1 Introduction

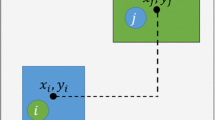
The single row facility layout problem (SRFLP) is the problem of obtaining a linear layout of facilities so as to minimize the weighted sum of the distances between all pairs of facilities. The weights for each of the pairs of facilities as well as the lengths of each of the facilities are known, and the distance between a pair of facilities is defined as the distance between their centroids. The number of facilities in a particular instance is called the size of the instance. This problem was first proposed in [28] and was shown to be NP-Hard [8]. Formally stated the objective of SRFLP is to minimize the cost expression

$$\begin{aligned} z = \sum _{1 \le i < j \le n} c_{ij} d_{ij}, \end{aligned}$$
(1)

where \(c_{ij}\) is the weight and \(d_{ij}\) is the distance between the pair of facilities \((i,j)\). Since the distance \(d_{ij}\) between the pairs of facilities depends on the linear arrangement of the facilities, the solution to the SRFLP is a permutation of facilities that minimizes the above cost expression.

The SRFLP has been used to model numerous practical situations. It has been used as a model for arrangement of rooms in hospitals, departments in office buildings or in supermarkets [28], arrangement of machines in flexible manufacturing systems [14], assignment of files to disk cylinders in computer storage, and design of warehouse layouts [23].

In the literature, several exact methods have been applied to solve the SRFLP to optimality. These methods include branch and bound [28], mixed-integer programming [1, 2, 15, 21], cutting planes [3], dynamic programming [23], branch and cut [4], and semidefinite programming [5–7, 16]. Currently, the best exact algorithms available are those in [3] and [16] and the largest SRFLP instance that has been solved to optimality has 42 facilities (see [16]).

Researchers have focused on heuristics for solving large sized SRFLP instances. These heuristics are of two types; construction and improvement. Construction heuristics for the SRFLP have been presented in [14, 24]. However these have later been superseded by improvement heuristics. Most improvement heuristics for the SRFLP are metaheuristics, e.g., simulated annealing [10, 13, 25], ant colony optimization [29], scatter search [17], tabu search [10, 26], particle swarm optimization [27], and genetic algorithms [9, 22]. Among these the genetic algorithm implementation in [22] yields best results for benchmark SRFLP instances of large sizes.

In the literature, genetic algorithms have been applied to the SRFLP in [9] and [22]. A closely related algorithm called the imperialist competitive algorithm has been presented in [20]. References [9] and [20] have reported results on benchmark instances with up to 80 facilities, while [22] has reported results on a limited set of benchmark instances with up to 110 facilities. We present a simple yet powerful genetic algorithm and test its performance on all the large size SRFLP benchmark instances available in the literature.

Our paper is organized as follows. In Sect. 2 we introduce our genetic algorithm GENALGO for solving large SRFLP instances. We then report the results of our computational experiments on SRFLP benchmark instances in Sect. 3 and compare them with those available in the published literature. We conclude the paper in Sect. 4 with a summary of the work.

2 Our genetic algorithm

A genetic algorithm (see, e.g., [12]) is an evolutionary search algorithm which simulates the natural evolution based on the principle of the survival of the fittest. Feasible solutions to the problem being solved are coded as individuals, and a population of individuals is iteratively improved using genetic operators such as selection, crossover, and mutation to create individuals of high fitness. In optimization problems the fitness of an individual is usually measured in terms of the objective function value of the solution it represents. Thus for the SRFLP, an individual corresponding to a solution with low cost is said to be of high fitness. The solution corresponding to an individual with the highest fitness encountered in the course of a genetic algorithm is output as an approximation to an optimal solution of the concerned SRFLP instance.

In this paper we present a genetic algorithm called GENALGO to solve the SRFLP. The algorithm is a generic algorithm with the exception that periodically, all the individuals in a generation are subjected to local search to improve their fitnesses. The pseudocode of the algorithm is provided below, and details of several of the steps are explained thereafter.

figure a1

In the GENALGO algorithm, an individual corresponding to a solution is coded as a permutation of the facilities, and the fitness of an individual is given by the cost expression (1) of the solution it corresponds to.

In Step 1 of the algorithm GENALGO generates an initial population of a user-specified number \(N\) individuals. In order to allow the algorithm to start with a sufficiently diverse population, the solutions corresponding to the \(N\) individuals were randomly generated permutations of the set of facilities. Given a generation of solutions, the first step in creating the next generation is to create a mating pool for reproduction in a genetic algorithm. This is done in Step 4 of GENALGO.

In GENALGO, the mating pool is created using a binary tournament selection [11] in which the fitter of the two randomly selected individuals from the population enter the mating pool. This may allow multiple copies of the same solution in the mating pool. The solutions in the mating pool thus generated are subsequently subjected to crossover and mutation operations to create candidate solutions for the next generation. We use the partially matched crossover (PMX) operator [18] in Step 5 to cross individuals with a user-defined crossover probability \(p_c\) to create the child pool. After generating the child pool, each child is subjected to a mutation operator in Step 6 of GENALGO. With a user-defined mutation probability \(p_m\), the solution corresponding to each individual is changed in the following minor way. Two facilities in the solution are selected at random and the second facility is moved so as to follow the first facility in the solution. All the remaining facilities are adequately shifted. This mutation is known in the literature as insertion mutation [18]. Step 7 of GENALGO is the elite preservation operation, which ensures that individuals with high fitness in the previous generation are carried over to the next generation, and individuals with low fitness obtained after crossover and mutation are eliminated. This ensures that the average fitness of individuals in populations does not degrade over generations. Step 9 is a local search operation that is carried out after regular intervals to improve the fitnesses of individuals in populations. We use an insertion neighborhood for local search in this step since experience in the literature suggests that the insertion neighborhood is the best neighborhood for local search for the SRFLP [25]. The pseudocode of the local search used in Step 9 is provided below. GENALGO terminates after generating a user-specified maximum number of generations.

figure a2

GENALGO differs from existing genetic algorithms [9, 22] in several ways. The first difference is in the selection of solutions for the initial population. In the genetic algorithm proposed in [9] each solution in the initial population is generated using four methods chosen at random. This ensures an initial population whose average solution fitness is high, but which is not sufficiently diverse. GENALGO populates the initial population with randomly generated solutions. This ensures diversity but does not guarantee a high average solution fitness. In this respect, GENALGO is similar to the algorithm in [22]. The second difference in terms of the crossover operator. The genetic algorithm in [9] uses a crossover operator designed by the authors, while the one in [22] uses the OX crossover operator designed for permutation problems. GENALGO uses the PMX crossover operator, also designed for permutation problems, because in our initial experiments, the PMX crossover operator performed better than the OX crossover operator. The mutation parameter value is self-adaptive in the genetic algorithm in [9] while it is fixed in GENALGO. Finally, the local search operation used in Step 9 of GENALGO is different from the one used in [22]. The genetic algorithm in [9] does not include any local search operation.

In the next section we describe the results of our computational experience with GENALGO on large sized SRFLP instances.

3 Computational experience

We coded our genetic algorithm GENALGO in C and compiled it using a gcc4 compiler. We ran our experiments on a personal computer with Intel i-5 2500 3.30 GHz processor with 4GB RAM running Ubuntu Linux version 12.04. We allowed the crossover probability \(p_c\) to be randomly chosen among values 0.6, 0.7, 0.8, 0.9, and 0.95, and the mutation probability \(p_m\) to be randomly chosen between 0.001 and 0.05. Each run of GENALGO was allowed to generate a maximum of 5,000 generations or till the population converged. Since GENALGO is stochastic, we performed 200 GENALGO runs and chose the best solution obtained as the output of GENALGO.

We compared the performance of GENALGO with results from the published literature on three classes of benchmark instances. The first class of 20 instances are the Anjos instances used in [5] and subsequently by most researchers. This class contains five instances each of size 60, 70, 75, and 80. The second class of 35 instances was used in [7, 16]. It consists of instances based on QAP benchmarks and are called sko instances. There are five instances each of sizes 42, 49, 56, 64, 72, 81, and 100. The third class is a set of three instances of size 110 introduced in [19]. This makes our computational experiments the most comprehensive, since it includes all the large size benchmark SRFLP instances which have been tested in recent studies [4, 16] but have not been tested in existing studies with genetic algorithms [9, 22].

3.1 Testing with 20 instances by Anjos et al. [5]

Table 1 compares the costs of solutions output by the 200 runs of GENALGO with the best costs known in the literature for Anjos instances (reported in [22]). The first two columns of the table give the name of the instance and its size. The third column presents the best costs reported in [22]. The fourth column reports the cost of the best solution that GENALGO outputs in any run, and the fifth and sixth columns report the mean and standard deviation of the costs of the solutions output by the 200 runs of GENALGO. The seventh column reports the median of the costs of the solution output by GENALGO. The last column of the table reports the worst of the costs output in all the runs of GENALGO for the corresponding instance.

Table 1 Solution costs output by GENALGO for Anjos instances of sizes from 60 to 80
Full size table

From Table 1, we observe that for each of the 20 Anjos instances, the best costs output by GENALGO matched the best costs reported in the literature. The mean costs were found to be higher than the median costs for all instances, thus suggesting that in most runs, GENALGO output solutions with costs close to the best cost.

Table 2 compares the times in CPU seconds required by GENALGO to execute on the Anjos instances with the times reported in [22]. The structure of the table is similar to that of Table 1; with the first two columns describing the instance, the third column presenting the times reported in [22], and the remaining five columns reporting the minimum, mean, median, worst, and standard deviation of the times required by GENALGO during its 200 runs for the corresponding instance.

Table 2 Execution times required by GENALGO for Anjos instances of sizes from 60 to 80
Full size table

From Table 2 we see that for the Anjos instances, the mean execution time required by GENALGO is less than that reported in [22]. Further, we see that GENALGO becomes progressively faster than the algorithm in [22] as problem sizes increase. The machine that we use is approximately 3.3 times faster than the one used in [22] (based on CPU speed comparisons using data from http://www.cpubenchmark.net). However the execution times for the two implementations are not strictly comparable, since the languages and compilers used are different.

3.2 Testing with sko instances

Table 3 presents a comparison of the costs of solutions output by the 200 runs of GENALGO with the best costs from the literature for the QAP based sko instances. The structure of Table 3 is similar to that of Table 1. Since no single study reports the best cost for all the instances, in the third column, each cost reported has a superscript indicating the source that reports the cost.

Table 3 Solution costs output by GENALGO for sko instances of sizes from 42 to 100
Full size table

The costs marked in boldface in Table 3 indicate those in which GENALGO generates solutions with costs lower than those previously known in the literature. From the table, we find that GENALGO outperforms the previously best known results in 19 out of the 35 sko instances. In the remaining 16 instances the cost output by GENALGO equals those obtained previously in the literature. Interestingly, in six of the instances, the median cost output by GENALGO is better than the best cost previously known in the literature. As with the Anjos instances, in most of the QAP based sko instances, the median cost of the output of GENALGO is less than the mean cost, indicating that GENALGO outputs low cost solutions in most of its runs.

Table 4 presents a comparison of the execution times in CPU seconds required by GENALGO with execution times of other algorithms generating the best solutions to these instances. The structure of Table 4 is similar to that of Table 2. For instances with sizes between 64 and 81, the best solution costs are reported in [4]; but the exact execution times required to obtain these solutions are not provided. For these instances, we present the limits on the execution times that have been reported in [4].

Table 4 Executions times required by GENALGO for sko instances of sizes from 42 to 100
Full size table

3.3 Testing with instances with 110 facilities by Letchford and Amaral [19]

Table 5 presents a comparison of the costs of the solutions output by the 200 runs of GENALGO with those reported in [22] for three instances of size 110 introduced by Letchford and Amaral [19]. The best costs known in the literature for these instances have been reported in [22]. The first column gives the name of the instance, the second column reports the best costs known in the literature, and the remaining columns provide the details about the solution costs output by GENALGO. The results show that the best output of GENALGO matches the best costs reported in [22] in two of the three instances and is marginally worse for the other instance. Table 6 presents details about the execution times in CPU seconds required by GENALGO for these instances.

Table 5 Solution costs output by GENALGO for three instances of size 110
Full size table
Table 6 Execution times required by GENALGO for three instances of size 110
Full size table

From our computational experiments it is clear that the GENALGO algorithm is competitive for solving large SRFLP instances.

4 Conclusions

In this paper, we propose an efficient genetic algorithm incorporating local search called GENALGO for solving large instances of the single row facility layout problem (SRFLP). We compared the performance of GENALGO with that of other algorithms known in the literature for solving large sized SRFLP instances. Our test bed consisted of 58 instances with sizes ranging from 42 to 110. We found that in 19 instances, GENALGO produced solutions which are superior to the best solutions known in the literature. In another 37 instances, GENALGO output solutions that matched the best known solutions in the published literature. In the other two instances, the solutions output by GENALGO were marginally worse. Hence the GENALGO algorithm that we propose in this paper is a competitive algorithm for solving large sized single row facility layout problems.

The current study is limited in that it uses fairly standard basic operators in its execution. This has the advantage of making it easy to implement, but more advanced operators may yield better results. So one direct direction for further research is to test the performance of heuristic GENALGO with more advanced operators. Other local search methods, like the 2-opt or the 3-opt neighborhood can be used to drive local search in Step 9 of the algorithm. Testing different crossover and mutation operators can also lead to better heuristics to solve large sized SRFLP instances. One may also look at developing other population based heuristics for solving large instances of SRFLP.