1 Introduction

The energy consumption in cloud data centers has been steadily increasing over the last few years (Zhou et al. 2018). As a result, the minimization of power and energy consumption in a cloud environment has become an urgent problem that is now receiving significant attention (Marek and Hoon 2018).

Applying a sleep mode is an effective method for reducing energy consumption in cloud data centers (Khojandi et al. 2018). For the purpose of minimizing energy consumption during runtime, Duan et al. (2015) presented a dynamic idle interval prediction scheme to estimate the future idle interval length of a CPU and thereby choose the most cost-effective sleep state. Chou et al. (2016) proposed a fine-grain power management scheme for data center workloads. This proposed scheme could dynamically postpone the processing of some tasks, create longer idle periods and promote the use of a deeper sleep mode. Luo et al. (2017) based on flow preemption and power-aware routing, Luo et al. proposed a dynamic adaptive scheduling algorithm to reduce energy consumption by decreasing the ratio of low utilization devices and putting more devices into sleep mode. In the literature mentioned above, we note that a sleep mode was only applied to a physical machine (PM) rather than a virtual machine (VM). This weakens the application flexibility of sleep modes.

Queuing models with vacations are used as an important way to evaluate the performance measures of the cloud data centers with sleep modes (Do et al. 2018). Multiple-server queueing models with various types of vacations have been studied by many researchers. Jin et al. (2018) proposed a novel type of M/M/c queue with an N-policy and synchronous vacations. Tian et al. (2001) analyzed the equilibrium theory for an M/M/c queue with an N-policy and asynchronous vacations. Jin et al. (2017) proposed a queueing system with synchronous vacations of partial servers. The research mentioned above has contributed to enriching the queueing system with an N-policy and synchronous vacations, an N-policy and asynchronous vacations, as well as asynchronous vacations of partial servers. However, there has so far been no research on a queueing system with an N-policy and asynchronous vacations of partial servers.

Teaching–learning-based optimization (TLBO) is an effective tool for function optimization (Cao et al. 2016). Since the appearance of TLBO, many researchers have directed their efforts into improving the searching capability of TLBO algorithms. Yu et al. (2016) an effort to enhance the performance of TLBO algorithms, Yu et al. introduced the mutation crossover operation to increase population diversity, and applied the chaotic perturbation mechanism to make the TLBO algorithm avoid falling into the local optimum. Ji et al. (2017) inspired by the concept of historical population, Ji et al. added two new process, namely the self-feedback learning process as well as the mutation and crossover processes to the TLBO algorithm. The added processes improved the exploration ability of the new algorithm in comparison to the original TLBO algorithm. Li et al. (2017) in order to enhance the diversification of population, Li et al. increased the number of teachers, introduced new students, and performed local searches around the potentially optimal solutions. To the best of our knowledge, the application of the improved TLBO algorithm in the optimization of the VM allocation strategy has not been studied yet.

Inspired by the research mentioned above, in this paper, we propose a clustered VM allocation strategy based on a sleep-mode with a wake-up threshold. For one thing, allowing that all the VMs in a cloud data center go to sleep may degrade the quality of cloud service. Thus, we divide the VMs in a cloud data center into two pools: Pool I and Pool II. The VMs in Pool I always stay awake to provide a timely cloud service for processing tasks, whereas the VMs in Pool II independently go to sleep whenever possible to reduce energy consumption. Another, for a VM, frequently switching from a sleep state to a awake state may cause additional energy consumption. To get around this problem, in this paper we make the VMs in Pool II to wake up only if the number of tasks waiting in the system buffer reaches a wake-up threshold and the corresponding sleep timer expires. This wake-up mechanism improves the energy conservation by delaying the instant at which a VM wakes up. To analyze the proposed strategy, we first build a type of queue with an N-policy and asynchronous vacations of partial servers by using a matrix-geometric method, and investigate the system performance through analysis experiments and simulation experiments. Finally, for the purpose of optimizing the proposed strategy, we construct a cost function to trad off different system performance, and develop the TLBO algorithm to optimize the system parameters settings.

The rest of this paper is organized as follows. In Sect. 2, we propose a clustered VM allocation strategy based on a new type of sleep-mode in a cloud environment and build a system model accordingly. In Sect. 3, we analyze the system model using the method of a matrix-geometric solution. In Sect. 4, we derive the performance measures in terms of the average latency of tasks and the energy saving rate of the system with the proposed strategy. In Sect. 5, we demonstrate the influence of system parameters on the system performance by using numerical results. In Sect. 6, we develop an intelligent searching algorithm to jointly optimize the number of the VMs in Pool II, the wake-up threshold and the sleeping parameter. Finally, Sect. 7 is devoted to the conclusion.

2 VM allocation strategy and system model

In this section, in order to enhance the energy efficiency in a cloud environment, we firstly propose a clustered VM allocation strategy based on a sleep-mode with a wake-up threshold. And then, we establish a queue with an N-policy and asynchronous vacations of partial servers to capture the proposed strategy.

2.1 VM allocation strategy

It should be noted that additional energy will be consumed when a VM frequently switches from the sleep state to the awake state, while the system performance will be degraded when all the VMs are put into a sleep-mode. To get around these problems, based on a sleep-mode with a wake-up threshold, we propose a clustered VM allocation strategy.

The VMs in a cloud data center are clustered into two pools, namely, Pool I and Pool II. The VMs in Pool I remain awake all the time and operate on a higher speed. The VMs in Pool II will go to sleep independently when there are no tasks in the system buffer. For the purpose of improving the energy efficiency of cloud data centers, we introduce a wake-up threshold to a periodic sleep mode. At the end epoch of a sleep period, if the number of the tasks gathered in the system buffer reaches or exceeds a certain value, namely the wake-up threshold, the corresponding VM in Pool II will wake up independently and operate on a lower speed. Otherwise, the VM in Pool II will begin another sleep period with a new sleep timer.

Under the proposed strategy, all the VMs are dominated by a control server, where several sleep timers, a task counter, and a VM scheduler are deployed. When a VM in Pool II is scheduled to go to sleep from the awake state or begin another sleep period, a sleep timer with a random value will be started to control the time length of a sleep period. The task counter keeps working and counts the tasks waiting in the system buffer. At the moment that a sleep timer expires, the VM scheduler adjusts the state of the corresponding VM according to the value on the task counter.

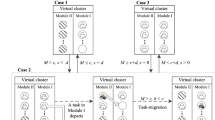
Figure 1 illustrates the working flow of a VM with the clustered VM allocation strategy based on a sleep-mode with a wake-up threshold.

Fig. 1
figure 1

The working flow of a VM with the strategy proposed in this paper

Full size image

As shown in Fig. 1, the VMs in Pool I remain awake all the time, while the VMs in Pool II switch between the sleep state and the awake state. Next, we discuss the state transition for the VMs in Pool II.

  1. 1.

    Awake state to sleep state

For a busy VM in Pool II, the state transition from awake state to sleep state occurs only at the instant when a task either in Pool I or Pool II is completely processed. When a task is completely processed in Pool I, if the VM scheduler monitors that the value on the task counter is zero and there is at least one task being processed in Pool II, one of the tasks being processed in Pool II will migrate Pool I, and then the evacuated VM in Pool II will go to sleep. When a task is completely processed in Pool II, if the VM scheduler monitors that the value on the task counter is zero, the evacuated VM in Pool II will go to sleep directly. We note that the task-migration considered in this paper is a kind of online VM-migration between different pools within a cloud data center, and this task-migration is to make the VMs in Pool II go to sleep earlier.

  1. 2.

    Sleep state to awake state

For a sleeping VM in Pool II, the state transition from sleep state to awake state occurs only at the end epoch of a sleep period. When a sleep timer expires, if the VM scheduler monitors that the value on the task counter is equal to or greater than the wake-up threshold, the corresponding VM in Pool II will wake up to process the first task waiting in the system buffer on a lower speed. Otherwise, a new sleep timer will be started and the VM in Pool II will begin another sleep period.

To summarize, at the moment that a sleep timer expires, the VMs in Pool II will wake up only if the number of the tasks waiting in the system buffer reaches the wake-up threshold. The wake-up mechanism in our proposed strategy effectively improves the energy conservation via extending sleep time by delaying the instant at which a VM wakes up. This is exactly the starting point for the sleep-mode with a wake-up threshold within our proposed strategy.

2.2 System model

According to the proposed VM allocation, we establish a queue with an N-policy and asynchronous vacations of partial servers. In this system model, the tasks are regarded as customers, each VM is regarded as an independent server, a sleep period is regarded as a vacation, and multiple sleep periods are regarded as multiple vacations.

In this system model, the buffer capacity is supposed to be infinite. Moreover, the number of the VMs in Pool I and Pool II are denoted as c and d, respectively. Let \(i_{t}\) be the total number of tasks in the system at instant t. \(i_{t}\) is called the system level, \(i_{t}\geqslant 0\). Let \(j_{t}\) be the number of busy VMs in Pool II at instant t. \(j_{t}\) is called the system stage, \(j_{t}=\overline{0, d}\), where \(\overline{0, d}\) represents the range of integers from 0 to d.

Thus, the behavior of the system under consideration can be described in terms of the two-dimensional continuous-time stochastic process as follows:

$$\begin{aligned} \xi _t = \{i_t, j_t \}, \quad t\geqslant 0. \end{aligned}$$
(1)

The state-space \(\varvec{\varOmega }\) of the two-dimensional continuous-time stochastic process \(\xi _t\) is given as follows:

$$\begin{aligned} \varvec{\varOmega }= & {} \{(i, 0): i=\overline{0, c}\} \cup \ \{(i,j):i=\overline{c+1, c+d}, \quad j=\overline{0, i-c}\}\ \nonumber \\&\cup \ \{(i, j): i\geqslant c+d+1, \quad j=\overline{0, d}\}. \end{aligned}$$
(2)

We assume that all the tasks in the system are homogenous and all the VMs in a pool are identical, where each task is for one VM. The arrival intervals of tasks are assumed to have an exponential distribution with parameter \(\lambda ~(\lambda >0)\). In addition, the service times of tasks processed in Pool I and in Pool II are assumed to be exponentially distributed with parameters \(\mu _{1}~(\mu _{1}>0)\) and \(\mu _{2}~(0<\mu _{2}<\mu _{1})\), respectively. Furthermore, the time length of a sleep timer is assumed to follow an exponential distribution with parameter \(\theta ~(\theta >0)\). Here, the parameter \(\theta \) is called the sleeping parameter.

Based on the assumptions above, the two-dimensional continuous-time stochastic process \(\xi _{t}\) can be seen as a two-dimensional continuous-time Markov chain (CTMC).

Taking \(c=2, \ d=3\) and \(N=2\) as an example, we show the state transition of the two-dimensional CTMC \(\xi _{t}\) in Fig. 2, where \(N=2\) shows this CTMC with a 2-policy.

Fig. 2
figure 2

The state transition of the the two-dimensional CTMC \(\xi _{t}\) with \(c=2, \ d=3\) and \(N=2\)

Full size image

We define \(\pi _{i,j}\) as the steady-state probability distribution of the system model for the system level being equal to i and the system stage being equal to j. \(\pi _{i,j}\) is then given as follows:

$$\begin{aligned} {\pi _{i,j}=\lim _{t\rightarrow \infty }P\{i_t=i,j_t=j\}}, \quad i\geqslant 0, \quad j=\overline{0,d}. \end{aligned}$$
(3)

And then, we form the row vectors \(\varvec{\pi }_i\) as follows:

$$\begin{aligned} \varvec{\pi }_i=\left\{ \begin{array}{ll} \pi _{i,0}, &{}\quad i=\overline{0,c} \\ (\pi _{i,0},\pi _{i,1},\ldots ,\pi _{i,i-c}), &{}\quad i=\overline{c+1,c+d} \\ (\pi _{i,0},\pi _{i,1},\ldots ,\pi _{i,d}), &{}\quad i\geqslant c+d+1.\\ \end{array} \right. \end{aligned}$$
(4)

The steady-state probability distribution \(\varvec{\pi }\) of the two-dimensional CTMC is composed of \(\varvec{\pi }_i~(i\geqslant 0)\). \(\varvec{\pi }\) is given as follows:

$$\begin{aligned} {\varvec{\pi }}=(\varvec{\pi }_{0}, \varvec{\pi }_{1},\ldots ). \end{aligned}$$
(5)

3 Model analysis

In this section, we first investigate the transition rate matrix of the two-dimensional CTMC. And then, we derive the steady-state probability distribution of the system model.

3.1 Transition rate matrix

We denote Q as the one-step state transition rate matrix of the two-dimensional CTMC \(\xi _t\). According to the system level, we separate the one-step state transition rate matrix Q of the two-dimensional CTMC \(\xi _t\) into some sub-matrices with different orders. To clearly represent the sub-matrices, we denote \(\varvec{Q}_{k, k'}\) as the one-step state transition rate sub-matrix for the system level changing from \(k\ (k\geqslant 0)\) to \(k'\ (k'\geqslant 0)\). Based on the initial system level k, we discuss the one-step state transition rate sub-matrix \(\varvec{Q}_{k, k'}\) in relation to three cases.

  1. 1.

    Initial system level is \(k=\overline{0, c}\): the number of busy VMs in Pool I is k, while the number of busy VMs in Pool II is 0.

\(k=0\) means no tasks exist in the system at all. Therefore, the possible state transitions are from state (0, 0) to state (1, 0) and from state (0, 0) to state (0, 0). If there is a task arrival at the system, the system level will be increased by one, while the system stage will not change, and the transition rate from state (0, 0) to state (1, 0) is \(\lambda \). If no task arrival occurs in the system, the system state will be fixed at state (0, 0), and the transition rate is \(-\,\lambda \). Consequently, the sub-matrices \({{\varvec{Q}}}_{0, 1}\) and \({{\varvec{Q}}}_{0, 0}\) are actually quantities given as follows:

$$\begin{aligned} {{\varvec{Q}}}_{0, 1}=\lambda ,\quad {{\varvec{Q}}}_{0, 0}=-\,\lambda . \end{aligned}$$

\(k=\overline{1, c}\) means all the tasks in the system are receiving service from the VMs in Pool I. If one of the tasks is completely processed and departs the system, the system level will drop by one, while the system stage will not change, and the transition rate from state (k, 0) to state \((k-1,0)\) is \(k\mu _{1}\). If there is a task arrival at the system, the system level will increase by one, while the system stage will not change, and the transition rate from state (k, 0) to state \((k+1,0)\) is \(\lambda \). If neither an arrival nor a departure occurs, the system state will be fixed at state (k, 0), the transition rate is \(-(\lambda +k\mu _{1})\). Consequently, the sub-matrices \({{\varvec{Q}}}_{k,k-1}\), \({{\varvec{Q}}}_{k,k+1}\) and \({{\varvec{Q}}}_{k,k}\) are also actual quantities given as follows:

$$\begin{aligned} {{\varvec{Q}}}_{k,k-1}=k\mu _{1},\quad {{\varvec{Q}}}_{k,k+1}=\lambda ,\quad {{\varvec{Q}}}_{k,k}=-(\lambda +k\mu _{1}),\quad k=\overline{1,c}. \end{aligned}$$
  1. 2.

    Initial system level is \(k=c+x, \ x=\overline{1, d-1}\): the number of busy VMs in Pool I is c, while the number of busy VMs in Pool II is less than or equal to x.

If there is at least one task queueing in the system buffer when a task is completely processed on a VM, whether the VM belongs to Pool I or Pool II, the task waiting at the head of the system buffer will be scheduled to the evacuated VM. In this case, the system level will drop by one, while the system stage will not change. Therefore, the transition rate from state (k, n) to state \((k-1,n)\) will be \((c\mu _{1}+n\mu _{2})\), where n \(( n=\overline{0, x-1})\) is the number of busy VMs in Pool II.

If there are no tasks queueing in the system buffer when a task is completely processed on a VM, whether the VM belongs to Pool I or Pool II, the number of sleeping VMs will increase by one. If the evacuated VM belongs to Pool I, one of the tasks receiving service in Pool II will be migrated to the evacuated VM in Pool I, and the just-evacuated VM in Pool II will go to sleep. If the evacuated VM belongs to Pool II, the evacuated VM in Pool II will start sleeping directly. In both of these two cases, both the system level and the system stage will drop by one. Therefore, the transition rate from state (k, x) to state \((k-1,x-1)\) will be \((c\mu _{1}+x\mu _{2})\).

Consequently, the sub-matrix \({{\varvec{Q}}}_{k,k-1}\) is a rectangular \((x+1)\times x\) matrix given as follows:

Before any of the sleep timers in Pool II expire, if there is a task arrival at the system, the newly arriving task has to queue in the system buffer. In this case, the system level will increase by one, while the system stage will not change. Therefore, the transition rate from state (k, n) to state \((k+1,n)\) will be \(\lambda \). Consequently, the sub-matrix \({{\varvec{Q}}}_{k,k+1}\) is a rectangular \((x+1)\times (x+2)\) matrix given as follows:

At the moment that one of the sleep timers expires, the corresponding VM in Pool II will decide whether to wake up or continue sleeping according to the number of tasks queueing in the system buffer. If this number is equal to or greater than the wake-up threshold N, the corresponding VM in Pool II will wake up and prepare to process the task waiting at the head of the queue. In this case, the system level will not change, while the system stage will increase by one. Therefore, the transition rate from state (k, n) to state \((k,n+1)\) will be \((d-n)\theta \), where n \((n=\overline{0, x})\) is the number of busy VMs in Pool II. Otherwise, the corresponding VM in Pool II will continue sleeping and there will be no state transitions at all.

Before any of the sleep timers in Pool II expire, if neither an arrival nor a departure occurs, the system state will not change. When the number of tasks queueing in the system buffer is equal to or greater than the wake-up threshold N, the transition rate will be \(\left( -\,h_{n}-(d-n)\theta \right) \), where \(h_{n}=\lambda +c\mu _{1}+n\mu _{2}\). When the number of tasks queueing in the system buffer is less than the wake-up threshold N, the transition rate will be \(-h_{n}\).

Consequently, the sub-matrix \({{\varvec{Q}}}_{k,k}\) is a rectangular \((x+1)\times (x+1)\) matrix given as follows:

  1. 3.

    Initial system level is \(k=c+x, \ x\geqslant d\): the number of busy VMs in Pool I is c, while the number of busy VMs in Pool II is less than or equal to d.

In the case of \(k= c+d\), \({{\varvec{Q}}}_{k, k-1}\) is a rectangular matrix of order \((d+1)\times d\). In the case of \(k=c+x, \ x\geqslant d+1\), \({{\varvec{Q}}}_{k, k-1}\) is square matrices of the order \((d+1)\times (d+1)\). In the case of \(k=c+x, \ x\geqslant d\), \({{\varvec{Q}}}_{k, k+1}\) and \({{\varvec{Q}}}_{k, k}\) are all square matrices of the order \((d+1)\times (d+1)\). Referencing the discussions in Item (2), the sub-matrices \({{\varvec{Q}}}_{k,k-1}\), \({{\varvec{Q}}}_{k,k+1}\) and \({{\varvec{Q}}}_{k,k}\) are given as follows:

So far, all the sub-matrices in the one step state transition rate matrix Q have been addressed. In the one-step state transition rate matrix Q, the sub-matrices \({{\varvec{Q}}}_{k,k-1}\) are repeated forever starting from the system level \((c+d+1)\), the sub-matrices \({{\varvec{Q}}}_{k,k+1}\) are repeated forever starting from the system level \((c+d)\), and the sub-matrices \({{\varvec{Q}}}_{k,k}\) are repeated forever starting from the system level \((c+d+N)\). For presentation purposes, the repetitive sub-matrices \({{\varvec{Q}}}_{k,k-1}\), \({{\varvec{Q}}}_{k,k+1}\) and \({{\varvec{Q}}}_{k}\) are represented by \({{\varvec{B}}}\), \({{\varvec{C}}}\) and \({{\varvec{A}}}\), respectively. Then, the one step state transition rate matrix Q is written as follows:

Obviously, the obtained form of the one step state transition rate matrix Q is a quasi-birth-and-death (QBD) matrix, so the CTMC \(\xi _{t}\) is also called a QBD CTMC (Tian and Zhang 2006).

Different methods can be used to resolve the steady-state transition probabilities. In our study, we consider a matrix-geometric solution method which is commonly used to analyze the QBD CTMC in the steady state.

3.2 Steady-state probability distribution

To analyze the QBD CTMC \(\xi _{t}\) by using the matrix-geometric solution method, we need to solve for the minimal non-negative solution of the matrix quadratic equation

$$\begin{aligned} {{\varvec{R}}}^2{{\varvec{B}}} + {{\varvec{R}}}{{\varvec{A}}} + {{\varvec{C}}} = \mathbf 0 , \end{aligned}$$
(6)

and this solution, called the rate matrix and denoted by \({{\varvec{R}}}\), can be explicitly determined.

In Sect. 3.1, the sub-matrices \({{\varvec{B}}}\), \({{\varvec{A}}}\) and \({{\varvec{C}}}\) are deduced to be upper-triangular matrices. Thus, the rate matrix \({{\varvec{R}}}\) is an upper-triangular matrix. We denote the unknown element of the rate matrix \({{\varvec{R}}}\) in line \(u \ (u=\overline{0,d})\) column \(v \ (v=\overline{0,d})\) as \(r_{u,v}\), and \(r_{u}=r_{u,u} \ ( u=\overline{0,d})\). The rate matrix \({{\varvec{R}}}\) can be written as follows:

$$\begin{aligned} {{\varvec{R}}}= \begin{pmatrix} \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} r_{0}&{}r_{0,1}&{}r_{0,2}&{}\cdots &{}r_{0,d-1}&{}r_{0,d}\\ &{}r_{1}&{}r_{1,2}&{}\cdots &{}r_{1,d-1}&{}r_{1,d}\\ &{}&{}r_{2}&{}\cdots &{}r_{2,d-1}&{}r_{2,d}\\ &{}&{}&{}\ddots &{}\vdots &{}\vdots \\ &{}&{}&{}&{}r_{d-1}&{}r_{d-1,d}\\ &{}&{}&{}&{}&{}r_{d}\\ \end{array} \end{pmatrix}. \end{aligned}$$
(7)

And then, using the elements in \({{\varvec{R}}}\), we calculate the elements of \({{\varvec{R}}}^{2}\) as follows:

$$\begin{aligned} ({{\varvec{R}}}^{2})_{u,u}=r^{2}_{u},\quad u=\overline{0, d}, \quad ({{\varvec{R}}}^{2})_{u,v}=\sum \limits ^{v}_{i=u}r_{u,i}r_{i,v},\quad u=\overline{0, d-1}, \quad v=\overline{u+1,d}. \end{aligned}$$

Next, by substituting the \({{\varvec{R}}}^{2}\), \({{\varvec{R}}}\), \({{\varvec{B}}}\), \({{\varvec{A}}}\) and \({{\varvec{C}}}\) into Eq. (6), we obtain a set of equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}(c\mu _{1}+u\mu _{2})r_{u}^{2}-(h_{u}+(d-u)\theta )r_{u} +\lambda =0,\quad u=\overline{0, d}\\ &{}(c\mu _{1}+v\mu _{2})\sum \limits ^{v}_{i=u}r_{u,i}r_{i,v}-(h_{v}+(d-v)\theta )r_{u,v}+(d-v+1)\theta r_{u,v-1}=0,\\ &{} \qquad \qquad \qquad u=\overline{0, d-1},\quad v=\overline{u+1, d}. \end{aligned} \end{array}\right. } \end{aligned}$$
(8)

With the constraint that the traffic load \(\rho =\lambda (c\mu _{1}+d\mu _{2})^{-1}<1\), we prove that the first equation of Eq. (8) has two real roots \(r_{u}~ (0<r_{u}<1)\) and \(r_{u}^{*}~(r_{u}^{*} \geqslant 1)\). It should be noted that the diagonal elements of \({{\varvec{R}}}\) are \(r_{u}~(u=\overline{0, d})\).

It is too arduous to deduce a general expression of \(r_{u,v} \ (u=\overline{0, d-1}, v=\overline{u+1, d})\) in closed-form. So, based on the last equation of Eq. (8), we recursively compute the off-diagonal elements starting from the diagonal elements obtained in the first equation of Eq. (8).

By using the matrix-geometric solution method (Neuts 1981), we have

$$\begin{aligned} \varvec{\pi }_i = \varvec{\pi }_{c+d+N}{{\varvec{R}}}^{i-(c+d+N)}, \ i\geqslant c+d+N, \end{aligned}$$
(9)

and the unknown steady-state probability distribution \(\varvec{\pi }_{0}\), \(\varvec{\pi }_{1}\), \(\ldots \), \(\varvec{\pi }_{c+d+N}\) can be obtained by solving the augmented matrix equation as follows:

(10)

where \(\varvec{e}_{1}\) is a \(\left( c+\left( \frac{d}{2}+N\right) (d+1) \right) \times 1\) vector, all of elements equal 1, \(\varvec{e}_{2}\) is a \((d+1)\times 1\) vector, all of elements equal 1, \(\mathbf 0 \) is a 1\(\times \left( c+\left( \frac{d+2}{2}+N\right) (d+1)\right) \) vector, all of elements equal 0, and

Finally, we obtain \(\varvec{\pi }_i \ (i=\overline{0,c+d+N})\) by applying the Gauss–Seidel method (Chen et al. 2017) to solve Eq. (10), and obtain \(\varvec{\pi }_i\ (i\geqslant c+d+N+1)\) by substituting \(\varvec{\pi }_{c+d+N}\) obtained in Eq. (10) into Eq. (9). So far, the steady-state probability distribution \(\varvec{\Pi }=(\varvec{\pi }_{0}, \varvec{\pi }_{1}, \ldots )\) of the system are given mathematically.

4 Performance measures

In this section, we mathematically evaluate the performance measures in terms of the average latency of tasks and the energy saving rate of the system.

We define the average latency of tasks as the average duration from the instant a task arrives at the system to the instant this task is completely processed.

Based on Little’s law and the steady-state probability distribution of the system model given in Sect. 3.2, the average latency W of tasks is given as follows:

$$\begin{aligned} W=\frac{1}{\lambda } \left( \sum ^{c}_{i=0}i\pi _{i0}+\sum ^{c+d}_{i=c+1}\sum ^{i-c}_{j=0}i\pi _{i,j}+\sum ^{m_{w}}_{i=c+d+1}\sum ^{d}_{j=0}i\pi _{i,j} \right) . \end{aligned}$$
(11)

\(m_{w}\) shown in Eq. (11) is a sufficiently large number that is set with the following condition:

$$\begin{aligned} 1 - \sum ^{m_{w}}_{i=0}\sum ^{d}_{j=0}\pi _{i,j}<\varepsilon _{1} \end{aligned}$$
(12)

where \(\varepsilon _{1}\) is an arbitrarily small number, such as \(\varepsilon _{1}=10^{-13}\). The smaller the value of \(\varepsilon _{1}\) is, the more precise the average latency of tasks will be.

We define the energy saving rate of the system as the energy conservation per unit time.

With the proposed strategy, the energy consumption of a VM in the awake state is higher than that in the sleep state. Indeed, additional energy will be consumed when a task is migrated from Pool II to Pool I, when a VM in Pool II listens to the system buffer, as well as when a VM in Pool II wakes up from a sleep state.

Based on the discussions above and the steady-state probability distribution of the system model given in Sect. 3.2, the energy saving rate E of the system with our proposed strategy is given as follows:

$$\begin{aligned} E&= (\omega _{}-\omega _{s})\sum ^{m_{e}}_{i=0}\sum ^{d}_{j=0}(d-j)\pi _{ij}- \left( \omega _{m}\sum ^{c+d}_{i=c+1}\sum ^{d}_{j=1}c\mu _{1}\pi _{ij} \right. \nonumber \\&\quad \,\, \left. + \ \omega _{l}\sum ^{m_{e}}_{i=0}\sum ^{d}_{j=0}\theta (d-j)\pi _{ij}+ \omega _{u}\sum ^{m_{e}}_{i=c+j+N}\sum ^{d-1}_{j=0}\theta (d-j)\pi _{ij} \right) \end{aligned}$$
(13)

where \(\omega \ (\omega >0)\) is the energy consumption per unit time for a busy VM in Pool II, \(\omega _{s}\ (\omega _{s}>0)\) is the energy consumption per unit time for a sleeping VM in Pool II, \(\omega _{m}\ (\omega _{m}>0)\) is the energy consumption for each task-migration, \(\omega _{l}\ (\omega _{l}>0)\) is the energy consumption for each listening, and \(\omega _{u}\ (\omega _{u}>0)\) is the energy consumption for each wake-up from a sleep state to an awake state. Moreover, \(m_{e}\) shown in Eq. (13) is a sufficiently large number that is set with the following condition:

$$\begin{aligned} 1 - \sum ^{m_{e}}_{i=0}\sum ^{d}_{j=0}\pi _{i,j}<\varepsilon _{2} \end{aligned}$$
(14)

where \(\varepsilon _{2}\) is also an arbitrarily small number, such as \(\varepsilon _{2}=10^{-13}\). The smaller the value of \(\varepsilon _{2}\) is, the more precise the energy saving rate of the system will be.

5 Numerical experiments

In this section, we provide numerical experiments with analysis and simulation to further analyze the impacts of the system parameters on the system performance in terms of the average latency of tasks and the energy saving rate of the system.

Based on Eqs. (11) and (13), the analysis results are carried out in Matlab 2016a on Intel(R) Core(TM) i7-4790 CPU @ 3.60 GHz 3.60 GHz, 8.00 GB RAM. Java language has the object-oriented features supporting the representation of multiple attributes through the definition of a class. Simulation experiments are implemented in the MyEclipse 2014 environment using Java language. In the simulation experiment, a TASK class is defined to include the attributes of UNARRIVE, WAIT, RUNHIGH, RUNLOW and FINISH. A VM class is defined to include the attributes of SLEEP, IDLE, BUSYLOW and BUSYHIGH.

Referencing to Jin et al. (2018), we set the experimental parameters as follows: \(c+d=50\), \(\lambda =7.00\ \mathrm s^{-1}\), \(\mu _{1}=0.20\ \mathrm s^{-1}\), \(\mu _{2}=0.10\ \mathrm s^{-1}\), \( \omega _{} =0.50\) mW, \(\omega _{s}=0.10\) mW, \(\omega _{m}=0.20\) mJ, \(\omega _{l}=0.15\) mJ and \(\omega _{u}=0.20\) mJ.

Figure 3 depicts the resulting average latency W of tasks vs. the sleeping parameter \(\theta \) for different numbers d of the VMs in Pool II and different wake-up thresholds N.

Fig. 3
figure 3

The average latency L of tasks versus the sleeping parameter \(\theta \) for different numbers d of the VMs in Pool II and different wake-up thresholds N

Full size image

Figure 3a indicates that the average latency W of tasks increases with an increase of the number d of the VMs in Pool II. For a given wake-up threshold and a given sleeping parameter, the more VMs there are deployed in Pool II, the weaker the system capability becomes, and the longer the tasks will sojourn in the system. This results in a larger average latency of tasks.

Figure 3b indicates that the average latency W of tasks increases with an increase in the value for threshold N. This is due to the fact that, when the number of the VMs in Pool II and the sleeping parameter are given, as the value for the wake-up threshold increases, the more likely it is that the VMs in Poiol II will continue sleeping, even when their sleep timers expire. That is to say, more tasks will accumulate in the system buffer before being processed. Consequently, the average latency of tasks will increase.

From Fig. 2, we also observe that for any number d of VMs in Pool II and any value for the wake-up threshold N, as the sleeping parameter \(\theta \) increases, the average latency W of tasks will initially decrease sharply and then decrease gradually. When the sleeping parameter \(\theta \) is smaller (such as \(0< \theta < 0.4\) for \(N=11\) and \(d=15\)), the time length of a sleep period is relatively long, so the tasks arriving during the sleep period have to wait longer in the system buffer. This leads to a larger average latency of tasks. In this case, the sleeping parameter has a greater impact on the average latency of tasks than any of the other factors, such as the arrival rate of tasks and the service rate of a task on a VM. Thus, the average latency of tasks will decrease sharply as the sleeping parameter increases.

When the sleeping parameter \(\theta \) is larger (such as \(0.4< \theta < 1.6\) for \(N=11\) and \(d=15\)), the time length of a sleep period is relatively short, so the tasks arriving during the sleep period will be processed earlier. This leads to a lower average latency of tasks. In this case, the arrival rate of tasks and the service rate of VMs play a dominate role in influencing the average latency of tasks. Thus, the average latency of tasks will decrease gradually as the sleeping parameter increases.

Figure 4 depicts the resulting energy saving rate E of the system vs. the sleeping parameter \(\theta \) for different numbers d of the VMs in Pool II and different wake-up thresholds N.

Fig. 4
figure 4

The energy saving rate E of the system versus the sleeping parameter \(\theta \) for different numbers d of the VMs in Pool II and different wake-up thresholds N

Full size image

Figure 4a indicates that deploying either relatively too few or too many VMs in Pool II will result in a lower energy saving rate E of the system. When the number of VMs in Pool II is smaller (such as \(d=5\) for \(N=11\)), even though all the VMs in Pool II are asleep, less energy will be saved. This leads to a lower energy saving rate of the system. When the number of VMs in Pool II is bigger (such as \(d=25\) for \(N=11\)), the system capability is relatively weaker. This is to say, once a VM in Pool II wakes up, that VM has little opportunity to go to sleep again. This also leads to a lower energy saving rate of the system.

Figure 4b indicates that a larger value for the wake-up threshold N will result in a higher energy saving rate E of the system. This is due to the fact that when the number of the VMs in Pool II and the sleeping parameter are given, the higher the value for the wake-up threshold is, the later a VM in Pool II will wake up from sleep state, and the longer the VMs in Pool II will remain asleep. This leads to a higher energy saving rate of the system.

From Fig. 4, we also notice that for any number d of VMs in Pool II and for any value for the wake-up threshold N, the energy saving rate E of the system decreases as the sleeping parameter \(\theta \) increases. The larger the sleeping parameter is, the shorter the time length of a sleep period is, and the earlier a VM in Pool II will wake up from a sleep state. That is to say, less energy will be saved. Additionally, the larger the sleeping parameter is, the more frequently the VM in Pool II listens to the system buffer or wakes up from sleep state. That is to say, additional energy will be consumed. Consequently, the energy saving rate of the system will decrease.

Combining the results shown in Figs. 2 and 3, we find that a lower average latency of tasks can be obtained with a smaller number of VMs in Pool II, a smaller value for the wake-up threshold and a larger sleeping parameter, whereas a higher energy saving rate of the system can be obtained with a moderate number of VMs in Pool II, a larger value for the wake-up threshold, and a smaller sleeping parameter. In the actual application of the proposed strategy, both the response performance and the energy saving effect should be taken into consideration. So, the number of the VMs in Pool II, the wake-up threshold and the sleeping parameter should be jointly optimized to balance the system performance.

6 Performance optimization

In this section, we improve the TLBO algorithm to optimize the proposed strategy.

For the optimization of the proposed strategy, we need to minimize the average latency of tasks while at the same time maximize the energy saving rate of the system. The criteria of such optimization problem are a function for the average latency of tasks to be minimized and another function for the energy saving rate of the system to be maximized. From the numerical results illustrated in Sect. 5, we find that the criteria are in conflict: a shorter average latency of tasks will certainly involve a lower energy saving rate of the system.

Considering the trade-off between the average latency of tasks and the energy saving rate of the system, we establish a system cost function \(F(d,N,\theta )\) as follows:

$$\begin{aligned} F(d,N,\theta )=f_{w}W-f_{e}E \end{aligned}$$
(15)

where \(f_{w}\) and \(f_{e}\) are the impact factors for the average latency W of tasks and the energy saving rate E of the system to the system cost function.

Table 1 Improved TLBO algorithm to obtain the optimal combination \((d^{*},N^{*},\theta ^{*})\)
Full size table

The optimization of the proposed strategy turns to minimize the system cost function and obtaining the optimal combination \((d^{*}, N^{*}, \theta ^{*})\). That is as follows:

$$\begin{aligned} (d^{*}, N^{*}, \theta ^{*})={argmin} \ F(d,N,\theta ). \end{aligned}$$
(16)

For a synchronous sleep-mode, in order to make sure that all the tasks waiting in the system buffer can be processed immediately once all the sleeping VMs wake up, the maximum wake-up threshold N is set as the number of the sleeping VMs. Obviously, the maximum wake-up threshold N in an asynchronous sleep-mode should not be higher than that in a synchronous sleep-mode. In the clustered VM allocation strategy based on an asynchronous sleep-mode proposed in this paper, we set the maximum wake-up threshold N as the number d of the VMs in Pool II. Therefore, when solving the optimization problem in Eq. (16), the value range for the wake-up threshold N is [1, d].

We note that it is difficult to express a system cost function in a closed-form, and also it is difficult to determine the monotonicity of the system cost function. Moreover, we note that the system cost function is not differentiable and there are possible more than one extreme point in the system cost function. In a result, the optimum point of the system cost function can not be searched by using classical numerical methods. In order to jointly optimize the number of VMs in Pool II, the wake-up threshold and the sleeping parameter with the minimum system cost function, we turn to an intelligent optimization algorithm, TLBO algorithm.

TLBO is one of the most efficient algorithms for providing good quality solutions in a reasonable computation time (Buddala and Mahapatra 2018). However, there are still some drawbacks with the TLBO algorithm, such as low population diversity and poor searching ability (Wang et al. 2018; Liu et al. 2018). For the purpose of improving the TLBO algorithm, we introduce a cube chaotic mapping mechanism to disperse the initial grades of students, and use an exponentially decreasing strategy for the teaching process to enhance the searching ability of the algorithm. The main steps for the improved TLBO algorithm are given in Table 1.

For the given system parameters, such as the total number \((c+d)\) of VMs in a cloud data center, the arrival rate \(\lambda \) and the service rate \(\mu _{1}\) of a task on the VM in Pool I, etc., the optimal combination \((d^{*}, N^{*}, \theta ^{*})\) for the number of VMs in Pool II, the wake-up threshold and the sleeping parameter can be obtained with the proposed strategy by performing the improved TLBO algorithm in Table 1.

Using the system parameters given in Sect. 5, and setting \(Num=100\), \({ iter}_{{ max}}=200\), \(\omega _{{ max}}=0.8\), \(\omega _{{ min}}=0.1\), \(\theta _{{ max}}=2\), \(X=50\), \(f_{w}=4\) and \(f_{e}=1\) as an example, we execute the improved TLBO algorithm given in Table 1. With a different service rates \(\mu _{2}\) of a task on the VM in Pool II, we obtain the optimal combination \((d^{*},N^{*},\theta ^{*})\) for the number of VMs in Pool II, the wake-up threshold and the sleeping parameter with the minimum system cost function \(F^{*}\) in Table 2.

Table 2 Optimization outcomes: \((d^{*},N^{*},\theta ^{*})\) and \(F^{*}\)
Full size table

The cloud capacity, the arrival intensity of tasks and the serving capability of VMs greatly influence the optimal outcomes in Table 2. With the optimization outcomes shown in Table 2, we can trade off the average latency of tasks and the energy saving rate of the system in the proposed strategy.

7 Conclusions

In this paper, we proposed a clustered VM allocation strategy with a novel sleep mode. Considering the sleep-mode with wake-up threshold in the proposed strategy, we established a queue with an N-policy and asynchronous vacations of partial servers. Based on the stochastic behavior of tasks with the proposed strategy, we built the QBD matrix and resolved the steady-state transition probabilities using the matrix-geometric solution method. Moreover, we evaluated the system performance in terms of the average latency of tasks and the energy saving rate of the system. Numerical results with analysis and simulation show that the average latency of tasks is lower with a smaller number of the VMs in Pool II, a smaller value for the wake-up threshold and a larger sleeping parameter, while the energy saving rate of the system is higher with a moderate number of VMs in Pool II, a larger value for the wake-up threshold and a smaller sleeping parameter. For this, we constructed a system cost function to balance different performance measures. By introducing a cube chaotic mapping mechanism for the grade initialization and an exponentially decreasing strategy for the teaching process, we developed an improved TLBO algorithm, and optimized the proposed strategy with the minimum system cost function.