Keywords

1 Introduction

According to the current “Cisco Global Cloud Index”, more than four fifths of the workload in data centers will be handled in cloud data centers by 2019 [1]. As a result, energy efficiency is becoming increasingly important in a cloud environment [2].

The use of a sleep mode improves energy efficiency in cloud data centers [3]. In [4], Duan et al. proposed a dynamic idle interval prediction scheme that could estimate the future idle interval length of a CPU and thereby choose the most cost-effective sleep state to minimize the energy consumption during runtime. In [5], Chou et al. proposed a fine-grain power management scheme for data center workloads. This scheme dynamically postponed the processing of some requests, created longer idle periods and promoted the use of a deeper sleep mode. In [6], Luo et al. proposed a dynamic adaptive scheduling algorithm based on flow preemption and power-aware routing. This algorithm saved energy by decreasing the ratio of low utilization devices and putting more devices into sleep mode. In the literature mentioned above, we note that a sleep mode was only applied to a Physical Machine (PM) rather than a Virtual Machine (VM).

In this paper, taking advantage of virtualization technology in cloud computing, we propose a clustered VM allocation strategy based on an N-threshold sleep-mode, and build an N-policy partially asynchronous multiple vacations queueing model. Then, we evaluate the system performance in terms of the energy saving rate of the system, both mathematically and numerically.

The rest of this paper is organized as follows. In Sect. 2, we propose a clustered VM allocation strategy based on an N-threshold sleep-mode in a cloud environment and build a system model accordingly. In Sect. 3, we analyze the system model using the method of matrix geometric solution. In Sect. 4, we derive the energy saving rate of the system. With numerical experiments, we investigate the system performance with the proposed strategy in Sect. 5. Finally, Sect. 6 concludes the whole paper.

2 VM Allocation Strategy and System Model

In this section, to improve the energy efficiency in a cloud environment, we first propose a clustered VM allocation strategy based on an N-threshold sleep-mode. Then, we develop an N-policy partially asynchronous multiple vacations queueing model to analyze the system with the proposed strategy.

2.1 VM Allocation Strategy

We note that additional energy will be consumed when the VM frequently switches from the sleep state to the awake state, and the system performance will be degraded when all the VMs are put in an imposed sleep-mode. To get around this problem, a clustered VM allocation strategy based on an N-threshold sleep-mode is proposed.

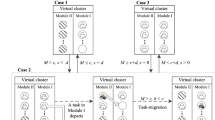
All the VMs in a cloud data center are clustered into two modules, namely, Module I and Module II. The VMs in Module I stay awake and operate on a higher speed. The VMs in Module II will go to sleep independently when there are no requests in the system buffer. At the end of a sleep period, if the requests gathered in the system buffer reaches or exceeds a certain value, namely threshold N, the corresponding VM in Module II will wake up independently and operate on a lower speed. Otherwise, the VM in Module II will restart a sleep timer and begin another sleep period.

In the proposed strategy, all the VMs are dominated by a control server, in which several sleep timers, a request counter, and a VM scheduler are deployed. Each sleep timer determines the time length of a sleep period. The request counter records the number of the requests waiting in the system buffer. Based on the sleep timers and the request counter, the VM scheduler adjusts the system state.

In Fig. 1, we demonstrate the workflow of VMs with the clustered VM allocation strategy based on an N-threshold sleep-mode.

Fig. 1.
figure 1

The workflow diagram of a VM with the proposed strategy.

Full size image

2.2 System Model

Regarding a request as a customer, a VM as an independent server, and a sleep period as a vacation, we model the proposed strategy as an N-policy partially asynchronous multiple vacations queueing model.

In this system model, the numbers of the VMs in Module I and Module II are denoted as c and d, respectively. The arrival intervals of requests are assumed to follow an exponential distribution with parameter \(\lambda ~(\lambda >0)\). The service times of requests processed in Module I and in Module II are assumed to follow exponential distributions with parameters \(\mu _{1}~(\mu _{1}>0)\) and \(\mu _{2}~(0<\mu _{2}<\mu _{1})\), respectively. Furthermore, the sleep timer length is assumed to follow an exponential distribution with parameter \(\theta ~(\theta >0)\). Here, the parameter \(\theta \) is called the sleeping parameter.

The system model is described with an infinite buffer capacity. Let \(S(t)=i, i\in \{0,1,\ldots \}\) be the total number of requests in the system at instant t. S(t) is also called the system level. Let \(J(t)=j, j\in \{0,1,\ldots ,d\}\) be the number of busy VMs in Module II at instant t. J(t) is also called the system stage. Based on the assumptions above, \(\{S(t), J(t), t\ge 0\}\) can be regarded as a two-dimensional continuous time Markov chain (CTMC).

We define \(\pi _{i,j}\) as the steady-state probability distribution of the system model for the system level being equal to i and the system stage being equal to j.

We define \(\varvec{\pi }_i\) as the steady-state probability distribution when the system level is i. The steady-state probability distribution \(\mathbf {\Pi }\) of the two-dimensional CTMC is composed of \(\varvec{\pi }_i~(i\ge 0)\). \(\mathbf {\Pi }\) is given as follows:

$$\begin{aligned} \mathbf{{\Pi }}=(\varvec{\pi }_{0},\varvec{\pi }_{1},\ldots ). \end{aligned}$$
(1)

3 Model Analysis

Based on the system level, the one-step state transition rate matrix Q of the two-dimensional CTMC \(\left\{ (S(t),J(t)),t\ge 0\right\} \) can be written in a block-tridiagonal form as follows:

In the one-step state transition rate matrix Q, the sub-matrices \({{\varvec{B}}}_{k}\) are repeated forever starting from the system level \((c+d+1)\), the sub-matrices \({{\varvec{A}}}_{k}\) are repeated forever starting from the system level \((c+d+N)\), and the sub-matrices \({{\varvec{C}}}_{k}\) are repeated forever starting from the system level \((c+d)\). The repetitive sub-matrices \({{\varvec{B}}}_{k}\), \({{\varvec{A}}}_{k}\) and \({{\varvec{C}}}_{k}\) are represented by \({{\varvec{B}}}\), \({{\varvec{A}}}\) and \({{\varvec{C}}}\), respectively.

\(B_{k}\ (k=1,2,\ldots ,c)\), \(\varvec{B}_{k}\ (k=c+1,c+2,\ldots ,c+d)\) and \(\varvec{B}\ (k=c+d+1,c+d+2,\ldots )\) are the one-step state transition rate sub-matrices for the system level k decreasing by one.

\(B _{k}=k\mu _{1},\ k=1,2,\ldots ,c, \)

$${{\varvec{B}}}_{k}=\left( \begin{array}{cccc} c\mu _{1} &{} \ &{} \ &{} \ \\ \ &{} c\mu _{1}+\mu _{2} &{} \ &{} \ \\ \ &{} \ &{} \ddots &{} \ \\ \ &{} \ &{} \ &{} c\mu _{1}+(x-1)\mu _{2} \\ \ &{} \ &{} \ &{} c\mu _{1}+x\mu _{2} \\ \end{array} \right) ,\ k=c+x, \ x=1,2,\ldots ,d,$$

\({{\varvec{B}}}={\text {diag}}\left( c\mu _{1},c\mu _{1}+\mu _{2},\ldots ,c\mu _{1}+d\mu _{2} \right) ,\ k=c+x, \ x=d+1,d+2,\ldots .\)

\(A_{k}\ (k=1,2,\ldots ,c)\), \(\varvec{A}_{k}\ (k=c+1,c+2,\ldots ,c+d+N-1)\) and \(\varvec{A}\ (k=c+d+N,c+d+N+1,\ldots )\) are the one step state transition rate sub-matrices for the system level k remaining fixed. For convenience of presentation, we introduce \(h_{y}\) \((h_{y}=\lambda +c\mu _{1}+y\mu _{2},\ 0\leqslant y\leqslant d\)) to simplify the sub-matrices \(\varvec{A}_{k}\) and A.

\(A_{k}=-(\lambda +k\mu _{1}),\ k=0,1,\ldots ,c, \)

\({{\varvec{A}}}_{k}= {\text {diag}}\left( -h_{0},-h_{1},\ldots , -h_{x} \right) ,\ k=c+x,\ x=1,2,\ldots ,{\text {min}}\{N,d\}-1.\)

For the case of \(N>d\),

\({{\varvec{A}}}_{k}= {\text {diag}}\left( -h_{0},-h_{1},\ldots , -h_{d} \right) ,\ k=c+x,\ x=d,d+1,\ldots ,N-1.\)

For the case of \(N\leqslant d\),

$$\begin{aligned} {{\varvec{A}}}_{k}= \begin{aligned}&\left( \begin{array}{ccccccccc} -h_{0}-d\theta &{} d\theta &{} \ &{} \ &{} \ \\ \ddots &{} \ddots \\ &{} -h_{x-N}-(d-(x-N))\theta &{}(d-(x-N))\theta \\ &{} &{}-h_{x-N}&{}0 \\ &{} &{}\ddots &{}\ddots \\ &{} &{} &{}-h_{x-1} &{}0 \\ &{} &{} &{} &{}-h_{x} \\ \end{array} \right) , \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad k=c+x,\ x=N,N+1,\ldots ,d-1. \end{aligned}\\ \end{aligned}$$
$$\begin{aligned} {{\varvec{A}}}_{k}= \begin{aligned}&\left( \begin{array}{ccccccccc} -h_{0}-d\theta &{} d\theta &{} \ &{} \ &{} \ \\ \ddots &{} \ddots \\ &{} -h_{x-N}-(d-(x-N))\theta &{}(d-(x-N))\theta \\ &{} &{}-h_{x-N}&{}0 \\ &{} &{}\ddots &{}\ddots \\ &{} &{} &{}-h_{d-1} &{}0 \\ &{} &{} &{} &{}-h_{d} \\ \end{array} \right) , \\&\qquad \qquad \qquad k=c+x, x={\text {max}}\{N,d\},{\text {max}}\{d,N\}+1,\ldots ,d+N-1. \end{aligned}\\ \end{aligned}$$
$$\begin{aligned} {{\varvec{A}}}= \begin{aligned}&\left( \begin{array}{ccccc} -h_{0}-d\theta &{} d\theta &{} \ &{} \ &{} \ \\ \ &{} -h_{1}-(d-1)\theta &{} (d-1)\theta &{} \ &{} \ \\ \ &{} \ &{} \ddots &{} \ddots &{} \ \\ \ &{} \ &{} \ &{} -h_{d-1}-\theta &{} \theta \\ \ &{} \ &{} \ &{} \ &{} -h_{d} \\ \end{array} \right) ,\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \,\, k=c+x,x=d+N,d+N+1,\ldots . \end{aligned}\\ \end{aligned}$$

\(C_{k}\ (k=1,2,\ldots ,c)\), \(\varvec{C}_{k}\ (k=c+1,c+2,\ldots ,c+d-1)\) and \(\varvec{C}\ (k=c+d,c+d+1,\ldots )\) are the one-step state transition rate sub-matrices for the system level k increasing by one.

Obviously, the state transitions of the CTMC occur only between adjacent system levels. The two-dimensional CTMC \(\{S(t),J(t),t\ge 0\}\) can be seen as a type of Quasi Birth-and-Death (QBD) process.

To analyze the QBD process \(\{S(t),J(t),t\ge 0\}\) by using the matrix geometric solution method, we need to solve for the minimal non-negative solution of the matrix quadratic equation \({{\varvec{R}}}^2{{\varvec{B}}} + {{\varvec{R}}}{{\varvec{A}}} + {{\varvec{C}}} = \mathbf 0 \). This solution is called the rate matrix \({{\varvec{R}}}\).

Based on the discussions above, we find that the sub-matrices B, A and C are upper-triangular matrices. So, the rate matrix R must be an upper-triangular matrix, and can be explicitly determined.

Applying the Gauss-Seidel method [7], we can obtain \(\varvec{\pi }_i \ (i=0,1,\ldots ,c+d+N)\). Based on the matrix geometric solution form \(\varvec{\pi }_i = \varvec{\pi }_{c+d+N}{} \mathbf R ^{i-(c+d+N)}, \ i\ge c+d+N,\) we can obtain \(\varvec{\pi }_i\ (i=c+d+N+1, c+d+N+2,\ldots )\).

4 Performance Measures

We define the energy saving rate of the system as the energy conservation per unit time. Energy saving rate of the system is a measure to compare the total energy consumption in our proposed strategy and that in the conventional strategy. Based on the steady-state probability distribution of the system model given in Sect. 3, the energy saving rate E of the system with our proposed strategy is given as follows:

$$\begin{aligned} E = E_{1}-(E_{2}+E_{3}) \end{aligned}$$
(2)

where \(E_{1}\) is the energy saving rate during the sleep period, \(E_{2}\) and \(E_{3}\) are the additional energy consumption rates caused by a request-migration and by a listening at the boundary of the sleep period.

$$\begin{aligned} \begin{aligned} E_{1} \ =&\ (\omega _{}-\omega _{s})\sum ^{\infty }_{i=0}\sum ^{d}_{j=0}(d-j)\pi _{ij},\\ E_{2} \ =&\ \omega _{m}\sum ^{c+d}_{i=c+1}\sum ^{d}_{j=1}c\mu _{1}\pi _{ij},\\ E_{3} \ =&\ \omega _{l}\sum ^{\infty }_{i=0}\sum ^{d}_{j=0}\theta (d-j)\pi _{ij} \end{aligned} \end{aligned}$$

where \(\omega \ (\omega >0)\) is the energy consumption per unit time for a busy VM in Module II. \(\omega _{s}\ (\omega _{s}>0)\) is the energy consumption per unit time for a sleeping VM in Module II. \(\omega _{m}\ (\omega _{m}>0)\) is the energy consumption for each request-migration. \(\omega _{l}\ (\omega _{l}>0)\) is the energy consumption for each listening.

5 Numerical Experiments

In order to quantify the impact of the sleeping parameter on the energy saving rate of the system for the different number of the VMs in Module II and the different thresholds N, we provide numerical experiments. Referencing to [8], we set the experimental parameters as follows: \(c+d=50\), \(\lambda =7.00\) (requests/ms), \(\mu _{1}=0.20\) (requests/ms), \(\mu _{2}=0.10\) (requests/ms), \( \omega _{} =0.50\) mW, \(\omega _{s}=0.10\) mW, \(\omega _{m}=0.50\) mW and \(\omega _{l}=0.15\) mW.

Figure 2 examines the influence of the sleeping parameter \(\theta \) on the energy saving rate E of the system for the different number d of the VMs in Module II and the different thresholds N.

Fig. 2.
figure 2

Energy saving rate E of the system.

Full size image

From Fig. 2(a), we notice that when the sleeping parameter \(\theta \) and the threshold N are given, a larger number d of the VMs in Module II will lead to a higher energy saving rate E of the system. As the number of the VMs in Module II increases, more VMs have the opportunity to take a sleep, so the energy saving rate of the system improves.

From Fig. 2(b), we notice that when the sleeping parameter \(\theta \) and the number d of the VMs in Module II are given, a bigger threshold N will lead to a higher energy saving rate E of the system. The higher the threshold N is, the later a VM in Module II will wake up from sleeping, so the VMs in Module II will stay in the sleep state for longer. This results in a higher energy saving rate of the system.

Combining Figs. 2(a) and 2(b), we also observe that for any number d of the VMs in Module II and any value for threshold N, the energy saving rate E of the system decreases as the sleeping parameter \(\theta \) increases. On the one hand, the larger the sleeping parameter is, the shorter the time length of a sleep period is, and the later a VM in Module II will wake up from sleeping, so less energy will be saved. On the other hand, the larger the sleeping parameter is, the more frequently the VM in Module II listens to the system buffer, so additional energy will be consumed. Therefore, the energy saving rate of the system will decrease.

6 Conclusions

In this paper, we proposed a clustered VM allocation strategy. Considering an N-threshold sleep-mode with the proposed strategy, we established an N-policy partially asynchronous multiple vacations queueing model. The queueing model quantified the effects of the number of VMs in Module II, the threshold N and the sleeping parameter on the energy saving rate of the system. In future research, we aim to extend our study to investigate the average latency of requests and to optimize the proposed strategy by making trade-offs between different performance measures.