An improvement on parametric $\nu$-support vector algorithm for classification

Abstract

One effective technique that has recently been considered for solving classification problems is parametric $\nu$-support vector regression. This method obtains a concurrent learning framework for both margin determination and function approximation and leads to a convex quadratic programming problem. In this paper we introduce a new idea that converts this problem into an unconstrained convex problem. Moreover, we propose an extension of Newton’s method for solving the unconstrained convex problem. We compare the accuracy and efficiency of our method with support vector machines and parametric $\nu$-support vector regression methods. Experimental results on several UCI benchmark data sets indicate the high efficiency and accuracy of this method.

1 Introduction

Classification has numerous practical applications including medical science, letter and number recognition, voice recognition, face recognition and hand-writing (Joachims 1998; Cao and Tay 2001; Osuna et al. 1997; Ivanciuc 2007). The first idea of classification as a support vector machine (SVM) was introduced by Vapnik and Chervonenkis (1974). A new method to obtain the separating hyperplane has recently been considered, the parametric v-support vector classification (Par $\nu$-SVC) (Hao 2010).

To date, many methods have been proposed for the classification of data by SVM as a hyperplane with maximum margin [The maximum margin hyperplane was shown to minimize an upper bound of the generalization error according to the Vapnik theory (Vapnik and Chervonenkis 1974; Bennett and Bredensteiner 2000)], regression classifier, etc (Deng et al. 2012; Pappu et al. 2015; Xanthopoulos et al. 2014). The $\nu$-support vector regression is a new class of SVM. It can handle both classification and regression (Schölkopf et al. 2000; Schölkopf and Smola 2001; Pontil et al. 1998). Schölkopf et al. introduced a new parameter $\nu$ which can control the number of support vectors and training errors.

Finally, a new method for obtaining the regression line that has recently been considered is the parametric $\nu$-support vector regression (Par $\nu$-SVR) (Hao 2010; Wang et al. 2014).

All the above-mentioned methods are used to solve constrained quadratic problems.

In this paper, we introduce a new idea for converting the constrained convex quadratic problem into an unconstrained convex problem.There are several approaches for solving unconstrained convex optimization problems (Resende and Pardalos 2002). One important and fast established methods for convex unconstrained problems is Newton’s method. Because in our case the objective function is not twice differentiable, we use the generalized Newton’s method.

Our notations are described as follows:

Let $a = [a_i]$ be a vector in $R^n$. By $a_+$ we mean a vector in $R^n$ whose ith entry is 0 if $a_i <0$ and equals $a_i$ if $a_i \ge 0$. If f is a real valued function defined on the n-dimensional real space $R^n$, the gradient of f at x is denoted by $\bigtriangledown f(x)$ which is a column vector in $R^n$, and the $n \times n$ Hessian matrix of second partial derivatives of f at x is denoted by $\bigtriangledown ^2f(x)$. By $A^T$ we mean the transpose of matrix A, and $\nabla f(x)^Td$ is called directional derivative of f at x in direction d. For the two vectors x and y in the $~n-$dimensional real space, $x^Ty$ denotes the scalar product. For $x\in R^n$, $\Vert x\Vert$ denotes $2-$norm. A column vector of ones of arbitrary dimension will be indicated by e. For $A \in R^{m \times n}$ and $B \in R^{n \times l}$ ; the kernel K(A; B) is an arbitrary function which maps $R^{m \times n} \times R^{n \times l}$ into $R^{m \times l}$. In particular, if x and y are column vectors in $R^n$ then, $K(x^T; y)$ is a real number, $K(x^T;A^T)$ is a row vector in $R^m$ , and $K(A;A^T)$ is an $m \times m$ matrix. The convex hull of a set S has been shown by $co\{S\}$. The identity $n \times n$ matrix will be denoted by $I_{n \times n}$.

2 Parametric $\nu$-support vector classification

For a classification problem, a data set $(x_i,y_i)$ is given for training with the input $x_i \in R^n$ and the corresponding target value or label $y_i = 1$ or $-1$ i.e.:

$$\begin{aligned} (x_1,y_1),\ldots ,(x_n,y_n)\in \mathbb {R}^\mathrm{n} \times \{\pm 1 \}. \end{aligned}$$

A classification problem finds the unique hyperplane $w^Tx+b=0$$(w,x\in R^n, \ b\in R)$ that best separates the two classes of data.

Schölkopf et al. proposed a new class of support vector machines which called $\nu$-support vector machine or $\nu$-support vector classification ($\nu$-SVC) (Schölkopf et al. 2000; Schölkopf and Smola 2001). In $\nu$-SVC, there is a parameter $\nu$ for controlling the number of support vectors and this parameter also can eliminate one of the other free parameters of the original support vector algorithms (Schölkopf and Smola 2001).

A modification of the $\nu$-SVC algorithm, called Par $\nu$-SVC, which considers a parametric-margin model of arbitrary shape (Hao 2010). In fact, in the Par $\nu$-SVC we consider a parametric margin $g\left( x \right) ={{c}^{T}}x+d$ and hyperplane $f\left( x \right) ={{w}^{T}}x+b$ that classify data if and only if:

$$\begin{aligned} {{y}_{i}}\left( {{w}^{T}}{{x}_{i}}+b \right) \ge {{c}^{T}}{{x}_{i}}+d,\ \ y_i \in \{\pm 1 \}, \ \ i=1,\ldots ,n. \end{aligned}$$

(1)

For finding function $f\left( x \right)$ and $g\left( x \right)$ as follows using the minimization problem (Hao 2010)

$$\begin{aligned}&\mathop {\min }\limits _{w, b, c, d,\xi } \frac{1}{2}{{\left\| w \right\| }^{2}}+C\left( -\nu \left( \frac{1}{2}\Vert c\Vert ^2-d\right) + \frac{1}{n}\sum \limits _{i=1}^{n}{ \xi _{i} }\right) \nonumber \\&s.t.\, y_i \left( {{w}^{T}}{{x}_{i}}+b \right) \ge (c^T x_i+d) - {{\xi }_{i}}, \nonumber \\&\xi _{i} \ge 0 , \ \ \ i=1,\ldots ,n, \end{aligned}$$

(2)

where C and $\nu$ are the penalty parameters.

In Par $\nu$-SVC, a margin of separation between the two pattern classes is maximized, and the solutions are those examples that lie closest to this margin (Boser et al. 1992).

Also, it is obvious that the objective function of Par $\nu$-SVC is an non-convex function and so we are motivated to consider other techniques for finding an approximate solution of (2).

We know that the regression is more general than classification and if we apply Par $\nu$-SVR to a binary classification dataset, then under some conditions, Par $\nu$-SVR gives the same solution as Par $\nu$-SVC. For this reason, we review $\nu$-SVR and Par $\nu$-SVR formulation for a linear two-class classifier.

In the $\varepsilon$-support vector regression ($\varepsilon$-SVR) (Schölkopf and Smola 2001) for classification, our goal is to solve the following constrained optimization problem

$$\begin{aligned}&\mathop {\min }\limits _{w ,b , \xi , \xi ^{*}} \frac{1}{2}{{\left\| w \right\| }^{2}}+C \frac{1}{n}\sum \limits _{i=1}^{n}{ (\xi _{i}+\xi _{i}^{*}) }\nonumber \\&s.t.\, \left( {{w}^{T}}{{x}_{i}}+b \right) -{{y}_{i}}\le \varepsilon +{{\xi }_{i}}, \nonumber \\&{{y}_{i}}-\left( {{w}^{T}}{{x}_{i}}+b \right) \le \varepsilon +\xi _{i}^{*}, \nonumber \\&\xi _{i}^{*},{{\xi }_{i}}\ge 0. \ \ \ i=1,\ldots ,n \end{aligned}$$

(3)

The $\nu$-SVR algorithm alleviates the problem (3) by considering $\varepsilon$ part of the optimization problem because it is difficult to select appropriate value of the $\varepsilon$ in $\varepsilon$-SVR (Schölkopf et al. 2000; Schölkopf and Smola 2001).

Then the minimization problem of $\nu$-SVR is as follows:

$$\begin{aligned}&\mathop {\min }\limits _{w ,b, \xi , \xi ^{*}, \varepsilon } \frac{1}{2}{{\left\| w \right\| }^{2}}+C \left( \nu \varepsilon + \frac{1}{n}\sum \limits _{i=1}^{n}({ \xi _i + \xi _{i}^{*}}) \right) \nonumber \\&s.t. \left( {{w}^{T}}{{x}_{i}}+b \right) -{{y}_{i}}\le \varepsilon +{{\xi }_{i}}, \nonumber \\&{{y}_{i}}-\left( {{w}^{T}}{{x}_{i}}+b \right) \le \varepsilon +\xi _{i}^{*}, \nonumber \\&\xi _{i}^{*},{{\xi }_{i}}\ge 0. \ \ \ i=1,\ldots ,n \end{aligned}$$

Everything above $\varepsilon$ is captured in slack variables $\xi _{i}$ and $\xi _{i}^{*}$, which are penalized in the objective function via a regularization constant C, chosen a priori (Vapnik 1998). The size of $\varepsilon$ is traded off against model complexity and slack variables via a constant $\nu >0$.

In a Par $\nu$-SVR, we consider a parametric margin $g\left( x \right) ={{c}^{T}}x+d$ instead of $\varepsilon$ in $\nu$-SVR. Especially the hyperplane $f\left( x \right) ={{w}^{T}}x+b$ classifies data if and only if (Hao 2010; Wang et al. 2014):

$$\begin{aligned}&\left( {{w}^{T}}{{x}_{i}}+b \right) \ge {{c}^{T}}{{x}_{i}}+d \quad for \ \ y_i=+1,\\&\left( {{w}^{T}}{{x}_{i}}+b \right) \le {-{c}^{T}}{{x}_{i}}-d \quad for \ \ y_i=-1. \end{aligned}$$

Using the following minimization problem, we find $f\left( x \right)$ and $g\left( x \right)$ simultaneously

$$\begin{aligned}&\mathop {\min }\limits _{w,b,c,d,\xi ^{*},\xi \,\,\,} \, \frac{1}{2}{{\left\| w \right\| }^{2}}+C\left( \nu \left( \frac{1}{2}{{\left\| c \right\| }^{2}}+d \right) +\frac{1}{n}\sum \limits _{i=1}^{n}{\left( {{\xi }_{i}}+\xi _{i}^{*} \right) } \right) \nonumber \\&s.t. \, \left( {{w}^{T}}{{x}_{i}}+b \right) +\left( {{c}^{T}}{{x}_{i}}+d \right) \ge {{y}_{i}}-{{\xi }_{i}},\nonumber \\&\left( {{c}^{T}}{{x}_{i}}+d \right) -\left( {{w}^{T}}{{x}_{i}}+b \right) \le {{y}_{i}}+\xi _{i}^{*},\nonumber \\&\xi _{i}^{*},{{\xi }_{i}}\ge 0, \ i=1,\ldots ,n, \end{aligned}$$

(4)

where C and $\nu$ are positive penalty parameters.

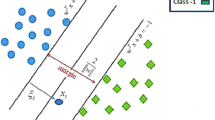
The point that is important here is that the Par $\nu$-SVR for classification leads to a convex problem. Figure 1 illustrates the Par $\nu$-SVR for classification graphically.

Fig. 1

Illustration of parametric $\nu$-SVR for classification

The Lagrangian corresponding to the problem (4) is given by

$$\begin{aligned} L( w,b,c,d,\alpha , \alpha ^*, \beta , \beta ^*, \xi , \xi ^* )= & {} \frac{1}{2}{{\left\| w \right\| }^{2}}+C\left( \nu \left( \frac{1}{2}{{\left\| c \right\| }^{2}}+d \right) +\frac{1}{n}\sum \limits _{i=1}^{n}{\left( {{\xi }_{i}}+\xi _{i}^{*} \right) } \right) \\&-\sum \limits _{i=1}^{n}{{{\alpha }_{i}}\left[ \left( {{w}^{T}}{{x}_{i}}+b \right) +\left( {{c}^{T}}{{x}_{i}}+d \right) -{{y}_{i}}+{{\xi }_{i}} \right] } \\&-\sum \limits _{i=1}^{n}{\alpha _{i}^{*}\left[ \left( {{w}^{T}}{{x}_{i}}+b \right) -\left( {{c}^{T}}{{x}_{i}}+d \right) +{{y}_{i}}+\xi _{i}^{*} \right] } \\&-\sum \limits _{i=1}^{n}{{{\beta }_{i}}{{\xi }_{i}}}-\sum \limits _{i=1}^{n}{\beta _{i}^{*}\xi _{i}^{*}}, \end{aligned}$$

where $\alpha _i$ , ${\alpha _i}^*$, $\beta _i$ and ${\beta _i}^*$ are the nonnegative Lagrange multipliers.

By using the Karush–Kuhn–Tucker (KKT) conditions, we obtain the dual optimization problem of (4) as (Boyd and Vandenberghe 2004)

$$\begin{aligned} \mathop {\max }\limits _{\alpha , \alpha ^*}&-\frac{1}{2}\sum \limits _{i=1}^{n}{\sum \limits _{j=1}^{n}{\left( \alpha _i-\alpha _i^* \right) }}\left( \alpha _j-\alpha _j^* \right) {x_i}^T{x_j} \\&\quad -\frac{1}{2C\nu }\sum \limits _{i=1}^{n}{\sum \limits _{j=1}^{n}{\left( {{\alpha }_{i}}+\alpha _{i}^{*} \right) }}\left( {\alpha _j}+\alpha _j^{*} \right) {x_i}^T{x_j} +\sum \limits _{i=1}^{n}{\left( {{\alpha }_{i}}-\alpha _{i}^{*} \right) {{y}_{i}}} \\ s.t.&\sum \limits _{i=1}^{n}{\left( {{\alpha }_{i}}-\alpha _{i}^{*} \right) =0,} \\&\sum \limits _{i=1}^{n}{\left( {{\alpha }_{i}}+\alpha _{i}^{*} \right) =C\nu ,} \\&0\le {{\alpha }_{i}}\le \frac{C}{n},\,\,0\le \alpha _{i}^{*}\le \frac{C}{n}. \ \ i=1,\ldots ,n \end{aligned}$$

By solving the above dual problem, we obtain the Lagrange multipliers $\alpha _i$ and $\alpha _i^*$, which give the weight vector w and c as a linear combination of $x_i$:

$$\begin{aligned} w= & {} \sum \limits _{i=1}^{n}{(\alpha _i-\alpha _i^*) x_i},\\ c= & {} \frac{1}{C\nu }\sum \limits _{i=1}^{n}{(\alpha _i+\alpha _i^*) x_i}, \end{aligned}$$

while the bias terms b and d are determined by exploiting the KKT conditions, which are

$$\begin{aligned} b= & {} \frac{-1}{2} \left( w^T x_i + w^T x_j + c^T x_i - c^T x_j - y_i - y_j\right) ,\\ \nonumber d= & {} \frac{-1}{2} \left( w^T x_i - w^T x_j + c^T x_i + c^T x_j - y_i + y_j\right) , \end{aligned}$$

for some i, j such that $\alpha _i , \alpha _j^* \in (0,\frac{C}{n})$.

The regression function f(x) and the corresponding parametric insensitive function g(x) can be obtained as follows [see Chen et al. (2012a)]:

$$\begin{aligned} f(x)= & {} \sum \limits _{i=1}^{n} (\alpha _i-\alpha _i^*)(x_i^Tx) +b, \\ g(x)= & {} \frac{1}{C\nu }\sum \limits _{i=1}^{n} (\alpha _i+\alpha _i^*)(x_i^Tx) +d. \end{aligned}$$

In the next section, we focus on solving the minimization problem (4).

3 Solving quadratic constrained programming problem

We see that the classical Par $\nu$-SVR formulation is equivalent to finding the f(x) and g(x) simultaneously . Using 2-norm slack variables $\xi _i$ and $\xi _i^*$ in objective function of (4) leads to the following minimization problem (Lee and Mangasarian 2001).

$$\begin{aligned}&\mathop {\min }\limits _{w,b,c,d,\xi ^{*},\xi \,\,\,} \, \frac{1}{2}{{\left\| w \right\| }^{2}}+C\left( \nu \left( \frac{1}{2}{{\left\| c \right\| }^{2}}+d \right) +\frac{1}{n}\sum \limits _{i=1}^{n}{\left( {\left\| {\xi }_{i} \right\| }^2+ \left\| \xi _{i}^{*}\right\| ^2 \right) } \right) \nonumber \\&s.t. \left( {{w}^{T}}{{x}_{i}}+b \right) +\left( {{c}^{T}}{{x}_{i}}+d \right) \ge {{y}_{i}}-{{\xi }_{i}},\nonumber \\&-\left( {{c}^{T}}{{x}_{i}}+d \right) +\left( {{w}^{T}}{{x}_{i}}+b \right) \le {{y}_{i}}+\xi _{i}^{*},\nonumber \\&\xi _{i}^{*},{{\xi }_{i}}\ge 0. \ \ i=1,\ldots ,n \end{aligned}$$

(5)

With respect to the Lagrangian function of (5) and KKT condition we have

$$\begin{aligned}&\xi \ge Y-\left[ \left( {{A}^{T}}w+be \right) +\left( {{A}^{T}}c+de \right) \right] , \end{aligned}$$

(6)

$$\begin{aligned}&{{\xi }^{T}}\left( \xi -Y+\left( {{A}^{T}}w+be \right) +\left( {{A}^{T}}c+de \right) \right) =0, \end{aligned}$$

(7)

$$\begin{aligned}&\xi \ge 0, \end{aligned}$$

(8)

where $\xi ={{\left[ {{\xi }_{1}},\ldots ,{{\xi }_{n}} \right] }^{T}}$, $Y={{\left[ {{y}_{1}},\ldots ,{{y}_{n}} \right] }^{T}}$ and $A=\left[ {{x}_{1}},\ldots ,{{x}_{n}} \right] ^{T}$. According to the inequalities (6)–(8) we have (Lee and Mangasarian 2001)

$$\begin{aligned} \xi ={{\left( Y-\left[ \left( {{A}^{T}}w+be \right) +\left( {{A}^{T}}c+de \right) \right] \right) }_{+}}, \end{aligned}$$

and similarly, we can show

$$\begin{aligned} {{\xi }^{*}}={{\left( \left[ \left( {{A}^{T}}w+be \right) -\left( {{A}^{T}}c+de \right) \right] -Y \right) }_{+}}. \end{aligned}$$

Thus the problem (5) is equivalent to the following problem:

$$\begin{aligned} \underset{w,b,c,d }{\mathop {\min }} \ \ \varphi (w,b,c,d)= & {} \underset{w,b,c,d}{\mathop {\min }} \frac{1}{2}{{\left\| w \right\| }^{2}}+C\nu \left( \frac{1}{2}{{\left\| c \right\| }^{2}}+d \right) \nonumber \\&\quad +\,\frac{C}{n}{{\left\| {{\left( Y-\left[ \left( {{A}^{T}}w+be \right) +\left( {{A}^{T}}c+de \right) \right] \right) }_{+}} \right\| }^{2}}\nonumber \\&\quad +\,\frac{C}{n}{{\left\| {{\left( \left[ \left( {{A}^{T}}w+be \right) -\left( {{A}^{T}}c+de \right) \right] -Y \right) }_{+}} \right\| }^{2}}. \end{aligned}$$

(9)

In this way, we made some modifications of Par $\nu$-SVR that led to unconstrained convex problem (9) which we call Par $\nu$-SVRC$^+$.

The main advantage of Par $\nu$-SVRC$^+$ over Par $\nu$-SVC (Hao 2010) and Par $\nu$-SVR is solving an unconstrained convex problem rather than a large complexity of quadratic programming problem (QPP).

Our goal here is to solve the unconstrained problem (9). The objective function to problem (9) is piecewise quadratic, convex, and differentiable, but it is not twice differentiable (Chen et al. 2012b; Ketabchi and Moosaei 2012; Pardalos et al. 2014). To solve the problem (9), we have provided some definitions that deal with the objective function of this problem.

Class $LC^1$ of functions is defined as follows (Hiriart-Urruty et al. 1984):

Definition 1

A function f is said to be an $LC^1$ function on an open set A if:

• 1. f is continuously differentiable on A,

• 2. $\nabla f$ is locally Lipschitz on A.

We know that if f is a $LC^1$ function on an open set A , then the $\nabla f$ is differentiable almost everywhere in A, and its generalized Jacobian in Clarkes sense can be defined (Clarke 1990).

Now, the generalized Hessian of f at x to be the set $\partial ^2 f(x)$ of $n \times n$ matrices is defined by:

$\partial ^2 f(x) = co\{H \in R^{n \times n} : \exists x_k \rightarrow x \ ~~with ~~\nabla \ f \ differentiable \ at \ x_k \ and \ \partial ^2 \ f(x_k) \rightarrow H\}$.

By considering (9), we have

$$\begin{aligned} \frac{\partial \varphi }{\partial w}= & {} w+\frac{2}{n}(-A)\left( {\left( Y-\left[ \left( {{A}^{T}}w+be \right) +\left( {{A}^{T}}c+de \right) \right] \right) }_{+}\right. \\&\left. -\,{\left( \left[ \left( {{A}^{T}}w+be \right) -\left( {{A}^{T}}c+de \right) \right] -Y \right) }_{+}\right) ,\\ \frac{\partial \varphi }{\partial b}= & {} \frac{2}{n}\left( -e^T\right) \left( {\left( Y-\left[ \left( {{A}^{T}}w+be \right) +\left( {{A}^{T}}c+de \right) \right] \right) }_{+}\right. \\&\left. -\,{\left( \left[ \left( {{A}^{T}}w+be \right) -\left( {{A}^{T}}c+de \right) \right] -Y \right) }_{+}\right) ,\\ \frac{\partial \varphi }{\partial c}= & {} C \nu c+\frac{2}{n}(-A)\left( {\left( Y-\left[ \left( {{A}^{T}}w+be \right) +\left( {{A}^{T}}c+de \right) \right] \right) }_{+}\right. \\&\left. +\,{\left( \left[ \left( {{A}^{T}}w+be \right) -\left( {{A}^{T}}c+de \right) \right] -Y \right) }_{+}\right) ,\\ \frac{\partial \varphi }{\partial d}= & {} C \nu +\frac{2}{n}(-e^T)\left( {\left( Y-\left[ \left( {{A}^{T}}w+be \right) +\,\left( {{A}^{T}}c+de \right) \right] \right) }_{+}\right. \\&\left. +\,{\left( \left[ \left( {{A}^{T}}w+be \right) -\left( {{A}^{T}}c+de \right) \right] -Y \right) }_{+}\right) . \end{aligned}$$

The formulation can be written

$$\begin{aligned} \frac{\partial \varphi }{\partial w}=T_1u-\frac{2}{n}A\left( (Y-T_2u)_+-(T_3u-Y)_+\right) , \end{aligned}$$

(10)

where $T_1=[I_{n \times n} \ \ \ 0_{n \times n} \ \ \ 0_{n \times 1} \ \ \ 0_{n \times 1}]$, $T_2= [A \ \ \ A^T \ \ \ e \ \ \ e]$, $T_3=[A \ \ \ -A^T \ \ \ e \ \ \ -e]$ and $u=[w^T \ \ c^T \ \ b^T \ \ d^T]^T$.

Note, we know (10) is not differentiable, but it satisfies Lipschitz conditions.

Theorem 1

$\frac{\partial \varphi }{\partial w}$ is globally Lipschitz.

Proof

From (10) we have that

$$\begin{aligned} \left\| \frac{\partial \varphi }{\partial w}(s)-\frac{\partial \varphi }{\partial w}(z)\right\|= & {} \left\| T_1s-\frac{2}{n}A\left( (Y-T_2s)_+-(T_3s-Y)_+\right) -T_1z\right. \nonumber \\&\left. \quad +\,\frac{2}{n}A\left( (Y-T_2z)_++(T_3z-Y)_+\right) \right\| \nonumber \\\le & {} \Vert T_1(s-z)-\frac{2}{n}A\left[ (Y-T_2s)-(T_3s-Y)\right] +\frac{2}{n}A\left( (Y-T_2z)+(T_3z-Y)\right) \Vert \nonumber \\\le & {} \Vert T_1(s-z)\Vert +\frac{2}{n}\Vert A\Vert \Vert T_2(s-z)+T_3(s-z)\Vert \nonumber \\\le & {} \left( \Vert T_1\Vert +\frac{2}{n}\Vert A^T\Vert \Vert T_2+T_3\Vert \right) \Vert s-z\Vert . \end{aligned}$$

(11)

Then from (11) we conclude that is globally Lipschitz with constant $K=\Vert T_1\Vert +\frac{2}{n}\Vert A\Vert \Vert T_2+T_3\Vert$. $\square$

Similarly, $\frac{\partial \varphi }{\partial b}$, $\frac{\partial \varphi }{\partial c}$ and $\frac{\partial \varphi }{\partial d}$ are globally Lipschitz.

Theorem 2

$\nabla \varphi (u)$ is globally Lipschitz continuous and the generalized Hessian of $\varphi (u)$ is $\partial ^2 \varphi (u) = (T_1+AD_1(u)T_2+AD_2(u)T_3 )$ where $D_1(u)$ denotes the diagonal matrix whose ith diagonal entry $u_i$ is equal to 1 if $(Y-T_2u)_i > 0$ ; $u_i$ is equal to 0 if $(Y-T_2u)_i \le 0$ and $D_2(u)$ also denotes the diagonal matrix whose ith diagonal entry $u_i$ is equal to 1 if $(T_3u-Y)_i > 0$; $u_i$ is equal to 0 if $(T_3u-Y)_i \le 0$ .

Proof

See (Hiriart-Urruty et al. 1984). $\square$

From the previous discussion and according to the above theorem, we know that the $\nabla \varphi$ is differentiable almost everywhere, and the generalized Hessian of $\varphi$ exists everywhere.

Therefore, to solve unconstrained problem (9), we can use the generalized Newton method.

3.1 A brief expression for nonlinear par $\nu$-SVRC$^+$

In the nonlinear case, we have the following minimization problem (Hao 2010):

$$\begin{aligned}&\underset{w,b,c,d,\xi ,\xi _{{}}^{*} }{\mathop {\min }}\,\,\, \ \ \ \frac{1}{2}{{\left\| w \right\| }^{2}}+C\left( \nu \left( \frac{1}{2}{{\left\| c \right\| }^{2}}+d \right) +\frac{1}{n}\left( {{\left\| \xi \right\| }^{2}}+{{\left\| {{\xi }^{*}} \right\| }^{2}} \right) \right) \\&s.t. \left( K{{\left( A,D \right) }^{T}}w+be \right) +\left( K{{\left( A,D \right) }^{T}}c+de \right) \ge Y-\xi , \\&-\left( K{{\left( A,D \right) }^{T}}c+de \right) +\left( K{{\left( A,D \right) }^{T}}w+be \right) \le Y+{{\xi }^{*}}, \\&{{\xi }^{*}},\ \xi \ge 0, \end{aligned}$$

where K( ., .) is any arbitrary kernel function and $D=[A;B]$. Similarly, this constrained problem can be considered an unconstrained problem as follows:

$$\begin{aligned} \underset{w,b,c,d }{\mathop {\min }} \ \ \varphi (w,b,c,d)= & {} \underset{w,b,c,d}{\mathop {\min }} \frac{1}{2}{{\left\| w \right\| }^{2}}+C\nu \left( \frac{1}{2}{{\left\| c \right\| }^{2}}+d \right) \\&\quad +\,\frac{C}{n}{{\left\| {{\left( Y-\left[ \left( {K{{\left( A,D \right) }^{T}}}w+be \right) +\left( {K{{\left( A,D \right) }^{T}}}c+de \right) \right] \right) }_{+}} \right\| }^{2}} \\&\quad +\,\frac{C}{n}{{\left\| {{\left( \left[ \left( {K{{\left( A,D \right) }^{T}}}w+be \right) -\left( {K{{\left( A,D \right) }^{T}}}c+de \right) \right] -Y \right) }_{+}} \right\| }^{2}}. \end{aligned}$$

4 Numerical experiments

In this section, we discuss our approach using two different performances: the accuracy and the learning speed of a classifier. Throughout this experimental part, we used the Gaussian kernel (i.e. $K(x,y)=exp(-\gamma \Vert x-y\Vert ^2)$ , $\gamma > 0$) for all data. The method was implemented in MATLAB 8 and carried out on a PC with Corei5 2310 (2.9 GHz) and 8 GB main memory. In order to examine the efficiency of Par $\nu$-SVRC$^+$, two samples of n-dimensional problems are given and we derive the separating hyperplanes by means of aforesaid algorithm. In the first problem, we determine randomly some arbitrary points in two classes of A and B which are approximately separated from each other linearly based on given MATLAB code in the “Appendix A” (here, we created 150 points for class A and 100 points for class B). These data are produced randomly within the interval $[-\,50,50]$. In Fig. 2, the given separating hyperplane has been shown by means of rendering Par $\nu$-SVRC$^+$ with red color and also the parametric margin hyperplane are indicated by blue and violet color. The accuracy rate of separating in this problem is $99.61\%$.

It is noted that by means of MATLAB code the problems with large-scale size are produced and the separating hyperplanes are derived by implementing the Par $\nu$-SVRC$^+$.

The average accuracy of separation is approximately $99\%$.

Fig. 2

Classification results of linear Par $\nu$-SVRC$^+$ on generated dataset

In another example, Ripleys synthetic standard data set have been adapted (Ripley 1996). These data comprise of 250 data samples out of which 125 data are placed in class of A and the next 125 of them in class B and they are not linearly separated (see Fig. 3). In Fig. 3 the separating hyperplane has been shown by red color. Likewise, the parametric margin hyperplanes, which have been derived by rendering this program, are identified by blue and violet dotted line. The accuracy rate of separating in this problem is $84.80\%$.

Fig. 3

Classification results of linear Par $\nu$-$\hbox {SVRC}^+$ on Ripleys dataset

In the following, demonstrate applications to two real data expression profiles for lung cancer and colon tumor. Lung cancer data set was used by Hong and Young to show the power of the optimal discriminant plane even in ill-posed settings. Applying the KNN method in the resulting plane gave $77\%$ accuracy (Hong and Yang 1991). Colon tumor data set contains 62 samples collected from colon-cancer patients. Among them, 40 tumor biopsies are from tumors (labeled as “negative”) and 22 normal (labeled as “positive”) biopsies are from healthy parts of the colons of the same patients. 2000 out of around 6500 genes were selected (Alon et al. 1999).

When we apply our method on these data sets we gain an accuracy of $87.50\%$ for lung cancer and $87.38\%$ colon tumor while MATLAB Quadprog gain 85.83% and $84.29\%$, respectively. In Fig. 4 accuracy between the proposed method and the method of quadratic programming in MATLAB can be seen.

Fig. 4

Performance comparisons of lung cancer and colon tumor data across Par $\nu$-SVR and Par $\nu$-$\hbox {SVRC}^+$ methods

Table 1 Comparison of linear SVM, Par $\nu$-SVR and Par $\nu$-$\hbox {SVRC}^+$ on benchmark data sets

Table 2 Comparison of non-linear SVM, Par $\nu$-SVR and Par $\nu$-$\hbox {SVRC}^+$ on benchmark data sets

To further test the performance of Par $\nu$-SVRC$^+$, we run this algorithm on several UCI benchmark data sets (Lichman 2013). We tested 13 UCI benchmark data sets, which are shown in Tables 1 and 2. To accelerate model selection, we tuned a set comprising randomly $20\%$ of the training samples to select optimal parameters.

As we noted in the discussion on Par $\nu$-SVRC$^+$, the generalization errors of the classifier depend on the values of the kernel parameter $\gamma$, the regularization parameter C, and parameter $\nu$. Tenfold cross-validation was used to evaluate the performance of the classifier and estimate the accuracy. Tenfold cross-validation followed these steps

• The datasets were divided into ten disjoint subsets of equal size.

• The classifier was trained on all the subsets except one.

• The validation error was computed by testing it on the omitted subset left out.

• This process was repeated for ten trials.

Tables 1 and 2, respectively, give the average accuracies, times, and kernel operations, of this method in the linear and nonlinear case of classification. In Par $\nu$-SVR we solve a constrained convex quadratic programming problem by using dual problem with MATLAB Quadprog optimization toolbox (the bolded values in the Tables 1, 2 represent highest accuracies obtained by corresponding classifiers).

In Table 1, we see that the accuracy of our linear Par $\nu$-SVRC$^+$ is higher than linear Par $\nu$-SVR on various datasets. For example, for House-votes dataset the accuracy of our Par $\nu$-SVRC$^+$ is 95.65% , while the accuracy of SVM is 94.96% and Par $\nu$-SVR is 78.62%. Beside on the another example, for Sonar datasets the accuracy of our Par $\nu$-SVRC$^+$ is 77.01% , while the accuracy of SVM is 79.98% and Par $\nu$-SVR is 70.72%. Although SVM win in the accuracy, so our method is still winner in time. In other datasets, we also obtain similar results. Our Par $\nu$-SVRC$^+$ is much far faster than the original SVM and Par $\nu$-SVR, indicating that the unconstrained optimization technique can improve the calculation speed. It can also be see that our Par $\nu$-SVRC$^+$ is the fastest on all of datasets. The results in Table 2 are better condition in time and accuracy with that appeared in Table 1, and therefore confirm the above conclusions further.

As mentioned above, we have solved an unconstrained convex minimization problem instead of a constrained convex one. The Experimental results in Tables 1 and 2 demonstrate the high speed, efficiency and accuracy of the proposed method.

5 Concluding remarks

In this paper, we presented a new idea for solving the Par $\nu$-SVR classification problem. By using 2-norm of the slack variables in the objective function of (4) and the KKT conditions associated with this obtained problem, we converted the constrained quadratic minimization problem (4) into an unconstrained convex problem. Since the objective function of Par $\nu$-SVRC$^+$ is an $LC^1$ function, the generalized Newton method was proposed for solving it. In this way, we have derived much faster and accurately method than Par $\nu$-SVR which solves a constrained quadratic problem. The experimental results on several UCI benchmark data sets have shown that this method has high efficiency and accuracy both in the linear and nonlinear case.

Matlab code

% Generate random M,N;

%Input: m1,m2 n; Output:M N

pl=inline(’(abs(x)+x)/2’);

M=rand(m1,n); M=100*(M-0.5*spones(M));

M(:,2)=M(:,1)+1*ones(m1,1)+100*rand(m1,1)+100*rand(m1,1);

N=rand(m2,n); N=100*(N-0.5*spones(N));

N(:,2)=N(:,1)-1*ones(m2,1)-100*rand(m2,1)-100*rand(m2,1);

uu=5*rand(3,n); uu1=uu;uu1(:,2)= uu1(:,1)+1*ones(3,1);

uu2=uu;uu2(:,2)= uu2(:,1)-1*ones(3,1);

M=[M;uu1;10 0]; N=[N;uu2;30 -20];m1=m1+4;m2=m2+4;m=m1+m2;

xM=[-50:40*rand: 50];yM=xM+1;xN=[-50:20*rand:50];yN=xN-1;

plot(M(:,1),M(:,2),’oblack’,N(:,1),N(:,2),’*bl’);

axis square

format short ;[m1 m2 n toc],[max(M(:,1)) min( N(:,1))]