1 Introduction

Abiding by the structural risk minimization (SRM) principle [1], support vector machine (SVM) [1, 2] with its transformations such as C-SVC [3] and ν-SVC [4], being useful classification tools for supervised machine learning, have already obtained many achievements in pattern classification problems [5–11]. In the SVMs, a quadratic programming problem (QPP) often needs to be solved, which spends much time on getting its solution. In order to speed up the learning process, on the one hand, several approaches such as Chunking [12], SMO [13], and SOR [14] were proposed to accelerate for solving the QPPs appeared in the SVMs. Further, some softwares have been built based on these approaches, such as SVMlight [15] and Libsvm [16]. On the other hand, different from directly solving the QPPs appeared in the SVMs, the proximal support vector machine (PSVM) [17] was proposed by modifying the inequality constraints QPP of the SVM to the equality constraints QPP, which makes the learning speed of the PSVM be much faster than the SVMs’ by solving a system of linear equations in the learning process. In addition, the SRM principle vanishes, whereas a new principle is obtained in the PSVM which be interpreted as regularized mean square error optimization (MSE) [18].

Different from maximizing the margin between two parallel hyperplanes in the SVMs, Hao et al. [19] proposed a parametric-margin ν-support vector machine (par-ν-SVM), which maximizes a parametric-margin by two nonparallel separating hyperplanes. Due to this parametric-margin, the par-ν-SVM suits for many cases, especially the case of heteroscedastic noise [19]. The par-ν-SVM already has some excellent numerical results [19, 20], and there are some achievements based on par-ν-SVM [21–23]. Though computing results [19, 20] show that the par-ν-SVM is better than the ν-SVC on the generalization ability, the scale of the QPP in the par-ν-SVM is the same as the ν-SVC, which limits the learning speed and restricts the application of the par-ν-SVM to the large-scaled problems.

In this paper, in the spirit of the PSVM, we improve the inequality constraints QPP of the par-ν-SVM to equality one and propose a novel and fast proximal parametric-margin support vector classifier (PPSVC). The main characteristics of our PPSVC are: (1) different from maximizing the parametric-margin in the par-ν-SVM, the PPSVC maximizes a novel proximal parametric-margin between two nonparallel proximal hyperplanes; (2) in the PPSVC, only a small system of linear equations needs to be solved, which significantly speeds up the learning process; (3) for nonlinear PPSVC, the reduced kernel technique [24] is introduced, which made our nonlinear PPSVC can deal with 1 million data with faster learning speed. In addition, we investigate the application of our PPSVC on real text categorization (TC) problems.

This paper is organized as follows. In Sect. 2, a brief review of the par-ν-SVM is given. Our linear and nonlinear PPSVC are formulated in Sect. 3, and experiments on several artificial and benchmark datasets are arranged in Sect. 4. In Sect. 5, we investigate the performance of the PPSVC on TC problems. Finally, Sect. 6 gives the conclusions.

In this paper, vector will be column vector on the absence of pointing out. Given the training set \(\{(x_i,y_i)|x_i\in R^n,y_i=\pm1,i=1,\ldots,l\}\), we use two matrices A and D instead of it. The ith row of A is the sample x i , and D is a diagonal matrix where d ii  = y i . ξ is a slack vector, and e indicates a vector of ones of appropriate dimension, and so do the identity matrix I. w, b, c, d, ρ are used to define the hyperplane in different methods, where \(w,c\in R^n\) and \(b,d,\rho\in R\). \(C,\nu\in R\) are positive parameters. There is a form of vector compares with vector, that means comparing all its elements with the corresponding ones. \(|\cdots|\) denotes the absolute value, and \(||\cdots||\) is the \(L_2\) norm.

2 Review of par-ν-SVM

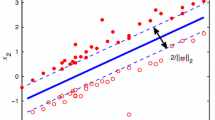
Par-ν-SVM [19] classifies samples by two nonparallel separating hyperplanes \(w^\top x+b=\pm(c^\top x+d)\), and the classification hyperplane is half of them (see Fig. 1a), by solving the following inequality constraints QPP

$$ \begin{array}{*{20}l} {\mathop {\min }\limits_{{w,b,c,d,\xi }} } \hfill & {\frac{1}{2}w^{ \top } w + C( - \nu (\frac{1}{2}c^{ \top } c + d) + \frac{1}{l}\xi ^{ \top } e)} \hfill \\ {{\text{s}}{\text{.t}}{\text{.}}} \hfill & {D(Aw + eb) \ge Ac + ed - \xi ,\xi \ge 0,d \ge 0} \hfill \\ \end{array} $$
(1)
Fig. 1
figure 1

Geometric interpretations of the par-ν-SVM and our PPSVC. The cross stands for the negative class sample, and the triangle stands for the positive class sample. The black real lines \(w^\top x+b=0\) correspond to the classification hyperplanes. The nonparallel dash lines \(w^\top x+b=\pm(c^\top x+d)\) (or \(w^\top x+b=\pm(1+c^\top x+d)\)) determine the parametric-margin (or the proximal one) \(|c^\top x+d|/||w||\) and \(|1+c^\top x+d|/||w||\), respectively. a par-ν-SVM, b PPSVC

Full size image

After solving the dual QPP of the problem (1) by the Karush–Kuhn–Tucker (KKT) [25] conditions, the classification hyperplane can be described as \(f(x)=w^\top x+b\).

Compared with the ν-SVC, the par-ν-SVM replaces ρ with \(c^\top x+d\) with respect to the support vectors, which are defined as the samples on two separating hyperplanes or with a positive slack vector ξ. By appropriately adjusting the parameters C and ν, the par-ν-SVM can get the optimal classifier with the idea of maximizing the parametric-margin \(|c^\top x+d|/||w||\) between the support vectors and the classification hyperplane. The margin where the definition differs in the ν-SVC has been parameterized to a trapezoid region \(|c^\top x+d|/||w||\). Thus, the par-ν-SVM turns into a parametric insensitive model and is useful especially when the noise is heteroscedastic [19].

Here, we point out that (i) in the par-ν-SVM, \(c^\top c+d\) optimized in (1) is an approximation of the parametric-margin \(|c^\top x+d|/||w||\) and (ii) in the par-ν-SVM, it leads to solve a dual QPP with l variables, which will be time-consuming on the large-scaled dataset.

3 The PPSVC formulation

3.1 Linear PPSVC

Similar to the par-ν-SVM, our PPSVC also determines a classification hyperplane \(w^\top x + b = 0\). However, different from maximizing the parametric-margin in par-ν-SVM, we introduce a proximal parametric-margin in our PPSVC. To measure the proximal parametric-margin, the proximal hyperplanes are defined as \(w^\top x+b = \pm(1+c^\top x+d)\), and then, we define the sum of the distances between the training samples of each class on the corresponding proximal hyperplane and the classification hyperplane as the proximal parametric-margin. Precisely, we have the following definition.

Definition

Suppose N + and N − are index sets of the positive and negative inputs, respectively. The proximal parametric-margin M pp is defined as

$$ M_{\rm pp}={\frac{|w^{\top} X_++b|}{||w||}}={\frac{|w^\top X_-+b|}{||w||}} $$

where \(w\in R^n, b\in R\) and X  ±  are the positive and negative inputs, \(|\cdot|\) is the absolute value.

By setting \(w^\top X_\pm+b=\pm(1+c^\top X_\pm+d)\), where \(c\in R^n\) and \(d\in R,\,M_{\rm pp}\) can be written as

$$ M_{\rm pp}:={\frac{|1+c^\top X_\pm+d|}{||w||}} $$

Using the idea of maximizing the above proximal parametric-margin M pp (see Fig. 1b), we get the following optimization problem

$$ \begin{array}{*{20}l} {\mathop {\min }\limits_{{w,b,c,d,\xi }} } \hfill & {\frac{1}{2}(w^{ \top } w + b^{2} ) + C\left( {\frac{{ - \nu }}{2}\left( {c^{ \top } c + d^{2} } \right) + \frac{1}{{2l}}\xi ^{ \top } \xi } \right)} \hfill \\ {{\text{s}}{\text{.t}}{\text{.}}} \hfill & {D(Aw + eb) = Ac + ed + e - \xi } \hfill \\ \end{array} $$
(2)

where C and ν are positive parameters.

Now we discuss the difference of the primal problems between the par-ν-SVM and our PPSVC: first, in our PPSVC, an extra regularization term b 2 is added in the objective function the same as was done in [17, 26–28], which makes the QPP stable and has a global optimal solution on b; second, in the spirit of proximal hyperplanes instead of separating hyperplanes [17], the constraints in (1) is modified from inequality to equality, and e is added in the constraints, this strategy leads our method to be more theoretically sound, avoiding two proximal hyperplanes invariably intersect at zero; third, the remanent term in the objective function (1) is modified from 1-norm formulation to 2-norm, for the norm formulation should be uniform and this helps us to get the solution from solving a system of linear equations.

The solution of the problem (2) can be obtained by introducing the KKT conditions [25] as follows

$$ w=A^{\top}D\alpha $$
(3)
$$ b=e^\top D\alpha $$
(4)

where \(\alpha\in R^l\) is the Lagrange multiplier, and an explicit expression of α

$$ \alpha=\left(DHH^\top D-{\frac{1}{C\nu}}HH^{\top}+{\frac{l}{C}}I\right)^{-1}e $$
(5)

where \(H=(A,e)\in R^{l\times (n+1)}\).

The solution of the Eq. (5) entails the inversion of l × l matrix, which may lead expensive time cost when encountering large-scaled dataset. Here, if necessary, we use the Sherman–Morrison–Woodbury (SMW) formula [29] for matrix inversion as was done in [17, 30, 31]. By defining \(U=(DH,{\frac{1}{\sqrt{C\nu}}}H), V=(H^\top D;-{\frac{1}{\sqrt{C\nu}}}H^\top)\), one gets

$$ \alpha=\left({\frac{l}{C}}I+UV\right)^{-1}e ={\frac{C}{l}}\left(I-U\left({\frac{l} {C}}I+VU\right)^{-1}V\right)e $$
(6)

The above expression involves the inversion of a matrix with the order (2n + 2) × (2n + 2), and one can easily get the solution by solving a system of linear equations, thus avoids solving a large-order system of linear equations and completely works out the classification problem.

The class \(\hat{y}\) of a new sample \(\hat{x}\) is predicted by the final decision function as follows

$$ \hat{y}={\text{sign}}\{w^{\top}\hat{x}+b\}={\text{sign}}\{(\hat{x}\,1)H^{\top} D\alpha\} .$$
(7)
figure aa

3.2 Nonlinear PPSVC

In order to extend the linear PPSVC to the nonlinear one, we project the input space to its feature space by the kernel function \(K(\cdot,\cdot)\) as in [17]. In the feature space, likewise, the classification hyperplane \(f(x)=K(x,A^\top)Dw+b\) is obtained by altering the equality constraints QPP (2) into its kernel version as follows

$$ \begin{array}{*{20}l} {\mathop {\min }\limits_{{w,b,c,d,\xi }} } \hfill & {\frac{1}{2}(w^{ \top } w + b^{2} ) + C\left( {\frac{{ - \nu }}{2}(c^{ \top } c + d^{2} ) + \frac{1}{{2l}}\xi ^{ \top } \xi } \right)} \hfill \\ {{\text{s}}{\text{.t}}{\text{.}}} \hfill & {D(K(A,A^{ \top } )Dw + eb) = K(A,A^{ \top } )c + ed + e - \xi } \hfill \\ \end{array} $$
(8)

Similar to the linear PPSVC, we get an explicit expression for the Lagrange multiplier \(\beta\in R^l\) in terms of training data K and D by the KKT conditions [25] as follows

$$ w=DK^{\top}D\beta $$
(9)
$$ b=e^\top D\beta $$
(10)

and

$$ \beta=\left(DKK^{\top} D+Dee^{\top} D-{\frac{1}{C\nu}}KK^{\top}-{\frac{1} {C\nu}}ee^{\top}+{\frac{l}{C}}I\right)^{-1}e $$
(11)

where \(K:=K(A,A^\top)\).

Define G = (K, e), then we need to solve the following

$$ \beta=\left(DGG^{\top} D-{\frac{1}{C\nu}}GG^{\top}+{\frac{l}{C}}I\right)^{-1}e $$
(12)

We can straightly get the solution of the inverse matrix in (12) but cannot get a simple formula similar to (6) in the linear PPSVC, because K is a l × l matrix instead of A with l × n in the linear PPSVC, where generally n ≪ l. However, if necessary, the reduced kernel technique [24] can be utilized to reduce the order l × l of the kernel K to a much smaller order \(l\times \bar{l}\), where \(\bar{l}\ll l\). Such reduced kernel technique not only makes most large problems tractable, but also avoids data overfitting [24]. While the reduced kernel technique is used in our nonlinear PPSVC, the SMW formula can be utilized by defining \(S=(D\bar{G},{\frac{1}{\sqrt{C\nu}}}\bar{G}), T=(\bar{G}^\top D;-{\frac{1}{\sqrt{C\nu}}}\bar{G}^\top)\), where \(\bar{G}=(\bar{K},e)\) and K in (11) is replaced by a \(l\times \bar{l}\) matrix \(\bar{K}\) which is the result of the reduced kernel technique, and then

$$ \beta=\left({\frac{l}{C}}I+ST\right)^{-1}e ={\frac{C}{l}}\left(I-S\left({\frac{l}{C}}I+TS\right)^{-1}T\right)e $$
(13)

In short, whether we obtain the Lagrange multiplier β by using some techniques or straightly solving the equation (12), the solution can always be obtained by solving a system of linear equations, where the difference in the order of this system of linear equations is l × l or \(\bar{l}\times\bar{l}\). The class \(\hat{y}\) of a new sample \(\hat{x}\) can be predicted by following

$$ \hat{y}={\text{sign}}\{K(\hat{x},A^{\top})Dw+b\}={\text{sign}}\{(K(\hat{x},A^{\top})\,1)G^{\top} D\beta\} $$
(14)
figure ba

4 Experimental results

In this section, we analyze the performance of our PPSVC. We compared our implementation with the par-ν-SVM and ν-SVC on several artificial and public available benchmark datasets. All the methods were implemented on a PC with an Intel P4 processor (2.5 GHz) with 2 GB RAM. The par-ν-SVM and PPSVC were implemented by Matlab (2008a) [32], and the ν-SVC was implemented by Libsvm(2.9) [16]. In the experiments, the system of linear equations in the PPSVC is solved by the operator “\” in Matlab, to be more specific, the linear and nonlinear PPSVC are summarized in Algorithms 1 and 2, respectively. To realize our PPSVC, we give its native Matlab code in the following “Code 4.1”. From Code 4.1, we can see that our PPSVC only consists of 5 lines of native Matlab code, that is to say, it is very easy to implement.

figure ca

4.1 Artificial examples

Firstly, we simulated our PPSVC on an artificial dataset. The implementations of the nonlinear ν-SVC, par-ν-SVM and our PPSVC with Gaussian kernel [33] K(x i , x j ) = exp{− μ||x i  − x j ||} on a two-dimensional artificial dataset were given. The positive class samples consist of uniform points satisfying \(x_1\in[-\pi/2,2\pi]\), \(\sin x_1-0.25\leq x_2\leq\sin x_1+0.25\), while the negative class samples consist of uniform points satisfying \(x_1\in[-\pi/2,2\pi]\), \(0.6\sin(x_1/1.05+0.4)-1.35\leq x_2\leq0.6\sin(x_1/1.05+0.4)-0.85\), where \(x=[x_1,x_2]^\top\), either the margin corresponding to the ν-SVC or the (proximal) parametric-margin corresponding to the par-ν-SVM and PPSVC depends on the input location. Figure 2a, c, e shows the one-run results of these four methods. Obviously, the classification hyperplanes of these classifiers get the similar results. However, our PPSVC obtains a pair of more suitable proximal hyperplanes according to the input data distribution compared with the others, while the pair of separating hyperplanes either in the ν-SVC or in the par-ν-SVM separates the class samples well but cannot catch the input data distribution especially the positive class samples. This indicates that the proposed PPSVC has an effective proximal parametric-margin to determine the flexible margin.

Fig. 2
figure 2

Results of the nonlinear ν-SVC, par-ν-SVM, and PPSVC on artificial dataset [(a, c, e) without noise, and (b, d, f) with noise]

Full size image

Secondly, we implemented these methods on the above artificial example with some noise samples. Figure 2b, d, f shows the one-run results of these three methods. It can be seen that the result of our PPSVC in Fig. 2f is similar with that appeared in Fig. 2e, while the par-ν-SVM cannot catch the input data distribution, which indicates our PPSVC has a better interference immunity on the noise points than the others.

4.2 Benchmark datasets

To further test the performance of our PPSVC, we implemented it on several public available datasets compared with the par-ν-SVM and ν-SVC. For linear classifiers, the optimal parameter C in the par-ν-SVM and PPSVC was selected from the set of \(\{10^i|i=-2,-1,\ldots,6\}\), and the parameter ν in the ν-SVC, par-ν-SVM and PPSVC from \(\{0.1,0.2,\ldots,0.9\}\). For nonlinear classifiers, the Gaussian kernel K(x i , x j ) = exp{−μ||x i  − x j ||} was used and its optimal parameter μ was selected from \(\{2^i|i=-9,-8,\ldots,4\}\). The best results are marked bold. Tables 1 and 2 show the average classification accuracies of these methods with linear and nonlinear classifiers on several UCI datasets [34] by standard ten-fold cross validation methodology, respectively. Tables 1 and 2 indicate that our PPSVC is much better than the par-ν-SVM on many of the datasets considered in terms of classification accuracy. It also reveals that our PPSVC performs comparable with the ν-SVC. Tables 1 and 2 also show the optimal values of the parameters for these methods. From Tables 1 and 2, we can see that the value range of μ from (0,1) in our PPSVC always can achieve better classification results.

Table 1 Classification accuracy with corresponding parameter(s) for linear classifiers
Full size table
Table 2 Classification accuracy with corresponding parameters for Gaussian kernel classifiers
Full size table

In order to study the training time of our PPSVC, we also conducted experiments on David Musicant’s NDC Data Generator [35] to get a clear picture of how the computing time of all these methods scale with respect to number of samples. For experiments with NDC datasets, we selected the samples from 102 to 106 as the training set and fixed penalty parameters of all methods to be one (i.e., C = 1, ν = 0.1 and μ = 0.0001). Table 3 shows the CPU time of the par-ν-SVM, ν-SVC and our PPSVC on these NDC datasets for linear and nonlinear classifiers. The reduced kernel technique was used in the nonlinear PPSVC. When the dataset size l was increased, the kernel size \(\bar{l}\) was decreased. Table 3 indicates that our PPSVC has a much faster learning speed compared with the par-ν-SVM and ν-SVC, which the par-ν-SVM spends so much time to get the classifier and is terminated when learning more than 4,000 samples because of out of the memory. Although the ν-SVC is as fast as the PPSVC on small-scaled datasets (no more than 1,000), it is too slow to learn a classifier on large-scaled datasets, especially 1 million samples. In addition, the linear or nonlinear PPSVC, whose solution is obtained by solving a system of linear equations, can deal with 1 million samples less than 10 s.

Table 3 CPU time cost for the ν-SVC, par-ν-SVM and PPSVC
Full size table

5 Application to text categorization

In this section, we further apply our PPSVC to text categorization (TC) problem [36, 37]. Automatic TC is a supervised machine learning problem which involves training a classifier with a labeled large text corpus. After getting the classifier, one can use it to predict the labels of unlabeled documents. Each document may have several labels or one label or no label at all in the corpus. Often, a binary classifier learns for each category to form a complete TC system. We perform experiments on two well-known corpora in TC research, reuters-21578 [38] and 20 Newsgroups (20NG) [39]. To generate a TC classifier, text preprocessing is an important stage so we introduced first as below, and the corpora we used and the experiment results were replied all in this section.

5.1 Document representation

Documents which have the title and content typically are string of characters and have to be transformed into a representation suitable for the learning algorithm of classifier. Here, we use a simple representation ‘bag of words’ which means a document be represented as a numerical vector, and the element of the vector denotes a corresponding word in the document. This transformation involves several steps like dimensionality reduction, feature subset selection, and term weighting. In text preprocessing, first we use a stop word list [40] to filter many useless words in the text content and then perform words stemming using Porter stemmer algorithm [41]. After dimensionality reduction, a feature dictionary is built by χ2 value [42] which measures the independence between a feature t and category c, given by

where A,  B,  C, and D above in the table is the frequency of feature t occurrence or not, and N is the number of the training documents.

Once obtained the feature dictionary, the dimension of the data samples is set to the number of the words used in this dictionary. For each document, the numerical value of a word in the feature dictionary is calculated by log TFIDF [43] as follows

$$ w_{td}=\log_2(tf_{td}+0.5)*\log_2(N/(D_{td}+0.01)) $$
(15)

where tf td is the occurrence of feature t in document d,  D td is the number of document d containing the feature t, the constant 0.5 or 0.01 is used to avoid tf td or D td equals 0.

In our experiments, we scale this value w td using cosine normalization as follows

$$ w_{td}^*={\frac{w_{td}}{\sqrt{\sum_{t=1}^{k}w_{td}^2}}} $$
(16)

where k is the number of feature selected in feature dictionary.

After this step, a corpus will be transformed to a numerical matrix as the dataset treated in Sect. 2.

5.2 Data collections

David Lewis et al. applied a dataset named reuters-21578 [38] where the documents came from the reuters newswire before the year 2007. There are 21,578 news articles each belongs to one or more categories through different points of view. We split the dataset to 120 categories (different from the description 135 topics in the dataset) by the tag <TOPICS>. If one document belongs to two or more labels between the beginning <TOPICS> and the end <\TOPICS>, then it will be used many times if needed just as it has many copies each belongs to one of the categories. In our experiments, the top 10 categories having highest number of documents (9,555 documents totally) were used. We extracted the title and the content in each document and ignored other artificial information such as several tags. After word stemming and stop word removal, the χ2 measure helped us to select the top 300 words as features to build the feature dictionary, and then, we got the numerical representation of each document through the feature value computation method mentioned in Sect. 5.1.

The 20Newsgroups (20NG) corpus [39], applied by Lang, contains 19,952 articles (after deleting several which have no content) which came from the Usenet newsgroups evenly distributed to 20 categories. Yet, ten categories were used in the experiment and the process described in Sect. 5.1 was executed the same as reuters-21578, where the difference was the size of feature dictionary extended to 500, for this corpus had larger vocabulary and words that had more meanings.

5.3 Evaluation methodology

We use the standard information retrieval metrics: precision and recall [44], to evaluate each binary classifier. Table 4 shows the confusion matrix, and the criteria can be obtained from it. The formulas are

$$ {\text{Precision}}={\frac{{\text{TP}}}{{\text{TP\,+\,FP}}}},\quad {\text{Recall}}={\frac{{\text{TP}}}{{\text{TP\,+\,FN}}}} $$
(17)
Table 4 Confusion matrix
Full size table

Neither precision nor recall is meaningful in isolation of the other [44]. Therefore, we use precision-recall breakeven point (BEP) and F 1 measures to compare our PPSVC with other classifiers. BEP is the point where precision is equal to recall and is often determined by calculating the arithmetic mean of them. BEP performance metric is to be computed for each category separately and the overall performance of a classifier can be found with the help of macroaverage and microaverage of BEP. Macroaverage gives equal weight to each category, while microaverage gives equal weight to each document. F 1 is defined as harmonic mean of the criteria, and its formula is

$$ F_1={\frac{2*{\text{Precision}}*{\text{Recall}}}{{\text{Precision}}+{\text{Recall}}}} $$
(18)

5.4 Experimental results

All the text categorization steps discussed in Sect. 5.1 were performed in JDK7.0 platform, and we tested the performance of ν-SVC and our PPSVC using Matlab 2008a [32] after getting the numerical datasets. From Table 3, we knew the par-ν-SVM’s time cost was expensive, whereas this is sensitive to text categorization, so we did the experiment on ν-SVC and our PPSVC merely. Here, the linear forms were used, because this is often more effective than the nonlinear forms when encountering large number of features especially TC problem [45]. In fact, it is known that the training data with large number of features are linear separability.

For binary classifier applying to TC problem which has n categories, n*(n + 1)/2 binary classifiers are often generated and one may use the results in some way like ‘voting strategy’ in predicting process. We followed this idea and made every training set balance for binary classification. Table 5 shows the BEP performance of binary classifiers on datasets reuters-21578 and 20NG respectively, and Table 6 shows the average of BEP and F 1. Table 5 indicates that our PPSVC achieves higher BEP rating than ν-SVC on many binary classifiers (14/20), and Table 6 indicates the effectiveness of our PPSVC, especially on the dataset reuters-21578.

Table 5 BEP performance of 20 largest categories from reuters-21578 and 20NG
Full size table
Table 6 Average BEP and F 1 performance on reuters-21578 and 20NG
Full size table

6 Conclusions

In this paper, a novel and fast proximal parametric-margin support vector classifier (PPSVC) is proposed. In the PPSVC, we maximize a novel proximal parametric-margin by solving a small system of linear equations, which makes our PPSVC has a much faster learning speed compared with the par-ν-SVM. We evaluated the PPSVC in both generalization ability and computational time on several artificial and public available datasets. Computational comparisons show the PPSVC obtains a comparable classification accuracy with several state-of-art SVMs with a very fast learning speed, particularly it handles the large-scaled datasets better than other SVMs. We further investigated the applications of our PPSVC on TC problems. Comparisons with the SVM on two benchmark datasets reuster-21578 and 20NG demonstrate the practicability and effectiveness of our PPSVC according to BEP and F 1 measures. Since our PPSVC has the advantages both on generalization ability and learning speed, the extension on multi-class classification problems and other practical application problems will be the avenue of our future work.