1 Introduction

In most scheduling literature, the processing time of jobs was often assumed to be fixed and known before the processing (Pinedo 2002). However, in many practical environments, the workers can acquire experience and the production efficiency improves continuously with time after they repetitiously operate the same or similar tasks. As a result, the later a job is processed, the shorter its processing time. This phenomenon is so-called the “learning effect” in the literature (Biskup 1999). Biskup (1999) was the pioneer introducing the learning effect into scheduling problems, where a position-dependent learning model was developed, and since then the learning effect has received extensive discussion in the scheduling field (Mosheiov and Sidney 2003; Janiak and Rudek 2009; Teyarachakul et al. 2011). In particular, much research on the batch scheduling problems with the learning effect can be found in the last decade (Yang and Kuo 2009; Kumar and Tan 2015; Paul et al. 2015; Tan et al. 2016; Tan and Carrillo 2017). However, all these studies focus on the parallel-batching scheduling problems. Whereas the other major type of batch scheduling problems, the serial-batching problems, with learning effect are relatively unexplored.

Our study was motivated by a practical production scenario of the aluminum-making process in an aluminum plant. In this particular scenario, cylindrical aluminum ingots are processed on an extrusion machine, which is a batch processing machine that processes batches of aluminum ingots for the extrusion process in the form of serial-batching, i.e., one after another in the same batch. Before processing each batch of aluminum ingots, a time-dependent linear setup time is required. The production efficiency improves continuously over time, and the processing time of an aluminum ingot depends on its processing position or sequence in a batch. That is, if an aluminum ingot is processed in a later position, then it takes less time to complete the extrusion process. Therefore, the processing times of aluminum ingots can be modeled as a decreasing function of their positions. In this production scenario, both single-machine and parallel-machine configurations are required for different production demands. Thus, in this paper we focus on both single-machine and parallel-machine scheduling situations according to the actual production requirements.

There have been many studies on the problems of single-machine scheduling with the learning effect. Cheng and Wang (2000) studied a single-machine scheduling problem where the job processing times decrease following a volume-dependent piecewise linear learning function, and the objective was to minimize the maximum lateness. Wang et al. (2008) considered a single-machine scheduling problem with the time-dependent learning effect, in which a job’s processing time is assumed to be a function of the total normal processing time of all the other jobs scheduled in front of the job, and the objectives were to minimize the weighted sum of completion times, the maximum lateness, and the number of tardy jobs. Lee et al. (2010) investigated a single-machine problem with the learning effect and release times, and the objective was to minimize the makespan. A branch-and-bound algorithm was developed to derive the optimal solution. More recent papers which have addressed single-machine scheduling problems with learning effect include Lu et al. (2012), Zhu et al. (2013), Wang et al. (2014a), Wang and Wang (2014).

In addition to single-machine scheduling problem, some researchers also focus on the parallel-machines scheduling with the learning effect. Mosheiov (2001) studied parallel-machine scheduling problems flow-time minimization with a learning effect, and the objective was to minimize the flow-time. Eren (2009) investigated the bicriteria parallel machine scheduling problem with a learning effect of setup and removal times, and the objective function of the problem was to minimize of the weighted sum of total completion time and total tardiness. Three heuristic approaches were proposed to solve large-size problems. Eren and Güner (2009) also studied m-parallel machine scheduling problem for minimizing the weighted sum of total completion time and total tardiness based on the learning effect. Some other works on parallel-machine scheduling with learning effect can be found in Hsu et al. (2011), Okołowski and Gawiejnowicz (2010), etc. Although the scheduling problems under single-machine and parallel-machine settings have been separately studied, these two settings are rarely considered simultaneously. Meanwhile, the previous studies mainly focused on the general processing jobs way, and few papers studied the special processing way, e.g., serial-batch processing according to the practical production scenario.

The group scheduling problems with the learning effect are similar to the problem studied in this paper. In the group scheduling problems, the jobs are classified into certain groups in advance based on similar production requirements. Yang and Chard (2008) studied a group scheduling problem with learning and forgetting effects, and the objective was to minimize the total completion time of jobs. Three basic models were developed and some comparisons were made through computational experiments to analyze the impact of effects on learning and forgetting on this problem. Pan et al. (2014) studied an integrated single machine group scheduling problem, where the effects of learning and forgetting and preventive maintenance planning were simultaneously considered. More recent papers on the group scheduling problems with the learning effect include Bai et al. (2012), Huang et al. (2011), and Wang et al. (2012, 2014b), etc. Although some similarity can be found between the serial-batching problems and group scheduling problems, that is, the jobs in a batch or group are processed one after another. However, there are several significant differences between them, as concluded in Pei et al. (2015a).

We have also studied the serial-batching scheduling problems with learning effect in the past research, while many key significant differences can be found in them. Different from Pei et al. (2017a), our paper only focuses on the learning effect, different argument jobs batching and jobs sequencing are obtained, and parallel-machine scheduling problems are studied and the hybrid VNS–GSA is proposed to solve them. Different from Pei et al. (2016), the machines are available all the time in this paper, and different learning effects are investigated. In addition, we also investigated the scheduling problems with the deteriorating jobs in the past research (Pei et al. 2015a, b, 2017b), and the deterioration phenomenon is also a typical characteristic during the practical production. We compare and contrast the related papers with our work in the following Table 1.

Table 1 Key comparisons on our previous paper, other related research, and current study
Full size table

The main contributions of this paper can be summarized as follows:

  1. (1)

    Both single-machine and parallel-machine scheduling problems with the learning effect using the processing way of serial-batching are studied, and the objectives of minimizing maximum earliness and total number of tardy jobs are considered in these two types of scheduling problems. The integer programming models for all the studied problems are constructed.

  2. (2)

    For the single-machine scheduling problems, structural properties are derived for the problems of minimizing maximum earliness and number of tardy jobs, and optimization algorithms are developed to solve them.

  3. (3)

    Based on the derived structural properties of the single-machine scheduling problems, the hybrid VNS–GSA algorithm is proposed to solve the parallel-machine scheduling problems with these two objectives.

The reminder of this paper is organized as follows. The notation and problem description are given in Sect. 2. The single-machine and parallel-machine scheduling problems are studied in Sects. 3 and 4, respectively. Finally, the conclusion is given in Sect. 5.

2 Notation and problem definition

The notation used in this paper is first described as Table 2.

Table 2 The list of the notation
Full size table

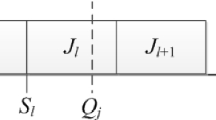
There is a given set of n non-preemptive jobs to be processed at time zero. Two types of scheduling problems are studied. In the first type of problem, all jobs are processed on a single serial-batching machine, while in the second one, all jobs are first assigned into parallel machines, and then the assigned jobs are processed on each machine with serial-batching processing way. For both single-machine and parallel-machine scheduling problems, the objectives to minimize maximum earliness and total number of tardy jobs are considered, respectively. The jobs are firstly partitioned into multiple serial batches on each serial-batching machine and then they are processed on the serial-batching machine. Serial batches require that all the jobs within the same batch are processed consecutively in a serial fashion (Xuan and Tang 2007), and the completion times of all jobs are equal to that of their belonged batch, which is defined as the completion time of the last job in that batch. The capacity of the serial-batching machine is defined as c, that is, the maximum number of jobs in a batch is equal to c, and each machine has the same capacity c in the parallel-machine scheduling problems. A time-dependent setup time is required before processing each batch. In this paper, we extend the application of Biskup’s model (Biskup 1999) in the serial-batching scheduling problem. The learning effect is reflected on the varying job processing time. Specifically, the actual processing time of \(J_i \) is defined as

$$\begin{aligned} p_{ir} =p_{\left[ r \right] } =p_i r^{a},\quad i,r=1,2,\ldots ,n \end{aligned}$$

where r is the position of \(J_i \), and a is the learning index of processing time and \(a\le 0\).

Moreover, as in Cheng et al. (2011), the batch’s setup time is also defined as a simple linear function of its starting time t, that is,

$$\begin{aligned} s=\theta t \end{aligned}$$

where \(\theta >0\) is the setup time’s deterioration rate.

We adopt \(E_{max} =\mathop {\max }\limits _{i=1,2,\ldots ,n} \left\{ {0,d-C_i } \right\} \) and \(\mathop \sum \nolimits _{i=1}^n U_i \) to denote the maximum earliness and total number of tardy jobs, respectively. All jobs have a common due date, where \(U_i =1\) if \(C_i >d\) and 0 otherwise. In the remaining sections of the paper, we use the three-field notation schema \(\alpha \left| \beta \right| \gamma \) introduced by Graham et al. (1979) to denote all the problems.

3 Single-machine scheduling problems

In this section, we firstly derive the completion time of each batch, which will be used in the problems with the objectives of minimizing maximum earliness and total number of tardy jobs. Then, the problems with the objectives of minimizing maximum earliness and total number of tardy jobs are studied in Sects. 3.1 and 3.2, respectively.

Lemma 1

For any given schedule \(\pi =\left( {b_1 ,b_2 ,\ldots ,b_f ,\ldots ,b_m } \right) \), the completion time of \(b_f \) in schedule \(\pi \) is

$$\begin{aligned} C\left( {b_f } \right) =\mathop {\sum }\limits _{k=1}^f \mathop {\sum }\limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop {\sum }\limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{f-k} \end{aligned}$$
(3.1)

where \(f=1,2,\ldots ,m\).

Proof

This lemma can be proved by the mathematical induction based on the number of batches. Firstly for \(f=1\), we have

$$\begin{aligned} C\left( {b_1 } \right) =s_1 +\mathop \sum \limits _{r=1}^{n_1 } p_{\left[ r \right] } =\mathop \sum \limits _{r=1}^{n_1 } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} . \end{aligned}$$

Thus, Eq. (3.1) holds for \(f=1\). Suppose for all \(2\le f\le m-1\), Eq. (3.1) is satisfied. We have

$$\begin{aligned} C\left( {b_f } \right) =\mathop \sum \limits _{k=1}^f \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{f-k}. \end{aligned}$$

Then, for the \(\left( {f+1} \right) \) th batch \(b_{f+1} \),

$$\begin{aligned} C\left( {b_{f+1} } \right)= & {} C\left( {b_f } \right) +s_{f+1} +\mathop \sum \limits _{r=1+{\sum }_{j=1}^f n_j }^{{\sum }_{j=1}^{f+1} n_j } p_{\left[ r \right] }\\= & {} \mathop \sum \limits _{k=1}^f \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{f-k}\nonumber \\&+\,\theta \mathop \sum \limits _{k=1}^f \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{f-k}\\&+\mathop \sum \limits _{r=1+{\sum }_{j=1}^f n_j }^{{\sum }_{j=1}^{f+1} n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir}\\= & {} \mathop \sum \limits _{k=1}^{f+1} \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{f+1-k}. \end{aligned}$$

Thus, Eq. (3.1) holds for \(C\left( {b_{l+1} } \right) \), and the lemma is proved by the induction. \(\square \)

3.1 Problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \)

In this section, we study the single-machine scheduling problem with the objective of minimizing the maximum earliness of all jobs. For this problem, all jobs are restricted to be completed no later than the common due date d, which is usually assumed in many previous works involving earliness (Yin et al. 2012), and otherwise if without this assumption each job may be trivially scheduled sufficiently late to avoid earliness cost. Hence, it should be \(d\ge t+{\sum }_{k=1}^m s_k +{\sum }_{i=1}^n p_i \), where t is the starting time of processing jobs. We denote the earliness of job \(J_i \) and the maximum earliness of all jobs as \(E_i =max\left\{ {0,d-C_i } \right\} \) and \(E_{max} =\mathop {\hbox {max}}\limits _{i=1,2,\ldots ,n} E_i \), respectively. Next, the model is given in Sect. 3.1.1, and then some structural properties are derived and an optimization algorithm is proposed to solve the problem based on the properties.

3.1.1 Mixed integer programming model for the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max}\)

$$\begin{aligned}&\hbox {Minimize} \,\,E_{max} \end{aligned}$$
(3.2)
$$\begin{aligned}&\hbox {Subject} \hbox { to}{:}\nonumber \\&\mathop \sum \limits _{i=1}^n y_{ik} \le c,\quad k=1,2,\ldots ,m \end{aligned}$$
(3.3)
$$\begin{aligned}&\mathop \sum \limits _{k=1}^m y_{ik} =1,\quad i=1,2,\ldots ,n\end{aligned}$$
(3.4)
$$\begin{aligned}&S\left( {b_{k+1} } \right) \ge C\left( {b_k } \right) \left( {1+\theta } \right) ,\quad k=1,2,\ldots ,m-1\end{aligned}$$
(3.5)
$$\begin{aligned}&d\ge t+\mathop \sum \limits _{k=1}^m s_k +\mathop \sum \limits _{i=1}^n p_i ,\end{aligned}$$
(3.6)
$$\begin{aligned}&C\left( {b_k } \right) -C\left( {b_l } \right) +Mz_{kl} -C\left( {b_k } \right) \left( {1+\theta } \right) -P\left( {b_k } \right) \ge 0,\quad k,l=1,2,\ldots ,m\end{aligned}$$
(3.7)
$$\begin{aligned}&y_{ik} ,z_{kl} =0\,or\,1,\quad k,l=1,2,\ldots ,m_i ,i,p=1,2,\ldots ,n \end{aligned}$$
(3.8)

The objective function (3.2) is to minimize the maximum earliness of all jobs. Constraint set (3.3) prohibits that the job number of any batch more than the machine capacity. Constraint set (3.3) guarantees that each job should be only assigned to one batch. Constraint set (3.4) makes sure that setup time is required before processing each batch. Constraint sets (3.6) ensures that all jobs are restricted to be completed no later than the common due date d in this studied problem. Constraint set (3.7) indicates that there is no overlapping situation between two continuous batches. Constraint set (3.8) defines the ranges of the variables.

3.1.2 The structural properties and the proposed optimization algorithm

The structural properties on the jobs sequencing and batching argument are proposed as follows.

Lemma 2

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \), there is an optimal schedule in which there are no idle times between any consecutive batches or consecutive jobs in the same batch, and the first batch \(b_1 \) starts at time t such that

$$\begin{aligned} t\left( {1+\theta } \right) ^{m}+\mathop \sum \limits _{k=1}^m \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}=d \end{aligned}$$
(3.9)

Then, the maximum earliness is

$$\begin{aligned} E_{max} =d-\frac{d-\mathop \sum \nolimits _{k=2}^m \mathop \sum \nolimits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \nolimits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}}{\left( {1+\theta } \right) ^{m-1}} \end{aligned}$$
(3.10)

Proof

Apart from satisfying the constraint that all jobs’ completion times should be no later than the common due date, they need to be completed as late as possible to minimize the maximum earliness. Hence, the completion time of the last batch should be just equal to the common due date. Similar to the proof of Lemma 1, it can be derived that

$$\begin{aligned} t\left( {1+\theta } \right) ^{m}+\mathop \sum \limits _{k=1}^m \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}=d. \end{aligned}$$

If there is any idle time between consecutive batches or consecutive jobs in the same batch, then the starting time t will be earlier and the maximum earliness will be increased. Thus, there should be no idle times in the optimal schedule. Then, we have

$$\begin{aligned} E_{max} =d-t\left( {1+\theta } \right) -\mathop \sum \limits _{r=1}^{n_1 } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} . \end{aligned}$$

Based on Eq. (3.9), it should be

$$\begin{aligned}&E_{max} =d-\left( {1+\theta } \right) \nonumber \\&\quad \quad \cdot \frac{d-\mathop \sum \nolimits _{r=1}^{n_1 } \mathop \sum \nolimits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-1}-\mathop \sum \nolimits _{k=2}^m \mathop \sum \nolimits _{r=1+\mathop \sum \nolimits _{j=1}^{k-1} n_j }^{\mathop \sum \nolimits _{j=1}^k n_j } \mathop \sum \nolimits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}}{\left( {1+\theta } \right) ^{m}}\\&\qquad -\mathop \sum \limits _{r=1}^{n_1 } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir}\\&\quad =d-\frac{d-\mathop \sum \nolimits _{k=2}^m \mathop \sum \nolimits _{r=1+\mathop \sum \nolimits _{j=1}^{k-1} n_j }^{\mathop \sum \nolimits _{j=1}^k n_j } \mathop \sum \nolimits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}}{\left( {1+\theta } \right) ^{m-1}}. \end{aligned}$$

The proof is completed. \(\square \)

Lemma 3

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \), if \(m\ge 2\), then the processing time of an arbitrary job in \(b_1 \) is no smaller than that in other batches.

Proof

Let \(\pi ^{*}\) and \(\pi \) be an optimal schedule and a job schedule. The difference between the two schedules is the pairwise interchange of these two jobs \(J_u \in b_1 \) and \(J_v \in b_p \), and \(J_u \) and \(J_v \) are assigned to the orders e and w in the optimal schedule \(\pi ^{*}\). \(\pi ^{*}=\left( {b_1 ,W_1 ,b_p ,W_2 } \right) \), \(\pi =\left( {\left( {\left( {b_1 /\left\{ {J_u } \right\} } \right) \cup \left\{ {J_v } \right\} } \right) ,W_1 ,\left( {\left( {b_p /\left\{ {J_v } \right\} } \right) \cup \left\{ {J_u } \right\} } \right) ,W_2 } \right) \), where \(n_p \ge 2\), \(p=2,\ldots ,m\), \(W_1 \) and \(W_2 \) represent two partial sequences, and \(W_1 \) or \(W_2 \) may be empty. We assume that \(p_u <p_v \).

For \(\pi ^{*}\), the maximum earliness is

$$\begin{aligned} E_{max} \left( {\pi ^{*}} \right) =d-\frac{d-\mathop \sum \nolimits _{k=2}^m \mathop \sum \nolimits _{r=1+\mathop \sum \nolimits _{j=1}^{k-1} n_j }^{\mathop \sum \nolimits _{j=1}^k n_j } \mathop \sum \nolimits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}}{\left( {1+\theta } \right) ^{m-1}}. \end{aligned}$$

For \(\pi \), the maximum earliness is updated to

$$\begin{aligned}&E_{max} \left( \pi \right) \\&\quad =d-\frac{1}{\left( {1+\theta } \right) ^{m-1}}\left( {d-\left( {\mathop \sum \limits _{k=2}^{p-1} \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}} \right. } \right. \\&\qquad +\mathop \sum \limits _{r=1+{\sum }_{j=1}^{p-1} n_j }^{{\sum }_{j=1}^p n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-p}-p_v w^{a}\left( {1+\theta } \right) ^{m-p}\\&\qquad +p_u w^{a}\left( {1+\theta } \right) ^{m-p}+\left. {\left. {\mathop \sum \limits _{k=p+1}^m \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}} \right) } \right) \end{aligned}$$

Then,

$$\begin{aligned} E_{max} \left( {\pi ^{*}} \right) -E_{max} \left( \pi \right) =\frac{\left( {p_v -p_u } \right) w^{a}\left( {1+\theta } \right) ^{m-p}}{\left( {1+\theta } \right) ^{m-1}}>0. \end{aligned}$$

It can be derived that \(E_{max} \left( {\pi ^{*}} \right) >E_{max} \left( \pi \right) \), which conflicts with the optimal solution. Thus, it should be \(p_u \ge p_v \). The proof is completed. \(\square \)

Lemma 4

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \), if \(n\ge c\), then the first batch is full, i.e., \(n_1 =c\).

Proof

Let \(\pi ^{*}\) and \(\pi \) be an optimal schedule and a job schedule. The difference between the two schedules is the transferring of a job \(J_u \), and \(J_u \) is assigned to the position e in the optimal schedule \(\pi ^{*}\). That is, \(\pi ^{*}=\left( {b_1 ,b_2 ,W} \right) \), \(\pi =\left( {\left( {b_1 \cup \left\{ {J_u } \right\} } \right) ,\left( {b_2 /\left\{ {J_u } \right\} } \right) ,W} \right) \), W represents a partial sequence, and it may be empty. We assume that \(n\ge c\) and \(n_1 <c\). \(J_u \) is the first one in \(b_2 \) and updated to the last one in \(b_1 \). After the transferring, we obtain that \(J_u \) is still in the position e.

For \(\pi ^{*}\), the maximum earliness is

$$\begin{aligned} E_{max} \left( {\pi ^{*}} \right) =d-\frac{d-\mathop \sum \nolimits _{k=2}^m \mathop \sum \nolimits _{r=1+\mathop \sum \nolimits _{j=1}^{k-1} n_j }^{\mathop \sum \nolimits _{j=1}^k n_j } \mathop \sum \nolimits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}}{\left( {1+\theta } \right) ^{m-1}}. \end{aligned}$$

For \(\pi \), the maximum earliness is updated to

$$\begin{aligned} E_{max} \left( \pi \right) =d-\frac{d-\left( {\mathop \sum \nolimits _{k=2}^m \mathop \sum \nolimits _{r=1+\mathop \sum \nolimits _{j=1}^{k-1} n_j }^{\mathop \sum \nolimits _{j=1}^k n_j } \mathop \sum \nolimits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{m-k}-p_u e^{a}\left( {1+\theta } \right) ^{m-2}} \right) }{\left( {1+\theta } \right) ^{m-1}}. \end{aligned}$$

Then,

$$\begin{aligned} E_{max} \left( {\pi ^{*}} \right) -E_{max} \left( \pi \right) =\frac{p_u e^{a}\left( {1+\theta } \right) ^{m-2}}{\left( {1+\theta } \right) ^{m-1}}. \end{aligned}$$

It can be derived that \(E_{max} \left( {\pi ^{*}} \right) >E_{max} \left( \pi \right) \), which conflicts with the optimal solution. Thus, we can transfer the jobs from \(b_2 \) (or other batches) to \(b_1 \) until \(b_1 \) is full. The proof is completed. \(\square \)

Based on the swapping and transferring operations of jobs, we obtain the following two lemmas.

Lemma 5

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \), if \(n\ge c\), then the jobs following \(b_1 \) belonged to the same batch should be sequenced in the non-decreasing order of \(p_i \) in an optimal schedule.

Lemma 6

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \), if \(n\ge c\), then each batch following \(b_1 \) is full except possibly the second batch in an optimal schedule.

Based on Lemma 6, we have the following corollary.

Corollary 1

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \), if \(n\ge c\), then \(n_1 =c, n_2 =n-\left( \lceil \frac{n}{c}\rceil -1 \right) c\), \(n_k =c\left( {k>2} \right) \) in an optimal schedule.

On the basis of the above lemmas and corollary, we design the following Algorithm 1 for solving the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \).

figure a

Theorem 1

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \), an optimal schedule can be obtained by Algorithm 1 in \(O\left( {n\log n} \right) \) time, and the optimal maximum earliness is

$$\begin{aligned}&E_{max}^{*}\nonumber \\&\quad = {\left\{ \begin{array}{ll} 0&{}{n>c}\\ d-{\frac{d-\left( \sum _{r=c+1}^{c+n-\left( \left\lceil \frac{n}{c}\right\rceil -1\right) c} \sum _{i=1}^{n} {p_i}{{i}^{a}} x_{ir}{(1+\theta )}^{\left\lceil \frac{n}{c}\right\rceil -2} +{\sum }_{k=3}^{\left\lceil \frac{n}{c}\right\rceil } {\sum }_{r=c+n-\left( \left\lceil \frac{n}{c}\right\rceil -1\right) c+(k-3)c+1}^{c+n-\left( \left\lceil \frac{n}{c}\right\rceil -1\right) c+(k-3)c+c} {\sum }_{i=1}^{n}{p_i}{{i}^{a}}x_{ir}{(1+\theta )}^{\left\lceil \frac{n}{c}\right\rceil -k}\right) }{{(1+\theta )}^{\left\lceil \frac{n}{c}\right\rceil -1}}}&{}{n\le c}\\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(3.11)

Proof

Based on Lemmas 2-6 and Corollary 1, an optimal solution can be generated by Algorithm 1, and also the result of the optimal solution can be obtained as Eq. (3.11). The time complexity of step 1 is \(O\left( {n\log n} \right) \), and the time complexity of steps 2, 3, and 4 is at most \(O\left( n \right) \). Thus, the total time complexity of Algorithm 1 is \(O\left( {n\log n} \right) \). The proof is completed.   \(\square \)

3.2 Problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \)

In this section, the problem with the objective of minimizing the number of tardy jobs is studied. We first give some properties for the optimal schedules, and then an optimization algorithm is developed to solve this problem. Here, the job sets of which the completion times are no later than and later than the common due date d are denoted as O (i.e., ordinary jobs) and L (i.e., late jobs), respectively. Similar to the problem in Sect. 3.1, the model, structural properties, and optimization algorithm are proposed as follows.

3.2.1 Mixed integer programming model for the problem \(1\big | s-batch,p_{ir} =p_i r^{a},s=\theta t \big |{\sum }_{i=1}^n U_i \)

$$\begin{aligned}&\hbox {Minimize} \,\,{\sum }_{i=1}^n U_i\\&\hbox {Subject to}\,\, (3.3)-(3.5),(3.7)-(3.8)\nonumber \end{aligned}$$
(3.12)

The objective function (3.12) is to minimize the number of tardy jobs.

3.2.2 The structural properties and the proposed optimization algorithm

The structural properties on the jobs sequencing and batching argument are also proposed as follows.

Lemma 7

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \), the following properties are satisfied in an optimal schedule:

  1. (1)

    All jobs should be sequenced in the non-decreasing order of \(p_i\) in O, and all batches are full except possibly the first batch and the highest indexed batch in O;

  2. (2)

    The processing time of an arbitrary job in O is no more than that of other jobs in L.

  3. (3)

    If there exists a batch \(b_k \) in L satisfying that \(S\left( {b_k } \right) <d\) and \(C\left( {b_k}\right) >d\), then it should be \(C\left( {b_{k-1} } \right) \left( {1+\theta } \right) \left( {1+p_i w^{a}} \right) >d\) for an arbitrary job \(J_i \in L\), where \(w={\sum }_{i=1}^{k-1} n_i +1\) and it is the first position after \(b_{k-1} \).

Proof

(1) This property can be proved by swapping and transferring operations of jobs. We omit the proof.

(2) Let \(\pi ^{*}\) and \(\pi \) be an optimal schedule and a job schedule. The difference between the two schedules is the pairwise interchange of these two jobs \(J_u \) and \(J_v \) (suppose \(J_u \) and \(J_v \) are in the e-th and w-th orders, and \(e<w\)), that is, \(\pi ^{*}=\left( {W_1 ,b_p ,W_2 ,b_q ,W_3 } \right) \), \(\pi =\left( {W_1 ,\left( {b_p /\left\{ {J_u } \right\} } \right) \cup \left\{ {J_v } \right\} ,W_2 ,\left( {b_q /\left\{ {J_v } \right\} } \right) \cup \left\{ {J_u } \right\} ,W_3 } \right) \). \(W_1 \), \(W_2 \), and \(W_3 \) represent three partial sequences, where \(W_1 \), \(W_2 \), or \(W_3 \) may be empty, \(b_p \subseteq O\), and \(b_q \subseteq L\). Here we assume that \(p_u >p_v \).

The completion time of \(b_p \) in \(\pi ^{*}\) is

$$\begin{aligned} C\left( {b_p \left( {\pi ^{*}} \right) } \right) =\mathop \sum \limits _{k=1}^p \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{p-k}. \end{aligned}$$

The completion time of \(b_p \) in \(\pi \) is

$$\begin{aligned} C\left( {b_p \left( \pi \right) } \right) =\mathop \sum \limits _{k=1}^p \mathop \sum \limits _{r=1+{\sum }_{j=1}^{k-1} n_j }^{{\sum }_{j=1}^k n_j } \mathop \sum \limits _{i=1}^n p_i i^{a}x_{ir} \left( {1+\theta } \right) ^{p-k}-p_u e^{a}+p_v e^{a}. \end{aligned}$$

Then, \(C\left( {b_p \left( {\pi ^{*}} \right) } \right) -C\left( {b_p \left( \pi \right) } \right) =p_u e^{a}-p_v e^{a}\). Since \(p_u >p_v \), it can be derived that \(C\left( {b_p \left( {\pi ^{*}} \right) } \right) >C\left( {b_p \left( \pi \right) } \right) \), which conflicts with the optimal solution. Hence, it should be \(p_u \le p_v \) in an optimal schedule.

(3) If there exist a batch \(b_k \) and a job \(J_i \) in L satisfying that \(S\left( {b_k } \right) <d\), \(C\left( {b_k } \right) >d\), and \(C\left( {b_{k-1} } \right) \left( {1+\theta } \right) \left( {1+p_i w^{a}} \right) \le d\), then the solution can be improved after \(J_i \) is placed into a single batch, which contradicts with the optimal schedule. Thus, it can be derived that \(C\left( {b_{k-1} } \right) \left( {1+\theta } \right) \left( {1+p_i w^{a}} \right) >d\) for any job \(J_i \in L\).

This completes the proof. \(\square \)

Based on Lemma 7, we develop the following Algorithm 2 to solve the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| \mathop \sum \limits _{i=1}^n U_i \).

figure b

Theorem 2

For the problem \(1\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \), an optimal schedule can be obtained by Algorithm 2 in \(O\left( {n\log n} \right) \) time.

Proof

Based on Lemma 7, an optimal solution can be obtained by Algorithm 2. The time complexity of step 1 is \(O\left( {n\log n} \right) \), the total time complexity of steps 2, 3, 4, 5, and 6 is \(O\left( n \right) \). Thus, the time complexity of Algorithm 2 is at most \(O\left( {n\log n} \right) \). \(\square \)

4 Parallel-machine scheduling problems

In this section, the hybrid VNS–GSA algorithm is used to solve the parallel-machine scheduling problems with the objective of minimizing the maximum earliness and total number of tardy jobs, respectively.

4.1 Mixed integer programming models for the parallel-machine scheduling problems

4.1.1 Mixed integer programming model for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \)

Minimize \(\left( {3.2} \right) \)

Subjec to:

$$\begin{aligned}&\mathop \sum \limits _{i=1}^n y_{gik} \le c,\quad k=1,2,\ldots ,m_g ,g=1,2,\ldots ,q\end{aligned}$$
(4.1)
$$\begin{aligned}&\mathop \sum \limits _{k=1}^{m_g } y_{gik} =1,\quad i=1,2,\ldots ,n,g=1,2,\ldots ,q\end{aligned}$$
(4.2)
$$\begin{aligned}&S\left( {b_{g\left( {k+1} \right) } } \right) \ge C\left( {b_{gk} } \right) \left( {1+\theta } \right) ,\quad k=1,2,\ldots ,m-1,g=1,2,\ldots ,q\end{aligned}$$
(4.3)
$$\begin{aligned}&d\ge t_g +\mathop \sum \limits _{k=1}^m s_{gk} +\mathop \sum \limits _{i=1}^n p_i ,\quad g=1,2,\ldots ,q \end{aligned}$$
(4.4)
$$\begin{aligned}&C({b}_{gk})-C({b}_{gl})+{Mz}_{gkl}-C({b}_{gk})(1+\theta )\nonumber \\&\quad -P({b}_{gk})\ge 0,\quad k,l=1,2\ldots ,m, g=1,2,\ldots ,q \end{aligned}$$
(4.5)
$$\begin{aligned}&{y}_{gik},{z}_{kl}=0 \,\,or\,\, 1, \quad k,l=1,2,\ldots ,{m}_{g}, g=1,2,\ldots ,q,i=1,2, \ldots ,n \end{aligned}$$
(4.6)

Constraint set (4.1) assures that the number of jobs in any batch should be no more than the machine capacity on each machine. Constraint set (4.2) guarantees that each job should be only assigned to one batch on each machine. Constraint set (4.3) makes sure that setup time is required before processing each batch on each machine. Constraint set (4.4) ensures that all jobs should be completed no later than the common due date d on each machine, and here \(t_g \) denotes the starting time to process the batches. Constraint set (4.5) indicates that there is no overlapping situation between two continuous batches on each batch. Constraint set (4.6) defines the ranges of the variables.

4.1.2 Mixed integer programming model for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \)

Minimize \(\left( {3.12} \right) \)

Subject to \(\left( {4.1} \right) \!-\!\left( {4.3} \right) ,\left( {4.5} \right) \!-\!\left( {4.6} \right) \)

4.2 Key procedures of VNS–GSA

Variable neighborhood search (VNS) was proposed by Mladenović and Hansen (1997), since when this algorithm has been extensively studied by many researchers and applied in many practical combinatorial optimization problems. Gravitational search algorithm (GSA), proposed by Rashedi et al. (2009), is a population-based heuristic algorithm based on Newton’s theory of gravity and mass interactions. In this paper, we combine the main features and steps of VNS and GSA to develop a novel hybrid VNS–GSA algorithm for solving the parallel-machine scheduling problems. The key procedures of VNS–GSA are described as follows:

4.2.1 Coding scheme

In the proposed VNS–GSA, for ensuring the continuity of search space in GSA algorithm, the random key encoding way is applied in our problem, which was first proposed by Bean (1994) to keep feasibility from parent to offspring in genetic algorithm. In this paper, a solution to the problem of assigning jobs to the parallel-machine is an array with the length equal to \(n+q-1\), and each position value is a decimal between 0 and 1.

4.2.2 Encoding scheme

We should map this decimal array into the jobs number array on each machine before encoding. Firstly, we map this decimal array into an integer array, and each decimal sequenced in the non-decreasing order of the value is transformed to the order number. For example, the smallest decimal is transformed to the integer 1, and the second smallest decimal is transferred to the integer 2, and so on. Then, if the value of any position is greater than n, then this position is marked as a flag to assign the following jobs into a different machine, and this flag mechanism has been applied in Wang and Chou (2010).

Assume that there are five jobs to be processed on two serial-batching machines. In Fig. 1 there is an example of a decimal array (0.67, 0.78, 0.54, 0.98, 0.45, 0.08) and the mapping process. The jobs {\(J_4 \), \(J_5 \), \(J_3 \)} are assigned on \(M_1 \) and {\(J_2 \), \(J_1 \)} on machine \(M_2 \).

Fig. 1
figure 1

An example of encoding mapping

Full size image

Then, we can obtain the jobs set assigned on each machine, and different encoding strategies are designed for different objective functions. The detail of encoding strategy for problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \) is described as follows:

Encoding strategy for problem \({\varvec{P}}\left| {{\varvec{s-batch}},{\varvec{p}}_{{\varvec{ir}}} ={\varvec{p}}_{\varvec{i}} {\varvec{r}}^{{\varvec{a}}},{\varvec{s}}={\varvec{\theta }} {\varvec{t}}} \right| {\varvec{E}}_{{\varvec{max}}} \)

Step 1.

Set \(g=1\),\(E_{max} =0\)

Step 2.

Apply Algorithm 1 to sequence and batch all jobs assigned on \(M_g \), and \(E_{max}^g \) is obtained for \(M_g \)

Step 3:

If \(E_{max} <E_{max}^g \), then \(E_{max} =E_{max}^g \)

Step 4:

If \(g<q\), set \(g=g+1\), then go to step 2. Otherwise, output the result of \(E_{max} \)

The detail of encoding strategy for problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \) is described as follows:

Encoding strategy for problem \({\varvec{P}}\left| {{\varvec{s-batch}},{\varvec{p}}_{{\varvec{ir}}} ={\varvec{p}}_{\varvec{i}} {\varvec{r}}^{{\varvec{a}}},{\varvec{s}}={\varvec{\theta }} {\varvec{t}}} \right| {\sum }_{{\varvec{i}}=\mathbf 1 }^{\varvec{n}} {\varvec{U}}_{\varvec{i}} \)

Step 1.

Set \(g=1\),\({\sum }_{i=1}^n U_i =0\)

Step 2.

Apply Algorithm 2 to sequence and batch all jobs assigned on \(M_g \), and \({\sum }_{i=1}^n U_i^g \) is obtained for \(M_g \) Set \({\sum }_{i=1}^n U_i ={\sum }_{i=1}^n U_i +{\sum }_{i=1}^n U_i^g \)

Step 3.

If \(g<q\), set \(g=g+1\), then go to step 2. Otherwise, output the result of \({\sum }_{i=1}^n U_i =0\)

4.2.3 Neighborhood structure

Swap operator is widely applied in neighborhood structure of combinatorial optimization problem. A multiple swap-based neighborhood structure is applied in this paper, which can be described as follows: randomly select two different positions from the solution and swap them to form a new solution, and the above process is defined as 1-swap, and then repeat to randomly swap two different positions from the new solution, it is defined as 2-swap, and so on.

4.2.4 GSA-based local search in variable neighborhood search

In order to improve the efficiency of local search in VNS, we use GSA as local search operator to strengthen the optimization ability of the algorithm. The detail of GSA-Based Local Search operation is described as follows (Rashedi et al. 2009):

GSA-Based Local Search operation

Step 1.

Randomly select m solutions from a certain neighborhood of the current optimal solution in variable neighborhood search

Step 2.

Calculate the fitness of each solution

Step 3.

Update best and worst of the population

Step 4.

Calculate mass and acceleration for each solution

Step 5.

Update velocity and position for each solution

Step 6.

If termination condition is met, then stop the iteration

4.3 The main steps and framework of VNS–GSA

In our problem, the initial solution is denoted by x, the neighborhood of the solution is denoted by \(N_o \left( x \right) \), and the current iteration step is denoted by it. We initialize the following parameters \(o,o_{min} ,o_{max} ,t_{max} ,o_{step} \), where o is the current neighborhood, \(o_{min} \) is the first neighborhood, \(o_{max} \) is the last neighborhood, \(t_{max} \) is the maximum number of iterations, \(o_{step} \) is the step length of iteration.

Main steps of VNS–GSA

Step 1.

Set \(it=1\), execute local search procedure to find a local optimal solution for initial solution and set it as the optimal solution \(x_{best} \)

Step 2.

Set \(o=o_{min} \)

Step 3.

Execute GSA-Based Local Search for \(N_o \left( {x_{best} } \right) \) to obtain a solution \({x}'\)

Step 4.

If solution \({x}'\) is better than \(x_{best} \), then set \(x_{best} ={x}'\) Otherwise, set \(o=o+1\), if \(o\le o_{max} \) and go to step 3

Step 5.

If \(it\le t_{max} \), then stop the iteration. Otherwise, set \(it=it+1\) and go to step 2

Fig. 2
figure 2

The framework of VNS–GSA

Full size image
Table 3 Parameters setting
Full size table
Table 4 Computational results for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \)
Full size table

The framework of VNS–GSA is shown in Fig. 2 to solve the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \) and \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \).

4.4 Computational experiments and comparison

In this sub-section, a serial of computational experiments are conducted to test the performance of our proposed algorithm VNS–GSA, compared with VNS (Lei and Guo 2016), GSA (Rashedi et al. 2009), and SA (Damodaran and Vélez-Gallego 2012). We also conducted computational experiments for the problems of \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \) and \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \). The parameters of the test problems were randomly generated according to the practical production situations of an aluminum factory, as shown in Table 3.

Fig. 3
figure 3

Convergence curves for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \) with small size. a Convergence curves for problem 1, b convergence curves for problem 2, c convergence curves for problem 3, d convergence curves for problem 4, e convergence curves for problem 5

Full size image
Fig. 4
figure 4

Convergence curves for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \) with large size. a Convergence curves for problem 6, b convergence curves for problem 7, c convergence curves for problem 8, d convergence curves for problem 9, e convergence curves for problem 10

Full size image

4.4.1 Experiments and comparison for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \)

In order to test the performance of proposed VNS–GSA, the proposed algorithm and another three algorithms have been applied to solve the problem \(P\left| s-batch,p_{ir} =p_i r^{a},s=\theta t \right| E_{max} \) for comparison. In Table 4, the average objective value (Avg.Obj) and the maximum objective value (Max.Obj) for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| E_{max} \) are listed. It is easy to find that the VNS–GSA can obtain better solutions than compared algorithms, especially for the large-size problems.

We also compared the proposed algorithm with other compared algorithms on the convergence speed and efficiency. Figures 3 and 4 show the convergence performance of VNS–GSA, GSA, VNS and SA for small-size and large-size problem instances, respectively. Compared to GSA, VNS, and SA, the proposed VNS–GSA converges faster and has better optimization capability.

Table 5 Computational results for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| \mathop \sum \limits _{i=1}^n U_i \)
Full size table
Fig. 5
figure 5

Convergence curves for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \) with small size. a Convergence curves for problem 11, b convergence curves for problems 12, c convergence curves for problem 13, d convergence curves for problem 14, e convergence curves for problem 15

Full size image
Fig. 6
figure 6

Convergence curves for the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \) with large size. a Convergence curves for problem 16, b convergence curves for problem 17, c convergence curves for problem 18, d convergence curves for problem 19, e convergence curves for problem 20

Full size image

4.4.2 Experiments and comparison for the problem \(P\big | s-batch,p_{ir} =p_i r^{a},s=\theta t \big |{\sum }_{i=1}^n U_i \)

In Table 5, we list the Ave.obj and Max.obj of the problem \(P\left| s-batch,p_{ir} =p_i r^{a},s=\theta t \right| {\sum }_{i=1}^n U_i \) generated by the proposed algorithm and other algorithms. It is also obvious that VNS–GSA has better optimization capability than other algorithms.

Figures 5 and 6 show the convergence performance of the proposed algorithm and compared algorithms when solving the problem \(P\left| {s-batch,p_{ir} =p_i r^{a},s=\theta t} \right| {\sum }_{i=1}^n U_i \) with small and large problem instances, respectively. It is obvious that the proposed algorithm has better convergence than compared algorithms.

In all, from the above results we can conclude that the proposed VNS–GSA has faster convergence speed when solving problems compared with VNS (Lei and Guo 2016), GSA (Rashedi et al. 2009), and SA (Damodaran and Vélez-Gallego 2012). Then, it can be inferred that the proposed VNS–GSA is very stable and robust in terms of solution quality and convergence speed.

5 Conclusions

In this paper, we study single-machine and parallel-machine serial-batching scheduling problems with learning effect, considering the time-dependent set-up time. Under the setting of single-machine, we propose the models and structural properties for the problems with the objectives of minimizing the maximum earliness and the number of tardy jobs, and develop optimization algorithms to solve these two problems, respectively. Under the setting of the parallel-machine, we propose a hybrid VNS–GSA algorithm to solve the scheduling problems with the same two objectives. In future research, we will investigate more general serial-batching scheduling models with the learning effect, take different objective functions into consideration, and extend our models to the background of supply chain scheduling.