An interactive approach to stochastic programming-based portfolio optimization

Abstract

We consider expected return, Conditional Value at Risk, and liquidity criteria in a multi-period portfolio optimization setting modeled by stochastic programming. We aim to identify a preferred solution of the decision maker (DM) by obtaining information on her/his preferences. We use a weighted Tchebycheff program to generate representative sets of solutions. Our approach models the stochasticity of market movements by stochastic programming. Working with multiple scenario trees, we construct confidence ellipsoids around representative solutions, and present them to the DM for her/him to make a choice. With each iteration of the approach, an increasingly concentrated set of ellipsoids around the DM’s choices are generated. The procedure is demonstrated with tests performed using stocks traded on Borsa Istanbul.

1 Introduction

Portfolio optimization (PO) is the problem of choosing between available investment instruments in the financial market. Examples of these instruments are stocks, bonds, mutual funds, options and deposit accounts. The decision maker (DM) of the problem, the investor, may be personal or corporate. The primary goal is to maximize the wealth resulting from the investment; but the uncertainty of financial markets complicates the problem. Since Markowitz (1959) pioneered the Modern Portfolio Theory, it has been an active field in finance. The classical mean-variance portfolio model has two objectives: maximizing expected return in terms of weighted expected returns of financial securities, and minimizing portfolio risk in terms of variance of return.

Following the parametric approach of Markowitz to the mean-variance portfolio model, several other approaches were proposed for PO. Initially, the primary concern was to make the risk objective easier to handle. The covariance matrix was diagonalized to decrease its density for reduced computational complexity. Linear risk measures were also proposed. One of the most popular was Mean Absolute Deviation (MAD) by Konno and Yamazaki (1991). In this measure, risk is defined as the absolute deviation from the mean return. Other researchers like Konno (1990) and Michalowski and Ogryczak (2001) studied variations of MAD where only downside deviations are considered and bigger ones are penalized more. Mansini et al. (2003) provided an overview of linear programming-solvable models for PO. They looked into several linear risk measures like variations of MAD, Conditional Value at Risk (CVaR), Gini’s Mean Difference and minimax risk. CVaR is a measure of extreme losses; and its use in the portfolio literature has increased lately. Mansini et al. (2007) studied linear programming models for PO that are related to CVaR. Ogryczak and Ruszczynski (2002) justified CVaR as a suitable risk measure by showing that it is consistent with the second degree stochastic dominance and it has attractive computational properties.

As the literature on PO expanded, needs of unconventional investors had to be taken into account. Steuer et al. (2006) argued that there are investors who would like to consider several additional criteria besides return such as dividends, liquidity, social responsibility, turnover and amount of shortselling. Moreover, risk of the portfolio can be modeled with multiple measures. Multiple Criteria Decision Making (MCDM) has therefore been a valuable tool in the developing PO theory. A popular approach to solve PO with two or more objectives is to compute a number of discrete efficient points to represent the efficient frontier. With the $\upvarepsilon$-constraint method of Haimes et al. (1971), one of the objectives is optimized by systematically changing the levels of the remaining ones. There are also variations such as in Ballestero and Romero (1996) and Bana e Costa and Soares (2004) where, rather than generating a sample from the whole frontier, they generate certain discrete points with desired characteristics. More recently, Roman et al. (2007) used expected return, variance and CVaR criteria. They used the $\upvarepsilon$-constraint method by treating variance as the objective and the other two criteria as constraints. Xidonas et al. (2011) considered expected return, MAD, dividend yield and market risk in a PO problem with complicating constraints on portfolio compositions. Binary variables included in some constraints led to a multiobjective mixed-integer model that was solved with the augmented $\upvarepsilon$-constraint method. To guide the DM to her/his most preferred solution among the set of solutions generated, they applied an interactive filtering procedure. Xidonas et al. (2010) added two criteria to this study: relative price/earnings ratio and marketability. Fang et al. (2009) also employed the $\upvarepsilon$-constraint method to generate efficient solutions with the criteria of transaction costs-adjusted expected return, semi-absolute deviation and a fuzzy liquidity measure of turnover rates of securities. Şakar and Köksalan (2013a) studied the effects of multiple criteria on PO using expected return, variance, CVaR and liquidity criteria. They also considered constraints on the weights of securities and the number of securities contained in the portfolio; and looked into the effects of these on the results.

Stochastic programming (SP) models have been used to explicitly account for the uncertainty of portfolio outcomes, and also to handle multi-period PO problems. Generally speaking, SP involves mathematical programming models to handle problems that involve uncertainty. We discuss SP in the context of our approach in the next section. Ballestero (2001) proposed a stochastic goal programming model to mean-variance PO and utilized the connection between classical expected utility theory and linear weighted goal programming model under uncertainty. Abdelaziz et al. (2009) also proposed a stochastic goal programming approach to PO by utilizing discrete scenarios on equities that are generated from a number of historical observations. They used one deterministic and four random objectives; and measured the deviations from the goals of the random objectives for each scenario. Aouni et al. (2005) included DM’s preferences in a stochastic goal programming model by means of satisfaction functions. They applied their model to portfolio selection with stocks from the Tunisian stock exchange. Abdelaziz et al. (2007) proposed a new deterministic formulation to multicriteria SP by combining compromise programming and chance constrained programming models for PO. They considered rate of return, exchange flow ratio and the risk coefficient as criteria. Ibrahim et al. (2008) studied single-stage and two-stage SP models that minimize maximum downside deviation. They treated past returns of stocks as equiprobable scenarios. Yu et al. (2004) used SP in the bond market with a dynamic model of maximizing the difference between the expected wealth at the end of the investment horizon and the weighted sum of shortfall cost. Gülpınar et al. (2003) considered transaction costs with four asset classes, a number of liabilities and riskless assets. They minimized risk for given wealth levels and experimented with different numbers of scenarios. Pınar (2007) developed and tested multistage PO models using a linear objective composed of expected wealth and downside deviation from a target. He used a simulated market model to randomly generate scenarios. Balibek and Köksalan (2010) developed a SP model for a multicriteria public debt management problem, which can be considered as a reverse PO problem. They generated scenarios on multiple factors by utilizing vector autoregressive models. Yu et al. (2003) provided a survey on SP models in financial optimization. They provided an introduction to SP and discussed SP models for asset allocation, fixed-income security management and asset/liability management problems.

In multicriteria problems, the DM has a set of efficient solutions to choose from. Unless she/he is provided a form of guidance, this choice can be difficult. The DM can be included in the optimization process through an interactive approach. Balibek and Köksalan (2012) developed an interactive approach to stochastic multicriteria problems in the context of public debt management. Their method makes use of the Visual Interactive Approach of Korhonen and Laakso (1986).

In this study, we develop an interactive approach to a SP-based PO problem with three criteria: expected return, CVaR and a measure of liquidity. Our approach addresses several important issues related to PO. Specifically, it captures the multi-period and multiple criteria aspects, it incorporates the preferences of the DM interactively, and it represents the future behavior of markets well. We utilize SP to make multi-period decisions regarding the portfolio compositions. We employ stocks as financial securities, and utilize discrete scenarios in three-month PO settings. In our scenario trees, the utilization of larger number of scenarios represents the market behavior better, but results in increased complexity. Hence, we first generate a large number of scenarios and then cluster them. We also account for the stochasticity of our solutions that occur as a result of the randomness involved in the scenario generation process. The DM is integrated into the decision process by adopting the interactive weighted Tchebycheff procedure of Steuer and Choo to our problem (see Steuer 1986, pp. 419-455).

The paper is organized as follows: Sect. 2 covers the basics of SP and our SP approach to multicriteria PO. In Sect. 3, we introduce our interactive approach and provide results of our experiments with stocks from Borsa Istanbul (BIST). We conclude in Sect. 4.

2 The stochastic programming approach to portfolio optimization

SP approaches consist of models to handle problems that involve uncertainty. In PO context, this uncertainty is a result of the behavior of random parameters that affect the portfolio outcome. If these random parameters can be represented by discrete distributions, SP can work with scenario trees. These scenario trees model the future movement of problem-related factors by assigning probabilities to different possible outcomes. A general scenario tree starts with a set of initial possible outcomes for the first period; and then continues with future periods with possible outcomes conditional on the realizations of the previous periods. When all periods of the planning horizon are accounted for, we obtain a scenario path for each chain of realization with a corresponding probability. Scenario trees have nodes from which possible branches grow. The DM is expected to make decisions at these nodes evaluating the information that became available on past realizations and the possible future evolution of factors.

Our SP approach deals with a multi-period multicriteria PO problem where stocks are considered as investment options that have uncertain future progress. We consider expected return, CVaR, and liquidity criteria in our approach and make use of discrete scenarios on a stock market-representative index. Our model provides us with portfolio decisions for the whole planning horizon. We build upon our original approach in Şakar and Köksalan (2013b). We review that approach in Sects. 2.1–2.3. We further improve the efficiency of the approach in Sect. 2.4 by developing clustered scenarios.

2.1 Scenario generation

Scenario generation is a fundamental component of SP and it has been studied by several researchers. Yu et al. (2003) discussed three approaches to scenario generation: bootstrapping historical data utilizes random historical occurrences of asset returns; time series analysis estimates volatilities and correlation matrices of assets using historical data; and vector autoregressive models capture the progress of multiple time series that have interdependencies. Guastaroba et al. (2009) limited their study to single-period PO; and studied and compared historical data technique, bootstrapping technique, block bootstrapping technique, Monte Carlo simulation techniques and multivariate generalized ARCH process technique. They found that historical data technique gives comparable results despite its simplicity. Dupacova et al. (2000) discussed random walk models, binomial and trinomial models and autoregressive models to generate scenario trees for multi-stage stochastic programs. Hoyland and Wallace (2001) proposed a method that generates a limited number of discrete scenarios that possess DM-specified statistical properties; and they implemented it with single and three-period scenario trees.

Our scenario generation technique is a result of our conclusions and assumptions about financial markets in general and the Turkish Stock Market (TSM) in particular. Several researchers and finance practitioners have tried to understand and predict the behavior of financial markets. The question of whether the progress of financial securities’ prices can be predicted is related to the efficient market hypothesis. Basically, efficient market hypothesis argues that prices of securities cannot be predicted with gathering information about the financial market, because such information is already reflected in prices. No investor can earn abnormal profits by studying the trend of prices or factors that are assumed to affect prices. Numerous researchers tested financial markets for efficient market hypothesis, see for example Lo and MacKinlay (1988), Poterba and Summers (1988), Fama and French (1993) and Seyhun (1986). We consider the most common result to be that, even if there are some opportunities for predicting the market, the time, energy and cost required to exploit these opportunities level off abnormal profits. Random walk models are closely related to market efficiency. They argue that if information related to prices is already accounted for, the change in the price of a security for the next period can only be random. We refer the reader to Campbell et al. (1997) for models and tests of random walk hypotheses, and Bodie et al. (2009) for detailed discussions on efficient market hypotheses, their tests and random walk models.

Tests of market efficiency and random walk models offer mixed results for the TSM. Smith and Ryoo (2003), Buguk and Brorsen (2003) and Odabasi et al. (2004) confirmed random walk behavior for the TSM. Based on these studies and also our observations about the progress of Turkish stock prices, we assume that the TSM follows a random walk model.

To keep our scenario trees computationally manageable, we generate scenarios on the return of a market-representative index and then derive individual stock returns from the index return by using the Single Index Model. This model relates the return of assets to a common macroeconomic factor using historical data and regression analysis. Since we use stocks as securities, a representative BIST index, BIST-100, is used for this purpose. The regression equation for the Single Index Model is:

$$\begin{aligned} r_i \left( t \right) =\alpha _i +\beta _i .r_M \left( t \right) +e_i \left( t \right) \end{aligned}$$

(1)

where $r_i \left( t \right)$ and $r_M \left( t \right)$ are the returns of security $i$ and the market-representative index at time $t$, respectively, $\beta _i$ and $\alpha _i$ are the sensitivity to the index and individual return premium of security $i$, respectively, and $e_i$ is the zero-mean, security-specific surprise in the return of security $i$

The expected value of (1) is given by:

$$\begin{aligned} E\left( {r_i } \right) =\alpha _i +\beta _i .E\left( {r_M } \right) \end{aligned}$$

(2)

We estimate the alpha and beta values of securities by regression, and estimate individual stock returns using these and scenarios on the return of BIST-100.

The random walk model we use to generate scenarios on the return of the BIST-100 index is:

$$\begin{aligned} r_t =\mu +\sigma . e_t \qquad e_t \sim N\left( {0,1} \right) \end{aligned}$$

(3)

where $r_t$ is the return of the index and $e_t$ is a standard normal error term at time $t,\, \mu$ is the mean and $\sigma$ is the standard deviation of the return of the index. We use constant variation as it is supported by empirical evidence from BIST. Normal distribution is frequently used in the literature for asset returns and we observe that the historical return distribution of BIST-100 is in line with the applications in the literature.

In our scenario generation procedure, (3) is used to generate BIST-100 returns for each branch of the scenario tree by using random sampling from the error term; and individual stock returns on these branches are derived from the index return by (2).

2.2 The criteria

We consider three criteria: expected return, liquidity and CVaR. The procedure to model expected return is discussed in the previous section. We use monthly percentage returns of stocks and BIST-100 for the random walk model and the Single Index Model. Liquidity can be defined as the degree to which a security can be traded swiftly within fair price levels. Sarr and Lybek (2002) review several liquidity measures. We use a turnover ratio as our liquidity measure: the number of shares of stocks that are traded in a fixed time unit divided by the publicly outstanding number of shares of that stock. We use the most recent month for the number of outstanding shares of stocks and take the daily average number as the number of shares traded. Our last criterion is a risk measure of extreme losses, CVaR. CVaR at $\lambda$ probability is the expected value of losses in the worst (1–$\lambda$) of probable cases. When we are working with discrete scenarios, CVaR can be optimized using a linear programming model as given in Rockafellar and Uryasev (2000). In line with their discussions, the following model can be used to optimize CVaR in the presence of discrete scenarios on stock returns:

$$\begin{aligned}&\hbox {Minimize }\tau +\frac{1}{(1-\lambda )} \sum \limits _{s=1}^{q} a_s p_s \end{aligned}$$

(4)

$$\begin{aligned}&a_s \ge -x^{T}r^{s}-\tau \qquad \forall \,\, s=1,\ldots ,\,q \end{aligned}$$

(5)

$$\begin{aligned}&a_s \ge 0 \qquad \forall \, s=1,\ldots ,\,q \end{aligned}$$

(6)

where $x$ is the vector of proportions of stocks in the portfolio and $r^{s}$ is the vector of stock returns in scenario $s,\, p_s$ and $a_s$ are the probability and auxiliary variable corresponding to scenario $s$, respectively, and $\tau$ is an auxiliary variable used to find excess losses.

2.3 The stochastic programming model

The mathematical model for our SP approach that we present here is taken from Şakar and Köksalan (2013b), where we used it with the $\upvarepsilon$-constraint method to present the DM a discrete representation of the efficient frontier.

Parameters:

$I$ :

set of all stocks

$S$ :

set of all scenarios

$N$ :

set of all nodes in the scenario tree

$n_{s}$ :

the final node of scenario $s\in S$

$n^{\prime }$ :

immediate predecessor node of $n\in N$

$R(n)$ :

set of all predecessor nodes of $n\in N$

$m(n^{\prime },n)$ :

market return corresponding to branch between nodes $n^{\prime }$ and $n$

$p(n^{\prime },n)$ :

probability corresponding to branch between nodes $n^{\prime }$ and $n$

$p_n$ :

probability of the partial scenario up to node $n$, where $p_n = p_{n^{\prime }}.p\left( {n^{\prime },n} \right) \quad \forall n \,{\in }\, N, n = 0$ is the root node of the scenario tree, and $p_{0}= 1$.

$liq_{i}$ :

liquidity value of stock $i\in I$

$\lambda$ :

probability level for CVaR

$D$ :

number of periods in the scenario tree

Decision variables:

$VaR$ :

Value at Risk value

$x_{ni}$ :

allocation of stock $i\in I$ at node $n\in N\backslash \left\{ {n_s :s\in S} \right\}$

Structural variables:

$Ret_{s}$ :

value (return) obtained if scenario $s$ is realized, $s\in S$

$liquidity_{s}$ :

resulting liquidity if scenario $s$ is realized, $s\in S$

$aux_{s}$ :

auxiliary variable corresponding to scenario $s\in S$

$$\begin{aligned} \hbox {Max }z_1&= \sum \limits _{s\in S} p_{n_s}. Ret_s \end{aligned}$$

(7)

$$\begin{aligned} \hbox {Min }z_2&= VaR+\left[ {\frac{1}{1-\lambda } \sum \limits _{s\in S} (p_{n_s } .aux_s )} \right] \end{aligned}$$

(8)

$$\begin{aligned} \hbox {Max }z_3&= \sum \limits _{s\in S} p_{n_s}. liquidity_{s}\end{aligned}$$

(9)

$$\begin{aligned} \sum \limits _{i\epsilon I} x_{ni}&= \sum \limits _{i\epsilon I} x_{n^{{\prime }}i} (1+\alpha _i +\beta _i .m(n^{\prime },n)) \qquad \forall \, n\in N\backslash \left( {\left\{ 0 \right\} \cup \left\{ {n_s: s\in S} \right\} } \right) \end{aligned}$$

(10)

$$\begin{aligned} Ret_s&= \sum \limits _{i \epsilon I} x_{n_s^{\prime } i} (1+\alpha _i +\beta _i .m(n_s^{\prime } ,n_s )) \qquad \forall \,s\in S \end{aligned}$$

(11)

$$\begin{aligned} aux_s&\ge 1-Ret_s -VaR \qquad \forall \,s\in S \end{aligned}$$

(12)

$$\begin{aligned} liquidity_s&= \frac{\sum \nolimits _{k\in R(n_s )} (\sum \nolimits _{i\in I} x_{ki} .liq_i )}{D} \qquad \forall \, s\in S \end{aligned}$$

(13)

$$\begin{aligned} \sum \limits _{i\in I} x_{0i}&= 1 \end{aligned}$$

(14)

$$\begin{aligned} x_{ni}&\ge 0 \qquad \forall \, n\in N\backslash \left\{ {n_s : s\in S} \right\} ,\,i\in I \end{aligned}$$

(15)

$$\begin{aligned} aux_s&\ge 0 \qquad \forall \,s\in S \end{aligned}$$

(16)

For the expected return criterion, we maximize the compounded return over all periods. With (14), we choose the initial percentages of stocks. (10) ensures that we allocate the ending value of each node, except for the final stage nodes, to stocks chosen at its successor node. (11) gives the values of final nodes, thus the ending values of scenarios. With (7), we maximize the expected value of the scenario tree, and $z_1$ –1 gives the compounded expected return over all periods. (8), (12) and (16) are adopted from the CVaR model (4)–(6). (12) and (16) makes use of auxiliary variables to account for the excess loss of each scenario, and (8) gives the CVaR value. In (13) we calculate the weighted sums of the liquidity measures of the stocks for nodes of each scenario, and then use their average as the liquidity measure corresponding to that scenario. (9) gives the liquidity criterion in which we take the weighted sum of the liquidity measures of scenarios by their corresponding probabilities. In sign restrictions of (15), we exclude the final nodes from the set of stock allocation decision variables since these nodes are the ending points of scenarios and no decisions are made at those points.

2.4 Scenario clustering

In our SP approach, we use scenario trees to model the stochasticity of the TSM. Each scenario represents a possible path of progress for the market-representative index. We now want to increase the approximation capabilities of our scenario trees to represent the behavior of the TSM better. For this purpose, we consider generating a large number of scenarios. As the number of scenarios gets larger, we will have an increased probability of covering all possible outcomes. However, this approach increases computational complexity. To deal with this issue we employ a two-stage procedure. We first generate a large number of scenarios, and then, classify them into clusters based on their similarity. This procedure is adapted from the SP approach to public debt management in Balibek and Köksalan (2012).

Clustering is basically assigning items to groups so that they are more similar to the other items in the same group than the ones in other groups. Similarity between items is measured by a distance metric. We use the $K$-means algorithm (MacQueen 1967) for clustering. The $K$-means algorithm clusters data points into a predetermined number of $(K)$ disjoint classes.

Below is our routine to obtain clustered scenario trees. Let $t$ be the time counter, $y$ be the number of periods in the scenario tree, $c$ be the desired number of scenario paths stemming from each decision node, and $M$ be the number of scenario paths to be clustered down to $c$.

• 1. Set $t$ = 0, decide on the values of $y,\, M$ and $c$.

• 2. For each node of time $t$, generate $M$ scenario paths on the BIST-100 return with the random walk model (3) by using random sampling from the error term.

• 3. Cluster each set of the $M$ scenario paths to $c$ classes.

• 4. Compute the probability of each scenario path by dividing the number of elements in the related cluster by $M$.

• 5. Set $t=t +1$ and repeat steps 2 to 4 until $t=y-1$.

• 6. Connect the scenario paths of time 0 to $t$ to form final scenarios covering all periods and compute their corresponding probabilities.

We generate clustered scenario trees that have equal number of branches coming out of each decision node since we make applications with such trees. Nevertheless, the above routine can easily be modified so that each node can have a different number of clustered paths.

We compare the quality of clustered scenario trees against scenario trees that are formed without clustering. For this purpose, we use the measure proposed by Kaut and Wallace (2003) that tests the stability of the scenario tree generator. They assert that the optimal objective function values obtained by different scenario trees generated by a certain method should be distributed with a small variance. That is, the results should be stable across different replications. For our comparisons, we use the same stock and index data used in Şakar and Köksalan (2013b). The estimated mean and standard deviation of the BIST-100 index return that are fed to the random walk model are calculated from the monthly closing prices of the index during January 2003–June 2010¹. The monthly percentage return values of 100 random stocks from BIST are taken from the period January 2003–December 2009 (see footnote 1) , and this period is utilized for the regression analysis. For the liquidity measure, we use the number of shares traded (see footnote 1) and the total number of outstanding shares² corresponding to December 2010. To obtain clustered scenarios, we set $y =3,\, c =5$ and $M =100$. We make 50 independent replications with both clustered scenario trees and trees that are formed without clustering. In each replication, we optimize for the expected return and CVaR criterion separately. We do not optimize for liquidity since it is independent of the index return modeled by scenarios. Table 1 shows the estimated mean and standard deviation of the expected return and CVaR criteria for scenario trees that are formed with and without clustering. Clustered scenario trees result in about a 76 % decrease in the standard deviation of expected return, and a 68 % decrease in the standard deviation of CVaR. Hence we achieve substantial improvement in robustness of scenarios by clustering them.

Table 1 Stability results for unclustered and clustered scenarios

3 An interactive approach

With our SP approach covered in Sect. 2, the DM is expected to select an individual solution among the set of efficient solutions presented to her/him. This may be a difficult decision considering the possibly large number of solutions. We now develop an interactive multistage approach to guide the DM towards her/his preferred solutions. DM preferences will be elicited by the help of the comparison of a limited number of solutions in consecutive iterations. Our approach is based on the interactive weighted Tchebycheff procedure of Steuer and Choo (see Steuer 1986, pp. 419–455). This procedure makes use of the augmented weighted Tchebycheff program which is formulated as follows:

$$\begin{aligned}&Min\,\, \alpha +\rho \sum \limits _{i=1}^k (z_i^*-z_i) \end{aligned}$$

(17)

$$\begin{aligned}&s.t.\quad \alpha \ge w_i \left( {z_i^*-z_i } \right) \quad \forall \,i=1,\, \ldots ,k \end{aligned}$$

(18)

$$\begin{aligned}&\qquad \qquad z_i =f_i \left( x \right) \quad \qquad \forall \,i=1,\, \ldots ,k \end{aligned}$$

(19)

$$\begin{aligned}&\qquad \qquad x\in X \end{aligned}$$

(20)

where $z^{*}$ is the ideal vector in the presence of $k$ criteria, $w_i$ is the weight of criterion $i$ and $\rho$ is a small positive constant used as the augmentation coefficient. This program minimizes the maximum weighted distance from the ideal point in $k$ criteria.

The augmented Tchebycheff program given by (17)–(20) is a powerful model since it can generate any efficient solution with appropriately chosen weights. Our procedure requires the DM to choose among a small number of solutions in each iteration.

3.1 The procedure

In essence, the Interactive Weighted Tchebycheff Procedure aims to converge the best solution by eliciting preference information from the DM in consecutive iterations and contracting the weight space accordingly. We explain the procedure further by discussing its steps briefly. First, an ideal criterion vector is computed and objectives are normalized. A given number of random weight vectors are generated for the criteria (initially, they are freely chosen from the interval [0,1]), and they are reduced to a predetermined number of most-different weight vectors using a filtering approach. Using each of the resulting weight vectors, (17)–(20) is solved to determine solutions with minimum weighted Tchebycheff distances from the ideal point. The resulting solutions are filtered to a preset number of solutions and presented to the DM. After the DM chooses her/his most preferred solution, the weight vector corresponding to this solution is determined. Centered around this weight vector, new, narrowed down ranges for weights of criteria are calculated. Another set of random weight vectors that obey the new ranges are generated and filtered. Again solving (17)–(20) for each weight vector, a new set of solutions concentrated in a neighborhood of the previously selected solution is generated. These are filtered and presented to the DM for her/him to make a selection. This procedure is continued for a predetermined number of iterations unless the DM wants to stop prematurely.

We adopt this procedure to include the preferences of the DM to our SP approach. To make our scenario trees more representative of the TSM, we use clustered scenario trees that are generated as explained in Sect. 2.4. As another issue, we also want to account for the stochasticity of our solutions due to the randomness involved in the scenario generation process as in Balibek and Köksalan (2012). That is, there is randomness in the estimated criteria values of each solution due to the randomness inherent in the scenarios. To statistically account for this randomness, instead of a single scenario tree, we work with multiple scenario trees and generate confidence ellipsoids around solutions. Observing these ellipsoids, the DM will have an understanding about the stability of each of the solutions, where the criteria values of some solutions may have more variation than others. This may affect the DM’s choices. The DM is asked to choose between solutions represented by the ellipsoids. Another modification we make to the Interactive Weighted Tchebycheff Procedure is to carry the preferred solution (ellipsoid) of one iteration to the next. In the original procedure, in each iteration, only new solutions concentrated around the previously selected solution are presented to the DM. There is no guarantee that we will proceed to a better solution in each iteration with this procedure. The solution of the previous iteration may have a better utility value for the DM than the newly generated solutions. As a remedy, in each iteration, we also present the DM the best solution obtained so far.

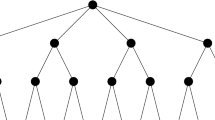
We provide a flowchart of our approach in Fig. 1. We refer to each stage in the flow chart by a stage number (given in boxes to the left of the stages). $N$ is the number of scenarios used to construct ellipsoids. $V$ is the number of weight vectors generated in each iteration later to be filtered. $P$ corresponds to the sample size of ellipsoids to be presented to the DM. Let us further explain the mechanisms used in some of the steps.

Fig. 1

Flowchart of the interactive approach to SP-based PO

In step 1, we generate a large number of scenarios for better market representation purposes and then cluster them to decrease complexity. In step 4, we use a filtering mechanism to achieve the most-different weight vectors. The method we use is the Method of First Point Outside the Neighborhoods (see Steuer 1986, pp. 314–318). This method is also used in step 7, where we filter ellipsoids to determine the ones to present to the DM. The centroids of ellipsoids are utilized for this purpose. At the first iteration, $2P$ ellipsoids found with the weights of the iteration are filtered down to $P$. At other iterations, the selected ellipsoid of the previous iteration is added to the top of the list of $2P$ ellipsoids. Due to the working mechanism of the filtering method, the first ellipsoid is always retained. As a result, we ensure that the best ellipsoid so far is not lost and it is presented to the DM at each iteration.

In step 5, for every weight vector filtered, we solve (17)–(20) and obtain $N$ solutions for each. Utilizing the approach of Balibek and Köksalan (2012), we use these solutions to construct ellipsoids of their criteria values in step 6. (The reader is referred to (Johnson and Wichern (2002), pp. 210–238) for the theory on constructing confidence regions for multivariate means.) When the sample size is large, inferences about a population mean vector can be made without the normality assumption. Large-sample inferences about a mean vector are based on the $\chi ^{2}$ distribution. Let $X_{j}$’s ($j=1,\ldots ,n$) be $k$-dimensional vectors sampled from a population with mean $\mu$ and covariance matrix $S$. When $n-k$ is large, $n(\bar{{X}}-\mu )^{\prime }S^{-1}(\bar{{X}}-\mu )$ is approximately $\chi ^{2}$ distributed with $k$ degrees of freedom. Thus,

$$\begin{aligned} P\left[ {n(\bar{{X}}-\mu )^{\prime }S^{-1}(\bar{{X}}-\mu )\le \chi _k^2 (\gamma )} \right] =1-\gamma \end{aligned}$$

(21)

The above equality defines an ellipsoid which gives a 100($1-\gamma$)% confidence region for the mean of $X_{j}$’s. If we want to build simultaneous confidence intervals for the individual component means, we can project the ellipsoid on the axes of each component. This gives us the following 100($1-\gamma$)% simultaneous confidence intervals:

$$\begin{aligned} \bar{{x}}_{i} \mp \sqrt{\chi _k^2 (\gamma )\frac{s_{ii} }{n}} \qquad i=1,\ldots ,k \end{aligned}$$

(22)

where $s_{ii}$ is the variance for component $i$.

As mentioned before, centroids of the constructed $2P$ ellipsoids are used to filter them down to $P$ in step 7.

For the DM to choose her/his most preferred ellipsoid in step 8, confidence intervals of all criteria corresponding to each ellipsoid are presented to her/him. This approach is preferred because ellipsoids are difficult to present and also hard to visualize for the DM with more than two criteria.

After the DM selects an ellipsoid, in step 9, new ranges for weights of criteria are generated. We require that these are concentrated around the weight vector corresponding to the solution in the ellipsoid that is closest to the centroid. We use Euclidean distance and normalized values to determine this solution, and refer to it as the ‘pseudo centroid’. We apply the procedures defined by Steuer and Choo at this stage. Let $z^{h}$ be the pseudo centroid of the chosen ellipsoid of iteration h. Then the most appropriate weight vector corresponding to $z^{h}$, denoted by $w^{h}$, is found as follows (see Steuer 1986, pp. 448):

$$\begin{aligned} w_i^h =\left\{ {{\begin{array}{ll} \frac{1}{(z_i^*-z_i^h)}\left[ {\sum \limits _{i=1}^k \frac{1}{(z_i^*-z_i^h )}} \right] ^{-1} &{}\quad \hbox {if } \, z_i^h \ne z_i^*\,\hbox { for all } \, i \\ 1&{}\quad \hbox {if } \, z_i^h =z_i^*\\ 0&{}\quad \hbox {if } \, z_i^h \ne z_i^*\, \hbox { but } \, \exists j\ni \,z_j^h =z_j^*\\ \end{array}}} \right. \end{aligned}$$

(23)

Next, the ranges of weights that are concentrated around $w^{h}$ are formed as follows (see Steuer 1986, pp. 449):

$$\begin{aligned} {[}LB_i^{h+1} ,UB_i^{h+1}{]}=\left\{ \begin{array}{ll} {[}0,r^{h}{]} &{} \hbox {if } \, w_i^h -r^{h}/2 \le 0 \\ {[}1-r^{h},1{]} &{} \hbox {if } \, w_i^h +r^{h}/2\ge 1 \\ {[}w_i^h -r^{h}/2,w_i^h +r^{h}/2] &{} \hbox {otherwise} \\ \end{array} \right. \end{aligned}$$

(24)

where $r$ is a pre-determined reduction factor for weights.

In the next section, we demonstrate our approach with stocks from BIST.

3.2 Results of experiments

We use the same 100 stocks used in Şakar and Köksalan (2013b) and Sect.  2.4 for our experiments. The estimated mean and standard deviation of the BIST-100 index used in the random walk model are calculated from monthly closing prices of the index during January 2008–December 2009.³ This period is also utilized for regression analysis. For the liquidity measure, we use the number of shares traded (see footnote 3) and the total number of outstanding shares⁴ corresponding to June 2011. Expected return, CVaR at 90 % probability level and liquidity are used as criteria. We use a three-month SP setting where decisions are made at the beginning of each month. We use clustered scenario trees where five branches stem from each decision node, resulting in 5$^{3}=125$ scenarios.

The number of scenario trees to generate ellipsoids of solutions, $N$, is taken as 50. We use 90 % confidence level for constructing ellipsoids. Ideal and nadir vectors of all scenario trees are computed individually. The nadir vectors are required for normalization purposes, and we approximate them by payoff nadirs. Normalized values are also used for filtering, and we use Euclidean distance as the distance metric of the filtering method.

Based on preliminary tests to determine good parameters for the approach, the number of iterations is set to 5. The sample size of solutions that are presented to the DM, $P$, is selected as 6. The number of weight vectors generated in each iteration, $V$, is chosen as 150, and 0.5 is used as $r$, the reduction factor for weights.

To make experiments with our approach, we need to assume an underlying preference function for the DM to simulate her/his selection of ellipsoids. With three types of distance metrics, we assume that the DM tries to minimize the weighted distance of normalized ellipsoid centroids from the ideal vector. These centroids are found by utilizing average normalized expected return, CVaR and liquidity values of the solutions in the ellipsoids. As distance metrics, we utilize Rectilinear, Euclidean and Tchebycheff distances. The weights of the DM used for expected return, CVaR and liquidity for all distances are 0.5, 0.25 and 0.25, respectively. We make three replications each for the three distance metrics. First, we present the details of the first iteration of one replication with the Tchebycheff distance to illustrate our approach. Later, we summarize all of our results.

In normalization routines used for the weighted Tchebycheff programs and also the simulation of DM preferences of ellipsoids, we aim to scale criteria values between 0 and 1, where 0 is the worst and 1 is the best possible value for all criteria. However, because of the approximation of the nadir point by the payoff nadir, there may be cases where the lower bound is violated. Even so, the progress of the algorithm and the validity of results will not be affected. When simulating DM preferences, the ideal vector is taken as (1, 1, 1).

Expected return, CVaR and liquidity are denoted as ret, cvar and liq in vector representations. Let $\bar{{v}}_j^i =(v_{ret} ,\,v_{cvar} ,\,v_{liq})$ denote the weight vector numbered $j\, (j=1, 2,\ldots , 6)$ of iteration $i$ that leads to one of the six ellipsoids in step 7 of the algorithm that are to be presented to the DM, where $v_k$ denotes the weight of criterion $k$.

3.2.1 The first iteration

150 random weight vectors are generated from the following ranges:

$$\begin{aligned}&\left[ {LB_{ret}^1 ,UB_{ret}^1 } \right] =\left[ {0,\,1} \right] \\&\left[ {LB_{cvar}^1 ,UB_{cvar}^1 } \right] =\left[ {0,1} \right] \\&\left[ {LB_{liq}^1 ,UB_{liq}^1 } \right] =\left[ {0,1} \right] \end{aligned}$$

150 weight vectors are filtered to 12. 50 augmented weighted Tchebycheff programs (one for each scenario tree) are solved with each of these 12 weight vectors. 12 ellipsoids of solutions are generated and filtered down to six by utilizing normalized ellipsoid centroids. For illustration purposes, Fig. 2 shows the solutions used to construct the six ellipsoids. Ellipsoids are abbreviated as ‘E’ in illustrations.

Fig. 2

Plot of the solutions of the six ellipsoids

Six vectors of weights that led to these ellipsoids are:

• $\bar{{v}}_1^1 \,\, =$ (0.4145, 0.4065, 0.1790)

• $\bar{{v}}_2^1 \,\, =$ (0.0829, 0.5416, 0.3754)

• $\bar{{v}}_3^1 \,\, =$ (0.5798, 0.0853, 0.3348)

• $\bar{{v}}_4^1 \,\, =$ (0.7705, 0.2223, 0.0073)

• $\bar{{v}}_5^1 \,\, =$ (0.0690, 0.3625, 0.5684)

• $\bar{{v}}_6^1 \,\, =$ (0.2279, 0.1643, 0.6078)

For the six ellipsoids retained by the filter, the confidence regions of criteria are found by projecting the ellipsoids to individual criterion axes. Then the DM is asked to determine her/his most preferred one. Figure 3 illustrates the confidence regions of the six ellipsoids that are presented to the DM. The criteria values of the centroids of the ellipsoids are provided for the reader in Table 2, where we also include normalized values and the weighted Tchebycheff distances of the centroids of the ellipsoids from the ideal vector. These weighted Tchebycheff distances of the ellipsoids from the ideal point are assumed to represent the DM’s preferences and are used to simulate the DM’s responses.

Table 2 Criteria values of the centroids of ellipsoids of iteration 1

Fig. 3

Presenting the DM ellipsoid projections

As observed from Table 2, the centroid of Ellipsoid 1 has the smallest weighted Tchebycheff distance from the ideal vector. Accordingly, the DM is assumed to select Ellipsoid 1, and we continue to find the most appropriate weight vector corresponding to the pseudo centroid of this ellipsoid by using (23):

$$\begin{aligned} w^{1}=(w_{ret}^1 ,w_{cvar}^1 ,w_{liq}^1 )\,\, = (0.4145, 0.4065, 0.1790) \end{aligned}$$

Centered around $w^{1}$, the new ranges of weights for the next iteration found by (24) are:

$$\begin{aligned}&\left[ {LB_{ret}^2 ,UB_{ret}^2 } \right] =\left[ {0.1645,0.6645} \right] \\&\left[ {LB_{cvar}^2 ,UB_{cvar}^2 } \right] =\left[ {0.1565,0.6565} \right] \\&\left[ {LB_{liq}^2 ,UB_{liq}^2 } \right] =\left[ {0,0.5} \right] \end{aligned}$$

3.2.2 Summary of the Results of Experiments

Table 3 summarizes the three replications performed while assuming the DM tries to minimize weighted Tchebycheff distance from the ideal point. The first iteration of replication 1 was discussed in the previous section. As a result of the three replications, the DM is presented solutions that have weighted Tchebycheff distances of 0.1654, 0.1698 and 0.1768 from the ideal point. To evaluate the results, we find the solution closest to the ideal point by using DM’s weights of criteria: 0.5, 0.25 and 0.25 for expected return, CVaR and liquidity, respectively. This solution in normalized terms is (expected return, CVaR, liquidity) = (0.6725, 0.3561, 0.3450) with a distance value of 0.1637. We see that the algorithm produces solutions that are close to the best solution of the DM, and the achieved distance values are close to the minimum distance.

Table 3 Results of experiments with a Tchebycheff preference function for the DM

Tables 4 and 5 summarize the results with underlying preference functions of the DM with Rectilinear and Euclidean distances. With Rectilinear distance, the best solution for the DM in normalized terms is (expected return, CVaR, liquidity) = (0.9723, 0.9895, $-$0.0068), and it has a distance value of 0.2907. With Euclidean distance, the solution is (0.7974, 0.8049, 0.1630) with a distance of 0.2375. We can observe that the algorithm can approach the best solution for the DM in these cases too. The distances of solutions attained while assuming a Euclidean distance for the DM are particularly good.

Table 4 Results of experiments with a Rectilinear preference function for the DM

Table 5 Results of experiments with a Euclidean preference function for the DM

4 Conclusions

In this study, we studied an interactive approach to a multicriteria multi-period PO problem modeled by SP. In our SP approach, we generate scenarios on the return of a stock market-representative index and estimate individual stock returns from these scenarios. We use expected return, CVaR and liquidity as criteria. In our former work that covers our SP approach, we had presented the DM a discrete representation of the efficient frontier. We developed an interactive approach to provide the DM with a highly-preferred single solution. The approach is based on the Interactive Weighted Tchebycheff Procedure, which aims at converging the best solution by eliciting preference information from the DM in consecutive iterations and contracting the weight space accordingly. In our approach, we also took the stochasticity of market movements modeled by scenarios into account and provided the DM with statistical information. Working with multiple clustered scenarios, we constructed confidence ellipsoids around solutions and the DM was asked to make her/his preferences considering these ellipsoids. According to her/his selection, an increasingly concentrated set of ellipsoids were generated in each iteration. Another modification we made to the Interactive Weighted Tchebycheff Procedure is preserving the best solution generated so far throughout the process.

We carried out experimental studies by simulating DM preferences with three types of underlying preference functions. Using Tchebycheff, Rectilinear and Euclidean distances of the centroids of the ellipsoids from the ideal vector to represent the DM’s preferences, we made replications utilizing stocks from BIST. In all replications, the solution obtained by our approach was close to the best solution of the DM as measured by the assumed preference function. This result was achieved with only five iterations, indicating a small cognitive load on the DM.

The contributions of the current research to PO literature are several fold. It supports the DM with portfolio decisions over multiple periods. The scenario trees used in the SP approach are tailored to represent the uncertain financial markets well. The DM is included in the optimization process in an interactive manner and guided toward preferred solutions without requiring a heavy cognitive burden. We modify the Interactive Weighted Tchebycheff Procedure in order to quickly reach the preferred solutions of the DM. We address the stochasticity in the estimated multiple criteria statistically using confidence regions. We believe that these contributions will attract other researchers to address multiple criteria, multi-period PO.