Two-stage portfolio optimization with higher-order conditional measures of risk

Abstract

We describe a study of application of novel risk modeling and optimization techniques to daily portfolio management. In the first part of the study, we develop and compare specialized methods for scenario generation and scenario tree construction. In the second part, we construct a two-stage stochastic programming problem with conditional measures of risk, which is used to re-balance the portfolio on a rolling horizon basis, with transaction costs included in the model. In the third part, we present an extensive simulation study on real-world data of several versions of the methodology. We show that two-stage models outperform single-stage models in terms of long-term performance. We also show that using high-order risk measures is superior to first-order measures.

1 Introduction

The main objective of this paper is to evaluate the usefulness of several risk modeling and optimization techniques for daily stock portfolio optimization. In the portfolio optimization problem in its simplest form, the return rates of $n$ assets are represented by an $n$-dimensional random vector $R$, with $R_j$ denoting the return rate of asset $j=1,\ldots ,n$. The $n$-dimensional vector $z$ represents the distribution of the capital among assets: $z_j$ is equal to the fraction of the capital invested in asset $j$. The total return rate of the portfolio at the end of the investment period is

$$\begin{aligned} R^{\top }z = \sum _{j=1}^n R_j z_j. \end{aligned}$$

The portfolio problem is to find an “optimal” way to distribute the initial capital among the $n$ assets, under the condition that $z\in Z$, where $Z\subset \mathfrak {R}^n$ is a convex and compact set of feasible asset allocations. As the return rates of the assets are random, the portfolio return rate is a random variable, and thus the meaning of “optimal” depends of the modeling approach.

In a pioneering study, Markowitz (1952) argued that portfolio performance can be measured by using two scalar characteristics: the mean of the portfolio return, ${E}\big [R^{\top }z\big ]$, and the variance of the return, $\text {Var}\big [R^{\top }z\big ]$, which characterizes its riskiness. We can then minimize the variance for a fixed value of the mean, or maximize the mean, while keeping the variance bounded. Since then, numerous theoretical and practical studies evaluated the usefulness of the mean–variance approach in portfolio optimization.

Further improvement was made by considering more general mean–risk models, with different measures of variability (Kijima and Ohnishi 1993). By considering consistency with stochastic dominance, the papers (Ogryczak and Ruszczyński 1999, 2001, 2002), introduced a family of mean–semideviation models, which are particularly useful for portfolio models (see, e.g., Mansini et al. 2003; Ruszczyński and Vanderbei 2003).

In the last decade, axiomatic models of risk have been studied extensively, in particular, coherent risk measures, introduced by Artzner et al. (1999). In the following definition, the uncertain outcomes $X$ and $Y$ represent losses, and $\mathbb {1}$ denotes the sure loss of 1. Coherent risk measures are functionals $\rho :\fancyscript{X} \rightarrow \mathfrak {R}$ defined on a suitable vector space $\fancyscript{X}$ of random outcomes, which satisfy the following axioms:

• Convexity: $\rho (\alpha X + (1-\alpha )Y) \le \alpha \rho (X) + (1-\alpha )\rho (Y),\quad \forall X,Y \in \fancyscript{X}$, $\alpha \in [0,1]$;

• Monotonicity: If $X, Y \in \fancyscript{X}$, and $X\le Y$, then $\rho (X) \le \rho (Y)$;

• Translation Property: If $a \in \mathfrak {R}$ and $X \in \fancyscript{X}$,then $\rho (X + a\mathbb {1}) = \rho (X) + a$;

• Positive Homogeneity: If $\beta \ge 0$ and $X \in \fancyscript{X}$, then $\rho (\beta X) = \beta \rho (X)$.

The inequality in the monotonicity axiom is understood in the almost sure sense.

Important examples of coherent risk measures are models of the form

$$\begin{aligned} \rho (x) = E[X] + \gamma r[X], \end{aligned}$$

(1)

where $r(\cdot )$ is the upper semideviation of order $p \ge 1$, given in Eq. (2), or a weighted mean-deviation from quantile in Eq. (3):

$$\begin{aligned}&\displaystyle r(X) = E[(X - E[X])_{+}^p]^{1/p}, \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle r_\alpha (X) = \min _\eta E\left[ \max \left( \frac{1-\alpha }{\alpha }(X-\eta ),\eta -X\right) \right] , \quad \alpha \in (0,1). \end{aligned}$$

(3)

For these both cases, when $\gamma \in [0, 1]$, the mean-risk model is coherent (Ruszczyński and Shapiro 2006b). It is also worth mentioning that the deviation from quantile (3) is related to the Average (Conditional) Value at Risk (see, Rockafellar and Uryasev 2000, 2002) by the formula [cf. (Shapiro et al. 2009, sec. 6.2.4)]

$$\begin{aligned} E[X] + r_\alpha [X] = \text {AVaR}_\alpha [X] = \frac{1}{\alpha } \int _{1-\alpha }^1 F_X^{-1}(\beta )\;d\beta = \min _{\eta }\left\{ \eta + \frac{1}{\alpha }E\big [( X-\eta )_+\big ]\right\} . \end{aligned}$$

Here $F_X^{-1}(\cdot )$ is the quantile function of $X$.

We can formulate the general one-stage portfolio problem with a risk measure $\rho (\cdot )$ as an objective function as follows:

$$\begin{aligned} \min _{z\in Z} \rho [-R^{\top } z]. \end{aligned}$$

(4)

We adapt the convention that the argument of the risk measure $\rho [\cdot ]$ represents cost (losses) and that is why we use the minus sign in front of the return rate. A fundamental modeling issue is to choose the risk function $r(\cdot )$ used in this model. For the measures of risk (2) with $p=1$ and (3), the resulting optimization problem (4) is a linear programming problem, which can be efficiently solved by specialized techniques (Mansini et al. 2003). Parametric methods of Ruszczyński and Vanderbei (2003) allow for generating a family of solutions, corresponding to a range of values of the parameter $\gamma$ in (1).

However, if a portfolio optimization model is used in a rolling horizon fashion, as in Matmoura and Penev (2013), with re-balancing in regular time intervals, it makes sense to include the re-balancing action and associated transaction costs into the model. To address this issue in the simplest possible way, a two-stage model can be formulated. In this model, an option to re-balance the portfolio at the end of the first period is available. Let us denote by $R^t_j$ the return rate of asset $j= 1,\ldots ,n$ in stage $t \in \left\{ 1,2\right\}$. Asset allocations are denoted by $n$-dimensional vectors $z$ and $y$, where $z_j$ represents the amount of capital invested in asset $j$ at stage 1, and $y_j$ the amount invested at stage 2. The vector $y$ may depend on the observations gathered in stage 1. The end portfolio value in stage $1$ is given by $(\xi ^1)^{\top } z$ and the end value at stage 2 is $(\xi ^2)^{\top } y$, where

$$\begin{aligned} \xi ^t = \mathbb {1} + R^t, \end{aligned}$$

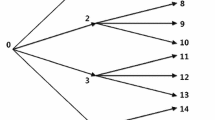
with $\mathbb {1}$ denoting the sure outcome of 1. The random vectors $\xi ^1$ and $\xi ^2$ are, in general, dependent. If they have have finite numbers of realizations, the most transparent way is to represent them in a form of a scenario tree. An example of such a tree is depicted in Fig. 1. The nodes at levels one and two represent realizations of $\xi ^1$ and $\xi ^2$, respectively. The node at level zero is known as the root node and represents the beginning of the process. Each node at level one represents a different realization of $\xi ^1$. It is connected to a set of children nodes at level two, which represent possible outcomes of $\xi ^2$, following the first stage outcome. With each arc of the tree, a probability is associated. Probabilities of arcs leading to nodes at level one are the probabilities of realizations of $\xi ^1$. The probabilities of arcs leading to nodes at level 2, are conditional probabilities of realizations of $\xi ^2$.

Fig. 1

Scenario tree

The two-stage portfolio problem allows us to model the re-allocation option within an optimization problem. In stage 1, asset allocations $z$ are to be determined. Then a realization of $\xi ^1$ is observed, and the allocations can be changed to $y$. In the scenario tree setting, there can be a different value of $y$ for each node at level 1. Finally, the realization of $\xi ^2$ is observed. As a result, the final portfolio value can be calculated. Such an approach, with the use of dynamic measures of risk, has been first developed in Miller (2008) and Miller and Ruszczyński (2011). We formally define the two-stage model in Sects. 2 and 3.

Our intention is to advance these ideas, by exploring new scenario tree generation methods and using higher order measures of risk.

In Sect. 2, several scenario tree generation methods are described. First, a multivariate GARCH model is used to generate an adequate number of scenarios to model the random returns. Then, three different tree construction algorithms are developed: K-means and Two-Step cluster algorithms in forward and backward forms, and a backward multi-facility location algorithm. In order to evaluate the quality of the scenario trees, Monge–Kantorovich transportation model is formulated to compare the probability distributions of the “original” probability distribution (empirical distribution supported on the scenarios generated) with the probability distributions supported on the constructed scenario trees.

In Sect. 3, a two-stage portfolio problem with an option to re-balance is modeled by using higher-order conditional risk measures. A risk-averse multicut method is proposed to solve this model.

In Sect. 4, computational results will be presented to compare scenario generation techniques and performance of the constructed portfolios on portfolios constructed from the components of the Dow Jones Index.

Finally, at the conclusion of this study, an overall summary of our contribution and a list of some possible future research directions will be presented.

2 Scenario tree generation

2.1 Background

A substantial body of literature exists about generating scenario trees for stochastic optimization models. Heitsch and Romisch (2009) proposed a theory-based heuristics for generating scenario trees from an initial set of scenarios, and applied these heuristics in electric power management. Their proposed heuristics have a recursive scenario reduction algorithm and also bundling steps based on forward or backward scenario tree generation methods. They used the stability result in multi-stage stochastic programs from the study in Heitsch et al. (2006) to compare the closeness of the original probability distribution to its scenario tree approximation. The conditions on the initial approximation in applications is constructed from a discrete probability distribution by using a sampling method or from a general probability distribution by using discretization schemes. However, the algorithm can be used as a heuristics for scenario tree generation in other applications.

Hochreiter and Pflug (2007) showed that the problem of obtaining accurate and valuable scenario tree approximations can be viewed as the problem of optimally approximating a given distribution by using a distance function. In that paper, it is found that the best approach is to use the Wasserstein distance in tree approximation. The resulting optimization problem can be formulated as a multi-dimensional facility location problem, and then well-known heuristic algorithms for multi-facility location problems can be applied. They also showed that a scenario tree is constructed as a nested facility location problem to use in multi-stage stochastic programs. A multi-stage stochastic mean-risk financial programming problem is used to test the model. They concluded that if the objective of the approximation is to achieve a controlled matching of certain moments and a controllable coverage of heavy tails, scenario tree generation based on multidimensional facility location will be the best fit.

Our approach builds on these contributions, with the intention to be able to handle huge trees arising in financial applications.

2.2 Scenario generation

Financial data are insufficient for construction optimization models based on empirical distributions alone. It is imperative to generate scenarios that were not observed in practice, but are possible according to statistics. For this purpose, we need a model for scenario generation.

The first step in scenario generation is to obtain data to construct scenarios. In this study, daily stock price data of the 30 companies included in the Dow Jones index are obtained for a period of three years, from September 2, 2008, to November 30, 2011.

Next, in order to model the probabilistic information in the data, an adequate number of scenarios must be generated. As we are interested in an adequate modeling of the tail behavior, multivariate GARCH models appear to be particularly useful. In multivariate GARCH models, the most important issue is the parametrization of the covariance matrix, at a minimum loss of generality. In this study, we will use multivariate GO-GARCH(1,1) (Van Der Weide 2002) model to generate scenarios. Its structure can be summarized as follows.

We assume that the observed vector-valued time series $\left\{ x_t\right\}$ (of dimension $m=30$) is a linear combination of unobserved $m$-dimensional normal vectors $\left\{ y_t\right\}$ having uncorrelated components, that is,

$$\begin{aligned} x_t = Z y_t, \quad t=0,1,2,\ldots \end{aligned}$$

The square matrix $Z$ is assumed to be constant over time and invertible.

Unobserved components have a diagonal covariance matrix $H_t = \text {diag}\{h_{i,t},\ i=1,\ldots ,m\}$, and thus the covariance matrix of $x_t$ is $V = E \big [x_t x_t^{T}\big ] = Z H_t Z^{T}$. The crucial component of the model is the evolution of the diagonal elements $h_{i,t}$ of the covariance matrix $H_t$:

$$\begin{aligned} h_{i,t+1} = (1 - \alpha _i - \beta _i) + \alpha _i y^2_{i,t} + \beta _i h_{i,t}, \quad i =1,\ldots ,m, \quad t=0,1,2,\ldots , \end{aligned}$$

where the initial matrix $H_0 = I$.

The historical data are used to calculate the least-squares estimates of the matrix $Z$ and the coefficients $(\alpha _i,\beta _i),\, i=1,\ldots ,m$.

Once the model is constructed, it can be used to generate an arbitrary number of scenarios. Assuming that the data were collected for the period $t=0,1,\ldots ,T$, we generate scenarios for times $T+1,T+2,\ldots$. In our case, we use only two next steps, that is, $T+1$ and $T+2$, to prepare scenarios for $\xi ^1$ and $\xi ^2$.

2.3 Tree generation

Raw scenarios are not suitable for two-stage optimization models, because after stage 1, while deciding about allocations $y$ for the second stage, we would know not only the past return realizations $\xi ^1$, but also the future realizations $\xi ^2$ (see the left part of Fig. 2). Constructing a scenario tree eliminates this problem as it can be seen in the right part of Fig. 2.

Fig. 2

First-stage clustering in a forward tree construction

There are two different ways to design scenario tree generation methods, forward and backward. In a forward tree construction, starting at the first stage, one merges selected nodes into clusters and moves forward until the last stage. Forward tree construction is illustrated in Figs. 2 and 3. In a backward tree construction, one starts at the last stage, merges selected nodes into clusters and this will join all their predecessors as well. In this way, we move backward until the first stage. Backward tree construction is illustrated in Figs. 4 and 5. In scenario tree generation, it is important to maintain probability information while reducing the number of scenarios, that is, to assign to a scenario representing a group of scenarios the sum of their probabilities.

Fig. 3

Second-stage clustering in a forward tree construction

Fig. 4

Second-stage clustering in a backward tree construction

Fig. 5

First-stage clustering in a backward tree construction

Since the quality of multi-stage stochastic optimization models depends heavily on the quality of the underlying scenario model, this study will focus on constructing a scenario tree for two-stage portfolio optimization problem, so that portfolio optimization problem with rebalancing can be solved in a more time-efficient way.

Five different scenario generation methods are used in this study: $K$-means and two-step clustering methods in forward and backward versions, and a backward scenario generation method based on the idea of a multi-facility location problem. Then, these five models will be compared by using a mass-transportation model.

2.4 Multi-facility-location-based scenario tree generation method

We will use a hybrid method which is composed of two different algorithms within a backward scenario tree generation method. In the first part, a nearest centroid based heuristic is used to form a given number of clusters in the second stage.

Choosing initial centroids is very important in a clustering algorithm since bad initialization can lead to poor results. The fastest and easiest way to choose initial centroids is pure random. However, it will very likely lead to poor results since it can choose these initial centroids close to each other. In the initialization part of our algorithm, we want to choose the initial centroids that are spread out from each other. We will use a very similar initialization approach as in Arthur and Vassilvitskii (2007). Nearest centroid based heuristic is explained in Algorithm 1.

The distance measure used in this algorithm is as follows:

$$\begin{aligned} d_{ij} = \sqrt{\sum \limits _{n=1}^{30} \left[ (r^1(i,n) - r^1(j,n))^2 + (r^2(i,n) - r^2(j,n))^2\right] }, \end{aligned}$$

(5)

where $r^1$ represents the return rate at the first stage, $r^2$ represents the return rate at the second stage, $i$ and $j$ represent the scenarios, and $n$ represents the security.

In the second part of this hybrid method, in order to aggregate first-stage nodes, a multi–facility location problem is formulated.

We denote by $J$ the total number of scenarios (after the initial greedy aggregation) and by $I<J$ the desired number of first-stage nodes. For $i,j=1,\ldots ,J$ we use $d_{ij}$ to denote the distance calculated according to formula (5). The multi-facility location problem can be formulated as follows:

$$\begin{aligned} \min&\sum _{i=1}^{J}\sum _{j=1}^{J} d_{ij} x_{ij} \\ {\mathrm {s.t.}}&\sum \limits _{i=1}^{J} x_{ij} = 1, \quad \forall j=1,\ldots ,J, \\&\sum \limits _{i=1}^{J} v_{i} = I, \\&x_{ij} \le v_{i}, \quad \forall i, j=1,\ldots ,J, \\&\text {all } x \text { and } v \text { variables are binary.} \end{aligned}$$

In the problem above, $v_i$ is the decision to use scenario $i$ as a first-stage node, and $x_{ij}$ represents the assignment of scenario $j$ to node $i$. It is a large-scale problem, and we solve it by a greedy method using the linear programming relaxation, in which the binary variables $x$ and $v$ are allowed to take any values in [0,1]. After a relaxed problem is solved, all $v_i = 1$ are permanently fixed; if none is equal to 1, we choose the one that is closest to 1, and fix it at 1. After that, a reduced problem with a smaller number of variables is solved, etc. Our experience indicates that this procedure does not lead to significant errors and allows for processing large data sets.

2.5 $K$-means scenario tree generation method

$K$-means is a clustering method in which a set of $n$ observations $S=\{x_1, x_2,\ldots ,x_n\}$ are partitioned into $k$ clusters ($k \le n$). Each scenario is a $d$-dimensional vector, where $d=30$ in this study (the number of Dow Jones stocks). Let $S = S_1\cup S_2\cup \cdots \cup S_k$ be the partition of the set; the objective of the $K$-means method is to minimize the sum of squares within clusters:

$$\begin{aligned} \min _{S_1,\ldots ,S_k}\quad&\sum \limits _{i=1}^{k}\sum \limits _{x_j\in S_i} \left\| x_j - m_i(S_i)\right\| ^2\\ \text {subject to}\quad&S_1\cup S_2\cup \cdots \cup S_k = S,\\&S_i\cap S_j=\emptyset \ \text {if}\ i\ne j. \end{aligned}$$

In the problem above, $m_i(S_i)$ is the mean of the points in $S_i$.

The first $k$ initial means are randomly selected from the scenario set. Then, every scenario is associated with the nearest mean. Next, the centroid of each cluster becomes the new mean for that cluster. Finally, when no new centroids are created, the method stops.

The $K$-means algorithm is used to construct scenario trees in two-stage stochastic portfolio problem is given in Algorithm 2.

In the $K$-means model, Euclidean distance is used as a metric, and the number of first-stage clusters $k$, and second stage clusters $l$, are input parameters. Therefore, good results from this method depend on the appropriate choice of $k$ and $l$.

2.6 Two-step clustering

IBM’s (SPSS Inc 2004) two-step clustering scenario tree generation method is designed for very large data sets. The method requires only one pass of the data, and has two major steps. In the first step, scenarios are grouped into many small preclusters. Then, these preclusters are clustered into a desired number of clusters. The method is explained in Algorithm 3.

As it is in $K$-means model, Euclidean distance is used as a metric, and the number of clusters at the first stage $k$, and at the second stage $l$, are input parameters.

2.7 Quality of scenario trees

No universally good scenario tree generation method exists. Therefore, we need a measure to evaluate the quality of the trees generated. One possibility is use error values of methods or convergence of the objective function values can be used. Pflug defined an approximation error in Pflug (2001) as follows. Let the original problem be

$$\begin{aligned} \min \limits _{x \in X} \quad F(x; \tilde{\xi }), \end{aligned}$$

and the tree-based problem be

$$\begin{aligned} \min \limits _{x \in X} \quad F(x; \tilde{\eta }), \end{aligned}$$

with the solution $x^*$. Then, the approximation error can be calculated as follows:

$$\begin{aligned} e_f(\tilde{\eta },\tilde{\xi }) = F(x^*; \tilde{\xi }) - \min \limits _x F(x; \tilde{\xi }) \ge 0. \end{aligned}$$

However, to calculate this error function is not easy because we need to find the true objective value for a given solution $x$, and the true optimal solution, which is practically impossible. Therefore, in this study a mass transportation model will be formulated to compare the original distribution with the distribution in the scenario tree. The model evaluates the Monge–Kantorovich metric.

In the model below, we use the following data:

We look for the cheapest way to move the probability mass from the “original” distribution (the empirical distribution supported on the generated scenarios) and the distribution on the tree. The variables $f_{ij}$ represent the probability mass to be moved from path $i$ in the original distribution to path $j$ in the tree:

$$\begin{aligned} \begin{aligned} \min&\quad \sum _{i} \sum _{j} d_{ij} f_{ij} \\ \text {subject to}&\quad \sum _{j} f_{ij} = p_i,\quad \forall \;i, \\&\quad \sum _{i} f_{ij} = q_j, \quad \forall \;j, \\&\quad f_{ij} \ge 0, \quad \forall i, j. \end{aligned} \end{aligned}$$

(6)

The optimal value of this problem will be used as a measure of the quality of the tree.

3 Two-stage portfolio optimization problem with risk measures

3.1 General formulation

The problem (4), when the risk function is a semideviation of order 1, or weighted mean-deviation from quantile, can be formulated and solved as a linear programming problem (see Mansini et al. 2003; Ruszczyński and Vanderbei 2003 and also Miller and Ruszczyński 2011 for additional insights). We shall focus on the two-stage version, as outlined in Sect. 1. In what follows, we assume that the sequence of returns $(R^1,R^2)$ has a distribution supported on a scenario tree.

Let $p^1$ be the first-stage probability vector, with $p_i^1$ denoting the probability of outcome $R^1_i$ at the first stage, and let $p_i^2$ be the conditional probability vector for each node $i$ in the first level, with $p_{il}^2$ denoting the probability of moving to node $l$ in the second-stage from node $i$. The corresponding realizations $R^2_{il}$ with probabilities $p_{il}^2$ represent the conditional distribution of $R^2$, given that the realization $R^1_i$ occurred.

The two-stage portfolio optimization problem can be formulated as follows

$$\begin{aligned} \min _{z\in Z} \rho _1\big [ V(z)\big ], \end{aligned}$$

(7)

where $V(z)$ is a random variable representing the conditional risk measure at stage 2. Its realizations, $V_i(z)$, are the optimal values of the second stage problem:

$$\begin{aligned} V_i(z) = \min _{y_i\in Y_i(z)} \rho _{2i}\big [-(\xi ^2_i)^{\top } y_i\big ]. \end{aligned}$$

(8)

In Eq. (8), the argument of the conditional measure of risk $\rho _{2i}[\cdot ]$ is the negative of the total wealth after stage 2. The feasible set $Y_i(z)$ depends on the initial investments $z$ and the realization of the returns in the first stage, which is represented by the branch index $i$. In the absence of transaction costs, it would have the form resulting from the simple cash balance equation:

$$\begin{aligned} Y_i = \bigg \{y \in Y: \big (\xi ^1\big )^{\top } z = \mathbb {1}^{\top } y\bigg \}. \end{aligned}$$

However, the presence of transaction costs makes this formulation insufficient. In the next section, we describe a detailed model for the case of a mean–semideviation measure of risk.

The use of composition risk measures in (7)–(8) follows form the general theory of time-consistent dynamic measures or risk (see, Ruszczyński 2010 and the references therein).

For the main concepts and results of the theory of dynamic measures of risk, see Artzner et al. (2007), Cheridito et al. (2006), Föllmer and Penner (2006), Fritelli and Scandolo (2006), Pflug and Römisch. (2007), Riedel (2004) and Ruszczyński and Shapiro (2006a) and the references therein.

3.2 The mean-semideviation model

In this section, risk averse two-stage portfolio problem will be formulated with the mean-semideviation risk function of order $r$.

Indices:

       $i \in \{1,\ldots ,I\}$—First-stage scenarios,

       $l \in \{1,\ldots ,L(i)\}$—Second-stage scenarios for each first-stage scenario,

       $j \in \{1,\ldots ,n\}$—Securities.

Parameters:

       $p_i$—probability of a first-stage scenario $i$,

       $p_{il}$—conditional probability of second-stage scenario $l$ after the first-stage scenario $i$,

       $R_{ji}$—return rate of security $j$ in first-stage scenario $i$,

       $R_{jil}$—return rate of security $j$ in second-stage scenario $l$ after the first-stage scenario $i$,

       $\varepsilon _j$—relative transaction cost of security $j$,

       $\gamma$—risk aversion constant,

First-Stage Variables:

       $z_j$—amount invested in security $j$ in the first-stage,

       $\xi$—auxiliary variables representing shortfalls at the first-stage,

       $u$—expectation at the first-stage,

Second-Stage Variables:

       $y_{ji}$—new position in security $j$ in scenario $i$ after the first-stage,

       $b_{ji}$—amount spent to buy security $j$ in scenario $i$ after the first-stage,

       $s_{ji}$—value of security $j$ sold in scenario $i$ after the first-stage,

       $\sigma$—auxiliary variables representing shortfalls at the second-stage,

       $m$—conditional expectation at the second-stage.

We assume that the initial capital is 1, and thus (in the simplest version)

$$\begin{aligned} z \in Z = \Bigg \{z \in {\mathbb {R}}^n : \sum _{j=1}^{n}{z_j} = 1, \ z_j \ge 0, \ j = 1,\ldots ,n \Bigg \}; \end{aligned}$$

more complex restrictions on the initial investments are possible as well, as long as they define a polyhedral set $Z$. In order to estimate the (relative) transaction costs, the following bid-ask spread formula is used:

$$\begin{aligned} \varepsilon _j = \frac{(\text {AskPrice}_j - \text {BidPrice}_j) / 2}{\text {AskPrice}_j}, \quad j=1,\ldots ,n. \end{aligned}$$

This formula assumes that a “fair price” is half-way between the bid and the ask prices, and ignores transaction costs due to the price impact of large trades. The link between the first-stage variables $z$ and the second-stage variables $y$ is provided by the cash balance equation:

$$\begin{aligned} y_{ji} = (1 + R_{ji}) z_j + (1 - \varepsilon _j) b_{ji} - (1 + \varepsilon _j) \cdot s_{ji}, \end{aligned}$$

(9)

in which we symmetrically assign transaction costs to the sales and purchases. The first-stage problem (7) with mean-semideviation risk functions of order $r \ge 1$ can be now formulated as follows:

$$\begin{aligned} \min _{z\in Z} \quad \sum _{i=1}^I p_i V_i(z) + \gamma \Bigg (\sum _{i=1}^I p_i \bigg (\max (V_i(z) - p^{\top } V(z), 0)\bigg )^r\Bigg )^{1/r}, \end{aligned}$$

where $V_i(z)$ is the optimal value of $i$th second-stage problem (8).

The first-stage problem can be rewritten as follows:

$$\begin{aligned} \begin{aligned} \min&\quad u + \gamma \Big (\sum _{i=1}^I p_i \xi _i^r\Big )^{1/r} \\ \text {s.t.}&\quad u = \sum _{i=1}^I p_i V_i(z), \\&\quad u \le V_i(z) + \xi _{i},\quad i=1,\ldots ,I, \\&\quad \xi \ge 0, \\&\quad z \in Z. \end{aligned} \end{aligned}$$

(10)

The second-stage problem (8) with mean-semideviation risk function of order $r \ge 1$ is formulated in scenario $i$ as follows:

$$\begin{aligned} \begin{aligned} \min&\quad -m_i + \gamma \Big (\sum _{l=1}^{L(i)} p_{il}\sigma _{il}^r\Big )^{1/r} \\ \text {s.t.}&\quad y_{ji} = (1 + R_{ji}) z_j + (1 - \varepsilon _j) b_{ji} - (1 + \varepsilon ) s_{ji},\quad j=1,\ldots ,n, \\&\quad \sum _{j=1}^n \big ( b_{ji} - s_{ji}\big )=0, \\&\quad W_{il} = \sum _{j=1}^n (1 + R_{jil}) y_{ji}, \quad l = 1,\ldots , L(i), \\&\quad m_i = \sum _{l=1}^{L(i)} p_{il} W_{il}, \\&\quad m_i \le W_{il} + \sigma _{il},\quad l=1,\ldots ,L(i), \\&\quad b \ge 0, \quad s \ge 0, \quad \sigma \ge 0. \end{aligned} \end{aligned}$$

(11)

The optimal value of this problem is denoted by $V_i(z)$. In a more general formulation, we may use different risk-aversion parameters $\gamma$ in the first-stage problem (10) and in the second stage problems (11), making them dependent on the scenario $i$. We can also add to problem (11) additional restrictions on the allocations $y_{ji}$, $j=1,\ldots ,n$, as long as they define a nonempty polyhedral set. In particular, keeping the first-stage investments unchanged, that is, setting $y_{ji} = (1 + R_{ji}) z_j$, $j=1,\ldots ,n$, should be feasible for problem (11).

3.3 Risk-averse multicut method for higher-order conditional measures of risk

If $r=1$, the problems (10) and (11) (for $i=1,\ldots ,I$) can be put together into a large-scale linear programming problem, with $V_i$, $i=1,\ldots ,I$, treated as variables [given by the formula in the first row of (11)]. The dimension of this problem, however, is of order $I\times (L + n)$ variables and constraints, which becomes unmanageable for realistic sizes of scenario trees. If $r>1$, an additional complication arises from the fact that we have to deal with a large-scale nonlinear optimization problem.

We shall, therefore, develop a decomposition method for solving problem (10)–(11), based based on Benders decomposition. In order to describe this method, we have to recall the dual representation of measures of risk. For a coherent measure of risk $\rho :\fancyscript{X}\rightarrow \mathfrak {R}$, where $\fancyscript{X}$ is the vector space of random variables on a finite probability space having $I$ elementary events, a closed convex set $\fancyscript{A}$ of probability measures on this space exists, such that

$$\begin{aligned} \rho (V) = \max _{\mu \in \fancyscript{A}} \ \sum _{i=1}^I \mu _i V_i,\quad V\in \fancyscript{X}. \end{aligned}$$

(12)

This representation, first proved in Artzner et al. (1999), is valid in a much more general setting as well (see, Ruszczyński and Shapiro 2006b; Shapiro et al. 2009 and the references therein). The set $\fancyscript{A}$ is the subdifferential of $\rho (\cdot )$ at zero. Analytical expressions for the sets $\fancyscript{A}$ for popular measures of risk (including the mean-semideviation measure) are available (see Shapiro et al. 2009).

Owing to (12), the first-stage problem (7) becomes

$$\begin{aligned} \min _{z \in Z} \max _{\mu \in \fancyscript{A}} \ \sum _{i=1}^I \mu _i V_i(z), \end{aligned}$$

(13)

Two main issues arise from this formulation. First, solving the “$\max$” problem above is hard by using all of the elements in $\fancyscript{A}$, especially, when $r>1$. Second, there is no easy expression for $V_i(z)$, $i=1,\ldots ,I$, which are optimal values of problems (11).

In order to handle the first issue, rather than using $\fancyscript{A}$, it approximation from within, $\text {conv}\big (\{\mu ^0,\mu ^1,\ldots ,\mu ^{k-1}\}\big )$ will be used. Here $\text {conv}(C)$ denotes the convex hull of a set $C$, and $\mu ^1,\ldots ,\mu ^{k-1}$ are elements of $\fancyscript{A}$ collected in iterations $1,\ldots ,k-1$ of the method. For $\mu ^0$ we substitute the nominal probability distribution $p$, which is an element of $\fancyscript{A}$ for all practically relevant measures of risk, including the mean–semideviation measure.

We construct an approximation of problem (13) as

$$\begin{aligned} \min _{z \in Z} \max _{\kappa = 0,1,\ldots ,k-1} \ \sum _{i=1}^I \mu _i^\kappa V_i(z). \end{aligned}$$

It is an approximation from below, because the maximum is evaluated over a subset of $\fancyscript{A}$ rather than over $\fancyscript{A}$. Equivalently, the problem above can be written as linear programming problem:

$$\begin{aligned} \begin{aligned} \min&\quad \alpha \\ \mathrm {s.t.}&\quad \alpha \ge \sum _{i=1}^I \mu _i^\kappa V_i(z), \quad \kappa = 0,1,\ldots ,k-1. \end{aligned} \end{aligned}$$

It is essential to stress that when new points $\mu ^\kappa$ are added, then these approximations become more and more accurate, leading eventually to the solution of the original problem, as in standard cutting-plane methods of convex optimization.

To deal with the second issue, the unknown functions $V_i(z)$ will be replaced with piecewise linear convex functions constructed from cuts, derived from the solutions of subproblems (11) at earlier iterations. This is a standard way of dealing with parameter dependent subproblems, similar to expected-value two-stage problems (see, Ruszczyński 2003 and the references therein). In general, each cut is an inequality

$$\begin{aligned} V_i(z) \ge \hat{v}_{i}^{\kappa } + \big (g_{i}^{\kappa }\big )^{\top } \big (z - z^\kappa \big ), \end{aligned}$$

where $\hat{v}_{i}^{\kappa }$ is an optimal value of problem (11) for scenario $i$ in iteration $\kappa$ of the method, with $z=z^\kappa$. The subgradient $g_{i\kappa }$ can be calculated from the Lagrange multipliers $\pi _{i}^\kappa$ associated with the constraints of problem (11) involving the parameters $z$:

$$\begin{aligned} g_{ij}^{\kappa } = (1 + R_{ji}) \pi _{ji}^\kappa . \end{aligned}$$

(14)

The reader may consult (Miller and Ruszczyński 2011) for details of the cut construction in two-stage risk-averse linear programming, which is identical in our case.

The algorithm for risk-averse multicut method is presented below.

Risk-averse multicut method

Step 0: :

Set $k = 1$.

Step 1: :

Solve the master problem,

$$\begin{aligned} \begin{aligned} \min \limits _{z, v, \alpha }&\quad \alpha \\ \mathrm {s.t.}&\quad \alpha \ge \sum _{i=1}^I \mu _i^\kappa v_i, \quad \kappa = 0,1,\ldots , k-1, \\&\quad v_i \ge \bar{v}_{i\kappa } + g_\kappa ^{\top } (z - z^\kappa ),\quad \kappa = 1,\ldots , k-1, \quad i = 1,\ldots , I, \\&\quad z \in Z, \quad {v} \ge {v}_{\min }. \end{aligned} \end{aligned}$$

Denote the solution by $z^k$, $\alpha ^k$, $v^k$.

Step 2: :

For each $i=1,\ldots ,I$: Solve the second-stage problem (11) and let $\hat{v}_i^{k}$ be its optimal value and $\pi _{ji}^k$ the Lagrange multiplier associated with the re-balancing constraint for security $j$ in constraint (9). Then, calculate $g_\kappa$ by using Eq. (14).

Step 3: :

Calculate $\rho _1^k = \rho _1\big [\hat{v}^k\big ]$ and $\mu ^k \in \partial \rho _1\big [\hat{v}^k\big ]$.

Step 4: :

If $\rho _1^k = \alpha ^k$, then stop; otherwise, increase $k$ by 1 and go to Step 1.

In the risk-averse multicut method we assume that the set $Z$ is compact, and that we know lower bounds $\hat{v}_{\min }$ for the optimal values of each second stage problem.

From general convergence results in Ruszczyński (2006), convergence of this method is finite with the mean-semideviation risk function of order 1. If $r\ge 2$, convergence still can be proved, by the general properties of cutting plane methods for convex programming (see, e.g., (Ruszczyński 2006, Thm 7.7)).

The calculation of $\mu$ in Step 3 depends on the risk measure applied. For mean-semideviation risk function of order $r$, the subgradient can be calculated as follows. We calculate the shortfall values

$$\begin{aligned} \sigma _i = \max \Big (0, \hat{v}^k_i - \sum _{m=1}^I p_m \hat{v}^k_i\Big ),\quad i=1,\ldots ,I, \end{aligned}$$

and the semideviation of order $r$,

$$\begin{aligned} \varphi = \Big (\sum _{i=1}^I p_i (\sigma _i)^r\Big )^{1/r}. \end{aligned}$$

Then, by applying the rules of subdifferential calculus (see, e.g., (Ruszczyński 2006, sec. 2.5)), we can obtain $\mu ^k \in \partial \rho _1\big [\hat{v}^k\big ]$ from the following formula:

$$\begin{aligned} \mu _i^k = p_i \left[ 1 + \frac{\gamma }{(\varphi )^{r-1}} \Big ((\sigma _i)^{r-1} - \sum _{m=1}^I (\sigma _m)^{r-1} p_k\Big ) \right] , \quad i=1,\ldots ,I. \end{aligned}$$

(15)

4 Computational results

First, daily returns of Dow Jones companies’ from September 2, 2008 to November 30, 2011 were used to calibrate a multivariate GO-GARCH(1,1) model of the returns. The model was used to generate a large number of scenarios for the next two days. The generated scenarios were used to construct two-stage scenario trees by employing all five scenario tree generation methods discussed in Sect. 2. The methods were compared in terms of their time and solution quality. The results in Table 1 show that two-step clustering methods are slightly faster in terms of CPU times compared to other methods.

Table 1 CPU Time (in secs) of scenario tree generation methods

Table 2 Accuracy of scenario tree generation methods

Because of computational complexity, for the purpose of comparing tree generation methods, the sizes of the scenario trees were restricted to 10,000 and 20,000 scenarios. Table 2 contains the comparison of the quality of scenario trees obtained by different methods: the optimal value of the Monge–Kantorovich metric given by (6). The results show that tree quality is stable for each scenario tree generation technique. However, the multi-facility location clustering method is better with scenario trees constructed from both 10,000 and 20,000 scenarios. Therefore, in the next part of the study, we used the multi-facility location-based method to generate scenario trees in a rolling horizon fashion.

In the next part of the study, a simulation analysis was carried out. Each day, the preceding 619 days of data were used to calibrate a multivariate GO-GARCH(1,1) model. The model was then used to generate 80,000 scenarios for the following two days. The multi-facility location clustering method was used to construct a scenario tree for the next two days. Then the tree model with conditional measures of risk was solved, the investments were re-balanced, and the method continued. On the next day, new return data were available, new scenario trees were generated, new models solved, etc. The steps of the simulation study are depicted in Fig. 6.

Fig. 6

Simulation analysis

The simulation study had two objectives. First, we compared the two-stage portfolio model with the static model where $b_{ji} = s_{ji} = 0$. Based on the cumulative wealth graphs in Figs. 7 and 8, we can say that two-stage portfolio model performs better than the static model for both mean-semideviation risk functions of order 1 and 2. This was partly due to the reduced volume of trades, which resulted in significantly lower transaction costs, but also to a better portfolio composition.

Fig. 7

Performance of the static and two-stage portfolios with mean-semideviation (Order 1)

Fig. 8

Performance of the static and two-stage portfolios with mean-semideviation (Order 2)

Secondly, we compared two-stage portfolio models with the mean-semideviation risk measures of first-order and higher orders (2 and 3) with static minimum variance model where $b_{ji} = s_{ji} = 0$. In each case we used fixed $\gamma = 0.9$ and bid-ask spread transaction costs. The two-stage portfolio optimization problem was solved with the risk-averse multi-cut method, implemented in MATLAB with the CPLEX solver. We observed that there is no significant difference between two-stage portfolio problem with mean-semideviation risk measure of second order and third order. As we can see from Figs. 8 and 9, using the second-order methods leads to significant improvements in cumulative wealth trajectories compared to first order and Markowitz’s minimum variance models. This is consistent with the findings of Matmoura and Penev (2013), where other higher-order risk measures were employed (with a static model and no transaction costs).

Finally, we can compare the performance of the portfolios with mean-semideviation of order 1 and 2 with Dow Jones Index. Based on the following graph, the simulation analysis shows that portfolio with mean-semideviation of order 2 performs better than other portfolios.

Fig. 9

Performance of the two-stage portfolios and Dow Jones Index

Next, we compare $\beta$ values of the portfolios with mean-semideviation of order 2 when risk aversion constant is either $\gamma = 0.9$ or $\gamma = 0.5.\, \beta$ value of portfolio (0.92) with $\gamma = 0.5$ is slightly more than $\beta$ value of portfolio (0.85) with $\gamma = 0.9$. This means both portfolios generally move in the same direction as the benchmark (Dow Jones). However, movement of the mean-semideviation portfolio of order 2 with $\gamma = 0.9$ is generally less than the movement of the mean-semideviation portfolio of order 2 with $\gamma = 0.5$.

5 Conclusion

In this study, two-stage portfolio models with higher-order conditional risk measures are studied. First, adequate number of scenarios are generated to model the probabilistic information on random data. Next, scenario trees are constructed by different methods, and the best one is chosen based on the distance between the probability distribution on the scenario tree and the empirical distribution on the raw scenarios. It is found that the two-step forward clustering method is most efficient in terms of the CPU time, because it passes over the data just once. However, that multi-facility location clustering method is the most accurate, in terms of the Monge-Kantorovich metric.

Next, conditional mean-semideviation risk functions of first-order and higher-orders (Order 2 and 3) are used to formulate the risk-averse two-stage portfolio problem on the trees generated from the multi-facility location clustering method. The problems are solved by a generic risk averse multicut algorithm for any higher-order risk function. The results show that the portfolio allocations for mean-semideviation models of first-order and higher-orders are similar. However, portfolios with the mean-semideviation of second-order and third-order perform better compared to mean-semideviation of first-order, minimum variance model, and the Dow Jones index. All two-stage models outperform the static model.