1 Introduction

Planar microwave low pass filters (LPFs) with flat and low loss passband, sharp transition band and ultra wide stopband have attracted considerable attention in recent years. Moreover, in the modern wireless applications, apart from good frequency response, the dimension of a filter is also an important issue [1]. Filters are frequently required in many RF and microwave wireless applications [2, 3], such as diplexers, power dividers [4,5,6], power dividers [7] and power amplifiers [8].

So far, LPFs with wide stopband, which utilize meandered lines and radial patches have been presented [9, 10], but the frequency responses of the transition band were not sufficiently sharp in these works. To obtain sharp transition band, an LPF using the symmetrical T-shaped and U-shaped resonators has been reported in [11], which shows a sharp response but this filter is rather large. LPFs using stepped impedances and hairpin resonators were proposed in [12, 13]. However, they have inappropriate size and insertion loss. Another filter with wide stopband and sharp roll-off using circular-shaped patches and open stubs was presented in [14], but the designed structure was asymmetric.

An LPF using high impedance lines and T-structured resonators is presented in [15]. The overall size of this filter is very compact and the insertion loss is acceptable, however, the suppression band of this LPF is not ultra wide.

In this paper, a new compact LPF with ultra wide stopband is designed. The designed LPF shows good specifications, compared to the recent works.

2 Main resonator

The layout and frequency response of the presented triangular resonator are illustrated in Fig. 1. As seen in Fig. 1(b), the resonator can generate a transmission zero at 3.2 GHz, with high attenuation value.

Fig. 1
figure 1

a Layout structure, b frequency response of the triangular resonator

Full size image

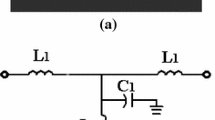
To obtain the LC equivalent circuit (LCEC) of the presented triangular resonator, the LCECs of some typical transmission lines should be discussed at first. The LCEC for a typical transmission line and an open-ended stub are illustrated in Fig. 2(a, b) [1].

Fig. 2
figure 2

The LCEC for a atypical transmission line, b an open-ended stub

Full size image

The equivalent elements of the presented LCEC can be recognized by using Fig. 2 equalizing procedures. The LCEC of the triangular resonator is shown in Fig. 3.

Fig. 3
figure 3

The LCEC of the proposed triangular resonator

Full size image

In the presented LCEC, C4 and L1 are corresponding to the capacitance and inductance of the transmission line. Besides, C1, C2 and L2, L3 are capacitances and inductances of high impedance lossless line. It can be seen that Ls and Cs are elements in π-equivalent circuit. The calculated values for elements in the π-equivalent circuit using Eqs. (1) and (2) are summarized in Table 1.

$$L_{\text{s}} = \frac{1}{\omega} \times z_{\text{s}} \times \sin \left({\frac{2\pi}{{\lambda_{\text{g}}}}l_{\text{s}}} \right)$$
(1)
$$C_{\text{s}} = \frac{1}{\omega} \times \frac{1}{{z_{\text{s}}}} \times \tan \left({\frac{\pi}{{\lambda_{\text{g}}}}l_{\text{s}}} \right)$$
(2)

where \(\omega\) is the angular frequency, \(z_{s}\) is characteristic impedance, \(l_{\text{s}}\) denotes length, and \(\lambda_{g}\) is the guided wavelength. The equivalent capacitance of the open-circuited stub line [Fig. 2(b)] is given as [1]:

$$C_{\text{p}} = \frac{{\Delta l \cdot \sqrt {\varepsilon_{\text{re}}}}}{{c \cdot Z_{\text{s}}}}\quad \Delta l = \frac{{\xi_{1} \xi_{3} \xi_{5}}}{{\xi_{4}}} \cdot h$$
(3)

where \(\varepsilon_{\text{re}}\) is the effective dielectric constant and \(c\) is the light velocity in the free space. Also, \(\xi_{1}\), \(\xi_{2}\), \(\xi_{3}\), \(\xi_{4}\) and \(\xi_{5}\) are given below:

$$\xi_{1} = 0.434907\frac{{\varepsilon_{\text{re}}^{0.81} + 0.26(W/h)^{0.8544} + 0.235}}{{\varepsilon_{\text{re}}^{0.81} - 0.189(W/h)^{0.8544} + 0.87}}$$
(4)
$$\xi_{2} = 1 + \frac{{(W/h)^{0.371}}}{{2.3\varepsilon_{\text{r}} + 1}}$$
(5)
$$\xi_{3} = 1 + \frac{{0.5274\tan^{- 1} \left[{0.084(W/h)^{{1.9413/\xi_{2}}}} \right]}}{{\varepsilon_{\text{re}}^{0.9236}}}$$
(6)
$$\xi_{4} = 1 + 0.037\tan^{- 1} \left[{0.067(W/h)^{1.456}} \right]\cdot \left\{{6 - 5\exp \left[{0.036(1 - \varepsilon_{\text{r}})} \right]} \right\}$$
(7)
$$\xi_{5} = 1 - 0.218\exp (-\, 7.5W/h)$$
(8)

The dimensions of the triangular resonator in Fig. 1(a) are calculated as follows: W1 = 0.1, L1 = 8.5, W2 = 4.1, L2 = 4, W3 = 0.3 and L3 = 7.1 (all in millimeter). The capacitance and inductance values of the equivalent circuit, which was shown in Fig. 3, can be approximated by the Eqs. (1–8) as listed in Table 1.

The electromagnetic (EM) simulation and LCEC results of the triangular resonator are compared in Fig. 4. As seen, the LCEC results of the triangular resonator and the EM simulation are in good agreement as shown in Fig. 3.

Table 1 Calculated values for LCEC of the proposed triangular resonator
Full size table
Fig. 4
figure 4

A comparison between EM simulation and LCEC results of the triangular resonator

Full size image

To improve the sharpness and pass band of the triangular shaped resonators, two rectangular shaped resonators are inserted in the structure to form the main resonators as shown in Fig. 5(a). The applied dimensions of the rectangular shaped resonators are as follows: Wa4 = 2.4 and La4 = 2.4 (all in millimeter).

Fig. 5
figure 5

a Structure, b frequency response of the main resonator

Full size image

The frequency response of the main resonator is depicted in Fig. 5(b). As seen, better pass band and sharper transition band are obtained, compared to the triangular resonator response. The LCEC of the proposed main resonator is extracted similar to triangular resonator as shown in Fig. 6.

The calculated parameters of the main resonator LCEC are summarized in Table 2. The parameters C5 and L1 are corresponding to the capacitance and inductance of the transmission line; C1, C2, C3 and L2, L3 are capacitances and inductances of high impedance line, respectively.

Table 2 Calculated parameters of the main resonator LCEC
Full size table
Fig. 6
figure 6

The LCEC of the main resonator

Full size image

The EM simulation and LCEC results of the main resonator are compared in Fig. 7. As seen, the LCEC results and the EM simulation of the main resonator are in the good agreement.

Fig. 7
figure 7

EM simulation and LCEC results of the main resonator

Full size image

The transfer function of the main resonator LCEC results is presented in Eq. (9). The transition band sharpness and main frequency of the LPF can be controlled by the first transmission zero. Equation of the first transmission zero is presented in Eq. (10). It should be noted that the values of r in Eq. (9) is considered 50 ohms, refers to the resistance of matching

$$\frac{{V_{o} }}{{V_{i} }} = \frac{{\left( {a^{2} br} \right)}}{{\begin{array}{*{20}l} {(a^{2} r^{2} + 2abr^{2} - 2a^{2} bL_{1} s + 2a^{2} L_{7} rs + 4abL_{7} rs} \hfill \\ { + 2aL_{1} r^{2} s + 2bL_{1} r^{2} s - a^{2} L_{1}^{2} s^{2} + a^{2} L_{7}^{2} s^{2} + 2abL_{7}^{2} s^{2} } \hfill \\ { + 4aL_{1} L_{7} rs^{2} + 4bL_{1} L_{7} rs^{2} + L_{1}^{2} r^{2} s^{2} + 2aL_{1} L_{7}^{2} s^{3} } \hfill \\ {2bL_{1} L_{7}^{2} s^{3} + 2L_{1}^{2} L_{7} rs^{3} + L_{1}^{2} L_{7}^{2} s^{4} )} \hfill \\ \end{array} }}$$
(9)

where a and b parameters are defined as follows

$$\begin{aligned} a & = \frac{{\begin{array}{*{20}l} {(s(c_{1} + c_{2} + 2(c_{3} + c_{4} ) + (c_{2} (c_{3} + c_{4} )L_{3} } \hfill \\ { + (c_{2} + 2c_{3} )c_{4} L_{4} + c_{1} (c_{2} L_{2} + (c_{3} + c_{4} )(2L_{2} + L_{3} )} \hfill \\ { + c_{4} L_{4} ))s^{2} + (c_{1} c_{2} (c_{3} + c_{4} )L_{2} L_{3} + c_{4} (c_{1} (c_{2} + 2c_{3} )L_{2} } \hfill \\ { + (c_{1} + c_{2} )c_{3} L_{3} )L_{4} )s^{4} + c_{1} c_{2} c_{3} c_{4} L_{2} L_{3} L_{4} s^{6} ))} \hfill \\ \end{array} }}{{\begin{array}{*{20}l} {(1 + s^{2} (c_{4} (2L_{2} + L_{3} + L_{4} ) + c_{3} (2L_{2} + L_{3} )(1 + c_{4} L_{4} s^{2} )} \hfill \\ { + c_{2} L_{2} (1 + (c_{3} L_{3} + c_{4} (L_{3} + L_{4} ))s^{2} + c_{3} c_{4} L_{3} L_{4} s^{4} )))} \hfill \\ \end{array} }} \\ b & = \frac{{(1 + c_{5} L_{5} s^{2} + c_{6} L_{5} s^{2} + c_{6} L_{6} s^{2} + c_{5} c_{6} L_{5} L_{6} s^{4} )}}{{\begin{array}{*{20}l} {((2c_{5} s + 2c_{6} s + c_{7} s + c_{5} c_{7} L_{5} s^{3} + c_{6} c_{7} L_{5} s^{3} } \hfill \\ { + 2c_{5} c_{6} L_{6} s^{3} + c_{6} c_{7} L_{6} s^{3} + c_{5} c_{6} c_{7} L_{5} L_{6} s^{5} ))} \hfill \\ \end{array} }} \\ T_{Z} & = \sqrt {\frac{ - C}{3D} - \frac{{2^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} B}}{{\begin{array}{*{20}l} {\left( { - 2C^{3} + 9BCD - 27AD^{2} + \left( {\sqrt {4( - C^{2} + 3BD)^{3} + \left( { - 2C^{3} + 9BCD - 27AD^{2} } \right)^{2} } } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} } \hfill \\ {\frac{{2^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} C^{2} }}{{ + 3D\left( { - 2C^{3} + 9BCD - 27AD^{2} + \left( {\sqrt {4( - C^{2} + 3BD)^{3} + \left( { - 2C^{3} + 9BCD - 27AD^{2} } \right)^{2} } } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }}} \hfill \\ {\frac{{\left( { \pm 2C^{3} + 9BCD - 27AD^{2} + \left( {\sqrt {4( - C^{2} + 3BD)^{3} + ( - 2C^{3} + 9BCD - 27AD^{2} )^{2} } } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }}{{32^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} D}}} \hfill \\ \end{array} }}} \\ \end{aligned}$$
(10)

where

$$\begin{aligned} A &= (c_{1} + c_{2} + 2(c_{3} + c_{4}) + (c_{2} (c_{3} + c_{4})L_{3} \hfill \\ B &= (c_{2} + 2c_{3})c_{4} L_{4} + c_{1} (c_{2} L_{2} + (c_{3} + c_{4})(2L_{2} + L_{3}) + (c_{4} L_{4})) \hfill \\ C &= (c_{1} c_{2} (c_{3} + c_{4})L_{2} L_{3} + c_{4} (c_{1} (c_{2} + 2c_{3})L_{2} + (c_{1} + c_{2})c_{3} L_{3})L_{4}) \hfill \\ D &= c_{1} c_{2} c_{3} c_{4} L_{2} L_{3} L_{4} \hfill \\ \end{aligned}$$

For example, if L1 increases to 3.17 nH, 3.5 nH and 4 nH, the transmission zero will increase to 2.1 GHz, 2.45 GHz, and 2.68 GHz, respectively. So, L1 can be used to control transmission zero. Also, the transmission zero location can be changed by C3, C4 and, L4. The mentioned lumped elements are calculated by Wa4. The effects of the Wa4 different values on the position of transmission zero for the main resonator are shown in Fig. 8. In this figure, the impact of changing the Wa4 values of 0.1, 0.5, 1, 2 and 2.4 mm, on frequency responses of the main resonator is shown. With these changes, the frequency of transmission zero is moved to 3.25, 2.9, 2.7, 2.3, 2.1 GHz and the value of C4 is changed to 14, 41, 97, 152, 170 fF, respectively.

Fig. 8
figure 8

The effects of the Wa4 different values on the position of transmission zero for the main resonator

Full size image

3 Low pass filter design

T-shaped suppressor resonators are added to the main resonator to make an ultra-wide stop-band as depicted in Fig. 9(a). The frequency response of the T-shaped resonators is illustrated in Fig. 9(b). As can be seen in this figure, some harmonics can be eliminated by the T-shaped resonators. The dimensions of the T-shaped resonator in Fig. 9(a) are as follows: W5 = 3.9, L5 = 7.5, W6 = 0.3, L6 = 0.8, A = 2.6 (All in millimeter). The frequency response of the T-shaped resonator is depicted in Fig. 9(b).

Fig. 9
figure 9

a Layout structure, b frequency response of T-shaped resonator

Full size image

After adding the T-shaped resonators to the main resonator, the initial filter structure will be obtained which is shown in Fig. 10(a). Therefore microstrip prototype filter which is shown in Fig. 10(a) is achieved. Frequency response of this structure is depicted in Fig. 10(b). The dimensions of the prototype in Fig. 10(a) are as follows: X = 0.3 mm and Y = 0.6 mm.

Fig. 10
figure 10

a Layout structure, b frequency response of the initial filter

Full size image

There are two unwanted harmonics in the initial filter response at 2.3 GHz and 9.2 GHz. To eliminate these harmonics, another T-shaped (second T-shaped) resonator is added, which is depicted in Fig. 11(a). The frequency response of the second T-shaped resonator is illustrated in Fig. 11(b).

Fig. 11
figure 11

a Layout structure, b frequency response of the second T-shaped resonator

Full size image

To conclude this section, the final design of microstrip filter and its frequency response are illustrated in Fig. 12(a, b).

Fig. 12
figure 12

a Layout structure, b frequency response of the final proposed filter

Full size image

The stopband of the proposed LPF is achieved from 1.81 to 29.4 GHz with more than 20 dB attenuation. Furthermore, the cut of frequency of the proposed LPF is 1.663 GHz. The frequency response and LCEC of the proposed LPF is depicted in Fig. 13. As seen, the LCEC results and EM simulation are in the good agreements.

Fig. 13
figure 13

a The LCEC, b the frequency response of the proposed LPF

Full size image

The calculated values of the extracted LCEC for the proposed filter are listed in Table 3.

Table 3 Calculated values of the extracted LCEC for the proposed filter
Full size table

4 Simulation and measurement results

The fabricated LPF results are illustrated in Fig. 14. As seen, the measured data follow the simulation results. Also, the picture of the fabricated proposed filter is shown in Fig. 15.

Fig. 14
figure 14

The fabricated LPF results

Full size image
Fig. 15
figure 15

Photograph of the fabricated proposed filter

Full size image

A transition band from 1.663 GHz up to 1.88 GHz corresponding with 3–40 dB attenuations is achieved for the proposed LPF. The proposed LPF is fabricated on a RO-4003 substrate with a thickness of 32 mil and a dielectric constant of 3.38. The results are measured using an HP8757A vector network analyzer.

The performance of the proposed LPF is listed in Table 4, which is compared with other published paper. According to the Table 4, high figure-of-merit of 33,813 is obtained for the proposed LPF.

Table 4 Performance comparisons between published LPFS and this work
Full size table

In the Table 4, the parameter roll-off rate denotes the transition band sharpness. Also, the parameters SF, RSB and NCS are suppression factor, relative stopband bandwidth, and normalized circuit size, respectively. The FOM can be calculated as defined in Eq. (11)

$$FOM = \frac{{\left({\text{Roll-off rate}} \right) \times SF \times RSB}}{AF \times NCS}$$
(11)

where the architecture factor (AF) is considered as 1 or 2, when the design is 2D or 3D, respectively.

5 Conclusions

In this article, a compact microstrip LPF with a sharp response and ultra wide stopband is designed and fabricated. The simulation and measurement result shows a good agreement. Besides, figure-of-merit of 33,813 is obtained which is very high compared to the other reported works. The designed LPF can be applied to the modern communication systems because of the obtained good features.