1 Introduction

Narrowband technique for long range and acceptably low data rate gives us a favorable tradeoff between range and the transmission time. In order to have a good resistant to interference, using the least spectrum has been suggested. Hence, narrowband microwave devices such as narrowband microstrip filters [1, 2], narrowband diplexers and multiplexers have been introduced in [3,4,5,6]. These devices can select the required frequencies and remove harmonics in the crowded frequency bands. Especially narrowband multi-channel diplexers and multiplexers have been needed to separate the desired signals from a crowded frequency band in multi-service communication systems [5, 6]. With developing in the modern multi-service communication systems, multi-channel microstrip diplexers [7,8,9,10] and multiplexers [11,12,13] have been reported recently. Since, the design of a multi-channel diplexer is harder than multiplexers and diplexers [14, 15], they have been less designed. Two-channel diplexers in [3, 4] have been obtained using microstrip triangular open loops and semi-spiral cells, respectively. In order to design the quad-channel diplexers, microstrip spiral stub-loaded resonators in [6], stepped-impedance resonator (SIR) inserted T-junctions in [7], the coupled stepped impedance resonators in [8], a stub loaded step impedance microstrip line in [9] and coupled hairpin resonators in [10] have been utilized. Tri-mode net-type resonators [11], coupled hairpins [12] and coupled uniform open loops [13] have been used to design quad-channel multiplexers. Despite the importance of being small, among all mentioned diplexers and multiplexers only the authors in [6] could somewhat save the size. A high performance diplexer or multiplexer should be able to suppress unwanted harmonics. However only in [3, 10, 12] the harmonics have been attenuated while they could not reduce the insertion losses simultaneously. Improving the loss is another problem, which has been solved in [4,5,6, 14, 15]. Meanwhile the other mentioned diplexers and multiplexers have undesired common port return loss or high insertion loss.

In this paper, a narrowband quad-channel diplexer is proposed which is compact with a high performance. It is designed based on a novel miniaturized microstrip structure. It has four passbands at 1.67, 2.54, 3.45 and 4.57 GHz for multi-service RF communication systems. For examples, 1.67 GHz channel can be employed for GSM while 3.45 GHz channel separates the signals for IEEE 802.16 WiMAX applications. Meanwhile, 2.67 GHz channel provides desired signals from 2.6 GHz omnidirectional antenna series, which covers 2.5–2.7 GHz frequency range for IEEE 802.16 and 802.20 WiMAX technology such as sprint/Clearwire 4G WiMAX, Europe LTE and wireless internet service. The realized multi-channel diplexer not only has improved insertion and return losses but also its harmonics are attenuated up to 8 GHz with a maximum level of − 27.5 dB. These advantages are obtained where there is a reasonable isolation better than − 30 dB between the ports. In order to improve the stopband properties several transmission zeros are created above and below the passbands.

2 Designing process

In order to design a quad-channel diplexer, we performed the following steps: first, we designed a novel single-mode resonator. Then, it was converted to a dual-mode resonator by adding an internal stub without size increment. To have four channels, we need to a new dual-mode resonator. It can be obtained by changing the dimensions of proposed dual-mode resonator. Finally, we integrated two dual-mode resonators to create a four-channel diplexer.

Figure 1(a) depicts the proposed single-mode resonator. It consists of a simple step impedance U-shape resonator, which is coupled to two step impedance feed structures. Figure 1(b) shows an equivalent LC model of the proposed single-mode resonator. In the proposed LC circuit, open ends are replaced by the capacitors Co. The feeding structures are replaced by the capacitors CF. The effects of step in widths and bents are significant at the frequencies higher than 10 GHz, hence they can be ignored in the LC circuit. The capacitors C1 and C2 illustrate the coupling between the thin and wider lines. The inductor L1 presents the effect of a half of a thin line (with the width wc and length 0.5l c ) and the inductor L2 presents the effect of a half of a wider line (with the width wb and length 0.5l c ). The equivalent LC circuit of coupled lines is an approximated model while in the exact model, there are too many coupling capacitors and subsequently the number of inductors will be increased. The inductor L3 is related to the microstrip line with the width wd.

Fig. 1
figure 1

a Proposed single mode resonator and b its equivalent LC circuit

Full size image

Ignoring the open end capacitors due to their small values helps to calculate the input impedance of LC circuit as follows:

$$\begin{aligned} & Z_{in} = \frac{2}{{j\omega C_{F} }} + 2Zc + j\omega L_{3} \\ & where{:} \\ & Zc = \frac{{\left[ {\frac{{\left( {\frac{1}{{j\omega C_{1} }} + j\omega (L_{1} + L_{2} )} \right) \times \frac{1}{{j\omega C_{2} }}}}{{\frac{1}{{j\omega C_{1} }} + j\omega (L_{1} + L_{2} ) + \frac{1}{{j\omega C_{2} }}}} + j\omega (L_{1} + L_{2} )} \right] \times \frac{1}{{j\omega C_{1} }}}}{{\frac{{\left( {\frac{1}{{j\omega C_{1} }} + j\omega (L_{1} + L_{2} )} \right) \times \frac{1}{{j\omega C_{2} }}}}{{\frac{1}{{j\omega C_{1} }} + j\omega (L_{1} + L_{2} ) + \frac{1}{{j\omega C_{2} }}}} + j\omega (L_{1} + L_{2} ) + \frac{1}{{j\omega C_{1} }}}} \\ \end{aligned}$$
(1)

The even mode resonance angular frequency ωe can be obtained where the input admittance is zero. Accordingly, the even mode angular resonance frequency can be extracted from Eq. (1) as follows:

$$\begin{aligned} & \left( {\frac{1}{{j\omega C_{1} }} + j\omega (L_{1} + L_{2} )} \right) \times \frac{1}{{j\omega C_{2} }} + \left[ {\frac{1}{{j\omega C_{1} }} + j\omega (L_{1} + L_{2} ) + \frac{1}{{j\omega C_{2} }}} \right]\left[ {j\omega (L_{1} + L_{2} ) + \frac{1}{{j\omega C_{1} }}} \right] = 0 \\ & \quad \Rightarrow - 2\frac{{\omega_{e}^{2} (C_{1} + C_{2} )(L_{1} + L_{2} )}}{{C_{2} C_{1} }} + \frac{1}{{C_{1}^{2} }} + \frac{2}{{C_{2} C_{1} }} + \omega_{e}^{4} (L_{1} + L_{2} )^{2} = 0 \\ & \quad \Rightarrow \omega_{e} = \frac{{\sqrt {\frac{{(C_{1} + C_{2} )(L_{1} + L_{2} )}}{{C_{2} C_{1} }} \pm \sqrt {\left[ {\frac{{(C_{1} + C_{2} )(L_{1} + L_{2} )}}{{C_{2} C_{1} }}} \right]^{2} - \left( {\frac{1}{{C_{1}^{2} }} + \frac{2}{{C_{2} C_{1} }}} \right)(L_{1} + L_{2} )^{2} } } }}{{(L_{1} + L_{2} )}} \\ \end{aligned}$$
(2)

From Eq. (1), ωe is obtained when the denominator of Zc is Zero. The odd mode angular resonance frequency ωo can be obtained when Zin = 0. Accordingly, the odd mode angular resonance condition is calculated from Eq. (1) as follows:

$$\begin{aligned} & \frac{{1 - 0.5\omega_{o}^{2} L_{3} C_{F} }}{{C_{F} }} + \frac{{\omega_{o}^{4} C_{2} (L_{1} + L_{2} )^{2} - \omega_{o}^{2} (L_{1} + L_{2} )(2C_{1} + C_{2} ) + 1}}{{\omega_{o}^{4} (L_{1} + L_{2} )^{2} C_{1}^{3} C_{2} - \omega_{o}^{2} C_{1}^{2} (L_{1} + L_{2} )(1 + 2C_{2} + C_{1} ) + (1 + C_{2} + C_{1} )C_{1} }} = 0 \\ & \quad \Rightarrow \omega_{o}^{6} [0.5L_{3} C_{F} (L_{1} + L_{2} )^{2} \,C_{1}^{3} C_{2} ] - \omega_{o}^{4} [(L_{1} + L_{2} )^{2} \,C_{2} (C_{1}^{3} + C_{F} ) + 0.5L_{3} C_{F} C_{1}^{2} (L_{1} + L_{2} )(1 + 2C_{2} + C_{1} )] \\ & \quad \quad + \omega_{o}^{2} [0.5L_{3} C_{F} (1 + C_{2} + C_{1} )C_{1} + (L_{1} + L_{2} )(C_{1}^{2} (1 + 2C_{2} + C_{1} ) + C_{F} (2C_{1} + C_{2} ))] - [C_{F} + (1 + C_{2} + C_{1} )C_{1} ] = 0 \\ \end{aligned}$$
(3)

In order to solve Eq. (3), we ignore the small terms against larger terms. Since the coupling capacitors are generally small values in fF, while the other capacitors are in nF and the inductors are in the range of nH, the coefficient ω 6o is a very small value so that we can ignore it. Applying additional approximation in Eq. (3) results in the following formulas:

$$\begin{aligned} & \omega_{o}^{4} [(L_{1} + L_{2} )^{2} C_{2} C_{F} ] - \omega_{o}^{2} [0.5L_{3} C_{F} C_{1} + C_{F} (2C_{1} + C_{2} )] + C_{F} = 0 \\ & \quad \Rightarrow \omega_{o} = \sqrt {\frac{{[0.5L_{3} C_{F} C_{1} + C_{F} (2C_{1} + C_{2} )] \pm \sqrt {[0.5L_{3} C_{F} C_{1} + C_{F} (2C_{1} + C_{2} )]^{2} - 4C_{F} (L_{1} + L_{2} )^{2} C_{2} C_{F} } }}{{(L_{1} + L_{2} )^{2} \,C_{2} C_{F} }}} \\ \end{aligned}$$
(4)

A microstrip single-mode resonator can resonate at several frequencies, which one of them is desired and the others are unwanted. An unwanted resonance frequency acts as a harmonic [16]. Our primary single-mode resonator has four resonance frequencies obtained from Eqs. (2) and (4). One of these resonance frequencies is desired while three of them are harmonics. In order to attenuate these harmonics, there are the conditions in which one of the second-order equations has no real answer and another equation has only a real answer. Under this condition, we have a main resonance frequency and three attenuated harmonics. According to Eqs. (2) and (4), tuning the dimensions of coupled lines leads to only an angular resonance frequency. The proposed single-mode resonator is simulated, where the corresponding dimensions in Fig. 1 are in mm. Figure 2(a) depicts the simulation results of the single-mode resonator. The lengths of coupled lines and the thin stub with the length l b affect the passband of the single-mode resonator. Accordingly, these passbands as a function of l b and l c are presented in Fig. 2(b, c) respectively.

Fig. 2
figure 2

Single-mode resonator a simulation results, b resonance frequency as a function of lb, c resonance frequency as a function of lc

Full size image

From Fig. 2(b, c) it is clear that decreasing the dimensions of proposed resonator shifts the resonance frequency to the right. Since l b is an effective parameter in the resonance frequency, its corresponding inductor (L3) is impressive. Therefore, this resonance frequency is obtained based on the odd mode resonance condition. Meanwhile the calculated resonance modes in Eq. (2) are harmonics. In order to remove these harmonics, the effective parameters are selected so that we have only a resonance mode.

According to above analysis, a harmonic attenuator single-mode resonator is obtained. In order to create another resonance frequency without size increment, we added two internal stubs as shown in Fig. 3(a). The dimensions of the proposed dual-mode resonator are similar to single-mode while the dimensions of additional internal stubs and their positions are in mm. The frequency responses of the proposed dual-mode resonator as a function of the effective parameters are presented in Fig. 3(b–e). As shown in Fig. 3(a), decreasing the space “D”, moves both channels to the left. Figure 3(c) illustrates the effect of internal stub with the length L so that increasing this length shifts the second resonance frequency to the left. Integrating two similar dual-mode resonators with different dimensions results in a quad-channel diplexer presented in Fig. 4, where the corresponding dimensions are in mm. The other dimensions are complying with the proposed dual-mode resonator. In order to save the size, the resonators are coupled without any large additional integrators. Three middle coupled lines make a good isolation between two channels.

Fig. 3
figure 3

Proposed dual-mode resonator a layout, b frequency response as a function of D, c frequency response as a function of L, d frequency response as a function of W1, e frequency response as a function of W2

Full size image
Fig. 4
figure 4

Proposed quad-channel diplexer

Full size image

3 Results and discussion

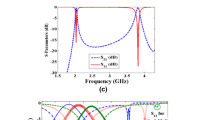
The proposed diplexer is simulated by Advanced Design System (ADS) full wave EM simulator. It is fabricated on a Rogers_RT_Duroid5880 substrate with εr = 2.22, h = 31 mil and a loss tangent of 0.0009. An Agilent network analyser N5230A performed the measurements. The proposed diplexer is compact with the overall size of 0.22 λg × 0.13 λg (29.6 mm × 17.9 mm), where λg is the guided wavelength calculated at the first resonance frequency. Figure 5(a) depicts the simulated and measured S21 and S31. The proposed quad-channel diplexer operates at 1.67, 2.54, 3.45 and 4.57 GHz for multi-service RF communication systems. The channels are narrow with the fractional bandwidths of 1.2, 1.96, 1.15 and 1.09%, which make it suitable for the long-range communication applications. As shown in Fig. 5(a) the harmonics are attenuated up to 8 GHz. This means that 4th harmonic is well attenuated. Figure 5(b) shows the simulated and measured common port return loss (S11) and isolation (S23). The results show that the insertion losses are 0.5, 0.38, 0.53 and 0.58 dB while the common port return losses at the passbands are better than 20, 21, 25 and 22 dB. The simulated and measured isolations between ports 2 and 3 are better than − 26 dB from 1 to 7 GHz. The return losses from ports 2 and 3 are demonstrated in Fig. 5(c). From Fig. 5(c) it is clear that the simulated and measured S22 and S33 are better than − 20 dB. Figure 5(d) shows a photograph of the fabricated diplexer. The results are compared to the previous reported dual-channel diplexers, quad-channel diplexers and quadruplexers. The comparison results are listed in Table 1, where f1 is the first resonance frequency. According to Table 1, the proposed diplexer is miniaturized so that it occupies the smallest area. Moreover, in comparison with the previous works, the proposed diplexer not only has the good insertion and return losses but also a good harmonic attenuation is carried out while most of the previous works could not suppress the harmonics. Only, the presented multiplexer in [12] has a better harmonic suppression, in comparison with our work. Nevertheless, it occupies a large area while it has relatively high insertion losses at all channels. The insertion losses in [5, 6, 15] are a little better than our diplexer. However, they only could suppress the harmonics up to 1.01 f1, 1.4 f1 and 2.08 f1 respectively while the proposed diplexer can attenuate the harmonics up to 4.79 f1. Also, the proposed structures in [5, 6, 15] are larger than our diplexer.

Fig. 5
figure 5

a Simulated and measured S21 and S31, b simulated and measured common port return loss and isolation, c return losses from ports 2 and 3, d a photograph of the fabricated diplexer

Full size image
Table 1 Comparison between the proposed diplexer and previous works
Full size table

4 Conclusion

In this work, a multi-channel diplexer is designed based on a novel microstrip stub loaded resonator. It has four channels at 1.67 GHz (for GSM), 2.54 GHz (for IEEE 802.16 and 802.20 WiMAX technology), 3.45 (IEEE 802.16 WiMAX which covers 3.17–4.2 GHz) and 4.57 GHz (for IEEE C-band applications that covers 4–8 GHz). The channels of the proposed diplexer are narrow which give a good resistant to interference. In order to miniaturize the overall size, the stubs are loaded inside the main resonator so that it has a compact size of 0.029/529.84 (λ 2g /mm2). The introduced diplexer is compared to the previous works. The comparison results show that it not only has good insertion losses but also the common port return losses are improved. Another advantage of our quad-channel diplexer was its capability of harmonics suppression where most of the previous works did not try to solve this problem.