Robust model selection with covariables missing at random

Abstract

Let $f_{Y|X,Z}(y|x,z)$ be the conditional probability function of Y given (X, Z), where Y is the scalar response variable, while (X, Z) is the covariable vector. This paper proposes a robust model selection criterion for $f_{Y|X,Z}(y|x,z)$ with X missing at random. The proposed method is developed based on a set of assumed models for the selection probability function. However, the consistency of model selection by our proposal does not require these models to be correctly specified, while it only requires that the selection probability function is a function of these assumed selective probability functions. Under some conditions, it is proved that the model selection by the proposed method is consistent and the estimator for population parameter vector is consistent and asymptotically normal. A Monte Carlo study was conducted to evaluate the finite-sample performance of our proposal. A real data analysis was used to illustrate the practical application of our proposal.

1 Introduction

Model selection has been a hot spot in statistical analysis for a long time. Significant practicality and theoretical advances have been made in the field of model selection over the past five decades. The main advances, however, focus on the case where data are observed completely (see, e.g., Mallow 1973; Claeskens and Hjort, 2003; Jiang et al., 2008; Rolling and Yang, 2014; Shao and Yang, 2017; Zhang et al., 2017), while less attention has been paid to the case of missing data (see, e.g., Hens et al., 2006; Claeskens and Consentino, 2008; Ibrahim et al., 2008; Jiang et al., 2015; Wei et al., 2021). Missing data occur commonly in the study of many practical problems such as socioeconomic research, medical research, observational research and so on. Therefore, it is of great practical importance to develop model selection strategies which are applicable to missing data. This paper considers the model selection problem in the presence of missing data.

In many scientific areas, a basic task is to assess the simultaneous influence of several factors (covariates) on a quantity of interest (response variable) (Wang and Rao, 2002a). In this paper, we are interested in the model selection problem for the conditional probability function of Y given (X, Z), denoted by $f_{Y|X,Z}(y|x,z)$, where Y is the scalar response variable, while (X, Z) is the covariable vector. Throughout this paper, a generic notation $f_{V_1|V_2}(v_1|v_2)$ is utilized to denote the conditional probability function of the variable $V_1$ given the variable $V_2$. Missing data mechanism plays an important role in the study of missing data problems. In this paper, we consider the case where X is missing at random (MAR) which has been commonly assumed in the analysis of missing data. See, e.g, Little and Rubin (2002). In short, this paper considers the model selection problem for $f_{Y|X,Z}(y|x,z)$ with X missing at random.

There are several alternative model selection approaches that can be applied for the considered model selection problem. These approaches can be roughly classified into the following four types. The first type of approach is developed based on Bayesian point of view (see, e.g., Celeux et al., 2006; Gelman et al., 2005). A drawback of this type is that it needs to set prior distributions for parameters in the candidate models. In general, it is not easy to obtain reasonable priors and meanwhile make sure that these priors are not in conflict with each other. The second type of approach is established based on the expectation-maximization (EM) algorithm (see, e.g., Claeskens and Consentino, 2008; Ibrahim et al., 2008; Jiang et al., 2015). A drawback of this type is that it requires a correctly specified parametric model for the condition probability function $f_{X|Z}(x|z)$. In practice, it may be hard to get a correct specification for $f_{X|Z}(x|z)$, not mention X is missing. The third type is the bias corrected model selection criterion of Wei et al. (2021), and it does not need that $f_{X|Y,Z}(x|y,z)$ is specified correctly. Hence, it improves the model selection approaches based on EM algorithm. However, it requires a correctly specified parametric model for the selection probability function. The final type of approach is the weighted AIC (Hens et al., 2006) which is developed based on the inverse probability weighted (IPW) method (Horvitz and Thompson, 1952; Robins et al., 1994), a widely used method in the study of missing data problems. Comparing to the previous three types of approaches, the advantages of the weighted AIC are that it is a frequentist model selection approach so that it does not need to set prior distributions, and its calculation is irrelevant to $f_{X|Z}(x|z)$ or $f_{X|Y,Z}(x|y,z)$, so that it does not need to specify parametric model for $f_{X|Z}(x|z)$ or $f_{X|Y,Z}(x|y,z)$. However, a drawback of the weighted AIC is that it requires a consistent estimate of the selection probability function. If the selection probability function is estimated parametrically, then a correctly specified parametric model for the selection probability function is required. And if the selection probability function is estimated nonparametrically, the problem of “curse of dimension” occurs. Unfortunately, the theoretical properties of the weighted AIC are lacked in Hens et al. (2006).

This paper proposes a robust inverse probability weighting Kullback–Leibler divergence (RIPW-KL) criterion-based method by estimating the weight function semiparametrically. The main idea of this method can be described as follows. We first postulate several possible parametric models for the selection probability function and then combine the information contained in these estimated parametric models through a nonparametric smoothing method to get a semiparametric estimator of a conditional probability function conditional on the assumed models. With the inverse of this estimator as the weight, an inverse probability weighted estimator of the Kullback–Leibler divergence can be obtained immediately. And further, the proposed criterion can be established by minimizing the weighted Kullback–Leibler divergence with a suitable penalty term. Under some conditions, we prove that the model selection by our proposed criterion is consistent and the estimator of population parameter vector corresponding to the selected model is asymptotically normal. Unlike the weighted AIC which makes a choice between parametric and nonparametric methods, our semiparametric weighting criterion makes a balance between these two kinds of methods and thus alleviates the problems of model misspecification and “curse of dimension” simultaneously. Concretely, under certain conditions, it is shown that the consistency of model selection by our proposal is valid as long as the selection probability function is a function of its assumed models. Hence, comparing to the parametrically weighted AIC, our proposed RIPW-KL criterion is more robust to misspecification of the selection probability function. This alleviates the problem of model misspecification. Besides, for the purpose of weights, our proposal applies the kernel smoothing method to estimate regression on the assumed models for the selection probability function, while the nonparametrically weighted AIC applies the kernel smoothing method to estimate the selection probability regression function on the observed variables. Usually, the number of these assumed models is far smaller than the number of the observed variables, and thus, the proposed method also alleviates the problem of “curse of dimension”. That is, the proposed method has following significant advantages over the existing methods:

• 1. The RIPW-KL criterion does not need to set prior distributions as Bayesian methods;

• 2. The RIPW-KL criterion does not need a correct specification for $f_{X|Z}(x|z)$ or $f_{X|Y,Z}(x|y,z)$ comparing to EM algorithm.

• 3. The RIPW-KL criterion does not need a correct specification of the selection probability function as the parametrically weighted AIC method due to Hens et al. (2006) and the corrected method due to Wei et al. (2021).

• 4. The RIPW-KL criterion alleviates the problem of “curse of dimension” comparing to the nonparametrically weighted AIC method due to Hens et al. (2006).

The rest of this paper is organized as follows. In Sect. 2, we describe the model framework and then establish the RIPW-KL criterion. In Sect. 3, the theoretical properties of our proposal are presented, and the finite-sample performance of our proposal is investigated through a Monte Carlo study in Sect. 4. And a real data analysis is implemented in Sect. 5. And all the technical details are relegated in the “Appendix”.

2 Methodology

Let $\{(Y_i, X_i, Z_i,\delta _i), 1\le i\le n\}$ be the independent and identically distributed sample from $(Y, X, Z,\delta )$, where $Y_i$ and $Z_i$ are observed completely, and $\delta _i=0$ if $X_i$ is missing, otherwise $\delta _i=1$. Throughout this paper, we assume that X is missing at random (MAR), that is,

$$\begin{aligned} P(\delta =1|Y,X,Z)=P(\delta =1|Y,Z):=\pi (Y,Z). \end{aligned}$$

Suppose that a finite set of candidate parametric models can be obtained for $f_{Y|X,Z}(y|x,z)$. For the candidate model M, we have a parametric model $g_M(y|x,z;\theta _M)$, where $\theta _M$ is an unknown parameter vector, while $g_M(\cdot |x,z;\theta _M)$ is a known function. It’s well known that the Kullback–Leibler (KL) divergence is a widely used measure on the closeness between the assumed parametric model and the true model that generates data. For the candidate model M, the KL divergence from $f_{Y|X,Z}(y|x,z)$ to $g_M(y|x,z;\theta _M)$ is

$$\begin{aligned} KL(M,\theta _M)=E\left\{ \log f_{Y|X,Z}(Y|X,Z)\right\} -E\left\{ \log g_M(Y|X,Z;\theta _M)\right\} . \end{aligned}$$

(1)

Clearly, we take $E\left\{ \log g_M(Y|X,Z;\theta _M)\right\}$ to measure the closeness of $f_{Y |X,Z} (y|x, z)$ to $g_M (y|x, z;\theta _M)$ and denote it by $D(M,\theta _M)$, since $E\left\{ \log f_{Y|X,Z}(Y|X,Z)\right\}$ is irrelevant to the candidate models. Clearly, the larger $D(M,\theta _M)$ is, the smaller KL divergence is.

We assume a parametric model $\pi (y,z;{\bar{\alpha }})$ for the selection probability function $P(\delta =1|y,z)$, where ${\bar{\alpha }}$ is the unknown parameter vector. Inspired by Hens et al. (2006), an inverse probability weighting estimator of $D(M,\theta _M)$ is given by

$$\begin{aligned} {{\hat{D}}}(M,{{\hat{\alpha }}},\theta _M)=\frac{1}{n} \sum _{i=1}^n \frac{\delta _i}{\pi (Y_i,Z_i;{{\hat{\alpha }}})}\log g_M(Y_i|X_i, Z_i;\theta _M), \end{aligned}$$

where ${{\hat{\alpha }}}$ is the maximum likelihood estimate (MLE) of ${\bar{\alpha }}$.

For writing convenience, we abbreviate $\pi (y,z;{\bar{\alpha }})$ to $\pi ({\bar{\alpha }})$. Obviously, if $\pi ({\bar{\alpha }})$ is misspecified, ${{\hat{D}}}(M,{{\hat{\alpha }}},\theta _M)$ defines an inconsistent estimator for $D(M,\theta _M)$. In this case, one may use the augmented inverse probability weighting approach. This method, however, needs that $f_{X|Y,Z}(x|y,z)$ is specified correctly when $\pi ({\bar{\alpha }})$ is misspecified. Nevertheless, it is impractical to specify $f_{X|Y,Z}(x|y,z)$ correctly since $f_{Y|X,Z}(y|x,z)$ is unknown, not to mention that X is missing. Another strategy is to use the nonparametric kernel method to estimate the selecting probability function. However, this approach leads to “curse of dimension” problem if the dimension of (Y, Z) is large. These motivate us to develop a robust model selection approach based on the inverse probability weighting KL divergence with a semiparametric weight.

Specify multiple possible parametric models $\{\pi _{j}({y,z};{\alpha }_{j}), j = 1,\dots ,J \}$ for $\pi \left( {y,z}\right)$. Define $\phi _{\pi }\left( {y,z};\alpha \right) = \left( \pi _{1}\left( {y,z}; {\alpha }_{1}\right) ,\dots ,\pi _{J}\left( {y,z}; {\alpha }_{J}\right) \right) ^{\top }$, where $\alpha = \left( {\alpha }^{\top }_{1}, \dots ,{\alpha }^{\top }_{J}\right) ^{\top }$. Usually, the number of the assumed models J is less than the dimension of the observed variables.

Let

$$\begin{aligned} {\hat{p}}_{\alpha ,n}(v)=\frac{\sum _{l=1}^n K\left( \frac{\{v-\phi _{\pi }({Y_l,Z_l};\alpha )\}}{h_n}\right) \delta _l}{\sum _{l=1}^n K\left( \frac{\{v-\phi _{\pi }({Y_l,Z_l};\alpha )\}}{h_n}\right) }, \end{aligned}$$

(2)

and

$$\begin{aligned} {\hat{r}}_{\alpha ,n}(v)=\frac{1}{nh_n^J}\sum _{l=1}^n K\left( \frac{\{v-\phi _{\pi }({Y_l,Z_l};\alpha )\}}{h_n}\right) \delta _l, \end{aligned}$$

(3)

where $h_n$ is a scalar bandwidth, $K(\cdot )$ is the multivariate kernel function. Then, a robust estimator of $D(M,\theta _M)$ can be defined as follows:

$$\begin{aligned} {{\hat{D}}}_{\text {IP}}(M,\theta _M,{\hat{\alpha _n}}) = \frac{1}{n}\sum _{i=1}^n \left\{ \frac{\delta _i}{{{\hat{p}}}_{{{\hat{\alpha _n}}},b_n}\left( \phi _{\pi }\left( {Y_i,Z_i};{{{\hat{\alpha }}}_n}\right) \right) }\log g_M(Y_i|X_i,Z_i;\theta _M)\right\} , \end{aligned}$$

(4)

where ${\hat{\alpha _n}}$ is the MLE of $\alpha$, ${\hat{p}}_{\alpha ,b_n}(v)={\hat{p}}_{\alpha ,n}(v){\hat{r}}_{\alpha ,b_n}(v)/{\hat{r}}_{\alpha ,n}(v)$, $b_n$ is a positive constant sequence tending to 0, and ${\hat{r}}_{\alpha ,b_n}(v)=\max \{{\hat{r}}_{\alpha ,n}(v),b_n\}$. It is obvious that ${{\hat{D}}}_{\text {IP}}(M,\theta _M,{\hat{\alpha _n}})$ is a dimension reduction estimation comparing to the nonparametric inverse probability weighting approach since J is usually taken less than the dimension of (Y, Z). Specially, J is taken to be 1 if one can specify a correct model for $\pi (y,z)$.

Further, let us denote the maximizer of ${{\hat{D}}}_{\text {IP}}(M,\theta _M,{\hat{\alpha _n}})$ with respect to $\theta _M$ as ${{{\hat{\theta }}}}^{\text {IP}}_M$, that is,

$$\begin{aligned} {{{\hat{\theta }}}}^{\text {IP}}_M=\mathop {\arg \max }_{\theta _M \in \Theta _M}{{\hat{D}}}_{\text {IP}}(M,\theta _M,{\hat{\alpha _n}}), \end{aligned}$$

(5)

where $\Theta _M$ is the parameter space of $\theta _M$. Then, the proposed RIPW-KL criterion is given by

$$\begin{aligned} {\text {IC}}_{\text {IP}}(M)=-{{\hat{D}}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})+\lambda _nd_M, \end{aligned}$$

(6)

where $d_M$ is the dimension of the unknown parameter vector $\theta _M$ and $\lambda _n$ is a positive tuning parameter tending to zero. Define

$$\begin{aligned} {{\hat{M}}}_{\text {IP}}=\mathop {\arg \min }_{M \in {\mathcal {M}}}{\text {IC}}_{\text {IP}}(M), \end{aligned}$$

(7)

where ${\mathcal {M}}$ is the set of all the candidate models. Then, ${{\hat{M}}}_{\text {IP}}$ is the selected model and the parameter vector can be estimated using ${{{\hat{\theta }}}}^{\text {IP}}_{{\hat{M}}_{\text {IP}}}$.

3 Theoretical properties

Before giving the main results, we first give some notations and some required conditions. To prove the consistency of model selection by the proposed criterion, firstly, we need to prove the asymptotic normality of the estimator ${{{\hat{\theta }}}}^{\text {IP}}_M$ in (5) for each candidate model M. Let $f_{\alpha }(\cdot )$ be the density function of $\phi _\pi (y,z;\alpha )$. Clearly, ${\hat{r}}_{\alpha ,n}(v)$ in (3) is the J-dimensional kernel density estimate of $f_{\alpha }(v)$. And denote $r_\alpha (v)=p_\alpha (v)f_\alpha (v)$, where $p_{\alpha }(v) = E\{\delta \mid \phi _{\pi }({Y,Z};\alpha )=v\}$. Then, ${\hat{p}}_{\alpha ,n}(v)$ in (2) is the nonparametric regression estimate of $p_{\alpha ^*}(v)$ where $\alpha ^*$ is the probability limit of ${\hat{\alpha _n}}$. And denote $||\cdot ||$ as Euclidean norm. Now, we present the required conditions as follows.

• (C.1) $\Theta _M$ is a compact set. And the KL divergence $KL(M,\theta _M)$ has a unique minimum point at $\theta ^*_{M}$, where $\theta ^*_{M}$ is an inner point of $\Theta _M$.

• (C.2) $E\left\{ -\frac{\partial ^{2}\log g_M(Y|X,Z;\theta _M)}{\partial \theta _M \partial \theta ^T_M}|_{\theta _M=\theta ^*_{M}}\right\}$ is positive definite. $\frac{\partial ^{3}\log g_M(y|x,z;\theta _M)}{\partial \theta ^3_M}$ is continuous with respect to $\theta _M$. And $E\{\sup \limits _{\theta _M \in \Theta _M}\log ^2 g_M(Y|X,Z;\theta _M)\}<\infty$.

• (C.3) $p_\alpha (v)$, $f_\alpha (v)$ have bounded partial derivatives up to order $k (k>J)$.

• (C.4) $\inf _{y,z}p(\delta =1|Y=y,Z=z)>0$.

• (C.5) (i) $||\phi _\pi (y,z;\alpha )-\phi _\pi (y,z;\alpha ^{'})||\le l(y,z)||\alpha -\alpha ^{'}||$, with $El(Y,Z)\le \infty$. (ii) $E[\sup _{\alpha }||\nabla _\alpha p_\alpha (\phi _\pi (Y,Z;\alpha ))||]<\infty$ and $E[\sup _{\alpha }||\nabla _\alpha r_\alpha (\phi _\pi (Y,Z;\alpha ))||]<\infty$. (iii) $\sup _{z,x} E[Y^2|Z=z,X=x]<\infty$.

• (C.6) The multivariate function K(v) is bounded and continuous kernel function of order $k(k>J)$ defined on the compact support.

• (C.7) $b_n$ is a constant sequence satisfying $\sqrt{n}h^{J+1}_nb^2_n/\log n\rightarrow \infty ,\sqrt{n}h^{\kappa }_n/b^2_n\rightarrow 0,\kappa >J+1$.

• (C.8) $\sqrt{n}E\left[ \left| \frac{1}{p_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))}\right| I[f_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))<b_n]\right] \rightarrow 0$, where I is the indicator function.

Remark

Condition (C.1) is the same as Condition 3 and Condition 5 of Fang and Shao (2016), which is an identifiability condition in model selection. Condition (C.2) defines the smoothness of $\log g_M(Y|X,Z;\theta _M)$. Condition (C.5)(i) controls the complexity of the multiple possible models $\phi _\pi (y,z;\alpha )$ for $\pi \left( {y,z}\right)$, which is identical to the Condition (C.3) in Wang et al. (2021). Condition (C.7) is a regular condition in nonparametric regression (see, Condition (C.$h_n$) in Wang and Rao (2002a) and Conditions (C.5), (C.6) in Wang et al. (2021). Condition (C.8) is similar to Condition (C.gm$b_n$) in Wang and Rao (2002a), which controls the rates of $b_n$ tending to zero.

Theorem 1

Under Conditions (C.1)–(C.8), we have $\sqrt{n} ({\hat{\theta }}^{\text {IP}}_M-\theta ^*_{M})$ is asymptotically mean-zero normal if $\pi \left( {y,z}\right)$ is a function of $\phi _{\pi }\left( {y,z};\alpha ^*\right)$.

Before establishing the consistency of model selection of the proposed method, we first present the definition of correct model. If $g_M(y|x,z;\theta _M)$ is a correctly specified model for $f_{Y|X,Z}(y|x,z)$, then we say that the model M is a correct model. Otherwise, we say that the model M is an incorrect one. Let $M_{\text {opt}}$ be the optimal model with the smallest dimension among all correct models in the class of candidate models. To prove the consistency of model selection by our proposal, we assume that there is at least one correct model among the class of candidate models. Such an assumption guarantees the existence of $M_{\text {opt}}$ and is commonly used in the model selection literature such as Jiang et al. (2015); Fang and Shao (2016) and Wei et al. (2021).

Theorem 2

Under Conditions (C.1)-(C.8), if $\lambda _n\rightarrow 0$, $\sqrt{n}\lambda _n\rightarrow \infty$ and satisfies that $\pi \left( {y,z}\right)$ is a function of $\phi _{\pi }\left( {y,z};\alpha ^*\right)$, then we have $P(\hat{M}_{\text {IP}}=M_{\text {opt}})\rightarrow 1$ as $n\rightarrow \infty$.

Theorem 2 indicates that the model selection by our proposed criterion is consistent. Our proposed criterion is robust to the model specifications for $\pi (y,z)$ as long as $\pi (y,z)$ is a function of $\phi _{\pi }\left( {y,z};\alpha ^*\right)$. In addition, according to Theorem 2, it is clear that Theorem 1 is still valid if M in Theorem 1 is replaced by ${\hat{M}}_{\text {IP}}$.

There are many choices of $\lambda _n$ that meet its restrictions given in Theorem 2. This arouses the interest of a referee in the question of how to select $\lambda _n$. As pointed out by Fang and Shao (2016), no optimal solution has been derived for this question in the model selection literature even for the case of no missing data. In this article, we mainly put our efforts into developing model selection methods with consistency of model selection rather than finding the best ways of choosing $\lambda _n$, because the latter is to some extent outside the scope of this article and we leave it for future study. At last, it should be pointed out that, following the strategy taken in Fang and Shao (2016), the tuning parameter $\lambda _n$ was set to be $\{0.25\log \log n\}^{0.25}n^{-1/2}$ in the following simulation studies and the real data analysis. And based on our simulation results, we believe that this setting of $\lambda _n$ is, if not the best, quite competitive.

4 Simulations

In this section, we conduct a Monte Carlo study with two designs to investigate the finite-sample performance of the proposed RIPW-KL criterion. The first design is concerned with the case where the assumed models $\{\pi _{j}({y,z};{\alpha }_{j}), j = 1,\dots ,J\}$ are all misspecified, but $\pi (y,z)$ is approximately a function of $\phi _{\pi }(y,z;\alpha ^*)$. And the second design is considered with the case where one of the assumed models $\{\pi _{j}({y,z};{\alpha }_{j}), j = 1,\dots ,J\}$ is correctly specified. A comparison between our proposal and two related existing model selection strategies based on KL divergence are made. The first model selection strategy uses classical Bayesian information criterion (BIC; Schwartz, 1978) with complete-case analysis which just ignores all the individuals that contain the missing. And we term this method as CC-KL. The second model selection strategy is the weighted AIC whose weight is selected by Akaike’s information criterion (Claeskens and Hjort, 2008) from the assumed models $\{\pi _{j}({y,z};{\alpha }_{j}), j = 1,\dots ,J\}$. We term this method as wAIC-KL. We also consider the classical BIC based on the complete data as a gold standard and term this method as CD-KL. The details and results of the Monte Carlo study are given below.

Design 1: In this design, we consider the case where $\{\pi _{j}({y,z};{\alpha }_{j}), j = 1,\dots ,J\}$ are all misspecified, while $\pi (y,z)$ is a function of $\phi _{\pi }(y,z;\alpha ^*)$. The data-generating process is

$$\begin{aligned} Y_{i}=\vartheta _{0}+\vartheta _{1}Z_{i,1}+\vartheta _{2}Z_{i,2}+\vartheta _{3}X_{i}+e_{i},\quad (\vartheta _{0},\vartheta _{1},\vartheta _{2},\vartheta _{3})^{\top }=(0, -0.5, 0, 1)^{\top }, \end{aligned}$$

(8)

where $\{Z_{i,1},Z_{i,2},X_{i},e_{i}\}$ are independent standard normal random variables for $i=1, 2,\cdots ,n$. The selection probability function is

$$\begin{aligned} \pi (y,z)=\Phi (\tilde{\alpha }_{0}+\tilde{\alpha }_{1}z_{1}y+\tilde{\alpha }_{2}z_{2}y), \end{aligned}$$

(9)

where $\Phi (\cdot )$ is the cumulative distribution function of the standard normal distribution. We consider the following two settings of $\tilde{\alpha }=(\tilde{\alpha }_{0},\tilde{\alpha }_{1},\tilde{\alpha }_{2})^{\top }$

$$\begin{aligned} \text {Case 1}: \tilde{\alpha }=(0.9, 0.5, -0.5)^{\top },\quad \text {Case 2}: \tilde{\alpha }=(0.2, 0.5, -0.5)^{\top }. \end{aligned}$$

The corresponding average missing rates are approximated $30\%$ and $50\%$, respectively. For the conditional probability function $f_{Y|X,Z}(y|x,z)$, we consider the following four candidate models:

$$\begin{aligned}&M_{1}: Y_{i}=\theta _0+\theta _{3}X_{i}+\sigma e_{i}, \\&M_{2}: Y_{i}=\theta _0+\theta _{1}Z_{i,1}+\theta _{3}X_{i}+\sigma e_{i}, \\&M_{3}: Y_{i}=\theta _0+\theta _{2}Z_{i,2}+\theta _{3}X_{i}+\sigma e_{i}, \\& M_{4}: Y_{i}=\theta _0+\theta _{1}Z_{i,1}+\theta _{2}Z_{i,2}+\theta _{3}X_{i}+\sigma e_{i}. \end{aligned}$$

According to the data-generating process (8), it is easy to see that $M_{2}$ is the optimal model. For the selection probability function $\pi (y,z)$, we consider the following two parametric models,

$$\begin{aligned} \pi _{1}({y,z};{\alpha }_{1})=\frac{\exp (\alpha _{10}+\alpha _{11}z_{1}y)}{1+\exp (\alpha _{10}+\alpha _{11}z_{1}y)},\quad \pi _{2}({y,z};{\alpha }_{2})=\frac{\exp (\alpha _{20}+\alpha _{22}z_{2}y)}{1+\exp (\alpha _{20}+\alpha _{22}z_{2}y)}. \end{aligned}$$

According to (9), it is easy to see that both $\pi _{1}({y,z};{\alpha }_{1})$ and $\pi _{2}({y,z};{\alpha }_{2})$ are misspecified, and $\pi (y,z)$ is neither a function of $\pi _{1}({y,z};{\alpha }_{1})$ nor a function of $\pi _{2}({y,z};{\alpha }_{2})$. Consider the following function of $\pi _{1}({y,z};{\alpha }_{1})$ and $\pi _{2}({y,z};{\alpha }_{2})$,

$$\begin{aligned} l_{\pi }(\pi _{1}({y,z};{\alpha }_{1}),\pi _{2}({y,z};{\alpha }_{2})) =c_{1}^{-1}\log \left\{ \frac{\pi _{1}({y,z};{\alpha }_{1})}{1-\pi _{1}({y,z};{\alpha }_{1})}\right\} +c_{2}^{-1}\log \left\{ \frac{\pi _{2}({y,z};{\alpha }_{2})}{1-\pi _{2}({y,z};{\alpha }_{2})}\right\} , \end{aligned}$$

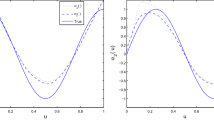
where $c_{1}$ and $c_{2}$ are some suitable constants. We analyze the relationship between $\pi (y,z)$ and $l_{\pi }(\pi _{1}({y,z};{\alpha }_{1}),\pi _{2}({y,z};{\alpha }_{2}))$ based on 500 simulated sample points. And the result is displayed in Fig. 1.

Fig. 1

Relationship between the selection probability function $\pi (y,z)$ and the function $l_{\pi }(\pi _{1}({y,z};{\alpha }^*_{1}),\pi _{2}({y,z};{\alpha }^*_{2}))$ based on 500 simulated sample points

From Fig. 1, it can be seen that $\pi (y,z)$ is a function of $l_{\pi }(\pi _{1}({y,z};{\alpha }^*_{1}),\pi _{2}({y,z};{\alpha }^*_{2}))$, and hence a function of {$\pi _{1}({y,z};{\alpha }^*_{1}),\pi _{2}({y,z};{\alpha }^*_{2})$}. This means that the assumed models $\{\pi _{1}({y,z};{\alpha }^*_{1}),\pi _{2}({y,z};{\alpha }^*_{2})\}$ for the selection probability function can approximately recover information of $\pi (y,z)$. This actually presents an example that the function is nonlinear since $l_{\pi }(\cdot , \cdot )$ is nonlinear.

In order to implement our proposal, following Wang et al. (2021), we use the Epanechnikov kernel function of order 4 which is

$$\begin{aligned} K(t)=\frac{3}{4\sqrt{5}}\left( \frac{15}{8}-\frac{7t^{2}}{8}\right) \left( 1-\frac{t^{2}}{5}\right) 1_{\{|t|\le \sqrt{5}\}}, \end{aligned}$$

and set $h_{n}=1.5n^{-1/(J+4+1)}, b_{n}=cn^{-1/4(J+4+1)}\log n$, where c is a constant. The sample size is considered to be $n=100,200$ and 400. Table 1 reports the number of times that a model is selected in 1000 simulation runs for the considered four methods.

From Table 1, some simulation results can be summarized as follows. First, our proposed RIPW-KL criterion is significantly better than wAIC-KL and CC-KL for all the combinations of simulation conditions. In addition, under the same average missing rate, the performance of our proposed criterion gets better and gets closer to the performance of CD-KL as the sample size increases. This is a significant advantage of our proposal over other model selection methods. Finally, it is worth noting that when the average missing rate is high, both wAIC-KL and CC-KL perform poorly even if the sample size is large. The reason may be that wAIC-KL depends on a correct specification of $\pi (y,z)$ and CC-KL may lead to inconsistency of model selection. The simulation results suggest that our proposed criterion is robust to the misspecified models for $\pi (y,z)$ as long as the selection probability function is a function of its assumed models.

Table 1 Number of times that each candidate model was selected by the considered four methods in 1000 simulation runs under Design 1

Design 2: In this design, we consider the case where one of the assumed models $\{\pi _{j}({y,z};{\alpha }_{j}), j = 1,\dots ,J\}$ is correctly specified. In fact, it is almost impossible to correctly specify one of the assumed models for the selection probability function $\pi (y,z)$. However, in order to make a comparison with Design 1 and fully understand the effect of misspecified parametric model for $\pi (y,z)$ on our proposed criterion, we take this special case into consideration. The current design is the same as Design 1 except for the following three changes. The selection probability function is now changed to the following

$$\begin{aligned} \pi (y,z)=\frac{\exp (\tilde{\alpha }_{0}+\tilde{\alpha }_{1}z_{1}y+\tilde{\alpha }_{2}z_{2}y)}{1+\exp (\tilde{\alpha }_{0}+\tilde{\alpha }_{1}z_{1}y+\tilde{\alpha }_{2}z_{2}y)}. \end{aligned}$$

(10)

And the settings of $\tilde{\alpha }$ are changed to the following two cases

$$\begin{aligned} \text {Case 1}: \tilde{\alpha }=(1.2, 0.5, -0.5)^{\top },\quad \text {Case 2}: \tilde{\alpha }=(0.2, 0.5, -0.5)^{\top }, \end{aligned}$$

such that the corresponding average missing rates are also approximated 30% and 50%, respectively. Furthermore, we change $\pi _{1}({y,z};{\alpha }_{1})$ to

$$\begin{aligned} \pi _{1}({y,z};{\alpha }_{1})=\frac{\exp (\alpha _{10}+\alpha _{11}z_{1}y+\alpha _{12}z_{2}y)}{1+\exp (\alpha _{10}+\alpha _{11}z_{1}y+\alpha _{12}z_{2}y)}, \end{aligned}$$

and keep $\pi _{2}({y,z};{\alpha }_{2})$ unchanged, so that $\pi _{1}({y,z};{\alpha }_{1})$ now becomes a correct specification for the selection probability function $\pi (y,z)$ in (10), and $\pi _{2}({y,z};{\alpha }_{2})$ is misspecified. Table 2 reports the number of times that a model is selected in 1000 simulation runs with the considered four methods.

Table 2 Number of times that each candidate model was selected by the considered four methods in 1000 simulation runs under Design 2

From Table 2, some results can be summarized as follows. Under this special case, the performances of both RIPW-KL and wAIC-KL perform well except for CC-KL. It is what we expect since the model selection proposed by wAIC-KL is also consistent when $\pi _{1}({y,z};{\alpha }_{1})$ is correctly specified for the selection probability function $\pi (y,z)$. As the sample size increases, the performance of our proposed RIPW-KL gets better. Note that, the performance of our proposed RIPW-KL is superior to wAIC-KL when $n=400$. Thus, our proposed RIPW-KL is still comparable in this case. Generally, it is impossible to correctly specify the models for the selection probability function $\pi (y,z)$ in real life as in Design 2. However, it is relatively easy to assume that the selection probability function $\pi (y,z)$ is a function of its assumed models. Hence, the RIPW-KL criterion we propose is more robust and more feasible.

All in all, the proposed RIPW-KL criterion performs competitively in the presence of missing data.

5 Real data analysis

In this section, we apply the proposed criterion to the automobile data set from the Machine Learning Repository at the University of California Irvine (http://mlr.cs.umass.edu/mldatasets/Automobile). The raw data contain 205 sample points. And we analyze the relationship between the price of the car and its corresponding car attributes. Following Wei et al. (2021), we take the logarithm of the price of the car as the response variable Y and choose normalized-losses (X), wheel-base ($Z_1$), length ($Z_2$), width ($Z_3$), height ($Z_4$), curb-weight ($Z_5$), engine-size ($Z_6$), bore ($Z_7$), stroke ($Z_8$), compression-ratio ($Z_9$), horsepower ($Z_{10}$), peak-rpm ($Z_{11}$), city-mpg ($Z_{12}$), highway-mpg ($Z_{13}$), symboling ($Z_{14}$), fuel-type ($Z_{15}=1$, diesel; $Z_{15}=2$, gas), aspiration ($Z_{16}=1$, std; $Z_{16}=2$, turbo), num-of-doors ($Z_{17}$), and num-of-cylinders ($Z_{18}$) as predictors. Among the 18 predictors, the $Z_{14}$, $Z_{15}$, $Z_{16}$, $Z_{17}$, and $Z_{18}$ are discrete predictors and the remaining are continuous predictors. Denote $Z=(Z_1, Z_2, \cdot \cdot \cdot ,Z_{18})$. Note that, there are 4 sample points in Y and 8 samples points in Z contain missing values, and we simply delete these sample points. Thus, the response variable Y and covariates Z are observed completely, while there are 34 missing values for covariates X. Further, we standardize each continuous predictors based on complete cases. Thus, for the conditional probability linear function $f_{Y|X,Z}(y|x,z)$, we have $2^{19}-1$ candidate models. To the candidate model M, we have

$$\begin{aligned} Y=\theta _0+\sum _{i\in \Upsilon _M} \theta _iT_i+e, \end{aligned}$$

where $T=(Z,X)$, $\Upsilon _M\subset \{1,2,\cdot \cdot \cdot ,19\}$, $\theta _i$ is the unknown parameter vector, and e is a normal error vector which is independent of T with mean zero and unknown variance $\sigma ^2$. Clearly, the sheer number of models is not conducive to implementing our proposed criterion. Thus, to obtain a series of candidate models, we take full advantage of FW/BW procedure in Jiang et al. (2015). Similar to Jiang et al. (2015), due to missing data, we calculate $RSS(M,T,\theta )$ based on the complete cases and denote it as $RSS_{cc}(M,T,\theta )$, where $RSS(M,T,\theta )=\sum \limits _{i=1}^n(Y_i-\theta _0-\sum \limits _{i\in \Upsilon _M}\theta _iT_i)^2$ and $RSS_{cc}(M,T,\theta )=\sum \limits _{i=1}^n\delta _i(Y_i-\theta _0-\sum \limits _{i\in \Upsilon _M}\theta _iT_i)^2$. Then, taking FW/BW procedure, we can obtain the candidate models for $f_{Y|X,Z}(y|x,z)$ based on $RSS_{cc}(M,T,\theta )$.

Similarly, we assume that X is missing at random (MAR). As for the selection probability function $\pi (y,z)$, we consider the following two cases:

Case1:

$$\begin{aligned}&\pi _1(y,z;\alpha _1)=\exp (\alpha _{10}+\alpha _{11}y+\alpha _{11}z)/\left\{ 1+\exp (\alpha _{10}+\alpha _{11}y+\alpha _{11}z)\right\} ,\\&\pi _2(y,z;\alpha _2)=\exp (\alpha _{21}y+\alpha _{22}z)/\left\{ 1+\exp (\alpha _{21}y+\alpha _{22}z)\right\} , \end{aligned}$$

where $\alpha _1$, $\alpha _2$ are the corresponding parameter vectors.

Case2:

$$\begin{aligned}&\pi _1(y,z;\beta _1)=\exp (\beta _{10}+\beta _{11}y+\beta _{12}z+\beta _{13}zy)/\left\{ 1+\exp (\beta _{10}+\beta _{11}y+\beta _{12}z+\beta _{13}zy)\right\} ,\\&\pi _2(y,z;\beta _2)=\exp (\beta _{20}+\beta _{21}y+\beta _{22}z)/\left\{ 1+\exp (\beta _{20}+\beta _{21}y+\beta _{22}z)\right\} , \end{aligned}$$

where $\beta _1$, $\beta _2$ are the corresponding parameter vectors.

Table 3 reports the models selected by the two methods, respectively.

Table 3 The models selected by RIPW-KL criterion, wAIC-KL, respectively, for the automobile data set

From Table 3, it can be observed that RIPW-KL criterion is more robust than wAIC-KL since our proposal selects the same model under two different specifications of $\pi (y,z)$. Clearly, in real data analysis, it is hard to select the true model for the selection probability function. However, it is relatively reliable to assume some models for the selection probability function. Similar to Wang et al. (2021), we can see that the spirit of RIPW-KL criterion is like the idea of model averaging that can combine the information of each assumed models for the selection probability function, while the wAIC-KL simply uses the information of one model in the end. This may be the reason that the RIPW-KL criterion is more robust than wAIC-KL.

Appendix

We present proofs of theorems as follows.

Proof of Theorem 1

In order to prove Theorem 1, we need to prove the existence and consistency of ${{{\hat{\theta }}}}^{\text {IP}}_M$ defined in (5) firstly. Based on Property 24.1 in Gourieroux and Monfort (1995), the existence of ${{{\hat{\theta }}}}^{\text {IP}}_M$ can be guaranteed under (C.1), (C.2), (C.5) and (C.6). Recalling the definition of ${{\hat{D}}}_{\text {IP}}(M,\theta _M,{{\hat{\alpha }}}_n)$ given in (4), based on Theorem 2.1 in Newey and Mcfadden (1994) and (C.1), (C.2), it suffices to prove the consistency of the ${\hat{\theta }}^{\text {IP}}_M$ by verifying the following equation:

$$\begin{aligned} \sup _{\theta _M \in \Theta _M}|{{\hat{D}}}_{\text {IP}}(M,\theta _M,\hat{\alpha }_n)-D(M,\theta _M)|=o_p(1). \end{aligned}$$

Note that,

$$\begin{aligned}&|{{\hat{D}}}_{\text {IP}}(M,\theta _M,{{\hat{\alpha }}}_n)-D(M,\theta _M)| \\&\quad \le |{{\hat{D}}}_{\text {IP}}(M,\theta _M,{{\hat{\alpha }}}_n)-{\tilde{D}}_{\text {IP}}(M,\theta _M,\alpha ^*)|+|{\tilde{D}}_{\text {IP}}(M,\theta _M,\alpha ^*)-D(M,\theta _M)|, \end{aligned}$$

where ${{\tilde{D}}}_{\text {IP}}(M,\theta _M,\alpha ^*) = n^{-1}\sum \limits _{i=1}^n\left\{ \frac{\delta _i}{p_{\alpha ^*}\left( \phi _{\pi }\left( {Y_i,Z_i};\alpha ^*\right) \right) }\log g_M(Y_i|X_i,Z_i;\theta _M)\right\}$, in which $p_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))$ is defined in the first paragraph of Sect. 3. We need only to prove,

$$\begin{aligned} \sup _{\theta _M \in \Theta _M}|{{\hat{D}}}_{\text {IP}}(M,\theta _M,\hat{\alpha }_n)-{{\tilde{D}}}_{\text {IP}}(M,\theta _M,\alpha ^*)|=o_p(1), \end{aligned}$$

(11)

and

$$\begin{aligned} \sup _{\theta _M \in \Theta _M}|{\tilde{D}}_{\text {IP}}(M,\theta _M,\alpha ^*)-D(M,\theta _M)|=o_p(1). \end{aligned}$$

(12)

According to Lemma 2.4 in Newey and Mcfadden (1994), with (C.1) and (C.2), it is direct to prove (12) by noting

$$\begin{aligned} E\{\delta |\phi _\pi (y,z;\alpha ^*)\}=\pi (y,z). \end{aligned}$$

(13)

Note that,

$$\begin{aligned}&{{\hat{D}}}_{\text {IP}}(M,\theta _M,{\hat{\alpha _n}})-{{\tilde{D}}}_{\text {IP}}(M,\theta _M,\alpha ^*)\nonumber \\&\quad =\frac{1}{n}\sum _{i=1}^n\delta _i \log g_M(Y_i|X_i,Z_i;\theta _M)\{{{\hat{q}}}_{{{\hat{\alpha _n}}},b_n}\left( \phi _{\pi }\left( {Y_i,Z_i} ;{{{\hat{\alpha }}}_n}\right) \right) -{\hat{q}}_{\alpha ^*,b_n}(\phi _\pi (Y_i,Z_i;\alpha ^*))\}\nonumber \\+&\frac{1}{n}\sum _{i=1}^n\delta _i \log g_M(Y_i|X_i,Z_i;\theta _M)\{{\hat{q}}_{\alpha ^*,b_n}(\phi _\pi (Y_i,Z_i;\alpha ^*))-q_{\alpha ^*,b_n}(\phi _\pi (Y_i,Z_i;\alpha ^*))\}\nonumber \\&\qquad +\frac{1}{n}\sum _{i=1}^n\delta _i \log g_M(Y_i|X_i,Z_i;\theta _M)\{q_{\alpha ^*,b_n}(\phi _\pi (Y_i,Z_i;\alpha ^*))- q_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))\}\nonumber \\ {}&\quad :=Q_{n1}+Q_{n2}+Q_{n3}, \end{aligned}$$

(14)

where ${\hat{q}}_{\alpha ,n}(u)=1/{\hat{p}}_{\alpha ,n}(u)$, ${\hat{q}}_{\alpha ,b_n}(u)=1/{{\hat{p}}}_{\alpha ,b_n}(u)={\hat{q}}_{\alpha ,n}(u){\hat{r}}_{\alpha ,n}(u)/{\hat{r}}_{\alpha ,b_n}(u)$, $q_{\alpha }(u)=1/p_{\alpha }(u)$, $q_{\alpha ,b_n}(u)=q_\alpha (u)r_\alpha (u)/r_{\alpha ,b_n}(u)$, $r_{\alpha ,b_n}(u)=\max \{r_{\alpha }(u),b_n\}$, in which $p_\alpha (v)$ and $r_\alpha (v)$ are given at the first paragraph of Sect. 3. By (2) and (3), we know that the definition of ${\hat{q}}_{\alpha ,n}(u)$, ${\hat{q}}_{\alpha ,b_n}(u)$, $q_\alpha (u)$ and $q_{\alpha ,b_n}(u)$ are similar to ${\hat{a}}_{\gamma ,n}(v)$, ${\hat{a}}_{\gamma ,b_n}(u)$, $a_\gamma (u)$ and $a_{\gamma ,b_n}(u)$ in Wang et al. (2021), respectively. By (C.2), we have $E\{\sup \limits _{\theta _M\in \Theta _M}\delta \log g_M(Y|X,Z;\theta _M)\}<\infty$. This together with conditions (C.3)-(C.7) proves $\sup \limits _{\theta _M \in \Theta _M}Q_{n1}=o_p(1)$ and $\sup \limits _{\theta _M \in \Theta _M}Q_{n2}=o_p(1)$, respectively, using the similar arguments to that of Lemma S1 and S2 in Wang et al. (2021). Clearly,

$$\begin{aligned} |Q_{n3}|\le \frac{2}{n}\sum _{i=1}^n|\delta _i \log g_M(Y_i|X_i,Z_i;\theta _M)q_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))|I[r_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))<b_n]. \end{aligned}$$

By (C.2), (C.3) and (C.4), $\forall \epsilon >0$, we then have

$$\begin{aligned}&P(|\sup _{\theta _M\in \Theta _M}Q_{n3}|>\epsilon )\\&\quad \le \frac{2}{\epsilon }E\{|\sup _{\theta _M \in \Theta _M}\delta \log g_M(Y|X,Z;\theta _M)q_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))|I[r_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))<b_n]\}\\&\quad \rightarrow 0. \end{aligned}$$

This yields

$$\begin{aligned}&\sup _{\theta _M \in \Theta _M}|{{\hat{D}}}_{\text {IP}}(M,\theta _M,\hat{\alpha }_n)-{{\tilde{D}}}_{\text {IP}}(M,\theta _M,\alpha ^*)|\\ {}&\quad \le \left| \sup _{\theta _M\in \Theta _M}Q_{n1}\right| +\left| \sup _{\theta _M\in \Theta _M}Q_{n2}\right| +\left| \sup _{\theta _M\in \Theta _M}Q_{n3}\right| =o_p(1). \end{aligned}$$

This completes the proof of (11).

Now, in what follows, we prove the asymptotically normality of $\hat{\theta }_M^{\text {IP}}$. By (14), we know that

$$\begin{aligned} {{\hat{D}}}_{\text {IP}}(M,\theta _M,{{\hat{\alpha }}}_n) ={\tilde{D}}_{\text {IP}}(M,\theta _M,\alpha ^*)+Q_{n1}+Q_{n2}+Q_{n3}. \end{aligned}$$

Lemma 1 in the supplementary material proves that

$$\begin{aligned} Q_{n1}=&n^{-1}\sum _{i=1}^n\{\delta _i\log g_M(Y_i|X_i,Z_i;\theta _M)\}\{\partial q_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))/\partial \alpha \}({\hat{\alpha _n}}-\alpha ^*)\nonumber \\ {}&+o_p(n^{-1/2}). \end{aligned}$$

(15)

Further, according to Lemma 2 in the supplementary material, we have

$$\begin{aligned} Q_{n2}=&n^{-1}\sum _{i=1}^n\{1-\delta _iq_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))\}q_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))\nonumber \\&\times \delta _i\log g_M(Y_i|X_i,Z_i;\theta _M)+o_p(n^{-1/2}). \end{aligned}$$

(16)

For $Q_{n3}$, by (C.2), (C.8) and Markov’s inequality, we have

$$\begin{aligned}&P(n^{1/2}|Q_{n3}|>\epsilon )\nonumber \\ \le&P(n^{-1/2}\sum _{i=1}^n2\left| C_iq_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))\right| I[r_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))<b_n]>\epsilon ) \nonumber \\&\quad \le 2\epsilon ^{-1}E\{\sqrt{n}\left| Cq_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))\right| I[r_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))<b_n]\} \rightarrow 0, \end{aligned}$$

(17)

where $C_i=\delta _i\log g_M(Y_i|X_i,Z_i;\theta _M)$. Then, we have $Q_{n3}=o_p(n^{-1/2})$. Thus, we have

$$\begin{aligned}&{{\hat{D}}}_{\text {IP}}(M,\theta _M,{\hat{\alpha _n}}) ={\tilde{D}}_{\text {IP}}(M,\theta _M,\alpha ^*)+Q_{n1}+Q_{n2}+o_p(n^{-1/2}). \end{aligned}$$

(18)

Let $\Psi (u,v)$ be a general vector-valued or matrix-valued function, and we denote

$$\begin{aligned} \Psi ^{'}_{\{u\}}(u,v)=\frac{ \partial \Psi (u,v)}{\partial u}, \end{aligned}$$

$$\begin{aligned} K_M(\theta _M,{\hat{\alpha _n}})={{\hat{D}}}^{'}_{IP\{\theta _M\}}(M,\theta _M,{\hat{\alpha _n}}). \end{aligned}$$

Then, by (4), we have

$$\begin{aligned} K_M(\theta _M,{\hat{\alpha _n}})=n^{-1}\sum _{i=1}^n \left\{ \frac{\delta _i}{{{\hat{p}}}_{{{\hat{\alpha _n}}},b_n}\left( \phi _{\pi }\left( {Y_i,Z_i};{\hat{\alpha }_n}\right) \right) }t_{M,i}(\theta _M)\right\} , \end{aligned}$$

where $t_{M,i}(\theta _M)=\frac{\partial \log g_M(Y_i|X_i,Z_i;\theta _M)}{\partial \theta _M}$, for $i=1,2,\cdot \cdot \cdot ,n$. With the same technique of (18), under (C.2)-(C.8), we can obtain that

$$\begin{aligned}&K_M({\hat{\theta _M}}^{\text {IP}},{\hat{\alpha _n}})=n^{-1}\sum _{i=1}^nq_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))\delta _it_{M,i}({\hat{\theta _M}}^{\text {IP}})\nonumber \\&\quad +n^{-1}\sum _{i=1}^n\delta _it_{M,i}({\hat{\theta _M}}^{\text {IP}})\{\partial q_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))/\partial \alpha \}({\hat{\alpha _n}}-\alpha ^*) \nonumber \\+&\quad n^{-1}\sum _{i=1}^n\{1-\delta _iq_{\alpha ^{*}}(\phi _{\pi }({Y_i,Z_i};\alpha ^{*}))\}q_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))\delta _i t_{M,i}({\hat{\theta _M}}^{\text {IP}})+o_p(n^{-1/2}). \end{aligned}$$

(19)

From (5), it follows that $K_M({\hat{\theta _M}}^{\text {IP}},\hat{\alpha }_n)=0$. Thus, applying Taylor expansion to $K_M({\hat{\theta _M}}^{\text {IP}},{{\hat{\alpha }}}_n)$ around the point $(\theta ^*_{M},\alpha ^*)$, we have

$$\begin{aligned}&0=n^{-1}\sum _{i=1}^n\bigg \{q_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))\delta _it_{M,i}(\theta ^*_M) +[1-\delta _iq_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))]\nonumber \\&\quad \times q_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))\delta _i t_{M,i}(\theta ^*_M)\bigg \}+n^{-1}\sum _{i=1}^n\bigg \{q_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))\delta _it^{'}_{M,i}(\theta ^*_M) \nonumber \\&\quad +[1-\delta _iq_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))] q_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))\delta _i t^{'}_{M,i}(\theta ^*_M)\bigg \}({\hat{\theta _M}}^{\text {IP}}-\theta ^*_M) \nonumber \\ {}&\quad +n^{-1}\sum _{i=1}^n\bigg \{\delta _it_{M,i}(\theta ^*_M)\partial q_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))/\partial \alpha \bigg \}({\hat{\alpha _n}}-\alpha ^*) +o_p(n^{-1/2})\nonumber \\ {}&\quad :=H_{n1}(M,\theta ^*_M,\alpha ^*)+H_{n2}(M,\theta ^*_M,\alpha ^*)({\hat{\theta _M}}^{\text {IP}}-\theta ^*_M)+H_{n3}(M,\theta ^*_M,\alpha ^*)({\hat{\alpha _n}}-\alpha ^*) \nonumber \\ {}&\quad +o_p(n^{-1/2}), \end{aligned}$$

(20)

where $\alpha ^*$ is the probability limit of ${\hat{\alpha _n}}$ and $\theta ^*_{M}$ is given in Condition (C.1). Let

$$\begin{aligned} t_\pi (\alpha )=\frac{\delta -\phi _\pi (y,z;\alpha )}{\phi _\pi (y,z;\alpha )\{1-\phi _\pi (y,z;\alpha )\}}\cdot \phi ^{'}_{\pi {\{\alpha \}}}(y,z;\alpha ). \end{aligned}$$

And by a standard argument, one can easily obtain the following equation:

$$\begin{aligned} \sqrt{n}({\hat{\alpha _n}}-\alpha ^*)=I^{-1}_{\alpha ^*}\frac{1}{\sqrt{n}}\sum _{i=1}^n t_{\pi ,i}(\alpha ^*)+o_p(1), \end{aligned}$$

(21)

where $I_{\alpha ^*}=-E[t^{'}_\pi (\alpha )_{\{\alpha ^T\}}(\alpha ^*)]$.

Similarly, by the law of larger numbers, we can obtain that

$$\begin{aligned} H_{n2}(M,\theta ^*_M,\alpha ^*)=-I_{\theta ^*_{M}}+o_p(1),\ \ H_{n3}(M,\theta ^*_M,\alpha ^*)=-A_{M,\alpha ^*}+o_p(1), \end{aligned}$$

(22)

where

$$\begin{aligned}&I_{\theta ^*_{M}}=-E\big [\delta q_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))t^{'}_{M\{\theta ^T_M\}}(\theta ^*_{M})+\{1-\delta q_{\alpha ^*}(\phi _{\pi }(Y,Z;\alpha ^*))\}\\&\times q_{\alpha ^*}(\phi _{\pi }(Y,Z;\alpha ^*))\delta t^{'}_{M\{\theta ^T_M\}}(\theta ^*_{M})\big ],\\&\quad A_{M,\alpha ^*}=-E\left\{ \delta \frac{\partial q_{\alpha ^*}(\phi _\pi (Y,Z;\alpha ^*))}{\partial \alpha ^*}t_M(\theta ^*_M)\right\} . \end{aligned}$$

Thus, (20) together with (21) and (22), we prove

$$\begin{aligned} \sqrt{n} ({\hat{\theta }}^{\text {IP}}_M-\theta ^*_{M})=\frac{1}{\sqrt{n}}\sum _{i=1}^n R_{M,i}+o_p(1), \end{aligned}$$

where

$$\begin{aligned}&R_{M,i}=I^{-1}_{\theta ^*_{M}}\bigg \{\delta _i q_{\alpha ^*}(\phi _\pi (Y_i,Z_i;\alpha ^*))t_{M,i}(\theta ^*_{M})+[1-\delta _iq_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))]\\&\quad \times q_{\alpha ^*}(\phi _{\pi }({Y_i,Z_i};\alpha ^*))\delta _i t_{M,i}(\theta ^*_M) -A_{M,\alpha }I^{-1}_{\alpha ^*}t_{\pi ,i}(\alpha ^*)\bigg \}. \end{aligned}$$

By the central limit theorem and the above prove process, we prove that ${\hat{\theta }}^{\text {IP}}_M$ is asymptotically normal with zero mean, as $n\rightarrow \infty$. This completes the proof of Theorem 1. $\square$

Proof of Theorem 2

Obviously, in order to prove Theorem 2, it suffices to prove the following equation:

$$\begin{aligned} P\{{\text {IC}}_{\text {IP}}({\hat{M}}_{\text {IP}})={\text {IC}}_{\text {IP}}(M_{\text {opt}})\}\rightarrow 1 \ \ (n\rightarrow \infty ). \end{aligned}$$

(23)

Recalling the definition of ${\hat{M}}_{\text {IP}}$ in (7), ${\hat{M}}_{\text {IP}}$ is the minimizer of ${\text {IC}}_{\text {IP}}(M)$ with respect to M. So, it is obvious that we have ${\text {IC}}_{\text {IP}}({\hat{M}}_{\text {IP}})\le {\text {IC}}_{\text {IP}}(M_{\text {opt}})$. Thus, to prove (23), we only need to prove that

$$\begin{aligned} P\{{\text {IC}}_{\text {IP}}({\hat{M}}_{\text {IP}})\ge {\text {IC}}_{\text {IP}}(M_{\text {opt}})\}\rightarrow 1 \ \ (n\rightarrow \infty ). \end{aligned}$$

(24)

To prove (24), it’s enough to prove the following equation:

$$\begin{aligned} P\{{\text {IC}}_{\text {IP}}(M)\ge {\text {IC}}_{\text {IP}}(M_{\text {opt}})\}\rightarrow 1 \ \ (n\rightarrow \infty ), \end{aligned}$$

(25)

for each candidate model M. By the definition of ${\text {IC}}_{\text {IP}}(M)$ defined in (6), we know that in order to prove (25), it’s equivalent to prove the following equation, when $n\rightarrow \infty$,

$$\begin{aligned} P({\hat{D}}_{\text {IP}}(M_{\text {opt}},{{\hat{\theta }}}^{\text {IP}}_{M_{\text {opt}}},{\hat{\alpha _n}})-{\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})+\lambda _n(d_M-d_{M_{\text {opt}}})\ge 0)\rightarrow 1. \end{aligned}$$

(26)

If $M=M_{\text {opt}}$, (26) is clearly true. Thus, we consider the case where the model M is not $M_{\text {opt}}$ only. By Theorem 1, applying Taylor-expansion to ${{\hat{D}}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})$, we have

$$\begin{aligned} {{\hat{D}}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})&={{\hat{D}}}_{\text {IP}}(M,\theta ^{*}_M,\alpha ^*)+ {{\hat{D}}}^{'}_{IP\{\theta ^T_M\}}(M,\theta ^{*}_M,\alpha ^*)({\hat{\theta }}^{\text {IP}}_M-\theta ^{*}_M)\\ {}&+{{\hat{D}}}^{'}_{IP\{\alpha ^T\}}(M,\theta ^{*}_M,\alpha ^*)({\hat{\alpha _n}}-\alpha ^*)+o_p(n^{-1/2}), \end{aligned}$$

where the definition of ${\hat{\theta }}^{\text {IP}}_{M_{\text {opt}}}$ is similar to ${\hat{\theta }}^{\text {IP}}_M$. By (C.2), (C.4) and (C.5)(ii) as well as the root n consistency of ${\hat{\theta }}^{\text {IP}}_M$ and ${\hat{\alpha _n}}$, we have

$$\begin{aligned}&{{\hat{D}}}^{'}_{IP\{\theta ^T_M\}}(M,\theta ^{*}_M,\alpha ^*)({\hat{\theta }}^{\text {IP}}_M-\theta ^{*}_M)=O_p(n^{-1/2}),\\&\quad {{\hat{D}}}^{'}_{IP\{\alpha ^T\}}(M,\theta ^{*}_M,\alpha ^*)({\hat{\alpha _n}}-\alpha ^*)=O_p(n^{-1/2}). \end{aligned}$$

Thus, we have

$$\begin{aligned} {{\hat{D}}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})={{\hat{D}}}_{\text {IP}}(M,\theta ^{*}_M,\alpha ^*)+O_p(n^{-1/2}). \end{aligned}$$

(27)

Similarly, we have

$$\begin{aligned} {{\hat{D}}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_{M_{\text {opt}}},{\hat{\alpha _n}})={{\hat{D}}}_{\text {IP}}(M,\theta ^{*}_{M_{\text {opt}}},\alpha ^*)+O_p(n^{-1/2}), \end{aligned}$$

(28)

where the definition of $\theta ^{*}_{M_{\text {opt}}}$ is similar to $\theta ^{*}_M$. Note that, $\pi (y,z)$ is a function of $\phi _\pi (y,z;\alpha ^*)$, together with (13) and (18) and the law of large numbers, we have

$$\begin{aligned} {\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})=D(M,\theta ^*_{M})+O_p(n^{-1/2}). \end{aligned}$$

(29)

Obviously, (29) is also true for $M=M_{\text {opt}}$, we then have

$$\begin{aligned}&{\hat{D}}_{\text {IP}}(M_{\text {opt}},{\hat{\theta }}^{\text {IP}}_{M_{\text {opt}}},{\hat{\alpha _n}})-{\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})\nonumber \\&\quad =D(M_{\text {opt}},\theta ^*_{M_{\text {opt}}})-D(M,\theta ^*_{M})+O_p(n^{-1/2}). \end{aligned}$$

(30)

Recalling the definition of $D(M,\theta _M)$ given below (1), it follows that $D(M_{\text {opt}},\theta ^*_{M_{\text {opt}}})-D(M,\theta ^*_{M})$ is non-negative in probability. Recalling that $\lambda _n$ is a positive tuning parameter tending to zero as $n\rightarrow \infty$. By Fang and Shao (2016), we consider the following three cases to prove (26):

Case 1. M is an incorrect model and $d_{M_{\text {opt}}}<d_M$. In this case, we then have ${\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_{M_{\text {opt}}},{\hat{\alpha _n}})-{\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})>0$ in probability, and hence (26) is clearly true.

Case 2. M is an incorrect model but $d_{M_{\text {opt}}}\ge d_M$. Similar to Case 1, we have ${\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_{M_{\text {opt}}},{\hat{\alpha _n}})-{\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})>0$ in probability, (26) then holds by noting $\lambda _n\rightarrow 0$.

Case 3. M is a correct model but $d_{M_{\text {opt}}}< d_M$. In this case, we then have ${\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_M,{\hat{\alpha _n}})-{\hat{D}}_{\text {IP}}(M,{\hat{\theta }}^{\text {IP}}_{M_{\text {opt}}},{\hat{\alpha _n}})=O_p(n^{-\frac{1}{2}})$, and hence (26) is true as long as $\sqrt{n}\lambda _n\rightarrow \infty$.

This completes the proof of (26) and hence the proof of Theorem 2. $\square$