Estimation in partially linear varying-coefficient errors-in-variables models with missing response variables

Abstract

In this paper, a partially linear varying-coefficient model with measurement errors in the nonparametric component as well as missing response variable is studied. Two estimators for the parameter vector and nonparametric function are proposed based on the locally corrected profile least squares method. The first estimator is constructed by using the complete-case data only, and another by using an imputation technique. Both proposed estimators of the parametric component are shown to be asymptotically normal, and the estimators of nonparametric function are proved to achieve the optimal strong convergence rate as the usual nonparametric regression. Some simulation studies are conducted to compare the behavior of these estimators and the results confirm that the estimators based on the imputation technique perform better than the complete-case data estimator in finite samples. Finally, an application to a real data set is illustrated.

1 Introduction

The partially linear varying-coefficient model, as a very important semi-parametric model, takes the form as

$$\begin{aligned} Y=\mathbf{X} ^T\varvec{\beta }+\mathbf{Z} ^T\varvec{\alpha }(U)+{\varepsilon }, \end{aligned}$$

(1)

where Y is the response variable, $\mathbf{X} \in R^p,\mathbf{Z} \in R^q$ and U are the associated covariates, $\varvec{\beta }=(\beta _1,\ldots ,\beta _p)^T$ is a p-dimensional vector of unknown parameter and $\varvec{\alpha }(.)=(\alpha _1(.),\ldots ,\alpha _q(.))^T$ is a q-dimensional vector of unknown coefficient function, $\varepsilon$ is the random error that is assumed to be independent of $(U,\mathbf{X} , \mathbf{Z} )$ with mean zero and finite variance $\sigma ^2$. Since model (1) keeps both the interpretation power of parametric model and the flexibility of nonparametric model, it has been extensively studied by researches (Ahmad et al. 2005; Fan and Huang 2005; Kai et al. 2011; Long et al. 2013; You and Zhou 2006; Zhang et al. 2002; among others).

With the development of science and technology, the study of data with missing observations has been attracted more attention in various scientific fields, such as economics, engineering, biology and epidemiology. Dealing with missing data, several problems may arise when traditional statistical inference procedures for complete data sets are applied directly. There has been extensive research on statistical models with missing observations. In the partially linear model with the missing response data, Wang et al. (2004) proposed a class of semiparametric estimators for the regression coefficient and the response mean. Wang and Sun (2007) developed the imputation, semi-parametric surrogate regression and inverse marginal probability weighted methods to estimate unknown parameter. Xue and Xue (2011) proposed the bias-corrected method to calibrate the empirical likelihood ratios so that the estimator has asymptotically chi-squared distribution. Besides, with the missing response data in the partially linear varying-coefficient model (1), Wei (2012a) presented a profile least squares estimator for the parametric part based on the complete-case data.

Besides missing data, error-in-variables(EV) data, as another complex data can always be seen in real problems. It is well known that, if the measurement errors are ignored directly, the resulting estimators will not be unbiased. A great deal of researches on regression models with EV data have been studied. The simple specification of EV data is that the variables are measured with additive errors. Instead of observing certain covarites $\mathbf{X}$, we observe $\mathbf{W} =\mathbf{X} +\varvec{\xi }$, where the measurement error $\varvec{\xi }$ is independent of other variables. Taking model (1) as an example, under the situation of $\mathbf{X}$ is measured with additive error, You and Chen (2006) proposed a locally corrected profile least squares procedure to estimate the parameter and showed that the estimator is consistent and asymptotically normal. Zhang et al. (2011) and Wei (2012b) developed a restricted modified profile least squares estimator of the parameter under some additional linear restrictions. Hu et al. (2009) and Wang et al. (2011) constructed confidence regions for the unknown parameters with the empirical likelihood inference. On the other hand, when the nonparametric part $\mathbf{Z}$ is measured with additive error in model (1), Feng and Xue (2014) conducted a locally bias-corrected restricted profile least squares estimators of both parameter and nonparametric functions. Fan et al. (2016a) used some auxiliary information to construct empirical log-likelihood ratios and Fan et al. (2016b) extended the penalized empirical likelihood to the high-dimensional model. Fan et al. (2018) suggested a bias-correction penalized profile least squares variable selection method in high dimensional models. Moreover, when $\mathbf{X}$ is measured with additive errors as well as the response Y is missing in model (1), Wei and Mei (2012) applied the empirical likelihood method to construct confidence regions for parameters and Yang and Xia (2014) obtained restricted estimators under the linear constraint. However, the simultaneous existence of missing response and measurement error in the nonparametric part of model (1) has been seldom discussed. In addition, it should be noted that the assumption of additive measurement errors may be too simple in some applications. To analyze data from certain biomedical and health-related studies, one cannot directly observe some covariates and the response variable, but may obtain their distorted observations by certain functions of an observed confounding variable. Zhang et al. (2018) considered the nonlinear regression model under the assumption that both the response and predictors are unobservable and distorted by the multiplicative effects of some observable confounding variables. More interesting work for further study with model (1) will consider this situation.

In this paper, we study partially linear varying-coefficient models in which the response variable Y cannot be observed completely and the covariate $\mathbf{Z}$ cannot be observed accurately. Throughout this paper, we introduce an indicator variable $\delta$ such that $\delta =1$ means that Y is observed and $\delta =0$ indicates that Y is missing. We assume that data missing mechanism follows

$$\begin{aligned} \mathrm{Pr}(\delta =1|Y,\mathbf{X},Z, U)=\mathrm{Pr}(\delta =1|\mathbf{X},Z, U)=\pi (\mathbf{X},Z, U). \end{aligned}$$

(2)

Meanwhile, the variable $\mathbf{Z}$ is measured with additive errors. That is

$$\begin{aligned} \mathbf{W} =\mathbf{Z} +\varvec{\xi }, \end{aligned}$$

(3)

where $\varvec{\xi }$ is the measurement error and independent of $(Y,\mathbf{X} , \mathbf{Z} ,U,\varvec{\varepsilon }, \delta )$ and has mean zero and known covariance $\mathrm{Cov}(\varvec{\xi })=\Sigma _{\varvec{\xi }}$. Even if covariance $\Sigma _{\varvec{\xi }}$ is unknown, a consistent and unbiased estimator can still be obtained by repeatedly observing $\mathbf{W} _i$ (see Liang et al. (2007) for details). If $\mathbf{Z}$ is observed exactly, then the probability of missingness is independent of missing responses and the resulting mechanism is called missing at random (MAR). However, considering model (1) under assumption (3), the covariate $\mathbf{Z}$ is observed with measurement error and therefore Y is not missing at random which has been pointed out by Wei and Mei (2012) and Liang et al. (2007).

The rest of this paper is organized as follows. In Sect. 2, the locally corrected profile linear least squares estimation procedure with complete-case data is proposed, and then the asymptotic properties of the estimators are proved under some assumptions. In Sect. 3, an imputation technique is used to improve the accuracy of the estimator and corresponding asymptotic results are obtained. Some simulation studies are conducted in Sect. 4 to assess the performances of the proposed two estimators. In Sect. 5, the methodologies are illustrated by a real data example. Sect. 6 is conclusion and the proofs of the main Theorems are left in the “Appendix”.

2 Estimation method based on complete-case data

Firstly, we assume that measurement errors do not exist thus covariate $\mathbf{Z}$ can be observed exactly. Suppose that the observation data $\{{Y_i;\delta _i,\mathbf{X} _i,\mathbf{Z} _i,U_i}\}_{i=1}^n$ is generated from model (1) under assumption (2), then we have the following equation

$$\begin{aligned} \delta _i Y_i=\delta _i \mathbf{X} _{i}^T\varvec{\beta }+\delta _i \mathbf{Z} _i^T\varvec{\alpha }(U_i)+\delta _i\varepsilon _i,\quad i=1,\ldots ,n. \end{aligned}$$

(4)

We assume that $\varvec{\beta }$ is known, then the model (4) can be rewritten as the following varying coefficient regression model,

$$\begin{aligned} \delta _i Y_i-\delta _i \mathbf{X} _{i}^T\varvec{\beta }=\delta _i \sum _{j=1}^q Z_{ij}\alpha _j(U_i)+\delta _i\varepsilon _i, \end{aligned}$$

(5)

where $Z_{ij}$ is the jth element of $\mathbf{Z} _{i}$ and $\alpha _j(.)$ is the jth function of $\varvec{\alpha }(.),j=1,\ldots ,q$. We can estimate the coefficient functions ${\alpha }_j(.),j=1\cdots ,q$ by the local linear fitting procedure. Specifically, for u in a small neighborhood of $u_0$, ${\alpha }_j(u)$ can be locally approximated by a linear function as following:

$$\begin{aligned} \alpha _j(u)\approx \alpha _j(u_0)+\alpha _j^{(1)}(u_0)(u-u_0)=a_j+b_j(u-u_0),\quad j=1,\ldots ,q, \end{aligned}$$

where $\alpha _j^{(1)}(u)={\partial \alpha _j(u)}/{\partial u}$ denotes the first order derivative of $\alpha _j(u)$. Then, the estimators of $\alpha _j(.)$ can be obtained by selecting $\{(a_j,b_j),j=1,\ldots ,q\}$ to minimize:

$$\begin{aligned} \sum _{i=1}^{n}\left\{ Y_i-\mathbf{X} _i^T\varvec{\beta }-\sum _{j=1}^{q}[a_j+b_j(U_i-u)]Z_{ij}\right\} ^2 K_{h_1}(U_i-u)\delta _i, \end{aligned}$$

(6)

where $K_{h_1}(.)=K(./{h_1})/{h_1}$, K(.) is a kernel function and ${h_1}$ is the bandwidth. The solution to problem (6) is obtained by

$$\begin{aligned} \hat{\varvec{\alpha }}(u;\varvec{\beta })= (\mathbf{I} _q,\mathbf 0 _{q}) \left[ (\mathbf{D} _u^\mathbf{Z} )^T \varvec{\omega } ^\delta _u \mathbf{D} ^\mathbf{Z} _u\right] ^{-1}(\mathbf{D} _u^\mathbf{Z} )^T \varvec{\omega } _u ^\delta (\mathbf{Y} -\mathbf{X} \varvec{\beta }), \end{aligned}$$

(7)

where $\mathbf{Y} =(Y_1,\ldots ,Y_n)^T$, $\mathbf{X} =(\mathbf{X} _1,\ldots ,\mathbf{X} _n)^T$, $\varvec{\omega }^\delta _u=\mathrm{diag}(K_{h_1}(U_1-u)\delta _1,\ldots ,K_{h_1}(U_n-u)\delta _n)$, and

$$\begin{aligned} \mathbf{D} _u^\mathbf{Z} =\left( \begin{array}{cc} \mathbf{Z} _1^T&{}h_1^{-1}(U_1-u) \mathbf{Z} _1^T\\ \vdots &{}\vdots \\ \mathbf{Z} _n^T&{}h_1^{-1}(U_n-u) \mathbf{Z} _n^T\\ \end{array} \right) . \end{aligned}$$

Now consider $\mathbf{Z} _i$’s are not observed due to measurement error and $\mathbf{W} _i$’s are the observable surrogate data. Thus, $\hat{\varvec{\alpha }}(u;\varvec{\beta })$ is not consistent and unbiased if $\mathbf{W} _i$ is replaced by $\mathbf{Z} _i$ directly in (7). Based on the idea of Feng and Xue (2014), a modified locally corrected linear estimators of $\varvec{\alpha }(.)$ can be given by

$$\begin{aligned} \hat{\varvec{\alpha }}(u;\varvec{\beta })= (\mathbf{I} _q,\mathbf 0 _{q})\left[ (\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u^\delta \mathbf{D} _u^\mathbf{W} -\varvec{\Omega }_u^\delta \right] ^{-1}(\mathbf{D} _u^\mathbf{W} )^T\varvec{\omega }_u^\delta (\mathbf{Y} -\mathbf{X} \varvec{\beta }), \end{aligned}$$

(8)

where $\mathbf{D} _u^\mathbf{W}$ has the same form as $\mathbf{D} _u^\mathbf{Z}$ except that $\mathbf{Z} _i$ is replaced by $\mathbf{W} _i$ and

$$\begin{aligned} \varvec{\Omega }_u^\delta =\sum _{i=1}^n\varvec{\Sigma }_\xi \otimes \left( \begin{array}{cc} 1&{} \frac{U_i-u}{h_1}\\ \frac{U_i-u}{h_1}&{}\left( \frac{U_i-u}{h_1}\right) ^2\\ \end{array} \right) K_{h_1}(U_i-u)\delta _i, \end{aligned}$$

with $\otimes$ is the Kronecker product.

Taking u to be $U_1,\ldots ,U_n$ in (8), we can get that $\hat{\varvec{\alpha }}(U_i;\varvec{\beta })=\mathbf{Q} _i(\mathbf{Y} -\mathbf{X} \varvec{\beta })$, where $\mathbf{Q} _i=(\mathbf{I} _q,\mathbf 0 _{q})[(\mathbf{D} _{U_i}^\mathbf{W} )^T \varvec{\omega }_{U_i}^\delta \mathbf{D} _{U_i}^\mathbf{W} -\varvec{\Omega }^\delta _{U_i}]^{-1}(\mathbf{D} _{U_i}^\mathbf{W} )^T\varvec{\omega }_{U_i}^\delta .$ For the convenience of expression, let

$$\begin{aligned} \mathbf{S} _c=\left( \begin{array}{cc} (\mathbf{W} _1^T,0_{1 \times q})[(\mathbf{D} _{U_1}^\mathbf{W} )^T \varvec{\omega }_{U_1}^\delta \mathbf{D} _{U_1}^\mathbf{W} -\varvec{\Omega }_{U_1}^\delta ]^{-1}(\mathbf{D} _{U_1}^\mathbf{W} )^T\varvec{\omega }_{U_1}^\delta \\ \vdots \\ (\mathbf{W} _n^T,0_{1 \times q})[(\mathbf{D} _{U_n}^\mathbf{W} )^T \varvec{\omega }_{U_n}^\delta \mathbf{D} _{U_n}^\mathbf{W} -\varvec{\Omega }_{U_n}^\delta ]^{-1}(\mathbf{D} _{U_n}^\mathbf{W} )^T\varvec{\omega }_{U_n}^\delta \\ \end{array} \right) , \end{aligned}$$

and denote $\tilde{Y}_i={Y}_i-\sum _{k=1}^n \mathbf{S} _{ik}^{c} Y_k$ and $\tilde{\mathbf{X }}_i=\mathbf{X }_i-\sum _{k=1}^n \mathbf{S} _{ik}^{c}{} \mathbf{X} _k$, where $\mathbf{S} _{ik}^{c}$ is the (i, k)th component of matrix $\mathbf{S} _c$.

Then, the locally corrected profile least squares estimator $\varvec{{\hat{\beta }}}_c$ of $\varvec{{\beta }}$ based on complete-case data is obtained by minimizing

$$\begin{aligned} \sum _{i=1}^n\delta _i\left[ Y_i-\mathbf{X} _i^T\varvec{\beta }-\mathbf{W} _i^T\hat{\varvec{\alpha }}(U_i;\varvec{\beta })\right] ^2 -\sum _{i=1}^n\delta _i \hat{\varvec{\alpha }}^T(U_i;\varvec{\beta })\varvec{\Sigma }_\xi \hat{\varvec{\alpha }}(U_i;\varvec{\beta }). \end{aligned}$$

(9)

It is noted that the second term on the right hand side of (9) is included to avoid underestimating for $\varvec{\beta }$ which is caused by measurement errors. By simple calculation, estimator $\hat{\varvec{\beta }}_c$ can be obtained by

$$\begin{aligned} \hat{\varvec{\beta }}_c=\left[ \sum _{i=1}^n\delta _i\left( \tilde{\mathbf{X }}_i\tilde{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{Q} _i^T\varvec{\Sigma }_\xi \mathbf{Q} _i\mathbf{X} \right) \right] ^{-1} \left[ \sum _{i=1}^n\delta _i\left( \tilde{\mathbf{X }}_i\tilde{Y}_i-\mathbf{X} ^T\mathbf{Q} _i^T\varvec{\Sigma }_\xi \mathbf{Q} _i\mathbf{Y} \right) \right] .\nonumber \\ \end{aligned}$$

(10)

Then, substituting $\varvec{\hat{\beta }}_c$ into $\hat{\varvec{\alpha }}(u;\varvec{\beta })$ of (8) gives the estimator $\hat{\varvec{\alpha }}(u;\varvec{\hat{\beta }}_c)$ of ${\varvec{\alpha }}(u)$,that is

$$\begin{aligned} \hat{\varvec{\alpha }}_c(u)=\hat{\varvec{\alpha }}(u;\varvec{\hat{\beta }}_c)= (\mathbf{I} _q,\mathbf 0 _{q})\left[ (\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u^\delta \mathbf{D} _u^\mathbf{W} -\varvec{\Omega }_u^\delta \right] ^{-1}(\mathbf{D} _u^\mathbf{W} )^T\varvec{\omega }_u^\delta (\mathbf{Y} -\mathbf{X} \hat{\varvec{\beta }}_c).\nonumber \\ \end{aligned}$$

(11)

The asymptotic properties of $\varvec{{\hat{\beta }}}_c$ and $\hat{\varvec{\alpha }}_c(u)$ are given in the following Theorems.

Theorem 1

Suppose that the Conditions in the Appendix C1–C5 hold. Then we have

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\beta }}_c-\varvec{\beta }){\mathop {\longrightarrow }\limits ^{d}}N(0,\varvec{\Sigma }_1^{-1}\varvec{\Omega }_1 \varvec{\Sigma }_1^{-1}), \end{aligned}$$

where “${\mathop {\longrightarrow }\limits ^{d}}$” denotes convergence in distribution,

$$\begin{aligned} \varvec{\Sigma }_1= & {} \mathrm{E}\{\delta _1[ \mathbf{X} _1-\varvec{\Phi }_c^T(U_1)\varvec{\Gamma }_c^{-1}(U_1) \mathbf{Z} _1]^{\otimes 2}\},\\ \varvec{\Omega }_1= & {} \mathrm{E}\{\delta _1({\varepsilon }_1-\varvec{\xi }_1^T\varvec{\alpha }(U_1))^2\varvec{\Sigma }_1\}+\sigma ^2\mathrm{E}\{\delta _1[\varvec{\Phi }_c^T(U_1)\varvec{\Gamma }_c^{-1}(U_1)\varvec{\Sigma }_\xi \varvec{\Gamma }_c^{-1}(U_1)\varvec{\Phi }_c(U_1)]\}\\&+\,\mathrm{E}\{\delta _1[\varvec{\Phi }_c^T(U_1)\varvec{\Gamma }_c^{-1}(U_1)(\varvec{\xi }_1\varvec{\xi }^T_1-\varvec{\Sigma }_{\xi })\varvec{\alpha }(U_1)]^{\otimes 2}\},\\&\quad with\;\; \varvec{\Gamma }_c(u)=\mathrm{E}(\delta _1 \mathbf{Z} _1\mathbf{Z} _1^T|U=u)\;\; and \;\; \varvec{\Phi }_c(u)=\mathrm{E}(\delta _1 \mathbf{Z} _1\mathbf{X} _1^T|U=u). \end{aligned}$$

When we make statistical inference for $\varvec{\beta }$ by Theorem 1, asymptotic variance of $\varvec{\beta }$ is required to be estimated firstly. $\varvec{\Sigma }_1^{-1}\varvec{\Omega }_1 \varvec{\Sigma }_1^{-1}$ is estimated by $\varvec{\hat{\Sigma }}_1^{-1}\varvec{\hat{\Omega }}_1 \varvec{\hat{\Sigma }}_1^{-1}$ with plug-in method, where $\varvec{\hat{\Sigma }}_1=\frac{1}{n}\sum _{i=1}^n \delta _i \{ \tilde{\mathbf{X }}_i\tilde{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{Q} _i^T \varvec{\Sigma }_{\xi } \mathbf{Q} _i \mathbf{X} \},$ and $\varvec{\hat{\Omega }}_1=\frac{1}{n}\sum _{i=1}^n \delta _i \big \{ \tilde{\mathbf{X }}_i(\tilde{\mathbf{Y }}_i-\tilde{\mathbf{X }}_i^T\hat{\varvec{\beta }}_c) -\mathbf{X} ^T \mathbf{Q} _i^T\varvec{\Sigma }_\xi \mathbf{Q} _i [\mathbf{Y} -\mathbf{X} \hat{\varvec{\beta }}_c]\big \}^{\otimes 2}.$

Theorem 2

Suppose that the Conditions C1–C5 in the Appendix hold and $h_1=c n^{-1/5}$, where c is a constant. Then we have

$$\begin{aligned} \underset{{1\le j\le p}}{\mathrm{max}}\underset{{u\in \Pi }}{\mathrm{sup}}|\hat{\alpha }_{cj}(u)-\alpha _j(u)|=O(n^{-2/5}+(\mathrm{log} n)^{1/2}),~~~~ a.s. \end{aligned}$$

3 Estimation method based on imputation technique

It is noted that the estimator $\hat{\varvec{\beta }}_c$ defined by (10) use complete-case data only and discard sample when $Y_i$ is missing. This procedure may reduce the efficiency of the estimators of $\varvec{\beta }$ which is caused without making full use of sample information.

When we are dealing with missing data, an imputation technique is prevalent which has been applied to various semi-parametric models, such examples can be found in Yang et al. (2011) and Xue and Xue (2011). The main idea of this method is to firstly impute a reasonable value for each missing data and then make statistical inference as if the data set is complete. Specifically, if covariate $\mathbf{Z}$ can be observed directly, based on the estimator $\hat{\varvec{\beta }}_c$ and $\hat{\varvec{\alpha }}_c(u;\hat{\varvec{\beta }}_c)$, we have $(\hat{H}_i^0;\mathbf{X} _i,\mathbf{Z} _i,U_i)_{i=1}^n$, where

$$\begin{aligned} \hat{H}_i^0=\delta _iY_i+(1-\delta _i)[\mathbf{X} _i^T\hat{\varvec{\beta }}_c+\mathbf{Z} _i^T\hat{\varvec{\alpha }}_c(U_i;\hat{\varvec{\beta }}_c)]. \end{aligned}$$

However, $\hat{H}_i^0$ can not be obtained since $\mathbf{Z} _i$ can not be observed in practice. Instead, $\hat{H}_i=\delta _iY_i+(1-\delta _i)[\mathbf{X} _i^T\hat{\varvec{\beta }}_c+\mathbf{W} _i^T\hat{\varvec{\alpha }}_c(U_i;\hat{\varvec{\beta }}_c)]$ is available. Based on data $(\hat{H}_i;\mathbf{X} _i,\mathbf{W} _i,U_i)_{i=1}^n$, the following partially linear varying-coefficient model with measurement errors in both covariate and response can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{H}_i^0=\mathbf{X} _i^T{\varvec{\beta }}+\mathbf{Z} _i^T{\varvec{\alpha }}(U_i)+e_i\\ \mathbf{W} _i=\mathbf{Z} _i+\varvec{\xi }_i\\ \hat{H}_i=\hat{H}_i^0+(1-\delta _i)\varvec{\xi }_i^T\hat{\varvec{\alpha }}_c(U_i;\hat{\varvec{\beta }}_c)\\ \end{array}\right. } \end{aligned}$$

(12)

where $e_i=\hat{H}_i^0-Y_i+\varepsilon _i$ is the model error.

Then, the estimator $\hat{\varvec{\beta }}_I$ of parameter $\varvec{\beta }$ based on model (12) can be obtained by minimizing

$$\begin{aligned}&\sum _{i=1}^n \left[ \hat{H}_i-\mathbf{X} _i^T\varvec{\beta }-\mathbf{W} _i^T\check{\varvec{\alpha }}(U_i;\varvec{\beta })\right] ^2 -\sum _{i=1}^n\check{\varvec{\alpha }}^T(U_i;\varvec{\beta })\varvec{\Sigma }_\xi \check{\varvec{\alpha }}(U_i;\varvec{\beta })\nonumber \\&\quad +\,\sum _{i=1}^n (1-\delta _i)\check{\varvec{\alpha }}^T(U_i;\varvec{\beta })\varvec{\Sigma }_\xi \hat{\varvec{\alpha }}(U_i;\hat{\varvec{\beta }}_c), \end{aligned}$$

(13)

where $\check{\varvec{\alpha }}(u;\varvec{\beta })$ has the same form as $\hat{\varvec{\alpha }}(u;\varvec{\beta })$ defined in (8), except that $\varvec{\omega }_u^\delta$ and $\varvec{\Omega }_u^\delta$ are replaced by $\varvec{\omega }_u$ and $\varvec{\Omega }_u$, respectively. That is

$$\begin{aligned} \check{\varvec{\alpha }}(u;\varvec{\beta })= (\mathbf{I} _q,\mathbf 0 _{q})\left[ (\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u \mathbf{D} _u^\mathbf{W} -\varvec{\Omega }_u\right] ^{-1}(\mathbf{D} _u^\mathbf{W} )^T\varvec{\omega }_u(\hat{\mathbf{H }}-\mathbf{X} \varvec{\beta }), \end{aligned}$$

(14)

with $\varvec{\omega }_u=\mathrm{diag}(K_{h_2}(U_1-u),\ldots ,K_{h_2}(U_n-u))$, $\hat{\mathbf{H }}=(\hat{H}_1,\hat{H}_2,\ldots ,\hat{H}_n)^T$, and

$$\begin{aligned} \varvec{\Omega }_u=\sum _{i=1}^n\varvec{\Sigma }_\xi \otimes \left( \begin{array}{cc} 1&{} \frac{U_i-u}{h_2}\\ \frac{U_i-u}{h_2}&{}\left( \frac{U_i-u}{h_2}\right) ^2\\ \end{array} \right) K_{h_2}(U_i-u), \end{aligned}$$

and $K_{h_2}(.)=K(./{h_2})/{h_2}$ with a kernel function K(.) and a bandwidth ${h_2}$.

Besides the second term in (13), the third term is added to correct the bias which is induced by $\mathbf{W} _i$ contained in $\hat{H}_i$. Similarity, denote $\mathbf{R} _i=(\mathbf{I} _q,\mathbf 0 _{q})[(\mathbf{D} _{U_i}^\mathbf{W} )^T \varvec{\omega }_{U_i} \mathbf{D} _{U_i}^\mathbf{W} -\varvec{\Omega }_{U_i}]^{-1}(\mathbf{D} _{U_i}^\mathbf{W} )^T\varvec{\omega }_{U_i},$ then $\check{\varvec{\alpha }}(U_i;\varvec{\beta })=\mathbf{R} _i(\hat{\mathbf{H }}-\mathbf{X} \varvec{\beta })$. Let

$$\begin{aligned} \mathbf{S} _I=\left( \begin{array}{cc} (\mathbf{W} _1^T,0_{1 \times q})\left[ (\mathbf{D} _{U_1}^\mathbf{W} )^T \varvec{\omega }_{U_1} \mathbf{D} _{U_1}^\mathbf{W} -\varvec{\Omega }_{U_1}\right] ^{-1}(\mathbf{D} _{U_1}^\mathbf{W} )^T\varvec{\omega }_{U_1}\\ \vdots \\ (\mathbf{W} _n^T,0_{1 \times q})\left[ (\mathbf{D} _{U_n}^\mathbf{W} )^T \varvec{\omega }_{U_n} \mathbf{D} _{U_n}^\mathbf{W} -\varvec{\Omega }_{U_n}\right] ^{-1}(\mathbf{D} _{U_n}^\mathbf{W} )^T\varvec{\omega }_{U_n}\\ \end{array} \right) . \end{aligned}$$

Denote $\bar{H}_i=\hat{H}_i-\sum _{k=1}^n \mathbf{S} _{ik}^{I} \hat{H}_k$ and $\bar{\mathbf{X }}_i=\mathbf{X }_i-\sum _{k=1}^n \mathbf{S} _{ik}^{I}{} \mathbf{X} _k$, where $\mathbf{S} _{ik}^{I}$ is the (i, k)th component of matrix $\mathbf{S} _I$.

By simple calculation, the estimator $\hat{\varvec{\beta }}_I$ based on the imputation method is obtained by

$$\begin{aligned} \hat{\varvec{\beta }}_I= & {} \left[ \sum _{i=1}^n(\bar{\mathbf{X }}_i\bar{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_\xi \mathbf{R} _i\mathbf{X} )\right] ^{-1}\nonumber \\&\left[ \sum _{i=1}^n(\bar{\mathbf{X }}_i{\bar{H}}_i-\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_\xi \mathbf{R} _i{\hat{\mathbf{H }}})+ (1-\delta _i)\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_\xi \mathbf{Q} _i(\mathbf{Y} -\mathbf{X} \hat{\varvec{\beta }}_c)\right] .\nonumber \\ \end{aligned}$$

(15)

Then, the corresponding imputation estimator $\hat{\varvec{\alpha }}_I(u)$ of ${\varvec{\alpha }}(u)$ is defined as

$$\begin{aligned} \hat{\varvec{\alpha }}_I(u)=\check{\varvec{\alpha }}(u;\hat{\varvec{\beta }}_I)= (\mathbf{I} _q,\mathbf 0 _{q})\left[ (\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u \mathbf{D} _u^\mathbf{W} -\varvec{\Omega }_u\right] ^{-1}(\mathbf{D} _u^\mathbf{W} )^T\varvec{\omega }_u(\hat{\mathbf{H }}-\mathbf{X} \hat{\varvec{\beta }_I}). \end{aligned}$$

(16)

The asymptotic normality of $\varvec{{\hat{\beta }}}_I$ and the convergence of $\hat{\varvec{\alpha }}_I(u)$ are given in the following Theorems.

Theorem 3

Suppose that the Conditions C1–C5 in the Appendix hold. Then we have

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\beta }}_I-\varvec{\beta }){\mathop {\longrightarrow }\limits ^{d}}N(0,\varvec{\Sigma }^{-1}\varvec{\Omega }_2 \varvec{\Sigma }^{-1}), \end{aligned}$$

where

$$\begin{aligned} \varvec{\Sigma }= & {} \mathrm{E}\{[\mathbf{X} _1-\varvec{\Phi }^T(U_1)\varvec{\Gamma }^{-1}(U_1) \mathbf{Z} _1]^{\otimes 2}\},\\ \varvec{\Omega }_2= & {} (\varvec{\Sigma }_2+\varvec{\Sigma }_1)\varvec{\Sigma }_1^{-1} \varvec{\Omega }_1\varvec{\Sigma }_1^{-1}(\varvec{\Sigma }_2+\varvec{\Sigma }_1),\\ \varvec{\Sigma }_2= & {} \mathrm{E}\{ (1-\delta _1)[\mathbf{X} _1-\varvec{\Phi }^T(U_1)\varvec{\Gamma }^{-1}(U_1) \mathbf{Z} _1][\mathbf{X} _1-\varvec{\Phi }_c^T(U_1)\varvec{\Gamma }_c^{-1}(U_1) \mathbf{Z} _1]^T\}\\&\quad with\;\; \varvec{\Gamma }(u)=\mathrm{E}( \mathbf{Z} _1\mathbf{Z} _1^T|U=u)\;\; and \;\; \varvec{\Phi }(u)=\mathrm{E}( \mathbf{Z} _1\mathbf{X} _1^T|U=u). \end{aligned}$$

where $\varvec{\Sigma }_1$ and $\varvec{\Omega }_1$ are defined in Theorem 1.

Theorem 4

Suppose that the Conditions C1–C5 in the Appendix hold and $h_2=c n^{-1/5}$, where c is a constant. Then we have

4 Simulation study

In this section, we conduct some simulations to assess the performances of the proposed estimators in finite samples. The data are generated from the following partially linear varying-coefficient measurement error model with missing responses

$$\begin{aligned} {\left\{ \begin{array}{ll} {Y}_i=\mathbf{X} _{i}^T\varvec{\beta }+Z_{1i}{\alpha }_1(U_i)+Z_{2i}{\alpha }_2(U_i)+\varepsilon _i,\\ W_{ji}=Z_{ji}+\xi _{ji},\quad j=1,2,\quad i=1,\ldots ,n, \end{array}\right. } \end{aligned}$$

where parameter vector $\varvec{\beta }=(\beta _1,\beta _2,\beta _3,\beta _4,\beta _5)^T=(1,1.5,2,1.5,1)^T$, coefficient functions $\alpha _1(u)=\mathrm{cos}(2\pi u)$ and $\alpha _2(u)=\mathrm{sin}(2\pi u)$. The covariate variables $X_1,X_2,$ $X_3,X_4,X_5$ are independently generated from N(1, 1), $Z_1,Z_2$ are independently generated from $N(-1,1)$ and U is independently drawn from a uniform distribution on [0,1]. In addition, the model error $\varepsilon \sim N(0,1)$ and the measurement error ${\varvec{\xi }}=(\xi _1,\xi _2)^T \sim N(\mathbf 0 ,\Sigma _{\xi })$ with $\Sigma _{\xi }=0.2 I_2$ and $\Sigma _{\xi }=0.4 I_2$, respectively. $I_2$ is identity matrix with order 2. We consider the following two missing schemes as

Case (i). $\mathrm{Pr}(\delta =1|X_1=x_1,X_2=x_2,X_3=x_3,X_4=x_4,X_5=x_5,Z_1=z_1,Z_2=z_2,U=u)=0.8$ for all $x_1,x_2,x_3,x_4,x_5,z_1,z_2,u$.

Case (ii). $\mathrm{Pr}(\delta =1|X_1=x_1,X_2=x_2,X_3=x_3,X_4=x_4,X_5=x_5,Z_1=z_1,Z_2=z_2,U=u)=0.8+0.6(|z_1|+|z_2|+|u-0.5|)$ if $|z_1|+|z_2|+|u-0.5|<1$, and otherwise 0.8. In this case, the mean response rates is approximately 0.87.

Kernel function K(t) is chosen as Epanechnikov kernel $K(t)=(3/4)(1-t^2)$ if $|t|\le 1$, and 0 otherwise. In our simulation, we set the sample size n to be 100, 200 and 300. For each sample size, we generate 1000 random samples.

Some simulation results are reported in Tables 1, 2, 3, 4, 5, 6 and 7 to evaluate the performances of the proposed estimators $\varvec{\hat{\beta }}_c$ and $\varvec{\hat{\beta }}_I$. Firstly, to determine whether the choice of bandwidth has influences on the performance of the estimators, we choose three bandwidths with $h_1=h_2=h_{opt}=2.34*\mathrm{{sd}}(U)*n^{-1/5}$, where $\mathrm{{sd}}(U)$ is the standard deviation of the observations of $U_1,U_2,\ldots ,U_n$. The average estimation errors $||\varvec{\hat{\beta }}_c-\varvec{\beta }||$ and $||\varvec{\hat{\beta }}_I-\varvec{\beta }||$ in $L_2$-norm are computed with three different bandwidths in Table 1. We can see that the choice of bandwidth shows a very slight impact on the estimators $\varvec{\hat{\beta }}_c$ and $\varvec{\hat{\beta }}_I$, especially when the sample size is large. Hence, we choose $h_{opt}$ as the selected bandwidth for the later examples.

Table 1 The average estimation errors of estimators for the parametric components with $\Sigma _\xi =0.2 I_2$ under missing case (i)

Secondly, in Tables 2, 3, 4, 5 and 6, “Bias” and “SD” denote the bias and the standard deviation of the 1000 estimators, respectively. For comparison, we not only report the proposed estimates $\hat{\beta }_c$ and $\hat{\beta }_I$, but also $\hat{\beta }_T$ and $\hat{\beta }_N$, which stand respectively for the true and naive estimates. The true estimate $\hat{\beta }_T$ is obtained via the standard profile least squares approach by using the complete data $(Y_i;X_i,Z_i,U_i), i =1,\ldots , n$. However, $\hat{\beta }_T$ is not applicable in practice since some observations of $Y_i$ are not available due to missing and $Z_i$ can not be obtained as a result of measurement errors. The naive estimate $\hat{\beta }_N$ is calculated by ignoring the measurement errors, not performing the bias correction as in equations (8) and (9), and applying the complete-case data only.

Table 2 Finite sample performance of estimator $\hat{\beta }_T$, $\hat{\beta }_c$, $\hat{\beta }_I$ and $\hat{\beta }_N$ for $\beta _1$

Table 3 Finite sample performance of estimator $\hat{\beta }_T$, $\hat{\beta }_c$, $\hat{\beta }_I$ and $\hat{\beta }_N$ for $\beta _2$

Table 4 Finite sample performance of estimator $\hat{\beta }_T$, $\hat{\beta }_c$, $\hat{\beta }_I$ and $\hat{\beta }_N$ for $\beta _3$

Table 5 Finite sample performance of estimator $\hat{\beta }_T$, $\hat{\beta }_c$, $\hat{\beta }_I$ and $\hat{\beta }_N$ for $\beta _4$

Table 6 Finite sample performance of estimator $\hat{\beta }_T$, $\hat{\beta }_c$, $\hat{\beta }_I$ and $\hat{\beta }_N$ for $\beta _5$

From Tables 2, 3, 4, 5 and 6, it is observed that the bias and SD of both estimators $\hat{\beta }_c$ and $\hat{\beta }_I$ are relatively small, which show that the proposed estimation procedures in this paper can work well in finite samples. The estimators $\hat{\beta }_c$ and $\hat{\beta }_I$ are comparable to $\hat{\beta }_T$, though it is impossible to obtain in practice. The bias and the SD of $\hat{\beta }_N$ is much larger than other three estimators, which indicate that the measurement error should not be ignored directly. It is noted that the estimator $\hat{\beta }_I$ based on the imputation technique outperform the complete-case estimator $\hat{\beta }_c$ in terms that it gives smaller SD in most cases. This is due to the fact that $\hat{\beta }_I$ can make full use of the sample information. Furthermore, the values of SD in the missing data case (i) are usually greater than those in case (ii). The reason for this is that the number of observed responses generated from the missing data case (i) is less than that from case (ii). In addition, the larger variance of measurement error $\Sigma _\xi$ yields larger SD. It can also be observed that all methods perform better with smaller bias and SD as the sample size increases.

To illustrate the effect of the variance of model error $\varepsilon$ on the proposed estimation methods, we compare the average mean square error(MSE) of vector $\beta$ in Table 7. The smaller variance of model error $\varepsilon$, the smaller MSE. It can be seen that all the proposed estimation procedures perform better with the small variance of model error.

Table 7 The average MSE of estimator $\hat{\beta }_T$, $\hat{\beta }_c$, $\hat{\beta }_I$ and $\hat{\beta }_N$

In addition, we report the performances of the proposed estimation procedures for the nonparametric function. We plot the estimated curve of the nonparametric function when the measurement error covariance is $\Sigma _\xi =0.2I_2$ and the missing scheme is case (i) with sample size 200 in Fig. 1. We also evaluate the performance of the estimator $\varvec{\alpha }(.)$ by using the square root of mean-squared errors (RMSE) which is defined as

$$\begin{aligned} \mathrm{{RMSE}}=\left\{ \frac{1}{N} \sum _{k=1}^N ||\varvec{\hat{\alpha }}(U_k)-\varvec{\alpha }(U_k)||^2\right\} ^{1/2} \end{aligned}$$

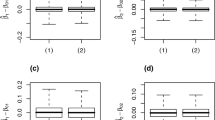
where $U_k,k=1,\ldots ,N$ are the grid points at which the function is evaluated. In our simulation, we set $N = 200$ and $U_k$ is equally taken on interval (0,1). Figure 2 shows the box-plots for 1000 RMSE values for the nonparametric functions $\varvec{\alpha }(.)$ with different methods.

Fig. 1

The plot of the nonparametric estimator. The dotted, the dashed and the solid lines respectively denote $\hat{\alpha }_c(.),$ $\hat{\alpha }_I(.)$ and the true curve $\alpha (.)$

Fig. 2

The boxplots of the 1000 RMSE values for the nonparametric functions based on the complete-case data (left panel) and imputation technique (right panel)

From Fig. 1, we can see that the estimators $\hat{\alpha }_c(.)$ and $\hat{\alpha }_I(.)$ are almost same, and they all approximate the real curve. It shows that both the proposed methods can perform well in terms of nonparametric functions. From Fig. 2, it is observed that the RMSE values, obtained by the complete-case data and imputation technique, both decrease as the sample size increases. In addition, $\hat{\alpha }_I(.)$ performs better than $\hat{\alpha }_c(.)$ since it has smaller RMSE values.

In this simulation, we assume that the dimension p of the parameter $\beta$ is fixed. In a general setup, the dimension p can grow with the sample size n, and thus model (1) extends to a high-dimensional partially linear varyingcoefficient model. As there would be some spurious covariates in the parametric component, some penalized profile least squares estimation procedures should be developed. The assumption that there are simultaneous missing response observations and additive errors in the nonparametric component in high-dimensional partially linear varying-coefficient model (1), would be more practical, but more challenging, which is left for the future research.

5 A real example

In this section, we apply our proposed estimation procedures to the Boston housing data set, which has been analyzed by several researches, such as Fan and Huang (2005), Wang and Xue (2011) and Li and Mei (2013) via different regression models. The median value of houses and several associated variables which might explain the variation of housing values are our main interest. In this study, we take the median value of owner-occupied homes in $1000s(MEDV) as the response variable Y, per capita crime rate by town(CRIM), nitric oxide concentration parts per 10 million(NOX), average number of rooms per dwelling(RM), full-value property tax per $10,000(TAX), proportion of owner-occupied units built prior to 1940(AGE) and pupil-teacher ratio by town school district(PTRATIO) as covariates, denoted by $Z_2,Z_3,Z_4,Z_5, X_1$ and $X_2$,respectively. We take $Z_1=1$ as the intercept term and as the index variable, where LSTAT means lower status of the population. We employ the following partially linear varying-coefficient model

$$\begin{aligned} Y=X_1\beta _1+X_2\beta _2+\sum _{i=1}^5 Z_i\alpha _i(U)+\varepsilon . \end{aligned}$$

(17)

to fit the given data.

Before building the model, the response and covariate variables should be standardized for mean zero and unit sample standard deviation. In addition, the index variable U is transformed so that its marginal distribution is U[0,1]. To illustrate our method to this data set, as mentioned in Feng and Xue (2014), we consider the situation that covariate $Z_5$ has measurement error and can not be observed directly. Instead of $Z_5$, $W_5$ can be observed and has the following form

$$\begin{aligned} W_5=Z_5+U_5, \end{aligned}$$

(18)

where $U_5\sim N(0,0.3^2)$. Firstly, we fit the data set by models (17) and (18) without response missing. The estimator of $\varvec{\beta }$, denoted by $\hat{\varvec{\beta }}_0=(0.0435,-0.1446)^T$ is obtained with all observation data. Secondly, we remove 10%,15% and 20% of the response Y values at random. Since $\delta$ is randomly generated, we estimate $\varvec{\beta }$ from 100 simulation runs and the average results can be found in Table 8.

Table 8 The estimates of $\beta _1$ and $\beta _2$

From Table 8, we can obtain that two estimates of the parameter with complete-case data and imputation technique are almost same, and close to the case with no response missing. In addition, the missing rate is smaller, the estimator value is closer to the case of no missing.

The estimated coefficient functions when the missing rata is $20\%$ are depicted in Fig. 3. From Fig. 3, we can observe that the shapes of the $\hat{\alpha }_c(.)$ and $\hat{\alpha }_I(.)$ are very similar in five different coefficient functions.

Fig. 3

The estimated coefficient functions, where the solid line and the dotted line represent the estimated coefficient functions $\hat{\alpha }_c(.)$ and $\hat{\alpha }_I(.)$, respectively

6 Conclusions

In this paper, we study the partially linear varying-coefficient model when the nonparametric component is measured with additive error and the response variable is missing simultaneously. Firstly, we propose a locally corrected profile linear least squares estimation procedure based on the complete-case data only. Furthermore, a semiparametric imputation technique is applied to construct another estimator for improving the accuracy of the estimator. We establish the asymptotic normality property of the proposed two estimators of the parameters. As well, we show that the estimator of nonparametric component converge at an optimal rate. Theoretically, the estimator based on the imputation technique has advantages compared to the complete-case data method because it makes full use of information of the observation data. This conclusion is confirmed by the simulation studies and a real example.

However, we only consider the case in which there are a fixed number of predictors in this study. Currently highdimensional data analysis has attracted extensive attention. One important aspect of a regression model for highdimensional data is that the number of covariates is diverging. There has been some remarkable results on variable selection and parameter estimation in partially linear varying coefficient errors-invariables model with no missing data (Fan et al. 2016b, 2018). The simultaneous existence of missing response observations as well as measurement errors in the covariates would be extremely challenge in the highdimensional data modeling. We may apply some penalization methods for variable selection. Specifically, a penalty function could be added to Eqs. (9) or (13). The penalized estimator of $\beta$ based on complete-case data can be obtained by minimizing the following bias-corrected penalized least square function

$$\begin{aligned} \frac{1}{2}\sum _{i=1}^n\delta _i\left[ Y_i-\mathbf{X} _i^T\varvec{\beta }-\mathbf{W} _i^T\hat{\varvec{\alpha }}(U_i;\varvec{\beta })\right] ^2 -\frac{1}{2}\sum _{i=1}^n\delta _i \hat{\varvec{\alpha }}^T(U_i;\varvec{\beta })\varvec{\Sigma }_\xi \hat{\varvec{\alpha }}(U_i;\varvec{\beta })+n\sum _{j=1}^p p_\lambda (|\beta _j|).\nonumber \\ \end{aligned}$$

(19)

where $p_\lambda (.)$ is a pre-specified penalty function, such as the SCAD penalty. The tuning parameter $\lambda$ can be selected by some data-driven criteria, such as BIC, AIC, CV. Since the SCAD penalty function is irregular at the origin, the commonly used gradient method is not applicable. To solve this difficulty, an iterative algorithm is proposed by Fan and Li (2001). The penalty function is locally approximated by a quadratic function and then Newton–Raphson algorithm can be used to minimize problem (19). This method can significant reduce the computational burden and should be studied in the future work.

Appendix: Proofs of the main results

We begin with the following assumption conditions required to derive the main results. These conditions are quite mild and can be easily satisfied.

C1: The random variable u has a bounded support $\Pi$. Its probability density function f(.) is Lipschitz continuous and bounded away from 0 on its support.

C2: The $q\times q$ matrix $\mathrm{E}(\mathbf{ZZ} ^T|U)$ and $\mathrm{E}(\delta \mathbf{ZZ} ^T|U)$ are nonsingular for each $U\in \Pi$. The matrix $\mathrm{E}(\mathbf{ZZ} ^T|U)$, $\mathrm{E}(\mathbf{ZZ} ^T|U)^{-1}$, $\mathrm{E}(\delta \mathbf{ZZ} ^T|U)$, $\mathrm{E}(\delta \mathbf{ZZ} ^T|U)^{-1}$, $\mathrm{E}(\mathbf{ZX} ^T|U)$ and $\mathrm{E}(\delta \mathbf{ZX} ^T|U)$ are all Lipschitz continuous.

C3: There exists an $s>0$ such that $\mathrm{E}||\mathbf{X} ||^{2s}<\infty$,$\mathrm{E}||\mathbf{Z} ||^{2s}<\infty$ and for some $k<2-s^{-1}$ such that $n^{2k-1}h\longrightarrow \infty .$

C4: $\alpha _j(u),j=1,\ldots ,q$ have continuous second derivative for $u\in \Pi$.

C5: The Kernel K(.) is a symmetric probability density function with compact support and the bandwidth h satisfies $nh^8\longrightarrow 0$ and $nh^2/(\mathrm{log} n)^2\longrightarrow \infty$ when $n\longrightarrow \infty$.

In order to prove the main results, we first give several Lemmas. The following notations will be used in the proof of the Lemmas and Theorems. Let $c_n=(\mathrm{log}n/nh)^{1/2}$, $\mu _i=\int _0^{\infty } t^i K(t)\mathrm{d}t$, $\mathbf{M} =[\mathbf{Z} _1^T\varvec{\alpha }(U_1),\dots ,\mathbf{Z} _n^T\varvec{\alpha }(U_n)]^T$, $\mathbf{M} ^\mathbf{W }=[\mathbf{W} _1^T\varvec{\alpha }(U_1),\ldots ,\mathbf{W} _n^T\varvec{\alpha }(U_n)]^T$, $\tilde{\varepsilon }_i={\varepsilon }_i-\sum _{k=1}^n \mathbf{S} _{ik}^{c} \varepsilon _k$ and $\tilde{\mathbf{Z }}_i=\mathbf{Z }_i-\sum _{k=1}^n \mathbf{S} _{ik}^{c} \mathbf{Z} _k.$

Lemma 1

Suppose that conditions C1–C5 hold. Then the followings hold uniformly

$$\begin{aligned} (\mathbf{D} _u^\mathbf{Z} )^T \varvec{\omega }_u\mathbf{D} _u^\mathbf{Z} -\varvec{\Omega }_u=nf(u)\varvec{\Gamma }(u)\otimes \left( \begin{array}{ll} 1&{} \mu _1\\ \mu _1&{} \mu _2 \\ \end{array}\right) [1+O_p(c_n)]. \end{aligned}$$

(20)

$$\begin{aligned} (\mathbf{D} _u^\mathbf{Z} )^T \varvec{\omega }_u \mathbf{X} =nf(u)\varvec{\Phi }(u)\otimes (1, \mu _1)^{T}[1+O_p(c_n)]. \end{aligned}$$

(21)

$$\begin{aligned} (\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u^\delta \mathbf{D} _u^\mathbf{W} -\varvec{\Omega }_u^\delta =nf(u)\varvec{\Gamma }_c(u)\otimes \left( \begin{array}{ll} 1&{} \mu _1\\ \mu _1&{} \mu _2 \\ \end{array} \right) [1+O_p(c_n)]. \end{aligned}$$

(22)

$$\begin{aligned} (\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u^\delta \mathbf{X} =nf(u)\varvec{\Phi }_c(u)\otimes (1, \mu _1)^{T}[1+O_p(c_n)]. \end{aligned}$$

(23)

Proof

Equations (20) and (21) are given in Lemma 2 in Feng and Xue (2014). Similarly, Eqs. (22) and (23) can also be obtained.

Lemma 2

Suppose that conditions C1–C5 hold. Then

$$\begin{aligned} \frac{1}{{n}}\sum _{i=1}^{n}\delta _i(\tilde{\mathbf{X }}_i\tilde{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{Q} _i^T\varvec{\Sigma }_{\xi } \mathbf{Q} _i\mathbf{X} ) \longrightarrow \varvec{\Sigma _1}, ~~a.s, \end{aligned}$$

$$\begin{aligned} \frac{1}{{n}}\sum _{i=1}^{n}(\bar{\mathbf{X }}_i\bar{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_{\xi } \mathbf{R} _i\mathbf{X} ) \longrightarrow \varvec{\Sigma }, ~~a.s, \end{aligned}$$

$$\begin{aligned} \frac{1}{{ n}}\sum _{i=1}^{n}(1-\delta _i)(\bar{\mathbf{X }}_i \tilde{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_{\xi } \mathbf{Q} _i \mathbf{X} )\longrightarrow \varvec{\Sigma }_2,~~a.s, \end{aligned}$$

where $\varvec{\Sigma _1}$ is defined in Theorem 1, $\varvec{\Sigma }$ and $\varvec{\Sigma }_2$ are defined in Theorem 3.

Proof

The proof of this Lemma is similar to that of Lemma 7.2 in Fan and Huang (2005). Hence, the details are omitted.

Proof of Theorem 1

Let

$$\begin{aligned} B_n=\frac{1}{{n}}\sum _{i=1}^{n}\delta _i(\tilde{\mathbf{X }}_i\tilde{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{Q} _i^T\varvec{\Sigma }_{\xi } \mathbf{Q} _i\mathbf{X} ), \end{aligned}$$

and

$$\begin{aligned} A_n=\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}\delta _i\left[ \tilde{\mathbf{X }}_i(\tilde{Y}_i-\tilde{\mathbf{X }}_i^T \varvec{\beta }) -\mathbf{X} ^T\mathbf{Q} _i^T\varvec{\Sigma }_\xi \mathbf{Q} _i(\mathbf{Y} -\mathbf{X} \varvec{\beta })\right] . \end{aligned}$$

Then,

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\beta }}_c-\varvec{\beta })=B_n^{-1}A_n. \end{aligned}$$

(24)

For $A_n$, by simple calculation and similar proof of Lemma 4 in Feng and Xue (2014), we have

$$\begin{aligned} A_n= & {} \frac{1}{\sqrt{n}}\sum _{i=1}^{n}\delta _i\left[ \tilde{\mathbf{X }}_i(\tilde{\mathbf{Z }}_i^T\varvec{\alpha }(U_i)+\tilde{\varepsilon }_i) -\mathbf{X} ^T\mathbf{Q} _i^T\varvec{\Sigma }_\xi \mathbf{Q} _i(\mathbf{M} +\varvec{\varepsilon })\right] \nonumber \\= & {} \frac{1}{\sqrt{n}}\sum _{i=1}^{n}\delta _i \left\{ [\mathbf{X} _i-\varvec{\Phi }_c^T(U_i)\varvec{\Gamma }_c^{-1}(U_i)\mathbf{Z} _i] [\varepsilon _i-\varvec{\xi }_i^T\varvec{\alpha }(U_i)]\right. \nonumber \\&\left. -\,\varvec{\Phi }_c^T(U_i)\varvec{\Gamma }_c^{-1}(U_i)\varvec{\xi }_i\varepsilon _i +\varvec{\Phi }_c^T(U_i)\varvec{\Gamma }_c^{-1}(U_i)(\varvec{\xi }_i \varvec{\xi }_i^T-\varvec{\Sigma }_\xi )\varvec{\alpha }(U_i)\right\} +o_p(1)\nonumber \\= & {} \frac{1}{\sqrt{n}}\sum _{i=1}^{n} \mathbf{G} _i +o_p(1). \end{aligned}$$

(25)

It is easy to see that $\mathbf{G} _i$ is independent and identical distributed with mean zero and $\mathrm {Cov}(\mathbf{G} _i)=\varvec{\Omega }_1.$

Thus, by the Slutsky theorem, Lemma 2 and the central limit theorem, we complete the Theorem.

Proof of Theorem 2

By the definition of $\hat{\varvec{\alpha }}_c(u)$, we can obtain that

$$\begin{aligned} \hat{\varvec{\alpha }}_c(u)= & {} (\mathbf{I} _q,\mathbf 0 _{q})[(\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u^\delta \mathbf{D} _u^\mathbf{W} -\varvec{\Omega }_u^\delta ]^{-1}(\mathbf{D} _u^\mathbf{W} )^T\varvec{\omega }_u^\delta \mathbf{M} \\ \nonumber&+\, (\mathbf{I} _q,\mathbf 0 _{q})[(\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u^\delta \mathbf{D} _u^\mathbf{W} -\varvec{\Omega }_u^\delta ]^{-1}(\mathbf{D} _u^\mathbf{W} )^T\varvec{\omega }_u^\delta \varvec{\varepsilon }\\\nonumber&+\, (\mathbf{I} _q,\mathbf 0 _{q})[(\mathbf{D} _u^\mathbf{W} )^T \varvec{\omega }_u^\delta \mathbf{D} _u^\mathbf{W} -\varvec{\Omega }_u^\delta ]^{-1}(\mathbf{D} _u^\mathbf{W} )^T\varvec{\omega }_u^\delta \mathbf{X} (\varvec{\beta }-\hat{\varvec{\beta }}_c). \end{aligned}$$

By Theorem 1, similar to the proof of Theorem 3.1 in Xia and Li (1999), it is easy to show that

$$\begin{aligned} \underset{{1\le j\le p}}{\mathrm {max}}\underset{{u\in \Pi }}{\mathrm {sup}}|\hat{\alpha }_{cj}(u)-\alpha _j(u)|=O\{h_1^2+(\mathrm {log}n/{nh_1})^{1/2}\},~~~~ a.s. \end{aligned}$$

Let $h_1=cn^{-1/5}$, where c is a constant. Then it yields that

$$\begin{aligned} \underset{{1\le j\le p}}{\mathrm {max}}\underset{{u\in \Pi }}{\mathrm {sup}}|\hat{\alpha }_{cj}(u)-\alpha _j(u)|=O(n^{-2/5}+(\mathrm {log} n)^{1/2}),~~~~a.s. \end{aligned}$$

Proof of Theorem 3

Similar to Theorem 1, it can be shown that

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\beta }}_I-\varvec{\beta })=D_n^{-1}E_n, \end{aligned}$$

(26)

where

$$\begin{aligned} D_n=\frac{1}{{n}}\sum _{i=1}^{n}(\bar{\mathbf{X }}_i\bar{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_{\xi } \mathbf{R} _i\mathbf{X} ), \end{aligned}$$

and

For convenience, we denote $[\mathbf{S} _c(\mathbf{A} )]_i$ and $[\mathbf{S} _I(\mathbf{A} )]_i$ to respectively be the ith row of product of $\mathbf{S} _c \mathbf{A}$ and $\mathbf{S} _I\mathbf{A}$ for a given matrix $\mathbf{A}$.

By simple calculation, it is obtained that

By Lemma 1, we have

$$\begin{aligned} I_1=\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}(\mathbf{X} _i-\varvec{\Phi }(U_i)\varvec{\Gamma }^{-1}(U_i) \mathbf{W} _i)\delta _i (\varepsilon _i-\varvec{\xi }_i^T\varvec{\alpha }(U_i))+o_p(1). \end{aligned}$$

(27)

In view of Theorem 1 and the law of large numbers, it follows that

$$\begin{aligned} \nonumber I_2= & {} \frac{1}{{ n}}\sum _{i=1}^{n}(1-\delta _i) \bar{\mathbf{X }}_i \tilde{\mathbf{X }}_i^T \sqrt{n} (\hat{\varvec{\beta }}_c-\varvec{\beta })\\\nonumber= & {} \frac{1}{{ n}}\sum _{i=1}^{n}(1-\delta _i)(\bar{\mathbf{X }}_i \tilde{\mathbf{X }}_i^T-\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_{\xi } \mathbf{Q} _i \mathbf{X} ) \sqrt{n} (\hat{\varvec{\beta }}_c-\varvec{\beta })\\\nonumber&+\,\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}(1-\delta _i)\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_{\xi } \mathbf{Q} _i \mathbf{X} (\hat{\varvec{\beta }}_c-\varvec{\beta })+o_p(1)\\= & {} \varvec{\Sigma }_2 \varvec{\Sigma }_1^{-1} \frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}{} \mathbf{G} _i +\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}(1-\delta _i)\mathbf{X} ^T\mathbf{R} _i^T\varvec{\Sigma }_{\xi } \mathbf{Q} _i \mathbf{X} (\hat{\varvec{\beta }}_c-\varvec{\beta })+o_p(1),\nonumber \\ \end{aligned}$$

(28)

where $\mathbf{G} _i$ is defined in Theorem 1.

$I_3$ can be written as

$$\begin{aligned} I_3= & {} \frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}(1-\delta _i)\mathbf{X }_i [\mathbf{S} _{c}(\varvec{\varepsilon }-\varvec{\xi }^T\varvec{\alpha }(u))]_i -\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}(1-\delta _i)[\mathbf{S} _I(\mathbf{X })]_i^T [\mathbf{S} _{c}(\varvec{\varepsilon }-\varvec{\xi }^T\varvec{\alpha }(u))]_i\\= & {} I_{31}-I_{32}. \end{aligned}$$

By Lemma 1, it can be shown that

$$\begin{aligned} I_{31}= & {} \frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}(1-\delta _i)\mathbf{X }_i \mathbf{W} _i^T(n f(U_i)\varvec{\Gamma }_c(U_i))^{-1}\sum _{j=1}^nK_{h_1}(U_j-U_i)\mathbf{W} _j(\varepsilon _j-\varvec{\xi }_j^T\varvec{\alpha }(U_j))\delta _j\\= & {} \frac{1}{{\sqrt{n}}}\sum _{i=1}^{n} \varvec{\Phi }(U_i)\varvec{\Gamma }_c^{-1}(U_i) \mathbf{W} _i \delta _i(\varepsilon _i-\varvec{\xi }_i^T\varvec{\alpha }(U_i))\\&-\,\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n} \varvec{\Phi }_c(U_i)\varvec{\Gamma }_c^{-1}(U_i) \mathbf{W} _i \delta _i(\varepsilon _i-\varvec{\xi }_i^T\varvec{\alpha }(U_i))+o_p(1). \end{aligned}$$

In a similar way, we obtain that,

$$\begin{aligned} I_{32}= & {} \frac{1}{{\sqrt{n}}}\sum _{i=1}^{n} \varvec{\Phi }(U_i)\varvec{\Gamma }_c^{-1}(U_i) \mathbf{W} _i \delta _i(\varepsilon _i-\varvec{\xi }_i^T\varvec{\alpha }(U_i))\\&-\,\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n} \varvec{\Phi }(U_i)\varvec{\Gamma }^{-1}(U_i) \mathbf{W} _i \delta _i(\varepsilon _i-\varvec{\xi }_i^T\varvec{\alpha }(U_i))+o_p(1) \end{aligned}$$

Therefor,

$$\begin{aligned} I_3=\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}[ \varvec{\Phi }(U_i)\varvec{\Gamma }^{-1}(U_i) \mathbf{W} _i - \varvec{\Phi }_c(U_i)\varvec{\Gamma }_c^{-1}(U_i) \mathbf{W} _i ]\delta _i(\varepsilon _i-\varvec{\xi }_i^T\varvec{\alpha }(U_i))+o_p(1).\nonumber \\ \end{aligned}$$

(29)

$I_4$ can be expressed as

$$\begin{aligned} I_4= & {} \frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}\bar{\mathbf{X }}_i (\mathbf{W} _i^T\varvec{\alpha }(U_i)-[\mathbf{S} _I(\mathbf{M} ^\mathbf{W} )]_i) -\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}\bar{\mathbf{X }}_i \delta _i [\mathbf{S} _{I}(\varepsilon -\varvec{\xi }^T\varvec{\alpha }(u))]_i\\&-\,\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}\bar{\mathbf{X }}_i (1- \delta _i) [\mathbf{S} _I(\mathbf{X} )]_i^T(\hat{\varvec{\beta }}_c-\varvec{\beta }) -\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}\bar{\mathbf{X }}_i (1- \delta _i)[\mathbf{S} _I(\hat{\mathbf{M }}_c^\mathbf{W }-\mathbf{M }^\mathbf{W })]_i\\= & {} I_{41}+I_{42}+I_{43}+I_{44} \end{aligned}$$

where $\hat{\mathbf{M }}_c^\mathbf{W }=[\mathbf{W} _1^T\hat{\varvec{\alpha }}_c(U_1),\ldots ,\mathbf{W} _n^T\hat{\varvec{\alpha }}_c(U_n)]^T$. By Lemma 1, it can be shown that $I_{41}=o_p(1)$ and $I_{42}=o_p(1)$. By the fact that $\hat{\varvec{\beta }}_c-\varvec{\beta }=O_p(n^{-1/2})$ from Theorem 1 and $\frac{1}{{ n}}\sum _{i=1}^{n}\bar{\mathbf{X }}_i[\mathbf{S} _I(\mathbf{X} )]_i=o_p(1)$, $I_{43}=o_p(1)$ is obtained. $I_{44}=o_p(1)$ can also be proved similarly. Thus, we have

$$\begin{aligned} I_{4}=o_p(1). \end{aligned}$$

(30)

Similar to the calculation of $I_4$, we can show that

$$\begin{aligned} I_5= & {} \frac{1}{{\sqrt{n}}}\sum _{i=1}^{n}(1-\delta _i)\bar{\mathbf{X }}_i ([\mathbf{S} _I(\mathbf{M} ^\mathbf{W} )]_i-\mathbf{W} _i^T\varvec{\alpha }(U_i))\\\nonumber= & {} o_p(1). \end{aligned}$$

(31)

Invoking (26)–(31), it can be obtained that

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\beta }}_I-\varvec{\beta })=\Sigma ^{-1}(\Sigma _1+\Sigma _2)\Sigma _1^{-1}\frac{1}{{\sqrt{n}}}\sum _{i=1}^{n} \mathbf{G} _i+o_p(1). \end{aligned}$$

Thus, by the Slutsky theorem, Lemma 2 and the central limit theorem, we concludes the theorem.

Proof of Theorem 4

The proof of Theorem 4 is similar to Theorem 2, then, we omit it.