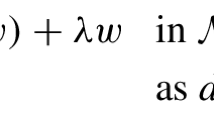Sobolev spaces and $\nabla$-differential operators on manifolds I: basic properties and weighted spaces

Abstract

We study covariant Sobolev spaces and $\nabla$ -differential operators with coefficients in general Hermitian vector bundles on Riemannian manifolds, stressing a coordinate-free approach that uses connections (which are typically denoted $\nabla$). These concepts arise naturally from geometric partial differential equations, including some that are formulated on plain Euclidean domains, for instance, from problems formulated on the boundary of smooth domains or in relation to the weighted Sobolev spaces used to study PDEs on polyhedral domains. We prove several basic properties of the covariant Sobolev spaces and of the $\nabla$-differential operators on general manifolds. For instance, we prove mapping properties for our differential operators and the independence of the covariant Sobolev spaces on the choices of the connection $\nabla$, as long as the new connection is obtained using a totally bounded perturbation. We also introduce the Fréchet finiteness condition (FFC) for totally bounded vector fields, which is satisfied, for instance, by open subsets of manifolds with bounded geometry. When (FFC) is satisfied, we provide several equivalent definitions of our covariant Sobolev spaces and of our $\nabla$-differential operators. We also introduce and study the notion of a $\nabla$-bidifferential operator (a bilinear version of differential operators), obtaining results similar to those obtained for $\nabla$-differential operators. Bilinear differential operators are necessary for a global, geometric discussion of variational problems. We tried to write the paper so that it is accessible to a large audience.

1 Introduction

Even if one is interested only in partial differential equations (PDEs) on Euclidean domains, one is quickly lead to consider also equations on vector bundles on manifolds, as noticed in many earlier works, including [16, 23] and [41, 44, 46]. Sobolev spaces on manifolds are useful, for instance, for the study of problems formulated on the boundary of smooth domains or for the investigation of the weighted Sobolev spaces that arise in the study of PDEs on polyhedral domains. Vector bundles arise when one considers systems, as explained below. This motivates our interest in Sobolev spaces and differential operators with coefficients in a general Hermitian vector bundle $E \rightarrow M$ on a Riemannian manifold (M, g) possibly with boundary. (The boundary will play a very small role in this paper. However, when considering non-integer and negative order Sobolev spaces, we shall assume that M does not have a boundary.)

The main goal of this paper is to investigate the first steps in an approach to the study of Sobolev spaces and of bounded differential operators on general Riemannian manifolds that is as independent as possible from local coordinates on M and local trivializations of the coefficient bundle $E \rightarrow M$. This requires us to use connections $\nabla$ instead of derivatives in our definitions. Thus, in this paper, as, for instance, in [37], we introduce Sobolev spaces and differential operators using iterations $\nabla ^j$ of the connection $\nabla$. The resulting objects will be called covariant Sobolev spaces and $\nabla$ -differential operators. We stress that we are not making any general assumptions on our manifold M that is valid throughout the paper since one of the main points of our paper is to keep the setting as general as possible, in particular, to go beyond the bounded geometry setting. For instance, we are not assuming M to be complete.

In this general setting of a plain manifold M, we prove a few basic, elementary properties of the covariant Sobolev spaces and $\nabla$-differential operators such as multiplication properties, mapping and restriction properties, and the independence of these definitions on totally bounded perturbations of the connection $\nabla$. (A section of a vector bundle will be called totally bounded if it is bounded and all its covariant derivatives are bounded.) We also recall the connection between weighted Sobolev spaces and the usual Sobolev spaces on manifolds (for a conformally equivalent metric).

To obtain more in depth results, we consider the set

$$\begin{aligned} {\mathcal {W}}_b(M) \mathrel {\ := \ }W_{\nabla }^{\infty ,\infty }(M; TM) \end{aligned}$$

(1)

of totally bounded vector fields on M (i.e. vector fields that are bounded together with all of their covariant derivatives). We then say that M satisfies the Fréchet finiteness condition (FFC) if ${\mathcal {W}}_b(M)$ is finitely generated as a Fréchet module over $W_{\nabla }^{\infty , \infty }(M)$, the space of functions all of whose covariant derivatives are bounded (see Definition 5.8). This condition is somewhat close to M being of bounded geometry and is satisfied if, for instance, M is an open subset of a manifold with bounded geometry. If (FFC) is satisfied, we provide several additional equivalent definitions of our covariant Sobolev spaces and our $\nabla$-differential operators.

We note that our covariant Sobolev spaces and our $\nabla$-differential operators depend on the underlying metric g on the manifold M and on the choice of the connection $\nabla$ on the coefficient vector bundle E. While very many works have been devoted to the role of the underlying metric g of the manifold M in the study of the properties of Sobolev spaces and differential operators, much fewer works have been devoted to role of the of the coefficient vector bundle E, which is encoded in the choice of the connection $\nabla$. Notable exceptions are the papers on “magnetic Sobolev spaces” by Nguyen et al. [56] and by Iftimie et al. [42]. From a practical point of view, considering operators with coefficients in a vector bundle has practical applications, as it is a framework that is necessary for the modeling of systems, as mentioned above. Systems arise in solid or continuum mechanics (examples are the Lamé—and the elasticity operator, in general—and the Stokes and Navier–Stokes systems and their generalizations), in the study of the Hodge-Laplacian and the Yamabe problem [1, 7, 14, 26, 53, 65], and in the study of relativistic or spin quantum mechanics. For instance, fluid mechanics in a relativistic setting (on a curved space-time) was considered recently by Disconzi et al. [29] (see also [45, 50]). We are planning some geometric applications of our results, but these applications would require some results that will be included in the second part of this project [34].

The role of the the underlying metric g of the manifold M in the study of the properties of Sobolev spaces and differential operators was much studied and we cannot do justice to all the people who have worked on the subject; nevertheless, let us mention a few of the most important contributions that have influenced our paper. In an early paper, Aronszajn and Milgram [16] have studied scalar differential operators on general Riemannian manifolds, obtaining, in particular, adjoint and Green-type formulas. The reader will find there a lot of useful geometric background material accessible to analysts. Browder [23] has also worked in the scalar case and has studied PDEs on a class of Euclidean domains that these days are called “manifolds with boundary and bounded geometry.” More recently, Sobolev spaces and differential operators on manifolds have been studied in very many papers, see, for instance, [2, 3, 6, 17, 25, 38, 53, 60] and the references therein. The monographs by Aubin [18], Hebey [37], and Taylor [62] provide even more references. Recently Herbert Amann and his collaborators have started a general program to study maximal regularity and general PDEs on certain singular spaces that can be modelled by manifolds with boundary and bounded geometry, see, for instance [3,4,5, 30]. A related program (but with a completely different motivation and mostly devoted to elliptic theory) was pursued by the second named author together with several collaborators, see, for instance [12, 35, 51]. This paper fits into this program of the second named author, but the role of the metric in the study of covariant Sobolev and $\nabla$-differential operators will mostly be relegated to the second paper of this series [34], since it takes us too far afield from the results obtained in this paper.

1.1 Contents of the paper

In Sect. 2, we fix some notation and recall some basic definitions concerning vector bundles and connections. In Sect. 3, we introduce our covariant Sobolev spaces and prove a few of their basic properties. In Sect. 4, we define the $\nabla$-differential operators, which are the natural differential operators acting on covariant Sobolev spaces since they are also defined starting with the connection. We also prove some of their mapping properties. The next section is devoted to totally bounded vector fields and to differential operators generated by covariant derivatives $\nabla _X$. We call them mixed differential operators since they are placed between the $\nabla$-differential operators and the classical differential operators. In addition, we introduce the Fréchet finiteness condition (FFC) for the set ${\mathcal {W}}_b(M)$ of totally bounded vector fields on M as a main tool in the study of mixed differential operators. We show that if (FFC) is satisfied, then the mixed differential operators coincide with the $\nabla$-differential operators. We also obtain various properties of mixed differential operators when (FFC) is satisfied. Among of them, we obtain a finite generation property for the algebra of bounded mixed differential operators and we show that the adjoint of a mixed differential operator is again a mixed differential operator. We also describe equivalent definitions of covariant Sobolev spaces in terms of $\nabla$-differential and mixed differential operators. In Sect. 6, we introduce the notion of $\nabla$-bidifferential operator (a bilinear version of a differential operator), and provide a parallel discussion to that of $\nabla$-differential operators. Bilinear differential operators are necessary for a global, geometric discussion of variational problems, thus motivating the results of this paper. The last section provides further motivation by making some connections with weighted Sobolev spaces.

In general, our results for differential operators come in “pairs,” one result in the smooth category (i.e., for ${{\mathcal {C}}}^{\infty }$-coefficients or morphisms) and one in the $W_{\nabla }^{\infty , \infty }$ category (i.e., for $W_{\nabla }^{\infty , \infty }$-coefficients or morphisms). The results for the ${{\mathcal {C}}}^{\infty }$ category are usually easier than the ones for the $W_{\nabla }^{\infty , \infty }$ category, and are usually not new. We include them, however, for the benefit of the reader and for comparison with the results for the $W_{\nabla }^{\infty , \infty }$ category, which are the ones needed when dealing with Sobolev spaces.

2 Preliminaries: vector bundles and connections

In this section, we recall some basic definitions and set up some notation. For simplicity, we shall stay as much as possible in the smooth category: smooth manifolds, smooth vector bundles, smooth coefficients, .... All along the paper, n will be the dimension of the underlying space: M, ${\mathbb {R}}^n$, and so on.

We shall use the following conventions for the many types of dual spaces that we use. First, $V'$ denotes the dual space to a real or complex topological vector space V and, if $T : V \rightarrow W$ is a linear map, then $T' : W' \rightarrow V'$ is its dual. Similarly, if V and W are complex vector spaces endowed with inner products, then $T^* : W \rightarrow V$ is the adjoint of $T : V \rightarrow W$. In case of real vector spaces (still endowed with an inner product), instead of the adjoint we have the transpose $T^\top : W \rightarrow V$. We let ${\mathbb {Z}}_+ = \{0, 1, 2, \ldots , \}$ and ${\mathbb {N}}= {\mathbb {Z}}_+ \smallsetminus \{0\}$.

It will be convenient to use the language of manifolds and vector bundles as in [16, 40, 59, 62], for example, but there are many other possible references. In this paper, we follow [12] to which we refer for concepts not defined here, as well as for some other details. Thus, in the following, M will be a smooth Riemannian manifold (with or without boundary) with metric g. Unless otherwise stated, we are not making any assumptions on M. Moreover, most of the time M will be allowed to be non-complete. We shall often consider manifolds that are subsets of some Euclidean space, in which case, they will typically be denoted by $\Omega$, possibly decorated with various subscripts. In this section, we present known, basic results needed in what follows. See [18, 20, 37, 43] for more background on differential geometry and for the unexplained concepts and results.

The space of smooth sections of a vector bundle $E \rightarrow M$ will be denoted ${{\mathcal {C}}}^{\infty }(M; E)$, whereas the space of those sections that in addition have compact support will be denoted ${{\mathcal {C}}}^{\infty }_{\text {c}}(M; E)$. We can use the fixed metric on M to identify the dual ${{\mathcal {C}}}^{\infty }_{\text {c}}(M; E)'$ with a space of distributions [39]. All the vector bundles considered in this paper will be smooth. As usual, $TM \rightarrow M$ is the tangent bundle to M and $T^*M \rightarrow M$ is the cotangent bundle to M (the dual of TM). Recall that a connection $\nabla = \nabla ^E$ on E is a first order (linear) differential operator

$$\begin{aligned} \nabla ^E : {{\mathcal {C}}}^{\infty }(M; E) \rightarrow {{\mathcal {C}}}^{\infty }(M; T^*M \otimes E)\,, \quad \nabla ^E (fu) = \hbox {d}f \otimes u + f \nabla ^E (u)\, , \end{aligned}$$

where $f \in {{\mathcal {C}}}^{\infty }(M)$ and $u \in {{\mathcal {C}}}^{\infty }_{\text {c}}(M; E).$ (All differential operators in this paper will be linear.) If $X \in {{\mathcal {C}}}^{\infty }(M; TM)$ is a smooth vector field, then $i_X : {{\mathcal {C}}}^{\infty }(M; T^*M \otimes E) \rightarrow {{\mathcal {C}}}^{\infty }(M; E)$ is the contraction with X and we have $\nabla ^E_X := i_X \circ \nabla ^E$. We shall need also the following extension of this construction.

Definition 2.1

Let $E, F \rightarrow M$ be vector bundles. If $X \in {{\mathcal {C}}}^{\infty }(M; E \otimes TM)$ and $\omega \in {{\mathcal {C}}}^{\infty }(M; T^*M \otimes F)$, then $i_X(\omega ) \in {{\mathcal {C}}}^{\infty }(M; E \otimes F)$ will denote the image of $X \otimes \omega$ under the contraction map $E \otimes TM \otimes T^*M \otimes F \rightarrow E \otimes F$.

If $E, F \rightarrow M$ are two vector bundles endowed with connections $\nabla ^E$ and $\nabla ^F$, respectively, then we shall endow the tensor product vector bundle $E\otimes F$ with the induced connection: $\nabla _X^{E \otimes F} = \nabla _X^{E} \otimes 1 + 1 \otimes \nabla _X^{F}$. Let $\tau : E \otimes T^*M \otimes F \rightarrow T^*M \otimes E \otimes F$ be the natural isomorphism permuting the first two factors. Then, $\nabla ^{E \otimes F} = \nabla ^E \otimes 1 + \tau \circ (1 \otimes \nabla ^F)$, which we shall write, by abuse of notation, in the form

$$\begin{aligned} \nabla ^{E \otimes F} = \nabla ^{E} \otimes 1 + 1 \otimes \nabla ^{F}\,. \end{aligned}$$

(2)

We extend $\nabla ^E$ to connections $\nabla$ on the bundles $T^{*\otimes k}M \otimes E$, $k \in {\mathbb {N}}$, using the Levi-Civita connection $\nabla ^{LC}$ on TM (here and below, we sometimes omit the superscripts of connections to lighten the notation). This gives then that

$$\begin{aligned} {{\mathcal {C}}}^{\infty }(M; E) \, = \,\{ u : M \rightarrow E \, \mid \, \nabla ^k u \text{ is } \text{ a } \text{ measurable } \text{ section } \text{ for } \text{ all } \ k\in {\mathbb {Z}}_+\}\,, \end{aligned}$$

(3)

where the section $\nabla ^k u$ is defined in distribution sense.

We shall proceed similarly with endomorphism bundles.

Remark 2.2

Let E and F be two complex vector bundles on M endowed with connections. We endow ${\text {Hom}}(E, F)$ with the induced connection. More precisely, let $\kappa : T^*M \otimes {\text {Hom}}(E; F) \simeq {\text {Hom}}(E; T^*M \otimes F)$ denote the natural isomorphism. Then, the connection on ${\text {Hom}}(E; F)$ is such that, for all $u \in {{\mathcal {C}}}^{\infty }(M; E)$ and $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E; F))$,

$$\begin{aligned} \nabla ^{F} (a u) = \kappa \nabla ^{{\text {Hom}}(E; F)}(a) u + (1 \otimes a) \nabla ^{E} u\,. \end{aligned}$$

The natural morphism $\kappa$ will be omitted from the notation from now on. In particular, this construction for $F = {\mathbb {C}}$, yields the connection on the dual bundle $E':= {\text {Hom}}(E; {\mathbb {C}})$, where the trivial bundle ${\mathbb {C}}$ is endowed with the trivial connection. Thus, if we denote by $\langle \, , \, \rangle : E' \otimes E \rightarrow {\mathbb {C}}$ the natural pairing, then the connection $\nabla ^{E'}$ is such that, for all vector fields X and all smooth, compactly supported sections u and w of the vector bundles E and $E'$, we have

$$\begin{aligned} \langle \nabla _X^{E'} u, w \rangle \, = \,X \langle u, w \rangle - \langle u, \nabla _X^{E} w \rangle \,. \end{aligned}$$

Whenever there is no danger of confusion, we shall drop the superscripts of the connection, thus write $\nabla = \nabla ^E$.

A Hermitian vector bundle $E \rightarrow M$ is a complex vector bundle endowed with a (smoothly varying, sesquilinear) inner product $(\cdot , \cdot )_E$. Its bounded sections are denoted $L^\infty (M; E)$. A connection $\nabla = \nabla ^E : {{\mathcal {C}}}^{\infty }(M; E) \rightarrow {{\mathcal {C}}}^{\infty }(M; T^*M \otimes E)$ is called metric preserving if, for all $\xi , \eta \in {{\mathcal {C}}}^{\infty }_{\text {c}}(M; E)$, we have

$$\begin{aligned} X(\xi , \eta )_E \, = \,(\nabla _X^E \xi , \eta )_E + (\xi , \nabla _X^E \eta )_E \,. \end{aligned}$$

(4)

Notation 2.3

The category of finite-dimensional, Hermitian vector bundles on M with metric preserving connection will be denoted ${\mathcal {H}}(M)$. We shall also use the notation

$$\begin{aligned} V^{\otimes k} \mathrel {\ := \ }\underbrace{V \otimes V \otimes \ldots \otimes V}_{\mathrm{{k-times}}} \ \text{ and } \ V^{\otimes 0} \mathrel {\ := \ }{\mathbb {C}}\,. \end{aligned}$$

In particular, $T^{*\otimes j}M := (T^*M)^{\otimes j}$ will denote the repeated tensor products of the cotangent space $T^*M$, which appears in the range of the iterated connection map

$$\begin{aligned} \nabla ^j \mathrel {\ := \ }\nabla ^{T^{* \otimes (j-1)} M \otimes E} \circ \ldots \circ \nabla ^{T^{*} M \otimes E} \circ \nabla ^{E} : {{\mathcal {C}}}^{\infty }(M; E) \rightarrow {{\mathcal {C}}}^{\infty }(M; T^{*\otimes j}M \otimes E)\,, \end{aligned}$$

where $T^*M$ and TM are endowed with the Levi–Civita connection $\nabla = \nabla ^{TM} = \nabla ^{LC}$. The Levi–Civita connection is the unique torsion-free, metric preserving connection on TM, a concept that we recall next.

The space of bounded sections u of E such that all their covariant derivatives $\nabla ^j u \in {{\mathcal {C}}}^{\infty }(M; T^{*\otimes j} M \otimes E)$ are also bounded is denoted by $W_{\nabla }^{\infty , \infty }(M; E)$. If the curvature of E and all its covariant derivatives are bounded (i.e. if the curvature is in $W_{\nabla }^{\infty , \infty }$), we shall say that E has totally bounded curvature [12].

3 Global, geometric covariant Sobolev spaces

In this section, we recall the definition of Sobolev spaces using connections, as in [37], but see also [12]. The goal of this definition is to provide a definition of Sobolev spaces that is independent of coordinate charts or of trivializations of the coefficient bundle. By $\,d{\text {vol}}_g$ we shall denote the induced volume form (that is, measure) on M associated to the metric g on M. For the sake of brevity, in the following, we will employ the notation $\,d{\text {vol}}$ instead of $\,d{\text {vol}}_g$, since, for most of this paper, the metric g will be fixed. We assume, $E, F \in {\mathcal {H}}(M)$, that is, $E, F \rightarrow M$ will be finite dimensional, Hermitian vector bundles with metric preserving connections. (We have used the notation introduced in 2.3. Also, whenever we shall consider $L^p$ or, more generally, $W^{s,p}$ spaces, we shall assume that the underlying vector bundles are Hermitian vector bundle with a metric preserving connection.)

3.1 Definition of covariant Sobolev spaces

We then let, as usual,

$$\begin{aligned} \Vert u\Vert _{L^p(M,g; E)} \mathrel {\ := \ }{\left\{ \begin{array}{ll} \ \Big ( \int _{M} \Vert u(x)\Vert _E^p \,d{\text {vol}}(x) \Big )^{1/p} &{} \quad \text{ if } 1 \le p < + \infty \\ \ \inf _{{\text {vol}}(N) = 0} \, \sup _{x \in M \smallsetminus N} \Vert u(x)\Vert _E &{} \quad \text{ if } p = + \infty \end{array}\right. } \end{aligned}$$

(5)

Of course $\Vert u\Vert _{L^\infty (M; E)}$ is the essential supremum, ${\text {ess-sup}}\Vert u(x)\Vert _E$, of u, and we allow $\Vert u\Vert _{L^p(M,g; E)} \in [0, \infty ]$. As usual, we identify sections of E that coincide outside a set of measure zero to define the $L^p$–spaces:

$$\begin{aligned} L^p(M,g; E) \mathrel {\ := \ }\{ u : M \rightarrow E \, \vert \ \Vert u\Vert _{L^p(M, g; E)} < + \infty \}/\ker (\Vert \cdot \Vert _p)\,. \end{aligned}$$

(6)

The spaces $L_{{\text {loc}}}^p$ are defined similarly, as in the classical case.

3.1.1 Definition of positive order covariant Sobolev spaces

We now introduce the Sobolev spaces in which we are interested in a global way, as in [12, 37]. We need to use the index $\nabla$ in their notation since their definition depends on the choice of the connection (in general) and since we will consider also alternative definitions of Sobolev spaces. We consider only complex Sobolev spaces, but the real case can be treated similarly. Recall the definition of the $L^p$-spaces and norms, Eqs.  (5) and (6).

Definition 3.1

Let M be a Riemannian manifold with metric g and volume form $\,d{\text {vol}}= \,d{\text {vol}}_g$. Let $E \in {\mathcal {H}}(M)$, that is, a finite dimensional, Hermitian vector bundle with metric preserving connection $\nabla ^E$. Let $\ell \in {\mathbb {Z}}_+$. Then,

$$\begin{aligned} W_{\nabla }^{\ell , p}(M; E) \mathrel {\ := \ }\{u \, \vert \ \nabla ^j(u) \in L^p(M,g;T^{*\otimes j } M \otimes E) \,,\, \text{ for } \, 0 \le j \le \ell \} \end{aligned}$$

is the order $\ell$, $L^p$–type $\nabla$–Sobolev space of sections of E (so $W_\nabla ^{0, p} = L^p$) with norm

$$\begin{aligned} \Vert u\Vert _{W_{\nabla }^{\ell ,p}(M; E)} \mathrel {\ := \ }\ell ^p\text{--norm } \text{ of } \{ \Vert \nabla ^j (u)\Vert _{L^p(M,g;T^{* \otimes j} M \otimes E)}\,,\ 0 \le j \le \ell \} \,. \end{aligned}$$

The vector bundle E will be referred to as the coefficient bundle of the respective covariant Sobolev space.

Remark 3.2

The elements of the spaces $W_{\nabla }^{\ell , p}(M; E)$ are thus (equivalence classes of) sections of $E \rightarrow M$. Occasionally, E will only be assumed to have a smoothly fiberwise norm (which does not necessarily come from an inner product). The definitions extend to this case without change. This will be used exclusively for endomorphisms bundles of Hermitian bundles with the operator norm.

Also, in particular,

$$\begin{aligned} \Vert u\Vert _{W_{\nabla }^{\ell , \infty }(M;E)} \mathrel {\ := \ }{\max }_{j=0}^\ell \Vert \nabla ^j (u)\Vert _{L^\infty (M,g;T^{*\otimes j } M \otimes E)}\,. \end{aligned}$$

When there is no danger of confusion, we shall write $\Vert u\Vert _{L^p(M)}$ and even $\Vert u\Vert _{L^p}$ for $\Vert u\Vert _{L^p(M,g; E)}$ and $\Vert u\Vert _{W_{\nabla }^{\ell , p}(M)}$ (or even $\Vert u\Vert _{W_{\nabla }^{\ell , p}}$) for $\Vert u\Vert _{W_{\nabla }^{\ell , p}(M; E)}$. As we will see below, in Example 3.11, some care needs to be taken when dealing with the covariant Sobolev spaces. The space

$$\begin{aligned} W_{\nabla }^{\infty , \infty }(M; E) \mathrel {\ := \ }\bigcap _{\ell \in {\mathbb {Z}}_+} W_{\nabla }^{\ell ,\infty }(M; E) \subset {{\mathcal {C}}}^{\infty }(M; E) \,, \end{aligned}$$

(7)

introduced above, that is, the space of bounded sections of E such that all their covariant derivatives are also bounded, will play an important role in what follows. It is a Fréchet space endowed with the increasing family of semi-norms $\Vert \cdot \Vert _{W_{\nabla }^{s,\infty }(M; E)}$. The last inclusion in Eq. (7) is a consequence of Eq. (3). Recall that a subset S of a Fréchet space is bounded if, and only if, it is bounded in every semi-norm (see, e.g., [58, Theorem 1.37]).

3.1.2 Negative and non-integer order covariant Sobolev spaces

We now turn to the case $s \notin {\mathbb {Z}}_+$ in our definition of the spaces $W_{\nabla }^{s, p}(M; E)$. With our definition, if M happens to have a non-empty boundary $\partial M$, then $W_{\nabla }^{s, p}(M; E) = W_{\nabla }^{s, p}(M \smallsetminus \partial M; E)$ for $s \in {\mathbb {Z}}_+$, so we could as well assume that M does not have a boundary for this range of s. This is no longer true, however, if $s \notin {\mathbb {Z}}_+$. So, in this subsection (for the purpose of defining negative and non-integer order Sobolev spaces), we shall assume that M does not have a boundary.

Let next $\mathring{W}_{\nabla }^{s,p}(M; E)$, $s \in {\mathbb {N}}$, be the closure of the space ${{\mathcal {C}}}^{\infty }_{\text {c}}(M;E)$ in $W_{\nabla }^{s,p}(M; E)$. If M is complete, then, for any $1 \le p < \infty$, $\mathring{W}_{\nabla }^{1,p}(M;E)= W_{\nabla }^{1,p}(M; E)$ (see [37, Theorem 2.7]). Moreover, if $s \in {\mathbb {N}}$, $s\ge 2$, and M is complete with positive injectivity radius and Ricci curvature bounded up to the order $s-2$, then, for any $1 \le p < \infty$, $\mathring{W}_{\nabla }^{s,p}(M;E) = W_\nabla ^{s,p}(M; E)$ (see [37, Theorem 2.8]).

We shall use the spaces $\mathring{W}_{\nabla }^{s,p}(M; E)$, for $1<p<+\infty$, to define the Sobolev spaces with negative index

$$\begin{aligned} W_{\nabla }^{-s,p}(M; E^*) \mathrel {\ := \ }\mathring{W}_{\nabla }^{s,p'}(M; E)^* \,, \end{aligned}$$

(8)

where $V^*$ is the complex conjugate dual of V and $\frac{1}{p}+\frac{1}{p'}=1$. For simplicity, in the following, we shall identify $E^*$ with E using the Hermitian metric on E, so $W_{\nabla }^{-s,p}(M; E^*)\simeq W_{\nabla }^{-s,p}(M; E)$. We also define the spaces $W_{\nabla }^{s,p}(M; E)$ for $s \notin {\mathbb {Z}}$ by complex interpolation between consecutive integers (see [49, 64] for further details).

Let $p = 2$, $M = {\mathbb {R}}^n$ with the Euclidean metric, and $E = {\mathbb {C}}$ be trivial. Then, the spaces $W^{s, 2}(M) = W^{s, p}(M; {\mathbb {C}})$ can be also obtained using the Fourier transform (Bessel-potential spaces). For this case, all the results in this paper are, of course, well known.

3.2 Elementary properties of covariant Sobolev spaces

We now prove the first properties of the covariant Sobolev spaces. We also provide an example to show that the choice of the metric preserving connection on the coefficient bundle E does play a role in their definition, and hence it is important. We allow M to have a boundary, but this makes little difference in this paper, especially when dealing with positive integer order Sobolev spaces, since the boundary has measure zero. We begin with a few simple lemmas that will eventually be generalized.

In this subsection, $E, F \in {\mathcal {H}}(M)$, that is, they will be two finite dimensional, Hermitian vector bundles on M endowed with metric preserving connections $\nabla ^E$ and $\nabla ^F$. Recall that M is a Riemannian manifold and that, when considering Sobolev spaces, all our vector bundles are endowed with a metric and a metric preserving connection. Also, we will often drop the superscripts, and thus the connections will be denoted simply by $\nabla$. Also, we shall usually simply write $\Vert u\Vert _{W_{\nabla }^{s, p}} = \Vert u\Vert _{W_{\nabla }^{s, p}(M; E)}$, but if M is replaced by a subset U, we keep it in the notation $\Vert u\Vert _{W_{\nabla }^{s, p}(U)} = \Vert u\Vert _{W_{\nabla }^{s, p}(U; E)}$, and the same comment applies to the case when the vector bundle is not implicit.

Proposition 3.3

Let $s \in {\mathbb {R}}$ and $p \in [1, \infty ]$, but $p \ne 1, \infty$ if $s < 0$. Then, the space $W_{\nabla }^{s,p}(M; E)$ is complete. Moreover, for $p=2$, $W_{\nabla }^{s,p}(M; E)$ is a Hilbert space.

Proof

For $s = 0$, the statement is known since $W_{\nabla }^{0, p}(M; E) = L^{p}(M; E)$ with equality of norms (see Eqs. 5, 6 ). Let us assume then that $s \in {\mathbb {N}}$. The graph of the map $\nabla$ with domain $W_{\nabla }^{1, p}(M; E)$ and codomain $L^p(M; T^*M \otimes E)$ is closed in $L^p(M; E) \times L^p(M; T^*M \otimes E)$ since $\nabla$ is continuous in the topology of distributions. Let $X \mathrel {\ := \ }\oplus _{j=0}^s L^p(M; T^{* \otimes j} M \otimes E)$. For each $0 \le k < s$, we consider the subspace $X_k := \{ \xi = (\xi _j) \in X \mid \nabla \xi _k = \xi _{k+1}\}$. Then, the space $X_k$ is the product of a Banach space with the graph of $\nabla$ (with a suitable domain). So $X_k$ is closed in X. Hence, $W_{\nabla }^{s,p}(M; E) := \cap _{k=0}^{s-1} X_k$ is a closed subspace of a Banach space, and hence it is complete. Moreover, if $p = 2$, X is a closed subspace of a Hilbert space, hence a Hilbert space on its own.

The statement for $s \notin {\mathbb {Z}}_+$ then follows since the constructions used to define the spaces $W_{\nabla }^{s,p}(M; E)$, namely duality and interpolation, preserve the class of Banach spaces (respectively, Hilbert spaces, if $p = 2$). $\square$

The above proof also spells out the precise form of the inner product on the space $W_{\nabla }^{s, p}(M; E)$ for $p=2$ and $s \in {\mathbb {Z}}_+$:

$$\begin{aligned} ( u, v )_{W_{\nabla }^{s,p}} \mathrel {\ := \ }\sum _{j=0}^s \int _M ( \nabla ^j(u) ,\nabla ^j(v) )_{E}\ dvol \,, \end{aligned}$$

(9)

and this is a Hilbert space. The statement that $W_{\nabla }^{s, p}(M; E)$ is also a Hilbert space for $p=2$ and $s \notin {\mathbb {Z}}_+$ follows by duality and interpolation.

The following few lemmas, while easy, are emblematic for our approach.

Lemma 3.4

Let $\varphi : E \rightarrow F$ be a measurable linear map satisfying

$$\begin{aligned} \nabla (\varphi ) \mathrel {\ := \ }\nabla ^F \circ \varphi - (1 \otimes \varphi ) \circ \nabla ^E = 0 \,. \end{aligned}$$

Then, $\Vert \varphi (x)\Vert$ is constant in $x \in M$ and $\varphi \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; F))$ (see Eq. 7). In particular, $\varphi$ is smooth and bounded. Moreover, the induced map $\varphi : W_{\nabla }^{s, p}(M; E) \rightarrow W_{\nabla }^{s, p}(M; F)$ is continuous of norm $\le \Vert \varphi \Vert _{L^\infty }$ for all $s \in {\mathbb {R}}$ and all $p \in (1, \infty )$ (also for all $1 \le p \le \infty$ if $s \ge 0$).

Proof

We drop the superscripts E and F in the connections. The assumption $\nabla (\varphi ) := \nabla \circ \varphi - (1 \otimes \varphi ) \circ \nabla = 0$ implies, by induction, that $\nabla ^j(\varphi ) = 0$ and $(1 \otimes \varphi ) \circ \nabla ^j = \nabla ^j \circ \varphi$ for all $j \in {\mathbb {N}}$. This, in turn, gives that $\Vert \varphi (x)\Vert$ is constant, since parallel transport by $\nabla$ preserves the norm. Therefore, $\varphi \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; F))$. We also obtain that that $\nabla ^j \circ \varphi (u) = 1 \otimes \varphi ( \nabla ^j (u))$. Since $\Vert 1 \otimes \varphi \Vert _{L^\infty } = \Vert \varphi \Vert _{L^\infty }$, this ultimately implies that

$$\begin{aligned} \Vert \nabla ^j \big ( \varphi (u) \big ) \Vert _{L^p}\, \le \, \Vert \varphi \Vert _{L^\infty } \Vert \nabla ^j (u) \Vert _{L^p}\,. \end{aligned}$$

This proves our result for all $s \in {\mathbb {N}}$. Since $\varphi$ preserves supports, it maps continuously $\mathring{W}_{\nabla }^{s,p}(M; E) \rightarrow \mathring{W}_{\nabla }^{s,p}(M; F)$, again if $s \in {\mathbb {N}}$. The result for $s \in {\mathbb {Z}}$, $s < 0$, and $p \ne 1, \infty$ then follows by duality from the definition of the spaces $W_{\nabla }^{s,p}$. For $s \in {\mathbb {R}}\smallsetminus {\mathbb {Z}}$, the result follows by interpolation. $\square$

The basic maps $\tau : E \rightarrow {\text {Hom}}(F; E\otimes F) {\simeq F' \otimes F \otimes E}$, $\epsilon : F' \otimes F \otimes E \rightarrow E$, and $\tau _{1} : {\text {End}}(F) \rightarrow {\text {End}}(E\otimes F)$ defined next satisfy the assumptions of the above lemma. Indeed, let

$$\begin{aligned} \begin{gathered} \tau _\xi (\eta ) \mathrel {\ := \ }\xi \otimes \eta \,, \\ \epsilon (\eta ' \otimes \eta \otimes \xi ) \mathrel {\ := \ }\eta '(\eta ) \xi \,, \\ \tau _{1}(\varphi ) \mathrel {\ := \ }1 \otimes \varphi \mathrel {\ := \ }id_E \otimes \varphi \,, \quad \text{ and } \\ g : TM \rightarrow T^*M\,. \end{gathered} \end{aligned}$$

(10)

The last map is simply the isomorphism induced by the metric. We endow the endomorphism bundles with the operator norm, see Remark 3.2.

Corollary 3.5

The maps $\tau$, $\epsilon$, $\tau _1$, and g of Eq. (10) have norm one and zero covariant derivative, that is, $\nabla (\tau ) = 0$, $\nabla (\epsilon )=0$, $\nabla (\tau _1) = 0$, and $\nabla (g)=0$. Consequently, they induce contractions between the corresponding $W_{\nabla }^{s,p}$ spaces of Lemma 3.4.

Proof

The fact that the four maps have norm one is elementary and follows from the definition of the norms on tensor products and homomorphism spaces. We note however that, in spite of the isomorphism ${\text {Hom}}(F; E\otimes F) \simeq F' \otimes F \otimes E$, the norms on these spaces are different. As we have already mentioned, we use the same notation $\nabla$ for all connections, for simplicity. In view of Lemma 3.4, it thus suffices to check that the covariant derivatives vanish. First, we use Remark 2.2 defining the connection on endomorphism bundles and then Eq.  (2) defining the tensor product connection to obtain

$$\begin{aligned} \nabla (\tau )_v (\xi )&= \nabla \big ( \tau _v(\xi ) \big ) - \tau _{\nabla v}(\xi ) - \tau _{v}(\nabla \xi )\\&= \nabla ( v \otimes \xi ) - \nabla v \otimes \xi - v \otimes \nabla \xi = 0\,. \end{aligned}$$

The other relation is similar:

$$\begin{aligned} \nabla (\epsilon )(v' \otimes v \otimes \xi )&= \nabla \big [ \epsilon (v'\otimes v \otimes \xi )\big ] - \epsilon \big [ \nabla (v'\otimes v \otimes \xi )\big ]\\&= \nabla \big (\langle v', v\rangle \otimes \xi \big ) - \epsilon \big [ \nabla (v' \otimes v) \otimes \xi + v' \otimes v \otimes \nabla (\xi ) \big ]\\&= \big [ d\langle v', v \rangle - \epsilon \nabla (v'\otimes v) \big ] \otimes \xi \\&= \big [ d\langle v', v \rangle - \langle \nabla (v'), v \rangle - \langle v', \nabla (v) \rangle \big ] \otimes \xi \, = \,0 \,. \end{aligned}$$

The proofs for $\tau _1$ and g are completely similar using also the relations $\nabla (id_E) = 0$, $\nabla (\psi \otimes \varphi ) = \nabla (\psi ) \otimes \varphi + \psi \otimes \nabla (\varphi )$, and $\nabla _X g(Y, Z) = g(\nabla _X Y, Z) + g(Y, \nabla _X Z)$. $\square$

We also have the following easy lemma, a stronger version of which will be obtained later on.

Lemma 3.6

For all $\ell \in {\mathbb {Z}}_+$ and $p \in [1, \infty ]$, the map $\nabla : W_{\nabla }^{\ell +1, p}(M; E) \rightarrow W_{\nabla }^{\ell , p}(M; T^*M \otimes E)$ is contractive, that is, $\Vert \nabla u \Vert _{W_{\nabla }^{\ell , p}} \le \Vert u \Vert _{W_{\nabla }^{\ell +1, p}}$.

Proof

For all $j \le \ell$ and $u \in W_{\nabla }^{\ell +1, p}(M; E)$, we have $\nabla ^j \nabla u \in L^p(T^{* \otimes (j+1)} M \otimes E)$, by definition, and hence $\nabla u \in W_{\nabla }^{\ell , p}(M; T^{*} M \otimes E)$, again by definition. The inequality of the norms follows in the same way since the $\ell _p$-norm of $(a_0, a_1, \ldots , a_\ell )$ is $\ge$ the $\ell _p$-norm of $(a_1, a_2, \ldots , a_\ell )$. $\square$

3.3 Further properties of covariant Sobolev spaces

We have the following basic multiplicative property.

Proposition 3.7

Let $\ell \in {\mathbb {Z}}_+$ and $p,q,r \in [1, \infty ]$ with $\frac{1}{p}+\frac{1}{q}=\frac{1}{r}$. Then, for all $a \in W_{\nabla }^{\ell ,p}(M; {\text {Hom}}(E; F))$ and $u \in W_{\nabla }^{\ell ,q}(M; E)$, we have $a u = a(u) \in W_{\nabla }^{\ell ,r}(M; F)$ and

$$\begin{aligned} \Vert au\Vert _{W_{\nabla }^{\ell ,r}(M; F)}\, \le \, 3^\ell \, \Vert a\Vert _{W_{\nabla }^{\ell ,p}(M; {\text {Hom}}(E; F))} \Vert u\Vert _{W_{\nabla }^{\ell ,q}(M; E)}\,. \end{aligned}$$

In particular, the evaluation in E defines a continuous bilinear map

$$\begin{aligned} W_{\nabla }^{\ell ,p}(M; {\text {Hom}}(E; F))\times W_{\nabla }^{\ell ,q}(M; E) \ni (a, u)\, \mapsto \, au := a(u) \in W_{\nabla }^{\ell ,r}(M; F)\,. \end{aligned}$$

Proof

We show our property by induction on $\ell$. If $\ell = 0$, the result is known. Indeed, if $r = \infty$, then $p = q = \infty$, and the inequality follows from the pointwise inequality $\Vert (au)(x) \Vert \le \Vert a(x)\Vert \Vert u(x)\Vert$. Let us assume then that $r < \infty$. Then, if $(a,u)\in L^p (M,g; {\text {Hom}}(E; F))\times L^q(M,g; E)$, using again this pointwise inequality of norms as well as the Hölder inequality for $\frac{r}{p} + \frac{r}{q} = 1$ and for the functions $\Vert a(x)\Vert$ and $\Vert u(x)\Vert$, we obtain

$$\begin{aligned} \Vert au\Vert _{L^{r}}^r&\mathrel {\ := \ }\int _{M} \Vert (au)(x)\Vert ^r \,d{\text {vol}}(x)\\&\le \int _{M} \big ( \Vert a(x)\Vert \Vert u(x)\Vert \big )^r \,d{\text {vol}}(x)\\&\le \Big ( \int _{M} \Vert a(x)\Vert ^p \,d{\text {vol}}(x) \Big )^{r/p}\ \Big ( \int _{M} \Vert u(x)\Vert ^q \,d{\text {vol}}(x) \Big )^{r/q}\\&\, = \,\Vert a\Vert _{L^p}^r \Vert u\Vert _{L^q}^r\,. \end{aligned}$$

Assume now that our statement is valid for $\ell -1 \ge 0$, and show that it holds also for $\ell$. Let $(a, u)\in W_{\nabla }^{\ell ,p}(M; {\text {Hom}}(E; F)) \times W_{\nabla }^{\ell ,q}(M; E)$. Then, in view of the embedding $W_{\nabla }^{\ell ,p}(M; {\text {Hom}}(E; F)) \times W_{\nabla }^{\ell ,q}(M; E)\hookrightarrow W_{\nabla }^{\ell -1,p}(M; {\text {Hom}}(E; F))\times W_{\nabla }^{\ell -1,q}(M; E)$ and by the induction hypothesis we obtain that $au\in W_{\nabla }^{\ell -1,r}(M; F)$. Thus,

$$\begin{aligned} \nabla ^{j}(au)\in L^{r}(M,g; T^{* \otimes j }M \otimes F),\ \ 0\le j\le \ell -1\,. \end{aligned}$$

(11)

It remains to show that $\nabla ^{\ell }(au)\in L^{r}(M,g; T^{* \otimes \ell }M \otimes F)$. To this end, we use the formula

$$\begin{aligned} \nabla (au) = \nabla (a)u + (1\otimes a)\nabla u \end{aligned}$$

(12)

(see Remark 2.2) and obtain that

$$\begin{aligned} \nabla ^{\ell }(au) =\nabla ^{\ell -1}\left( \nabla (au)\right) = \nabla ^{\ell -1}\left( \nabla (a)u + (1\otimes a)\nabla u\right) \,. \end{aligned}$$

(13)

By Lemma 3.6, we have $\nabla a\in W_{\nabla }^{\ell -1,p}(M; {\text {Hom}}(E, T^*M \otimes F))$ and $u\in W_{\nabla }^{\ell -1,q}(M; E)$ and, thus, $\nabla (a)u\in W_{\nabla }^{\ell -1,r}(M; F)$ by the induction hypothesis. The same argument using also Lemma 3.4 gives that $(1\otimes a)\nabla u\in W_{\nabla }^{\ell -1,r}(M; F)$. Therefore, $\nabla ^{\ell }(au)\in L^r(M; F)$ by formulas (11) and (13) with continuous dependence. Hence $au\in W_{\nabla }^{\ell ,r}(M; F)$ and the induced map is continuous, as asserted. To obtain the precise form of our result, we track the constants in the above reasoning as follows:

$$\begin{aligned} \Vert au\Vert _{W_\nabla ^{\ell , r}}&\le \, \Vert au\Vert _{W_\nabla ^{\ell -1, r}} + \Vert \nabla (au)\Vert _{W_\nabla ^{\ell -1,r}}\\&\le 3^{\ell -1} \Vert a\Vert _{{W_\nabla ^{\ell -1,p}}}\Vert u\Vert _{{W_\nabla ^{\ell -1, q}}} + \Vert \nabla (a)u + (1\otimes a)\nabla u\Vert _{W_\nabla ^{\ell -1, r}}\\&\le 3^{\ell } \Vert a\Vert _{W_\nabla ^{\ell ,p}}\Vert u\Vert _{W_\nabla ^{\ell , q}} \,, \end{aligned}$$

where we have used the induction hypothesis. $\square$

Proposition 3.7 extends to tensor products as follows.

Corollary 3.8

Using the notation and assumptions of Proposition 3.7, we have that the tensor product defines a continuous bilinear map

$$\begin{aligned} W_\nabla ^{\ell , p}(M; E) \times W_\nabla ^{\ell , q}(M; F) \ni (u,v) \, \mapsto \, u \otimes v \in W_\nabla ^{\ell , r}(M; E \otimes F) \,, \end{aligned}$$

and $\Vert u \otimes v\Vert _{W_\nabla ^{\ell ,r}(M; E \otimes F)} \le 3^\ell \Vert u\Vert _{W_\nabla ^{\ell ,p}(M; E)} \Vert v\Vert _{W_\nabla ^{\ell ,q}(M; F)}.$

For the proof of the second part of this result, one could repeat the same arguments as for Proposition 3.7. We prefer, however, to reduce its proof to that proposition using the natural map $\tau _\xi (\eta ) = \xi \otimes \eta$ of Corollary 3.5.

Proof

Recall from Corollary 3.5 that the natural map $\tau : E \rightarrow {\text {Hom}}(F, E \otimes F)$ is contractive. Since $u \otimes v = \tau _u(v)$, the result follows from Proposition 3.7. $\square$

Although we shall not use the following result in this paper, we include it since it is an interesting general result that may allow us to compare Sobolev norms with their Euclidean counter-parts. Let ${\mathcal {U}}= (U_i)_{i \in I}$ be a covering of M, that is, $M = \cup _{i \in I} U_i$. Recall that its covering multiplicity $N({\mathcal {U}}) = N((U_i)_{i \in I})$ is defined by

$$\begin{aligned} N({\mathcal {U}}) \mathrel {\ := \ }\max \{r \, \vert \ \exists i_1 , i_2, \ldots , i_r \in I \text{ distinct } \text{ with } U_{i_1} \cap U_{i_2} \cap \ldots \cap U_{i_r} \ne \emptyset \}\,. \end{aligned}$$

(14)

Also, recall that the covering ${\mathcal {U}}= (U_i)_{i \in I}$ of M is uniformly locally finite if $N({\mathcal {U}}) < \infty$. Assume that the index set I labeling the open sets of the covering ${\mathcal {U}}$ is countable. Then, we also let

$$\begin{aligned} ||| u |||_{{\mathcal {U}}, s, p} \mathrel {\ := \ }{\left\{ \begin{array}{ll} \, \Big ( \sum _{j \le s, i \in I} \Vert \nabla ^i u\Vert ^p_{L^p(U_i)} \Big )^{1/p} &{} \quad \text{ if } 1 \le p < \infty \\ \ \sup _{j \le s, i \in I} \Vert \nabla ^i u\Vert _{L^\infty (U_i)} &{} \quad \text{ if } p = \infty \,. \end{array}\right. } \end{aligned}$$

(15)

Proposition 3.9

We have $||| u |||_{{\mathcal {U}}, s, \infty } = \Vert u\Vert _{W_{\nabla }^{s, \infty }(M)}$. If $1 \le p < \infty$, then $\Vert u\Vert _{W_{\nabla }^{s, \infty }(M)} \le ||| u |||_{{\mathcal {U}}, s, p} \le N({\mathcal {U}})^{1/p} \Vert u\Vert _{W_{\nabla }^{s, \infty }(M)}.$

Proof

This follows from the definitions of the norms $\Vert \, \cdot \, \Vert _{W_{\nabla }^{s, \infty }(M)}$ and $||| \, \cdot \, |||_{{\mathcal {U}}, s, p}$ and, for $f \ge 0$ measurable, the inequalities

$$\begin{aligned} \int _M f \,d{\text {vol}}\, \le \, \sum _{i \in I} \, \int _{U_i} f \,d{\text {vol}}\, \le \, N({\mathcal {U}}) \int _M f \,d{\text {vol}}\,. \end{aligned}$$

This completes the proof. $\square$

The spaces $W_{\nabla }^{s, p}$ do have many of the usual properties of the Sobolev spaces on compact, smooth manifolds (with or without boundary), especially if M has bounded geometry, this will follow from standard results on bounded geometry manifolds, see [12, 36, 37, 63] and the references therein, once we will establish a few more technical results in [34]. (See, however, [31, 32] for related papers using Sobolev spaces that go beyond the bounded geometry setting.) The reader should be cautioned, however, not to take all the properties of classical Sobolev spaces for granted in the case of covariant Sobolev spaces, since, for instance, the spaces $W_{\nabla }^{s,p}$ do depend on the choice of the connection $\nabla ^E$ on the coefficient bundle E. Indeed, this will be seen shortly in the following example on “magnetic Sobolev spaces” [42, 56]. Let us introduce first some notation.

Notation 3.10

Assume $M \subset {\mathbb {R}}^n$, so we have global coordinates $x_j$. We shall use the following notation:

• (i) $I \mathrel {\ := \ }\{1, 2, \ldots , n\}$ and $J_{\mu } \mathrel {\ := \ }\{\emptyset \} \cup I \cup I^2 \cup \ldots \cup I^{\mu }$;

• (ii) $(e_j := \partial _j := \frac{\partial }{\partial x_j})_{j \in I}$ and $(e_j^* := dx_j)_{j \in I}$, are the standard basis of TM and, respectively, $T^*M$ and $e_{\mathbf {i}} := e_{i_0} \otimes e_{i_1} \otimes \ldots e_{i_r}$ and $e^*_{\mathbf {i}} := e^*_{i_0} \otimes e^*_{i_1} \otimes \ldots e^*_{i_r}$, where $\mathbf {i} =(i_1, i_2, \ldots , i_r) \in I^r \subset J_\mu$ and $e_\emptyset = e^*_\emptyset = 1 \in {\mathbb {C}}$;

• (iii) for $\mathbf {i} = (i_1, i_2, \ldots ,i_r) \in I^r \subset J_\mu$, we let $|\mathbf {i}| := r$;

• (iv) for $\mathbf {i} = (i_1, i_2, \ldots ,i_r) \in I^r$, we let $\nabla _{\mathbf {i}} \mathrel {\ := \ }\nabla _{i_1} \nabla _{i_2} \ldots \nabla _{i_r}$, and we agree that $\nabla _{\emptyset } u = u$.

Example 3.11

(Magnetic Sobolev spaces) Let us assume that $M = {\mathbb {R}}^n$ with the flat metric, but that the trivial bundle $E := M \times V \rightarrow M$ has a non-trivial connection, where V is some given real vector space. Let $\nabla _j = \nabla _{e_j}$ be the covariant derivative with respect to the vector field $e_j := \frac{\partial }{\partial x_j}$. Then, $\nabla _j (dx_k) = 0$ and

$$\begin{aligned} \nabla _j(\xi ) \mathrel {\ := \ }\partial _j \xi + A_j \xi \, , \end{aligned}$$

(16)

where $\partial _j$ is the partial derivative with respect to jth variable (which is defined since $E \rightarrow M = {\mathbb {R}}^n$ is a trivial bundle) and $A_j \in {{\mathcal {C}}}^{\infty }(M; {\text {End}}(V))$. Recall the notation of 3.10 (in particular, recall that we agreed that $\nabla _{\emptyset } u = u$).

By induction, we then obtain that

$$\begin{aligned} \nabla ^r u \, = \,\sum _{\mathbf {i} \in J^r} e^*_{\mathbf {i}} \otimes \nabla _{\mathbf {i}} u\, . \end{aligned}$$

(17)

We obtain, in particular, that

$$\begin{aligned} u \in W_{\nabla }^{r,p}(M; E) \ \Leftrightarrow \ \forall \mathbf {i} \in J_r\,,\ \nabla _{\mathbf {i}} u \in L^p(M,g; T^{*\otimes |\mathbf {i}|} M \otimes E)\,. \end{aligned}$$

(18)

Because of the lack of commutation (in general) of the operators $\nabla _i$, these conditions may be more stringent than in the classical case. To see this more clearly, let us look at the explicit example when $n = 2$, $V = {\mathbb {C}}^2$, $A_1 = 0$, and

$$\begin{aligned} A_2 \mathrel {\ := \ }\left( \begin{array}{cc} 0 &{} e^{\imath x_1^3}\\ - e^{-\imath x_1^3} &{} 0 \end{array} \right) \,. \end{aligned}$$

(19)

(Notice that $A_2^* = - A_2$.) Then, $H^1_{\nabla }(M; E) = H^1(M; E)$, but $H^2_{\nabla }(M; E) \ne H^2(M; E)$. Indeed, let us use Eq. (16). We shall write $\nabla _{\mathbf {i}} = \nabla _{(1,1)} = \nabla _{e_1}^2$ when $\mathbf {i} = (1, 1)$, and so on, according to 3.10. Then, we obtain

$$\begin{aligned} \begin{aligned} \nabla _{(1,1)}\xi&=\partial _1^2\xi \,,\quad \nabla _{(2,1)}\xi =\partial _2\partial _1\xi + \left( e^{\imath x_1^3}\partial _1\xi _2, -e^{-\imath x_1^3}\partial _1\xi _1 \right) ,\, \\ \nabla _{(1,2)}\xi&=\partial _1\partial _2\xi + \left( 3\imath x_1^2e^{\imath x_1^3}\xi _2 + e^{\imath x_1^3}\partial _1\xi _2,\ 3 \imath x_1^2e^{-\imath x_1^3}\xi _1-e^{-\imath x_1^3}\partial _1\xi _1 \right) \\ \nabla _{(2,2)}\xi&=\partial _2^2\xi + 2\left( e^{\imath x_1^3}\partial _2\xi _2, -e^{-\imath x_1^3}\partial _2\xi _1 \right) -\xi \,. \end{aligned} \end{aligned}$$

See [42, 56] for related results.

To continue our study of covariant Sobolev spaces, we need to take a look at the natural differential operators in our setting, called “$\nabla$-differential operators,” which we introduce in the next section.

4 Global, geometric $\nabla$-differential operators

We now introduce the class of differential operators that we will study, namely the class of $\nabla$-differential operators. Again, one of our main goals is to provide definitions that are independent of local coordinate charts and local trivializations. We shall consider globally defined differential operators on M with smooth coefficients acting on sections of smooth vector bundles. We provide several equivalent definitions. We are especially interested in definitions that do not rely on local coordinates (unlike the classical one).

As mentioned already, all our vector bundles will be smooth. Also, we shall consider differential operators with smooth coefficients, unless otherwise mentioned. The case of differential operators with non-smooth coefficients is to a large extent very similar. In order to define our $\nabla$-differential operators, we do not need our vector bundles to have metrics; however, in order to obtain mapping properties for these operators, we will need to assume that the coefficient are suitably bounded and hence that our vector bundles are endowed with Hermitian metrics and metric preserving connections.

Recall that $V^{\otimes k} \mathrel {\ := \ }V \otimes V \otimes \ldots \otimes V$ (k-times) and that $V^{\otimes 0} \mathrel {\ := \ }{\mathbb {C}}\,.$ It will be convenient to consider the “truncated Fock space”

$$\begin{aligned} {\mathcal {F}}^M_\mu (E) \mathrel {\ := \ }\oplus _{j=0}^\mu \, T^{*\otimes j}M \otimes E \,. \end{aligned}$$

(20)

We endow the truncated Fock space ${\mathcal {F}}^M_m(E)$ with the induced connection from E and $T^*M$. Given a measurable section a of the morphism bundle ${\text {Hom}}( {\mathcal {F}}_\mu ^M (E); F)$, we shall write $a^{[j]}$ for the corresponding components of a in ${\text {Hom}}(T^{*\otimes j} M \otimes E; F)$, $j=0,\ldots ,\mu$, using Eq. (20). We shall also write

$$\begin{aligned} a \cdot \nabla ^{tot} \mathrel {\ := \ }\sum _{j=0}^{\mu }a^{[j]}\nabla ^j \,. \end{aligned}$$

(21)

Definition 4.1

Let $E, F \rightarrow M$ be vector bundles, with E endowed with a connection and let $a = (a^{[0]}, a^{[1]}, \ldots , a^{[\mu ]})$ be measurable section of ${\text {Hom}}({\mathcal {F}}_\mu ^M (E); F)$. We let $\nabla ^0 = id$. A $\nabla$ -differential operator (on E with values in F) is a map

$$\begin{aligned} P \, = \,a \cdot \nabla ^{tot} \mathrel {\ := \ }\sum _{j=0}^{\mu }a^{[j]}\nabla ^j: {{\mathcal {C}}}^{\infty }(M;E) \rightarrow {{\mathcal {C}}}^{\infty }(M; F) \,. \end{aligned}$$

We let ${\text {ord}}(P)$ denote the least $\mu$ for which such a writing exists and call it the order of P. Suitable extensions by continuity of P will also be called $\nabla$-differential operators and will be denoted by the same letter.

We note that, in order to define $\nabla$-differential operators on E with values in F, only E needs to be endowed with a connection. Moreover, neither E nor F need to be endowed with a metric and the connection on E need not be metric preserving (although most of the time it will be).

Notation 4.2

Let us introduce now further notation and terminology pertaining to a $\nabla$-differential operator $P := a \cdot \nabla ^{tot} := \sum _{j=0}^{\mu }a^{[j]}\nabla ^j$ (as in Definition 4.1).

• If $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}({\mathcal {F}}_\mu ^M (E); F))$, we shall say that P has ${{\mathcal {C}}}^{\infty }$-coefficients. The set of such operators is denoted ${\text {Diff}}_{\nabla }^\mu (M; E, F)$.

  Assume now also that $E, F \in {\mathcal {H}}(M)$.

• If $a \in W_{\nabla }^{\ell ,\infty }(M; {\text {Hom}}({\mathcal {F}}_\mu ^M (E); F))$, we shall say that P has coefficients in $W_{\nabla }^{\ell ,\infty }$.

• If, in fact, $\ell = 0$, we shall say that P has bounded coefficients.

• On the other hand, if $\ell = \infty$, we shall say that P has totally bounded (or $W_{\nabla }^{\infty , \infty }$) coefficients. The set of operators with such coefficients is denoted ${\text {Diff}}_{b, \nabla }^\mu (M; E, F)$.

Unless stated otherwise, all our differential operators will have smooth coefficients. Thus, by “a $\nabla$-differential operator,” we will mean a “$\nabla$-differential operator with smooth coefficients.” The case of operators with non-smooth coefficients will only rarely be considered, but it usually can be treated in a similar way. Here are some comments.

Remark 4.3

We use the notation of Definition 4.1.

• (1) If $j \ge 2$, the coefficient $a^{[j]}$ in $a = (a^{[0]}, a^{[1]}, \ldots , a^{[\mu ]}) \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}({\mathcal {F}}_\mu ^M (E); F))$ is not uniquely determined by the map $P = a \cdot \nabla ^{tot} := \sum _{j=0}^{\mu } a^{[j]} \nabla ^j :{{\mathcal {C}}}^{\infty }(M; E) \rightarrow {{\mathcal {C}}}^{\infty }(M; F)$.

• (2) Peetre’s Theorem [40, 57] characterizes the explicit structure of $\nabla$-differential operators and shows that such an operator is, indeed, a classical differential operator in any coordinate chart.

• (3) Note that in our approach avoiding local coordinates, one also needs to consider vector valued Sobolev spaces (with values in tensor products of the cotangent bundle) even if one is interested only in scalar equations.

We have the following “easy” continuities.

Lemma 4.4

Let $E \rightarrow M$ be a vector bundle. We assume that $E \in {\mathcal {H}}(M)$ (finite dimensional, Hermitian with metric preserving connection), to be able to define Sobolev spaces. Let $\ell \in {\mathbb {Z}}_+$ be given and let $P := a \cdot \nabla ^{tot}$ be a $\nabla$-differential operator with coefficients in $W_{\nabla }^{\ell , \infty }$ (see Definition 4.1). Then, for all $s \in [0, \ell ]$, the induced map

$$\begin{aligned} P \, = \,\sum _{j=0}^\mu a_j \nabla ^j :{W_{\nabla }^{s+\mu , p}}(M; E) \, \rightarrow \, W_{\nabla }^{s, p}(M; F) \end{aligned}$$

is well-defined and continuous.

Proof

The continuity for $s \in [0, \ell ] \cap {\mathbb {Z}}_+$ follows by combining Lemma 3.6 with Proposition 3.7, which gives the continuity of the maps

$$\begin{aligned} W_{\nabla }^{ s, \infty }(M; {\text {Hom}}( TM^{*\otimes j} \otimes E; F)) \otimes W_{\nabla }^{ s ,p}(M; T^*M^{\otimes j}\otimes E) \, \rightarrow \, W_{\nabla }^{ s, p}(M; F)\, . \end{aligned}$$

In particular, P is well defined with the stated domain and range for $s \in [0, \ell ] \cap {\mathbb {Z}}_+$. For $s \in [0, \ell ]$ non-integer, the result follows by interpolation, since the non-integer Sobolev spaces are defined by interpolation, see Sect. 3.1.2. $\square$

We want to extend this mapping property to other spaces. It extends to $\ell \ge 0$ real immediately by interpolation, since our fractional order Sobolev spaces were defined by interpolation, see, for instance, [49, 62], or [64, Chapter 2]. To extend to $\ell \le 0$, we shall need also the following basic algebraic properties.

Proposition 4.5

We use the notation introduced in 4.2.

• (i) For any $\mu \in {\mathbb {Z}}_+$, the spaces ${\text {Diff}}_{\nabla }^{\mu }(M; E, F)$ and ${\text {Diff}}_{b, \nabla }^{\mu }(M; E, F)$ are linear vector spaces.

• (ii) Let $P \in {\text {Diff}}_{\nabla }^j(M; E, F)$ and $Q \in {\text {Diff}}_{\nabla }^N(M; F, G)$, then $QP \in {\text {Diff}}_{\nabla }^{N+j}(M; E, G)$.

• (iii) If P and Q have $W_{\nabla }^{\infty , \infty }$–coefficients, then QP has $W_{\nabla }^{\infty , \infty }$-coefficients as well.

• (iv) In particular,

  $$\begin{aligned} {\text {Diff}}_{\nabla }^\infty (M; E) \mathrel {\ := \ }\bigcup _\mu {\text {Diff}}_{\nabla }^\mu (M; E, E) \text{ and } {\text {Diff}}_{b, \nabla }^\infty (M; E) \mathrel {\ := \ }\bigcup _\mu {\text {Diff}}_{b, \nabla }^\mu (M; E, E) \end{aligned}$$

  are algebras.

Proof

The statement (i) follows right away from the definitions of the spaces ${\text {Diff}}_{b, \nabla }^{\mu }(M; E, F) \subset {\text {Diff}}_{\nabla }^{\mu }(M; E, F)$ and the fact that the spaces of $W_{\nabla }^{\infty , \infty }$-sections (of various vector bundles over M) are vector spaces.

Next, by linearity (proved in part (i)), it is enough to assume that $Q = b \nabla ^j$ and $P = a \nabla ^N$, where a and b are suitable sections of endomorphism bundles, as in Definition 4.1. We shall prove the statements (ii) and (iii) by induction on j.

Let us prove the statement (ii). If $j = 0$, then $QP = ba \nabla ^N$ where ba is a smooth endomorphism, and hence, the statement is true. Next, let us assume that the statement is true for $j-1 \ge 0$ and let us prove it for j. Remark 2.2 gives

$$\begin{aligned} (b \nabla ^j) \circ (a \nabla ^N) (u) \, = \,b \nabla ^{j-1} \big [\nabla (a)\nabla ^N u + (1 \otimes a)\nabla ^{N+1}u \big ]\,. \end{aligned}$$

(22)

We know that if $a \in {{\mathcal {C}}}^{\infty }$, then $\nabla (a)$ and $1 \otimes a$ are also in ${{\mathcal {C}}}^{\infty }$. Hence, $\nabla (a)\nabla ^N + (1 \otimes a)\nabla ^{N+1}$ is also a $\nabla$-differential operator with smooth coefficients and this proves (ii) by induction.

For the statement (iii), let us assume that P and Q have $W_{\nabla }^{\infty , \infty }$-coefficients and prove that QP has the same property. We then proceed in exactly the same way as in the proof of (ii), using the formula (22). So assume $a, b \in W_{\nabla }^{\infty , \infty }$. When $j = 0$, we obtain similarly that $QP = ba\nabla ^N$ and ba is in $W_{\nabla }^{\infty , \infty }$ due to Proposition 3.7. For $j > 0$, we notice that $(\nabla a)\nabla ^N + (1 \otimes a)\nabla ^{N+1}$ has $W_{\nabla }^{\infty , \infty }$ coefficients (if $a \in W_{\nabla }^{\infty , \infty }$, then $\nabla (a)$ and $1 \otimes a$ are also in $W_{\nabla }^{\infty , \infty }$), which yields the induction step.

The statement (iv) follows right away from the previous two. $\square$

We can now prove the independence on the connection $\nabla$ of our differential operators with smooth coefficients (no boundedness assumption). We first notice that ${{\mathcal {C}}}^{\infty }(M; E)$ does not depend on the connection on E.

Proposition 4.6

Let $E \rightarrow M$ be a fixed vector bundle and let ${{\widetilde{\nabla }}} = \nabla + A$, for some $A \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E; T^*M \otimes E))$. Then, ${\text {Diff}}_{\nabla }^\mu (M; E, F) = {\text {Diff}}_{{{\widetilde{\nabla }}}}^\mu (M; E, F)$, for all $\mu \in {\mathbb {Z}}_+$ and all vector bundles $F \rightarrow M$.

Proof

Let us observe that if we are given two connections, ${{\widetilde{\nabla }}}$ and $\nabla$ on E, then ${{\widetilde{\nabla }}} - \nabla =: A \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E; T^*M \otimes E) )$. Hence, ${{\widetilde{\nabla }}} \in {\text {Diff}}_{\nabla }^\mu (M; E, F)$. The composition property of Proposition 4.5 then yields that all operators of the form $a\cdot {{\widetilde{\nabla }}}^{tot}$ are in ${\text {Diff}}_{\nabla }^\mu (M; E, F)$. Hence ${\text {Diff}}_{{{\widetilde{\nabla }}}}^\mu (M; E, F) \subset {\text {Diff}}_{\nabla }^\mu (M; E, F)$. By symmetry, we obtain the other inclusion, and hence the equality ${\text {Diff}}_{\nabla }^\mu (M; E, F) = {\text {Diff}}_{{{\widetilde{\nabla }}}}^\mu (M; E, F)$. $\square$

In view of this result, we may drop the index $\nabla$ in the notation for differential operators. We shall thus use the following notation.

Notation 4.7

We let ${\text {Diff}}^{\mu }(M; E, F)$ denote the set of $\nabla$-differential operators ${{\mathcal {C}}}^{\infty }(M; E) \rightarrow {{\mathcal {C}}}^{\infty }(M; F)$ of order $\le \mu$ with smooth coefficients. However, we keep $\nabla$ in the notation for ${\text {Diff}}_{b, \nabla }^{\mu }(M; E, F)$, the set of $\nabla$-differential operators of order $\le \mu$ with $W_{\nabla }^{\infty , \infty }$-coefficients. We shall also write:

• ${\text {Diff}}^\mu (M; E) := {\text {Diff}}^\mu (M; E, E)$ and ${\text {Diff}}_{b, \nabla }^\mu (M; E) := {\text {Diff}}_{b, \nabla }^\mu (M; E, E)$;

• ${\text {Diff}}^\infty (M; E) = \cup _\mu {\text {Diff}}^\mu (M; E)$ and ${\text {Diff}}_{b, \nabla }^\infty (M; E) = \cup _\mu {\text {Diff}}_{b, \nabla }^\mu (M; E)$ (they were seen to be algebras in the last proposition);

• ${\text {Diff}}^\mu (M) := {\text {Diff}}^\mu (M; {\mathbb {C}})$ and ${\text {Diff}}_{b, \nabla }^\mu (M) := {\text {Diff}}_{b, \nabla }^\mu (M; {\mathbb {C}})$ (that is, we omit E and F from the notation when $E = F = {\mathbb {C}}$).

We now consider the case of totally bounded coefficients. In this case, our spaces will depend on the choice of connection.

Proposition 4.8

Let $E \in {\mathcal {H}}(M)$, $A = - A^* \in {{\mathcal {C}}}^{\infty }(M; T^*M \otimes {\text {End}}(E) )$, and ${{\widetilde{\nabla }}} : = \nabla + A$.

• (i) If $\ell \in {\mathbb {N}}$ and $A \in W_{\nabla }^{\ell -1, \infty }(M; {\text {Hom}}(E; T^*M \otimes E) )$, then there exists $c_{\ell , p} \ge 1$ that depends only on $\Vert A\Vert _{W_{\nabla }^{\ell -1,\infty }(M)}$ such that, for all $u \in {{\mathcal {C}}}^{\infty }(M; E)$,

  $$\begin{aligned} c_{\ell , p}^{-1} \Vert u\Vert _{W_{\nabla }^{\ell , p}(M; E)} \le \Vert u\Vert _{W_{{{\widetilde{\nabla }}}}^{\ell , p}(M; E)} \le c_{\ell , p} \Vert u\Vert _{W_{\nabla }^{\ell , p}(M; E)}\,. \end{aligned}$$

  This holds also for $\ell = 0$ and $c_{0, p} = 1$ with no condition on A. Consequently,

  $$\begin{aligned} W_{\nabla }^{\ell , p}(M; E) \, = \,W_{{{\widetilde{\nabla }}}}^{\ell , p}(M; E)\,, \quad \ell \ge 0 \,. \end{aligned}$$

• (ii) We have ${\text {Diff}}_{b, \nabla }^\mu (M; E, F) = {\text {Diff}}_{b, \widetilde{\nabla }}^\mu (M; E, F)$ for all $\mu \in {\mathbb {Z}}_+$ and all $F \in {\mathcal {H}}(M)$ if, and only if, $A \in W_{\nabla }^{\infty , \infty }(M; T^*M \otimes {\text {End}}(E) )$.

Proof

To prove (i), we proceed by induction on $\ell$ using Propositions 3.7 and 4.5. First, we have that $W_{\nabla }^{0, p}(M; E)=L^p(M,g; E)= W_{{{\widetilde{\nabla }}}}^{0, p}(M; E)$ with the same norms, since the definition of these spaces (and of their norms) does not involve the connection. This gives the result for $\ell =0$ with $c_{0,p}=1$. Assume now that (i) holds for $\ell - 1 \ge 0$ and show it for $\ell$. The definition of the norm in $W_{\nabla }^{\ell , p}(M;E)$, Proposition 3.7, and the induction hypothesis imply that

$$\begin{aligned} \Vert u\Vert _{W_{\nabla }^{\ell , p}}&\le \Vert u\Vert _{W_{\nabla }^{\ell -1,p}} + \Vert \nabla u\Vert _{W_{\nabla }^{\ell -1,p}} \\&= \Vert u\Vert _{W_{\nabla }^{\ell -1,p}} + \Vert {{\widetilde{\nabla }}} u - A u\Vert _{W_{\nabla }^{\ell -1,p}} \\&\le c_{\ell -1,p} \Vert u\Vert _{W_{{{\widetilde{\nabla }}}}^{\ell -1,p}} + \Vert {{\widetilde{\nabla }}} u\Vert _{W_{\nabla }^{\ell -1,p}} + \Vert A u \Vert _{W_{\nabla }^{\ell -1,p}} \\&\le 2 c_{\ell -1,p} \Vert u \Vert _{W_{\widetilde{\nabla }}^{\ell , p}} + 3^{\ell -1}\Vert A\Vert _{W_{\nabla }^{\ell -1,\infty }} \Vert u \Vert _{W_{\nabla }^{\ell -1,p}} \\&\le c_{\ell -1,p} \Big [2+ 3^{\ell -1}\Vert A\Vert _{W_{\nabla }^{\ell -1,\infty }} \Big ] \Vert u \Vert _{W_{{{\widetilde{\nabla }}}}^{\ell ,p}} \,, \end{aligned}$$

Since we can also bound $\Vert A\Vert _{W_{{{\widetilde{\nabla }}}}^{\ell -1,\infty }} \le c_{\ell -1 , \infty } \Vert A\Vert _{W_{\nabla }^{\ell -1,\infty }}$, by the induction hypothesis, the second of the desired inequalities for the norms follows by symmetry for $c_{\ell , p} := c_{\ell -1,p}\big [2 + 3^{\ell -1} c_{\ell -1, \infty } \Vert A\Vert _{W_{\nabla }^{\ell -1,\infty }} \big ].$ In particular, we deduce the equality $W_{\nabla }^{\ell , p}(M; E) \, = \,W_{{{\widetilde{\nabla }}}}^{\ell , p}(M;E)$ (with equivalence of the norms).

Let us now prove (ii). The equality of the spaces of differential operators if A is totally bounded (i.e. in $W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; T^*M \otimes E) )$ follows from Propositions 3.7 and 4.5 and (i) just proved. Indeed, Proposition 4.5 (iii) combined with the assumption that $A \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; T^*M \otimes E) )$ shows that ${{\widetilde{\nabla }}}^j = (\nabla +A)^j \in {\text {Diff}}_{b, \nabla }^j(M; E, T^{*\otimes j}M \otimes E)$, for all $0\le j \in {\mathbb {N}}$. Moreover, any operator P in ${\text {Diff}}_{b, \widetilde{\nabla }}^\mu (M; E, F)$ has the form $P =\sum _{j=0}^{\mu }\widetilde{a}^{[j]}{{\widetilde{\nabla }}}^j$, where the coefficients ${{\widetilde{a}}}^{[j]}$ are in $W_{\nabla }^{\infty , \infty }$. Thus, P can be written in the equivalent form $P=\sum _{j=0}^{\mu }{\widetilde{a}}^{[j]}(\nabla +A)^j=\sum _{j=0}^{\mu }b^{[j]}\nabla ^j$, where $b^{[j]}$ are in $W_{\nabla }^{\infty , \infty }$ as well, by Proposition 3.7. This shows the inclusion ${\text {Diff}}_{b, {{\widetilde{\nabla }}}}^\mu (M; E, F)\subseteq {\text {Diff}}_{b, \nabla }^\mu (M; E, F)$. The converse inclusion follows by symmetry since $A \in W_{{{\widetilde{\nabla }}}}^{\infty , \infty }(M; {\text {Hom}}(E; T^*M \otimes E))$, by (i).

Next we assume that ${\text {Diff}}_{b, \nabla }^\mu (M; E, T^*M \otimes E) = {\text {Diff}}_{b, {{\widetilde{\nabla }}}}^\mu (M; E, T^*M \otimes E)$. Then, the operators $\nabla$ and ${{\widetilde{\nabla }}} =\nabla +A$ belong to ${\text {Diff}}_{b, \nabla }^1(M; E, T^*M \otimes E)$, and, thus, $A = {{\widetilde{\nabla }}} - \nabla \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; T^*M \otimes E) )$, since the ${\text {Diff}}_{b, \nabla }^1(M; E, T^*M \otimes E)$ is a vector space. This proves the converse statement in (ii) and hence completes the proof. $\square$

5 Mixed differential operators and totally bounded vector fields

In this section, we consider a different approach to differential operators, using what we call “mixed differential operators,” since they will be used to relate the $\nabla$-differential operators of the previous section to the classical differential operators. One of the main results is that the classes of mixed and $\nabla$-differential operators coincide. Under certain circumstances, this holds true also if we require totally bounded coefficients. More precisely, we introduce the “Fréchet finiteness condition” (FFC) and we show that if (FFC) is satisfied, then the classes of mixed and $\nabla$-differential operators with totally bounded coefficients coincide.

5.1 Mixed differential operators

In this subsection, we introduce mixed differential operators and we show that, as long as we do not impose growth conditions on the coefficients, the set of mixed differential operators is the same as the set of $\nabla$-differential operators. It is known [52, p. 71] that every vector bundle $E \rightarrow M$ on a manifold has a vector bundle embedding $\Phi : E \rightarrow M \times {\mathbb {R}}^N$ into a trivial bundle. In this subsection, we shall use the existence of such an embedding for $E = TM$ and we shall deduce some geometric consequences.

Remark 5.1

Let $\Phi : TM \rightarrow M \times {\mathbb {R}}^N$ be a smooth vector bundle embedding of the tangent bundle into a trivial vector bundle. We endow the trivial vector bundle with the constant metric. Then, the transpose $\Phi ^\top : M \times {\mathbb {R}}^N \rightarrow TM$ is onto. (The transpose is the analog of the adjoint, but in the real case.) Moreover, $\Phi ^\top \Phi$ is a smooth, invertible section of ${\text {End}}(TM)$. Let $\Psi := (\Phi ^\top \Phi )^{-1} \Phi ^\top$, so that $\Psi \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}({\mathbb {R}}^N ; TM))$ and $\Psi \Phi = 1$. Let

$$\begin{aligned} Z_1 \mathrel {\ := \ }\Psi (e_1),\ Z_2 \mathrel {\ := \ }\Psi (e_2),\ \ldots \ ,\ Z_N \mathrel {\ := \ }\Psi (e_N) \, \in \, {{\mathcal {C}}}^{\infty }(M; TM) \end{aligned}$$

be the vector fields corresponding to the constant basis $(e_j)_{j=1}^N$ of ${\mathbb {R}}^N$ via $\Phi ^\top$. Since $\Psi \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}({\mathbb {R}}^N; TM))$, we have that $Z_j$ are all in ${{\mathcal {C}}}^{\infty }(M; TM)$. Let

$$\begin{aligned} \xi _j \mathrel {\ := \ }p_j \circ \Phi : TM \rightarrow {\mathbb {R}}\end{aligned}$$

be the 1-form obtained from the projection of ${\mathbb {R}}^N$ onto the jth component. Then $\xi _j \in {{\mathcal {C}}}^{\infty }(M; T^*M)$ and the relation $\Psi \Phi = 1$ gives, for every $X \in {{\mathcal {C}}}^{\infty }(M; TM)$,

$$\begin{aligned} X \, = \,\Psi (\Phi (X)) \, = \,\Psi \Big (\sum _{j=1}^N \xi _j(X) e_j \Big ) \, = \,\sum _{j=1}^N \xi _j(X) Z_j\,. \end{aligned}$$

Let $\omega \in {{\mathcal {C}}}^{\infty }(M; T^*M).$ By evaluating $\omega$ in the above relation, we obtain that

$$\begin{aligned} \omega (X) = \sum _{j=1}^N \xi _j(X) \omega (Z_j) \,, \end{aligned}$$

and hence we have the dual relation $\omega \, = \,\sum _{j=1}^N \omega (Z_j) \xi _j\,.$ In particular, ${{\mathcal {C}}}^{\infty }(M; TM) \, = \,\sum _{j=1}^N {{\mathcal {C}}}^{\infty }(M) Z_j$ and ${{\mathcal {C}}}^{\infty }(M; T^*M) \, = \,\sum _{j=1}^N {{\mathcal {C}}}^{\infty }(M) \xi _j.$

The following consequence of this remark will be useful. We shall write $\mathbf {k} = (k_1, k_2, \ldots , k_\mu )$, $1 \le k_1, k_2, \ldots k_\mu \le N$.

Lemma 5.2

Any measurable section w of $T^{*\otimes \mu }M \otimes E$ can be written as

$$\begin{aligned} w \, = \,\sum _{|\mathbf {k}| = \mu } \xi _{k_1} \otimes \xi _{k_2} \otimes \ldots \otimes \xi _{k_\mu } \otimes i_{Z_{k_\mu }}i_{Z_{k_{\mu - 1}}} \ldots i_{Z_{k_1}}(w)\,, \end{aligned}$$

where $\mathbf {k} = (k_1, k_2, \ldots , k_\mu ) \in \{1, 2, \ldots , N\}^\mu$.

Proof

Let us prove our result by induction on $\mu$. For a 1-form, we have $\omega (Z_j) = \langle \omega ,Z_j\rangle = i_{Z_j}(\omega )$. Remark 5.1 then yields the relation

$$\begin{aligned} \langle \omega , X \rangle \, = \,\omega (X) \, = \,\sum _{j=1}^N \xi _j(X) \omega (Z_j) \, = \,\big \langle \, \sum _{j=1}^N i_{Z_j}(\omega ) \xi _j , X \, \big \rangle \,. \end{aligned}$$

Hence, if v is a section of E, we obtain that

$$\begin{aligned} \omega \otimes v \, = \,\sum _{j=1}^N i_{Z_j}(\omega ) \xi _j \otimes v \, = \,\sum _{j=1}^N \xi _j \otimes i_{Z_j} (\omega \otimes v) \,. \end{aligned}$$

This proves our result for $\mu = 1$. Let us assume next that our result is true for $\mu -1 \ge 1$ and let us prove it for $\mu$. Let v be a section of $T^{*\otimes (\mu -1)}M \otimes E$ and $\omega$ be a one form. Then, the calculations for the case $\mu = 1$ combined with the case $\mu -1$ for v give (using the notation $\mathbf {k} = (k_1, \mathbf {k'})$ and $k_1 =j$)

$$\begin{aligned} \omega \otimes v&\, = \,\sum _{j=1}^N \xi _j \otimes i_{Z_j}(\omega ) v\\&\, = \,\sum _{j=1}^N \xi _j \otimes \sum _{|\mathbf {k'}| = \mu -1} \xi _{k_2} \otimes \ldots \otimes \xi _{k_\mu } \otimes i_{Z_{k_\mu }} \ldots i_{Z_{k_2}}\big ( i_{Z_j} (\omega \otimes v) \big )\,, \end{aligned}$$

which is the desired result. $\square$

We now take a look at a different global definition of differential operators.

Definition 5.3

We let $\widetilde{{\text {Diff}}}_{\nabla }^\mu (M; E, F)$ be the set of all linear operators of order $\le \mu$ linearly generated by $a \nabla _{X_1} \ldots \nabla _{X_r}$, $0 \le r \le \mu$, $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E, F))$, $X_j \in {{\mathcal {C}}}^{\infty }(M; TM)$. An operator P of this type will be called a mixed differential operator of order $\le \mu$. If $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E, F))$ and all $X_j \in {\mathcal {W}}_b(M) := W_{\nabla }^{\infty , \infty }(M; TM)$, then P is called a mixed differential operator of order $\le \mu$ with $W_{\nabla }^{\infty , \infty }$ -coefficients, and we let $\widetilde{{\text {Diff}}}_{b, \nabla }^\mu (M; E, F)$ denote the set of all such operators.

As we will see in Sect. 5.3, mixed differential operators are, sometimes, easier to deal with than $\nabla$-differential operators and form a convenient intermediate class between $\nabla$- and classical differential operators. The following lemma is standard, except for the fact that the system $(Z_j)$ is only a system of generators of ${{\mathcal {C}}}^{\infty }(M; TM)$ as a ${{\mathcal {C}}}^{\infty }(M)$-module, and not a basis. Let ${\text {div}}:= - d^\prime$ be the negative of the dual map $d^\prime : {{\mathcal {C}}}^{\infty }(M; TM) \rightarrow {{\mathcal {C}}}^{\infty }(M)$ of $d : {{\mathcal {C}}}^{\infty }(M) \rightarrow {{\mathcal {C}}}^{\infty }(M; T^*M)$, as usual.

Lemma 5.4

Let $Z_j$ and $\xi _j$ be as in Remark 5.1.

• (i) If $X \in {{\mathcal {C}}}^{\infty }(M; TM)$, then $\nabla _X \in {\text {Diff}}^{1}(M; E)$.

• (ii) $\nabla ^E = \sum _{j=1}^N \xi _j \otimes \nabla ^E_{Z_j} : {{\mathcal {C}}}^{\infty }(M; E) \rightarrow {{\mathcal {C}}}^{\infty }(M; T^*M \otimes E)$.

• (iii) For any $X \in {{\mathcal {C}}}^{\infty }(M; TM)$, we have ${\text {div}}(X) \in {{\mathcal {C}}}^{\infty }(M)$.

• (iv) We have $\nabla _{Z_i}Z_j= \sum _{k} G_{ij}^k Z_k$, where $G_{ij}^k \in {{\mathcal {C}}}^{\infty }(M)$.

• (v) We have $[Z_i, Z_j] = \sum _{k} L_{ij}^k Z_k$, where $L_{ij}^k \in {{\mathcal {C}}}^{\infty }(M)$.

Proof

Let $Z_1, Z_2, \ldots , Z_N \in {{\mathcal {C}}}^{\infty }(M; TM)$ be the vector fields and $\xi _1, \xi _2, \ldots , \xi _N \in {{\mathcal {C}}}^{\infty }(M; T^*M)$ be the 1-forms introduced in Remark 5.1. Let $i_X : T^*M \otimes E \rightarrow E$, $i_X(u) = \langle X, u \rangle$, be the contraction with the vector $X \in {{\mathcal {C}}}^{\infty }(M ;TM)$.

To prove (i), we notice that $i_X \in {{\mathcal {C}}}^{\infty }(M; T^*M \otimes {\text {End}}(E))$, since $X \in {{\mathcal {C}}}^{\infty }(M; TM)$, and hence $\nabla _X = i_X \circ \nabla$ is a $\nabla$-differential operator with smooth coefficients, by definition.

To prove (ii), let $u \in {{\mathcal {C}}}^{\infty }(M; E)$ and $X \in {{\mathcal {C}}}^{\infty }(M; TM)$ be arbitrary. Then, the formula $X = \sum _{j=1}^N \xi _j(X) Z_j$ of Remark 5.1 gives

$$\begin{aligned} \langle X, \nabla ^E(u) \rangle \, = \,\nabla ^E_X (u) \, = \,\sum _{j=1}^N \xi _j(X) \nabla ^E_{Z_j}(u) \, = \,\Big \langle X, \sum _{j=1}^N \xi _j \otimes \nabla ^E_{Z_j}(u) \Big \rangle \,. \end{aligned}$$

Since $u \in {{\mathcal {C}}}^{\infty }(M ; T^*M)$ and $X \in {{\mathcal {C}}}^{\infty }(M; TM)$ were arbitrary, the result follows.

We recall the proof of the well-known relation (iii) for the benefit of the reader. Let $X_1, X_2, \ldots , X_n$ be a local orthonormal basis of TM. Since the map $T^*M \ni \xi \rightarrow \big ( (\xi , X_j) \big )_{j=1}^n$ is an isometry, we then obtain that $\sum _{j, k, l=1 }^n \xi _k (X_j) \xi _l(X_j) = (\xi _k, \xi _l)$. Therefore we obtain

$$\begin{aligned} {\text {div}}(X)&\, = \,\mathop {\mathrm {tr}}(\nabla X)\\&\, = \,\sum _{j=1}^n (\nabla _{X_j}X , X_j)\\&\, = \,\sum _{j, k, l=1 }^n \xi _k (X_j) \xi _l(X_j) (\nabla _{Z_k}X, Z_l)\\&\, = \,\sum _{j, k, l=1}^n (\xi _k, \xi _l) (\nabla _{Z_k}X, Z_l) \ \in \, {{\mathcal {C}}}^{\infty }(M)\,. \end{aligned}$$

To prove (iv), we notice that since $\nabla _{Z_i}Z_j \in {{\mathcal {C}}}^{\infty }(M; TM)$, we have $\nabla _{Z_i}Z_j = \sum _{k=1}^N \xi _k(\nabla _{Z_i}Z_j) Z_k$, by Remark 5.1, and hence we can take $G_{ij}^k := \xi _k(\nabla _{Z_i}Z_j)$, which is in ${{\mathcal {C}}}^{\infty }(M)$. For (v), we proceed in exactly the same way since the Lie bracket of vector fields $[Z_i, Z_j] \in {{\mathcal {C}}}^{\infty }(M; TM)$. $\square$

We have the following generation property for mixed differential operators.

Proposition 5.5

Let $\mu ,\nu \in {\mathbb {Z}}_+$.

• (i) $\widetilde{{\text {Diff}}}_{\nabla }^{\nu }(M; F, G) \widetilde{{\text {Diff}}}_{\nabla }^\mu (M; E, F) \subset \widetilde{{\text {Diff}}}_{\nabla }^{\mu + \nu }(M; E, G)$.

• (ii) $\widetilde{{\text {Diff}}}_{\nabla }^\mu (M; E, F) = {\text {Diff}}^\mu (M; E, F)$.

• (iii) Let $Z_1, Z_2, \ldots , Z_N \in {{\mathcal {C}}}^{\infty }(M)$ be a systems of generators for ${{\mathcal {C}}}^{\infty }(M)$ as in Remark 5.1, then ${\text {Diff}}^\mu (M; E, F)$ is linearly generated by $a \nabla _{Y_1}\nabla _{Y_2} \ldots \nabla _{Y_r}$, where $r \le \mu$, $Y_1, Y_2, \ldots , Y_r \in \{Z_1, Z_2, \ldots , Z_N\}$ and $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E, F))$.

Proof

We prove the first statement by induction on $\mu$. For $\mu = 0$, the property (i) follows from the multiplication properties

$$\begin{aligned} {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(F; G)) {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E; F)) \subset {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E; G)) \,. \end{aligned}$$

The induction step is obtained using the equation $\nabla _{X} a = \nabla _X(a) + a \nabla _X$.

To prove (ii), let us notice that Lemma 5.4(i) states that $\nabla _X \in {\text {Diff}}^1(M; E, F)$. The composition property of Proposition 4.5(ii) yields the inclusion ${{\widetilde{{\text {Diff}}}}}_\nabla ^\mu (M; E, F)\subset {\text {Diff}}^\mu (M; E, F)$. Let us prove now the opposite inclusion.

Let $\tau _\xi (\zeta ) := \xi \otimes \zeta ,$ as in Lemma 3.5. Then, $\nabla \, = \,\sum _{i=1}^N \tau _{\xi _i}\nabla _{Z_i},$ by Lemma 5.4(ii). This gives $\nabla \in {\widetilde{{\text {Diff}}}}_\nabla ^1(M; E, T^*M \otimes E)$. Part (i), already proved, then gives by induction on j that $a \nabla ^j \in {{\widetilde{{\text {Diff}}}}}_\nabla ^\mu (M; E, F)$ if $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(T^{* \otimes j}M \otimes E; F))$ and $j \le \mu$. Therefore, ${\text {Diff}}^\mu (M; E, F) \subset \widetilde{\text {Diff}}_\nabla ^\mu (M; E, F)$. Hence, we have equality.

Let ${\mathcal {D}}_\mu$ be the linear span of $a \nabla _{Y_1}\nabla _{Y_2} \ldots \nabla _{Y_r}$, where $Y_1, Y_2, \ldots , Y_r \in \{Z_1, Z_2, \ldots , Z_N\}$, $r \le \mu$, and $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E, F))$. In view of (ii) just proved, it is enough to prove that ${\mathcal {D}}_\mu = {\text {Diff}}^\mu (M; E, F)$. To this end, let $Q := a \nabla _{Y_1}\nabla _{Y_2} \ldots \nabla _{Y_r}$, where $Y_1, Y_2, \ldots , Y_r \in {{\mathcal {C}}}^{\infty }(M; TM )$, $r \le \mu$, and $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E, F))$. We shall prove, by induction on r, that $Q \in {\mathcal {D}}_\mu$, that is, that Q is a linear combination of terms of the same kind, but with all $Y_j \in \{Z_1, Z_2, \ldots , Z_N\}$. By induction, we can assume that this is true for products of up to $r - 1$ covariant derivatives. The induction step is obtained using the equation $\nabla _{X} a = \nabla _X(a) + a \nabla _X$. Indeed, let us consider then a and b be ${{\mathcal {C}}}^{\infty }$–endomorphisms, $Y_2, Y_3, \ldots , Y_r \in \{Z_1, Z_2, \ldots , Z_N\}$, and $Y_1$ an arbitrary smooth vector field. Then

$$\begin{aligned} Q_1 \mathrel {\ := \ }a \nabla _{Y_1} b \nabla _{Y_2} \ldots \nabla _{Y_r} \, = \,a \big [Y_1(b) + b \sum _{j=1}^N \xi _j(Y_1) \nabla _{Z_j} \big ] \nabla _{Y_2} \ldots \nabla _{Y_r} \end{aligned}$$

We thus have $Q_1 \in {\mathcal {D}}_\mu$. This proves the equality of ${\mathcal {D}}_\mu$ and ${\widetilde{{\text {Diff}}}}^\mu (M; E, F)$. $\square$

We again obtain that if we do not impose growth conditions on the coefficients, then the space $\widetilde{{\text {Diff}}}_{\nabla }^\mu (M; E, F)$ of mixed differential operators of order $\le \mu$ does not depend on $\nabla$, so we will drop $\nabla$ from the notation and write $\widetilde{{\text {Diff}}}^\mu (M; E, F)$, or even ${\text {Diff}}^\mu (M; E, F)$, instead of $\widetilde{{\text {Diff}}}_{\nabla }^\mu (M; E, F)$, since we have proved that these spaces are the same. We also obtain the following consequence.

Corollary 5.6

Let $(Z_j)$, $1 \le j \le N$, $Z_j \in {{\mathcal {C}}}^{\infty }(M; TM)$ be as in Remark 5.1. Then, ${\text {Diff}}^\mu (M; E, F) = \widetilde{{\text {Diff}}}^\mu (M; E, F)$ is linearly generated by $a \nabla ^E_{Z_{k_1}} \ldots \nabla ^E_{Z_{k_r}}$, where $1 \le k_1 \le k_2 \le \ldots \le k_r \le N$, $r \le \mu$, and $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E; F))$.

Proof

We know that ${\text {Diff}}^\mu (M; E, F)$ is linearly generated by terms of the form $a \nabla ^E_{Z_{k_1}} \ldots \nabla ^E_{Z_{k_r}}$, where $k_1, k_2, \ldots , k_r \in \{1, 2, \ldots , N\}$, $r \le \mu$, $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E; F))$. It just remains to show that we can choose the indices k to form a non-decreasing sequence. To this end, we shall use the relation

$$\begin{aligned} R^E(X, Y) \mathrel {\ := \ }[\nabla _X^E, \nabla _Y^E]-\nabla _{[X, Y]}^E \in {{\mathcal {C}}}^{\infty }(M; {\text {End}}(E))\,. \end{aligned}$$

(23)

This shows that, up to lower order terms, we can commute the operators $\nabla _{Z_j}^E$. The proof is completed by induction. $\square$

5.2 Totally bounded vector fields and (FFC)

In this subsection, we introduce and study the Fréchet Finiteness Condition or (FFC), which will be needed in order to control the boundedness of the coefficients of our differential operators. In this subsection, we shall assume that the vector bundle $E \in {\mathcal {H}}(M)$ (we recall that this means that E is finite dimensional, Hermitian with a metric preserving connection).

Recall that we write ${\text {Diff}}_{b, \nabla }^\infty (M) := {\text {Diff}}_{b, \nabla }^\infty (M; {\mathbb {C}})$ for the algebra of scalar $\nabla$-differential operators on M with $W_{\nabla }^{\infty , \infty }(M)$-coefficients introduced in Proposition 4.5(iv) (see also the notation 4.7); “scalar” here refers to the fact that the vector bundle E in that proposition is the trivial vector bundle with fiber ${\mathbb {C}}$. Then, by separating the order zero part of a differential operator, we obtain

$$\begin{aligned} {\text {Diff}}^1_b(M) \, = \,W_{\nabla }^{\infty , \infty }(M) \oplus W_{\nabla }^{\infty , \infty }(M; TM) \,. \end{aligned}$$

Since the space $W_{\nabla }^{\infty , \infty }(M; TM)$ will play an important role in what follows, it will be convenient to simplify the notation by writing

$$\begin{aligned} {\mathcal {W}}_b(M) \mathrel {\ := \ }W_{\nabla }^{\infty , \infty }(M; TM) \end{aligned}$$

as in the Introduction, Eq. (1). Then, ${\mathcal {W}}_b(M)$ is a module over $W_{\nabla }^{\infty , \infty }(M)$ with respect to multiplication by Proposition 3.7. This space (which will turn out to be a Lie algebra) will play an important role in what follows and this section is devoted, to a large extent, to the study of their role in the definition of covariant Sobolev spaces and $\nabla$-differential operators. We have the following result analogous a part of Lemma 5.4.

Lemma 5.7

Let ${\mathcal {W}}_b(M) \mathrel {\ := \ }W_{\nabla }^{\infty , \infty }(M; TM)$ and $E \in {\mathcal {H}}(M)$.

• (i) If $X \in {\mathcal {W}}_b(M)$, then $i_X \in W_{\nabla }^{\infty , \infty }(M; T^*M, {\mathbb {C}})$, and hence $\nabla _X^E \in {\text {Diff}}_{b, \nabla }^{1}(M; E)$.

• (ii) ${\mathcal {W}}_b(M)$ is a Lie algebra, that is, $[X, Y] := XY - YX \in {\mathcal {W}}_b(M)$ for all $X, Y \in {\mathcal {W}}_b(M)$.

• (iii) If $X, Y \in {\mathcal {W}}_b(M)$, then $\nabla _X^{LC} Y \in {\mathcal {W}}_b(M)$.

Proof

We denote all connections with the same letter. To prove (i), we first notice that $\nabla ^k i_X = i_{\nabla ^k X}$, where the contraction with $\nabla ^k X$ is given by Definition 2.1. Then we notice that, if $X \in {\mathcal {W}}_b(M)$, then $i_X$ defines a totally bounded map in view of that Definition, of Corollary 3.5, and of Proposition 3.7. That is, if $X \in {\mathcal {W}}_b(M)$, we obtain that $i_X \in W_{\nabla }^{\infty , \infty }(M; T^*M \otimes {\text {End}}(E))$. Therefore, $\nabla _X = i_X \circ \nabla \in {\text {Diff}}_{b, \nabla }(M; {\text {End}}(E))$, by definition

The property (ii) follows from (i) since ${\text {Diff}}_{b, \nabla }^\infty (M) = {\text {Diff}}_{b, \nabla }^\infty (M; {\mathbb {C}})$ is an algebra (see Proposition 4.5(iv)) and, for $E = M \times {\mathbb {C}}$ with the trivial connection,

$$\begin{aligned}{}[X, Y] \, = \,XY - YX \, = \,\nabla _X^{\mathbb {C}}\nabla _Y^{\mathbb {C}}- \nabla _Y^{\mathbb {C}}\nabla _X^{\mathbb {C}}\,. \end{aligned}$$

Property (iii) follows from (i) and the “easy” mapping property of Lemma 4.4 (which gives, in particular, that $P \in {\text {Diff}}_{b, \nabla }^{\mu }(M; E, F)$ maps $W_{\nabla }^{\infty , \infty }(M; E)$ to $W_{\nabla }^{\infty , \infty }(M; F)$ continuously). $\square$

Definition 5.8

We say that (M, g) satisfies the Fréchet finiteness condition (FFC) if, there exists $N \in {\mathbb {N}}$ and an isometric (vector bundle) embedding

$$\begin{aligned} \Phi : TM \rightarrow M \times {\mathbb {R}}^N\,, \quad \Phi \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(TM; {\mathbb {R}}^N))\,, \end{aligned}$$

where on the trivial vector bundle $M \times {\mathbb {R}}^N \rightarrow M$ we consider the trivial connection.

The condition $\Phi \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(TM; {\mathbb {R}}^N))$ is one of the main points of the above definition, since, if one drops it, then the existence of $\Phi$ is standard (and was already used). However, the condition $\Phi \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(TM; {\mathbb {R}}^N))$ is actually pretty strong, but it was proved in Lemma 3.1 of [35] that it is satisfied by a manifold with bounded geometry. (In fact, in that paper, instead of constructing a $\Phi$ with the property that it is an isometry, it was proved that $\Phi ^{-1} \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}({\mathbb {R}}^N; TM))$. By replacing $\Phi$ with its polar part, one can assume it to be isometric.)

Remark 5.9

The condition (FFC) is hereditary, in the sense that if it is satisfied by a manifold M, then it is satisfied by any open subset $M_0 \subset M$. Indeed, it is enough to restrict $\Phi$ to $M_0$. This shows then that every open subset of a manifold with bounded geometry satisfies (FFC) [35].

We have the following analog of Remark 5.1.

Remark 5.10

We use the notation of Remark 5.1, which remains, of course valid, since it was proved without the assumption $\Phi \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(TM; {\mathbb {R}}^N))$. If our manifold satisfies (FFC), then the condition $\Phi \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(TM; {\mathbb {R}}^N))$ yields some additional properties. Indeed, since we have assumed that $\Phi$ is an isometry now, we have $\Psi = \Phi ^\top : M \times {\mathbb {R}}^N \rightarrow TM$ and, for all $1 \le j \le N$, we have

$$\begin{aligned} \begin{aligned} Z_j&\mathrel {\ := \ }\Phi ^\top (e_j) \in {\mathcal {W}}_b(M) \mathrel {\ := \ }W_{\nabla }^{\infty , \infty }(M; TM) \ \text{ and } \\ \xi _j&\mathrel {\ := \ }p_j \circ \Phi \in W_{\nabla }^{\infty , \infty }(M; T^*M) \end{aligned} \end{aligned}$$

so that ${\mathcal {W}}_b(M) = \sum _{j=1}^N W_{\nabla }^{\infty , \infty }(M) Z_j$. The relations $X \, = \,\sum _{j=1}^N \xi _j(X) Z_j$ and $\omega \, = \,\sum _{j=1}^N \omega (Z_j) \xi _j$ remain, of course, valid. The set $\{Z_1, Z_2, \ldots , Z_N\}$ will be called a Fréchet system of generators for ${\mathcal {W}}_b(M)$.

We shall need the following result analogous the remaining part Lemma 5.4 (the part not extended already in Lemma 5.7).

Lemma 5.11

Assume M satisfies (FFC) and let $Z_j \in {\mathcal {W}}_b(M) := W_{\nabla }^{\infty , \infty }(M; TM)$ and $\xi _j \in W_{\nabla }^{\infty , \infty }(M; T^*M)$, $j = 1, \ldots , N$, be as in Remark 5.10.

• (i) For any $X \in {\mathcal {W}}_b(M)$, we have ${\text {div}}(X) \in W_{\nabla }^{\infty , \infty }(M)$.

• (ii) We have $[Z_i, Z_j] = \sum _{k} L_{ij}^k Z_k$, where $L_{ij}^k \in W_{\nabla }^{\infty ,\infty }(M)$.

• (iii) We have $\nabla _{Z_i}Z_j= \sum _{k} G_{ij}^k Z_k$, where $G_{ij}^k \in W_{\nabla }^{\infty ,\infty }(M)$.

Proof

To prove (i), let $X_1, X_2, \ldots , X_n$ be a local orthonormal basis of TM. Then, we obtain

$$\begin{aligned} {\text {div}}(X)&\, = \,\sum _{i=1}^n (\nabla _{X_i}X , X_i)\\&\, = \,\sum _{j , k, l=1 }^n \xi _k (X_j) \xi _l(X_j) (\nabla _{Z_k}X , Z_l)\\&\, = \,\sum _{j, k, l=1}^n (\xi _k, \xi _l) (\nabla _{Z_k}X , Z_l) \end{aligned}$$

by the isometry property of the map $T^*M \ni \xi \rightarrow \big ( (\xi , X_j) \big )_{j=1}^n$ (since $(X_i)$ was chosen to be an orthonormal basis). Then (i) follows using also Propositions 3.7 and Lemma 5.7(i), since X, $Z_j$, and $\xi _j$ are all in $W_{\nabla }^{\infty , \infty }$.

Let us prove (ii). Lemma 5.7(ii) gives that $[Z_i, Z_j] \in {\mathcal {W}}_b(M)$. Hence $[Z_i, Z_j] = \sum _{k=1}^N \xi _k([Z_i, Z_j]) Z_k$ and we can take $L_{ij}^k := \xi _k([Z_i, Z_j])$, which is in $W_{\nabla }^{\infty , \infty }(M)$ by Proposition 3.7 since $Z_j$ and $\xi _j$ are all in $W_{\nabla }^{\infty , \infty }$. This proves (ii). For (iii), we proceed in exactly the same way by using (iii) of Lemma 5.7 instead of (ii) of that lemma. $\square$

We can now formulate and prove the following proposition, which provides us with the usual properties of the Hilbert space adjoints $\nabla _X^*$ and $\nabla ^*$.

Proposition 5.12

Let us assume that M satisfies (FFC) and that $E \in {\mathcal {H}}(M)$. Then, we also have the following properties.

• (i) If $X \in {\mathcal {W}}_b(M)$, then $\nabla _X^* = - \nabla _X - {\text {div}}(X) \in {\text {Diff}}_{b, \nabla }^{1}(M; T^*M \otimes E, E)$.

• (ii) $\nabla ^* \in {\text {Diff}}_{b, \nabla }^{1}(M; T^*M \otimes E, E)$.

Proof

To prove (i), let ${\text {div}}= -d^\prime : {{\mathcal {C}}}^{\infty }(M; T^*M) \rightarrow {{\mathcal {C}}}^{\infty }(M)$, the negative of the restriction of the dual of the de Rham differential. Then, ${\text {div}}(fX) = f{\text {div}}(X) + X(f)$. Let us write $\nabla _X$ for $\nabla _X^E$, to simplify the notation. Then, using also formula (4), we obtain for all $\xi , \eta \in {{\mathcal {C}}}^{\infty }(M; E)$

$$\begin{aligned} (\nabla _X \xi , \eta )_E&\, = \,X(\xi , \eta )_E - (\xi , \nabla _X \eta )_E \\&\, = \,{\text {div}}\left( (\xi , \eta )_E X\right) - (\xi , \eta )_E{\text {div}}(X) - (\xi , \nabla _X \eta )_E\,, \end{aligned}$$

and then, integrating over M and using the assumption that $\xi$ and $\eta$ have compact support (so the integral of the “div” part is zero), we get

$$\begin{aligned} \int _M(\nabla _X \xi , \eta )_E \,d{\text {vol}}&\, = \,- \int _M (\xi , {\text {div}}(X)\eta +\nabla _X \eta )_E\,d{\text {vol}}\,. \end{aligned}$$

Thus, $\nabla _X^* \, = \,-\nabla _X - {\text {div}}(X),$ as stated, and hence $\nabla _X^*$ belongs to ${\text {Diff}}_{b, \nabla }^{1}(M; T^*M \otimes E, E)$ by Lemma 5.7(i) and by Lemma 5.11(i).

Let $\tau _\xi (\zeta ) := \xi \otimes \zeta$. Then, using the notation of Remarks 5.1 and 5.10, we can reformulate the result of Lemma 5.11(ii) as

$$\begin{aligned} \nabla \, = \,\sum _{i=1}^N \tau _{\xi _i}\nabla _{Z_i}\,. \end{aligned}$$

(24)

The relation (ii) thus follows from this relation by taking adjoints and by using (i), that $Z_j$ and $\xi _j$ are in $W_{\nabla }^{\infty , \infty }$, and the composition property of Proposition 4.5(ii). $\square$

We can now prove the following extension of the standard continuity of differential operators. Recall the spaces $\mathring{W}_{\nabla }^{s,p}$ introduced in Sect. 3.1.2. Recall the category ${\mathcal {H}}(M)$ of 2.3.

Corollary 5.13

Assume that M satisfies (FFC). Let $1< p < \infty$, $\mu \in {\mathbb {Z}}_+$, and $E,F \in {\mathcal {H}}(M)$. If $P = \sum _{j=0}^{\mu } a_j \nabla ^j$ and $a_{j} \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; F))$, then P extends by continuity to maps

$$\begin{aligned} \begin{gathered} \mathring{W}_{\nabla }^{s+\mu ,p}(M; E) \rightarrow \mathring{W}_{\nabla }^{s,p}(M; F)\,, \quad s\in {\mathbb {Z}}_+, \\ W_{\nabla }^{s+\mu ,p} (M; E) \rightarrow W_{\nabla }^{s,p}(M; F)\,, \quad s \in {\mathbb {R}}\,. \end{gathered} \end{aligned}$$

Proof

We have already seen that $P:W_{\nabla }^{s+\mu ,p}(M; E) \rightarrow W_{\nabla }^{s,p}(M; F)$ is continuous if $s \in {\mathbb {Z}}_+$, see Lemma 4.4. Moreover, a differential operator will send compactly supported sections to compactly supported sections. The first statement thus follows.

Let us turn now to the second statement. Since for non-integer s, the spaces $W_{\nabla }^{s, p}$ are defined by interpolation between consecutive integers, it suffices to prove our statement for integer values of s. (The general case is obtained by interpolation.) Furthermore, using Propositions 3.7 and 4.5, we see that it is also enough to consider the case $P = \nabla$ (so $\mu = 1$). (The case P of order zero follows from Proposition 3.7.) We have then two possibilities for s, either $s \ge \mu = 1$ or $s \le 0$. The first case was already proved, as we have just mentioned. To prove the case $s \le 0$, recall that the adjoint operator $P^* = \nabla ^*$ is also a $\nabla$-differential operator by Proposition 5.12 and that the negative order Sobolev spaces $W_{\nabla }^{-s,p}(M; E) \mathrel {\ := \ }\mathring{W}_{\nabla }^{s,p'}(M; E)^*$, see Eq. (8). The second statement is known for $\nabla ^* : \mathring{W}_{\nabla }^{1-s,p'}(M; E) \rightarrow \mathring{W}_{\nabla }^{-s,p'}(M; E)$ since $\nabla ^* \in {\text {Diff}}_{b, \nabla }^{1}(M; T^*M \otimes E, E)$ by the first part (since we reduced to $s \in {\mathbb {Z}}_+$). The desired (second) statement is then obtained by taking adjoints. $\square$

5.3 Bounded mixed differential operators

The (FFC) condition allows us now to control the boundedness of the coefficients of the mixed differential operators. For the rest of this section, we shall thus assume that our vector bundles are in ${\mathcal {H}}(M)$, see 2.3. In particular, it gives the following finite generation property for the algebra of $\nabla$-differential operators with $W_{\nabla }^{\infty , \infty }$-coefficients. This property is analogous to Proposition 5.5.

Proposition 5.14

Let $\mu , \nu \in {\mathbb {Z}}_+$. Assume M satisfies (FFC) and let $Z_1, Z_2, \ldots , Z_N \in W_{\nabla }^{\infty , \infty }(M; TM)$ be a Fréchet systems of generators for $W_{\nabla }^{\infty , \infty }(M; TM)$ (see 5.1). Let $E, F, G \in {\mathcal {H}}(M)$.

• (i) $\widetilde{{\text {Diff}}}_{b, \nabla }^{\nu }(M; F, G) \widetilde{{\text {Diff}}}_{b, \nabla }^\mu (M; E, F) \subset \widetilde{{\text {Diff}}}_{b, \nabla }^{\mu + \nu }(M; E, G)$.

• (ii) $\widetilde{{\text {Diff}}}_{b, \nabla }^\mu (M; E, F) = {\text {Diff}}_{b, \nabla }^\mu (M; E, F)$.

• (iii) Consequently, ${\text {Diff}}_{b, \nabla }^\mu (M; E, F)$ is linearly generated by $a \nabla _{X_1}\nabla _{X_2} \ldots \nabla _{X_r}$, where $r \le \mu$, $X_1, X_2, \ldots , X_r \in \{Z_1, Z_2, \ldots , Z_N\}$ and $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E, F))$.

Proof

The proof is completely similar to that of Proposition 5.5, but using Lemma 5.11 instead of 5.4, and by using the composition property

$$\begin{aligned} W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(F; G)) W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; F)) \subset W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; G))\,, \end{aligned}$$

and the properties $\nabla _X \in {\text {Diff}}_{b, \nabla }^1(M; E, F)$ if $X \in {\mathcal {W}}_b(M) := W_{\nabla }^{\infty , \infty }(M; TM)$, $\nabla \in \widetilde{{\text {Diff}}}_{b, \nabla }^1(M; E, T^*M \otimes E)$, and $\nabla _{X} a = \nabla _X(a) + a \nabla _X \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E, F))$ if $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E, F))$ and $X \in {\mathcal {W}}_b(M)$ instead of the corresponding statements in that proof. $\square$

Let us recall that a vector bundle $E \rightarrow M$ is said to have totally bounded curvature if its curvature $R^E \in W_{\nabla }^{\infty , \infty }(M; \Lambda ^2 T^*M \otimes {\text {End}}(E))$. Recall that if M satisfies (FFC), then ${{\widetilde{{\text {Diff}}}}}^\mu = {\text {Diff}}^\mu$ and $\widetilde{{\text {Diff}}}_{b, \nabla }^\mu = {\text {Diff}}_{b, \nabla }^\mu$. We next show that we can choose the vector fields $X_j$ in the above proposition in the right order.

Corollary 5.15

Assume M satisfies (FFC) and let $(Z_j)$, $1 \le j \le N$, be a Fréchet generating system for ${\mathcal {W}}_b(M)$. Let us assume also that $E \in {\mathcal {H}}(M)$ has totally bounded curvature.

• (i) If $X, Y \in {\mathcal {W}}_b(M)$, then $\nabla _X^E \nabla _Y^E -\nabla _Y^E \nabla _X^E - \nabla _{[X, Y]}^E \in W_{\nabla }^{\infty , \infty }(M; {\text {End}}(E))$.

• (ii) Consequently, ${\text {Diff}}_{b, \nabla }^\mu (M; E, F)$ is linearly generated by $a \nabla ^E_{Z_{k_1}} \ldots \nabla ^E_{Z_{k_r}}$, where $1 \le k_1 \le k_2 \le \ldots \le k_r \le N$, $r \le \mu$, and $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; F))$.

Proof

The statement (i) follows also from the formula (23) taking into account that, in this case, $R^E(X, Y) \in W_{\nabla }^{\infty , \infty }(M; {\text {End}}(E))$, since $R^E \in W_{\nabla }^{\infty , \infty }(M; \Lambda ^2 T^*M \otimes {\text {End}}(E))$ and $X, Y \in {\mathcal {W}}_b(M)$. Finally, the last part is proved in the same way as Corollary 5.6, but taking into account also (i). $\square$

5.4 Equivalent definitions of covariant Sobolev spaces

Using (FFC), we also obtain some equivalent definitions of our covariant Sobolev spaces. Let $Z_1, Z_2, \ldots , Z_N \in {\mathcal {W}}_b(M) := W_{\nabla }^{\infty , \infty }(M; TM)$ be a Fréchet system of generators of ${\mathcal {W}}_b(M)$ as $W_{\nabla }^{\infty , \infty }$-module, and let $\{\xi _1, \xi _2, \ldots , \xi _\mu \}$ be the dual system, as in Remark 5.10.

The following result gives several alternative descriptions of Sobolev spaces $W_\nabla ^{s, p}(M; E)$, $s \in {\mathbb {N}}$, $1 \le p \le \infty$, in terms of vector fields similar to [35, Proposition 3.2], where part of this result was proved for manifolds with bounded geometry. Let us record the following easy lemma. We recall that in this subsection we continue to assume that all our vector bundles are finite dimensional, Hermitian and have a metric preserving connection (that is, they are in ${\mathcal {H}}(M)$).

Lemma 5.16

Assume that M satisfies (FFC). Then, $w \in L^p(M,g; T^{*\otimes \mu }M \otimes E)$ if, and only if, $a w \in L^p(M,g; E)$ for all $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(T^{*\otimes \mu }M \otimes E; E))$.

Proof

If $w \in L^p(M,g; T^{*\otimes \mu }M \otimes E)$ and $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(T^{*\otimes \mu }M \otimes E; E))$, then we have already seen that $aw \in L^p(M,g; E)$.

Let us now turn to the proof of the converse. Let $Z_1, Z_2, \ldots , Z_N \in {\mathcal {W}}_b(M) := W_{\nabla }^{\infty , \infty }(M; TM)$ be a Fréchet system of generators of ${\mathcal {W}}_b(M)$ as $W_{\nabla }^{\infty , \infty }(M)$-module, as in Remark 5.10. Let $\{\xi _1, \xi _2, \ldots , \xi _\mu \} \subset W_{\nabla }^{\infty , \infty }(M; T^*M)$ be the dual system, again as in that remark. Let $\mathbf {k} = (k_1, k_2, \ldots , k_\mu )$, $1 \le k_1, k_2, \ldots k_\mu \le N$. Then, Lemma 5.2 implies that

$$\begin{aligned} w \, = \,\sum _{\mathbf {k}} \xi _{k_1} \otimes \xi _{k_2} \otimes \ldots \otimes \xi _{k_\mu } \otimes i_{Z_\mu }i_{Z_{\mu - 1}} \ldots i_{Z_1}(w)\,. \end{aligned}$$

(25)

To prove the converse, let us consider w be such that $aw \in L^p(M,g; E)$ for all $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(T^{*\otimes \mu }M \otimes E; E))$. We shall choose $a := i_{Z_\mu }i_{Z_{\mu - 1}} \ldots i_{Z_1}$, which is in $W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(T^{*\otimes \mu }M \otimes E; E))$ by Lemma 5.7(i). The hypothesis and Corollary 3.8 then implies that

$$\begin{aligned} \xi _{k_1} \otimes \xi _{k_2} \otimes \ldots \otimes \xi _{k_\mu } \otimes i_{Z_\mu }i_{Z_{\mu - 1}} \ldots i_{Z_1}(w) \in L^p(M,g; T^{*\otimes \mu }M \otimes E) \end{aligned}$$

for all $k_i$, because all $\xi _j \in W_{\nabla }^{\infty , \infty }(M; T^*M)$. Therefore, $w \in L^p(M,g; T^{*\otimes \mu }M \otimes E)$, by Equation (25). $\square$

The following type of descriptions is often used in the setting of weighted Sobolev spaces, see, for instance, [15, 19, 24, 27, 28, 46, 47, 55]. If M satisfies (FFC), $Z_1, Z_2, \ldots , Z_N \in {\mathcal {W}}_b(M) := W_{\nabla }^{\infty , \infty }(M; TM)$ will continue to denote a Fréchet system of generators of ${\mathcal {W}}_b(M)$ as $W_{\nabla }^{\infty , \infty }$-module, as in Remark 5.10.

Proposition 5.17

Let $\ell \in {\mathbb {N}}$ and $1 \le p \le \infty$. Then, the following spaces all coincide with $W_{\nabla }^{\ell , p}(M; E)$ under the listed additional conditions:

• (i) $\{ u \, \vert \ P u \in L^p(M,g; E)\,, \ \forall P \in {\text {Diff}}_{b, \nabla }^\ell (M; E, F)\}$.

• (ii) $\{ u \, \vert \ P u \in L^p(M,g; E)\,, \ \forall P \in \widetilde{{\text {Diff}}}_{b, \nabla }^\ell (M; E)\}$, provided that M satisfies (FFC).

• (iii) $\{\, u \, \vert \ \nabla ^E_{Z_{k_1}} \nabla ^E_{Z_{k_2}} \ldots \nabla ^E_{Z_{k_j}} u \in L^p(M,g; E),\ j \le \ell , \ 1 \le k_1, k_2, \ldots , k_j \le N \, \}$, provided that M satisfies (FFC).

• (iv) $\{\, u \, \vert \ \nabla ^E_{Z_{k_1}} \nabla ^E_{Z_{k_2}} \ldots \nabla ^E_{Z_{k_j}} u \in L^p(M,g; E),\ j \le \ell , \ 1 \le k_1 \le k_2 \le \ldots \le k_j \le N \, \}$ provided that M satisfies (FFC) and E has totally bounded curvature.

Proof

The first characterization of the Sobolev spaces $W_\nabla ^{\ell , p}(M; E)$ follows from the definition of covariant Sobolev spaces (Definition 3.1) and $\nabla$-differential operators (Definition 4.1), since it is enough to take P among the monomials $\nabla ^j$, $0 \le j \le \ell$. (Indeed, any $P \in {\text {Diff}}_{b, \nabla }^\ell (M; E, F)$ has the form $P = \sum _{j=0}^{\ell } a_j \nabla ^j$ with $a_{j} \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; F))$.)

The second point is similar. Indeed, we have $w \in L^p(M,g; T^{*\otimes k}M \otimes E)$ if, and only if, $a w \in L^p(M,g; T^{*\otimes k}M \otimes E)$ for all $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(T^{*\otimes k}M \otimes E)$. By applying this observation to $w := \nabla ^j u$, $j \le \ell$, and using Lemma 5.16, the definitions of covariant Sobolev spaces and $\nabla$-differential operators, we obtain the result.

The third and fourth points are also similar. They follow by combining (i) with Lemma 5.16 and Proposition 5.14 (for (iii)), respectively, Corollary 5.15 (for (iv)). $\square$

6 Bidifferential operators and Dirichlet forms

In order to treat variational problems in a manner that does not require local coordinate charts or local trivializations of our coordinate bundles, we found it convenient to consider $\nabla$ -bidifferential operators, which are analogous to the $\nabla$-differential operators studied in the previous sections. Variational problems arise prominently in analysis and geometry. In this section, we extend to bidifferential operators some of the properties we have proved for differential operators. In the first subsection of this section, we do not require our vector bundles to be Hermitian (unless explicitly stated), but we will do so in the second subsection, in order to deal with mapping properties.

6.1 $\nabla$-Bidifferential operators

We begin with some geometric preliminary discussions. Let $M_1$ and $M_2$ be two topological spaces and let

$$\begin{aligned} \pi _j : M_1 \times M_2 \rightarrow M_j \end{aligned}$$

be the projection onto the jth component, $j = 1, 2$. For any two real or complex vector bundles $E_j \rightarrow M_j$, we let

$$\begin{aligned} E_1 \boxtimes E_2 \mathrel {\ := \ }\pi _1^*(E_1) \otimes \pi _2^*(E_2) \rightarrow M_1 \times M_2 \end{aligned}$$

be the external tensor product of $E_1$ and $E_2$. It is a vector bundle on $M_1 \times M_2$. More concretely, if $x_j \in M_j$ and $E_{j,x_j}$ is the fiber of $E_j$ above $x_j$, then the fiber of $E_1 \boxtimes E_2$ above $(x_1, x_2)$ is $E_{1, x_1} \otimes E_{2, x_2}$. If $M_1 = M_2 = M$, in which case we shall always regard M as being diagonally embedded in $M \times M$, then, of course,

$$\begin{aligned} E_1 \boxtimes E_2 \vert _{M} \, = \,E_1 \otimes E_2 \,. \end{aligned}$$

The following long remark summarizes some of the properties of connections on the product $M_1 \times M_2$.

Remark 6.1

If $M_j$ are smooth manifolds and $E_j \rightarrow M_j$ are smooth vector bundles endowed with connections, $j = 1, 2$, then $E_1 \boxtimes E_2$ is endowed with the canonically induced connection from $\pi _j^*(E_j)$ (which acts trivially on the fiber $M_{3-j}$ of $\pi _j : M_1 \times M_2 \rightarrow M_j$). Let us take a closer look at this induced connection on $E_1 \boxtimes E_2$. We first notice that we have a canonical isomorphism

$$\begin{aligned} T(M_1 \times M_2) \simeq TM_1 \times TM_2 \simeq \pi _1^*(TM_1) \oplus \pi _2^*(TM_2)\,, \end{aligned}$$

and similarly for the cotangent bundles. Let $p_j : T^*(M_1 \times M_2) \rightarrow \pi _j^*(T^*M_j)$ be the induced projections and let

$$\begin{aligned} \nabla ^{E_1 \boxtimes E_2} \, = \,\nabla _1 + \nabla _2 \ \text{ where } \ \nabla _j \mathrel {\ := \ }(p_j \otimes id_{E_1 \boxtimes E_2}) \circ \nabla ^{E_1 \boxtimes E_2}\,. \end{aligned}$$

If $u_j \in {{\mathcal {C}}}^{\infty }(M_j; E_j)$, $j = 1, 2$, we let $v := u_1 \otimes u_2 \in {{\mathcal {C}}}^{\infty }(M_1 \times M_2 ; E_1 \boxtimes E_2)$, that is, $v(x_1, x_2) \mathrel {\ := \ }(u_1 \otimes u_2) (x_1, x_2) \mathrel {\ := \ }u(x_1) \otimes u_2(x_2).$ We then obtain

$$\begin{aligned} \nabla _1 v \, = \,\nabla u_1 \otimes u_2\,,\ \nabla _2 v \, = \,u_1 \otimes \nabla u_2\,,\, \text{ and } \text{ hence } \, \nabla _1 \nabla _2 v \, = \,\nabla _2 \nabla _1 v\,. \end{aligned}$$

Elementary tensor products of the form $v := u_1 \otimes u_2$ are dense (in a suitable sense) in ${{\mathcal {C}}}^{\infty }(M_1 \times M_2; E_1 \boxtimes E_2)$, and hence $\nabla _1 \nabla _2 = \nabla _2 \nabla _1$ on ${{\mathcal {C}}}^{\infty }(M_1 \times M_2; E_1 \boxtimes E_2)$.

We shall also need the following result.

Lemma 6.2

We use the notation of the previous remark. The projection $p_{i, j} : \Lambda ^{i + j} T^*(M_1 \times M_2) \rightarrow \pi _1^*(\Lambda ^{i} T^*M_1) \otimes \pi _2^*(\Lambda ^{j} T^*M_2)$ is totally bounded (i.e. in $W_{\nabla }^{\infty , \infty }$). For $i, j \in {\mathbb {Z}}_+$, here exists a $\nabla$-differential operator $P_{i,j}$ on $M_1 \times M_2$ such that, for all $v := u_1 \otimes u_2$, we have

$$\begin{aligned} P_{i,j} v \, = \,\nabla _1^{i}u_1 \otimes \nabla _2^{j}u_2\,. \end{aligned}$$

Proof

Let us notice that

$$\begin{aligned} \Lambda ^{i} \pi ^*(T^*M_1) \otimes \Lambda ^{j} \pi ^*(T^*M_2) \subset \Lambda ^{i + j} T^* (M_1 \times M_2) \end{aligned}$$

(26)

is a direct summand, and hence, we can take $P_{i,j} := p_{i, j} \nabla ^{i + j}$. $\square$

Let V be a complex vector space or vector bundle and let ${\overline{V}}$ denote the conjugate space to V. More precisely, ${\overline{V}} = V$ as additive groups, but with the external multiplication ${{{\overline{z}}}}\, {{{\overline{v}}}}= \overline{z v}$, $z \in {\mathbb {C}}$, $v \in V$, where ${\overline{v}}$ denotes the image in ${\overline{V}}$ of an element $v \in V$.

Definition 6.3

Let $E, F \rightarrow M$ be two smooth vector bundles endowed with connections. A $\nabla$-bidifferential operator on (E, F) is a linear map

$$\begin{aligned} {\mathfrak {b}}^{\nabla } : {{\mathcal {C}}}^{\infty }(M \times M ; E \boxtimes {\overline{F}}) \rightarrow {{\mathcal {C}}}^{\infty }(M) \end{aligned}$$

of the form ${\mathfrak {b}}^{\nabla } v = P v\vert _{M}$, where $P : {{\mathcal {C}}}^{\infty }(M \times M; E \boxtimes {\overline{F}}) \rightarrow {{\mathcal {C}}}^{\infty }(M \times M)$ is a $\nabla$-differential operator with smooth coefficients. If we can choose P to have $W_{\nabla }^{\infty , \infty }$-coefficients (that is, in ${\text {Diff}}_{b, \nabla }(M \times M; E \boxtimes {\overline{F}}, {\mathbb {C}})$), then we say that ${\mathfrak {b}}^{\nabla }$ has $W_{\nabla }^{\infty , \infty }$-coefficients as well.

Bidifferential operators appeared also in the framework of deformation quantization, see [21, 48, 61]. We could have tried to consider continuous bilinear maps $B_0 : {{\mathcal {C}}}^{\infty }(M; E) \otimes {{\mathcal {C}}}^{\infty }(M; F) \rightarrow {{\mathcal {C}}}^{\infty }(M)$ with the property that ${\text {supp}}(B_0(u, v)) \subset {\text {supp}}(u) \cap {\text {supp}}(v)$. The relation between this property, a “Peetre theorem” for bilinear forms, and our definition of bidifferential operators will be discussed in [34]. Let us obtain a more explicit form of the $\nabla$-bidifferential operators.

Remark 6.4

We use the notation of Definition 6.3 and let $\pi _ j: M \times M \rightarrow M$, $j = 1, 2$, be the two projections. Let $\nabla ^{E \boxtimes {\overline{F}}} \, = \,\nabla _1 + \nabla _2$ be the decomposition of Remark 6.1. Thus, if $u \in {{\mathcal {C}}}^{\infty }(M; E)$, $w \in {{\mathcal {C}}}^{\infty }(M; F)$, and $v := u \otimes {\overline{w}} \in {{\mathcal {C}}}^{\infty }(M \times M ; E \boxtimes {\overline{F}})$, then $\nabla _1 v = \nabla u \otimes {\overline{w}}$, $\nabla _2 v = u \otimes \nabla {\overline{w}}$. Let P be as in Definition 6.3. Therefore, for $v := u \otimes w$, we have

$$\begin{aligned} P v \mathrel {\ := \ }a \cdot \nabla ^{tot}v&\, = \,\sum _{j=0}^\mu a^{[j]} \nabla ^j v \, = \,\sum _{i + j \le \mu } a_{ij} \big ( \nabla _1^i \nabla _2^j v \big )\\&\, = \,\sum _{i + j \le \mu } a_{ij} \big [ (\nabla ^iu) \otimes (\nabla ^j {\overline{w}}) \big ] \in {{\mathcal {C}}}^{\infty }(M \times M) \,, \end{aligned}$$

where each $a_{ij} \in {{\mathcal {C}}}^{\infty }\Big (M \times M; \big [ (T^{* \otimes i} M \otimes E) \boxtimes (T^{* \otimes j} M \otimes {\overline{F}})\big ]^\prime \Big )$ is obtained in a canonical (linear) way from $a \in {{\mathcal {C}}}^{\infty }\big (M \times M; {\mathcal {F}}_\mu ^{M \times M}(E \boxtimes {\overline{F}})^\prime \big )$. In particular, if $a \in W_{\nabla }^{\infty , \infty }$, then all $a_{ij} \in W_{\nabla }^{\infty , \infty }$ as well and their bounds are controlled by the bounds for a. Let us assume also that F is endowed with a Hermitian metric $(\,,\,)_F$, regarded as a bilinear form on $F \otimes {\overline{F}}$. We let $(\,,\,)_{T^{*\otimes j}M \otimes F}$ be the corresponding Hermitian form on $T^{*\otimes j}M \otimes F$ (i.e. linear form on $T^{*\otimes j}M \otimes F \otimes T^{*\otimes j}M \otimes {\overline{F}}$). Then, there exist unique

$$\begin{aligned} {\mathfrak {a}}_{ij} \in {{\mathcal {C}}}^{\infty }\big (M; {\text {Hom}}(T^{*\otimes i}M \otimes E; T^{*\otimes j}M \otimes F)\big ) \end{aligned}$$

such that $({\mathfrak {a}}_{ij} \xi , \eta ) = a_{ij} \vert _M (\xi \otimes {\overline{\eta }})$.

Consequently, we have the following canonical form for ${\mathfrak {b}}^\nabla$.

Lemma 6.5

Let ${\mathfrak {b}}^{\nabla } : {{\mathcal {C}}}^{\infty }(M \times M ; E \boxtimes {\overline{F}}) \rightarrow {{\mathcal {C}}}^{\infty }(M)$ be a $\nabla$-bidifferential operator. Then, there exist ${\mathfrak {a}}_{ij} \in {{\mathcal {C}}}^{\infty }\big (M; {\text {Hom}}(T^{*\otimes i}M \otimes E; T^{*\otimes j}M \otimes F)\big )$, $i, j \le \mu$, such that

$$\begin{aligned} {\mathfrak {b}}^{\nabla } v(x) \, = \,{\mathfrak {b}}^{\nabla } (u \otimes {\overline{w}})(x) \, = \,\sum _{i + j \le \mu } \big ({\mathfrak {a}}_{ij}(x) \nabla ^iu(x), \nabla ^j w(x) \big )_{T^{*\otimes j} M \otimes F}\,. \end{aligned}$$

If ${\mathfrak {b}}^\nabla$ has $W_{\nabla }^{\infty , \infty }$-coefficients, we can assume that ${\mathfrak {a}}_{ij}$ are also in $W_{\nabla }^{\infty , \infty }$ with bounds controlled by those of ${\mathfrak {b}}^\nabla$. The converse is also true, in the sense that the expression on the right hand side of the displayed equation defines a $\nabla$-bidifferential operators that has $W_{\nabla }^{\infty , \infty }$-coefficients if all the ${\mathfrak {a}}_{ij}$ are in $W_{\nabla }^{\infty , \infty }$.

Proof

The existence of the coefficients ${\mathfrak {a}}_{ij}$ was explained in Remark 6.4. The converse follows similarly, but using Lemma 6.2. Indeed, let $q_G \in {\text {Hom}}(G \otimes {\overline{G}}, {\mathbb {C}})$ be the inner product on $G := T^{*\otimes j} M \otimes F$. Then, we can take

$$\begin{aligned} {\mathfrak {b}}^\nabla := \sum _{i, j} q_G \circ ({\mathfrak {a}}_{i, j} \otimes 1) \circ p_{i, j} \circ \nabla ^{i+j}\,. \end{aligned}$$

The boundedness of the coefficients of ${\mathfrak {b}}^\nabla$ follows from the fact that $p_{i, j}$ is bounded (Lemma 6.2). $\square$

If ${\mathfrak {a}}_{ij} = 0$ for $i > m$ or $j > m'$ in Lemma 6.5, we shall say that ${\mathfrak {b}}^\nabla$ has order $\le (m, m')$.

Corollary 6.6

Let $Q_1 \in {\text {Diff}}_\nabla ^m(M; E_1, G)$ and $Q_2 \in {\text {Diff}}_\nabla ^{m'}(M; E_2, G)$, where G is a Hermitian vector bundle. Then, ${\mathfrak {b}}(u \otimes {\overline{w}}):= (Q_1u, Q_2w)_G$ is a $\nabla$-bidifferential operator ${{\mathcal {C}}}^{\infty }(M \times M ; E \boxtimes {\overline{F}}) \rightarrow {{\mathcal {C}}}^{\infty }(M)$ of order $\le (m,m')$ with smooth coefficients. If P and Q have $W_{\nabla }^{\infty , \infty }$-coefficients, then ${\mathfrak {b}}$ will also have $W_{\nabla }^{\infty , \infty }$-coefficients.

Proof

We need to find a $\nabla$-differential operator ${\mathfrak {b}}^\nabla$ as in Definition 6.3. By linearity and by the definition of $\nabla$-differential operators, we can assume that $Q_j = a_j\nabla ^{i_j}$. The result then follows from the formula

$$\begin{aligned} (Q_1 u_1, Q_2 u_2) = (a_2^*a_1 \nabla ^{i_1} u_1, \nabla ^{i_2} u_2) \end{aligned}$$

and from Lemma 6.5. $\square$

Recall that $\,d{\text {vol}}$ denotes the volume form on M (associated to its metric g).

Definition 6.7

The sesquilinear form

$$\begin{aligned} B_{\mathfrak {b}}^{\nabla }(u, w) \mathrel {\ := \ }\int _M {\mathfrak {b}}^{\nabla } (u \otimes {\overline{w}}) \,d{\text {vol}}\ \end{aligned}$$

is called the Dirichlet form associated with ${\mathfrak {b}}^{\nabla }$. It has $W_{\nabla }^{\infty , \infty }$-coefficients if ${\mathfrak {b}}^{\nabla }$ has $W_{\nabla }^{\infty , \infty }$-coefficients and it has the same order as ${\mathfrak {b}}^{\nabla }$. The induced map $P_{\mathfrak {b}}^\nabla : {{\mathcal {C}}}^{\infty }(M; E) \rightarrow {{\mathcal {C}}}^{\infty }(M; F)^*$,

$$\begin{aligned} \langle P_{\mathfrak {b}}^\nabla u, {\overline{w}} \rangle \, = \,B_{\mathfrak {b}}^{\nabla }(u, w)\,, \quad u \in {{\mathcal {C}}}^{\infty }(M; E), w \in {{\mathcal {C}}}^{\infty }(M; F)\,, \end{aligned}$$

is called the $\nabla$ -differential operator in divergence form associated with ${\mathfrak {b}}^\nabla$ (or to $B_{\mathfrak {b}}^\nabla$). If ${\mathfrak {a}}_{ij} = 0$, if $i > m$ or $j > m'$, then we shall say that $P_{\mathfrak {b}}^\nabla$ has order $\le (m,m')$.

We shall see in the last part of this section that $P_{\mathfrak {b}}^\nabla$ is indeed a $\nabla$-differential operator. We shall continue to use the notation of Remark 6.4. In particular, ${\mathfrak {b}}^{\nabla }$ will be a $\nabla$-bidifferential operator.

Remark 6.8

It follows from definitions that all of the following sets are vector spaces:

• (1) The set $bi{\text{- }}\!{\text {Diff}}_{\nabla }^{(m,m')}(M; E, F)$ of $\nabla$-bidifferential operators ${\mathfrak {b}}^\nabla : {{\mathcal {C}}}^{\infty }(M \times M; E \boxtimes {\overline{F}}) \rightarrow {{\mathcal {C}}}^{\infty }(M)$ of order $\le (m,m')$ (with smooth coefficients).

• (2) The set of Dirichlet forms $B_{\mathfrak {b}}^{\nabla }$ (with smooth coefficients) associated with some ${\mathfrak {b}}^\nabla \in bi{\text{- }}\!{\text {Diff}}_{\nabla }^{(m,m')}(M; E, F)$.

• (3) The set of differential operators $P_{\mathfrak {b}}^{\nabla }$ in divergence form (with smooth coefficients) associated with some ${\mathfrak {b}}^\nabla \in bi{\text{- }}\!{\text {Diff}}_{\nabla }^{(m,m')}(M; E, F)$.

  For the following sets, we also assume that $E, F \in {\mathcal {H}}(M)$.

• (4) The set $bi{\text{- }}\!{\text {Diff}}_{b, \nabla }^{(m,m')}(M; E, F)$ of $\nabla$-bidifferential operators ${\mathfrak {b}}^\nabla \in bi{\text{- }}\!{\text {Diff}}_{\nabla }^{(m,m')}(M; E, F)$ with $W_{\nabla }^{\infty , \infty }$-coefficients.

• (5) The set of Dirichlet forms $B_{\mathfrak {b}}^{\nabla }$ associated with some ${\mathfrak {b}}^\nabla \in bi{\text{- }}\!{\text {Diff}}_{b, \nabla }^{(m,m')}(M; E, F)$ (thus with $W_{\nabla }^{\infty , \infty }$-coefficients).

• (6) The set of differential operators $P_{\mathfrak {b}}^{\nabla }$ in divergence form associated with some ${\mathfrak {b}}^\nabla \in bi{\text{- }}\!{\text {Diff}}_{b, \nabla }^{(m,m')}(M; E, F)$ (thus with $W_{\nabla }^{\infty , \infty }$-coefficients).

The coefficients ${\mathfrak {a}}_{ij}$ in the canonical form for ${\mathfrak {b}}^\nabla$ (see Remark 6.1) are not unique (except for $i + j \le 1$). So when we say that one of the above objects has $W_{\nabla }^{\infty , \infty }$-coefficients, we mean that we can choose the coefficients ${\mathfrak {a}}_{ij}$ to be in $W_{\nabla }^{\infty , \infty }$.

Proposition 6.9

A linear map ${\mathfrak {b}}^\nabla : {{\mathcal {C}}}^{\infty }(M \times M ; E \boxtimes {\overline{F}}) \rightarrow {{\mathcal {C}}}^{\infty }(M)$ is a $\nabla$ -bidifferential operator of order $\le (m, m')$ if, and only if, it is a linear combination of maps of the form $u \otimes {\overline{w}} \rightarrow (Pu, Qw)_G$, with $P \in {\text {Diff}}^m(M; E, G)$ and $Q \in {\text {Diff}}^{m'}(M; F, G)$. If ${\mathfrak {b}}^\nabla$ has $W_{\nabla }^{\infty , \infty }$-coefficients, then we can choose P and Q also to have $W_{\nabla }^{\infty , \infty }$-coefficients (in this case $E, F, G \in {\mathcal {H}}(M)$). In particular, if $Z_j$ are as in Remark 5.1, then $bi{\text{- }}\!{\text {Diff}}^{(m,m')}(M; E, F)$ is linearly generated by sesquilinear maps of the form $u \otimes {\overline{w}} \rightarrow \big (a \nabla ^E_{Z_{k_1}} \ldots \nabla ^E_{Z_{k_r}} u, b \nabla ^E_{Z_{j_1}} \ldots \nabla ^E_{Z_{j_s}} w\big )_G$, where $1 \le k_1 \le k_2 \le \ldots \le k_r \le N$, $1 \le j_1 \le j_2 \le \ldots \le j_s \le N$, $r\le m$, $s\le m'$, and $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(E; G))$ and $b \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(F; G))$. We can even assume $b = 1$.

Proof

This follows from definitions and Corollary 6.6 and Lemma 6.5. $\square$

Proposition 6.10

Let $A \in {{\mathcal {C}}}^{\infty }(M; T^*M \otimes {\text {End}}(E))$ and ${{\widetilde{\nabla }}} = \nabla + A$. Let also $p \in [1, \infty ]$ and $m, m' \in {\mathbb {Z}}_+$. We then have the following results:

• (i) $bi{\text{- }}\!{\text {Diff}}_{\nabla }^{(m,m')}(M; E, F) = bi{\text{- }}\!{\text {Diff}}_{\widetilde{\nabla }}^{(m,m')}(M; E, F)$.

• (ii) If $A= -A^*\in W_{\nabla }^{\infty , \infty }(M; T^*M \otimes {\text {End}}(E))$, then

  $$\begin{aligned} bi{\text{- }}\!{\text {Diff}}_{b, \nabla }^{(m,m')}(M; E, F) \, = \,bi{\text{- }}\!{\text {Diff}}_{b, {{\widetilde{\nabla }}}}^{(m,m')}(M; E, F)\,. \end{aligned}$$

Proof

This follows with arguments similar to those for the proof of Proposition 4.8. $\square$

Thus, from now on, we shall write $bi{\text{- }}\!{\text {Diff}}^{(m,m')}(M; E, F)$ instead of $bi{\text{- }}\!{\text {Diff}}_{\nabla }^{(m,m')}(M; E, F)$.

6.2 Mixed bidifferential operators and (FCC)

We now introduce mixed bidifferential operators in analogy with the set of mixed $\nabla$-differential operators. They will serve the same intermediate purpose. Recall that ${\text {Diff}}_\nabla ^m(M; E, G)$ denotes the set of mixed differential operators ${{\mathcal {C}}}^{\infty }(M; F) \rightarrow {{\mathcal {C}}}^{\infty }(M; G)$.

Definition 6.11

A linear map ${\mathfrak {b}}^{mix} : {{\mathcal {C}}}^{\infty }(M \times M ; E \boxtimes {\overline{F}}) \rightarrow {{\mathcal {C}}}^{\infty }(M)$ is a mixed bidifferential operator of order $\le (m,m')$ if it is a linear combination of maps of the form $u \otimes {\overline{w}} \rightarrow (Pu, Qw)_G$, where $P \in {{\widetilde{{\text {Diff}}}}}_\nabla ^m(M; E, G)$ and $Q \in {{\widetilde{{\text {Diff}}}}}_\nabla ^{m'}(M; F, G)$. If P and Q have $W_{\nabla }^{\infty , \infty }$-coefficients, then we shall say that ${\mathfrak {b}}$ will also have $W_{\nabla }^{\infty , \infty }$-coefficients.

Let ${{{\widetilde{bi{\text{- }}\!{\text {Diff}}}}}}{}^{(m, m')}(M; E, F)$ denote the set of mixed bidifferential operators of order $\le (m, m')$ with smooth coefficients. Let also ${{{\widetilde{bi{\text{- }}\!{\text {Diff}}}}}}{}_{b, \nabla }^{(m, m')}(M; E, F)$ be the set of mixed bidifferential operators of order $\le (m, m')$ with $W_{\nabla }^{\infty , \infty }$-coefficients. Let us assume now that M satisfies (FFC) and derive then the equality of the space of $\nabla$-bidifferential operators and that of mixed bidifferential operators, in analogy with the corresponding result for differential operators. It follows from the definition of mixed bidifferential operators and from Propositions 5.5 and 6.9 that ${{{\widetilde{bi{\text{- }}\!{\text {Diff}}}}}}{}^{(m, m')}(M; E, F) = bi{\text{- }}\!{\text {Diff}}^{(m, m')}(M; E, F)$, that is, every $\nabla$-bidifferential operator is a mixed bidifferential operator and conversely. We thus concentrate in what follows on the case of totally bounded coefficients, and thus we shall assume for the rest of this paper that our vector bundles over M are in ${\mathcal {H}}(M)$ (that is, finite dimensional, Hermitian, with a metric preserving connection).

Proposition 6.12

Let $m,m' \in {\mathbb {Z}}_+$ and assume that M satisfies (FFC) and that $E, F \in {\mathcal {H}}(M)$.

• (i) We have ${{{\widetilde{bi{\text{- }}\!{\text {Diff}}}}}}{}_{b, \nabla }^{(m, m')}(M; E, F) = bi{\text{- }}\!{\text {Diff}}_{b, \nabla }^{(m, m')}(M; E, F)$.

• (ii) Let $Z_1, Z_2, \ldots , Z_N \in {\mathcal {W}}_b(M)$ be Fréchet systems of generators for ${\mathcal {W}}_b(M)$ of Remark 5.10, then ${{{\widetilde{bi{\text{- }}\!{\text {Diff}}}}}}{}_{b, \nabla }^{(m,m')}(M; E, F)$ is linearly generated by sesquilinear maps of the form

  $$\begin{aligned} u \otimes {\overline{w}} \rightarrow (a \nabla _{Y_1}\nabla _{Y_2} \ldots \nabla _{Y_r} u, \nabla _{Y_{r+1}}\nabla _{Y_{r+2}} \ldots \nabla _{Y_{r+s}} w)_{G}\,, \end{aligned}$$

  where $r \le m$, $Y_1, Y_2, \ldots , Y_{r+s} \in \{Z_1, Z_2, \ldots , Z_N\}$, $G := T^{*\otimes s}M \otimes F$, and $a \in {{\mathcal {C}}}^{\infty }(M; {\text {Hom}}(T^{*\otimes r}M \otimes F, G))$.

Proof

This follows from Propositions 5.5 and Lemma 6.5. $\square$

Proposition 6.13

Assume M satisfies (FFC) and let $(Z_j)$, $1 \le j \le N$, be a Fréchet generating system for ${\mathcal {W}}_b(M)$. Let us assume also that $E, F \in {\mathcal {H}}(M)$ and have totally bounded curvature. Then, $bi{\text{- }}\!{\text {Diff}}_{b, \nabla }^{(m,m')}(M; E, F)$ is linearly generated by sesquilinear maps ${\mathfrak {b}}$ of the form ${\mathfrak {b}}(u \otimes {\overline{w}}) = \big (a \nabla ^E_{Z_{k_1}} \ldots \nabla ^E_{Z_{k_r}} u, \nabla ^E_{Z_{j_1}} \ldots \nabla ^E_{Z_{j_s}}\big )_G$, where $1 \le k_1 \le k_2 \le \ldots \le k_r \le N$, $1 \le j_1 \le j_2 \le \ldots \le j_s\le N$, $r\le m$, $s\le m'$, and $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(E; G))$.

Proof

This follows from Corollary 5.15(ii) and Proposition 6.9. $\square$

We conclude with the following proposition.

Proposition 6.14

Assume that M satisfies (FFC) and $E, F \in {\mathcal {H}}(M)$. Let $m,m'\in {\mathbb {Z}}_+$, $p,p'\in [1,\infty ]$ be such that $\frac{1}{p}+\frac{1}{p'}=1$, and ${\mathfrak {b}}\in bi{\text{- }}\!{\text {Diff}}_{b, \nabla }^{(m,m')}(M; E, F)$. Then, $B_{\mathfrak {b}}^{\nabla }$ of Definition 6.7 extends to a continuous, sesquilinear map

$$\begin{aligned} B_{\mathfrak {b}}^{\nabla } : W_{\nabla }^{m,p}(M; E) \times W_{\nabla }^{m',p'}(M; F) \rightarrow {\mathbb {C}}\,. \end{aligned}$$

and, consequently, $P_{\mathfrak {b}}^\nabla$ extends to a continuous map

$$\begin{aligned} P_{\mathfrak {b}}^{\nabla } : W_{\nabla }^{m,p}(M; E) \rightarrow W_{\nabla }^{m',p'}(M; F)^*. \end{aligned}$$

Moreover, the induced map $W_{\nabla }^{m,p} (M; E) \rightarrow W_{\nabla }^{-m',p}(M; F)$ is a $\nabla$-differential operator of order $\le m +m'$ with $W_{\nabla }^{\infty , \infty }$-coefficients. More precisely, if ${\mathfrak {b}}^\nabla$ is as in Lemma 6.5, then

$$\begin{aligned} P_{\mathfrak {b}}^{\nabla } \, = \,\sum _{i=1}^m\sum _{j=1}^{m'}(\nabla ^j)^* {\mathfrak {a}}_{ij} \nabla ^i \in {\text {Diff}}_{b, \nabla }^{(m,m')}(M; E, F) \,. \end{aligned}$$

Proof

By linearity, we can assume that ${\mathfrak {b}}(u \otimes {\overline{w}}) = (a \nabla ^i u, \nabla ^j w)_{T^{*\otimes j}M \otimes F}$, where $a \in W_{\nabla }^{\infty , \infty }(M; {\text {Hom}}(T^{*\otimes i}M \otimes E; T^{*\otimes j}M \otimes F)$. Then $P = (\nabla ^j)^* a \nabla ^i \in {\text {Diff}}_{b, \nabla }^{(m,m')}(M; E, F)$ by Propositions  4.5 and 5.12(ii). The result then follows from definitions. $\square$

7 Weighted Sobolev spaces

One of the main reasons for our interest in general Sobolev spaces on manifolds is that they are useful in the study of weighted Sobolev spaces. In turn, weighted Sobolev spaces are useful in the study geometric problems on singular spaces, such as the Yamabe problem [1, 26, 65]. As with the Sobolev spaces on manifolds, we need to consider connections. Thus, in this section, we introduce the $\nabla$-weighted Sobolev spaces and provide some of their main properties that follow from the corresponding properties for the non-weighted spaces. Recall that M is a smooth Riemannian manifold with a given metric g; however, since we will consider more than one metric on M, we shall indicate the metric in the notation of Sobolev spaces.

7.1 Non-negative order weighted Sobolev spaces

We begin with the definition of non-negative order weighted Sobolev spaces and discuss their relation with the standard Sobolev spaces (Definition 3.1).

Definition 7.1

Let $\rho , f_0: M \rightarrow (0, \infty )$ be given measurable functions. Let $s\in {{\mathbb {N}}}$ and $p\in [1,+\infty ]$. Then,

$$\begin{aligned} f_0 {\mathcal {W}}_{\nabla , \rho }^{s, p} (M,g; E) \mathrel {\ := \ }\{u \, \vert \ \rho ^j \nabla ^j (f_0^{-1} u) \in L^p(M,g; E) \,,\, \text{ for } \, 0 \le j \le s\}\,, \end{aligned}$$

(27)

is the order s, $L^p$–type weighted Sobolev space of sections of E (in particular, $f_0{\mathcal {W}}_{\nabla , \rho }^{0, p} = f_0L^p$), endowed with the norm

$$\begin{aligned} \Vert u\Vert _{f_0 {\mathcal {W}}_{\nabla , \rho }^{s, p}} \mathrel {\ := \ }\ell ^p\text{--norm } \text{ of } \{ \Vert \rho ^j \nabla ^j (f_0^{-1} u)\Vert _{L^p}\,,\ 0 \le j \le s \} \,. \end{aligned}$$

(28)

In the above definition, the connection $\nabla$ denotes, as usual, either the connection on E or the connections induced on $T^{*\otimes j} M \otimes E$ using also the Levi–Civita connection associated with g. We stress that in the definition of weighted spaces, we are not making more general assumptions on $\rho$ and $f_0$ other than that they are measurable. However, often in applications, we shall assume that $\rho$ and $f_0$ are “admissible weights” [10], a concept recalled next.

Definition 7.2

Let $f_0 : M_0 \rightarrow (0, \infty )$ be a function defined on a smooth Riemannian manifold $M_0$ endowed with a metric $g_0$ and associated Levi–Civita connection $\nabla _0$. We shall say that $f_0$ is $g_0$-admissible (or, simply, admissible if the metric $g_0$ is implicit) if it is smooth and $f_0^{-1} df_0 \in W^{\infty ,\infty }_{\nabla _0}(M_0, g_0;T^*M_0)$.

The weighted spaces are quite important in applications to geometry [2, 11, 32, 33, 35, 54] or to PDEs [19, 22, 27,28,29, 46, 47]. In fact, we think that our results will lead to geometric applications, but that would require the results of our second paper in this series [34], which is more geometric in nature and deals, among other things, with issues related to the Christoffel’s symbols. The study of the weighted Sobolev spaces considered in this paper is similar to that of the standard (unweighted) Sobolev spaces, since, in fact, we can relate the weighted and non-weighted spaces through conformal changes of metric, see, for instance, [3, 9, 10], by Proposition 7.3. One leads to consider weighted spaces even if one is interested only on PDEs on domains in ${\mathbb {R}}^n$, since they are useful in the study of polyhedral domains and of other singular spaces. If $f_0 = \rho = 1$, these spaces, of course, reduce to the standard $L^p$–type Sobolev space $W_{\nabla }^{s, p} = 1{\mathcal {W}}_{\nabla , 1}^{s,p}$ considered above.

7.2 Negative and non-integer order weighted Sobolev spaces

As in the case of the usual covariant Sobolev spaces, when considering negative and non-integer order weighted Sobolev spaces, we assume that the boundary $\partial M = \emptyset$. Let now $\ell \in {\mathbb {N}}$, $1<p<+\infty$, and $f_0 \mathring{\mathcal {W}}_{\nabla ,\rho }^{\ell ,p}(M,g; E)$ be the closure of the space ${{\mathcal {C}}}^{\infty }_{\text {c}}(M;E)$ in $f_0 {\mathcal {W}}_{\nabla , \rho }^{\ell ,p} (M,g; E)$. We use the space $f_0 \mathring{\mathcal {W}}_{\nabla ,\rho }^{\ell ,p}(M,g; E)$ to define the weighted Sobolev space with negative index

$$\begin{aligned} f_0 {\mathcal {W}}_{\nabla ,\rho }^{-\ell ,p} (M,g; E^*) \mathrel {\ := \ }\left( f_0^{-1} \mathring{\mathcal {W}}_{\nabla ,\rho }^{\ell , p'}(M,g; E)\right) ^* \,, \end{aligned}$$

(29)

where $\frac{1}{p}+\frac{1}{p'}=1$. Recall that we identify $E^*$ with E using the Hermitian metric on E, so $f_0 {\mathcal {W}}_{\nabla ,\rho }^{-\ell ,p}(M,g; E^*) \simeq f_0 {\mathcal {W}}_{\nabla ,\rho }^{-\ell ,p}(M,g; E)$.

Then, if $s \in {\mathbb {R}}$ is not an integer, we define the spaces $f_0{\mathcal {W}}_{\nabla , \rho }^{s , p} (M,g;E)$ by interpolation, so that the relation of Proposition 7.3 is still satisfied.

7.3 Properties of weighted Sobolev spaces

Recall that g is the given metric of the n-dimensional manifold M and $\nabla$ is its associated Levi–Civita connection. Assume that $\rho : M \rightarrow (0,\infty )$ is a smooth function. Let $g_0 := \rho ^{-2}g$ and $\nabla _0$ be the associated Levi-Civita connection. We assume also that $\rho :M\rightarrow (0,\infty )$ is an admissible weight with respect to the metric $g_0$, that is, $\rho$ is smooth and $\rho ^{-1}d\rho \in W_{\nabla _0}^{\infty , \infty }(M, g_0; T^*M)$ (see Definition 7.2). Let ${{\text {grad}}}_{g_0}\phi$ denote the vector field that represents the image of $d\phi$ in TM under the metric $g_0$. If $\rho = e^\phi$, then we have the following relation between $\nabla$ and $\nabla _0$:

$$\begin{aligned} A(X, Y) \mathrel {\ := \ }(\nabla -\nabla _0)_X Y \, = \,X(\phi )Y + Y(\phi )X - g_0(X,Y) {{\text {grad}}}_{g_0}\phi \,, \end{aligned}$$

(30)

(see, for instance, formula (5) in [8]).

We then obtain the following folklore result (but see, for instance, [3, 9, 10, 13])

Proposition 7.3

Let A be as in Eq. (30), then $A \in W_{\nabla _0}^{\infty , \infty }(M, g_0; T^{* \otimes 2} M \otimes TM)$. Let $\ell \in {\mathbb {Z}}_+$ and $p\in [1, \infty ]$. Consequently,

$$\begin{aligned} f_0{\mathcal {W}}_{\nabla , \rho }^{\ell , p} (M,g;E) \, = \,f_0 \rho ^{-\frac{n}{p}} W_{\nabla }^{\ell , p}(M,g_0; E) \, = \,f_0 \rho ^{-\frac{n}{p}} W_{\nabla _0}^{\ell , p}(M,g_0; E)\,, \end{aligned}$$

with equality of the norms for the first two spaces and equivalence of the norms for the last two spaces.

Proof

First, we have that $f_0{\mathcal {W}}_{\nabla , \rho }^{\ell , p} (M,g;E) \, = \,f_0 \rho ^{-\frac{n}{p}} W_{\nabla }^{\ell , p}(M,g_0; E)$ with equality of norms since this just amounts to a scaling of the norm on $T^*M$ and of the volume form (the covariant derivative does not change).

To prove the second equivalence of normed spaces, let $\phi := \ln \rho$, as above. Our assumption is that $d\phi \in W_{\nabla _0}^{\infty , \infty }(M; T^*M)$. We have

$$\begin{aligned} A = d \phi \otimes id_{TM} + id_{TM} \otimes d \phi + g_0 {{\text {grad}}}_{g_0}\phi . \end{aligned}$$

Hence $A \in W_{\nabla _0}^{\infty , \infty } (M, g_0; T^{* \otimes 2} M \otimes TM)$ by Lemma 3.4 and Corollary 3.5. Proposition 4.8 then gives that $W_{\nabla _0}^{\ell , p}(M,g_0; E) = W_{\nabla }^{\ell , p}(M,g_0; E)$. $\square$

This relation between weighted and unweighted Sobolev spaces proves that the weighted Sobolev spaces are also Banach spaces and it provides a strong motivation for our work, even if one is not interested in PDEs on manifolds, since weighted spaces appear naturally in the study of PDEs on polyhedral domains (thus even in the flat space). If $g_0$ has bounded geometry and the admissible weight $\rho$ is bounded, then the triple $(M, g_0, \rho )$ is called an Amann triple [10]. We have the following result.

Proposition 7.4

Let $\ell \in {\mathbb {Z}}_+$ and $p,q,r \in [1, \infty ]$ be such that $\frac{1}{p} + \frac{1}{q}=\frac{1}{r}$, $E, F \in {\mathcal {H}}(M)$. Let $\rho : M\rightarrow (0,\infty )$ be an admissible weight with respect to the metric $g_0 = \rho ^{-2}g$, then the bilinear map

$$\begin{aligned} f_0 {\mathcal {W}}_{\nabla , \rho }^{\ell , p}(M,g; {\text {Hom}}(E; F))\times h_0{\mathcal {W}}_{\nabla , \rho }^{\ell ,q}(M,g;E) \ni (a, u)\, \mapsto \, au \in f_0 h_0 {\mathcal {W}}_{\nabla , \rho }^{\ell ,r}(M,g; F) \end{aligned}$$

is continuous.

Proof

In view of Proposition 3.7, we obtain the continuity of the natural tensor product map (of the product of classical Sobolev spaces defined with respect to the metric $g_0$)

$$\begin{aligned} W_{\nabla _0}^{\ell , p}(M,g_0; {\text {Hom}}(E; F))\times W_{\nabla _0}^{\ell ,q}(M,g_0;E) \hookrightarrow W_{\nabla _0}^{\ell ,r}(M,g_0;E)\,. \end{aligned}$$

Then, Proposition 7.3 implies the continuity of the natural product map

$$\begin{aligned}&f _0 {\mathcal {W}}_{\nabla , \rho }^{\ell , p}(M,g; {\text {Hom}}(E; F))\times h_0{\mathcal {W}}_{\nabla , \rho }^{\ell ,q}(M,g;E)\\&\quad = f_0\rho ^{-\frac{n}{p}} W_{\nabla _0}^{\ell , p}(M,g_0;{\text {Hom}}(E; F)) \times h_0\rho ^{-\frac{n}{q}} W_{\nabla _0}^{\ell ,q}(M,g_0;E)\\&\qquad \hookrightarrow (f_0h_0)\rho ^{-(\frac{n}{p}+\frac{n}{q})} W_{\nabla _0}^{\ell ,r}(M,g_0;E)\\&\quad = f_0h_0 \rho ^{-\frac{n}{r}} W_{\nabla _0}^{\ell ,r}(M,g_0;E) = f_0h_0 {\mathcal {W}}_{\nabla , \rho }^{\ell ,r}(M,g;E)\,, \end{aligned}$$

that is, the desired result. $\square$

We shall use P to denote all the maps in Corollary 5.13 induced by the original P. Recall that M is an n-dimensional manifold with metric g and $\nabla$ is the associated Levi–Civita connection.

Corollary 7.5

Let $1<p<\infty$ and $E, F \in {\mathcal {H}}(M)$. Let $\rho , f_0: M \rightarrow (0, \infty )$ be admissible weights with respect to the metric $g_0=\rho ^{-2}g$ with $\rho$ bounded. Let $P = \sum _{j=0}^{\mu } a_j \nabla ^j$ and $a_{j} \in W_{\nabla _0}^{\infty , \infty }(M,g_0;{\text {Hom}}(E; F))$, that is P is a $\nabla$-differential operator with coefficients in $W_{\nabla _0}^{\infty , \infty }$ with respect to the metric $g_0$. Then, P extends by continuity to maps

$$\begin{aligned} f_0 {\mathcal {W}}_{\nabla , \rho }^{s , p}(M,g; E) \, \rightarrow \, f_0 \rho ^{-\mu } {\mathcal {W}}_{\nabla , \rho }^{s -\mu , p}(M,g; F)\,, \quad s \in {\mathbb {R}}\,. \end{aligned}$$

Proof

The assumption that $\rho$ and $f_0$ are $g_0$-admissible shows that $f_0^{-1} \rho ^{\mu }Pf_0$ is a $\nabla$-differential operator with coefficients in $W_{\nabla _0}^{\infty , \infty }$ with respect to the metric $g_0$. Then, in view of Corollary 5.13, this operator extends by continuity to the maps

$$\begin{aligned} W_{\nabla _0}^{s , p}(M,g_0;E)\rightarrow W_{\nabla _0}^{s -\mu ,p}(M,g_0;F)\,, \quad s \in {{\mathbb {N}}}\,. \end{aligned}$$

(31)

Then, Proposition 7.3 and the mapping property (31) show that P extends by continuity to the maps given in the statement. $\square$

Many operators with non-smooth coefficients can be treated by observing that the set of $\nabla$-differential operators with coefficients in $W_{\nabla }^{\ell , \infty }$ is $W_{\nabla }^{\ell , \infty }(M; {\text {End}}(F)) {\text {Diff}}_{b, \nabla }^{\infty }(M; E, F)$. In particular, this set does not depend on the connection if we perturb it with an $A \in W_{\nabla }^{\ell , \infty }$. We can prove mapping properties for these operators as before. These results can easily be stated and proved by the reader. Also, one could deal with the continuity of operators of the form $P_{\mathfrak {b}}$, as in the preceding section, but we leave this for another paper, where we will also discuss applications of these results.