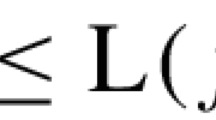Abstract
We study the \(L^p\)-spectrum of the Dirac operator on complete manifolds. One of the main questions in this context is whether this spectrum depends on p. As a first example where p-independence fails we compute explicitly the \(L^p\)-spectrum for the hyperbolic space and its product with compact spaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The \(L^p\)-spectrum of the Laplacian and its p-(in)dependence was and still is studied by many authors, e.g. in [17, 18, 22]. On closed manifolds one easily sees that the spectrum is independent of \(p\in [1,\infty ]\). For open manifolds, independence only holds under additional geometric conditions. Hempel and Voigt [22, 23] proved such results for Schrödinger operators in \(\mathbb {R}^n\) with potentials admitting certain singularities. Then Kordyukov [27] generalized this result to uniformly elliptic operators with uniformly bounded smooth coefficients on a manifold of bounded geometry with subexponential volume growth. Independently, Sturm [34] showed the independence of the \(L^p\)-spectrum for a class of uniformly elliptic operators in divergence form on manifolds with uniformly subexponential volume growth and Ricci curvature bounded from below. Both results include the Laplacian acting on functions. Later the Hodge-Laplacian acting on k-forms was considered. E.g. under the assumptions of the result by Sturm from above, Charalambous proved the \(L^p\)-independence for the Hodge-Laplacian in [14, Proposition 9]. The machinery used to obtain these independence results uses estimates for the heat kernel as in [32].
In contrast, the \(L^p\)-spectrum of the Laplacian on the hyperbolic space does depend on p [16, Theorem 5.7.1]. Its \(L^p\)-spectrum is the convex hull of a parabola in the complex plane, and this spectrum degenerates only for \(p=2\) to a ray on the real axis, cf. Remark 10.1.
In addition to the intrinsic interest of the p-independence of the \(L^p\)-spectrum, such results were used to get information on the \(L^2\)-spectrum by considering the \(L^1\)-spectrum, as in particular examples the \(L^1\)-spectrum can be easier to control. The result of Sturm was used for example by Wang [37, Theorem 3] to prove that the spectrum of the Laplacian acting on functions on complete manifolds with asymptotically non-negative Ricci curvature is \([0,\infty )\).
Some explicit calculations for the \(L^p\) spectrum of the Laplace–Beltrami operator on symmetric spaces were already carried by Lahoué and Rychener in the 1980’s [29], and Taylor [36] was able to determine the \(L^p\)-spectrum of this operator for all symmetric spaces of non-compact type. For locally symmetric spaces important progress was made recently by Ji and Weber, see e.g. [24–26, 39].
About the \(L^p\)-spectrum of the Dirac operator much less is known. As before, on closed manifolds the spectrum is independent on \(p\in [0,\infty ]\). Kordyukov’s methods [27] do not apply directly to the Dirac operator D, but following a remark of [27, Page 224] his methods generalize to suitable systems, and thus also to the square \(D^2\). Unfortunately, the system case is not completely worked out, but it seems to us, that the case of systems is completely analogous to the case of operators on functions. Assuming this, Kordyukov has shown that the spectrum of \(D^2\) is p-independent for \(1\le p<\infty \) on manifolds with bounded geometry and subexponential volume growth. For many such manifolds (e.g. for all such manifolds of even dimension or all manifolds of dimension \(4k+1\)), this already implies the p-independence of the \(L^p\)-spectrum of D, see our Lemma B.8 together with the following symmetry considerations.
Many of the results and techniques that were constructed up for Laplace operators are not yet developed for Dirac operators. It is interesting to compare the properties of the Dirac and Laplace operator. Furthermore, the \(L^p\)-spectrum of the Dirac operator is important for non-linear variational problems based on the Dirac operator, e.g., for (classical) Dirac operators certain \(L^p\)-spaces and \(L^p\)-spectral gaps naturally occur when considering a spinorial Yamabe-type problem which was our motivation to enter into this subject, see [5] and below.
In this paper we determine explicitly the \(L^p\)-spectrum for a special class of complete manifolds—products of compact spaces with hyperbolic spaces. More precisely, we study the following manifolds:
Let \((N^n,g_N)\) be a closed Riemannian spin manifold. Let \(M=\mathbb {M}_c\) be the product manifold \((\mathbb {M}_c^{m,k}= \mathbb {H}_c^{k+1}\times N^n, g_M=g_{\mathbb {H}_c^{k+1}}+g_N)\) where \(\mathbb {H}_c^{k+1}\) is the \((k+1)\)-dimensional hyperbolic space scaled such that its scalar curvature is \(-c^2k(k+1)\) for \(c\ne 0\) and \(\mathbb {H}_0^{k+1}\) is the \((k+1)\)-dimensional Euclidean space. For those manifolds we obtain the following result which is also illustrated in Fig. 1:
Theorem 1.1
We use the notions from above. Let \(p\in [1,\infty ]\), \(c\ge 0\), and \(k\in \mathbb {N}\cup \{0\}\). The \(L^p\)-spectrum of the Dirac operator on \(\mathbb {M}_c^{m,k}=\mathbb {H}_c^{k+1}\times N^n\) is given by the set
where \(\lambda _0^2\) is the lowest eigenvalue of \((D^N)^2\), \(\lambda _0\ge 0\), and \(D^N\) is the Dirac operator on \((N, g_N)\). In particular, the Dirac operator \(D:H_1^p\rightarrow L^p\) on \(\mathbb {M}_c^{m,k}\) has a bounded inverse if and only if \(\lambda _0> ck | \frac{1}{p}-\frac{1}{2}|\).
Note that we also allow the case \(n=0\), i.e. the case that N is a finite set. In this case we define \(\lambda _0:=0\).
For an overview of the structure of the proof, see the end of the introduction.
From the Theorem 1.1 one can directly read off the \(L^p\)-spectrum of \(D^2\) and compare it to the known spectrum of the Laplacian acting on functions which is done in Remark 10.1.
The shaded region (including the boundary) illustrates the \(L^p\)-spectrum of the Dirac operator on \(\mathbb {M}_c^{m,k}=\mathbb {H}_c^{k+1}\times N^n\), \(k\ge 1\), cf. Theorem 1.1. Left \(\lambda _0=0\) \((x_L= ck|\frac{1}{p}-\frac{1}{2}|)\). Middle \(0<\lambda _0<ck|\frac{1}{p}-\frac{1}{2}|\) \((x_M=( c^2k^2(\frac{1}{p}-\frac{1}{2})^2-\lambda _0^2)^{\frac{1}{2}} )\). Right \(\lambda _0>ck|\frac{1}{p}-\frac{1}{2}|\) \((x_R=( \lambda _0^2-c^2k^2(\frac{1}{p}-\frac{1}{2})^2)^{\frac{1}{2}} )\)
As mentioned above our interest in the \(L^p\)-spectrum for the Dirac operator on such spaces comes from an application in conformal spin geometry which we want to sketch very briefly: In the article [3] the first named author studied the behavior of a spinorial analogue of the Yamabe invariant under surgeries. In these Gromov–Lawson type constructions an important role was played by spinorial Yamabe-type invariants on the spaces \(\mathbb {H}_c^{k+1}\times \mathbb {S}^n\) where c is in [0, 1] and where \(\mathbb {S}^n\) is the standard sphere. When these invariants were studied in [21], the important role of the \(L^p\)-spectrum of the Dirac operator on such spaces became apparent. The results of the present article are preliminaries for some theorems about spinorial Yamabe-type invariants in [5].
The paper is structured as follows: Notations and preliminaries are collected in Sect. 2. Results on the Green function of the Dirac operator acting on \(L^2\)-spinors can be found in Sect. 3. General remarks and results for the Dirac operator acting on \(L^p\)-sections are given in Appendix B.
In Sect. 4, the Dirac operator on the model spaces \(\mathbb {M}_c^{m,k}\) is written in polar coordinates and the action of \(\mathrm{Spin}(k+1)\) on \(\mathbb {M}_c^{m,k}\) is studied. This is used in Sect. 5 to prove a certain symmetry property of the Green function on \(\mathbb {M}_c^{m,k}\) and in Sect. 6 to study its decay.
After these preparations we are ready to prove the main theorem (Theorem 1.1). In Sect. 7 we decompose the Green function into a singular part and the integral kernel of a smoothing operator. Using the homogeneity of the hyperbolic space we show in Proposition 7.1 that the singular part gives rise to a bounded operator from \(L^p\) to itself for all \(p\in [1,\infty ]\). In Proposition 7.2 we show that under certain assumptions on the decay of the Green function also the smoothing part gives rise to a bounded operator from \(L^p\) to \(L^p\) for certain p. Using the decay estimate obtained in Sect. 6 we then see in Sect. 8 that the \(L^p\)-spectrum of \(\mathbb {M}_c^{m,k}\) is contained in the set \(\sigma _p\) given in Theorem 1.1.
Thus, it only remains to show that each element of \(\sigma _p\) is already in the \(L^p\)-spectrum of \(\mathbb {M}_c^{m,k}\). For that we construct test spinors on \(\mathbb {H}_c^{k+1}\) in Sect. 9 and finish the proof for product spaces in Sect. 10.
2 Preliminaries
2.1 Notations and conventions
In the article we will use the convention that a spin manifold is a manifold which admits a spin structure together with a fixed choice of spin structure.
Let (M, g) be a spin manifold and \(\Sigma _M\) the corresponding spinor bundle, see Sect. 2.3.
\(\Gamma (\Sigma _M)\) denotes the space of spinors, i.e., sections of \(\Sigma _M\). The space of smooth compactly supported sections is denoted by \(C_c^\infty (M, \Sigma _M)\), or shortly \(C_c^\infty (\Sigma _M)\). The hermitian metric on fibers of \(\Sigma _M\) is denoted by \(\langle .,.\rangle \), the corresponding norm by |.|. For \(s_1,s_2\in \Gamma (M, \Sigma _M)\) we define the \(L^2\)-scalar product
For \(s\in [1,\infty ]\) \(\Vert . \Vert _{L^s(g)}\) is the \(L^s\)-norm on \((M^n,g)\). In case the underlying metric is clear from the context we abbreviate shortly by \(\Vert . \Vert _s\).
\(\mathrm Spec_{L^s}^M(D)\) denotes the spectrum of the Dirac operator on M viewed as an operator from \(L^s\) to \(L^s\), cf. Appendix B.
We denote by \(\pi _i:M\times M\rightarrow M\), \(i=1,2\), the projection to the i-th component. Moreover, we set \(\Sigma _M \boxtimes \Sigma _M^*:=\pi _1^*(\Sigma _M)\otimes \pi _2^*(\Sigma _M^*)\).
\(C^i(M)\) denotes the space of i-times continuously differentiable functions on M.
\(B_\epsilon (x)\subset M\) is the ball around \(x\in M\) of radius \(\epsilon \) w.r.t. the metric given on M.
A Riemannian manifold is of bounded geometry, if its injectivity radius is positive and the curvature tensor and all derivatives are bounded.
The metric on the k-dimensional sphere \(\mathbb {S}^k\) with constant sectional curvature 1 will be denoted by \(\sigma ^k\). For \(\mathbb {S}^k\) with metric \(r^2\sigma ^k\) we write \(\mathbb {S}^k_r\).
2.2 Coordinates and notations for \(\mathbb {H}_c^{k+1}\) and its product spaces.
We use polar coordinates on \(\mathbb {H}_c^{k+1}\). Namely, we fix a point \(p_0\in \mathbb {H}_c^{k+1}\) and an identification of \(T_{p_0}\mathbb {H}_c^{k+1}\) with \(\mathbb {R}^{k+1}\). Often we also use the exponential map to identify \(T_{p_0}\mathbb {H}_c^{k+1}\cong \mathbb {R}^{k+1}\) with \(\mathbb {H}_c^{k+1}\). In polar coordinates the metric is then \(g_{\mathbb {H}_c^{k+1}}=\mathrm {d}r^2 +f(r)^2\sigma ^k \) where \(\sigma ^k\) is the standard metric on \(\mathbb {S}^k\) and
In particular, the distance \(r=\mathrm {dist}_{\mathbb {H}_c^{k+1}}(y,p_0)\) of y to \(p_0\cong 0\) w.r.t. \(g_{\mathbb {H}_c^{k+1}}\) coincides with the euclidean one on \(\mathbb {R}^{k+1}\). The subset \(\{ y\in \mathbb {H}_c^{k+1}\ |\ \mathrm {dist}_{\mathbb {H}_c^{k+1}}(y,0)=r\}\) is isometric to \(\mathbb {S}_{f(r)}^k\) and its (unnormalized) mean curvature is given by
Let N be a closed Riemannian spin manifold. Note that we include the case where N is just a point. Set \(\mathbb {M}_c^{m,k}:= \mathbb {H}_c^{k+1}\times N\), and \(\pi _{\mathbb {H}}\) shall denote the projection of \(\mathbb {M}_c^{m,k}\) onto its \(\mathbb {H}_c^{k+1}\)-coordinates.
2.3 General preliminaries about spin geometry
The following can e.g. be found in [19]. A spin structure on \(M^m\) is a pair \((P_\mathrm{Spin}(M),\alpha )\) where \(P_\mathrm{Spin}(M)\) is a principal \(\mathrm{Spin}(m)\)-bundle and where \(\alpha :P_\mathrm{Spin}(M)\rightarrow P_\mathrm{SO}(M)\) is a fiber map over the identity of M that is compatible with the double covering \(\Theta :\mathrm{Spin}(m)\rightarrow \mathrm{SO}(m)\) and the corresponding group actions, i.e., the following diagram commutes

Let \(\Sigma _m\) be an irreducible representation of \(\mathrm{Cl}_m\). In case m is odd there are two such irreducible representations. Both of them coincide if considered as \(\mathrm{Spin}(m)\)-representations. For m odd we fix one of the two representations for the whole article. If m is even, there is only one irreducible \(\mathrm{Cl}_m\)-representation of \(\Sigma _m\), but it splits into non-equivalent subrepresentations \(\Sigma _m^{(+)}\) and \(\Sigma _m^{(-)}\) as \(\mathrm{Spin}(m)\)-representations.
Define \(\omega _M=\mathrm {i}^{[\frac{m+1}{2}]} e_1\cdot e_2\cdot \cdots \cdot e_m\) with \((e_i)_i\) being a positively oriented orthonormal frame on M. We have \(\omega _M^2=1\). If m is odd, then \(\omega _M\) commutes with the Clifford multiplication and thus acts as \(+1\) or \(-1\) on \(\Sigma _m\). If m is even, the it acts as \(\pm 1\) on \(\Sigma _m^{(\pm )}\). Sections of \(\Sigma _m^{(+)}\) (resp. \(\Sigma _m^{(-)}\)) are called positive (resp. negative) spinors.
In the article it will be convenient to use the notation \(\Sigma _{m}^{(\epsilon )}\), \(\epsilon \in \{0+,-\}\) also in the case m odd as well, by setting \(\Sigma _{m}^{(\epsilon )}=\Sigma _m\) for both choices of \(\epsilon \).
The spinor bundle \(\Sigma _M\) is defined as \(\Sigma _M=P_\mathrm{Spin}(M)\times _{\rho _m} \Sigma _m\) where \(\rho _m:\mathrm{Spin}(m)\rightarrow \mathrm{End}(\Sigma _m)\) is the complex spinor representation. Moreover, the spinor bundle is endowed with a Clifford multiplication, denoted by ’\(\cdot \)’, \(\cdot :TM\rightarrow \mathrm{End}(\Sigma _M)\). Then, the Dirac operator acting on the space of smooth sections of \(\Sigma _M\) is defined as the composition of the connection \(\nabla \) on \(\Sigma _M\) (obtained as a lift of the Levi-Civita connection on TM) and the Clifford multiplication. Thus, in local coordinates this reads as
where \((e_i)_{i=1,\ldots ,m}\) is a local orthonormal basis of TM. The Dirac operator is formally self-adjoint as an operator on \(L^2\), i.e., for \(\psi \in C^\infty (M, \Sigma _M)\) and \(\varphi \in C_c^\infty (M, \Sigma _M)\) we have \((\varphi , D\psi )=(D\varphi , \psi )\).
As M is complete, the Dirac operator is not only formally self-adjoint, but actually has a unique self-adjoint extension that is a densely defined unbounded operator \(D:H_1^2(\Sigma _M)\subset L^2(\Sigma _M)\rightarrow L^2(\Sigma _M)\), see [41]. Here \(H_1^2(\Sigma _M)\) is the subset of all \(\varphi \in L^2(\Sigma _M)\) such that \(\nabla \varphi \), defined in the distributional sense, is again in \(L^2\). The notation above indicates that \(H_1^2(\Sigma _M)\) is the domain of the operator, and that “densely defined” and “self-adjoint” should be understood as an unbounded operator from \(L^2(\Sigma _M)\) to \(L^2(\Sigma _M)\). From the spectral theorem it follows that \(D-\mu :H_1^2(\Sigma _M)\subset L^2(\Sigma _M)\rightarrow L^2(\Sigma _M)\) is invertible for all \(\mu \not \in \mathbb {R}\), in the sense that the inverse is a bounded operator from \(L^2(\Sigma _M)\) to \(L^2(\Sigma _M)\). See also Appendices A and B for more details.
2.4 Dual spinors
The hermitian metric induces a natural isomorphism from \(\Sigma _M^*\) to \(\bar{\Sigma }_M\). In this way we obtain a metric connection and a Clifford multiplication on \(\Sigma _M^*\) and this allows us to define a Dirac operator \(D^\mathrm{t}:C^\infty (\Sigma _M^*)\rightarrow C^\infty (\Sigma _M^*)\). Locally \(D^\mathrm{t}f=\sum _i e_i\cdot \nabla _{e_i} f\) where \(f\in C^\infty (\Sigma _M^*)\) and \(e_i\) is a local orthonormal frame on M. Completely analogously to the proof that the usual Dirac operator is formally self-adjoint, one proves that for \(f\in C^\infty (\Sigma _M^*)\), \(\varphi \in C^\infty (\Sigma _M)\) such that \(\mathrm supp\, f\cap \mathrm supp\, \varphi \) is relatively compact we have
2.5 Spinors on product manifolds
In this subsection our notation is close to [8]. Let \((P^{m+n}=M^m\times N^n\), \(g_P=g_M +g_N)\) be a product of Riemannian spin manifolds \((M,g_M)\) and \((N,g_N)\). We have
where \(\xi :\mathrm{Spin}(m)\times \mathrm{Spin}(n)\rightarrow \mathrm{Spin}(m+n)\) is the Lie group homomorphism lifting the standard embedding \(\mathrm{SO}(m)\times \mathrm{SO}(n)\rightarrow \mathrm{SO}(m+n)\). Note that \(\xi \) is not an embedding, its kernel is \((-1,-1)\), where \(-1\) denotes the non-trivial element in the kernel of \(\mathrm{Spin}(m)\rightarrow \mathrm{SO}(m)\) resp. \(\mathrm{Spin}(n)\rightarrow \mathrm{SO}(n)\).
The spinor bundle can be identified with
and the Levi-Civita connection acts as \(\nabla ^{\Sigma _M\otimes \Sigma _N}= \nabla ^{\Sigma _M}\otimes {\text {Id}}_{\Sigma _N} + {\text {Id}}_{\Sigma _M}\otimes \nabla ^{\Sigma _N}\). This identification can be chosen such that for \(X\in TM\), \(Y\in TN\), \(\varphi \in \Gamma (\Sigma _M)\), and \(\psi =(\psi _1, \psi _2)\in \Sigma _N\oplus \Sigma _N\) for both n and m odd and \(\psi \in \Gamma (\Sigma _N)\) otherwise, we have
where for both n and m odd we set \(\omega _N\cdot _N (\psi _1, \psi _2):= \mathrm {i}(\psi _2, -\psi _1)\) and \(Y\cdot _N (\psi _1, \psi _2):= (Y\cdot _N \psi _2, Y\cdot _N \psi _1)\).
The Dirac operator is then given by
where \(\tilde{D}^N=\mathrm{diag} (D^N, -D^N)\) if both m and n are odd and \(\tilde{D}^N=D^N\) otherwise.
Since \(\omega _N\cdot \) and \(\tilde{D}^N\) anticommute, \(D^M\otimes \omega _N\) and \(\mathrm{id}\otimes \tilde{D}^N\) anticommute as well. Thus
If we additionally assume that M and N are compact, then this equation implies together with the spectral theorem that the \(L^2\)-spectrum of the square of the Dirac operator on the product space \(M\times N\) is given by
2.6 The \(L^2\)-spectrum of the Dirac operator
The simplest case of Theorem 1.1 is when \(p=2\) and when N is a point. In this case we have by definition \(\lambda _0=0\). The theorem then states that the \(L^2\)-spectrum of the Dirac operator on \(\mathbb {H}_c^{k+1}\) is the whole real line \(\mathbb {R}\subset \mathbb {C}\). This fact was already known before, by scaling it suffices to consider the Euclidean case \(c=0\) and the hyperbolic case \(c=1\).
On Euclidean space \(\mathbb {R}^{k+1}=\mathbb {H}^{k+1}_0\) it is an easy calculation. The spinor bundle is trivialized by parallel orthonormal sections \(s_1,\ldots , s_t\) with t the rank of the spinor bundle. The Dirac operator preserves \(V_i:=C^\infty (\mathbb {R}^{k+1})\cdot s_i\), anticommutes with the Clifford action by parallel vector fields, and its square maps \(f\cdot s_i\) to \((\Delta f)\cdot s_i\). As \(\Delta \) has \(L^2\) spectrum \([0,\infty )\) on \(\mathbb {R}^{k+1}\), the statement follows.
On hyperbolic space, the \(L^2\)-spectrum of the Dirac operator was calculated by representation theoretical methods in [11]. Unfortunately [11] contains a small error, and the value 0 is not an eigenvalue of the Dirac operator in contrast to what is claimed in [11]. The argument can be repaired, and it follows that the spectrum is as claimed. A complete proof was given in [13], using similar techniques as in the present article.
We will not give a proof of this special case of Theorem 1.1, instead we will use this special case for the proof of the full version of Theorem 1.1.
Using the results of the previous subsection, we also get the \(L^2\)-spectrum of the Dirac operator on \(\mathbb {M}_c^{m,k}= \mathbb {H}_c^{k+1}\times N\): With Lemma B.8 we get
Together with Lemma B.11, Example B.12 and Lemma B.8 this yields
2.7 A covering lemma
Lemma 2.1
(Covering lemma) Let (M, g) be a Riemannian manifold of bounded geometry, and let \(R>0\). Then there are points \((x_i)_{i\in I}\subset M\) where I is a countable index set such that
-
(i)
the balls \(B_R(x_i)\) are pairwise disjoint and
-
(ii)
\((B_{2R}(x_i))_{i\in I}\) and \((B_{3R}(x_i))_{i\in I}\) are both uniformly locally finite covers of M.
Proof
Choose a maximal family of points \((x_i)_{i\in I}\) in M such that the sets \(B_{R}(x_i)\) are pairwise disjoint. Then \(\bigcup _{i\in I} B_{2R}(x_i)=M\). For \(y\in M\) let \(L(y)= \{ i\in I \ |\ y\in B_{3R}(x_i)\}\). For \(i\in L(y)\) we have \(B_{R}(x_i)\subset B_{4R}(y)\) and, thus,
where \(\sqcup \) denotes disjoint union. Comparing the volumes of both sides and using the bounded geometry of M we see that there exists a number \(L_R\) such that \(|L(y)|\le L_R\) for all \(y\in M\). Thus, the covering by sets \(B_{3R}(x_i)\), and hence the one by \(B_{2R}(x_i)\), is uniformly locally finite. \(\square \)
2.8 Interpolation theorems
Theorem 2.2
(Riesz–Thorin Interpolation Theorem, [40, Theorem II.4.2]) Let T be an operator defined on a domain \(\mathcal {D}\) that is dense in both \(L^q\) and \(L^{p}\). Assume that \(Tf\in L^q\cap L^p\) for all \(f\in \mathcal {D}\) and that T is bounded in both norms. Then, for any r between p and q the operator T is a bounded operator from \(L^r\) to \(L^r\).
Theorem 2.3
(Stein Interpolation Theorem, [16, Section 1.1.6], [30, Theorem IX.21]) Let \(p_0,q_0,p_1,q_1\in [1,\infty ]\), \(0<t<1\), and \(S=\{z\in \mathbb {C}\ |\ 0\le \mathrm {Re\,}z\le 1\}\). Let \(A_z\) be linear operators from \(L^{p_0}\cap L^{p_1}\) to \(L^{q_0}+L^{q_1}\) for all \(z\in S\) with the following properties
-
(i)
\(z\mapsto \langle A_zf, g\rangle \) is uniformly bounded and continuous on S and analytic in the interior of S whenever \(f\in L^{p_0}\cap L^{p_1}\) and \(g\in L^{r_0}\cap L^{r_1}\) where \(r_i\) is the conjugate exponent to \(q_i\).
-
(ii)
There is \(M_0>0\) such that \(\Vert A_{\mathrm {i}y}f\Vert _{q_0}\le M_0\Vert f\Vert _{p_0}\) for all \(f\in L^{p_0}\cap L^{p_1}\) and \(y\in \mathbb {R}\).
-
(iii)
There is \(M_1>0\) such that \(\Vert A_{1+\mathrm {i}y}f\Vert _{q_1}\le M_1\Vert f\Vert _{p_1}\) for all \(f\in L^{p_0}\cap L^{p_1}\) and \(y\in \mathbb {R}\).
Then, for \(1/p=t/p_1+(1-t)/p_0\) and \(1/q=t/q_1+(1-t)/q_0\)
for all \(f\in L^{p_0}\cap L^{p_1}\). Hence, \(A_t\) can be extended to a bounded operator from \(L^p\) to \(L^q\) with norm at most \(M_1^tM_0^{1-t}\).
3 The Green function
In this section, we collect results on existence and properties of the Green function of the Dirac operator D and its shifts \(D-\mu \), \(\mu \in \mathbb {C}\). They are obvious applications of standard methods, but a suitable reference does not exist yet. Unless otherwise stated we only assume in this section that the Riemannian spin manifold (M, g) is complete. Let \(\Delta :=\{(x,x)\mid x\in M\}\subset M\times M\) be the diagonal.
Definition 3.1
[6, Definition 2.1] A smooth section \(G_{D-\mu }:M\times M {\setminus } \Delta \rightarrow \Sigma _M\boxtimes \Sigma _M^*\) that is locally integrable on \(M\times M\) is called a Green function of the shifted Dirac operator \(D-\mu \) if
in the sense of distributions, i.e., for any \(y\in M\), \(\psi _0\in \Sigma _M|_y \), and \(\varphi \in C_c^\infty (\Sigma _M)\)
and \(G_{D-\mu }(., y)\in L^2(M{\setminus } B_r(y))\) for any \(r>0\).
In case that the operator \(D-\mu \) is clear from the context, we shortly write \(G=G_{D-\mu }\).
Proposition 3.2
If M is a closed Riemannian spin manifold with invertible operator \(D-\mu :H_1^2(\Sigma _M)\subset L^2(\Sigma _M)\rightarrow L^2(\Sigma _M)\), then a unique Green function exists. This Green function is the integral kernel of the inverse of \(D-\mu :H_1^2(\Sigma _M)\subset L^2(\Sigma _M)\rightarrow L^2(\Sigma _M)\).
To prove the well-known proposition, one usually starts by showing the existence of a parametrix.
Lemma 3.3
[28, III.§4] Let M be a closed Riemannian spin manifold. Then there is a smooth section \(P_{D-\mu }:M\times M {\setminus } \Delta \rightarrow \Sigma _M\boxtimes \Sigma _M^*\), called parametrix, which is \(L^1\) on \(M\times M\) and which satisfies
in the distributional sense for a smooth section \(R:M\times M \rightarrow \Sigma _M\boxtimes \Sigma _M^*\).
Let \(\epsilon >0\) be smaller than the injectivity radius. We choose \(\chi :[0,\infty )\rightarrow [0,1]\) smooth with support in \([0,\epsilon ]\) and constant to 1 in a neighborhood of 0. The statement of the lemma is still true is we replace \(P_{D-\mu }(x,y)\) by \(\chi (\mathrm {dist}(x,y))P_{D-\mu }(x,y)\) and an appropriately modified R. We thus can assume without loss of generality that the support \(P_{D-\mu }(x,y)\) and thus the support of R is in \((M\times M)_\epsilon :=\{(x,y)\in M\times M\,|\, \mathrm {dist}(x,y)<\epsilon \}\).
Convolution with \(P_{D-\mu }\) defines an operator \(\mathtt {P}_{D-\mu }\) by
for all \(\psi ,\varphi \in C_c^\infty (\Sigma _M)\). Then, \(\mathtt {P}_{D-\mu }\) is a right inverse to \({D-\mu }\) up to infinitely smoothing operators. We thus call it a right parametrix. The existence of such a right parametrix follows using the symbol calculus from the fact that D is an elliptic operator. An efficient and very readable overview over how to construct a right parametrix for an elliptic differential operator on a compact manifold can be found e.g. in [28, III.§4], although the reader should pay attention to the fact that it is not so obvious that the different notions of infinitely smoothing operators used in there are in fact all equivalent. The latter fact follows from standard techniques used in the theory of pseudo differential operators, see e.g. [1] or [35] for textbooks on this subject.
Proof of Proposition 3.2
From the last Lemma we have the existence of a parametrix \(P_{D-\mu }(x,y)\). We will use the notations of that Lemma. Since \(D-\mu \) is assumed to be invertible, there is a section \(P_{D-\mu }':M\times M\rightarrow \Sigma _M\boxtimes \Sigma _M^*\) with \((D_x-\mu ) P'_{D-\mu }(x,y)=R(x,y)\). By elliptic regularity \(P'_{D-\mu }(x,y)\) is smooth in x for each \(y\in M\). Again by elliptic regularity \((D-\mu )^{-1}\) is a continuous linear operator \(C_c^\infty (\Sigma _M)\rightarrow C^\ell (\Sigma _M)\) for any \(\ell \in \mathbb {N}\). Further \(P'_{D-\mu }(\,\cdot \,,y)\) is the composition
where the first map is the smooth map that maps \(\varphi \in \Sigma _M|_y\) to \(R(\,\cdot \,,y)\varphi \). This implies that \(P'_{D-\mu }(x,y)\) is smooth as function in both x and y. We set \(G_{D-\mu }(x,y)=P_{D-\mu }(x,y)-P'_{D-\mu }(x,y)\) and obtain \((D_x-\mu )(G_{D-\mu }(x,y))=\delta _y {\text {Id}}_{\Sigma _M|_y}\). Moreover, since \(P_{D-\mu }\) is \(L^1\) on \(M\times M\) and \(P_{D-\mu }'\) is smooth in both entries the Green function \(G_{D-\mu }\) is \(L^1\) as well. Furthermore, \(P_{D-\mu }(.,y)\) is smooth on \(M{\setminus } B_r(y))\) for any \(r>0\) and, hence, the same is true for \(G_{D-\mu }(.,y)\). In particular, \(G_{D-\mu }(.,y)\in L^2(M{\setminus } B_r(y))\). If \(\tilde{G}_{D-\mu }\) is a possibly different Green function of \(D-\mu \) then \((D-\mu )({G}_{D-\mu }(.,y)- \tilde{G}_{D-\mu }(.,y))=0\) for all \(y\in M\). As \(D-\mu \) is invertible we have \({G}_{D-\mu }=\tilde{G}_{D-\mu }\). \(\square \)
As for \(P_{D-\mu }\), convolution with \(G_{D-\mu }\) defines an operator \(\mathtt {G}_{D-\mu }\) by
for all \(\psi ,\varphi \in C_c^\infty (\Sigma _M)\). By construction \(\mathtt {G}_{D-\mu }\) is the right inverse of \(D-\mu \), and is thus even defined on \(L^2\). Since the inverse of \(D-\mu \) exists by assumption, \(\mathtt {G}_{D-\mu }=(D-\mu )^{-1}\), and \(\mathtt {G}_{D-\mu }\) is in particular also a left inverse of \(D-\mu \).
Lemma 3.4
Let M be a closed Riemannian spin manifold, and let \(D-\mu \) be invertible. Then \(G_{D-\mu }(x,y)\) is the adjoint of \(G_{D-\bar{\mu }}(y,x)\), i.e. \(G_{D-\bar{\mu }}(y,x)\) is the integral kernel of the adjoint operator of \(\mathtt {G}_{D-\mu }\).
Proof
Using the definitions and discussions from above and Lemma B.3(ii) we have \(\mathtt {G}_{D-\mu }^*=((D-\mu )^{-1})^*=(D-\bar{\mu })^{-1}=\mathtt {G}_{D-\bar{\mu }}\). In particular, we get for all \(\psi , \varphi \in L^2(\Sigma _M)\) that
\(\square \)
Moreover, we have
Lemma 3.5
In the situation of Lemma 3.4 we have \((D_y^\mathrm{t}-\mu ) G_{D-\mu }(x,y)=\delta _x{\text {Id}}_{\Sigma _M^*|_x}\), i.e., for \(f_0\in \Gamma ({\Sigma _M^*}|_{x})\), \(\varphi \in C_c^\infty (\Sigma _M)\)
Proof
where the last step uses that \(\mathtt {G}_{D-\mu }\) is also the left inverse of \(D-\mu \). \(\square \)
Now, M has no longer to be closed, but we assume bounded geometry.
Proposition 3.6
Let (M, g) be a Riemannian spin manifold of bounded geometry. Let \(D-\mu :H_1^2(\Sigma _M)\subset L^2(\Sigma _M)\rightarrow L^2(\Sigma _M)\) be invertible. Then there exists a unique Green function.
Proof
We choose \(R>0\) such that 3R is smaller than the injectivity radius. Let \((x_i)_{i\in I}\) be as in the Covering Lemma 2.1. Recall that \((M\times M)_\epsilon :=\{(x,y)\in M\times M\,|\, \mathrm {dist}(x,y)<\epsilon \}\). Because of \(M=\bigcup _{i\in I} B_{2R}(x_i)\) we have
We embed each ball \(B_{3R}(x_i)\) isometrically into a closed connected manifold \(M_{x_i}\), which is diffeomorphic to a sphere and \(D^{M_{x_i}}-\mu \) is invertible. This can always be achieved by local metric deformation on \(M_{x_i}{\setminus } B_{3R}(x_i)\), see Proposition C.1.
Thus, by Proposition 3.2 the operator \(D^{M_{x_i}}-\mu \) possesses a Green function \(G^{x_i}(x,y)\) with \((D^{M_{x_i}}_x-\mu )G^{x_i}(x,y)=\delta _y {\text {Id}}_{\Sigma _y}\). By abuse of notation we will view \(G^{x_i}(x,y)\) for \(x,y\in B_{3R}(x_i)\) also as a partially defined section of \(\Sigma _M\boxtimes \Sigma _M^*\rightarrow M\times M\), which is defined on \(B_{3R}(x_i)\times B_{3R}(x_i)\).
Now we choose smooth functions \(a_i\) on \(M\times M\) such that \(\mathrm supp\, a_i\subset B_{3R}(x_i)\times B_{3R}(x_i)\subset (M\times M)_{6R}\) and such that \(\sum _{i\in I}a_i\) equals to 1 on \((M\times M)_{R/2}\). Now we set
This implies \(\mathrm supp\, H\subset (M\times M)_{6R}\). Moreover, \(H(.,y)\in L^2(M{\setminus } B_r(y))\) for all \(r>0\) since this is true for each summand.
Our next goal is to prove that \((D_x-\mu ) H(x,y) - \delta _y {\text {Id}}_{\Sigma _y}\) is smooth. Note that \(G^{x_i}(x,y)\) and \(G^{x_j}(x,y)\) are both defined for \((x,y)\in (B_{3R}(x_i)\times B_{3R}(x_i))\cap (B_{3R}(x_j)\times B_{3R}(x_j))\), but they will not coincide in general. On the other hand their defining property and the locality of the differential operator D (cp. Lemma 3.5) imply that
Thus,
Since P is an elliptic operator, elliptic regularity implies that \(G^{x_i}(x,y)-G^{x_j}(x,y)\) viewed as a difference of distributions is a smooth function on \((B_{3R}(x_i)\times B_{3R}(x_i))\cap (B_{3R}(x_j)\times B_{3R}(x_j))\), and thus \(a_j(x,y)(G^{x_i}(x,y)-G^{x_j}(x,y))\) as well. On \(B_{3R}(x_j)\times B_{3R}(x_j)\) we rewrite
and we conclude that \((D_x-\mu )H(x,y)=\delta _y {\text {Id}}_{\Sigma _y} + F(x,y)\) where F(x, y) is a smooth section of \(\Sigma _M\boxtimes \Sigma _M^*\) with support in \((M\times M)_{6R}\).
There is a unique section \(H'\) of \(\Sigma _M\boxtimes \Sigma _M^*\) such that \((D_x-\mu )H'(x,y)=F(x,y)\) and such that \(H'(.,y)\) is \(L^2\) for all y. This follows for each y from the assumption that \(D-\mu \) is invertible. As \(D-\mu \) is a linear operator with continuous inverse and by elliptic regularity \(H'\) is smooth in x and y.
We set \(G(x,y)=H(x,y)-H'(x,y)\), and this gives a Green function for \(D-\mu \). Smoothness of G follows by smoothness of all \(G^{x_i}\), and smoothness of F and \(H'\).
Assume that G and \(\tilde{G}\) are two Green functions for D. We set \(\psi _y(x):=(G-\tilde{G})(x,y))\). For almost all \(y\in M\) the properties of the Green function imply \((D-\mu )\psi _y=0\) in the sense of distributions, \(\psi _y\in L^1_\mathrm{loc}(M)\) and \(\psi _y|_{M{\setminus } B_r(y)}\in L^2(M{\setminus } B_r(y))\). Local regularity implies \(\psi _y\in L^2(M)\). By the invertibility of \(D-\mu \) we btain \(\psi _y=0\) for almost all \(y\in M\) and thus \(G=\tilde{G}\). \(\square \)
Note that due to the last Proposition Lemmata 3.4 and 3.5 also hold true for manifolds M of bounded geometry.
We finish this section by stating another property of the Green function:
Lemma 3.7
Let (M, g) be a Riemannian spin manifold of bounded geometry, and let \(D-\mu \) be invertible. Then the Green function also decays in \(L^2\) in the second entry, i.e., \(G_{D-\mu }(x,.)\in L^2(M{\setminus } B_r(x))\) for all \(r>0\).
Proof
The Green function \(G_{D-\bar{\mu }}(.,x)\) is in \(L^2(M{\setminus } B_r(x))\) in the first component. Then the claim follows from Lemma 3.4 in the extended version to manifolds M of bounded geometry. \(\square \)
4 The Dirac operator on hyperbolic space and its products
In this section we examine the Dirac operator on the model spaces \(\mathbb {M}_c^{m,k}=\mathbb {H}_c^{k+1}\times N\). Note that we also allow the case where N is zero dimensional. First, we introduce polar coordinates on \(\mathbb {H}_c^{k+1}\) and write the Dirac operator in these coordinates. For this purpose it is convenient to introduce three foliations on the space \(M:=(\mathbb {H}_c^{k+1}\times N){\setminus } (\{p_0\}\times N)\), and to relate the associated Dirac operator with the Dirac operator on the total space. Then, we study the canonical action of \(\mathrm{Spin}(k+1)\) on \(\mathbb {M}_c^{m,k}\) and its spinor bundle.
4.1 The Dirac operator on a foliation
In this subsection we want to keep the notation rather general to allow other applications in future work. So we recall some well-known facts about Dirac operators on foliations, and describe them in a way suitable for our needs.
We assume that M is a Riemannian spin manifold with the Levi-Civita connection \(\nabla ^M\). To define foliations on M, we will choose our terminology close to Warner’s book, see [38, 1.56–1.64].
We assume that \(\mathcal {F}=\bigcup _{x\in M}\mathcal {F}_x\) is an \(\ell \)-dimensional distribution on M, so for each \(x\in M\), \(\mathcal {F}_x\) is an \(\ell \)-dimensional subspace of \(T_xM\), depending smoothly on x. In particular a distribution \(\mathcal {F}\) on M defines a vector bundle over M, denoted by \(\mathcal {F}\rightarrow M\). A vector field \(X\in C^\infty (M,TM)\) is called tangential to \(\mathcal {F}\) if for all \(x\in M\) we have \(X_x\in \mathcal {F}_x\), and we then simply write \(X\in C^\infty (M,\mathcal {F})\). The distribution \(\mathcal {F}\) is called involutive if \(X,Y\in C^\infty (M,\mathcal {F})\) implies \([X,Y]\in C^\infty (M,\mathcal {F})\). A foliation is defined as an involutive distribution.
It follows from Frobenius’ Theorem that there exists a family of disjoint connected \(\ell \)-dimensional submanifolds \((Z_b)_{b\in B}\), the leaves of the foliations, such that \(M= \bigcup _{b\in B}Z_b\) and such that \(T_xZ_b=\mathcal {F}_x\) for all \(x\in Z_b\subset M\) and all \(b\in B\).
Note that in general B is just a set. In the cases considered in the following subsections, we can achieve that B is a smooth manifold with \(Z_b\) depending smoothly on b and such that all manifolds \(Z_b\) are diffeomorphic to each other, but we will not assume this in this subsection.
For each \(x\in M\) let \(\nu _x\) be the orthogonal complement of \(\mathcal {F}_x\) in \(T_xM\). We obtain a vector bundle \(\nu :=\bigcup _{x\in M} \nu _x\) over M, the normal bundle. As vector bundles with scalar product we have \(TM=\mathcal {F}\oplus \nu \).
Each leaf will be equipped with the Riemannian metric induced from M. Then the Levi-Civita connection provides a connection, called the intrisic connection \(\nabla ^\mathrm{int}\), on the bundle \(TZ_b\rightarrow Z_b\) for every \(b\in B\). Also the restriction of \(\nu \) to a leaf \(Z_b\) carries a natural connection, also denoted by \(\nabla ^\mathrm{int}\); for \(X\in C^\infty (Z_b,TZ_b)\) and \(W\in C^\infty (Z_b,\nu |_{Z_b})\) we define \(\nabla ^\mathrm{int}_XW\) as the normal component of \(\nabla ^M_XW\).
Remark 4.1
These connections actually yield a partial connections on M, i.e. a bilinear maps \(\nabla ^\mathrm{int}:C^\infty (M,\mathcal {F})\times C^\infty (M,\mathcal {F})\rightarrow C^\infty (M,\mathcal {F})\) resp. \(\nabla ^\mathrm{int}:C^\infty (M,\mathcal {F})\times C^\infty (M,\nu )\rightarrow C^\infty (M,\nu )\) which are \(C^\infty (M)\)-linear in the first argument and which satisfy the usual product rule for \(C^\infty (M)\)-multiplication in the second argument. The partial connection on \(C^\infty (M,\mathcal {F})\) is characterized by being torsionfree and metric. However both partial connections are not a connections in the ordinary sense on M as \(\nabla _X^\mathrm{int}\) is not defined if X is not tangential to \(\mathcal {F}\).
Although \(TM=\mathcal {F}\oplus \nu \) holds in the sense of vector bundles, it does not hold for vector bundles with partial connection. The difference between the (partial) connection on TM and the partial connection of the sum \(\mathcal {F}\oplus \nu \) is the second fundamental form \(\mathrm{II}\). More exactly for \(X\in T_xZ_b\), \(Y\in C^\infty (TZ_B)\) and \(W\in C^\infty (\nu _B)\) we have
The bundle of positively oriented orthornormal frames of M will be denoted by \(P_{\mathrm{SO}}(M)\), and let \(P_{\mathrm{Spin}}(M)\rightarrow P_{\mathrm{SO}}(M)\) be a spin structure on M. We restrict these principal bundles to \(Z_b\) and obtain principal bundles \(P_{\mathrm{Spin}}(M)|_{Z_b}\) and \(P_{\mathrm{SO}}(M)|_{Z_b}\) over \(Z_b\). On \(TM|_{Z_b}=TZ_b\oplus \nu |_{Z_b}\) we have a connection defined by \(\nabla ^M\) and another connection defined by \(\nabla ^\mathrm{int}\). Both connections define connection-1-forms on \(P_{\mathrm{SO}}(M)|_{Z_b}\) and they lift to connection-1-forms on \(P_{\mathrm{Spin}}(M)|_{Z_b}\). Finally both connection-1-forms yield a connection on the associated spinor bundle again denoted by \(\nabla ^M\) and \(\nabla ^\mathrm{int}\). Note that the associated spinor bundle coincides with \(\Sigma _M|_{Z_b}\), and \(\nabla ^M\) is just the restriction of the standard connection on \(\Sigma _M\) to \(Z_b\). These connections are in fact partial connections on the bundle \(\Sigma _M\).
A calculation shows for all \(X\in C^\infty (M,\mathcal {F})\) and all spinors \(\varphi \in C^\infty (M,\Sigma _M)\)
where \((e_i)_i\) is a local positively oriented orthonormal frame on \(\mathcal {F}\), cp. [8, around (9)].
Remark 4.2
In [8] a slightly different notation is used, as can be seen in the following dictionary of notations
Bär [8] | Q | M | \(\nabla ^Q\) and | \(\nabla ^M\oplus \nabla ^N\) and | \(\widehat{D}\) | \(\tilde{D}\) |
|---|---|---|---|---|---|---|
\(\nabla ^{\Sigma Q}\) | \(\nabla ^{\Sigma M}\otimes \mathrm{id}+ \mathrm{id}\otimes \nabla ^{\Sigma N}\) | |||||
Our article | \(M\subset \mathbb {H}_c^{k+1}\times N\) | Z | \(\nabla ^M\) | \(\approx \nabla ^\mathrm{int}\) | \(D^Z_\partial \) | \(D_\mathrm{int}^Z\) |
Furthermore, in [8] one single submanifold is considered whereas we foliated the space. But this is not an essential difference.
In order to avoid missunderstandings, let us mention that a slightly different formalism is used in [9], it introduces an internal and an ambient Clifford multiplication, which differ by multiplication with a unit normal field. This is convenient if the submanifold is a hypersurface. However as we need arbitrary codimensions this is not helpful for our purpose.
In fact, in [9] the Clifford multiplication of the ambient manifold coincides with the Clifford multiplication on the hypersurface only up to Clifford multiplication with the normal vector field. In contrast to this in our notation the Clifford multiplication of the ambient space M coincides with the one on the submanifolds \(Z_b\).
The partial Dirac operator \(D^\mathcal {F}_\partial \) is now defined as \(D^\mathcal {F}_\partial =\sum _{i=1}^\ell e_i\cdot \nabla ^M_{e_i}\), and the intrinsic Dirac operators are given by \(D_\mathrm{int}^\mathcal {F}=\sum _{i=1}^\ell e_i\cdot \nabla ^\mathrm{int}_{e_i}\). As this definition does not depend on the choice of frame, it yields a global definition. Note that \((D^\mathcal {F}_\partial \varphi )|_{Z_b}\) and \((D_\mathrm{int}^\mathcal {F})|_{Z_b}\) only depend on \(\varphi |_{Z_b}\), each of them defines a family of Dirac-type operators on the leaves. On each leaf the intrinsic Dirac operator is locally a twisted Dirac operator on the submanifold N, the twist bundle is either the normal bundle if \(\ell (\dim M- \ell )\) is even, or two copies of the normal bundle \(\ell (\dim M- \ell )\) is odd.
In the applications in the following subsections all normal bundles have a parallel trivialization, hence, in this case the intrinsic Dirac operator coincides on each leaf with several copies of the Dirac operator on this leaf. As multiplicities are irrelevant for our discussion we have chosen the name ’intrinsic Dirac operator’ for \(D_\mathrm{int}\), slightly abusing the language.
By (3), the intrinsic Dirac operator \(D_\mathrm{int}^\mathcal {F}\) is related to the partial Dirac operator \(D_\partial ^\mathcal {F}\) via
where \({\vec {H}}_\mathcal {F}=\mathrm{tr}\, \mathrm{II}_\mathcal {F}\in C^\infty (M,\nu )\) is the unnormalised mean curvature vector field of the leaves \(Z_b\) in M, see [8, Lemma 2.1].
4.2 The Dirac operator in polar coordinates
The goal of this subsection is to study spinors in suitable polar coordinates on \(\mathbb {M}_c^{m,k}=\mathbb {H}_c^{k+1}\times N\).
We express the hyperbolic metric in polar normal coordinates centered in a fixed point \(p_0\) which will be sometimes identified with 0. In these polar coordinates \(M=(\mathbb {H}_c^{k+1}{\setminus } \{p_0\})\times N\) is parametrized by \(\mathbb {R}^+\times \mathbb {S}^k\times N\).
Define the following foliations on M:
-
The radial foliation \(\mathcal {F}_r\) where the leaves are the 1-dimensional submanifolds \(\mathbb {R}^+\times \{x\}\times \{y\}\). The radial vector field \(\partial _r\) on hyperbolic space generates \(\mathcal {F}_r\) pointwise.
-
The spherical foliation \(\mathcal {F}_{\mathbb {S}^k}\) where the leaves are the k-dimensional manifolds \(\{r\}\times \mathbb {S}^k\times \{y\}\).
-
The N-folation \(\mathcal {F}_N\), where the leaves are the n-dimensional manifolds \(\{r\}\times \{x\}\times N^n\).
On an open subset of M we choose an orthonormal frame \(e_1,\ldots ,e_m\), \(m=n+k+1=\dim M\), such that \(e_{k+2},\ldots ,e_m\) is an orthonormal frame for \(\mathcal {F}_N\), and \(e_{2},\ldots , e_{k+1}\) is an orthonormal frame for \(\mathcal {F}_{\mathbb {S}^k}\) and where \(e_1:=\partial _r\). The notation should be read such that \(\frac{\nabla }{dr}\) and \(\partial _r\) denote essentially the same (radial) vector, but \(\partial _r\) is viewed as a vector which acts via Clifford multiplication whereas \(\frac{\nabla }{dr}\) acts as a covariant derivative. The three foliations provide three partial Dirac operators \(\partial _r \cdot \frac{\nabla }{dr}= D_\partial ^{\mathcal {F}_r}\), \(D_\partial ^{\mathbb {S}^k}:= D_\partial ^{\mathcal {F}_{\mathbb {S}^k}}\) and \(D_\partial ^N:= D_\partial ^{\mathcal {F}_N}\). The partial Dirac operators along N and \(\mathbb {S}^k\) are locally defined as
for \(\varphi \in C^\infty (\Sigma _M)\). Note that we allow \(k=0\) which simply gives \(D_\partial ^{\mathbb {S}^0}=0\). The Dirac operator D on \((r_0,\infty )\times \mathbb {S}^k\times N\) is the sum of partial Dirac operators
The intrinsic Dirac operators along N and \(\mathbb {S}^k\) are given by
We denote the second fundamental form of \(\mathbb {S}^k\) in \(\mathbb {H}^{k+1}_c\) as \(\mathrm{II}_{\mathbb {S}^k}\) and set \({\vec {H}}_{\mathbb {S}^k}:= \mathrm{tr}\, \mathrm{II}_{\mathbb {S}^k}\). Then using natural identifications \(\mathrm{II}_{\mathbb {S}^k}\) and \({\vec {H}}_{\mathbb {S}^k}\) do not depend on whether they represent the second fundamental form and the mean curvature field of \(\mathbb {S}^k\) in \(\mathbb {H}^{k+1}_c\), or of \(\mathbb {S}^k\) in \(\mathbb {H}^{k+1}_c\times N\) or of \(\mathbb {S}^k\times N\) in \(\mathbb {H}^{k+1}_c\times N\).
Using \({\vec {H}}_N=0\) and \(f(r)=\sinh _c(r)\), cp. Sect. 2.2,
we obtain \(D^N:=D_\partial ^N=D_\mathrm{int}^N\) and \(D_\partial ^{\mathbb {S}^k}=D_\mathrm{int}^{\mathbb {S}^k}+\frac{k}{2}\coth _c(r)\partial _r\cdot \).
We set \(D^{\mathbb {S}^k}:= f(r)D_\mathrm{int}^{\mathbb {S}^k}\) which is on each spherical submanifold up to multiplicity the standard Dirac operator on \(\mathbb {S}^k\) and obtain
Lemma 4.3
The following operators anticommute: \(D^N\) with \(D^{\mathbb {S}^k}\), \(D^N\) with \(\partial _r\cdot \), \(D^N\) with \( \partial _r\cdot \frac{\nabla }{dr}\), \(D^{\mathbb {S}^k}\) with \( \partial _r\cdot \), and \(D^{\mathbb {S}^k}\) with \(\partial _r\cdot \frac{\nabla }{dr}\). However \(\partial _r\cdot \) commutes with \( \partial _r\cdot \frac{\nabla }{dr}\), and \((D^{\mathbb {S}^k})^2\) commutes with D.
Proof
Let \(P_\mathrm{Spin}(\mathbb {H}^{k+1}_c)\rightarrow P_\mathrm{SO}(\mathbb {H}^{k+1}_c)\) and \(P_\mathrm{Spin}(N)\rightarrow P_\mathrm{SO}(N)\) be the fixed spin structures on \(\mathbb {H}^{k+1}_c\) and N. Then we write as in Sect. 2.5
where \(\zeta \) is the composition \(\mathrm{Spin}(k+1)\times \mathrm{Spin}(n)\mathop {\rightarrow }\limits ^{\xi } \mathrm{Spin}(m)\mathop {\rightarrow }\limits ^{\rho _m} \mathrm End(\Sigma _m)\). The bundle P carries the Levi-Civita connection-1-form \(\alpha ^{LC}_{\mathbb {M}_c}\) and another connection-1-form \(\alpha ^\mathrm{int}\) as explained before.
We obtain a connection preserving bundle homomorphism \(I_c\), which is fiberwise an isometric isomorphism, and

commutes. Note that \(I_c\) is also compatible with the Clifford multiplication in the sense that for \(X\in TZ\) we have
Then the lemma follows immediately by the corresponding statements for \(\Sigma _{\mathbb {R}^+\times \mathbb {S}^k\times N}\). \(\square \)
We will also use the map \(\hat{I}_c:=I_0^{-1}\circ I_c: \Sigma _{\mathbb {H}^{k+1}_c{\setminus }\{p_0\}\times N}\rightarrow \Sigma _{\mathbb {R}^{k+1}{\setminus }\{0\}\times N}\) which allows to identify \(\Sigma _{\mathbb {H}^{k+1}_c\times N}|_{(x,y)}\) with \(\Sigma _{\mathbb {R}^{k+1}\times N}|_{(x,y)}\) and thus with \(\Sigma _{\mathbb {R}^{k+1}\times N}|_{(0,y)}\), \(0\cong p_0\).
4.3 The action of \(\mathrm{Spin}(k+1)\) on \(\mathbb {M}_c^{m,k}=\mathbb {H}_c^{k+1}\times N\)
We identify \(T_{p_0}\mathbb {H}^{k+1}_c\) with \(\mathbb {R}^{k+1}\). The left action \(a_1\) of the spin group \(\mathrm{Spin}(k+1)\) on \(\mathbb {R}^{k+1}\) obtained by composing the double covering \(\mathrm{Spin}(k+1)\rightarrow \mathrm{SO}(k+1)\) with the standard representation yields a left action on \(\mathbb {H}^{k+1}_c\) via the exponential map \(\exp _{p_0}:\mathbb {R}^{k+1}\rightarrow \mathbb {H}^{k+1}_c\) which is a diffeomorphism. As this action is isometric it yields a left action on \(P_\mathrm{Spin}(\mathbb {H}^{k+1}_c)\) – also called \(a_1\). Thus, we obtain a \(\mathrm{Spin}(k+1)\)-action on \(P_\mathrm{Spin}(\mathbb {H}^{k+1}_c)\times P_\mathrm{Spin}(N)\times \Sigma _m\) as \(\hat{a}_1=a_1\times \mathrm{id}\times \mathrm{id}\). Since \(a_1\) and the principal \(\mathrm{Spin}(k+1)\)-action which acts from the right commute, the \(\hat{a}_1\)-action descends to a \(\mathrm{Spin}(k+1)\)-action from the left – denoted by \(a_2\) – on the spinor bundle \(\Sigma _{\mathbb {H}^{k+1}_c\times N}= (P_\mathrm{Spin}(\mathbb {H}^{k+1}_c)\times P_\mathrm{Spin}(N)) \times _\zeta \Sigma _m\) (for \(\zeta \) as in (5)) such that

commutes.
By construction, the action \(a_1\) does not depend on c. Thus, Diagram (6) commutes with this \(\mathrm{Spin}(k+1)\)-action.
Moreover, note that \(a_1\) preserves the spheres \(\mathbb {S}_{r,y}^k:=\{r\}\times \mathbb {S}^k \times \{y\}\subset \mathbb {H}_c^{k+1}\times N\); for \(k>0\) this action is even transitive on \(\mathbb {S}_{r,y}^k\). Hence, the diagram above can be restricted to this submanifold. Furthermore, \((p_0,y)\) is a fixed point of \(a_1\times \mathrm{id}\) for all \(y\in N\). Thus, the \(a_2\)-action can be restricted to an action that maps \(\Sigma _{\mathbb {H}_c^{k+1}\times N}|_{(p_0,y)}\) to itself.
4.4 Spinors on \(\mathbb {S}^k\subset \mathbb {R}^{k+1}\)
We will now analyse the special case \(N=\{y\}\) and \(c=0\), thus \(\mathbb {H}^{k+1}_c=\mathbb {R}^{k+1}\). This well-known case is not only important as an example, but will also be used to derive consequences for the general case.
We obtain immediately from (3) and \(\mathrm{II}_{\mathbb {S}_r^k}= -\frac{1}{r} g|_{\mathbb {S}_r^k} \partial _r\) where \(\mathbb {S}_r^k\) is the sphere of radius r canonically embedded in \(\mathbb {R}^{k+1}\):
Lemma 4.4
Assume that \(\varphi \) is a parallel spinor on \(\mathbb {R}^{k+1}\). Then for any \(X\in T\mathbb {S}_r^k\) we have
In particular, we have
Using Lemma 4.3 and \(\nabla ^\mathrm{int}_X \partial _r=0\) this implies
5 Modes of \(\mathrm{Spin}(k+1)\)-equivariant maps
In this section we assume \(k\ge 1\). We now have a \(\mathrm{Spin}(k+1)\)-action on \(\Sigma _{\mathbb {R}^{k+1}}|_{0}\cong \Sigma _{k+1}\), \(\{r\}\times \mathbb {S}^k\) and \(\Sigma _{\mathbb {R}^{k+1}}|_{\{r\}\times \mathbb {S}^k}\), and thus one on \(C^\infty (\mathbb {S}^k, \Sigma _{\mathbb {R}^{k+1}}|_{\{r\}\times \mathbb {S}^k})\) given by \((\gamma \cdot f)(x)= a_2(\gamma )f(a_1(\gamma )^{-1} x)\). To simplify notations we mostly write \(\mathbb {S}^k\) for \(\{r\}\times \mathbb {S}^k\).
We now have to classify \(\mathrm{Spin}(k+1)\)-equivariant functions \(\Sigma _{\mathbb {R}^{k+1}}|_{0} \rightarrow C^\infty (\mathbb {S}^k, \Sigma _{\mathbb {R}^{k+1}}|_{\mathbb {S}^k})\).
For \(\psi _0\in \Sigma _{\mathbb {R}^{k+1}}|_{0}\) let the parallel spinor on \(\mathbb {R}^{k+1}\) with value \(\psi _0\) at 0 be denoted by \(\Psi _0\). For k odd, the positive and negative parts of \(\Psi _0\) are denoted by \(\Psi _0^{(\pm )}\).
Lemma 5.1
Let \( F:\Sigma _{k+1} \rightarrow C^\infty (\mathbb {S}^k, \Sigma _{\mathbb {R}^{k+1}}|_{\mathbb {S}^k})\) be a linear \(\mathrm{Spin}(k+1)\)-equivariant map. Then for k even F has the form
and for k odd F has the form
for suitable constants \(a_i, a_{ij}\in \mathbb {C}\).
The lemma is in fact a special case of Frobenius reciprocity as partially explained in the proof.
Proof
In the case k even, one easily checks that \(\psi _0\mapsto \Psi _0|_{\mathbb {S}^k}\) and \(\psi _0\mapsto \partial _r\cdot \Psi _0|_{\mathbb {S}^k}\) are linear \(\mathrm{Spin}(k+1)\)-equivariant maps. The same statement holds for k odd for \(\psi _0\mapsto \Psi _0^{(+)}|_{\mathbb {S}^k}\), \(\psi _0\mapsto \partial _r\cdot \Psi _0^{(+)}|_{\mathbb {S}^k}\) \(\psi _0\mapsto \Psi _0^{(-)}|_{\mathbb {S}^k}\) and \(\psi _0\mapsto \partial _r\cdot \Psi _0^{(-)}|_{\mathbb {S}^k}\).
The converse will be checked using Frobenius reciprocity. Since \(\partial _r\) is a \(\mathrm{Spin}(k+1)\)-equivariant vector field, we obtain a \(\mathrm{Spin}(k+1)\)-equivariant inclusion \(P_\mathrm{SO}(\mathbb {S}^{k})\hookrightarrow P_\mathrm{SO}(\mathbb {R}^{k+1})|_{\mathbb {S}^k}\), \((e_1,\ldots ,e_k)\mapsto (e_1,\ldots ,e_k,\partial _r)\). Via the inclusion \(\mathrm{SO}(k)\rightarrow \mathrm{SO}(k+1)\) we can view \(P_\mathrm{SO}(\mathbb {R}^{k+1})|_{\mathbb {S}^k}\) as an \(\mathrm{SO}(k)\)-principal bundle, then the inclusion commutes with the \(\mathrm{SO}(k)\) action of the \(\mathrm{SO}(k)\)-principle bundles. It follows from the construction of the spin structure on \(\mathbb {S}^{k}\) that this inclusion lifts to a \(\mathrm{Spin}(k+1)\)-equivariant inclusion \(P_\mathrm{Spin}(\mathbb {S}^{k})\hookrightarrow P_\mathrm{Spin}(\mathbb {R}^{k+1})|_{\mathbb {S}^k}\) of \(\mathrm{Spin}(k)\)-principal bundles. Note that the \(\mathrm{Spin}(k+1)\) action is the one described above which commutes with the \(\mathrm{Spin}(k)\)-actions from the principal bundles. Thus we have the \(\mathrm{Spin}(k+1)\)-equivariant isomorphism of \(\mathrm{Spin}(k+1)\)-principal bundles.
We apply Frobenius reciprocity [33, Theorem 7.47] for the homogeneous space \(\mathbb {S}^k=G/H\), \(G=\mathrm{Spin}(k+1)\), \(H=\mathrm{Spin}(k)\) which states that
for any G-representation W and any H-representation V. Here \(W|_H\) denotes the restriction of the G action on W to an H action on W. Further, \(\mathrm{Ind}^G_H(V)\) is the induced representation, defined as
and the action of G on \(f\in \mathrm{Ind}^G_H(V)\) is given by
So let \(W=V=\Sigma _{k+1}\) be the standard spinor representation with the standard action of G, resp. its restriction to H. Then
as a G-equivariant bundle over \(\mathbb {S}^k=G/H\).
Thus its space of sections \(C^\infty (\mathbb {S}^k, \Sigma _{\mathbb {R}^{k+1}}|_{\mathbb {S}^k})\) equals \(\mathrm{Ind}^G_H(\Sigma _{k+1})\), see also [33, Theorem 7.46]. Hence, \(\mathrm{Hom}_G(W, \mathrm{Ind}^G_H(V))\) is the space of all F satisfying the assumptions of the lemma. The lemma follows by calculating
This follows from Schur’s theorem as V is the sum of two non-isomorphic irreducible representations if k is even and as V is the sum of two isomorphic irreducible representations if k is odd. \(\square \)
Then using Lemma 4.4 we obtain immediately
Corollary 5.2
Let \( F:\Sigma _{k+1} \rightarrow C^\infty (\mathbb {S}^k, \Sigma _{\mathbb {R}^{k+1}}|_{\mathbb {S}^k})\) be a linear \(\mathrm{Spin}(k+1)\)-equivariant map. Let \(\psi _0\in \Sigma _{k+1}\) and \(\varphi =F\psi _0\). Then \((D^{\mathbb {S}^k})^2\varphi =\frac{k^2}{4}\varphi \).
We say that \(\varphi \) is in the spherical mode \(\frac{k^2}{4}\), and thus \(\varphi \) is in the mode of lowest energy on the sphere.
Now we want to carry over the last result to \(\mathbb {M}_c^{m,k}\). In the following \(p_0\in \mathbb {H}_c^{k+1}\) denotes again the fixed point of the \(\mathrm{Spin}(k+1)\)-action, and let \(y_0, y\in N\).
Lemma 5.3
Let \( F:\Sigma _{\mathbb {H}_c^{k+1}\times N}|_{(p_0, y_0)} \rightarrow C^\infty (\mathbb {S}^k, \Sigma _{\mathbb {H}_c^{k+1}\times N}|_{\mathbb {S}^k\times \{y\}})\) be a linear \(\mathrm{Spin}(k+1)\)-equivariant map. Let \(\psi _0\in \Sigma _{\mathbb {H}_c^{k+1}\times N}|_{(p_0, y_0)}\) and \(\varphi =F\psi _0\). Then \((D^{\mathbb {S}^k})^2\varphi =\frac{k^2}{4}\varphi \).
Proof
Note that the composition \(\hat{I}_c:=I_0^{-1}\circ I_c\) where \(I_c\) is defined as in (6) maps the spinor bundle over \((\mathbb {H}_c^{k+1}{\setminus }\{p_0\})\times N\) to the spinor bundle over \((\mathbb {R}^{k+1}{\setminus }\{0\})\times N\). This map preserves the intrinsic connection \(\nabla ^\mathrm{int}\) and uniquely extends into \(p_0\cong 0\). Via pullback we then obtain a \(\mathrm{Spin}(k+1)\)-equivariant vector space isomorphism
Moreover, we can write in the sense of \(\mathrm{Spin}(k+1)\)-modules \(\Sigma _{\mathbb {R}^{k+1}\times N}|_{(x, y)}\cong \Sigma _m\cong \Sigma _{k+1}\otimes V\) if k is even or \(\Sigma _{\mathbb {R}^{k+1}\times N}|_{(x, y)}\cong \Sigma _{k+1}^{(+)}\otimes V^{(+)} \oplus \Sigma _{k+1}^{(-)}\otimes V^{(-)}\) if k is odd, where \(V^{(\epsilon )}:=\mathrm{Hom}_{\mathrm{Spin}(k+1)}(\Sigma _{k+1}^{(\epsilon )}, \Sigma _{\mathbb {R}^{k+1}\times N}|_{(x, y)})\) is a vector space which is independent of \(x\in \mathbb {R}^{k+1}\).
Let now k be odd. Then any \(\alpha \in (V^{(\epsilon )})^*\) defines a map \(\Sigma _{\mathbb {H}_c^{k+1}\times N}|_{(x, y)}\rightarrow \Sigma _{k+1}^{(\epsilon )}\).
Let \(A:\Sigma _{k+1}^{(\delta )}\rightarrow \Sigma _{\mathbb {H}^{k+1}_c\times N}|_{(p_0,y_0)}\) be a \(\mathrm{Spin}(k+1)\)-equivariant map. By composition we obtain for fixed A, \(\alpha \) and \(\delta , \epsilon \in \{+, - \}\) a \(\mathrm{Spin}(k+1)\)-equivariant map
Let now k be even. Then the argumentation is analogous to the one above when replacing \(V^{(\epsilon )}\) by V and \(\Sigma ^{(\epsilon )}_{k+1}\) by \(\Sigma _{k+1}\).
Then the Lemma follows from Corollary 5.2 together with the identification by \(J_{r,y}\). \(\square \)
Corollary 5.4
Let G(q, p) be the Green function of the operator \(D-\mu \), \(\mu \not \in \mathrm Spec_{L^2}^{\mathbb {M}_c}(D)\). Let \(q=(r,x,y)\in \mathbb {M}_c^{m,k}\) be the polar coordinates when using \(p_0\) as the origin, \(r>0\). Let \(\psi _0\in \Sigma _{\mathbb {M}_c^{m,k}}|_{(p_0, y_0)}\), \(y_0\in N\). Set \(\varphi (q):=G(q,(p_0, y_0))\psi _0\). Then
Proof
Now we consider the Green function of the shifted Dirac operator \(D-\mu \) for \(\mu \not \in \mathrm Spec_{L^2}^{\mathbb {M}_c}(D)\) as a map
It follows from the definition of G, in particular from its uniqueness, and from the equivariance of D under \(\mathrm{Spin}(k+1)\) that \(G(\,\cdot \,,(p_0,y_0))\) is \(\mathrm{Spin}(k+1)\)-equivariant as well. In particular, \(G(\,\cdot \,,(p_0,y_0))|_{\mathbb {S}^k\times \{y\}}\) is a \(\mathrm{Spin}(k+1)\)-equivariant map as considered in Lemma 5.3. Thus, together with Lemma 5.3 the corollary follows. \(\square \)
6 Decay estimates for a fixed mode
Let \(\mu \not \in \mathrm Spec_{L^2}^{\mathbb {M}_c^{m.k}}(D)\). Then, by Theorem 3.6 there exists a unique Green function for \(D-\mu \). The goal of this section is to estimate the decay of this Green function at infinity. For that, let \(y=(p_0,y_N)\in \mathbb {H}_c^{k+1}\times N\) and \(\psi _0\in \Sigma _{\mathbb {M}_c}|_{y}\) be fixed. Set \(\varphi (x):=G(x,y)\psi _0\). The Definition of the Green function, cf. (2), implies that \(\varphi \) is an \(L^2\)-eigenspinor of D to the eigenvalue \(\mu \) outside a neighbourhood of y. Moreover, by Corollary 5.4 we know that \(\varphi \) is in the spherical mode \(\frac{k^2}{4}\).
Recall from Sect. 2.6 that
In the following the complement of this spectrum is denoted by \(I_{\lambda _0}:=(\mathbb {C}{\setminus } \mathbb {R})\cup (-\lambda _0,\lambda _0)\).
Now we decompose the space of spinors restricted to \(\{r_1\}\times \mathbb {S}^k\times N\) into complex subspaces of minimal dimensions which are invariant under \(D^N\), \(\partial _r\cdot \), \(D^{\mathbb {S}^k}\). For \(k>0\) such spaces have a basis of the form \(\psi \), \(\partial _r\cdot \psi \), \(P\psi \), and \(\partial _r\cdot P\psi \), where \(\psi \) satisfies \(D^N\psi =\lambda \psi \), \((D^{\mathbb {S}^k})^2\psi =\rho ^2\psi \), \(\rho \in \frac{k}{2}+ \mathbb {N}_0\), and \(P:=D^{\mathbb {S}^k}/\rho \). All these operations commute with parallel transport in r-direction, so by applying parallel transport in r-direction we obtain spinors \(\psi \), \(\partial _r\cdot \psi \), \(P\psi \), and \(\partial _r\cdot P\psi \) on \(\mathbb {R}^+\times \mathbb {S}^k\times N\) with similar relations, and the space of all spinors of the form
is preserved under the Dirac operator D on \(\mathbb {M}_c^{m,k}\) because of (4). Then the operators discussed above restricted to such a minimal subspace are represented by the matrices, cp. Lemma 4.3,
For \(k=0\) we have \(D^{\mathbb {S}^0}=0\) and one can proceed analogously with a basis \(\psi , \partial _r\cdot \psi \) and obtains
Proposition 6.1
Assume that \(\varphi \) is an \(L^2\)-solution to the equation \(D\varphi =\mu \varphi \), \(\mu \in I_{\lambda _0}\) on \((\mathbb {M}_c^{m,k})_{>r_0}:=(\mathbb {H}_c^{k+1}{\setminus } B_{r_0}(p_0))\times N\). Assume that \(\varphi \) has the form given in (7) with parameters \(\rho \) and \(\lambda \). Let \(\kappa \) satisfy \(\kappa ^2=\lambda ^2-\mu ^2\), \(\mathrm {Re\,}\kappa \ge 0\). Then \(\mathrm {Re\,}\kappa >0\). Moreover, let \(\kappa _{\lambda _0}^2=\lambda _0^2-\mu ^2\). If \(\mathrm {Re\,}\kappa _{\lambda _0}> 0\), then there is are positive constants C and \(r_1\) such that
where C is a constant that only depends on \(c, k,r_1,\lambda _0, \mu \) and \(\rho \) but not on \(\lambda \). For \(c=0\) an analogous estimate holds when replacing \(e^{-(ck/2)d(x_1,p_0)}\) by \(r^{-k/2}\) where \(r=d(x_1,p_0)\).
Proof
We prove first the case \(k>0\): By assumption \(\varphi \) can be written as in (7). We view the components of \(\varphi \) as a vector in \(\mathbb {C}^4\), i.e., \(\Phi (r):=(\varphi _1(r),\varphi _2(r),\varphi _3(r),\varphi _4(r))\). So by (4) the following equation is equivalent to \(D\varphi =\mu \varphi \):
Thus using \({{1}\mathrm{l}}\) for the identity matrix and setting
we obtain
We start with the case \(c\ne 0\): We now substitute \(t=e^{-cr}\), \(\widetilde{\Phi }(t)=\Phi (-c^{-1}\log t)\). Then
Such singular ordinary differential equations are well understood, see [15, Chap. 4, Sec. 1–3]. In particular, \(t=0\) is a singular point of first kind, and [15, Chap. 4 Thm. 2,1] yields that \(t=0\) is a so-called “regular singular point”, and the associated theory applies. However, in our situation it is more efficient to analyse the equation directly.
We set \(h(t):= (\log t -\log (t+1) -\log (1-t)) k/2\), then \(h'(t)= \frac{k(1+t^2)}{2(t-t^3)}\). We define
and we calculate
As B anticommutes with A, we have \(t^{A/c} B t^{-{A/c}}= t^{2{A/c}}B\), and as B is an isometry of \(\mathbb {C}^4\), we see that
where \(\Vert \,.\,\Vert \) denotes the operator norm and where
are the (complex) eigenvalues of A. It follows that for \(0<t<1/2\)
Thus the solution extends to \(t=0\), and
This estimate yields explicit asymptotic control for \(\widehat{\Phi }(t)\), and thus for \(\varphi \). Namely, assume \(cr_0\ge 1> \log 2\), there are two fundamental solutions \(\varphi _\pm \) of \(D\varphi _\pm =\mu \varphi _\pm \) such that \(\widehat{\Phi }_\pm (0)\) is an eigenvector of A to the eigenvalue \(\kappa _\pm \) and such that
This implies that for every \(\delta \in (0,1)\) there is \(\tilde{r}_0\) such that
From
and the left inequality of (8) we see that \(\varphi _\pm \) is in \(L^2((\mathbb {M}_c^{m,k})_{>\tilde{r}_0})\) if and only of \(\mathrm {Re\,}\kappa _\pm <0\). In the following we call this \(\kappa _\pm \) just \(\kappa _\lambda \) and also replace the ± index by \(\lambda \) in all other occurrences. We note that \(|\mathrm {Re\,}\kappa _\lambda |\) is increasing in \(|\lambda |\). Thus, \(\delta \) and \(\tilde{r}_0\) from above can be chosen independent on \(\lambda \).
Next, we multiply the first inequality of (8) by \(|\widehat{\Phi }_\lambda (0)|\) and then integrate its square:
Hence, we obtain an upper bound
where \(C_1\) is a constant independent on \(\lambda \).
Using this again with the right inequality of (8) we get for all x with \(r=\mathrm {dist}(x, p_0)> \tilde{r}_0\) that
For \(r>\tilde{r}_0\) we see that \((-2\mathrm {Re\,}\kappa _\lambda )e^{2\mathrm {Re\,}\kappa _{\lambda } (r-\tilde{r}_0)}\) is monotonically decreasing in \(|\mathrm {Re\,}\kappa _\lambda |\), and we obtain from (9)
for all x with \(r=d(x_1,p_0)>\tilde{r}_0\). Here, C can be chosen such that it only depends on c, k, \(\tilde{r}_0\), \(\lambda _0\), \(\mu \) and \(\rho \) but not on \(\lambda \). Note that the \(\kappa \) in the claim is simply \(-\kappa _{\lambda _0}\).
Next we consider the case \(c=0, k>0\):
Set \(\hat{\Phi }(r)=r^{\frac{k}{2}}e^{-Ar}\Phi (r)\). Then, \(\hat{\Phi }'(r)= \frac{\rho }{r} e^{-Ar} B e^{Ar} \hat{\Phi }=\frac{\rho }{r} e^{-2Ar} B \hat{\Phi } \). Then we can proceed as above and obtain the claim.
It remains the case \(k=0\): Then
and direct calculation gives the claim. \(\square \)
In order to estimate the decay of \(\varphi (x)=G(x,y)\psi _0\), \(\psi _0\in \Sigma _{\mathbb {M}_c^{m,k}}|_{y}\) at infinity we will decompose \(\varphi \) into its modes in \(\mathbb {S}^k\) and N direction, respectively. Lemma 6.1 provides an estimate of the decay of each mode which is independent of the mode in direction of N. Moreover, from Corollary 5.4 we know that \(\varphi \) has spherical mode \(\frac{k^2}{4}\). Thus, we obtain a decay estimate for \(\varphi \):
Lemma 6.2
Let \(\mu \not \in \mathrm Spec_{L^2}^{\mathbb {M}_c}(D)\), and let G be the unique Green function of \(D-\mu \). We set \(M_y(r):= \{x\in \mathbb {M}_c\ |\ \mathrm {dist}(x, N^y) =r\}\) where \(N^y = \{p_0\}\times N\) and \(y=(p_0,y_N)\in \mathbb {H}_c^{k+1}\times N\). Let \(\kappa \) satisfy \(\kappa ^2=\lambda _0^2-\mu ^2\) and \(\mathrm {Re\,}\kappa \ge 0\). Then for all \(\epsilon >0\) and \(r_0\) sufficiently large there is a constant \(C>0\) independent on y such that
Proof
Let \(\psi _0 \in \Sigma _{\mathbb {M}_c}|_{y}\). Set \(\varphi (x):=G(x,y)\psi _0\). Then, for \(k>0\) the spinor \(\varphi \) decomposes into a sum of spinors \(\varphi _{\rho ^2,\lambda }\) of the form (7) with \((D^{\mathbb {S}^k})^2\varphi _{\rho ^2,\lambda }=\rho ^2\varphi _{\rho ^2,\lambda }\) and \(D^N\varphi _{\rho ^2,\lambda }=\lambda \varphi _{\rho ^2,\lambda }\), respectively. By Corollary 5.4 \(\rho ^2\) may only take the value \(\frac{k^2}{4}\). For \(k=0\) the spinor \(\varphi \) decomposes into a sum of spinors \(\varphi _{0,\lambda }\) with \(D^N\varphi _{0,\lambda }=\lambda \varphi _{0,\lambda }\). Thus, for all k \(\int _{M_y(r)} |\varphi (x)|^2 dx = \sum _{\lambda } \Vert \varphi _{k^2/4, \lambda }\Vert _{L^2(M_y(r))}^2\).
Together with Proposition 6.1 we obtain for \(c\ne 0\)
The case \(c=0\) follows analogously. \(\square \)
7 Decomposition of the Green function
We decompose the Green function G of the shifted Dirac operator \(D-\mu \) on \(M=\mathbb {M}_c^{m,k}\) into a singular part and a smoothing operator. Both operators will be shown to be bounded operators from \(L^p\) to \(L^p\) for all \(p\in [1,\infty ]\).
At first we choose a smooth cut-off function \(\chi :\mathbb {R}\rightarrow [0,1]\) with \(\mathrm supp\, \chi \subset [-R,R]\) and \(\chi _{|_{(-R/2,R/2)}}\equiv 1\). Let \(\rho :M\times M\rightarrow [0,1]\) be given by \(\rho (x,y)=\chi (\mathrm {dist}_{\mathbb {H}_c^{k+1}}(\pi _{\mathbb {H}}(x),\pi _{\mathbb {H}}(y)))\).
Let now
Then \(G_2\) is zero on a neighbourhood of the diagonal, and thus smooth everywhere. The singular part is only contained in \(G_1\).
Proposition 7.1
Let \(M=\mathbb {M}_c^{m,k}\) and \(G_1\) be as defined above. Then, for all \(1\le p\le \infty \) the map \(P_1:\varphi \mapsto \int _M G_1(.,y)\varphi (y)\mathrm {d}y\) defines a bounded operator from \(L^p\) to \(L^p\).
Proof
We start with a smooth spinor \(\varphi \) compactly supported in \( B_{2R}(0)\times N\subset M\). For such a \(\varphi \) the spinor \(P_1\varphi \) is supported in \(B_{3R}(0) \times N\subset M\). We embed \(B_{3R}(0)\) isometrically into a closed Riemannian manifold \(M_R\). Let \(M_R \times N\). The metric on \(M_R\) can be chosen such that \(D^{M_R \times N}-\mu \) is invertible, cf. Proposition C.1. The norm of \((D^{M_R \times N}-\mu )^{-1}:L^p \rightarrow L^p\) is denoted by \(C_R(p)\).
For \(p<\infty \) we estimate
Next we want to consider arbitrary \(\varphi \in L^p(M,\Sigma _M)\), \(p<\infty \). Then \(C_c^\infty (M,\Sigma _M)\) is dense in \(L^p(M,\Sigma _M)\), and it suffices to consider \(\varphi \in C_c^\infty (M,\Sigma _M)\). Choose points \((x_i)_{i\in I}\subset \mathbb {H}_c^{k+1}\) as in Lemma 2.1. Then \((B_{2R}(x_i)\times N)_{i \in I}\) and \((B_{3R}(x_i)\times N)_{i \in I}\) both cover \(\mathbb {M}_c^{m,k}\) uniformly locally finite. We denote the multiplicity of the second cover by L and choose a partition of unity \(\eta _{i}\) subordinated to \((B_{2R}(x_i)\times N)_{i\in I}\).
Let \(\varphi =\sum \varphi _{i}\) where \(\varphi _{i}=\eta _{i}\varphi \in C_c^\infty (B_{2R}(x_i) \times N,\Sigma _M)\). Hence, \(P_1\varphi _i\in C_c^\infty (B_{3R} (x_i)\times N, \Sigma _M)\). Moreover, let \(\bar{f}_i:M\rightarrow M\) be given by \(\bar{f}_i=({\text {Id}}, f_i)\) where \(f_i\) is an isometry of \(\mathbb {H}_c^{k+1}\) that maps \(x_i\) to \(p_0\). We choose a lift of \(\tilde{f}_i\) to an isometry on the spinor bundle. Due to the homogeneity of \(\mathbb {H}_c^{k+1}\) we have \(P_1(\tilde{f}_i\circ \varphi \circ \bar{f}_i^{-1})=\tilde{f}_i\circ (P_1\varphi )\circ \bar{f}_i^{-1}\).
Then, by triangle inequality and Hölder inequality and since for fixed x the value \(P_1\varphi _i(x)\) is nonzero for at most L spinors \(\varphi _i\), we have
Thus, we obtain
It remains the case \(p=\infty \). Let \(\eta _i\) as above, and let \(\varphi \in L^\infty \). We decompose again \(\varphi =\sum \varphi _i\) where \(\varphi _i=\eta _i\varphi \) is compactly supported. Then, we obtain as above that
\(\square \)
We now turn to the off-diagonal part \(G_2\).
Note that \(\mathbb {H}_c^{k+1}\) is homogeneous for all c. In particular, the representation of the metric in polar coordinates—\(\mathrm {d}r^2+\sinh _c^2(r)\,\sigma ^k\) (cf. Sect. 2.2)—is independent of the chosen origin of the polar coordinates on \(\mathbb {H}_c^{k+1}\). We set \(M_y(r):= \{x\in \mathbb {M}_c^{m,k}\ |\ \mathrm {dist}(x, N^y) =r\}\) where \(N^y = \{y_1\}\times N\) where \(y=(y_1,y_2)\in \mathbb {H}_c^{k+1}\times N\). Then, the volume \(\mathrm{vol}(M_y(r))=f(r)^k\mathrm{vol}(N)\mathrm{vol}(S^k)=\sinh _c^k(r)\mathrm{vol}(N)\mathrm{vol}(S^k)\) is independent of y. We will subsequently leave out the y in the notation and write \(\mathrm{vol}(M(r))\).
Proposition 7.2
Using the notations from above, assume that there are constants \(C, \rho >0\) with
Let \(p=1\) and \(p=\infty \). Then, for \(\rho >\frac{ck}{2}\) the operator \(P_2:\varphi \mapsto \int _M G_2(.,y)\varphi (y)\mathrm {d}y\) from \(L^p\) to \(L^p\) is bounded.
Proof
We start with \(p=1\) and estimate for \(\varphi \in C_c^\infty (M, \Sigma _M)\)
where \(\tilde{x}\) is the angular part and r the radial part of x.
For \(\rho >\frac{ck}{2}\) the integral \(\int _{r\ge r_0} \sinh _c^\frac{k}{2}(r) e^{-\rho r}\,\mathrm {d}r \) is bounded. Hence, \(P_2:L^1\rightarrow L^1\) is invertible.
Next, we consider the other case \(p=\infty \). Then for \(\varphi \in L^\infty (M, \Sigma _M)\)
where for \(\rho > \frac{ck}{2}\) the last inequality follows as above. Thus, \(\Vert P_2\varphi \Vert _\infty \le \tilde{C} \Vert \varphi \Vert _\infty \). \(\square \)
8 \(\sigma _p\) contains the \(L^p\)-spectrum on \(\mathbb {M}_c^{m,k}\)
In this section we prove one direction of Theorem 1.1.
Proposition 8.1
Let \(p\in [1,\infty ]\). Let \(\lambda _0^2\), \(\lambda _0\ge 0\), be the lowest eigenvalue of the Dirac square on the closed Riemannian spin manifold N. The \(L^p\)-spectrum of the Dirac operator on \(\mathbb {M}_c^{m,k}\) is a subset of
Proof
We will show that \(D-\mu :H_1^p\subset L^p\rightarrow L^p\) has a bounded inverse for all \(\mu \in \mathbb {C}{\setminus } \sigma _p\). Fix \(\mu \in \mathbb {C}{\setminus } \sigma _p\), and let \(\kappa \in \mathbb {C}\) such that \(\mu ^2=\lambda _0^2+\kappa ^2\). For \(p=2\), the lemma follows from Sect. 2.6.
Let now \(p\in \{ 1,\infty \}\) and \(\mu \not \in \sigma _1=\sigma _\infty \). Then \(\mu \not \in \sigma _2\) and \((D-\mu ):H_1^2(\mathbb {M}_c^{m,k}) \subset L^2(\mathbb {M}_c^{m,k})\rightarrow L^2(\mathbb {M}_c^{m,k})\) has a bounded inverse given by \(P_\mu :\varphi \mapsto \int _{\mathbb {M}_c} G_\mu (x,y)\varphi (y)dy\). By Propositions 7.1, 7.2 and Lemma 6.2 the operator \(P_\mu :L^p \rightarrow L^p\) is bounded for \(| \mathrm {Im\,}\kappa |>ck|\frac{1}{p}-\frac{1}{2}|=c\frac{k}{2}\). Hence, the \(L^1\)- and the \(L^\infty \)-spectrum of D on \(\mathbb {M}_c^{m,k}\) have to be contained in \(\sigma _1=\sigma _\infty \).
First we deal with the case that \(\mathrm {Im\,}\kappa >0\). For \(p\in [1,2]\) we use the Stein Interpolation Theorem 2.3: Fix \(\epsilon >0\) and \(y_0\in \mathbb {R}\). We set \(h(z):=\mu (z)^2:=\lambda _0^2+\kappa (z)^2:=\lambda _0^2+(y_0+\frac{ck}{2}\mathrm {i}z+\mathrm {i}\epsilon )^2\) and \(A_z=(D^2-h(z))^{-1}\). By Sect. 2.6 the operators
for \(0\le w\le 1\) and \(y\in \mathbb {R}\), are bounded as operators from \(L^2\) to \(L^2\). Furthermore
is bounded from \(L^1\) to \(L^1\) as seen above. Thus—as required to apply the Stein interpolation theorem—\(A_{\mathrm {i}y}\) and \(A_{1+\mathrm {i}y}\) are bounded operators from \(L^1 \cap L^2\) to \(L^1+L^2\).
Let now \(\varphi \in L^1\cap L^2\) and \(\psi \in L^\infty \cap L^2\). Set \(S:=\{z\in \mathbb {C}\ |\ 0\le \mathrm {Re\,}z\le 1\}\). We define \(b_{\varphi ,\psi }(z)=\langle A_z\varphi ,\psi \rangle \). The map \(b_{\varphi ,\psi }\) is analytic in the interior of S, since the resolvent is, see Lemma B.5. Moreover, \(|b_{\varphi ,\psi }(z)|\le \Vert A_z\Vert \Vert \varphi \Vert _{L^2}\Vert \psi \Vert _{L^2} \le (\max _{0\le \mathrm {Re\,}z\le 1} \Vert A_z\Vert ) \Vert \varphi \Vert _{L^2}\Vert \psi \Vert _{L^2}\) where \(\Vert A_z\Vert \) denotes the operator norm for \(A_z:L^2\rightarrow L^2\). Thus, \(b_{\varphi ,\psi }(z)\) is uniformly bounded and continuous on \(S:=\{z\in \mathbb {C}\ |\ 0\le \mathrm {Re\,}z\le 1\}\). Thus, we can apply Theorem 2.3 and obtain for \(t\in (0,1)\) and \(p= \frac{2}{1+t}\) that \(A_t=(D^2-h(\frac{2}{p}-1))^{-1}=(D^2-(\lambda _0^2+(y_0+ck\mathrm {i}(\frac{1}{p} -\frac{1}{2})+\mathrm {i}\epsilon )^2))^{-1}\) is bounded from \(L^p\) to \(L^p\).
In the case \(\mathrm{Im} \kappa <0\) we set analogously \(A_z=(D^2-g(z))^{-1}\) for \(g(z)=\lambda _0^2+(y_0-\frac{ck}{2}\mathrm {i}z-\mathrm {i}\epsilon )^2\) and obtain that \(A_t=(D^2-g(\frac{2}{p}-1))^{-1}\) is bounded from \(L^p\) to \(L^p\). Since \(y_0\in \mathbb {R}\) and \(\epsilon >0\) can be chosen arbitrarily, we get for all \(\mu \in \mathbb {C}{\setminus } \sigma _p\) that \(\mu ^2\) is not in the \(L^p\)-spectrum of \(D^2\). Using Lemma B.8 the claim follows for \(p\in [1,2]\) and with Lemma B.3.(i) for \(p\in [2,\infty )\). \(\square \)
9 Construction of test spinors on \(\mathbb {H}^{k+1}\)
In this section we determine the Dirac \(L^p\)-spectrum of the hyperbolic space. The general case for \(\mathbb {M}_c\) is given in the next section.
Proposition 9.1
Let \(p\in [1,\infty ]\). The \(L^p\)-spectrum of the Dirac operator D on the hyperbolic space \(\mathbb {H}^{k+1}\) is given by the set
Proof
From Proposition 8.1 we know that the \(L^p\)-spectrum is contained in \(\sigma _p^{\mathbb {H}}\). Thus, it remains to show that each element \(\mu \) of \(\sigma _p^{\mathbb {H}}\) is contained in the \(L^p\)-spectrum of D. For that we start with a similar ansatz as was used in [18, Lemma 7] for the Laplacian.
Let the hyperbolic space \(\mathbb {H}^{k+1}\), \(k\ge 0\), be modelled by the space \(\{(y,x_1,\ldots ,x_k)\ |\ y>0\}\) equipped with the metric \(g=y^{-2}(dx_1^2 + \cdots + dx_k^2+dy^2)\). We set \(e_i= y \frac{\partial }{\partial x_i}=y\partial _i\) for \(i=1,\ldots , k\) and \(e_y=y\frac{\partial }{\partial y}=y\partial _y\). Then, \((e_y,e_1,\ldots ,e_k)\) forms an orthonormal basis, which can assumed to be positively oriented. Further we have \([e_y,e_i]=e_i=-[e_i,e_y]\). All other commutators vanish. Then, \(-\Gamma _{iy}^i=\Gamma _{ii}^y=1\) and all other Christoffel symbols vanish. The orthonormal frame \((e_y,e_1,\ldots ,e_k)\) can be lifted to the spin structure \(\vartheta :P_\mathrm{Spin}(\mathbb {H}^{k+1})\rightarrow P_\mathrm{SO}(\mathbb {H}^{k+1})\), namely we choose a map \(E:\mathbb {H}^{k+1}\rightarrow P_\mathrm{Spin}(\mathbb {H}^{k+1})\) with \(\vartheta (E)=(e_y, e_1,\ldots ,e_k)\). A spinor is by definition a section of the associated bundle \(\Sigma _{\mathbb {H}^{k+1}}= P_\mathrm{Spin}(\mathbb {H}^{k+1})\times _{\rho _{k+1}}\Sigma _{k+1}\), so every spinor can be written as \(x\mapsto [E(x),\varphi (x)]\) for a function \(\varphi :\mathbb {H}^{k+1}\rightarrow \Sigma _{k+1}\).
Hence, identifying \((e_y,e_1,\ldots ,e_k)\) with the standard basis of \(\mathbb {R}^{k+1}\) we obtain [12, (4.8)], [7, Lemma 4.1]
and
Let \(\psi _0\in \Sigma _{k+1}\) be a unit-length eigenvector of the Clifford multiplication with the vector \(e_y=(1,0,\ldots ,0)^t\in \mathbb {R}^{k+1}\) to the eigenvalue \(\pm \mathrm {i}\), i.e. \(e_y\cdot \psi _0=\pm \mathrm {i}\psi _0\). Set \(\varphi _n(x,y)=b(x)c_n(\log y) y^{\alpha } \psi _0\) where \(\alpha \in \mathbb {C}\), b(x) is any compactly supported function on \(\mathbb {R}^{k}\), and where \(c_n:\mathbb {R}\rightarrow \mathbb {R}\) is chosen to be a smooth cut-off function compactly supported on \((-4n, -n)\), \(c_n|_{[-3n,-2n]}\equiv 1\) and \(|c_n'|\le 2/n\). Then for \(p\in [1,\infty )\) one estimates \(\Vert c_n'\Vert _p^p/\Vert c_n\Vert _p^p\le C n^{-p}\rightarrow 0\) as \(n\rightarrow \infty \). For \(p=\infty \) we have \(\Vert c_n'\Vert _\infty /\Vert c_n\Vert _\infty \le 2/n \rightarrow 0\) as \(n\rightarrow \infty \). Then we set \(\Phi _n:=[E,\varphi _n]\) and obtain
In the following we will use the notation \((X\cdot \,.\,)\in \mathrm End(\Sigma _{k+1})\) for the Clifford multiplication by \(X\!\in \! \mathbb {R}^{k+1}\), and obviously its operator norm \(|(X\cdot \,.\,)|\) equals to the usual norm of X.
Let \(\mu = s \pm \mathrm {i}k(\frac{1}{p} - \frac{1}{2})\), \(s\in \mathbb {R}\). We choose \(z=\log y\) and \(\alpha =\frac{k}{2}\mp \mathrm {i}\mu =\frac{k}{p}\mp \mathrm {i}s\). Thus, the last summand in (11) vanishes and \(p\mathrm {Re\,}\alpha =k\). Then, for \(p\in [1,\infty )\) we have
where the last inequality uses
For \(p=\infty \) we have \(\mu =s\pm \mathrm {i}\frac{k}{2}\), \(\alpha =\mp s\) and the estimate above is done analogously.
Summarizing, we have shown that \(\partial \sigma _p^{\mathbb {H}}\), the boundary of \(\sigma _p^{\mathbb {H}}\), is a subset of the Dirac \(L^p\)-spectrum for \(\mathbb {H}^{k+1}\) for \(p\in [1,\infty ]\). Note that \(\sigma _s^{\mathbb {H}}=\bigcup _{2\ge r\ge s}\partial \sigma _r^{\mathbb {H}}\) for \(s<2\) and \(\sigma _s^{\mathbb {H}}=\bigcup _{2\le r\le s}\partial \sigma _r^{\mathbb {H}}\) for \(s>2\), respectively. Thus, using the Riesz–Thorin interpolation theorem we see that \(\sigma _p^{\mathbb {H}}\) is a subset of the \(L^p\)-spectrum of D on \(\mathbb {H}^{k+1}\) for \(p\in [1,\infty ]\). \(\square \)
Remark 9.2
From (10) we obtain
We use \(\mu \) and \(\varphi _n=b(x)c_n(\log y) y^\alpha \psi _0\) of the last proposition with b, \(\alpha \), \(c_n\) and \(\psi _0\) as therein. For \(c_n\) we require additionally \(|c_n''|\le 8n^{-2}\). Hence, \(\Vert c_n''\Vert _p/\Vert c_n\Vert _p\rightarrow 0\) as \(n\rightarrow \infty \) for \(p\in [1,\infty ]\). Then we have
and by analogous estimates as in Proposition 9.1 we have \(\Vert (D^2-\mu ^2) [E,\varphi _n]\Vert _p/\Vert [E, \varphi _n]\Vert _p\rightarrow 0\) as \(n\rightarrow \infty \).
Remark 9.3
Note that while the \(L^2\)-spectrum of the hyperbolic space only consists of continuous spectrum, this is no longer true for the \(L^p\)-spectrum for \(p\ne 2\) as can be seen by considering \(0\in \sigma _p^H\): We view the hyperbolic space \((\mathbb {H}^{k+1},g_{\mathbb {H}})\) modelled on the unit ball \(B_1(0)\subset \mathbb {R}^{k+1}\) of the Euclidean space and equipped with the metric \(g_{\mathbb {H}}= f^2g_E\) where \(f(x)=\frac{2}{1-|x|^2}\) and |.| denotes the Euclidean norm. Take a constant spinor \(\psi \) on \(B_1(0)\) normalized such that \(\Vert \psi \Vert _{L^p(B_1(0), g_E)}=1\). Then \(D^{g_E}\psi =0\). Using the identification of spinors of conformal metrics set \(\varphi :=f^{-\frac{k}{2}} \psi \). Then \(D^{g_{\mathbb {H}}}\varphi =0\) and \(\Vert \varphi \Vert _{L^p(g_{\mathbb {H}})}^p=\int _{B_1(0)} f^{k+1-\frac{k}{2}p} |\psi |^p \mathrm {dvol}_{g_E}\). Thus, \(\varphi \) is an \(L^p\)-harmonic spinor if and only if \( \int _{B_1(0)} (1-|x|^2)^{-k-1+\frac{k}{2}p}\mathrm {dvol}_{g_E}<\infty \), i.e., if and only if \( \int _{0}^1 (1-r^2)^{-1+\frac{k}{2}(p-2)}r^{k}\mathrm {d}r<\infty \). This is true precisely if \(p>2\) and \(k>0\). Thus, for all \(p>2\) and \(k>0\) the \(L^p\)-kernel of the Dirac operator on \((\mathbb {H}^{k+1}, g_{\mathbb {H}})\) is nontrivial.
10 The \(L^p\)-spectrum on \(\mathbb {M}_c^{m,k}\) contains \(\sigma _p\)
In this section we complete the proof of Theorem 1.1. In Proposition 8.1 it was shown that the \(L^p\)-spectrum on \(\mathbb {M}_c^{m,k}\) is contained in \(\sigma _p\). Thus, the converse remains to be shown. The case \(N=\{y\}\) was solved in Proposition 9.1.
Recall that by Lemma B.11 and Example B.12 the Dirac \(L^p\)-spectrum on \(\mathbb {M}_c^{m,k}\) is point symmetric, i.e., it is symmetric with respect to the reflection \(\lambda \mapsto -\lambda \).
Let now \(\mu \in \partial \sigma _p\) with \(\mu ^2=\lambda _0^2+\kappa ^2\), \(|\mathrm {Im\,}\kappa |= ck| \frac{1}{p}-\frac{1}{2}| \) be given. By Proposition 9.1 and scaling, we see that \(\kappa \) is in the spectrum of the Dirac operator of \(\mathbb {H}_c^{k+1}\). Then, by Lemma B.8 \(\kappa ^2\) is in the \(L^p\)-spectrum of \((D^{\mathbb {H}_c^{k+1}})^2\), and by Remark 9.2 there is a sequence \(\psi _i\in \Gamma (\Sigma _{\mathbb {H}_c^{k+1}})\) with \(\Vert ((D^{\mathbb {H}_c^{k+1}})^2-\kappa ^2)\psi _i\Vert _{L^p(\mathbb {H}_c^{k+1})}\rightarrow 0\) while \(\Vert \psi _i\Vert _{L^q(\mathbb {H}_c^{k+1})}=1\). Moreover, by Remark B.7 there is a \(\psi \in \Gamma (\Sigma _N)\) with \(\Vert \psi \Vert _{L^q(N)}=1\) and \((D^N)^2\psi =\lambda _0^2\psi \).
Assume that at least one of the dimensions of N and \(\mathbb {H}_c^{k+1}\) is even. Then \(\Sigma _{\mathbb {M}_c}=\Sigma _{\mathbb {H}_c^{k+1}} \otimes \Sigma _N\) and by (1) we have \(D^2=({D}^{\mathbb {H}_c^{k+1}})^2+({D}^N)^2\). We set \(\varphi _i=\psi _i\otimes \psi \). Then
Thus, \(\mu ^2\) is in the \(L^p\)-spectrum of \(D^2\). By the point symmetry of the spectrum and by Lemma B.8 both \(\mu \) and \(-\mu \) are in the \(L^p\)-spectrum of D.
Similarly we obtain the result if both the dimensions of N and \(\mathbb {H}_c^{k+1}\) are odd by setting \(\varphi _i:=\psi _i\otimes (\psi , \psi )\) in notation of Sect. 2.5.
Up to now we have shown that all \(\mu \in \partial \sigma _p\) are in the \(L^p\)-spectrum of the Dirac operator on \(\mathbb {M}_c\). Following the same arguments as in the last lines of the proof of Proposition 9.1 the proof of Theorem 1.1 is completed.
Remark 10.1
From Theorem 1.1 and Lemma B.8, we can immediately read off the \(L^p\)-spectrum of \(D^2\) on \(\mathbb {M}_c^{m,k}\). This consists of the closed parabolic region bounded by
Let us compare the \(L^p\)-spectrum for \(D^2\) on \(\mathbb {M}_c^{k+1,k}=\mathbb {H}^{k+1}\) (\(c=1\) and \(\lambda _0=0\))
with the one of the Laplacian on functions whose \(L^p\)-spectrum is given by the closed parabolic region bounded by [18, (1.5)]
Up to a shift in the real direction this is the same spectrum. However the qualitative difference is that for \(p\ne 2\) the spectrum of \(D^2\) contains negative real numbers, in contrast to the Laplacian.
References
Abels, H.: Pseudodifferential and Singular Integral Operators. An Introduction with Applications. De Gruyter Graduate Lectures. De Gruyter, Berlin (2012)
Ammann, B.: A variational problem in conformal spin geometry. Habilitation thesis. University of Hamburg, Germany (2003)
Ammann, B., Dahl, M., Humbert, E.: Surgery and the spinorial \(\tau \)-invariant. Commun. Partial Differ. Equ. 34(10–12), 1147–1179 (2009)
Ammann, B., Dahl, M., Humbert, E.: Harmonic spinors and local deformations of the metric. Math. Res. Lett. 18(5), 927–936 (2011)
Ammann, B., Große, N.: Relations between threshold constants for Yamabe type bordism invariants. J. Geom. Anal. 26(4), 2842–2882 (2016). doi:10.1007/s12220-015-9651-1. arXiv:1502.05232
Ammann, B., Humbert, E., Morel, B.: Mass endomorphism and spinorial Yamabe type problems on conformally flat manifolds. Commun. Anal. Geom. 14(1), 163–182 (2006)
Bär, C.: Das Spektrum von Dirac-Operatoren. Bonner Mathematische Schriften [Bonn Mathematical Publications], vol. 217. Universität Bonn, Mathematisches Institut, Bonn, 1991. Dissertation, Rheinische Friedrich-Wilhelms-Universität Bonn, Bonn (1990)
Bär, C.: Extrinsic bounds for eigenvalues of the Dirac operator. Ann. Glob. Anal. Geom. 16(6), 573–596 (1998)
Bär, C., Gauduchon, P., Moroianu, A.: Generalized cylinders in semi-Riemannian and spin geometry. Math. Z. 249(3), 545–580 (2005)
Bourguignon, J.-P., Gauduchon, P.: Spineurs, opérateurs de Dirac et variations de métriques. Commun. Math. Phys. 144(3), 581–599 (1992)
Bunke, U.: The spectrum of the Dirac operator on the hyperbolic space. Math. Nachr. 153, 179–190 (1991)
Cahen, M., Gutt, S., Lemaire, L., Spindel, P.: Killing spinors. Bull. Soc. Math. Belg. Sér. A 38(1986), 75–102 (1987)
Camporesi, R., Higuchi, A.: On the eigenfunctions of the Dirac operator on spheres and real hyperbolic spaces. J. Geom. Phys. 20(1), 1–18 (1996)
Charalambous, N.: On the \(L^p\) independence of the spectrum of the Hodge Laplacian on non-compact manifolds. J. Funct. Anal. 224(1), 22–48 (2005)
Coddington, E.A., Levinson, N.: Theory of Ordinary Differential Equations. McGraw-Hill Book Company Inc., New York (1955)
Davies, E.B.: Heat Kernels and Spectral Theory, vol. 92 of Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge (1990)
Davies, E.B.: \(L^p\) spectral theory of higher-order elliptic differential operators. Bull. Lond. Math. Soc. 29(5), 513–546 (1997)
Davies, E.B., Simon, B., Taylor, M.: \(L^p\) spectral theory of Kleinian groups. J. Funct. Anal. 78(1), 116–136 (1988)
Friedrich, T.: Dirac Operators in Riemannian Geometry. Graduate Studies in Mathematics, vol. 25. AMS, Providence (2000)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Classics in Mathematics. Springer, Berlin (2001) (Reprint of the 1998 edition)
Große, N.: Solutions of the equation of a spinorial Yamabe-type problem on manifolds of bounded geometry. Commun. Partial Differ. Equ. 37, 58–76 (2012)
Hempel, R., Voigt, J.: The spectrum of a Schrödinger operator in \(L_p({ R}^\nu )\) is \(p\)-independent. Commun. Math. Phys. 104(2), 243–250 (1986)
Hempel, R., Voigt, J.: On the \(L_p\)-spectrum of Schrödinger operators. J. Math. Anal. Appl. 121(1), 138–159 (1987)
Ji, L., Weber, A.: Dynamics of the heat semigroup on symmetric spaces. Ergod. Theory Dyn. Syst. 30(2), 457–468 (2010)
Ji, L., Weber, A.: \(L^p\) spectral theory and heat dynamics of locally symmetric spaces. J. Funct. Anal. 258(4), 1121–1139 (2010)
Ji, L., Weber, A.: The \(L^p\) spectrum and heat dynamics of locally symmetric spaces of higher rank. Ergod. Theory Dyn. Syst. 35(5), 1524–1545 (2015)
Kordyukov, Y.A.: \(L^p\)-theory of elliptic differential operators on manifolds of bounded geometry. Acta Appl. Math. 23(3), 223–260 (1991)
Lawson, H.B., Michelsohn, M.-L.: Spin Geometry. Princeton University Press, Princeton (1989)
Lohoué, N., Rychener, T.: Die Resolvente von \(\Delta \) auf symmetrischen Räumen vom nichtkompakten Typ. Comment. Math. Helv. 57(3), 445–468 (1982)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics II. Fourier Analysis, Self-adjointness. Academic Press Inc. [Harcourt Brace Jovanovich Publishers], New York (1975)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics I. Functional Analysis, 2nd edn. Academic Press Inc. [Harcourt Brace Jovanovich Publishers], New York (1980)
Saloff-Coste, L.: Uniformly elliptic operators on Riemannian manifolds. J. Differ. Geom. 36(2), 417–450 (1992)
Sepanski, M.R.: Compact Lie Groups, vol. 235 of Graduate Texts in Mathematics. Springer, New York (2007)
Sturm, K.-T.: On the \(L^p\)-spectrum of uniformly elliptic operators on Riemannian manifolds. J. Funct. Anal. 118(2), 442–453 (1993)
Taylor, M.E.: Pseudodifferential Operators. Princeton University Press, Princeton (1981)
Taylor, M.E.: \(L^p\)-estimates on functions of the Laplace operator. Duke Math. J. 58(3), 773–793 (1989)
Wang, J.: The spectrum of the Laplacian on a manifold of nonnegative Ricci curvature. Math. Res. Lett. 4(4), 473–479 (1997)
Warner, F.W.: Foundations of Differentiable Manifolds and Lie Groups. Reprint. Graduate Texts in Mathematics, vol. 94, p. IX, 272. Springer, New York (1983)
Weber, A.: Heat kernel estimates and \({L}^p\)-spectral theory of locally symmetric spaces. Dissertation (2007). doi:10.5445/KSP/1000005774
Werner, D.: Funktionalanalysis, extended edn. Springer, Berlin (2000)
Wolf, J.A.: Essential self-adjointness for the Dirac operator and its square. Indiana Univ. Math. J. 22, 611–640 (1972/73)
Yosida, K.: Functional Analysis, vol. 123 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 6th edn. Springer, Berlin (1980)
Acknowledgments
We thank an anonymous referee for many helpful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by J. Jost.
Appendices
Appendix A: Function spaces
We want to recall some analytical facts which are helpful to define spinorial function spaces on manifolds.
Let \((M^n,g)\) be an n-dimensional Riemannian spin manifold with the classical Dirac operator \(D:H_1^2(M, \Sigma _M)=\mathrm{dom}\, D\subset L^2(M, \Sigma _M) \rightarrow L^2(M, \Sigma _M)\). The set of compactly supported spinors \(C_c^\infty (M, \Sigma _M)\) is a core of D, i.e., D is the closure of \(D|_{C_c^\infty (M, \Sigma _M)}\) w.r.t. the graph norm \(H_1^2\).
A distributional spinor (or distribution with spinor values) is a linear map \(C_c^\infty (M, \Sigma _M)\rightarrow \mathbb {C}\) with the usual continuity properties of distributions. Any spinor with regularity \(L^1_{loc}\) defines a distributional spinor by using the standard \(L^2\)-scalar product on spinors.
Then \(D\varphi \) can be defined in the sense of distributions. Let \(H_1^s(M, \Sigma _M)\) be the set of distributional spinors \(\varphi \), such that \(\varphi \) und \(D\varphi \) are in \(L^s\), \(s\in [1,\infty ]\). Equipped with the norm \(\Vert \varphi \Vert _{H_1^s}:=\Vert \varphi \Vert _s+ \Vert D\varphi \Vert _s\) this is a Banach space. This norm is the graph norm of D viewed as an operator in \(L^s\) to \(L^s\). If we consider the operator \(D:H_1^s\subset L^s\rightarrow L^s\), we will shortly write \(D_s\) in the following.
Lemma A.1
Let \(1\le s<\infty \). \(C^\infty _c(M, \Sigma _M)\) is dense in \(H_1^s(M, \Sigma _M)\).
Proof
Assume that \(\varphi \in H_1^s(M, \Sigma _M)\), \(s<\infty \), is given. For a given point \(p\in M\) and for any \(R>0\) one can find a compactly supported smooth function \(\eta _R:M\rightarrow [0,1]\) such that \(\eta _R\equiv 1\) on \(B_R(p)\) and such that \(|\nabla \eta _R|\le R^{-1}\). Then one easily sees \(\lim _{R\rightarrow \infty } \Vert \varphi -\eta _R \varphi \Vert _s=0\). Further we calculate
Thus the elements with compact support are dense in \(H_1^s(M, \Sigma _M)\). Now if \(\psi \in H_1^s(M, \Sigma _M)\) has compact support, it follows from standard results that it can be approximated by smooth compactly supported spinors. \(\square \)
Thus, for \(s<\infty \), \(H_1^s(M, \Sigma _M)\) is equal to the completion of \(C^\infty _c(M, \Sigma _M)\) with respect to the graph norm of \(D:L^s\rightarrow L^s\). In particular this implies that for \(s<\infty \) the operator \(D_s\) is a closed extension of \(D|_{C_c^\infty (M, \Sigma _M)}\) with core \(C_c^\infty (M, \Sigma _M)\). Note that \(D_\infty \) is a closed extension of \(D|_{C_c^\infty (M, \Sigma _M)}\) as well but \(C_c^\infty (M, \Sigma _M)\) is in general no longer a core for this operator. Moreover, in the standard literature for \(L^p\)-theory of the Laplacian, e.g. [18], the operator for \(s=\infty \) is directly defined to be the adjoint operator for \(s=1\).
Lemma A.2
Let \(1<s<\infty \). On manifolds with bounded geometry, the \(H_1^s\)-norm is equivalent to the norm \(\Vert \varphi \Vert _s+\Vert \nabla \varphi \Vert _s\).
The proof of the lemma relies on local elliptic estimates which follow from the Calderon-Zygmund inequality, e.g. [20, Theorem 9.9], see also [2, Lemma 3.2.2] for the geometric adaptation.
Appendix B: General notes on the \(L^p\)-spectrum
In this section we collect general facts on the \(L^p\)-spectrum of the Dirac operator. Unless stated otherwise, we only assume that (M, g) is complete.
We examine the adjoint of the operator \(D_s:L^s\rightarrow L^s\) with respect to the duality pairing \(\langle .,.\rangle :L^s\times (L^s)^*\rightarrow \mathbb {C}\) whose restriction to compactly supported spinors coincides with the hermitian \(L^2\)-product. We use the convention that this pairing is antilinear in the second component. The adjoint \(D_s^*\) is an operator in \((L^s)^*\). For \(1\le s<\infty \) and \(s^{-1}+(s^*)^{-1}=1\), \((L^s)^*=L^{s^*}\) whereas \((L^\infty )^*\) is larger than \(L^1\). From the formal self-adjointness of D we see, that \(D_{s^*}|_{C_c^\infty (M, \Sigma _M)} = D_s^*|_{C_c^\infty (M, \Sigma _M)}\). Moreover, we have
Lemma B.1
For all \(\varphi \in H_1^s\) and \(\psi \in H_1^{s^*}\), \(1\le s \le \infty \), we have
Proof
For \(1<s< \infty \), let \(\varphi _i, \psi _j\in C_c^\infty (M, \Sigma _M)\) with \(\varphi _i\rightarrow \varphi \) in \(H_1^s\) and \(\psi _j\rightarrow \psi \) in \(H_1^{s^*}\). Then,
as \(i,j\rightarrow \infty \). Let now \(s=1\). For \(\varphi \in C_c^\infty (M, \Sigma _M)\) the equality follows from the distributional definition of \(D_\infty \). The rest follows since \(C_c^\infty (M, \Sigma _M)\) is dense in \(H_1^1\). The remaining case \(s=\infty \) just follows from the last one by interchanging s and \(s^*\). \(\square \)
Lemma B.2
For all \(1\le s<\infty \) the operators \(D_{s^*}\) and \(D_s^*\) coincide.
Proof
For \(\psi \in H_1^{s^*}\) Lemma B.1 yields \((D_s\varphi , \psi )=(\varphi , D_{s^*}\psi )\) for all \(\varphi \in H_1^s=\mathrm{dom}\, D_s\). This implies \(\psi \in \mathrm{dom}\, D_s^*\) and \(D_s^*\psi =D_{s^*}\psi .\) Hence, \(H_1^{s^*}\subset \mathrm{dom}\, D_s^*\) and \(D_s^*|_{H_1^{s^*}}=D_{s^*}:H_1^{s^*}\subset L^{s^*}\rightarrow L^{s^*}\). It remains to show that \(\mathrm{dom}\, D_s^*\subset H_1^{s^*}\): Let \(\psi \in \mathrm{dom}\, D_s^*\subset (L^s)^*=L^{s^*}\). Then there is a \(\rho \in L^{s^*}\) such that for all \(\varphi \in \mathrm{dom}\, D_s\) it holds \((D_s\varphi , \psi )= (\varphi , \rho )\). In particular, this is true for all \(\varphi \in C_c^\infty (M, \Sigma _M)\). In other words \(D_s^*\psi =\rho \) in the sense of distributions. Thus, \(\psi \in H_1^{s^*}\). \(\square \)
Since \(\varphi \in H_1^s\cap H_1^r\) implies \(D_s\varphi =D_r\varphi \) we often denote all those Dirac operators in the following just by D.
Moreover, a closed operator \(P:\mathrm{dom}\, P\subset V_1\rightarrow V_2\) between Banach spaces \(V_i\), and with dense domain \(\mathrm{dom}\, P\), will be called invertible if there exists a bounded inverse \(P^{-1}:V_2\rightarrow V_1\). We will use the phrase “P has a bounded inverse” synonymously.
Lemma B.3
Let \(1 \le s<\infty \).
-
(i)
If \(\overline{\mu }\) is in the \(L^{s^*}-\)spectrum of the Dirac operator where \((s^*)^{-1}+s^{-1}=1\), then \(\mu \) is in its \(L^s-\)spectrum.
-
(ii)
Let \(D_s-\mu \) be invertible. Then, \((D_{s^*}-\bar{\mu })^{-1}=((D_s-\mu )^{-1})^*\) and \(\Vert (D_{s^*}-\bar{\mu })^{-1}\Vert =\Vert (D_s-\mu )^{-1}\Vert \).
Proof
We prove this for \(\mu =0\). For arbitrary \(\mu \) this is done analogously. Assume that 0 is not in the \(L^s\)-spectrum of D, i.e., it has a bounded inverse \(E=D^{-1}:L^s\rightarrow L^s\) with range \(\mathrm{ran}\, E=H_1^s\). Let \(\varphi \in L^{s^*}\). Since E is bounded, \(f:L^s \rightarrow \mathbb {C}, \rho \mapsto (E\rho , \varphi )\) is a bounded functional and, thus, f is in the dual space of \(L^s\), i.e., there is \(\psi \in L^{s^*}\) with \((\rho ,\psi )=f(\rho )=(E\rho ,\varphi )\) for all \(\rho \in L^s\). Hence, \(\varphi \in \mathrm{dom}\, E^*\), i.e., \(\mathrm{dom}\, E^*=L^{s^*}\).
Now we can estimate for all \(\varphi \in H_1^s\) and all \(\psi \in L^{s^*}\) that \((D\varphi , E^*\psi )=(ED\varphi ,\psi )=(\varphi , \psi )\) which implies \(E^*\psi \in \mathrm{dom}\, D^*\) and \(D^*E^*\psi =\psi \). Thus, \(\mathrm{ran}\, D^*=L^{s^*}\) and \(D^*E^*={\text {Id}}:L^{s^*}\rightarrow L^{s^*}\).
If \(\rho \in L^s\) and \(\varphi \in \mathrm{dom}\, D^*\), we get \((\rho , E^*D^*\varphi )= (E\rho , D^*\varphi )=(DE\rho ,\varphi )=(\rho ,\varphi )\). Hence, \(E^*D^*={\text {Id}}:\mathrm{dom}\, D^*\rightarrow \mathrm{dom}\, D^*\). Together with the corresponding statement from above this gives that \((D^{-1})^*=(D^*)^{-1}\). Thus, 0 is not in the \(L^{s^*}\)-spectrum of D. This proves (i) and the first claim of (ii). The operator norm of an operator and its adjoint coincide, see [31, Thm VI.2]. Thus, the equality of the operator norms follows. \(\square \)
Corollary B.4
If \(D:H_1^q\rightarrow L^q\) has a bounded inverse for some \(q\in (1,\infty )\). Then as an operator from \(H_1^s \rightarrow L^s\) it has a bounded inverse for all \(s\in [q_1, q_2]\) where \(q_1=\min \{q,q^*\}\), \(q_2=\max \{q,q^*\}\), and \((q^*)^{-1}+q^{-1}=1\). In particular, the \(L^2\)-spectrum of D is a subset of the \(L^q\)-spectrum.
Proof
This Lemma follows directly from the Riesz–Thorin Interpolation Theorem 2.2 (using \(\mathcal {D}=C_c^\infty (M, \Sigma _M)\)) and Lemma B.3. \(\square \)
Lemma B.5
Let \(1\le s\le \infty \). Let \(R_s=\mathbb {C}{\setminus } \mathrm Spec_{L^s}(D)\) be the resolvent set of \(D:L^s\rightarrow L^s\). Then, the resolvent
is analytic, i.e., the map is locally given by a convergent power series with coefficients in \(\mathcal {B}(L^s)\). Here, \(\mathcal {B}(L^s)\) denotes the set of bounded operators from \(L^s\) to itself.
See [42, VIII.2 Theorem 1] for a proof.
For rounding up our presentation we will next add a lemma not needed in our context but maybe helpful to other applications.
Lemma B.6
-
(1)
The operator \(D:H_1^s\subset L^s\rightarrow L^s\), \(s\in [1,\infty ]\), is an invertible map onto its image if and only if there is a constant \(C>0\) with \(\Vert D\varphi \Vert _{s}\ge C\Vert \varphi \Vert _s\) for all \(\varphi \in H_1^s\).
-
(2)
Under the above conditions the image \(D(H_1^s)\) is closed.
-
(3)
Let \(s^{-1}+(s^*)^{-1}=1\), \(s<\infty \), and assume the conditions from above. Then D is surjective if and only if there is a \(C>0\) with \(\Vert D\varphi \Vert _{s^*}\ge C\Vert \varphi \Vert _{s^*}\) for all \(\varphi \in H_1^{s^*}\).
Proof
-
(1)
The proof is straightforward.
-
(2)
The operator \(D:H_{1}^s\rightarrow D(H_{1}^s)\), where the latter space is equipped with the \(L^s\)-norm, is a bijective bounded linear map. Hence, \(D(H_{1}^s)\) is a complete subspace of \(L^s\) and thus closed.
-
(3)
Suppose that \(D(H_1^s)\) is a proper subspace of \(L^s\). Due to Hahn-Banach there is a non-zero continuous functional \(\psi :L^s\rightarrow \mathbb {C}\) vanishing on \(D(H_1^s)\). We interpret \(\psi \) as an element in \(L^{s^*}\) using the Riesz representation theorem, i.e. \(\psi \in L^{s^*}\) is orthogonal on \(D(H_1^s)\). Then, \(\psi \in \mathrm{dom}\, (D_{s})^*\), and we even have \(D_{s}^*\psi =0\). Hence, by Lemma B.2 \(\psi \in H_1^{s*}\). This contradicts the estimate. Now assume that D is surjective. Then there is a bounded operator \(D^{-1}:L^s\rightarrow L^s\), inverse to D. Thus \((D^{-1})^*:L^{s^*}\rightarrow L^{s^*}\) is bounded as well, and \((D^{-1})^*\) is the inverse of \(D^*:H_1^{s^*}\rightarrow L^{s^*}\). The fact that the latter map has a bounded inverse is equivalent to the existence of a constant \(C>0\) with \(\Vert D\varphi \Vert _{s^*}\ge C\Vert \varphi \Vert _{s^*}\).
\(\square \)
Remark B.7
The \(L^s\)-spectrum of the Dirac operator D on a closed manifold \((M^m,g)\) is independent of s. We sketch the proof: Let \(\varphi \) be an \(L^2\)-eigenspinor of D. Then regularity theory implies that \(\varphi \in C^\infty (M, \Sigma _M)\) and, hence, \(\varphi \in L^s\) for all \(1\le s\le \infty \). In particular, \(\mathrm Spec_{L^2}^M(D)\subset \mathrm Spec_{L^s}^M(D)\). Let now \(\mu \not \in \mathrm Spec_{L^2}^M(D)\), i.e., \((D-\mu )^{-1}:L^2\rightarrow L^2\) is bounded. Let G(x, y) be the unique Green function of \(D-\mu \), see Proposition 3.2. Then, \(\int _M |G(.,y)|^2 dy\) is bounded uniformly in y. Hölder’s inequality implies that also \(\int _M |G(.,y)| dy\) is bounded uniformly in y. Hence, \((D-\mu )^{-1}:L^1\rightarrow L^1\) is a bounded operator. Then interpolation gives that \((D-\mu )^{-1}:L^s\rightarrow L^s\) is bounded for all \(1\le s<2\). Because of \(\mathrm Spec_{L^2}(D)\subset \mathbb {R}\) the same is true for \((D-\bar{\mu })^{-1}:L^s\rightarrow L^s\), and by using Lemma B.3 we get that \((D-\mu )^{-1}:L^s\rightarrow L^s\) is bounded for all \(2< s<\infty \). It remains \(s=\infty \): Let \(r>m\). Then by the Sobolev Embedding Theorem \(H_1^r\hookrightarrow L^\infty \) is bounded. Moreover, by the discussion above and using the fact that \(H_1^r\) carries the graph norm of D we know that \((D-\mu )^{-1}:L^r\rightarrow H_1^r\) is bounded for \(\mu \not \in \mathrm Spec_{L^2}^M (D)\) the Hölder inequality gives that
is bounded.
Lemma B.8
Let \(1\le s\le \infty \), and let \(\mathrm Spec_{L^s}^M(D)\ne \mathbb {C}\). Then the complex number \(\mu ^2\) is in the \(L^s\)-spectrum of \(D^2\) if and only if \(\mu \) or \(-\mu \) is in the \(L^s\)-spectrum of D.
Proof
We start with the “only if” part. So assume that both \(\mu \) and \(-\mu \) are not in the \(L^s\)-spectrum of D. Then we have bounded operators \((D-\mu )^{-1}:L^s\rightarrow L^s\) and \((D+\mu )^{-1}:L^s\rightarrow L^s\). It is then easy to verify that \((D-\mu )^{-1}\circ (D+\mu )^{-1}:L^s\rightarrow L^s\) is a bounded inverse of \(D^2-\mu ^2=(D+\mu )\circ (D-\mu )\). Thus \(\mu ^2\) is not in the \(L^s\)-spectrum of \(D^2\).
In order to prove the “if” statement, we assume that \(\mu ^2\) is not in the spectrum of \(D^2\). Then \(D^2-\mu ^2\) has a bounded inverse \(P:=(D^2-\mu ^2)^{-1}:L^s\rightarrow L^s\). Let \(\psi \in P(L^s)\). Then \(\psi \in L^s\) and \(D^2\psi \in L^s\). Next we will show that this implies \(D\psi \in L^s\). For that we choose \(\lambda \not \in \mathrm Spec_{L^s}^M(D)\). Then \(D\psi =(D-\lambda )^{-1}(D^2-\lambda ^2)\psi -\lambda \psi \), and hence \(D\psi \in L^s\). Thus, \(P(L^s)\subset H_{1}^s\). Hence \(Q_1:=(D\pm \mu )\circ P\) is a bounded operator with \(\mathrm{dom}\, Q_1=L^s\), and one easily checks that this a right inverse to \((D\mp \mu )\). Similarly, one shows that \(Q_2:=P\circ (D\pm \mu )\) is a left inverse of \((D\mp \mu )\). A priori \(Q_2\) is only defined on \(H_{1}^s\), but using \(Q_1=Q_1\circ (D\mp \mu )\circ Q_2=Q_2\) it is clear that \(Q_2\) and \(Q_1\) coincide on \(H_1^s\). So the integral kernels of \(Q_1\) and \(Q_2\) have to coincide, so \(Q_1\) is a left and right inverse of \((D\mp \mu )\) and thus \(\pm \mu \) is not in the spectrum of D. \(\square \)
Remark B.9
In the case \(1<s<\infty \) and M of bounded geometry, one can also prove that \(\mathrm Spec_{L^s}^M(D)=\mathbb {C}\) implies \(\mathrm Spec_{L^s}^M(D^2)=\mathbb {C}\): As in the proof of the “if” statement from above one has to show that \(D\psi \in L^s\). This can be proven using regularity theory on manifolds of bounded geometry.
Lemma B.10
(Pointwise symmetries) Let \(1\le s\le \infty \). Let (M, g) be an m-dimensional Riemannian spin manifold.
-
(i)
\(m\equiv 0 \mathrm{mod} 2\): The number \(\mu \) is in the \(L^s\)-spectrum of D if and only if \(-\mu \) is in the \(L^s\)-spectrum of D if and only if \(\bar{\mu }\) is in the \(L^s\)-spectrum of D.
-
(ii)
\(m\equiv 1 \mathrm{mod} 4\): The number \(\mu \) is in the \(L^s\)-spectrum of D if and only if \(-\bar{\mu }\) is in the \(L^s\)-spectrum of D.
-
(iii)
\(m\equiv 3 \mathrm{mod} 4\): The number \(\mu \) is in the \(L^s\)-spectrum of D if and only if \(\bar{\mu }\) is in the \(L^s\)-spectrum of D.
Proof
By [19, Prop. p. 31] we have a map \(\alpha :\Sigma _m\rightarrow \Sigma _m\) that is
-
a \(\mathrm{Spin}(m)\)-equivariant real structure that anticommutes with Clifford multiplication if \(m\equiv 0,1 \mathrm{mod} 8\).
-
a \(\mathrm{Spin}(m)\)-equivariant quaternionic structure that commutes with Clifford multiplication if \(m\equiv 2,3 \mathrm{mod} 8\).
-
a \(\mathrm{Spin}(m)\)-equivariant quaternionic structure that anticommutes with Clifford multiplication if \(m\equiv 4,5 \mathrm{mod} 8\).
-
a \(\mathrm{Spin}(m)\)-equivariant real structure that commutes with Clifford multiplication if \(m\equiv 6,7 \mathrm{mod} 8\).
Note that by definition real structure means that \(\alpha ^2={\text {Id}}\) and \(\alpha (\mathrm{i} v)=-\mathrm{i}\alpha (v)\). Moreover, quaternionic structure means that \(\alpha ^2=-{\text {Id}}\) and \(\alpha (\mathrm{i} v)=-\mathrm{i}\alpha (v)\).
Due to the \(\mathrm{Spin}(m)\)-equivariance \(\alpha \) induces a fiber preserving map \(\tilde{\alpha }\) on the spinor bundle with the same properties as above. Thus,
Thus, if \(\mu \) is in the \(L^s\)-spectrum of D then \(-\bar{\mu }\) (resp. \(\bar{\mu }\)) in the \(L^s\)-spectrum of D for \(m\equiv 0,1\) (resp. 2,3) \(\mathrm{mod}\) 4. This gives (ii) and (iii).
If m is even, then \(D (\omega _M\cdot \varphi )=-\omega _M\cdot D\varphi \). Thus, the spectrum is symmetric when reflected on the imaginary axis. Together with the symmetries from above, (i) follows. \(\square \)
Lemma B.11
(Orientation reversing isometry) Let \(1\le s\le \infty \). Assume there is an orientation reversing isometry \(f:M^m\rightarrow M^m\) that “lifts” to the spin structure as described in the proof. Then \(\mu \) is in the \(L^s\)-spectrum of D if and only if \(-\mu \) is in the \(L^s\)-spectrum of D.
Proof
The proof follows the lines of [4, Appendix A]. In this reference, f is required to be a reflection at a hyperplane of M. But this doesn’t change the part we need: We lift f to the bundle \(P_{\mathrm{SO}(m)}M\) of oriented orthonormal frames by mapping the frame \(\mathcal {E}=(e_1,\ldots , e_m)\) to \(f_*\mathcal {E}=(-\mathrm {d}f(e_1),\mathrm {d}f(e_2),\ldots , \mathrm {d}f(e_m))\), so \(f_*:P_{\mathrm{SO}(m)}M\rightarrow P_{\mathrm{SO}(m)}M\). Since f is an orientation reserving isometry,
where \(J=\mathrm{diag}(-1, 1,1,\ldots , 1)\). The map f is assumed to lift to the spin structure, i.e., there is a lift \(\tilde{f}_* :P_{\mathrm{Spin}(m)}(M)\rightarrow P_{\mathrm{Spin}(m)}(M)\) with \(\vartheta \circ \tilde{f}_*=f_*\circ \vartheta \) where \(\vartheta \) denotes the double covering \(\vartheta :P_{\mathrm{Spin}(m)}(M)\rightarrow P_{\mathrm{SO}(m)}(M)\). By [4, Lemma A.1 and Lemma A.4], f then lifts to a map \(f_\sharp :\Sigma _M\rightarrow \Sigma _M\) on the spinor bundle which fulfils \(f_\sharp (D\varphi )=-D (f_\sharp \varphi )\). \(\square \)
Example B.12
-
(i)
Let \(M^{n+1}\) be a Riemannian spin manifold with a spin structure \(\vartheta \) as above. Assume that up to isomorphism this is the unique spin structure on M. Let \(f:M\rightarrow M\) be an orientation reversing isometry. By pulling back the double covering \(P_{\mathrm{Spin}}M\rightarrow P_{\mathrm{SO}}M\) by \(f_*\) we obtain the double covering \(f^*\vartheta : f^*P_{\mathrm{Spin}}M\rightarrow P_{\mathrm{SO}}M\). We then turn \(f^*P_{\mathrm{Spin}}M\) into a \(\mathrm{Spin}(n+1)\)-principal bundle by conjugating the action of \(\mathrm{Spin}(n+1)\) on \(P_{\mathrm{Spin}}M\) with Clifford multiplication with \(e_0\). Then \(f^*\vartheta \) is a spin structure on M. Thus an isomorphism from \(\vartheta \) to \(f^*\vartheta \) yields a map \(f_\sharp \) as above.
-
(ii)
Consider the map \(f=f_1\times \mathrm{id}:\mathbb {M}_c^m=\mathbb {H}_c^{k+1}\times N^n\rightarrow \mathbb {M}_c^{m,k}\) where \(f_1\) is an orientation reversing isometry as in (i). Then, f is again an orientation reversing isometry. Using \(P_\mathrm{SO}(\mathbb {H}_c\times N)= (P_\mathrm{SO}(\mathbb {H}_c^{k+1})\times P_\mathrm{SO}(N))\times _{\bar{\xi }} \mathrm{SO}(m)\) where \(\bar{\xi }:\mathrm{SO}(k+1)\times \mathrm{SO}(n)\rightarrow \mathrm{SO}(m)\) is the standard embedding and using the analogous describtion for \(P_{\mathrm{Spin}}(\mathbb {H}_c\times N)\), see Sect. 2.5, one see that also f lifts to the spin structure.
Appendix C: Dirac eigenvalues of generic metrics
Proposition C.1
Let (M, g) be a closed, connected Riemannian spin manifold, let \(\mu \in \mathbb {R}\). Let \(U\subset M\) be a nonempty open subset. In case that \(\mu =0\), assume additionally that the \(\alpha \)-genus of M is zero. Then, there is a metric \(\tilde{g}\) on M with \(\tilde{g}=g\) on \(M{\setminus } U\) and \(\ker \, (D^{\tilde{g}}-\mu )=\{0\}\).
Proof
For \(\mu =0\), the proposition follows from [4, Theorem 1.1]. For \(\mu \ne 0\), the proof is a direct consequence of the following lemma. \(\square \)
Lemma C.2
Let (M, g) be a closed, connected Riemannian spin manifold, let \(\mu \in \mathbb {R}{\setminus } \{0\}\), and let \(U\subset M\) be a nonempty open subset. Then there is a function \(f\in C^\infty (M, \mathbb {R}^+)\) with \(f|_{M{\setminus } U}\equiv 1\) such that \(\ker \, (D^{fg}-\mu )=\{0\}\).
Proof
Choose \(f\in C^\infty (M, \mathbb {R}^+)\) with \(f|_{M{\setminus } U}\equiv 1\) such that \(d=\dim (E_{f,\mu }:=\ker \, (D^{fg}-\mu ))\) is minimal. Assume \(d>0\), and set \(g_0=fg\). For \(\alpha \in C^\infty (M)\) with \(\mathrm supp\, \alpha \subset U\) and t close to 0 we define \(g_t:=(1+t\alpha )fg\). Then by [10] there are real analytic functions \(\mu _1, \ldots , \mu _d:(-\epsilon , \epsilon )\rightarrow \mathbb {R}\) with \(\mu _i(0)=\mu \) such that \(\mathrm Spec_{L^2}^M(D^{g_t})\cap (\mu -\delta , \mu +\delta )=\{\mu _1(t), \ldots , \mu _d(t)\}\) including multiplicities. It is shown in [10] that there is an orthonormal basis \((\psi ^{(1)}, \ldots , \psi ^{(d)})\) of \(E_{f,\mu }\) depending on the choice of \(\alpha \) such that
where \(Q_{\psi }(X,Y)=\frac{1}{2}\mathrm {Re\,}\langle X\cdot \nabla _Y \psi + Y\cdot \nabla _X \psi , \psi \rangle .\) Thus,
As d is minimal, we see that \( \frac{\mathrm {d}}{\mathrm {d}t}|_{t=0} \mu _i(t)=0\), and thus for all \(\alpha \) as above
Note that \(\varphi :=\sum _{i=1}^d |\psi ^{(i)}|^2\in C^\infty (M)\) does not depend on the choice of \(\alpha \). This can be seen by direct calculation with base change matrices or alternatively by observing that \(\varphi \) is the pointwise trace of the integral kernel of the projection to \(E_{f,\mu }\). With \(\mu \ne 0\) this implies that \(\varphi \) and thus all \(\psi ^{(i)}\) vanish on U. The unique continuation principle implies then \(\psi ^{(i)}\equiv 0\) which gives a contradiction. \(\square \)
Rights and permissions
About this article
Cite this article
Ammann, B., Große, N. \(L^p\)-spectrum of the Dirac operator on products with hyperbolic spaces. Calc. Var. 55, 127 (2016). https://doi.org/10.1007/s00526-016-1046-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-016-1046-z