1 Introduction

Diabetes is a long-term (chronic) health condition that affects how the body transforms food into energy. Most food is broken down into sugar (glucose) by the body and released into the bloodstream. When blood sugar levels rise, the pancreas releases insulin, which is necessary for transporting blood sugar into cells for use as energy. Type 1 diabetes, type 2 diabetes, and gestational diabetes are the three forms of diabetes (https://www.cdc.gov/diabetes/basics/gestational.html).

  1. 1.

    Type 1 diabetes is caused by an autoimmune reaction (the body accidentally fights itself). Insulin synthesis is halted as a result of this response.

  2. 2.

    With type 2 diabetes, the body does not utilize insulin well and cannot maintain normal blood sugar levels.

  3. 3.

    Pregnant women who have never had diabetes acquire the third type of diabetes, i.e., gestational diabetes.

In our work, we focused on the mechanism of type 2 diabetes. Diabetes mellitus type 2 (T2DM) is a major global health concern linked to the obesity pandemic. Insulin resistance is widely regarded as the primary cause of type 2 diabetes. Insulin resistance raises plasma fatty acids, decreasing glucose delivery into muscle cells and boosting fat breakdown, increasing hepatic glucose production. Diabetes type 2 must result from insulin resistance and pancreatic cell failure [1]. People with type 2 diabetes mellitus are at an increased risk for both microvascular complications (such as retinopathy, nephropathy, and neuropathy) and macrovascular complications (such as cardiovascular comorbidities) due to hyperglycemia and individual components of the insulin resistance (metabolic) syndrome [2].

Interdisciplinary research of chronic disease dynamics has grown rapidly in recent decades. Mathematical, physics, biology, computer science, statistics, and epidemiological contributions are critical for improving public health [3]. Mathematical modeling is very important. In this setting, mathematical modeling is critical for understanding the complexities of disease dynamics [4, 5]. Many mathematical models have been developed to understand the mechanism of type 2 diabetes [2, 6–10]. In 2000, Topp et al. [6] created a model illustrating beta-cell mass dynamics along with the evolution of type 2 diabetes. The model was a foundation for various diabetes progression models [6]. De Winter et al. [11] created a population pharmacodynamic model comprised of glucose, insulin, and glycosylated hemoglobin differential equations to characterize the impact of treatment on the time course of insulin sensitivity and gradually reduced beta-cell function. Banzi et al. [12] devised a mathematical model to explore the dynamic behavior of glucose-insulin which is specific for type 2 diabetic patients. Bergman et al. [13] proposed a simple compartmental model of diabetes dynamics in 1981. This mathematical model has been employed in diabetic research [14]. To explain why fasting hyperinsulinemia can occur decades before hyperglycemia, Joon et al. [15] expanded Topp’s model by connecting beta-cell proliferation to beta-cell secretory burden, which can magnify the impact of modest changes in glucose. The model accurately predicted the effect of weight loss and bariatric surgery on the glucose-regulating system. Despite these efforts, a model that depicts the long-term history of diabetes while incorporating diabetogenic elements (such as an obesogenic environment) is only a few. Recently, Yang et al. [7] developed a mathematical model to study the role of beta-cell dysfunction on diabetes progression. Environmental and genetic factors contribute to the pathophysiological abnormalities that cause poor glucose homeostasis in type 2 diabetes mellitus [2, 7].

According to various studies [2, 7], obesity, physical inactivity, a high-fat diet, and a diet rich in saturated fatty acids have all been associated with an elevated risk of diabetes. Obesity has become a major global concern due to its rising prevalence and the accompanying cluster of diseases degrading life quality and longevity. It is the abnormal fat deposition in the adipose tissue due to prolonged overeating, limited physical activity, or inherited factors [10]. It raises the chance of developing type 2 diabetes, cardiovascular disease, cancer, and dying prematurely. The global obesity and type 2 diabetes epidemic is worsening. According to the World Health Organisation (WHO) data, global obesity has nearly doubled since 1990 [16]. Over 1.1 billion individuals are considered overweight, with approximately 320 million classified as obese [17]. Obesity and diabetes are firmly connected, with around 80\(\%\) of people with diabetes being obese. Obesity worsens the glucose content in the bloodstream; as a result, the pancreas becomes overworked and wears out. It begins to produce less insulin. Diabetes develops and rapidly worsens if fat resistance persists (https://health.clevelandclinic.org/diabesity-the-connection-between-obesity-and-diabetes/).

The current paper focuses on how beta-cell dysfunction due to the obesity-related factor can worsen the diabetic condition. The following is the outline for the paper: The model is framed in Sect. 2. Section 3 contributes to the model’s analysis (boundedness, equilibrium points, and stability analysis). Section 4 contributes to the bifurcation analysis. In Sect. 5, we extend our model and incorporate a delay term. This section is also devoted to the analysis of the delay model. Section 6 deals with the optimal control problem. Numerical results for both non-delay and delay models are illustrated in Sect. 7. Section 8 is where we interpret our results.

2 Formulation of Model

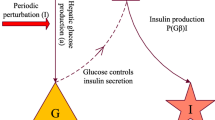
Obesity and diabetes are complex; however, many studies show that obesity and being overweight increase the likelihood of acquiring type 2 diabetes [7, 18, 19]. Mathematical models are used for depicting the progression and analyzing its nature. It is a combination of low pancreatic-cell insulin production and peripheral insulin resistance. Saturated fats have been linked to insulin resistance and beta-cell malfunction, according to [9]. To function normally, the human body relies on strict management of blood glucose levels. Insulin, produced in the pancreas by beta cells, stimulates glucose utilization by target cells and is essential for blood glucose control. High blood glucose levels stimulate the release of insulin from beta-cell secretory granules, which aids in the restoration of glucose concentrations to normal. When the glucose level drops, insulin secretion eventually stops. The glucose regulatory system can maintain glucose homeostasis for individuals free from diabetogenic events [7].

What happens when a person is obese is still a controversial question. However, findings suggest that if a person is obese or overweight, the amount of glucose level increases in his body [1]. Increased glucose levels, combined with increased NEFA (non-esterified fatty acids), can synergistically affect beta-cell health and insulin function [20, 21]. Type 2 diabetes is a heterogeneous condition characterized most commonly by insulin resistance, which is a state of decreased insulin-mediated glucose absorption caused by the pancreatic beta cells’ failure to make and produce adequate insulin to fulfill the required demands [17, 22]. The findings suggest that increased fat breakdown leads to increased hepatic glucose generation [1]. When blood glucose levels rise, beta-cells in the pancreatic islets secrete insulin, further decreasing blood glucose levels by acting on specific tissues [8]. Few mathematical models are designed in this direction [7, 23].

Motivated by the above-described mechanism, we have formulated an obesity-based diabetes model. The model is organized into four compartmental representations of the human body, with each compartment representing an organ or tissue that is connected by blood flow, namely, glucose concentration \((G)\), insulin concentration \((I)\), beta-cell mass \((B)\), and obesity-related factor \((F)\). In this work, we have considered the following assumptions:

  • As glucose growth and death occur naturally, the parameter \(a\) represents the average daily glucose infusion rate (with meal consumption as the primary source), including hepatic glucose generation. The term \(d_{1} G\) refers to the insulin-independent elimination of glucose [6].

  • Yang et al., [7], designed the enhanced hepatic glucose production to be a power function of obesity-related factor as \(F^{\alpha}\), which can be estimated by the extent to which the pathogenic factor affects the rate of glucose generation. In our work, we employ the same power function by assuming \(\alpha \) as 1 (\(F ^{1}\)) to show the role of obesity-related factors in glucose growth.

  • We suggest a novel functional response, \(\dfrac{bIG}{1+pG+qF}\), to imitate the mechanism of insulin and fat-dependent glucose swings. It is similar to the Holling type 2 functional response but includes an additional term that describes mutual interference by an obesity-related factor (\(q F\)). Glucose consumption saturates the Holling type II functional response, and glucose has high per-capita mortality at low densities and falling mortality as density increases. Here, \(b\) denotes the rate of decrease in glucose level due to insulin, \(q\) describes the rate of mutual interference by the obesity-related factor, and \(p\) is the glucose saturation constant. Figure 1, describes the behavior of the function. We can observe that the function attains its maxima when no obesity-related factors are present and glucose levels are normal. This means that the natural glucose removal process due to insulin is working effectively. However, at high-fat levels, the function’s value tends to zero, thus depicting low removal of glucose due to hampering insulin function by obesity-related factors.

    Fig. 1
    figure 1

    3D plot showing the behaviour of the function \(\dfrac{G}{1+pG+qF}\)

    Full size image

  • We have considered Holling type-II functional response, \(\dfrac{\mu B G }{ k_{1} + G}\), to model the interaction between glucose and beta-cells, which results in insulin production. This functional response accounts for the fact that beta and glucose interaction produces insulin; however, the production rate saturates at high glucose levels, and declining glucose levels can increase insulin density.

  • Holling type-II response, \(\dfrac{h G }{ k_{2} + G}\), is also considered to model glucose and beta-cell interaction resulting in beta-cell growth.

  • There is growing evidence that accumulating harmful compounds within beta-cells in obese patients promotes beta-cell death, eventually leading to diabetes [7]. We have demonstrated that beta-cell dysfunction is caused by an obesity-related component \((\delta F^{2} B)\).

  • Considering that obesity-related factors grow slowly to a maximum limit in humans, we employ logistic growth [7].

The ODE model is developed and illustrated below based on the aforementioned assumptions:

$$\begin{aligned} \dfrac{dG}{dt} =&a-\dfrac{bIG}{1+pG+qF}+ c F -d_{1} G, \end{aligned}$$
(1)
$$\begin{aligned} \dfrac{dI}{dt} =&\dfrac{\mu B G}{k_{1}+G}-d_{2} I, \end{aligned}$$
(2)
$$\begin{aligned} \dfrac{dB}{dt} =&\left (\dfrac{h G }{ k_{2} + G}- \delta F^{2} -d_{3} \right )B, \end{aligned}$$
(3)
$$\begin{aligned} \dfrac{dF}{dt} =&rF \left (1-\dfrac{F}{k_{3}}\right ). \end{aligned}$$
(4)

All of the model’s parameters are positive, and their descriptions are shown in Table 1. In addition, Fig. 2 depicts the schematic diagram of the obesity-based diabetes model.

Fig. 2
figure 2

Schematic diagram for obesity-based diabetes model (1)-(4)

Full size image
Table 1 Parameters description for the model (1)-(4)
Full size table

3 Analysis of the Model

In this section, we examine the boundedness, positivity, existence, and stability behavior of the system’s (1)-(4) steady-state solutions.

3.1 Boundedness

To ensure that the model (1)-(4) is well-posed, we examine the boundedness in this section.

Theorem 3.1

Assume that all the initial conditions are non-negative and the condition \(\dfrac{h \bar{G}}{k_{2}} < d_{3}\), holds, where \(\bar{G} = max\left(G(0),\dfrac{a + c \bar{F}}{d_{1}}\right)\), then the solutions of the system (1)-(4) is bounded in \(\mathbb{R}_{+}^{4}\).

Proof

From Eq. (4), we have

$$\begin{aligned} \dfrac{ d F}{dt} = r F \left (1 - \dfrac{F}{k_{3}}\right ) \end{aligned}$$

Hence, we get

$$\begin{aligned} \limsup_{t\to \infty}~F(t) \leq k_{3}. \end{aligned}$$

Then, we call the upper bound of \(F\) as

$$ \bar{F} = max(F(0), k_{3}). $$
(5)

From Eq. (1), we have

$$\begin{aligned} \dfrac{dG}{dt} =& a -\dfrac{b I G}{1 + pG + q F} +c F - d_{1} G \\ \leq & a + c \bar{F} - d_{1} G, ~~~~ \text{where }\bar{F}\text{ is taken from Eq. (5)} \end{aligned}$$

Hence, we have

$$\begin{aligned} G(t) \leq \dfrac{a + c \bar{F}}{d_{1}} + C_{4} e ^{- d_{1} t}, \end{aligned}$$

where \(C_{4}\) is a constant.

Taking,

$$\begin{aligned} \limsup_{t\to \infty}~G(t) \leq \dfrac{a + c \bar{F}}{d_{1}}. \end{aligned}$$

Hence, we get the upper bound of \(G\) as

$$ \bar{G} = max\left(G(0),\dfrac{a + c \bar{F}}{d_{1}}\right). $$
(6)

From Eq. (3), we have

$$\begin{aligned} \dfrac{d B}{d t} =& \dfrac{h B G}{k_{2} +G} -\delta F^{2} B - d_{3} B \\ \leq & \dfrac{h B \bar{G}}{k_{2}} - d_{3} B, \hspace{50pt} \text{where }\bar{G}\text{ is defined in Eq. (6)} \end{aligned}$$

Hence, we have

$$\begin{aligned} B(t) \leq e^{\left(\dfrac{h \bar{G}}{k_{2}}-d_{3}\right)t} + e^{C_{6}} \end{aligned}$$

where \(C_{6}\) is a constant.

Taking,

$$\begin{aligned} \limsup_{t\to \infty} ~B(t) \leq e^{C_{6}}~ if ~\dfrac{h \bar{G}}{k_{2}} < d_{3}. \end{aligned}$$

Then, we get the upper bound of \(B\) as

$$ \bar{B} = max(B(0), e^{C_{6}}). $$
(7)

From Eq. (2), we have

$$\begin{aligned} \dfrac{d I}{d t} =& \dfrac{\mu B G}{k_{1} +G} - d_{2} I, \\ \leq & \dfrac{\mu \bar{B} \bar{G}}{k_{1}} - d_{2} I, \hspace{50pt} \text{where }\bar{G}\text{ and }\bar{B}\text{ is taken from Eq. (6) and Eq. (7)} \end{aligned}$$

Hence, we get

$$\begin{aligned} I(t) \leq \dfrac{\mu \bar{B} \bar{G}}{k_{1} d_{2}} + C_{5} e^{-d_{2} t}, \end{aligned}$$

where \(C_{5}\) is a constant.

Taking,

$$\begin{aligned} \limsup_{t\to \infty} ~I(t) \leq \dfrac{\mu \bar{B} \bar{G}}{k_{1} d_{2}}. \end{aligned}$$

Hence, we have the upper bound of \(I\) as

$$ \bar{I} = max(I(0),\dfrac{\mu \bar{B} \bar{G}}{k_{1} d_{2}}). $$
(8)

Hence, from above, we conclude that our system is bounded. □

3.2 Positivity of the Solutions

To ensure that the system solution (1)-(4) is positive for all \(t \geq 0\), we calculate the lower bound as follows:

From the first equation of the system (1)-(4), we have,

$$\begin{aligned} \dfrac{dG}{dt} =& a - \dfrac{b I G}{1 + p G + q F} + c F - d_{1} G, \\ \geq & - b \bar{I} G - d_{1} G, \text{where }\bar{I}\text{ is taken from Eq. (8)} \end{aligned}$$

Hence, we have

$$\begin{aligned} G(t) \geq & C_{0} e^{-(b \bar{I}+ d_{1}) t}, \end{aligned}$$

where \(C_{0}\) is a constant.

Taking \(\lim {t \to \infty}\), we get

$$ G(t) \geq 0. $$

From the second equation of the system (1)-(4), we have,

$$\begin{aligned} \dfrac{d I}{d t} =& \dfrac{\mu B G}{k_{1} + G} - d_{2} I \\ \geq & - d_{2} I \end{aligned}$$

Hence, we have

$$ I(t) \geq C_{1} e ^{- d_{2} t}, $$

where \(C_{1}\) is a constant.

Taking \(\lim {t \to \infty}\), we get

$$ I(t) \geq 0. $$

From third equation of the system (1)-(4), we have,

$$\begin{aligned} \dfrac{d B}{d t} =& \dfrac{h B G}{k_{2} + G} - \delta F^{2} B -d_{3} B, \\ \geq & - \delta \bar{F}^{2} B - d_{3} B, \hspace{50pt} \text{where }\bar{F}\text{ is taken from Eq. (5)} \end{aligned}$$

Hence, we have

$$ B(t) \geq C_{2} e ^{- (d_{3} + \delta \bar{F}^{2}) t}, $$

where \(C_{2}\) is a constant.

Taking \(\lim {t \to \infty}\), we get

$$ B(t) \geq 0. $$

From the last equation of the system (1)-(4), we have,

$$\begin{aligned} \dfrac{d F}{d t} =& r F (1 - \dfrac{F}{k_{3}}) \end{aligned}$$

Hence, we have

$$ F(t) \geq C_{3} e^{-r t}, $$

where \(C_{3}\) is a constant.

Taking \(\lim {t \to \infty}\), we get

$$ F(t) \geq 0. $$

3.3 Existence of Equilibrium Points

Proposition 1

For system (1)-(4), there exist four potential equilibrium points as follows:

  1. 1.

    Totally glucose point: \(E_{1} = (G_{1}, I_{1}, B_{1}, F_{1}) = \left ( \dfrac{a}{d_{1}}, 0, 0 ,0\right )\) has only glucose level present and it always exist.

  2. 2.

    Glucose and obesity-related factor point : \(E_{2} = (G_{2}, I_{2}, B_{2}, F_{2})= \left ( \dfrac{a + c k_{3}}{d_{1}}, 0, 0, k_{3} \right )\) has only glucose level and obesity-related factor present, and it always exists.

  3. 3.

    Free from obesity-related factor point :

    $$E_{3} = (G_{3}, I_{3}, B_{3}, F_{3}) = \left (- \dfrac{d_{3} k_{2}}{d_{3} - h}, \dfrac{ X Y}{b d_{3} (d_{3} - h) k_{2}}, - \dfrac{Z X Y}{b d_{3}^{2} (d_{3} - h) k_{2}^{2} \mu} ,0\right ), $$

    where \(X = (a d_{3} - a h + d_{1} d_{3} k_{2}) \), \(Y = ( h + d_{3} k_{2} p - d_{3}) \) and \(Z= d_{2} (d_{3} k_{1} - h k_{1} - d_{3} k_{2}) \) is free from obesity-related factor and it exists if the following condition holds: \(d_{3} < h\) and \(d_{3} (a + d_{1} k_{2}) < a h\).

  4. 4.

    Disease-endemic point :

    $$E_{4} = (G_{4}, I_{4}, B_{4}, F_{4}) = \left ( \dfrac{d_{3} k_{2} + \delta k_{2} k_{3}^{2}}{ h - d_{3} - \delta k_{3}^{2}}, \dfrac{U W}{b k_{2} (d_{3} + \delta k_{3}^{2}) (h - d_{3} - \delta k_{3}^{2})}, \dfrac{T U W }{V} ,k_{3}\right ),$$

    where \(U = a d_{3} - a h + d_{1} d_{3} k_{2} + c d_{3} k_{3} - c h k_{3} + a \delta k_{3}^{2} + d_{1} \delta k_{2} k_{3}^{2} + c \delta k_{3}^{3} \), \(V= b k_{2}^{2} (d_{3} + \delta k_{3}^{2})^{2} (h - d_{3} - \delta k_{3}^{2}) \mu \), \(T=d_{2} (d_{3} k_{1} - h k_{1} - d_{3} k_{2} + \delta k_{1} k_{3}^{2} - \delta k_{2} k_{3}^{2})\) and \(W = d_{3} - h + \delta k_{3}^{2} - d_{3} k_{2} p - \delta k_{2} k_{3}^{2} p + d_{3} k_{3} q - h k_{3} q + \delta k_{3}^{3} q \) has all factors present and it exists if the following condition holds: \(h > d_{3} + \delta k_{3}^{2}\), \(\left (a > 0\text{ and }c \geq - \dfrac{d_{1} k_{2} (d_{3} + \delta k_{3}^{2})}{k_{3} (d_{3} - h + \delta k_{3}^{2})} \right )\).

3.4 Stability Analysis

The general Jacobian form of (1)-(4) model is as follows:

$$J= \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \dfrac{b G I p}{(1 + G p + F q)^{2}} - \dfrac{b I}{1 + G p + F q}& - \dfrac{b G}{1 + G p + F q} -d_{1}& 0 & c + \dfrac{b G I q}{(1+ G p + F q)^{2}} \\ \dfrac{B \mu}{ G+k_{1}} -\dfrac{B G \mu}{( G +k_{1})^{2}}& -d_{2}& \dfrac{G \mu}{ G + k_{1}}&0 \\ \dfrac{B h}{G + k_{2}} - \dfrac{B G h}{(G + k_{2})^{2}}& 0 & \dfrac{G h}{G + k_{2}} -d_{3} - \delta F^{2}& -2 B \delta F \\ 0&0&0&(1 - \dfrac{F}{k_{3}}) r - \dfrac{F r}{k_{3}} \end{array}\displaystyle \right ) $$

To test the stability of the equilibrium points, we execute the following:

  1. 1.

    For the equilibrium point \(E_{1}\): The eigenvalues are \(\left ( -d_{1}, -d_{2},\dfrac{a h}{a + d_{1} k_{2}} -d_{3} , r \right )\). Here, one of the eigenvalue is positive so \(E_{1}\) is always unstable.

  2. 2.

    For the equilibrium point \(E_{2}\): The eigenvalues are \(\bigg(-d_{1}, -d_{2}, \dfrac{h (a + c k_{3})}{a + d_{1} k_{2} + c k_{3}} -d_{3} - \delta k_{3}^{2}, -r \bigg)\) and \(E_{2}\) is stable if the following condition hold \(d_{3} > \dfrac{h (a + c k_{3})}{a + d_{1} k_{2} + c k_{3}}\).

  3. 3.

    For the equilibrium point \(E_{3}\): The eigenvalues are \(\left (r,\lambda _{1},\lambda _{2},\lambda _{3}\right )\), where \(\lambda _{i}'s\) are roots of the characteristic polynomial

    $$ \lambda ^{3} + R_{1} \lambda ^{2} + R_{2} \lambda +R_{3} $$

    where

    $$\begin{aligned} R_{1} &= \dfrac{a (d_{3} - h)^{2} + d_{3} k_{2} (d_{2} ( h -d_{3}) + (d_{1} + d_{2}) d_{3} k_{2} p)}{d_{3} k_{2} (h + d_{3} ( k_{2} p - 1))},\\ R_{2} &= \dfrac{d_{1} d_{2} d_{3} k_{2} ( d_{3}^{2} k_{2}^{2} p -(d_{3} - h)^{2} k_{1}) + a d_{2} (d_{3} - h)^{2} (2 h k_{1} + d_{3} (k_{2} + k_{1} k_{2} p -2 k_{1} ))}{d_{3} k_{2} (h k_{1} + d_{3} ( k_{2} -k_{1})) (h + d_{3} ( k_{2} p -1))} ,\\ R_{3} &= \dfrac{d_{2} (d_{3} - h) (a (d_{3} - h) + d_{1} d_{3} k_{2})}{h k_{2}}. \end{aligned}$$

    One of the eigenvalues, i.e., \('r'\), is always positive, so \(E_{3}\) is always unstable.

  4. 4.

    For the equilibrium point \(E_{4}\): The eigenvalues are \(\left ( -r,\sigma _{1},\sigma _{2},\sigma _{3}\right )\), where \(\sigma _{i}'s\) are roots of the characteristic polynomial

    $$ F(\sigma ) = \sigma ^{3} + S_{1} \sigma ^{2} + S_{2} \sigma +S_{3} $$
    (9)

    where

    $$\begin{aligned} S_{1} =& d_{2} + \dfrac{d_{1} k_{2}^{2} (d_{3} + \delta k_{3}^{2})^{2} p + a (d_{3} - h + \delta k_{3}^{2})^{2} (1 + k_{3} q) + c k_{3} (d_{3} - h + \delta k_{3}^{2})^{2} (1 + k_{3} q) }{k_{2} (d_{3} + \delta k_{3}^{2}) (h (1 + k_{3} q) - d_{3} (1 - k_{2} p + k_{3} q) - \delta k_{3}^{2} (1 - k_{2} p + k_{3} q))}, \\ S_{2} =& \dfrac{A}{k_{2} (d_{3} + \delta k_{3}^{2}) (h k_{1} + d_{3} C + \delta C k_{3}^{2})} \\ &{}+ \dfrac{B}{h (1 + k_{3} q) - d_{3} (1 - k_{2} p + k_{3} q) - \delta k_{3}^{2} (1 - k_{2} p + k_{3} q)}, \end{aligned}$$

    where

    \(A = d_{2} (d_{3} - h + \delta k_{3}^{2}) (d_{1} k_{1} k_{2} (d_{3} + \delta k_{3}^{2}) + a (2 d_{3} k_{1} - 2 h k_{1} - d_{3} k_{2} + \delta (2 k_{1} - k_{2}) k_{3}^{2}) + c k_{3} (2 d_{3} k_{1} - 2 h k_{1} - d_{3} k_{2} + \delta (2 k_{1} - k_{2}) k_{3}^{2}))\),

    \(B= d_{2} (d_{1} k_{2} (d_{3} + \delta k_{3}^{2}) + a (d_{3} - h + \delta k_{3}^{2}) + c k_{3} (d_{3} - h + \delta k_{3}^{2})) p\),

    \(C = k_{2} -k_{1}\),

    \(S_{3} = \dfrac{d_{2} (d_{3} - h + \delta k_{3}^{2}) (d_{1} k_{2} (d_{3} + \delta k_{3}^{2}) + a (d_{3} - h + \delta k_{3}^{2}) + c k_{3} (d_{3} - h + \delta k_{3}^{2}))}{h k_{2}}\).

    The first eigenvalue is always negative and from Routh-Hurwitz conditions [24], \(E_{4}\) is locally asymptotically stable if

    $$ S_{1} > 0,~ S_{2} > 0, ~S_{3} > 0,~ S_{1} S_{2} - S_{3} > 0 $$

    holds.

Proposition 2

If \(S_{1} > 0\), \(S_{2} > 0\), \(S_{3} > 0\), and \(S_{1} S_{2} - S_{3} > 0\) hold, the equilibrium point \(E_{4}\) is locally asymptotically stable.

3.5 Global Stability

The following theorem gives us sufficient conditions for the equilibrium point \(E_{4}\) to be globally asymptotically stable.

Theorem 3.2

Assume that the following conditions hold

$$\begin{aligned} a ~ \geq &~ \dfrac{2 G_{4} k_{3}}{r}\left ((\dfrac{c}{\bar{G}} + \dfrac{b q I_{4}}{(1 + p \bar{G} + q \bar{F})(1 + p G_{4} + q F_{4})} \right )^{2}, \\ \dfrac{c F_{4} d_{2}}{2 G_{4}} ~ \geq &~ \dfrac{\mu ^{2} k_{1}^{2} }{(k_{1} + \bar{G})^{2}(k_{1} + G_{4})^{2}}, \\ d_{2} d_{3} ~ \geq &~ \dfrac{2 \mu ^{2} G_{4}^{2}}{(k_{1} + \bar{G})^{2}}, \\ b ~p ~ \geq &~ \dfrac{h k_{2}^{2} (1 + p G_{4} + q F_{4})}{(k_{2} + \bar{G})^{2}(k_{2} + G_{4})G_{4}}, \\ r \geq & \dfrac{2 \delta F_{4}^{2} k_{3}}{\bar{F}^{2}}. \end{aligned}$$
(10)

where \(\bar{F}\) and \(\bar{G}\) are defined in Eqs. (5) and (6) respectively.

Then the equilibrium point \(E_{4} = (G_{4}, I_{4}, B_{4}, F_{4})\) of system (1)-(4) is globally asymptotically stable.

Proof

Let us choose a positive definite function,

$$\begin{aligned} V(t) = G - G_{4} - G_{4}~ ln \left (\dfrac{G}{G_{4}} \right ) + \frac{1}{2}\left (I - I_{4} \right )^{2} + \frac{1}{2}\left (B - B_{4} \right )^{2} + F - F_{4} - F_{4}~ ln \left (\dfrac{F}{F_{4}} \right ). \end{aligned}$$

Finding the derivatives along the positive solution of system (1)-(4) yields

$$\begin{aligned} \frac{d V}{d t} &= \frac{d G}{d t}\left (\dfrac{G - G_{4}}{G}\right ) + \frac{d I}{d t}\left (I - I_{4}\right ) + \frac{d B}{d t}\left (B - B_{4} \right ) + \frac{d F}{d t}\left (\dfrac{F - F_{4}}{F}\right ), \\ =& \left (\dfrac{G - G_{4}}{G}\right )\left [a- \dfrac{bIG}{1+pG+qF}+ c F -d_{1} G\right ] + \left (I - I_{4}\right ) \left [\dfrac{\mu B G}{k_{1}+G}-d_{2} I\right ] \\ &+ \left (B - B_{4}\right )\left [\left (\dfrac{h G }{ k_{2} + G}- \delta F^{2} -d_{3}\right )B\right ] + \left (\dfrac{F - F_{4}}{F} \right )\left [r F (1 -\dfrac{F}{k_{3}})\right ]. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \dfrac{d V}{d t} =& -\left [\dfrac{a}{G G_{4}}(G - G_{4})^{2}\right. \\ &-\left. \left (\dfrac{c}{G} + \dfrac{b q I_{4}}{(1 + p G + q F)(1 + p G_{4} + q F_{4})} \right )(F -F_{4})(G - G_{4}) + \dfrac{r}{2 k_{3}}(F - F_{4})^{2}\right ] \\ & -\left [\dfrac{c F_{4}}{G G_{4}}(G - G_{4})^{2}- \dfrac{\mu k_{1} B}{(k_{1} + G)(k_{1}+ G_{4})}(G - G_{4})(I - I_{4}) + \dfrac{d_{2}}{2}(I - I_{4})^{2}\right ] \\ & -\left [\dfrac{d_{2}}{2}(I - I_{4})^{2} - \dfrac{\mu G_{4}}{k_{1} + G}(I - I_{4})(B - B_{4}) + d_{3}(B - B_{4})^{2} \right ] \\ & -\left [- \dfrac{- h G_{4}}{(k_{2} + G_{4})}(B - B_{4})^{2} - \dfrac{k_{2} h B}{(k_{2} + G_{4})(k_{2} + G)}(B-B_{4})(G - G_{4})\right. \\ &\left. - \dfrac{b p I}{(1 + p G + q F)(1 + p G_{4} + q F_{4})}(G - G_{4})^{2} \right ] \\ & - \left [ \delta F^{2} (B - B_{4})^{2} + \delta B (F + F_{4}) (F - F_{4})(B - B_{4}) + \dfrac{r}{2 k_{3}} (F - F_{4})^{2}\right ]. \end{aligned}$$

Let \(A^{*}_{0} = \dfrac{a}{G G_{4}}\), \(B^{*}_{0} = \dfrac{r}{2 k_{3}} \), \(C^{*}_{0} = \dfrac{c}{G} + \dfrac{b q I_{4}}{(1 + p G + q F)(1 + p G_{4} + q F_{4})}\).

For \(\dfrac{dV}{dt}\) to be negative definite we must have the following,

$$\begin{aligned} A^{*}_{0}B^{*}_{0} - C^{*^{2}}_{0} ~\geq ~ 0&\implies \dfrac{a}{G G_{4}}\dfrac{r}{2 k_{3}} - \left (\dfrac{c}{G} + \dfrac{b q I_{4}}{(1 + p G + q F)(1 + p G_{4} + q F_{4})}\right )^{2} ~ \geq ~ 0 \\ &\implies \dfrac{a}{G_{4}}\dfrac{r}{2 k_{3}} - \left ( \dfrac{c}{\bar{G}} + \dfrac{b q I_{4}}{(1 + p \bar{G} + q \bar{F})(1 + p G_{4} + q F_{4})} \right )^{2} ~\geq ~ 0, \end{aligned}$$

where \(\bar{F}\) and \(\bar{G}\) are defined in Eqs. (5) and (6)

$$\begin{aligned} &\implies a ~\geq ~ \dfrac{2 G_{4} k_{3}}{r}\left (\dfrac{c}{\bar{G}} + \dfrac{b q I_{4}}{(1 + p \bar{G} + q \bar{F})(1 + p G_{4} + q F_{4})} \right )^{2}. \end{aligned}$$

Again, let \(A^{*}_{1} = \dfrac{c F_{4}}{G G_{4}}\), \(B^{*}_{1} = \dfrac{d_{2}}{2} \), \(C^{*}_{1} = \dfrac{\mu k_{1} B}{(k_{1} + G)(k_{1}+ G_{4})} \).

Similarly,

$$\begin{aligned} A^{*}_{1} B^{*}_{1} - C_{1}^{*^{2}} ~\geq ~ 0\implies \dfrac{c F_{4}}{G G_{4}} \dfrac{d_{2}}{2} - \left ( \dfrac{\mu k_{1} B}{(k_{1} + G)(k_{1}+ G_{4})}\right )^{2} ~\geq ~ 0, \\ \implies \dfrac{c F_{4} d_{2}}{2 G_{4}} ~\geq ~ \dfrac{\mu ^{2} k_{1}^{2}}{(k_{1} + \bar{G})^{2}(k_{1} + G_{4})^{2}}, \text{where }\bar{G}\text{ is defined in Eq. (6)}. \end{aligned}$$

Again, let \(A^{*}_{2} = \dfrac{d_{2}}{2}\), \(B^{*}_{2} = d_{3} \), \(C^{*}_{2} = \dfrac{\mu G_{4}}{(k_{1} + G)} \).

Similarly,

$$\begin{aligned} A^{*}_{2} B^{*}_{2}- C_{2}^{*^{2}} ~\geq ~ 0\implies \dfrac{d_{2} d_{3}}{2} - \left (\dfrac{\mu G_{4}}{k_{1}+G}\right )^{2} ~\geq ~ 0 \\ \implies d_{2} d_{3} ~\geq ~ \dfrac{2 \mu ^{2} G_{4}^{2}}{(k_{1} + \bar{G})^{2}}, \text{where $\bar{G}$ is defined in Eq. (6)}. \end{aligned}$$

Again, let

$$\begin{aligned} A^{*}_{3} =& -\dfrac{h G_{4}}{(k_{2} + G_{4})},\qquad B^{*}_{3} = - \dfrac{b p I}{(1 + p G + q F)(1 + p G_{4} + q F_{4})}, \\ C^{*}_{3} =& - \dfrac{k_{2} h B }{(k_{2} + G)(k_{2} + G_{4})} . \end{aligned}$$

Similarly,

$$\begin{aligned} A^{*}_{3} B^{*}_{3} - C_{3}^{*^{2}} ~\geq ~ 0\implies& \dfrac{h G_{4}}{(k_{2} + G_{4})} \dfrac{b p I}{(1 + p G + q F)(1 + p G_{4} + q F_{4})} \\ & - \left (- \dfrac{k_{2} h B }{(k_{2} + G)(k_{2} + G_{4})}\right )^{2} ~\geq ~ 0 \\ \implies& b ~p ~\geq ~ \dfrac{h k_{2}^{2} (1 + p G_{4} + q F_{4})}{(k_{2} + \bar{G})^{2}(k_{2} + G_{4})G_{4}}, \text{where }\bar{G}\text{ is defined in Eq. (6)}. \end{aligned}$$

Again, let \(A^{*}_{4} = \delta F^{2}\), \(B^{*}_{4} = \dfrac{r}{2 k_{3}}\), \(C^{*}_{4} = - \delta B (F + F_{4})\).

Similarly,

$$\begin{aligned} A^{*}_{4} B^{*}_{4} - C_{4}^{*{2}} ~\geq ~ 0 &\implies \delta F^{2} \dfrac{r}{2 k_{3}} - \left (- \delta B (F + F_{4})\right )^{2} ~\geq ~ 0 \\ &\implies r \geq \dfrac{2 \delta F_{4}^{2} k_{3}}{\bar{F}^{2}}, \text{where }\bar{F}\text{ is defined in Eq. (5)}. \end{aligned}$$

Under the assumption (10), we have \(\dfrac{d V(t)}{d t} < 0\). As a result of Lasalle’s invariance principle [25], the global asymptotic stability of \(E_{4}\) follows. This completes the proof. □

4 Bifurcation Analysis

The bifurcations and related dynamical behaviors of many human disease models are studied thoroughly by many researchers [23, 26]. In this section, we will also investigate the existence of bifurcation in model system (1)-(4).

Theorem 4.1

Let \(d_{1c} = \dfrac{(a + c k_{3}) ( h -d_{3} - \delta k_{3}^{2})}{k_{2} (d_{3} + \delta k_{3}^{2})}\). For system (1)-(4), the equilibrium point \(E_{2}\left ( \dfrac{a + c k_{3}}{d_{1}}, 0, 0, k_{3} \right )\) is

  • stable if \(d_{1} > d_{1c}\).

  • unstable if \(d_{1} < d_{1c}\).

  • a saddle node if \(d_{1} = d_{1c}\).

Proof

From the Jacobian \((J)\) provided in Sect. 3.4, we get the characteristic equation at \(E_{2}\left ( \dfrac{a + c k_{3}}{d_{1}}, 0, 0, k_{3} \right )\) as

$$ (d_{1} + \lambda ) (d_{2} + \lambda ) (r + \lambda ) (d_{1} k_{2} (d_{3} + \delta k_{3}^{2} + \lambda ) + a (d_{3} - h + \delta k_{3}^{2} + \lambda ) + c k_{3} (d_{3} - h + \delta k_{3}^{2} + \lambda )) = 0, $$

which have three negative roots i.e. \(\lambda _{1} = - d_{1}\), \(\lambda _{2} = -d_{2}\), \(\lambda _{3} = -r\) and the fourth root is \(\lambda _{4} = \dfrac{h (a + c k_{3})}{a + d_{1} k_{2} + c k_{3}} -d_{3} - \delta k_{3}^{2} \), therefore \(\lambda _{4} = 0\) if \(d_{1} = d_{1c} = - \dfrac{(a + c k_{3}) (d_{3} - h + \delta k_{3}^{2})}{k_{2} (d_{3} + \delta k_{3}^{2})} \) and \(\lambda _{4} > 0\ (< 0)\) if \(d_{1} < (> ) \ d_{1c}\).

This analysis shows that when \(d_{1}\) crosses a critical value \(d_{1c}\), \(E_{2}\) becomes locally asymptotically stable. It may be noted that below this critical point, two equilibriums \(E_{2}\) and \(E_{4}\) exist. However, the equilibrium \(E_{4}\) vanishes as \(d_{1} > d_{1c}\). □

Example 4.1

Consider \(d_{1} = 0.091\), \(d_{2} = 0.075\), \(k_{2} = 900\), \(\delta = 0.01\), \(k_{3} = 5.7\) and other parameters as defined in Table 2. We note that a saddle point occurs (represented by BP) at \(d_{1} = d_{1c} = 11.882115\). At this critical point the eigenvalues are \(\lambda _{1} = -11.8821\), \(\lambda _{2} = -0.075\), \(\lambda _{3} = -0.55\), \(\lambda _{4} = 0\). When \(d_{1}\) < \(d_{1c}\), the equilibrium point \(E_{2}\) is unstable, and as \(d_{1}\) > \(d_{1c}\), \(E_{2}\) becomes stable, i.e., a stable branch is observed (c.f. 3).

Fig. 3
figure 3

Bifurcation diagram at \(E_{2}\) for bifurcating parameter \(d_{1}\). Here, BP, represents the saddle point. When \(d_{1}\) < BP, \(E_{2}\) is unstable, when \(d_{1}\) > BP, \(E_{2}\) is stable

Full size image
Table 2 Parameter values used for numerical simulation
Full size table

Theorem 4.2

The equilibrium point \(E_{4}(G_{4}, I_{4}, B_{4}, F_{4})\) undergoes two Hopf bifurcation with respect to bifurcation parameter \(d_{3}\).

Proof

The equilibrium point \(E_{4}\) has two pure complex eigenvalues if

$$ S_{2} S_{1} = S_{3}, $$

let these two eigenvalues be represented as

$$ \sigma _{1,2} = \pm \iota \alpha , $$

for some positive real number \(\alpha \).

Since the sum of three zeros of Eq. (9) is \(\sum _{i=1}^{3}\sigma _{i} = - S_{1}\), then we get \(\sigma _{3} = -S_{1}\). Then we have \(F(\sigma _{3}) = 0\), which gives us the critical values of \(d_{3}\),

i.e.

$$ d_{3} = d_{3_{c_{1}}} \text{and} ~d_{3} = d_{3_{c_{2}}}. $$

Now, to verify the transversality condition, let us consider,

$$ F(\sigma _{j}) \equiv \sigma ^{3}_{j} + S_{1} \sigma ^{2}_{j} + S_{2} \sigma _{j} +S_{3} = 0, ~~~\text{for $j = 1$, 2} $$

therefore,

$$ \frac{ \partial F}{ \partial d_{3}}=(3\sigma _{j}^{2}+2\sigma _{j} S_{1}+ S_{2})\frac{ \partial \sigma _{j}}{ \partial d_{3}}+\sigma ^{2}_{j} S_{1}^{ \prime}+\sigma _{j} S_{2}^{\prime}+S_{3}^{\prime}=0, $$

hence

$$\begin{aligned} \frac{\partial \sigma _{j}}{ \partial d_{3}} &= - \dfrac{\sigma _{j}^{2}S_{1}^{\prime}+\sigma _{j} S_{2}^{\prime}+S_{3}^{\prime}}{S_{2} + 2 S_{1} \sigma _{j} + 3 \sigma _{j}^{2}}, \end{aligned}$$

we get

$$\begin{aligned} \Re \left (\frac{ \partial \sigma _{j}}{ \partial d_{3}}\right ) \Biggl| _{d_{3} =d_{3_{c_{1,2}}}}=& - \dfrac{(3\alpha ^{4}S_{1}^{\prime}-\alpha ^{2}S_{1}^{\prime}S_{2}-3S_{3}^{\prime}\alpha ^{2}+S_{3}^{\prime} S_{2}+2\alpha ^{2}S_{2}^{\prime} S_{1})}{(S_{2} -3\alpha ^{2})^{2}+4\alpha ^{2}S_{1}^{2}} \neq 0. \end{aligned}$$

Hence, the system undergoes Hopf bifurcation at \(E_{4}\) for some critical values of \(d_{3}\).

It is difficult to find the critical points analytically, thus prompting the exploration of numerical alternatives. Subsequently, we validate these findings numerically. Following the procedure presented in [27] and considering the parameters value same as discussed in Example 4.1, the equilibrium point \(E_{4}(G_{4}, I_{4}, B_{4}, F_{4})\), in terms of \(d_{3}\) is given by

$$\begin{aligned} G_{4} =& \dfrac{292.41 + 900. d_{3}}{(1.6591 - d_{3})}, \\ I_{4} =& \dfrac{d_{3} ( 68851.5 d_{3} -85584.7)-39044.3}{( d_{3} - 1.6591 )(0.3249 + d_{3})}, \\ B_{4} =& \dfrac{d_{3} ( d_{3} ( 46.4854 d_{3} -16.3292)-77.8892 )-23.5075}{( d_{3} + 0.3249)^{2}( d_{3} - 1.6591)}, \\ F_{4} =& 5.7. \end{aligned}$$

The feasibility condition for \(E_{4}\) to exist requires \(0 < d_{3} < 1.59792\) (see Fig. 4). In this \(d_{3}\) feasible range, \(S_{1}\) is positive and \(S_{3}\) is positive whenever \(E_{4}\) is feasible, that is, in the range \(d_{3} \in (0,1.59792)\) while \(S_{1} S_{2} - S_{3}\) is positive for \(d_{3} \in (0, 0.109415)\) and \(d_{3} \in (1.52208, 1.59792)\) (see Fig. 5 and for magnified version see Fig. 6 ).

Fig. 4
figure 4

Feasible region of \(d_{3}\) for the co-existence of all the four densities

Full size image
Fig. 5
figure 5

Plot showing the occurrence of Hopf bifurcation at \(H_{1} = 0.109415\) and \(H_{2} = 1.52205\) when curve \(S_{1} S_{2} - S_{3}\) crosses the \(x\)-axis

Full size image
Fig. 6
figure 6

(a) Plot showing the magnified version of region \(R_{1}\) of Fig. 5. This figure clearly shows the occurrence of 1st Hopf Bifurcation (\(H_{1}\)) at \(d_{3} = d_{3_{c_{1}}} = 0.109415\), (b) Plot showing the magnified version of region \(R_{2}\) of Fig. 5. This figure shows the occurrence of 2nd Hopf Bifurcation (\(H_{2}\)) at \(d_{3} = d_{3_{c_{2}}} = 1.52205\)

Full size image

Since the existence of this equilibrium point \(E_{4}\) is upto \(d_{3} = 1.59792\), hence we discuss the scenario of stability for \(d_{3}\) ∈ \((0, 1.59792)\).

  • At \(d_{3} = d_{3_{c_{1}}} = 0.109415\), we have

    $$ S_{1} > 0,~ S_{2} > 0 ~\text{and} ~S_{1} S_{2} - S_{3} \approx ~ 0 ~ \text{with}~ \frac{d }{d d_{3} } (S_{1} S_{2} - S_{3})\Biggl|_{d_{3} =d_{3_{c_{1}}}} \neq 0. $$

    This establishes the first Hopf bifurcation point \((H_{1})\).

  • At \(d_{3} = d_{3_{c_{2}}} = 1.52205\), we have

    $$ S_{1} > 0,~ S_{2} > 0 ~\text{and}~ S_{1} S_{2} - S_{3} \approx ~ 0 ~ \text{with}~ \frac{d}{d d_{3} } (S_{1} S_{2} - S_{3})\Biggl|_{d_{3} =d_{3_{c_{2}}}} \neq 0. $$

    This establishes the second Hopf bifurcation point \((H_{2})\).

Fig. 7(a, c) shows the branch of \(E_{4}\) and its stability w.r.t bifurcation parameter \(d_{3}\). We observe that the equilibrium point \(E_{4} (G_{4}, I_{4}, B_{4}, F_{4})\) is stable for \(d_{3} < d_{3_{c_{1}}}\) and unstabilizes through Hopf-bifurcation \((H_{1})\) at \(d_{3} = d_{3_{c_{1}}} = 0.109415\) and it again stabilizes through Hopf-bifurcation (\(H_{2}\)) giving us another critical value of \(d_{3}\) i.e. \(d_{3} = d_{3_{c_{2}}} = 1.52205\). In the bifurcation diagram 7 the variations of the glucose and beta-cells densities are examined in the ranges of \(0< G < 30000\) and \(0 < B < 7000\), as a function of \(d_{3}\) which varies in the range \(0 < d_{3}< 2\).

Fig. 7
figure 7

(a) Bifurcation analysis (\(G\) vs \(d_{3}\)) showing occurrence of two supercritical hopf points. (b) Same as in (a) to visualize the family of limit cycles bifurcating between the Hopf point \(H_{1}\) and \(H_{2}\). (c) Bifurcation analysis (\(B\) vs \(d_{3}\)) showing occurrence of two supercritical hopf points. (d) Same as in (c) but shown on a different scale to visualize the family of limit cycles bifurcating between the Hopf point \(H_{1}\) and \(H_{2}\). The dotted line represents unstable branch and the solid line represents stable branch

Full size image

We will now plot the phase portrait and time series around two Hopf-bifurcations (\(H_{1}\) and \(H_{2}\))

  • when \(d_{3}\) ∈ \((0, d_{3_{c_{1}}})\) i.e. \(d_{3} < d_{3_{c_{1}}}\), a stable behaviour is observed around \(E_{4}\) (see Fig. 8).

    Fig. 8
    figure 8

    (a) Phase Portrait, (b) Time series solution of system (1)–(4). Both diagrams are plotted with \(d_{3} = 0.06\) (\(d_{3}< d_{3_{c_{1}}}\)). Here, we observe that the system is stable

    Full size image

  • when \(d_{3_{c_{1}}} < d_{3} < d_{3_{c_{2}}}\), we observe a stable limit cycle as a result of 1st supercritical Hopf bifurcation (see Fig. 9).

    Fig. 9
    figure 9

    (a) Phase Portrait, (b) Time series solution of system (1)–(4). Both diagrams are plotted with \(d_{3} = 1\) (\(d_{3_{c_{1}}}< d_{3}< d_{3_{c_{2}}}\)). Here, we observe that the equilibrium point \(E_{4}\) becomes unstable giving rise to stable limit cycle ranging between two Hopf bifurcation points (\(H_{1}\) and \(H_{2}\))

    Full size image

  • At \(d_{3}=d_{3_{c_{2}}}\) the system encounters 2nd Hopf Bifurcation and as the result of it when \(d_{3} > d_{3_{c_{2}}}\), system restores its stability (see Fig. 10). □

    Fig. 10
    figure 10

    (a) Phase Portrait, (b) Time series solution of system (1)–(4). Both diagrams are plotted with \(d_{3} = 1.53\) (\(d_{3}>d_{3_{c_{2}}}\)). Here, we observe that the system again regains stability as it exceeds 2nd Hopf bifurcation point (\(H_{2}\))

    Full size image

5 Delayed Model and Its Dynamics

The lags, referred to as delays, can group along complex biological processes, merely indicating the time required for these processes to occur [28]. Time-delay models are becoming more familiar and widespread in several biological modeling fields [29]. These models have been seen in epidemiology [30], chemostat model theory [31], brain networks [32, 33], circadian rhythms [34], diabetes [6]. Chuedoung et al. [35] investigated the oscillatory behavior of the glucose and insulin dynamic system as a single-compartment model.

In diabetic patients, as glucose level increases, beta-cell come under more pressure to work, leading to its disruption, affecting insulin production. Beta cells usually work in starting, but they disrupt as the load increases. To investigate the consequences of the time delay in handling increased glucose levels, we introduced lag in insulin production due to beta-cell disruption. The modified model (1)–(4) with delay term is given as follows:

$$\begin{aligned} \dfrac{dG}{dt} =&a-\dfrac{bIG}{1+pG+qF}+ c F -d_{1} G, \end{aligned}$$
(11)
$$\begin{aligned} \dfrac{dI}{dt} =&\dfrac{\mu B(t-\tau ) G}{k_{1}+G}-d_{2} I, \end{aligned}$$
(12)
$$\begin{aligned} \dfrac{dB}{dt} =&\left (\dfrac{h G }{ k_{2} + G}- \delta F^{2} -d_{3} \right )B, \end{aligned}$$
(13)
$$\begin{aligned} \dfrac{dF}{dt} =&rF \left (1-\dfrac{F}{k_{3}}\right ). \end{aligned}$$
(14)

with initial conditions \(G(\zeta ) = \phi _{1}(\zeta ) \geq 0\), \(I(\zeta ) = \phi _{2}(\zeta ) \geq 0\), \(B(\zeta ) = \phi _{3}(\zeta ) \geq 0\), \(F(\zeta ) = \phi _{4}(\zeta ) \geq 0\), \(\zeta \in [-\tau , 0]\), \(\phi _{i}(0) > 0\), \(i=1,2,3,4\), where (\(\phi _{1}(\zeta ), \phi _{2}( \zeta ), \phi _{3}(\zeta ), \phi _{4}(\zeta )) \in C([-\tau , 0]\), \(R^{4}_{+0}\)) is the Banach space of continuous functions mapping the interval [\(-\tau \), 0] into \(R^{4}_{+0}\), where \(R^{4}_{+0}= \{(G, I, B, F): G\geq 0, I\geq 0, B\geq 0, F\geq 0\}\).

\(\tau \) denotes the time delay in insulin synthesis due to beta cell dysfunction, and all other parameters are same as described in Table 1.

5.1 Stability Analysis of Delay Model

The system (11)- (14) has been linearized around \(E_{4}\) and represented as follows:

$$\begin{aligned} \dfrac{dG}{dt} =&A_{11} G(t) + A_{12} I(t) + A_{13} B(t) + A_{14} F(t), \end{aligned}$$
(15)
$$\begin{aligned} \dfrac{dI}{dt} =&A_{21} G(t) + A_{22} I(t) + A_{23} B(t-\tau ) + A_{24} F(t), \end{aligned}$$
(16)
$$\begin{aligned} \dfrac{dB}{dt} =&A_{31} G(t) + A_{32} I(t) + A_{33} B(t) + A_{34} F(t), \end{aligned}$$
(17)
$$\begin{aligned} \dfrac{dF}{dt} =&A_{41} G(t) + A_{42} I(t) + A_{43} B(t) + A_{44} F(t). \end{aligned}$$
(18)

where the values of \(A_{11}\), \(A_{12}\), \(A_{13}\), \(A_{14}\), \(A_{21}\), \(A_{22}\), \(A_{23}\), \(A_{24}\), \(A_{31}\), \(A_{32}\), \(A_{33}\), \(A_{34}\), \(A_{41}\), \(A_{42}\), \(A_{43}\), \(A_{44}\) are discussed in appendix A. The characteristic equation of lineralized system (15)-(18) is given as,

$$ \eta ^{4} + p_{1} \eta ^{3} + p_{2} \eta ^{2} + p_{3} \eta + p_{4} + e^{- \eta \tau} (q_{1} \eta + q_{2}) = 0, $$
(19)

where the values of \(p_{1}\), \(p_{2}\), \(p_{3}\), \(p_{4}\), \(q_{1} \) and \(q_{2}\) are mentioned in appendix A.

The requirement for \(E_{4}\) to be asymptotically stable with \(\tau = 0\) is given by proposition 2, and the solutions approach \(E_{4}\) as the time \(t \to \infty \).

Now, to analyze the condition that guarantees system (11)–(14) to remain stable as \(\tau \) increases from zero. By the continuity of \(\tau \), equation (19) will have roots with a positive real part if it crosses the imaginary axis. It is clear that \(\eta = \iota \omega\) (\(\iota = \sqrt{-1}\), \(\omega > 0\)) is a root of equation (19) if and only if

$$ (\iota \omega )^{4} + p_{1} (\iota \omega )^{3} + p_{2} (\iota \omega )^{2} + p_{3} \iota \omega + p_{4} + e^{-\iota \omega \tau} (q_{1} (\iota \omega ) + q_{2}) = 0. $$

By Euler’s formula, \(e^{-\iota \omega \tau} = \cos ( \omega \tau ) - \iota \sin ( \omega \tau )\), we have

$$\begin{aligned} \begin{alignedat}{2} \omega ^{4} - \omega ^{2} p_{2} + p_{4} + q_{2} \cos (\omega \tau ) + q_{1} \omega \sin (\omega \tau ) = 0, \\ - \omega ^{3} p_{1} + p_{3} \omega + q_{1} \omega \cos (\omega \tau ) - q_{2} \sin (\omega \tau ) = 0. \end{alignedat} \end{aligned}$$
(20)

Now, we have from above equation

$$ \sin \tau \omega = \dfrac{ \omega ^{3} (p_{2} q_{1} - q_{2} p_{1}) -\omega ^{5} q_{1} - p_{4} q_{1} \omega + p_{3} q_{2} \omega}{q_{1}^{2} \omega ^{2} + q_{2}^{2}} $$

and

$$ \cos \tau \omega =- \dfrac{ q_{1} p_{3} \omega ^{2} -q_{1} \omega ^{4} p_{1} + q_{2} \omega ^{4} - \omega ^{2} p_{2} q_{2} + p_{4} q_{2}}{q_{1}^{2} \omega ^{2} + q_{2}^{2}}, $$

using the trigonometric property \(\sin ^{2}{\omega \tau} +\cos ^{2}{\omega \tau} = 1 \), we get

$$ \omega ^{8} + \omega ^{6} ( p_{1}^{2} - 2 p_{2}) + \omega ^{4}(p_{2}^{2} - 2 p_{1} p_{3} + 2 p_{4}) + \omega ^{2} (p_{3}^{2} - q_{1} ^{2} - 2 p_{2} p_{4}) + p_{4}^{2} - q_{2}^{2} =0. $$
(21)

By Descarte’s rule of signs, Eq. (21) has at least one positive real root defined by \(\omega _{0}\). Thus, from Eq. (20) we have

$$\begin{aligned} \tan \tau \omega =- \dfrac{ \omega ^{3} (p_{2} q_{1} - q_{2} p_{1})-\omega ^{5} q_{1} - p_{4} q_{1} \omega + p_{3} q_{2} \omega}{ q_{1} p_{3} \omega ^{2} -q_{1} \omega ^{4} p_{1} + q_{2} \omega ^{4} - \omega ^{2} p_{2} q_{2} + p_{4} q_{2}}. \end{aligned}$$

Therefore,

$$\begin{aligned} \tau _{j}^{*}=\dfrac{1}{\omega _{0}} {\tan ^{-1}} \left [ - \dfrac{ \omega _{0}^{3} (p_{2} q_{1} - q_{2} p_{1}) -\omega _{0}^{5} q_{1} - p_{4} q_{1} \omega _{0} + p_{3} q_{2} \omega _{0}}{ q_{1} p_{3} \omega _{0}^{2} -q_{1} \omega _{0}^{4} p_{1} + q_{2} \omega _{0}^{4} - \omega _{0}^{2} p_{2} q_{2} + p_{4} q_{2}} \right ]+\frac{2 \pi j}{\omega _{0}} \end{aligned}$$
(22)

where \(j=0,1,2,3,\ldots \). Let \(\tau _{0} = \tau _{0}^{*}\) be the first critical value for equation (19) to have roots on the imaginary axis.

\(E_{4}\) remains stable for \(\tau \in [0, \tau _{0}^{*})\) and unstable for \(\tau > \tau _{0}^{*}\). The system stability (11)–(14) is changed at the critical value of delay \(\tau _{0}^{*}\) and cannot occur again for greater delays [36]. We choose \(\tau \) as the bifurcation parameter because system (11)–(14) loses stability at \(\tau = \tau _{0}^{*}\). We demonstrated that, equation (19) has roots on the imaginary axis, namely \(\eta = \iota \omega _{0}\) at each \(\tau = \tau _{0}^{*}\).

Now, in order to establish the Hopf bifurcation condition [37], we check the transversality requirement. Differentiating (19) w.r.t. \(\tau \), we get

$$\begin{aligned} \left ( 4 \eta ^{3} +3 \eta ^{2} p_{1} + 2 \eta p_{2} +p_{3} + q_{1} e^{- \eta \tau} - \tau e^{-\eta \tau}(q_{1} \eta + q_{2})\right ) \dfrac{d \eta}{\tau} =& \eta e^{-\eta \tau}(q_{1} \eta +q_{2}) \end{aligned}$$

Using \(e^{-\eta \tau} = - \dfrac{ \eta ^{4} + p_{1} \eta ^{3} + p_{2} \eta ^{2} + p_{3} \eta + p_{4}}{q_{1} \eta + q_{2}}\), we get

$$\begin{aligned} \left (\dfrac{d\eta}{d \tau}\right )^{-1} =& \dfrac{ 4 \eta ^{3} +3 \eta ^{2} p_{1} + 2 \eta p_{2} +p_{3}}{-\eta (\eta ^{4} + p_{1} \eta ^{3} + p_{2} \eta ^{2} + p_{3} \eta + p_{4})} + \dfrac{q_{1}}{\eta (q_{1} \eta + q_{2})} - \dfrac{\tau}{\eta} \end{aligned}$$

Since for \(\tau = \tau ^{*}_{0}\) and \(\eta =\iota \omega _{0}\), we have

$$\begin{aligned} \dfrac{\tau}{\eta} =& -\iota \dfrac{\tau ^{*}_{0}}{\omega _{0}}, \\ \eta (q_{1} \eta + q_{2}) =& \iota q_{2} \omega _{0} -q_{1} \omega _{0}^{2}, \\ 4 \eta ^{3} +3 \eta ^{2} p_{1} + 2 \eta p_{2} +p_{3} =& 2 \iota \omega _{0} p_{2} + p_{3} -4 \iota \omega _{0}^{3} - 3\omega _{0}^{2} p_{1}, \\ -\eta (\eta ^{4} + p_{1} \eta ^{3} + p_{2} \eta ^{2} + p_{3} \eta + p_{4}) =& - (\iota \omega ^{5}_{0} + p_{1} \omega ^{4}_{0} - p_{2} \iota \omega ^{3}_{0} -p_{3} \omega ^{2}_{0} + \iota p_{4} \omega _{0}). \end{aligned}$$

Then

$$\begin{aligned} \left [ \Re \left ( \frac{d\eta}{d\tau} \right )^{-1} \right ]_{\tau = \tau ^{*}_{0}} =& \left [ \dfrac{ 4 \eta ^{3} +3 \eta ^{2} p_{1} + 2 \eta p_{2} +p_{3}}{-\eta (\eta ^{4} + p_{1} \eta ^{3} + p_{2} \eta ^{2} + p_{3} \eta + p_{4})} + \dfrac{q_{1}}{\eta (q_{1} \eta + q_{2})} - \dfrac{\tau}{\eta} \right ]_{\eta = \iota \omega _{0}} \\ =& \dfrac{1}{\omega _{0}^{2}}[ \dfrac{3 \omega _{0}^{2} p_{1} - p_{3}}{p_{1} \omega _{0}^{2} - p_{3} } - 1] \\ =& \dfrac{2 p_{1}}{p_{1} \omega _{0}^{2} - p_{3} } \end{aligned}$$

Hence,

$$\begin{aligned} sign \Bigg\{ \dfrac{d\Re (\eta (\tau ))}{d\tau}\Bigg\} _{\tau = \tau ^{*}_{0}} > 0 \end{aligned}$$

if

$$\begin{aligned} p_{1} w_{0}^{2} - p_{3} > 0. \end{aligned}$$

Therefore, a Hopf bifurcation is established at the equilibrium point \(E_{4}\) when \(\tau = \tau ^{*}_{0}\).

Theorem 5.1

Considering the system (11)-(14),

  • As \(\tau \) increases from zero, there exists \(\tau _{j}^{*}\) given by equation (22) such that \(\tau _{0} = \tau _{0}^{*}\) is the initial critical-value of delay. The disease-endemic equilibrium \(E_{4}\) is locally asymptotically stable for \(\tau \in [0, \tau _{0}^{*})\) and unstable when \(\tau > \tau _{0}^{*}\). Furthermore, the system undergoes Hopf bifurcation at \(E_{4}\) when \(\tau = \tau _{0}^{*}\).

6 The Optimal Control Problem

A crucial part of health facilities is the prevention of diabetes complications. The financial cost of diabetes is mostly related to long-term diabetic implications in terms of medication. This section proposes an optimal control strategy to lower the incidence and consequences of diabetes while keeping the relative cost of applying measures as low as possible. We quantify two forms of control interventions in this paper, namely, \(w_{1}(t)\) and \(w_{2}(t)\). Each intervention is discussed as follows:

Let \([0, T]\) denote the time when the optimal control technique is applied to the system (1)–(4). In this study, we quantify two types of control interventions: \(w_{1}(t)\) and \(w_{2}(t)\). Each intervention is explained as follows:

  • Control variable \(w_{1}(t)\): Due to the prevalence of the disease, the control \(w_{1}(t)\) is used to lower glucose production by using medication such as Metformin, the best prescription to reduce blood glucose levels and help keep blood sugar levels at a healthy range.

  • Control variable \(w_{2}(t)\): This intervention reduces the obesity-related factor by exercising daily, buying exercise equipment, eating healthy food, following a regular diet, and keeping a healthy weight.

Due to limited medical resources, it is necessary to put some boundaries on controls, such as \(0 \leq w_{1}(t)\), \(w_{2}(t) \leq 1\). If \(w_{1}(t)\) and \(w_{2}(t)\) are zero, no effort is placed into these controls at time \(t\), whereas one represents the maximum capacity of applied interventions. Considering the preceding assumptions, the system (1)–(4) is modified as follows to customize control variables:

$$\begin{aligned} \begin{alignedat}{2} \dfrac{dG}{dt}&=a-\dfrac{w _{1}(t)IG}{1+pG+qF}+ c F -d_{1} G, \\ \dfrac{dI}{dt}&=\dfrac{\mu B G}{k_{1}+G}-d_{2} I, \\ \dfrac{dB}{dt}&=\left (\dfrac{h G }{ k_{2} + G}- \delta F^{2} -d_{3} \right )B, \\ \dfrac{dF}{dt}&= (1 - w_{2}(t))F \left (1-\dfrac{F}{k_{3}}\right ). \end{alignedat} \end{aligned}$$
(23)

For our convenience, we write \(w_{1}(t) = w_{1}\) and \(w_{2}(t) = w_{2}\) for future analysis.

6.1 Controls Cost Construction and Characterization

This section is divided into two parts. These involve determining the total cost of disease and its controls and the analytical forms of the controls.

6.1.1 Total Cost Determination

Here, we calculate the overall cost incurred as a result of the control measures that are to be minimised.

  1. (i.)

    Cost incurred in lowering the glucose level: Cost involved in treatment policy is given as: \(\int _{0}^{T}\!A^{*} w_{1}^{2} \,\mathrm{d}t\ \).

    The term \(A^{*} w_{1}^{2}\) refers to the cost of treatment policy and related activities such as medicine, diagnostic expenses, and hospitalization. For the cost of the treatment policy, we used typical quadratic non-linearity \(w_{1}^{2} \).

  2. (ii.)

    Cost related to obesity-related factor and its treatment: The overall cost resulting from disease burden and treatment policy is stated as: \(\int _{0}^{T}\! \left [U_{1} F(t) + D^{*} w_{2}^{2} \right ] \, \mathrm{d}t\ \).

Consider the control problem of minimizing the objective function over time \(T\).

$$ L(w_{1},w_{2}) = \int _{0}^{T}\!\left [U_{1} F(t) + A^{*} w_{1}^{2} + D^{*} w_{2}^{2} \right ]\,\mathrm{d}t\ $$
(24)

subject to the model system (23).

where \(U_{1} > 0\), \(A^{*} > 0\), \(D^{*} > 0\) are positive weight constants that balance the unit of integrands and measure the relative costs.

Our target is to search the optimal controls \(w_{1}^{*}\), \(w_{2}^{*}\) such that

$$ L(w_{1}^{*}, w_{2}^{*}) = \underset{w_{1}, w_{2} \in U}{min} L(w_{1}, w_{2}) $$

where \(U\) is the set of admissible controls defined by

$$ U = \{ w_{1}, w_{2}~ |~ 0 \leq w_{1},~ w_{2} \leq 1,~ t \in [~0,~ T~] ~ \}. $$

The controls in this situation are bounded and measurable.

6.1.2 Existence of an Optimal Control

To begin, we demonstrate the existence of optimal control functions that minimize the cost function in a finite period. We follow the results proven in [38–40] to achieve this. This problem’s Lagrangian is described as follows:

$$ L_{1}(G, I, B, F, w_{1}, w_{2})= U_{1} F(t) + A^{*} w_{1}^{2} + D^{*} w_{2}^{2}. $$

The following conclusion ensures the existence of the ideal control functions.

Theorem 6.1

Consider the control problem with system (23), \(\exists \) an optimal control \((w_{1}^{*}, w_{2}^{*}) \in U\) such that \(L(w_{1}^{*}, w_{2}^{*}) = \underset{w_{1}, w_{2} \in U}{min} L(w_{1}, w_{2})\).

Proof

The existence of the optimal control can be determined using Theorem 4.1 of [41].

  • For each bounded control coming from the control set \(U\), all state variables are bounded, as was previously explained. The right-hand portion of the model system (23), about state variables, also satisfies the Lipschitz criterion.

  • The model system (23) is linear in control variables, and the control variable set \(U\) is convex and closed by definition.

  • The integrand \(L_{1}( G, I, B, F, w_{1}, w_{2}) = U_{1} F(t) + A^{*} w_{1}^{2} + D^{*} w_{2}^{2} \), is convex in U due to quadratic nature of control variables. Also, \(L_{1}( G, I, B, F, w_{1}, w_{2}) = U_{1} F(t) + A^{*} w_{1}^{2} + D^{*} w_{2}^{2} \geq A^{*} w_{1}^{2} + D^{*} w_{2}^{2} \). Now, we consider \(e_{1} = min(A^{*}, D^{*}) > 0\) and \(g(w_{1}, w_{2}) = e_{1}(w_{1}^{2} + w_{2}^{2})\). Hence, \(L_{1} \geq g(w_{1}, w_{2})\) is true and \(g\) is continuous and satisfies \(|(w_{1}, w_{2})|^{-1} g(w_{1}, w_{2}) \to \infty \) whenever \(|(w_{1}, w_{2})| \to \infty \).

Therefore, all conditions for the existence of controls are fulfilled. Hence, the result. □

6.1.3 Characterization of Optimal Control Functions

Here, we employ Pontryagin’s Maximum Principle to create the prerequisites for ideal control functions and examine the routes of ideal control functions for the control system (23)-(24). For this, the associated Hamiltonian ℋ is defined by

$$ \mathcal{H} = L_{1} + \lambda _{1} \dfrac{d G}{ d t} + \lambda _{2} \dfrac{d I}{ d t} + \lambda _{3} \dfrac{d B}{ d t} + \lambda _{4} \dfrac{d F}{ d t} $$
(25)

where \(\lambda = (\lambda _{1}, \lambda _{2}, \lambda _{3}, \lambda _{4})^{T}\) is known as adjoint variable. In the following theorem, we characterize the optimal controls.

Theorem 6.2

Let \(w_{1}^{*}\) and \(w_{2}^{*}\), be two optimal control functions, and \(G^{*}\), \(I^{*}\), \(B^{*}\) and \(F^{*}\) are the state variables of the optimal control problem (23)-(24). Then \(\exists \) adjoint variable \(\lambda = (\lambda _{1}, \lambda _{2}, \lambda _{3}, \lambda _{4})^{T}\) ∈ \(\mathcal{R}^{4}\) which satisfies the following canonical equations:

$$\begin{aligned} \begin{alignedat}{2} \dfrac{d\lambda _{1}}{dt}={}& \left ( d_{1} - \dfrac{ G I p w_{1}}{(1 + pG + q F)^{2}} + \dfrac{ I w_{1}}{(1 + p G + q F)}\right )\lambda _{1} \\ &{}- \left ( \dfrac{B \mu}{k_{1} + G} - \dfrac{B G \mu}{(k_{1} + G)^{2}}\right ) \lambda _{2} - \left ( \dfrac{h B}{k_{2} + G} - \dfrac{h G B }{(k_{2} + G )^{2}}\right )\lambda _{3}, \\ \dfrac{d\lambda _{2}}{dt}={}& d_{2} \lambda _{2} + \left ( \dfrac{ G w_{1}}{1 + p G + q F }\right )\lambda _{1}, \\ \dfrac{d\lambda _{3}}{dt}={}&\left ( d_{3} + \delta F^{2} - \dfrac{h G }{ k_{2} + G}\right )\lambda _{3} - \left ( \dfrac{ \mu G}{k_{1} + G}\right )\lambda _{2}, \\ \dfrac{d\lambda _{4}}{dt}={}& \left ( \dfrac{ F (1-w_{2})}{k_{3}} - \left (1 - \dfrac{F}{k_{3}}\right ) (1 - w_{2})\right )\lambda _{4} - U_{1} +2 B \delta F \lambda _{3} \\ &{}- \left ( c + \dfrac{ G I q w_{1}}{(1 + p G + q F)^{2}}\right )\lambda _{1}. \end{alignedat} \end{aligned}$$
(26)

with transversality conditions

$$ \lambda _{i} (T) = 0 ~\forall ~ 1\leq i \leq 4. $$
(27)

Also, the corresponding optimal controls \(w_{1}^{*}\) and \(w_{2}^{*}\) are given as,

$$\begin{aligned} \begin{alignedat}{2} w_{1}^{*} &= min \Biggl\{ max\Biggl\{ 0, \left ( \dfrac{\lambda _{1} G^{*} I^{*}}{2 A^{*}(1 + pG^{*} + q F^{*})} \right )\Biggr\} , 1\Biggr\} , \\ w_{2}^{*} &= min \Biggl\{ max\Biggl\{ 0, \dfrac{\lambda _{4} F^{*}}{2 D^{*}}\left (1-\dfrac{ F^{*}}{ k_{3}} \right )\Biggr\} , 1\Biggr\} . \end{alignedat} \end{aligned}$$
(28)

Proof

Let \(w_{1}^{*}\) and \(w_{2}^{*}\) be the given optimal control functions and \(G^{*}\), \(I^{*}\), \(B^{*}\) and \(F^{*}\) are the corresponding optimal state variables of the system (23), which minimize the cost functional (24). Then by the Pontryagin’s Maximum Principle, \(\exists \) adjoint variable \(\lambda = (\lambda _{1}, \lambda _{2}, \lambda _{3}, \lambda _{4})^{T} \in \mathcal{R}^{4}\) which satisfies the following canonical equations:

$$ \dfrac{d \lambda _{1}}{d t} = - \dfrac{ \partial \mathcal{H}}{ \partial G}, ~ \dfrac{d \lambda _{2}}{d t} = - \dfrac{ \partial \mathcal{H}}{ \partial I}, ~ \dfrac{d \lambda _{3}}{d t} = - \dfrac{ \partial \mathcal{H}}{ \partial B} ~and~ \dfrac{d \lambda _{4}}{d t} = - \dfrac{ \partial \mathcal{H}}{ \partial F} $$

with transversality conditions (27).

Here, ℋ is the Hamiltonian and given in (25). Then, we get the adjoint system (26) with transversality conditions (27).

Now, using the optimality condition, we have

$$ \dfrac{ \partial \mathcal{H}}{d w_{i}} = 0, ~~ at ~ w_{i} = w_{i}^{*} ~ for ~ i = 1,2. $$

Hence, we get

\(w_{1}^{*} = \dfrac{1}{2 A^{*}}\lambda _{1} \left ( \dfrac{ G^{*} I^{*}}{1 + pG^{*} + q F^{*}}\right ) \) and \(w_{2}^{*} = \dfrac{1}{2 D^{*}}\lambda _{4} \left ( F^{*} \left (1- \dfrac{ F^{*}}{ k_{3}}\right )\right )\).

By following the above along with the properties of the control space \(U\), we have the optimal controls \(w_{1}^{*}\) and \(w_{2}^{*}\) as given in (28). □

7 Numerical Analysis

Numerical analysis is used to examine the global dynamical behavior of the systems (1)-(4), (11)-(14) and (23). Table 2 mentions the parameter value and is either assumed or derived from the literature.

7.1 ODE Simulation: Effect of \(\delta \)

In this part, we simulate numerically the (1)–(4) system. The numerical results in this section were produced using MATLAB’s built-in ODE 45 function with the initial conditions (100, 20, 300, 0.01). Here, we vary \(\delta \), i.e., the death rate of beta-cells due to obese-related factors. We consider three values of \(\delta \): (i) \(\delta = 0.00001\), (ii) \(\delta = 0.0001\), and (iii) \(\delta = 0.001\) for our simulation, and the other parameters are the same as given in Table 2. At a low death rate of beta-cells due to obesity-related factors, say \(\delta = 0.00001\), we observe high insulin level and beta-cell density. However, one can keep a low level of glucose (see Fig. 11 (a)). This is due to proper beta-cell functioning, showing healthy conditions. When \(\delta \) slightly increases to 0.0001, the beta-cells with insulin density start decreasing with a corresponding rise in glucose level (see Fig. 11 (b)). Finally, when \(\delta \) increases to 0.001, the beta-cells with insulin density start to decrease rapidly with a corresponding increase in glucose level, showing the worst scenario (see Fig. 11 (c)). This simulation clearly states that an obesity-related factor increases the glucose level in the bloodstream.

Fig. 11
figure 11

Solution for system (1)-(4) with parameter values given in the Table 2 and when (a) \(\delta = 0.00001\), (b) \(\delta = 0.0001\), (c) \(\delta = 0.001\). These figures indicates as obese related death among beta cells increases, glucose levels correspondingly increase

Full size image

Our findings suggest that when the death rate of beta-cells due to obese-related factors is less (negligible), glucose levels can be controlled in the body, and this represents the healthy condition everyone wants, i.e., free from type 2 diabetes, and for this, one needs to follow a proper well-maintained routine like by having a nutritious diet, by proper daily exercise, whether by performing yoga or doing it with the help of gym equipment.

7.2 ODE Simulation: Effect of r

Here, we vary \(r\), i.e., the growth rate of obese-related factors. We consider \(r\) as: (i) \(r = 0.01\) and (ii) \(r= 0.1\) for our simulation, and the other parameters are the same as given in Table 2. Here, when \(r = 0.01\) (see Fig. 12 (a)), we see insulin as well as beta-cell density increases with time. However, glucose levels decrease, showing healthy conditions. When \(r\) is increased to \(r = 0.1\) after a few days, the glucose level crosses a critical value, resulting in beta-cell dysfunction, thus causing low insulin production (see Fig. 12 (b)). An uncontrolled growth in glucose is observed after the disruption of beta cells. By this simulation, we can clearly state that beta-cell dysfunctions as the growth rate of obese-related factors increases. Due to this, insulin production decreases, resulting in insulin resistance. As a result, glucose level increases in the body and hyperglycemia occurs, and the condition of a person who suffers from type two diabetes worsens.

Fig. 12
figure 12

Solution for system (1)-(4) with parameter values given in the Table 2 and when (a) \(r = 0.01 \), (b) \(r = 0.1\). These figures suggest that excessive fat disrupts beta cells, leading to unchecked glucose levels

Full size image

Our result suggests that when \(r\) is less, i.e., there is a control level of obese-related factor in the body, then beta-cells function properly, and this is the healthiest condition everyone wants, i.e., free from type 2 diabetes, and to achieve this, one needs to perform a healthy diet and routine and avoid the chances of getting obesity.

7.3 Numerical Simulation of the Model with Delay

Delay differential equations are an exciting type of differential equation with numerous applications, particularly in biology and medicine. In this section, a numerical analysis is performed to investigate the dynamical behavior of the system (11)- (14). We have considered the same initial conditions as in the case without delay. We took the same parameters as discussed in Example 4.1.

Here, we vary \(\tau \) from 0.01 to 1.2. The simulation showed periodic doubling bifurcation occurs when delay crosses a critical value (see Fig. 13). A period-doubling bifurcation in dynamical systems theory happens when a slight change in a system’s parameters results in the emergence of a new periodic trajectory from an existing one, the new one having twice the original period. The numerical values acquired by the system repeat themselves twice as slowly with a twofold period. For \(\tau \in [0.01, 0.68)\), the density of glucose level, insulin, and beta cells converge to a stable fixed point. And once \(\tau \geq \) 0.68, the component’s densities break in two, oscillating back and forth between two values and never settling to a single constant value. The cycle then continues. These are period-doubling bifurcations since the cycle’s or period’s duration has doubled. Also, from here, we note that the critical value of \(\tau =\tau _{0}^{*} = 0.68\); also, we identify a critical delay point at \(\tau =0.68\) (\(\omega =0.547134\)), marking the transition of the system’s stability from a stable state to an unstable state. Figure 14 show the system (11)-(14) solution corresponding to \(\tau = 0.3 \) and \(\tau = 4.5\) illustrating the impact of the time delay in generating periodic solutions; from here, when \(\tau < \tau _{0}^{*}\), we observe the stable behavior of our system (see Fig. 14(a)). As \(\tau > \tau _{0}^{*}\), we see the oscillatory behavior of the system (see Fig. 14(b)).

Fig. 13
figure 13

Bifurcation diagram for system (11)-(14) considering \(\tau \) as a bifurcation parameter. At \(\tau = \tau ^{*}_{0} = 0.68\) occurrence of Hopf bifurcation leading to period doubling is observed

Full size image
Fig. 14
figure 14

Solution of the system (11)-(14) showing the impact of different rate of delays (\(\tau \)), (a) \(\tau =0.3\); (b) \(\tau =4.5\)

Full size image

From a biological perspective, we may argue that as \(\tau \) grows, the density of all the components oscillates, with more followed by less, and so on.

7.4 Numerical Simulation of the Optimal Control Problem

This part focuses on running numerical simulations for the control problem to investigate how control interventions affect disease transmission dynamics. To verify the predictability of the controlled system (23), a graph compares the evolution of glucose levels in a diabetic patient without control to a diabetic patient with control.

To compile the numerical simulations, we set \(k_{3}= 15\), and others are the same as discussed in Example 4.1. The time period for controls to be applied is \(T = 300\) days, along with the same initial conditions [100, 20, 300, 0.01]. We choose the positive weight parameters as \(A^{*}= 10\), \(U_{1} =30\), \(D^{*}= 5\).

From Fig. 15, it is clear that due to measures like medication, exercise, and having a healthy diet, the glucose level starts to decrease, showing the positive effect of measures that are imposed.

Fig. 15
figure 15

Profile of glucose level with and without controls

Full size image

This represents the importance of control in disease transmission. It is observed that as controls are imposed, disease invasion is controlled. If the individual suffers from diabetes and does not adopt any measures, his/her health may worsen due to uncontrolled glucose rise.

8 Conclusion

A mathematical model has been developed to elucidate the interaction between obesity and diabetes. The primary objective of this study is to demonstrate the significant role of obesity in the progression of type 2 diabetes. The constructed model exhibits four biologically plausible equilibria. Our investigation encompasses both local and global stability analyses. Local and global stability conditions are defined using the Routh-Hurwitz criterion and constructing appropriate Lyapunov function. We have established that the system’s positive equilibrium is globally asymptotically stable under specific parameter assumptions. Furthermore, we have provided analytical evidence for the existence of Hopf bifurcations. Numerical simulations have been conducted to validate these findings.

Bifurcation analysis reveals that a lower death rate of beta cells (\(d_{3}\)) ensures the proper cyclic elimination of glucose. The intricate balance of anabolism and catabolism in response to variations in calorie intake, food composition, and physical activity influences the equilibrium of insulin and blood glucose levels. However, when this rate exceeds a critical value, glucose removal does not occur periodically due to beta cell dysfunction, necessitating external insulin administration. Our numerical simulations also indicate that an excessive growth rate of obesity-related factors impairs beta cells, leading to uncontrolled glucose levels.

Beta cells, responsible for producing and releasing insulin in response to glucose levels, may exhibit impaired function in individuals with type 2 diabetes. Consequently, this dysfunction can lead to delays in insulin secretion, disrupting the delicately balanced feedback mechanisms responsible for regulating blood glucose levels. We have introduced a time delay term to our proposed model to integrate this fact. This delay factor accounts for beta cell dysfunction in insulin production. Our analysis demonstrates that the system exhibits stable behavior when the delay parameter (\(\tau \)) is in the range [0, 0.68). However, beyond the critical value of 0.68, the system undergoes period doubling, transforming stable dynamics into periodic dynamics in the presence of delay. Period doubling exhibits non-linear behavior and thus, underscores the complex interplay between insulin dynamics, beta cell function, and glucose regulation in type 2 diabetes. We simulate the effect of reducing obesity through exercise and medication and formulate an optimal control model using the Pontryagin maximum principle to identify the best control solution [42]. This analysis is conducted with a sense of urgency, recognizing the imperative need for prompt action to curb the advancement of diabetes and to introduce accessible treatment solutions to counteract this alarming trend. Our findings corroborate this urgency, as evidenced by the results in Fig. 15. It is evident that the glucose level gradually decreases over time with the implementation of control measures. This reduction aligns with our objectives, as it signifies the effective management of the disease dynamics. By adhering to lifestyle modifications such as regular exercise and maintaining a healthy diet, individuals can control the disease’s progression. Conversely, failure to adopt these healthy lifestyle measures can exacerbate the condition of diabetic individuals. Thus, our analysis underscores the critical importance of proactive intervention and lifestyle management in mitigating the adverse effects of diabetes and improving overall health outcomes.

While our model exhibits several strengths, it is not without its limitations. One significant challenge is measuring beta-cell mass, a pivotal parameter within the model. Obtaining precise measurements of beta-cell mass presents inherent difficulties, as current methodologies often lack the necessary sensitivity and specificity. Moreover, reliable data about beta-cell mass are frequently scarce or unavailable, further complicating efforts to validate and refine the model. Furthermore, the scarcity of empirical evidence necessitates assuming certain parameter values within the model. While necessary for model development, these assumptions introduce uncertainty to the analysis and interpretation of results. The complex nature of the disease epidemic, encompassing multifaceted interactions between various physiological, genetic, environmental, and behavioral factors, underscores the need for ongoing research efforts. Addressing the intricacies of diabetes requires a comprehensive approach that extends beyond the scope of any single model. Future research endeavors must elucidate the complex mechanisms underlying diabetes pathogenesis and progression, integrating diverse datasets and methodologies to capture the full spectrum of disease dynamics. Continued research efforts are imperative to overcome these challenges and refine our understanding of diabetes, ultimately paving the way for more effective prevention and management strategies.

The global prevalence of diabetes is rapidly escalating, with an alarming increase in mortality rates associated with the disease. Factors such as obesity, unhealthy dietary habits, and sedentary lifestyles are identified as key contributors to this epidemic. These factors are largely preventable, underscoring the importance of raising public awareness about their detrimental effects. Research studies [1, 43–45] highlight the profound impact of these lifestyle choices on the onset and progression of diabetes. Surgical interventions, particularly bariatric surgery, emerge as highly effective strategies for addressing both obesity and type 2 diabetes [45]. These procedures offer promising outcomes in weight loss and glycemic control, emphasizing the potential for targeted interventions to mitigate the burden of diabetes. The findings presented in this paper collectively support the conclusion that the developed model is physiologically consistent and holds promise as a valuable tool for advancing our understanding of diabetes. By delving deeper into the intricacies of diabetes dynamics and exploring innovative interventions, we can strive to mitigate the economic and humanistic burden of this widespread disease.