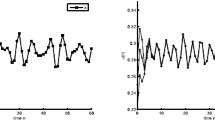Existence and Convergence Dynamics of Pseudo Almost Periodic Solutions for Nicholson’s Blowflies Model with Time-Varying Delays and a Harvesting Term

Abstract

In this paper, an Nicholson’s blowflies model with time-varying delays and a harvesting term is investigated. By applying the fixed point theorem, the properties of pseudo almost periodic function, inequality analysis technique and constructing appropriate Lyapunov functionals, we establish some new criteria for the existence and convergence dynamics of pseudo almost periodic solutions for the model. An illustrative example with its numerical simulation is presented to demonstrate the effectiveness of the derived results. Our results complement some previous studies.

1 Introduction

To describe the population of the Australian sheep-blowfly Lucilia cuprina, Nicholson [1] and Gurney et al. [2] proposed an Nicholson’s blowflies model which takes the form

$$ \dot{x}(t)=-\delta x(t)+px(t-\tau )e^{-a x(t-\tau )},\quad \delta ,p, \tau , a\in (0,\infty ), $$

(1.1)

where $x(t)$ stands for the size of population at time $t$, $p$ represents the maximum per capita daily egg production rate, $\delta$ stands for the per capita daily adult death rate, $\frac{1}{a}$ denotes the size at which the blowfly population reproduces at its maximum rate, $\tau$ is the generation rate. Since then, considerable effort has been devoted to investigating the dynamical behavior of model (1.1) and its modifications. For example, Ding and Li [3] investigated the stability and bifurcation of numerical discretization version of (1.1), Kulenovic et al. [4] considered the global attractivity of system (1.1), So and Yu [5] focused on the stability and uniform persistence of the discrete version of model (1.1). For more details, we refer the reader to [6–21].

It is well known that in real natural word, the change of the environment and impulsive effect play an important role in many biological and ecological dynamical systems [22]. Inspired by the viewpoint, Alzabut [22] investigated the following delay Nicholson’s blowflies model with impulsive effect which is a generalized form of model (1.1)

$$ \left \{ \textstyle\begin{array}{l} \displaystyle \dot{x}(t)=-\alpha (t)x(t)+\sum_{i=1}^{n}\beta_{i}(t)x(t-\tau )e^{- \lambda_{i}(t)x(t-\tau )}+h(t),\quad t\neq \theta_{k}, \\ \displaystyle \Delta x(\theta_{k})=\gamma_{k}x(\theta_{k})+\delta_{k},\quad k\in {\mathbb{N}}, \end{array}\displaystyle \right . $$

(1.2)

where $\alpha (t), \beta_{i}(t),\lambda_{i}(t),h(t)\in [{\mathbb{R}} ^{+},{\mathbb{R}}^{+}], \tau >0$ and $\gamma_{k}, \delta_{k}\in {\mathbb{R}}, k\in {\mathbb{N}}$, $h(t)$ is a harvesting function, $\Delta x(t)$ represents the difference $x(t^{+})-x(t^{-})$, where $x(t^{+})$ and $x(t^{-})$ define the limits from right and left, respectively, $\theta_{k}$ denotes the instants at which size of the population suffers an increment of $\delta_{k}$ units. By applying the contraction mapping principle and Gronwall-Bellman’s inequality, Alzabut [22] obtained some sufficient conditions which guarantee the existence and exponential stability of positive almost periodic solution for the model (1.2).

Here we would like to point out that many authors investigate the dynamical behavior of Nicholson’s blowflies model with constant or periodic environment. However, the real living environments of species are not always like this due to the ecological effects of human activities and industry, for example, the location of manufacturing industries and pollution of the atmosphere, soil, rivers, and so on [23–30]. Based on this situation, it is more reasonable to assume that the parameters of the models are pseudo almost periodic functions, which allow complex repetitive phenomena to be represented as an almost periodic process plus an ergodic component. As pointed out by Dads and Ezzinbi [31], it would be of great interest to investigate the pseudo almost periodic systems with delay. Stimulated by the aforementioned discussions, we will consider the pseudo almost periodic solution of the following modified system of model (1.2)

$$ \dot{x}(t)=-\alpha (t)x(t)+\sum_{i=1}^{n} \beta_{i}(t)x\bigl(t-\tau (t)\bigr)e ^{-\lambda_{i}(t)x(t-\tau (t))}+h(t). $$

(1.3)

The main aim of this article is to establish some sufficient conditions for the existence, convergence and exponential convergence of pseudo almost periodic solutions of (1.3). The obtained results will show that the criteria for convergence and exponential convergence of pseudo almost periodic solution of (1.3) are both delay and harvesting rate dependent. Recently, although there are some papers that deal with the pseudo almost periodic solutions of differential equations [32–42]. To the best of our knowledge, it is the first time to focus on the existence, convergence and exponential convergence of pseudo almost periodic solutions of (1.3). The obtained results of this article are completely new and complement some previous studies.

The remainder of the paper is organized as follows. In Sect. 2, we introduce some notations, lemmas and definitions, which can be used to check the existence of pseudo almost periodic solutions of system (1.3). In Sect. 3, we present some new sufficient conditions for the existence of the continuously differentiable pseudo almost periodic solution of (1.3). Some sufficient conditions on the convergence and exponential convergence of pseudo almost periodic solutions of (1.3) are established in Sect. 4. An example and its numerical simulations are given to illustrate the effectiveness of the obtained results in Sect. 5. Finally, a brief conclusion is drawn.

2 Preliminary Results

In this section, we would like to recall some notations, basic definitions and lemmas which are used in what follows. Throughout this paper, we will use the notations as follows:

$$\begin{aligned} u^{+}=\sup_{t\in \mathbb{R}} \bigl|u(t)\bigr|,\qquad u^{-}=\inf_{t\in \mathbb{R}}\bigl|u(t)\bigr|, \end{aligned}$$

where $u(t)$ is a bounded continuous function. Let $\mathit{BC}(\mathbb{R}, \mathbb{R})$ denote the set of bounded continued functions from ℝ to ℝ, and $\mathit{BUC}(\mathbb{R}, \mathbb{R})$ be the set of all bounded and uniformly continuous functions from ℝ to ℝ. Obviously, $(\mathit{BC}(\mathbb{R},\mathbb{R}), \|.\|)$ is a Banach space where $\|.\|$ denotes the sup norm $\|.\|:= \sup_{t\in \mathbb{R}}\|u(t)\|$. Let $C=C([-\tau^{+},0], \mathbb{R})$ be the continuous functions space equipped with the supremum norm $\|.\|$ and denote $C_{+}=C([-\tau^{+},0],\mathbb{R} _{+})$, where $\mathbb{R}_{+}=[0,+\infty )$. If $x(t)$ is continuous and defined on $[-\tau^{+}+t_{0},\rho )$ with $t_{0}, \rho \in \mathbb{R}$, then for all $t\in [t_{0}, \rho )$, we define $x_{t}\in C$, in which $x_{t}(\vartheta )=x(t+\vartheta )$ for all $\vartheta \in [-\tau^{+},0]$.

Considering the biological interpretation of model (1.3), we only investigate the positive solution. The initial conditions are given by

$$ x_{t_{0}}=\varphi , \varphi \in C_{+},\quad \varphi (0)>0. $$

(2.1)

Let $x_{t}(t_{0},\varphi )$ (or $x(t;t_{0},\varphi )$) be a solution of the initial value problem (1.3) and (2.1) with $x_{t_{0}}(t_{0}, \varphi )=\varphi \in C_{+}$ and $t_{0}\in \mathbb{R}$. In addition, let $[t_{0}, \zeta (\varphi ))$ be the maximal right interval of existence of $x_{t}(t_{0},\varphi )$.

Definition 2.1

(see [43, 44])

Let $u(t)\in \mathit{BC}( \mathbb{R},\mathbb{R}),u(t)$ is said to be almost periodic on ℝ if, for any $\varepsilon >0$, the set $T(u,\varepsilon )= \{\delta :\|u(t+\delta )-u(t)\|< \varepsilon \mbox{ for all } t \in \mathbb{R}\}$ is relatively dense; that is, for any $\varepsilon > 0$, it is possible to find a real number $l=l(\varepsilon ) >0$; for any interval with length $l(\varepsilon )$, there exists a number $\delta =\delta (\varepsilon )$ in this interval such that $\|u(t+\delta )-u(t)\|< \varepsilon$, for all $t\in \mathbb{R}$.

We denote by $\mathit{AP}(\mathbb{R},\mathbb{R})$ the set of the almost periodic functions from ℝ to ℝ. Besides, the concept of pseudo almost periodicity (PAP) was introduced by Zhang [43] in the early nineties. It is a natural generalization of the classical almost periodicity. Precisely, define the class of functions $\mathit{PAP}_{0}(\mathbb{R},\mathbb{R})$ as follows:

$$\begin{aligned} \biggl\{ u\in \mathit{BC}(\mathbb{R},\mathbb{R})\biggm| \lim_{T\rightarrow +\infty } \frac{1}{2T} \int_{-T}^{T}\bigl|u(t)\bigr|dt=0 \biggr\} . \end{aligned}$$

A function $u\in \mathit{BC}(\mathbb{R},\mathbb{R})$ is called pseudo almost periodic if it can be expressed as $u=u_{1}+u_{2}$, where $u_{1} \in \mathit{AP}(\mathbb{R},\mathbb{R})$ and $u_{2}\in \mathit{PAP}_{0}( \mathbb{R},\mathbb{R})$. The collection of such functions will be denoted by $\mathit{PAP}(\mathbb{R},\mathbb{R})$. The functions $u_{1}$ and $u_{2}$ in the above definition are, respectively, called the almost periodic component and the ergodic perturbation of the pseudo almost periodic function $u$. The decomposition given in definition above is unique. Observe that $(\mathit{PAP}(\mathbb{R},\mathbb{R}),\|.\|)$ is a Banach space and $\mathit{AP}(\mathbb{R},\mathbb{R})$ is a proper subspace of $\mathit{PAP}(\mathbb{R},\mathbb{R})$ since the function $u_{2}(t)= \sin ^{2}t+\sin^{2}\sqrt{7}t + \exp (-t^{4}\sin^{2}t)$ is pseudo almost periodic function but not almost periodic.

Lemma 2.2

(see [23])

If $u(t)\in \mathit{PAP}(\mathbb{R},\mathbb{R}), \tau (t)\in \mathit{AP}(\mathbb{R},\mathbb{R})$ and $\dot{\tau }(t)\leq \tau _{0}<1$, then $u(t-\tau (t))\in \mathit{PAP}(\mathbb{R},\mathbb{R})$.

Lemma 2.3

(see [23])

If $u(t),v(t)\in \mathit{PAP}(\mathbb{R}, \mathbb{R})$, then $u(t)v(t)\in \mathit{PAP}(\mathbb{R},\mathbb{R})$.

Definition 2.4

(see [20, 45])

Let $x\in \mathbb{R}^{n}$ and $Q(t)$ be a $n\times n$ continuous matrix defined on ℝ. The linear system

$$ \dot{x}(t)=Q(t)x(t) $$

(2.2)

is said to admit an exponential dichotomy on ℝ if there exist positive constants $k_{i},\alpha_{i}$, $i=1,2$ and projection $P$ and the fundamental solution matrix $X(t)$ of (2.2) satisfying

$$\begin{aligned} \bigl\| X(t)PX^{-1}(s)\bigr\| \leq& k_{1} e^{-\alpha_{1}(t-s)},\quad \mbox{for } t \geq s,\\ \bigl\| X(t) (I-P)X^{-1}(s)\bigr\| \leq& k_{2} e^{-\alpha_{2}(s-t)},\quad \mbox{for } t \leq s, \end{aligned}$$

where $I$ is the identity matrix.

Lemma 2.5

(see [43])

Assume that $Q(t)$ is an almost periodic matrix function and $g(t)\in \mathit{PAP}(\mathbb{R},\mathbb{R}^{p})$. If the linear system (2.2) admits an exponential dichotomy, then pseudo almost periodic system

$$ \dot{x}(t)=Q(t)x(t)+g(t) $$

(2.3)

has a unique pseudo almost periodic solution $x(t)$, and

$$ x(t)= \int_{-\infty }^{t}X(t)PX^{-1}(s)g(s)ds- \int_{t}^{+\infty }X(t) (I-P)X ^{-1}(s)g(s)ds. $$

(2.4)

Proof

It is check that (2.4) is a solution of (2.3). Now we only show that the solution (2.4) is bounded. By (2.4), we have

$$\begin{aligned} \bigl|x(t)\bigr| =& \int_{-\infty }^{t} \bigl|X(t)PX^{-1}(s)\bigr| \bigl|g(s)\bigr|ds+ \int_{t}^{+ \infty } \bigl|X(t) (I-P)X^{-1}(s)\bigr| \bigl|g(s)\bigr|ds \\ \leq &\|g\| \biggl[ \int_{-\infty }^{t}k_{1}e^{-\alpha_{1}(t-s)}ds+ \int _{t}^{+\infty }k_{2}e^{-\alpha_{2}(s-t)}ds \biggr] \\ \leq &\|g\| \biggl[ \frac{k_{1}}{\alpha_{1}}+\frac{k_{2}}{\alpha_{2}} \biggr] . \end{aligned}$$

Since $g$ is bounded, then $x$ is bounded. The bounded solution is unique because the homogeneous equation (2.2) has no nontrivial bounded solution.

Next we will prove that $g\in \mathit{PAP}(\mathbb{R},\mathbb{R}^{p})$. Let $I_{1}(t)=\int_{-\infty }^{t}X(t)PX^{-1}(s)g(s)ds$ and $I_{2}(t)=- \int_{t}^{+\infty }X(t)(I-P)X^{-1}(s)g(s)ds$. Then $x(t)=I_{1}(t)+I _{2}(t)$. In view of Definition 2.4, we have

$$\begin{aligned} \frac{1}{2T} \int_{-T}^{T}\bigl|I_{1}(t)\bigr|dt \leq & \frac{1}{2T} \int_{-T} ^{T}dt \int_{-\infty }^{t}\bigl|X(t)PX^{-1}(s)\bigr| \bigl|g(s)\bigr|ds \\ \leq &\frac{1}{2T} \int_{-T}^{T}dt \int_{-\infty }^{t} k_{1}e^{-\alpha _{1}(t-s)}\bigl|g(s)\bigr|ds \\ =&\frac{1}{2T} \int_{-T}^{T}dt \biggl[ \int_{-\infty }^{-T}k_{1}e^{- \alpha_{1}(t-s)}\bigl|g(s)\bigr|ds+ \int_{-T}^{t} k_{1}e^{-\alpha_{1}(t-s)}\bigl|g(s)\bigr|ds \biggr] \\ \leq & \frac{1}{2T} \int_{-\infty }^{-T}\bigl|g(s)\bigr|ds \int_{-T}^{T} k_{1}e ^{-\alpha_{1}(t-s)}dt+ \frac{1}{2} \int_{-T}^{T}\bigl|g(s)\bigr|ds \int_{s}^{T}k _{1}e^{-\alpha_{1}(t-s)}dt \\ =& I_{1}^{*}+I_{2}^{*}, \end{aligned}$$

where $I_{1}^{*}=\frac{1}{2T}\int_{-\infty }^{-T}|g(s)|ds \int_{-T} ^{T} k_{1}e^{-\alpha_{1}(t-s)}dt$ and $I_{2}^{*}=\frac{1}{2}\int_{-T} ^{T}|g(s)|ds\int_{s}^{T}k_{1}e^{-\alpha_{1}(t-s)}dt$. To prove that $I_{1}(t)\in \mathit{PAP}(\mathbb{R},\mathbb{R}^{p})$, we need to prove that both $I_{1}^{*}\rightarrow 0$ and $I_{2}^{*}\rightarrow 0$ when $T\rightarrow \infty$. We know that

$$\begin{aligned} I_{1}^{*} =&\frac{1}{2T} \int_{-\infty }^{-T}\bigl|g(s)\bigr|ds \int_{-T}^{T} k _{1}e^{-\alpha_{1}(t-s)}dt \\ \leq & \frac{1}{2T}\|g\|\frac{k_{1}}{\alpha_{1}}\bigl[e^{\alpha_{1}T}-e ^{-\alpha_{1}T}\bigr] \int_{-\infty }^{-T}e^{\alpha_{1} s}ds \\ \leq &\frac{1}{2T}\|g\|\frac{k_{1}}{\alpha_{1}^{2}}\bigl[1-e^{-2\alpha _{1}T}\bigr]. \end{aligned}$$

Then $I_{1}^{*}\rightarrow 0$ as $T\rightarrow \infty$.

$$\begin{aligned} I_{2}^{*} =&\frac{1}{2T} \int_{-T}^{T}\bigl|g(s)\bigr|ds \int_{s}^{T} k_{1}e^{- \alpha_{1}(t-s)}dt \\ \leq & \frac{1}{2T} \int_{-T}^{T}\frac{k_{1}}{\alpha_{1}}\bigl[1-e^{-\alpha _{1}(s-T)} \bigr]\bigl|g(s)\bigr|ds \\ \leq &\frac{1}{2T}\|g\|\frac{k_{1}}{\alpha_{1}} \int_{-T}^{T}\bigl|g(s)\bigr|ds. \end{aligned}$$

Note that $|g(.)|\in \mathit{PAP}(\mathbb{R},\mathbb{R}^{p})$, we can conclude that $I_{2}^{*}\rightarrow 0$ as $T\rightarrow \infty$. In a similar way, we can also prove that $I_{2}(t)\in \mathit{PAP}( \mathbb{R},\mathbb{R}^{p})$. The proof of Lemma 2.5 is complete. □

Lemma 2.6

(see [20, 45])

Let $b_{i}(t)$ be an almost periodic function on ℝ and

$$ M[b_{i}]=\lim_{T\rightarrow +\infty }\frac{1}{T} \int_{t}^{t+T}b_{i}(s)ds>0,\quad ij\in \varLambda . $$

(2.5)

Then the linear system

$$ \dot{x}(t)=\mathrm{diag}\bigl(-b_{1}(t),-b_{2}(t),\ldots ,-b_{n}(t)\bigr)x(t) $$

(2.6)

admits an exponential dichotomy on ℝ.

Lemma 2.7

(see [23])

Let $l$ be a real number and $u$ be a nonnegative function defined on $[l,+\infty )$ such that $u$ is integrable on $[l,+\infty )$ and is uniformly continuous on $[l,+\infty )$. Then $\lim_{t\rightarrow +\infty }u(t)=0$.

Throughout this paper, we make the following assumptions for system (1.3):

(H1) For $i=1,2,\ldots ,n$, $\alpha^{-}$, $\lambda_{i}^{-}$ are positive, $\alpha (t), \beta_{i}(t),\lambda_{i}(t), h(t)\in \mathit{PAP}(\mathbb{R},(0,+ \infty )), \tau (t)\in \mathit{AP}(\mathbb{R},\mathbb{R}_{+})$ and $\tau (t)$ are continuously differential functions which satisfies

$$\begin{aligned} 0\leq \tau (t)\leq \tau^{+},\qquad 0\leq \dot{\tau }(t)\leq\tau_{0}< 1. \end{aligned}$$

(H2) There exist two constants $\gamma_{1}>0$ and $\gamma_{2}>0$ such that

$$\begin{aligned} \gamma_{1}< \gamma_{2},\quad\sum_{i=1}^{n} \frac{\beta_{i}^{+}}{\lambda_{i} ^{-}}\frac{1}{\alpha^{-}e}+\frac{h^{+}}{\alpha^{-}}< \gamma_{2},\qquad \frac{1}{ \alpha^{+}}\sum_{i=1}^{n}{ \beta_{i}^{-}}\gamma_{2}e^{-\lambda_{i}^{+} \gamma_{2}} + \frac{h^{-}}{\alpha^{+}}>\gamma_{1}\geq \frac{1}{\lambda ^{-}}, \end{aligned}$$

where $\lambda^{-}=\min_{1\leq i\leq n}\{\lambda_{i}^{-}\}$.

(H3) The following condition holds.

$$\begin{aligned} \frac{1}{e^{2}\alpha^{-}}\sum_{i=1}^{n} \beta_{i}^{+}< 1. \end{aligned}$$

(H4) The following condition holds.

$$\begin{aligned} \alpha^{-}-\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau _{0}}< 1. \end{aligned}$$

(H5) The following condition holds.

$$\begin{aligned} \alpha^{-}-\frac{1}{e^{2}}\sum_{i=1}^{n}{ \beta_{i}^{+}}-\frac{1}{e ^{2}}\sum _{i=1}^{n}\beta_{i}^{+} \frac{1}{1-\tau_{0}}>0. \end{aligned}$$

Remark 2.1

We know that $\beta_{i}$ represents the per capita daily egg production rate, $\alpha$ stands for the per capita daily adult death rate, $\frac{1}{\lambda_{i}}$ denotes the size at which the blowfly population reproduces at its rate, $\tau$ is the generation rate. Thus all the conditions (H1)–(H5) have practical biological meanings. When these biological variables satisfy some suitable conditions, then the pseudo almost periodic solutions of the model will exist and all the other pseudo almost periodic solutions of the model will convergence exponentially to its unique pseudo almost periodic solution. In this sense, all the conditions (H1)–(H5) represent some problem of applied nature.

3 Existence of Pseudo Almost Periodic Solutions

In this section, we will establish sufficient conditions on the existence of pseudo almost periodic solutions of (1.3).

Lemma 3.1

Let $C_{0}=\{\varphi |\varphi \in C, \gamma_{1}< \varphi (t)<\gamma_{2}, t\in [-\tau^{+},0]\}$. Assume that (H1) and (H2) are satisfied. Then, for any $\varphi \in C$, the solution $x(t;t_{0}, \varphi )$ of system (1.3) satisfies

$$ \gamma_{1}< x(t;t_{0},\varphi )< \gamma_{2},\quad t\in[t_{0},\zeta (\varphi )) $$

(3.1)

and the existence interval of each solution of system (1.3) can be extended to $[t_{0}, +\infty )$.

Proof

Denote $x(t)=x(t;t_{0},\varphi )$. Let $[t_{0}, t^{*}) \subseteq [t_{0},\zeta (\varphi ))$ be an interval such that

$$\begin{aligned} x(t)>0,\quad \forall t\in [t_{0},t^{*}). \end{aligned}$$

First, we claim that

$$ 0< x(t)< \gamma_{2},\quad \forall t\in [t_{0},t^{*}). $$

(3.2)

In fact, if (3.1) does not hold, then there exists $t_{1}\in (t_{0},t ^{*})$ such that

$$ x(t_{1})=\gamma_{2},\quad\mbox{and}\quad 0< x(t)< \gamma_{2}\quad \forall t\in [t _{0}-\tau^{+},t_{1}). $$

(3.3)

In view of the fact $\sup_{y\geq 0}\frac{y}{e^{y}}=\frac{1}{e}$ and (3.1)–(3.3), we have

$$\begin{aligned} 0 \leq &\dot{x}(t_{1}) \\ =&-\alpha (t_{1})x(t_{1})+\sum _{i=1}^{n}\beta_{i}(t_{1})x \bigl(t_{1}- \tau (t_{1})\bigr)e^{-\lambda_{i}(t_{1})x(t_{1}-\tau (t_{1}))}+h(t_{1}) \\ =&-\alpha (t_{1})x(t_{1})+\sum _{i=1}^{n}\frac{\beta_{i}(t_{1})}{ \lambda_{i}(t_{1})}\lambda_{i}(t_{1})x \bigl(t_{1}-\tau (t_{1})\bigr)e^{-\lambda _{i}(t_{1})x(t_{1}-\tau (t_{1}))}+h(t_{1}) \\ \leq &-\alpha^{-}x(t_{1})+\sum _{i=1}^{n}\frac{\beta_{i}^{+}}{\lambda _{i}^{-}}\frac{1}{e}+h^{+} \\ =&\alpha^{-} \Biggl[ -\gamma_{2}+\sum _{i=1}^{n}\frac{\beta_{i}^{+}}{ \lambda_{i}^{-}}\frac{1}{\alpha^{-}e}+ \frac{h^{+}}{\alpha^{-}} \Biggr] < 0, \end{aligned}$$

which is a contradiction and implies that (3.2) holds.

Next we prove that

$$ x(t)>\gamma_{1},\quad \forall t\in [t_{0},\zeta (\varphi )). $$

(3.4)

If (3.4) does not hold, then there exists $t_{2}\in (t_{0}, \zeta ( \varphi ))$ such that

$$ x(t_{2})=\gamma_{1},\quad \mbox{and}\quad x(t)>\gamma_{1}\quad \forall t\in [t _{0}-\tau^{+},t_{2}). $$

(3.5)

In view of (3.2) and (H2), we have

$$ \gamma_{1}< x(t)< \gamma_{2}, \lambda_{i}^{+} x(t)\geq \lambda_{i}^{+}\frac{1}{ \lambda_{i}^{-}}\geq 1,\quad \forall t\in [t_{0}-\tau^{+},t_{2}). $$

(3.6)

By (1.3), (3.5), (3.6), (H2) and the fact $\min_{1\leq v\leq \mu }\frac{v}{e ^{v}}=\frac{\mu }{e^{\mu }}$, we have

$$\begin{aligned} 0 \geq &\dot{x}(t_{2}) \\ =&-\alpha (t_{2})x(t_{2})+\sum _{i=1}^{n}\beta_{i}(t_{2})x \bigl(t_{2}- \tau (t_{2})\bigr)e^{-\lambda_{i}(t_{2})x(t_{2}-\tau (t_{2}))}+h(t_{2}) \\ =&-\alpha (t_{2})x(t_{2})+\sum _{i=1}^{n}\frac{\beta_{i}(t_{2})}{ \lambda_{i}(t_{2})}\lambda_{i}(t_{2})x \bigl(t_{2}-\tau (t_{2})\bigr)e^{-\lambda _{i}(t_{2})x(t_{2}-\tau (t_{2}))}+h(t_{2}) \\ \geq &-\alpha^{+}x(t_{2})+\sum _{i=1}^{n}\frac{\beta_{i}^{-}}{\lambda _{i}^{+}}\lambda_{i}^{+}x \bigl(t-\tau (t_{2})\bigr)e^{-\lambda_{i}^{+}x(t_{2}- \tau (t_{2}))} +h^{-} \\ \geq &-\alpha^{+}x(t_{2})+\sum _{i=1}^{n}\frac{\beta_{i}^{-}}{\lambda _{i}^{+}}\lambda_{i}^{+} \gamma_{2}e^{-\lambda_{i}^{+}\gamma_{2}} +h ^{-} \\ \geq &\alpha^{+} \Biggl[ -\gamma_{1}+\frac{1}{\alpha^{+}} \sum_{i=1}^{n} {\beta_{i}^{-}} \gamma_{2}e^{-\lambda_{i}^{+}\gamma_{2}} +\frac{h^{-}}{ \alpha^{+}} \Biggr] >0, \end{aligned}$$

which is a contradiction and implies that (3.4) holds. In view of (3.2) and (3.4), we can conclude that (3.1) holds which implies that $x(t)$ is bounded. Thus it follows from the continuation theorem in Hale [46, Theorem 12.2.4] that the existence interval of each solution for system (1.3) can be extended to $[t_{0},+\infty )$. The proof of Lemma 3.1 is complete. □

We define a nonlinear operator $\varGamma$ as follows.

$$ (\varGamma \phi ) (t):=x^{\phi }(t)= \int_{-\infty }^{t}e^{-\int_{s}^{t} \alpha (\xi )d\xi }U(s)ds, $$

(3.7)

where $\phi \in \mathit{PAP}(\mathbb{R},\mathbb{R})$ and

$$\begin{aligned} U(s)=\sum_{i=1}^{n}\beta_{i}(s)x \bigl(s-\tau (s)\bigr)e^{-\lambda_{i}(s)x(s- \tau (s))}+h(s). \end{aligned}$$

Lemma 3.2

If (H1) holds, then $\varGamma$ maps $\mathit{PAP}( \mathbb{R}, \mathbb{R})$ into itself.

Proof

In view of Lemma 2.2, Lemma 2.3 and the composition theorem of pseudo almost periodic solution functions (see [47]), we know that $U(s)\in \mathit{PAP}(\mathbb{R},\mathbb{R})$. Thus $U(s)$ can be expressed as

$$\begin{aligned} U(s)=U_{1}(s)+U_{1}(s), \end{aligned}$$

where $U_{1}(s)\in \mathit{PAP}(\mathbb{R},\mathbb{R})$ and $U_{2}(s)\in \mathit{PAP} _{0}(\mathbb{R},\mathbb{R})$. Then we have

$$\begin{aligned} (\varGamma \phi ) (t) =& \int_{-\infty }^{t}e^{-\int_{s}^{t} \alpha ( \xi )d\xi }U_{1}(s)ds+ \int_{-\infty }^{t}e^{-\int_{s}^{t} \alpha ( \xi )d\xi }U_{2}(s)ds \\ =& (\varGamma U_{1}) (t)+(\varGamma U_{2}) (t). \end{aligned}$$

We first prove the almost periodicity of $(\varGamma U_{1})(t)$. It follows from the almost periodicity of $U_{1}$ that for any $\varepsilon >0$, there exists a number $l(\varepsilon )$ such that in any interval $[\varrho ,\varrho +l(\varepsilon ) ]$, one can find a number $\sigma$ which has the following property

$$\begin{aligned} \sup_{s\in \mathbb{R}}\bigl|U_{1}(s+\sigma )-U_{1}(s)\bigr|< \varepsilon . \end{aligned}$$

Hence

$$\begin{aligned} \bigl|(\varGamma U_{1}) (t+\sigma )-(\varGamma U_{1}) (t)\bigr| =& \biggl\vert \int_{-\infty } ^{t+\sigma }e^{-\int_{s}^{t+\sigma }\alpha (\xi )d\xi }U_{1}(s)ds - \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d\xi }U_{1}(s)ds \biggr\vert \\ \leq & \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d\xi } \bigl|U_{1}(s+\sigma )-U_{1}(s)\bigr|ds \\ \leq &\frac{\varepsilon }{\alpha^{-}}. \end{aligned}$$

Thus $(\varGamma U_{1})(t)\in \mathit{AP}(\mathbb{R},\mathbb{R})$.

We next prove $(\varGamma U_{2})(t)\in \mathit{PAP}(\mathbb{R},\mathbb{R})$. We only need to prove

$$\begin{aligned} \lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T}\biggl\vert \int_{- \infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d\xi }U_{2}(s)ds \biggr\vert dt=0. \end{aligned}$$

In fact,

$$\begin{aligned} &\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T}\biggl\vert \int_{- \infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d\xi }U_{2}(s)ds \biggr\vert dt \\ &\quad{}\leq \lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T}\biggl\vert \int _{-\infty }^{t}e^{-\alpha^{-}(t-s)}U_{2}(s)ds \biggr\vert dt \\ &\quad{}\leq L_{1}+L_{2}, \end{aligned}$$

where

$$\begin{aligned} L_{1}=\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int _{-T}^{t}\bigl\vert e^{-\alpha^{-}(t-s)}U_{2}(s) \bigr\vert ds \biggr] dt, \end{aligned}$$

$$\begin{aligned} L_{2}=\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int_{- \infty }^{-T}\bigl\vert e^{-\alpha^{-}(t-s)}U_{2}(s) \bigr\vert ds \biggr] dt. \end{aligned}$$

In the sequel, we will estimate $L_{1}$ and $L_{2}$. Let $t-s=\chi$. In view of Fubin’s theorem, we have

$$\begin{aligned} L_{1} =&\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int _{-T}^{t}\bigl\vert e^{-\alpha^{-}(t-s)}U_{2}(s) \bigr\vert ds \biggr] dt \\ =& \lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int _{-T}^{t}e^{-\alpha^{-}(t-s)}\bigl|U_{2}(s)\bigr|ds \biggr] dt \\ =&\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int _{0}^{t+T}e^{-\chi \alpha^{-}} \bigl|U_{2}(t-\chi )\bigr|d\chi \biggr] dt \\ \leq &\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int _{0}^{+\infty }e^{-\chi \alpha^{-}} \bigl|U_{2}(t-\chi )\bigr|d\chi \biggr] dt \\ =& \int_{0}^{+\infty }e^{-\chi \alpha^{-}} \biggl[ \frac{1}{2T} \int_{-T} ^{T}\bigl|U_{2}(t-\chi )\bigr|dt \biggr] d \chi \\ =& \int_{0}^{+\infty }e^{-\chi \alpha^{-}} \biggl[ \frac{1}{2T} \int_{-T-\chi }^{T-\chi }\bigl|U_{2}(\upsilon )\bigr|d\upsilon \biggr] d\chi \\ \leq & \int_{0}^{+\infty }e^{-\chi \alpha^{-}} \biggl[ \frac{T+\chi }{T}\frac{1}{2(T+ \chi )} \int_{-T-\chi }^{T+\chi }\bigl|U_{2}(\upsilon )\bigr|d\upsilon \biggr] d \chi . \end{aligned}$$

Denote

$$\begin{aligned} U^{*}(T,\chi )= \int_{-T-\chi }^{T+\chi }\bigl|U_{2}(\upsilon )\bigr|d\upsilon . \end{aligned}$$

Since $U_{2}\in \mathit{PAP}_{0}(\mathbb{R},\mathbb{R})$, then we can conclude that $U^{*}(T,\chi )$ is bounded and satisfies $\lim_{T\rightarrow +\infty }U^{*}(T,\chi )=0$. In view of the Lebesgue’s dominated convergence theorem, we get

$$\begin{aligned} L_{1}=\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int _{-T}^{t}\bigl\vert e^{-\alpha^{-}(t-s)}U_{2}(s) \bigr\vert ds \biggr] dt=0. \end{aligned}$$

Notice that $\|U_{2}\|=\sup_{t\in \mathbb{R}}|U_{2}(s)|<+\infty$, then

$$\begin{aligned} L_{1} =&\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int _{-\infty }^{-T}\bigl\vert e^{-\alpha^{-}(t-s)}U_{2}(s) \bigr\vert ds \biggr] dt \\ =&\lim_{T\rightarrow +\infty }\frac{1}{2T} \int_{-T}^{T} \biggl[ \int_{- \infty }^{-T}e^{-\alpha^{-}(t-s)}\bigl|U_{2}(s)\bigr|ds \biggr] dt \\ \leq &\lim_{T\rightarrow +\infty }\frac{1}{2T} \frac{1}{(\alpha^{-})^{2}} \bigl(1-e^{-2\alpha^{-}T}\bigr)\|U_{2}\|=0, \end{aligned}$$

which implies that $(\varGamma U_{2})(t)\in \mathit{PAP}_{0}(\mathbb{R}, \mathbb{R})$. Then $\varGamma (U)(t)\in \mathit{PAP}(\mathbb{R},\mathbb{R})$. Thus $\varGamma (\phi )(t)\in \mathit{PAP}(\mathbb{R},\mathbb{R})$. The proof of Lemma 3.2 is completed. □

Theorem 3.1

If (H1)–(H3) hold, then system (1.3) has an unique pseudo almost periodic solution in the region

$$\begin{aligned} \varOmega =\bigl\{ x \bigm| x\in \mathit{PAP}(\mathbb{R},\mathbb{R}), \gamma_{1}< x(t)< \gamma _{2},\ t\in \mathbb{R}\bigr\} . \end{aligned}$$

Proof

For any $\phi \in \mathit{PAP}(\mathbb{R},\mathbb{R})$, we consider the auxiliary equation which takes the form:

$$ \dot{x}(t)=-\alpha (t)x(t)+\sum_{i=1}^{n} \beta_{i}(t)\phi \bigl(t-\tau (t)\bigr)e ^{-\lambda_{i}(t)\phi (t-\tau (t))}+h(t). $$

(3.8)

Noticing that $M[\alpha ]>0$, we can conclude from Lemma 2.6 that the following linear equation

$$ \dot{x}(t)=-\alpha (t)x(t) $$

(3.9)

admits an exponential dichotomy on ℝ. In view of Lemma 2.5, we know that system (1.3) has exactly one solution expressed by

$$ {x}^{\phi }(t)= \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d \xi } \Biggl[ \sum _{i=1}^{n}\beta_{i}(s)\phi \bigl(s-\tau (s) \bigr)e^{-\lambda_{i}(s) \phi (s-\tau (s))}+h(s) \Biggr] ds. $$

(3.10)

By Lemma 3.2, it is easy to see that ${x}^{\phi }(t)\in \mathit{PAP}( \mathbb{R},\mathbb{R})$. Let

$$\begin{aligned} \varOmega =\bigl\{ x\bigm| x\in \mathit{PAP}(\mathbb{R},\mathbb{R}), \gamma_{1}< x(t)< \gamma _{2},\ t\in \mathbb{R}\bigr\} . \end{aligned}$$

Clearly, $\varOmega$ is closed subset of $\mathit{PAP}(\mathbb{R},\mathbb{R})$. We define an operator on $\varOmega$ as follows:

$$ (\varGamma \phi ) (t)= \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d \xi } \Biggl[ \sum _{i=1}^{n}\beta_{i}(s)\phi \bigl(s-\tau (s) \bigr)e^{-\lambda_{i}(s) \phi (s-\tau (s))}+h(s) \Biggr] ds. $$

(3.11)

Obviously, to prove that system (1.3) has an unique pseudo almost periodic solution, it suffices to show that $\varGamma$ has a fixed point in $\varOmega$.

We first prove that the operator $\varGamma$ is a self-mapping from $\varOmega$ to $\varOmega$. In fact, for any $\phi \in \varOmega$, according to (3.11) and the fact $\sup_{v\geq 0}\frac{v}{e^{v}}=\frac{1}{e}$, we get

$$\begin{aligned} (\varGamma \phi ) (t) =& \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d \xi } \Biggl[ \sum _{i=1}^{n}\beta_{i}(s)\phi \bigl(s-\tau (s) \bigr)e^{-\lambda_{i}(s) \phi (s-\tau (s))}+h(s) \Biggr] ds \\ =& \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d\xi } \Biggl[ \sum _{i=1}^{n}\frac{\beta_{i}(s)}{\lambda_{i}(s)}\lambda_{i}(s) \phi \bigl(s- \tau (s)\bigr)e^{-\lambda_{i}(s)\phi (s-\tau (s))}+h(s) \Biggr] ds \\ \leq & \int_{-\infty }^{t}e^{-\alpha^{-}(t-s)} \Biggl[ \frac{1}{e}\sum_{i=1}^{n} \frac{\beta_{i}(s)}{\lambda_{i}(s)}+h(s) \Biggr] ds \\ \leq &\sum_{i=1}^{n}\frac{\beta_{i}^{+}}{\lambda_{i}^{-}} \frac{1}{e \alpha^{-}}+\frac{h^{+}}{\alpha^{-}}< \gamma_{2},\quad \forall t\in \mathbb{R}. \end{aligned}$$

(3.12)

By (H2) we have

$$\begin{aligned} \lambda_{i}^{+} \phi (t)\geq \lambda_{i}^{+} \frac{1}{\lambda_{i}^{-}} \geq 1,\quad \forall t\in [t_{0}-\tau^{+},t_{2}). \end{aligned}$$

In view of the fact $\min_{1\leq v\leq \mu }\frac{v}{e^{v}}=\frac{ \mu }{e^{\mu }}$, we get

$$\begin{aligned} (\varGamma \phi ) (t) =& \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d \xi } \Biggl[ \sum _{i=1}^{n}\beta_{i}(s)\phi \bigl(s-\tau (s) \bigr)e^{-\lambda_{i}(s) \phi (s-\tau (s))}+h(s) \Biggr] ds \\ =& \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d\xi } \Biggl[ \sum _{i=1}^{n}\frac{\beta_{i}(s)}{\lambda_{i}(s)}\lambda_{i}(s) \phi \bigl(s- \tau (s)\bigr)e^{-\lambda_{i}(s)\phi (s-\tau (s))}+h(s) \Biggr] ds \\ \geq & \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d\xi } \Biggl[ \sum _{i=1}^{n}\frac{\beta_{i}(s)}{\lambda_{i}^{+}}\lambda_{i}^{+} \phi \bigl(s- \tau (s)\bigr)e^{-\lambda_{i}^{+}\phi (s-\tau (s))}+h^{-} \Biggr] ds \end{aligned}$$

$$\begin{aligned} \geq & \int_{-\infty }^{t}e^{-\int_{s}^{t}\alpha (\xi )d\xi } \Biggl[ \sum _{i=1}^{n}\frac{\beta_{i}(s)}{\lambda_{i}^{+}}\lambda_{i}^{+} \phi \bigl(s- \tau (s)\bigr)e^{-\lambda_{i}^{+}\phi (s-\tau (s))}+h^{-} \Biggr] ds \\ \geq & \frac{1}{\alpha^{+}}\sum_{i=1}^{n} \frac{\beta_{i}^{-}}{\lambda _{i}^{+}}\gamma_{2}e^{-\lambda_{i}^{+}\gamma_{2}} +\frac{h^{-}}{\alpha ^{+}}> \gamma_{1},\quad \forall t\in \mathbb{R}. \end{aligned}$$

(3.13)

It follows from (3.12) and (3.13) that the mapping $\varGamma$ is a self-mapping from $\varOmega$ to $\varOmega$.

We now prove that the mapping $\varOmega$ is a contraction mapping on $\varOmega$. In fact, for any $\phi ,\bar{\phi }\in \varOmega$, we have

$$\begin{aligned} \bigl\| \varGamma (\phi ) (t)-\varGamma (\bar{\phi }) (t)\bigr\| =& \sup_{t\in \mathbb{R}} \bigl|( \varGamma \phi ) (t)-(\varGamma \bar{\phi })(t)\bigr| \\ =&\sup_{t\in \mathbb{R}} \Biggl|\int_{-\infty}^{t}e^{-\int_{s}^{t} \alpha (\xi )d\xi } \Biggl[ \sum _{i=1}^{n}\beta_{i}(s) \bigl(\phi \bigl(s- \tau (s)\bigr)e^{-\lambda_{i}(s)\phi (s-\tau (s))} \\ &{}-\bar{\phi }\bigl(s-\tau (s)\bigr)e^{-\lambda_{i}(s)\bar{\phi }(s-\tau (s))} \bigr) \Biggr]ds \Biggr| \\ =&\sup_{t\in \mathbb{R}} \Biggl| \int_{-\infty }^{t}e^{-\int_{s}^{t} \alpha (\xi )d\xi } \Biggl[ \sum _{i=1}^{n}\frac{\beta_{i}(s)}{\lambda _{i}(s)} \bigl( \lambda_{i}(s)\phi \bigl(s-\tau (s)\bigr)e^{-\lambda_{i}(s)\phi (s- \tau (s))} \\ &{}-\lambda_{i}(s)\bar{\phi }\bigl(s-\tau (s)\bigr)e^{-\lambda_{i}(s)\bar{ \phi }(s-\tau (s))} \bigr) \Biggr]ds \Biggr|. \end{aligned}$$

(3.14)

Since $\sup_{v\geq 1}\vert \frac{1-v}{e^{v}}\vert =\frac{1}{e^{2}}$, then we have

$$ \biggl\vert \frac{u}{e^{u}}-\frac{v}{e^{v}}\biggr\vert =\biggl\vert \frac{1-(u+\chi ^{*}(v-u))}{e^{u+\chi^{*}(v-u)}}\biggr\vert |u-v| \leq \frac{1}{e^{2}}|u-v|, $$

(3.15)

where $u,v\in [1,+\infty ), 0<\chi^{*}<1$. In view of (H2), we get

$$ \lambda_{i}(s)\phi \bigl(t-\tau (t)\bigr)\geq \lambda_{i}(s) \gamma_{1}\geq \lambda_{i}(s)\frac{1}{\lambda_{i}^{-}}\geq 1,\quad \forall t\in \mathbb{R}. $$

(3.16)

According (3.14)–(3.16) and (H1), we have

$$\begin{aligned} \bigl\| \varGamma (\phi ) (t)-\varGamma (\bar{\phi }) (t)\bigr\| =&\sup _{t\in \mathbb{R}} \Biggl|\int_{-\infty}^{t}e^{-\int_{s}^{t}\alpha (\xi )d \xi } \Biggl[ \sum _{i=1}^{n}\beta_{i}(s)\frac{1}{e^{2}} \bigl|\phi \bigl(s-\tau (s)\bigr)-\bar{ \phi }\bigl(s-\tau (s)\bigr)\bigr| \Biggr] ds\Biggr| \\ \leq &\sup_{t\in \mathbb{R}} \Biggl|\int_{-\infty}^{t}e^{-\int_{s} ^{t}\alpha (\xi )d\xi } \Biggl[ \sum _{i=1}^{n}\beta_{i}(s) \frac{1}{e^{2}} \Biggr] ds\bigl\| \phi -\bar{\phi }\bigr\| \Biggr| \\ \leq & \frac{1}{e^{2}\alpha^{-}}\sum_{i=1}^{n} \beta_{i}^{+}\|\phi -\bar{ \phi }\|. \end{aligned}$$

(3.17)

By (H3), we know that $\varGamma$ is a contraction mapping. Thus, applying the Banach fixed point theorem, $\varGamma$ has an unique fixed point. The proof of Theorem 3.1 is complete. □

4 Convergence and Exponential Convergence of Pseudo Almost Periodic Solution

In this section, we will obtain the convergence and exponential convergence of pseudo almost periodic solution of system (1.3).

Theorem 4.1

If (H1)–(H4) are satisfied, then all the solutions of system (1.3) in the region $\varOmega$ converge to its unique pseudo almost periodic solution.

Proof

Let $u(t)$ be any solution of system (1.3) and $u^{*}(t)$ be a pseudo almost periodic solution of system (1.3). We define a Lyapunov function as follows:

$$ V_{1}(t)=\bigl|u(t)-u^{*}(t)\bigr|+\frac{1}{e^{2}}\sum _{i=1}^{n}\beta_{i}^{+} \frac{1}{1- \tau_{0}} \int_{t-\tau (t)}^{t}\bigl|u(s)-u^{*}(x)\bigr|ds $$

(4.1)

Calculating the upper right derivative of $V_{1}(t)$ along the solutions of system (1.3), we have

$$\begin{aligned} D^{+}V_{1}(t) =&\mathrm{sgn}\bigl\{ u(t)-u^{*}(t) \bigr\} \Biggl\{ -\alpha (t) \bigl(u(t)-u ^{*}(t)\bigr) \\ &{}+\sum_{i=1}^{n}\beta_{i}(t) \bigl[ u\bigl(t-\tau (t)\bigr)e^{-\lambda_{i}(t)u(t- \tau (t))}-u^{*}\bigl(t-\tau (t) \bigr)e^{-\lambda_{i}(t)u^{*}(t-\tau (t))} \bigr] \Biggr\} \\ &{}+\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}}\bigl|u(t)-u ^{*}(t)\bigr| \\ &{}-\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1- \dot{\tau }(t)}{1-\tau_{0}}\bigl|u\bigl(t-\tau (t) \bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ =&\mathrm{sgn}\bigl\{ u(t)-u^{*}(t)\bigr\} \Biggl\{ -\alpha (t) \bigl(u(t)-u^{*}(t)\bigr) \\ &{}+\sum_{i=1}^{n}\frac{\beta_{i}(t)}{\lambda_{i}(t)} \bigl[ \lambda _{i}(t)u\bigl(t-\tau (t)\bigr)e^{-\lambda_{i}(t)u(t-\tau (t))} \\ &{}-\lambda_{i}(t)u ^{*}\bigl(t-\tau (t)\bigr)e^{-\lambda_{i}(t)u^{*}(t-\tau (t))} \bigr] \Biggr\} \\ &{}+\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}}\bigl|u(t)-u ^{*}(t)\bigr| \\ &{}-\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1- \dot{\tau }(t)}{1-\tau_{0}}\bigl|u\bigl(t-\tau (t) \bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ \leq &-\alpha^{-}\bigl|u(t)-u^{*}(t)\bigr|+\frac{1}{e^{2}}\sum _{i=1}^{n}{\beta _{i}^{+}} \bigl|u\bigl(t-\tau (t)\bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ &{}+\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}} \bigl|u(t)-u ^{*}(t)\bigr| \\ &{}- \frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau _{0}} \bigl|u\bigl(t-\tau (t)\bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ \leq &-\alpha^{-}\bigl|u(t)-u^{*}(t)\bigr|+\frac{1}{e^{2}}\sum _{i=1}^{n}{\beta _{i}^{+}} \bigl|u\bigl(t-\tau (t)\bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ &{}+\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}} \bigl|u(t)-u ^{*}(t)\bigr|- \frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+} \bigl|u\bigl(t-\tau (t)\bigr)-u ^{*} \bigl(t-\tau (t)\bigr)\bigr| \\ =&- \Biggl( \alpha^{-}-\frac{1}{e^{2}}\sum _{i=1}^{n}\beta_{i}^{+} \frac{1}{1- \tau_{0}} \Biggr) \bigl|u(t)-u^{*}(t)\bigr|,\quad t>t_{0}. \end{aligned}$$

(4.2)

It follows from (H4) and (4.2) that there exists a constant $\nu_{1}>0$ such that

$$ D^{+}V_{1}(t)\leq -\nu_{1}\bigl|u(t)-u^{*}(t)\bigr|,\quad t>t_{0}. $$

(4.3)

Integrating on both sides of (4.3) from $t_{0}$ to $t$ leads to

$$ V_{1}(t)+\nu_{1} \int_{t_{0}}^{t}\bigl|u(t)-u^{*}(t)\bigr|ds< V_{1}(t_{0})< + \infty ,\quad t>t_{0}, $$

(4.4)

then

$$ \int_{t_{0}}^{t}\bigl|u(t)-u^{*}(t)\bigr|ds< +\infty ,\quad t>t_{0}, $$

(4.5)

which implies $|u(t)-u^{*}(t)|\in L^{1}(t_{0},+\infty )$. From Lemma 3.1, we know that $u(t)$, $u^{*}(t)$ and their derivatives are bounded on $[t_{0},+\infty )$. Thus $|u(t)-u^{*}(t)|$ is uniformly continuous on $[t_{0},+\infty )$. Applying Lemma 2.7, we have

$$ \lim_{t\rightarrow +\infty }\bigl|u(t)-u^{*}(t)\bigr|=0. $$

(4.6)

This completes the proof of Theorem 4.1. □

Theorem 4.2

If (H1)–(H5) are satisfied, then all the solutions of system (1.3) in the region $\varOmega$ exponentially converge to its unique pseudo almost periodic solution.

Proof

Similar to the proof of Theorem 4.1, we know that system (1.3) has an unique pseudo almost periodic solution. Define a continuous functions $\varTheta (\varrho )$ as follows:

$$ \varTheta (\varrho )=\alpha^{-}-\varrho -\frac{1}{e^{2}}\sum _{i=1}^{n} {\beta_{i}^{+}} -\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1- \tau_{0}}e^{\varrho \tau^{+}},\quad \varrho \geq 0. $$

(4.7)

Then

$$ \varTheta (0)=\alpha^{-}-\frac{1}{e^{2}}\sum _{i=1}^{n}{\beta_{i}^{+}} - \frac{1}{e ^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}}>0. $$

(4.8)

In view of the continuity of $\varTheta (\varrho )$, we can choose a sufficiently small positive constant $\varepsilon$ such that

$$ \varTheta (\varrho )=\alpha^{-}-\varrho -\frac{1}{e^{2}}\sum _{i=1}^{n} {\beta_{i}^{+}} -\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1- \tau_{0}}e^{\varrho \tau^{+}}>0 $$

(4.9)

Let $u(t)$ be any solution and $u^{*}(t)$ be a pseudo almost periodic solution of (1.3). Define a Lyapunov function as follows:

$$ V_{2}(t)=\bigl|u(t)-u^{*}(t)\bigr| e^{\varepsilon t}+ \frac{1}{e^{2}}\sum_{i=1} ^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}} \int_{t-\tau (t)}^{t}\bigl|u(s)-u^{*}(x)\bigr|e ^{\varepsilon (s+\tau^{+})} ds. $$

(4.10)

Calculating the upper right derivative of $V_{2}(t)$ along the solutions of system (1.3), we have

$$\begin{aligned} D^{+}V_{2}(t) =&\varepsilon e^{\varepsilon t}\bigl|u(t)-u^{*}(t)\bigr|+e^{ \varepsilon t} \mathrm{sgn}\bigl\{ u(t)-u^{*}(t)\bigr\} \Biggl\{ -\alpha (t) \bigl(u(t)-u ^{*}(t)\bigr) \\ &{}+\sum_{i=1}^{n}\beta_{i}(t) \bigl[ u\bigl(t-\tau (t)\bigr)e^{-\lambda_{i}(t)u(t- \tau (t))}-u^{*}\bigl(t-\tau (t) \bigr)e^{-\lambda_{i}(t)u^{*}(t-\tau (t))} \bigr] \Biggr\} \\ &{}+\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}}e ^{\varepsilon (t+\tau^{+})}\bigl|u(t)-u^{*}(t)\bigr|- \frac{1}{e^{2}}\sum_{i=1} ^{n} \beta_{i}^{+}\frac{1-\dot{\tau }(t)}{1-\tau_{0}}e^{\varepsilon (t- \tau (t)+\tau^{+})} \\ &{}\times \bigl|u\bigl(t-\tau (t)\bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ =&\varepsilon e^{\varepsilon t}\bigl|u(t)-u^{*}(t)\bigr|+e^{\varepsilon t} \mathrm{sgn}\bigl\{ u(t)-u^{*}(t)\bigr\} \Biggl\{ -\alpha (t) \bigl(u(t)-u^{*}(t)\bigr) \\ &{}+\sum_{i=1}^{n}\frac{\beta_{i}(t)}{\lambda_{i}(t)} \bigl[ \lambda _{i}(t) u\bigl(t-\tau (t)\bigr)e^{-\lambda_{i}(t)u(t-\tau (t))} \\ &{}- \lambda_{i}(t)u ^{*}\bigl(t-\tau (t)\bigr)e^{-\lambda_{i}(t)u^{*}(t-\tau (t))} \bigr] \Biggr\} \\ &{}+\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}}e ^{\varepsilon (t+\tau^{+})}\bigl|u(t)-u^{*}(t)\bigr| \\ &{}- \frac{1}{e^{2}}\sum_{i=1} ^{n} \beta_{i}^{+}\frac{1-\dot{\tau }(t)}{1-\tau_{0}}e^{\varepsilon (t- \tau (t)+\tau^{+})} \bigl|u\bigl(t-\tau (t)\bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ \leq &\varepsilon e^{\varepsilon t}\bigl|u(t)-u^{*}(t)\bigr| - \alpha^{-}e^{ \varepsilon t}\bigl|u(t)-u^{*}(t)\bigr| \\ &{}+\frac{1}{e^{2}}\sum_{i=1}^{n}{ \beta_{i}^{+}}e^{\varepsilon t}\bigl|u\bigl(t- \tau (t) \bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ &{}+\frac{1}{e^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}}e ^{\varepsilon (t+\tau^{+})}\bigl|u(t)-u^{*}(t)\bigr| \\ &{}-\frac{1}{e^{2}}\sum_{i=1} ^{n} \beta_{i}^{+}e^{\varepsilon t}\bigl|u\bigl(t-\tau (t) \bigr)-u^{*}\bigl(t-\tau (t)\bigr)\bigr| \\ =&-e^{\varepsilon t} \Biggl( \alpha^{-}-\varepsilon - \frac{1}{e^{2}} \sum_{i=1}^{n}{ \beta_{i}^{+}}-\frac{1}{e^{2}}\sum _{i=1}^{n}\beta_{i} ^{+} \frac{1}{1-\tau_{0}}e^{\varepsilon \tau^{+}} \Biggr) \bigl|u(t)-u^{*}(t)\bigr| \\ < &0,\quad t>t_{0}. \end{aligned}$$

(4.11)

By (4.10) and (4.11), we have

$$ \bigl|u(t)-u^{*}(t)\bigr|\leq V_{2}(t_{0})e^{-\varepsilon t}. $$

(4.12)

Thus we can conclude that all the pseudo almost periodic solutions of (1.3) convergence exponentially to its unique pseudo almost periodic solution. The proof of Theorem 4.2 is completed. □

5 An Example and Computer Simulations

In this section, we will give an example to illustrate the feasibility and effectiveness of our main results obtained in previous sections. Considering the following Nicholson’s blowflies model with a harvesting term

$$ \dot{x}(t)=-\alpha (t)x(t)+\sum_{i=1}^{2} \beta_{i}(t)x\bigl(t-\tau (t)\bigr)e ^{-\lambda_{i}(t)x(t-\tau (t))}+h(t), $$

(5.1)

where

$$\begin{aligned} &\alpha (t)=\frac{6}{e^{2}}+\bigl|\sin \sqrt{3}t\bigr|,\qquad \beta_{1}(t)=0.1+0.2\cos^{2}t+0.2\bigl|\sin \sqrt{5}t\bigr|,\\ &\tau (t)=0.5+0.5|\sin t|, \\ &\beta_{2}(t)=0.1+0.2\sin^{2}t+0.2|\cos \sqrt{3}t|,\qquad \lambda_{1}(t)=6+ \cos^{2}t+\sin^{2}\sqrt{3}t, \\ & \lambda_{2}(t)=6+\sin^{2}t+\cos^{2} \sqrt{5}t,\qquad h(t)= \frac{e^{2}}{14} \biggl( 0.5\sin^{2}t+0.5 \cos^{2}\sqrt{5}t+\frac{1}{1+t ^{2}} \biggr) . \end{aligned}$$

Then

$$\begin{aligned} &\alpha^{+}=\frac{6}{e^{2}}+1,\qquad \alpha^{-}=\frac{6}{e^{2}},\qquad \beta_{1} ^{+}=\beta_{2}^{+}=0.5,\qquad \beta_{1}^{-}=\beta_{2}^{-}=0.1, \\ & \lambda_{1}^{+}=\lambda_{2}^{+}=8,\qquad \lambda_{1}^{-}=\lambda_{2}^{-}=\lambda^{-}=6,\qquad h^{+}=\frac{2e^{2}}{14},\qquad h^{-}=\frac{e^{2}}{14},\qquad \tau ^{+}=1. \end{aligned}$$

Choose $\tau_{0}=0.9,\gamma_{1}=0.7, \gamma_{2}=3.1$. Hence,

• (H1)
  $$0\leq \tau (t)\leq 1=\tau^{+},\qquad 0\leq \dot{\tau }(t) \leq 0.9=\tau_{0}< 1, $$
• (H2)
  $$\begin{aligned} &\gamma_{1}< \gamma_{2},\quad \sum_{i=1}^{2}\frac{\beta_{i}^{+}}{ \lambda_{i}^{-}}\frac{1}{\alpha^{-}e}+ \frac{h^{+}}{\alpha^{-}}= \frac{0.1}{6}\times \frac{e}{6}\times 2+ \frac{e^{2}}{6}\times \frac{2e ^{2}}{6}\approx 3.0483< 3.1= \gamma_{2},\\ &\phantom{\gamma_{1}< \gamma_{2},\quad}\frac{1}{\alpha^{+}}\sum_{i=1}^{2}{ \beta_{i}^{-}}\gamma_{2}e^{-\lambda _{i}^{+}\gamma_{2}} + \frac{h^{-}}{\alpha^{+}}=\frac{1}{ \frac{6}{e^{2}}+1} \bigl( {0.5}\times 3.1\times e^{-8\times 3.1} \bigr) \times 2+\frac{\frac{e^{2}}{6}}{\frac{6}{e^{2}}+1}\\ &\phantom{\gamma_{1}< \gamma_{2},\quad\frac{1}{\alpha^{+}}\sum_{i=1}^{2}{ \beta_{i}^{-}}\gamma_{2}e^{-\lambda _{i}^{+}\gamma_{2}} + \frac{h^{-}}{\alpha^{+}}}\approx 0.6796>0.7=\gamma_{1}\geq \frac{1}{6}= \frac{1}{\lambda^{-}}, \end{aligned}$$
• (H3)
  $$\frac{1}{e^{2}\alpha^{-}}\sum_{i=1}^{2} \beta_{i}^{+}=\frac{1}{e ^{2}\times \frac{6}{e^{2}}}(0.5+0.5)= \frac{1}{6}< 1, $$
• (H4)
  $$\alpha^{-}-\frac{1}{e^{2}}\sum _{i=1}^{n}\beta_{i}^{+} \frac{1}{1- \tau_{0}}=\frac{6}{e^{2}}-\frac{1}{e^{2}}\times 10=- \frac{4}{e^{2}}< 1, $$
• (H5)
  $$\alpha^{-}-\frac{1}{e^{2}}\sum _{i=1}^{n}{\beta_{i}^{+}}- \frac{1}{e ^{2}}\sum_{i=1}^{n} \beta_{i}^{+}\frac{1}{1-\tau_{0}}=\frac{6}{e^{2}}- \frac{1}{e ^{2}}-\frac{1}{e^{2}}=\frac{4}{e^{2}}>0. $$

Then all the conditions in Theorem 3.1, Theorem 4.1 and Theorem 4.2 are fulfilled, then system (5.1) has an unique positive pseudo almost periodic solution

$$\begin{aligned} u^{*}(t)\in \varOmega =\bigl\{ u\bigm|u\in \mathit{PAP}(\mathbb{R},\mathbb{R}),\ 0.7< u(t)< 3.1,\ \forall t\in \mathbb{R}\bigr\} . \end{aligned}$$

Moreover, if

$$\begin{aligned} \varphi \in C_{0}=\bigl\{ \varphi \bigm|\varphi \in C,\ 0.7< \varphi (t)< 3.1, \ \forall t\in [-1,0]\bigr\} , \end{aligned}$$

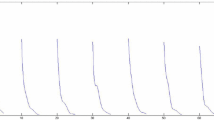
then $u^{*}(t;t_{0},\varphi )$ locally converges (exponentially) to $u^{*}(t)$ as $t\rightarrow +\infty$. The results are illustrated in Fig. 1.

Fig. 1

The Numerical solution of system (5.1)

6 Conclusions

In this paper, an Nicholson’s blowflies model with time-varying delays and a harvesting term is investigated. Applying the fixed point theorem, the properties of pseudo almost periodic function, inequality analysis technique and constructing appropriate Lyapunov functionals, we have established some new sufficient conditions to ensure the existence and convergence and exponential convergence of pseudo almost periodic solution for the Nicholson’s blowflies model. All the conditions are expressed in simple algebraic methods which are very easily checked in practice. We support the theoretical findings by an example with its computer simulations. Here we would like to point out that there are a lot of work which deal with the dynamics of equilibrium point, periodic solution and almost periodic solution of Nicholson’s blowflies model in recent years. But there are few results on the pseudo almost periodic behavior of model (1.3), which implies that the obtained results in this present paper are essentially new and complement and extend the previously known studies to some extent.