Introduction

Cardiovascular disorders are the primary cause of mortality globally. The expected number of fatalities is 17.7 billion, accounting for 31% of world mortality [1]. Recently, many researchers have been interested in studying and simulating blood flow in healthy and pathological blood vessels. The difficulty of the problem is related firstly to the complexity of human blood, which is a complex fluid constituted mostly of blood cells and plasma [2]. Red blood cells, also known as erythrocytes, white blood cells, and platelets, make up the majority of the blood cells [2]. Plasma operates similarly to a Newtonian fluid; however, entire blood behaves differently. In addition, the structure of blood vessels is complex [3]. Blood vessels are classified into three types: arteries, veins, and capillaries. The blood is transported from the heart by arteries at higher physiologic pressures. At lower physiologic pressures, veins return blood to the heart, and capillaries, relate between arteries and veins. Three layers make up the vessel wall: the adventitia, media, and intima. The intimal layer is the innermost layer of all blood vessels, composed of two structures: the endothelium and a subendothelial layer, and does not contribute to the overall mechanical behavior of the vessel wall because of its relatively small thickness and low stiffness. The thickest layer of the vessel wall is called the media, it is made of elastic lamina and smooth muscle cells, it has great strength and elasticity, and it is responsible of the most of the vessel mechanical properties. The adventitia is the outer layer of the wall, composed of a loose connective tissue of elastin and collagen fibers [3]. The proportions and composition of the different layers vary in different types of blood vessels. The media is less elastic, the collagen adventitia is thicker, and the vein wall is thinner. Endothelial cells, which are highly permeable, make up the sole layer of the capillary walls, which are incredibly thin [4]. The movement of blood in the body is affected by several factors, including the size of blood vessels and how they change during constriction and dilation, as well as the presence of bifurcations and junctions. Blood flow also depends on the difference in pressure between the arterial and venous ends of the vessels and on the viscosity of the blood [5]. In the case of larger blood vessels, blood typically flows in a smooth and orderly manner called laminar flow. However, blood artery diseases such as stenosis, atherosclerosis, and aneurysm can induce turbulence and lower flow, disrupting blood flow and leading to organ failure [5]. In order to identify diseases related to blood vessels, it is crucial to possess extensive knowledge about the circulation of blood. Blood flow must be thoroughly understood to diagnose vascular disorders. Magnetohydrodynamics (MHD) plays a crucial role in understanding the behavior of conducting fluids in the presence of a magnetic field. MHD blood flow refers to the study of blood flow in the presence of magnetic fields. When a conductive fluid, such as blood, flows in the presence of a magnetic field, it experiences electromagnetic forces that can significantly influence its behavior. This field of study is particularly relevant in the context of pathological vessels, where the understanding of blood flow dynamics is crucial for diagnosing and treating various cardiovascular diseases. It can provide insights into conditions like atherosclerosis, aneurysms, thrombosis, embolism, and stenosis. By simulating blood flow and considering the influence of magnetic fields, MHD modeling helps understand disease progression, assess treatment strategies, predict complications, and optimize drug delivery.

In order to solve real engineering problems, different numerical methods have been developed for the treatment of partial differential equations. The finite-element method (FEM) is based on a rigorous mathematical basis [6]. A variational (or weak) formulation of the system of partial differential equations is established first and then the weak formulation is transformed to an algebraic system of equations using a double discretization of both space and the unknown fields. The solutions precision and validity depend on the mesh applied [6]. In retrospect, the historical origins of the FEM reveal that its functionality was initially acknowledged by Richard Courant during the early 1940s. FEM was applied in the first time in 1956 by Turner et al. [7], in order to solve problems related to structural mechanics. In the end of 1960, FEM became a powerful method allowing to solve problems of heat transfer and fluid mechanics [8,9,10]. In the same period, the finite difference method (FDM) was proposed to solve fluid mechanics problems [11]. The present methodology encompasses solving differential equations through the implementation of finite differences as a means of approximating derivatives. During the process of solving mathematical problems, discretization is often utilized to approximate solutions in both the spatial domain and time interval. This approach involves the utilization of algebraic equations containing finite differences, as well as values obtained from neighboring points, to obtain an approximation of the solution at discrete points. The Finite Volume Method (FVM) was originated in 1980, specifically to solve fluid dynamics problems [12, 13]. Later, the method was developed by Spalding and Patankar [14] to treat transport phenomenon. The fundamental concept of FVM is predicated upon the integration of equations, expressed in the form of conservation laws, over basic volumes of uncomplicated geometry. As a consequence, FVM inherently affords discrete conservative approximations. Consequently, it is highly pertinent for the mathematical equations utilized in the field of fluid mechanics. The three methods are all based on the concept of weighted residual methods. The difference between them lies only in the type of weighting functions used. In pathological vessels, such as those affected by atherosclerosis or aneurysms, the blood flow characteristics deviate from those in healthy vessels. The presence of stenosis (narrowing of the vessel lumen), irregular geometries, and altered mechanical properties of vessel walls can lead to disturbed blood flow patterns, turbulence, and the formation of pathological phenomena, like thrombosis or embolism. To accurately model and predict these complex flow behaviors, a mesoscopic modeling approach is often required. The mesoscopic modeling approach aims to bridge the gap between the macroscopic (whole organ) and microscopic (individual cell) scales by considering the intermediate-scale phenomena that occur within blood vessels. This approach takes into account the interactions between individual blood cells, the vessel wall, and the magnetic field, which can have a significant impact on the overall flow behavior. The need for a mesoscopic modeling approach arises due to the limitations of both macroscopic and microscopic models in capturing the intricacies of blood flow in pathological vessels. Macroscopic models, such as computational fluid dynamics (CFD) simulations, offer a global view of blood flow but may oversimplify the behavior of individual cells and fail to capture local phenomena. On the other hand, microscopic models, such as particle-based simulations, provide detailed information about cell-level interactions but struggle to simulate large-scale flows within entire vessels. The LBM as a mesoscopic approach simulates interactions between molecules in order to ascertain significant physical quantities including velocity, pressure, and temperature at a large scale [15]. The LBM evolved from the lattice gas automata (LGA) [15,16,17,18] and has gained prominence in recent years as a numerical approach for addressing an extensive diversity of hydrodynamic problems. To simplify the Lattice Boltzmann Equation, Higuera and Jimenez [19] proposed the utilization of a linearized form to approximate the collision operator, which considers an assumption that the distribution of the system is in proximity to a state of equilibrium. Koelman [20] and Chen et al. [21] independently introduced a simple linearized collision operator that relies on the Bhatnagar–Gross–Krook collision model. A Chapman–Enskog analysis [22] recovers the Navier–Stokes equations using the Bhatnagar–Gross–Krook (BGK) model. The LBM is a way of describing fluids on a large scale and can also provide reliable numerical calculations for macroscopic behavior [15]. The popularity of LBM is owing to the BGK collision operator, which is known for its straightforward implementation and simplicity. It has contributed significantly to the achievement of this method. In recent years, the LBM has become increasingly popular [23,24,25,26,27,28,29,30,31] and has been utilized for modeling a variety of systems, involving immiscible liquids [32], multi-phase flows [33], heat transfer [34,35,36,37,38,39,40,41], heat and mass transfer [42,43,44], isotropic turbulence [45], magnetohydrodynamics [46], and porous media [47, 48].

The LBM confers a conspicuous advantage over other numerical methods on account of its capability to transform intricate partial differential system into a less complex first-order system [15]. In contradistinction to macroscopic numerical techniques, the LBM does not require the solving of a comprehensive system of equations; it solely relies on information obtained from neighboring nodes to progress the variables. The LBM presents itself as a viable and economical strategy for inter-processor communication due to its explicit computation involving locality, making it an excellent choice for parallel computation [49,50,51,52,53]. In addition, for incompressible unsteady flows, Laplace equation does not need to be solved at each time step to satisfy the continuity, contrary to the case in solving the Navier–Stokes (NS) equation. Moreover, the iterations on the time steps are relatively inexpensive because they involve simple arithmetic calculations.

The process of mathematically modeling and conducting numerical simulations concerning blood magnetohydrodynamic problems is of considerable relevance to medical science. In this review paper, researches related to the study of hemodynamics and blood magnetohydrodynamics in pathological vessels are presented and an alternative numerical model based on LBM is introduced. This paper classifies the applications of magnetohydrodynamics in biological system into two categories: simple and pulsatile flow. Furthermore, the literature review has furnished valuable insights that allow for the formulation of conclusive recommendations and avenues for further research.

A Review of the Literature on Blood Flow Modeling and Methods

Despite the advancements made in experimental studies and blood flow measurement methods conducted by applying either in vitro [54,55,56,57,58,59,60], in vivo [61,62,63,64,65], or ex vivo [66,67,68] approaches, there are still some obstacles to overcome [69,70,71,72,73,74]. Measurement of in vitro wall shear stress (WSS) poses a significant challenge due to its intricate nature. Additionally, measurements of velocity also encounter substantial errors. In vivo, the precise quantification of quantities of interest, such as shear stress, poses a significant challenge, thereby necessitating the adoption of numerical simulation as a valuable investigatory mechanism. However, owing to the complex nature of blood flow, many simplifications of the flow boundary conditions, geometry, and blood flow nature are made by researchers, leading in some cases to unrealistic, weak, and uncertain results [75].

Rheological Behavior of Blood

Researchers have developed many rheological models to present the rheological behavior of blood (see Table 1). A common simplification in literature is to consider blood as Newtonian fluid. The validity of this assumption is constrained to cases where the shear rate is in excess of 100\(s^{-1}\) [76, 77]. The non-Newtonian character of fluids is notably pronounced in situations where the rate of shear is relatively low. This is particularly relevant within the context of small diameter blood vessels, like in arterioles and capillaries [78]. Regarding the rheological properties of blood, it is deemed acceptable to regard blood as a Newtonian fluid within the context of large arterial vessels, namely the aorta [76, 79, 80]. Various authors have pointed out the necessity of considering the non-Newtonian behavior of blood [81,82,83], while others consider it as unnecessary approximation [84, 85]. Chaichana et al. [86] compared velocity fields and WSS given by Newtonian and non-Newtonian power law generalized model and obtained similar results. In the other hand, Cebral et al. [87] explored the effect of the viscous stress model on blood flow properties using Newtonian and non-Newtonian Casson model while simulating blood flow in four cerebral aneurysms. The findings show that the blood flow properties are only impacted by the viscous stress in low flow rate case. Kumar et al. [88] employed Newtonian and non-Newtonian Casson model to investigate the velocity distribution, wall pressure, and WSS in an aortal vessel. The WSS values obtained are widely impacted by the meshing, a difference of 15.84% in the maximum WSS value is noticed which occurs when using medium mesh instead of coarse mesh. According to their findings, the non-Newtonian flow has a larger WSS value than the Newtonian flow [89,90,91] and show similarity in results for the other parameters for Newtonian and non-Newtonian model. The authors concluded that a Newtonian model can lead to unrealistic results. Gaudio et al. [92] carried out a similar investigation, comparing between the Newtonian rheological model of blood and the non-Newtonian Carreau–Yasuda model. The findings revealed that the velocity for the Newtonian model is higher than for the Carreau–Yasuda model and shear stress is smaller for the Newtonian model. Carvalho et al. [93] obtained similar results using the Carreau non-Newtonian model.

Table 1 Blood rheological models
Full size table

Blood Vessels Assumptions

Blood vessels are not rigid and static. In reality, the blood flow is affected by the movement of the vessel wall and its surrounding tissue and vice versa, in healthy and diseased blood vessels. In addition, wave propagation phenomena cannot be modeled without taking into consideration the deformability of the vessel wall. Due to the complexity of treating and modeling the interaction between blood flow and vessel wall deformation, the majority of researchers have assumed the wall to be rigid. Berin Seta et al. [98] have studied blood flow through the aortic arch by considering a simplified model. The aorta walls are considered rigid and smooth. For more accurate results, the aorta wall deformability has to be integrated to the model as well as the interaction of blood and the wall. Recently, Lijian Xu et al. [99] have studied blood flow in aorta with a specific aortopathy, namely aortic dilatation using laminar and LES modeling methods. The two approaches give approximately the same results. Despite the high performance of LES method in simulating blood flow in an artery with potential turbulence, it suffers from limited spatio-temporal resolution [100,101,102]. In the other hand, direct numerical simulation is expensive in terms of computational cost [103, 104]. In their investigation, the aorta wall is considered to be rigid; this technique reduces computing effort and simplifies the analysis. However, this statement overlooks the interplay between the fluid and adjacent tissue, resulting in the exclusion of the impact of wall deformation on the circulation of blood. This simplification can have severe influence on the simulation results due to the fact that the aerotic walls actively deform during a cardiac cycle in reaction to blood pressure pulsations [105, 106]. Many studies have pointed out that neglecting the deformation of aortic wall causes an excess in WSS [107, 108]. An investigation into the level of accuracy regarding estimations is required. The rigid wall assumption in blood flow simulations, done in many researches, have lead researchers to investigate the impact of this assumption on the results.

Fluid–Structure Interaction (FSI)

Lopes et al. [111] conducted a fluid–structure interaction investigation of carotid blood flow using COMSOL Multiphysics software with the comparison of the Newtonian and Carreau viscosity models. The results reveal that velocity at the geometry center are similar for the Newtonian and non-Newtonian models; however, blood viscosity affects WSS, which is significantly greater for the Carreau model. Additionally, it is demonstrated that blood viscosity has no effect on the arterial wall displacement, which is dependent on fluid pressure. Saeedi et al. [112] conducted a simulation of 3-dimensional blood flow within an aneurysm located in the Circle of Willis, a crucial region of the middle cerebral artery (MCA) utilizing fluid–structure interaction (FSI). This study aims to assess how a partially blocked artery affects an aneurysm. The Mooney–Rivlin model and the Carreau model have been utilized to take into account the hyperelastic feature of the wall and the blood non-Newtonian properties. The outcomes of the study reveal that in the case of partly blocked vessel, the maximum WSS is 12% greater resulting in an increase in the aneurysm growth and rupture risks. Zhao et al. [113] showed that the simulated flow behavior obtained using fluid–structure interaction models is universally equivalent to that attained by invoking the supposition of a rigid wall. Nevertheless, a comprehensive analysis of the wall dynamics elicits a discernible decline in the amplitude of the WSS. Another comparison between the FSI and rigid wall models is done by Torii et al. [114], which exhibits irrelevant difference in time-averaged WSS (TAWSS) and oscillatory shear index OSI. In contrast, variations in instantaneous WSS profiles were remarkable, especially in the distal region of the artery. Blessy Thomas and Sumam [115] concluded, based on their literature review, that considering the vessel wall and the blood flow interaction give more realistic results. However, consideration of three-dimensional FSI problem increases the computational work.

For more details, Tables 1, 2, and 3 summarize the several geometries, boundary conditions, and flow characteristics used by various researchers in recent years. Regardless of the geometry, it can be observed that the majority of researchers perceive blood as a non-Newtonian fluid and used Carreau–Yasuda model to approximate its behavior. In addition, for boundary conditions, rigid wall assumption was applied by almost all the authors. The CFD solvers employed are based principally on FVM and FEM (Table 4).

Table 2 Computational models of blood flow and the related assumptions
Full size table
Table 3 Computational models of blood flow and the related assumptions
Full size table
Table 4 Computational models of blood flow and the related assumptions
Full size table

A Review on Blood Flow Modeling Using LBM

LBM is a numerical mesoscopic approach employed in simulating complex flows. It presents a powerful alternative of traditional computational fluid dynamic CFD methods. The LBM method is efficient in treating complex problems, including multi-phase flows [135] and non-Newtonian flows [136]. In addition, the process of programming is inherently less complex and amenable to computational parallelization [137]. The blood flow simulations applying Lattice Boltzmann approach, found in literature, treat mainly aneurysm. Fang et al. [138] developed a lattice Boltzmann model for modeling viscous flow in large distensible blood veins by incorporating a boundary condition for elastic and moving boundaries, with blood considered to be Newtonian fluid. The findings presented evince consonance with both experimental and analytical outcomes. Tamagawa et al. [139] predicted thrombus formation, by considering shear rates and adhesion force to wall, using LBM. The results show that the accuracy of LBM is as almost the same as experiment and FDM in predicting the flow field in the orifice pipe. Artoli et al. [140] employed the LBM to model a steady blood flow in a two-dimensional (2D) symmetric bifurcation. The flow fields and stress tensor components acquired were juxtaposed with those produced by a Navier–Stokes (NS) solver. Boyd et al. [141] implemented a two-dimensional model to simulate stenosis development in the human carotid artery. The walls are considered as rigid and blood is assumed to be Newtonian. The present study examines the variability of wall shear under conditions of stenosis progression. Persistent zones of low velocity and near-wall shear have been identified, specifically located in close proximity to the wall upstream from the growth of the stenosis. A second-order accurate lattice Boltzmann non-Newtonian flow model was developed by Boyd et al. [142]. The findings of the study indicate that the application of the LBM is well suited for modeling non-Newtonian flows. The authors [142] have conducted an investigation on both steady and unsteady flows utilizing the LBM in conjunction with the Casson and Carreau–Yasuda models. The findings of the study highlight discernible distinctions between the outcomes of these respective models. A comparative study to analyze the distinctive features of the Newtonian and non-Newtonian Carreau–Yasuda models was conducted by Boyd and Buick [143] to simulate blood flow in 2D carotid artery geometry. The results show that the non-Newtonian behavior of blood can be neglected under certain conditions. Bernsdorf and Wang [144] simulated cerebral aneurysms using Newtonian and non-Newtonian Carreau–Yasuda models. The results indicate that the non-Newtonian model displays a lower WSS and lower viscosity near the walls relative to the Newtonian flow. Hence, when non-Newtonian impacts are ignored within the simulation, an overestimation of the WSS values happens. Ashrafizaadeh and Bakhshaei [145] simulated non-Newtonian blood flows using K–L model, Casson, and Carreau–Yasuda. The predicted velocity profiles show great agreement with those of exact solutions. However, different results are acquired from the three models showing the importance of selecting the adequate model for more realistic blood flow simulations. Chopard et al. [146] conducted research on the cerebrovascular blood flow dynamics in cases of cerebral aneurysms. The utilization of Palabos, an open source software predicated on LBM, is deployed to simulate shear stress and velocity in the aneurysm. Recently, Cherkaoui et al. [147, 148] conducted a numerical study using LBM based on BGK approximation to investigate the impact of magnetic field intensity on laminar blood flow in a stenotic artery. The study outcomes show that the increase in magnetic field strength decreases the flow velocity and reduces the recirculation zones and the WSS in the constricted region.

A Review of the Literature on Modeling MHD Blood Flow

Blood is regarded as a vital biofluid, possessing intrinsic biomagnetic properties [149,150,151,152,153]. Since there are numerous diseases, including cancer, there is a need to improve therapeutic modalities that are both cost-effective and minimally intrusive. The widespread use of Magnetic Resonance Imaging (MRI) as a standard medical procedure has increased exposure to high magnetic fields, raising concerns in the research community and providing an incentive to study the impact of magnetic fields on human physiology and their effects on patient health. In this regard, scientists have been interested in researching the effect of magnetic fields on blood flow. The magnetohydrodynamics principles control how a conducting fluid, like blood, moves under the influence of an external magnetic field. When the body is subjected to a magnetic field, the Lorentz force deflects charged blood particles running transverse to the field, resulting in electrical currents and voltages across vessel walls and in surrounding tissues. Furthermore, a reduction in the rate of flow can arise as a consequence of the interplay between the currents produced and the magnetic field [154]. Several researchers have demonstrated the interaction of magnetic fields with blood flow through in vitro and in vivo assessments, wherein the measurement of pressure and flow rate was recorded. Higashi et al. [155] studied experimentally the impact of magnetic field up to 8T on red blood cells. The findings demonstrate that the orientation of red blood cells are strongly impacted by the application of magnetic field. Research has proven that red blood cells line up completely at 4T. The change in red blood cells orientation affect the macroscopic properties of blood. It was revealed experimentally by Haik et al. [156] that the magnetic field affect the apparent viscosity of blood, which increase considerably resulting in a decline in blood flow rate.

However, theoretical calculations for the blood flow caused by magnetohydrodynamics have been made far earlier, dating back to the early 1960s. Under the presumption that blood is Newtonian, Korchevskii, and Marochnik [157] initially provided a solution for the velocity profile of blood flow between two parallel plates subjected to a uniform pressure gradient and influenced by a magnetic field normal to the plane of the plates. In order to enhance the precision of arterial blood flow modeling, select studies have directed their focus toward flow within a non-deformable circular conduit, characteristically possessing non-conducting walls, that is subjected to a transverse magnetic field. In this instance, R. Gold [158] presented the most comprehensive solution to the magnetohydrodynamic equations of a conducting fluid. Gold [158] derived formulas for the velocity profile and the induced magnetic field through the utilization of a uniform pressure gradient. Sud et al. [159] used a sinusoidal pressure gradient to characterize the pulsed pattern of blood flow in arteries later on, while Abdallah et al. [160] recently offered a more realistic arterial flow solution based on a physiological pressure gradient model under the assumption of rigid vessel walls and Newtonian fluid. Recently, Shit and Roy [161] examined analytically the influence of a magnetic field on blood flow through a restricted tube, using a nonlinear micropolar fluid model. The investigation demonstrates that as the strength of the magnetic field amplifies, the flow toward the channel wall accelerates, while the axial velocity at the channel center line decreases. The complexity of analytical resolution of magnetohydrodynamics problem has introduced several numerical investigations.

Simple Blood Flow

Loukopoulos and Tzirtzilakis [162] conducted a numerical investigation on the magnetic field impact on biomagnetic fluid flow in a channel. The findings show that a vortex is developing near the magnetic source and get wider with the increase of magnetic intensity. Kenjereš [163] conducted a study to examine the hemodynamic behavior of blood flow in anatomically accurate arterial structures under the influence of a significantly non-uniform magnetic field. The momentum equations include both the Lorentz and magnetization forces. The results show that by imposing non-uniform magnetic field on blood flow can create noticeable changes in the local pressure and the secondary flow patterns. Ikbal et al. [164] employed the finite difference method to examine the hemodynamics in stenosed artery under the impact of a transverse magnetic field. The study treated blood as a non-Newtonian fluid governed by the generalized Power law model. The findings demonstrate that the flow rate is dropped considerably by the magnetic field and the gradient nature of the magnetic field has a significant influence in determining the flow field. Mustapha et al. [165] conducted an examination into the impact of a magnetic field on the flow of blood that exhibits unsteadiness within an artery that is characterized by an irregular, double stenosed shape. This analysis was performed through the utilization of a finite difference scheme that is founded on staggered grids. The particularity of this work remains in considering a couple of constrictions in the vessel lumen and with the wall irregularities. The outcomes of the study prove that it is possible to greatly regulate the flow separation that results from such a complicated flow situation by applying a magnetic field to the fluid stream. A computational study on the non-steady and laminar flow behavior of a biomagnetic fluid that is viscous, incompressible, Newtonian, and electrically conductive is carried out within an infinitely long channel, featuring multiple unsymmetrical stenoses. The system is exposed to an externally applied magnetic field that varies spatially. This investigation is conducted through implementation of a finite-element methodology by Turk et al [166]. The results show an increase in the vortices length with the increase of the magnetic field intensity and the constriction severity. Shit and Majee [167] use the finite difference approach to computationally model the unsteady magnetohydrodynamics and heat transfer properties. The flow pattern in an aneurysmal artery was the focus of the authors in this paper. The findings show that vortices size in the aneurysm decrease with the increase of the magnetic field intensity (see Fig. 1), additionally, it is shown that the quantity of low WSS area within the aneurysm lowers when exposed to magnetic field strength, making the arterial state less severe. Tzirtzilakis [168] looked into the movement of biomagnetic Newtonian fluid in an aneurysm under a concentrated magnetic field. The statistics on skin friction, heat transfer, and velocity and temperature fields all demonstrate that the magnetic field has a considerable impact on the flow. Using the finite volume approach, Sharifi et al. [169] conducted a study to investigate the influence of a magnetic field generated by two wires on the conduction of heat and flow of electrically conducting Newtonian fluid within an aneurysm. The findings of the study indicate that the employment of magnetic fields reduces the probability of aneurysm rupture risk factors. Javadzadegan et al. [170] conducted a study on magnetohydrodynamic blood flow in individuals diagnosed with coronary artery disorder. The findings of the investigation reveal a considerable decrease in the maximum WSS (MWSS), alongside diminished zones featuring low WSS (ALWSS) and decreased size of vortex attributable to the application of a magnetic field, more specifically in coronaries that exhibit moderate to severe stenosis (see Fig. 2) (Tables 5).

Fig. 1
figure 1

(Figure reprinted from Shit and Majee [167])

Streamlines for various values of Hartmann number, a Ha = 0, b Ha = 2, c Ha = 4, and d Ha = 6, at Re = 300, Pr = 21, t = 2

Full size image
Fig. 2
figure 2

(Figure reprinted from Javadzadegan et al. [170])

Streamline patterns pertaining to a representative artery exhibiting a diameter stenosis of 60%, under varying magnetic field intensities ranging from 0 T to 10 T. The abbreviation “RL” denotes the length of recirculation zones

Full size image
Table 5 Computational simulations of magnetohydrodynamics and the related assumptions
Full size table

Pulsatile Blood Flow

Pressure and flow in a pulsatile system vary with time, and the velocity profile varies during the cardiac cycle. The flow waveform of blood in an artery is presented in terms of the instantaneous Reynolds number during one cardiac cycle (see Fig. 3).

Fig. 3
figure 3

A typical Reynolds number in an artery during the cardiac cycle [190]

Full size image

Numerous investigations have been undertaken to examine the physiological fluid dynamics occurring in stenosed arterial systems in the presence of a magnetic field. The fundamental objectives of these studies are to assess the flow patterns and shear stresses experienced by the arterial walls under pulsatile conditions. An in vivo experimental investigation was conducted by Chi et al. [171] to examine pulsatile flow in a patient-specific cerebral aneurysm located on the lateral aspect. The empirical observations suggest that, as the frequency of pulsatile inflow increases, there is a concurrent elevation in the oscillation of wall deformation. Shit and Roy [161] conducted an inquiry into the impact that externally applied body acceleration and magnetic field have upon pulsatile blood flow within a stenosed artery, utilizing the FDM. The results show that by applying a magnetic field on blood flow, the erythrocytes align their disk plane parallel to the magnetic field’s axis adding an additional viscosity and causing a drop in blood velocity. Shit and Majee [172] conducted a numerical study of pulsatile blood flow in overlapping constricted artery in the presence of magnetic field in a vibration environment. The outcomes of the study show a reduction in blood velocity by 10% under 8-T magnetic field strength. A numerical study of pulsatile magnetohydrodynamics in a constricted tube is conducted by Bandyopadhyay and Layek [173] using finite difference approach. It is observed that when the magnetic field strength increases, the axial velocity gradually flattens. Alimohamadi and Imani [174] investigated numerically the impact of external magnetic field on pulsatile blood flow through a constricted artery. It is shown that the stenosis region experiences a rise in shear stress value due to the applied external magnetic field, which can help in reducing the fatty deposits on the plaques. Abbas et al. [126] computationally modeled blood flow through an overlapping stenosed arterial blood artery under the influence of externally imposed body acceleration and a uniform magnetic field. The Sutterby fluid model is used to represent blood rheology. The problem equations are solved using FDM and the results show that the flow velocity reduces considerably by increasing the magnetic field intensity. Using the commercial program COMSOL Multiphysics 5.1, Sedeghi et al. [175] conducted an investigation to examine the impact of uniform magnetic fields with varying degrees of intensity on pulsatile non-Newtonian blood flow in a vessel with elastic wall, characterized by axial symmetry and featuring single and double stenosis. The findings suggest that increasing the stenosis degree causes a rise in pressure drop, which is especially pronounced in double stenosis. Furthermore, exposure to a magnetic field elicits an elevation in arterial pressure, particularly discernible during instances of maximal flow rate. Teimouri et al. [176] conducted an analysis on the impact of magnetic field on the pulsatile blood flow within a curved artery exhibiting stenosis. The results demonstrate that the proportion of variations in blood flow is associated to the magnetic field intensity. These effects are more drastic in areas of the vessel subjected to a stronger magnetic field (see Fig. 4). Ali et al. [177] performed an analysis of the pulsating movement of micropolar (MP) non-Newtonian fluid in a tube with symmetrical constrictions. The results obtained using a finite difference-based solver reveal that the streamlines got smoother as the magnetic field intensity increased, and the flow separation area was minimized by increasing the magnetic field intensity (Table 6). Recently, Cherkaoui et al. [191] investigated numerically the effect of magnetic field on pulsatile non-Newtonian blood flow in an aneurysmal artery. The application of a magnetic field has been observed to decrease the size of recirculation zones and elevate the WSS. Such effects act as a preventive measure against the development and rupture of vascular disorders, particularly in the region of an aneurysm.

Fig. 4
figure 4

(Figure reprinted from Teimouri et al. [176])

WSS contour of artery consisting of deoxygenated blood for a Mn = 0, b Mn = 8.5, and c Mn = 11.5 (upper set: front view, lower set: back view)

Full size image
Table 6 Computational simulations of pulsatile magnetohydrodynamics and the related assumptions
Full size table

Magnetohydrodynamic problems have practical utility and relevance in the field of medical science, as evidenced by their application in mathematical modeling and numerical simulations. In the next section, an accurate and efficient mathematical model of blood magnetohydrodynamics, based on LBM with single relaxation time (SRT) is presented.

Modeling MHD Blood Flow Using LBM

Mathematical Equations

The governing equations that describe the magnetohydrodynamics phenomenon can be mathematically formulated by the combination of the incompressible Navier–Stokes equations and the Maxwell equations, as outlined below [163]:

Electromagnetics

The following equations depict the magnetic field elements:

$$\begin{aligned}{} & {} \nabla .B=0 \end{aligned},$$
(1)
$$\begin{aligned}{} & {} \frac{\partial B}{\partial t}= \frac{1}{\mu _{0}\varrho }\nabla ^{2}B \end{aligned}.$$
(2)

The electrical field elements are given by

The Poisson’s equation:

$$\begin{aligned}{} & {} \nabla ^2 \Phi =\nabla .(V \times B) \end{aligned}.$$
(3)
$$\begin{aligned}{} & {} E=-\nabla \Phi \end{aligned}.$$
(4)

The Ohm’s law:

$$\begin{aligned} J=\sigma (E+V\times B) \end{aligned}.$$
(5)

Fluid Dynamics

$$\begin{aligned}{} & {} \nabla .V=0 \end{aligned},$$
(6)
$$\begin{aligned}{} & {} \frac{\partial V}{\partial t}+(V.\nabla )V=\nu \nabla ^2 V +\frac{1}{\varrho }\left[ -\nabla p+(J \times B)+\mu _0(M.\nabla )H\right] \end{aligned}.$$
(7)

The Lorentz force \((J \times B)\) and magnetization force \(\mu _0(M.\nabla )H\), which affect the fluid, are two forms of body forces included in the momentum equation. Electromagnetic fields that are applied produce these forces. The Lorentz force is produced by the fluid’s electrical conductivity as it moves in the presence of a magnetic field, while the magnetisation force is produced by the fluid becoming magnetized as a result of the magnetic field’s non-uniformity.

LBM with Single Relaxation Time (SRT-LBM)

The problem of obtaining a solution to the magnetohydrodynamic equations may be approached via the utilization of two interdependent lattice Boltzmann equations. The initial equation presents a forecast of the development of the distribution function for particles, denoted as \(F_{i}\), while the subsequent equation encompasses a function of a vector nature, given by \(h_{i}\), depicting the magnetic field progression. The utilization of the D2Q9 lattice Boltzmann model relying on the BGK collision operator is presented for the purpose of investigating fluid dynamics and magnetic field progression.

The dynamics are characterized by a particle distribution function exhibiting an evolution over discretized time and space. Hence, the Lattice Boltzmann Equation (LBE) can be expressed as follows:

$$\begin{aligned} F_{i}\left( \textbf{x}+\mathbf {{\kappa }_{i}} \Delta t,t+\Delta t\right) -F_{i}\left( \textbf{x},t\right) =\Omega _{i}\left( F\right) \end{aligned}.$$
(8)

The collision operator, denoted by \(\Omega _i\), encompasses the alteration of particle distribution following particle collisions. The estimation of the collision term can be carried out through the utilization of the BGK approximation, which has been extensively employed in the field of academic writing. In order to replicate two-dimensional fluid flows, it is possible to utilize various models, such as the \(D_{2}Q_{4}\), \(D_{2}Q_{5}\), \(D_{2}Q_{7}\), or \(D_{2}Q_{9}\) approaches. The present study employs the \(D_{2}Q_{9}\) model as illustrated in Fig. 5.

Fig. 5
figure 5

\(D_{2}Q_{9}\) model

Full size image

The lattice Boltzmann BGK equation may be expressed as follows:

$$\begin{aligned} F_{i}\left( \textbf{x}+\mathbf {{\kappa }_{i}} \Delta t,t+\Delta t\right) -F_{i}\left( \textbf{x},t\right) =-\frac{1}{\tau }\left[ F_{i}\left( \textbf{x},t\right) -F_{i}^{eq}\left( \textbf{x},t\right) \right] \end{aligned}.$$
(9)

The collision step is represented as following:

$$\begin{aligned} F_{i}^{*}\left( \textbf{x},t\right) =F_{i}\left( \textbf{x},t\right) -\frac{1}{\tau }\left[ F_{i}\left( \textbf{x},t\right) -F_{i}^{eq}\left( \textbf{x},t\right) \right] \end{aligned}.$$
(10)

The streaming step is presented by

$$\begin{aligned} F_{i}\left( \textbf{x}+\mathbf {\kappa }_{i} \Delta t,t+\Delta t\right) =F_{i}^{*}\left( \textbf{x},t\right) \end{aligned}.$$
(11)

The superscript * denotes the post-collision variables.

In the present context, the relaxation parameter denoted by \(\tau\) is correlated with the fluid kinematic viscosity, wherein the relation is specified as \(\nu =\left( \tau -0.5\right) c_{s}^2\), which necessitates the selection of \(\tau >0.5\) since viscosity is positive. The equilibrium distribution function denoted as \(F_{i}^{eq}\) is defined in terms of the local fluid velocity and density. Specifically, it is expressed as follows:

$$\begin{aligned} F_{i}^{eq}=\psi _{i}\varrho \left[ 1+\frac{3\mathbf {\kappa _{i}}.\textbf{u }}{c^{2}}+\frac{9\left( \mathbf {\kappa _{i}}.\textbf{u}\right) ^{2} }{2c^{4}}-\frac{3 \textbf{u}.\textbf{u}}{2c^{2}}\right] \ \ \ \ \ \ \ \ i=0\rightarrow 8 \end{aligned}.$$
(12)

The weighing factor, denoted as \(\psi _i\), is defined as follows:

$$\begin{aligned} \left\{ \begin{array}{c} \psi _{i}=\frac{4}{9} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=0 \\ \psi _{i}=\frac{1}{9} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=1,2,3,4 \\ \psi _{i}=\frac{1}{36} \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=5,6,7,8 \end{array} \right. \end{aligned}.$$
(13)

The quantity denoted by \(c_{s}\) refers to the sound speed, which can be expressed as \(c_{s}^{2}=\Delta x^{2}/3\Delta t^{2}\). The notations \(\Delta x\) and \(\Delta t\) denote the dimensions of the lattice width and time step, consecutively. The values of \(\Delta x\) and \(\Delta t\) have been selected to be equivalent, with both being equal to 1. As a result, the velocity constant, c, is equal to 1. The D2Q9 model comprises a total of nine lattice velocities, expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{c} \mathbf {{\kappa }_{i}}=(0,0)\,\, \,\,\,\,\,\,\,\, \,\,\,\,\ \,\,\,\,\ \,\,\,\, \,\,\,\, \,\, \,\, \,\, \,\,\,\, \,\, \,\, \,\, \,\, \,\, \,\, \, \,\,\,\, \,\, \,\, \,\, \,\,\,\, \,\, \,\, \,\, \,\, \,\, \,\, \, \,\,\,\, \,\, \,\, \,\, \,\,\,\, \,\, \,\, \,\, \, i=0 \\ \mathbf {\kappa _{i}}=\left( \cos \left[ \left( i-1\right) \frac{\pi }{2} \right] ,\sin \left[ \left( i-1\right) \frac{\pi }{2}\right] \right) c \,\,\,\,\,\,\,\, \,\,\,\, \,\,\,\, \,\, \,\, \,\, \,\,\,\, \,\, \,\, \,\, \,\, \,\, \,\, \,\,i=1,2,3,4 \\ \mathbf {\kappa _{i}}=\left( \cos \left[ \left( 2i-9\right) \frac{\pi }{4} \right] ,\sin \left[ \left( 2i-9\right) \frac{\pi }{4}\right] \right) c\sqrt{2} \,\,\,\,\,\,\,\, \,\,\,\, \,\,\,\,\, \,\,\,\,\, \,\,\,i=5,6,7,8 \end{array} \right. \end{aligned}.$$
(14)

The fluid density (denoted by \(\varrho\)) and velocity (represented by \(\textbf{u}\)) can be readily determined using the density distribution function at each discrete lattice point.

$$\begin{aligned} \varrho =\sum \limits _{i=0}^{8} F_{i}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ and\ \ \ \ \ \ \ \ \ \ \varrho \textbf{u}=\sum \limits _{i=0}^{8} F_{i}\mathbf {\kappa _{i}} \end{aligned}.$$
(15)

The application of the LBM has been utilized in the investigation of the spatial and temporal changes that occur during the magnetic field evolution. Consequently, the magnetic lattice Boltzmann equation can be denoted as follows:

$$\begin{aligned} h_{i}\left( \textbf{x}+\mathbf {\kappa }_{i} \Delta t,t+\Delta t\right) =h_{i}\left( \textbf{x},t\right) -\frac{\Delta t}{\tau _{m}}\left[ h_{i}\left( \textbf{x},t\right) -h_{i}^{eq}\left( \textbf{x},t\right) \right] \end{aligned},$$
(16)

where \(\Delta t\) is the time step and \(\tau _{m}\) is the relaxation parameter. \(h_{i}=\left[ h_{ix}, h_{iy}\right]\) presents the evolution of the magnetic field

$$\begin{aligned}{} {} h_{ix}\left( \textbf{x}+\mathbf {\kappa }_{i} \Delta t,t+\Delta t\right) -h_{ix}\left( \textbf{x},t\right) & =-\frac{\Delta t}{\tau _{m}}\nonumber \\{} & {} \quad \left[ h_{ix}\left( \textbf{x},t\right) -h_{ix}^{eq}\left( \textbf{x},t\right) \right] \end{aligned},$$
(17)
$$\begin{aligned}{} {} h_{iy}\left( \textbf{x}+\mathbf {\kappa }_{i} \Delta t,t+\Delta t\right) -h_{iy}\left( \textbf{x},t\right) & =-\frac{\Delta t}{\tau _{m}}\nonumber \\{} & {} \quad \left[ h_{iy}\left( \textbf{x},t\right) -h_{iy}^{eq}\left( \textbf{x},t\right) \right] \end{aligned}$$
(18)

with i=0,...,8 in the \(D_{2}Q_{9}\) space.

$$\begin{aligned}{} & {} h_{ix}\left( \textbf{x}+\mathbf {\kappa }_{i} \Delta t,t+\Delta t\right) =h_{ix}^{*}\left( \textbf{x},t\right) \end{aligned},$$
(19)
$$\begin{aligned}{} & {} h_{iy}\left( \textbf{x}+\mathbf {\kappa }_{i} \Delta t,t+\Delta t\right) =h_{iy}^{*}\left( \textbf{x},t\right) \end{aligned}.$$
(20)

The post-collision distributions are presented by

$$\begin{aligned}{} & {} h_{ix}^{*}\left( \textbf{x},t\right) = h_{ix}\left( \textbf{x},t\right) +\omega _{\eta }[h_{ix}^{eq}\left( \textbf{x},t\right) -h_{ix}\left( \textbf{x},t\right) ] \end{aligned},$$
(21)
$$\begin{aligned}{} & {} h_{iy}^{*}\left( \textbf{x},t\right) = h_{iy}\left( \textbf{x},t\right) +\omega _{\eta }[h_{iy}^{eq}\left( \textbf{x},t\right) -h_{iy}\left( \textbf{x},t\right) ] \end{aligned}.$$
(22)

The relaxation frequencies, represented by \(\omega _{\eta }\) satisfying the inequality \(\omega _{\eta }<2\), are associated with the magnetic resistivity of the fluid according to the following relationship:

$$\begin{aligned} \eta =\left( \frac{1}{\omega _{\eta }}-0.5\right) c_{s}^2 \end{aligned}.$$
(23)

The interconnection of the velocity field and magnetic field is manifested in the equilibrium functions denoted as follows:

$$\begin{aligned}{} & {} F_{i}^{eq}=\psi _{i}\varrho \left[ 1+\frac{\mathbf {\kappa _{i}}.\textbf{u }}{c_{s}^{2}}+\frac{\left( \mathbf {\kappa _{i}}.\textbf{u}\right) ^{2} }{2c_{s}^{4}}-\frac{\textbf{u}.\textbf{u}}{2c_{s}^{2}}\right] \nonumber \\{} & {} \qquad +\frac{\zeta _{i}}{2c_{s}^{4}}\left[ \frac{1}{2} {\mid {\mathbf {\kappa _{i}}}\mid } ^{2} {\mid {\textbf{b}}\mid }^{2} -{\left( \mathbf {\kappa _{i}}.\textbf{b} \right) } ^{2}\right] \end{aligned},$$
(24)
$$\begin{aligned}{} & {} h_{ix}^{eq}=\zeta _{i}\left[ b_{x}+\frac{{\kappa _{iy}}}{c_{s}^{2}} \left( u_{y}b_{x}-u_{x}b_{y} \right) \right] \end{aligned},$$
(25)
$$\begin{aligned}{} & {} h_{iy}^{eq}=\zeta _{i}\left[ b_{y}+\frac{{\kappa _{ix}}}{c_{s}^{2}} \left( u_{x}b_{y}-u_{y}b_{x} \right) \right] \end{aligned},$$
(26)

where \(\zeta _{i}\) is the weighting factor defined in \(D_2Q_9\) as follows:

$$\begin{aligned} \left\{ \begin{array}{c} \zeta _{i}=\frac{4}{9} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=0 \\ \zeta _{i}=\frac{1}{9} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=1,2,3,4 \\ \zeta _{i}=\frac{1}{36} \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=5,6,7,8 \end{array} \right. \end{aligned}.$$
(27)

The magnetic macroscopic variables are expressed as follows:

$$\begin{aligned}{} & {} b_{x}=\sum \limits _{i=0}^{8} h_{ix} \end{aligned},$$
(28)
$$\begin{aligned}{} & {} b_{y}=\sum \limits _{i=0}^{8} h_{iy}. \end{aligned}.$$
(29)

Lattice Boltzmann Approach for Non-Newtonian Flows

Numerous studies in the literature have presented a variety of numerical findings pertaining to non-Newtonian flows using LBM. Aharonov and Rothman presented the first work [178]. The researchers successfully demonstrated the feasibility of utilizing the LBM for addressing non-Newtonian flows that conform to the power law model. This was achieved through the introduction of modifications to the relaxation time of the BGK collision model, which enabled its alignment with the local viscosity of the fluid. The accuracy of the LBM has been thoroughly examined by Gabbanelli et al. [136] with regard to the scenarios involving the rheological behaviors of shear-thinning and shear-thickening truncated power law fluids. A linear decline in relative error with respect to analytical solutions was observed as the lattice resolution increased. The authors conducted an experimental analysis to validate their LBM approach in re-entrant flow geometry. The study revealed that the solutions obtained through LBM precisely corresponded to those generated by finite-element techniques. It was confirmed once more that LBM is suitable for non-Newtonian flows and shear-dependent viscosity using a variable parameter [179]. Vikhansky [180] presented a variation of the LBM approach for the yield stress liquids by resolving a nonlinear algebraic equation linking the local stress and shear rate. These studies further illustrated LBM’s adaptability in simulating non-Newtonian flows. The LBM enables simple computations of the local shear rate to second-order precision because of its kinetic nature. Thus, it is used to imitate the non-Newtonian blood flows.

Power Law Model for Blood

The power law model is a fundamental model employed in blood modeling due to its simplicity. This model allow expressing both pseudo-plastic and dilatant material behavior, when applied in LBM. In the power law model, the apparent viscosity is a function of strain rate and it is given by

$$\nu (\dot{\gamma }) = k{\gamma^{\prime\prime}}^{{n - 1}}$$
(30)

with m which is the consistency constant and n is the power law model exponent, n<1 for blood. The shear rate is determined by

$$\begin{aligned} \dot{\gamma }=2 \sqrt{D_{\amalg }} \end{aligned}.$$
(31)

The second invariant of the strain rate tensor, denoted by \(D_{amalg}\), is expressed by

$$\begin{aligned} D_{\amalg } = \sum _{\alpha ,\beta =1}^l S_{\alpha \beta } S_{\alpha \beta } \end{aligned}.$$
(32)

In a two-dimensional model scenario, the parameter l is assigned a value of 2.

In the lattice Boltzmann approach, the shear rate tensor is locally calculated and written according to the non-equilibrium distribution function, as follows [181]:

$$\begin{aligned} {\textbf {S}}= \frac{-1}{2c_s^2\varrho \tau }\sum \limits _{i=0}^{8} (F_{i}-F_{i}^{eq})\mathbf {\kappa _{i}}.\mathbf {\kappa _{i}} \end{aligned}.$$
(33)

The local and instantaneous relaxation times for each lattice are calculated once the apparent viscosity has been established. The power law model suggests that the apparent viscosity of blood flow exhibits a shear-thinning behavior, characterized by an exponent n which is less than unity. Under this framework, it is observed that the apparent viscosity shows an increasing trend as the shear rate decreases and eventually diverges when the shear rate approaches zero. To circumvent this difficulty, a truncated power law model for LBM [136] was formulated, incorporating predefined constraints on the upper and lower bounds of relaxation times. Furthermore, when the value of the relaxation time approaches \(\tau \ge 0.5\) (\(\nu \le 0.001\)), the LBM scheme becomes unstable and its accuracy degrades as \(\tau \le 1\) (\(\nu \ge 1/6\)). An approach entails decomposing the collective non-Newtonian viscous force into two distinct components, a Newtonian viscous force and an externally generated force, which is suggested by Wang and Ho in order to overcome the possible instabilities that the varied relaxation times may generate.

Boundary Conditions

The significance of boundary conditions in the simulation of blood flow, particularly in intricate geometries, is considerable. Inadequate consideration of boundary conditions can result in outcomes that are weak, misleading, and not reflective of reality. Typically, in hemodynamic research, a velocity profile is imposed at the inlet, while a no-slip condition is applied to the internal surface of the wall. Furthermore, a combination of velocity and traction-free constraints are enforced at the outlet. The appropriateness of these boundary conditions is contingent upon a prior knowledge of the flow distribution. In different cases, where the pressure and velocity fields need to be predicted or in the case where the wall is compliant, boundary conditions have to be selected in a way to tolerate the blood domain to be coupled to deformable wall models at the lateral surface. This approach pointed out new challenges, such as considering the mechanics of the wall and modeling the fluid–solid interactions between the blood and the blood vessel. In LBM, many boundary conditions have been proposed [30, 182,183,184,185,186,187,188]. Implementing boundary conditions in LBM is a significant challenge since it requires translating supplied information from macroscopic variables to particle distribution function. In this section, most common boundary conditions, used in LBM to treat blood flow pathologies, such as aneurysm and stenosis, are introduced.

Bounce-Back

The bounce-back scheme serves as an instantiation of the “no-slip” boundary constraint, denoting the absence of fluid motion in the close proximity of the boundaries. The bounce-back boundary condition, as described by reference number [189], postulates that when particles reach a boundary, they scatter back to the fluid in the direction from which they originally arrived. The utilization of the bounce-back boundary condition on the boundary nodes results in the provision of initial order precision. The implementation of the bounce-back boundary condition results in second-order accuracy when a wall is positioned at a location that is half of the grid spacing away from both a flow node and a bounce-back node (Fig. 6).

Fig. 6
figure 6

Bounce-back boundary condition

Full size image

The unknown distribution functions, for a D2Q9 model, are expressed by

$$\begin{aligned} \begin{array}{lcl} F_{5}(x,y,t)= F_{7}(x,y,t) \\ F_{2}(x,y,t)= F_{4}(x,y,t) \\ F_{6}(x,y,t)= F_{8}(x,y,t) \end{array} \end{aligned}.$$
(34)

Improved Bounce-Back Boundary Condition

Yu et al. [188] proposed an improved bounce-back boundary condition, valid for curved wall, based on linear interpolation scheme, given by

$$\begin{aligned} F_{\overline{i}}(x_{w})= F_{\overline{i}}(x_{w})+\frac{\Delta }{1+\Delta } (F_{\overline{i}}(x_{f}+c_{i})-F_{\overline{i}}(x_{w})) \end{aligned}.$$
(35)

with

$$\begin{aligned} 0\le \Delta \le 1 \end{aligned},$$
(36)

where \(F_{\overline{i}}\) indicates post-collision state.

Curved Boundary Condition

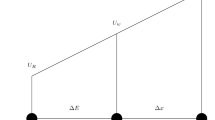
Bouzidi et al. [30] proposed a treatment for curved boundaries that fulfills the no-slip condition to the second order in \(\Delta x\) and maintains the geometric boundary integrity of the wall. The boundary condition is given by the following equation (Fig. 7):

$$\begin{aligned} F_{\overline{i}}(x_{f},t+\Delta t)= \overline{F}_{{i}}(x_{f},t)+\frac{2\Delta -1}{2\Delta } F_{\overline{i}}(x_{f},t+\Delta t) \end{aligned},$$
(37)

\(x_{w}\) represent nodes on the wall boundary, \(x_{f}\) represent nodes in the fluid domain, and \(x_{b}\) represent nodes in the solid region. \(\Delta\) presents the fraction of an intersected lattice with the wall boundary that is placed within the fluid region. It is given by

$$\begin{aligned} \Delta = \frac{{x_{F}-x_{w}}}{{x_{F}-x_{b}}} \end{aligned}.$$
(38)
Fig. 7
figure 7

Layout of the regularly spaced lattices and the boundary of the curved wall

Full size image

Zou–He Boundary Condition

The velocity boundary condition of Zou–He [35] is applied at the flow inlet. The velocity profile at the inlet is expressed by Poiseuille profile (\(u_x(y)\) and \(u_y=0\)). After streaming \(F_2, F_3, F_4, F_6, F_7\) are known at the inlet. The unknown density \(\rho , F_1, F_5, F_8\) can be determined by

$$\begin{aligned} \begin{array}{lcl} \rho = \frac{1}{1-u_{x}}\left[ F_0+F_2+F_4+2(F_3+F_6+F_7) \right] , \\ F_{1}= F_{3}+\frac{2}{3}\rho u_{x}, \\ F_{5}= F_{7}-\frac{1}{2}(F_2-F_4)+\frac{1}{2}\rho u_{y}+\frac{1}{6}\rho u_{x}, \\ F_{8}= F_{6}+\frac{1}{2}(F_2-F_4)-\frac{1}{2}\rho u_{y}+\frac{1}{6}\rho u_{x}. \end{array} \end{aligned}.$$
(39)

Numerical Model Applications

Using the lattice Boltzmann approach based on the BGK approximation, laminar flow simulation of magnetohydrodynamic blood flow in stenosed artery in two dimensions is carried out by Cherkaoui et al. [147, 148]. It is an application of the suggested lattice Boltzmann model with certain boundary conditions (bounce-back and Zou–He) and the consideration of blood as Newtonian fluid. The model has been verified in the absence and in the presence of various magnetic field intensities, and it exhibits strong concurrence with various findings in the literature. The various comparisons show the efficacy and precision of the LBM-BGK suggested model of magnetohydrodynamics.

Magnetic Field Impact on Streamlines

Figures 8, 9, and 10 depict the effect of magnetic field intensity, presented by various Hartmann number values (Ha= 0, Ha= 10, Ha= 50, Ha= 75 and Ha= 100) on blood velocity for Re= 400, Re= 600, and Re= 800.

Fig. 8
figure 8

(Figure reprinted from Cherkaoui et al. [147])

Effect of Hartmann number on streamlines at \(Re=400\)

Full size image
Fig. 9
figure 9

(Figure reprinted from Cherkaoui et al. [147])

Effect of Hartmann number on streamlines at \(Re=600\)

Full size image
Fig. 10
figure 10

(Figure reprinted from Cherkaoui et al. [147])

Effect of Hartmann number on streamlines at \(Re=800\)

Full size image

According to the study [147], an increase in the magnetic field strength reduces the recirculation zones considerably and reduces the flow rate. The red blood cells (RBCs) aggregation, which increased as blood is exposed to a magnetic field, is the reason of the decrease in velocity. The results reported in the literature and our findings are fairly consistent. In the approaches based on FEM, FDM, and FVM, the introduction of a Lorentz force term into the Navier–Stokes equations results in the imposition of a single, unequivocal direction for the magnetic field. In our approach, it is noteworthy that the magnetic field direction could be predicted at each node due to the association of a vector possessing nine conceivable orientations which serve to provide a magnetic field to every individual particle within the given flow.

Magnetic Field Impact on Pressure Drop

The magnetic field intensity impact on pressure drop across a constricted zone with various degrees of stenosis (DOS) at different Reynolds and Hartmann numbers is presented in Fig. 11.

Fig. 11
figure 11

(Figure reprinted from Cherkaoui et al. [147])

Pressure drop across stenosis at varying degrees of stenosis and Reynolds numbers, while considering three distinct values of Hartmann number (namely, Ha=0, Ha=10, and Ha=50)

Full size image

Research [147] has demonstrated that as stenosis degree increases, pressure drop also increases. However, the application of a magnetic field with a Hartmann number value of 10 results in a 90% reduction in pressure drop, while a Hartmann number value of 50 leads to a decrease of 98.25%. This reduction is attributed to a decrease in velocity caused by the magnetic field. Nonetheless, across all cases, there has been a sudden surge in pressure from DOS 80% to 85%. The study concludes that powerful magnetic fields are highly effective in decreasing pressure drop in a stenotic artery.

Magnetic Field Impact on WSS

Fig. 12
figure 12

WSS at Re= 360 and Ha= 0, 5, 15, and 20. (Figure reprinted from Cherkaoui et al. [148])

Full size image

In cardiovascular diseases, WSS is a crucial hemodynamic variable that significantly affects stenosis progression. Figure 12 demonstrates how an external magnetic field affects WSS in a stenotic artery at various Hartmann number values and Reynolds number of 360. The study [148] reveals that the maximum WSS occurs in the restricted zone, where the diameter is reduced. The non-Newtonian behavior of blood is particularly pronounced in the stenotic region, owing to the clustering of red blood cells within that particular zone. Fig. 12 shows that an external magnetic field considerably reduces WSS in the stenotic region.

The outcomes of the study have applications in the management of hypertension and several cardiovascular diseases. Furthermore, the regulation of blood circulation can be facilitated via the utilization of a magnetic field, a valuable technique particularly in the field of surgical procedures.

Conclusion

In this review, numerical simulations of hemodynamics and magnetohydrodynamics of blood in pathological vessels using FVM, FEM, FDM, and LBM are presented. The LBM is an accurate alternative approach to simulate complex flows, such as blood flow. In addition, complex boundary shapes can be easily dealt with in the LBM. The majority of studies presented in this review treat blood flow in large vessels, such as arteries. Simulations of blood flow in small vessels such as veins and capillaries are required. The consideration of non-Newtonian behavior of blood in small vessels is necessary to identify the flow related properties, such as WSS; however, the selection of non-Newtonian model is crucial. Based on this review, Carreau–Yasuda, generalized power law, and Casson models seem to give more accurate predictions of blood behavior compared to other models. For more realistic results, consideration of deformable vessels and the interaction between the vessel wall and blood flow are necessary. The analysis of wall mechanics and characterization of fluid–solid interactions between the blood and the blood vessel are pertinent areas of investigation. The great majority of LBM simulations presented in the review implemented single relaxation time collision model; however, the effects of collision model selection on predicted velocity fields in pathological blood flow need further research. LBM proved its precision in two dimensions in the simulation of steady and time-varying fluid flow within complex geometries. On the contrary, the three-dimensional LBM has poor accuracy due to the lack of adequate boundary conditions. Additional research is required to thoroughly explore the velocity and pressure boundary conditions, particularly for complex geometries. The implementation of LBM has the potential to advance the medical field and can contribute to advancements in medicine. The LBM can simulate the blood flow through complex geometries, such as blood vessels and heart chambers. By accurately modeling the behavior of blood cells and the interactions between blood and vessel walls, LBM can help in understanding diseases, like atherosclerosis, thrombosis, and aneurysms. It can also aid in modeling drug transport within the body and in optimizing medical devices, such as stents and artificial heart valves.