Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

10.1 Introduction

Blood flow simulations constitute a rapidly growing field for the medical, engineering, and basic sciences communities. The study of blood in the macrovasculature, as much as in capillaries, has deep implications in understanding and prevention of the most common cardiovascular pathologies, with atherosclerosis being perhaps the best known example. Atherosclerosis is responsible for ∼ 35% of annual deaths in developed countries, and its development depends on the presence of systemic risk factors. The disease results from the accumulation of lipid molecules within the wall of the blood vessels, as well as from enhanced exposure to intramural penetration of nano-sized biological bodies [19]. The build up of the resultant soft tissue and the eventual changes in its consistency leads to serious atherosclerotic pathologies, including catastrophic events such as plaque rupture. Atherosclerotic plaques appear in regions of disturbed blood flow where the local endothelial shear stress (ESS) is low ( < 1. 0 Pa) or of alternating direction [9]. Hence, plaques tend to form near arterial bifurcations where the flow is always altered compared to unbranched regions [8, 39].

Atherosclerosis primarily affects the coronary arteries, and the evidence that low average ESS has a key role in the disease localization and progression is widely accepted [8, 23, 43, 9]. Predictions of where and how the illness is likely to develop can be obtained by fluid-dynamics simulations as a routine methodology to study blood flow patterns in human arteries. As a matter of fact, the shape and the structure of endothelium play a number of important roles in the vascular system, and its dysfunction may lead to several pathological states, including early development of atherosclerosis [30]. The microscopic shape of the endothelium is defined by the presence of endothelial cells (ECs henceforth), making the arterial wall undulated. This effect becomes more pronounced in small-sized vessels, where the corrugation degree increases. The study of blood flow over a regularly undulating wall made of equally aligned and distributed ECs has been recently carried out in [34] where the variation of wall shear stress over the ECs has been computed. Furthermore, the endothelium is coated by long-chained macromolecules and proteins which form a thin porous layer, called the glycocalyx [44]. The glycocalyx has a brushlike structure and a thickness which varies with the vessel diameter, but its average is 100 nm for arterioles. It has several roles: it serves as a transport barrier, to prevent ballistic red blood cell (RBC) interactions with the endothelium, and as a sensor and transducer of mechanical forces, such as fluid shear stress, to the surface of ECs. Actually, it has been recognized that the glycocalyx responds to the flow environment and, in particular, to the fluid stress, but the mechanism by which these proteins sense the shearing forces and transduce mechanical into biochemical signals is still not fully understood [30]. The glycocalyx itself is remodeled by the shearing flow and by the compression exerted by the deformed erythrocytes in capillaries [38]. Flow-induced mechano transduction in ECs has been studied over the years with emphasis on correlation between disturbed flow and atherosclerosis. Recently, some mathematical modelling work has been carried out, using a porous medium to model the endothelial surface layer (ESL henceforth) [1, 42]. However, none of these works includes the effect of the roughness, or wavy nature, of the wall, which should be incorporated for a more realistic description. In the following sections we also present a coarse-grained model that attempts to include some of the basic physical microscale effects of the ESL attached to the EC surface and hence, examine to what extent the wall shear stress may vary due to this layer in addition to the previously examined EC shape and particulate transport.

Simulations of blood flows based on the Lattice Boltzmann (LB) method provide a particularly efficient and flexible framework in handling complex arterial geometries. In the past, the LB method has been applied to a broad range of fluid-dynamic problems, including turbulence and multiphase flows [41], as well as in blood flow simulations in steady and pulsatile regimes and with non-Newtonian flows through stenoses [32]. A direct benefit of the joint use of simulation and imaging techniques is to understand the connection between fluid-mechanical flow patterns and plaque formation and evolution, with important implications for predicting the course of atherosclerosis and possibly preventing or mitigating its effects, in particular by non-invasively and inexpensively screening large numbers of patients for incipient arterial disease, and to intervene at clinical level prior to the occurrence of a catastrophic event. One option is to obtain the arterial wall shape, plaque morphology, and lumen anatomy from the non-invasive multi-detector computed tomography (MDCT) imaging technique, as in the newest systems with 320-detector rows, a technology that enables 3D acquisition of the entire arterial tree in a single heart beat and high accuracy of nominal resolution of 0. 1 mm [36].

The LB method is particularly flexible for handling complex arterial geometries, since most of its simplicity stems from an underlying Cartesian mesh over which fluid motion is represented. LB is based on moving information along straight-line trajectories, associated with the constant speed of fictitious molecules which characterize the state of the fluid at any instant and spatial location. This picture stands in sharp contrast with the fluid-dynamic representation, in which, by definition, information moves along the material lines defined by fluid velocity itself, usually a very complex space-time-dependent vector field. This main asset has motivated the increasing use over the last decade of LB techniques for large-scale simulations of complex hemodynamic flows [29, 12, 27, 3].

The main aim of this chapter is to show that the inclusion of crucial components such as RBC and the glycocalyx, can be done within a single unified computational framework. This would allow us to reproduce blood rheology in complex flows and geometrical conditions, including the non-trivial interplay between erythrocytes and wall structure. The possibility of embedding suspended bodies in the surrounding plasma and the glycocalyx representation over an undulated endothelial wall addresses major steps forward to model blood from a bottom-up perspective, in order to avoid unnecessary and sometimes wrong assumptions in blood dynamics.

10.2 The Lattice Boltzmann Framework

In the last decade, the LB method has captured increasing attention from the fluid-dynamics community as a competitive computational alternative to the discretization of the Navier–Stokes equations of continuum mechanics. LB is a hydrokinetic approach and a minimal form of the Boltzmann kinetic equation, based on the collective dynamics of fictitious particles on the nodes of a regular lattice. The dynamics of fluid particles is designed in such a way as to obey the basic conservation laws ensuring hydrodynamic behavior in the continuum limit, in which the molecular mean free path is much shorter than typical macroscopic scales [41]. This condition is clearly met in blood flow regimes, together with the Newtonian rheological behavior of blood in large arterial systems. Non-Newtonian rheological models appropriate for simulating blood flow in medium or small-sized arteries, such as the Casson, Carreau, or Carreau-Yasuda models, can be also incorporated within the LB approach [6, 20].

The LB method is based on the collective dynamics of fictitious particles on the nodes of a regular lattice where the basic quantity is \({f}_{p}({x},t)\), representing the probability of finding a “fluid particle p” at the mesh location \({x}\) and at time t and traveling with discrete speed \({{c}}_{p}\). “Fluid particles” represent the collective motion of a group of physical particles (often referred to as populations). We employ the common three-dimensional 19-speed cubic lattice (D3Q19) with mesh spacing Δx, where the discrete velocities c p connect mesh points to first and second neighbors [2]. The fluid populations are advanced in a time step Δt through the following evolution equation:

$${f}_{p}(\mathbf{x} +{ \mathbf{c}}_{p}\Delta t,t + \Delta t) = {f}_{p}(\mathbf{x},t) - \omega ({f}_{p} - {f}_{p}^{eq})(\mathbf{x},t) + {F}_{ p}(\mathbf{x},t).$$
(10.1)

The right-hand side of (10.1) represents the effect of fluid-fluid molecular collisions, through a relaxation towards a local equilibrium, typically a second-order expansion in the fluid velocity of a local Maxwellian with speed u,

$${f}_{p}^{eq} = {w}_{ p}\rho \left [1 + \frac{\mathbf{u} \cdot {\mathbf{c}}_{p}} {{c}_{\mathrm{ s}}^{2}} + \frac{\mathbf{u}\mathbf{u} : ({\mathbf{c}}_{p}{\mathbf{c}}_{p} - {c}_{\mathrm{ s}}^{2}\mathbf{I})} {2{c}_{\mathrm{ s}}^{4}} \right ],$$
(10.2)

where \({c}_{\mathrm{ s}} = 1/\sqrt{3}\) is the speed of sound, w p is a set of weights normalized to unity, and I is the unit tensor in Cartesian space. The relaxation frequency ω controls the kinematic viscosity of the fluid, \(\nu = {c}_{\mathrm{ s}}^{2}\Delta t\left ( \frac{1} {\omega } -\frac{1} {2}\right )\). The kinetic moments of the discrete populations provide the local mass density ρ(x, t) =  ∑ p  f p (x, t) and momentum ρu(x, t) =  ∑ p c p f p (x, t). The last term F p in (10.1) represents a momentum source, given by the presence of suspended bodies, if RBCs are included in the model, as discussed in the following sections. In the incompressible limit, (10.1) reduces to the Navier–Stokes equation

$$\begin{array}{lll} \nabla \cdot \mathbf{u}& = 0, \\\frac{\partial \mathbf{u}} {\partial t} + (\mathbf{u} \cdot \nabla )\mathbf{u}& = -\frac{1} {\rho }\nabla P + \nu {\nabla }^{2}\mathbf{u} + \mathbf{F},\end{array}$$
(10.3)

where P is the pressure and F is any body force, corresponding to F p in (10.1).

The LB is a low-Mach, weakly compressible fluid solver and presents several major advantages for the practical implementation in complex geometries. In particular, in hemodynamic simulations, the curved blood vessels are shaped on the Cartesian mesh scheme via a staircase representation, in contrast to body-fitted grids that can be employed in direct Navier–Stokes simulations. This apparently crude representation of the vessel walls can be systematically improved by increasing the mesh resolution. In addition, at the high mesh resolution required to sample low-noise ESS data, the LB method requires rather small time steps (of the order of 10 − 6 s for a resolution of 20 μm).

The wall shear stress, which is central to hemodynamic applications, can be computed via the shear tensor \(\mathbf{\sigma }(\mathbf{x},t) \equiv \nu \rho \left (\nabla \mathbf{u} + \nabla {\mathbf{u}}^{T}\right )\) evaluated via its kinetic representation

$$\sigma (\mathbf{x},t) = \frac{-3\nu \omega } {{c}_{S}^{2}} { \sum \nolimits }_{p}{\mathbf{c}}_{p}{\mathbf{c}}_{p}({f}_{p} - {f}_{p}^{eq})(\mathbf{x},t).$$
(10.4)

The tensor second invariant is the endothelial shear stress or ESS:

$$ \mathcal{S}({\mathbf{x}}_{w},t) = \sqrt{\frac{1} {2}(\sigma : \sigma )({\mathbf{x}}_{w},t)},$$
(10.5)

where x w represents the position of sampling points in close proximity to the mesh wall nodes. \(\mathcal{S}({\mathbf{x}}_{w},t)\) provides a direct measure of the strength of the near-wall shear stress [5]. It is worth mentioning that the ESS evaluation via (10.4) is completely local and does not require any finite-differencing procedure. Thus it is particularly advantageous near boundaries where the computation of gradients is very sensitive to morphological details and accuracy. In order to sample high signal/noise ESS data, the LB mesh needs high spatial resolution, with mesh spacing being as small as Δx ≃ 50 μm for standard fluid-dynamic simulations, or being as small as Δx ≃ 10 μm in order to account for the presence of RBCs.

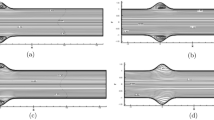
For the multiscale simulations of blood flows, we have developed the MUPHY software [3]. Such simulations in extended arterial systems, are based on the acquisition of MDCT data which are segmented into a stack of slices, followed by a mesh generation from the segmented slices. For a typical coronary artery system, the procedure to build the LB mesh from the MDCT raw data starts from a single vessel, formatted as stacked bi-dimensional contours (slices), with a nominal resolution of 100 μm. In spite of recent technological progress, this resolution is still insufficient, and the inherently noisy geometrical data pose a problem in the evaluation of ESS, a quantity that proves extremely sensitive to the details of the wall morphology. Raw MDCT data present a mild level of geometric irregularities, as shown in Fig. 10.1, that can affect the quality of the LB simulations. For the simulation, we resort to regularize the initial geometry by smoothing the sequence of surface points via a linear filter along the longitudinal direction. Similarly, one could filter out surface points along the azimuthal contour. We have shown that such smoothing is necessary in order to avoid strong artifacts in the simulation results [28]. Even if the precise shape of the vessel is unknown, as it falls within the instrumental indeterminacy, the numerical results converge to a common fluid-dynamic pattern as the smoothing procedure reaches a given level. The regularized geometries are still of great interest because they obey the clinical perception of a smooth arterial system, and, moreover, the smoothing procedure falls within the intrinsic flexibility of the arterial system.

Fig. 10.1
figure 1

Details of a multi-branched artery as obtained from MDCT (left) and after smoothing have been applied as used in simulations (right)

Full size image

When studying coronary arteries as a prototypical system for plaque formation and development, one issue regards the inclusion of deformable vessels in simulation. Whereas larger arteries undergo high deformations, a simple calculation shows that the distensibility index of a coronary artery of sectional area A is b  − 1 ≃ 1. 5 mmHg. Therefore, the arterial section during a heartbeat has a maximal deformation of \(\delta A/A = b\Delta P\), with ΔP the maximal pressure variation over a cardiac cycle. For a pressure jump of 40 mmHg, the deformation is less than 3%, and considering rigid coronary systems does not introduce major artifacts in the computed flow and pressure distributions.

LB allows to impose no-slip boundary conditions at the endothelium by employing the bounce-back method; this consists of reversing at every time step the post-collisional populations pointing toward a wall node, providing first-order accuracy for irregular walls [41]. In the bounce-back method, the points corresponding to the exact no-slip hydrodynamic surface fall at intermediate positions between the external fluid mesh nodes and the nearby wall mesh nodes. Owing to its simplicity, the method handles irregular vessel boundaries in a seamless way, although more sophisticated alternatives with higher-order accuracy are available [4, 21, 17].

In a branched portion of arteries, boundary conditions at the inlet and multiple outlets can be chosen in different ways, typically by following the flow-pressure, pressure-pressure, or flow-flow prescriptions. The first two options are more popular in fluid-dynamic models, and pressure conditions at the outlets reflect the presence of a recipient medium. Even flow-flow conditions have found some applicability, as they can accommodate some type of metabolic autoregulation as encoded by Murray’s law [40]. It is worth mentioning that flow-flow conditions can give rise to numerical instabilities in simple pipe flows, as long-lived transients can develop and a certain strain is exhorted on the simulation method. The absence of a peripheral system in real-life simulations can be compensated by using an equivalent RCL circuit at each system outlet, where the auxiliary circuitry introduces an external viscous dissipation (R), vessel compliance (C), and fluid inertia (L) and compensates for the missing components (lumped parameter model).

In the framework of the LB method, boundary conditions at the inlet and multiple outlets can be imposed as follows. A constant velocity (with plug or parabolic profile) is enforced at the entrance of the main artery, as a way to control the amplitude of the flow. Even if the inlet profiles are not the real ones for irregular geometries, they fulfill the purpose of imposing the total flow rate in the chosen region. The fluid spontaneously and rapidly develops the consistent profile already at a short distance downstream. A constant pressure is imposed on the several outlets of the main artery, as well as on the outlet of all secondary branches (of the order of 10 in typical coronary systems). This leaves the simulation with the freedom of creating an appropriate velocity profile in the outlet regions, and building up a pressure drop between the inlet and the several outlets. The Zou-He method [46] is used to implement both the velocity inlet and the pressure outlets. This method exploits information streamed from fluid bulk nodes onto boundary cells and imposes a completion scheme for particle populations which are unknown because their neighboring nodes are not part of the fluid domain. The boundary cells are treated as normal fluid cells where to execute the conventional LB scheme. Thanks to this natural integration of the boundary scheme, the method is second-order accurate in space, compatible with the overall accuracy of the LB method (see [22]). The method handles in a natural way time-dependent inflow conditions for pulsatile flows. The algorithm requires that all nodes of a given inlet or outlet are aligned on a plane which is perpendicular to one of the three main axes, although the injected flow profile and direction can be arbitrary. However, since the inlet section is typically a critical region of simulation in terms of numerical stability due to the high fluid velocities, it is preferable to have an incoming flow direction aligned with one of the Cartesian axes. This requirement can be fulfilled by rotating the artery in such a way as to secure that alignment, the inlet axis with one of the Cartesian axis, which guarantees an exact control of the flow imposed at the inlet. Conversely, the outlet planes are not in general normal to the orientation of the blood vessels. However, this does not lead to noticeable problems, because the pressure drop along typical arterial systems is mild, and the error due to imposing a constant pressure along an inclined plane is negligible.

10.3 Red Blood Cells

RBCs or erythrocytes are globules that present a biconcave discoidal form, and a soft membrane that encloses a high-viscosity liquid made of hemoglobin: they exhibit both rotational and orientational responses that deeply modulate blood rheology. While blood rheology is quasi-Newtonian away from the endothelial region, the presence of RBCs strongly affects blood flow in proximity of the endothelium, where the interplay of RBC crowding for hematocrit levels up to 50%, depletion due to hydrodynamic forces, and RBC arrangement in rouleaux takes place.

In order to consider these different factors, we have recently proposed a model that focuses on three independent components: the far-field hydrodynamic interaction of a RBC in a plasma solvent, the raise of viscosity of the suspension with the hematocrit level, and the many-body collisional contributions to viscosity [26]. These three critical components conspire to produce large-scale hemorheology and the local structuring of RBCs. The underlying idea is to represent the different responses of the suspended bodies, emerging from the rigid body as much as the vesicular nature of the globule, by distinct coupling mechanisms. These mechanisms are entirely handled at kinetic level, that is, the dynamics of plasma and RBC’s is governed by appropriate collisional terms that avoid to compute hydrodynamic forces and torques via the Green’s function method, as employed in Stokesian dynamics [7]. The fundamental advantage of hydrokinetic modeling is to avoid such an expensive route and, at the same, enabling to handle finite Reynolds conditions and complex boundaries or irregular vessels within the simple collisional approach. At the macroscopic scale, the non-trivial rheological response emerges spontaneously as a result of the underlying microdynamics.

The presence of suspended RBCs is included via the following forcing term [see (10.1)]:

$${F}_{p} = {w}_{p}\left [\frac{\mathbf{G} \cdot {\mathbf{c}}_{p}} {{c}_{S}^{2}} + \frac{(\mathbf{G} \cdot {\mathbf{c}}_{p})(\mathbf{u} \cdot {\mathbf{c}}_{p}) - {c}_{S}^{2}\mathbf{G} \cdot \mathbf{u}} {{c}_{S}^{4}} \right ],$$
(10.6)

where G(x, t) is a local force-torque. This equation produces first-order accurate body forces within the LB scheme. Higher-order methods, such as Guo’s method [16], could be adopted. However, given the non-trivial dependence of the forces and torques on the fluid velocity and vorticity, Guo’s method would require an implicit numerical scheme, whereas it is preferable to employ an explicit, first-order accurate numerical scheme.

The fluid-body hydrodynamic interaction is constructed according to the transfer function \(\tilde{\delta }({\mathbf{r}}_{i})\) centered on the i-th particle position r i and having ellipsoidal symmetry and compact support. The shape of the suspended body can be smaller than the mesh spacing, allowing to simulate a ratio of order 1 : 1 between suspended bodies and mesh nodes. In addition, the body is scale-adaptive, since it is possible to reproduce from the near-field to the far-field hydrodynamic response with desired accuracy [25]. The fluid-particle coupling requires the computation of the following convolutions over the mesh points and for each configuration of the N suspended bodies:

$$\begin{array}{lll} \tilde{{\mathbf{u}}}_{i}& = \sum\nolimits_{\mathbf{x}}\mathbf{u}(\mathbf{x})\tilde{\delta }(\mathbf{x} -{\mathbf{r}}_{i}), \\\tilde{{\Omega }}_{i}& = \sum\nolimits_{\mathbf{x}}\Omega (\mathbf{x})\tilde{\delta }(\mathbf{x} -{\mathbf{r}}_{i}), \\\tilde{{\mathbf{t}}}_{i}& = \sum\nolimits_{\mathbf{x}}\mathbf{t}(\mathbf{x}) \times (\mathbf{x} -{\mathbf{r}}_{i})\tilde{\delta }(\mathbf{x} -{\mathbf{r}}_{i}),\end{array}$$
(10.7)

where Ω is the fluid vorticity and t is the fluid traction vector, quantities that are directly obtained from the LB computational core. The three convolutions allow to compute the drag force and drag torque, inclusive of tank trading components. On the fluid side, the body-induced forces are encoded by the term

$$\mathbf{G}(\mathbf{x}) = -\sum\limits_{i=1}^{N}\left [{\mathbf{D}}_{ i}\tilde{\delta }(\mathbf{x} -{\mathbf{r}}_{i}) + \frac{1} {2}{\mathbf{T}}_{i} \times \nabla \tilde{\delta }(\mathbf{x} -{\mathbf{r}}_{i})\right ],$$

where D i and T i are the drag forces and torques acting on the particles, constructed starting from the quantities featuring in (10.7). The explicit expression of the drag forces and torques are not given here, and can be found in [25].

Besides hydrodynamic interactions, mechanical forces regulate the direct interactions and the packing attitude of suspended bodies. The interactions are modeled as pairwise by means of the Gay-Berne (GB) potential [14], the pairwise GB energy being a function of the relative distance between pairs of RBCs and their mutual orientation. In addition, the mutual interaction depends on the eccentricity of each interacting particle, so that, as for the hydrodynamic coupling, mixtures of particles of different shapes can be handled within a unified framework. Once the forces and torques standing from both hydrodynamics and direct mechanical forces are computed, the rigid-body dynamics is propagated via a time second-order accurate algorithm [24, 10].

Numerical results have shown that the particulate nature of blood cannot be omitted when studying the non-trivial rheology of the biofluid and the shear stress distribution in complex geometries. Regions of low shear stress can appear as the hematocrit reaches physiological levels as a result of the non-trivial organization of RBCs and the irregular morphology of vessels, with far reaching consequences in real-life cardiovascular applications, where the organization of RBCs impacts both the local flow patterns and the large-scale flow distribution in vascular networks.

A crucial advantage of the hydrokinetic model in the presence of physiological levels of RBCs is its reduced computational cost, thus enabling the investigation of systems of physiological relevance (Fig. 10.2). To a large extent, both the LB method and the RBC dynamics have been proved to scale over traditional CPU-based computers such as on Blue Gene architectures, as much as over massive assemblies of graphic processing units (see [31] and references therein).

Fig. 10.2
figure 2

Snapshot of a multi-branched artery in presence of red blood cells for 50% hematocrit

Full size image

10.4 A Closer View to Blood-Wall Interaction

At a lower scale, new intriguing aspects come to light in hemodynamics. For example, the vessel wall surface is covered by endothelial cells (EC), that give a wavy structure, so far neglected (Fig. 10.3): this does not imply a significant variation in the flow field, but it can be relevant in computing ESS, which is constant in a flat-walled artery. Indeed, the ECs (a single EC has been estimated to be about 15 μm long by 0.5 μm high [35]) form a continuous, undulated wall layer above which blood is flowing. At such mesoscopic scale, the wall may be considered as a smoothly corrugated idealized surface constituted by a regular array of equal, repeated EC’s. The pressure-driven axi-symmetric flow of a continuum fluid over such a surface has been recently modelled by Pontrelli et al. [34]. It was shown that, despite no great change in velocity profiles, there can occur significant ESS variations between the ECs wall peaks and throats, especially in small-sized arteries. Differently than in Sect. 10.3, the mesoscopic particulate nature of the blood is now addressed in the context of a bicomponent fluid model: RBC are here deformable, neutrally buoyant liquid drops constrained by a uniform interfacial tension and suspended in the plasma.

Fig. 10.3
figure 3

The rough surface of the endothelium as imaged using scanning force microscopy (from [35]). Arrows point to granular structures on EC’s surfaces, white line marks scanning line for height profile evaluation, and scale bar corresponds to 5 μm

Full size image

In addition, the endothelial surface is not only wavy in its geometry, but, at a smaller scale, it is covered by fibrous filaments and long protein chains forming a thin layer called the endothelial surface layer (ESL) or glycocalyx [44]. From a fluid-dynamics point of view, the ESL can be modelled as a porous layer of constant thickness which suits the wall undulation, through which the flow of the continuous phase (plasma) is possible. This would alter the boundary condition of the problem, specifically the classical no-slip condition at the vessel wall may have to be replaced to allow for plasma penetration through the ESL. The LB method readily accommodates a model of the glycocalyx itself, as it is particularly well suited to address what would now become a multiscale model. Conceptually, the idea is to solve a two-domain problem, whereby the bulk flow (in the lumen) is governed by the multicomponent Navier–Stokes equations and the near-wall region by a porous-medium Brinkman flow formulation (see below). At the mesoscale, the glycocalyx is not modelled in a detailed form, but its effect on the flow is still properly addressed, using methods which are amenable to coupling other, more detailed, simulations with experiments. We develop here a two-way coupled model where the drop interface is forced by compression of the ESL, and the effect of perturbed or compressed glycocalyx is then communicated to the flow [33]. We assume here that the filaments are strongly anchored in the endothelium, where they are most resistant to deformation and that they deform preferably at their tip, that is toward the vessel lumen.

The mesoscale LB method is still used to solve the governing hydrodynamic equations, that involves multicomponent fluid flow, off-lattice, or sub-grid, boundary surfaces and a porous-layer representative of the ESL. The governing hydrodynamic equations for flow in a porous media, with constant or variable porosity ε, are an extension of (10.3) as in [15]:

$$\begin{array}{lll} \nabla \cdot \mathbf{u} = 0, \\ \frac{\partial \mathbf{u}} {\partial t} + (\mathbf{u} \cdot \nabla )\frac{\mathbf{u}} {\varepsilon }= -\frac{1} {\rho }\nabla (\varepsilon P) + \nu {\nabla }^{2}\mathbf{u} +\mathbf{F}.\end{array}$$
(10.8)

Here, F is the total body force due to the presence of both the porous material (drag) and other external forces:

$$\mathbf{F} = \frac{\varepsilon \nu } {K}\mathbf{u} -\frac{\varepsilon{F}_{\varepsilon}}{\sqrt{K}}\mathbf{u}\mathbf{\vert u\vert } + \varepsilon \mathbf{H},$$
(10.9)

where H is the extra body force that will be used to incorporate further details of the ESL and particulate effects, such as the RBC interface force density (pressure step) defined below. To solve governing Equations (10.8) and (10.9) we combine the LB methods of Guo and Zhao [15] with the model of Halliday et al. [18], that allows for the introduction of two immiscible fluid components and the formation of interfaces that embed correct kinematic and surface tension laws. To complete the algorithm, we must mention that, for multiple fluid LB, the propagation step is augmented by a fluid segregation process that ensures the correct kinematics and dynamics and good integrity for an interface between completely immiscible fluid components, representing RBC and plasma, as discussed above [18]. The propagation step is expressed as:

$$\begin{array}{lll} {R}_{p}(\mathbf{x} +{ \mathbf{c}}_{p}\Delta t,t + \Delta t)=\frac{R} {\rho } {f}_{p}^{+} + {w}_{ p}\beta \frac{RB} {\rho } \cdot {\mathbf{c}}_{p} \cdot \mathbf{n},\\{B}_{p}(\mathbf{x} +{ \mathbf{c}}_{p}\Delta t,t + \Delta t)= \frac{B} {\rho } {f}_{p}^{+} - {w}_{ p}\beta \frac{RB} {\rho } \cdot {\mathbf{c}}_{p} \cdot \mathbf{n},\end{array}$$
(10.10)

where the density of each fluid component is given by R =  ∑ p   R p (x, t) and B = ∑ p   B p (x, t), the combined particle distribution function is \({f}_{p} = {R}_{p} + {B}_{p}\), and f  + p accounts for the propagated combined distribution. In (10.10) β represents an interfacial segregation parameter and n the interfacial unit normal vector. We also note that, if only one fluid component exists, (10.10) reduce to the standard LB propagation step (10.1). Returning to the definition of the extra body force term, H in (10.9), this incorporates both particulate and glycocalyx forces and is defined as

$$\mathbf{H} = \frac{\sigma } {2\rho }\pi \nabla {\rho }_{N} + \mathbf{E}.$$
(10.11)

The left-hand side term imposes an interfacial tension σ on multicomponent particles. Here, π =  ∇  ⋅n is the local curvature, and \({\rho }_{N} = (R - B)/(R + B)\) is a phase field indicator. The right-hand term E is a glycocalyx force that acts upon the particles as defined in the next section.

10.5 The RBC: Glycocalyx Interplay

In the proposed model of the ESL as a porous layer, the porosity is reduced by a compressive encounter with an erythrocyte. As a consequence, the ESL is squashed locally transporting the same mass into a smaller volume and consequently decreasing the porosity in that region. Even in the simplest situation, the ESL-lumen boundary should not be regarded as sharp, and there is an uncertainty region between bulk, lumen, and glycocalyx material [33]. Let us define a variable porosity ε(x, y) that tends to 1 in the lumen region and gradually reduces, as we enter the glycocalyx region, where it approaches a minimum value, εG. This porosity transition is modelled through the increasing smooth function:

$$\varepsilon (\mathbf{x}) = {\varepsilon }_{\mathrm{ G}} + \frac{1 - {\varepsilon }_{\mathrm{ G}}} {2} \left [1 -\tanh (\xi (s - l))\right ],$$
(10.12)

where l is the mean ESL thickness and the parameter 1 ∕ ξ determines the distribution of (i.e., the effective standard deviation of) protein chain lengths, while s(x) denotes distance measured normally to the endothelial boundary. Note that εG ≤ ε(x) ≤ 1 and that, for ε → 1, we have F → H [see (10.9)], and (10.8)–(10.9) reduce to the multicomponent LB Navier–Stokes equations for free multicomponent fluid flows, and the described procedure reduces to the standard LB method for two-component, incompressible fluid. On the other hand, an additional, fictitious, repulsive body force density acts on the drop interface which enters the ESL region, impinging on the lumen. This force distribution is so designed that its accumulation produces an effective Hookean force acting at the center of the local volume. Specifically, the erythrocyte is subjected to a surface force distribution, effective in the ESL only, which is directed everywhere in the drop-surface normal direction. This force device effectively models the glycocalyx as a continuum of elastic springs, with modulus E, gradually decaying from a maximum value, and E G (in the ESL) to 0 (towards the bulk):

$$E(x) = \frac{{E}_{\mathrm{ G}}} {2} \left [1 -\tanh (\xi (s - l))\right ],$$
(10.13)

where all notations are given in correspondence to (10.12). It is important to note that the above force acts solely on the red fluid (drop) and not upon the plasma. Hence, the relative density of the material which comprises the drop may be modelled by appropriate choice of the spring constant E G in the above equation.

A number of simulations have been carried out in the case of an axi-symmetric channel having the same corrugation repeated along the length. Its size (of order of μm) is slightly larger than a single RBC flowing through it, driven by a constant pressure gradient with periodic conditions. At such fine scale, for accuracy purposes, the off-lattice non-slip endothelial surface uses continuous bounce-back conditions [4]. The ESL structure has been modelled as a porous layer of constant thickness over the undulated wall. As one may expect, the average velocity of the drop is slower in the presence of the glycocalyx, which constitutes a hindrance for the lumen flow. Also, the mean deformation of the drop is more pronounced with the glycocalyx force (Fig. 10.4). Hence, when the drop is in the ESL influence region, it is subjected to the elastic force which squeezes and lifts it away from the boundary while making its shape more elongated. Considering the action of the glycocalyx as a sensor of mechanical forces, it is worth computing the shear stress at the ESL/lumen boundary. Our results evidence, in the latter case with ESL, a reduction of the shearing stress either at the wall (due to the plasma only) and at the ESL top (due to the particulate fluid) [33]. It is seen that ESL is more likely to protect the endothelial cells from ESS fluctuations associated with particle transits.

Fig. 10.4
figure 4

The velocity field for the particulate fluid in the region of the endothelium. The extent of the ESL is indicated by the broken line. An enhanced recirculation region is induced by the porous media (bottom), with respect to an experiment without glycocalyx (top). The single deformable drop has been acted on by encountering the glycocalyx body force field. The flow appears to be deflected up which would tend to protect the endothelial cell surface from increased WSS

Full size image

10.6 The MUPHY Software

The simulation of real-life blood flows involves five basic steps: (1) acquisition of MDCT data, (2) data segmentation into a stack of slices, (3) mesh generation from the segmented slices, (4) flow simulation; (5) data analysis and visualization. The MUPHY simulation package is designed to handle generic geometries, such as those provided by the MDCT acquisitions, and to run large-scale simulations on commodity or high-performance hardware resources. The major advantage of MUPHY is the possibility of concurrently simulating fluid dynamics together with suspended bodies at cellular and molecular scales. This multi-scale methodology arises from the combined use of LB and molecular dynamics techniques and has been discussed in previous sections and in paper [3].

In the design of MUPHY, we have followed some basic guidelines that allow us to use the software as is, for a number of diverse applications. The cornerstone of our approach is to use an indirect addressing scheme [11, 37]. At variance with most Navier–Stokes solvers, the LB mesh is Cartesian, providing extreme simplicity in data management and algorithms. At the working resolution, given the size of a reconstructed arterial tree (linear edge ≃ 10 cm), the resulting simulation box would have a size ∼ 1011 Δx 3, clearly beyond the capabilities of most commodity and high-end computers. Hence, for the LB simulation and all the ancillary stages of simulation (mesh construction and data analysis), only the active computational nodes, those residing inside the arterial vessel, should be taken into account, resulting in huge savings in memory (about three orders of magnitude) and CPU time. The scheme relies on representing sparse mesh regions as a compact one-dimensional primary array, complemented by a secondary array that contains the Cartesian location of each element. In addition, neighboring mesh points are accessed by constructing a connectivity matrix whose elements are pointers to the primary storage array. For the LB mesh topology, this matrix requires the storage of 18 ×N mesh elements, where N mesh is the number of active computational nodes. The indirect addressing approach demands some extra programming effort and may result in a minor (and very reduced on modern computing platforms) computational penalty in simulating non-sparse geometries. This choice provides strategic advantages in handling sparse and generic systems, allowing us to handle a number of fluid nodes of the order 109, a size sufficient to study extended arterial systems with a high degree of ramification. We further mention the possibility of simulating the dynamical trajectories of active and passive tracers. Different ways to exchange hydrodynamic information locally between tracers and mesh nodes can be cast within the indirect addressing framework, without major efficiency penalties [13].

To exploit the features of modern computing platforms, the MUPHY code has been highly tuned and parallelized. The code takes advantage of optimizations like (a) removal of redundant operations; (b) buffering of multiply used operations [45], and (c) fusion of the collision and streaming in a single step. This last technique, already in use in other high-performance LB codes [45], significantly reduces data traffic between main memory and processor. With these optimizations in place, we achieve ∼ 30% of the peak performance of a single core of a modern CPU, in line with other highly tuned LB kernels [45]. Indeed, the algorithm for the update of the LB populations has an unfavorable ratio between number of floating point operations and number of memory accesses, no optimized libraries are available as for other computational kernels (e.g., matrix operations or FFTs), and it is not possible to exploit the SIMD-like operations on many modern processors since the LB method has a scattered data access pattern.

10.7 Conclusions

Studying the cardiovascular system and capturing the essence of blood circulation cogently requires to cope with the complexity of such biological fluid, as much as the details of the anatomy under study. From the computational standpoint, taming such complexity is not a trivial task, as it requires to handle several computational actors. Choosing the right computational framework, therefore, is a delicate issue that has been addressed in the present chapter. It was shown that the LB method is an extremely powerful framework to deal simultaneously with blood plasma, RBCs, and the glycocalyx in a unified and consistent form. The versatility of this framework is such to be a good candidate to study biological fluids of different types and at different scales without major differences.

When dealing specifically with blood and the development of cardiovascular disease, it is key to address the detailed structure and dynamics of blood in the surroundings of the endothelium, as recent work has revealed a correlation between the flow-induced mechano-transduction in the glycocalyx and the development of atherosclerosis. The presence of the glycocalyx is supposed necessary for the endothelial cells to respond to fluid shear, and its role is characterized by studying its response to shear stress. A coarse-grained model and a preliminary numerical simulation of the blood flow over the exact, microscale, corrugated EC shape covered by a prototype ESL have been proposed. Another direction we are undertaking is to enhance our current, simplistic, interfacial tension model with additional stresses and bending properties associated with elastic structures. Our current effort is to modify and extend the behaviour our fluid-fluid interface so as to enrich and adapt its existing mechanical properties, in a manner which mimics the thin membrane of erythrocytes.

If, at one hand, the microscopic blood-wall interaction has a noticeable importance for pathological states, on the other hand, the simulation of large-scale circulatory systems relies on sophisticated imaging techniques and powerful simulation methodologies. Owing to the basic assets of hydrokinetic modeling, the unifying LB methodology provides a reliable and robust approach to the understanding of cardiovascular disease in multiple-scale arterial systems, with great potential for impact on biophysical and biomedical applications. The inclusion of RBCs allows to reproduce non-trivial blood rheology and represents a step forward for clinical purposes, as much as for the basic understanding of biomechanics in model and physiological scenarios.