Modeling of Cyclic Bending of Thin Foils Using Higher-Order Strain Gradient Plasticity

Abstract

The plastic behaviors of thin metallic foils, including size effect, Bauschinger effect, and passivation effect, are studied under cyclic bending condition using the strain gradient visco-plasticity theory. The finite element simulations are performed on the cyclic bending of the elasto-viscoplastic thin foils with passivated and unpassivated surfaces. The study is also conducted on the transition from a passivated surface to an unpassivated one. The roles of the dissipative and energetic gradient terms are emphasized. From the results, it is found that the dissipative gradient terms increase the yield strength, while the energetic gradient terms increase the strain hardening, resulting in an anomalous Bauschinger effect. Further, it is observed that the surface passivation effect increases both the normalized bending moment at initial yielding and strain hardening. The comparison between the numerical results of cases with and without passivation demonstrates that the switching of boundary conditions significantly affects the plastic behavior of the foils under cyclic bending.

1 Introduction

Many measurements have revealed that the strength of small-scaled metallic structures undergoing non-uniform plastic deformation is size-dependent [1,2,3,4,5,6,7,8,9,10,11,12]. The conventional plasticity theories are unable to characterize these size-dependent phenomena because such theories do not contain intrinsic material length scales. Many authors [4, 10, 13,14,15,16,17,18,19,20,21,22] have developed various phenomenological gradient theories to describe the mechanical response of materials at small scales. These theories are mainly based on the connection between the plastic strain gradient and geometrically necessary dislocations (GNDs) introduced by Nye [23] and Ashby [24]. The crucial step in constructing the phenomenological strain gradient plasticity (SGP) theories was to express the plastic work in terms of plastic strain and its gradient, thereby introducing one or more length scales into the material description. Later, it was accepted that the higher-order SGP theories are necessary as they include both dissipative (unrecoverable) and energetic (recoverable) gradient contributions [17, 19, 21, 22]. Additional nonstandard boundary conditions are required to solve equilibrium states in higher-order SGP theories.

The exposure of metals to air results in forming a dense oxide layer on the surface [25]. The passivation layer could block the dislocation motion, resulting in dislocation pile-ups, and hindering the plastic flow as the material exceeds the elastic limit [26, 27]. Further, the experiments on hardening and strengthening due to restricted plastic flow have drawn attention in dealing with the effect of surface passivation in the plastic behavior of materials. For example, Xiang and Vlassak [28] showed that a copper film bonded to a substrate could support a larger stress than the independent counterpart. Further experiments on the evaluation of confined shear were reported by Mu et al. [29, 30]. They found that the dependence of shear flow stress on the thickness of the metal layer sandwiched between rigid solids was remarkable, with the smaller being stronger. Recent experiments on the bending of foils with passivation layers showed that the flow stress was enhanced due to the passivation layer [31]. The influence of passivation layers on the bending behavior of thin foils was theoretically analyzed by Evans and Hutchinson [26]. The authors obtained that the higher-order SGP theory was indispensable since the conventional plasticity theory or the lower-order SGP theory could not capture the passivation effect due to the lack of higher-order stress and additional boundary conditions. Several authors analyzed the mechanical behaviors of thin foils and wires with the passivated surface within higher-order SGP theories [32,33,34,35,36,37,38,39]. However, few experimental or theoretical studies focused on investigating the passivation effect during cyclic bending of thin foils.

Most small-scale experimental and theoretical studies adopt monotonic straining and loading conditions that do not deviate significantly from proportional straining. Only a few attempts [6, 28, 32, 33, 40,41,42,43] were made to address the non-proportional straining issues at a small scale. The size effects and the Bauschinger effect were distinctly represented in early cyclic experiments at a small scale. For example, tests on thin foils under cyclic bending showed that a pronounced Bauschinger effect exists [40, 44, 45], i.e., the yield strength under reverse loading is much smaller than that under forward loading. This study is devoted to studying the size effect and passivation effect in the cyclic bending of thin foils with and without passivation.

The paper is organized as follows. The basic equations for Gudmundson’s theory and its finite element (FE) implementation are described briefly in Sect. 2. The boundary value problems of the cyclic bending of thin foils with unpassivated surface, passivated surface, and switching from passivated to unpassivated surface are presented in Sect. 3. The detailed numerical results and discussion are given in Sect. 4. Finally, the conclusions are provided in Sect. 5.

2 Theoretical Basis and Finite Element Implementation

2.1 Strain Gradient Plasticity

The flow theory of strain gradient plasticity proposed by Gudmundson [17] is utilized in this work. The full plastic strain tensor is adopted in Gudmundson’s theory rather than the effective plastic strains used by Fleck and Hutchinson [16]. Both elastic and plastic strains and plastic strain gradients contribute to the internal power during small deformations. Under the assumption that the volume force is ignored, the principle of virtual power of Gudmundson’s theory can be shown as

$$\begin{aligned} \int _V {\left[ {\sigma _{ij} \dot{{\varepsilon }}_{ij} +\left( {q_{ij} -s_{ij} } \right) \dot{{\varepsilon }}_{ij}^{\mathrm{P}} +\tau _{ijk} \dot{{\varepsilon }}_{ij,k}^{\mathrm{P}} } \right] \text{ d }V} =\int _S {\left( {T_{i} \dot{{u}}_{i} +t_{ij} \dot{{\varepsilon }}_{ij}^{\mathrm{P}} } \right) {\text {d}}S} \end{aligned}$$

(1)

where $\sigma _{ij}$ is the Cauchy stress, $s_{ij} =\sigma _{ij} -\delta _{ij} {\sigma _{kk} } {\big /} 3$ is the deviatoric stress, $q_{ij}$ is the microstress power-conjugate to the plastic strain rate $\dot{{\varepsilon }}_{ij}^{\mathrm{P}}$, $\dot{{\varepsilon }}_{ij}$ is the strain rate, and $\tau _{ijk}$ is the higher-order stress power-conjugate to the plastic strain gradient rate $\dot{{\varepsilon }}_{ij,k}^{\mathrm{P}}$. The external virtual power is applied on the boundary S by the conventional traction $T_{i}$, and by the microscopic traction $t_{ij}$. The strain rates satisfy the kinematic relations

$$\begin{aligned} \dot{{\varepsilon }}_{ij} ={\left( {\dot{{u}}_{i,j} +\dot{{u}}_{j,i} } \right) } \big / 2,{\, }\dot{{\varepsilon }}_{ij} =\dot{{\varepsilon }}_{ij}^{\mathrm{E}} +\dot{{\varepsilon }}_{ij}^{\mathrm{P}} ,{\, }\dot{{\varepsilon }}_{ii}^{\mathrm{P}} =0 \end{aligned}$$

(2)

where $\dot{{\varepsilon }}_{ij}^{\mathrm{E}}$ is the elastic strain rate, and $\dot{{u}}_{i}$ is the velocity. According to Eq. (1) and the divergence theorem, the equilibrium equations are

$$\begin{aligned}&\sigma _{ij,j} =0,{\, \, \, }q_{ij} -s_{ij} -\tau _{ijk,k} =0{\, \, \, {\text{ in }}\, }V \end{aligned}$$

(3)

$$\begin{aligned}&\sigma _{ij} n_{j} =T_{i} ,{\, \, \, }\tau _{ijk} n_{k} =t_{ij} {\, \, \, \, \, \, \, \, \, \, \, \, {\hbox {on}}\, }S \end{aligned}$$

(4)

where $\sigma _{ij} =\sigma _{ji}$, $q_{ij} =q_{ji}$, $q_{ii} =0$, $\tau _{ijk} =\tau _{jik}$, $\tau _{iik} =0$, and $n_{i}$ is the outward unit normal to S. The second formulae in Eqs. (3) and (4) are the microscopic force balance and the microscopic traction condition, respectively. The higher-order stress, $\tau _{ijk}$, can be divided into a dissipative part, $\tau _{ijk}^{\mathrm{D}}$, and an energetic part, $\tau _{ijk}^{\mathrm{E}}$,

$$\begin{aligned} \tau _{ijk} =\tau _{ijk}^{\mathrm{D}} +\tau _{ijk}^{\mathrm{E}} \end{aligned}$$

(5)

It is generally considered that microstress is completely dissipative in nature, so

$$\begin{aligned} q_{ij} =q_{ij}^{\mathrm{D}} \end{aligned}$$

(6)

In consideration of the influence of GNDs, it is assumed that the bulk free energy depends upon the elastic strain, $\varepsilon _{ij}^{\mathrm{E}}$, and the plastic strain gradient, $\varepsilon _{ij,k}^{\mathrm{P}}$,

$$\begin{aligned} \varPsi \left( {\varepsilon _{ij}^{\mathrm{E}} ,\varepsilon _{ij,k}^{\mathrm{P}} } \right) =\frac{1}{2}\left( {\varepsilon _{ij} -\varepsilon _{ij}^{\mathrm{P}} } \right) C_{ijkl} \left( {\varepsilon _{kl} -\varepsilon _{kl}^{\mathrm{P}} } \right) +\frac{1}{2}GL^{2}\varepsilon _{ij,k}^{\mathrm{P}} \varepsilon _{ij,k}^{\mathrm{P}} \end{aligned}$$

(7)

where $C_{ijkl}$ is the isotropic elastic stiffness tensor of solids, G is the shear modulus, and L is the energetic length scale. The Cauchy stress is obtained by

$$\begin{aligned} \sigma _{ij} =\frac{\partial \varPsi }{\partial \varepsilon _{ij}^{E} }=C_{ijkl} \left( {\varepsilon _{kl} -\varepsilon _{kl}^{\mathrm{P}} } \right) \end{aligned}$$

(8)

while the energetic higher-order stress can be deduced as

$$\begin{aligned} \tau _{ijk}^{\mathrm{E}} =\frac{\partial \varPsi }{\partial \varepsilon _{ij,k}^{\mathrm{P}} }=GL^{2}\varepsilon _{ij,k}^{\mathrm{P}} \end{aligned}$$

(9)

The effective stress, $\varSigma$, power-conjugate to the effective plastic strain rate, $\dot{{E}}_{\mathrm{P}}$, was defined by Gudmundson [17]. To make sure the dissipation is always non-negative, there is

$$\begin{aligned} \dot{{D}}=\varSigma \dot{{E}}_{\mathrm{P}} =q_{ij} \dot{{\varepsilon }}_{ij}^{\mathrm{P}} +\tau _{ijk}^{\mathrm{D}} \dot{{\varepsilon }}_{ij,k}^{\mathrm{P}} \ge 0 \end{aligned}$$

(10)

and

$$\begin{aligned} \dot{{E}}_{\mathrm{P}}= & {} \sqrt{\frac{2}{3}\dot{{\varepsilon }}_{ij}^{\mathrm{P}} \dot{{\varepsilon }}_{ij}^{\mathrm{P}} +\ell ^{2}\dot{{\varepsilon }}_{ij,k}^{\mathrm{P}} \dot{{\varepsilon }}_{ij,k}^{\mathrm{P}} } \end{aligned}$$

(11)

$$\begin{aligned} \varSigma= & {} \sqrt{\frac{3}{2}q_{ij} q_{ij} +\ell ^{-2}\tau _{ijk}^{\mathrm{D}} \tau _{ijk}^{\mathrm{D}} } \end{aligned}$$

(12)

where $\ell$ is the dissipative length scale. The microstress and dissipative stress are given as

$$\begin{aligned} q_{ij}= & {} \frac{2}{3}\frac{\varSigma }{\dot{{E}}_{\mathrm{P}} }\dot{{\varepsilon }}_{ij}^{\mathrm{P}} \end{aligned}$$

(13)

$$\begin{aligned} \tau _{ijk}^{\mathrm{D}}= & {} \frac{\varSigma }{\dot{{E}}_{\mathrm{P}} }\ell ^{2}\dot{{\varepsilon }}_{ij,k}^{\mathrm{P}} \end{aligned}$$

(14)

Gudmundson’s theory is able to account for a back stress, and hence for the Bauschinger effect. The back stress for Gudmundson’s theory can be explicitly provided by following the procedures outlined by Gurtin and Anand [19]. By Eqs. (5) and (6), the microscopic force balance (3) can be rewritten as

$$\begin{aligned} s_{ij} +\tau _{ijk,k}^{\mathrm{E}} =q_{ij}^{\mathrm{D}} -\tau _{ijk,k}^{\mathrm{D}} \end{aligned}$$

(15)

Following Gurtin and Anand [19], we consider the negative of the energetic term $\tau _{ijk,k}^{E}$ as the back stress. In view of Eq. (9), we have

$$\begin{aligned} \sigma _{ij}^{\mathrm{back}} {=}-\tau _{ijk,k}^{\mathrm{E}} {=}-GL^{2}\varepsilon _{ij,kk}^{\mathrm{P}} \end{aligned}$$

(16)

The back stress is simpler than that in the Gurtin–Anand theory [19]. This is because, from the outset, Gudmundson’s theory allows the plastic free energy to be dependent on the gradient of plastic strain, whereas, Gurtin and Anand’s theory allows the free energy to be dependent on the Burgers tensors. By accounting for Eqs. (13) and (14), the flow rule yields

$$\begin{aligned} s_{ij} +GL^{2}\varepsilon _{ij,kk}^{\mathrm{P}} =\frac{2}{3}\frac{\varSigma }{\dot{{E}}_{\mathrm{P}} }\dot{{\varepsilon }}_{ij}^{\mathrm{P}} -\frac{\varSigma }{\dot{{E}}_{\mathrm{P}} }\ell ^{2}\dot{{\varepsilon }}_{ij,k}^{\mathrm{P}} \end{aligned}$$

(17)

The deviatoric stress $s_{ij}$ represents a second-order partial differential equation for the plastic strain. Unlike conventional plasticity theories, the flow rule here is nonlocal and needs to be augmented by appropriate boundary conditions.

We introduce the flow stress $\sigma _{y} (E_{\mathrm{P}} )$ by taking the gradient effect into account,

$$\begin{aligned} \sigma _{y} \left( {E_{\mathrm{P}} } \right) =\sigma _{Y} \left( {1+{EE_{\mathrm{P}} } \big / {\sigma _{Y} }} \right) ^{N} \end{aligned}$$

(18)

where $\sigma _{Y}$ and E denote the standard uniaxial yield stress and Young’s modulus, respectively; N is the hardening exponent, while $0\le N\le 1$; and $E_{\mathrm{P}} =\int {\dot{{E}}_{\mathrm{P}} \text{ d }t}$, with ${\dot{E}}_{\mathrm{p}}$ being defined in Eq. (11).

The generalized effective visco-plastic equation is established as

$$\begin{aligned} \varSigma \left( {E_{\mathrm{P}} ,\dot{{E}}_{\mathrm{P}} } \right) =\sigma _{y} \left( {E_{\mathrm{P}} } \right) V\left( {\dot{{E}}_{\mathrm{P}} } \right) \end{aligned}$$

(19)

where $V\left( {\dot{{E}}_{\mathrm{P}} } \right) =\left( {{\dot{{E}}_{\mathrm{P}} } {\big / } {\dot{{\varepsilon }}_{0} }} \right) ^{m}$ is the visco-plastic function, and m is the rate sensitivity exponent. According to Panteghini and Bardella [46], $V\left( {\dot{{E}}_{\mathrm{P}} } \right)$ is defined as

$$\begin{aligned} V\left( {\dot{{E}}_{\mathrm{P}} } \right) =\left\{ {\begin{array}{ll} {\dot{{E}}_{\mathrm{P}} } \big / {\left( {2\dot{{\varepsilon }}_{0} } \right) }&{}\quad \text{ if }\,\,{\dot{{E}}_{\mathrm{P}} } \big /{\dot{{\varepsilon }}_{0} }\le \text{1 } \\ 1-{\dot{{\varepsilon }}_{0} } \big / {\left( {2\dot{{E}}_{\mathrm{P}} } \right) }&{}\quad \text{ if }\,\,{\dot{{E}}_{\mathrm{P}} } \big / {\dot{{\varepsilon }}_{0} }{>1 } \\ \end{array}} \right. \end{aligned}$$

(20)

where $\dot{{\varepsilon }}_{0}$ is a constant representing the reference strain rate. When $\dot{{\varepsilon }}_{0} \rightarrow 0$, a rate-independent limit case is obtained [32]. More detailed discussions of $\dot{{\varepsilon }}_{0}$ have been given by Panteghini and Bardella [46] and Fuentes-Alonso and Martínez-Pañeda [47]. More recently, a mixed energetic–dissipative potential was proposed by Panteghini et al. [48], consisting of the sum of quadratic higher-order potentials transitioning into linear terms at different threshold values. Such a potential incorporated in distortion gradient plasticity could give reliable predictions on the cyclic torsion responses of thin metallic wires [43].

2.2 Boundary Conditions

The classical static boundary conditions are

$$\begin{aligned} \sigma _{ij} n_{j} =T_{i}^{0} {\, \, {\text{ on }}\, \, }S_{t} \end{aligned}$$

(21)

whereas the homogeneous higher-order static boundary conditions are adopted, which are called microfree boundary conditions as they describe the dislocations free to exit from the body.

$$\begin{aligned} \tau _{ijk} n_{k} =0{\, \, \text{ on }\, \, }S_{t}^{\mathrm{free}} \end{aligned}$$

(22)

The classical kinematic boundary conditions are

$$\begin{aligned} \dot{{u}}=\dot{{u}}^{0}{\, \, \text{ on }\, \, }S_{u} \end{aligned}$$

(23)

whereas the homogeneous higher-order kinematic boundary conditions called micro-hard boundary conditions are adopted as they describe the dislocations piling up at the boundary.

$$\begin{aligned} \dot{{\varepsilon }}_{ij}^{\mathrm{P}} =0{\, \, \text{ on }\, \, }S_{u}^{\mathrm{hard}} \end{aligned}$$

(24)

2.3 Finite Element Implementation

A backward Euler implementation of Gudmundson’s theory was developed by Martínez-Pañeda et al. [49]. The FE framework uses a user element (UEL) subroutine to implement into the commercial package ABAQUS, which is briefly summarized here. It contains both dissipative and energetic strain gradient contributions. The explicit FE implementations of the higher-order theories of SGP were also described by Danas et al. [50], and Nielsen et al. [51]

The displacements and plastic strains are used as the primary kinematic variables of the FE framework. The nodal variables for the displacement field ${\varvec{u}}$ and the plastic strain field ${\varvec{\varepsilon }}^{\mathrm{P}}$at position ${\varvec{x}}$ are interpolated according to their respective nodal components ${\hat{\varvec{u}}}_{n}$ and ${\hat{\varvec{\varepsilon }}}_{n}^{\mathrm{P}}$, while using a quadratic function in the element as

$$\begin{aligned} {\varvec{u}}=\sum \limits _{n=1}^k {{\varvec{N}}_{n}^{u} {\hat{\varvec{u}}}_{n} } \,\hbox {and}\,{\varvec{\varepsilon }}^{\mathrm{P}}=\sum \limits _{n=1}^k {{\varvec{N}}_{n}^{\varepsilon ^{\mathrm{P}}} {\hat{\varvec{\varepsilon }}}_{n}^{\mathrm{P}} } \end{aligned}$$

(25)

where ${\varvec{N}}_{n}^{u}$ and ${\varvec{N}}_{n}^{\varepsilon ^{\mathrm{P}}}$ are the shape functions related to the displacement and plastic strain, respectively; n is the degree of freedom, and k is the total number of degrees of freedom for the nodal displacements or the nodal plastic strain components. The gradient quantities can be discretized as

$$\begin{aligned} {\varvec{\varepsilon }}=\sum \limits _{n=1}^k {{\varvec{B}}_{n}^{u} } {\hat{\varvec{u}}}_{n} \, \hbox {and}\, \nabla {\varvec{\varepsilon }}^{\mathrm{P}}=\sum \limits _{n=1}^k {{\varvec{M}}_{n}^{\varepsilon ^{\mathrm{P}}} } {\hat{\varvec{\varepsilon }}}_{n}^{\mathrm{P}} \end{aligned}$$

(26)

through matrices ${\varvec{B}}_{n}^{u}$ and ${\varvec{M}}_{n}^{\varepsilon ^{\mathrm{P}}}$. The details of ${\varvec{N}}_{n}^{u}$, ${\varvec{N}}_{n}^{\varepsilon ^{\mathrm{P}}}$, ${\varvec{B}}_{n}^{u}$ and ${\varvec{M}}_{n}^{\varepsilon ^{\mathrm{P}}}$ are given in the supplementary material of Ref. [49]. Eventually, by using the above relations, the internal virtual work shown in Eq. (1) is discretized and can be written as

$$\begin{aligned} \delta W_{i} =\int _V {\left\{ {\left( {{\varvec{B}}_{n}^{u} } \right) ^{\mathrm{T}}\mathbf {\sigma }\delta {\hat{\varvec{u}}}_{n} +\left[ {\left( {{\varvec{N}}_{n}^{\varepsilon ^{\mathrm{P}}} } \right) ^{\mathrm{T}}\left( {{\varvec{q}}-\mathbf {\sigma }} \right) +\left( {{\varvec{M}}_{n}^{\varepsilon ^{\mathrm{P}}} } \right) ^{\mathrm{T}}\mathbf {\tau }} \right] \delta {\hat{\varvec{\varepsilon }}}_{n}^{\mathrm{P}} } \right\} \text{ d }V} \end{aligned}$$

(27)

By solving the global system of linear equations, the increments for each time step $\Delta t$ in nodal displacements and plastic strains are calculated as

$$\begin{aligned} \left[ {{\begin{array}{ll} {{\varvec{K}}^{u,u}} \quad &{} {{\varvec{K}}^{u,\varepsilon ^{\mathrm{p}}}} \quad \\ {{\varvec{K}}^{\varepsilon ^{\mathrm{p}},u}} \quad &{} {{\varvec{K}}^{\varepsilon ^{p},\varepsilon ^{\mathrm{p}}}} \quad \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\Delta {\hat{\varvec{u}}}_{n} } \quad \\ {\Delta {\hat{\varvec{\varepsilon }}}_{n}^{\mathrm{P}} } \quad \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {{\varvec{R}}_{n}^{u} } \quad \\ {{\varvec{R}}_{n}^{\varepsilon ^{\mathrm{P}}} } \quad \\ \end{array} }} \right] \end{aligned}$$

(28)

where ${\varvec{R}}_{n}^{u}$ and ${\varvec{R}}_{n}^{\varepsilon ^{\mathrm{P}}}$ denote the nodal residuals of the displacement and the plastic strain at a given node, respectively; ${\varvec{K}}$ denotes the consistent stiffness matrix defined as the differentiation of ${\varvec{R}}$ with respect to the incremental nodal variables. And,

$$\begin{aligned} {\varvec{R}}_{n}^{u}= & {} \int _V {\left( {{\varvec{B}}_{n}^{u} } \right) ^{\mathrm{T}}\mathbf {\sigma }\text{ d }V} \end{aligned}$$

(29)

$$\begin{aligned} {\varvec{R}}_{n}^{\varepsilon ^{\mathrm{P}}}= & {} \int _V {\left[ {\left( {{\varvec{N}}_{n}^{\varepsilon ^{\mathrm{P}}} } \right) ^{\mathrm{T}}\left( {{\varvec{q}}-\mathbf {\sigma }} \right) +\left( {{\varvec{M}}_{n}^{\varepsilon ^{\mathrm{P}}} } \right) ^{\mathrm{T}}\mathbf {\tau }} \right] \text{ d }V} \end{aligned}$$

(30)

For a detailed FE implementation, the reader is referred to Martínez-Pañeda et al. [49]

3 Modeling the Cyclic Bending of Thin Foils

Responses of the cyclic bending of thin foils with and without passivation, and transitioning from a passivated surface to an unpassivated one are studied here. This work focuses on comparing the differences between the mechanical responses of thin foils with different boundary conditions. The study is conducted in the rate-independent plasticity and cyclic loading conditions. The plane strain and 8-node quadrilateral elements are used in all the cases.

The schematic representation of a foil with length W along $x_{1}$ and thickness H along $x_{2}$ undergoing bending moment in the $x_{3}$-direction is shown in Fig. 1. The aspect ratio is $W/H=4$. At both ends of the foil, longitudinal displacement components are imposed. The surface strain amplitude to deform the foil is shown in Fig. 2. The displacement fields are given as

$$\begin{aligned} u_{1} =\kappa x_{1} x_{2} ,\, {\hbox {at}}\, x_{1} =\pm W/2 \end{aligned}$$

(31)

where $\kappa$ is the curvature bent around the $x_{3}$-axis. In the simulation, different boundary conditions are applied to the foil. For an unpassivated foil, the dislocations can freely slip out from the surface. Therefore, the traction-free boundary conditions are adopted at the top and bottom surfaces of the foil, i.e., $T_{i} =t_{ij} =0$ at $x_{2} =\pm H/2$. Further, the dislocations would pile up around the passivation layer for a passivated foil, with non-vanished GNDs and higher-order stress. At the passivated surfaces, the corresponding higher-order boundary conditions are micro-hard, resulting in the disappearance of plastic strain and plastic strain rate at the surface, i.e., $\dot{{\varepsilon }}_{11}^{\mathrm{P}} =\dot{{\varepsilon }}_{22}^{\mathrm{P}} =0$ at $x_{2} =\pm H/2$ for $\forall x_{1}$. For the symmetry reason, we simplify the simulations by modeling one-fourth of the foil in the structure described as follows. A foil consisting of a total of 400 quadratic quadrilateral elements, with 1301 nodes, is used for the simulation. The bending moment is evaluated as the standard expression

$$\begin{aligned} M=2b\int _0^{H/2} {\sigma _{11} x_{2} \text{ d }x_{2} } \end{aligned}$$

(32)

where the bending moment is normalized by the initial yield moment $M_{Y} ={\sigma _{Y} bH^{2}} {\big /} {\left( {6\sqrt{1-\nu +\nu ^{2}} } \right) }$ [38] and $\nu$ is Poisson’s ratio.

Fig. 1

Schematic of a thin foil under bending: a the foil under bending; b a quarter of the foil with partial boundary conditions

Fig. 2

Applied strain amplitude of the foils under bending

4 Results and Discussion

Numerical results are obtained for the materials with the normalized yield strength $\sigma _{Y} /E=0.002$, Poisson’s ratio $\nu =0.3$, and the rate sensitivity exponent $m=0.05$. The reference strain rate in the visco-plastic function is $\dot{{\varepsilon }}_{0} =10^{-4}\text{ s}^{-1}$. The total loading time is set to be $t=21\, \text{ s }$, while a total loading and unloading cycle lasts for 4 s. Since the determination of the material length scales L and $\ell$ is still an open issue, we employ the dimensionless ratio between the material length scale and the foil dimension to analyze the problems.

4.1 Cyclic Bending Response of Unpassivated Foils

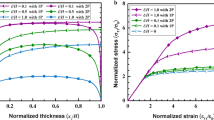
Initially, the cyclic bending of unpassivated foils is considered. The cyclic responses in terms of the normalized moment versus surface strain are shown in Fig. 3. Figure 3a–c show the cases with strain-hardening $N=0.1$, while Fig. 3d presents the case about elastic-perfectly plastic solid (i.e. $N=0)$. The cases of $\ell /H=0$, $L/H=0$ and $\ell /H=L/H=0$ all correspond to the predictions based on classical plasticity theory. For the cyclic bending case with only one dissipative length scale (see Fig. 3a), increasing $\ell /H$ leads to the increase of the bending moment on initial yielding, while the hardening rate is hardly affected. For the cyclic bending case with one energetic length scale (see Fig. 3b), increasing L/H results in an increase in strain hardening, while the yield strength is hardly affected. Comparing Fig. 3a with b, it is observed that, in Fig. 3a, the yield strength under reverse loading is the same as during initial loading; while in Fig. 3b, the yield strength under reverse loading is significantly lower than in forwarding loading. Therefore, it is observed that there is a significant Bauschinger effect in the energetic cases but not in the dissipative cases. Further, for the case $L/H=1.0$, an anomalous Bauschinger effect is found, i.e., recoverable plasticity occurs upon unloading. The reason is the back stress induced by the GNDs residing in the thin foil. This indicates that the GNDs induced by the inhomogeneous deformation are an important origin of the Bauschinger effect. Moreover, the kinematic hardening effect arises from the influence of higher-order stresses on effective stress, according to Eq. (12). Figure 3c, d ($N=\text{0 })$ show the cyclic bending response of thin foils with combined dissipative and energetic gradient effects. The results are presented for $\ell /H=0,{\, }0.1,\,\text{ and }\, 0.3$, while $L/H=0,{\, }0.5,{\, \text{ and }\, }1.0$. It is also demonstrated that combining the two different kinds of gradient effects increases yield strength, additional strain hardening, and the Bauschinger effect. The loading cycle in Fig. 3c ($N=0.1)$ is found to be an open-loop due to the increase in yield stress during plastic deformation, which in Fig. 3d ($N=0)$, is a closed-loop.

Fig. 3

Cyclic bending responses for elastic-plastic foils: a dissipative gradient effects, $N=0.1$; b energetic gradient effects, $N=0.1$; c combination of dissipative and energetic gradient effects, $N=0.1$; d combination of dissipative and energetic gradient effects, $N=0$

Fig. 4

Distributions of plastic strain and stress quantities through half-thickness of the foil at $\kappa H/2=0.01$: a plastic strain $\varepsilon _{11}^{\mathrm{P}}$ for Points I–V; b stress $\sigma _{11}$ for Points I–V

Fig. 5

Distributions of different stress quantities through half-thickness of the foil at $\kappa H/2=0.01$ for Points II–V

Figures 4 and 5 show the distributions of several normalized quantities across half-thickness of the foil for Points I–V, with the foil at the maximum deformation level (i.e., at the surface strain $\kappa H/2=0.01)$. In Fig. 4, it is evident that the curve of Point I, which corresponds to classical plasticity (i.e., $\ell /H=L/H=0)$, is very different from other points with the strain gradient effects considered. For Point I, the plastic strain is zero at the neutral plane. Thereafter, it increases linearly with $x_{2}$, while the stress increases linearly with the thickness initially and then becomes a plateau near the free surface. Further, the classical plastic theory predicts an elastic core near the neutral plane, as shown in Fig. 4. For Points II–V, the plastic strain initially increases linearly with $x_{2}$, then tends to become a platform near the free surface for $\varepsilon _{11,2}^{\mathrm{P}} =0$ at $x_{2} =H {\big /} 2$, and the stress has a significant increase near the free surface. Furthermore, when the plastic strain gradient goes to zero, an elastic boundary layer arises near the free surface of the foil (see Fig. 4a).

Fig. 6

Contours of $\varepsilon _{11}^\mathrm{P}$ (a), $\tau _{{112}}^\mathrm{D}$ (b), $\tau _{{112}}^\mathrm{E}$ (c) , $E_\mathrm{P}$ (d) and $\varvec{\varSigma }$ (e) at $\kappa H/2=0.01$. The hardening exponent is assumed to be $N = 0.1$

Fig. 7

Cyclic bending responses for the passivated foils: a dissipative gradient effects, $N = 0.1$; b energetic gradient effects, $N = 0.1$; c combination of dissipative and energetic gradient effects, $N = 0.1$; d combination of dissipative and energetic gradient effects, $N = 0$

Evolutions of the quantities not included in the conventional plasticity theory are illustrated in Fig. 5. These include the microstress, $q_{11}$, the dissipative higher-order stress, $\tau _{112}^{\mathrm{D}}$, and the energetic higher-order stress, $\tau _{112}^{\mathrm{E}}$, which are normalized by $\sigma _{Y}$, $\ell \sigma _{Y}$ and $L\sigma _{Y}$, respectively. From Fig. 5, it is observed that the microstress $q_{11}$ increases with $x_{2}$ to a plateau. The microstress $q_{11}$ reaches its maximum value at the free surface, and is almost zero near the neutral plane except at Point III. Point III takes only the energetic gradient effects into account, as shown in Fig. 5b, and the value of the microstress near the neutral plane ($x_{2} =0)$ is non-zero. According to the higher-order balance equation (3), this is explained, leading to $q_{11} =\tau _{112,2}^{\mathrm{E}}$ at the neutral plane ($x_{2} =0)$ while $s_{11}$ is about zero. Further, it is also noted that there is an increase in $\tau _{112}^{\mathrm{E}}$ at ${x_{2} } \big / {\left( {H \big / 2} \right) }\in \left[ {0,0.3} \right]$ for Point III, which brings about a non-zero $\tau _{112,2}^{\mathrm{E}} (=q_{11} )$ around $x_{2} =0$. At all the points except Point III, the higher-order stress quantities $\tau _{112}^{\mathrm{D}}$ and $\tau _{112}^{\mathrm{E}}$ almost all vanish at the free surface as a result of the micro-free boundary condition according to Eq. (19), and achieve their maximum value at the neutral plane as the plastic strain gradients $\varepsilon _{11,2}^{\mathrm{P}}$ are the largest. Comparing Fig. 5c with d, it is observed that Point V (the case with $N=0)$ has a larger $\tau _{112}^{\mathrm{E}}$ and smaller $q_{11}$ and $\tau _{112}^{\mathrm{D}}$ than Point IV (the case with $N=0)$. This can be explained by Eqs. (15) and (16). The case with $N=0$ indicates that smaller effective stress $\varSigma$ leads to smaller $q_{11}$ and $\tau _{112}^{\mathrm{D}}$, while a lager $\tau _{112}^{\mathrm{E}}$ is affected by a larger plastic strain gradient as seen in Fig. 4a.

To observe the distributions of higher-order quantities intuitively, the contours obtained for $\varepsilon _{11}^{\mathrm{P}}$, $\tau _{112}^{\mathrm{D}}$ , $\tau _{112}^{\mathrm{E}}$, $E_{\mathrm{P}}$, and $\varSigma$ through half-thickness of the foil at the maximum deformation level $\kappa H/2 = 0.01$ are captured, as shown in Fig. 6. The influences of different values of $\ell$ and L are examined by assuming different cases including $\ell = L = 0$, $\ell = 0.1$ and $L = 0.5$, and $\ell = 0.3$ and $L = 1.0$. It is observed that both dissipative and energetic higher-order stresses increase with corresponding length scales, respectively. Moreover, the plastic strain $\varepsilon _{11}^\mathrm{{P}}$ and the effective plastic strain ${E_\mathrm{{P}}}$ decrease with increasing length scales, showing a strong size effect.

4.2 Responses of Passivated Foils Under Cyclic Bending

In this section, we take the effect of surface passivation into account in the cyclic bending of foils. The passivated boundary condition is modelled as micro-hard boundary conditions at the foil surfaces, requiring that the plastic strain and the plastic strain rate vanish, i.e., $\dot{\varepsilon }_{11}^\mathrm{{P}} = \dot{\varepsilon }_{22}^\mathrm{{P}} = 0$ at ${x_2} = \pm H/2$ for $\forall {x_1}$ . In Fig. 7, it is observed that the influences of both the dissipative and energetic gradient effects are the same as discussed in Sect. 4.1. However, the Bauschinger effect additionally exists in this condition. The main difference is that the bending moment at initial yielding and strain hardening is enhanced, leading to a shrunk hysteresis loop. By considering the passivation effect, the micro-hard boundary conditions require $\varepsilon _{11}^\mathrm{{P}} = 0$ at the surface of foil (i.e. ${x_2} = H/2$), resulting in a solid elastic layer around the surface of the foil.

Fig. 8

Distributions of plastic strain, stress and GND quantities through half-thickness of the foil at $\kappa H/2 = 0.01$: a plastic strain $\varepsilon _{11}^\mathrm{{P}}$ for Points I–V; b stress ${\sigma _{11}}$ for Points I–V; c distribution of GNDs for Point IV; d convergence of the plastic strain

Fig. 9

Distributions of different stress quantities through half-thickness of the foil at $\kappa H/2 = 0.01$ for Points II–V

Fig. 10

Cyclic bending responses with passivation followed by continued cyclic bending with no passivation: a dissipative gradient effects, $N = 0.1$; b energetic gradient effects, $N = 0.1$; c combination of dissipative and energetic gradient effects, $N = 0.1$; d combination of dissipative and energetic gradient effects, $N = 0$

Figures 8 and 9 show the distributions of several normalized quantities across half-thickness of the foil for Points I–V in Fig. 7. In Fig. 8a, it is observed that there is a sharp decline in the value $\varepsilon _{11}^\mathrm{{P}}$ of near the passivated surface due to the micro-hard boundary conditions (i.e., $\varepsilon _{11}^\mathrm{{P}} = 0$ at ${x_2} = H/2$). With consideration of gradient effects, the overall distributions of $\varepsilon _{11}^\mathrm{{P}}$ with ${x_2}$ are found to be much smaller than those in free surface cases (see Figs. 4a and 8a). Figure 8b shows that there is a significant increase in the stress ${\sigma _{11}}$ near the passivated surface, and all stress quantities reach the same value at the surface due to the disappearance of surface plastic strain. The distributions of GND density for Point IV are shown in Fig. 8c. The density of GNDs is expressed by ${\rho _{\mathrm{{GND}}}} = {b^{ - 1}}{\mathop {\mathrm{d}}\nolimits } \varepsilon _{11}^{\mathrm{{P}}}/{\mathop {\mathrm{d}}\nolimits } y$ [4]. The dislocations exit through an unpassivated surface (a dislocation pile-up cannot be sustained), whereupon, at the surface, ${\rho _{\mathrm{{GND}}}} = 0$. By contrast, dislocations pile up at the passivated surface with non-zero ${\rho _{\mathrm{{GND}}}}$, while the plastic strain vanishes (see Fig. 8a). Further, 400 elements are used for all the simulations here as the convergence is verified, as shown in Fig. 8d. As the exact solution is unknown, the simulations are conducted by increasing the number of elements until a satisfactory result is achieved, i.e., no apparent change. The simulations are performed with 400, 800, and 2000 elements to examine the convergence. The plastic strain distributions for the passivated foil $L/H = 0.5,\ell /H = 0.1$ are plotted in Fig. 8d. It is demonstrated that the convergence for the case of 400 elements is satisfactory.

Figure 9a–d show the distributions of different stress quantities through half-thickness of the passivated foil under cyclic bending. The distributions are much different from those in the free surface cases (Fig. 5). All the higher-order stresses for the passivated cases gradually decrease into a negative value with the minimum value at ${x_2} = H/2$. These phenomena result from the sharp decline of $\varepsilon _{11}^{\mathrm{P}}$ near the passivated surface, leading to a negative plastic strain gradient $\varepsilon _{11,2}^{\mathrm{P}}$. The magnitude of microstress $q_{11}$ along $x_{2}$ begins and ends at zero since $q_{11}$ is a function of $\varepsilon _{11}^{\mathrm{P}}$ (see Eq. 13).

4.3 Influence of Switching Boundary Conditions

The boundary-value problem is studied for the cyclic bending of thin foils by switching the micro-hard boundary conditions at the top and bottom surfaces to the micro-free boundary conditions. During the initial 8-s loading, the micro-hard boundary condition is imposed; then, at the end of 8 s, i.e., the position indicated by Point $\alpha$ in Fig. 10a, the micro-free boundary condition is applied. As a result, the hysteresis loop has a significant change after changing the higher-order boundary conditions. Comparing Figs. 10a–d with Figs. 3 and 7, it is observed that the passivation loading stage in Fig. 10 is the same as the pure passivation loading cases, while the un-passivation loading stage is different from the pure un-passivation loading cases. Furthermore, the case $N=0$ shows that the loading cycle becomes an open-loop after switching the higher-order boundary conditions (see Fig. 10d).

In order to investigate the influence of boundary conditions, the cyclic responses are considered in terms of the normalized moment versus loading time, as shown in Fig. 11. Figure 11a shows that, after the boundary conditions change, for the dissipative case (i.e., $\ell /H = 0.3, L/H = 0$), the bending moment at initial yielding in forward loading decreases with loading time, while the yield strength increases in reverse loading. However, for the energetic case (i.e., $\ell /H = 0, L/H = 1.0$), an opposite phenomenon occurs. The classical plasticity theory (i.e., $\ell /H = L/H = 0$) predicts a nearly unchangeable yield strength. At the time point where the switching of boundary conditions is changed, it turns out to be slightly different from Fig. 11a, as can be seen in Fig. 11b. Further, both dissipative and energetic gradient effects increase the yield strength with time in forwarding loading, while the yield strength decreases with time in reverse loading. Comparing Fig. 11a with b, it is observed that, as the boundary condition changes, the size effect decreases as a whole due to the disappearance of passivation layers. In summary, Gudmundson’s theory predicts that the plastic flow restarts after removing passivation and that switching the boundary conditions at different times leads to different mechanical responses.

Fig. 11

Cyclic bending responses of thin foils with boundary conditions changing: a switching of boundary conditions at the beginning of 8 s; b switching of boundary conditions at the beginning of 11 s

5 Conclusions

The plastic responses for the cyclic bending of foils with unpassivated and passivated surfaces, and transitioning from a passivated surface to an unpassivated one, are studied within Gudmundson’s higher-order SGP theory. The numerical scheme includes both energetic and dissipative higher-order stresses, and the size effect under non-proportional loading is investigated. It is shown that the dissipative gradient term controls the strengthening size effect, increasing initial yielding strength, while the energetic gradient term has a notable impact on the strain hardening and the Bauschinger effect. The GNDs induced by the inhomogeneous deformation are an essential origin of the Bauschinger effect. The surface passivation gives rise to the increase of both initial yield strength and strain hardening. Further, the FE simulations show that Gudmundson’s theory can differentiate between the unpassivated and passivated surfaces and predict the recovery of plastic flow after switching from a passivated surface to an unpassivated one.