1 Introduction

The mathematical models that characterize mechanical properties of materials are a continuing issue in engineering research. The simplest and more friendly models for this proposal are the Kelvin–Voigt and Maxwell models [1,2,3,4,5] because of their linearity. The models are not equivalent: the first can explain creep, but not relaxation phenomena, and the second does the opposite. Both models correspond to materials that show only one characteristic time. In order to fit a model to materials showing several characteristic times, generalized linear viscoelastic models are used, connecting several Kelvin–Voigt or Maxwell elements. Every generalized Maxwell (GM) model has an equivalent generalized Kelvin–Voigt (GKV) model. These models correspond to the use of Prony series to adjust creep and relaxation functions. This is a usual option in a variety of engineering applications involving viscoelastic materials [6,7,8,9,10,11,12,13,14,15,16], and the identification of the parameters of the material models is nowadays still a challenging issue [17,18,19,20,21,22,23,24,25,26,27,28].

The engineering practitioner, when using different tools for calculation, must use these viscoelastic models under a specific form [29]. This fact can be relatively important, because commercial software is usually implemented with only some specific viscoelastic models. Therefore, it is necessary for the user to know the conversions to pass from one model to another. Although the existence of these relationships is a well-known fact [4, 5, 30,31,32], it usually implies some numerical methods. A number of these numerical methods have been developed and published [32,33,34,35,36,37]. A recent work [37] offers an interconversion method between the different models by explicit expressions, except for the determination of the zeros of certain polynomials. For some cases it is possible to establish quite explicit formulas of interconversion, which are presented in Ref. [4], but only for the simplest cases.

This work presents the complete set of explicit expressions of the relationships between GKV and GM models of first and second, as well as relaxation and creep coefficients. To the best of our knowledge, there is not a set of explicit formulas published as we propose. From this study, it is also possible to study singular points as maximums, minimums or inflexion points. These relationships allow to move from one model to another equivalent easily and quickly.

2 Characterization of Prony series

In this section, the GKV and GM models as combination of springs and dashpots are characterized.

In the GKV model, only creep, storage and loss compliances are presented. The other way round occurs in the GM model, which presents values for relaxation, storage and loss moduli. As the number of terms n in the models is increased, the equations found in the Laplace domain are more complicated to express in the time or frequency domains. Only in two cases (in the GKV model with compliances and in GM model with moduli), these transformations are simple, since every term in the Laplace domain can be separately transformed in an inverse exponential in the time domain.

The difficulty arises when passing from the coefficients of the creep function to the relaxation moduli, for example. Conversely, the same happens when it is interesting to obtain the compliance coefficients from the relaxation function. In this work, these interconversions are solved when n = 1 or n = 2, in an explicit form. However, in other cases, with n > 2, the expressions as a function of n in the Laplace domain contain a denominator with a polynomial equation of degree n. There is no expression to pass easily from Laplace domain to time domain when a polynomial equation of degree three or more appears in the denominator. For this reason, all coefficients are just solved for n = 1 and n = 2.

In the following sub-sections, the explicit expressions to obtain the coefficients of the relaxation function from the GKV model for n = 1 and n = 2 have been developed. Also, explicit expressions for the creep coefficients from the GM model up to second order have been obtained. Moreover, the general expressions of compliances for GKV models and moduli for GM models are shown.

2.1 GKV model

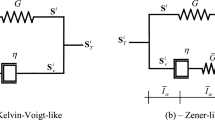
A Kelvin–Voigt element is a set of one spring and one dashpot connected in parallel. The GKV model is a series of Kelvin–Voigt elements with a spring, all them connected in series (Fig. 1). The elastic (E) and viscous (η) parameters are defined as usual

$$\sigma = E \cdot \varepsilon ,$$
(1a)
$$\sigma = \eta \cdot \frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}},$$
(1b)

where σ is the stress and ε is the strain, and the prime indicates the time derivative. The stress along the model is the same for each block in Fig. 1, and the total strain of the model results of the strain summation of every block.

Fig. 1
figure 1

GKV model of order n

Full size image

2.1.1 First order GKV model

By definition, the GKV model of first order has the representation of Fig. 2. This is a commonly used material model and is also known as a linear standard model, or three-parameter model.

Fig. 2
figure 2

GKV model with n =1

Full size image

Considering Eq. (1), the Laplace transform leads to

$$E_{{0_{K} }} \cdot {\mathcal{L}}\left[ {\varepsilon_{0} } \right] = \left( {E_{{1_{K} }} + \eta_{{1_{K} }} \cdot s} \right) \cdot {\mathcal{L}}\left[ {\varepsilon_{1} } \right],$$
(2a)
$${\mathcal{L}}\left[ \varepsilon \right] = {\mathcal{L}}\left[ {\varepsilon_{0} } \right] + \frac{{E_{{0_{\text{K}} }} }}{{E_{{1_{K} }} + \eta_{{1_{K} }} \cdot s}} \cdot {\mathcal{L}}\left[ {\varepsilon_{0} } \right].$$
(2b)

And, taking \({\mathcal{L}}\left[ \sigma \right] = E_{{0_{K} }} \cdot {\mathcal{L}}\left[ {\varepsilon_{0} } \right]\), one has

$${\mathcal{L}}\left[ \varepsilon \right] = \left( {\frac{1}{{E_{0_K} }} + \frac{1}{{E_{{1_K}} + \eta_{1_K} \cdot s}}} \right) \cdot {\mathcal{L}}\left[ \sigma \right].$$
(3)

Then, the mechanical resistance Z, the transfer function of the system, considering the stress as the input and the strain as the output is

$$Z\left( s \right) = \frac{1}{{E_{0_K} }} + \frac{1}{{E_{1_K} + \eta_{1_K} \cdot s}} .$$
(4)

Also, from Eq. (3), the differential equation associated to the GKV model with n = 1 is

$$\sigma + \frac{{\eta_{1_K} }}{{E_{0_K} + E_{1_K} }} \cdot \frac{{\rm d}\sigma }{{\rm d}t} = \frac{{E_{0_K} E_{1_K} }}{{E_{0_K} + E_{1_K} }}\varepsilon + \frac{{E_{0_K} \eta_{1_K} }}{{E_{0_K} + E_{1_K} }} \cdot \frac{{\rm d}\varepsilon }{{\rm d}t}.$$
(5)

The relaxation modulus is the stress response for a constant strain. This is \({\mathcal{L}}\left[ \varepsilon \right] = 1/s\) in the Laplace domain. Therefore, the relaxation modulus is the transfer function from strain to stress. This is the inverse of the product between the mechanical resistance and s. Through conversion from Laplace domain to time domain, the relaxation modulus for the GKV model with n = 1 gives

$$Y = Y_{0} \left[ {1 - p_{1} \left( {1 - {\text{e}}^{{ - \frac{t}{{\tau_{1} }}}} } \right)} \right],$$
(6a)

with

$$Y_{0} = G_{0} = E_{0_K} ,\;p_{1} = \frac{{E_{0_K} }}{{E_{0_K} + E_{1_K} }},\;\tau_{1} = \frac{{\eta_{1_K} }}{{E_{0_K} + E_{1_K} }}.$$
(6b)

The creep compliance in the Laplace domain is the strain of the material under a constant unitary stress: \(\sigma = 1 , t > 0\). This means \({\mathcal{L}}\left[ \sigma \right] = 1/s\). Therefore, \(Y\left( s \right) \cdot J\left( s \right) = s^{ - 2}\), as it is pointed out in Ref. [37]. From Eq. (3), and converting from Laplace domain to time domain, the creep compliance J for the GKV model with n = 1 is

$$J = J_{0} \left[ {1 + q_{1} \left( {1 - {\text{e}}^{{ - \frac{t}{{\lambda_{1} }}}} } \right)} \right],$$
(7a)

with

$$J_{0} = \frac{1}{{E_{0_K} }},\;q_{1} = \frac{{E_{0_K} }}{{E_{1_K} }},\;\lambda_{1} = \frac{{\eta_{1_K} }}{{E_{1_K} }}.$$
(7b)

The frequency response function can be easily found from the expression of the mechanical resistance Eq. (4) just changing the s parameter by iω, where “i” is the imaginary unit. After algebraic operation, the result is a complex function of ω. This function of the angular frequency ω describes the response (strain) of the material under harmonic stresses. The storage compliance (J′) is the real part of this number

$$J^{\prime} = J_{0} \left( {1 + \frac{{q_{1} }}{{1 + \lambda_{1}^{2} \omega^{2} }}} \right).$$
(8a)

The loss compliance (J″) is the absolute value of the imaginary part

$$J^{\prime\prime} = J_{0} \frac{{q_{1} \cdot \lambda_{1} \omega }}{{1 + \lambda_{1}^{2} \omega^{2} }}.$$
(8b)

Storage and loss moduli, in the frequency domain, are defined as the real and imaginary part of the inverse of the creep compliance. This is the response (stress) of the material under harmonic strains. The storage modulus is

$$G^{\prime} = G_{0} \left( {1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }}} \right).$$
(9a)

The loss modulus is

$$G^{\prime\prime} = G_{0} \frac{{p_{1} \cdot \tau_{1} \omega }}{{1 + \tau_{1}^{2} \omega^{2} }}.$$
(9b)

The tangent of the phase angle is the ratio of loss modulus (Eq. (9b)) to storage modulus (Eq. (9a))

$$\tan \delta = \frac{{\frac{{p_{1} \tau_{1} \omega }}{{1 + \tau_{1}^{2} \omega^{2} }}}}{{1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }}}}.$$
(10)

2.1.2 Second order GKV model

Adding a new Kelvin–Voigt element, the GKV model with n = 2 (second order) has the representation of Fig. 3.

Fig. 3
figure 3

GKV model with n = 2

Full size image

Following a deduction analogous to that of the previous section, for the mechanical resistance, the GKV model with n = 2 gives

$$Z = \frac{1}{{E_{0_K} }} + \frac{1}{{E_{1_K} + \eta_{1_K} \cdot s}} + \frac{1}{{E_{2_K} + \eta_{2_K} \cdot s}}.$$
(11)

The differential equation for the GKV model with n = 2, using Laplace transform, presents the following form

$$\begin{aligned} \sigma & + \frac{{E_{0_K} \left( {\eta_{1_K} + \eta_{2_K} } \right) + E_{1_K} \eta_{2_K} + E_{2_K} \eta_{1_K} }}{{E_{0_K} E_{1_K} + E_{0_K} E_{2_K} + E_{1_K} E_{2_K} }} \cdot \frac{{{\text{d}}\sigma }}{{{\text{d}}t}} \\ &+ \frac{{\eta_{1_K} \eta_{2_K} }}{{E_{0_K} E_{1_K} + E_{0_K} E_{2_K} + E_{1_K} E_{2_K} }} \cdot \frac{{{\text{d}}^{2} \sigma }}{{{\text{d}}t^{2} }}\\ &= \frac{{E_{0_K} E_{1_K} E_{2_K} }}{{E_{0_K} E_{1_K} + E_{0_K} E_{2_K} + E_{1_K} E_{2_K} }}\varepsilon\\ & + \frac{{E_{0_K} \left( {E_{1_K} \eta_{2_K} + E_{2_K} \eta_{1_K} } \right)}}{{E_{0_K} E_{1_K} + E_{0_K} E_{2_K} + E_{1_K} E_{2_K} }} \cdot \frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}}\\ &+ \frac{{E_{0_K} \eta_{1_K} \eta_{2_K} }}{{E_{0_K} E_{1_K} + E_{0_K} E_{2_K} + E_{1_K} E_{2_K} }} \cdot \frac{{{\text{d}}^{2} \varepsilon }}{{{\text{d}}t^{2} }}. \\ \end{aligned}$$
(12)

The creep compliance is \(Z\left( s \right)/s\), which is, for the time domain

$$J = J_{0} \left[ {1 + q_{1} \left( {1 - {\text{e}}^{{ - \frac{t}{{\lambda_{1} }}}} } \right) + q_{2} \left( {1 - {\text{e}}^{{ - \frac{t}{{\lambda_{2} }}}} } \right)} \right],$$
(13)

with

$$J_{0} = \frac{1}{{E_{0_K} }},$$
(14a)
$$q_{i} = \frac{{E_{0_K} }}{{E_{i_K} }} ,\quad i = 1,2 ,$$
(14b)
$$\lambda_{i} = \frac{{\eta_{i_K} }}{{E_{i_K} }} ,\quad i = 1,2.$$
(14c)

Following the same procedure as explained to obtain the relaxation modulus in Sect. 2.1.1, the relaxation modulus for the GKV model with n = 2 is defined as

$$Y = Y_{0} \left[ {1 - p_{1} \left( {1 - {\text{e}}^{{ - \frac{t}{{\tau_{1} }}}} } \right) - p_{2} \left( {1 - {\text{e}}^{{ - \frac{t}{{\tau_{2} }}}} } \right)} \right] .$$
(15)

For this model, when analyzing the relaxation coefficients, these coefficients are found as a function of the auxiliary coefficients used in the previous expressions. Creep coefficients can be related to spring and dashpot parameters

$$Y_{0} = E_{{0_K }} ,$$
(16a)
$$p_{1} = \frac{{C_{2_K} \left( {C_{4_K} + C_{5_K} - C_{3_K} } \right)}}{{2C_{4_K} \left( {C_{1_K} + C_{2_K} } \right)}},$$
(16b)
$$p_{2} = \frac{{C_{2_K} \left( {C_{4_K} - C_{5_K} + C_{3_K} } \right)}}{{2C_{4_K} \left( {C_{1_K} + C_{2_K} } \right)}},$$
(16c)
$$\tau_{1} = \frac{1}{{C_{3_K} - C_{4_K} }},$$
(16d)
$$\tau_{2} = \frac{1}{{C_{3_K} + C_{4_K} }},$$
(16e)

with

$$C_{1_K} = \frac{{E_{0_K} E_{1_K} E_{2_K} }}{{E_{0_K} E_{1_K} + E_{0_K} E_{2_K} + E_{1_K} E_{2_K} }},$$
(17a)
$$C_{2_K} = \frac{{E_{0_K}^{2} \left( {E_{1_K} + E_{2_K} } \right)}}{{E_{0_K} E_{1_K} + E_{0_K} E_{2_K} + E_{1_K} E_{2_K} }},$$
(17b)
$$C_{3_K} = \frac{{E_{0_K} \left( {\eta_{1_K} + \eta_{2_K} } \right) + E_{1_K} \eta_{2_K} + E_{2_K} \eta_{1_K} }}{{2\eta_{1_K} \eta_{2_K} }},$$
(17c)
$$C_{4_K} = \frac{{\sqrt {\left( {E_{0_K} \left( {\eta_{1_K} + \eta_{2_K} } \right) + E_{1_K} \eta_{2_K} + E_{2_K} \eta_{1_K} } \right)^{2} - 4\eta_{1_K} \eta_{2_K} \left( {E_{0_K} E_{1_K} + E_{0_K} E_{2_K} + E_{1_K} E_{2_K} } \right)} }}{{2\eta_{1_K} \eta_{2_K} }},$$
(17d)
$$C_{5_K} = \frac{{E_{1_K}^{2} \eta_{2_K} + E_{2_K}^{2} \eta_{1_K} }}{{\eta_{1_K} \eta_{2_K} \left( {E_{1_K} + E_{2_K} } \right)}}.$$
(17e)

Following the same procedure as explained to obtain the storage modulus in Sect. 2.1.1, the storage modulus and the loss modulus are

$$G^{\prime} = G_{0} \left( {1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }} - \frac{{p_{2} }}{{1 + \tau_{2}^{2} \omega^{2} }}} \right),$$
(18)
$$G^{\prime\prime} = G_{0} \left( {\frac{{p_{1} \tau_{1} \omega }}{{1 + \tau_{1}^{2} \omega^{2} }} + \frac{{p_{2} \tau_{2} \omega }}{{1 + \tau_{2}^{2} \omega^{2} }}} \right),$$
(19)

where

$$G_{0} = E_{0_K} .$$
(20)

The storage compliance and the loss compliance are, respectively

$$J^{\prime} = J_{0} \left( {1 + \frac{{q_{1} }}{{1 + \lambda_{1}^{2} \omega^{2} }} + \frac{{q_{2} }}{{1 + \lambda_{2}^{2} \omega^{2} }}} \right),$$
(21)
$$J^{\prime\prime} = J_{0} \left( {\frac{{q_{1} \lambda_{1} \omega }}{{1 + \lambda_{1}^{2} \omega^{2} }} + \frac{{q_{2} \lambda_{2} \omega }}{{1 + \lambda_{2}^{2} \omega^{2} }}} \right).$$
(22)

The tangent of the phase angle is the ratio of loss modulus (Eq. (19)) to storage modulus (Eq. (18))

$$\tan \delta = \frac{{\frac{{p_{1} \tau_{1} \omega }}{{1 + \tau_{1}^{2} \omega^{2} }} + \frac{{p_{2} \tau_{2} \omega }}{{1 + \tau_{2}^{2} \omega^{2} }}}}{{1 - \left( {\frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }}} \right) - \left( {\frac{{p_{2} }}{{1 + \tau_{2}^{2} \omega^{2} }}} \right)}}.$$
(23)

2.1.3 GKV model with n elements

This subsection is devoted to the general case (Fig. 1) with n Kelvin–Voigt elements. The elastic (E) and viscous (η) parameters are defined as usual Eq. (1). The stress along the model is the same for each block in Fig. 3, and the total strain of the model results of the strain summation of every block

$$\varepsilon = \varepsilon_{0} + \mathop \sum \limits_{i = 1}^{n} \varepsilon_{i} ,$$
(24a)
$$\sigma = \sigma_{i} ,\quad i = 0,1, \ldots,\, n.$$
(24b)

For every block, i = 1, 2, …, n, the stress is

$$\sigma = E_{{0_{K} }} \cdot \varepsilon_{0} = E_{{i_{K} }} \cdot \varepsilon_{i} + \eta_{{i_{K} }} \cdot \frac{{{\text{d}}\varepsilon_{i} }}{{{\text{d}}t}} ,\quad i = 1,2,\, \ldots, n.$$
(25)

Taking Laplace transformation of Eqs. (24) and (25) and combining them, one can define the mechanical resistance Z, the transfer function of the system (considering the stress as the input and the strain as the output)

$$Z\left( s \right) = \frac{{{\mathcal{L}}\left[ \varepsilon \right]}}{{{\mathcal{L}}\left[ \sigma \right]}} = \frac{1}{{E_{0_K} }} + \mathop \sum \limits_{i = 1}^{n} \frac{1}{{E_{i_K} + \eta_{i_K} \cdot s}}.$$
(26)

Coming back to time domain, one can obtain the following differential equation

$$\begin{aligned} \sigma + \frac{B}{A}\frac{{\text{d}}\sigma }{{\text{d}}t} + \frac{C}{A}\frac{{{\text{d}}^{2} \sigma }}{{{\text{d}}t^{2} }} + \frac{D}{A}\frac{{{\text{d}}^{3} \sigma }}{{{\text{d}}t^{3} }} + \cdots + \frac{Y}{A}\frac{{{\text{d}}^{n - 1} \sigma }}{{{\text{d}}t^{n - 1} }} + \frac{Z}{A}\frac{{{\text{d}}^{n} \sigma }}{{{\text{d}}t^{n} }} = \frac{a}{A}\varepsilon + \frac{b}{A}\frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}} + \frac{c}{A}\frac{{{\text{d}}^{2} \varepsilon }}{{{\text{d}}t^{2} }} + \frac{d}{A}\frac{{{\text{d}}^{3} \varepsilon }}{{{\text{d}}t^{3} }} + \cdots + \frac{y}{A}\frac{{{\text{d}}^{n - 1} \varepsilon }}{{{\text{d}}t^{n - 1} }} + \frac{z}{A}\frac{{{\text{d}}^{n} \varepsilon }}{{{\text{d}}t^{n} }}. \hfill \\ \end{aligned}$$
(27)

The constant values in Eq. (27) can be found in Appendix A. 1.

The creep compliance in the Laplace domain is the strain of the material under a constant unitary stress: \(\sigma = 1 , t > 0\). This means \({\mathcal{L}}\left[ \sigma \right] = 1/s\). From Eq. (26), and converting from Laplace domain to time domain, the creep compliance J for the GKV model results

$$J = J_{o} \left[ {1 + \mathop \sum \limits_{i = 1}^{n} q_{i} \cdot \left( {1 - { {\text{e}}^{- \frac{t}{\lambda_{i}} }}} \right)} \right],$$
(28)

with

$$J_{0} = \frac{1}{{E_{0_K} }},$$
(29a)
$$q_{i} = \frac{{E_{0_K} }}{{E_{i_K} }},$$
(29b)
$$\lambda_{i} = \frac{{\eta_{i_K} }}{{E_{i_K} }}.$$
(29c)

As in previous sections, the frequency response function can be found from the expression of the mechanical resistance Eq. (26). The storage compliance (J′) is the real part of this number

$$J^{\prime} = J_{0} \left( {1 + \mathop \sum \limits_{i = 1}^{n} \frac{{q_{i} }}{{1 + \lambda_{i}^{2} \omega^{2} }}} \right).$$
(30)

The loss compliance (J″) is the absolute value of the imaginary part

$$J^{\prime\prime}= J_{0} \mathop \sum \limits_{i = 1}^{n} \frac{{q_{i} \lambda_{i} \cdot \omega }}{{1 + \lambda_{i}^{2} \cdot \omega^{2} }}.$$
(31)

2.2 GM model

A Maxwell element is a set of one spring and one dashpot connected in series. The GM model (also known as Maxwell–Wiechert model) is a set of n Maxwell elements with a spring, all connected in parallel (Fig. 4).

Fig. 4
figure 4

GM model

Full size image

The elastic (E) and viscous (η) components are defined as usual Eq. (1). The strain along the model is the same for each block in Fig. 4, and the total stress of the model results of the stress summation of every block.

2.2.1 First order GM model

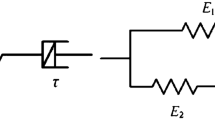
The GM model with n = 1 has the representation of Fig. 5. It is also known as the Zener model.

Fig. 5
figure 5

GM model with n = 1

Full size image

The mechanical resistance Z is the transfer function of the system, considering the stress as the input and the strain as the output

$$Z\left( s \right) = \left( {E_{\infty_M} + \frac{{E_{1_M} \eta_{1_M} \cdot s}}{{E_{1_M} + \eta_{1_M} \cdot s}}} \right)^{ - 1}$$
(32)

The differential equation for the GM model with n = 1, leads to

$$\sigma + \frac{{\eta_{1_M} }}{{E_{1_M} }} \cdot \frac{{{\text{d}}\sigma }}{{{\text{d}}t}} = E_{\infty_M} \cdot \varepsilon + \frac{{\eta_{1_M} }}{{E_{1_M} }}\left( {E_{\infty_M} + E_{1_M} } \right)\frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}}.$$
(33)

As in the previous section, the relaxation modulus can be determined by the relationship \(Z\left( s \right) \cdot Y\left( s \right) = 1/s\)

$$Y = Y_{0} \left[ {1 - p_{1} \left( {1 - {\text{e}}^{{ - \frac{t}{{\tau_{1} }}}} } \right)} \right].$$
(34)

Also, the storage modulus and the loss modulus are the real and imaginary parts of \(Y\left( {{\text{i}}\omega } \right)\)

$$G^{\prime} = G_{0} \left( {1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }}} \right),$$
(35)
$$G^{\prime\prime} = G_{0} \frac{{p_{1} \tau_{1} \omega }}{{1 + \tau_{1}^{2} \omega^{2} }},$$
(36)

with

$$Y_{0} = G_{0} = E_{\infty_M} + E_{1_M} ,$$
(37a)
$$p_{1} = \frac{{E_{1_M} }}{{E_{\infty_M} + E_{1_M} }},$$
(37b)
$$\tau_{1} = \frac{{\eta_{1_M} }}{{E_{1_M} }}.$$
(37c)

The tangent of the phase angle is the ratio of loss modulus (Eq. (36)) to storage modulus (Eq. (35))

$$\tan \delta = \frac{{\frac{{p_{1} \tau_{1} \omega }}{{1 + \tau_{1}^{2} \omega^{2} }}}}{{1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }}}}.$$
(38)

Since \(J\left( s \right) = Z\left( s \right)/s\) and \(J\left( {{\text{i}}\omega } \right) = J^{\prime}\left( \omega \right) + {\text{i}} \cdot J^{\prime\prime}\left( \omega \right)\), the creep compliance, the storage compliance and the loss compliance are

$$J = J_{0} \left[ {1 + q_{1} \left( {1 - {\text{e}}^{{ - \frac{t}{{\lambda_{1} }}}} } \right)} \right],$$
(39)
$$J^{\prime} = J_{0} \left( {1 + \frac{{q_{1} }}{{1 + \lambda_{1}^{2} \omega^{2} }}} \right),$$
(40)
$$J^{\prime\prime} = J_{0} \cdot \frac{{q_{1} \lambda_{1} \omega }}{{1 + \lambda_{1}^{2} \omega^{2} }},$$
(41)

with

$$J_{0} = \frac{1}{{E_{\infty_M} + E_{1_M} }},$$
(42a)
$$q_{1} = \frac{{E_{1_M} }}{{E_{\infty_M} }},$$
(42b)
$$\lambda_{1} = \eta_{1_M} \left( {\frac{1}{{E_{\infty_M} }} + \frac{1}{{E_{1_M} }}} \right).$$
(42c)

2.2.2 Second order GM model

The GM model with n = 2 has the representation of Fig. 6.

Fig. 6
figure 6

GM model with n = 2

Full size image

The mechanical resistance of the GM model with n = 2 is

$$Z = \left( {E_{\infty_M} + \frac{{E_{1_M} \eta_{1_M} \cdot s}}{{E_{1_M} + \eta_{1_M} \cdot s}} + \frac{{E_{2_M} \eta_{2_M} \cdot s}}{{E_{2_M} + \eta_{2_M} \cdot s}}} \right)^{ - 1} .$$
(43)

The differential equation for this model, using Laplace transform, shows the following expression

$$\begin{aligned} \sigma + \frac{{E_{1_M} \eta_{2_M} + E_{2_M} \eta_{1_M} }}{{E_{1_M} E_{2_M} }} \cdot \frac{{{\text{d}}\sigma }}{{{\text{d}}t}} + \frac{{\eta_{1_M} \eta_{2_M} }}{{E_{1_M} E_{2_M} }} \cdot \frac{{{\text{d}}^{2} \sigma }}{{{\text{d}}t^{2} }} = E_{\infty_M} \cdot \varepsilon + \left[ {\frac{{E_{\infty_M} }}{{E_{1_M} E_{2_M} }}\left( {E_{1_M} \eta_{2_M} + E_{2_M} \eta_{1_M} } \right)} + {\eta_{1_M} + \eta_{2_M} } \right] \cdot \frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}} + \frac{{\eta_{1_M} \eta_{2_M} }}{{E_{1_M} E_{2_M} }}\left( {E_{\infty_M} + E_{1_M} + E_{2_M} } \right) \cdot \frac{{{\text{d}}^{2} \varepsilon }}{{{\text{d}}t^{2} }}. \hfill \\ \end{aligned}$$
(44)

The relaxation modulus, the storage modulus and the loss modulus, are defined as follows

$$Y = Y_{0} \left[ {1 - p_{1} \left( {1 - {\text{e}}^{{ - \frac{t}{{\tau_{1} }}}} } \right) - p_{2} \left( {1 - {\text{e}}^{{ - \frac{t}{{\tau_{2} }}}} } \right)} \right],$$
(45)
$$G^{\prime} = G_{0} \left( {1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }} - \frac{{p_{2} }}{{1 + \tau_{2}^{2} \omega^{2} }}} \right),$$
(46)
$$G^{\prime\prime} = G_{0} \left( {\frac{{{{{p}}_{1}} {\tau_{1}} \omega }}{{1 + {{\tau }}_{1}^{2}} \omega^{2} }} + \frac{{{{{p}}_{2}} {{\tau }}_{2}} \omega }{{1 + {{\tau }}_{2}^{2}} {\omega^{2}} } \right),$$
(47)

with

$$Y_{0} = G_{0} = E_{\infty_M} + E_{1_M} + E_{2_M} ,$$
(48a)
$$p_{i} = \frac{{E_{i_M} }}{{E_{\infty_M} + E_{1_M} + E_{2_M} }} ,\quad i = 1,2,$$
(48b)
$$\tau_{\text{i}} = \frac{{\eta_{{{\text{i}}M}} }}{{E_{{{\text{i}}M}} }} ,\quad i = 1,2.$$
(48c)

For this model, when analyzing the creep coefficients, these coefficients are found as a function of auxiliary coefficients used in the previous expressions. Creep coefficients can be related to spring and dashpot parameters. The creep compliance, the storage compliance and the loss compliance are

$$J = J_{0} \left[ {1 + q_{1} \left( {1 - {\text{e}}^{{ - \frac{t}{{\lambda_{1} }}}} } \right) + q_{2} \left( {1 - {\text{e}}^{{ - \frac{t}{{\lambda_{2} }}}} } \right)} \right],$$
(49)
$$J^{\prime} = J_{0} \left( {1 + \frac{{q_{1} }}{{1 + \lambda_{1}^{2} \omega^{2} }} + \frac{{q_{2} }}{{1 + \lambda_{2}^{2} \omega^{2} }}} \right),$$
(50)
$$J^{\prime\prime} = J_{0} \left( {\frac{{q_{1} \lambda_{1} \omega }}{{1 + \lambda_{1}^{2} \omega^{2} }} + \frac{{q_{2} \lambda_{2} \omega }}{{1 + \lambda_{2}^{2} \omega^{2} }}} \right).$$
(51)

The tangent of the phase angle is the ratio of loss modulus (Eq. (47)) to storage modulus (Eq. (46))

$$\tan \delta = \frac{{\frac{{{{p}}_{1} \tau_{1} \omega }}{{1 + \tau_{1}^{2} \omega^{2} }} + \frac{{{{p}}_{2} \tau_{2} \omega }}{{1 + \tau_{2}^{2} \omega^{2} }}}}{{1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }} - \frac{{p_{2} }}{{1 + \tau_{2}^{2} \omega^{2} }}}},$$
(52)

with

$$J_{0} = C_{1_M} + C_{2_M} ,$$
(53a)
$$q_{1} = - \frac{{C_{2_M} \left( {C_{4_M} + C_{5_M} - C_{3_M} } \right)}}{{2C_{4_M} \left( {C_{1_M} + C_{2_M} } \right)}},$$
(53b)
$$q_{2} = - \frac{{C_{2_M} \left( {C_{4_M} - C_{5_M} + C_{3_M} } \right)}}{{2C_{4_M} \left( {C_{1_M} + C_{2_M} } \right)}},$$
(53c)
$$\lambda_{1} = \frac{1}{{C_{3_M} - C_{4_M} }},$$
(53d)
$$\lambda_{2} = \frac{1}{{C_{3_M} + C_{4_M} }},$$
(53e)

with

$$C_{1_M} = \frac{1}{{E_{\infty_M} }},$$
(54a)
$$C_{2_M} = - \frac{{E_{1_M} + E_{2_M} }}{{E_{\infty_M} \left( {E_{\infty_M} + E_{1_M} + E_{2_M} } \right)}},$$
(54b)
$$C_{3_M} = \frac{{E_{\infty_M} \left( {E_{1_M} \eta_{2_M} + E_{2_M} \eta_{1_M} } \right) + E_{1_M} E_{2_M} \left( {\eta_{1_M} + \eta_{2_M} } \right)}}{{2\eta_{1_M} \eta_{2_M} \left( {E_{\infty_M} + E_{1_M} + E_{2_M} } \right)}},$$
(54c)
$$C_{4_M} = \frac{{\sqrt {\left[ {E_{\infty_M} \left( {E_{1_M} \eta_{2_M} + E_{2_M} \eta_{1_M} } \right) + E_{1_M} E_{2_M} \left( {\eta_{1_M} + \eta_{2_M} } \right)} \right]^{2} - 4E_{\infty_M} E_{1_M} E_{2_M} \eta_{1_M} \eta_{2_M} \left( {E_{\infty_M} + E_{1_M} + E_{2_M} } \right)} }}{{2\eta_{1_M} \eta_{2_M} \left( {E_{\infty_M} + E_{1_M} + E_{2_M} } \right)}},$$
(54d)
$$C_{5_M} = \frac{{E_{1_M} E_{2_M} \left( {\eta_{1_M} + \eta_{2_M} } \right)}}{{\eta_{1_M} \eta_{2_M} \left( {E_{1_M} + E_{2_M} } \right)}}.$$
(54e)

2.2.3 GM model with n elements

The mechanical resistance of the GM model, in the frequency domain, is defined as follows

$$Z = \left( {E_{\infty_M} + \mathop \sum \limits_{i = 1}^{n} \frac{{E_{i_M} \eta_{i_M} \cdot s}}{{E_{i_M} + \eta_{i_M} \cdot s}}} \right)^{ - 1} .$$
(55)

The differential equation of the GM model, using Laplace transforms, presents the following form

$$\begin{aligned} \sigma + \frac{B}{A}\frac{{{\text{d}}\sigma }}{{{\text{d}}t}} + \frac{C}{A}\frac{{{\text{d}}^{2} \sigma }}{{{\text{d}}t^{2} }} + \frac{D}{A}\frac{{{\text{d}}^{3} \sigma }}{{{\text{d}}t^{3} }} + \cdots + \frac{Y}{A}\frac{{{\text{d}}^{n - 1} \sigma }}{{{\text{d}}t^{n - 1} }} + \frac{Z}{A}\frac{{{\text{d}}^{n} \sigma }}{{{\text{d}}t^{n} }} = \frac{a}{A}\varepsilon + \frac{b}{A}\frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}} + \frac{c}{A}\frac{{{\text{d}}^{2} \varepsilon }}{{{\text{d}}t^{2} }} + \frac{d}{A}\frac{{{\text{d}}^{3} \varepsilon }}{{{\text{d}}t^{3} }} + \cdots + \frac{y}{A}\frac{{{\text{d}}^{n - 1} \varepsilon }}{{{\text{d}}t^{n - 1} }} + \frac{z}{A}\frac{{{\text{d}}^{n} \varepsilon }}{{{\text{d}}t^{n} }}. \hfill \\ \end{aligned}$$
(56)

The values of the constants in Eq. (56) can be found in Appendix A.1.2.

The relaxation modulus, the storage modulus and the loss modulus for the GM model are defined

$$Y = Y_{0} \left[ {1 - \mathop \sum \limits_{i = 1}^{n} p_{i} \left( {1 - {\text{e}}^{{ - \frac{t}{{\tau_{i} }}}} } \right)} \right],$$
(57)
$$G^{\prime} = G_{0} \left[ {1 - \mathop \sum \limits_{i = 1}^{n} \left( {\frac{{p_{i} }}{{1 + \tau_{i}^{2} \omega^{2} }}} \right)} \right],$$
(58)
$$G^{\prime\prime} = G_{0} \cdot \mathop \sum \limits_{i = 1}^{n} \frac{{p_{i} \tau_{i} \omega }}{{1 + \tau_{i}^{2} \omega^{2} }},$$
(59)

with

$$Y_{0} = G_{0} = E_{\infty_M} + \mathop \sum \limits_{i = 1}^{n} E_{i_M} ,$$
(60a)
$$p_{i} = \frac{{E_{i_M} }}{{E_{\infty_M} + \mathop \sum \nolimits_{i = 1}^{n} E_{i_M} }},$$
(60b)
$$\tau_{i} = \frac{{\eta_{i_M} }}{{E_{i_M} }}.$$
(60c)

3 Plots

It is possible to plot the relaxation modulus vs time, or the creep compliance vs. time, for every viscoelastic model. Also, it is possible to plot storage/loss modulus/compliance and phase angle in the frequency domain. These plots, for each viscoelastic material model, related to a differential Eqs. (27) and (56), have some characteristics that can be determined and can allow to recognize the kind of model one is dealing with.

It is worth noting that the plots for GKV and GM models with n = 1 and with n = 2 are the same, as a function of either relaxation or creep coefficients, regardless of whether they are subsequently expressed as a function of the creep or relaxation coefficients. The reason is that, although the dispositions of springs and dashpots are different for each model, the general expression for moduli and compliances for this number of terms is identical, expressed as relaxation or creep coefficients, respectively.

In order to draw the plots, first the mechanical parameter in question is represented as a function of time or frequency. So, a general plot is represented without any fixed values in both axes. The coefficients of the equations are expressed in a general way.

Once the plot is represented, the maximums and minimums are found with the first order derivative of the mathematical expression, set equal to zero (Appendices A.2.1.1 and A.2.2.1). The inflexion points are found with the second order derivative of the previous mathematical expression also set equal to zero (Appendices A.2.1.2 and A.2.2.2).

Relaxation moduli and creep compliances do not have maximums, minimums or inflexion points. In these cases, the characteristic points are just at zero and at infinite time.

It is important to emphasize that, for models of order greater than two, the determination of the relative extrema and inflexion points depends on the obtaining of the roots of a polynomial of grade greater than four. This avoids getting analytical expressions for these models.

3.1 Models with n = 1

Figure 7 shows a sketch of the characteristic plots of relaxation modulus and creep compliance along the time (Eqs. (6a), (7a), (34) and (39). Both curves are monotonic. The initial values and the limit values for time tending to infinity are characteristics of the model.

Fig. 7
figure 7

Relaxation modulus/creep compliance vs. time: characteristic values. Models with n = 1

Full size image

Figure 8a shows the plot of the storage modulus versus frequency (Eqs. (9a) and (35)): there is one inflexion point and the limits at infinity are also determined. The plot of the loss modulus vs. frequency (Eqs. (9b) and (36)) has also one inflexion point and one maximum (Fig. 8b). The loss modulus tends to zero when the frequency tends to infinity. The plots of the storage and loss compliances (Eqs. (8a), (8b), (40), (41)) have a quite similar structure (Fig. 8a, b).

Fig. 8
figure 8

a, b Storage/loss modulus and c, d compliance vs. frequency: characteristic values. Models with n = 1. The horizontal axes are in logarithmic scale

Full size image

Finally, Fig. 9 plots the phase angle along the frequency (Eqs. (10) and (38)). This plot has also a maximum and one inflexion point (and another theoretical one for frequency zero).

Fig. 9
figure 9

Phase angle vs. frequency: characteristic values. Models with n = 1. The horizontal axes is in logarithmic scale

Full size image

3.2 Plots with n = 2

The general plots between the different mechanical properties versus time or frequency are represented in Figs. 10–12, for the cases when there are two summations in the corresponding Prony series. Figure 10 shows the relaxation modulus and the creep compliance vs. time (Eqs. (13), (15), (45) and (49)). Both curves are monotonic and have a simple value when time tends to infinity.

Fig. 10
figure 10

a Relaxation modulus and b creep compliance vs. time: characteristic values. Models with n = 2

Full size image
Fig. 11
figure 11

Sketches of typical graphs of a, b storage/loss modulus and c, d compliance vs. frequency for models with n = 2. The arrows mark the inflexion points. The horizontal axes are in logarithmic scale

Full size image
Fig. 12
figure 12

Sketch of a typical graph of the tangent of phase angle vs. frequency for models with n = 2. The arrows mark the inflexion points. The horizontal axes are in logarithmic scale

Full size image

From the expression of the storage modulus ((Eqs. (18) and (46)), one can calculate the limit values at frequency zero and tending to infinity. The function is strictly increasing so there are no relative extrema. There are three inflexion points (Fig. 11a) that can be calculated by setting the second derivative of Eqs. (18) and (46) equal to zero. This leads to the fourth grade equation (A.10 found in Appendix A.2.2.2, set equal to zero)

$$\begin{aligned} & x^{4} + \frac{{9\tau_{1}^{4} \tau_{2}^{4} \left( {p_{1} + p_{2} } \right) - p_{1} \tau_{2}^{4} + p_{2} \tau_{1}^{4} }}{{3\tau_{1}^{2} \tau_{2}^{2} \left( {p_{1} \tau_{2}^{2} + p_{2} \tau_{1}^{2} } \right)}}x^{3} + \frac{{3\left( {p_{1} \tau_{1}^{2} + p_{2} \tau_{2}^{2} } \right) - \left( {p_{1} \tau_{2}^{2} - p_{2} \tau_{1}^{2} } \right)}}{{\tau_{1}^{2} \tau_{2}^{2} \left( {p_{1} \tau_{2}^{2} + p_{2} \tau_{1}^{2} } \right)}}x^{2} + \frac{{\left( {\tau_{1}^{2} - \tau_{2}^{2} } \right)\left( {p_{1} \tau_{1}^{2} - p_{2} \tau_{2}^{2} } \right)}}{{\tau_{1}^{4} \tau_{2}^{4} \left( {p_{1} \tau_{2}^{2} + p_{2} \tau_{1}^{2} } \right)}}x - \frac{{p_{1} \tau_{1}^{2} + p_{2} \tau_{2}^{2} }}{{3\tau_{1}^{4} \tau_{2}^{4} \left( {p_{1} \tau_{2}^{2} + p_{2} \tau_{1}^{2} } \right)}} = 0, \\ \end{aligned}$$
(61)

where \(x = \omega^{2}\). This equation can be solved in explicit form. The resulting frequencies for the inflexion points are (Appendix A.3.2)

$$\omega_{{{\text{infl }}i}} = \sqrt {x_{i + 1} } ,\quad i = 1,2,3.$$
(62a)
$$G^{\prime}_{{{\text{infl }}i}} = G_{0} \left( {1 + \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega_{{{\text{infl }}i}}^{2} }} + \frac{{p_{2} }}{{1 + \tau_{2}^{2} \omega_{{{\text{infl }}i}}^{2} }}} \right).$$
(62b)

The loss modulus (Fig. 11b) has two maximums and one minimum, with three inflexions points (Eq. (A.6) in Appendix A.2.2.1). The maximums and the minimum can be localized by deriving the Eqs. (19) and (47) and their frequencies are the roots of the cubic equation

$$x^{3} + \frac{{p_{1} \tau_{1} \tau_{2}^{2} \left( {2\tau_{1}^{2} - \tau_{2}^{2} } \right) + p_{2} \tau_{2} \tau_{1}^{2} \left( {2\tau_{2}^{2} - \tau_{1}^{2} } \right)}}{{\tau_{1}^{3} \tau_{2}^{3} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}x^{2} + \frac{{p_{1} \tau_{1} \left( {\tau_{1}^{2} - 2\tau_{2}^{2} } \right) + p_{2} \tau_{2} \left( {\tau_{2}^{2} - 2\tau_{1}^{2} } \right)}}{{\tau_{1}^{3} \tau_{2}^{3} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}x - \frac{{p_{1} \tau_{1} + p_{2} \tau_{2} }}{{\tau_{1}^{3} \tau_{2}^{3} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}} = 0,$$
(63)

where \(x = \omega^{2}\). This equation can be solved in explicit form. The resulting frequencies are (Appendix A.3.1)

$$\omega_{{{ \text{max} }1}} = \sqrt {x_{1} } < \omega_{{{ \text{max} }2}} = \sqrt {x_{3} } ,$$
(64a)
$$G_{{\rm max} i}^{\prime\prime} = G_{0} \left( {\frac{{{p_{1}}{\tau_{1}} {\omega_{{\rm max}i} } }}{{1 + {\tau_{1}^{2}}{\omega_{{\rm max} i}^{2}} }} + \frac{{{p_{2}} {\tau_{2}}{\omega_{{\rm max} i}} }}{{1 + {\tau_{2}^{2}} {\omega_{{\rm max}i}^{2}} }}} \right) , \ \ i = 1,2,$$
(64b)
$$\omega_{ \text{min} } = \sqrt {x_{2} } ,$$
(64c)
$$G_{ {\rm min} }^{\prime\prime} = G_{0} \left( {\frac{{{p_{1}} {\tau_{1}} {\omega_{ {\rm min} }} }}{{1 + {\tau_{1}^{2}} {\omega_{{\rm min} }^{2} }}} + \frac{{{p_{2}} {\tau_{2}} {\omega_{ {\rm min} }} }}{{1 + {\tau_{2}^{2}} {\omega_{ {\rm min} }^{2} }}}} \right).$$
(64d)

From Eqs. (19) and (47), using Eq. (A.11) (in Appendix A.2.2.2) set equal to zero, where \(x = \omega^{2}\), one obtains the following expression

$$ \begin{aligned} & x^{4} + \frac{{3 {\left( {\tau_{1}^{2} - \tau_{2}^{2} } \right)\left( {p_{1} \tau_{2} - p_{2} \tau_{1} } \right)}}}{{\tau_{1}^{2} \tau_{2}^{2} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}x^{3} + \frac{{3\left[ {\left( {p_{1} \tau_{1}^{3} + \tau_{2}^{3} } \right) - 3\tau_{1} \tau_{2} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)} \right]}}{{\tau_{1}^{3} \tau_{2}^{3} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}x^{2} + \frac{{p_{1} \tau_{1}^{5} + p_{2} \tau_{2}^{5} - 9\tau_{1}^{2} \tau_{2}^{2} \left( {p_{1} \tau_{1} + p_{2} \tau_{2} } \right)}}{{\tau_{1}^{5} \tau_{2}^{5} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}x - 3\frac{{p_{1} \tau_{1}^{3} + p_{2} \tau_{2}^{3} }}{{\tau_{1}^{5} \tau_{2}^{5} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}} = 0. \\ \end{aligned} $$
(65)

The inflexion points correspond to the roots of Eq. (65). This leads (see Appendix A.3.2) to the next frequencies for the three inflexion points (Fig. 11b)

$$\omega_{{G^{\prime\prime}{\text{infl}} 1}} = \sqrt {x_{2} } ,\, \omega_{{G^{\prime\prime}{\text{infl }}2}} = \sqrt {x_{3} } ,\, \omega_{{G^{\prime\prime}{\text{infl }}3}} = \sqrt {x_{4} } ,$$
(66a)
$$G^{\prime\prime}\left( {\omega_{{G^{\prime\prime}{\text{infl}} i}} } \right) = G_{0} \left( {\frac{{p_{1} \tau_{1} \omega_{{G^{\prime\prime}{\text{infl}} i}} }}{{1 + \tau_{1}^{2} \omega_{{G^{\prime\prime}{\text{infl}} i}}^{2} }} + \frac{{p_{2} \tau_{2} \omega_{{G^{\prime\prime}{\text{infl}} i}} }}{{1 + \tau_{2}^{2} \omega_{{G^{\prime\prime}{\text{infl}} i}}^{2} }}} \right) ,\quad i = 1,2,3,$$
(66b)

where the roots of \(x_{i} , i = 2,3,4\) have explicit expressions (Eqs. (A.20)–(A.22)); note that the first root, \(x_{1}\) (Eq. (A.19)) is always negative. Figure 11c, shows the sketch of a typical graph for the storage compliance. This graph is defined by three inflexion points. By deriving Eqs. (21) and (50) twice (Eq. (A.12), in Appendix A.2.2.2), and setting equal to zero, the following polynomial equation is obtained

$$\begin{aligned} x^{4} + {\frac{{9\lambda_{1}^{2} \lambda_{2}^{2} \left( {q_{1} + q_{2} } \right) - q_{1} \lambda_{2}^{4} - q_{2} \lambda_{1}^{4} }}{{3\lambda_{1}^{2} \lambda_{2}^{2} \left( {q_{1} \lambda_{2}^{2} + q_{2} \lambda_{1}^{2} } \right)}}} x^{3} + \frac{{3\left( {q_{1} \lambda_{1}^{2} + q_{2} \lambda_{2}^{2} } \right) - q_{1} \lambda_{2}^{2} - q_{2} \lambda_{1}^{2} }}{{\lambda_{1}^{2} \lambda_{2}^{2} \left( {q_{1} \lambda_{2}^{2} + q_{2} \lambda_{1}^{2} } \right)}}x^{2} + \frac{{\left( {\lambda_{1}^{2} - \lambda_{2}^{2} } \right)\left( {q_{1} \lambda_{1}^{2} - q_{2} \lambda_{2}^{2} } \right)}}{{\lambda_{1}^{4} \lambda_{2}^{4} \left( {q_{1} \lambda_{2}^{2} + q_{2} \lambda_{1}^{2} } \right)}}x - \frac{{q_{1} \lambda_{1}^{2} + q_{2} \lambda_{2}^{2} }}{{3\lambda_{1}^{4} \lambda_{2}^{4} \left( {q_{1} \lambda_{2}^{2} + q_{2} \lambda_{1}^{2} } \right)}} = 0, \hfill \\ \end{aligned}$$
(67)

where \(x = \omega^{2}\). Solving this equation (see Appendix A.3.2), the inflexion points of the graph are

$$\omega_{{J^{\prime}{\text{infl }}1}} = \sqrt {x_{2} } ,\, \omega_{{J^{\prime}{\text{infl }}2}} = \sqrt {x_{3} } ,\,\omega_{{J^{\prime}{\text{infl }}3}} = \sqrt {x_{4} } ,$$
(68a)
$$J^{\prime}\left( {\omega_{{J^{\prime}\inf i}} } \right) = J_{0} \left( {1 + \frac{{q_{1} }}{{1 + \lambda_{1}^{2} \omega_{{J^{\prime}{\text{infl }}i}}^{2} }} + \frac{{q_{2} }}{{1 + \lambda_{2}^{2} \omega_{{J^{\prime}{\text{infl }}i}}^{2} }}} \right) ,\quad i = 1,2,3.$$
(68b)

Figure 11d is the loss compliance versus frequency. The curve has two maximums, one minimum and three inflexion points. Deriving the Eqs. (22) and (51) (see Eq. (A.8), Appendix A in First order derivatives), and setting equal to zero, the resulting polynomial equation is as follows

$$x^{3} + \frac{{q_{1} \lambda_{2} \left( {2\lambda_{1}^{2} - \lambda_{2}^{2} } \right) + q_{2} \lambda_{1} \left( {2\lambda_{2}^{2} - \lambda_{1}^{2} } \right)}}{{\lambda_{1}^{2} \lambda_{2}^{2} \left( {q_{1} \lambda_{2} + q_{2} \lambda_{1} } \right)}}x^{2} + \frac{{q_{1} \lambda_{1} \left( {\lambda_{1}^{2} - 2\lambda_{2}^{2} } \right) + q_{2} \lambda_{2} \left( {\lambda_{2}^{2} - 2\lambda_{1}^{2} } \right)}}{{\lambda_{1}^{3} \lambda_{2}^{3} \left( {q_{1} \lambda_{2} + q_{2} \lambda_{1} } \right)}}x - \frac{{q_{1} \lambda_{2} + q_{2} \lambda_{2} }}{{\lambda_{1}^{3} \lambda_{2}^{3} \left( {q_{1} \lambda_{2} + q_{2} \lambda_{1} } \right)}} = 0,$$
(69)

where \(x = \omega^{2}\). This allows finding the maximums and minimum. The resulting values are

$$\omega_{{J^{\prime\prime}{ \text{max} }1}} = \sqrt {x_{1} } ,\, \omega_{{J^{\prime\prime}{ \text{min} }}} = \sqrt {x_{2} } ,\, \omega_{{J^{\prime\prime}{ \text{max} }2}} = \sqrt {x_{3} } ,$$
(70a)
$$J^{\prime\prime}\left( {\omega_{{J^{\prime\prime}i}} } \right) = J_{0} \left( {\frac{{q_{1} \lambda_{1} \omega_{{J^{\prime\prime}i}} }}{{1 + \lambda_{1}^{2} \omega_{{J^{\prime\prime}i}}^{2} }} + \frac{{q_{2} \lambda_{2} \omega_{{J^{\prime\prime}i}} }}{{1 + \lambda_{2}^{2} \omega_{{J^{\prime\prime}i}}^{2} }}} \right) ,\quad i = { \text{max} }1, { \text{min} }, {\text{max}}2.$$
(70b)

With a second derivation of C (Eq. (A.13), Appendix A.2.2.2), one obtains

$$\begin{aligned} & x^{4} + 3\frac{{ {\left( {\lambda_{1}^{2} - \lambda_{2}^{2} } \right)\left( {q_{1} \lambda_{2} - q_{2} \lambda_{1} } \right)} }}{{\lambda_{1}^{2} \lambda_{2}^{2} \left( {q_{1} \lambda_{2} + q_{2} \lambda_{1} } \right)}}x^{3} +3 \frac{{\left[ { {q_{1} \lambda_{1}^{3} + q_{2} \lambda_{2}^{3} } - 3\lambda_{1} \lambda_{2} \left( {q_{1} \lambda_{2} + q_{2} \lambda_{1} } \right)}\right] }}{{\lambda_{1}^{3} \lambda_{2}^{3} \left( {q_{1} \lambda_{2} + q_{2} \lambda_{1} } \right)}}x^{2} + \frac{{q_{1} \lambda_{1}^{5} + q_{2} \lambda_{2}^{5} - 9\lambda_{1}^{2} \lambda_{2}^{2} \left( {q_{1} \lambda_{1} + q_{2} \lambda_{2} } \right)}}{{\lambda_{1}^{5} \lambda_{2}^{5} \left( {q_{1} \lambda_{2} + q_{2} \lambda_{1} } \right)}}x - 3\frac{{q_{1} \lambda_{1}^{3} + q_{2} \lambda_{2}^{3} }}{{\lambda_{1}^{5} \lambda_{2}^{5} \left( {q_{1} \lambda_{2} + q_{2} \lambda_{1} } \right)}} = 0, \\ \end{aligned}$$
(71)

where \(x = \omega^{2}\). The inflexion points are

$$\omega_{{J^{\prime\prime}{\text{infl}}1}} = \sqrt {x_{2} } ,\, \omega_{{J^{\prime\prime}{\text{infl}}2}} = \sqrt {x_{3} } ,\, \omega_{{J^{\prime\prime}{\text{infl}}3}} = \sqrt {x_{4} } ,$$
(72a)
$$J^{\prime\prime}\left( {\omega_{{J^{\prime\prime}{\text{infl}}\, i}} } \right) = J_{0} \left( {\frac{{q_{1} \lambda_{1} \omega_{{J^{\prime\prime}{\text{infl}}\,i}} }}{{1 + {{\lambda }}_{1}^{2} \omega_{{J^{\prime\prime}{\text{infl}}\, i}}^{2} }} + \frac{{q_{2} \lambda_{2} \omega_{{J^{\prime\prime}{\text{infl}}\,i}} }}{{1 + {{\lambda }}_{2}^{2} \omega_{{J^{\prime\prime}{\text{infl}}\, i}}^{2} }}} \right) , i = 1,2,3.$$
(72b)

The typical curve of the tangent of the phase angle versus frequency has also two maximums, one minimum and three inflexion points (Fig. 12). The first derivative of Eqs. (23) and (52) leads to the polynomic equation (where \(x = \omega^{2}\))

$$ \begin{aligned} x^{3} + \frac{{p_{1} \tau_{2} \left[ {2\tau_{1}^{2} - \tau_{2}^{2} \left( {1 - p_{1} } \right)} \right] + p_{2} \tau_{1} \left[ {2\tau_{2}^{2} - \tau_{1}^{2} \left( {1 - p_{2} } \right)} \right] + p_{1} p_{2} \tau_{1} \tau_{2} \left( {\tau_{1} + \tau_{2} } \right)}}{{\tau_{1}^{2} \tau_{2}^{2} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}x^{2} + \frac{{p_{1} \tau_{1}^{3} + p_{2} \tau_{2}^{3} - 2\tau_{1} \tau_{2} \left[ {p_{1} \tau_{2} \left( {1 - p_{1} } \right) + p_{2} \tau_{1} \left( {1 - p_{2} } \right)} \right] + p_{1} p_{2} \left[ {\tau_{1}^{2} \left( {3\tau_{2} - \tau_{1} } \right) + \tau_{2}^{2} \left( {3\tau_{1} - \tau_{2} } \right)} \right]}}{{\tau_{1}^{3} \tau_{2}^{3} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}x + \frac{{p_{1} p_{2} \left( {\tau_{1} + \tau_{2} } \right) - p_{1} \tau_{1} \left( {1 - p_{1} } \right) - p_{2} \tau_{2} \left( {1 - p_{2} } \right)}}{{\tau_{1}^{3} \tau_{2}^{3} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}} = 0. \\ \end{aligned} $$
(73)

The maximums and minimum are

$$\omega_{{\tan \delta\, {\text{max}}1}} = \sqrt {x_{1} } , \,\omega_{{\tan \delta\, {\text{min}}}} = \sqrt {x_{2} } ,\, \omega_{{\tan \delta \, {\text{max}}2}} = \sqrt {x_{3} } ,$$
(74a)
$$\tan \delta \left( {\omega_{\tan \delta i} } \right) = {\frac{{\frac{{p_{1} \tau_{1} \omega_{\tan \delta i} }}{{1 + \tau_{1}^{2} \omega_{\tan \delta i}^{2} }} + \frac{{p_{2} \tau_{2} \omega_{\tan \delta i} }}{{1 + \tau_{2}^{2} \omega_{\tan \delta i}^{2} }}}}{{1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega_{\tan \delta i}^{2} }} - \frac{{p_{2} }}{{1 + \tau_{2}^{2} \omega_{\tan \delta i}^{2} }}}}},\quad i = \text{max} 1,\,\text{min} ,\,\text{max} 2.$$
(74b)

The second derivative of Eqs. (23) and (52) gives the following equation

$$\begin{aligned}& x^{4} + 3\frac{{ \left\{\tau_{1} \tau_{2} \left[ {p_{1} \tau_{1} \left( {1 + p_{2} } \right) + p_{2} \tau_{2} \left( {1 + p_{1} } \right)} \right] - \tau_{1}^{3} p_{2} \left( {1 - p_{2} } \right) - \tau_{2}^{3} p_{1} \left( {1 - p_{1} } \right)\right\} }}{{\tau_{1}^{2} \tau_{2}^{2} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}} x^{3}\\ & + 3\frac{{\tau_{1}^{3} p_{1} \left( {1 - p_{2} } \right) + \tau_{2}^{3} p_{2} \left( {1 - p_{1} } \right) + \tau_{1} \tau_{2} \left[ {p_{1} \tau_{2} \left( {4p_{1} + 3p_{2} - 3} \right) + p_{2} \tau_{1} \left( {4p_{2} + 3p_{1} - 3} \right)} \right]}}{{\tau_{1}^{3} \tau_{2}^{3} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}x^{2}\\& + \left\{ {\frac{{\tau_{1}^{5} p_{1} \left( {1 - p_{2} } \right)^{2} + \tau_{2}^{5} p_{2} \left( {1 - p_{1} } \right)^{2} + p_{1} p_{2} \tau_{1} \tau_{2} \left[ {\tau_{1}^{3} \left( {1 - p_{2} } \right) + \tau_{2}^{3} \left( {1 - p_{1} } \right)} \right]}}{{\tau_{1}^{5} \tau_{2}^{5} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}} + } {\frac{{p_{1} \tau_{1} \left[ {p_{2} \left( {10 + p_{1} - p_{2} } \right) - 9\left( {1 - p_{1} } \right)} \right] + p_{2} \tau_{2} \left[ {p_{1} \left( {10 + p_{2} - p_{1} } \right) - 9\left( {1 - p_{2} } \right)} \right]}}{{\tau_{1}^{3} \tau_{2}^{3} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}}} \right\}x\\& + 3\frac{{\left( {p_{1} + p_{2} - 1} \right)\left\{ {\left[ {p_{1} \tau_{1}^{3} \left( {1 - p_{2} } \right) + p_{2} \tau_{2}^{3} \left( {1 - p_{1} } \right)} \right] + p_{1} p_{2} \tau_{1} \tau_{2} \left( {\tau_{1} + \tau_{2} } \right)} \right\}}}{{\tau_{1}^{5} \tau_{2}^{5} \left( {p_{1} \tau_{2} + p_{2} \tau_{1} } \right)}} = 0. \\ \end{aligned}$$
(75)

The inflexion points are

$$\omega_{{\tan \delta\, {\text{infl}}1}} = \sqrt {x_{2} }, \omega_{{\tan\, \delta \,{\text{infl}}2}} = \sqrt {x_{3} }, \omega_{{\tan\, \delta \, {\text{infl}}3}} = \sqrt {x_{4} } ,$$
(76a)
$$\tan \delta \left( {\omega_{{\tan \delta \,{\text{infl}} \,i}} } \right) = {\frac{{\frac{{p_{1} \tau_{1} \omega_{{\tan \delta \,{\text{infl}} \,i}} }}{{1 + \tau_{1}^{2} \omega_{{\tan \delta \,{\text{infl}} \,i}}^{2} }} + \frac{{p_{2} \tau_{2} \omega_{{\tan \delta \,{\text{infl}}\,i}} }}{{1 + \tau_{2}^{2} \omega_{{\tan \delta \,{\text{infl}} \,i}}^{2} }}}}{{1 - \frac{{p_{1} }}{{1 + \tau_{1}^{2} \omega_{{\tan \delta \,{\text{infl}} \,i}}^{2} }} - \frac{{p_{2} }}{{1 + \tau_{2}^{2} \omega_{{\tan \delta \,{\text{infl}} \,i}}^{2} }}}}},\quad i = 1,\,2,\,3.$$
(76b)

4 Relationships between GKV and GM models and relaxation and creep coefficients

The equivalence of GKV and GM models of the same order is well known. Nevertheless, unfortunately, it is not easy to find the algebraic expressions of this equivalence. In this section, these expressions are determined and presented in a closed form, up to second order models. Moreover, the relaxation coefficients for the moduli equations and the creep coefficients for the compliance equations are also found. Furthermore, explicit formulas are presented for the parameters of the material models (GKV and GM) from relaxation or creep coefficients. These relationships, up to second order models, can be found in Appendices B.1 and B.2.

In the diagram of Fig. 13, an application of the formulas developed in this work is shown, by way of example. In this case, starting from a dynamic mechanical analysis (DMA) test, the parameters of the relaxation model can be obtained. This is carried out using the equations and their corresponding expressions in Appendix A. From these relaxation parameters, by means of the interconversion expressions of the table shown in Appendix B, the parameters corresponding to the creep test can be obtained. In addition, with the same table, the parameters of the material models are obtained, whether they are of the GM or GKV model.

Fig. 13
figure 13

Flowchart of an application: obtaining the creep and relaxation parameters, as well as the GM and GKV material models, from a dynamic thermomechanical analysis (DMA) test

Full size image

5 Conclusions

The GKV and GM models of the same order are related to each other. These relationships can be helpful for the engineering practitioner because computational simulators are implemented with just some specific combinations of springs and dashpots. The explicit relationships between the GKV and GM models, up to order two, are found. Moreover, explicit formulas are found for the position of the characteristic points (maxima, minima and inflexion points) of the storage and loss compliances/moduli.

The interconversion formulas for models of first and second order have also been developed. The complete set of interconversion formulas between GKV, GM, relaxation coefficients and creep coefficients have been presented. Therefore, the engineering practitioner can easily have a simple guide to change from one model to another if necessary.