Introduction

Landslide hazards are common in China, especially in Southwest China and the Three Gorges Reservoir area. For instance, there are over 4200 landslides distributed throughout the Three Gorges Reservoir area (Yin et al. 2010). The movement and failure of landslides can cause substantial damage and loss of life. Forecasting the displacement of continuously deforming landslides is considered an important and economical way of avoiding or reducing losses (Ma et al. 2017c).

Landslide displacement forecasting is complex and remains a key challenge in natural hazard research. This challenge arises because landslides are nonlinear, dynamic systems (Qin et al. 2002), and the associated movements can be induced by different causes, such as geological factors, morphological factors, and human activities (Ma et al. 2017b). To date, various growth theories and models have been proposed to predict landslide displacement. In additional, these studies can be divided into three categories: deterministic models, statistical models, and computational intelligence models (Ma et al. 2007c). Deterministic models, such as the Saito model (Saito 1965) and Fukuzono model (Fukuzono 1985), involve creep theory and physical mechanisms and provide clear physical explanations of landslides. However, they can be applied only in limited cases. Statistical models, such as the Verhulst model (Yin and Yan 1996) and autoregressive integrated moving average (ARIMA) (Carlà et al. 2016), have been applied to predict slope displacement. Because statistical models are inherently linear, the nonlinear characteristics of landslide processes are ignored. Other techniques are generally integrated with these approaches to improve the prediction performance (Du et al. 2013; Zhou et al. 2016). Computer intelligence methods, such as artificial neural networks (ANNs) (Du et al. 2013), extreme learning machines (ELMs) (Lian et al. 2013, 2014; Cao et al. 2016), and support vector machines (Ren et al. 2014; Zhou et al. 2016), have become increasingly popular approaches to driving forecasting models of landslide displacement. Among these methods, ANNs have been found capable of approximating arbitrary, nonlinear, and dynamic systems with high precision (Kilian and Siegelmann 1996). ANNs have been successfully applied to predict landslide displacement in a variety of cases (Neaupane and Achet 2004; Chen and Zeng 2012; Du et al. 2013; Lian et al. 2015).

However, most studies of landslide displacement forecasting mainly focused on deterministic point forecasting and did not consider the random variability in the predictions of displacement, nor do they consider the epistemic uncertainty in landslide systems. Different types of uncertainties exist in landslide systems (Wu et al. 2013), and these uncertainties represent considerable obstacles to landslide displacement forecasting. Determining how to evaluate the uncertainty in landslide displacement forecasting remains a problem that must be solved.

Probabilistic forecasting can be used to quantify the uncertainty associated with deterministic point forecasting (Wan et al. 2014). It can offer prediction intervals (PIs) and measure the confidence that we have in the output of a model for future inputs (Khosravi et al. 2010). Recently, probabilistic forecasting has attracted increased research interest and has been successfully applied to construct PIs in a variety of fields, including electricity market price prediction (Shrivastava and Panigrahi 2013; Khosravi et al. 2013; Wan et al. 2014), baggage handling system prediction (Khosravi et al. 2010), hydrologic river flow prediction (Shrestha and Solomatine 2006), and industrial equipment degradation prediction (Lins et al. 2015).

However, only a few studies have built probabilistic forecasting models of landslide displacement. Lian et al. (2016) applied an ANN with random hidden weights for the probabilistic forecasting of landslide displacement. The bootstrap approach is the simplest and most frequently used technique to evaluate uncertainties since it does not require complex computations (Srivastav et al. 2007). However, to the best of our knowledge, the bootstrap approach has yet to be used to evaluate the epistemic uncertainties in landslide displacement prediction. In this study, we propose a hybrid approach based on bootstrap, ELM, and ANN methods to construct PIs and evaluate the epistemic uncertainties that exist in landslide displacement forecasting. The Shuping landslide in the Three Gorges Reservoir area has been chosen as a case study to explore the usefulness of the Bootstrap-ELM-ANN-based approach.

Sources of epistemic uncertainty in landslide deformation analyses

Epistemic uncertainty is associated with imperfect or inadequate knowledge (Walker et al. 2003) and pervades all aspects of the natural and physical environment (Regan et al. 2002). Based on the classification of Regan et al. (2002), epistemic uncertainty in landslide deformation analyses can be divided into six categories: measurement error, systematic error, natural variation, inherent randomness, model uncertainty, and subjective judgment.

Measurement error is caused by imperfections in measuring instruments or techniques. This type of uncertainty can be managed by reporting measurements with bounds or using statistical methods if multiple or repeated measurements are taken.

Systematic error results from the bias in measuring instruments or sampling procedures, such as the erroneous calibration of measuring instruments or consistently incorrect recordings. Systematic error can be reduced by recognizing and removing the bias in an experimental procedure. However, this type of uncertainty is notoriously difficult to discern.

Natural variation exists in natural systems, such as landslides. A landslide system changes temporally and spatially (Ma et al. 2017a), as do the associated parameters of interest, such as the density, friction angle, and cohesive strength of landslide materials. This type of uncertainty can be qualified statistically.

Inherent randomness in a natural system occurs not due to the limited understanding of the driving processes of patterns but because the system is inherently random.

Model uncertainty results from the abstractions of a natural system. This type of uncertainty occurs in two main forms. First, only relevant and major variables and processes are included in models. However, less important variables and processes are excluded. For example, although snowmelt might have some effect on landslide movements in the Three Gorges Reservoir area, the effect is sufficiently weak as to be ignored when evaluating many problems. In the landslide area, the average number of days with precipitation that falls as snow per year is 3.9, i.e., there is very little snow in the winter in the landslide area. Thus, the ANN models currently used to predict landslide deformation do not explicitly include parameters that describe snowmelt. Second, model uncertainty results from the abstract methods of representing observed processes. For instance, curve fitting is a common approach used to build landslide forecasting models and provides a mathematical expression given empirical data points. Such abstraction and extrapolation are always associated with model uncertainty.

Subjective judgment results from the interpretation of data, and this is especially the case when insufficient data are available.

The abovementioned epistemic uncertainty in landslide systems is often compound, and impossible to distinguish or separate conclusively (Regan et al. 2002; Uusitalo et al. 2015). However, a clear understanding of the sources of epistemic uncertainty in landslide deformation analyses helps researchers identify, treat, and account for compound uncertainty.

Probabilistic forecasting of landslide displacement based on the Bootstrap-ELM-ANN method

Probabilistic forecasting

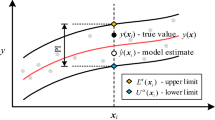
Probabilistic forecasting can provide PIs to quantify the uncertainty associated with traditional point forecasting. A PI consists of upper and lower limits (Shrestha and Solomatine 2006). These limits are called the upper bound and lower bound (Fig. 1). The future targets are expected to fall within the constructed PIs based on the nominal probability (1 − α) × 100%, which is deemed the PI nominal confidence (PINC). The α level, or significance level, represents the “lack of confidence” and is the probability of not capturing the value of the parameter.

Fig. 1
figure 1

Schematic diagram of PI construction

Full size image

The uncertainty in ANN prediction includes the model uncertainty and noise. Model uncertainty is mainly caused by the misspecification of the neural network structure and parameters, while noise is mainly caused by the stochastic characteristics of regression data (Wan et al. 2014).

Given a time series\( {\left\{\left({X}_i,{t}_i\right)\right\}}_{i=1}^N \), such as landslide displacement, the prediction target can be expressed as follows:

$$ {t}_i=g\left({X}_i\right)+\varepsilon \left({X}_i\right) $$
(1)

where t i is the ith prediction target, g(X i ) is the true regression mean, X i is the vector of inputs, and ε(Xi) is the noise, which is assumed to be normally distributed with mean zero and variance \( {\widehat{\sigma}}_{\varepsilon}^2 \) (Shrestha and Solomatine 2006; Shrivastava and Panigrahi 2013; Wan et al. 2014).

In practice, the output of the ANN, \( \widehat{g}\left({X}_i\right) \), can be regarded as an estimate of the true regression g(X i ). Thus, the prediction error can be expressed as follows:

$$ {t}_i-\overset{\hat{\mkern6mu} }{g}\left({X}_i\right)=\left[g\left({X}_i\right)-\widehat{g}\left({X}_i\right)\right]+\varepsilon \left({X}_i\right) $$
(2)

where \( {t}_i-\widehat{g}\left({X}_i\right) \) is the total prediction error and \( g\left({X}_i\right)-\widehat{g}\left({X}_i\right) \) is the error of the ANN estimate with respect to the true regression.

Assuming that the estimation error and the noise are statistically independent, the variance of the total prediction error, \( {\widehat{\sigma}}_t^2\left({X}_i\right) \), can be expressed as follows:

$$ {\widehat{\sigma}}_t^2\left({X}_i\right)={\widehat{\sigma}}_g^2\left({X}_i\right)+{\widehat{\sigma}}_{\varepsilon}^2\left({X}_i\right) $$
(3)

where \( {\widehat{\sigma}}_g^2\left({X}_i\right) \) and \( {\widehat{\sigma}}_{\varepsilon}^2\left({X}_i\right) \) are the variance of the model uncertainty and the variance of the noise, respectively.

PIs with a prescribed confidence level of (1 − α) × 100% can be constructed as follows:

$$ {L}_t^{\left(\alpha \right)}\left({X}_i\right)=\widehat{g}\left({X}_i\right)-{z}_{\alpha /2}\sqrt{{\widehat{\sigma}}_t^2\left({X}_i\right)} $$
(4)
$$ {U}_t^{\left(\alpha \right)}\left({X}_i\right)=\widehat{g}\left({X}_i\right)+{z}_{\alpha /2}\sqrt{{\widehat{\sigma}}_t^2\left({X}_i\right)} $$
(5)

where \( {L}_t^{\left(\alpha \right)}\left({X}_i\right) \) and \( {U}_t^{\left(\alpha \right)}\left({X}_i\right) \) are the lower bound and the upper bound, respectively, and zα/2 is the critical value of the standard normal distribution.

The prediction interval coverage probability (PICP) and average coverage error (ACE) are two indices used to evaluate the correctness of the approximated PIs.

The PICP reflects the degree of reliability of PIs and is defined as follows:

$$ \mathrm{PICP}=\frac{1}{N_t}\sum \limits_{i=1}^{N_t}{I}_i^{\left(\alpha \right)} $$
(6)

where N t is the number of test samples. \( {I}_i^{\left(\alpha \right)} \) is defined in Eq. (7):

$$ {I}_i^{\left(\alpha \right)}=\left\{\begin{array}{c}1\kern0.75em {t}_i\in \left[{L}_t^{\left(\alpha \right)}\left({X}_i\right),{U}_t^{\left(\alpha \right)}\left({X}_i\right)\right]\\ {}0\kern0.75em {t}_i\notin \left[{L}_t^{\left(\alpha \right)}\left({X}_i\right),{U}_t^{\left(\alpha \right)}\left({X}_i\right)\right]\end{array}\right. $$
(7)

The ACE reflects the difference between the PICP and PINC and is defined by Eq. (8):

$$ \mathrm{ACE}=\mathrm{PICP}\hbox{-} \mathrm{PINC} $$
(8)

For high-quality PIs, the value of the PICP should be as close to 100% as possible, and the value of ACE should be as close to zero as possible (Wan et al. 2014).

Bootstrapping

Bootstrapping (Efron 1979) is a general and robust statistical reference technique. The idea behind bootstrapping is to perform random sampling with replacement to estimate the unknown distribution. This technique allows the sampling distribution of almost any statistic to be estimated by uniform sampling of the original time series (Wan et al. 2014). Bootstrap sampling can be based on pairs or residuals (Lins et al. 2015). Paired bootstrapping involves sampling the observations from an original data set with replacement. Additionally, residual-based bootstrapping involves sampling the residuals determined via a regression model adjusted over the original data set with replacement. Paired bootstrapping was used in the present study.

Extreme learning machines

An ELM (Huang et al. 2006) is a novel feedforward neural network with a single hidden layer. The input weights in ELMs are randomly assigned, and the output weights are analytically determined using a simple matrix computation. An ELM-trained model can produce good prediction results and learn thousands of times faster than a neural network using backpropagation (Huang et al. 2006). Formally, the ELM algorithm can be stated as follows.

Given a time series with N samples \( {\left\{\left({X}_i,{t}_i\right)\right\}}_{i=1}^N \), such that X i  ∈ Rn and t i  ∈ Rm, a standard ELM with L hidden nodes and an activation function ψ(⋅) can be mathematically modeled as follows:

$$ {f}_L\left({X}_j\right)=\sum \limits_{i=1}^L{\beta}_i\psi \left({a}_i\cdot {X}_j+{b}_i\right)={t}_j,\kern0.5em j=1,\cdots, N $$
(9)

where a i  = [ai1, ai2, ⋯, a in ]T is the weight vector connecting the ith hidden node and the input nodes, β i  = [βi1, βi2, ⋯, β in ]T is the weight vector connecting the ith hidden node and the output nodes, b i is the threshold of the ith hidden node, and ψ(a i  ⋅ X i  + b i ) is the output of the ith hidden node with respect to the input X i .

For simplicity, the above equation can be written as follows:

$$ H\beta =T $$
(10)

where H is the output matrix of the hidden layer, β is the matrix of the output weight, and T is the matrix of targets. These variables can be expressed as follows:

$$ H={\left[\begin{array}{ccc}h\left({a}_1\cdot {X}_1+{b}_1\right)& \cdots & h\left({a}_L\cdot {X}_1+{b}_L\right)\\ {}\vdots & \vdots & \vdots \\ {}h\left({a}_1\cdot {X}_N+{b}_1\right)& \cdots & h\left({a}_L\cdot {X}_N+{b}_1\right)\end{array}\right]}_{N\times L} $$
(11)
$$ \beta ={\left[\begin{array}{c}{\beta}_1^T\\ {}\vdots \\ {}{\beta}_L^T\end{array}\right]}_{L\times m}\ \mathrm{and}\kern0.5em \mathrm{T}={\left[\begin{array}{c}{t}_1^T\\ {}\vdots \\ {}{t}_N^T\end{array}\right]}_{N\times m} $$
(12)

The ELM training process is used to find a least squares solution, \( \widehat{\beta} \), of Eq. (10). The least squares solution with the smallest norm is expressed as follows:

$$ {\beta}^{\ast }={H}^{+}T $$
(13)

where H+ is the Moore-Penrose generalized inversion of matrix H. Using the Moore-Penrose inverse method, an ELM can achieve a good generalization performance and an extremely efficient learning speed.

Bootstrap-ELM-ANN-based method for PIs construction

The overall framework of PIs construction based on the bootstrap, ELM, and ANN methods is shown in Fig. 2. This framework consists of four stages: (1) bootstrap sampling and ELM training, (2) estimation of model uncertainty, (3) estimation of noise, and (4) PIs construction.

Fig. 2
figure 2

The overall framework of PIs construction for landslide displacement based on the Bootstrap-ELM-ANN approach

Full size image
  1. (1)

    Bootstrap sampling and ELM training

A bootstrap sample set B1, B2, ⋯, B B with N samples is chosen by random sampling with replacement from the original time series \( {\left\{\left({X}_i,{t}_i\right)\right\}}_{i=1}^N \). After the generation of each bootstrap set, ELM training is performed. A total of B ELMs are trained.

  1. (2)

    Estimation of the true regression mean and model uncertainty

After the ELM models have been trained, it is possible to use the input data X i in the trained models. The true regression mean, \( {\widehat{g}}_q\left({X}_i\right) \), can be calculated by averaging the outputs of B trained ELMs as follows:

$$ \widehat{g}\left({X}_i\right)=\frac{1}{B}\sum \limits_{q=1}^B{\widehat{g}}_q\left({X}_i\right) $$
(14)

where \( {\widehat{g}}_q\left({X}_i\right) \) is a prediction value of input sample X i generated by the qth bootstrapped ELM. The variance in the model uncertainty, \( {\widehat{\sigma}}_g^2\left({X}_i\right) \), can be estimated from the variance in the outputs of the trained B ELMs using Eq. (15):

$$ {\widehat{\sigma}}_g^2\left({X}_i\right)=\frac{1}{B-1}\sum \limits_{q=1}^B{\left({\widehat{g}}_q\left({X}_i\right)-\widehat{g}\left({X}_i\right)\right)}^2 $$
(15)
  1. (3)

    Estimation of noise

According to Eq. (3), \( {\widehat{\sigma}}_{\varepsilon}^2\left({X}_i\right) \) can be obtained as follows:

$$ {\widehat{\sigma}}_{\varepsilon}^2\left({X}_i\right)\sim E\left(\left({t}_i-\widehat{g}\left({X}_i\right)\right)\right)-{\widehat{\sigma}}_g^2 $$
(16)

Then, a set of squared residuals, r2(X i ), is determined using Eq. (17):

$$ {r}^2\left({X}_i\right)=\max \left({\left[{t}_i-\widehat{g}\left({X}_i\right)\right]}^2-{\widehat{\sigma}}_g^2\left({X}_i\right),0\right) $$
(17)

After the squared residuals r2(X i ) are obtained, a new data set, \( {D}_{r^2} \), is generated using the residuals and corresponding inputs:

$$ {D}_{r^2}={\left\{{X}_i,{r}^2\left({X}_i\right)\right\}}_{i=1}^N $$
(18)

A new ANN can be trained using the data set \( {D}_{r^2} \) to estimate the variance in the noise \( {\widehat{\sigma}}_{\varepsilon}^2\left({X}_i\right) \). To ensure a positive variance, an exponential activation function is used in the new ANN.

  1. (4)

    PIs construction

After the true regression mean \( {\widehat{g}}_q\left({X}_i\right) \), the variance in the model uncertainty \( {\widehat{\sigma}}_g^2\left({X}_i\right) \), and the variance in the noise \( {\widehat{\sigma}}_{\varepsilon}^2\left({X}_i\right) \) are obtained, PIs with (1 − α) × 100% PINC can be obtained from Eqs. (3), (4), and (5).

Application to the Shuping landslide, Three Gorges Reservoir, China

Geological setting

The Shuping landslide, a colluvial landslide (Yin et al. 2016), is situated on the right bank of the Yangtze River, approximately 47 km northwest of the Three Gorges Reservoir Dam (110°37′00″ E, 30°59′37” N; see Fig. 3a for location). The landslide is an ancient landslide (Wang et al. 2005, 2008) composed of two blocks (Fig. 3b, c). The landslide is approximately 800 m long and 700 m wide. The thickness of the landslide body varies from 30 and 70 m. The entire planar area of the landslide is approximately 0.55 million square meters, and the landslide volume is approximately 27 million cubic meters. The planar area of block 1 is 0.35 million square meters and the volume of block 1 is approximately 15.75 million cubic meters. The landslide itself extends from approximately 65 to 400 m in elevation (Fig. 4). The mean inclination of the landslide surface is 22°.

Fig. 3
figure 3

a Location of the Shuping landslide, Three Gorges Reservoir area, China. b Topographic map of the Shuping landslide. c Overall view of the Shuping landslide

Full size image
Fig. 4
figure 4

Geological profile along sections A-A’ and B-B′ with monitoring instruments and reservoir level range

Full size image

Site investigation and borehole analysis (Wang et al. 2007) showed that the landslide materials are colluvial gravel soil (Fig. 4). The colluvial gravel soil is composed of yellow and brown silty clay and gravel clasts, with diameters varying from 1 to 15 cm. These clasts represent as much as 30–50% of the deposit by weight. The thickness of the sliding zone varies from 1.0 to 1.2 m. It is composed of approximately 70% magenta silty clay and 30% gravel clasts (Wang et al. 2005, 2007; Lu et al. 2014). The Quaternary deposit is underlain by argillaceous siltstone and marlstone of the Triassic Badong formation, with an average dip direction of 170° and a dip angle of 10–30° (Fig. 4).

Deformation characteristics

The Shuping landslide was reactivated by the initial impoundment of the Three Gorges Reservoir Dam in June 2003 (Huang et al. 2014). Cracks have been observed by the locals since the initial impoundment. The cracks were mainly distributed in block 1 between elevations of 310 and 370 m (Fig. 3b). Based on the distribution of the surface cracks, we can assume that block 1 is the main deformation zone. The surface cracks can be divided into transverse and longitudinal cracks. The transverse cracks (Fig. 5a) are perpendicular to the sliding direction, while the longitudinal cracks (Fig. 5b) are parallel to the sliding direction. Crack Cl1 was first observed by the locals in January 2004 and reached approximately 100 m in length. According to local reports, major transverse crack Ct appeared between elevations of 310 and 355 m in January 2004. Major crack Ct consists of a series of minor cracks that are approximately 20 to 50 m long and 5 to 10 cm wide.

Fig. 5
figure 5

a Transverse crack on the west boundary of block 1. b Longitudinal crack on the west boundary of block 1

Full size image

Nine GPS survey monuments were installed on the landslide slope (see Fig. 3b for locations): seven in the main deformation zone (block 1), one in the second deformation zone (block 2), and one on stable ground outside the deformation area. The GPS monuments were surveyed monthly.

Figure 6 shows the rainfall intensity as obtained from the Shazhenxi Meteorological Station near the Shuping landslide, the reservoir level before and after the initial impoundment of the Three Gorges Reservoir Dam, and the displacement from GPS survey monuments ZG87, ZG85, and SP2 over the 10-year period between October 2003 and October 2013. The available data indicate that the landslide is unstable and had continuously deformed during the entire monitoring period. The landslide exhibits step-like deformation behavior due to the periodic fluctuations in water level and heavy precipitation.

Fig. 6
figure 6

Time series of rainfall intensity, reservoir level and landslide displacement spanning the period of October 2003 to October 2013

Full size image

Driving factors of landslide movements

The step-like deformations shown in Fig. 6 represent two primary types of motion: short periods of rapid movements and longer periods of suspended activities. Rapid movements occurred at the end of reservoir drawdown (June and July of each year) and at the beginning of the rainfall season, from May to September. However, the rapid movement period ended before the end of the rainfall season. These findings indicate that rapid drawdown of the reservoir and prolonged heavy rainfall are the two main driving factors affecting movement in the Shuping landslide. Landslide movement was especially pronounced under prolonged periods of reservoir level decline; prolonged heavy rainfall had a weaker effect on landslide movement.

PIs construction

The proposed probabilistic forecasting approach was tested for the Shuping landslide to validate its effectiveness and efficiency. The PIs construction process for the Shuping landslide is as follows.

  1. (1)

    Data splitting

In the Three Gorges Reservoir area, rainfall and water level fluctuations are generally considered the two main hydrological causes of landslide movements. Landslide displacement was surveyed monthly, whereas reservoir water level and rainfall were monitored daily. Because of the different monitoring frequencies, the raw data were preprocessed on a monthly basis. Based on previous studies of landslide displacement prediction in the Three Gorges Reservoir area (Du et al. 2013; Cao et al. 2016; Zhou et al. 2016), seven indicators were chosen as inputs (X i ): the rainfall intensity over the past month (\( {x}_i^1 \)), the rainfall intensity over the past 2 months (\( {x}_i^2 \)), the average reservoir level in the current month (\( {x}_i^3 \)), the variation in reservoir level in the current month (\( {x}_i^4 \)), the displacement over the past 1 month (\( {x}_i^5 \)), the displacement over the past 2 months (\( {x}_i^6 \)), and the displacement over the past 3 months (\( {x}_i^7 \)). Additionally, displacement in the current month (t i ) was chosen as the output. A data set \( {\left\{\left({X}_i,{t}_i\right)\right\}}_{i=1}^N \) was generated based on the inputs and corresponding outputs.

Data from October 2003 to December 2012 were treated as the training set, and the data from January 2013 to October 2013 were regarded as the testing set. The training data set was used to train the ELM and ANN models, and testing data were used to evaluate the performance of the proposed method.

  1. (2)

    Bootstrap sampling

The training data set was resampled B times based on the paired-based bootstrap method. The bootstrap replicate number was set to 100 in the paired bootstrap method.

  1. (3)

    ELM training

B bootstrap data sets were used to train B ELM models. The original data were normalized in the range of [0,1] to eliminate dimensional effects. Then, the outputs of the ELM were denormalized to yield the correct values.

  1. (4)

    Estimation of the true regression mean and model uncertainty

The predicted value \( {\widehat{g}}_q\left({X}_i\right) \) of input sample X i can be obtained using the qth bootstrapped ELM. The true regression mean \( \widehat{g}\left({X}_i\right) \) and the variance in the model uncertainty \( {\widehat{\sigma}}_g^2\left({X}_i\right) \) can be estimated using Eqs. (14) and (15).

  1. (5)

    Estimation of noise

Data set \( {D}_{r^2}={\left\{{X}_i,{r}^2\left({X}_i\right)\right\}}_{i=1}^N \) was used to train a single ANN and estimate the variance in the noise.

  1. (6)

    PIs construction

The final PIs were obtained through Eqs. (3), (4) and (5). The PINC was set to 95% in this study.

Results and analysis

The constructed PIs with a nominal confidence level of 95% are shown in Fig. 7. The corresponding performance indices PICP and ACE are shown in Table 1. Figure 7 shows that the constructed PIs based on the bootstrap, ELM, and ANN methods encompass the majority of the observed samples, with percentages all greater than 90%. For example, the constructed PIs for monitoring point ZG87 have a PICP of 97.5%, which is close to the corresponding nominal confidence PINC of 95%. The ACE of the obtained PIs was 2.5%. The constructed PIs for monitoring point ZG85 have a PICP of 96.69% and an ACE of 1.69. Additionally, the constructed PIs for monitoring point SP2 have PICP and ACE values of 93.38% and − 1.62, respectively. These results indicate that the proposed approach provides satisfactory performance. Additionally, the proposed approach appropriately accounts for all existing uncertainties and can construct reliable PIs.

Fig. 7
figure 7

PIs with a nominal confidence level of 95% for landslide displacement obtained using the Bootstrap-ELM-ANN approach

Full size image
Table 1 Performance indices of the PIs for the Shuping landslide
Full size table

Figure 7 shows that the widths of constructed PIs vary from one sample to another. This result reflects one potential and important aspect of the proposed Bootstrap-ELM-ANN approach: how they respond to different levels of uncertainty in the constructed prediction model. Because the driving factors of landslide movements (e.g., water level or rainfall intensity) change over time, the level of uncertainty consequently changes. These variations are quantified by PIs and reflected in their widths. Figure 7 shows that incorrect predictions, or observations that do not fit predictions, occurred for some samples. In practical application, incorrect predictions cause underestimates or overestimates of risk and response. These failed predictions should not be interpreted as a criticism of those involved in the decision making process (Hungr et al. 2005). Instead, they demonstrate the inherent difficultly in landslide prediction, in which the controlling processes and deformation mechanisms are far from completely understood (Hungr et al. 2005; Yao et al. 2015).

In general, the proposed hybrid approach needs B + 1 neural network models to construct the PIs. Computational time is an important issue that should be considered. Table 1 shows that an average computation time of 5.30 s is required to train B (100) ELMs and a single ANN. Thus, the approach is computationally efficient. Simulations using the proposed approach and all the data sets were performed in MATLAB R2016b running on a Core I7-4700MQ @2.40 GHz CPU with 16-GB RAM. This significant computational efficiency benefits from the fast learning speed of the ELM. Therefore, the proposed probabilistic forecasting approach based on bootstrapping and ELM is practically applicable.

Discussion: deterministic point prediction versus probabilistic forecasting

Landslide deformation prediction is inherently uncertain. Evaluating the epistemic uncertainty and transforming the deterministic point prediction into probabilistic forecasting have several potential benefits. First, probabilistic forecasting is scientifically more “honest” and more realistic than is deterministic point prediction because it allows researchers to acknowledge uncertainty. Second, this approach enables users to make informed and appropriate decisions by explicitly considering risk. Variations in the widths of PIs are of practical importance in decision making and provide scientists and key officials with information about the accuracy and credibility of forecasting, while no additional information is available in traditional pointwise decision-making methods. A wide PI suggests that there is a high level of uncertainty in the forecasting, and sufficient attention and additional measures should be taken by scientists and key officials, especially when using certain types of point predictions. For insurance reasons, alternative options should be evaluated and established beforehand to mitigate risks. Alternatively, a narrow PI reflects low uncertainty in sample data, and decisions can be made more confidently based on point predictions. Thus, PIs constructed using the Bootstrap-ELM-ANN method can be employed as a complementary source of information along with point predictions to improve the efficiency and reliability of decision-making processes.

Although the benefits of probabilistic forecasting are many, the disadvantages can be considerable. The main disadvantage of the Bootstrap-ELM-ANN approach is that the computational cost of this method can become overly expensive with large data sets. Another disadvantage of probabilistic forecasting is that it can be difficult to understand and implement. An important aspect of deterministic point prediction is that it can offer a single number that is easy to comprehend and apply. In certain scenarios, e.g., for practical, more immediate, and operational-level planning, a quantitative input may be needed for decision making (Bijak et al. 2015). In contrast, probabilistic forecasting offers a prediction band instead of a single number. Thus, the results of probabilistic forecasting need to be reorganized in an approximate way that is more useful for end-users decision making. If a single number is needed, it can be obtained from quantiles determined from predictive distributions.

Conclusions

Probabilistic forecasting, which can be used to evaluate the epistemic uncertainties associated with landslide displacement forecasting by providing PIs, plays a critical role in the construction of reliable early warning systems. A probabilistic forecasting approach that combines bootstrap, ELM and ANN methods was used to construct PIs of landslide displacement. The proposed probabilistic forecasting approach is applied to a case study in the Three Gorges Reservoir area. The constructed PIs include the majority of the observed samples and appropriately account for all existing uncertainties. These results indicate that the proposed approach is effective and efficient. The successful implementation of this probabilistic forecasting approach suggests that the Bootstrap-ELM-ANN approach is valuable for landslide displacement forecasting in the medium term and long term, and can be used to quantify existing uncertainties for colluvial landslides with step-like deformation in the Three Gorges Reservoir area.

In practical application, PIs constructed with the Bootstrap-ELM-ANN approach can be efficiently used as a complementary source of information along with point predictions for informed and appropriate decision making. As the uncertainties associated with landslide displacement prediction are quantified and reflected in the varying widths of sample PIs, scientists and key officials have an indicator of the confidence or risk level associated with using point predictions.