A hybrid approach for interval prediction of concrete dam displacements under uncertain conditions

Abstract

Accurate and credible displacement prediction is essential to dam safety monitoring. However, due to the inherent uncertainties involved in dam systems, errors of conventional deterministic point predictions are inevitable and sometimes large. In this paper, prediction intervals (PIs) are used instead of deterministic values to quantify the associated uncertainties and improve the reliability of dam displacement prediction. A hybrid modeling approach is proposed to synthetically evaluate the aleatoric and epistemic uncertainties through PI construction, which integrates the non-parametric bootstrap, least squares support vector machine (LSSVM), and artificial neural network (ANN) algorithms. Specifically, the PIs of dam displacement are constructed in two stages. In the first stage, multiple bootstrap-based LSSVMs are utilized to estimate the true regression means of future displacements and the variance of model uncertainty. In the second stage, a modified ANN (MANN) is developed and applied to estimate the variance of data noise. The final PIs are calculated by combining the true regression means and the variances of model uncertainty and data noise. The performance of the bootstrap-LSSVM–MANN model is verified using monitoring data from a real concrete dam. The results show that the proposed method can generate computationally efficient high-quality PIs and can effectively deal with multiple uncertainties in data-driven modeling and prediction. The novel approach has great potential to support the decision-making activities in an environment characterized by uncertainties and risks.

1 Introduction

At present, most of the dams in the world higher than 100 m, both already built or under construction, are made of concrete. Such concrete dams play a vital role in the socio-economic development of any country by providing and facilitating flood control, power generation, navigation, etc. They not only have to cope with various dynamic and static cyclic loads and sudden disasters (e.g., floods and earthquakes), but are also affected by the ever-changing environmental loads (e.g., water level and air temperature) during their service life [1]. The local and overall structural performance of a dam gradually declines over its lifetime, which leads to an increase in the risk of failure. Water conservation projects using concrete dams as the main structure are mostly large-scale reservoirs, which will cause huge losses to the national economy and people’s lives and property in case of dam failure. Fortunately, catastrophic failures often do not happen suddenly but rather gradually [2]; thus it is crucial to use reliable data-driven safety monitoring algorithms to detect their anomalous behavior well in advance [3]. There may be many specialized sensors placed inside and around a dam to monitor its structural responses (e.g., displacements and seepages) and environmental quantities. A large amount of recorded monitoring data makes it possible to model and predict dam behavior. Among all the responses, displacements can conveniently represent the joint effect of various factors on dam structural performance, and thus their evolution is an important basis for assessing the safety status of a dam [4, 5]. It is thus essential to develop an effective prediction model for dam displacement based on in-situ monitoring data to estimate the trends and magnitudes of future behaviors, thereby identifying the potential safety hazards in time.

1.1 Related work on dam displacement modeling and prediction

In recent years, many researchers have carried out extensive studies on dam behavior modeling and established numerous data-driven displacement prediction models. These models can roughly be divided into two categories, namely numerical and mathematical models [6]. The former category mostly includes deterministic and mixed models based on the finite element method (FEM) or other numerical simulation techniques. Deterministic models utilize the FEM to predict and analyze the dam responses under a given load combination using physics-based models of the dam and its foundation. This traditional approach is relatively easy to interpret and is suitable for analyzing early filling periods, when the amount of monitoring data is small. However, such models have shortcomings, such as cumbersome geometric modeling and inefficient iterative calibration [7]. In the mixed models, only the displacement component caused by hydrostatic pressure is obtained by FEM, and the remaining components are calculated from statistical models. It has been proven that the prediction accuracy of the mixed models is higher than that of a single deterministic model and their calculation procedures are more convenient [8].

The long-term accumulation of monitoring data during the normal operation period promotes the application of data-driven mathematical models [9]. Such models are regression formulas based on the causal relationship between the influencing factors (e.g., water level, temperature, and time effect) and dam displacements, which can be classified into two types, namely linear (with explicit expressions) and nonlinear (without explicit expressions) models [10]. Linear models are so-called statistical models and mainly include the hydrostatic-seasonal-time (HST) models [11], hydrostatic-temperature–time (HTT) models [12], and their various variants [13, 14]. The unknown model coefficients can be found by multiple linear regression [12], stepwise regression [15], or principle component regression [16]. The advantages of linear models are simplicity of formulation, efficiency of execution, and ease of determining the contribution of each factor to the dam behavior [17]. Nevertheless, linear hypothesis-based models are not well-suited to characterize the complex nonlinear interactions between inputs and output and have poor robustness to noise. Recently, benefitting from their powerful data mining capabilities, the machine learning-based nonlinear models have been widely used in dam displacement modeling and prediction, including artificial neural networks (ANNs) [16,17,18], support vector machines (SVMs) [19,20,21], extreme learning machines (ELMs) [22,23,24], and random forest regression (RFR) [15, 25]. Among them, the SVM-based models have attracted increasing attention owing to their complete theory, global optimum finding performance, and good generalization ability. For example, Su et al. [26] combined the wavelet-SVM algorithm with phase space reconstruction and meta-heuristic optimization to establish a high-precision dam displacement prediction model. Ren et al. [11] introduced quantitative evaluation and hysteresis correction into the SVM-based dam behavior model, which improved its robustness and accuracy. Cheng and Zheng [19] used SVM to construct a dam monitoring model based on latent variables, and it was successfully applied to the displacement and seepage analysis of a concrete dam. Su et al. [20] built the time-varying identification model for dam behavior after structural reinforcement based on SVM and Bayesian approach. They also proposed the performance improvement method of SVM-based model monitoring dam safety [21]. Kang et al. [27] compared SVM and its variation, the least squares SVM (LSSVM), for separating the thermal effects from long-term measured air temperature and the results showed that both algorithms performed well in simulating dam behavior. The LSSVM algorithms have also been successfully applied in other fields, such as streamflow forecasting [28] and geological surveying [29]. These applications demonstrated that LSSVM is better fit to solve nonlinear regression problems with high dimensions and small sample sizes. Compared to the standard SVM, the improved LSSVM has a faster training speed without a significant loss in estimation accuracy [30] and thus it is adopted in this study. Last but not least, more and more excellent mathematical models such as ensemble learning and deep learning algorithms are being employed to monitor dam behavior. Due to limited space, the interested readers can refer to literature [9, 11] for comprehensive reviews of the advanced algorithms adopted for dam displacement modeling.

1.2 Problem statement

From the above literature survey, it can be concluded that most studies on dam displacement modeling focused on deterministic point predictions without considering the random variability of displacements or the inherent uncertainties involved in dam systems. In reality, however, there are different types of uncertainties in both the dam system itself and the modeling process, which challenge seriously the accurate estimation of future displacements [24]. Furthermore, while obtaining point predictions, dam operators also want to know the reliability and credibility of prediction results to make better-informed decisions, especially in risky situations [31, 32]. Therefore, the evaluation and quantification of uncertainties in dam displacement prediction are urgent research problems.

In this study, the aleatoric and epistemic uncertainties associated with dam displacement predictions are considered. The aleatoric uncertainty (also referred to as data noise uncertainty) is present in noisy monitoring datasets. It originates from the following two main sources: (1) dam displacement is a dynamic evolution process influenced by environmental conditions and mechanical characteristics of structural materials, which is inherently stochastic and variable. Also, the internal and external loads acting on the dam are time-varying, which further aggravates the uncertainty of modeling the dam and its foundation. (2) The imperfect monitoring instruments or techniques produce measurement errors, while the erroneous instrument calibration and recording procedures bring in systematic errors. In short, the random noise in the monitoring data is unavoidable. As for the epistemic uncertainty (also referred to as model uncertainty), it results from imperfect mathematical representations of nonlinear behavior due to the limited knowledge and simplified model conceptualization. This uncertainty mainly appears in two forms: (1) only the known or major influencing factors are included in model inputs, while the complex or less important factors are ignored, which greatly affects the model architecture. For example, some key factors, such as earthquakes and cracks, are often not added to the water level, temperature, and time effect as model inputs. (2) Both numerical and mathematical models are abstractions and simplifications of complex systems, i.e., they are based on various assumptions, which inevitably introduce model uncertainty. Moreover, any inconsistency of model parameters in each model run will intensify this uncertainty. Therefore, model uncertainty caused by its architecture and parameters accounts for the majority of epistemic uncertainty.

Because of these uncertainties, it is inevitable that errors, sometimes relatively large, will plague point predictions. In this work, instead of the traditional point prediction the interval prediction is used to quantify comprehensively the above two types of uncertainties. A prediction interval (PI) comprises an upper limit and a lower limit rather than a single value (usually expectation or median). PIs are more informative for dam operators as they allow preparing in advance for the worst and the best possible conditions. The future targets are expected to fall within the constructed PIs at a predefined PI nominal confidence level (PINC) $(1 - \alpha ) \times 100\%$, where $\alpha$ is the significance level. PIs have been successfully applied in various fields, such as evaporation estimation [33], solar power generation [34], and precipitation and temperature modeling [35]. To the best of our knowledge, however, there are few reports on uncertainty quantification for dam displacement prediction using PIs, while in the field of dam safety monitoring there are currently no studies that consider both aleatoric and epistemic uncertainties.

1.3 Research contributions

In this paper, to quantify the aleatoric and epistemic uncertainties and improve the reliability of displacement predictions, a hybrid approach combining the non-parametric bootstrap, LSSVM, and ANN algorithms is proposed to calculate the optimal PIs and regression means of future displacements. The constructed PIs consider the uncertainties in both the data (i.e., aleatoric uncertainty) and the regression model (i.e., epistemic uncertainty), while being computationally efficient and of high quality. In the proposed approach, non-parametric bootstrap is used as a general resampling statistical method [36]. Unlike the parametric bootstrap, it does not need to postulate a sample distribution and the unknown distribution moments (e.g., mean and variance) can be inferred through random sampling with replacement. Bootstrap is frequently used for PI construction owing to its simplicity and flexibility [24, 33,34,35]. The PIs of dam displacement are constructed in three steps as follows: (1) a specified number of pseudo-datasets are generated based on the measured monitoring datasets through pairs bootstrap (PB) sampling. (2) The estimations of model uncertainty and true regression mean are obtained using multiple LSSVM models trained on the pseudo-datasets. (3) A modified ANN (MANN) algorithm is adopted for estimation of data noise uncertainty using the reconstructed residual dataset. In this way, the aleatoric and epistemic uncertainties are quantitatively evaluated in the form of PIs by combining the estimations of both data noise and LSSVM-based predictive model. The performance of the proposed hybrid modeling approach is verified by using monitoring data collected from a real-world dam project. The obtained results suggest that the bootstrap-LSSVM–MANN (B-LSSVM–MANN) model performs well in quantifying the joint uncertainties associated with dam displacement modeling.

The main contributions of this paper can be summarized as follows:

• 1. The aleatoric and epistemic uncertainties involved in dam systems and monitoring models are quantified by PIs.

• 2. A hybrid approach for dam displacement interval prediction is proposed to generate high-quality PIs and accurate regression means of future displacements.

• 3. A real-life dam example is studied to verify the effectiveness of the proposed modeling approach through comprehensive analyses and simulations.

This paper is structured as follows: the fundamental theories of PI formulation and assessment are given in Sect. 2. Section 3 describes the mathematical principles of the bootstrap, LSSVM, and MANN algorithms and the developed model for dam displacement interval prediction. In Sect. 4, the feasibility and performance of the proposed model are analyzed and discussed by using long-term monitoring data from a concrete gravity dam. Finally, the conclusions and future research directions are given in Sect. 5.

2 PI formulation and assessment

2.1 PI formulation

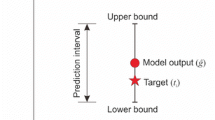
Given a set of prototype observation data, $D = \left\{ {({\mathbf{x}}_{i} ,t_{i} )} \right\}_{i = 1}^{N}$, where x_i is the vector or set of factors affecting the dam behavior, and t_i is the prediction target, namely the dam displacement observation value at the i-th moment in time. If there is a nonlinear mapping relationship, y(x), between the output target, t_i, and the input factor vector, x_i, then target t_i can be modeled as follows:

$$ t_{i} = y({\mathbf{x}}_{i} ) + \varepsilon ({\mathbf{x}}_{i} ), $$

(1)

where $y({\mathbf{x}}_{i} )$ is the true regression value, and $\varepsilon ({\mathbf{x}}_{i} )$ is the random noise, which is mainly derived from the aleatoric uncertainty and assumed to obey the standard normal distribution with a zero mean and variance $\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )$.

In practice, the output of a trained data-driven prediction model, $\hat{y}({\mathbf{x}}_{i} )$, can be regarded as an estimate of the true regression value, $y({\mathbf{x}}_{i} )$. Hence, the prediction error can be expressed as follows:

$$ t_{i} - \hat{y}({\mathbf{x}}_{i} ) = \left[ {y({\mathbf{x}}_{i} ) - \hat{y}({\mathbf{x}}_{i} )} \right] + \varepsilon ({\mathbf{x}}_{i} ), $$

(2)

where $t_{i} - \hat{y}({\mathbf{x}}_{i} )$ is the total prediction error, and $y({\mathbf{x}}_{i} ) - \hat{y}({\mathbf{x}}_{i} )$ is the error of model estimate with respect to the true regression, which primarily results from the epistemic uncertainty.

Suppose that the estimation error, $y({\mathbf{x}}_{i} ) - \hat{y}({\mathbf{x}}_{i} )$, and the data noise, $\varepsilon ({\mathbf{x}}_{i} )$, are statistically independent, the variance of the total prediction error, $\sigma_{t}^{2} ({\mathbf{x}}_{i} )$, can be calculated as follows [37]:

$$ \sigma_{t}^{2} ({\mathbf{x}}_{i} ) = \sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} ) + \sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} ), $$

(3)

where $\sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} )$ and $\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )$ are the variances of model uncertainty and of data noise, respectively.

When the significance level is set to $\alpha$, PIs with the corresponding PINC of $(1 - \alpha ) \times 100\%$ (usually 95%) for the output target, t_i, can be formulated as follows:

$$ I_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} ) = \left[ {L_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} ),U_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} )} \right], $$

(4)

where $U_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} )$ and $L_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} )$ are the upper and lower limits of the constructed PIs, respectively. The upper and lower limits are obtained by the following formulas:

$$ L_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} ) = \hat{y}({\mathbf{x}}_{i} ) - z_{1 - \alpha /2} \sqrt {\sigma_{{t_{i} }}^{2} ({\mathbf{x}}_{i} )} , $$

(5)

$$ U_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} ) = \hat{y}({\mathbf{x}}_{i} ) + z_{1 - \alpha /2} \sqrt {\sigma_{{t_{i} }}^{2} ({\mathbf{x}}_{i} )} , $$

(6)

where $z_{1 - \alpha /2}$ is the $1 - \alpha /2$ percentile of the standard normal distribution, which depends on the prescribed PINC $(1 - \alpha ) \times 100\%$. The schematic diagram of PI construction is shown in Fig. 1.

Fig. 1

Schematic diagram of PI construction

It can be seen from Eqs. (5) and (6) that the variance of the total prediction error, $\sigma_{t}^{2}$, is the key to PI construction. According to Eq. (3), we first have to calculate the variances of model uncertainty and data noise, $\sigma_{{\hat{y}}}^{2}$ and $\sigma_{\varepsilon }^{2}$, so as to obtain $\sigma_{t}^{2}$. In Sect. 3, $\sigma_{{\hat{y}}}^{2}$ and $\sigma_{\varepsilon }^{2}$ are computed by bootstrap-based LSSVM and MANN algorithms, respectively.

2.2 PI quality assessment measures

In order to assess the overall quality of the constructed PIs, two evaluation indices are introduced for their reliability and sharpness. The reliability and sharpness are measured by PI coverage probability (PICP) and mean PI width (MPIW) [24, 37], respectively, which are defined as follows:

$$ {\text{PICP}} = \frac{1}{{N_{v} }}\sum\limits_{i = 1}^{{N_{v} }} {c_{i} } , \, c_{i} = \left\{ \begin{gathered} 1, \, t_{i} \in \left[ {L_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} ),U_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} )} \right] \hfill \\ 0, \, t_{i} \notin \left[ {L_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} ),U_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} )} \right] \hfill \\ \end{gathered} \right., $$

(7)

$$ {\text{MPIW}} = \frac{1}{{N_{v} }}\sum\limits_{i = 1}^{{N_{v} }} {\left[ {U_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} ) - L_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} )} \right]} , $$

(8)

where $N_{v}$ is the number of validation samples. Variable $c_{i}$ is Boolean: if the target value falls within the PIs $c_{i} = 1$; otherwise, $c_{i} = 0$. Variables $L_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} )$ and $U_{{t_{i} }}^{\alpha } ({\mathbf{x}}_{i} )$ used in Eq. (8) were defined previously in Eq. (4).

Generally speaking, a larger coverage probability (i.e., PICP) and a smaller interval width (i.e., MPIW) are expected, and PICP should be quite close or greater than PINC related to the PIs. In brief, high-quality PIs correspond to relatively large PICP values and small MPIW values. However, large PICP values can easily be achieved by widening PIs. With the conflicting nature of the two goals, a synthetic coverage width-based criterion (CWC) [33, 34, 37] is applied herein, which is expected to be smaller for better PIs:

$$ {\text{CWC}} = {\text{MPIW}}\left[ {1 + \gamma ({\text{PICP}}){\text{e}}^{{ - \eta ({\text{PICP}} - {\text{PINC}})}} } \right],\quad \gamma ({\text{PICP}}) = \left\{ \begin{gathered} 0,{\text{ PICP}} \ge {\text{PINC}} \hfill \\ 1,{\text{ PICP}} < {\text{PINC}} \hfill \\ \end{gathered} \right., $$

(9)

where $\gamma ({\text{PICP}})$ is a control factor, and $\eta$ is a penalty parameter. When PICP is greater or equal to PINC $(1 - \alpha ) \times 100\%$, $\gamma ({\text{PICP}})$ eliminates the exponential term and thus the quality of PIs is only measured by MPIW. Conversely, if PICP is less than PINC $(1 - \alpha ) \times 100\%$, then it needs to be penalized. Parameter $\eta$ is set to a relatively large value, e. g., $\eta = 50$ is used in this study [24, 37].

3 Methodology

The aim of this study is to develop a hybrid framework based on the bootstrap algorithm for constructing the PIs of dam displacements. The variances of model uncertainty and data noise are estimated by the LSSVM and MANN algorithms, respectively. The principles of these algorithms are explained in this section.

3.1 Non-parametric PB method

Dam displacement prediction is a regression analysis problem, i.e., the input factor vector, x_i, and the output target, t_i, always appear in pairs. Among the non-parametric bootstrap methods, PB, proposed by Freedman [38], is used in the present study because it works well for resampling the predictor and response variables together from the original dataset. The prototype observation dataset, $D = \left\{ {({\mathbf{x}}_{i} ,t_{i} )} \right\}_{i = 1}^{N}$, whose overall distribution, F, is unknown, contains N data pairs, $({\mathbf{x}}_{i} ,t_{i} )$. The following scheme is used to estimate the unknown parameters (e.g., mean and variance):

Step 1: Resampling. The paired pseudo-samples (inputs and output) with the sample size N are generated N times with equal-probability (i.e., sampling probability of 1/N) by random sampling of the original dataset D with replacement. This is repeated B times and B pseudo-datasets, $D^{*} = \left\{ {D_{b}^{*} } \right\}_{b = 1}^{B}$, are obtained, as shown in Fig. 2.

Fig. 2

PB sampling scheme

Step 2: Parameter estimation. Every time a pseudo-dataset $D_{b}^{*}$ is generated, $F_{b}^{*}$ can be calculated using statistical expressions [39]. A dataset consisting of $F_{b}^{*}$ is then constructed to simulate the overall distribution F. In this way, the unknown parameters, including mean and variance, can be estimated based on the simulated distribution, $\hat{F}$. A more detailed scheme and discussion can be found in literature [38].

3.2 Least squares support vector machine

Suppose $\left\{ {({\mathbf{x}}_{i} ,y_{i} )} \right\}_{i = 1}^{N}$ denotes a given dataset, where ${\mathbf{x}}_{i} \in {\mathbf{R}}^{n}$ represents the input vector, and $y_{i} \in {\mathbf{R}}$ is the corresponding output. The basic idea of LSSVM is to map the data samples from the input space, ${\mathbf{R}}^{n}$, to a high-dimensional feature space, ${\mathbf{H}}$, by a nonlinear function, $\varphi ( \cdot )$, which can be considered as a convex optimization problem [27, 40]. The nonlinear estimation function is transformed into a linear estimation function in ${\mathbf{H}}$ by the optimal decision function:

$$ y({\mathbf{x}}) = {{\varvec{\upomega}}}^{T} \varphi ({\mathbf{x}}) + b, $$

(10)

where ${{\varvec{\upomega}}}$ is the weight vector, $\varphi ( \cdot )$ denotes the nonlinear mapping function, and $b$ is the bias term.

The slack variable, $\xi_{i}$, is introduced to determine ${{\varvec{\upomega}}}$ and $b$, and the regression is expressed as an optimization problem with equality constraints based on the structural risk minimization principle as follows:

$$ \left\{ \begin{gathered} \min J({{\varvec{\upomega}}},\xi ) = \frac{1}{2}\left\| {{\varvec{\upomega}}} \right\|^{2} + \frac{1}{2}C\sum\limits_{i = 1}^{N} {\xi_{i}^{2} } \hfill \\ {\text{s}}.{\text{t}}. \, y_{i} = {{\varvec{\upomega}}}^{T} \varphi ({\mathbf{x}}_{i} ) + b + \xi_{i} ,\quad i = 1,2, \cdots ,N \hfill \\ \end{gathered} \right., $$

(11)

where $C \ge 0$ is a regularization parameter, which trades off the model error and model complexity. The Lagrangian function is adopted to incorporate the constraint conditions into the objective function asfollows:

$$ L({{\varvec{\upomega}}},b,\xi_{i} ,\alpha_{i} ) = J({{\varvec{\upomega}}},\xi_{i} ) - \sum\limits_{i = 1}^{N} {\alpha_{i} ({{\varvec{\upomega}}}^{T} \varphi ({\mathbf{x}}_{i} ) + b + \xi_{i} - y_{i} )} , $$

(12)

where $\alpha_{i} \ge 0, \, i = 1,2, \ldots ,N$ are the Lagrangian multipliers. According to the Karush–Kuhn–Tucker conditions, the partial derivatives of ${{\varvec{\upomega}}}$, $b$, $\xi_{i}$, and $\alpha_{i}$ can be obtained from $L({{\varvec{\upomega}}},b,\xi_{i} ,\alpha_{i} )$. Subsequently, ${{\varvec{\upomega}}}$ and $\xi_{i}$ are eliminated and the following system of linear equations can be obtained in the dual space:

$$ \left[ {\begin{array}{*{20}c} 0 & {{\mathbf{e}}^{T} } \\ {\mathbf{e}} & {{\mathbf{K}} + C^{ - 1} {\mathbf{I}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ {{\varvec{\upalpha}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {\mathbf{y}} \\ \end{array} } \right], $$

(13)

where ${\mathbf{e}} = \left[ {1,1, \ldots ,1} \right]^{{\text{T}}}$, ${\mathbf{K}}$ is the kernel function matrix, ${\mathbf{I}}$ is the N-order unit matrix, ${{\varvec{\upalpha}}} = \left[ {\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{N} } \right]^{{\text{T}}}$, and ${\mathbf{y}} = \left[ {y_{1} ,y_{2} , \ldots ,y_{N} } \right]^{{\text{T}}}$. The kernel function is defined as ${\mathbf{K}} = K({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} ) = \varphi ({\mathbf{x}}_{i} )^{{\text{T}}} \varphi ({\mathbf{x}}_{j} ), \, i,j = 1,2, \ldots ,N$ in terms of Mercer’s theorem. The decision function, $y({\mathbf{x}}) = \sum\nolimits_{i = 1}^{N} {\alpha_{i} K({\mathbf{x}},{\mathbf{x}}_{i} ) + b}$, is eventually obtained when ${{\varvec{\upalpha}}}$ and $b$ in Eq. (13) are solved in the least squares sense [40, 41].

Several common kernel functions are available, such as linear, polynomial, and radial basis function (RBF). In this study, the RBF is selected as the kernel function because it has a stronger nonlinear mapping ability and fewer hyperparameters. The expression for RBF is $K({\mathbf{x}},{\mathbf{x}}_{i} ) = \exp ( - \left\| {{\mathbf{x}} - {\mathbf{x}}_{i} } \right\|^{2} /2\sigma^{2} )$, where $\sigma$ is the width of RBF. An equivalent parameter, $\gamma = (2\sigma^{2} )^{ - 1} , \, \gamma > 0$ is defined for convenience. As such, the prediction performance of LSSVM with RBF kernel mainly depends on two key hyperparameters, i.e., the regularization parameter, $C$, and the kernel parameter, $\gamma$. The schematic diagram of LSSVM architecture is illustrated in Fig. 3.

Fig. 3

General architecture of LSSVM network [42]

3.3 Standard artificial neural network

The ANNs are a class of universal approximators that are inspired by biological neural networks. Among many different types of ANN, the multilayer perceptron (MLP) with the error backpropagation mechanism is by far the most popular feedforward neural network learning model owing to its simplicity and efficacy [16]. The topology of MLP consists of an input layer, at least one hidden layer, and an output layer, which form a simple yet competitive regressor. In each layer of MLP, the neuron is the basic processing element. The neurons in each layer connect to the neurons in the next layer, while the neurons in the same layer or across layers do not connect to one another.

Theoretically, the output of MLP network depends on the connection weight, w, threshold, θ, and activation function, $f( \cdot )$, of the functional neuron. The activation functions, $f( \cdot )$, can be specified as required and are usually nonlinear (e.g., sigmoid or tanh) for complex regression tasks. By contrast, the connection weights, w, and thresholds, θ, cannot be solved for directly, but have to be learned from a given training dataset. A general optimization problem is formulated to adjust the values of w and θ in each layer. Specifically, in order to make the approximated outputs approach the expected ones, the gradient descent method [16] is utilized to minimize the mean square error (MSE)-based cost function, $C_{{{\text{MSE}}}} ({\mathbf{x}}_{i} ,{\mathbf{w}},\theta )$ [18]:

$$ C_{{{\text{MSE}}}} ({\mathbf{x}}_{i} ,{\mathbf{w}},\theta ) = \frac{1}{2N}\sum\limits_{i = 1}^{N} {\left\| {y_{e} ({\mathbf{x}}_{i} ) - y_{a} ({\mathbf{x}}_{i} ,{\mathbf{w}},\theta )} \right\|^{2} } , $$

(14)

where the sample size of the dataset is N, and $y_{e} ({\mathbf{x}}_{i} )$ and $y_{a} ({\mathbf{x}}_{i} )$ are the expected and approximated outputs of the input factor vector, x_i, respectively.

3.4 Proposed hybrid bootstrap-LSSVM–MANN model for dam displacement interval prediction

Using the above theoretical background, a hybrid modeling approach for dam displacement interval prediction considering both aleatoric and epistemic uncertainties is described in this section. The overall procedure of model implementation is shown in Fig. 4. Specifically, the proposed B-LSSVM–MANN model mainly includes the following four main steps:

Fig. 4

Implementation procedure of PI construction for dam displacement based on proposed hybrid B-LSSVM–MANN model

Step 1: Generate pseudo-datasets and train LSSVM models using PB method

• (1.1) The original dataset, D, with inputs and output (sample size N) is first min–max normalized and then divided into a training dataset, D_t, (sample size N_t) and a validation dataset, D_v, (sample size N_v).

• (1.2) According to the PB sampling scheme described in Sect. 3.1, the B pseudo-training datasets, $D_{t}^{*} = \left\{ {D_{t,b}^{*} } \right\}_{b = 1}^{B}$, are uniformly resampled from D_t with replacement. Note that the number of bootstrap replicates is equal to N_t in this study.

• (1.3) A total of B LSSVM models are trained on the B pseudo training datasets generated. For optimization purpose, the modified fruit fly optimization algorithm (MFOA), proposed in our previous work [11], and fivefold cross validation are combined to tune the LSSVM hyperparameters, C and $\gamma$, based on D_t.

Step 2: Estimate the regression mean, $\hat{y}({\mathbf{x}}_{i} )$, and the variance of model uncertainty, $\sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} )$, using LSSVMs

• (2.1) The B trained LSSVMs are tested on D_v in parallel. The ensemble models allow obtaining a less biased estimate of the true regression of the future targets [37, 43], thus, the true regression mean, $\hat{y}({\mathbf{x}}_{i} )$, is approximated by averaging the outputs of B trained LSSVMs as follows:

  $$ \hat{y}({\mathbf{x}}_{i} ) = \frac{1}{B}\sum\limits_{b = 1}^{B} {\hat{y}_{b} ({\mathbf{x}}_{i} )} , $$

  (15)

  where $\hat{y}_{b} ({\mathbf{x}}_{i} )$ is the predicted value of the i-th input sample generated by the b-th LSSVM model.

• (2.2) The variance of model uncertainty, $\sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} )$, can be estimated from the variance of the outputs of the B trained LSSVMs:

  $$ \sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} ) = \frac{1}{B - 1}\sum\limits_{b = 1}^{B} {\left[ {\hat{y}_{b} ({\mathbf{x}}_{i} ) - \hat{y}({\mathbf{x}}_{i} )} \right]^{2} } $$

  (16)

Step 3: Estimate the variance of data noise, $\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )$, using MANN

• (3.1) After determining the variance of model uncertainty, we also need to estimate the variance of data noise, $\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )$, to construct the PIs. From Eq. (3), $\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )$ can be obtained as follows:

  $$ \sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} ) \simeq E\left\{ {\left[ {t_{i} - \hat{y}({\mathbf{x}}_{i} )} \right]^{2} } \right\} - \sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} ), $$

  (17)

• (3.2) According to Eq. (17), a set of squared residuals, $r^{2} ({\mathbf{x}}_{i} )$, is calculated to form a model to fit the remaining residuals:

  $$ r^{2} ({\mathbf{x}}_{i} ) = \max \left( {\left[ {t_{i} - \hat{y}({\mathbf{x}}_{i} )} \right]^{2} - \sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} ), \, 0} \right) $$

  (18)

  where $\hat{y}({\mathbf{x}}_{i} )$ and $\sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} )$ are obtained from Eqs. (15) and (16), respectively. Subsequently, a new dataset, $D_{{r^{2} }} = \left\{ {({\mathbf{x}}_{i} ,r^{2} ({\mathbf{x}}_{i} ))} \right\}_{i = 1}^{{N_{t} }}$, is generated by linking the residuals to the set of corresponding inputs.

• (3.3) In order to estimate the unknown noise variance, $\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )$, an ANN-based model is developed using the residual dataset, $D_{{r^{2} }}$, which is required to maximize the probability of observing the samples in $D_{{r^{2} }}$. However, the standard ANN with MSE (see Eq. (14)) as the cost function cannot achieve this goal. To this end, the MANN model developed in this study uses an improved cost function. Generally, the data noise, $\varepsilon ({\mathbf{x}}_{i} )$, is normally distributed with zero mean (see Eq. (1)), and its conditional distribution can be expressed as follows:

  $$ P\left( {r^{2} ({\mathbf{x}}_{i} );\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )} \right) = \frac{1}{{\sqrt {2\pi \sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )} }}\exp \left( { - \frac{{r^{2} ({\mathbf{x}}_{i} )}}{{2\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )}}} \right) $$

  (19)

  The maximum likelihood estimation method is used in training of the MANN for noise variance approximation. The natural logarithm of the likelihood function, $L_{\varepsilon }$, is derived from Eq. (19) as follows:

  $$ L_{\varepsilon } = \sum\limits_{i = 1}^{{N_{t} }} {\ln \left[ {\frac{1}{{\sqrt {2\pi \sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )} }}\exp \left( { - \frac{{r^{2} ({\mathbf{x}}_{i} )}}{{2\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )}}} \right)} \right]} . $$

  (20)

  Our goal is to maximize $L_{\varepsilon }$ of Eq. (20), but the ANN cost function has to be minimized, which requires a negative sign transformation. Furthermore, the constant terms in Eq. (20) can be ignored. As such, the improved cost function for training the MANN model is defined as follows:

  $$ C_{\varepsilon } = \frac{1}{2}\sum\limits_{i = 1}^{{N_{t} }} {\left[ {\frac{{r^{2} ({\mathbf{x}}_{i} )}}{{\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )}} + \ln (\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} ))} \right]} . $$

  (21)

  To ensure that the estimated noise variance, $\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )$, is always positive, the sigmoid function is selected as the activation function of neurons in the MANN output layer. The minimization of $C_{\varepsilon }$ can be reached by combining the MFOA with the gradient descent method.

Step 4: Construct the optimal PIs for dam displacements

Using the $B + 1$ models (i.e., B LSSVMs and a single MANN) derived above, the dam displacement PIs can be constructed. The true regression mean, $\hat{y}({\mathbf{x}}_{i} )$, and the variance of model uncertainty, $\sigma_{{\hat{y}}}^{2} ({\mathbf{x}}_{i} )$, are estimated in Step 2 through the ensemble of B LSSVM models. The variance of data noise, $\sigma_{\varepsilon }^{2} ({\mathbf{x}}_{i} )$, is estimated using the MANN model from Step 3. Consequently, PIs with PINC $(1 - \alpha ) \times 100\%$ can be calculated using Eqs. (3), (5), and (6). Furthermore, in order to improve the reliability and robustness of the constructed PIs, the entire process is repeated ten times and the final PI of each target is the average of the ten PIs. The final regression mean is also obtained by averaging the ten estimates.

4 Engineering example and application

In the following subsections, a real concrete gravity dam is studied as a practical example to demonstrate the validity and performance of the proposed interval prediction model in quantifying both aleatoric and epistemic uncertainties. Also, the reliability and rationality of the PIs obtained from the B-LSSVM–MANN model are further explored through comprehensive analyses and simulation tests.

4.1 Project overview and data preparation

The analyzed dam is located on the Second Songhua River in Jilin Province, northeast China. While it is mainly used for hydropower generation, it also has other purposes, such as flood control and water supply. The construction of the dam began in 1937 and was completed in 1953. The maximum dam height is 91.7 m and the dam crest length is 1080 m. Figure 5 shows the upstream and downstream views of the dam. The dam comprises 60 sections along its axis and each section is 18 m long, as shown in Fig. 6. Dam sections 9–19 are crest overflow sections and the rest are non-overflow sections. Since the 1980s, an automatic safety monitoring system has been deployed to assess the operating status of the dam in real time. The system consists of numerous instruments and pieces of equipment that can measure and store data such as reservoir water level, ambient temperatures, displacements, stresses, strains, and others. Displacements are measured one to three times every month by a vacuum laser collimation system, while the water level and air temperature are recorded every day and stored in the monitoring database, which makes the interval prediction of dam displacements possible.

Fig. 5

Analyzed concrete gravity dam: a upstream view, and b downstream view

Fig. 6

Dam section layout (A denotes retaining dam sections, B denotes crest overflow sections, and C denotes taking dam sections. Also, the number in the circle indicates the serial number of dam section)

The horizontal displacements of the fourth and 36-th dam sections marked in orange in Fig. 6, which are denoted as D4 and D36, are investigated hereinafter. The fourth dam section is located on the bank slope, while the 36th section is almost in the middle of the dam. As illustrated in Fig. 7, the displacement time series of the two dam sections present different evolution patterns (e.g., amplitudes and fluctuations), which is helpful to test the generalization ability of the predictive models. Positive values indicate displacements in the downstream direction, while negative values indicate displacements in the upstream direction. The time series of the upstream water level and air temperature are also shown in Fig. 7. It should be noted that in Fig. 7 the water level and displacement time series are plotted with the same frequency, while the air temperature is plotted daily. All data used for modeling have been confirmed as reliable by the dam operators.

Fig. 7

Prototype observation data collected from automatic safety monitoring system: a upstream water level, b daily mean air temperature, and c horizontal displacements

The dataset extracted from the monitoring database for this study spans a 12-year period from January 1997 to December 2008 and contains 155 groups of data in total. A total of 126 observations between January 1997 and December 2006 were used for model training, whereas 29 observations between January 2007 and December 2008 for model validation. In order to reduce the dimensional effect, the raw data were normalized to the range [0, 1] before being fed into the LSSVM model, and the outputs of LSSVMs are denormalized to yield the original values.

4.2 Input factors and model parameters

In general, the input factors of the dam displacement prediction model can be selected using statistical models, among which the HST and HTT are the most commonly used ones [6, 9, 11]. In the statistical models, the horizontal displacement, $\delta$, at any measuring point is considered as the sum of components corresponding to the hydrostatic pressure, $\delta_{H}$, temperature, $\delta_{T}$, and time effect, $\delta_{\theta }$[2, 15]. For a concrete gravity dam, $\delta_{H}$ can be expressed as a cubic polynomial function in the upstream water level, H. Component $\delta_{\theta }$ is usually represented as a combination of a linear function and a logarithmic function of time, t. The expression for $\delta_{T}$ is the main difference between the HST and the HTT. In the HST, $\delta_{T}$ is described by the multiperiodic harmonics, while in the HTT it is computed from the measured temperature [12]. More recently, Kang et al. [17, 27] confirmed that using the long-term air temperature data, T, can lead to better prediction results of dam displacement. Therefore, the input factor set of the interval prediction model, $S_{{{\text{HTT}}}}$, is selected using HTT as follows:

$$ \begin{aligned} S_{{{\text{HTT}}}} &= \left\{ {x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ,x_{7} ,x_{8} ,x_{9} ,x_{10} ,x_{11} ,x_{12} ,x_{13} ,x_{14} } \right\} \\ &= \left\{ {H,H^{2} ,H^{3} ,T_{0} ,T_{1 - 2} ,T_{3 - 7} ,T_{8 - 15} ,T_{16 - 30} ,T_{31 - 60} ,T_{61 - 90} ,T_{91 - 120} ,T_{121 - 180} ,\theta ,\ln \theta } \right\}, \\ \end{aligned} $$

(22)

where $T_{0}$ denotes the air temperature on the day of displacement monitoring, $T_{p - q}$ denotes the mean air temperatures between p and q days before the monitoring date, t denotes the cumulative number of days since the initial monitoring date, and $\theta = t/100$ [26].

In the modeling process, the PB, LSSVM, and MANN algorithms used in the proposed hybrid approach have own parameters that need to be determined. In the bootstrap method, the number of replicates, B, is a critical parameter that trades off the prediction performance and computational efficiency of the model. As suggested in literature [44], B can be taken as equal to the number of training samples used. As mentioned in Sect. 3.4, the MFOA is adopted to tune the parameters of LSSVM and MANN using the training samples. The maximum iteration number and population size of MFOA are set to 100 and 20, respectively [11]. For the LSSVM, the search space of the hyperparameter combination, $(C, \, \gamma )$, is defined as $[0.01,100] \subset {\mathbf{R}} \, \times \, [0.01,100] \subset {\mathbf{R}}$. The MANN used is a single-hidden-layer architecture, and the number of hidden neurons is obtained by trial and error [45]. The search ranges of the connection weights and thresholds between the input and hidden layers (hidden and output layers) are all set to $[ - 1,1]$. As the number of MFOA iterations increases, the model parameters gradually approach the ideal solutions. In both the LSSVM and MANN, the parameter values at the end of MFOA search are regarded as the final choice. The parameters of all algorithms involved in the prediction models for D4 and D36 after model training are given in Table 1. According to the implementation steps described in Sect. 3.4, the optimized B-LSSVM–MANN models with these parameters can be used for interval prediction of future displacements.

Table 1 Parameters of algorithms used for interval prediction models for D4 and D36

4.3 Interval prediction results

The goal of the B-LSSVM–MANN model is to construct the dam displacement PIs with a certain PINC, thereby providing a basis for risk-based decision-making and control. In practice, high-confidence information is usually used for referencing decisions to ensure the accurate understanding of dam behavior. Therefore, PIs with three high PINCs of 90%, 95%, and 99%, respectively, are selected for comprehensive analyses in this section.

Figure 8 shows the dam displacement PIs with different PINCs for the validation samples of D4 and D36 obtained by the B-LSSVM–MANN models trained as explained in Sect. 4.2. Table 2 summarizes the evaluation results of the constructed PIs with three PINCs using the assessment measures defined in Sect. 2.2. From Fig. 8, it can be seen that the PI width (PIW) is relatively uniform and increases with the increase in confidence level, which is in accordance with previous studies [36, 43]. Taking D4 as an example, the MPIWs corresponding to the obtained PIs with PINCs of 90%, 95%, and 99% are 1.25 mm, 1.43 mm, and 1.84 mm, respectively. Also, Fig. 8 shows that regardless whether the PINC is 90%, 95%, or 99%, the constructed PIs for D4 and D36 can cover most of the measured samples. Table 2 further reveals that at the three high confidence levels, the PICP is about 1–10% larger than the specified PINC, which indicates that the obtained PIs for both D4 and D36 are reliable. In this case, the CWC value is relatively small and equal to MPIW. These results demonstrate that the proposed hybrid B-LSSVM–MANN approach has satisfactory performance, i.e., the model appropriately quantifies the joint uncertainties through PIs.

Fig. 8

PIs with different PINCs for validation samples obtained by proposed B-LSSVM–MANN model: a 90% PI for D4, b 90% PI for D36, c 95% PI for D4, d 95% PI for D36, e 99% PI for D4, and f 99% PI for D36

Table 2 Quantitative evaluation of constructed PIs with different PINCs for D4 and D36

The variation in PIW can describe the effect of dynamic change in the input factors on displacement predictions. For instance, Fig. 7 shows that the peaks and troughs of the dam displacement time series correspond exactly to those of the water level and temperature time series. The water level and temperature change more drastically at the peak and trough positions [17], which causes greater variability in the dam displacement predictions. As seen in the PIW bar charts of Fig. 8, the PIs are wider near the peaks and valleys, which is a good reflection of the variability. In addition to being affected by external factors, the PIW is also influenced by the magnitude of the displacement itself. Generally, the uncertainty involved in the displacement of larger magnitude is more significant. In Fig. 7c, the range for D36 is larger than that for D4 and thus the MPIW of D36 PIs is greater than that of D4 PIs (see Table 2). In summary, the extrinsic and intrinsic effects are well characterized by PIs and reflected in their widths.

The proposed B-LSSVM–MANN model can not only construct the PIs, but also provide point prediction results, namely the true regression means (see Fig. 8). The common performance measures, i.e., the coefficient of determination (R²), mean absolute error (MAE), and root mean square error (RMSE), are used to evaluate the quality of the regression mean [4, 11]. The closer the R² is to 100%, the smaller the MAE and RMSE are, and the better the point prediction performance of the model is. Table 3 lists the evaluation results of the regression mean for D4 and D36. It can be observed that at the three confidence levels, the indices of the regression mean are excellent ($R^{2} \ge 95\%$) and close ($\Delta R^{2} \le 1.5\%$), indicating that the point prediction performance of the model is stable. By contrast, the width of the constructed PIs varies with the PINC, which differs from the regression mean. Moreover, Fig. 8 shows that the point prediction errors at the peak and trough positions are larger than elsewhere, which correlates with the wider PIs near the peaks and troughs mentioned earlier. This consistency reconfirms that the calculated PIs are rational.

Table 3 Quantitative evaluation of regression means for D4 and D36

4.4 Simulation and comparison analysis

As demonstrated in Sects. 2.1 and 3.4, both aleatoric and epistemic uncertainties are considered in the hybrid B-LSSVM–MANN model. The former is mainly caused by data noise, while the latter results primarily from the misspecification of model architecture and abstraction. In Sect. 4.3, we have demonstrated that the joint uncertainties can be well quantified by the constructed PIs with three different PINCs. In this section, taking PINC 95% as an example, it is further verified that the proposed model can properly respond to the individual uncertainty through PIs. To that end, three types of simulations are set up, including adding data noise, changing input factor set and prediction algorithm.

4.4.1 Exploration of aleatoric uncertainty through adding data noise

According to Eq. (22), the HTT-based factors related to air temperature are processed by the moving average method, which reduces noise. In this section, Gaussian noise is added to the training data of measured upstream water level and horizontal displacements of D4 and D36 to produce training data with an increased level of noise. A comparison of the noiseless (i.e., measured data without additional noise) and noisy data is shown in Fig. 9. In the simulation, the measured data are replaced with noisy training data and fed into the model, however, only the water level data or displacement data are replaced each time, but not both concurrently. Following the procedure described in Sect. 3.4 and the parameter settings from Sect. 4.2, the B-LSSVM–MANN models trained using the noisy water level or noisy displacement data are obtained and then used for interval prediction of dam displacement.

Fig. 9

Comparison of noiseless and noisy data of upstream water level for D4 and D36 (μ denotes mean value of noise and σ denotes standard deviation of noise)

The displacement PIs with PINC 95% for D4 and D36 obtained using noisy data are shown in Figs. 10 and 11, respectively. Figure 12 compares the PIs and regression means of D4 and D36 obtained using noiseless and noisy data through evaluation indices. Notably, after adding Gaussian noise, the width of the PIs increases and the precision of the regression mean decreases. The added noise increases the aleatoric uncertainty to dam behavior modeling, thereby reducing the credibility and accuracy of the prediction results. Moreover, the added low noise can be identified by the interval predictions, which demonstrates that it is feasible to use a MANN to estimate the variance of data noise as explained in Sect. 3.4.

Fig. 10

PIs with PINC 95% for D4 obtained using: a noisy upstream water level, and b noisy D4

Fig. 11

PIs with PINC 95% for D36 obtained using: a noisy upstream water level, and b noisy D36

Fig. 12

Quantitative evaluation of interval prediction results obtained using noiseless and noisy data: a PIs with PINC 95% for D4, b regression mean of D4, c PIs with PINC 95% for D36, and d regression mean of D36

The PIs offer more information than the point prediction of the regression mean. For example, the 36-th dam section is close to the middle of the dam (see Fig. 6), and thus it is more sensitive to the changes in water level. In Fig. 12c, the PICP of the PIs with PINC 95% for D36 obtained using noisy water level is only 92% ($< 95\%$), which suggests a lower prediction reliability. Also, the corresponding CWC value is as high as 21.88 mm, which is far larger than the CWC value of 4.72 mm in the absence of noise. In contrast, there is no significant change in the evaluation indices of regression mean irrespective whether the water level data used is noisy or not (see Fig. 12d). In short, the point prediction fails to reflect the negative effect of the additional noise in the water level data on the displacement prediction, whereas the PIs do.

4.4.2 Exploration of epistemic uncertainty of model architecture through changing input factor set

The changes in the number and magnitude of input factors would directly affect the model architecture, thus changing the resulting epistemic uncertainty. In this simulation, the only change is to replace the HTT-based factors with the HST-based factors. For the difference between the two, see Sect. 4.2. The HST-based input factor set, $S_{{{\text{HST}}}}$, can be expressed as follows [11, 15]:

$$ \begin{aligned} S_{{{\text{HST}}}} &= \left\{ {x_{1}^{{\prime}} ,x_{2}^{{\prime}} ,x_{3}^{{\prime}} ,x_{4}^{{\prime}} ,x_{5}^{{\prime}} ,x_{6}^{{\prime}} ,x_{7}^{{\prime}} ,x_{8}^{{\prime}} ,x_{9}^{{\prime}} } \right\} \\ & = \left\{ {H,H^{2} ,H^{3} ,\sin \frac{2\pi t}{{365}},\cos \frac{2\pi t}{{365}},\sin \frac{4\pi t}{{365}},\cos \frac{4\pi t}{{365}},\theta ,\ln \theta } \right\}. \\ \end{aligned} $$

(23)

After the B-LSSVM–MANN model is retrained, the displacement PIs with PINC 95% for D4 and D36 obtained using input factor set S_HST are shown in Fig. 13. Table 4 evaluates quantitatively the PIs and regression mean of D4 and D36 obtained using input factor sets S_HTT and S_HST. Combining the interval prediction results shown in Fig. 8c, d, it can be observed that the overall performance of the proposed model established using the HTT-based input factors is better, which is also consistent with the findings of Kang et al. [12, 17, 27]. From Table 4, the MPIW of the constructed PIs is nearly the same after changing the input factors, but the PICP is greatly reduced, even lower than PINC 95%. Some of the data points falling outside the 95% PI bands are marked in Fig. 13. This is because the multiperiodic harmonics in HST do not simulate the thermal responses of dam concrete accurately, while the long-term measured temperature effect modelling used in the HTT is closer to reality [27]. We also notice that in Fig. 13, the measured samples falling outside the 95% PI bands have a large deviation with the point prediction (i.e., regression mean), but are close to the lower limit of the PIs. Therefore, in the case of extreme uncertainty the upper or lower limit of the PIs could be regarded as an alternative estimate of future displacements.

Fig. 13

PIs with PINC 95% obtained using S_HST: a D4, and b D36

Table 4 Quantitative evaluation of interval prediction results for D4 and D36 obtained using S_HTT and S_HST

4.4.3 Exploration of epistemic uncertainty of model abstraction through changing prediction algorithm

The dam monitoring instruments are properly maintained and thus the noise contained in the recorded data is generally low. In this simulation, the MANN algorithm for estimating the variance of data noise remains unchanged, but the LSSVM algorithm for estimating the regression mean and the variance of epistemic (or model) uncertainty is replaced with alternative algorithms. The LSSVM is essentially an abstraction of the real functional relationship between dam displacement and its influencing factors. The common prediction algorithms (e.g., LSSVM, ELM [22], and RFR [15]) have different levels of approximation to the function, resulting in the differences in the epistemic uncertainty of model abstraction. In order to investigate the impact of different prediction algorithms on uncertainty quantification, the LSSVM is replaced with the ELM or RFR to form the B-ELM–MANN and B-RFR–MANN models, respectively, to compare them with the proposed B-LSSVM–MANN model. In all three models, the HTT-based factor set (Eq. (22)) is used as model inputs. The LSSVM parameters are shown in Table 1, and the parameter settings of ELM and RFR are listed in Table 5. Following the steps outlined in Sect. 3.4, the three models are trained and verified using the same data samples.

Table 5 Parameters of ELM and RFR algorithms for interval prediction models for D4 and D36

Figure 14 shows the displacement PIs with PINC 95% for D4 and D36 obtained using B-ELM–MANN and B-RFR–MANN models, while the corresponding PIs obtained using B-LSSVM–MANN are illustrated in Fig. 8c, d. The evaluation results of both PIs and regression means obtained from the three models are shown in Fig. 15. The PICP of the three models is greater than PINC 95%, which indicates that the PIs constructed via them are all effective. The MPIW of B-ELM–MANN is larger than the other two, and the MPIW of B-LSSVM–MANN is the smallest of the three. The prediction results of LSSVM achieved by separate runs are relatively uniform so that the proposed B-LSSVM–MANN model can yield the narrower PIs. On the other hand, the connection weights and thresholds of ELM are randomly initialized and thus the variability of its prediction results is quite significant [22]. As for the point prediction performance, it can be seen from Fig. 15b, d that the three evaluation indices of the regression mean obtained using the B-LSSVM–MANN model are all optimal. Notably, its R² value is up to about 95% for both D4 and D36. In summary, there are differences in the uncertainty quantization with different prediction algorithms, but the proposed B-LSSVM–MANN model has an excellent performance in terms of both interval prediction and point prediction.

Fig. 14

PIs with PINC 95% obtained using different models: a B-ELM–MANN model for D4, b B-ELM–MANN model for D36, c B-RFR–MANN model for D4, and d B-RFR–MANN model for D36

Fig. 15

Quantitative evaluation of interval prediction results for D4 and D36 obtained using different models

The proposed hybrid modeling approach is based on bootstrap resampling. In practical applications, the computational efficiency is another important issue that should be considered in addition to prediction performance. Table 6 compares the average computation time of three predictive models for D4 and D36 in a single run. The B-ELM–MANN model takes the least time, followed by the proposed B-LSSVM–MANN model. Both these models are computationally efficient and only require less than 1.0 s to train 126 ELMs or LSSVMs and a single MANN for PIs construction. The ELM is a single-hidden-layer neural network [22], while the LSSVM applies linear least squares criteria for the loss function and works with equality instead of inequality constraints [27], so that their training is fast. In contrast, the RFR is a tree-based ensemble learning algorithm [15] and thus its training is time-consuming. From Table 6, its time cost is about 70–100 times that of the other two models. Among the three comparison models, therefore, only the proposed B-LSSVM–MANN model achieves a satisfactory balance between prediction performance and computational efficiency.

Table 6 Average computation time of three predictive models for D4 and D36 in a single run

4.5 Discussion: interval prediction versus point prediction

The traditional methods of point prediction produce only the deterministic values as the final predictions. In this study, the PIs constructed by the interval prediction model are used as the uncertain representation of future displacements, and the regression mean values serve as the deterministic point prediction results. Accordingly, the point prediction and interval prediction are both interrelated but different.

• Due to the complexity of dam systems and the inadequacy of cognitive level, dam displacement prediction is inherently uncertain. In contrast to the point prediction, the interval prediction is more realistic and informative, because it can reflect the associated uncertainties through PIs.

• The interval prediction can be used as a substitute of traditional point prediction to assist in risk decision-making. The variation in the width of PIs provides dam operators with additional information about the variability and credibility of displacement predictions. Wide PIs indicate a high degree of uncertainty of the predicted values and the need for more attention and precautionary measures before risk mitigation action are undertaken. On the other hand, narrow PIs suggest that the uncertainty of the predicted results is relatively low, and the appropriate decisions can be made more confidently based on point predictions. Therefore, interval prediction can provide a valuable reference for making better-informed decisions, thereby improving the efficacy and reliability of dam risk management.

• Although interval prediction has obvious advantages over point prediction, it is still less than perfect in some aspects. For instance, the computational efficiency of the proposed B-LSSVM–MANN model is better than that of the other two interval prediction approaches compared (see Sect. 4.4.3), but is not as good as the simple point prediction. Especially when face with large amounts of data, the computational cost of the model becomes extremely expensive, which will challenge the online monitoring capability. Fortunately, with the progress in computer technology and improvement in artificial intelligence algorithms, this issue will gradually be resolved.

5 Conclusions and future research directions

Compared to the deterministic point prediction, the proposed interval prediction can be used to quantify the aleatoric and epistemic uncertainties associated with dam displacement predictions through PI construction. A hybrid approach for interval prediction that combines the non-parametric bootstrap, LSSVM, and MANN algorithms is proposed to construct the PIs of future displacements. The effectiveness of the proposed B-LSSVM–MANN model is verified using the monitoring data of a concrete gravity dam located in northeast China. The comprehensive analyses and simulation tests are further conducted to substantiate the claim to superiority of the proposed model. The main conclusions of this work are as follows:

• 1. The hybrid B-LSSVM–MANN model can not only quantify the uncertainties related to the predicted values in the form of PIs, but also provide the point prediction of regression mean. The constructed PIs with different confidence levels are high-quality and can encompass the majority of the measured samples (i.e., ${\text{PICP}} \ge {\text{PINC}}$) with a smaller MPIW. The accuracy of the regression mean is also excellent, with the R² value of over 95% for both D4 and D36.

• 2. The variation in PIW can describe the effect of the dynamic change in input factors on dam displacement predictions. The PIW is also influenced by the magnitude of the displacement itself. Generally, the variability or uncertainty involved in the displacement data with larger magnitude is more significant. Therefore, the extrinsic and intrinsic effects are well characterized by the constructed PIs and reflected in their widths.

• 3. Through three types of simulation tests, we found that the displacement PIs obtained using the proposed model can appropriately account separately for the aleatoric or epistemic uncertainty. Additional artificial data noise increases aleatoric uncertainty of dam displacement modeling, while changing the input factor set or the prediction algorithm changes the inherent epistemic uncertainty. Nevertheless, the increased level of aleatoric or epistemic uncertainty can be identified by the interval prediction results.

• 4. The computation of the proposed B-LSSVM–MANN model is efficient owing to the rapid training of the LSSVM algorithm. The results demonstrate that for D4 and D36, the average time of running this model once is less than 1.0 s.

In future work, we first plan to investigate other sources of uncertainties associated with dam systems and predictive models (e.g., dam aging and model parameters) in addition to data noise and model misspecification discussed in this paper. Secondly, other advanced mathematical techniques (e.g., reinforcement learning and Bayesian optimization) can be introduced for further enhancement of the prediction performance and computational efficiency of the proposed hybrid approach for interval prediction of dam displacements. Finally, the applicability of the B-LSSVM–MANN model to other phenomena and data (e.g., seepage, stress, and strain) deserves further studies.