Introduction

A typical forest planning problem consists of finding the optimal combination of treatment schedules for the stands of a forest. Combinatorial optimization is commonly used in this task. The methods for combinatorial optimization fall into two categories: mathematical programming and heuristics (e.g., Bettinger et al. 2009). Heuristic methods have been increasingly used as an alternative to mathematical programming (e.g., Pukkala and Kangas 1993; Boston and Bettinger 1999, 2002; Falcão and Borges 2002; Liu et al. 2006). Other methods such as dynamic programming and nonlinear optimization are frequently used in stand management optimization where the optimized variables are continuous (e.g., Haight et al. 1985; Valsta 1992; Pukkala 2007).

Most of the used heuristics fall to the category of global, or centralized, methods since the quality of a solution and the effects of changes that are made in the solution are evaluated at the forest level (globally). Decentralized methods optimize the management of each individual stand, but, when doing this, they are able to take into account forest-level constraints. Examples of decentralized methods are cellular automata (Strange et al. 2002; Heinonen and Pukkala 2007; Mathey et al. 2007) and the method of reduced costs (Hoganson and Rose 1984; Pukkala et al. 2009).

The most common global heuristics are simulated annealing, tabu search and genetic algorithm (Reeves 1993; Borges et al. 2002). Simulated annealing (SA) is a cooling method since it mimics the cooling process of melted metal. Other heuristics that can also be called as cooling methods are threshold accepting (TA) and great deluge (GD, Bettinger et al. 2002). All these methods accept also inferior moves (such changes in the solution that make it worse), but the probability of accepting inferior moves decreases when the optimization proceeds and the process cools. The purpose of accepting inferior moves is to provide a way to get away from local optima.

Tabu search (TS) uses tabu lists for the same purpose. Recent moves are temporally forbidden, which forces the method to explore a wider set of alternative solutions. Typical of tabu search is that several candidate moves are generated, and the best non-tabu candidate is accepted (Reeves 1993). While tabu search and all cooling methods operate with one solution, genetic algorithms (GA) operate with a population of solutions, which are combined to obtain a new generation of solutions (Reeves 1993). The solutions are called chromosomes. The objective function value calculated for a solution is called fitness.

Ant colony optimization (AC) is another heuristic, which operates with more than one solution (Zeng et al. 2007). In AC, solutions are called ants. Pheromone tracks left by the ants affect the way in which new ants select treatment schedules for stands when they construct their solutions. AC is a widely used heuristic method (Blum 2005; Dorigo et al. 2006), but it has been used only once in forest management planning (Zeng et al. 2007).

The advantage of heuristics is their flexibility. They can be used in problems in which the additivity and proportionality requirements of linear programming are not met. The objective variables can be spatial or non-spatial. The only requirements of heuristics are that the objective variable is numerical and there is a method for calculating its value. Heuristics are easy to use in multiobjective optimization. The relationships between objective variables and objective function (OF) can be linear or nonlinear, and the effects of different objective variables on the objective function value can be additive, multiplicative or a combination of both. Although mathematical programming methods can be used in complicated spatial (Baskent and Keles 2005; Constantino et al. 2008; Könnyű et al. 2014.) and stochastic (Eyvidson and Kangas 2014) problems, it is likely that the use of heuristic methods continues to increase since the complexity of forest management problems is increasing due to the increasing number of products and services that should be considered in forest planning.

The problem of heuristic methods is that they do not necessarily find the optimal solution. Usually, they find a good solution, but it is not assured that the solution is the global optimum. However, the practical significance of this limitation may be small since there are much bigger sources of uncertainty in forest planning. These uncertainties include errors in inventory data and growth models, as well as uncertainties related to future timber prices, regeneration of trees, pest outbreaks, diseases and various abiotic hazards.

Another problem is the difficulty to find the best parameters for the heuristics. Each method has a few parameters which greatly affect the performance and time consumption of the method. The optimal parameter values depend on the type of the problem, which means that different parameter values should be used in different problems. It is extremely tedious to systematically analyze the effect of different parameter combinations on the performance of the heuristic. For example, if the heuristic has 5 parameters and 10 different values of each parameter are compared, the number of parameter combinations is 105 = 100,000. Therefore, when seeking good parameter values for the comparison of different heuristic methods (Bettinger et al. 2002; Pukkala and Kurttila 2005), it is common to examine one parameter at a time and ignore the interactions of parameters. However, due to the interrelationships between parameters, this approach does not guarantee that the best parameter values were found. This limitation has also an effect on the comparisons of alternative heuristic methods since the parameters used may be more optimal for certain heuristic than for the others.

An alternative to trial and error is to use optimization in the search for optimal parameter values. This would make the comparisons between different heuristic methods more ‘fair’ since none of the methods is impaired by poorly set parameters. There is already one study that used optimization to find the best parameter values for heuristic methods (Pukkala and Heinonen 2006). However, several of the well-known heuristic techniques (TS, GA, GD, AC) were not included in the optimizations.

This study aimed at providing a fair comparison of the most common global heuristics in non-spatial and spatial forest planning problems. The analysis consisted of two steps. First, the parameters of each method were optimized on the constraint that each method had the same time to find the solution. Second, the OF values produced by different heuristics with the optimal parameter values were compared.

Methods

The heuristic methods were used to find the optimal combination of treatment schedules generated for the stands of a forest. The treatment schedules were produced before running the heuristics. The CMForest software (Jin et al. 2016) was used to produce the schedules. In the case study area used in this study the average number of treatment schedules was 14.5 per stand, and the number of stands was 888. This means that the magnitude of the number of different combinations of treatment schedules (size of decision space) was 14.5888, which is a huge number. The task of the heuristic was to find the best of these combinations.

Each heuristic can be implemented in different ways. In this study SA, TS and GA were used as explained in Pukkala and Heinonen (2006), who in turn based their implementations on the advices given in Reeves (1993). TA and GD were implemented as described in Bettinger et al. (2002). Because there is plenty of literature on all these methods (e.g., Reeves 1993; Bettinger et al. 2002; Borges et al. 2002; Pukkala and Kurttila 2005), they are described only briefly below. The AC heuristic used in this study is based on the descriptions of Blum (2005) and Dorigo et al. (2006).

Simulated annealing

SA begins with an initial solution. The initial solution is the best of several random combinations of treatment schedules of stands. Moves (changes) are made to the initial solution by selecting first a random stand and then a random schedule for this stand from those produced beforehand. The schedule that is currently in the solution is replaced by the randomly selected alternative schedule. The replacement (move) is maintained if it improves the OF value; otherwise, it is maintained with the following probability:

$$p = \exp \left[ {\frac{{\left( {{\text{OF}}_{\text{Candidate}} - {\text{OF}}_{\text{Current}} } \right)}}{T}} \right]$$
(1)

where OFCurrent is the OF value of the solution before implementing the move, OFCandidate is the OF value after the move, and T is ‘temperature’ which determines the probability of accepting inferior moves. The temperature is decreased toward the end of the search, which means that the probability to accept inferior moves also decreases. Several candidate moves are produced at each temperature. The search is stopped when the temperature reaches a pre-defined low value, which is called freezing temperature. A new temperature is obtained by multiplying the current temperature by a multiplier smaller than 1. It is possible to increase or decrease the number of candidate moves per temperature when the process cools. An increase means that the search is intensified toward the end of the search.

SA has the following parameters:

  • P1: number of random searches done to obtain the initial solution

  • P2: starting temperature

  • P3: freezing temperature

  • P4: cooling multiplier (<1)

  • P5: search intensity at initial temperature, expressed as the proportion of the number of stands (1.0 means that the number of evaluated candidate moves is equal to the number of stands)

  • P6: multiplier of search intensity, to obtain the search intensity in the next temperature

Threshold accepting

TA is fairly similar to SA, and in this study, it was implemented in a nearly similar way as SA. The difference is that whereas SA accepts inferior moves with certain probability, TA accepts all moves which produce an OF value greater than the current value minus a threshold. For example, if the current OF value is 0.9 and the threshold is 0.05, all moves that produce a solution with OF value greater than 0.85 are accepted. Cooling is implemented so that the threshold is reduced toward the end of the search. Search is terminated once the threshold value is close zero. This threshold may be called as freezing threshold.

TA has the following parameters:

  • P1: number of random searches done to obtain the initial solution

  • P2: starting threshold

  • P3: freezing threshold

  • P4: cooling multiplier (<1), to obtain the next threshold

  • P5: search intensity at initial threshold, expressed as the proportion of the number of stands

  • P6: multiplier for search intensity, to obtain the search intensity at the next threshold

Great deluge

GD can also be classified as cooling method. Cooling is implemented via rising water level. Water level is the lowest accepted OF value. Water has an initial level. Always when a move improves the solution, there is a rain event, which rises the water level. The amount of rain gets smaller when the search continues. This type of search stops when the water level is equal to the current OF value. The search continues with another search mode, namely direct ascent (hill climbing). The direct ascent search mode selects a random stand and replaces its current treatment schedule by another, randomly selected schedule simulated for the same stand. All improving moves are accepted, and all moves which do not improve the solution are rejected. Direct ascent steps are repeated for a certain number of iterations.

GD has five parameters:

  • P1: number of random searches done to obtain the initial solution

  • P2: initial water level

  • P3: initial rain

  • P4: rain multiplier (<1), to obtain the magnitude of the next rain

  • P5: number of direct ascent iterations at the end of the search

Tabu search

TS is somewhat different from the cooling methods. The first difference is that several candidate moves are produced and only one of them is accepted. The number of candidates can be anything from two to the highest possible value (total number of schedules minus number of stands). The best non-tabu candidate is accepted even if it produces an OF value lower than the current value. If all candidate moves are in the tabu list (forbidden), the move that has the shortest tabu tenure is accepted (shortest tabu tenure means that the move will be the first to be removed from the tabu list). Moreover, if a move would produce a better OF value than the best found so far, the move is accepted even if it is tabu.

Another feature is the use of tabu lists, which prevent the search process from repeating recent moves. The two schedules that participate in a move go to a tabu list in which they stay for a certain number of iterations. Iteration refers to the generation of a set of candidate moves and selecting the best of them. For example, an initial tabu tenure 10 means that the schedule which goes to the list is tabu for 10 iterations. Every iteration reduces the remaining tabu tenures of all listed schedules by 1.

The tabu search heuristic used in this study has two tabu lists, one for the schedules that are replaced by another schedule (schedules that leave the solution) and the other list for schedules that replace the removed schedule (schedules that enter the solution). The whole stand is tabu as long as the entering schedule is tabu. Tabu search is terminated when a certain number of iterations are completed.

The parameters of TS are:

  • P1: number of iterations

  • P2: number of candidate moves produced per iteration

  • P3: length of the tabu tenure of leaving schedules

  • P4: length of the tabu tenure of entering schedules

Genetic algorithm

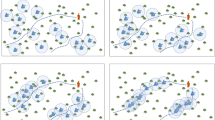
GA can be implemented in several different ways. Common to all implementations is that, opposite to all previous heuristics, they operate with several solutions. These solutions are called chromosomes. New chromosomes (off-spring) are produced by combining two parent chromosomes using crossing-over. The new chromosome may have mutations, i.e., small changes somewhere in the chromosome. When GA is applied to forest planning, a gene corresponds to a stand, and different treatment schedules of the stand are the alleles of the gene. A chromosome is a list of schedules which are included in the solution (Fig. 1).

Fig. 1
figure 1

Production of off-spring in genetic algorithm. Two parent chromosomes (solutions) and crossing-over points (thick vertical lines) are selected. The middle part of the off-spring is taken from the second parent, and the rest is taken from the first parent. Mutations can be made in the newly produced off-spring (the gray-shaded cells with boldface numbers show one mutation). The numbers in the chromosomes indicate the number of the treatment schedule which is included in the solution represented by the chromosome

Full size image

In this study, only one off-spring was produced per iteration (generation). Two parent chromosomes were selected from the current population. For the first parent, the probability of selection depended on the fitness value (OF value) of the chromosome, so that the best chromosome had the highest probability to become selected. The second parent was selected randomly, using the same probability for all chromosomes.

Then, two crossing-over places were selected randomly. The genes located in the chromosome before the first and after the second point were taken from the first parent, and the remaining genes were taken from the second parent (Fig. 1). For example, if the solution (chromosome) consisted of treatment schedules for 100 stands and the crossing-over places were 25 and 66, the schedules for stands 1–24 and 67–100 were taken from the first solution and the schedules of stands 25–66 were taken from the second solution.

Mutations were applied to the new off-spring. A mutation means that a random gene (stand) is selected, and its schedule is replaced by another, randomly selected schedule simulated for the same stand. Mutation rate changed during the GA search process.

After a new off-spring was produced, one chromosome was removed from the population. The probability of removal was inversely proportional to the ranking of the chromosome (worst chromosomes had the highest probability of removal). The search was stopped when a certain pre-defined number of generations were completed.

The parameters of GA are:

  • P1: number of chromosomes

  • P2: number of random searches that are used to produce an initial chromosome

  • P3: number of generations

  • P4: initial mutation rate (at first generation)

  • P5: final mutation rate (at last generation)

Mutation rate was changed gradually from the initial to the final rate. Rate 2.5 means that two mutations are made with certainty and a third mutation is made with the probability of 0.5.

Ant colony optimization

The original plan in this study was to use the AC algorithm proposed for forest planning by Zeng et al. (2007). However, preliminary analyses revealed that this algorithm was not working satisfactorily in the forest planning problems analyzed in this study. Therefore, each of the three variants of ant colony optimization described in Dorigo et al. (2006), namely Ant System, Max–Min Ant System, and Ant Colony System, was adapted to forest planning and tested. It turned out that the Ant System was inferior to the other variants, and the Ant Colony System was not better than the Max–Min Ant System. Therefore, the Max–Min Ant System was selected for parameter optimization.

In the Max–Min Ant System used in this study, all treatment schedules are given the same initial pheromone level. Each ant of the first ant iteration constructs a solution by selecting a random treatment schedule for each stand. The objective function value is calculated for each ant.

The pheromone levels of all treatment schedules are updated at the end of each iteration. In the Max–Min Ant System only the best ant updates the pheromones. This ant can be the best ant of the last iteration (iteration-best) or the best ant of all iterations completed so far (best-so-far). In our study, both the iteration-best ant and the best-so-far ant updated the pheromones of the treatment schedules. The pheromone update was done as follows:

$$\tau_{ij} \leftarrow \left[ {(1 - \rho ) \cdot \tau_{ij} + \Delta \tau_{ij}^{\text{best}} } \right]_{{{\kern 1pt} \tau_{\hbox{min} } }}^{{{\kern 1pt} \tau_{\hbox{max} } }}$$
(2)

where τ ij is the pheromone level of treatment schedule i of stand j, ρ is the pheromone evaporation rate, and τ min and τ max are the minimum and maximum pheromone levels, respectively. The amount of pheromone addition was equal to half of the objective function value of the solution generated by the iteration-best or best-so-far ant:

$$\Delta \tau_{ij}^{\text{best}} = \left\{ {\begin{array}{*{20}l} {OF_{\text{best}} /2} \hfill & {{\text{if}}\;i\;{\text{belongs}}\;{\text{to}}\;{\text{the}}\;{\text{solution}}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(3)

After completing the first iteration and updating the pheromone levels of all treatment schedules the same number of ants constructed new solutions so that the probability of selecting a schedule depended on the pheromone levels of the treatment schedules as follows:

$$p_{ij}^{k} = \frac{{\tau_{ij}^{\alpha } }}{{\sum\nolimits_{i = 1}^{{n_{j} }} {\tau_{ij}^{\alpha } } }}$$
(4)

where p k ij is the probability that ant k selects schedule i for stand j, τ ij is the pheromone of schedule i of stand j, and n j is the number of treatment schedules simulated for stand j. The heuristic information included in most ant colony algorithms (Dorigo et al. 2006) was not used in the AC heuristic tested in this study.

The same process of constructing solutions and updating pheromones was repeated for a certain number of ant iterations. The best solution constructed during the whole search process (best-so-far) was the solution found by the AC heuristic.

The parameters of AC are:

  • P1: number of ants

  • P2: number of iterations

  • P3: evaporation rate (ρ in Eq. 2)

  • P4: probability exponent (α in Eq. 4)

  • P5: initial pheromone

  • P6: minimum pheromone (τ min)

  • P7: maximum pheromone (τ max)

Case study problems

The heuristics were optimized and compared using data from the Mengjiagang Forest, located in the Heilongjiang Province in Northeast China. The forest has been divided into 93 compartments, and each compartment has been further divided into subcompartments so that the total number of subcompartments is 888. Subcompartment, which corresponds to stand, was the calculation unit in the simulation of treatment alternatives. The total area of the case study forest is 15,533 hectares.

The CMForest software (Jin et al. 2016) was used to simulate alternative treatment schedules for the stands for three 10-year periods. The total number of alternatives simulated for the 888 stands was 12,940, which gives an average of 14.57 schedules per stand. Schedules representing even-aged management were simulated for planted stands, and selective cuttings were simulated for all other stands. Details of the automated simulation tool of CMForest can be found in Jin et al. (2016).

The parameters of the heuristics were optimized for a non-spatial and spatial problem. The forest planning problems were formulated in a utility theoretic way as follows:

$$\hbox{max} \,U = \sum\limits_{i = 1}^{I} {a_{i} u_{i} (q_{i} )}$$
(5)

subject to

$$q_{i} = Q_{i} ({\mathbf{x}}),\quad i = \, 1, \ldots ,I$$
(6)

where U is total utility, a i is the weight, u i is the subutility function, and q i is the quantity of objective variable i. Q i is the procedure which calculates the value of objective variable i from the information of those treatment schedules that are included in the solution, and x is a vector which indicates the ID numbers of those schedules which are included in the solution (see Fig. 1).

Subutility functions scale all objective variables to range 0–1. In addition, a subutility function tells how the utility depends on the quantity of the objective variable. The weights (a i ) were scaled so that their sum was equal to 1. Therefore, the total utility also ranged from 0 to 1.

The utility function of the non-spatial problem was as follows

$$U = 0.25u_{1} \left( {H_{\text{I}} } \right) + 0.25u_{2} \left( {H_{\text{II}} } \right) + 0.25u_{3} \left( {H_{\text{III}} } \right) + 0.25u_{4} \left( {V_{30} } \right)$$
(7)

where H I, H II and H III are the harvested volumes of the first, second and third 10-year period and V 30 is the total growing stock volume at the end of the third 10-year period. The spatial problem had two additional objective variables:

$$U = 0.1667u_{1} \left( {H_{\text{I}} } \right) + 0.1667u_{2} \left( {H_{\text{II}} } \right) + 0.1667u_{3} \left( {H_{\text{III}} } \right) + 0.1667u_{4} \left( {V_{30} } \right) + 0.1667u_{5} \left( {\text{CC}} \right) + 0.1667u_{5} \left( {\text{CNC}} \right)$$
(8)

where CC is the length of the common boundary between such adjacent stands which are both cut during the same 10-year period, and CNC is the boundary between such adjacent stands of which one is cut and the other is not cut during a certain 10-year period (Kurttila et al. 2002; Palahí et al. 2004). Maximization of CC leads to aggregated harvest blocks and large total area of harvested stands, and minimization of CNC leads to compact harvest blocks and small total area of harvested stands. Previous research has shown that simultaneous use of these two variables as management objectives leads to good aggregation of harvest blocks (Islam et al. 2010).

The utility functions for harvested volumes were formulated so that a removal of 300,000 m3 gave the maximal subutility, and deviations to both directions decreased utility. The cutting target of 300,000 m3 is close to the 10-year volume increment of the case study forest. Linear subutility functions were used for V 30 and CC. The maximum possible value gave subutility 1, and if the value of the objective variable was zero, subutility was also zero. The subutility function of CNC was also linear, but now the maximum possible value of CNC resulted in subutility 0, and the lowest possible value of cut-uncut border (0 m) resulted in subutility 1. This means that CNC was minimized.

Optimization method

The method of Hooke and Jeeves (1961) was used to find the optimal values of the parameters of each heuristic. The direct search of the Hooke and Jeeves method consists of alternating steps of exploratory and pattern searches. The exploratory search changes the value of one variable at a time, and all changes that improve the objective function are accepted. After examining all optimized variables in the exploratory search the algorithm goes to pattern search, which makes simultaneous changes in more than one variable. Then the step size (magnitude of change) is halved, and the sequence of exploratory and pattern searches is repeated. This process is continued until the step size becomes smaller than the stopping criterion of the algorithm.

Since the Hooke and Jeeves direct search algorithm does not necessarily converge to the global optimum, the search was repeated a few times, starting from different initial solutions (different initial combinations of the parameters of the heuristic). The parameter optimizations for the non-spatial forest planning problem were repeated 5 times, and 2 or 3 repeated direct searches were used when the parameters were optimized for the spatial problem, for which the heuristic search was more time-consuming.

The starting point of the first direct search was an initial guess by the authors (‘Start’ in Table 1). The other direct searches started from the best of 100 random combinations of the parameters of the heuristic. The random parameter values were drawn from uniform distributions specified by the minimum and maximum values of the respective parameter (Low and High in Table 1). The initial step size of the direct search was 10 % of the range of variation (Low–High). The direct search was terminated when the step size was less than 1 % of the initial step size. Since the direct search was allowed to move beyond the Low–High range, every parameter was also given a minimum allowed and maximum allowed value (Min and Max in Table 1). All values beyond the Min–Max range were replaced by Min or Max.

Table 1 Ranges and starting values for the optimized parameters of the heuristic algorithms
Full size table

All tested parameter combinations were passed to the heuristic search algorithm, which solved the forest planning problem using these parameter values. The utility value of the management plan was passed to the Hooke and Jeeves algorithm. Based on this feedback the Hooke and Jeeves algorithm either accepted or rejected the change it made to the parameters of the heuristic.

Each heuristic method was given the same search time. The time limitation was implemented by using a penalty function. The penalty was zero if the used search time was less than the allowed limit and increased linearly up to one when the search time was twice the allowed time. This means that the objective function value (Utility–Penalty) was zero if the search time was equal to twice the allowed search time. All calculations were done with Lenovo ThinkCentre M8500t computer (CPU I7-3770, memory 24 GB).

The allowed time was found by applying all heuristics to the non-spatial and spatial forest planning problem, using parameters recommended in earlier literature (Reeves 1993; Bettinger et al. 2002; Pukkala and Kurttila 2005; Pukkala and Heinonen 2006). Based on these searches, two allowed search times were defined for the non-spatial and spatial problem. The first time, leading to ‘fast search,’ was the time that the quickest heuristics needed for the search, and the second, leading to ‘slow search,’ was the time that the slowest heuristics used to complete their search process. In the non-spatial problem, the fast time was 1 s and the slow time was 7 s. In the spatial problems, the fast search time was 10 s, and slow search time was 60 s.

Results

Optimal parameter values of the heuristics

Simulated annealing

For the fast solving of the non-spatial problem, the optimal parameters of SA were 44 initial random searches (the starting point was the best of 44 random solutions) with an initial temperature on 0.002674, freezing temperature of 0.000018 and cooling multiplier of 0.875 (Table 2, Non-spatial, fast). The number of generated candidate moves in the initial temperature was 0.740 times the number of stands (888) resulting in 657 candidates. The search intensity was increased by 5.1 % in every new temperature (iteration multiplier was 1.051). However, there was some variation between the five repeated Hooke and Jeeves optimizations. In the three best ones (2nd, 3rd and 4th solution in Table 2) the number of initial random searches was 18–149, initial temperature ranged from 0.001728 to 0.003150, and freezing temperature ranged from 0.000018 to 0.000098. The search intensity also varied and the two parameters related to search intensity were interrelated so that when the initial intensity was high, it decreased toward the end of the search, and vice versa.

Table 2 Optimal parameter values of simulated annealing for different problems and solution times found in two to five repeated Hooke and Jeeves optimizations
Full size table

When more time was allowed for the search, the number of initial random searches increased, initial temperature increased, freezing temperature was not much affected, cooling became slightly slower, and the search intensity became slightly higher (Table 2, Non-spatial, slow). These conclusions can be made when looking at the results of all repeated Hooke and Jeeves optimizations.

The number of initial random searches was smaller in the spatial problems (except in the second optimization for ‘Spatial, slow,’ which resulted in low utility value), and freezing temperatures were lower than in the non-spatial problems. The main difference between fast and slow search for the spatial problem was slightly higher initial temperature and more quickly increasing search intensity in the slow search.

Threshold accepting

Typical to TA was high variation in the number of initial random searches, suggesting that the search result is not sensitive to this parameter (Table 3). In the fast search for non-spatial problem, the initial threshold was 0.004437–0.009934 and the cooling multiplier was 0.814–0.867. A clear difference to SA was about two times more intensive search at the initial threshold with almost constant search intensity during the whole search process. Increasing search time led to higher number of initial random searches, slower decrease in threshold and more intensive search.

Table 3 Optimal parameter values of threshold accepting for different problems and solution times found in two to five repeated Hooke and Jeeves optimizations
Full size table

The optimal parameters for a fast search in the spatial problem did not differ much from those for a fast search in the non-spatial problem. The starting threshold was systematically lower, and the freezing threshold was always low in the spatial problem. For the slow search in spatial problem, TA adopted a higher number of initial random searches, slower cooling and gradually increasing search intensity.

Great deluge

In GD, fast search for the non-spatial problem used 114–200 initial random searches and 112–901 direct ascent search steps at the end of optimization (Table 4, Non-spatial, fast). Between them, the great deluge itself started from an initial water level of 0.663–0.899, initial rain of 0.000134–0.000464 and rain multiplier of 0.908–0.998. When more time was allowed for the search, the main and most systematic difference was smaller initial rain, which resulted in slower cooling (Table 4, Non-spatial, slow). The optimal parameters for the spatial problem were not systematically different from the optimal parameters for non-spatial problem. The same difference was found between fast and slow search: Initial rain was smaller when more time was allowed for the search, resulting in slower cooling.

Table 4 Optimal parameter values of great deluge for different problems and solution times found in two to five repeated Hooke and Jeeves optimizations
Full size table

Tabu search

In fast tabu search for the non-spatial problem, TS used 5000–7000 iterations, produced 4–12 candidate moves per iteration and forbade the treatment schedules that participated in the last move from participating in another move for 18 to 43 iterations (Table 5). Note that when the tabu tenure is longer for the entering schedule (P4 in Table 5) than for the leaving schedule (P3), parameter P3 has no effect on the search process since all schedules of the stands are tabu as long as the entering schedule is in the tabu list.

Table 5 Optimal parameter values of tabu search for different problems and solution times found in two to five repeated Hooke and Jeeves optimizations
Full size table

The number of iterations increased when 7 s was allowed for the search instead of 1 s. The other parameters were not systematically affected. The spatial problem seems to need a higher number of candidate moves and longer tabu tenures for those treatment schedules that a removed from the solution. The main difference between fast and slow search was higher number of iterations in the slow search.

Genetic algorithm

The overall observation that characterized the optimal parameter values of GA was very low number of chromosomes, which was the lowest possible (2) in a majority of optimizations (Table 6). This means that the algorithm operated with only two solutions that were combined to obtain an off-spring, after which one of the three solutions was removed from the population. Most probably, the reason for such a low number of solutions was the short allowed search time. With a ‘normal’ population size, GA would be clearly slower than the other heuristics analyzed in this study (except AC).

Table 6 Optimal parameter values of genetic algorithm for different problems and solution times found in two to five repeated Hooke and Jeeves optimizations
Full size table

In the fast search processes (both non-spatial and spatial), the number of random searches that were used to produce each of the chromosomes was 10–30, and the number of generations was 65–237. The number of mutated ‘genes’ (stands) was 1–10, which means that the treatment schedules of 1–10 stands out of the 888 stands of the case study forest were changed after the first version of the off-spring was produced by crossing-over. The mutation rate sometimes increased (final mutation rate, P5 was higher than P4) and sometimes decreased (P4 was higher than P5) during the search process. This suggests that it would be enough to use a constant mutation rate (of about 5/888) during the whole search.

Increasing search time increased the number of generations. Also the number of random searches that were used to produce an initial solution increased. These changes were fairly systematic.

Ant colony optimization

For fast AC search either the number of ants or the number of ant iterations was low (Table 7). It seems that fast search with reasonable results is only possible with a very low number of ants. In this respect, the results correspond to those obtained for GA: Small population size (chromosomes or ants) must be used in fast search. Both the number of ants and the number of iterations increased when more time was allowed for the search.

Table 7 Optimal parameter values of ant colony optimization for different problems and solution times found in two to five repeated Hooke and Jeeves optimizations
Full size table

Since the results still varied a lot between repeated optimizations, especially in terms of utility value, additional optimizations were conducted with a longer search time (very slow in Table 7) to see whether the results of repeated optimizations would stabilize, making it easier to make conclusions about suitable parameter values. Now the utility values stabilized, and the results suggested 12–30 ants with 89–244 ant iterations. If all optimizations for the non-spatial problem that resulted in good utility values are looked together, it may be concluded that a suitable maximum pheromone is 4–6, minimum pheromone is 0.001–0.15, and the initial pheromone should be 2–4. Parameter α of Eq. 4 should be 1.1–1.9. It seems that longer allowed search times lead to higher number of ants and iterations and lower evaporation rate.

Also in the spatial problem the number of ants or ant iterations tended to increase with increasing allowed search time. However, there seems to be much uncertainty about the optimal values of some parameters. This may be because of the interrelationships between parameters. For example, evaporation rate was often low when the initial pheromone was low and higher evaporation rates often occurred with high initial pheromone levels.

Search process with optimal parameter values

Figure 2 shows examples of the development of the utility value in the search process for the non-spatial problem in the slow search (7 s). The best parameter values (boldface in Tables 2–6) were used. Typical of all cooling methods (SA, TA and GD) was the high but decreasing oscillation of the utility value of the current solution and a gradual increase in the utility of the best solution found so far. The reason for the decreasing oscillation was decreasing probability to accept inferior moves, i.e., cooling. In GD, the lower limit of the range of oscillation increased steadily, which was a result of rising water level. The utility of SA reached a high level later than in TA, which is because of higher number of initial random searches in SA (334, see Table 2) than in TA (1, Table 3). However, the number of initial random searches varied a lot between repeated Hooke and Jeeves optimizations for both SA and TA, which means that since both of these methods are fast, they can spend a part of the allowed search time for initial random searches although these searches are not critically important for the outcome of the search.

Fig. 2
figure 2

Development of the utility of the current solution and the best solution found so far in the slow search for non-spatial problem when optimal parameter values are used for each heuristic. In genetic algorithm, which operates with several solutions, the mean utility of the current population of solution vectors is shown

Full size image

The corresponding diagram looked quite different for TS (Fig. 2, Tabu search), which quickly found a good solution, which could not be improved much during the rest of the search process. The range of oscillation did not decrease during the search process because there was no cooling. Inferior moves were to be accepted during the whole search process because of constant tabu tenures.

In GA, the utility of the best chromosome and the average utility of all chromosomes increased almost linearly during the whole search process. This means that GA needed the whole allowed time to find a good solution.

Figure 3 shows the development of the utility of the best-so-far and iteration-best ants and the mean utility of all ants of the current iteration in fast, slow and very slow AC search for the non-spatial problem. When the number of ants was 46, the iteration-best became almost always the new best-so-far ant. With fewer ants, the curve for the iteration-best ant often differed from the best-so-far curve, and sometimes it took several iterations to improve the best-so-far solution. When there were more than two ants, differences in their utility values decreased gradually and the mean utility approached the utility of the best ant.

Fig. 3
figure 3

Development of the utility of the best-so-far and iteration-best ant and the mean utility of all ants of the current iteration in the fast, slow and very slow search for non-spatial problem when optimal parameter values are used

Full size image

The development of the 10-year harvests during the search was similar in SA and TA (Fig. 4) after the end of the random searches, which lasted longer in SA. The pattern was completely different in GD, which needed almost the whole allowed time to find solutions in which the harvested volume was close to 300,000 m3 for all three 10-year periods. In this respect, GD and GA were similar, but there was less oscillation in GA (Fig. 4 bottom). Common to both methods was that they used the whole allowed computing time to reach a solution which satisfied the cutting targets and had a good utility value.

Fig. 4
figure 4

Development of 10-year harvests in the current solution in the slow search for non-spatial problem when optimal parameter values are used for each heuristic. For genetic algorithm, the harvested volumes of the best solution of the current population are shown. The Roman number (I, II and III) refers to the 10-year period

Full size image

TS very quickly found a solution in which the 10-year harvests were near 300,000 m3, after which they varied only little during the rest of the search. Common to all methods was the gradually increasing harvested volume of the first 10-year period and decreasing harvest of the third period.

In the fast AC search the harvest of the first 10-year period did not reach the required 300,000 m3 suggesting that 1 s was a too short search time for the AC heuristic to find good solutions (Fig. 5). The required harvested volumes were reached in the slow and very slow search, and the development of the periodical harvests resembled to those in GA. The smoother progress of the harvested volume in the slow search can be explained by the high number of ants resulting in a new best-so-far solution at every iteration.

Fig. 5
figure 5

Development of 10-year harvests for the iteration-best ant in the fast, slow and very slow AC search for non-spatial problem when optimal parameter values are used. The Roman number (I, II and III) refers to the 10-year period

Full size image

Ranking of the heuristics

In the fast search for the non-spatial problem, TA, SA and TS were the best methods and GA and AC were clearly worse than the other heuristics (Fig. 6, top). All methods benefitted from increased computing time, but the improvement of utility was much larger in GA and AC than in the other methods. SA was the best method with 7-s computing time, but TA was nearly as good. GA was again the worst method, and GD and TS were halfway between the two worst (GA and AC) and the two best (SA and TA) methods.

Fig. 6
figure 6

Utility values obtained with the optimal parameter values found for different heuristic methods in the fast (left, light tone) and slow (right, dark tone) search for the spatial and non-spatial forest planning problem

Full size image

In the spatial problem, SA was the best method in the fast search (10 s) and TA was the second, but the order was reversed when the search process was allowed to last for 60 s (Fig. 6, bottom). GA and AC were again clearly weaker than the other methods, and GD was better than TS. Based on all the optimizations, it is easy to rank the five tested heuristics as follows: SA and TA are the best methods, GD is the third in ranking, TS is the fourth, and GA and AC are the least satisfactory heuristics when the same computing time is allowed for all heuristics. AC was slightly better than GA.

Discussion

This study is the second one in which optimization was used to find the best combinations of parameters that guide the search processes of heuristic methods used in forest management planning (the first is Pukkala and Heinonen 2006). The study is the first one that optimized the parameters of great deluge, genetic algorithm and ant colony optimization. The Min–Max Ant System was used for first time in forest management planning.

The purpose of parameter optimization was to help other users of heuristic methods to set their parameters so that good solutions are found in reasonable computing time. Although the results of repeated optimizations varied, some conclusions on recommendable parameter values for similar forest planning problems can be given. For example, the cooling multiplier of SA should be about 0.9. This is a significant result since very fast cooling (e.g., 0.7 or 0.8) and very slow cooling (e.g., 0.95 or 0.99) could be ruled out. A suitable number of iterations in each temperature were 1–2 times the number of stands. If the search time does not need to be very short, the number of iterations could be increased by 5 % in every new temperature. The number of random searches that are done to obtain the initial solution for the SA heuristics is not an important parameter.

The results were equally clear for the TA heuristic. More problematic parameters, from the generalization point of view, are the initial and freezing temperatures of SA, and the initial and freezing thresholds of TA. However, generalization becomes easier if these parameters are related to the unit and range of variation of the objective function and the influence that one move (or stand) can have on the objective function value. For example, the optimal initial temperature of SA was found to be approximately 0.002 in most cases. In the utility maximization of this study, the maximum influence of a stand on the OF value of the solution is approximately 1/888 = 0.001126, i.e., the maximum possible utility divided by the number of stands. A suitable initial temperature was equal to the maximum value of the objective function divided by the number of stands and multiplied by two.

The results on starting and cooling temperature may be applied to other cases as follows. If the maximized variable is net present value, its maximum value is approximately 2,500,000 USD, and there are 1500 stands, a suitable starting temperature would be 2 × 2,500,000/1500 = 3333. The magnitude of freezing temperature should 0.5–1 % of the initial temperature, i.e., around 15–30. Similar rules apply to the initial and freezing thresholds of the TA heuristic. This shows that although the optimal parameters of the heuristics are problem-specific, some generalizations to similar forest planning problems can be made from the results of this study. Therefore, the results of this study make it easier for forest managers to find suitable parameters for the heuristic methods they use to solve forest planning problems.

Generalization would be easier if parameter optimizations are made for several forests and forest planning problems varying in size, objective function and constraints. This would make it possible to develop rules or even models for the optimal parameter values of the heuristics.

The optimal parameter values for the SA, TA and TS heuristics were reasonably close to those obtained by Pukkala and Heinonen (2006). This earlier study suggests slightly slower cooling in SA and TA (a cooling multiplier of 0.92–0.94) than found in our study (0.9). To compensate for the increased search time due to slower cooling, the number of iterations at the initial temperature or threshold was lower in the study of Pukkala and Heinonen (2006). They found that the number of candidate moves that are generated at each iteration of tabu search was mostly 1–5 % of the number of stands, whereas the corresponding proportion in our study was mostly 0.5–1.2 % of stands. The length of the tabu tenure was of the same magnitude in both studies.

Our study suggests that SA and TA are the best heuristics for typical combinatorial forest planning problems if the search time cannot be very long. Also in Pukkala and Heinonen (2006) TS was slightly inferior to SA and TA. Similarly to Zeng et al. (2007), our study suggests that SA works better in forest planning problems than the GA and AC heuristics. Bettinger et al. (2002) found that all cooling methods (SA, TA and GD) worked better than TS and GA, which is in line with our study. However, when tabu search was used with 2-opt moves, it was equally good as the cooling methods. A 2-opt move means that the move consists of a simultaneous change in the treatment schedule of two stands. Pukkala and Kurttila (2005) found that SA was better than TS and GA in simple forest planning problems, but GA was the best method in the most complicated problem that included two hierarchical levels and both spatial and non-spatial objective variables. However, similarly to our study, GA needed a longer time to find good solutions. Liu et al. (2006) found SA to be a better heuristic than the GA and hill climbing (HC) algorithms for solving a spatially constrained forest planning problem. SA and HC were approximately 10 times faster than GA.

As a conclusion, our study suggests that the cooling methods, especially SA and TA, are the most recommendable heuristics for solving combinatorial forest planning problems when short search time is important. When the solutions must be found quickly, for instance in an iterative analysis of the trade-offs between different objectives, the population-based heuristics GA and AC may not be good choices. However, if search time is not an issue, none of the heuristics should be ruled out. The results obtained for different heuristics depend on the way the methods are implemented as an algorithm and a computer program. There is much flexibility in the implementation of the heuristics, especially TS, GA and AC. Therefore, the results obtained for them in this study would improve if more efficient implementations are developed.