Estimations of Three Characteristic Stress Ratios for Rockfill Material Considering Particle Breakage

Abstract

The particle breakage during specimen shearing has a significant influence on the critical-state line (CSL) of the rockfill material. A series of large-scale triaxial compression tests on the rockfill material from Henan Province (HPR) were conducted in a wide range of initial void ratios and confining pressures. The influences of the particle breakage on the critical-state stress ratio $M_{\mathrm{c}}$, the peak stress ratio $M_{\mathrm{p}}$ and dilatancy stress ratio $M_{\mathrm{d}}$ were investigated. The deviatoric stress and particle breakage of the HPR at the critical state increase with the increase in confining pressure, while the influences of the initial void ratio on these behaviors are too little to be considered. The gradient of the CSL in the $q\hbox {-}p$ space of the rockfill, $M_{\mathrm{c}}$, was found to be passively correlated with the particle breakage index $B_{\mathrm{r}}$, rather than being a constant. Additionally, the observed values of $M_{\mathrm{c}}$ at low confining pressures (low particle breakage occur) will be substantially undervalued if $M_{\mathrm{c}}$ is estimated as a constant. In the critical-state-theory-based constitutive models, $M_{\mathrm{p}}$ and $M_{\mathrm{d}}$ are estimated as the combinations of $M_{\mathrm{c}}$ and state parameter $\psi$. It is believed that the simulations of $M_{\mathrm{p}}$ and $M_{\mathrm{d}}$ when $M_{\mathrm{c}}$ is correlated with $B_{\mathrm{r}}$ are obviously more favorable than those when $M_{\mathrm{c}}$ is constant.

1 Introduction

Rockfill materials are widely used in the construction of dams, offshore structures, and railroad embankments [1,2,3,4]. To model the strength and deformation behaviors of rockfills, numerous constitutive models have been proposed [5,6,7,8]. Among them, the peak stress ratio $M_{\mathrm{p}}$ and dilatancy stress ratio $M_{\mathrm{d}}$ are two key material parameters for expressing the strength behavior and dilatancy behavior of soils, respectively. Many existing empirical equations can only reflect the influence of stress levels on the peak and dilatancy stress ratios [5, 9,10,11,12], which are not sufficient to account for the influence of initial void ratios. To improve this limitation, the critical-state theory (CST) was introduced [8, 13, 14], which has played an increasingly important role in the study of constitutive models for the rockfill material with various initial void ratios and under different stress levels. In the CST-based constitutive models, $M_{\mathrm{p}}$ and $M_{\mathrm{d}}$ are estimated as the combination of the critical-state stress ratio $M_{\mathrm{c}}$ and state parameter $\psi$ [14,15,16,17]. Accordingly, the critical-state stress ratio $M_{\mathrm{c}}$ is also an important characteristic stress ratio for soils without doubt.

The critical-state lines (CSLs) in both the $q\hbox {-}p$ space and the $e\hbox {-}p$ space are thought to be the basis and core of the CST-based constitutive models. The CSL in the $e\hbox {-}p$ space, originally described as a linear curve in the $e\hbox {-ln}p$ space [18], is the reference state to define the state parameter $\psi$. However, it was found that the stress–strain–volume behaviors of rockfill material may be significantly affected by the particle breakage [19,20,21], which leads to the change of the CSL in the $e\hbox {-}p$ space. Therefore, new expressions of the CSL in the $e\hbox {-}p$ space were proposed to consider the influence of particle breakage, for instance the linear curve in the $e\hbox {-}(p/p_{\mathrm{a}})^{\xi }$ space [13, 16], the three-segment type curve in the $e\hbox {-ln}p$ space [22] and the breakage CSL in the $e\hbox {-}(p/p_{\mathrm{a}})^{\xi }$ space [23]. Additionally, many state parameters for the interlocking effect were defined and proposed, such as $\psi =e\hbox {-}e_{\mathrm{c}}$ [24], $\psi = e/e_{\mathrm{c}}$ [14], $\psi = p/p_{\mathrm{c}}$ [25] and $\psi ={ ep}/e_{\mathrm{c}}p_{\mathrm{c}}$ [8].

It is noted that the gradient of the CSL in the $q\hbox {-}p$ space is denoted as the critical-state stress ratio $M_{\mathrm{c}}$. Many investigations involving the CST have focused on the expression of the CSL in the $e\hbox {-}p$ space and the definition of $\psi$, while the importance of the CSL in the $q\hbox {-}p$ space was ignored. It is widely accepted that the gradient of CSL in the $q\hbox {-}p$ space for sand is a constant [16, 17, 19, 22, 26], indicating that the critical-state stress ratio $M_{\mathrm{c}}=q_{\mathrm{c}}/p_{\mathrm{c}}$ is a constant. Therefore, $M_{\mathrm{c}}$ was also regarded as a constant for the rockfill. However, the large-scale triaxial experimental results of rockfills [7, 8] indicate that the gradient of CSL in the $q\hbox {-}p$ space is nonlinear and dependent on the confining pressure because of particle breakage. The critical stress ratio $M_{\mathrm{c}}$, therefore, cannot be considered as a constant in the rockfill analysis. As a result, the estimations of $M_{\mathrm{p}}$ and $M_{\mathrm{d}}$ based on $M_{\mathrm{c}}$ also need to be reevaluated.

To investigate the influence of particle breakage on the estimations of the above-mentioned three characteristic stress ratios (i.e., $M_{\mathrm{c}}$, $M_{\mathrm{p}}$ and $M_{\mathrm{d}}$) for the rockfill material, a series of large-scale triaxial compression tests were carried out in this study. Then the critical-state stress behavior and particle breakage behavior of the rockfill material were discussed, with a nonlinear function proposed to describe the relationship between the critical-state stress ratio $M_{\mathrm{c}}$ and particle breakage index. Lastly, four different combinations of the critical-state stress ratio $M_{\mathrm{c}}$ and state parameter $\psi$ were designed and compared to simulate the peak and dilatancy stress ratios.

2 Triaxial Compression Tests

2.1 Rockfill Material

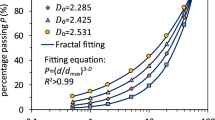
For the present study, the rockfill material was obtained from a dam located in Henan Province of central China (the rockfill material hereafter is called the HPR). The initial particle size distribution (PSD) of the HPR is shown in Fig. 1. The maximum particle size used in the tests is 60 m, the uniformity coefficient ($C_{\mathrm{u}}$) of the HPR is 12.7, and the curvature coefficient ($C_{\mathrm{c}}$) is 1.78.

Fig. 1

Initial particle size distribution of the HPR

In order to quantify the evolution of particle breakage and PSD after tests, the initial fractal dimension $D_{0}$ was analyzed using Eq. (1) and supposed to be 2.297, as shown in Fig 1. The fractal PSD of granular soils [27, 28] is described as:

$$\begin{aligned} F(d)=\left( {\frac{d}{d_{\max }}} \right) ^{3-D} \end{aligned}$$

(1)

where F is the percentage finer, d is the particle size, $d_{\mathrm{max}}$ is the maximum particle size and D is the fractal dimension.

2.2 Test Program

Figure 2a shows the large-scale triaxial apparatus.

Fig. 2

Large-scale triaxial compression test: a triaxial apparatus; b specimen

The specimen size is 700 mm in height and 300 mm in diameter. The HPR for one specimen, as shown in Fig. 2b, was divided into 5 equal parts, and each part was compacted with a vibrator at the frequency of 60 cycles/s. The procedure was evolved after several trials to acquire the designed initial void ratio (dry density). The specimen was first saturated using the vacuum saturation method with the B-value in excess of 0.95 and then subjected to the required consolidation pressure. The specimen was subjected to shear tests under the drained condition with a constant axial displacement of 1 mm/min until the axial strain was accumulated up to 20%, reaching the critical state.

Four different initial void ratios ($e_{0}=0.352, 0.320, 0.301$ and 0.272) were used in the triaxial compression tests. For each given confining pressure, four typical confining pressures ($\sigma _{3}=300, 600, 900$ and 1200 kPa) were tested to study the effects of stress level and void ratio on the mechanical behavior and particle breakage evolution of rockfill at the critical state. Details of the test program and test results are listed in Table 1.

Table 1 Test results of large-size triaxial compression of the HPR

3 Test Results

3.1 Critical-State Stress Behaviors

The critical state is defined as the state at which the volumetric strain and shear stress are both constant with the increase in shear strain. It is noted that, by the end of the test, some rockfills still have not reached the critical state (i.e., the axial strain $\varepsilon _{\mathrm{a}}=15\%$), especially at a low confining pressure or low initial void ratio. An effective way to obtain the critical-state data is to extrapolate the stress–strain data to zero volume change [20, 29, 30]. This way may not be applicable for this study, because the stress–strain–volume data can be extrapolated to the critical state according to their tendency, but the critical-state data for particle breakage are difficult to obtain in the same way. Therefore, the axial strain $\varepsilon _{\mathrm{a}}$ of all specimens were accumulated up to 20% to reach the real critical state. Figure 3 shows the stress–strain–volume behaviors of HPR at different initial confining pressures and initial void ratios. The test data on the volumetric strain and deviatoric stress of all 16 specimens have reached constant values at the end of the tests, indicating that all specimens have reached the critical state, as shown in Fig. 3.

Fig. 3

Stress–strain–volume behaviors of the HPR: a$\sigma _{3}=300~\hbox {kPa}$; b$\sigma _{3}=600~\hbox {kPa}$; c$\sigma _{3}=900~\hbox {kPa}$; d$\sigma _{3}=1200~\hbox {kPa}$

The main purpose is to investigate the critical-state stress behaviors of rockfill in this section. Therefore, the stress–strain–volume behaviors during shearing were not discussed. As can be seen from Fig. 3, even though the deviatoric stresses q of specimens at a given initial confining pressure $\sigma _{3}$ increase with the decrease in initial void ratio $e_{0}$ during shearing (e.g., $\sigma _{3}=1200~\hbox {kPa}$, as shown in Fig. 3d), they tend to reach the same critical state deviatoric stress $q_{\mathrm{c}}$. By contrast, the critical state deviatoric stress at a given initial void ratio increases with an increase in the confining pressure (e.g., for a given $e_{0}=0.272$, as shown in Fig. 3a–d). Consequently, the critical-state stress is only positively correlated with the confining pressure, while the initial void ratio has less influence on the critical-state stress.

3.2 Particle Breakage Behaviors

Many particle breakage indices have been proposed to comprehensively quantify the degree of particle breakage after loading, while the details of the individual fraction before and after tests were neglected. The change in percentage of the fractions (CPFs) is sometimes more essential and clearer to reflect the evolution of particle breakage. From this point of view, the CPFs for all 16 specimens were calculated and rearranged in terms of CPFs and particle size, as shown in Fig. 4.

Fig. 4

Changes in percentage of the fractions after test: a$\sigma _{3}=300~\hbox {kPa}$; b$\sigma _{3}=600~\hbox {kPa}$; c$\sigma _{3}=900~\hbox {kPa}$; d$\sigma _{3}=1200~\hbox {kPa}$

Three outstanding characteristics about the CPFs can be obtained from Fig. 4: (1) For any of the HPR specimens, the number of the larger particles in 60–40 mm and 40–20 mm decreases and that of the smaller particles in 20–10 mm, 10–5 mm and 5–0 mm increases after the test; (2) an increase in the confining pressure could result in an increase in the CPFs of specimens at a given initial void ratio (e.g., $e_{0}=0.272$, as shown in Fig. 4a–d); (3) nearly, no changes on the CPFs can be observed with an increase in the initial void ratio under a certain confining pressure (e.g., $\sigma _{3}=1200~\hbox {kPa}$, as shown in Fig. 4d). As a result, the confining pressure significantly influences the particle breakage behaviors of HPR, while the initial void ratio shows much less influence.

Furthermore, the HPR specimens at $e_{0}=0.272$ and $\sigma _{3}=1200~\hbox {kPa}$ were taken as the examples to investigate the behaviors of PSD after test. The PSDs after test and the fitting curves (by Eq. (1)) are plotted in terms of $\hbox {log}P$ and $\hbox {log}(d/d_{\mathrm{max}})$; thus, the gradient of the fitting line is 3D, as shown in Fig. 5. It can be seen from Fig. 5 that the linear fitting curve agrees well with the test data, indicating that the rockfill tends to be fractal at the critical state.

Fig. 5

Fractal dimensions for HPR specimens: a specimens under different confining pressures ($e_{0}=0.272$); b specimens at different initial void ratios ($\sigma _{3}=1200~\hbox {kPa}$)

Figure 5a, b also shows the evolutions of fractal gradation of HPR at the critical state with different confining pressures and initial void ratios, respectively. On the one hand, the PSD of the specimen uplifts with the confining pressure, indicating that a greater degree of particles breakage occurs with the larger confining pressure, as shown in Fig. 5a. On the other hand, the observed data of specimens at $\sigma _{3}=1200~\hbox {kPa}$ with various initial void ratios are basically coincident and can be described by the same fractal line with the fractal dimension of $D=2.421$, as shown in Fig. 5b. This again demonstrates that a greater degree of particle breakage or a larger fractal dimension occurs with the increase in confining pressure, while particle breakages of nearly the same degree occur with various initial void ratios.

The fractal dimensions of all the 16 specimens are plotted in the $D\sim \hbox {log}(\sigma _{3}/p_{\mathrm{a}})$ space, as shown in Fig. 6. It is noted that specimens of various initial void ratios at the same confining pressure tend toward the same fractal dimension, and the fractal dimension D in relation to $\hbox {log}(\sigma _{3}/p_{\mathrm{a}})$ can be expressed in a linear curve as:

$$\begin{aligned} D=D_0 +k_{\mathrm{D}} \log \left( {\frac{\sigma _3 }{p_{\mathrm{a}} }} \right) \end{aligned}$$

(2)

where $D_{0}$ is the initial fractal dimension and $k_{\mathrm{D}}$ is a material parameter.

Fig. 6

Relationship between fractal dimension and confining pressure

Figure 6 shows that the simulation by Eq. (2) is in good agreement with the test results, and parameter $k_{\mathrm{D}}$ is 0.101 for the HPR.

In summary, the stress and particle breakage (fractal dimension) behaviors of rockfill materials at the critical state are found to be positively correlated with the confining pressure, while the influence of the initial void ratio on these behaviors is too little to be considered.

4 Critical-State Stress Ratio

The gradient of the CSL in the $q\hbox {-}p$ space is denoted as $M_{\mathrm{c}}$, which is regarded as a constant when the CSL in the $q\hbox {-}p$ space is linear. The value of $M_{\mathrm{c}}$ for sand is constant [16, 19, 22, 26]. The CSL of HPR in the $q\hbox {-}p$ space (as shown in Fig. 7) can also be expressed by a linear function as $q_{\mathrm{c}}=M_{\mathrm{c}} p_{\mathrm{c}}$, with a constant $M_{\mathrm{c}}=1.722$, and the fitting correlation coefficient $R^{2}$ is as high as 0.997.

Fig. 7

Critical-state line of the HPR in the $q\hbox {-}p$ space

It seems that $M_{\mathrm{c}}$ is totally a constant. However, it will not be so convincing after the next example is discussed. The peak deviatoric stress points of the 16 specimens are plotted in the $q\hbox {--}p$ space, and fitted by the linear function as $q_{\mathrm{p}}=M_{\mathrm{p}} p_{\mathrm{p}}$, with a constant $M_{\mathrm{p}}=1.817$, as shown in Fig. 8a. It is interestingly noted that the fitting correlation coefficient $R^{2}$ is as high as 0.989. In this case, the peak stress ratio $M_{\mathrm{p}}$ also seems to be a constant.

Fig. 8

Behaviors of the peak stress ratio $M_{\mathrm{p}}$: a in the $q\hbox {-}p$ space; b relationships between $M_{\mathrm{p}}$ and void ratio, confining pressure

In fact, a number of triaxial tests [5,6,7, 11] have illustrated that the peak stress ratio $M_{\mathrm{p}}$ (or friction angle $\phi _{\mathrm{p}}$) of a rockfill material is significantly influenced by the confining pressure and initial void ratio. For example, a well-known function of the friction angle $\phi _{\mathrm{p}}$ and confining pressure $\sigma _{3}$ is expressed as [5]:

$$\begin{aligned} \phi _{\mathrm{p}} =\phi _{\mathrm{p}0} -\Delta \phi _{\mathrm{p}} \lg \left( {\frac{\sigma _3}{p_{\mathrm{a}} }} \right) \end{aligned}$$

(3)

where $\phi _{\mathrm{p0}}$ and $\Delta \phi _{\mathrm{p}}$ are material parameters. The relationships between stress ratio M and friction angle $\phi$ are given as:

$$\begin{aligned} \begin{array}{l} M=\frac{6\sin \phi }{3-\sin \phi } \\ \phi =\arcsin \left( {\frac{6M}{3-M}} \right) \\ \end{array} \end{aligned}$$

(4)

where M can be $M_{\mathrm{c}}$, $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$ in this paper and $\phi$ is the corresponding friction angle.

Figure 8b shows the observed $M_{\mathrm{p}}$ of HPR in terms of $M_{\mathrm{p}}$ and $\hbox {log}(\sigma _{3}/p_{\mathrm{a}})$. It is clear that an increase in the confining pressure or initial void ratio could result in a significant decrease in $M_{\mathrm{p}}$. The maximum $M_{\mathrm{p}}$ is 2.048 ($e_{0}=0.272$, $\sigma _{3}=300~\hbox {kPa}$) and the minimum $M_{\mathrm{p}}$ is 1.733 ($e_{0}=0.352$, $\sigma _{3}=1200~\hbox {kPa}$), both of which are very different from the constant value of $M_{\mathrm{p}}=1.817$, as shown in Fig. 8b.

Consequently, the high $R^{2}$-value of the fitting linear curve of peak deviatoric stress points in the $q\hbox {-}p$ space is not sufficient to prove that the peak stress ratio $M_{\mathrm{p}}$ is a constant for the HPR. Similarly, it will not be convincing to regard $M_{\mathrm{c}}$ as a constant, even though the $R^{2}$-value (0.997) of $M_{\mathrm{c}}$ is higher than that of $M_{\mathrm{p}}$ (0.989).

As discussed above, the HPR specimens under different confining pressures result in different particle breakages and critical-state stresses. Therefore, the critical-state stress ratio $M_{\mathrm{c}}$ should be related to the particle breakage and confining pressure. Actually, it has been pointed out that the value of $M_{\mathrm{c}}$ of rockfill material decreases slightly with an increase in the confining pressure [31]. In addition, this study attempts to correlate $M_{\mathrm{c}}$ with the extent of particle breakage. First of all, a particle breakage index is needed to quantify the extent of particle breakage. Among the widely accepted particle breakage indices, the $B_{\mathrm{r}}$ proposed by Einav [28] is an increasingly acceptable one. The definition of $B_{\mathrm{r}}=B_{\mathrm{t}}/B_{\mathrm{p}}$ is shown in Fig. 9a, where $B_{\mathrm{p}}$ is the breakage potential and $B_{\mathrm{t}}$ is the total breakage potential. $B_{\mathrm{r}}$ can be expressed as the function of the fractal dimensions [20, 28]:

$$\begin{aligned} B_{\mathrm{r}} =\frac{(D_{\mathrm{c}} -D_0 )(3-D_{\mathrm{u}} )}{(D_{\mathrm{u}} -D_0 )(3-D_{\mathrm{c}} )} \end{aligned}$$

(5)

where $D_{0}$, $D_{\mathrm{c}}$ and $D_{\mathrm{u}}$ are the fractal dimensions of the initial PSD, current PSD and ultimate PSD, respectively.

Fig. 9

Behaviors of critical-state stress ratio $M_{\mathrm{c}}$: a definition of relative breakage index $B_{\mathrm{r}}$; b relationship between $M_{\mathrm{c}}$ and $B\hbox {r}$

The ultimate PSD changes very little with much higher pressure, and $D_{\mathrm{u}}$ can be seen as a constant for a given rockfill material [20, 27, 28]. Therefore, the range of $B_{\mathrm{r}}$ is $0\sim 100\%$. $D_{\mathrm{u}}$ is regarded as 2.7 for the HPR according to another triaxial compression test under $\sigma _{3}=2.5~\hbox {MPa}$. $D_{0}$ is 2.297, and $D_{\mathrm{c}}$ of all specimens is listed in Table 1. Accordingly, $B_{\mathrm{r}}$ of all specimens is computed and listed in Table 1. A nonlinear relationship is proposed to describe the influence of particle breakage on $M_{\mathrm{c}}$:

$$\begin{aligned} M_{\mathrm{c}} =M_{\mathrm{c0}} +\chi \exp \left( {-\mu B_{\mathrm{r}} } \right) \end{aligned}$$

(6)

where $M_{\mathrm{c0}}$, $\chi$ and $\mu$ are material constants.

The observed $M_{\mathrm{c}} \sim B_{\mathrm{r}}$ and the simulation of Eq. (6) are shown in Fig. 9b, with the material constants of $M_{\mathrm{c0}}=1.710$, $\chi =0.161$ and $\mu =21.1$. As can be seen from Fig. 9b, $M_{\mathrm{c}}$ is passively correlated with the particle breakage index $B_{\mathrm{r}}$. When $B_{\mathrm{r}}=0$, $M_{\mathrm{c}}=M_{\mathrm{c0}}+\chi$; when $B_{\mathrm{r}}=100\%$, $M_{\mathrm{c}}=M_{\mathrm{c0}}$ (as exp($\hbox {-}\mu \hbox {B}_{\mathrm{r}}$) is too small to be considered when $B_{\mathrm{r}}=100\%$ and $\mu$ is a larger number). Since $B_{\mathrm{r}}$ is positively correlated with the confining pressure and tends to be 100% according to Eqs. (2), (3), $M_{\mathrm{c}}$ decreases to a constant $M_{\mathrm{c0}}$ with an increase in the particle breakage index $B_{\mathrm{r}}$. It is noted that the observed value of $M_{\mathrm{c}}$ is significantly larger than the constant $M_{\mathrm{c}}=1.722$ when $B_{\mathrm{r}}$ is small, while they are close when $B_{\mathrm{r}}$ is sufficiently large, as shown in Fig. 9b.

In summary, the critical-state stress ratio $M_{\mathrm{c}}$ is not a constant, and it is passively correlated with the particle breakage index $B_{\mathrm{r}}$ as well as the confining pressure. The observed value of $M_{\mathrm{c}}$ at a low confining pressure (where low particle breakage occurs) will be substantially undervalued if $M_{\mathrm{c}}$ is estimated as a constant in the $q\hbox {-}p$ space.

5 Peak and Dilatancy Stress Ratios

5.1 Roles of the Peak and Dilatancy Stress Ratios

Peak stress ratio $M_{\mathrm{p}}$ and dilatancy stress ratio $M_{\mathrm{d}}$ are two important material constants in the constitutive model. For example, the author [11] proposed a generalized plastic model and modeled the triaxial compression test data of a rockfill, and the stress–strain–volume behaviors of $\sigma _{3}=300~\hbox {kPa}$ and $\sigma _{3}=1200~\hbox {kPa}$ were taken as the examples, as the scatters shown in Fig. 10. Then by increasing or decreasing the peak and dilatancy stress ratios by a certain percentage (e.g., 10%) with other material constants unchanged, as shown in Fig. 10, it is found that the dilatancy stress ratio $M_{\mathrm{d}}$ has a significant influence on the volumetric strain, as shown in Fig. 10b, and the peak stress ratio $M_{\mathrm{p}}$ has a significant influence on both deviatoric stress and volumetric strain, as shown in Fig. 10a.

Fig. 10

Influences of $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$ on the prediction of stress–strain–volume behaviors of the rockfill: a the dilatancy stress ratio $M_{\mathrm{d}}$; b the peak stress ratio $M_{\mathrm{p}}$

5.2 Estimation Equations

Many empirical equations [5, 9,10,11] have been proposed to describe the peak and dilatancy stress ratios, and most of them express the influence of stress level alone, such as the well-known Eq. (3). In the CST, the state parameter $\psi$ and critical-state stress ratio $M_{\mathrm{c}}$ are used for estimating the peak and dilatancy stress ratios, which can reflect the combined influence of void ratio and stress level. Two typical definitions of the state parameter $\psi$ have been proposed to describe the behavior of granular material. The first one was proposed by Been and Jefferies [24], which is expressed as:

$$\begin{aligned} \psi =e-e_{\mathrm{c}} \end{aligned}$$

(7)

where e is the current void ratio and $e_{\mathrm{c}}$ is the void ratio on the critical-state line at the current effective stress p.

This state parameter $\psi$ was used to estimate the dilatancy stress ratio $M_{\mathrm{d}}$ and the peak stress ratio $M_{\mathrm{p}}$ directly as:

$$\begin{aligned} \begin{array}{l} M_{\mathrm{d}} =M\exp (n_{\mathrm{d}} \psi ) \\ M_{\mathrm{p}} =M\exp (-n_{\mathrm{p}} \psi ) \\ \end{array} \end{aligned}$$

(8)

where $n_{\mathrm{d}}$ and $n_{\mathrm{p}}$ are material constants.

The other one was originally proposed by Biarez and Hicher [15], which was defined as the ratio of the current void ratio e to the critical-state void ratio $e_{\mathrm{c}}$:

$$\begin{aligned} \psi =\frac{e}{e_{\mathrm{c}}} \end{aligned}$$

(9)

Similar to Eq. (8) but in an indirect way, this state parameter was used for estimating the dilatancy friction angle $\phi _{\mathrm{d}}$ and the peak friction angle $\phi _{\mathrm{p}}$ as follows:

$$\begin{aligned} \begin{array}{l} \phi _{\mathrm{d}} =\arctan (\psi ^{n_{\mathrm{d}} }\tan \phi _{\mathrm{c}} ) \\ \phi _{\mathrm{p}} =\arctan (\psi ^{-n_{\mathrm{p}} }\tan \phi _{\mathrm{c}} ) \\ \end{array} \end{aligned}$$

(10)

where $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$ can be calculated by $\phi _{\mathrm{d}}$ and $\phi _{\mathrm{p}}$ according to Eq. (4).

The current void ratio e can be computed as:

$$\begin{aligned} e=e_0 -(1+e_0 )\varepsilon _v \end{aligned}$$

(11)

where the critical-state void ratio $e_{\mathrm{c}}$ can be computed by the CSL in the $e \sim \hbox {ln}p$ or $e\sim (p/p_{\mathrm{a}})^{\xi }$ space.

Since the CSL in the $e\sim (p/p_{\mathrm{a}})^{\xi }$ space was thought to be more applicable for rockfill [13, 20], it is used in the current study, which is expressed as:

$$\begin{aligned} e_{\mathrm{c}} =e_\Gamma -\lambda \left( {\frac{p}{p_{\mathrm{a}} }} \right) ^{\xi } \end{aligned}$$

(12)

where $e_{\Gamma }$, $\lambda$ and $\xi$ are material constants. The CSL of HPR in the $e\sim (p/p_{\mathrm{a}})^{\xi }$ space is explicitly illustrated in Fig. 11, followed by the constants of $e_{\Gamma }=0.367$ and $\lambda =0.0066$, while $\xi$ is set to be 0.75.

Fig. 11

Critical-state line of the HPR in the $e\hbox {-}(p/p_{\mathrm{a}})^{\xi }$ space

5.3 Comparison

Four schemes for estimating $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$ are designed in this section according to the combinations of the above-mentioned two expressions of $M_{\mathrm{c}}$ and two expressions of $\psi$, as listed in Table 2.

Table 2 Schemes and constants of the simulations for $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$

The comparisons between the observed and the simulated values for $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$ are given in Figs. 12 and 13, respectively.

Fig. 12

Estimations of the dilatancy stress ratio $M_{\mathrm{d}}$: a Scheme 1; b Scheme 2; c Scheme 3; d Scheme 4

Since the behavior of $M_{\mathrm{p}}$ has been discussed above, more attention should be paid on the behavior of $M_{\mathrm{d}}$ in this section. The distribution of the observed $M_{\mathrm{d}}$ along the horizontal axis indicates that the increase in confining pressure results in a decrease in $M_{\mathrm{d}}$, and the simulations of Scheme 1 (Fig. 12a) and Scheme 3 (Fig. 12c) along the vertical axis can well reflect this characteristic. As a result, when $M_{\mathrm{c}}$ is related to particle breakage, it is favorable to express the dilatancy stress ratio $M_{\mathrm{d}}$, regardless of what the definition of $\psi$ is. By contrast, comparing Scheme 1 (Fig. 12a) with Scheme 2 (Fig. 12b), and Scheme 3 (Fig. 12c) with Scheme 4 (Fig. 12d), it can be found that the differences between the simulated and observed $M_{\mathrm{c}}$ of Scheme 2 and Scheme 4 are significantly larger than those of Scheme 1 and Scheme 3. Additionally, the simulations of Scheme 2 (Fig. 12b) and Scheme 4 (Fig. 12d) are distributed in a more concentrated range along the vertical axis, which is unreasonable. The reason might be that both $M_{\mathrm{c}}$ and $M_{\mathrm{d}}$ were thought to be influenced by particle breakage and are not constants as discussed above. Therefore, the observed particle breakage-related $M_{\mathrm{d}}$ is applicable to be described by the particle breakage-related $M_{\mathrm{c}}$, as shown in Fig. 12a, c, while the observed particle breakage-related $M_{\mathrm{d}}$ is less applicable to be described by the constant $M_{\mathrm{c}}$, as shown in Fig. 12b, d. Similarly, it is found that the behaviors of simulations of $M_{\mathrm{p}}$ are basically the same to those of $M_{\mathrm{d}}$, as shown in Fig. 13.

Fig. 13

Estimations of the dilatancy stress ratio $M_{\mathrm{p}}$: a Scheme 1; b Scheme 2; c Scheme 3; d Scheme 4

In summary, the value of $M_{\mathrm{c}}$ has a notable influence on the estimations of $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$, while the definition of the state parameter has less influence. The simulations of $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$ with $M_{\mathrm{c}}$ related to particle breakage are obviously more reasonable than those with constant $M_{\mathrm{c}}$.

6 Conclusions

A series of large-scale triaxial compression tests on the HPR were conducted. The influences of particle breakage on the critical-state stress ratio $M_{\mathrm{c}}$, peak stress ratio $M_{\mathrm{p}}$ and dilatancy stress ratio $M_{\mathrm{d}}$ were investigated. The main conclusions are as follows:

• 1. The deviatoric stress and particle breakage of the rockfill material at critical state were found to be positively correlated with the confining pressure, while the influence of the initial void ratio on these behaviors is too little to be considered.

• 2. The gradient of the CSL in the $q\hbox {--}p$ space of the HPR, $M_{\mathrm{c}}$, is not a constant, and it is passively correlated with the particle breakage index. The observed value of $M_{\mathrm{c}}$ at low confining pressures (where low particle breakage occurs) will be substantially undervalued if $M_{\mathrm{c}}$ is estimated as a constant in the $q\hbox {-}p$ space.

• 3. The value of $M_{\mathrm{c}}$ has a notable influence on the estimations of dilatancy stress ratio $M_{\mathrm{d}}$ and peak stress ratio $M_{\mathrm{p}}$ in the CST, while the definition of the state parameter has less influence. The simulations of $M_{\mathrm{d}}$ and $M_{\mathrm{p}}$ with $M_{\mathrm{c}}$ related to particle breakage are obviously more favorable than those with constant $M_{\mathrm{c}}$, regardless of what the definition of the state parameter is.