Unified model of critical state line for rockfill material with and without considering particle breakage

Abstract

The critical state line (CSL) is important for characterizing soils’ properties. However, particle breakage is inevitable for granular soils such as rockfill. Therefore, the impact of particle breakage on CSL has always been one of the main focuses. Unfortunately, it has not yet been adequately resolved how particle breakage influences CSL quantitatively. Large-scale drained triaxial shearing tests of rockfill materials under various initial gradations, initial void ratios and confining pressure have been conducted in this paper. It shows that particle breakage could result in decrements in both of the stress ratio and void ratio at the critical state. The equation for a critical state line with none breakage (NBCSL) was theoretically derived and demonstrated. The intercept and gradient of CSL and NBCSL are inextricably related because of particle breakage, which has been quantified as follows: the intercept of CSL is identical to NBCSL’s, and the gradient of CSL is a breakage-related constant plus that of NBCSL. In other words, the CSL and NBCSL of rockfill materials has actually been described by a unified equation. Based on this, the translation and rotation of CSL induced by changing gradation and void ratio can be explained from the essence of particle breakage.

1 Introduction

Rockfill material is a typical granular soil, which has been extensively used in the constructions of rockfill dams, railroad infrastructure, and other structures [1, 12, 16, 22, 26]. When the soil is deformed by shearing, it eventually reaches a critical point where shearing occurs at constant volume and stress. A critical state line or locus (CSL) is defined by the combinations of stress and volume at the critical state [6, 8, 18, 21, 23, 27]. The state-related constitutive models were mainly developed using a state parameter-a measurement of the distance between current state and the CSL. Among them, the most popular choice is the state parameter ψ introduced by Been and Jefferies [4]. The CSL is the cornerstone of the state-related constitutive model from this perspective, and its importance is clear [13, 22].

A significant characteristic of granular soil is particle breakage [9, 11, 15, 21, 25, 30]. Currently, the CSL of sands has been fully studied incorporating of particle breakage [3, 5, 7, 10, 18, 20]. Comparing to sand, the CSL properties of rockfill have shown many similarities. There are two commonly acknowledged facts regarding the translation and rotation rules of rockfill materials’ CSL: (1) the CSL is a straight line in e − (p/p_a)^ξ plane, which has been widely documented [13, 22, 26]. When the initial gradation is fixed, the CSLs are parallel under different initial void ratios [26], meaning that the intercept of CSL is related to the initial void ratio (CSL translation) but the gradient is not; (2) CSLs with different initial gradations are not parallel, uniformly graded soils tend to have steeper CSLs than well-graded soils (CSL rotation), which has been quantitively described by Li [17] and Chang and Deng [6].

Coop [9] stated that when a constant volume is achieved in triaxial tests on crushable granular soil, the apparent critical state may be “a result of counteracting dilative strains from particle rearrangement and compressive strains from particle breakage”. Therefore, the translation and rotation of rockfill materials’ CSL can be essentially explained by particle breakage. To formulate the link between particle breakage and CSL changes, Hanley [14] and Ciantia [7] enabled systematic exploration and clarification using discrete model, providing an answer to the crucial CSL-related topic of how particle breakage affects the location of CSL. The results obtained support the hypothesis of a multiplicity of CSLs in the compression plane for crushable granular materials. In particular, Ciantia [7] proposed an important reference line, which is known as the critical state line with fixed gradation (none breakage occurring, hereafter called as NBCSL). The proposal of NBCSL clarifies how particle breakage affects CSL of crushable granular materials.

In summary, the NBCSL is an important reference line for comprehending the translation and rotation of CSL. However, the CSL and NBCSL were determined by fitting the observed critical state points (CSPs) in finite element test [7, 14]. Since the particle breakage is unavoidable in laboratory tests, it is impossible to observe critical state points without particle breakage. As a result, the NBCSL is actually unknown. This prompts two inquiries: (1) How to obtain the NBCSL in the laboratory test; (2) The NBCSL and CSL were expressed by two separated groups of parameters. These two groups of parameters are independent test phenomena, or there is an inevitable connection caused by particle breakage?

The purpose of this contribution is to fill some of these gaps. Previous studies have directly studied the CSL by fitting the distribution of all tested CSPs. This study takes the opposing tack and concentrates on a single CSP. Therefore, the CSL and NBCSL are theoretically derived by tracking the single CSP, rather than fitting on all CSPs. Finally, it was determined and verified that CSL and NBCSL have a quantifiable relationship induced by particle breakage.

The paper is organized as follows. First, the 64 large-scale triaxial tests under various gradations and void ratios were conducted and analyzed, and the relationship between particle breakage index and void ratio reduction was quantitatively expressed. Then, the tracking law of the single CSP under various breakage indices was investigated. The NBCSL and CSL equations were derived on the basis of this. Additionally, a unified equation of rockfill’s CSL and NBCSL under various initial gradations and initial void ratios was proposed and discussed.

2 Test program

2.1 Rockfill material

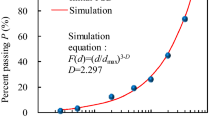
The earth-rockfill dam in Hekou village in central China provided the rockfill material for the current investigation (hereafter called as HKR). Figure 1 shows 4 different initial particle size distribution (PSD) of the HKR designed in the test, and the maximum particle sizes are all 60 mm. The main mineralogy of HKR is dolomitic limestone, and the specific gravity G_s is 2.77. Based on the fractal theory [11, 19], the PSD, i.e., a cumulative distribution by mass can be expressed as follows:

$$ P = \left( {\frac{d}{{d_{\max } }}} \right)^{3 - D} $$

(1)

where P is the percentage finer, d is the particle size, d_max is the maximum particle size, and D is the fractal dimension.

Fig. 1

Designed 4 initial particle size distributions (PSD) of the HKR

The designed 4 PSDs are also analyzed by Eq. (1), and the fractal dimensions are supposed to be D₀ = 2.082, 2.285, 2.425 and 2.531, respectively, as shown in Table 1. More basic details of HKR with the 4 PSDs are shown in Table 1. The designed 4 PSDs were classified as well-graded (GW) according to ASTM [2] because PCF4 [i.e., percentage of coarse fraction] > 50%, FC [i.e., fines content] < 5%, C_u [i.e., coefficient of uniformity] > 4 and 1 < C_c [i.e., coefficient of curvature] < 3.

Table 1 Basic details of HKR with the 4 PSDs

2.2 Triaxial compression test scheme

In Fig. 2a, the various HKR particle fractions are displayed, and Fig. 2b shows the large-scale triaxial apparatus (b). The specimen is 300 mm in diameter and 700 mm in height. Five equally sized layers of the HPR for a single specimen (Fig. 2c) were separated, and each layer was compressed using a vibrator at a frequency of 60 cycles/s.

Fig. 2

Large-scale triaxial compression test: (a) soil particles; (b) triaxial apparatus; (c) sample preparation

After multiple attempts, the technique was refined to achieve the desired initial void ratio (dry density). The specimen was saturated using the vacuum saturation method with a B-value greater than 0.95 after being originally subjected to the required consolidation pressure. Under draining conditions, the specimen was sheared at a constant axial displacement of 2 mm/min until the axial strain accumulated to 20%, at which point the critical state was reached.

For each HKR grading, 4 initial void ratio (e₀) are controlled, which were adopted by the relative densities of D_r = 0.60, 0.75, 0.90 and 1.0, respectively, as shown in Fig. 3.

Fig. 3

Designed various initial void ratios of HKR

The tests can be divided into 4 large groups and 16 small groups. The classification of the 4 large groups is based on the same initial PSD (Characterized by D₀), which are name as D1 ~ D4, respectively. Furthermore, the 16 small groups are based on the same initial PSD and initial void ratio (e₀), which are named as D1E1 ~ D4E4, respectively. The 16 small groups of triaxial consolidation drainage (CD) shear tests were conducted under 4 confining pressures (σ₃ = 300, 600, 1000, and 1500 kPa), and the complete test scheme is shown in Table 2.

Table 2 Large-scale triaxial compression test scheme of HKR

Prior to shearing, the specimens were initially isotropically consolidated at the designed confining pressures. The void ratio of specimens after isotropic consolidation were averagely measured (e_i), and the stress–strain-volume change behaviors during shearing were plotted. The particle breakage after shearing in each test was determined by sieving the dried rockfill material used in the specimen before and after testing.

Taking test results of Group D2 (D₀ = 2.285) as the examples, Fig. 4 shows the stress–strain-volume behaviors of HKR at various initial confining pressures σ₃ (= 300, 600, 1000, and 1500 kPa) and initial void ratios e₀ (= 0.390, 0.339, 0.287 and 0.250). Since the critical state is defined as the state at which the volumetric strain and shear stress are both constant. At the end of shearing, i.e., ε_a = 20%, the test data for the deviatoric stress and volumetric strain of all specimens have reached or come close to constant values. Therefore, this series of large-scale triaxial tests can be used to study the critical state.

Fig. 4

Stress–strain-volume behaviors of HKR: (a) e₀ = 0.390; (b) e₀ = 0.339; (c) e₀ = 0.287; (d) e₀ = 0.250

3 Test results

3.1 Isotropic consolidation line

It has been pointed out that the behavior of the isotropic consolidation line (ICL) in the e − (p/p_a)^ξ plane behaves similarly to that of the CSL [14]. The observed isotropic consolidation points (ICPs) and the fitting lines are plotted in the e − (p/p_a)^ξ plane, as shown in Fig. 5. As a result, the ICL of HKR can be written as follows:

$$ e_{i} = e_{0} - \lambda_{i} \left( {\frac{p}{{p_{a} }}} \right)^{\xi } $$

(2)

where λ_i is the material parameter, p_a is the standard atmospheric pressure, and empirical normalization exponent ξ was suggested as 0.7, which is recovered here was also recovered by Hanley [14], Xiao [26], Ciantia [7] and Nazanin [21].

Fig. 5

Observed ICPs and ICLs of HKR: (a) D₀ = 2.082; (b) D₀ = 2.285; (c) D₀ = 2.425; (d) D₀ = 2.531

It should be noted that when p in Eq. (2) is 0, it indicates that the specimen has not yet consolidated and that the void ratio is the original void ratio, e₀. In other words, e₀ represents the intercept of ICL. Furthermore, the gradient of ICL, λ_i, shows a linear decreasing relationship with D₀ (Fig. 6), and it can be expressed as follows:

$$ \lambda_{i} { = }\lambda_{i0} - \alpha_{\lambda i} D_{0} $$

(3)

where λ_i0 and α_λi are dimensionless material constants (Table 3).

Fig. 6

Relationship between λ_i and D₀

Table 3 Values of material constants

The substitution of Eq. (3) into Eq. (2) gives the ICL equation of the HKR under various initial PSD, initial void ratios and pressure conditions.

$$ e_{i} = e_{0} - \left( {\lambda_{i0} - \alpha_{\lambda i} D_{0} } \right)\left( {\frac{p}{{p_{a} }}} \right)^{\xi } $$

(4)

3.2 Particle breakage at critical state

A lot of breakage indices have been proposed to measure the degree of particle breakage; among them, the B_r proposed by Hardin [15] is a widely acceptable one. The definition of B_r = B_t/B_p is shown in Fig. 7, where B_t is the area between the initial grading of soil and the current grading of soil and B_p is the area between the initial grading of soil and the vertical line of sieve size 0.074 mm. B_r can be expressed as follows:

$$ B_{r} = \frac{{B_{t} }}{{B_{p} }} $$

(5)

Fig. 7

Definition of breakage index proposed by Hardin [15]

Accordingly, B_r of all specimens was computed based in Eq. (5). Increasing particle breakage B_r, as illustrated in Fig. 8, is a direct result of increased pressure, and the relationship is best represented as a line.

$$ B_{r} = b\left( {\frac{{p_{c} }}{{p_{a} }}} \right)^{\xi } $$

(6)

where p_c is the critical mean stress; b is the material parameter.

Fig. 8

Relationship between B_r and (p/p_a).^ξ: (a) D₀ = 2.082; (b) D₀ = 2.285; (c) D₀ = 2.425; (d) D₀ = 2.531

In accordance with different D₀ and e₀, Fig. 9 demonstrates that the parameter b is not a constant. Based on the observed appearance, a straightforward equation was presented to describe the impact of D₀ and e₀ on parameter b:

$$ b{ = }b_{0} - \alpha_{b} D_{0} - \chi_{b} e_{0} $$

(7)

where α_b and χ_b are material constants (Table 3)

Fig. 9

Relationship between parameter b and D₀ & e₀

According to Eq. (7), b decreases with D₀ and e₀, which will be covered subsequently. In essence, the B_r equation of HKR under varied initial PSD, initial void ratios, and pressure circumstances is obtained by substituting Eq. (7) into Eq. (6).

$$ B_{r} = \left( {b_{0} - \alpha_{b} D_{0} - \chi_{b} e_{0} } \right)\left( {\frac{{p_{c} }}{{p_{a} }}} \right)^{\xi } $$

(8)

3.3 Stress ratio at critical state

The critical state stress ratio, M_c, denotes the ratio of deviatoric stress q to mean stress p at the critical state. Under a variety of stress circumstances, the value of M_c is typically regarded as a constant [7, 10, 17]. The observed critical stress of HKR in q–p plane may be described by a linear function, q = M_cp, as illustrated in Fig. 10, using the test results of Group D2 as examples. The fitting correlation coefficient R² is 0.987, and the gradient M_c is 1.73. Similarly, the constant M_c values for Group D1, D3, and D4 are 1.71, 1.75 and 1.76, respectively.

Fig. 10

Constant M_c of the HKR (D₀ = 2.285)

However, it has been noted that despite the fitting linear curve's strong R²-value, this does not prove that M_c is a constant [13]. In fact, as confining pressure (or particle breakage) increases, the M_c of rockfill material actually slightly declines [13, 26].

The critical state stress ratio M_c = (q_c/p_c) are plotted in M_c − B_r plane, as shown in Fig. 11. It is clear that an increase in the B_r value could result in a non-ignorable decrease in M_c. In Group D2, for instance, the maximum M_c is 1.88 (e₀ = 0.250, σ₃ = 300 kPa) and the minimum M_c is 1.65 (e₀ = 0.390, σ₃ = 1500 kPa), both of which deviate significantly from the constant value of M_c = 1.73 (Fig. 11).

Fig. 11

Relationship between changing M_c and B_r: (a) D₀ = 2.082; (b) D₀ = 2.285; (c) D₀ = 2.425; (d) D₀ = 2.531

A linear relationship was proposed to describe the influence of B_r on M_c:

$$ M_{c} = M_{NBc} - mB_{r} $$

(9)

where M_NBc and m are material parameters.

Noting that, recent discrete element method (DEM) and laboratory investigations have shown that M_c is mainly influenced by morphology of particles rather than gradation curve (and thus, breakage) [28, 29]. The authors also believe that the change of particles morphology is the internal mechanism leading to the change of M_c, and the particle breakage is the surface-level explanation. Since the particle breakage index (e.g., B_r) is a more widely used and more easily characterized parameter than particles morphology in laboratory investigations, Eq. (9),i.e., $M_{c} = M_{NBc} - mB_{r}$, was proposed based on B_r, which can intuitively reflect the stress ratio when there is no occurrence of breakage (M_NBc).

The Fig. 11 also demonstrates that the physical significance of parameter M_NBc represents the critical state stress ratio when none particle breakage occurs.

It is interesting to find that gradient of fitted lines (Fig. 11), or the parameter m in Eq. (9), can be regarded as a constant, and its value is 3.14 for HKR. The intercept of fitted lines (Fig. 11), or the parameter M_NBc in Eq. (9), is decreasing with D₀ and e₀. A fitting line in terms of M_NBc ~ e₀, Eq. (10), was proposed to expressed the relationship between M_NBc and D₀, e₀, as shown in Fig. 12.

$$ M_{NBc} { = }M_{c0} - \alpha_{M} D_{0} - \chi_{M} e_{0} $$

(10)

where M_c0, α_M and χ_M are dimensionless material constants (Table 3).

Fig. 12

Relationship between parameter M_NBc and D₀ & e₀

The substitution of Eq. (10) into Eq. (9) gives the M_c equation of HKR under various initial PSD, initial void ratios and particle breakages:

$$ M_{c} { = }M_{c0} - \alpha_{M} D_{0} - \chi_{M} e_{0} - mB_{r} $$

(11)

4 Unified CSL model

4.1 Particle breakage-induced void ratio reduction

The ICPs and ICLs already been covered above. In fact, compared with the ICP, the CSP has additional shearing stress, void ratio and particle breakage.

First of all, the increment of the void ratio between an ICP and CSP (Δe_ci) is defined as

$$ \Delta e_{ci} = e_{c} - e_{i} $$

(12)

where e_c is the void ratio at the critical state, e_i is the void ratio after isotropic consolidation.

The ICPs and CSPs from Group D2E1 (D₀ = 2.285, e₀ = 0.390, σ₃ = 1500 kPa) and Group D2E4 (D₀ = 2.285, e₀ = 0.250, σ₃ = 300 kPa) were taken as an examples, as shown in Fig. 13. The specimen of D2E1 under σ₃ = 1500 kPa exhibits volumetric contraction; thus, the CSP is located below the ICP, and the increment of the void ratio Δe_ci occurs during shearing is negetive, as illustrated in Fig. 13a. On the contrary, the specimen of D2E4 under σ₃ = 300 kPa shows volumetric dilatation, and the increment of the void ratio Δe_ci occurs during shearing is positive, as illustrated in Fig. 13b.

Fig. 13

Definition of decrement of the void ratio occurs during shearing (Δe_ci): (a) volumetric contraction; (b) volumetric dilatation

Secondly, the critical state point with none breakage (NBCSP) is assumed; as shown in Fig. 14, discrete element triaxial tests [5, 7, 14] have demonstrated that the void ratio of NBCSP (e_NBc) will expand in comparison with the corresponding ICP’s (e_i). In their simulations, all samples dilated (i.e., e_NBc > e_i) when particles are uncrushable, even though the confining pressure is very high (e.g., 40 MPa, Bolton [5], Hanley [14]). Therefore, the expanded void ratio between the NBCSP and ICP is named as Δe_ΓB, and the Δe_ΓB value is positive without doubt (Fig. 14).

Fig. 14

Relationship of the void ratios between the ICP, CSP and NBCSP: (a) volumetric contraction; (b) volumetric dilatation; (c) volume expansion mechanism from ICP to NBCSP

In addition, the volume expansion mechanism from ICP to NBCSP can be explained in Fig. 14c. Initially, the particles are compressed to a stable state (ICP) under isotropic pressure (σ₃). Subsequently, the shear stress (σ₁ − σ₃) is applied in the direction of major principal stress, causing the particles to rearrange until reaching a new stable state (NBCSP). During the shear stress loading, the large-size particles rotation dominates the volume change (i.e., dilation).

Thirdly, because particle breakage will cause the void ratio to decrease during shearing, the measured critical void ratio with particle breakage (e_c) will be lower than that with none breakage (e_NBc). Assuming that the particle breakage-induced reduction in void ratio is proportional to particle breakage index B_r, the proportional coefficient is k. Therefore, the breakage-induced reduction in void ratio is kB_r (Fig. 14).

Eventually, as shown in Fig. 14, Δe_ci (= e_c − e_i) is the void ratio increment during particle crushable shearing, Δe_ΓB is the void ratio increment during particle uncrushable shearing, and kB_r is the particle breakage-induced void ratio reduction. Therefore, their relationship can be expressed as follows:

$$ \Delta e_{ci} = \Delta e_{\Gamma B} - kB_{r} $$

(13)

where Δe_ΓB and k are material parameters.

It is noted that, Eq. (13) is unaffected by whether the observed volumetric behavior is contraction (Δe_ci < 0) or dilatation (Δe_ci > 0), as shown in Fig. 14. In Eq. (13), the values of Δe_ci (= e_c − e_i) and breakage index B_r are observed, and the Δe_ΓB and k are assumed, which are the material parameters to be determined. Therefore, the assumed Eq. (13) may accurately explain the relationship between Δe_ci ~ B_r as indicated by the observed values and the simulations of Eq. (13) in Fig. 15.

Fig. 15

Observed and Eq. (13) fitted Δe_ci ~ B_r: (a) D₀ = 2.082; (b) D₀ = 2.285; (c) D₀ = 2.425; (d) D₀ = 2.531

The intercepts of the fitted lines, i.e., Δe_ΓB, are shown to be decreasing with e₀; additionally, we found that Δe_ΓB is also decreasing with D₀. Figure 16a demonstrates that Δe_ΓB can be linearly expressed as the function of D₀ and e₀:

$$ \Delta e_{\Gamma B}\, { = }\,\Delta e_{\Gamma B0} - \alpha_{\Gamma B} D_{0} - \chi_{\Gamma B} e_{0} $$

(14)

where Δe_ΓB0, α_ΓB and χ_ΓB are material constants. The values of e_ΓB0 = 0.448, α_ΓB = 0.104 and χ_ΓB = 0.423 are determined using the parameter data of Δe_ΓB by a least-squares analysis (R² = 0.987).

Fig. 16

Relationship between parameter Δe_ΓB & k with D₀ & e₀: (a) parameter Δe_ΓB; (b) parameter k

The parameter k is the gradient of the line in terms of Δe_ci ~ B_r. In fact, k is not a constant since the Eq. (14) fitted lines are not parallel. The values of k under various initial fractal dimension (D₀) and initial void ratio (e₀) are plotted in the k–e₀ plane, as shown in Fig. 16b. It shows that k is increasing with e₀ but decreasing with D₀, which can be expressed as follows:

$$ k = k_{0} - \alpha_{k} D_{0} + \chi_{k} e_{0} $$

(15)

where k₀ = 2.97, α_k = 0.94, χ_k = 2.48 are material constants (Table 3).

4.2 Critical state line with none breakage

For a given D₀ and e₀, e.g., D₀ = 2.285 and e₀ = 0.250, the observed Δe_ci ~ B_r of specimens under various confining pressures (σ₃ = 300, 600, 1000, and 1500 kPa) can be expressed by a line (Fig. 15), indicating that the values of Δe_ΓB and k are constant and independent of σ₃. It is simple to comprehend why parameter k is a constant. When the initial void ratio e₀ is constant, the particle breakage-induced void ratio reductions under different σ₃ are proportional to the breakage index B_r, and the proportional coefficient (k) is constant.

The fact that Δe_ΓB is also a constant, nevertheless, raises some confusions and needs to be clarified. For example, when D₀ = 2.285, e₀ = 0.250, the value of Δe_ΓB is 0.105 (Fig. 15b). That Δe_ΓB is a constant, according to the definition of Δe_ΓB (Fig. 14), means the expanded void ratios of all uncrushable triaxial CD specimens under various confining pressures are the same, i.e., 0.105. This fact cannot be explicitly demonstrated by laboratory testing, because the rockfill material cannot be uncrushable during shearing. In fact, this phenomenon has been verified by the discrete element triaxial tests conducted by Ciantia [7], Hanley [14] and Bono and McDowell [10]. For instance, the isotropically-compressed sand samples at confining pressures between 1 and 40 MPa (σ’₃ = 1, 2, 4, 8, 16, 24, 32 and 40 MPa) were subjected to uncrushable drained triaxial compression (Hanley et al. [15]), and the results showed that the critical volumetric strain is all about -6.5%, as shown in Fig. 17a. It means that, in the absence of particle breakage, the effect of confining pressure on expanded volume from ICP to NBCSP is minimal. Furthermore, the observed void ratios of ICPs and NBCSPs are shown in Fig. 17b and Table 4, and the expanded void ratios (Δe_ΓB) exhibit a minor variation within a narrow range of 0.0932 ~ 0.1012. Therefore, the parameter Δe_ΓB can be seen as a constant despite varying levels of confining pressures (1 ~ 40 MPa), and its estimated value is the mean value of 0.0970 (Table 4).

Fig. 17

Observed results in discrete element test after Hanley [14]: (a) volumetric strain; (b) ICPs and NBCSPs in the e-p plane

Table 4 DEM results from ICPs to NBCSPs after Hanley

As discussed above, the stress ratio of NBCSP (i.e., B_r = 0 in Eq. (9)) is M_NBc, according to the triaxial stress relationship ($p = {{\left( {\sigma_{1} { + }2\sigma_{3} } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{1} { + }2\sigma_{3} } \right)} 3}} \right. \kern-0pt} 3}q = \sigma_{1} - \sigma_{3} q = M_{c} p)$, the mean stress of NBCSP can be written as $p_{NBc} = \left[ {{3 \mathord{\left/ {\vphantom {3 {(3 - M_{NBc} )}}} \right. \kern-0pt} {(3 - M_{NBc} )}}} \right]\sigma_{3}$. If an ICP’s coordinates in the e–p plane are (e_i, σ₃), as shown in Fig. 18, the associated NBCSP can be written as follows:

$$ \left\{ \begin{aligned} e_{NBc} =\, & e_{i} + \Delta e_{\Gamma B} \hfill \\ p_{NBc} =\, & \frac{3}{{3 - M_{NBc} }}\sigma_{3} \hfill \\ \end{aligned} \right. $$

(16)

Fig. 18

Coordinate scaling transformation rule between NBCSP and ICP

Equation (16) shows that the e-coordinate of NBCSP essentially plus a constant Δe_ΓB compared to ICP’s e-coordinate, and the (p/p_a)^ξ-coordinate of NBCSP can be regarded as multiplying a fixed coefficient $\left[ {{3 \mathord{\left/ {\vphantom {3 {\left( {3 - M_{NBc} } \right)}}} \right. \kern-0pt} {\left( {3 - M_{NBc} } \right)}}} \right]^{\xi }$ on the ICP’s (p/p_a)^ξ-coordinate (Fig. 18). According to the coordinate scaling transformation rule, the NBCSL in e − (p/p_a)^ξ plane is also a line. In addition, the intercept of NBCSL is the ICL’s intercept plus Δe_ΓB, and the gradient of NBCSL is the ICL’s gradient divides $\left[ {{3 \mathord{\left/ {\vphantom {3 {\left( {3 - M_{NBc} } \right)}}} \right. \kern-0pt} {\left( {3 - M_{NBc} } \right)}}} \right]^{\xi }$. Therefore, the equation of NBCSL can be given as follows:

$$ e_{NBc} = e_{\Gamma NB} - \lambda_{NBc} \left( {\frac{p}{{p_{a} }}} \right)^{\xi } $$

(17)

where e_ΓNB and λ_NBc are material parameters representing the intercept and gradient of the NBCSL, respectively, which can be derived as follows:

$$ \left\{ \begin{gathered} e_{\Gamma NB} = e_{0} + \Delta e_{\Gamma B} \hfill \\ \lambda_{NBc} = \frac{1}{{\left[ {{3 \mathord{\left/ {\vphantom {3 {\left( {3 - M_{NBc} } \right)}}} \right. \kern-0pt} {\left( {3 - M_{NBc} } \right)}}} \right]^{\xi } }}\lambda_{i} \hfill \\ \end{gathered} \right. $$

(18)

Although Eq. (18) cannot be proved directly, the DEM example conducted by Hanley [14] is discussed again. The intercepts and gradients of ICL and NBCSL of a sand (Fig. 17b), obtaining by a least-squares analysis based on testing points from discrete element method, are e₀ = 0.503, $\lambda_{i}$ = 9.967 × 10⁻⁴ and e_NBc = 0.6003, $\lambda_{NBc}$ = 8.513 × 10⁻⁴, respectively [14]. The critical stress ratio without breakage is given by Hanley as $M_{NBc}$ = 0.687. Taking $\lambda_{i}$ = 9.967 × 10⁻⁴ and $M_{NBc}$ = 0.687 into Eq. (18), the predicted $\lambda_{NBc}$ value is 8.308 × 10⁻⁴, which is very close to 8.513 × 10⁻⁴. Taking e₀ = 0.503 and Δe_ΓB = 0.0970 (determined in Table 4) into Eq. (18), the predicted e_NBc is 0.60, which is much closed to 0.6003. As a result, the proposed equations of NBCSL and its parameters, i.e., Eqs. (17) and (18), are reasonable.

Combining Eqs. (18), (17), (14) and (11) gives

$$ \left\{ \begin{gathered} e_{\Gamma NB} = e_{0} + \Delta e_{\Gamma B0} - \alpha_{\Gamma B} D_{0} - \chi_{\Gamma B} e_{0} \hfill \\ \lambda_{NBc} = \frac{1}{{\left[ {{3 \mathord{\left/ {\vphantom {3 {\left( {3 - (M_{c0} - \alpha_{M} D_{0} - \chi_{M} e_{0} )} \right)}}} \right. \kern-0pt} {\left( {3 - (M_{c0} - \alpha_{M} D_{0} - \chi_{M} e_{0} )} \right)}}} \right]^{\xi } }}\left( {\lambda_{i0} - \alpha_{i} D_{0} } \right) \hfill \\ \end{gathered} \right. $$

(19)

Substitution of Eq. (19) into Eq. (17) gives

$$ e_{NBc} = \left( {e_{0} + \Delta e_{\Gamma B0} - \alpha_{\Gamma B} D_{0} - \chi_{\Gamma B} e_{0} } \right) - \frac{{\lambda_{i0} - \alpha_{i} D_{0} }}{{\left[ {{3 \mathord{\left/ {\vphantom {3 {\left( {3 - (M_{c0} - \alpha_{M} D_{0} - \chi_{M} e_{0} )} \right)}}} \right. \kern-0pt} {\left( {3 - (M_{c0} - \alpha_{M} D_{0} - \chi_{M} e_{0} )} \right)}}} \right]^{\xi } }}\left( {\frac{p}{{p_{a} }}} \right)^{\xi } $$

(20)

Equation (20) is the equation for NBCSLs under various initial gradations and initial void ratios.

4.3 Relationship between the parameters of CSL and NBCSL

The CSLs of HKR have not been discussed yet. Of course, the equation of CSL is known as

$$ e_{c} = e_{\Gamma } - \lambda_{c} \left( {\frac{p}{{p_{a} }}} \right)^{\xi } $$

(21)

where e_Γ and λ_c are material parameters representing the intercept and gradient of the CSL, respectively.

The values of e_Γ and λ_c can be obtained by fitting method as usual, but it can be directly deduced theoretically in this paper. Taking Test No. D2E4 (D₀ = 2.285, e₀ = 0.250) as the example, the observed ICPs (σ₃ = 300, 600, 1000, and 1500 kPa) and ICL (e₀ = 0.250, λ_i = 0.00626) are shown in Fig. 19, the NBCSPs are obtained based in Eq. (19), and the NBCSL (e_ΓNB = 0.355, λ_NBc = 0.00297) is drawn based in Eq. (20). The observed CSPs are also plotted in Fig. 19. As assumed before, the e-coordinate of a CSP can be obtained by subtracting the breakage-induced void ratio kB_r from NBCSP’s (Fig. 14). Therefore, when p is 0, B_r = 0, the CSP and NBCSP are coincident. It indicates that the intercept of CSL is same with the NBCSL’s, i.e., $e_{\Gamma } { = }e_{\Gamma NB}$.

Fig. 19

Observed ICPs, CSPs and derived NBCSPs of HKR at D₀ = 2.285 and e₀ = 0.250

Based on the fact that $e_{\Gamma } { = }e_{\Gamma NB}$ (Fig. 19), the gradient of CSL can be expressed as (Fig. 20):

$$ \lambda_{c} = \frac{{e_{\Gamma } - e_{c} }}{{\left( {{{p_{c} } \mathord{\left/ {\vphantom {{p_{c} } {p_{a} }}} \right. \kern-0pt} {p_{a} }}} \right)^{\xi } }} = \frac{{e_{\Gamma NB} - e_{c} }}{{\left( {{{p_{c} } \mathord{\left/ {\vphantom {{p_{c} } {p_{a} }}} \right. \kern-0pt} {p_{a} }}} \right)^{\xi } }} $$

(22)

Fig. 20

Derived gradient and intercept of the CSL

According to Fig. 20 and Eq. (17), $e_{\Gamma NB} - e_{c}$ can be given as follows:

$$ e_{\Gamma NB} - e_{c} = \left( {e_{\Gamma NB} - e_{NBc} } \right) + kB_{r} = \lambda_{NBc} \left( {\frac{{p_{NBc} }}{{p_{a} }}} \right)^{\xi } { + }kB_{r} $$

(23)

Substitution of Eq. (6) ($B_{r} = b\left( {{{p_{c} } \mathord{\left/ {\vphantom {{p_{c} } {p_{a} }}} \right. \kern-0pt} {p_{a} }}} \right)^{\xi }$) and Eq. (22) into Eq. (21) gives

$$ \lambda_{c} = kb + \lambda_{NBc} \left( {\frac{{p_{NBc} }}{{p_{c} }}} \right)^{\xi } $$

(24)

where $p_{NBc} = \left[ {{3 \mathord{\left/ {\vphantom {3 {(3 - M_{NBc} )}}} \right. \kern-0pt} {(3 - M_{NBc} )}}} \right]\sigma_{3}$, $p_{c} = \left[ {{3 \mathord{\left/ {\vphantom {3 {(3 - M_{c} }}} \right. \kern-0pt} {(3 - M_{c} }}} \right]\sigma_{3}$ and $M_{c} { = }M_{NBc} - mB_{r}$(Eq. (9)). Therefore, $\left( {{{p_{NBc} } \mathord{\left/ {\vphantom {{p_{NBc} } {p_{c} }}} \right. \kern-0pt} {p_{c} }}} \right)^{\xi }$ in Eq. (23) can be simplified into

$$ \left( {\frac{{p_{NBc} }}{{p_{c} }}} \right)^{\xi } { = }\left( {1{ + }\frac{{mB_{r} }}{{3 - M_{{NB{\text{c}}}} }}} \right)^{\xi } \approx 1 $$

(25)

It is noted that, the value of $\left( {{{p_{NBc} } \mathord{\left/ {\vphantom {{p_{NBc} } {p_{c} }}} \right. \kern-0pt} {p_{c} }}} \right)^{\xi }$ is increasing slightly with increasing B_r, but much closed to 1, as shown in Fig. 21 (e.g., Test D2, D₀ = 2.285). Based in Eq. (25) and Eq. (24), the intercept and gradient of CSL can be derived as follows:

$$ \left\{ \begin{gathered} e_{\Gamma } = e_{\Gamma NB} \hfill \\ \lambda_{c} = kb + \lambda_{NBc} \hfill \\ \end{gathered} \right. $$

(26)

Fig. 21

Values of $\left( {{{p_{NBc} } \mathord{\left/ {\vphantom {{p_{NBc} } {p_{c} }}} \right. \kern-0pt} {p_{c} }}} \right)^{\xi }$ under various breakages

In Eq. (26), the constant k is the breakage-induced void ratio reduction proportionality parameter, and b is the proportionality factor between B_r and p. In other words, the material constants k and b are both particle breakage-related. Therefore, the intercept and gradient of CSL are directly and quantitatively affected by particle breakage.

In short, the equation of CSL can also be given as follows:

$$ e_{c} = e_{\Gamma NB} - \left( {kb + \lambda_{NBc} } \right)\left( {\frac{p}{{p_{a} }}} \right)^{\xi } $$

(27)

If none breakage occurring, the values of k and b will be 0; Eq. (27) will degenerate into that of NBCSL’s. Therefore, Eq. (27) can be regarded as the unified equation of CSL and NBCSL.

4.4 Verification

In summary, the ICL, NBCSL, and CSL of rockfill are straight lines in the e − (p/p_a)^ξ plane. The parameters of the three lines, i.e., intercept and gradient, are quantitatively related, which are listed in Table 5. Among them, the parameters of CSLs incorporating initial gradation and initial void ratio can be given as follows:

$$ \left\{ \begin{gathered} e_{\Gamma } = e_{\Gamma NB} { = }e_{0} + \Delta e_{\Gamma B0} - \alpha_{\Gamma B} D_{0} - \chi_{\Gamma B} e_{0} \hfill \\ \lambda_{c} = kb + \lambda_{NBc} { = }\left( {k_{0} - \alpha_{k} D_{0} + \chi_{k} e_{0} } \right)\left( {b_{0} - \alpha_{b} D_{0} - \chi_{b} e_{0} } \right) + \lambda_{NBc} \hfill \\ \end{gathered} \right. $$

(28)

where $\Delta e_{\Gamma B}$, k, b and $M_{NBc}$ are material parameters depending on D₀ and e₀.

Table 5 Quantified relationship of intercept and gradient of ICL, CSL and NBCSL

The observed CPSs are plotted in Fig. 22, and the fitted CSLs (using Eq. (21), by least-squares analysis based on observed CPSs) and predicated CSLs (using Eq. (27), according to the parameters in Table 3) are also shown in Fig. 22. The distributions of the observed CPSs (under various D₀ and e₀) can be well described by both the fitted and predicted CSLs. In conclusion, the prediction effect is similar even if the predicted parameters of CSL are not totally compatible with the fitted values. It preliminarily proves that the proposed breakage-induced internal relationships between the ICL CSL and NBCSL (Table 5) of granular material are reasonable.

Fig. 22

Predicted and Fitted CSLs of HKR: (a) D₀ = 2.082; (b) D₀ = 2.285; (c) D₀ = 2.425; (d) D₀ = 2.531

5 Discussion

5.1 Parameter b

In essence, parameter b ($B_{r} = b\left( {{{p_{c} } \mathord{\left/ {\vphantom {{p_{c} } {p_{a} }}} \right. \kern-0pt} {p_{a} }}} \right)^{\xi }$, Eq. (6); $b{ = }b_{0} - \alpha_{b} D_{0} - \chi_{b} e_{0}$, Eq. (7)) essentially describes the potential of causing particle breaking under a certain stress. Particle breakage is undoubtedly less likely to occur as D₀ increases because it signals a decrease in the quantity of coarse particles and an increase in the content of fine particles, Therefore, b is decreasing with D₀. The increase in e₀ means that the rockfill is looser; therefore, the potential for occurring particle breakage (b) under a certain stress is also decreasing.

It is noted that, for HKR in this study, b is decreasing with e₀, but for some other granular materials, the observed results showed that, the effect of e₀ on b is very slight, which can be neglected [13]. In order to uniformly describe this phenomenon, the influence of e₀ on k has been considered in Eq. (7), and the material constant χ_b in Eq. (7) can be set as 0 if the influence of e₀ on k can be neglected.

Besides, the connection of B_r and (p/p_a)^ξ ($B_{r} = b\left( {{{p_{c} } \mathord{\left/ {\vphantom {{p_{c} } {p_{a} }}} \right. \kern-0pt} {p_{a} }}} \right)^{\xi }$, Eq. (6)) is expressed as a line in this paper. To be honest, this is a simplified approach of making the parameter b a constant. According to the ultimate gradation theory [11], the particle breakage increases with the increasing p, but it will eventually tend to a fixed value. Therefore, the gradient of B_r ~ (p/p_a)^ξ, i.e., parameter b, is not constant if the confining pressure is extremely high. At least under the existing conditions in large-scale triaxial test (confining pressure ≤ 3 MPa), Eq. (6) is acceptable.

5.2 Parameter k

Parameter k represents ($kB_{r} { = }\Delta e_{\Gamma B} - \Delta e_{ci}$, Eq. (13); $k = k_{0} - \alpha_{k} D_{0} + \chi_{k} e_{0}$, Eq. (15)) the potential for inducing void ratio reduction under specified breakage B_r. The increase in D₀ means less coarse particles and more fine particles, which causes a less specific surface area [24]; therefore, the same breakage-induced fine particles have less potential to fill the void, i.e., k is decreasing with D₀. The increase in e₀ means that the rockfill is looser; therefore, the potential for breakage-induced void ratio reduction (k) is larger, i.e., k is increasing with e₀.

5.3 Interpretation for initial void ratio’s effect on CSLs

It has been pointed that when the initial gradation (D₀) of rockfill material is fixed, the CSLs corresponding to different initial void ratio (e₀) are basically parallel [26], i.e., the slope of CSLs (λ_c) are same, but the intercepts (λ_Γ) are different under changing e₀.

Taking HKR as the example, assuming that the D₀ values are fixed at 2.2 and the e₀ values increase from 0.20 to 0.45 (in increments of 0.05), the predicted family of CSLs are shown in Fig. 23. According to Eq. (28), it is obvious that the intercept λ_Γ decreases with decreasing e₀.

Fig. 23

Predicted family of CSLs under various e₀

But the CSLs are almost parallel (Fig. 23), which is difficult to understand, because the slope λ_c is determined by three variables of k, b and λ_NBc. First of all, the curves of b ~ e₀ and k ~ e₀ are shown in Fig. 24a, and the curve of kb ~ e₀ is shown in Fig. 24b. It is interesting to find that b is decreasing with e₀ and k is increasing with e₀ (as discussed above), but their product kb is almost unchanged (about 0.01, Fig. 24b). Moreover, curves of λ_c ~ e₀ and λ_NBc ~ e₀ are also shown in Fig. 24b. The values of λ_NBc are significantly less than λ_c; therefore, the value of λ_c mainly depends on the value of kb, which is almost unchanged as discussed above (λ_c = 0.014).

Fig. 24

Relationship between material parameters and e₀: (a) parameters b and k; (b) parameters λ_c, bk and λ_NBc

Furthermore, that kb = kB_r/(p/p_a)^ξ (Eq. (6) and Eq. (23)) actually represents the breakage-induced void ratio reduction during shearing under specific pressure (Fig. 20), which is very little affected by e₀. As a result, from the point view of particle breakage, it explains why λ_c can be basically regarded as unchanged under various initial void ratios.

5.4 Interpretation for initial gradation’s effect on CSLs

The existing research [17] also shows that the change of initial gradation can lead to the rotation of rockfill materials’ CSL. If the initial gradation (D₀) changes, the slope of CSL will decrease with increasing D₀. The second-shearing tests performed by Bandini and Coop [3] are the most well-known example of this phenomena. They performed triaxial tests on the carbonate Dogs Bay sand with a pre-loading phase to induce crushing and recognized (initial D₀ has increased because of particle breakage) that the CSL of the sand changed.

This conclusion is based on the observed CSLs. According to the CSL parameters equations derived in this paper, it can be explained from another aspect.

Taking HKR as the example, assuming that the initial void ratio is fixed at 0.35 and the initial D₀ value increases from 1.6 to 2.6 (in increments of 0.2). The initial PSDs are shown in Fig. 25a, and the predicted CSLs according to Eq. (28) are shown in Fig. 25b. It is clear that both of the slope and intercept are decreasing with increasing D₀.

Fig. 25

Predicted family of CSLs under various D₀: (a) changing PSDs under various D₀; (b) family of CSLs

According to Eq. (28), the reason for the decrease in intercept (e_Γ) with increasing D₀ are obvious. The curves of b ~ D₀ and k ~ D₀ are shown in Fig. 26a, and the curve of kb ~ D₀ is shown in Fig. 26b. It is obvious that b and k are decreasing with D₀, therefore, the product kb is also decreasing. Moreover, curves of λ_c ~ D₀ and λ_NBc ~ D₀ are also shown in Fig. 26b. The values of λ_NBc are significantly less than λ_c; therefore, the value of λ_c mainly depends on the value of kb, which is decreasing with D₀ as discussed above.

Fig. 26

Relationship between material parameters and D₀: (a) parameters b and k; (b) parameters λ_c, bk and λ_NBc

In summary, the change of e₀ and D₀ essentially changes the potential of rockfills to produce particle breakage (b), and the potential of breakage-induced fine particles to fill the particles’ void (k), which will directly lead to the translation and rotation of CSL.

6 Conclusions

In this paper, a series of large-scale drained triaxial shearing tests of rockfill material under various initial gradations (D₀), initial void ratios (e₀) and confining pressure (σ₃) have been conducted, and how particle breakage affects the CSL was discussed quantitatively. The main conclusions are as follows:

(1) At the critical state, the particle breakage index B_r is positive proportional to the normalized mean stress. The particle breakage causes a reduction both in stress ratio and void ratio. In particular, the critical state stress ratio of rockfill materials cannot be considered as a constant under various particle breakages.

(2) The observed ICL and CSL are lines in the e-(p/p_a)^ξ plane, and the NBCSL in e-(p/p_a)^ξ plane was also proved to be a line. The parameters of the ICL, CSL and NBCSL, i.e., intercept and gradient, were inextricably related because of particle breakage, which has been quantitative descripted as follows: the intercept of NBCSL is the ICL’s intercept plus a constant, and the gradient of NBCSL is the ICL’s gradient divided by $\left[ {{3 \mathord{\left/ {\vphantom {3 {\left( {3 - M_{NBc} } \right)}}} \right. \kern-0pt} {\left( {3 - M_{NBc} } \right)}}} \right]^{\xi }$. The intercept of CSL is same to the NBCSL’s, and the gradient of CSL is a breakage-related constant plus that of NBCSL. Therefore, the CSL and NBCSL of rockfills can actually be described by a unified equation.

(3) The parameters of ICL, CSL and NBCSL can be generalized to consider the influence of D₀ and e₀. The change of e₀ and D₀ essentially changes the potential of rockfills to produce particle breakage (b), and the potential of breakage-induced fine particles to fill the particles’ void (k), which will directly lead to the translation and rotation of CSL.