1 Introduction

Since the carbon nanotubes (CNTs) were discovered by Iijima in early 1990s [1], they have caught enormous attention because of their remarkable mechanical and electronic properties which lead to extensive potential applications in different fields of nanoscience [2,3,4,5]. In particular, the wave propagation and vibration behavior of fluid-filled CNTs has been a challenging research topic of particular interest because CNTs are very much useful in nanobiological, nanomechanical and nanochemical applications such as nanofluid conveyance and drug delivery [6]. Experimental investigation and theoretical analysis are two main approaches to study the dynamic behavior of fluid-filled CNTs. However, the operation of experimental investigation is quite difficult to control and maneuver at nanoscale [4]. Thus, a number of analytical and computational methods on discrete and continuous models have been intensively developed.

Molecular dynamic simulation (MD) is a reasonable methodology among all kinds of theoretical simulations. However, MD is inefficient because it needs to consider every atom within a CNT molecule, resulting in time-consuming computations and numerical instability [7, 8]. Thus the elastic continuum models of CNTs have been rigorously developed. One of these continuum approaches is the classical elastic beam and shell modeling for fluid-filled CNTs. Yan used the classical continuum elastic beam and shell theory to study the instability and dynamic behaviors of multi-walled carbon nanotubes filled with fluid [9,10,11]. Yoon predicted the vibration and instability characteristics of fluid-conveying CNTs based on the classical Euler–Bernoulli beam models [12, 13].

Although the classical elastic theory is simple and convenient, direct application of these classical beam and shell models may lead to inaccurate solutions because the classical models cannot capture the influences of nanoscale size effects on the mechanical properties of CNTs, such as electrostatic attraction, surface effect, long-range forces between molecules, and so on.

Since the size effects are key factors that influence the material properties of CNTs and can’t be ignored directly, it is necessary to develop new analytical continuum models to investigate the scale effects on the material properties of CNTs. One of these new and effective models is the nonlocal elastic stress model proposed by Eringen [14]. Due to simplicity of the differential nonlocal constitutive relation, many research articles about the dynamic behaviors of fluid-filled CNTs based on these nonlocal models have been published in the last decade [15,16,17,18,19]. For instance, Bahaadini analyzed the small-scale effects on the vibration and stability of viscoelastic CNTs when conveying fluid [15]. Zhen used the nonlocal stress theory to study the nonlinear vibration of fluid-conveying single-walled CNTs [16]. Deng predicted the vibration of fluid-filled multi-walled CNTs based on the nonlocal elasticity theory. The results show that the vibration frequencies increase with increasing wave number and decrease with increasing length of CNTs. Also, the vibration frequencies decrease with the increase in the innermost radius and tend to constant values [18]. Filiz analyzed the wave propagation of embedded (coupled) functionally graded nanotubes conveying fluid. The effects of flow velocity, material property, nonlocal parameter and spring coefficient on wave propagation were considered in this study [19].

The nonlocal elastic models can only account for the softening stiffness with increasing nanoscale effects, which, however, cannot characterize the stiffness enhancement effect noticed from the experimental observation and other elasticity theories. Therefore, Lim first developed the nonlocal strain gradient theory by coupling the nonlocal elastic stress and the strain gradient together to simulate the nanoscale effects [20]. Based on this new kind of models, some research articles about buckling and wave propagation behaviors of nanostructures were published [21,22,23]. The analytical results of these studies indicated good agreements with the experimental and MD results. It can be predicted that the nonlocal strain gradient theory is also appropriate for the dynamic analysis of fluid-filled CNTs.

In this paper, the wave propagation behaviors of fluid-filled single-walled carbon nanotubes (SWCNTs) are studied by employing a high-order nonlocal strain gradient theory. New governing equations of motion based on the Timoshenko beam model are derived. The small-scale effects on CNTs and inside fluids are analyzed using the nonlocal/strain gradient theory and the slip boundary theory, respectively. The influences of nanoscale effects on the dynamic properties of fluid-filled CNTs are investigated in detail.

2 Establishment of the Fluid-Filled Timoshenko Beam Model

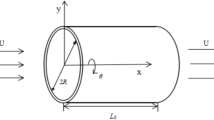
The fluid-filled CNT is simplified as a shear deformable Timoshenko beam in the Cartesian coordinate system, as shown in Fig. 1, where x and y denote the axial and vertical coordinates, respectively. In Fig. 1, w denotes the vertical deflection, U the flow velocity of the inner fluid, and L the beam length.

Fig. 1
figure 1

Simply supported fluid-filled SWCNT

Full size image

The governing equations for the free vibration of classical fluid-filled Timoshenko beam with respect to the rotation angle \(\varphi \) and the vertical deflection w are expressed as [24]:

$$\begin{aligned}&\frac{\partial Q}{\partial x}+\rho _f A_f U^{2}\frac{\partial ^{2}w}{\partial x^{2}}+2\rho _f A_f U\frac{\partial ^{2}w}{\partial x\partial t}+\left( \rho _f A_f +\rho _c A_c \right) \frac{\partial ^{2}w}{\partial t^{2}}=0 \end{aligned}$$
(1a)
$$\begin{aligned}&\frac{\partial M}{\partial x}-Q-\left( {\rho _f I_f -\rho _c I_c } \right) \frac{\partial ^{2}\varphi }{\partial t^{2}}=0 \end{aligned}$$
(1b)

In Eqs. (1a, 1b), M is the bending moment, Q is the shear force, \(\rho \) is the mass density, I is the second-order moment of inertia of SWCNT, A is the cross-sectional area, t is time, and the subindices f and c denote fluid and CNT, respectively. The bending moment and shear force in Eq. (1) are taken as

$$\begin{aligned} M=\int \limits _A {y\sigma \left( x \right) \hbox {d}A_c } \end{aligned}$$
(2)

and

$$\begin{aligned} Q=A_c G\kappa \left( {w^{\left\langle 1 \right\rangle }-\varphi } \right) \end{aligned}$$
(3)

In Eq. (3), \(\kappa \) is the Timoshenko shear correction factor, G is shear modulus, and \(\langle n \rangle \) denotes the nth derivatives with respect to x. According to the nonlocal strain gradient theory, the one-dimensional constitutive relation is presented as [20]

$$\begin{aligned} \sigma (x)-(ea)^{2}\frac{\partial ^{2}\sigma (x)}{\partial x^{2}}=E\left[ \varepsilon (x)-l^{2}\frac{\partial ^{2}\varepsilon (x)}{\partial x^{2}}\right] \end{aligned}$$
(4)

where \(\sigma (x)\) and \(\varepsilon (x)\) are the normal stress and strain with respect to the x coordinate, E is Young’s modulus, and \(\nabla ^{2}\) is the Laplace operator. In Eq. (4), ea and l are nonlocal stress and strain gradient parameters which account for the nanosize effects induced by nonlocality and the strain gradient field [20, 25,26,27,28]. The classical constitutive equation of stress and strain can be obtained when \(ea=0\) and \(l=0\).

The geometry relationship between strain and the rotation angle is taken as

$$\begin{aligned} \varepsilon (x)=-y\frac{\partial \varphi }{\partial x} \end{aligned}$$
(5)

By submitting Eqs. (4) and (5) into Eq. (2), the bending moment with size effects is obtained as

$$\begin{aligned} \left[ {1-(ea)^{2}\frac{\partial ^{2}}{\partial x^{2}}} \right] M=-EI_c \left[ 1-l^{2}\frac{\partial ^{2}}{\partial x^{2}}\right] \frac{\partial \varphi }{\partial x} \end{aligned}$$
(6)

where

$$\begin{aligned} I_c =\int \limits _A {y^{2}\hbox {d}A_c } \end{aligned}$$
(7)

By applying Eqs. (5) and (6), the governing equations shown in Eq. (1) can be changed as

$$\begin{aligned}&\kappa GA_c \left( \frac{\partial ^{2}w}{\partial x^{2}}-\frac{\partial \varphi }{\partial x}\right) +\rho _f A_f U^{2}\frac{\partial ^{2}w}{\partial x^{2}}+2\rho _f A_f U\frac{\partial ^{2}w}{\partial x\partial t}+\left( \rho _f A_f +\rho _c A_c \right) \frac{\partial ^{2}w}{\partial t^{2}}=0 \end{aligned}$$
(8a)
$$\begin{aligned}&\kappa GA_c \left[ 1-(ea)^{2}\frac{\partial ^{2}}{\partial x^{2}}\right] \left( \frac{\partial w}{\partial x}-\varphi \right) +EI\left( 1-l^{2}\frac{\partial ^{2}}{\partial x^{2}}\right) \frac{\partial ^{2}\varphi }{\partial x^{2}}=\left( \rho _f I_f +\rho _c I_c \right) \left[ 1-(ea)^{2}\frac{\partial ^{2}}{\partial x^{2}}\right] \frac{\partial ^{2}\varphi }{\partial t^{2}}\nonumber \\ \end{aligned}$$
(8b)

Since the nanoscale effects contributed by fluid also need to be considered, the dynamic model based on Eqs. (8a, 8b) should be further improved. According to the slip boundary theory, the flow velocity of fluid inside the CNT is affected by the nanoscale effects caused by the interaction between the CNT and the fluid molecules. Rashidi studied the ratio between the average flow velocities through the CNT with and without the nanoscale boundary effects, and defined the VCF number as [15]:

$$\begin{aligned} \hbox {VCF}\equiv \frac{U_\mathrm{slip} }{U}=(1+a\hbox {Kn})\left[ 4\left( \frac{2-\zeta _v }{\zeta _v }\right) \left( \frac{\hbox {Kn}}{1+\hbox {Kn}}\right) +1\right] \end{aligned}$$
(9)

where \(U_\mathrm{slip}\) and U are average flow velocities through the nanotube with and without slip boundary conditions at nanoscale, respectively; \(\hbox {Kn}\) is the Knudsen number, whose value represents the degree of fluid velocity affected by the nanoscale effects. The value of a is defined as:

$$\begin{aligned} a=\frac{64}{3\pi \left( 1-\frac{4}{b}\right) }\frac{2}{\pi }\left( {\tan ^{-1}4\hbox {Kn}^{0.4}} \right) \end{aligned}$$
(10)

\(\hbox {Kn}\) (the Knudsen number) is able to simulate the nanoscale effects induced by fluid. By substituting Eqs. (9) and (10) into Eqs. (8a, 8b), the governing equations for fluid-filled SWCNT beam are further derived as:

$$\begin{aligned}&\kappa GA_c \left( \frac{\partial ^{2}w}{\partial x^{2}}-\frac{\partial \varphi }{\partial x}\right) +\rho _f A_f U^{2}(\hbox {VCF})^{2}\frac{\partial ^{2}w}{\partial x^{2}}+2\rho _f A_f U(\hbox {VCF})\frac{\partial ^{2}w}{\partial x\partial t}+\left( \rho _f A_f +\rho _c A_c \right) \frac{\partial ^{2}w}{\partial t^{2}}=0\nonumber \\ \end{aligned}$$
(11a)
$$\begin{aligned}&\kappa GA_c \left[ 1-(ea)^{2}\frac{\partial ^{2}}{\partial x^{2}}\right] \left( \frac{\partial w}{\partial x}-\varphi \right) +EI\left( 1-l^{2}\frac{\partial ^{2}}{\partial x^{2}}\right) \frac{\partial ^{2}\varphi }{\partial x^{2}}=\left( \rho _f I_f +\rho _c I_c \right) \left[ 1-(ea)^{2}\frac{\partial ^{2}}{\partial x^{2}}\right] \frac{\partial ^{2}\varphi }{\partial t^{2}}\nonumber \\ \end{aligned}$$
(11b)

The solutions of Eq. (11) are assumed as

$$\begin{aligned} w= & {} W\hbox {e}^{\mathrm{{i}}(kx-\omega t)} \end{aligned}$$
(12a)
$$\begin{aligned} \varphi= & {} \varPhi \hbox {e}^{\mathrm{{i}}(kx-\omega t)} \end{aligned}$$
(12b)

where W is the amplitude of the wave, \(\omega \) the angular frequency, k the wave number, and \(\varPhi \) the angular amplitude. By substituting Eqs. (12a, 12b) into Eqs. (11a, 11b), a linear equation group of W and \(\varPhi \) is obtained as

$$\begin{aligned} \left( {{\begin{array}{ll} {\varDelta _1 }&{} \quad {\varDelta _2 } \\ {\varDelta _3 }&{} \quad {\varDelta _4 } \\ \end{array} }} \right) \left( {{\begin{array}{l} W \\ \varPhi \\ \end{array} }} \right) =0 \end{aligned}$$
(13)

where the entities of the coefficient matrix are expressed as

$$\begin{aligned} \varDelta _1= & {} 2\rho _f A_f U(\hbox {VCF})k\omega -\kappa GA_c k^{2}-\rho _f A_f U^{2}(\hbox {VCF})^{2}k^{2}-\left( \rho _f A_f +\rho _c A_c \right) \omega ^{2} \end{aligned}$$
(14a)
$$\begin{aligned} \varDelta _2= & {} -\kappa GA_c {\hbox {i}}k \end{aligned}$$
(14b)
$$\begin{aligned} \varDelta _3= & {} \kappa GA_c {\hbox {i}}k\left[ 1+(ea)^{2}k^{2}\right] \end{aligned}$$
(14c)
$$\begin{aligned} \varDelta _4= & {} \left( \rho _f A_f +\rho _c A_c \right) \left[ 1+(ea)^{2}k^{2}\right] \omega ^{2}-EIk^{2}\left( 1+l^{2}k^{2}\right) -\kappa GA_c \left[ 1+(ea)^{2}k^{2}\right] \end{aligned}$$
(14d)

As we know, a condition for the existence of nontrivial solutions of Eq. (18) is that the determinant of the coefficient matrix vanishes, namely

$$\begin{aligned} \varDelta _1 \varDelta _4 -\varDelta _2 \varDelta _3 =0 \end{aligned}$$
(15)

3 Results and Discussions

The material and geometry parameters of the SWCNT beam and the fluid used are taken as \(E=1\,\hbox { TPa}\), \(G=0.4\,\hbox { TPa}\), \(\kappa =1.1\), \(I_c =1.78\, \times \, 10^{-38}\,\hbox { m}^{4}\), \(I_f =1.43\,\times \, 10^{-38}\,\hbox { m}^{4}\), \(A_c =3.63\,\times \, 10^{-19}\,\hbox { m}^{2}\), \(A_f =3.0\times 10^{-19}\,\hbox { m}^{2}\), \(\rho _c =2.27\times 10^{3}\,\hbox { kgm}^{-3}\), and \(\rho _f =1.0\times 10^{3}\,\hbox { kgm}^{-3}\).

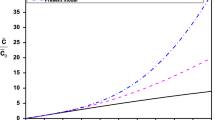
Figure 2a illustrates the dispersion relations for the fluid-filled SWCNT beam between the real part of \(\omega \) (Re(\(\omega \))) and the wave number k with different values of ea. The nonlocal parameters of SWCNT are, respectively, taken as \(ea=0.5\), 1, and 2 nm when \(l=1~\hbox {nm}\). As is shown in Fig. 2a, the value of Re\((\omega )\) keeps rising when the wave number increases, which is similar to the classical model [29]. However, the angular frequency decreases with the increase in the nonlocal parameter ea, which means the stiffness of SWCNT is weakened due to the nonlocal effect.

Fig. 2
figure 2

The real part of angular frequency versus wave number: a with different values of ea; b with different values of

Full size image

In Fig. 2b, the dispersion relations with different strain gradient parameters are indicated, where the values of l respectively take 0.5, 1, and 2 nm when \(ea=1~\hbox {nm}\). The increasing trend for angular frequency with wave number k is the same as that in Fig. 2a. However, the value of Re\((\omega )\) becomes higher since l varies from 0.5 to 2 nm, which means the stiffness is enhanced due to the strain gradient effects. Therefore, the scale effects contributed by the nonlocal stress and strain gradient fields lead to opposite influences on the stiffness of nanotubes, as illustrated by Fig. 2a, b.

Fig. 3
figure 3

The real part and imaginary part of angular frequency versus ea: a real part; b imaginary part

Full size image

Figure 3a, b shows the real and imaginary parts of frequency (Re(\(\omega \)) and Im(\(\omega \))) varying with the nonlocal parameter. In Fig. 3a, four different modes of frequency are illustrated. The values of Re(\(\omega \)) for the first and second modes take the same absolute value, but mode 1 is positive and mode 2 is negative. The absolute value of the two modes decreases when increases because the wave decaying is enhanced when the nonlocal effect increases. However, both modes approach a constant value when, which means the vibration of beams cannot be promoted or damped with high nonlocal effects. The third and fourth modes keep zero, since these two modes only contribute decaying effects to the wave. More information about Im(\(\omega \)) is illustrated in Fig. 3b, where modes 1 and 2 are positive, and modes 3 and 4 are negative. However, the absolute values of Im(\(\omega \)) for all these four modes are the same and keep decreasing when increases, which means the damping of wave is enhanced when the nonlocal effect becomes higher. Thus the damping of wave induced by the nonlocal effect is further confirmed.

Figure 4a, b illustrate the relationships between the frequency and the strain gradient parameter l. The real part Re(\(\omega \)) in Fig. 4a also contains four modes. The first mode takes positive Re(\(\omega \)) and the second mode takes negative Re(\(\omega \)), but the absolute values of Re(\(\omega \)) for both modes are the same and keep increasing as l increases; thus, the stiffness of beam is enhanced and the vibration and wave propagation are promoted due to the strain gradient effect. However, similar to the case in Fig. 3a, modes 3 and 4 take zero, since the strain gradient effect only contributes damping to higher-mode frequencies. In Fig. 4b, the imaginary parts of modes 1 and 2 are the same, and both negative, while those of modes 3 and 4 are also the same, but both positive. Furthermore, the absolute values of the four modes are the same and keep decreasing with increasing l. Therefore, comparing with the results obtained from Fig. 3a, b, the opposite results in Fig. 4a, b confirm the stiffness enhancement and vibration promotion caused by the strain gradient effect.

The information illustrated by Figs. 2, 3 and 4 indicates that the nonlocal stress effect leads to wave damping and stiffness decrease, especially for high-frequency waves, when the strain gradient effect induces opposite results. The physical explanation for this result can be deduced from the constitutive equation shown as Eq. (4). Comparing with the classical constitutive equation \(\sigma (x)=E\varepsilon (x)\), the nonlocal stress on the left side of Eq. (4) is reduced by the nonlocal term \(-(ea)^{2}\frac{\partial ^{2}\sigma (x)}{\partial x^{2}}\), which means the stiffness is decreased due to the nonlocal effect. On the contrary, the strain gradient term \(-l^{2}\frac{\partial ^{2}\varepsilon (x)}{\partial x^{2}}\) on the right side of Eq. (4) leads to smaller strain and higher stiffness as compared with the classical form. Therefore, the two kinds of nanoscale effects induce reverse consequences for materials, and the final influences of nanoscale effects depend on the values of ea and l illustrated by Figs. 2, 3 and 4. Similar results of stiffness prediction for nanostructure materials based on higher-order nonlocal strain gradient models have been confirmed and published [20,21,22,23].

Fig. 4
figure 4

The angular frequency versus l: a real part; b imaginary part

Full size image

Beside the scale effects contributed by nonlocality and the strain gradient of CNT, the slip boundary effects induced by fluid flow also influence the dynamic behaviors. Figure 5a shows the relationship between Re(\(\omega \)) and the Kn number. We can see that Re(\(\omega \)) keeps constant when \(\hbox {Kn}\) varies from 0 to 0.1. However, the values of Im(\(\omega \)) for the four modes shown in Fig. 5b all become higher when \(\hbox {Kn}\) increases; thus, the slip boundary effect from fluid only leads to promotions in wave and vibration.

Fig. 5
figure 5

The angular frequency versus \(\hbox {Kn}\): a real part; b imaginary part

Full size image

Because according to Eq. (9), the slip boundary effect directly affects the flow velocity, the relationships between frequency and flow velocity of Fig. 6a, b indicate similar trends with those of Fig. 5a, b. Firstly, the values of Re(\(\omega \)) in Figs. 6a and 5a are the same, where the frequencies for all modes keep constant with increasing U. Furthermore, the values of Im(\(\omega \)) for all the modes described in Fig. 6b also keep increasing when U becomes higher, which is similar to those in Fig. 5b. The reason for this can be explained by the analytical relationship between U and \(\hbox {Kn}\) in Eq. (9), where U keeps increasing when \(\hbox {Kn}\) becomes higher. However, Fig. 6b indicates the nonlinear relationships between Im(\(\omega \)) and U, while the relationships between Im(\(\omega \)) and \(\hbox {Kn}\) in Fig. 5b are linear. Therefore, the wave promotion caused by the slip boundary effect of fluid flow is further confirmed here.

Fig. 6
figure 6

The angular frequency versus flow velocity: a real part; b imaginary part

Full size image

Because of the difficult operation for experiments, the reasonable methodologies for verification of numerical solution are the MD simulation and the Monte Carlo simulation (MCS) [7, 8]. However, due to time-consuming computations and numerical instability, few studies on fluid-conveying CNTs have been conducted based on either MD simulation or MCS. Liu and his colleagues investigated the wave propagation behaviors of fluid-conveying CNTs by MCS and the interval analysis method (IAM) [30]. We now employ the dispersion relation proposed by Liu et al. to verify the present nonlocal models. The wave dispersion curves obtained by MCS, IAM and the nonlocal strain gradient model are compared and indicated in Fig. 7, where all physical and geometry parameters of the fluid-filled CNT take the same values as Ref. [30].

Fig. 7
figure 7

Dispersion relations by various approaches

Full size image

Figure 7 first illustrates the good agreement of numerical results based on the MCS and IAM proposed by Liu [30]. However, the frequency based on IAM is a little higher than the one by MCS according to Liu’s study, but the difference is very small. Thus MCS and IAM are both reliable for verification of other analytical models [30]. It is shown in Fig. 7 that the frequency predicted by the nonlocal strain gradient model is a little higher than those by MCS and IAM. However, the dispersion curve obtained by the nonlocal strain gradient model indicates the same trend with the MCS and IAM results, and the difference between the frequencies obtained by the nonlocal strain gradient model and MCS is very small. Therefore, the nonlocal strain gradient model is capable of providing accurate results at lower computational cost for wave propagation analysis of fluid-conveying CNTs. Similar results for CNTs without fluid have been verified by comparing with MD and other models [20]. Here the conclusions are further improved for fluid-conveying CNTs.

4 Conclusions

The wave propagation behaviors of fluid-filled CNTs are analyzed based on the Timoshenko beam model established according to new nonlocal strain gradient theory and slip boundary theory. The governing equations are derived and resolved to investigate the wave characteristics of CNTs. The numerical results show that the strain gradient effect leads to stiffness enhancement for CNTs, while the nonlocal stress effect causes stiffness to decrease. The dynamic behaviors of fluid-filled CNTs are affected by both scale effects. The flow velocity of fluid inside the CNT is increased by the slip boundary effect, resulting in the promotion of wave propagation in CNTs.