Introduction

In global navigation satellite system (GNSS) applications, high-precision positioning and navigation are mainly due to high-precision carrier phase observations. It is necessary to ensure that the integer ambiguities remain constant during continuous signal tracking and that they are determined correctly or converge to a certain accuracy. However, unknown integer bias called cycle slips may occur when phase observations are affected by receiver hardware issues or observation obstructions. This phenomenon is not rare; thus, processing cycle slips is essential in high precision GNSS positioning and navigation. Common methods for dealing with cycle slips include reintroducing a new ambiguity parameter and allowing it to re-converge or repairing the cycle slip. Although the method of re-initializing the ambiguity is simple and convenient, the convergence time to achieve high accuracy depends on the processing method of the observations. It can reach tens of minutes to reach the converged accuracy in worse cases. This method will result in the deteriorated availability of high precision positioning results where cycle slip occurs. Especially when multiple satellites need to re-converge their carrier phase ambiguities at the same time or the satellite observation redundancy is not high enough, the positioning accuracy may also be significantly lower. This situation seriously affects the real-time application of high-precision GNSS data. Therefore, in GNSS data processing, cycle slip repair is an important part of ensuring continuous high-precision positioning.

The cycle slips processing could be divided into two steps: cycle slip detection and reIn the past few decades, the GNSS research community has been working on cycle slip detection and repair algorithms. Cycle slip detection can be roughly categorized into two types. The first type is to detect abnormal changes in ambiguity through constructing cycle slips sensitive linear combinations. Among them, the TurboEdit algorithm proposed by Blewitt (1990) is the most popular dual-frequency linear combination algorithm for detecting cycle slips in the time-differenced Hatch–Melbourne–Wübbena (HMW) linear combination (Hatch 1983; Melbourne 1985; Wübbena 1985) and the time-differenced geometry-free linear combination. This method is effective in detection except for some small cycle slips (Liu 2011). Second, within the framework of quality control, the cycle slips are treated as outliers appearing in observation. They are usually detected based on relevant statistics through statistical testing. The detection, identification, and adaption (DIA) method is a well-known method (Teunissen and De Bakker, 2013). In addition, there are outlier detection methods that analyze the posterior residuals in the optimal estimation process, similar to the robust Kalman filtering method (Yang et al. 2001). Compared with the linear combination method, the quality control method can detect cycle slips that cannot be detected by the linear combination due to the strengthened model considering the satellite geometry.

In terms of cycle slip repair, the TurboEdit algorithm proposed by Blewitt (1990) also includes a method for dual-frequency cycle slip repair by using the linear combination. However, due to the small redundancy of the method, this method and its derivative methods still have shortcomings that severely rely on accurate ionospheric delay prediction; thus, these methods will be inevitably unavailable when the ionosphere is strongly active or in real-time processing (Cai et al. 2013; Liu 2011). Subsequently, the method to estimate the cycle slips by using the difference between adjacent epochs has been studied (Banville and Langley 2009, 2013; Zhang and Li 2012). This method considers the geometric relations between satellites, which can greatly improve the success rate of cycle slip repair compared with geometry-free cycle slip repair methods. In addition, triple-frequency and single-frequency situations are also similarly investigated (Fujita et al. 2013; Li et al. 2016, 2019a; Zangeneh-Nejad et al. 2017; Zhao et al. 2015). As the triple-frequency increases the redundant measurements and improves the redundancy, the success rate of cycle slip repair is significantly improved (Zhang and Li 2016).

The problem of repairing the cycle slip of the three frequencies has been basically solved, but the cycle slip repair for dual-frequency measurements is still challenging, especially in situations with strong ionospheric activities and few observed satellites. In many cases, the cycle slips cannot be repaired by only using two adjacent epochs in the estimation model. Based on this situation, real-time multi-epoch repair methods have been proposed. Among them, the method proposed by Li and Melachroinos (2019) is essentially a multi-epoch geometry-free cycle slip repair method, which extended the TurboEdit method to using more than one epoch. Although the success rate is significantly improved compared to the single-epoch geometry-free cycle slip repair method, the performance is still not ideal due to the limitation of the small redundancy of the geometry-free method. It will still rely on the accurate ionospheric delay prediction and wrong cycle slip repair caused by inaccurate ionospheric delay prediction is also observed by Li and Melachroinos (2019). Different from the geometry-free method, another real-time cycle slip repair method based on the undifferenced and uncombined model and Kalman filter proposed by Li et al. (2019c) utilized the geometry relations between satellites, and this method will be called as the undifferenced and uncombined model-based cycle slips repair method. Nevertheless, this method also has its limitations as well. Due to its reparameterization method, the terms of ambiguities and newly involved cycle slips are linearly dependent and estimated in the filter. Meanwhile, in the ionospheric-free (IF) model, using the same approach to group parameters will result in a loss of integer property of cycle slips. As a result, this method can only be applied to the undifferenced and uncombined PPP model but is not applicable in IF-PPP, and it can only repair the cycle slips in the observations whose ambiguities have converged. Therefore, it is still necessary to improve multi-epoch-based cycle slips repair methods which can overcome these limitations.

We propose a real-time multi-epoch time-differencing geometry-based cycle slip repair method. Compared with the multi-epoch geometry-free cycle slips repair method, this proposed method will significantly increase redundancy to ensure a better cycle-slip repair performance. Compared with the undifferenced and uncombined model-based cycle slips repair method, this method can be applied to the undifferenced and uncombined PPP model and other models such as IF PPP or Carrier to Code Levelling (CCL) model. In addition, the cycle slips in the observations whose ambiguities have not converged are also repairable in this method.

Mathematical models for cycle slip repair

In this section, functional models of the multi-epoch cycle slip repair methods will be presented. For easy understanding, a brief review of GNSS measurements and the positioning model will be illustrated.

Undifferenced and uncombined models and time-differencing models

The linearized form of undifferenced and uncombined equations can be written as

$$\begin{array}{*{20}c} {E\left( {P_{r,j}^{s} } \right) = \rho_{0_{r}}^{s} + G_{r}^{s} u_{r} + c{\rm d}t_{r} + b_{r,j}^{s} + T_{r}^{s} + I_{r,j}^{s} } \\ \end{array}$$
(1)
$$\begin{array}{*{20}c} {E\left( {L_{r,j}^{s} } \right) = \rho_{0_{r}}^{s} + G_{r}^{s} u_{r} + c{\rm d}t_{r} + \lambda_{j} \left( {N_{r,j}^{s} + B_{r,j}^{s} } \right) + T_{r}^{s} - I_{r,j}^{s} } \\ \end{array}$$
(2)

where E(*) is the notation of mathematical expectation, \(G\) is the (1 × 3) design matrix and \(u\) is the (3 × 1) difference matrix of unknown coordinates and linearized point; \(s\) and \(r\) identify the satellite and receiver respectively; the subscript \(j\) denotes the frequency; \(P\) and \(L\) represent the measurements of pseudorange and carrier observations; \({\uprho }\) is the distance between respective satellite and receiver pair; \(c\) and \({\rm d}t\) are the speed of light and time offsets respectively; \(\lambda\) is the wavelength and \(N\) is the integer ambiguity; \(b\) and \(B\) represent the hardware and phase delay, respectively; \(T\) and \(I\) denote tropospheric delay and ionospheric delay respectively. Satellite clock errors could be corrected by precise clock products and other unmentioned biases are corrected by models.

The between-epoch single-differenced observation for epoch \(t\) and \(t + n\) could be written as.

$$\begin{array}{*{20}c} {E\left( {\Delta_{t,t + n} P_{r,j}^{s} } \right) = \Delta_{t,t + n} \rho_{0_{r}}^{s} + \Delta_{t,t + n} G_{r}^{s} u_{r} + \Delta_{t,t + n} c{\rm d}t_{r} + \Delta_{t,t + n} b_{r,j}^{s} + \Delta_{t,t + n} T_{r}^{s} + \Delta_{t,t + n} I_{r,j}^{s} } \\ \end{array}$$
(3)
$$\begin{array}{*{20}c} {E\left( {\Delta_{t,t + n} L_{r,j}^{s} } \right) = \Delta_{t,t + n} \rho_{0_{r}}^{s} + \Delta_{t,t + n} G_{r}^{s} u_{r} + \Delta_{t,t + n} c{\rm d}t_{r} + \Delta_{t,t + n} \lambda_{j} N_{r,j}^{s} + n_{t,t + n} B_{r,j}^{s} } \\ { + \Delta_{t,t + n} T_{r}^{s} - \Delta_{t,t + n} I_{r,j}^{s} } \\ \end{array}$$
(4)

where \(\Delta_{t,t + n} \left( * \right) = \Delta_{t + n} \left( * \right) - \Delta_{t} \left( * \right)\) is the time-differencing notation.

$$\Delta _{{t,t + n}} Gu = G_{{t + n}} u_{{t + n}} - G_{t} u_{t} = \frac{{\left( {G_{{t + n}} + G_{t} } \right)\left( {u_{{t + n}} - u_{t} } \right)}}{2} + \frac{{\left( {G_{{t + n}} - G_{t} } \right)\left( {u_{{t + n}} + u_{t} } \right)}}{2}$$

It is noted that some of the errors are constant in a short period, including \(B_{r,j}^{s}\), \(T_{r}^{s}\), \(b_{r,j}^{s}\) (Li et al. 2019b); therefore, the between-epoch single-differenced observation could be written as:

$$\begin{array}{*{20}c} {E\left( {\Delta_{t,t + n} P_{r,j}^{s} } \right) = \Delta_{t,t + n} \rho_{0_{r}}^{s} + \Delta_{t,t + n} G_{r}^{s} u_{r} + \Delta_{t,t + n} c{\rm d}t_{r} + \Delta_{t,t + n} I_{r,j}^{s} } \\ \end{array}$$
(5)
$$\begin{array}{*{20}c} {E\left( {\Delta_{t,t + n} L_{r,j}^{s} } \right) = \Delta_{t,t + n} \rho_{0_{r}}^{s} + \Delta_{t,t + n} G_{r}^{s} u_{r} + \Delta_{t,t + n} c{\rm d}t_{r} + \lambda_{j} \Delta_{t,t + n} N_{r,j}^{s} - \Delta_{t,t + n} I_{r,j}^{s} } \\ \end{array}$$
(6)

Equations (5–6) demonstrate that the time-differenced observations could be expressed by a combination of unknowns including term \(N_{r,j}^{s}\); thus, they could be further reparametrized for cycle slip estimation.

Geometry-based cycle slip repair method

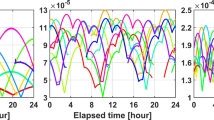
The geometry-based cycle slip repair method was first introduced by Banville and Langley (2009). From time-differencing (5–6), \(\Delta_{t,t + n} Gu\) is usually approximated as \(\frac{{\left( {G_{t + n} + G_{t} } \right)\left( {u_{t + n} - u_{t} } \right)}}{2}\). However, in order to ignoring \(\frac{{\left( {G_{t + n} - G_{t} } \right)\left( {u_{t + n} + u_{t} } \right)}}{2}\), \(\frac{{\left( {G_{t + n} - G_{t} } \right)\left( {u_{t + n} + u_{t} } \right)}}{2}\) should be small enough; otherwise, the linearization error should be taken into consideration. This is usually small enough for a single-epoch differenced method or high sampling rate data and it is usually ignored (Banville and Langley 2009, 2013; Li et al. 2019b). However, it should be carefully investigated in the enhanced multi-epoch differenced method, especially for low sampling rate data. Generally, the interval of low sampling-rate data is 30 s, so \(\left( {G_{t + n} - G_{t} } \right)\) in 30 s (1 epoch) and 120 s (4 epochs) is assessed. Taking ALGO station as an example, GPS and GLONASS magnitudes of \(\left( {G_{t + n} - G_{t} } \right)\) are shown in Fig. 1. Considering \(\left( {u_{t + n} + u_{t} } \right)\) could reach meter level if the prior values of coordinates are estimated by single point positioning (SPP) method or centimeter level to decimeter level estimated by the PPP method; thus, for 120 s interval, \(\frac{{\left( {G_{t + n} - G_{t} } \right)\left( {u_{t + n} + u_{t} } \right)}}{2}\) could reach the centimeter level. For the time-differencing equations, the noise level of carrier phases is usually centimeter or millimeter level, which may be smaller than \(\frac{{\left( {G_{t + 1} - G_{t} } \right)\left( {u_{t + 1} + u_{t} } \right)}}{2}\). As a result, the \(\frac{{\left( {G_{t + n} - G_{t} } \right)\left( {u_{t + n} + u_{t} } \right)}}{2}\) is not neglectable for large intervals and extremely high-speed kinematic datasets including low orbit satellites. Considering the effect of linearization error, \(\frac{{\left( {G_{t + n} - G_{t} } \right)\left( {u_{t + n} + u_{t} } \right)}}{2}\) could be treated as noise to mitigate its impact where \(\left( {G_{t + n} - G_{t} } \right)\) is calculable and the error of \(\left( {u_{t + n} + u_{t} } \right)\) can be approximated according to the positioning covariance. Therefore, the uncertainty of \(\frac{{\left( {G_{t + n} - G_{t} } \right)\left( {u_{t + n} + u_{t} } \right)}}{2}\) could be estimated by the law of error propagation. Thus, the approximation is implemented as:

$$\begin{array}{*{20}c} {\Delta _{{t,t + n}} Gu = G_{{t + n}} u_{{t + n}} - G_{t} u_{t} \approx \frac{{\left( {G_{{t + n}} + G_{t} } \right)\left( {u_{{t + n}} - u_{t} } \right)}}{2}~} \\ \end{array}$$
(7)
Fig. 1
figure 1

\(\left( {G_{t + n} - G_{t} } \right)\) magnitude of 30s (top) and 120s (bottom) interval, computed using the GPS+GLONASS data for ALGO on the DOY 1,2019. The difference \(\left( {G_{t + n} - G_{t} } \right)\) contains three vectors, and they are merged into the figure

Full size image

If cycle slips are detected, the equation (5–6) could be written as:

$$\begin{array}{*{20}c} {E\left( {\Delta_{t,t + n} \overline{P}_{r,j}^{s} } \right) = \Delta_{t,t + n} G_{r}^{s} u_{r} + \Delta_{t,t + n} c{\rm d}t_{r} + \mu_{j} \Delta_{t,t + n} I_{r,1}^{s} } \\ \end{array}$$
(8)
$$\begin{array}{*{20}c} {E\left( {\Delta_{t,t + n} \overline{L}_{r,j}^{s} } \right) = \Delta_{t,t + n} G_{r}^{s} u_{r} + \Delta_{t,t + n} c{\rm d}t_{r} - \mu_{j} \Delta_{t,t + n} I_{r,1}^{s} + \lambda_{j} z_{r,j}^{s} } \\ \end{array}$$
(9)

where \(\Delta_{t,t + n} \overline{P}_{r,j}^{s} = \Delta_{t,t + n} P_{r,j}^{s} - \Delta_{t,t + n} \rho_{0_{r}}^{s},\) \(\Delta_{t,t + n} \overline{L}_{r,j}^{s} = \Delta_{t,t + n} L_{r,j}^{s} - \Delta_{t,t + n} \rho_{0_{r}}^{s},\) \(\mu_{j} = \lambda_{j}^{2} /\lambda_{1}^{2}\) and \(z_{r,j}^{s}\) = \(\Delta_{t,t + n} N_{r,j}^{s}\) are the differences of ambiguities which are considered as cycle slips.

Let \(\Delta_{t,t + n} \overline{P}_{r}^{s} = \left[ {\Delta_{t,t + n} \overline{P}_{r,1}^{s} , \ldots ,\Delta_{t,t + n} \overline{P}_{r,f}^{s} } \right]^{\rm T},\) \(\Delta_{t,t + n} \overline{L}_{r}^{s} = \left[ {\Delta_{t,t + n} \overline{L}_{r,1}^{s} , \ldots ,\Delta_{t,t + n} \overline{L}_{r,f}^{s} } \right]^{\rm T},\) \(\Delta_{t,t + n}\) \(G^{s} = e_{f}^{\rm T} \otimes \Delta_{t,t + n} G_{r}^{s}\), \(\mu = \left[ {\mu_{1} , \ldots , \mu_{f} } \right]^{\rm T}\), \(z_{r}^{s} = \left[ {z_{r,1}^{s} , \ldots , z_{r,f}^{s} } \right]^{\rm T};\) \(\Delta_{t,t + n} \overline{P}_{r} = \left[ {\Delta_{t,t + n} \overline{P}_{r}^{1^{\rm T}} , \ldots ,\Delta_{t,t + n} \overline{P}_{r}^{m^{\rm T}} } \right]^{\rm T},\) \(\Delta_{t,t + n} \overline{L}_{r} = \left[ {\Delta_{t,t + n} \overline{L}_{r}^{1^{\rm T}} , \ldots ,\Delta_{t,t + n} \overline{L}_{r}^{m^{\rm T}} } \right]^{\rm T},\) \(\Delta_{t,t + n} G = \left[ {\Delta_{t,t + n} G^{1^{\rm T}} , \ldots ,\Delta_{t,t + n} G^{m^{\rm T}} } \right]^{\rm T},\)\(\Delta_{t,t + n} I_{r} = \left[ {\Delta_{t,t + n} I_{r,1}^{1} , \ldots ,\Delta_{t,t + n} I_{r,1}^{m} } \right]^{\rm T},\) \(z_{r} = \left[ {z_{r}^{1^{\rm T}} , \ldots ,z_{r}^{m^{\rm T}} } \right]^{\rm T},\) \(\lambda = {\rm diag}\left( {\lambda_{1} , \ldots , \lambda_{f} } \right)\) where \(m\) is the number of observed satellites and \(f\) denotes the number of frequencies. All the time-differencing observations for all frequencies could be written as:

$$\begin{array}{*{20}c} {E\left( {\Delta_{t,t + n} \overline{P}_{r} } \right) = \Delta_{t,t + n} Gu_{r} + e_{mf}^{\rm T} \Delta_{t,t + n} c{\rm d}t_{r} + \Delta_{t,t + n} I_{r} \otimes \mu } \\ \end{array}$$
(10)
$$\begin{array}{*{20}c} {E\left( {\Delta_{t,t + n} \overline{L}_{r} } \right) = \Delta_{t,t + n} Gu_{r} + e_{mf}^{\rm T} \Delta_{t,t + n} c{\rm d}t_{r} - \Delta_{t,t + n} I_{r} \otimes \mu + \left( {{\text{diag}}\left( {e_{m} } \right) \otimes \lambda } \right)z_{r}^{s} } \\ \end{array}$$
(11)

where \(\otimes\) is the notation of Kronecker product.

For high sampling rate data, the time-differenced ionospheric delay is usually neglectable, but for low sampling rate data, it is usually processed by adding a pseudo-observation for predicted ionospheric changes (Li et al. 2014). The pseudo observations of ionospheric delay changes could be expressed as:

$$\begin{array}{*{20}c} {E\left( {\iota_{r}^{s} } \right) = \Delta_{t,t + n} I_{r,1}^{s} ,D\left( {\iota_{r}^{s} } \right) = \sigma_{\iota }^{2} ,E\left( {\iota_{r} } \right) = \Delta_{t,t + n} I_{r} ,Q\left( {\iota_{r}^{s} } \right) = {\text{diag}}\left( {e_{m} \otimes \sigma_{\iota }^{2} } \right)} \\ \end{array}$$
(12)

where \(D\)(*) is the notation of variance,\(Q\left( * \right)\) is the notation of covariance matrix, and ι is the predicted ionospheric changes; \(\iota_{r} = \left[ {\iota_{r}^{1} , \ldots ,\iota_{r}^{m} } \right]^{\rm T}\), \(\Delta_{t,t + n} I_{r} = \left[ {\Delta_{t,t + n} I_{r}^{1} , \ldots ,\Delta_{t,t + n} I_{r}^{m} } \right]^{\rm T}\).

Defining \(e_{k}\) is the (1 × \(k\)) matrix \(\left[ {1, \ldots , 1} \right]_{k}\) and \(0_{{a \times {\text{b}} }}\) is the (\(a\) × \({\text{ b}}\)) zero matrix; for the single-epoch geometry-based time-differencing method, it could be written as:

$$\begin{array}{*{20}c} {E\left( y \right) = Ax + Bz\# \left( {13} \right)} \\ \end{array}$$
(13)
$$\begin{array}{*{20}c} {A = \left[ { \begin{array}{*{20}c} {\Delta_{t,t + n} G} & {e_{mf}^{\rm T} } & {{\text{diag}}\left( {e_{m} } \right) \otimes \mu } \\ {\Delta_{t,t + n} G} & {e_{mf}^{\rm T} } & {{\text{diag}}\left( {e_{m} } \right) \otimes - \mu } \\ {0_{m \times 3} } & {0_{m \times 1} } & {{\text{diag}}\left( {e_{m} } \right)} \\ \end{array} } \right],\,B = \left[ {\begin{array}{*{20}c} {0_{mf \times mf} } \\ {{\text{diag}}\left( {e_{m} } \right) \otimes \lambda } \\ {0_{m \times mf} } \\ \end{array} } \right],y = \left[ {\begin{array}{*{20}c} {\Delta_{t,t + n} \overline{P}_{r} } \\ {\Delta_{t,t + n} \overline{\Phi}_{r} } \\ {\iota_{r} } \\ \end{array} } \right],x = \left[ {\begin{array}{*{20}c} {u_{r} } \\ {\Delta_{t,t + n} c{\rm d}t_{r} } \\ {\Delta_{t,t + n} I_{r} } \\ \end{array} } \right],} \\ {z = z_{r} } \\ \end{array}$$
(14)

The corresponding columns of \(B\) and rows of \(z\) could be removed if a satellite has not been detected as a cycle slip.

For the multi-epoch time-differencing method, if it is assumed that no unrepaired cycle slips in previous \(n\) epochs, similar method proposed by Li and Melachroinos (2019) can be used to enhance this method to use multi-epoch data, which can be expressed as:

$$\begin{array}{*{20}c} {E\left( {y^{n} } \right) = A^{n} x^{n} + B^{n} z} \\ \end{array}$$
(15)
$$\begin{array}{*{20}c} {A^{n} = {\text{diag}}\left( {A_{1} , \ldots ,A_{n} } \right),B^{n} = \left[ {B_{1}^{\rm T} , \ldots ,B_{n}^{\rm T} } \right]^{\rm T} ,y^{n} = \left[ {y_{1}^{\rm T} , \ldots ,y_{n}^{\rm T} } \right]^{\rm T} ,x^{n} = \left[ {x_{1}^{\rm T} , \ldots ,x_{n}^{\rm T} } \right]^{\rm T} } \\ \end{array}$$
(16)

If there are existing unrepaired cycle slips in previous epoch, the respective rows and columns could be omitted in the matrices.

Method and strategy for implementation

In addition to the mathematical model mentioned above, the data processing procedure is also indispensable. The overall flowchart of cycle slip (detection and) repair in this research is shown in Fig. 2, and the new procedure of cycle slip repair is presented in the cycle slips repair block Details will be described in the following sections.

Fig. 2
figure 2

Overall flowchart of cycle slips (detection and) repair procedure of PPP in our research. The flowchart is separated into two blocks: detection Block (top) and repair block (bottom). A recursive repair and validation procedure is used to implement cycle slip repair using multiple epochs.

Full size image

Cycle slip detection strategy

In the geometry-based cycle slips repairing method, the correct detection of all cycle slips is essential; otherwise, the biased estimation may result in failed cycle slips repair. Therefore, even though the cycle slip detection method used in this study is not innovative, a clear illustration of the cycle slip detection strategy is required. For dual-frequency signals, the TurboEdit method proposed by Blewitt (1990) will be used to detect cycle slips at the first step. In this section, most of the cycle slips could be detected. As aforementioned, the HMW combination uses both pseudorange and carrier observations, and it is difficult to distinguish the effect of pseudorange measurement noise and small cycle slips. Meanwhile, the geometry-free combination detects cycle slips through analyzing the ionospheric changes, and this may also lead to small cycle slips indistinguishable from the true ionospheric delay changes. Therefore, the TurboEdit method may still ignore some small cycle slips, and it is necessary for further quality control processes to identify the small cycle slips. DIA procedures and residual assessment are used in this step to detect the rest cycle slips (Baarda 1968; Banville and Langley 2013; Teunissen 1990). A Chi-square test will detect outliers, and the outlier will be identified by the maximum standard residual assessment. When cycle slips are detected in one satellite, they are usually identified as cycle slips that exist in all frequencies.

The strategy we used for cycle slip detection is demonstrated below. The TurboEdit method is the first section for cycle slips detection to detect most cycle slips. Subsequently, the quality control section is implemented after the standard PPP processing section. When cycle slips are detected, the ambiguity will be initialized at first, and the recurrent quality control process will be used until it can pass the quality control section.

Real-time processing strategy

For the multi-epoch time-differencing cycle slip repair method, there are two choices for using multi-epoch data: using the previous epochs or later epochs. Some real-time multi-epoch cycle slip repair methods are using later epochs for cycle slip repair, and this strategy has a significant benefit in improving the repair rate because it can mitigate the effect when large noise or multipath effects appear in the epoch detected cycle slips. Nevertheless, it has inevitable shortcomings in real-world applications. If the integer ambiguities are not converged or fixed, it will generate difficulties in updating the ambiguity parameters and their covariance matrix of the optimal estimator. In addition, even if the cycle slips are fixed with the later multiple epochs, the positioning results before a successful repair will still be degraded. Therefore, using previous epochs for the time-differencing method can avoid these potential problems.

In addition, it could be noticed that the whole matrix for the multi-epoch geometry-based method is large and computing it may be time-consuming. Since the single-epoch geometry-based time-differencing method can repair most of the cycle slips, there is no need to use multiple epochs for every cycle slip repair. Inspired by the implementation method in the multi-epoch geometry-free time-differencing method (Li and Melachroinos 2019), the Kalman-filter-based method could be used for real-time processing to repair the cycle slips required using multiple epochs.

When cycle slips occur in epoch \(t\), single-epoch time-differencing method for epoch \(t\) and \(t - 1\) could be used for cycle slips repairing. The unknown parameters are estimated, and if cycles slips cannot pass the validation test, it yields:

$$\begin{array}{*{20}c} {x_{t - 1,t} = \left[ {\begin{array}{*{20}c} {u_{t - 1,t} } \\ {\Delta_{t - 1,t} c{\rm d}t_{r} } \\ {\Delta_{t - 1,t} I_{r} } \\ \end{array} } \right],\,z_{t - 1,t} = z_{r} } \\ \end{array}$$
(17)

Epoch time-differencing method for \(t\) and \(t - 2\) could be written in the form as (Welch and Bishop 1995):

$$\left[ {x_{t - 2,t}^{\rm T} ,z_{t - 2,t}^{\rm T} } \right]^{\rm T} = F\left[ {x_{t - 1,t}^{\rm T} ,z_{t - 1,t}^{\rm T} } \right]^{\rm T} + W\iota_{t - 2,t - 1} + \omega$$
$$\begin{array}{*{20}c} {F = \left[ {\begin{array}{*{20}c} {0_{4 \times 4} } & {0_{{4 \times \left( {{\text{m}} + {\text{mf}}} \right)}} } \\ {0_{{\left( {m + mf} \right) \times 4}} } & {{\rm diag}\left( {e_{m + mf} } \right)} \\ \end{array} } \right],W = \left[ {\begin{array}{*{20}c} {0_{m \times 4} } \\ {{\rm diag}\left( {e_{m} } \right)} \\ {0_{{m \times {\text{mf}}}} } \\ \end{array} } \right],Q\left( {\iota_{t - 2,t - 1} } \right) = {\rm diag}\left( {e_{m} \otimes \sigma_{\iota }^{2} } \right)} \\ \end{array}$$
(18)

where \(\iota_{t - 2,t - 1}\) denotes the predicted ionospheric changes from epoch \(t - 2\) to \(t - 1\) and \(\omega\) is the processing noise. If there is no unfixed cycle slips between epoch \(t - 1\) and \(t - 2\), the covariance matrix of noise \(\omega\) could be written as:\(\Omega = \left[ {\begin{array}{*{20}c} {{\rm diag}\left( {e_{4} \times \infty } \right)} & {0_{{4 \times \left( {{\text{m}} + {\text{mf}}} \right)}} } \\ {0_{{\left( {m + mf} \right) \times 4}} } & {0_{m + mf} } \\ \end{array} } \right]\), where \(\infty\) represents a large value, and if cycle slips exist between epoch \(t - 1\) and \(t - 2\), noise \(\sigma_{z}\) could be added to \(\Omega\) in the corresponding columns and rows, respectively.

Integer estimation and validation

After cycle slips are estimated with the optimal estimation method, integer candidates need to be selected based on the float results. The most popular method LAMBDA will be used to search the integer candidates (Teunissen et al. 1995).

Before accepting the integers searched by the LAMBDA method, the validation test is essential to verify if the integers are correct. Incorrect cycle slip fixing may contaminate the ambiguity and lead to unexpected accuracy loss. Therefore, bootstrapping success rate and R ratio test (Verhagen et al. 2013) may be used to reduce wrong fixing. Bootstrapping success rate is an indicator for the strength of the model, and the R ratio test may be used to analyze the ratio of two closest integer vectors based on the data quality. Here, the W-ratio is another option for use in ambiguity validation (Li and Wang 2014; Wang et al. 1998).

In addition, different from the geometry-free method, it is common to estimate multiple cycle slips from different satellites. When the noise or the ionospheric delay prediction error is too large, this may cause issues for the LAMBDA method to fix them simultaneously. In order to improve the fixing rate and reduce the effect of observation with low quality, the partial ambiguity resolution (PAR) method could be used to select a subset of cycle slips to be fixed to integers, and there are many existing types of research of the PAR method see for example Li et al. (2015); Li and Zhang (2015) Wang and Feng (2013). The PAR method proposed by Li and Zhang (2015) will be used in this research.

Experiments

We have discussed the following cycle slip repair methods:

  • Method A: the existing single-epoch cycle slip repair method (Banville and Langley 2009, 2013).

  • Method B: the multi-epoch geometry-free cycle-slip repair method proposed by Li and Melachroinos (2019).

  • Method C: our new cycle slip repair method using the multi-epoch geometry-based model.

  • Method D: undifferenced and uncombined model-based cycle slip repair method proposed by Li et al. (2019c).

They will be further analyzed in the experiments.

As aforementioned, in contrast to the undifferenced and uncombined model, the IF model can reveal the unfixed cycle slips more significantly, thus more efficient for reflecting the benefits of the cycle slip repairs. Therefore, the above cycle-slip repair methods will be tested under the framework of IF-based-PPP. As the cycle slip repair method proposed by Li et al. (2019c), Method D, does not work for such IF-based PPP processing, and the repair rates cannot perfectly represent the performance in this method. Therefore, we will compare the performance among Methods A, B, and C, and Method D will be discussed in the later section.

For illustrating the performance of these cycle slip repair methods, the repair rate is used as the most important indicator. However, if other indicators are used, the repair rate can be different, even for identical datasets and the same method. Therefore, a clear statement of the impact factors used in this research is essential.

Considering the potential impact of incorrectly fixed ambiguities on positioning, a strict threshold was used in experiments. For validation test in integer ambiguity resolution, a threshold of success rate and R ratio test was set to 0.99 and 6, respectively, the same as used by Li et al. (2019c). Another important factor affecting the repair rate is the method of ionospheric delay variation prediction. Different ionospheric delay variation prediction methods were applied to high sampling rate datasets and low sampling rate datasets in this research. The predicted ionospheric delay was fixed to zero for the high sampling rate data and a small variation based on the elevation angle. The variation of the ionospheric delay was predicted with a constantly changing rate model for the low sampling rate data. The ionospheric delay was predicted based on the geometry-free combination of the observations in previous epochs using linear extrapolation. The variation of the prediction was calculated based on the extrapolation error. The standard deviations (STD) of the pseudorange and carrier phase were set to 0.3 m and 0.003 m in the zenith direction. Meanwhile, the dual-frequency cycle slip can be repaired by wide-lane and narrow-lane separately. In this study, this strategy is not used in order to simplify the constant settings.

Experiments with static datasets

Datasets from International GNSS Service (IGS) stations, specifically, the datasets from the DOY 1 to the DOY 10 in 2019 were used in this experiment. The stations used are selected for different latitude and longitude, and their distribution is demonstrated in Fig. 3. In addition, the receiver types and antenna types are shown in Table 1.

Fig. 3
figure 3

Distribution of stations used in the static experiment

Full size image
Table 1 Receiver types and antenna types of test stations of IGS station information used in the static experiment
Full size table

GPS and GLONASS systems were used in experiments. The final orbit and clock products provided by the European Space Agency (ESA) were used to correct the error of satellites. For these low sampling rate data sets, cycle slips for all satellites were simulated every 120 epochs (1 h). Both simulated and original cycle slips are to be repaired in experiments, but only simulated cycle slips will be recorded.

The repair number of cycle slips and repair rates of using different methods are demonstrated in Tables 2 and 3, respectively. Considering the repair rates of Method B is too low, the results of Method B of only using the R ratio test are also listed. This strict threshold will reduce the repair rates; however, the wrong cycle slip repair in Li et al. (2019c) caused by the small number of model redundancies may also be reduced.

Table 2 Number of simulated and repaired cycle slips with using different cycle slip repair methods for different test stations. Repair rates in the brackets are the results only using R ratio test in the validation.
Full size table
Table 3 Repair rates using different cycle slip repair methods for different test stations. Repair rates in the brackets are the results only using R ratio test in the validation.
Full size table

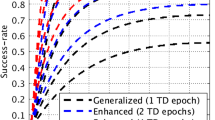
Considering that the bootstrapping success rate is a model-driven indicator, the success rate of the geometry-free method can be computed according to the stochastic model. Based on the assumption that the noise of measurements and ionospheric variations is an elevation-dependent parameter, the success rate of the geometry-free method is also elevation-dependent. It can be noticed that even if ignoring the data-driven ratio test (R ratio test in the experiment), still a large part of the cycle slips cannot pass the success rate validation test using Method B, as shown in Fig. 4. This represents a significant improvement of the proposed geometry-based method that most of them can pass the success rate threshold (shown in Tables 2 and 3), compared with the geometry-free method.

Fig. 4
figure 4

Success rate variation with different elevation angle in Method B with the same stochastic model used in the experiments

Full size image

Our proposed Method C (The multi-epoch geometry-based method) is more effective in improving the fixing rate compared to Method A for approximately 0.8% with 2 epochs and 1.3% with 4 epochs. Even though the number seems small, it represents that more than 30% of the unrepaired cycle slips in the single-epoch geometry-based method can be repaired by using four epochs geometry-based method. In addition, a more significant improvement compared to Method B. An example has been shown in Fig. 5 to illustrate the benefits of the proposed multi-epoch cycle slip repair method using the positioning result of station RGDG on the DOY6 in 2019. The unfixable cycle slip with the single-epoch method could be repaired by the proposed multi-epoch method at 03:00:00 of GPS time and it could mitigate the impact of re-convergence. It should be noted that unrepairable cycle slips in this experiment exist in the newly rising satellites, and there are not enough previous epochs observed for using the multi-epoch method. However, even though these satellites will reduce the repair rate in the experiment, in real-world applications, the initialization of these newly rising satellites will not significantly impact positioning results.

Fig. 5
figure 5

Comparative results of positioning error of JFNG station on DOY 2, 2019 in the east, north, up direction by using Method A (top) and Method C (bottom)

Full size image

We have analyzed the reason for the lowest fixing rate in our method for KOUR. Figure 6 clearly shows a constant HMW value of satellite G18 and G01 during the whole period, in which no cycle slips exist in the satellite in the high probability. However, a rapid variation of the value of geometry-free combination to the same satellites shown in Fig. 7 can be noticed, even though the elevation is high. Neglecting the impact of undetectable cycle slips by considering the constant HMW value, ionospheric variation derived from geometry-free combination has a high accuracy which substantiates the irregular ionospheric variation during this period. This is mainly caused by the active ionosphere happened near the equator, which impedes the precise ionospheric delay prediction. This finally results in the degrading of cycle slip repair. The reliable and real-time applicable ionospheric variation prediction method for the low sampling rate data is still one of GNSS research issues, considering its irregular characteristics.

Fig. 6
figure 6

Elevation angle variation (bottom) and HMW value (top and middle) of satellites G01 (red) and G18 (blue) for station KOUR on DOY 6, 2019

Full size image
Fig. 7
figure 7

Geometry-free combination variation (top) and ionospheric delay variation of adjacent epochs derived from the geometry-free combination (bottom) of satellites G01 (red) and G18 (blue) for station KOUR on the DOY 6, 2019

Full size image

In addition, 1hz high sampling rate datasets for ALGO, CUT0 and KOUR were also tested, which is selected based on the various cycle slip repair performance in the low sampling rate experiments which includes both high repair rate and low repair rates. The datasets on DOY 1 in 2019 are used with simulated cycle slips to all satellites in every 30 s. 100% of the cycle slips can be repaired in 1 epoch. This is also another evidence that inaccurate ionospheric variation predictions may cause unrepairable cycle slips.

Meanwhile, the Ambiguity Dilution of Precision (ADOP) proposed by Teunissen and Odijk (1997) can be used to indicate the model strength of ambiguity resolution. In this research, the ADOP is inherited for the cycle slip due to the high similarity between the cycle slip repair and the ambiguity resolution. The variation of the ADOP using a different number of epochs is used to analyze the precision of float cycle slip estimation. Since the geometry-based method is affected by the geometry of satellites, the ADOP will vary with different geometry. Thus, an example of high sampling rate ALGO station is taken to illustrate the ADOP variation. Figure 8 clearly demonstrates a significant improvement of ADOP with the increasing epoch number used in cycle slip repair. It can also be observed that the improvement from 1 to 2 epochs is most significant.

Fig. 8
figure 8

ADOP variation with epoch number used, computed with the first simulated cycle slips for ALGO on DOY 1, 2019

Full size image

Experiments with kinematic datasets

In order to analyze the performance of the enhanced cycle slip repair method in real-world applications, 1 Hz high sampling rate kinematic datasets were also processed. Three kinematic datasets with different types of vehicles are tested, details of the dataset information are shown in Table 4.

Table 4 Information of three datasets used in the kinematic experiment
Full size table

For the kinematic experiments, cycle slips for all satellites will be simulated in every 30 epochs after 10 min and end until the last 10 min. The comparative results of Method A, Method B and Method C are shown in Table 5. It can be noticed that significant improvements of Method C are observed compared with using Method A and Method B.

Table 5 Repair rates with using different cycle slip repair methods for different kinematic data sets. Repair rates in the brackets are the results only using R ratio test in the validation.
Full size table

In addition, the airborne dataset is also processed with Method D (undifferenced and uncombined model-based cycle slip repair method). Due to the better performance of geometry-based method, Method A and Method C are further compared with Method D. Figure 9 shows a comparison of using Method A, Method C, and Method D.

Fig. 9
figure 9

Comparative results of the STDs using airborne dataset of Method D (top), Method A (middle) and Method C (bottom) with simulated cycle slips in every 30 epochs

Full size image

Figure 9 clearly shows that Methods A and D achieve lower precision than Method C. In Method D, since the ambiguities were not fully converged within 10 min, a large part of cycle slips cannot be repaired by one epoch and this results in a worse precision for the unrepaired epochs. Subsequently, as time goes by, the changes of satellites and unrepaired cycle slips make the cycle slips unrepairable, and obvious convergence processes can be observed. This indicates that Method D is struggling with repairing cycle slips in the un-converged ambiguities. Cycle slips that cannot be repaired by Method A result in 1 more re-convergence process compared to Method C during the positioning. Compared with the single-epoch time-differencing method, more cycle slips can be repaired by using the multi-epoch cycle slip repair method. A significant improvement is demonstrated in this kinematic dataset.

Another experiment was conducted to analyze the performance of unrepairable cycle slips in the single-epoch geometry-based method. Only the unrepairable cycle slips with the single-epoch geometry-based method in the first experiment were simulated. Figure 10 illustrates that even though Method D can repair the cycle slips and avoid the re-convergence, the precision will still get worse until it is repaired.

Fig. 10
figure 10

Comparative results of the STDs of using airborne dataset of Method D (top), Method A (middle) and Method C (bottom) with unrepairable cycle slips in single-epoch geometry-based method

Full size image

Conclusion

We have proposed an enhanced multi-epoch geometry-based cycle slip repair method for precise GNSS positioning. Our proposed method utilizes previous epochs for time differences, which can be implemented in real-time processing. The results of our proposed method are compared with some existing methods, including the multi-epoch geometry-free cycle slip repair method, the single-epoch geometry-based cycle slip repair method and the undifferenced and uncombined model-based method. The repair rates for both static and kinematic datasets with simulated cycle slips are presented. Using the proposed multi-epoch method repairs a part of the cycle slips which could not be repaired by the existing methods. Thus, possible re-convergences are reduced. However, in large interval datasets, the ionospheric irregularity will still pose an important challenge to cycle slip repair. In the future, a reliable real-time ionospheric delay prediction method needs to be further investigated.