Introduction

In the past decade, precise Global Navigation Satellite System (GNSS) applications based on a single dual-frequency receiver have become increasingly popular. Precise point positioning (PPP) is a typical technique that uses only one GNSS receiver to achieve decimeter or even centimeter high precision positioning solutions (Zumberge et al. 1997; Kouba and Héroux 2001). In the PPP applications, a key limitation is the long ambiguity convergence time, typically about 30 min under normal GNSS observation conditions (Bisnath and Gao 2008). Thus, it is highly desired that the GNSS carrier phase signals be continuously tracked, ensuring continuous delivery of high precision PPP solutions as long as the initial ambiguities are resolved at the beginning. Any discontinuities in GNSS carrier phase signals are undesirable and must be repaired to maintain the continuity of high precision PPP solutions. A carrier phase cycle slip is an unpredictable but frequently encountered phenomenon. Basically, there are two approaches to treating the cycle slips. One is to introduce additional parameters to the PPP model. This is similar to re-initialization of the ambiguities and causes the solution to take a long time to converge. In case the frequency of cycle slip occurrences is high, a large number of parameters must be introduced and this might lead to a significant degradation of the PPP solution. The second approach is to directly detect and repair the cycle slips at the epoch in question. This is certainly a more desirable option compared to the first one.

Many cycle slip detection methods have been proposed since the early 1980s, including phase ionospheric residual (PIR) method (Goad 1985), Kalman filtering (Bastos and Landau 1988), polynomial fitting (Lichtenegger and Hofmann-Wellenhof 1989), and high-order and time-difference method (Kleusberg et al. 1993). Their limitations have been summarized in Miao et al. (2011). Recently, several new methods have been proposed for cycle slip detections based on undifferenced GPS observations. de Lacy et al. (2008) presented a Bayesian approach to detecting cycle slips. Liu (2011) developed a new cycle slip detection and repair approach based on the ionospheric total electron content (TEC) rate. But both approaches are most effective to high sampling rate data such as 1 Hz (de Lacy et al. 2008; Liu 2011). Wu et al. (2009) used triple-frequency carrier phase combinations to detect cycle slips. However, the triple-frequency data are not yet available for most GPS satellites. The use of dual-frequency GPS data will continue to dominate until the triple-frequency data are fully available. Many of these cycle slip detection methods implicitly have a presumption that the carrier phase observations are smooth. But this presumption may be violated when GPS observations are collected under high ionospheric activities. With the approach of the 24th solar cycle maximum in the coming years, the ionosphere will become highly active. The high ionospheric activities will very likely increase the occurrence of cycle slips.

The Melbourne–Wübbena (M–W) linear combination (Melbourne 1985; Wübbena 1985) has been widely applied to the cycle slip detection in undifferenced observations as well as double differences. A major advantage of M–W combination is that it is not only geometry-free but also ionosphere-free. Therefore, it can be used even if the GPS receiver undergoes high level of dynamics and/or ionospheric variation. Together with ionospheric combinations, the M–W linear combination was used in the TurboEdit algorithm to detect and repair cycle slips (Blewitt 1990). Miao et al. (2011) modified the TurboEdit algorithm for better applications to satellite-borne GPS observations by introducing a weighted factor that is a function of the satellite elevation angle. The M–W combination uses pseudorange observations which are much noisier than carrier phase observations. Under some observation conditions, the pseudorange noise may be much larger than usual, e.g. in the presence of multipath, increased ionospheric disturbance, and low satellite elevation angle. In such circumstances, the recursive averaging algorithm used in TurboEdit may fail to detect small cycle slips of 1–2 cycles.

We present a cycle slip detection and repair method based on undifferenced, dual-frequency GPS data for post-mission processing. This method integrates a forward and backward moving window averaging (FBMWA) algorithm with a second-order, time-difference phase ionospheric residual (STPIR) algorithm. Unlike the TurboEdit algorithm where the continuous averaging of widelane ambiguity is performed backward only, the averaging of widelane ambiguity in this method is conducted both forward and backward and the averaging is performed within a defined moving window size. The backward moving window averaging is performed on a given number of epochs prior to the epoch in question, and the forward one is performed on epochs within the moving window at and after the epoch in question. Thus, the effect of pseudorange noise prior to and after the epoch in question can be reduced, and the detection of small cycle slips at one cycle level becomes feasible. The only assumption is that there is no further cycle slip within the specified moving window.

The STPIR algorithm is proposed because it can further remove the influence of ionospheric variations, as opposed to the first-order, time-difference PIR. The integration of the FBMWA and STPIR algorithms allows the cycle slips to be determined uniquely. GPS observation data under different levels of ionospheric activities are chosen to test the proposed method. The numerical results indicate that the combined use of the two algorithms can effectively detect and repair cycle slips under active ionospheric conditions.

Cycle slip detection approaches

After reviewing the TurboEdit algorithm (Blewitt 1990), the FBMWA and STPIR algorithms are presented to jointly detect cycle slips. An example is provided for each algorithm for a better understanding.

TurboEdit algorithm

TurboEdit (Blewitt 1990) is an algorithm for cycle slip identification and repair as well as outlier removal using undifferenced, dual-frequency GPS data. In TurboEdit, the detection of cycle slips is based on M–W and the geometry-free combinations. With the measurements from a dual-frequency GPS receiver, the M–W combination observation can be described as follows:

$$ L_{MW} = \frac{{f_{1} \cdot \lambda_{1} \Upphi_{1} - f_{2} \cdot \lambda_{2} \Upphi_{2} }}{{f_{1} - f_{2} }} - \frac{{f_{1} \cdot P_{1} + f_{2} \cdot P_{2} }}{{f_{1} + f_{2} }} = \lambda_{WL} N_{WL} $$
(1)

where λ WL  = c/(f 1 − f 2) ≈ 0.86 m and N WL  = N 1 − N 2 are widelane wavelength and widelane ambiguity, Φ1 and Φ2 are carrier phases on L 1 and L 2 frequencies, P 1 and P 2 are the pseudoranges on L 1 and L 2 frequencies, λ 1 and λ 2 are the wavelengths of the L 1 and L 2 signals and f 1 and f 2 are the respective carrier frequencies, and N 1 and N 2 are the integer ambiguities on L 1 and L 2, respectively. The widelane ambiguity can be easily obtained from (1) as follows:

$$ N_{WL} = \frac{{L_{MW} }}{{\lambda_{WL} }} = \Upphi_{1} - \Upphi_{2} - \frac{{f_{1} \cdot P_{1} + f_{2} \cdot P_{2} }}{{\lambda_{WL} \left( {f_{1} + f_{2} } \right)}}. $$
(2)

As long as the phase observations are free of cycle slips, the widelane ambiguity remains quite stable over time.

In utilizing the M–W combination to detect cycle slips, a recursive averaging filter is used in TurboEdit as follows:

$$ \bar{N}_{WL} (k) = \bar{N}_{WL} (k - 1) + \frac{1}{k}[N_{WL} (k) - \bar{N}_{WL} (k - 1)] $$
(3a)
$$ \sigma^{2} (k) = \sigma^{2} (k - 1) + \frac{1}{k}[(N_{WL} (k) - \bar{N}_{WL} (k - 1))^{2} - \sigma^{2} (k - 1)] $$
(3b)

where \( \bar{N}_{WL} \) is the mean value of N WL , k and k − 1 represent the present and previous epochs, respectively. The standard deviation (SD) of \( \bar{N}_{WL} \) at epoch (k) is σ(k). When the following conditions are satisfied,

$$ \left| {N_{WL} (k) - \bar{N}_{WL} (k - 1)} \right| \ge 4\sigma (k) $$
(4a)
$$ \left| {N_{WL} (k + 1) - N_{WL} (k)} \right| \le 1 $$
(4b)

it is considered that a cycle slip occurs.

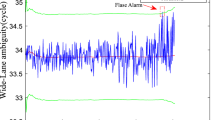
Figure 1 is an example of cycle slip detection with the TurboEdit algorithm using the GPS satellite PRN 26 dataset observed at International GNSS Service (IGS) station WUHN on July 14, 2000. One cycle and two cycle slips are simulated on the L 1 signal at GPS time of 3:50:00 and 5:10:00 (i.e. the 40th and 200th epochs) in the top and bottom panels, respectively. During the 6-h period (3:30–9:30 GPS time), the PRN 26 satellite rose from 11° to 85° and set at 15°. An initial SD value is set to 0.6 cycles. The blue curves represent the widelane ambiguity N WL (k) estimated using (2). The curves are shifted by a constant for the sake of clear display. The red curves represent the filtered ambiguity—recursively averaged widelane ambiguity \( \bar{N}_{WL} \). The green ones denote the sum of \( \bar{N}_{WL} \) and its ± 4σ. According to the judgment criteria in (4a), widelane ambiguity exceeding the bounds of the two green lines, i.e. \( N_{WL} (k) > [\bar{N}_{WL} (k - 1) + 4 \cdot \sigma (k)]{\text{ or }}N_{WL} (k) < [\bar{N}_{WL} (k - 1) - 4 \cdot \sigma (k)] \), suggests a possible cycle slip. Figure 1 indicates that the widelane ambiguity, represented by the blue curves, is well within the area bounded by the two green lines. This implies that no cycle slip can be detected in this case using the TurboEdit algorithm. This clearly indicates that in some cases the small cycle slips of 1–2 cycles are difficult to detect using the TurboEdit algorithm. New algorithms need to be developed to enhance the reliability of cycle slip detection.

Fig. 1
figure 1

Cycle slip detection using M–W combinations based on the TurboEdit algorithm

Full size image

This failure to detect the simulated cycle slips (1, 0) in the top panel and (2, 0) in the bottom panel is because of the large measurement noise, particularly pseudorange noise. The large measurement noise affects N WL (k) and σ(k) more than the filtered \( \bar{N}_{WL} (k - 1) \). When the noise level is high, the criteria (4a) might fail to detect small cycle slips, as shown in this example.

Forward and backward moving window averaging algorithm

A forward and backward moving window averaging (FBMWA) filter algorithm is proposed here. In this algorithm, the widelane ambiguity is smoothed in both forward and backward directions with a specified size of smoothing window in each direction. This differs from the regular TurboEdit algorithm where only the backward smoothing is performed and the window size continuously grows with the number of epochs. Note that the use of a forward smoothing algorithm implies that the FBMWA method is only suitable for post-mission GPS data processing. The FBMWA algorithm can be described as follows:

$$ \bar{N}_{{WL,B{\text{wd}}}} (k - 1) = \frac{1}{m}\sum\limits_{i = k - 1}^{k - m} {N_{WL} (i)} $$
(5a)
$$ \bar{N}_{{WL,F{\text{wd}}}} (k) = \frac{1}{n}\sum\limits_{i = k}^{k + n - 1} {N_{WL} (i)} $$
(5b)
$$ \Updelta \bar{N}_{WL} (k) = \bar{N}_{{WL,F{\text{wd}}}} (k) - \bar{N}_{{WL,B{\text{wd}}}} (k - 1) $$
(6)

where \( \Updelta \bar{N}_{WL} (k) \) is the difference between \( \bar{N}_{{WL,F{\text{wd}}}} (k) \) and \( \bar{N}_{{WL,B{\text{wd}}}} (k - 1) \), \( \bar{N}_{{WL,B{\text{wd}}}} (k - 1) \) is the backward smoothing widelane ambiguity over m epochs prior to epoch (k), \( \bar{N}_{{WL,F{\text{wd}}}} (k) \) is the forward smoothing widelane ambiguity over n epochs at and after epoch (k), m and n are the sizes of smoothing windows for the backward and forward smoothing, respectively. The window size of backward smoothing m may be different from that used in forward smoothing i.e. n. Equation (5a) is essentially same as the formula of (3a). The only difference is the number of smoothing epochs. There is no specific limitation on this number in the TurboEdit algorithm while it is specified as m in the FBMWA algorithm. The value of m can be predefined prior to cycle slip detection. The more significant difference is the use of \( \bar{N}_{{WL,F{\text{wd}}}} (k) \) in the FBMWA algorithm. In the TurboEdit algorithm as shown in (4a), the N WL (k) is used to detect cycle slip. When the noise level of N WL (k) is significant, the direct use of N WL (k) may result in incorrect cycle slip detection. In the FBMWA algorithm, the widelane ambiguity at epoch (k) is computed as a smoothed value over n epochs in a forward smoothing. When there are no cycle slips in the n epochs, the forward smoothing can significantly reduce the noise level of the widelane ambiguity. The standard deviation of smoothed ambiguity (i.e. \( \bar{N}_{{WL,F{\text{wd}}}} (k) \)) is only \( 1/\sqrt n \) of the unsmoothed one (i.e. N WL (k)). The effectiveness of the FBMWA method is tested and shown in Fig. 2.

Fig. 2
figure 2

Cycle slip detection results using the moving window average filter algorithm

Full size image

The dataset is the same as that used in Fig. 1. The size of the moving window used in Fig. 2 is 25. Similar to Fig. 1, the blue curves represent the unsmoothed widelane ambiguities, the red curves are the smoothed ones after performing the backward moving window average algorithm, and the green ones are the \( \Updelta \bar{N}_{WL} (k) \). It can be seen from the green curves of Fig. 2 that the 1-cycle slips in the top panel and the 2-cycle slips in the bottom panel can be readily identified. In the top panel, the detected cycle slip values \( \Updelta \bar{N}_{WL} \) at the 40th and 200th epochs are calculated as 0.969 and 0.971 cycles, respectively. They can be naturally rounded to their nearest integer 1 cycle. This 1-cycle slip is exactly the simulated value. Compared to the results shown in Fig. 1, the FBMWA algorithm is more effective to detect small cycle slips of 1–2 cycles, especially when the widelane ambiguity estimates are noisy. It is noted that the start points of the red and green curves are 25 epochs later than the blue ones. This is because the first 25 epochs are used in the backward moving window smoothing. Similarly, the end points of green curves terminate 25 epochs earlier than the blue and red ones, which is the window size of forward smoothing in the green curves.

The window sizes used in the forward and backward filters are empirically determined based on the noise level of the time-differenced widelane ambiguities. The window size may be approximately determined as 50 times of the noise level of the time-differenced widelane ambiguities. The larger window size can contribute to reducing the noise level of filtered ambiguities but the risk of having other cycle slips within a window will increase.

Second-order, time-difference phase ionospheric residual method

The cycle slip in the widelane observation can be effectively detected using (6) in the FBMWA algorithm. However, it is still unknown how large the individual cycle slips are and at which frequency the cycle slips occur. To uniquely determine the cycle slips at each frequency, another cycle slip equation must be obtained. Thus, this section develops the second-order, time-difference phase ionosphere residual (STPIR) algorithm to detect cycle slips. The phase ionospheric residual (PIR) method was first proposed by Goad (1985), and it is essentially a scaled geometry-free combination. The geometry-free combination is defined as follows:

$$ \Upphi_{GF} = \lambda_{1} \Upphi_{1} - \lambda_{2} \Upphi_{2} = \lambda_{1} N_{1} - \lambda_{2} N_{2} + (\gamma - 1)I $$
(7)

where I is the ionospheric range delay in unit of meter on L 1 and \( \gamma = f_{1}^{2} /f_{2}^{2} \). The PIR combination is defined as follows:

$$ \Upphi_{PIR} = N_{1} - \lambda_{2} /\lambda_{1} \cdot N_{2} + I_{{\text{Re} s}} $$
(8)

where I Res = (γ − 1)I/λ1 = 3.3997I is the residual ionospheric error in unit of cycles. The cycle slip at epoch (k), if any, can be estimated by differencing the PIR combinations at epochs (k) and (k − 1) as follows:

$$ [\Updelta N_{1} - \lambda_{2} /\lambda_{1} \Updelta N_{2} ] = \left[ {\Upphi_{PIR} (k) - \Upphi_{PIR} (k - 1)} \right] - \left[ {I_{{\text{Re} s}} (k) - I_{{\text{Re} s}} (k - 1)} \right]. $$
(9)

Equation (9) can be called the first-order, time-difference of PIR combination. As shown in this equation, the cycle slip term \( [\Updelta N_{1} - \lambda_{2} /\lambda_{1} \Updelta N_{2} ] \) is influenced by the ionospheric residual remaining in the right side that can be calculated as 3.3997[I(k) – I(k − 1)]. The standard deviation of ionospheric TEC change rate can be over 0.03 TECU/second during ionosphere disturbances based on the TEC observation data in the low latitude region of Hong Kong (Liu and Chen 2009). Thus, the ionospheric residual must be removed before the first-order, time-difference of PIR combination can be used to detect cycle slips, especially under the active ionospheric conditions.

To minimize the impact of ionospheric disturbances, we propose the second-order, time-difference PIR (STPIR) algorithm. The STPIR algorithm can be defined as follows:

$$ [\Updelta N_{1} - \lambda_{2} /\lambda_{1} \Updelta N_{2} ] = \left[ {\Upphi_{PIR} (k) - 2\Upphi_{PIR} (k - 1) + \Upphi_{PIR} (k - 2)} \right] - \left[ {I_{{\text{Re} s}} (k) - 2I_{{\text{Re} s}} (k - 1) + I_{{\text{Re} s}} (k - 2)} \right]. $$
(10)

In the STPIR, the ionospheric residual is significantly smaller than in the first-order, time-difference PIR.

The example in Fig. 3 illustrates the advantage of using the STPIR rather than the first-order, time-difference PIR combination, particularly when the ionosphere varies rapidly. The GPS data collected on July 14, 2000 from IGS station BJFS are used in the test. The simulated cycle slip pair on PRN 21 at GPS time 10:40:00 is (4, 3) on GPS L 1 and L 2 signals, respectively. For convenience of display, the value of undifferenced PIR combination was shifted by a constant. It is apparent that the simulated cycle slips do not show any effect on the undifferenced PIR combination. It can be seen that the first-order, time-difference PIR combination has large variations over the entire period of 3 h. There is an abrupt jump at the cycle slip simulation epoch 10:40:00, but it is hard to distinguish the cycle slip from the large ionospheric residuals. The time series of the STPIR in the bottom panel of Fig. 3 appear to be flat, except at the cycle slip simulation epoch 10:40:00. The bottom panel clearly suggests that the ionospheric residual in the STPIR combination approaches zero cycle, which allows a quick detection of cycle slips.

Fig. 3
figure 3

Cycle slip detection results for GPS PRN 21 using the phase ionospheric residual method at BJFS on July 14, 2000

Full size image

Repair of cycle slips by combining the FBMWA and STPIR algorithms

Using (6) or (10) alone, almost all the cycle slips can be detected except some special pairs of cycle slips on GPS L 1 and L 2 frequencies. For instance, when the cycle slip pair is (ΔN 1, ΔN 2) and ΔN 1 = ΔN 2, the detected cycle slip \( \Updelta \bar{N}_{WL} (k) \) value will be 0. This is because these cycle slip pairs will not result in a change in the widelane ambiguity \( \bar{N}_{{WL,F{\text{wd}}}} (k) \). Similarly, special cycle slip pairs such as \( (77 \cdot k,\,60 \cdot k),k = \pm 1, \pm 2, \ldots \)will not show an impact on the cycle slip term of (10). The first and last rows of Table 1 show the two cases. But the use of the STPIR algorithm can complement the drawbacks of the FBMWA algorithm. For instance, FBMWA is insensitive to the cycle slip pair (1, 1), but STPIR will have a value of −0.283 cycles, which is significant and can be detected. In addition, the combination of the FBMWA and STPIR algorithms can uniquely determine and repair the cycle slips at each frequency. The rows 2–4 of Table 1 refer to a few special cycle slip pairs that cause only a limited impact on the STPIR values.

Table 1 Several insensitive cycle slip pairs for the FBMWA and STPIR algorithms
Full size table

When using the detected cycle slip values from (6) and (10), any pair of cycle slips (ΔN 1, ΔN 2) can be uniquely determined by combining the equations:

$$ \Updelta N_{ 1} - \Updelta N_{2} = a $$
(11a)
$$ \Updelta N_{ 1} - \lambda_{2} /\lambda_{1} \cdot \Updelta N_{ 2} = b $$
(11b)

where a is the detected cycle slip value from (6), which has been rounded to an integer value. The detected cycle slip value b from (10) is a float value. Using (11a) and (11b), the float values of (ΔN 1, ΔN 2) are first estimated before rounding them to integers.

Numerical results and analyses

The FBMWA and STPIR algorithms are extensively tested using GPS data collected under significant ionospheric disturbances. Table 2 gives a summary of the used observation data. These GPS stations are distributed over different regions, covering equatorial, mid- and high latitudes. The data sampling rate of all these datasets was 30 s except that the datasets on March 31, 2001 had a higher data rate of 1 s.

Table 2 Summary of observation data used in the test
Full size table

Three days in the last solar maximum cycle with different levels of ionospheric disturbances are chosen for testing. Figure 4 shows the geomagnetic Kp indices for these days. The Kp index is a mean value of the geomagnetic disturbance levels indicating the severity of the global magnetic disturbances in near-earth space (Wing et al. 2005). The Kp indices in this figure indicate that the ionospheric activities for 3 days are at moderate and high levels. Especially for March 31, 2001, its maximum Kp index reached 9 as a strong interplanetary shock wave struck the earth and produced one of the largest geomagnetic storms (Baker et al. 2002). The ionosphere was very active on March 31, 2001, and its daily average Kp index was 7.6, which was the highest one in the past 20 years (1992–2011) and the 6th highest in the past 80 years (1932–2011). The ionospheric activities on the other 2 days were at medium level.

Fig. 4
figure 4

Geomagnetic Kp indices on three different testing days

Full size image

The datasets on July 14, 2000 and April 15, 2001 were collected under intensive solar flares. The solar flare classes for the 2 days are 5.7 and 14.4, representing medium and high levels, respectively. A solar flare is an abrupt brightening in an active region near a group of sunspots of the photosphere, which produces immediate increases in the ionospheric ionization and thereby causes a sudden increase in TEC. The solar flare intensity of 14.4 on April 15, 2001 was the highest one during the last solar maximum cycle of 2000–2002.

Figure 5 shows the ionospheric TEC increment that is caused by the solar flares on the first 2 testing days. Different colors represent different satellites. The sudden increments of TEC are significant, as can be seen from the time window defined by two vertical dashed lines. The conventional undifferenced PIR or geometry-free combination based cycle slip detection methods usually assume that the ionospheric TEC varies smoothly. This assumption cannot be satisfied for the time periods as specified in Fig. 5.

Fig. 5
figure 5

TEC increment caused by different classes of solar flares on two testing days

Full size image

As done previously, some simulated cycle slips are added to the original carrier phase observations. In this test, the cycle slip pair (5, 4) is added to the GPS L 1 and L 2 carrier phase data at an epoch located in the time window with increased ionospheric TEC, as indicated by two vertical dashed lines in Fig. 5. The pair (5, 4) was chosen because it is one of the most challenging pairs to detect, as suggested in Table 1.

Shown in Figs. 6 and 7 are the cycle slip detection results for the two testing days with solar flares using the FBMWA and STPIR algorithms. In each plot, the cycle slip detection results using the FBMWA algorithm are given in the left panel and the ones using the STPIR algorithm are shown in the right panel. The color lines have the same definition as above. The simulated cycle slips at the 180th (GPS time 10:30) and 120th (14:00) epochs have been indicated by two vertical dashed lines. As shown in the left panels, 1 cycle of slip, i.e. the difference of 5 cycles of slip on the L 1 frequency and 4 cycles of slip on the L 2 frequency, is successfully detected using the FBMWA algorithm. Especially, it is noted from Fig. 7e and f that the FBMWA algorithm still performs well even at high latitude stations with more active ionospheric conditions.

Fig. 6
figure 6

Cycle slip detection results on July 14, 2000. The horizontal axis is in GPS time. (a) BJFS, (b) URUM

Full size image
Fig. 7
figure 7figure 7

Cycle slip detection results on April 15, 2001. The horizontal axis is in GPS time. (a) AMC2, (b) MDO1, (c) KOUR, (d) AREQ, (e) KELY, (f) REYK

Full size image

Shown in the right panels of Figs. 6 and 7 are the cycle slip detection results using both first-order and second-order, time-difference PIR combinations. Examining the STPIR results reveals that there exists more than one peak value in addition to the one at the cycle slip epoch. According to the results detected by the FBMWA algorithm in the left panel, it can be concluded that at least one of the peaks is caused by the simulated cycle slips (5, 4). Due to the existence of cycle slip pairs to which the FBMWA algorithm is not sensitive, it is possible that special cycle slips (ΔN 1, ΔN 2) with ΔN 1 = ΔN 2 occur and that these cycle slips cannot be detected using the FBMWA algorithm. As indicated in Table 1, the cycle slip pair (1, 1) or (−1, −1) results in a change of 0.283 cycles to the STPIR result. For other special cycle slip pairs, the impact on the STPIR result will be a multiple of 0.283 cycles. The right panels in Figs. 6 and 7 show that the time series of the STPIR results (denoted by the red color) are flat to 0 cycle and that the peak values are significantly smaller than 0.283 cycles (except Fig. 7e and f). Therefore, it can be concluded that these peaks are not caused by the special cycle slip (ΔN 1, ΔN 2) with ΔN 1 = ΔN 2. Matching the only one jump at the cycle slip epoch indicated in the left panel of Figs. 6 and 7, it can be reasoned that only one STPIR peak value in the right panel is caused by the simulated cycle slips (5, 4). All the other STPIR peak values that do not match cycle slips in the left panel are not caused by the special cycle slips (ΔN 1, ΔN 2) with ΔN 1 = ΔN 2. They should be discarded since they are not cycle slip signals.

Table 3 summarizes the results of the cycle slip detection and repair using the FBMWA and STPIR algorithms. Statistical results indicate that the mean detection values in the FBMWA algorithms are less than 0.1 cycles in all but one of the 24 cases. This indicates that the measurement noises in both carrier phases and particularly pseudoranges have been well smoothed by the FBMWA algorithm. The peak values are significantly larger than the mean value of ~ 0.1 cycles in most cases. All the peak values are close to the simulated 1 cycle slip. Statistically, a Gaussian distribution is assumed for the time series of the FBMWA results. As shown in Table 3, all the peak values in column 3 are beyond the (mean ± 3σ) threshold limit. This suggests all 24 peak values detected should be regarded as cycle slips with a confidence coefficient of 99.7 %.

Table 3 Statistical results of cycle slip detection using the FBMWA and STPIR algorithms (cycle)
Full size table

Column 4 of Table 3 shows all the 24 cycle slips caused peak values calculated using the STPIR algorithm. These STPIR peak values are regarded to be resulting from cycle slips because the FBMWA values have peak values concurrently at the same epoch. The other STPIR peak values shown in Figs. 6 and 7 are not shown in this table because there are no peak FBMWA values concurrently at those epochs. The (mean ± 3σ) threshold limit is shown in column 6. If the cycle slip terms calculated from the STPIR algorithm is assumed to obey a Gaussian distribution, the peak values that exceed the (mean ± 3σ) threshold limits can be regarded as cycle slips. The column 8 shows that 21 of 24 peak values are successfully detected as cycle slips. The only undetected cycle slips are associated with satellite PRN 2 and PRN 11 at stations KELY and REYK. These two stations are located in the high latitude regions at 66.987° and 64.139° latitude, respectively. At KELY station, the satellite PRN 2 has an elevation angle varying from 20° to 41° during GPS time 13:00–16:00 on April 15, 2001. The elevation angle of PRN 11 varies from 23° to 48° during the same period. At REYK station, the elevation angle of PRN 11 changes from 21° to 64°. The combined effects of relatively low satellite elevation angle, high latitudes, and the strong solar flares may result in the inability to detect the cycle slip using the STPIR algorithm in the three cases as shown in Table 3. But this does not affect the cycle slip detection at these epochs because the cycle slips have been detected by the FBMWA algorithm. The STPIR result could still be utilized to determine the magnitude of cycle slips, together with the FBMWA peak values. It should be noted that some STPIR values larger than 0.283 cycles appear in Fig. 7e and f under high ionospheric activities. This will cause difficulty in identifying the cycle slip pair (1, 1) to which the FBMWA algorithm is insensitive. In principle, it is possible that the epochs with the large STPIR peak values may have special cycle slip pair (1, 1). In practice, it is usually deemed very unlikely that all these happen simultaneously. It is relatively safe to consider that the possibility of occurrence of (1, 1) is extremely small (Blewitt 1990).

Column 9 of Table 3 shows the cycle slip repair results using (11a) and (11b). The estimated cycle slip values are quite close to the simulated cycle slip (5, 4) on L 1 and L 2 frequencies. As a result, they can be easily rounded to their nearest integers, which can then be used to correct the cycle slips in the original carrier phase observations.

As stated above, there are some STPIR values larger than 0.283 cycles in Fig. 7e and f. An important reason is that the 30-s sampling rate of observations is not high enough for the STPIR algorithm to detect cycle slips in these special situations. Figure 8 shows the cycle slip detection results using observations of 1-s sampling rate at CHUR and ALGO stations on March 31, 2001 when a severe geomagnetic storm occurred. It can be seen from the right panels of Fig. 8 that all the STPIR values are significantly smaller than 0.283 cycles. As a result, the cycle slips can be easily identified and repaired using the FBMWA and STPIR algorithms. If the CHUR and ALGO station data are processed at an interval of 30 s, similar to Fig. 7e and f, there exist some STPIR values larger than 0.283 cycles. This suggests that the STPIR algorithm performs more reliably with high-rate observations under severe ionospheric conditions.

Fig. 8
figure 8

Cycle slip detection results on March 31, 2001. The horizontal axis is in GPS time. (a) CHUR, (b) ALGO

Full size image

Table 4 gives the window sizes used in the forward and backward filters in the above FBMWA data processing. The window sizes are determined by the noise level of the time-differenced widelane ambiguities.

Table 4 Window sizes used in the FBMWA algorithm
Full size table

Conclusions

A new cycle slip detection and repair approach is proposed for dual-frequency GPS data observed from a single receiver under high ionospheric activity. The approach jointly uses a forward and backward moving window averaging (FBMWA) algorithm and a second-order, time-difference phase ionospheric residual (STPIR) algorithm to determine the cycle slips. The FBMWA can significantly reduce the noise of widelane ambiguities in both forward and backward directions at the epoch in examination, particularly when the measurement noises (primarily from pseudorange) are high. The STPIR algorithm can precisely detect cycle slips with the use of only carrier phase observations but is sensitive to ionospheric disturbances. The integration of the FBMWA and STPIR algorithms allows the cycle slips to be uniquely detected and determined even under high ionospheric activities. The proposed approach has been tested using various GPS datasets under different levels of ionospheric activities. The results indicate that the approach is effective in detection and repair of cycle slips on each frequency.