Principles, methods and applications of cycle slip detection and repair under complex observation conditions

Abstract

With the popularity of global navigation satellite system (GNSS) applications, how to tackle the cycle slips under complex observation conditions is inevitable. Here, the complex observation condition means that one may face the challenges of harsh environment, single-frequency low-cost receiver, or real-time kinematic situation, etc. However, most currently existing cycle slip detection and repair methods are designed for specific scenarios, and little attention has been paid to the unified method, which limits the availability, precision and reliability of cycle slip processing, especially under complex observation conditions. This paper is the first to systematically and comprehensively study the principles, methods and applications of cycle slip detection and repair under complex observation conditions. Firstly, one unified method of cycle slip processing is proposed, which mainly has three aspects. Specifically, the geometry-free (GF), geometry-based (GB), and geometry-fixed (GFix) models are designed for the geometric term; the ionosphere-free, ionosphere-unbiased, and ionosphere-biased models are designed for the ionospheric delay; the observation-domain (OD)-, state-domain (SD)-, and coordinate-domain (CD)-aided approaches are used to assist the cycle slip processing. Secondly, three practical cycle slip processing methods are also proposed based on the above unified method, focusing on three typical complex observation conditions. They are the SD-aided GFix method, OD- and CD-aided GB method, and GF combined GB method. Three experiments were conducted and analyzed in detail to validate the effectiveness of these proposed methods. The results show that the unified method is feasible and superior, and the three new specific methods can detect and repair the small, multiple, and insensitive cycle slips better than the traditional methods under complex observation conditions. Typically, when applying the proposed methods, the success rate of ambiguity resolution can be improved by approximately 39%, and centimeter-level and millimeter-level positioning accuracy can be obtained in RTK and PPP.

1 Introduction

High-precision global navigation satellite systems (GNSS) positioning and navigation technologies such as real-time kinematic positioning (RTK), precise point positioning (PPP), network RTK, and PPP-RTK have been widely used in the mass market such as high-precision navigation, real-time monitoring and autonomous driving (Yang et al. 2020). However, the requirements of data processing are usually high at this time. One of the most critical steps is to resolve the ambiguities quickly and accurately (Xu et al. 2012). Nowadays, the observation conditions of the new related applications are usually complicated such as under the challenges of harsh environment, single-frequency low-cost receiver, and real-time kinematic situation. Therefore, the cycle slips inevitably exist more frequently in GNSS phase observations (Leick et al. 2015; Teunissen and Montenbruck 2017). Any incorrect cycle slip processing may lead to time-consuming re-initialization and even incorrect positioning results.

As usual, a typical cycle slip has two properties: integerness and inheritance. Specifically, a typical cycle slip is an integer in cycles and will affect subsequent observations by the same amount until another cycle slip occurs. Almost the cycle slip detection and repair methods are based on these two properties. The most popular method is called the TurboEdit (Blewitt 1990), which includes the geometry-free (GF) model and Hatch–Melbourne–Wübbena (HMW) combinations (Hatch 1982; Melbourne 1985; Wübbena 1985). The main limitation is that the method needs at least two frequencies, and the performance is affected by the ionospheric delay and the precision of code observations. Limitations on the precision of code signals can be alleviated since new bands and constellations exhibit precision enhancement, such as the Galileo transmitted at the E5a frequency band. Compared with the above easy-to-implement geometry-free method that is based on a satellite-by-satellite basis, the geometry-based (GB) method which involves the coordinate components has better model strength (Banville and Langley 2013; Li et al. 2019b), whereas the GB method cannot work well if there are many cycle slips simultaneously. Also, the ionospheric delays need to be treated carefully. Otherwise, the model will be biased.

Therefore, ionospheric delay is crucial during cycle slip detection and repair. Of course, using the ionosphere-free (IF) model (Chen et al. 2016) is a good approach, whereas it needs two frequencies and mixes the observations from the two frequencies. It is not easy to determine a specific number of cycle slips for each frequency. As a supplement, other methods to deal with the ionospheric delays are proposed, such as ionospheric total electron content rate (Liu 2011), moving window together with differenced phase ionospheric residual (Cai et al. 2013), etc. The above methods are somewhat effective, while the ionospheric delays are not treated rigorously. In more high-precision applications, the ionosphere-unbiased (IU) model can be used. Specifically, the ionospheric delays can be eliminated, modeled, or parameterized (Zhang and Li 2012; Li et al. 2019b), where the precision and reliability of cycle slip detection and repair are improved to a great extent.

Additional methods can be applied further to enhance the performance of cycle slip detection and repair. For instance, the polynomial fitting (de Lacy et al. 2008) or high-order differencing (Hofmann-Wellenhof et al. 2007) is effective. Also, the other types of data, such as Doppler (Lipp and Gu 1994; Carcanague 2012) or inertial navigation system (Lee et al. 2003; Li et al. 2021), can be considered. Similarly, a prior information on receiver position (Li et al. 2019a) is also feasible to alleviate the burden of cycle slip processing. However, the applicability of all these methods is relatively limited, and the accuracy needs to be higher.

Although the above methods are effective to some degree, most are designed for specific scenarios. Little attention has been paid to the unified method of cycle slip detection and repair, especially under complex observation conditions, such as a harsh environment, single-frequency low-cost receiver, and real-time kinematic situation. There are mainly two problems to be solved when dealing with cycle slips. The first one is the non-dispersive error, mainly including the geometric term, and the second one is the dispersive error, mainly referring to the ionospheric delay. Currently, almost all popular algorithms are directly or indirectly based on how to solve these two problems. Therefore, it is highly urgent to establish a unified method to make cycle slip processing more intelligent, ubiquitous, and integrated. In addition, since complex observation conditions are more common than before, the difficulty of cycle slip processing is significantly increased. At this time, the quality of observations is degraded and the residual systematic errors are more serious. Then various types of cycle slips inevitably exist in observations, such as multiple, small, insensitive cycle slips, etc. Unfortunately, although several studies have studied the problem of cycle slip detection and repair under specific complex observation conditions, the availability, precision, and reliability of these methods are often limited. Moreover, the connection, distinction, and intrinsic nature of these methods have not been explored in depth. Therefore, performing adaptive processing of cycle slips with changes in observation conditions and application scenarios is a tricky problem.

In this paper, the principles, methods and applications of cycle slip detection and repair under complex observation conditions are systematically and comprehensively studied for the first time. Firstly, one unified method of cycle slip detection and repair is proposed, where the basic models are deduced for the geometric term and ionospheric delay. Specifically, the GF, GB and geometry-fixed (GFix) models are for the geometric term, and the IF, IU and ionosphere-biased (IB) models are for the ionospheric delay. Theoretically, at least nine combinations can be formed depending on how the geometric term and ionospheric delays are treated. In addition, three types of aided approaches are also given to enhance the performance of cycle slip detection and repair, i.e., the observation-domain (OD), state-domain (SD), and coordinate-domain (CD)-aided approaches. One can propose any existent or new methods of cycle slip processing based on the above three geometry models, three ionospheric models, and three aided approaches. Secondly, focusing on three typical complex observation conditions by fully considering the characteristics and limitations of these complex conditions, three practical cycle slip processing schemes are also proposed according to the unified method. Three experiments were conducted and analyzed in detail to validate the effectiveness of these proposed methods.

2 Principles of cycle slip detection and repair

In this section, the principles of cycle slip detection and repair are studied comprehensively. First, three models for dealing with the geometric term are deduced; second, three models for dealing with the ionospheric delay are discussed; finally, three domains to assist the cycle slip processing are given.

2.1 Three models for dealing with the geometric term

The geometric term is the first error that needs to be considered. In this section, three basic models are given and discussed in detail. Actually, the other non-dispersive errors including the receiver clock offset, satellite clock offset, and tropospheric delay are usually processed together with the geometric term.

2.1.1 Geometry-free model

First, the typical undifferenced and uncombined GNSS observation equations for receiver $r$ and satellite $s$ on frequency $i$ read (Leick et al. 2015; Teunissen and Montenbruck 2017)

$${P}_{r, i}^{s}={\rho }_{r}^{s}+{c\tau }_{r}-{c\tau }^{s}+{\xi }_{r, i}-{\xi }^{s,i}+{I}_{r,i}^{s}+{T}_{r}^{s}+{\varepsilon }_{r,i}^{s}$$

(1)

$${\phi }_{r, i}^{s}={\rho }_{r}^{s}+{c\tau }_{r}-{c\tau }^{s}+{\zeta }_{r, i}-{\zeta }^{s,i}+{\lambda }_{i}{N}_{r,i}^{s}-{I}_{r,i}^{s}+{T}_{r}^{s}+{\epsilon }_{r,i}^{s}$$

(2)

where $P$ and $\phi$ denote the code and phase observations, respectively; $\rho$ denotes the satellite-to-receiver range; $c$ denotes the speed of light in a vacuum; ${\tau }_{r}$ and ${\tau }^{s}$ denote the clock offsets of receiver end and satellite end, respectively; $\xi$ and $\zeta$ denote the hardware delays of code and phase signals, respectively; $\lambda$ and $N$ denote the wavelength and ambiguity, respectively; $I$ and $T$ denote the ionospheric and tropospheric delays, respectively; $\varepsilon$ and $\epsilon$ denote the code and phase observation noise including unmodeled errors (Li et al. 2018), respectively. The other error terms such as phase center offset and variation, phase windup, relativistic effect, solid earth tide, ocean loading, and earth rotation are assumed to be corrected in advance.

In the GF model, the observation equations are parameterized in terms of the satellite-to-receiver ranges. When dealing with cycle slips, a time-differenced strategy is often applied, where the effects of constant or slowly varying parameters are eliminated. The time-differenced GF models of code and phase observations can be formed as

$$d{P}_{r,i}^{s}={d\widetilde{\rho }}_{r}^{s}+{dI}_{r,i}^{s}+d{\varepsilon }_{r,i}^{s}$$

(3)

$$d{\phi }_{r,i}^{s}=d{\widetilde{\rho }}_{r}^{s}+{\lambda }_{i}{Z}_{r,i}^{s}-d{I}_{r,i}^{s}+d{\epsilon }_{r,i}^{s}$$

(4)

with the equivalent satellite-to-receiver range ${d\widetilde{\rho }}_{r}^{s}=d{\rho }_{r}^{s}+{cd\tau }_{r}-{cd\tau }^{s}+{dT}_{r}^{s}$, where $d*$ denotes the operator of time differencing between adjacent epochs and $Z$ denotes the cycle slip which may exist. The GF model is linear, whereas it is rank deficient. In order to solve the problem of rank deficit, the minimum constraint datum could be applied. For instance, if there are two frequencies, the time-differenced phase-only GF model can be deduced as

$${d\phi }_{r,i}^{s}-{d\phi }_{r,j}^{s}={\lambda }_{i}{Z}_{r,i}^{s}-{\lambda }_{j}{Z}_{r,j}^{s}-\left(1-{\mu }_{j}\right){dI}_{r,i}^{s}+{d\epsilon }_{r,i}^{s}-d{\epsilon }_{r,j}^{s}$$

(5)

Then the compact form reads

$${\rm E}\left[d{\phi }_{\mathrm{GF}}\right]={\lambda }_{i}{Z}_{r,i}^{s}-{\lambda }_{j}{Z}_{r,j}^{s}-\left(1-{\mu }_{j}\right){dI}_{r,i}^{s}$$

(6)

with the ionospheric delay coefficient ${\mu }_{j}={\lambda }_{j}^{2}/{\lambda }_{i}^{2}$, where ${\rm E}\left[*\right]$ denotes the operator of expectation. Apparently, (6) is not sensitive to the equidistant cycle slips of two frequencies and cannot work well when the ionosphere changes drastically, or the sampling interval becomes larger. It is worth noting that if there is only one frequency, the GF model of code and phase combination can also be used, whereas the model error is enlarged due to the introduced code signal. In addition, the other non-dispersive errors can also be parameterized together with the geometric error, especially in the case of a multi-frequency situation. This approach may also be called the geometry-weighted model (Banville and Langley 2013; Zhang and Li 2016; Xiao et al. 2018). The biggest advantage of the GF model is that it is convenient, whereas it is easily influenced by external observation conditions and usually has some insensitive cycle slips.

2.1.2 Geometry-based model

In the GB model, the coordinated components are parameterized in the observation equations (Banville and Langley 2009; Li et al. 2019b). According to (1) and (2), the time-differenced GB models of code and phase observations read

$${dP}_{r,i}^{s}={\varvec{A}}{\varvec{x}}+{cd\tau }_{r}-{cd\tau }^{s}+d{I}_{r,i}^{s}+d{T}_{r}^{s}+d{\varepsilon }_{r,i}^{s}$$

(7)

$${d\phi }_{r,i}^{s}={\varvec{A}}{\varvec{x}}+{cd\tau }_{r}-{cd\tau }^{s}+{\lambda }_{i}{Z}_{r,i}^{s}-d{I}_{r,i}^{s}+d{T}_{r}^{s}+d{\epsilon }_{r,i}^{s}$$

(8)

with ${\varvec{A}}{\varvec{x}}={\varvec{A}}\left(t\right){\varvec{x}}\left(t\right)-{\varvec{A}}\left(t-1\right){\varvec{x}}\left(t-1\right)$ $\left(t>1\right)$, where ${\varvec{A}}\left(t\right)$ denotes a design matrix of station coordinates ${\varvec{x}}\left(t\right)={\left[x\left(t\right),y\left(t\right),z\left(t\right)\right]}^{\mathrm{T}}$ at epoch $t$, and ${\varvec{A}}\left(t-1\right)$ denotes a design matrix of station coordinates ${\varvec{x}}\left(t-1\right)={\left[x\left(t-1\right),y\left(t-1\right),z\left(t-1\right)\right]}^{\mathrm{T}}$ at epoch $t-1$. Unlike the GF model, the GB model is nonlinear and can connect the relationship between different satellites. Considering the triple-differenced observation equation is the mostly used for the cycle slip processing, the GB models of code and phase observations then can be deduced as follows

$${\Delta \nabla dP}_{qr,i}^{us}=\Delta \nabla {\varvec{A}}{\varvec{x}}+\Delta \nabla d{I}_{qr,i}^{us}+\Delta \nabla d{T}_{qr}^{us}+\Delta \nabla d{\varepsilon }_{qr,i}^{us}$$

(9)

$${\Delta \nabla d\phi }_{qr,i}^{us}=\Delta \nabla {\varvec{A}}{\varvec{x}}+{\lambda }_{i}{\Delta \nabla Z}_{qr,i}^{us}-\Delta \nabla d{I}_{qr,i}^{us}+{\Delta \nabla dT}_{qr}^{us}+\Delta \nabla d{\epsilon }_{qr,i}^{us}$$

(10)

where the superscript $u$ and subscript $q$ denote the reference satellite and reference station, respectively; $\Delta$ and $\nabla$ denote the operators of between-receiver differencing and between-satellite differencing, respectively. For the geometric term, $\Delta \nabla {\varvec{A}}{\varvec{x}}$ can be formulated as

$$\Delta \nabla {\varvec{A}}{\varvec{x}}=\Delta \nabla {\varvec{A}}\left(t\right)\Delta \nabla {\varvec{x}}\left(t\right)-\Delta \nabla {\varvec{A}}\left(t-1\right)\Delta \nabla {\varvec{x}}\left(t-1\right)$$

(11)

where $\Delta \nabla {\varvec{A}}\left(t\right)$ denotes the double-differenced design matrix of baseline components $\Delta \nabla {\varvec{x}}\left(t\right)$ at epoch $t$, and $\Delta \nabla {\varvec{A}}\left(t-1\right)$ denotes the double-differenced design matrix of baseline components $\Delta \nabla {\varvec{x}}\left(t-1\right)$ at epoch $t-1.$ To estimate the unknown parameters better, $\Delta \nabla {\varvec{A}}{\varvec{x}}$ can be rewritten as

$$ \begin{aligned} \Delta \nabla {\varvec{A}}{\varvec{x}} & =\frac{\Delta \nabla {\varvec{A}}\left(t\right)+\Delta \nabla {\varvec{A}}\left(t-1\right)}{2}\left[\Delta \nabla {\varvec{x}}\left(t\right)-\Delta \nabla {\varvec{x}}\left(t-1\right)\right]\\ &\quad +\frac{\Delta \nabla {\varvec{A}}\left(t\right)-\Delta \nabla {\varvec{A}}\left(t-1\right)}{2}\left[\Delta \nabla {\varvec{x}}\left(t\right)+\Delta \nabla {\varvec{x}}\left(t-1\right)\right]\end{aligned} $$

(12)

If $\Delta \nabla {\varvec{A}}\left(t\right)$ and $\Delta \nabla {\varvec{A}}\left(t-1\right)$ are almost the same within a certain period, $\Delta \nabla {\varvec{A}}\left(t\right)-\Delta \nabla {\varvec{A}}\left(t-1\right)$ is equal to 0. Then $\Delta \nabla {\varvec{A}}{\varvec{x}}$ can be given with a compact form

$$\Delta \nabla {\varvec{A}}{\varvec{x}}=\Delta \nabla {\varvec{A}}\left(t\right)\left[\Delta \nabla {\varvec{x}}\left(t\right)-\Delta \nabla {\varvec{x}}\left(t-1\right)\right]$$

(13)

Hence, the magnitude of $\frac{\Delta \nabla {\varvec{A}}\left(t\right)-\Delta \nabla {\varvec{A}}\left(t-1\right)}{2}[\Delta \nabla {\varvec{x}}\left(t\right)+\Delta \nabla {\varvec{x}}\left(t-1\right)]$ needs to be studied.

Since the $\Delta \nabla {\varvec{A}}\left(t\right)$ based on the differenced observations is related to the baseline length, the ${\varvec{A}}\left(t\right)$ with the equal amplitude based on the undifferenced observations is studied here. We will focus on the magnitudes of $\frac{{\varvec{A}}\left(t\right)-{\varvec{A}}\left(t-1\right)}{2}\left[{\varvec{x}}\left(t\right)+{\varvec{x}}\left(t-1\right)\right]$ and discuss whether and how we can ignore this term. For each satellite, the bias caused by the $\frac{{\varvec{A}}\left(t\right)-{\varvec{A}}\left(t-1\right)}{2}\left[{\varvec{x}}\left(t\right)+{\varvec{x}}\left(t-1\right)\right]$ equals to $\frac{1}{2}\left({A}_{x}x+{A}_{y}y+{A}_{z}z\right)$, where $\left[{A}_{x},{A}_{y},{A}_{z}\right]$ is the design matrix in terms of ${\varvec{A}}\left(t\right)-{\varvec{A}}\left(t-1\right)$ of each satellite, and ${\left[x,y,z\right]}^{\mathrm{T}}$ is the coordinate components in terms of ${\varvec{x}}\left(t\right)+{\varvec{x}}\left(t-1\right)$. Assuming $x=y=z=b$ with $b$ denoting the bias of each direction, we have $\frac{b}{2}\left({A}_{x}+{A}_{y}+{A}_{z}\right)$. Hence, the key question is how large is the $\left|{A}_{x}\right|+\left|{A}_{y}\right|+\left|{A}_{z}\right|$ as usual. Figures 1 and 2 illustrate the amplitudes of $\left|{A}_{x}\right|+\left|{A}_{y}\right|+\left|{A}_{z}\right|$ for BeiDou Navigation Satellite System (BDS) with a sampling interval of 1 s and 30 s, respectively. In each panel, each color denotes one satellite, where the Geostationary Earth Orbit (GEO), Inclined Geosynchronous Satellite Orbit (IGSO), and Medium Earth Orbit (MEO) satellites are all included. It can be seen that the amplitudes of GEO satellites are smaller than any other two satellite types, and the amplitudes of MEO satellites are the largest due to their relatively low orbital altitudes. That is, the amplitudes of $\left|{A}_{x}\right|+\left|{A}_{y}\right|+\left|{A}_{z}\right|$ are usually smaller than the $2.4\times {10}^{-4}$ for 1-s sampling interval, and $7.0\times {10}^{-3}$ for 30-s sampling interval, respectively. when the critical threshold is the widely used fixed-fraction strategy (i.e., 0.2 cycles) (Li et al. 2014; Zhang et al. 2020), the maximum allowable error is 4 cm in the case of 20-cm wavelength. Therefore, the biases $b=333.3$ m and $b=11.4$ m are allowed in 1-s and 30-s sampling intervals, respectively, which can meet the requirements of most scenarios. That is, the (13) can indeed be used in real applications especially when the sampling interval is 1 s. Hence, the GB model can process small cycle slips in theory, although it is a little complicated.

Fig. 1

24-h $\left|{A}_{x}\right|+\left|{A}_{y}\right|+\left|{A}_{z}\right|$ for BDS GEO (left), IGSO (middle), and MEO (right) satellites with a sampling interval of 1 s. Each color denotes one satellite

Fig. 2

24-h $\left|{A}_{x}\right|+\left|{A}_{y}\right|+\left|{A}_{z}\right|$ for BDS GEO (left), IGSO (middle), and MEO (right) satellites with a sampling interval of 30 s. Each color denotes one satellite

2.1.3 Geometry-fixed model

The third model for dealing with the geometric term is the GFix model, which estimates the satellite-to-receiver ranges in advance and treats them as known in the observation models (Zhang et al. 2021). The promising application of the GFix model is in a permanent station. Although this poses certain limitations, it is still an important model in theory and practice, especially when the receiver is a low-cost one or the observation environment is not ideal enough. According to (1) and (2), the time-differenced GFix models of code and phase observations read

$$d{P}_{r,i}^{s}-{d\widehat{\rho }}_{r}^{s}={cd\tau }_{r}-{cd\tau }^{s}+d{I}_{r,i}^{s}+d{T}_{r}^{s}+d{\varepsilon }_{r,i}^{s}$$

(14)

$$d{\phi }_{r,i}^{s}-d{\widehat{\rho }}_{r}^{s}={cd\tau }_{r}-{cd\tau }^{s}+{\lambda }_{i}{Z}_{r,i}^{s}-{dI}_{r,i}^{s}+{dT}_{r}^{s}+d{\epsilon }_{r,i}^{s}$$

(15)

where ${\widehat{\rho }}_{r}^{s}$ denotes the estimate of the satellite-to-receiver range. It can be seen that the GFix model is also linear and the problem of the rank deficit is alleviated compared with the GF model. For instance, if the between-receiver and between-satellite operation is conducted on (14) and (15), we have

$${\Delta \nabla dP}_{qr,i}^{us}-{\Delta \nabla d\widehat{\rho }}_{qr}^{us}=\Delta \nabla d{I}_{qr,i}^{us}+\Delta \nabla {dT}_{qr}^{us}+\Delta \nabla d{\varepsilon }_{qr,i}^{us}$$

(16)

$${\Delta \nabla d\phi }_{qr,i}^{us}-{\Delta \nabla d\widehat{\rho }}_{qr}^{us}={\lambda }_{i}{\Delta \nabla Z}_{qr,i}^{us}-\Delta \nabla {dI}_{qr,i}^{us}+{\Delta \nabla dT}_{qr}^{us}+\Delta \nabla d{\epsilon }_{qr,i}^{us}$$

(17)

The most critical question in the GFix model is whether this type of model can be used since the performance of the GFix model is highly dependent on the accuracy of the estimated satellite-to-receiver ranges. The geometric term ${\Delta \nabla d\rho }_{qr,i}^{us}$ are affected by both the coordinates of orbit and station. Since the precise coordinates of the station are usually known in the GFix model with the centimeter or even millimeter level, the factors from the stations are not considered here. In a standalone mode, the broadcast ephemerides will lead to signal-in-space ranging errors (SISRE), of which the values are nearly 0.6 to 1.9 m. Also, the precise ephemeris uncertainties of the SISRE are expected to be approximately 5 to 10 cm (Montenbruck et al. 2015). Hence, the cycle slip processing with the GFix model based on a standalone receiver needs to be treated carefully.

Since the orbit errors can be mitigated in a relative mode, the cycle slip detection and repair with the GFix model are more promising in theory. The ensuing question is how long the baseline can the GFix model still be used. The orbit accuracies in along-track, cross-track, and radial directions of broadcast ephemeris and precise ephemeris are approximately 100.0 cm and 2.5 cm, respectively (Montenbruck et al. 2017). Then the three-dimensional root mean squared (RMS) values of broadcast ephemeris and precise ephemeris reach approximately 173.2 cm and 4.3 cm, respectively. The relationship between the RMS of between-receiver single-differenced geometric error ${\sigma }_{\Delta \rho }$ and the RMS of orbit error ${\sigma }_{o}$ is shown below (Han 1997; Chen et al. 2016)

$${\sigma }_{\Delta \rho }=\frac{L}{\rho }{\sigma }_{o}$$

(18)

where $L$ denotes the baseline length. Since the satellite-to-receiver range for Medium Earth Orbit (MEO) satellite is approximately 20,000 km, the ${\sigma }_{\Delta \rho }$ per kilometer under the conditions of broadcast ephemeris and precise ephemeris is approximately 0.0866 mm or less. According to the error propagation law, for a triple-differenced situation, the corresponding ${\sigma }_{\nabla \Delta \rho \left(t\right)}$ per kilometer will reach approximately 0.1732 mm. If the $3\sigma$ criterion is applied, the impacts of orbit error per kilometer can be up to approximately 0.5196 mm. Since the wavelength of the phase signal is approximately 20 cm when the maximum allowable error is 4 cm as aforementioned. Theoretically, the GFix model can be used as long as the baseline length is less than 77 km, which can meet the requirements of most RTK baseline lengths in real applications. If the estimates of station coordinates are precisely enough, the GFix model can be applied in a relative mode where the baseline length does not exceed 77 km, and the threshold of baseline length can be longer if the precise ephemeris is used. In conclusion, although the availability of the GFix model is relatively limited, it is a critical supplement especially under complex observation conditions.

2.2 Three models for dealing with the ionospheric delay

The ionospheric delay is another crucial issue to be addressed since it is a dispersive error. In this section, also three basic models are comprehensively studied. Specifically, they are the IF, IU, and IB models, respectively.

2.2.1 Ionosphere-free model

The ionospheric delays are always existent, and hence they need to be processed carefully. The first widely used model is the IF model. That is, the ionospheric delays are mitigated by a linear combination, in which the first-order ionospheric delays are eliminated. The relationship of ionospheric delays between two frequencies $i$ and $j$ satisfies

$${I}_{r,j}^{s}={\mu }_{j}{I}_{r,i}^{s}$$

(19)

The most popular IF model in the cycle slip processing is a so-called HMW combination, which is composed of a wide-lane phase combination and a narrow-lane code combination as shown below

$$\begin{aligned} \text{HMW} & =\frac{1}{{f}_{i}-{f}_{j}}\left({f}_{i}{\phi }_{i}-{f}_{j}{\phi }_{j}\right)-\frac{1}{{f}_{i}+{f}_{j}}\left({f}_{i}{P}_{i}+{f}_{j}{P}_{j}\right)\\ & ={\lambda }_{\mathrm{HMW}}{N}_{\mathrm{HMW}}+{\epsilon }_{{\phi }_{\mathrm{HMW}}}\end{aligned} $$

(20)

where $f$ denotes the frequency. The HMW combination is actually a GF plus IF model. The wavelength of HMW combination satisfies ${\lambda }_{\mathrm{HMW}}=c/\left({f}_{i}-{f}_{j}\right)$, of which the value can reach approximately 86.2 cm in the case of global positioning system (GPS) L1 and L2. The ambiguity of HMW combination reads ${N}_{\mathrm{HMW}}={N}_{i}-{N}_{j}$. The cycle slips can be detected according to the behaviors of ${N}_{\mathrm{HMW}}$. When ignoring the correlations among the observations and considering the same standard deviation (STD) for the observations on the two frequencies, the STD of HMW combination can be computed according to the error propagation law when ignoring the correlations among the observations

$${\sigma }_{\mathrm{HMW}}^{2}=\frac{{f}_{i}^{2}+{f}_{j}^{2}}{{\left({f}_{i}-{f}_{j}\right)}^{2}}{\sigma }_{\phi }^{2}+\frac{{f}_{i}^{2}+{f}_{j}^{2}}{{\left({f}_{i}+{f}_{j}\right)}^{2}}{\sigma }_{P}^{2}$$

(21)

where ${\sigma }_{\mathrm{HMW}}$, ${\sigma }_{\phi }$ and ${\sigma }_{P}$ denote the STDs of HMW, phase, and code observations, respectively. If the two frequencies are the GPS L1 and L2, and the ${\sigma }_{\phi }$ and ${\sigma }_{P}$ are set to 3.0 mm and 0.2 m, respectively, the ${\sigma }_{\mathrm{HMW}}$ is equal to 0.1435 m. It is acceptable to detect the small cycle slips in theory.

However, the performance of the HMW combination will be affected under complex observation conditions since the code observations will be easily polluted. In addition, the method is insensitive to equivalent cycle slips of two frequencies and is impossible to tell which frequency the cycle slip comes from. The IF model is immune to the effects of the ionospheric delays, but at least two types of observations are needed.

2.2.2 Ionosphere-unbiased model

In the IU model, the ionospheric delays have been successfully corrected. For instance, the ionosphere-fixed, ionosphere-weighted, and ionosphere-float models can all be used (Odijk 2000). Since the ionosphere-weighted model is the most general one, it is emphasized here. First, we have the ionospheric constraints, of which a prior expectation and dispersion are as follows

$${\rm E}\left({\varvec{\iota}}\right)={{\varvec{\iota}}}_{0}$$

(22)

$$D\left({\varvec{\iota}}\right)={\sigma }_{{{\varvec{\iota}}}_{0}}^{2}{{\varvec{Q}}}_{0}$$

(23)

where ${{\varvec{\iota}}}_{0}$ denotes a prior expectation of ionospheric delay vector of raw observations on frequency $i$; ${\sigma }_{{{\varvec{\iota}}}_{0}}^{2}$ and ${{\varvec{Q}}}_{0}$ denote the corresponding a prior variance factor and cofactor matrix, respectively. The ionospheric constraints are actually acted as pseudo-observations. If it is a time-differenced GB model where the satellite clock offset and tropospheric delay have been corrected, the ionosphere-weighted model reads

$$ \begin{aligned} \text{E}\left[ {\begin{array}{*{20}c} {d{\varvec{P}}} \\ {d{\varvec{\phi}} } \\ {d{\varvec{\iota}}_{\mathbf{0}} } \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} {{\varvec{e}}_{m} \otimes {\varvec{G}}_{t} } & { - {\varvec{e}}_{m} \otimes {\varvec{G}}_{t - 1} } & {{\varvec{e}}_{mn} } & {\mathbf{0}} & {{\varvec{\mu}}_{m} \otimes {\varvec{I}}_{n} } \\ {{\varvec{e}}_{m} \otimes {\varvec{G}}_{t} } & { - {\varvec{e}}_{m} \otimes {\varvec{G}}_{t - 1} } & {{\varvec{e}}_{mn} } & {{\varvec{\lambda}}_{m} \otimes {\varvec{I}}_{n} } & { - {\varvec{\mu}}_{m} \otimes {\varvec{I}}_{n} } \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{I}}_{n} } \\ \end{array} } \right] \\ &\qquad \left[ {\begin{array}{*{20}c} {{\varvec{x}}\left( t \right)} \\ {{\varvec{x}}\left( {t - 1} \right)} \\ {cd\tau_{r} } \\ {\begin{array}{*{20}c} {\varvec{Z}} \\ {d{\varvec{\iota}}} \\ \end{array} } \\ \end{array} } \right] \end{aligned}$$

(24)

with $d{\varvec{P}}={\left[{d{\varvec{P}}}_{1}^{\mathrm{T}},\ldots ,{d{\varvec{P}}}_{m}^{\mathrm{T}}\right]}^{\mathrm{T}}$, $d{\varvec{\phi}}={\left[{d{\varvec{\phi}}}_{1}^{\mathrm{T}},\ldots ,{d{\varvec{\phi}}}_{m}^{\mathrm{T}}\right]}^{\mathrm{T}}$, ${d{\varvec{P}}}_{m}={\left[{dP}_{r, m}^{1},\ldots ,{dP}_{r, m}^{n}\right]}^{\mathrm{T}}$, $d{{\varvec{\phi}}}_{m}=[{d\phi }_{r, m}^{1},\ldots ,{d\phi }_{r,m}^{n}]^{\mathrm{T}}$, ${{\varvec{\lambda}}}_{m}=\mathrm{diag}\left({\lambda }_{1},\ldots ,{\lambda }_{m}\right)$, ${{\varvec{\mu}}}_{m}={\left[{\mu }_{1},\ldots ,{\mu }_{m}\right]}^{\mathrm{T}}$, where $m$ and $n$ denote the frequency and satellite numbers, respectively; ${{\varvec{e}}}_{m}$ and ${{\varvec{I}}}_{n}$ denote the $m$-column vector with one elements and identity matrix of order $n$, respectively; ${{\varvec{G}}}_{t}$ and ${{\varvec{G}}}_{t-1}$ denotes the design matrix of coordinate ${{\varvec{x}}}_{t}$ and ${{\varvec{x}}}_{t-1}$ on one frequency of $n$ satellites; $\otimes$ denotes the operator of Kronecker product of two matrices; $\mathrm{diag}$ denotes the operator of diagonal concatenation of elements. By combining the variance–covariance matrices of time-differenced observations and ionospheric delays, the IU model in (24) can be resolved with the generalized least squares (LS).

In fact, the ionosphere-fixed and ionosphere-float model are just two extreme cases of the ionosphere-weighted model. That is, the values of ${\sigma }_{{{\varvec{\iota}}}_{0}}^{2}$ in the ionosphere-fixed and ionosphere-float are 0 and $\infty$, respectively. Specifically, when the values of ${\sigma }_{{{\varvec{\iota}}}_{0}}^{2}\to 0$, ${{\varvec{\iota}}}_{0}$ is rather precise, and the observation model reads

$$\text{E}\left[\begin{array}{l}d{\varvec{P}}-{{\varvec{\mu}}}_{f}\otimes d{{\varvec{\iota}}}_{0}\\ d{\varvec{\phi}}+{{\varvec{\mu}}}_{f}\otimes d{{\varvec{\iota}}}_{0}\end{array}\right]=\left[\begin{array}{cccc}{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t}& -{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t-1}& {{\varvec{e}}}_{mn}& \mathbf{0}\\ {{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t}& -{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t-1}& {{\varvec{e}}}_{mn}& {{\varvec{\lambda}}}_{m}\otimes {{\varvec{I}}}_{n}\end{array}\right]\left[\begin{array}{l}{\varvec{x}}\left(t\right)\\ {\varvec{x}}\left(t-1\right)\\ {cd\tau }_{r}\\ \begin{array}{l}{\varvec{Z}}\end{array}\end{array}\right]$$

(25)

(25) is the ionosphere-fixed model. On the contrary, when the values of ${\sigma }_{{{\varvec{\iota}}}_{0}}^{2}\to \infty$, ${{\varvec{\iota}}}_{0}$ becomes rather untrustworthy, then the observation model reads

$$ \begin{aligned} \text{E}\left[\begin{array}{l}d{\varvec{P}}\\ d{\varvec{\phi}}\end{array}\right] & =\left[\begin{array}{ccccc}{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t}& -{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t-1}& {{\varvec{e}}}_{mn}& \mathbf{0}& {{\varvec{\mu}}}_{m}\otimes {{\varvec{I}}}_{n}\\ {{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t}& -{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t-1}& {{\varvec{e}}}_{mn}& {{\varvec{\lambda}}}_{m}\otimes {{\varvec{I}}}_{n}& -{{\varvec{\mu}}}_{m}\otimes {{\varvec{I}}}_{n}\end{array}\right]\\ &\qquad \left[\begin{array}{l}{\varvec{x}}\left(t\right)\\ {\varvec{x}}\left(t-1\right)\\ {cd\tau }_{r}\\ \begin{array}{l}{\varvec{Z}}\\ d{\varvec{\iota}}\end{array}\end{array}\right] \end{aligned}$$

(26)

(26) is the ionosphere-float model. The ionosphere-weighted, ionosphere-fixed, and ionosphere-float models can all be used as the IU model, where the choice mainly depends on the accuracy of a prior information of ionospheric delay. Hence, the theory of the IU model is rigorous, whereas the computational requirements are relatively high.

2.2.3 Ionosphere-biased model

If the ionospheric delays are directly ignored or just corrected by external ionospheric products, the strategy refers to the ionosphere-ignored or ionosphere-corrected model (Zhang et al. 2021). By using this way, since there may exist residual ionospheric delays during cycle slip detection and repair, it can be called the IB model. Apparently, this approach is easy to implement although the precision and reliability are not high enough. It is well known that the IU model should be used if the ionospheric delays are sufficiently large. However, the uncertainty is enlarged in the IU model compared with the IB model. Therefore, it is necessary to know when the IB model can be used during the cycle slip detection and repair.

Without loss of generality, the ionosphere-float model is acted as the IU model, then the ionosphere-ignored model is served as the IB model. According to the IU model (26), the compact form is given as

$${\varvec{L}}={\varvec{B}}{\varvec{X}}+{\varvec{U}}{\varvec{\iota}}+{\varvec{E}}$$

(27)

where ${\varvec{E}}$ denotes the observation noise vector of $d{\varvec{P}}$ and $d{\varvec{\phi}}$. Accordingly, the observation model of the IB model can be formed as

$$\text{E}\left[\begin{array}{l}d{\varvec{P}}\\ d{\varvec{\phi}}\end{array}\right]=\left[\begin{array}{cccc}{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t}& -{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t-1}& {{\varvec{e}}}_{mn}& \mathbf{0}\\ {{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t}& -{{\varvec{e}}}_{m}\otimes {{\varvec{G}}}_{t-1}& {{\varvec{e}}}_{mn}& {{\varvec{\lambda}}}_{m}\otimes {{\varvec{I}}}_{n}\end{array}\right]\left[\begin{array}{l}{\varvec{x}}\left(t\right)\\ {\varvec{x}}\left(t-1\right)\\ {cd\tau }_{r}\\ \begin{array}{l}{\varvec{Z}}\end{array}\end{array}\right]$$

(28)

The corresponding compact form reads

$${\varvec{L}}={\varvec{B}}{\varvec{X}}+{\varvec{E}}$$

(29)

In the IU model, the covariance matrix of ${\varvec{X}}$ follows

$$ \varvec{Q}_{{\varvec{\hat{X}\hat{X}}}}^{{\left\langle u \right\rangle }} = \varvec{N} + \varvec{NB}^{{\text{T}}} \varvec{Q}^{{ - 1}} \varvec{UQ}_{{\varvec{\hat{\iota }\hat{\iota }}}} \varvec{U}^{{\text{T}}} \varvec{Q}^{{ - 1}} \varvec{BN} $$

(30)

with ${{\varvec{N}}=\left({{\varvec{B}}}^{\mathrm{T}}{{\varvec{Q}}}^{-1}{\varvec{B}}\right)}^{-1}$, where ${\varvec{Q}}$ denotes the covariance matrix of ${\varvec{L}}$. The covariance matrix of ${\varvec{X}}$ in the IB model is ${{\varvec{Q}}}_{\widehat{{\varvec{X}}}\widehat{{\varvec{X}}}}^{\langle b\rangle }={\varvec{N}}$. It can be found that the uncertainty of ${\varvec{X}}$ is indeed enlarged in the IU model. However, the IB model will introduce a bias, which can be deduced as

$$ \varvec{b}_{{\varvec{\hat{X}}}} = \varvec{NB}^{{\text{T}}} \varvec{Q}^{{ - 1}} \varvec{U\hat{\iota }} $$

(31)

The mean squared error (MSE) of the ionospheric delays then can be obtained (Li et al. 2017; Teunissen and Khodabandeh 2021)

$$ {\text{MSE}} = \varvec{Q}_{{\varvec{\hat{X}\hat{X}}}}^{{\left\langle b \right\rangle }} + \varvec{b}_{{\varvec{\hat{X}}}} \varvec{b}_{{\varvec{\hat{X}}}}^{{\text{T}}} = \varvec{N} + \varvec{NB}^{{\text{T}}} \varvec{Q}^{{ - 1}} \varvec{U\hat{\iota }\hat{\iota }}^{{\text{T}}} \varvec{U}^{{\text{T}}} \varvec{Q}^{{ - 1}} \varvec{BN} $$

(32)

The difference between the covariance matrix of ${\varvec{X}}$ in the IU model and the MSE in the IB model satisfies

$$ \varvec{\Gamma } = \varvec{Q}_{{\varvec{\hat{\iota }\hat{\iota }}}} - \varvec{\hat{\iota }\hat{\iota }}^{{\text{T}}} $$

(33)

Taking the trace to (33) $\text{trace}\left(\varvec{\Gamma }\right)$, if ${\varvec{\Gamma }}_{kk}>0$ with $k$ denoting the row and column number of the matrix $\varvec{\Gamma }$, thus indicating that the IB model is better than the IU model. Otherwise, the IU model is more appropriate when dealing with the cycle slips. Assuming the precision of the ionospheric parameters is approximately 3 to 5 cm (Shi et al. 2012; Wang et al. 2019), there is not much need to use the IU model if the ionospheric delays to be estimated are smaller than 3 to 5 cm. In conclusion, although the precision of the IB model is limited, it still can be used if the ionospheric delays are not significant enough.

2.3 Three domains to assist the cycle slip processing

This section gives three different types of basic approaches mainly based on the internal data information assistance and external carrier motion constraint. Specifically, they are the OD-, SD-, and CD-aided approaches.

2.3.1 Observation-domain-aided approach

The first aided approach is based on the observation domain. The reason is that there is a specific law when the observations change over time. For instance, the method of polynomial fitting can be used to detect the cycle slips, where the undifferenced, single-differenced, and double-differenced observations can all be adopted. By comparing predicted phase observations with polynomial fitting, the existence of cycle slips in real phase observations can be found. For a given epoch window $w$ and the order of polynomial $p$, the observation equation can be formed as follows

$${\varvec{l}}=\varvec{H}{\varvec{\theta}}+{\varvec{\delta}}$$

(34)

with ${\varvec{l}}={\left[{\phi }_{1},{\phi }_{2},\ldots ,{\phi }_{w}\right]}^{\mathrm{T}}$, ${\varvec{\theta}}={\left[{\theta }_{1},{\theta }_{2},\ldots ,{\theta }_{p+1}\right]}^{\mathrm{T}}$, ${\varvec{\delta}}={\left[{\delta }_{1},{\delta }_{2},\ldots ,{\delta }_{w}\right]}^{\mathrm{T}}$, and

$$\varvec{H}=\left[\begin{array}{lllll}1& \left({t}_{1}-{t}_{0}\right)& {\left({t}_{1}-{t}_{0}\right)}^{2}& \cdots & {\left({t}_{1}-{t}_{0}\right)}^{p}\\ 1& \left({t}_{2}-{t}_{0}\right)& {\left({t}_{2}-{t}_{0}\right)}^{2}& \cdots & {\left({t}_{2}-{t}_{0}\right)}^{p}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1& \left({t}_{w}-{t}_{0}\right)& {\left({t}_{w}-{t}_{0}\right)}^{2}& \cdots & {\left({t}_{w}-{t}_{0}\right)}^{p}\end{array}\right]$$

where ${\varvec{\theta}}$ denotes the fitting coefficient vector; ${t}_{w}$ denotes the epoch number compared with the starting epoch ${t}_{0}$. The fitting coefficients can be estimated by the LS criterion

$$\widehat{{\varvec{\theta}}}={\left({\varvec{H}}^{\mathrm{T}}\varvec{H}\right)}^{-1}{\varvec{H}}^{\mathrm{T}}{\varvec{l}}$$

(35)

Based on the fitted residuals ${\varvec{v}}=\varvec{H}\widehat{{\varvec{\theta}}}-{\varvec{l}}$, the STD of unit weight reads

$$\sigma =\sqrt{\frac{{{\varvec{v}}}^{T}{\varvec{v}}}{w-\left(p+1\right)}}$$

(36)

The STD of unit weight usually can be used as the threshold such as $3\sigma$ or larger assuming the GNSS observations are normally distributed.

The orders of polynomial fitting are usually set to 2 or 5 according to the derivative of the satellite-to-receiver range concerning time. The between-epoch high-order differencing is another popular method, whereas it cannot be used in real time. The biggest drawback of this approach is that it usually cannot detect continuous and small cycle slips. It is worth noting that data from other sensors, such as Doppler data may also be adopted (Zhao et al. 2020).

2.3.2 State-domain-aided approach

The properties of integerness and inheritance can be used as a state-domain aid. For instance, the float cycle slips can be fixed to integers according to the integer constraint. If the triple-differenced model is applied, in the case of a short baseline, we have

$${\Delta \nabla dP}_{qr,i}^{us}={\Delta \nabla d\rho }_{qr,i}^{us}+\Delta \nabla {d\varepsilon }_{qr,i}^{us}$$

(37)

$${\Delta \nabla d\phi }_{qr,i}^{us}={\Delta \nabla d\rho }_{qr,i}^{us}+{\lambda }_{i}{\Delta \nabla Z}_{qr,i}^{us}+\Delta \nabla d{\epsilon }_{qr,i}^{us}$$

(38)

If there exist cycle slips in one or several triple-differenced observations, the cycle slips can be detected preliminary according to residuals or the float cycle slips. It is worth noting that the (37) and (38) are prone to be ill-conditioned. Hence, to avoid the potential problem to a great extent, the rounding, bootstrapping, or LAMBDA (Teunissen 1995) strategies can all be adopted to determine whether and how many cycle slips happen. The estimated integer cycle slips can be used to recover the corresponding observations. It is worth noting that the rounding method may encounter type I error of false alarm and type II error of wrong detection. Hence, one can employ the LAMBDA method, where the correlations among cycle slips are fully taken into account.

In addition, in HMW combination, according to the inheritance constraint, one judging criterion is often added to check whether the cycle slips are indeed existent at the epoch $k$

$$\left|{N}_{\mathrm{HMW},k+1}-{N}_{\mathrm{HMW},k}\right|<1$$

(39)

where ${N}_{\mathrm{HMW},k+1}$ and ${N}_{\mathrm{HMW},k}$ denote the ambiguity of HMW combination at the epoch $k+1$ and $k$, respectively. Moreover, when combing the HMW and GF combinations of two frequencies (i.e., the TurboEdit method), the property of integer can be applied

$$\left\{\begin{array}{l}{\widehat{Z}}_{\mathrm{HMW}}={Z}_{i}-{Z}_{j}\\ {Z}_{\mathrm{GF}}={\lambda }_{i}{Z}_{i}-{\lambda }_{j}{Z}_{j}\end{array}\right.$$

(40)

where ${\widehat{Z}}_{\mathrm{HMW}}$ and ${Z}_{\mathrm{GF}}$ are the cycle slips computed by the HMW and GF combinations, respectively. The ${\widehat{Z}}_{\mathrm{HMW}}$ is an integer and can be fixed by rounding in advance, then the specific cycle slips can be estimated as follows

$$\left\{\begin{array}{l}{Z}_{i}=\left({Z}_{\mathrm{GF}}-{\widehat{Z}}_{\mathrm{HMW}}\cdot {\lambda }_{j}\right)/\left({\lambda }_{i}-{\lambda }_{j}\right)\\ {Z}_{j}=\left({Z}_{\mathrm{GF}}-{\widehat{Z}}_{\mathrm{HMW}}\cdot {\lambda }_{i}\right)/\left({\lambda }_{i}-{\lambda }_{j}\right)\end{array}\right.$$

(41)

The ${Z}_{i}$ and ${Z}_{j}$ can also be determined whether the observations do exist cycle slips according to the rounding directly or significance testing. However, in real applications, the most limitation of this approach is that the estimated float cycle slips must be precise and reliable. Otherwise, the properties of integer and inheritance may deteriorate.

2.3.3 Coordinate-domain-aided approach

The approach of coordinate-domain assistance is important but often ignored. Specifically, the positions, velocities, and even accelerations of a station or vehicle can all be used to constrain the mathematical models of cycle slip detection and repair. The Kalman filter (Li et al. 2019c) and polynomial constraint (Li et al. 2019a) are all feasible. For instance, in a triple-differenced observation model where the ionospheric and tropospheric delays are ignored, we have

$${\Delta \nabla dP}_{qr,i}^{us}=\Delta \nabla {\varvec{A}}{\varvec{x}}+\Delta \nabla d{\varepsilon }_{qr,i}^{us}$$

(42)

$${\Delta \nabla d\phi }_{qr,i}^{us}=\Delta \nabla {\varvec{A}}{\varvec{x}}+{\lambda }_{i}{\Delta \nabla Z}_{qr,i}^{us}+\Delta \nabla d{\epsilon }_{qr,i}^{us}$$

(43)

If the baseline components $\Delta \nabla {\varvec{x}}\left(t\right)$ and $\Delta \nabla {\varvec{x}}\left(t-1\right)$ have a prior information, satisfying

$$\Delta \nabla {\varvec{x}}\left(t\right)={\varvec{\Psi }}_{t,t-1}\Delta \nabla {\varvec{x}}\left(t-1\right)+{\varvec{W}}\left(t\right)$$

(44)

where ${\varvec{\Psi }}_{t,t-1}$ denotes the state transition matrix; ${\varvec{W}}\left(t\right)$ denotes the state noise. Then the state equation is generated to the observation equations. Apparently, the cycle slips can be detected and repaired more precisely if the precision and reliability of the coordinate-domain assistance are high enough. For instance, if it is in the area of deformation monitoring or low dynamic scenario, the velocity constraint can be added

$$\Delta \nabla {\varvec{x}}\left(t\right)-\Delta \nabla {\varvec{x}}\left(t-1\right)=\Delta \nabla {\varvec{x}}\left(t-1\right)-\Delta \nabla {\varvec{x}}\left(t-2\right)={{\varvec{g}}}_{t}$$

(45)

with $t>2$. Then the triple-differenced observation equations between adjacent epochs read

$${\Delta \nabla dP}_{qr,i}^{us}\left(t-1\right)=\Delta \nabla {\varvec{A}}\left(t-1\right){{\varvec{g}}}_{t}+{\Delta \nabla d\varepsilon }_{qr,i}^{us}\left(t-1\right)$$

(46)

$${\Delta \nabla d\phi }_{qr,i}^{us}\left(t-1\right)=\Delta \nabla {\varvec{A}}\left(t-1\right){{\varvec{g}}}_{t}+\Delta \nabla d{\epsilon }_{qr,i}^{us}\left(t-1\right)$$

(47)

$${\Delta \nabla dP}_{qr,i}^{us}\left(t\right)=\Delta \nabla {\varvec{A}}\left(t\right){{\varvec{g}}}_{t}+\Delta \nabla {d\varepsilon }_{qr,i}^{us}\left(t\right)$$

(48)

$${\Delta \nabla d\phi }_{qr,i}^{us}\left(t\right)=\Delta \nabla {\varvec{A}}\left(t\right){{\varvec{g}}}_{t}+{\lambda }_{i}{Z}_{qr,i}^{us}+\Delta \nabla d{\epsilon }_{qr,i}^{us}\left(t\right)$$

(49)

It is worth noting that only the observations without the cycle slips can be used in (47) since the cycle slips have been processed before. The compact form can be obtained as follows

$$\text{E}\left[\begin{array}{l}{{\varvec{l}}}_{t-1}\\ {{\varvec{l}}}_{t}\end{array}\right]=\left[\begin{array}{lc}{{\varvec{e}}}_{2m}\otimes {\varvec{\Omega }}_{t-1}& \mathbf{0}\\ {{\varvec{e}}}_{2m}\otimes {\varvec{\Omega }}_{t}& {\varvec{B}}\otimes {{\varvec{I}}}_{{n}_{t}}\end{array}\right]\left[\begin{array}{l}{{\varvec{g}}}_{t}\\ \begin{array}{l}{\varvec{Z}}\end{array}\end{array}\right]$$

(50)

where ${{\varvec{l}}}_{t-1}={\left[\Delta \nabla d{{\varvec{P}}\left(t-1\right)}^{\mathrm{T}},\Delta \nabla d{{\varvec{\phi}}\left(t-1\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}$ with $\Delta \nabla d{\varvec{P}}\left(t-1\right)={\left[{\Delta \nabla d{{\varvec{P}}}_{1}\left(t-1\right)}^{\mathrm{T}},\ldots ,{\Delta \nabla d{{\varvec{P}}}_{m}\left(t-1\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}$, $\Delta \nabla d{\varvec{\phi}}\left(t-1\right)={\left[{\Delta \nabla d{{\varvec{\phi}}}_{1}\left(t-1\right)}^{\mathrm{T}},\ldots ,{\Delta \nabla d{{\varvec{\phi}}}_{m}\left(t-1\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}$, $\Delta \nabla d{{\varvec{P}}}_{m}\left(t-1\right)={\left[{\Delta \nabla dP}_{qr,m}^{u1}\left(t-1\right),\ldots ,{\Delta \nabla dP}_{qr,m}^{u{n}_{t-1}}\left(t-1\right)\right]}^{\mathrm{T}}$; $\Delta \nabla d{{\varvec{\phi}}}_{m}\left(t-1\right)={\left[{\Delta \nabla d\phi }_{qr,m}^{u1}\left(t-1\right),\ldots ,{\Delta \nabla d\phi }_{qr,m}^{u{n}_{t-1}}\left(t-1\right)\right]}^{\mathrm{T}}$; ${{\varvec{l}}}_{t}={\left[\Delta \nabla {d{\varvec{P}}\left(t\right)}^{\mathrm{T}},\Delta \nabla d{{\varvec{\phi}}\left(t\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}$ with $\Delta \nabla d{\varvec{P}}\left(t\right)={\left[{\Delta \nabla d{{\varvec{P}}}_{1}\left(t\right)}^{\mathrm{T}},\ldots ,{\Delta \nabla d{{\varvec{P}}}_{m}\left(t\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}$, $\Delta \nabla d{\varvec{\phi}}\left(t\right)={\left[{\Delta \nabla d{{\varvec{\phi}}}_{1}\left(t\right)}^{\mathrm{T}},\ldots ,{\Delta \nabla d{{\varvec{\phi}}}_{m}\left(t\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}$, $\Delta \nabla d{{\varvec{P}}}_{m}\left(t\right)= \Big[{\Delta \nabla dP}_{qr,m}^{u1}\left(t\right),\ldots ,{\Delta \nabla dP}_{qr,m}^{u{n}_{t-1}}\left(t\right)\Big]^{\mathrm{T}}$; $\Delta \nabla d{{\varvec{\phi}}}_{m}\left(t\right)=\Big[{\Delta \nabla d\phi }_{qr,m}^{u1}\left(t\right),\ldots ,{\Delta \nabla d\phi }_{qr,m}^{u{n}_{t-1}}\left(t\right)\Big]^{\mathrm{T}}$; ${\varvec{Z}}\!=\! \Big[{{\varvec{Z}}}_{1}^{\mathrm{T}},\ldots ,{{\varvec{Z}}}_{m}^{\mathrm{T}}\Big]^{\mathrm{T}}$ with ${{\varvec{Z}}}_{m}={\left[{Z}_{qr,m}^{u1},{Z}_{qr,m}^{u2},\ldots ,{Z}_{qr,m}^{u{n}_{t}}\right]}^{\mathrm{T}}$; ${\varvec{\Omega }}_{t-1}$ and ${\varvec{\Omega }}_{t}$ the design matrices of ${{\varvec{g}}}_{t}$, respectively; ${\varvec{B}}=\left[0\otimes {{\varvec{I}}}_{m};{{\varvec{\lambda}}}_{m}\right]$ the design matrix of ${\varvec{Z}}$. According to the law of covariance propagation, the stochastic model of (50) can be derived, and the parameters ${{\varvec{g}}}_{t}$ and ${\varvec{Z}}$ can be estimated by the LS criterion. The LAMBDA can be used to further determine the specific cycle slips. Besides, the velocity constraint ${{\varvec{g}}}_{t}$ can be strengthened, e.g., the ${{\varvec{g}}}_{t}=\mathbf{0}$ in a static case. With the help of coordinate-domain constraint, the observations of different epochs without cycle slips may also be added to the model, which will fully exploit the estimation of cycle slips with high precision and reliability.

3 Methods of cycle slip detection and repair under complex observation conditions

This section gives one unified method of cycle slip detection and repair, where the characteristics are analyzed comprehensively. Focusing on several typical complex conditions, corresponding specific methods are proposed.

3.1 One unified method of cycle slip detection and repair

Based on the preceding analysis, one unified cycle slip detection and repair method is given. Figure 3 illustrates the flowchart of the proposed method. There are three main steps when establishing a specific method of cycle slip processing. First, according to the positioning mode and observation condition, the GNSS observations that may need combination or differencing are obtained; second, to treat the geometric term and ionospheric delay, two basic models need to be determined. More than one method can be formed if insensitive cycle slips or significant defects exist. Third, any aided approaches can be added if necessary, and the cycle slip detection and repair method is finally established. Actually, almost all existing methods can be derived from this unified method. For instance, the most popular method TurboEdit is a combination of the GF plus IB method (i.e., GF combination), and the GF plus IF method (i.e., HMW combination). Also, new methods can be proposed according to the unified method if necessary.

Fig. 3

Flowchart of the unified method of cycle slip detection and repair

According to the flowchart of the proposed method, as shown in Fig. 3, nine typical methods can be formed, i.e., the GF plus IF (FF), GF plus IU (FU), GF plus IB (FB), GB plus IF (BF), GB plus IU (BU), GB plus IB (BB), GFix plus IF (XF), GFix plus IU (XU), and GFix plus IB (XB) methods. As aforementioned, different methods have different pros and cons. For instance, the methods based on the GF or GFix model ignore the connections between different satellites, but they do not need enough redundant observations. Although the calculation of the methods based on the GB or IU model is a little complicated, they are usually precise and reliable. The methods based on the IB model are easy to implement but may not be accurate enough. For the methods based on the IF model, it is trustworthy, but two or more types of observations are needed.

Under complex observation conditions, such as a harsh environment, single-frequency low-cost receiver, or real-time kinematic situation, it may cause a decrease in observation quality, the change of characteristics of errors, and the protrusion of residual systematic errors. Hence, the cycle slips cannot be detected and repaired easily, especially when there are small and multiple cycle slips. Also, since insensitive and even large cycle slips may frequently occur at this moment, the requirements of cycle slip processing are higher. Table 1 lists the applicability of the nine typical methods under different conditions. Specifically, the BF and BU methods can process the small cycle slips. The methods based on the GF and GFix models can work well for the multiple cycle slips, and the methods based on the GF model usually have insensitive cycle slips.

Table 1 Applicability analysis of the nine typical methods

3.2 Several schemes of cycle slip detection and repair under complex observation conditions

In this paper, as an example, three practical new cycle slip detection and repair methods are proposed for three specific complex conditions. Specifically, they are the harsh environment, single-frequency low-cost receiver, and real-time kinematic situation.

3.2.1 A practical method in harsh environment

In harsh environments including in canyons or during active ionosphere, since the multipath effects or the ionospheric delays are often significant which need to be considered, and the observation quality is also decreased, the most appropriate approach at this moment is the combination of several methods.

Without loss of generality, if the stations are continuously operating at this time, such as in deformation monitoring, the XU or XB method can be used first. Specifically, after the geometry-fixed and ionosphere-fixed models are adopted, the triple-differenced phase observation equation reads

$$\text{E}\left[{\Delta \nabla d\phi }_{qr,i}^{us}-{\Delta \nabla d\widehat{\rho }}_{qr}^{us}\right]={\lambda }_{i}{\Delta \nabla Z}_{qr,i}^{us}$$

(51)

To further enhance the performance of the above method such as repair the cycle slips, the SD-aided approach is added since the ${\Delta \nabla Z}_{qr,i}^{us}$ will be close to a non-zero integer, satisfying

$$\left\{\begin{array}{l}\left|{\Delta \nabla \widehat{Z}}_{qr,i}^{us}\right|\ge a\\ \left|{\Delta \nabla \widehat{Z}}_{qr,i}^{us}-\text{round}\left({\Delta \nabla \widehat{Z}}_{qr,i}^{us}\right)\right|\le b\end{array}\right.$$

(52)

where $a$ and $b$ denote the coefficients to be determined; $\text{round}\left(\cdot \right)$ denotes the operator of rounding. In real applications, if the $\left|{\Delta \nabla \widehat{Z}}_{qr,i}^{us}\right|$ is equal to or larger than the $a$, whereas the $\left|{\Delta \nabla \widehat{Z}}_{qr,i}^{us}-\text{round}\left({\Delta \nabla \widehat{Z}}_{qr,i}^{us}\right)\right|$ is larger than the $b$, one may not repair the potential cycle slip directly and only re-initialize the ambiguity for insurance since the model is biased at this time. It is worth noting that if it is a standalone positioning mode like PPP, one can apply the double-differenced phase observation equation if the precise ephemeris and other systematic error corrections are used

$$\text{E}\left[{\nabla d\phi }_{r,i}^{us}-{\nabla d\widehat{\rho }}_{r}^{us}\right]={\lambda }_{i}{\nabla Z}_{r,i}^{us}$$

(53)

Similar to (52), a corresponding cycle slip judgment method can be established.

The above method can be called SD-aided XU/XB (S-X) method, which is suitable for the harsh environment as long as the coordinates of the stations are precisely known and the unmodeled errors are successfully corrected. Moreover, the proposed practical method is easy to implement.

3.2.2 A practical method in single-frequency low-cost receiver

In a single-frequency low-cost receiver, the observation quality is decreased, and the characteristics of errors are changed. Also, the traditional TurboEdit method cannot work since only one frequency exists. Moreover, the relatively low-precision observations especially the code ones need to be handled with care. At this moment, the fundamental approach prefers to use the BU or BB method. Both the standalone mode like (7) and (8) or relative mode like (9) and (10) can be used. It is worth noting that if the baseline length in the relative mode is sufficiently short, the BB method can be treated as the BU method.

The OD- and CD-aided approaches can be added to the BU or BB method to overcome the potential shortcoming of the low-precision observations with outliers. That is, the OD-aided approach like (34) to (36) can detect large cycle slips, hence the robustness of the model in use will be enhanced. Suppose the state information of the low-cost device is also known. In that case, the CD-aided approach like (44) to (50) can be added to the model in use since the observation precision usually needs to be higher and there are usually inadequate redundant observations.

The above method can be called OD- and CD-aided BB/BU (OC-B) method, which is especially suitable for the single-frequency low-cost receiver. The biggest advantage of the proposed practical method is that the strength of the model is guaranteed to a great extent, where the adverse effects of the low-precision observations and outliers are reduced.

3.2.3 A practical method in real-time kinematic situation

One of the most common challenging scenarios is the real-time kinematic situation, where the cycle slips will inevitably exist in observations. Currently, the methods based on the GFix model are not appropriate. Since the vehicle is in high-speed motion, the GB model is recommended due to its best geometric strength. Therefore, if the ionospheric delays are not very serious, the BU or BB method is selected as the fundamental one, like (7) and (8) or (9) and (10).

Whereas the coordinate components are not easy to predict due to the frequent maneuver. In addition, there are many cycle slip parameters to be solved, and the equation is very prone to solvable and estimable problems and is even ill-conditioned. Therefore, the FB method like (3) to (6) and combined FF method like (20) are added before the BU or BB method. Specifically, using the FB plus FF method with large and small thresholds, the observations with large cycle slips and partial observations that must be free of cycle slips can be detected. After that, more redundant observations can be obtained, and only partial cycle slips need to be estimated. Finally, the cycle slips can be processed with high precision and high reliability. The segment processing of the FB plus FF method can be expressed as follows

$$ \left\{ {\begin{array}{*{20}l} {T_{{{\text{FB}}}} < c_{1} \;{\text{and}}\;T_{{{\text{FF}}}} < d_{1} ,} \hfill & {{\text{without }}\;{\text{cycle}}\;{\text{slip}}} \hfill \\ {T_{{{\text{FB}}}} \ge c_{2} \;{\text{and}}\;T_{{{\text{FF}}}} \ge d_{2} , } \hfill & {{\text{with}}\;{\text{large}}\;{\text{cycle }}\;{\text{slip}}} \hfill \\ {{\text{Others}}, } \hfill & {{\text{with}}\;{\text{or}}\;{\text{without}}\;{\text{cycle}}\;{\text{slip}}} \hfill \\ \end{array} } \right. $$

(54)

where ${T}_{\mathrm{FB}}$ and ${T}_{\mathrm{FF}}$ are the two statistics of FB and FF methods, respectively; ${c}_{1}$ and ${d}_{1}$ are the small thresholds of FB and FF methods, respectively; ${c}_{2}$ (${c}_{2}>{c}_{1}$) and ${d}_{2}$ (${d}_{2}>{d}_{1}$) are the large thresholds of FB and FF methods, respectively.

The above method can be called BU/BB combined FB and FF (F-B) method, which is the GF combined GB approach. The proposed practical method takes advantage of the pros and cons of both GF and GB approaches. The GF-based approach can be processed on a single satellite basis, whereas this approach has limited accuracy and then small cycle slips cannot be detected easily in such cases. Then, since the GB-based approach fully accounts for the links between satellites, the ability to detect and repair small cycle slips is strong. However, when there are many cycle slips simultaneously, this approach can only work some of the time. Hence, in the proposed practical method, segment processing is sufficiently efficient and accurate.

4 Results and discussion

To demonstrate the effectiveness of the unified method and the corresponding three new schemes, three different experiments under complex observation conditions were carried out. Specifically, they are the harsh environment, single-frequency low-cost receiver, and real-time kinematic situation.

4.1 Analysis in the harsh environment

This section adopts single- and dual-frequency mixed baseline dataset No. 1, of which the baseline length is 22.65 km. The 24-h GPS and BDS observations were collected with a sampling interval of 30 s. Hence, the ionospheric delays at this time cannot be totally eliminated by using the between-epoch differencing. The reference and rover stations are both located in Hong Kong, China. Besides, the data used here is from the day of year (DOY) 201 during the summer vacation of 2021. Figure 4 illustrates the geomagnetic Kp indices of this day. The Kp index can represent the ionospheric activity level. According to Fig. 4, the sum of Kp indices of that day is 18, thus indicating the ionosphere is relatively active.

Fig. 4

Geomagnetic Kp indices on DOY 201, 2021

As mentioned in Sect. 3.2.1, since the coordinates of the receivers are precisely known due to the long-term continuous observation, the S-X method can be applied here. For a comprehensive analysis, RTK and static PPP modes are both carried out. When dealing with the cycle slips, the broadcast ephemeris and precise ephemeris are used in RTK and PPP, respectively. The coefficients $a$ and $b$ in (52) are set to 0.75 cycles and 0.20 cycles, respectively. To confirm the effectiveness of the proposed S-X method, the TurboEdit method is also used for comparison, where the thresholds of GF and HMW combinations are 0.05 m and 4 cycles, respectively. The real cycle slips are all corrected previously by examining the positioning results, then simulated cycle slips are added to dataset No. 1 of several typical satellites. Specifically, they are GPS G05, G08, G15, G17 and G32, BDS C22 for MEO, BDS C16 for IGSO, and BDS C01 for GEO, where satellite types and periods are all taken into account. It notes that different types of cycle slips are considered here, including small (1 to 3 cycles), large, multiple, simultaneous cycle slips, etc. Some insensitive cycle slips of GF and HMW combinations, such as equivalent and equidistant cycle slips, are also adopted. Therefore, the simulated cycle slips are rather representative.

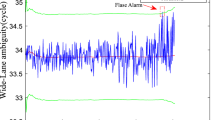
Figure 5 shows the fractional parts of the potential cycle slips. The orange points denote the values of ${\Delta \nabla \widehat{Z}}_{qr,i}^{us}-\text{round}\left({\Delta \nabla \widehat{Z}}_{qr,i}^{us}\right)$ based on RTK, and the green points denote the values of ${\nabla \widehat{Z}}_{r,i}^{us}-\text{round}\left({\nabla \widehat{Z}}_{r,i}^{us}\right)$ based on PPP. The data satisfying the $\left|{\Delta \nabla \widehat{Z}}_{qr,i}^{us}\right|<a$ or $\left|{\nabla \widehat{Z}}_{r,i}^{us}\right|<a$ is not shown here since they cannot be regarded as the potential cycle slips. According to Fig. 5, it can be easily found that the fractional part of the ${\Delta \nabla \widehat{Z}}_{qr,i}^{us}$ is highly concentrated in the interval − 0.1 to 0.1 cycles, where the maximum amplitude is the − 0.11 cycles in RTK and 0.13 cycles in PPP, respectively. Therefore, the coefficient $b$ can be set to 0.2 cycles with high reliability, and the SD-aided approach is indeed useful. Based on (52), as aforementioned, if the $\left|{\Delta \nabla \widehat{Z}}_{qr,i}^{us}\right|$ is equal or larger than the coefficient $a$, whereas the $\left|{\Delta \nabla \widehat{Z}}_{qr,i}^{us}-\text{round}\left({\Delta \nabla \widehat{Z}}_{qr,i}^{us}\right)\right|$ is larger than the coefficient $b$, the observations are polluted by other outliers with high possibility. Accordingly, the XU method may degenerate into the XB method, then the users may re-initialize the ambiguity for insurance.

Fig. 5

Fractional part of the potential cycle slips in RTK (up) and PPP (bottom) of dataset No. 1

In order to make a quantitative comparison, two types of success rate of cycle slip resolution are applied (Verhagen et al. 2013). The first one is based on the number of cycles slips ${P}_{\mathrm{sc}}$, and the second one is based on the number of epochs ${P}_{\mathrm{se}}$

$${P}_{\mathrm{sc}}=\frac{\text{number of correctly resolved cycle slips}}{\text{Number of total cycle slips}}$$

(55)

$${P}_{\mathrm{se}}=\frac{\text{Epoch number of correctly resolved cycle slips}}{\text{Number of total epochs with cycle slips}}$$

(56)

Of course, one may also use the easy-to-compute sharp lower bound of integer bootstrapping (Teunissen 1998). In dataset No. 1, the ${P}_{\mathrm{sc}}$ and ${P}_{\mathrm{se}}$ of S-X method are both 100%, whereas the ones of TurboEdit method are only approximately 24.8% and 17.4% in RTK and 26.6% and 19.6% in PPP. The main reason is that the TurboEdit method cannot work under the conditions of single frequency and insensitive cycle slip, which is very common in harsh environment.

To verify the performance of the cycle slip processing in terms of positioning, Figs. 6 and 7 show the positioning results of the TurboEdit and S-X methods in RTK and PPP, respectively. Three directions, including east–west (E–W), north–south (N–S), and up–down (U–D) directions, are all presented. The yellow and green points denote the float and fixed solutions in Fig. 6. The corresponding statistics including, STD and bias of positioning results, are listed in Tables 2 and 3. In this study, since the observation condition is not very good, the ratio when fixing the ambiguities is set to 1.5 in RTK mode. The LAMBDA method is adopted if the integer ambiguities need to be fixed. The success rates of the TurboEdit and S-X methods are 66.0%, and 89.4%, respectively. It indicates that 23.4% improvements of the S-X method can be obtained. In Fig. 7, due to the impact of cycle slips, the solution of the TurboEdit method is frequently initialized and cannot be converged. In contrast, the solution of the S-X method converges to centimeter-level after about 140 min. Taking a closer look at Figs. 6 and 7, and combining the estimated STD and bias, it can be found that the S-X method is more precise. Specifically, for the STD, approximately 78.4%, 48.8%, and 56.4% improvements can be obtained in E–W, N–S, and U–D directions in RTK mode, and 55.9%, 42.1% and 86.0% in PPP mode. Similarly, for the bias, 57.1%, 26.3%, and 30.0% improvements can be obtained by using the S-X method in RTK mode, and 54.1%, 39.6% and 86.1% in PPP mode. Therefore, the cycle slips must be handled carefully in harsh environments, and the proposed S-X method is practical and trustworthy to a great extent.

Fig. 6

Positioning errors of three directions by using the TurboEdit method (left) and the S-X method (right) in RTK. The yellow and green points denote the float and fixed solutions, respectively

Fig. 7

Positioning errors of three directions by using the TurboEdit method (left) and the S-X method (right) in PPP

Table 2 Statistics of fixed solutions of two different strategies in RTK of dataset No. 1

Table 3 Statistics of positioning results after three hours of two different strategies in PPP of dataset No. 1

4.2 Analysis in the single-frequency low-cost receiver

This section collects 24-h dataset No. 2 from the single-frequency low-cost receiver. The model of the low-cost receiver is HG-BX-RAG360 which only costs a few hundred USD. For miniaturization purposes, a built-in GNSS full-band antenna and low-cost board are integrated into the receiver. Here 5-s single-frequency GPS/BDS observations were adopted in a 54.50-m baseline. A short baseline is used because the observation condition is not good enough where the unmodeled errors inevitably exist. Hence, the atmospheric delays need to be eliminated better. Figure 8 illustrates the GPS/BDS satellite numbers of the rover and reference stations. The mean total satellite numbers of rover and reference stations are approximately 20.96 and 22.11, showing the unstable performance. The position dilution of precision (PDOP) of the rover station is shown in Fig. 9. It can be seen that the PDOP values fluctuate dramatically between approximately 1.2 to 2.8. Hence, it indicates that the signal reception is disturbed, which is most likely due to the internal low-cost receiver and external challenging environment. Therefore, the quality of the observations of dataset No. 2 is not very good, which is sufficiently representative.

Fig. 8

Total satellite numbers of the rover (up) and reference (bottom) stations of dataset No. 2

Fig. 9

PDOP values of the rover station of dataset No. 2

As aforementioned, the OC-B method is used in this section. Firstly, the BU or BB method is served as the fundamental one where the relative mode is adopted. In addition, the polynomial fitting based on the between-receiver single-differenced observations is treated as the OD-aided approach, where the epoch window and the polynomial order are set to 4 and 2, respectively. Since the polynomial fitting is not very precise and is just an aided approach, the threshold in (36) is set to 10, which will be explained later. For the CD-aided approach, the GB model is formulated in terms of (50) since dataset No. 2 is a baseline. The cycle slips can be detected and repaired by using the LAMBDA method.

Figure 10 depicts the fitting precision and residuals by using the polynomial fitting of dataset No. 2. It can be seen that the fitting precision of the top panel is approximately 2 cycles, where the maximum value is as high as 8 cycles, which can be further confirmed by the residuals of the bottom panel. It indicates that the polynomial fitting can indeed process the cycle slips to some extent, whereas the minimal detectable cycle slip in the case of the single-frequency low-cost receiver at hand is approximately 2 cycles. The reason is that the observation precision is limited, and then the ability of polynomial fitting is affected. Fortunately, the large cycle slips can be detected and repaired with high reliability since the maximum value of fitting precision is smaller than 8 cycles. Therefore, the polynomial fitting can be used to detect relatively large cycle slips (10 cycles in this study) in advance.

Fig. 10

Fitting precision (top) and residuals (bottom) by using the polynomial fitting of dataset No. 2

To certify the effectiveness of the CD-aided approach, three-dimensional time-differenced coordinate components based on the GB model in (50) are illustrated in Fig. 11. We can easily find that the time-differenced coordinate components in three directions are highly concentrated around 0 m. It is reasonable that the rover and reference stations are both relatively static during this period, and hence the time-differenced coordinate components are nearly 0 m. It proves that the CD-aided GB method is highly reliable. Moreover, the threshold of time-differenced coordinate components can be set (e.g., 0.1 m in this study). The CD-aided approach will be not be used if the resolved time-differenced coordinate components are larger than the above threshold. The accuracy and reliability of the CD-aided GB method can be further improved.

Fig. 11

Three-dimensional time-differenced coordinate components resolved in CD-aided GB method of dataset No. 2

Figure 12 shows the float solutions of the cycle slip parameters resolved in the OC-B method of dataset No. 2. It can be clearly seen that most float cycle slip parameters are nearly 0 cycles, thus indicating that there are no cycle slips at this time. Also, most of the other cycle slip parameters are usually close to an integer. Hence, the GB model is effective to a great extent. Taking a closer look at Fig. 12, the absolute values of the float cycle slip parameters are all smaller than 10 cycles since the potential large cycle slips (i.e., larger than 10 cycles) have been processed by the polynomial fitting before. In addition, there are small cycle slip parameters, especially those with an absolute value equal to 1 cycle, thus proving that the GB model can handle small cycle slips with the help of OD and CD-aided approaches.

Fig. 12

Float solutions of the cycle slip parameters resolved in the OC-B method of dataset No. 2

To further quantitatively confirm the superiority of the proposed OC-B method, Table 4 lists the statistics of ambiguity resolution and positioning results including the float and fixed solutions of three different strategies. Specifically, they are the OD-aided approach alone, CD-aided BB/BU (C-B) method, and the OC-B method, respectively. There are 31.7% and 15.8% fixed solutions using the OD and C-B methods, respectively. When using the OC-B method, the success rate can reach up to 74.4%, thus indicating the effectiveness and superiority of the proposed OC-B method. When comparing the STD and bias of the three methods, much improvement can be obtained after using the OC-B method. Specifically, almost 3.3 to 4.3 m of STD and 1.6 to 2.9 m of bias can be improved in the three-dimensional direction. By combining the OD- and CD-aided approaches to the BB/BU method, all types of cycles including multiple cycle slips, small cycles slips, and even large cycle slips can be processed appropriately. Hence, the proposed OC-B method is indeed valuable for a single-frequency low-cost receiver.

Table 4 Statistics of ambiguity resolution and positioning results of three different strategies of dataset No. 2

4.3 Analysis in the real-time kinematic situation

The real-time kinematic data is adopted in this section named dataset No. 3. The 1-s dual-frequency vehicle data was collected from P5 manufactured by Huace on DOY 061, 2022. The experiment site was located in the urban area of Nanjing, China, where the signals may be obstructed, reflected, etc. The experiment started and ended at 02:17:00 to 03:38:00 GPS time (GPST), which lasted 1 h and 21 min. Figure 13 shows the velocity values in three directions. It can be clearly seen that the speed of the vehicle fluctuates wildly over time. The mean velocity is approximately 23.11 km/h. Although real cycle slips inevitably exist in a such kinematic situation, several simulated cycle slips, including small, multiple, insensitive, and even large cycle slips, are added. Hence the performance of the proposed method can be validated better. Specifically, small cycle slips from 2 to 3 cycles are added on G04 at L1, G29 at L2, C04 at B2, and C05 at B1 every 20 s from 02:17:09; multiple cycles from 4 to 5 cycles on more than 60% of satellites except reference satellite every 200 s from 02:17:49; insensitive cycle slips of FB and FF combinations are added on G03 at L1 (1 cycle) and L2 (1 cycle), G22 at L1 (77 cycles) and L2 (60 cycles) every 20 s from 02:17:14; large cycle slips from 100 to 225 cycles are added on G31 at L2, G32 at L1, C01 at B1, and C02 at B2 every 20 s from 02:17:19.

Fig. 13

Velocity values in E-W, N-S, and U-D directions of dataset No. 3

The F-B method is applied here according to the Sect. 3.2.3. When using the FB and FF methods in (53), the small thresholds of FB and FF methods are set to ${c}_{1}=0.05 \mathrm{m}$ and ${d}_{1}=1 \mathrm{cycle}$, and the corresponding large thresholds are set to ${c}_{2}=0.18 \mathrm{m}$ and ${d}_{2}=10 \mathrm{cycles}$. That is, the observations with large cycle slips (10 cycles in this study) can be detected with high reliability in advance. Also, partial observations that must be free of cycle slips can be detected based on the small thresholds ${c}_{1}$ and ${d}_{1}$. For the rest observations to be processed, by using the BU or BB method, the triple-differenced observation Eqs. (9) and (10) are used where a nearby reference station is utilized. Finally, the small cycle slips can be processed by using the GB model.

Figures 14 and 15 illustrate the global and local values of the FB and FF methods of dataset No. 3, respectively. Based on Fig. 14, it can be found that the precision of the FB method is high, whereas there are several discontinuities since there are some insensitive cycle slips. For the FF method shown in Fig. 15, the precision is not high enough due to the use of code observations. Hence, small cycle slips cannot be detected easily in such cases. In conclusion, the FB and FF methods are effective to some extent, but some limitations will hinder the performance of cycle slip detection and repair.

Fig. 14

Global (top) and local (bottom) values of the FB method of dataset No. 3

Fig. 15

Global (top) and local (bottom) values of the FF method of dataset No. 3

Figures 16 and 17 show the float solutions and corresponding fractional parts of cycle slips based on the GB method alone and F-B method, respectively. Here the fractional part means the difference between the float solution of the cycle slip and its nearest integer. Based on the relatively concentrated fractional parts in Fig. 16, the GB method alone is effective to some extent. However, the GB method can only work some of the time. The reason may be that there are not enough redundant observations. Hence, the GB method alone cannot work well in case of multiple cycle slips. It can be confirmed in Fig. 17 that the fractional parts are more concentrated since some significant cycle slips are processed in advance by the FB and FF methods. Therefore, it proves the effectiveness of the proposed method.

Fig. 16

Float solutions and corresponding fractional parts of cycle slips based on the GB method alone

Fig. 17

Float solutions and corresponding fractional parts of cycle slips based on the F-B method

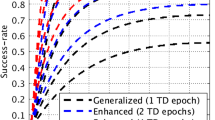
To verify the performance of the F-B method in terms of positioning, Table 5 lists the success rates of ambiguity resolution of three different strategies of dataset No. 3 under different ratio values. Specifically, they are the TurboEdit method, the GB method alone, and the F-B method, respectively. Here the TurboEdit method is the FB and FF methods, of which the thresholds are the same as in Sect. 4.1. The mean success rate of the TurboEdit method is only approximately 20.5%, whereas one of the GB method alone can reach approximately 56.0%. It can be found that the method based on the GF model is worse than the one based on the GB model. Moreover, after combining the GF and GB models (i.e., the F-B method), the success rates of ambiguity resolution are improved to a great extent, where the mean value is as high as 74.3%. It proves the effectiveness and superiority of the proposed F-B method again.

Table 5 Success rates of ambiguity resolution of three different strategies of dataset No. 3 under different ratio values (unit: %)

5 Conclusion

In this paper, the principles, methods, and applications of cycle slip detection and repair under complex observation conditions are thoroughly studied for the first time. Three basic models for dealing with the geometric term, three basic models for dealing with the ionospheric delay, and three basic aided approaches are all analyzed in depth. Based on this, one unified cycle slip detection and repair method is proposed. Almost all existing or potential new methods can be deduced according to the unified method. Focusing on three typical complex conditions, i.e., challenging environment, single-frequency low-cost receiver, and real-time kinematic situation, three specific cycle slip processing schemes are also proposed.

The results show that the idea of the unified method is feasible, and these three practical methods are more effective than the traditional methods. Specifically, in the harsh environment, the S-X method can detect and repair the cycle slips all the time, whereas the TurboEdit method cannot. In RTK and static PPP, one can obtain centimeter-level and millimeter-level positioning accuracy respectively, only after using the S-X method. In the single-frequency low-cost receiver, at least a 42.7% success rate of ambiguity resolution can be improved after using the OC-B method. Also, it can be increased by approximately 3.8 m and 2.3 m in terms of STD and bias, respectively. In the real-time kinematic situation, the positioning performance is also improved after using the F-B method, where the success rate of ambiguity resolution is improved by approximately 36.0% on average.

It is worth noting that although the three new specific methods are relatively effective and practicable, different specific methods can also be proposed based on the unified method under the above three typical complex observation conditions. According to the real observation conditions and application modes, the users do not need to restrict themselves to existing methods. Besides, the proposed unified method can be used in multi-frequency and multi-constellation situation. Only when the actual situation is fully considered, can one find an optimal approach based on the unified method.