Introduction

The satellite formation-flying technique has demonstrated its particular importance in implementing new and advanced concepts in earth observation missions in the past decades, such as the GRACE (Tapley et al. 2004), TanDEM-X (Krieger et al. 2007) and Swarm (Friis-Christensen et al. 2008) missions. To fulfill their respective mission goals, we prefer or even require orbits of high quality in both absolute and relative senses. For that purpose, the GNSS-based precise orbit determination (POD) is indispensable, where integer ambiguity resolution (IAR) plays a crucial role in achieving the best orbit accuracy. At present, IAR can be performed on both double- and single-difference levels. Resolving the double-difference (DD) ambiguities between-satellites-between-receivers has long been practiced to achieve the best accuracy for ground–ground, space–space and space-ground baselines (Allende-Alba and Montenbruck 2016; Allende-Alba et al. 2017; Dong and Bock 1989; Jäggi et al. 2007; Kroes et al. 2005). Regarding absolute orbit accuracy, however, the contribution of DD IAR was shown to be minor or even negative (Jäggi et al. 2007; Mao et al. 2017). In the past decade, single-receiver IAR by resolving the single-difference (SD) ambiguities between GNSS satellites (hereafter we also call it SD IAR) has demonstrated its great potential in improving positioning performance with respect to ambiguity-float solutions (Collins 2008; Ge et al. 2008; Laurichesse et al. 2008). As to POD for low earth orbiting (LEO) satellites, Laurichesse et al. (2009) showed that SD IAR was able to improve the Jason-1 orbit accuracy as evidenced by a reduction in the Satellite Laser Ranging (SLR) residuals by 1.5 mm. This approach was also successfully applied to POD for the Sentinel-3A and Swarm satellite missions and notably improved the orbits by about 30% as inferred from SLR residuals (Montenbruck et al. 2017; 2018). Li et al. (2015) generated the GPS satellite fractional-cycle biases (FCBs) required for SD IAR and their GRACE POD test spanning 30 days showed that accuracy of kinematic orbits was considerably improved by about 30% in 3D as inferred from comparison with the JPL reduced-dynamic orbit. However, Allende-Alba et al. (2018) reported that SD IAR could not achieve comparable relative orbit accuracy to that provided by DD IAR, particularly for formation-flying satellites with short/medium-size baselines, identical spacecraft and common orientation, e.g., GRACE.

Thus, both SD IAR and DD IAR have merits and drawbacks for formation-flying satellites. Neither of them can provide orbit solutions with the best accuracies in both absolute and relative senses. One may argue that this ultimate goal can be reached based solely upon DD IAR through joint processing of spaceborne and ground-based GPS data and by fixing the ambiguities on the ground–ground, space-ground, and space–space baselines. However, on the one hand, this will drastically complicate data processing. On the other hand, Jäggi et al. (2007) showed that the relative orbit accuracy was degraded in the joint processing mode due to a very low fixing rate of the space-ground baseline ambiguities. In this study, we process only spaceborne GPS data and propose a new IAR scheme for formation-flying satellites, where the SD IAR is integrated with the DD IAR, to simplify the data processing and enhance the orbit solutions. To demonstrate the added value of the proposed IAR scheme, we use the onboard GPS data collected by the GRACE mission. Considering that GRACE suffers from data gaps since 2011, we use the GPS data collected in 2010 for that purpose. In total, four types of orbits are derived, and each type of orbit consists of a kinematic and dynamic one. For the first type, the undifferenced (UD) ambiguities are estimated as float parameters. For the second one, we perform SD IAR at each GRACE satellite. For the third one, only the DD ambiguities between the twin GRACE satellites are resolved; and for the fourth one we make integrated SD and DD IAR, that is fix the SD and DD ambiguities simultaneously. These orbits will be compared with the reduced-dynamic orbit produced at the Jet Propulsion Laboratory (JPL), validated by independent SLR and K-Band ranging (KBR) measurements.

In the following, we first present the details of the strategy adopted for GRACE POD. Then, we focus on the different AR schemes to enhance POD. After that, the orbits derived from different AR schemes will be evaluated. Finally, we will make a discussion followed by conclusions of this study.

POD strategy

In this study, the data processing is performed with the Position And Navigation Data Analyst (PANDA) software, which is developed at the GNSS Research Center of Wuhan University and has been widely used in satellite POD and earth’s gravity field recovery (Guo et al. 2018; Liu and Ge 2003). For GRACE POD, we have used both the dynamic and kinematic orbit determination approach. The adopted POD strategy is listed in Table 1.

Table 1 GRACE POD strategy
Full size table

For dynamic POD, only a few deterministic dynamic parameters are estimated, and sophisticated force models are required for that purpose. Among others, the 8-plate macro model for the GRACE satellite is used to model the non-gravitational forces, which mainly result from atmospheric drag, solar and earth radiation pressure. As described in Table 1, the atmospheric density values required for atmospheric drag modeling are obtained with the DTM94 model (Berger et al. 1998). To account for deficiencies in DTM94 and/or the GRACE macro model, the drag coefficients, i.e., the scaling factors, are estimated freely once per orbital revolution in the course of dynamic POD. As to the solar and earth radiation pressure, we calculate them based on the satellite macro model as described in Marshall and Luthcke (1994). In contrast to atmospheric drag, a fixed scale factor of one is used for both the solar and earth radiation pressure, which indicates that the ‘datum’ of our dynamic orbit at the cross-track and radial components is defined by the applied force models rather than the GPS measurements. Additionally, 1 cycle-per-revolution (cpr) empirical accelerations are freely estimated to compensate for deficiencies in the adopted force models.

In view of the kinematic orbits, they are completely independent of the applied force models and are determined by a precise point positioning (PPP) approach (Švehla and Rothacher 2005).

For both dynamic and kinematic orbit determination, the same data and observation models have been used. The GRACE level 1B RL02 products (Case et al. 2010) are used here, which include the GPS data (GPS1B) and satellite attitude data (SCA1B) to perform POD. The GPS data are processed in an undifferenced manner, where the GPS orbits and clocks are fixed to a priori values. Furthermore, single-receiver IAR requires consistent GPS orbit, clocks and FCBs. For that purpose, we use the GPS phase clocks and FCBs (or phase biases) as described in Geng et al. (2019) which are consistent with the operational GPS orbits produced by the Center for Orbit Determination in Europe (CODE) (Bock et al. 2009). For the sake of further consistency, we have used the outdated IGS05.ATX model for GPS antenna phase center correction. The GRACE antenna phase center locations are modeled according to the VGN1B products, which provide L1/L2 antenna phase center offsets. To reduce the phase center model errors, we have estimated the phase center variations (PCVs) for the ionosphere-free L1/L2 combination for each satellite using the residual approach as described in Jäggi et al. (2009) and applied as observation corrections during the POD process. In addition, data processing in this study has been performed in 30-h arcs centered on the noon of each day, which leads to 6-h overlaps (21:00–03:00 h) between adjacent arcs, but only the orbits of the center 24-h are used in the orbit evaluation to avoid boundary effects.

Integer ambiguity resolution

In this section, we start with the basic GPS observation equations. Then, the different AR schemes are described in detail followed by a brief description about the adopted method for ambiguity fixing decision. Finally, we discuss the impact of ambiguity constraint on POD in case of different AR schemes.

Observation model

Pseudorange and carrier-phase observations between a satellite (superscript s) and a spaceborne receiver (subscript r) are usually described by the following observation equations (Blewitt 1989):

$$ \begin{aligned} & P_{r,j}^{s} = \rho_{r}^{s} + c\left( {dt_{r} - dt^{s} } \right) + I_{r,j}^{s} + b_{r,j} - b_{j}^{s} \\ & L_{r,j}^{s} = \rho_{r}^{s} + c\left( {dt_{r} - dt^{s} } \right) - I_{r,j}^{s} + \lambda_{j} \left( {N_{r,j}^{s} + B_{r,j} - B_{j}^{s} } \right){ + }\lambda_{j} \omega_{r}^{s} \\ \end{aligned} $$
(1)

where the subscript j denotes a given frequency \( f_{j} \), and \( \rho \) is the geometric range between the antenna phase center of the satellite (at the time of signal transmission) and receiver (at the time of signal reception). The antenna phase center offsets and variations, gravitational bending and relativistic corrections must be applied to the geometric range between the center of mass of the GNSS and LEO satellites. c is the speed of light in vacuum, \( dt_{r} {\text{ and }}dt^{s} \) denote the receiver and satellite clock offsets, I is the ionospheric path delay, which varies predominantly with the inverse square of the signal frequency. \( \lambda \) is the signal wavelength and N is the integer ambiguity, \( \omega_{r}^{s} \) is the phase wind up correction, \( b_{r} {\text{ and }}b^{s} \) are the hardware biases for the pseudorange observations at the receiver and satellite, respectively, while \( B_{r} {\text{ and }}B^{s} \) are hardware biases for the carrier phase. In reality, these biases are usually stable or at least vary slowly over time (Geng and Bock 2016; Geng et al. 2011). Finally, observation noise and unmodeled errors such as multipath effects and higher-order ionosphere delays have been ignored for brevity.

To eliminate the first-order ionospheric path delay, the orbit processing is based on the undifferenced ionospheric-free observations, which are formulated as follows:

$$ \begin{aligned} & P_{r,IF}^{s} = \rho_{r}^{s} + c\left( {dt_{r} - dt^{s} } \right) + b_{r,IF} - b_{IF}^{s} \\ & L_{r,IF}^{s} = \rho_{r}^{s} + c\left( {dt_{r} - dt^{s} } \right) + \lambda_{1} \left( {N_{r,IF}^{s} + B_{r,IF} - B_{IF}^{s} } \right) + \lambda_{1} \omega_{r,IF}^{s} \\ \end{aligned} $$
(2)

with \( \lambda_{1} \) the wavelength on L1 and

$$ \begin{aligned} & b_{{r,{\text{IF}}}} = {{\left( {f_{1}^{2} b_{r,1} - f_{2}^{2} b_{r,2} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1}^{2} b_{r,1} - f_{2}^{2} b_{r,2} } \right)} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}} \\ & b_{\text{IF}}^{s} = {{\left( {f_{1}^{2} b_{1}^{s} - f_{2}^{2} b_{2}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1}^{2} b_{1}^{s} - f_{2}^{2} b_{2}^{s} } \right)} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}} \\ & N_{\text{IF}} = {{f_{1} \left( {f_{1} N_{1} - f_{2} N_{2} } \right)} \mathord{\left/ {\vphantom {{f_{1} \left( {f_{1} N_{1} - f_{2} N_{2} } \right)} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}} \\ & B_{{r,{\text{IF}}}} = {{f_{1} \left( {f_{1} B_{r,1} - f_{2} B_{r,2} } \right)} \mathord{\left/ {\vphantom {{f_{1} \left( {f_{1} B_{r,1} - f_{2} B_{r,2} } \right)} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}} \\ & B_{\text{IF}}^{s} = {{f_{1} \left( {f_{1} B_{1}^{s} - f_{2} B_{2}^{s} } \right)} \mathord{\left/ {\vphantom {{f_{1} \left( {f_{1} B_{1}^{s} - f_{2} B_{2}^{s} } \right)} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1}^{2} - f_{2}^{2} } \right)}} \\ & \omega_{{r,{\text{IF}}}}^{s} = {{f_{1} \omega_{r}^{s} } \mathord{\left/ {\vphantom {{f_{1} \omega_{r}^{s} } {\left( {f_{1} + f_{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1} + f_{2} } \right)}} \\ \end{aligned} $$
(3)

Following the IGS analysis convention, the IF pseudorange biases \( b_{{r,{\text{IF}}}} \,{\text{and}}\,b_{\text{IF}}^{s} \) are assimilated into the respective receiver and satellite clock offsets in the data processing (Kouba 2009). Thus, Eqs. (2) are reformulated as:

$$ \begin{aligned} & P_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c\left( {\bar{d}t_{r} - \bar{d}t^{s} } \right) \\ & L_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c\left( {\bar{d}t_{r} - \bar{d}t^{s} } \right) + \lambda_{1} \bar{N}_{{r,{\text{IF}}}}^{s} + \lambda_{1} \omega_{{r,{\text{IF}}}}^{s} \\ \end{aligned} $$
(4)

with

$$ \begin{aligned} & \bar{d}t^{s} = dt^{s} + b_{\text{IF}}^{s} /c \\ & \bar{d}t_{r} = dt_{r} + {{b_{{r,{\text{IF}}}} } \mathord{\left/ {\vphantom {{b_{{r,{\text{IF}}}} } c}} \right. \kern-0pt} c} \\ & \bar{N}_{{r,{\text{IF}}}}^{s} = N_{{r,{\text{IF}}}}^{s} + d_{{r,{\text{IF}}}} - d_{\text{IF}}^{s} \\ & d_{{r,{\text{IF}}}} = B_{{r,{\text{IF}}}} - {{b_{{r,{\text{IF}}}} } \mathord{\left/ {\vphantom {{b_{{r,{\text{IF}}}} } {\lambda_{1} }}} \right. \kern-0pt} {\lambda_{1} }} \\ & d_{\text{IF}}^{s} = B_{\text{IF}}^{s} + {{b_{\text{IF}}^{s} } \mathord{\left/ {\vphantom {{b_{\text{IF}}^{s} } {\lambda_{1} }}} \right. \kern-0pt} {\lambda_{1} }} \\ \end{aligned} $$
(5)

The IF ambiguity \( \bar{N}_{{r,{\text{IF}}}}^{s} \) is usually estimated as a float parameter due to the existence of hardware biases in both pseudorange and carrier-phase observations.

Undifferenced float ambiguities

The UD IF ambiguities \( \bar{N}_{{r,{\text{IF}}}}^{s} \) are usually decomposed into combinations of integer wide-lane (WL) and float narrow-lane (NL) ambiguities to perform IAR, following Blewitt (1989):

$$ \bar{N}_{{r,{\text{IF}}}}^{s} = \frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{{r,{\text{WL}}}}^{s} + \frac{{f_{1} }}{{f_{1} + f_{2} }}\bar{N}_{{r,{\text{NL}}}}^{s} $$
(6)

with

$$ \begin{aligned} & N_{{r,{\text{WL}}}}^{s} = N_{r,1}^{s} - N_{r,2}^{s} \\ & \bar{N}_{{r,{\text{NL}}}}^{s} = N_{{r,{\text{NL}}}}^{s} + d_{{r,{\text{NL}}}} - d_{\text{NL}}^{s} \\ & d_{{r,{\text{NL}}}} = d_{{r,{\text{IF}}}} {{\left( {f_{1} + f_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} + f_{2} } \right)} {f_{1} }}} \right. \kern-0pt} {f_{1} }} \\ & d_{\text{NL}}^{s} = d_{\text{IF}}^{s} {{\left( {f_{1} + f_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} + f_{2} } \right)} {f_{1} }}} \right. \kern-0pt} {f_{1} }} \\ & N_{{r,{\text{NL}}}}^{s} = N_{r,1}^{s} \\ \end{aligned} $$
(7)

where \( \left( {d_{{r,{\text{NL}}}} ,d_{\text{NL}}^{s} } \right) \) are the so-called receiver- and satellite-dependent NL FCBs. The WL and NL ambiguities \( \left( {N_{{r,{\text{WL}}}}^{s} ,N_{{r,{\text{NL}}}}^{s} } \right) \) are usually fixed in two sequential steps.

First, the WL ambiguity \( N_{{r,{\text{WL}}}}^{s} \) is resolved with the Hatch–Melbourne–Wübbena combination \( \bar{N}_{{r,{\text{WL}}}}^{s} \) (Hatch 1982; Melbourne 1985; Wübbena 1985), which is defined as:

$$ \begin{aligned} \bar{N}_{{r,{\text{WL}}}}^{s} & = {{\left[ {{{\left( {f_{1} L_{r,1}^{s} - f_{2} L_{r,2}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} L_{r,1}^{s} - f_{2} L_{r,2}^{s} } \right)} {\left( {f_{1} - f_{2} } \right) - {{\left( {f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} } \right)} {\left( {f_{1} + f_{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1} + f_{2} } \right)}}}}} \right. \kern-0pt} {\left( {f_{1} - f_{2} } \right) - {{\left( {f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} } \right)} {\left( {f_{1} + f_{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1} + f_{2} } \right)}}}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{\left( {f_{1} L_{r,1}^{s} - f_{2} L_{r,2}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} L_{r,1}^{s} - f_{2} L_{r,2}^{s} } \right)} {\left( {f_{1} - f_{2} } \right) - {{\left( {f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} } \right)} {\left( {f_{1} + f_{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1} + f_{2} } \right)}}}}} \right. \kern-0pt} {\left( {f_{1} - f_{2} } \right) - {{\left( {f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} } \right)} {\left( {f_{1} + f_{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1} + f_{2} } \right)}}}}} \right]} {\lambda_{\text{WL}} }}} \right. \kern-0pt} {\lambda_{\text{WL}} }} \\ & = N_{{r,{\text{WL}}}}^{s} + d_{{r,{\text{WL}}}} - d_{\text{WL}}^{s} \\ \end{aligned} $$
(8)

with

$$ \begin{aligned} & d_{{r,{\text{WL}}}} = B_{r,1} - B_{r,2} - {{\left( {f_{1} b_{r,1} + f_{2} b_{r,2} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} b_{r,1} + f_{2} b_{r,2} } \right)} {{{\left( {f_{1} + f_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} + f_{2} } \right)} {\lambda_{\text{WL}} }}} \right. \kern-0pt} {\lambda_{\text{WL}} }}}}} \right. \kern-0pt} {{{\left( {f_{1} + f_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} + f_{2} } \right)} {\lambda_{\text{WL}} }}} \right. \kern-0pt} {\lambda_{\text{WL}} }}}} \\ & d_{\text{WL}}^{s} = B_{1}^{s} - B_{2}^{s} - {{\left( {f_{1} b_{1}^{s} + f_{2} b_{2}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} b_{1}^{s} + f_{2} b_{2}^{s} } \right)} {{{\left( {f_{1} + f_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} + f_{2} } \right)} {\lambda_{\text{WL}} }}} \right. \kern-0pt} {\lambda_{\text{WL}} }}}}} \right. \kern-0pt} {{{\left( {f_{1} + f_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{1} + f_{2} } \right)} {\lambda_{\text{WL}} }}} \right. \kern-0pt} {\lambda_{\text{WL}} }}}} \\ & \lambda_{\text{WL}} = {c \mathord{\left/ {\vphantom {c {\left( {f_{1} - f_{2} } \right)}}} \right. \kern-0pt} {\left( {f_{1} - f_{2} } \right)}} \\ \end{aligned} $$
(9)

where \( d_{{r,{\text{WL}}}} \) and \( d_{\text{WL}}^{s} \) are the receiver- and satellite-dependent WL FCBs. By applying these WL FCB corrections to \( \bar{N}_{{r,{\text{WL}}}}^{s} \), the WL ambiguity \( N_{{r,{\text{WL}}}}^{s} \) can be resolved according to (8) as:

$$ N_{{r,{\text{WL}}}}^{s} = \bar{N}_{{r,{\text{WL}}}}^{s} + d_{\text{WL}}^{s} - d_{{r,{\text{WL}}}} $$
(10)

Second, the resolved integer WL ambiguity and IF ambiguity estimated from the POD process are used to compute the float NL ambiguity \( \bar{N}_{{r,{\text{NL}}}}^{s} \) according to (6). Then, by applying the NL FCB corrections to \( \bar{N}_{{r,{\text{NL}}}}^{s} \), the integer NL ambiguity \( N_{{r,{\text{NL}}}}^{s} \) can be obtained according to (7) as follows:

$$ N_{{r,{\text{NL}}}}^{s} = \bar{N}_{{r,{\text{NL}}}}^{s} + d_{\text{NL}}^{s} - d_{{r,{\text{NL}}}} $$
(11)

Once the WL and NL ambiguities are fixed, the IF ambiguity can be constructed according to (6) as follows:

$$ \bar{N}_{{r,{\text{IF}}}}^{s} = \frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{{r,{\text{WL}}}}^{s} + \frac{{f_{1} }}{{f_{1} + f_{2} }}\left( {N_{{r,{\text{NL}}}}^{s} + d_{{r,{\text{NL}}}} - d_{\text{NL}}^{s} } \right) $$
(12)

In practice, the satellite-dependent FCBs can be estimated from a global network solution in advance, whereas the receiver-dependent FCBs are not available. Thus, the WL and NL UD ambiguities cannot be fixed and the UD IF ambiguities \( \bar{N}_{{r,{\text{IF}}}}^{s} \) can thus only be estimated as float parameters (hereafter, we denote the orbit solution based on the UD float ambiguity resolution (FAR) as a ‘FAR-UD’ solution).

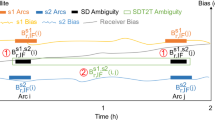
SD ambiguity resolution

In the case of SD ambiguities, between-satellite, receiver-dependent FCBs are canceled out. By applying satellite-dependent FCB corrections, the integer properties of the WL and NL SD ambiguities are recovered and can be fixed sequentially arc by arc according to (10) and (11). Then, the SD IF ambiguity can be derived from the fixed WL and NL SD ambiguities:

$$ \nabla \bar{N}_{{r,{\text{IF}}}}^{{s_{0} ,s}} = \frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}\nabla N_{{r,{\text{WL}}}}^{{s_{0} ,s}} + \frac{{f_{1} }}{{f_{1} + f_{2} }}\left( {\nabla N_{{r,{\text{NL}}}}^{{s_{0} ,s}} - \nabla d_{\text{NL}}^{{s_{0} ,s}} } \right) $$
(13)

where \( \nabla \) is the single-difference operator and s0,s denotes a satellite pair. As we process UD IF observables, the derived SD IF ambiguities are taken as pseudo-observations to constrain the UD IF ambiguity parameters during parameter estimation:

$$ \nabla \bar{N}_{{r,{\text{IF}}}}^{{s_{0} ,s}} = \bar{N}_{{r,{\text{IF}}}}^{s} - \bar{N}_{{r,{\text{IF}}}}^{{s_{0} }} ,\quad W_{r}^{{s_{0} ,s}} $$
(14)

where \( W_{r}^{{s_{0} ,s}} \) is the weight. Therefore, single-receiver IAR can be performed and hereafter we denote the orbit solution as an ‘IAR-SD’ solution.

DD ambiguity resolution

In the case of DD ambiguities, between-receiver-between-satellite, both receiver- and satellite-dependent FCBs are canceled out. Thus, the WL and NL DD ambiguities are theoretically integers and can thus again be fixed sequentially arc by arc according to (10) and (11). Then, the DD IF ambiguities can be constructed as follows:

$$ \Delta \nabla \bar{N}_{{r_{0} ,r,{\text{IF}}}}^{{s_{0} ,s}} = \frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}\Delta \nabla N_{{r_{0} ,r,{\text{WL}}}}^{{s_{0} ,s}} + \frac{{f_{1} }}{{f_{1} + f_{2} }}\Delta \nabla N_{{r_{0} ,r,{\text{NL}}}}^{{s_{0} ,s}} $$
(15)

where \( \Delta \nabla \) is the double-difference operator and r0,r denotes a receiver pair. Similarly, the constructed DD IF ambiguities are treated as pseudo-observations to constrain the UD IF ambiguity parameters:

$$ \Delta \nabla \bar{N}_{{r_{0} ,r,{\text{IF}}}}^{{s_{0} ,s}} = \bar{N}_{{r,{\text{IF}}}}^{s} - \bar{N}_{{r,{\text{IF}}}}^{{s_{0} }} - \bar{N}_{{r_{0} ,{\text{IF}}}}^{s} + \bar{N}_{{r_{0} ,{\text{IF}}}}^{{s_{0} }} ,\quad W_{{r_{0} ,r}}^{{s_{0} ,s}} $$
(16)

where \( W_{{r_{0} ,r}}^{{s_{0} ,s}} \) is the weight. Hereafter, we denote the orbit solution as an ‘IAR-DD’ solution.

Integrated SD and DD ambiguity resolution

Once the SD and DD ambiguities have been fixed, we can also constrain the UD IF ambiguity parameters with both (14) and (16) during parameter estimation. As SD and DD ambiguities are fixed simultaneously, only the SD ambiguities for a single LEO satellite (here we select GRACE A) are needed to be fixed. The obtained orbit solution is denoted as an ‘IAR-SD-DD’ solution hereafter. At this point, one may deduce that the IAR-SD-DD scheme is essentially equivalent to the IAR-SD one, where the SD ambiguities for GRACE A and B are fixed separately, due to the fact that the DD ambiguities between GRACE A and B are constructed from their respective SD ambiguities. Theoretically, this is true when assuming strictly common observations on both GRACE satellites. However, this is not the case in practice and in fact, one can obtain a better performance of the IAR-SD-DD scheme as will be shown later.

Fixing decision

In this study, the fixing decision is made according to the probability P0 (fixing to the nearest integer), which is calculated with the formula as proposed in Dong and Bock (1989). Given a confidence level \( \alpha \), the ambiguity can be fixed to its nearest integer if P0 is larger than \( 1 - \alpha \), otherwise not. In this study, we choose a confidence level of 0.1%, which has been proven feasible in practice (Dong and Bock 1989; Ge et al. 2005, 2008).

Ambiguity constraint

Concerning the weights of the pseudo-observations used to constrain the UD IF ambiguities, the situations are different for SD IAR and DD IAR. As shown in (15), once the WL and NL DD ambiguities are correctly fixed, the derived DD IF ambiguities can be treated as error-free. Thus, it allows assigning an arbitrarily large weight to the DD ambiguity pseudo-observation, i.e., Eq. (16). In this research, we impose strong constraints by setting the precision of the DD IF ambiguities \( \nabla \Delta \bar{N}_{{r_{0} ,r,{\text{IF}}}}^{{s_{0} ,s}} \) to be \( 1 \times 10^{ - 4} \) L1 cycles or about 0.02 mm in length unit.

Nevertheless, this is not the case for SD IAR. As shown in (13), even if the WL and NL SD ambiguities are correctly fixed, the SD ambiguity is still not free of error because the NL SD FCBs contain errors. Thus, the weights assigned to the SD ambiguity pseudo-observations may influence the orbits. To investigate the possible impacts, we produced three sets of orbit solutions, where precision of the SD ambiguity pseudo-observations was set to be 2, 0.2 and 0.02 mm, respectively. Note that a precision lower than 2 mm could not provide enough constraint to improve the orbits, while a precision of 0.02 mm was adequate, and a higher precision could not further change the orbits. The results revealed that, while orbit comparison to the JPL reduced-dynamic orbit and SLR validation were insensitive to the precision settings, the KBR validation was rather sensitive to them. While increasing the precision settings from 2 to 0.02 mm gradually improved the KBR validation in the case of the integrated IAR-SD solution, the KBR validation gradually degraded in the case of the IAR-SD-DD solution. This indicates that the current absolute orbit accuracy (usually at the centimeter level) is insensitive to the errors in the FCBs under consideration. On the other hand, this implies that FCB-induced orbit errors can be mitigated when forming baselines from the IAR-SD orbits, while they exist in the baselines constructed from the IAR-SD-DD orbits because SD IAR is only performed on GRACE A in that case. We, therefore, impose soft (2 mm) and hard (0.02 mm) constraint to the SD ambiguity pseudo-observations for the IAR-SD-DD and IAR-SD solution, respectively, in the following computations.

Results

Based on the POD strategy, four sets of GRACE orbits have been produced for the year 2010 using different AR schemes. Each set of the orbit consists of a dynamic and kinematic one. In this section, we first give a description about the quality of the employed FCB products. Then, the obtained orbits will be evaluated in a comprehensive way.

Quality of FCB products

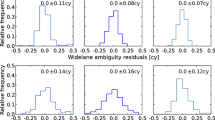
As the quality of the FCB products play a crucial role in performing single-receiver IAR, for the purpose of illustration, the distribution of the fractional parts of all the FCB-corrected WL and NL ambiguities on the twin GRACE satellites for a typical orbital arc (2009-12-31 21:00:00 to 2010-01-02 03:00:00) is shown in Fig. 1. In the given example, about 90% of the fractional parts are confined to 0.25 cycles for both WL and NL ambiguities. Another efficient way to validate the FCBs is to check the ambiguity fixing efficiency after applying these corrections. For that purpose, we have made a statistic for all the orbital arcs and the results show that on average about 97.1% of the SD NL ambiguities can be resolved to integers. In the case of the DD ambiguities, our statistics have revealed a slightly higher fixing rate (about 97.3%), which agrees well with those reported in the previous studies (Allende-Alba and Montenbruck 2016; Mao et al. 2017). Thus, the fixing rate for the SD ambiguities is in close accordance with that for the DD ambiguities. This confirms a good quality of the FCB products, as well as the feasibility of performing IAR at a single GRACE satellite.

Fig. 1
figure 1

Distribution of the fractional parts of all the FCB-corrected WL (top) and NL (bottom) SD ambiguities. The mean and standard deviations are displayed in the top right corners

Full size image

Orbit comparison

The obtained orbits are compared with the JPL reduced-dynamic orbits which have been released as the GRACE GNV1B RL02 product. JPL has proposed a distinctive approach to single-receiver IAR. In that approach, the wide-lanes and phase biases of the ground stations were derived in advance from a global network solution and introduced as known when resolving DD ambiguities between the local receiver being point-positioned and a receiver from the global network solution. Thus, single-receiver IAR can be performed in the sense that no other receiver data are required. This approach has been used to produce the GNV1B RL02 products (Bertiger et al. 2010).

Figure 2 shows the daily difference RMSs between the JPL reduced-dynamic orbit and our dynamic orbits derived from different AR schemes for GRACE B. The plots for GRACE A show similar patterns. Thus, they are not shown here. It can be seen that our dynamic orbits show impressive consistency with the JPL orbit: the differences are no more than 16 mm in 3D RMS for all cases (Table 2). Despite that, IAR is still able to improve the consistency, particularly when the SD ambiguities are fixed. In case of GRACE B, the mean difference RMSs are reduced by 36, 5 and 24% in the along-track, cross-track, and radial components, respectively, when compared to the FAR-UD orbit (Table 2). This is not strange, because JPL also performed single-receiver IAR during their POD process. On the other hand, the difference RMS values with respect to the JPL orbit for the IAR-SD and IAR-SD-DD orbits are hardly discernible for both satellites as can be seen from both Fig. 2 and Table 2. In the case of GRACE B, this indicates that the effect of IAR-SD-DD can be equivalent to that of IAR-SD. Note that in case of IAR-SD-DD, we only resolve the SD ambiguities at GRACE A and the DD ambiguities between GRACE A and B, whereas the SD ambiguities are separately resolved in the case of IAR-SD.

Fig. 2
figure 2

Daily RMS of differences between the JPL reduced-dynamic orbit and our dynamic orbits derived from different AR schemes for GRACE B

Full size image
Table 2 Mean RMS (mm) of differences between the JPL reduced-dynamic orbit and our dynamic orbits derived from different AR schemes
Full size table

Figure 3 displays the daily difference RMSs between the JPL orbit and our kinematic orbits derived from different AR schemes for GRACE B. The ambiguities from the dynamic orbit determination process have been used when computing the kinematic orbits. Again, the plots for GRACE A are not shown here due to their similar patterns as GRACE B. In general, the results are similar to those for the dynamic orbits.

Fig. 3
figure 3

Daily RMS of differences between the JPL reduced-dynamic orbit and our kinematic orbits derived from different AR schemes for GRACE B

Full size image

However, a comparison between Figs. 2 and 3 reveals that the improvements for the kinematic orbits obtained with IAR-SD are more significant than those for the dynamic orbits. For GRACE B, the mean difference RMSs are reduced substantially by 59, 54 and 42% for the along-track, cross-track and radial components, respectively, as opposed to the FAR-UD orbit (Table 3). Unlike the dynamic orbit, whose accuracy is largely dominated by the applied force models, the quality of the kinematic orbit is completely dependent on the precision and geometry of the observations. Thus, this indicates that single-receiver IAR can enhance the observation strength and considerably improve the quality of the kinematic orbit. Finally, it can be seen that the IAR-SD-DD scheme is able to provide orbits of the same quality as IAR-SD (Table 3), again demonstrating their equivalent effects regarding absolute orbit accuracy.

Table 3 Mean RMS (mm) of differences between the JPL reduced-dynamic orbit and our kinematic orbits derived from different AR schemes
Full size table

SLR validation

The international laser ranging service (ILRS) (Pearlman et al. 2002) provided SLR measurements to the GRACE satellites. Thus, the SLR measurements are used as an independent validation of the obtained orbits. For that purpose, coordinates of the SLR stations are referred to the SLRF2008 (v 16/08/08) frame (https://ilrs.cddis.eosdis.nasa.gov/science/awg/SLRF2008.html). In addition, site loading displacement induced by solid earth tides, ocean tides and pole tides is modeled according to IERS 2010 and applied as corrections to the station coordinates. As to the SLR observations, the slant tropospheric delay is computed with the zenith delay model (Mendes and Pavlis 2004) and mapping function (Mendes et al. 2002). The general relativistic time delay due to gravitational bending is modeled according to IERS 2010. Furthermore, due to the different performance of the SLR stations (Arnold et al. 2018a), a subset of 16 high-performance stations (Yarragadee, Matera, San Juan, Koganei, Graz, Greenbelt, Herstmonceux, Potsdam, Concepcion, Mount Stromlo, San Fernando, Papeete, Monument Peak, Zimmerwald, Grasse, Arequipa) have been selected for this validation, which contribute about 81% of the available observations. In addition, a threshold of 20 cm is applied to detect outliers, which further exclude about 1% of the observations from the selected 16 stations.

Figure 4 displays the SLR residuals for the kinematic orbits obtained from different AR schemes. It can be observed that the vast majority of them are confined to ± 5 cm, which indicates a good quality of the obtained kinematic orbits. This is particularly true when the SD ambiguities are fixed. In that case, residuals are distinctly less scattered for both satellites. The residual RMSs for the IAR-SD kinematic orbits are reduced considerably by 31% and 35% for GRACE A and B, respectively, when compared to those for the FAR-UD orbit (Table 4). Finally, the differences between the SLR validations are hardly discernible for the IAR-SD and IAR-SD-DD orbits as can be seen from Fig. 4 and Table 4. These results are consistent with those from the independent orbit comparisons and also demonstrate the equivalent effect of IAR-SD and IAR-SD-DD regarding absolute accuracy.

Fig. 4
figure 4

SLR residuals for GRACE kinematic orbits derived from different AR schemes

Full size image
Table 4 Mean, STD and RMS (mm) of the SLR residuals for dynamic and kinematic orbits derived from different AR schemes
Full size table

In view of the dynamic orbits, SLR validation reveals that the improvements obtained with IAR are insignificant as compared to the kinematic orbits (Table 4), as well as those reported in other studies (Montenbruck et al. 2017, 2018), which also indicates that the accuracy of our dynamic orbits is largely dominated by the applied force models. Finally, the results also show that IAR-SD-DD can provide the same absolute orbit accuracy as IAR-SD.

KBR validation

The K-Band ranging system onboard GRACE has measured the range (with a bias) between the twin satellites at the micron level (Dunn et al. 2003), which offers a unique possibility to validate the relative position accuracy of the twin satellites in the approximate along-track direction.

Figure 5 shows the daily STDs of KBR residuals (observed minus computed) for the dynamic (top) and kinematic (bottom) orbits derived from different AR schemes. It is clear that IAR has considerably reduced the STDs for both orbits. In view of dynamic orbits, IAR-SD improves the STD from 6.7 to 1.7 mm, a factor of about four, which is consistent with previous studies where relatively short periods of data have been processed (from several days to several tens of days) (Allende-Alba et al. 2018; Arnold et al. 2018b; Bertiger et al. 2010; Laurichesse et al. 2009). While the KBR validation performance of our IAR-SD orbit is slightly better than those in the above-mentioned investigations, it is still worse than IAR-DD as can be seen from Fig. 5 and Table 5. We explain this by the fact that the FCB products are not free of error and their errors might have degraded the KBR validation. In addition, the IAR-SD-DD orbit presents the same performance as the IAR-DD orbit as can be seen from Fig. 5 and Table 5. We also note that the achieved best relative accuracy (1.1 mm) still cannot reach the highest (sub-mm) level as reported in previous research, where single-differenced or double-differenced GPS data have been processed (Allende-Alba and Montenbruck 2016; Gu et al. 2017; Jäggi et al. 2007; Kroes et al. 2005; Mao et al. 2017). We attribute this to the fact that we have processed undifferenced data in this research (Table 1), thus common mode errors from the GPS satellites (and receivers) cannot be effectively mitigated as compared to the single-differenced (and double-differenced) data processing scheme.

Fig. 5
figure 5

Daily STDs of the KBR residuals for the dynamic (top) and kinematic (bottom) orbits derived from different AR schemes

Full size image
Table 5 Mean STDs (mm) of KBR residuals for the dynamic and kinematic orbits derived from different AR schemes
Full size table

Regarding kinematic orbits, as they occasionally suffer from large errors, the KBR residuals must be cleaned from outliers. In that regard, the residuals exceeding a given threshold (10 times the corresponding STD) are identified and then excluded from the statistics. The procedure is iterated until no more outliers are found. As a result, less than 0.3% of the residuals have been discarded in all four considered cases. STDs of the cleaned residuals are listed in Table 5. In general, the relative performances among different AR schemes are similar to those for dynamic orbits. But the KBR validation is still inferior to that of the dynamic orbits due to the relative poor model strength of the PPP approach with respect to the dynamic approach as can be seen in Table 5.

Discussion

Although IAR-SD can achieve the same relative orbit accuracy as IAR-DD from the theoretical point of view, all studies up to now show that IAR-SD still cannot compete with IAR-DD in terms of relative accuracy (Allende-Alba et al. 2018; Arnold et al. 2018b; Bertiger et al. 2010; Laurichesse et al. 2009). In our study, we point out that errors in the NL FCBs may partly explain this degradation. One may argue that the GPS orbit and clocks adopted in this study are not coming from one unique source and this may be considered crucial in the case of IAR-SD. On the one hand, we believe that our GPS clocks are consistent with the GPS orbits and can support SD IAR as shown in Geng et al., (2019). On the other hand, we note that all previous studies showed that IAR-SD performed worse than IAR-DD in terms of relative orbit accuracy, although the GPS orbits and clocks they used were from a unique source. In fact, we also produced the GRACE orbits using the GPS orbits and integer clocks released by CNES/CLS (Centre National d’Études Spatiales/Collecte Localisation Satellites) analysis center (Loyer et al. 2012). Unfortunately, this did not alter the conclusions and we did not observe any further improvements in the relative accuracy of the IAR-SD orbits. Thus, we speculate that errors in the GPS clocks cannot be thoroughly canceled out in case of SD IAR, although the GPS clocks have to be considered error-free in the data processing. It should be noted that this is also applicable in our case because of the 1-to-1 linear dependency between NL FCBs and GPS clock corrections. We suggest that the residual errors must be properly accounted for in data processing to achieve the best orbit accuracy. In our case, we have dealt with this issue through constraining the SD IF ambiguities in a proper manner as described in the section of ambiguity constraint.

Conclusions

In this study, we have proposed an integrated IAR scheme for formation-flying satellites to enhance the orbit solutions. To demonstrate the added value, four sets of orbits have been produced using 1 year of GPS data collected by GRACE. For the first set, we have estimated the UD ambiguities as float parameters (denoted as the ‘FAR-UD’ solution). For the second one, SD IAR has been performed (denoted as the ‘IAR-SD’ solution). For the third one, only the DD ambiguities between the twin GRACE satellites have been resolved (denoted as the ‘IAR-DD’ solution) and for the fourth one the SD and DD ambiguities have been fixed simultaneously (denoted as the ‘IAR-SD-DD’ solution). The obtained orbits are evaluated by comparison with the JPL reduced-dynamic orbit, external validation with independent SLR and KBR measurements. Based on this analysis, we have shown that the integrated IAR-SD-DD scheme is able to provide the best absolute and relative orbit accuracies simultaneously. These findings are likely applicable also to other formation-flying satellites, at least for those distributed in short/medium-size baselines and composed of identical spacecraft.