1 Introduction

The presence of stenosis is often related to the narrowing of blood vessels as a result of plaque formation. The blood flow characteristics in the microvascular stenosis contain important information related to circulatory disorders or microvascular diseases, such as lacunar infarct (Clark et al. 2017) and coronary microvascular disease (Labazi and Trask 2017). A high risk of microvascular blockage may lead to complete blood flow stopping in microvessels, depending on the severity of stenosis. Due to the complexity of blood flow and biophysical properties, the hemodynamic and hemorheological features have not yet been clearly explored.

The blood flow is significantly disturbed by the microstenosis (Ha and Lee 2013; Hu et al. 2015), such as pressure drop and red blood cell distribution. The pressure drops in stenosed microfluidic channel increase significantly with the increase in fluid viscosity (Hu et al. 2015). The severity of the stenosis determines the condition of blood flow stopping (Polwaththe-Gallage et al. 2016). In vivo experiments, it has been observed that the RBCs advance in narrow capillaries in a single file surrounded with plasma under normal conditions, while the flow of RBCs in the larger microvessels is usually multi-file and the transition to multi-file flow is also attributed to an increase in hematocrit (Bryngelson and Freund 2016, 2018; Pries and Secomb 2005). When flowing in a vessel, faster flow velocity promotes the migration of RBCs from the vessel wall toward the vessel center, resulting in a cell-rich central core and a cell-free layer (CFL) formation near the wall, and produces higher mean velocity of cells compared to plasma. This leads to a reduction in the tube hematocrit compared to the discharge hematocrit, which is called Fahraeus effect, and a reduction in the apparent blood viscosity with decreasing tube diameter, which is called Fahraeus–Lindqvist effect. Both the Fahraeus and Fahraeus–Lindqvist effects are observed to be significantly affected by the microstenosis (Vahidkhah 2015) and bifurcations (Bacher et al. 2018), which are common in vascular system. The distribution of RBCs/CFL thickness exhibits asymmetry up- and downstream the stenosis (Bacher et al. 2017; Fujiwara et al. 2009; Vahidkhah 2015). The experimental studies on microfluidic conduits with severe constrictions demonstrated that the CFL thickness downstream increases and even cell separation occurs (Vahidkhah 2015).

RBCs tend to aggregate under low-shear conditions or when certain plasma proteins or other long-chain macromolecules such as Dextran exist in the blood (Steffen et al. 2013). Under low-shear force, RBCs have a propensity to accumulate to form the stacks-of-coins-like rouleaux, and the aggregates can reversibly be broken into smaller aggregates or individual cells as the shear force increases under normal conditions (Bagchi et al. 2005). It has been experimentally demonstrated that at low-shear condition, RBC aggregation significantly affects the blood flow including cell-free layer, local hematocrit and local viscosity distribution, by investigating the transport of RBC aggregates in rectangular microchannels (Kaliviotis et al. 2016; Sherwood et al. 2014a) and in bifurcating flows (Kaliviotis et al. 2017; Sherwood et al. 2014b). It has been proved that the older RBCs exhibit great aggregability compared to younger cells (Rampling et al. 2004). Generally, the elevated levels of aggregation are often accompanied with a large number of pathological states, such as sepsis and diabetes (Ernst 1988). In vivo studies and viscometric measurements (Chien et al. 1966; Reinke et al. 1987) of whole blood viscosity have shown a steep viscosity increase for shear rates below 10 s−1, and the cell-free layer thickness increases with the reduction in shear rate due to cell aggregation. Due to technological limitations of experimental techniques and measurements, few studies provide detailed hemodynamic information in microvessels. With the advances in computer and simulation technology, numerical simulation facilitates investigations on blood flow in stenosed microvessels. A three-dimensional computational model of RBCs up to O(102) in semi-dense suspension based on immersed boundary method was developed, and the microrheological data were obtained (Doddi and Bagchi 2009). And a three-dimensional finite volume method combined with finite-discrete element method was established to compute the deformation of 49512 RBCs under the influence of aggregating forces (Xu et al. 2013). Also, Fedosov et al. (2010b) employed dissipative particle dynamics combined with an efficient parallel code, which has the potential to simulate the number of RBCs up to the order of O(104), to investigate the blood flow in tubes ranging from 10 to 40 µm for different hematocrits and capture the Fahraeus and Fahraeus–Lindqvist effects. Several numerical models combined with dissipative particle dynamics have been developed to simulate the transport of platelet in the stenotic microchannels to explain the mechanism of platelet-mediated thrombus formation (Gao et al. 2017; Yazdani and Karniadakis 2016; Yazdani et al. 2017). This numerical method has been used to investigate the motion and deformation of two red blood cells in a stenosed microvessel (Xiao et al. 2016b). It is necessary to further investigate the blood flow through the microvascular stenosis to measure the hemodynamics by numerical techniques.

In this study, dissipative particle dynamics (DPD) method combined with a spring-based network cell model is employed to carry out simulations of blood flows in stenosed microvessels. Cell–cell interaction is represented by a Morse potential function based on depletion model. Then, the simulation results of blood flow at different hematocrits in the tube ranging from 10 to 20 µm will be compared with the experimental results. Next, the blood flow properties in terms of CFL thickness, velocity profiles as well as Fahraeus–Lindqvist effect will be examined. Then, the effects of the presence of the stenosis on the blood flow properties will be discussed. Finally, the effects of RBC aggregation combined with decreased stenosis on the blood flow in the stenosed microvessels of 20 µm will be investigated.

2 Model and methods

2.1 DPD method, RBC membrane model and RBC aggregation model

The blood flow dynamics is simulated by dissipative particle dynamics method, which has been adopted in our previous studies (Xiao et al. 2016a, b). Introductions to DPD method have been presented in detail (Espanol 1995; Groot and Warren 1997; Hoogerbrugge and Koelman 1992). In brief, each DPD particle represents a soft lump of atoms and interacts with surrounding particles by three simple pairwise additive forces: conservative force, dissipative force and random force. Particle motion is governed by Newton’s equations of motion.

$$\begin{aligned} & {\text{d}}{\mathbf{r}}_{i} = {\mathbf{v}}_{i} {\text{d}}t \\ & m_{i} {\text{d}}{\mathbf{v}}_{i} = \sum\limits_{j \ne i} \left( {{\mathbf{F}}_{ij}^{\text{C}} - \gamma \left[ {\omega (r_{ij} )} \right]^{2} ({\mathbf{v}}_{ij} \cdot {\hat{\mathbf{r}}}_{ij} ){\hat{\mathbf{r}}}_{ij} + \sigma \omega (r_{ij} )\frac{{\xi_{ij} }}{{\sqrt {dt} }}{\hat{\mathbf{r}}}_{ij} } \right){\text{d}}t + {\mathbf{F}}_{\text{ext}} {\text{d}}t \\ \end{aligned}$$
(1)

where \({\mathbf{r}}_{i}\), \({\mathbf{v}}_{i}\) and \(\text{m}_{i}\) are the location, velocity and mass of the ith particle and the mass of the individual particle is set to 1; t is the time. \({\mathbf{F}}_{{i{\kern 1pt} j}}^{\text{C}}\) is conservative force between particle i and j. γ and σ reflect the strength of dissipative and random forces, respectively. \(\omega (r_{ij} )\) is a distance-dependent weight function. \({\hat{\mathbf{r}}}_{ij} = {\mathbf{r}}_{{{\mathbf{i}}j}} /r_{ij}\), \({\mathbf{r}}_{ij} = {\mathbf{r}}_{i} - {\mathbf{r}}_{j}\) and \({\mathbf{v}}_{ij} = {\mathbf{v}}_{i} - {\mathbf{v}}_{j}\). \(\xi_{ij}\) is a normally distributed random variable with zero mean, unit variance and \(\xi_{ij} = \xi_{ji}\); dt is the time step. \({\mathbf{F}}_{\text{ext}}\) is the external force acted on particle i.

The cell membrane is modeled as a collection of particles connected by elastic springs. These springs comprise a network, which is endowed with in-plane and bending energy as well as constraint of surface area and volume. The details of the RBC membrane model and the scaling procedure have been described in previous studies (Fedosov et al. 2010a; Li et al. 2014; Pivkin and Karniadakis 2008; Xiao et al. 2016b). To characterize the RBC aggregation, the depletion model introduced by Liu et al. (2004) was employed. In this model, the interaction energy is represented by a Morse potential function \(\psi (r)\).

$$\psi (r) = D_{\text{e}} [{\text{e}}^{{2\beta (r_{0} - r)}} - 2{\text{e}}^{{\beta (r_{0} - r)}} ]$$
(2)

where r is the distance between two plane elements of the opposing RBCs directly facing each other, \(r_{0}\) is the zero force length, \(D_{\text{e}}\) is the intercellular interaction strength and \(\beta\) is the scaling factor controlling the interaction decay behavior. The corresponding parameters setting also can be found in (Xiao et al. 2016b). Therefore, the total interaction energy (Ye et al. 2014) of a triangulated cell is expressed by

$$\psi (\{ {\mathbf{r}}_{i} \} ){\kern 1pt} = \sum\limits_{{j = 1,N_{\text{t}} }} {\psi (r_{jk} )} ({\mathbf{n}}_{j} \cdot {\mathbf{I}}_{j} )({\mathbf{n}}_{k} \cdot {\mathbf{I}}_{k} )A_{j}$$
(3)

where \(r_{jk}\) is the local distance between the jth and kth triangles located in cell 1 and 2, respectively. \(N_{\text{t}}\) is the number of the triangle elements which are linked by particle i. \({\mathbf{n}}_{j}\) and \({\mathbf{n}}_{k}\) are the outward unit normal vectors to the those curved elements, and \({\mathbf{I}}_{j}\) and \({\mathbf{I}}_{k}\) stand for the unit vectors parallel to the line joining the centers of two cells and directed toward each other. \(A_{j}\) is the area of jth triangle of cell 1, as shown in Fig. 1. A healthy unstressed RBC has a biconcave equilibrium shape with the minimum energy (Evans et al. 2013) and is described by

$$z = \pm \,D_{0} \sqrt {1 - \frac{{4(x^{2} + y^{2} )}}{{D_{0}^{2} }}} \left[ {a_{0} + a_{1} \frac{{x^{2} + y^{2} }}{{D_{0}^{2} }} + a_{2} \frac{{(x^{2} + y^{2} )^{2} }}{{D_{0}^{4} }}} \right]$$

where D0 = 7.82 is the average diameter, a0 = 0.0518, a1 = 2.0026, a2 = -4.491 The surface area and volume of the RBC are equal to 135 µm2 and 94 µm3, respectively. The RBC membrane model has been validated by comparing the simulated results with optical tweezer stretching results (Xiao 2016).

Fig. 1
figure 1

Schematic illustration of the intercellular force acting on the jth membrane particle of cell 1 from the kth particle of cell 2

Full size image

The interaction force acting on the membrane particle i in cell 1 is given by:

$${\mathbf{F}}_{i}^{\text{agg}} = - \frac{{\partial \psi (\left\{ {{\mathbf{r}}_{i} } \right\})}}{{\partial {\mathbf{r}}_{i} }}$$
(4)

It has been shown that the intercellular force is simply illustrated as a weak attractive force at far distance (r > r0), but a strong repulsive force at near distance (r < r0). Such repulsive interactions cannot prevent the neighboring RBCs from an overlap. To avoid this, a short-range Lennard–Jones potential combined with specular reflection of RBC vertices on membranes of other RBCs is employed (Fedosov et al. 2011).

2.2 Parallel algorithm implementation

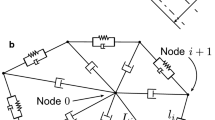
The 3D simulation of the blood flow is usually limited to the high computational cost. In order to improve the computing efficiency, the parallel computation message passing interface (MPI) technology was implemented in the simulation system. A domain decomposition method was employed to divide the computational domain into several sub-domains with approximately equal computational expense. So the global computation load was divided into sub-tasks and each sub-domain was assigned to a single processor, as illustrated in Fig. 2a. The particles located near the boundary of each sub-domain may interact with the particles in the neighboring ones. Therefore, the information of these particles should be passed through message communication. A ghost zone is created for each sub-domain, where the particles are equivalent to the particles near the boundary in the neighboring sub-domain (Alizadehrad et al. 2012). So the information of these particles is shared among the neighboring processors through MPI_SENDRECV operation, as shown in Fig. 2b. These ghost zone particles are only involved in the evaluation of forces on the particles located on the boundary of the sub-domain. The position of a particle changes gradually over time, and subsequently, it may exceed the boundary of the current sub-domain. When it enters into the adjacent sub-domain, the neighboring processor should take in charge of tracking this particle. The positions of the particles updated are used to determine if the particles located in boundary would be reassigned to neighboring processor every time step.

Fig. 2
figure 2

Sketch diagrams of domain decomposition (a) and communication between two neighboring processors (b) and the snapshot of cell across two processors (c)

Full size image

Regarding to the computation of forces on the membrane particles, it not only involves the interaction between the neighboring particles, neighboring triangles, but also involves that between the neighboring RBCs. Firstly, the initial information of the membrane particles representing the spontaneous parameter values related to the RBC network model is shared among all the processors since the simulation systems were not large enough. If the whole RBC membrane particles locate in a processor, there is no difference between this case and in serial computing. However, with the motion and deformation of the RBCs, an individual RBC may occupy several processors concurrently, as shown in Fig. 2c, identification of each part of the cell and communication is needed. Each membrane particle and each RBC have a global fixed identity number, which enables the recognition of each part for the RBC across several processors. Meanwhile, each membrane particle is assigned to a local identity number in the given processor to facilitate computing the membrane force. In addition, the information of RBC membrane particles near the boundary of the sub-domain is sent to the neighboring processor in the same way as fluid particles.

The computational efficiency of the implemented parallel code for the blood flow was not commented on in detail. But the simulation systems for the case of Ht= 0.3 and B = 0.64 in the stenosed microvessels with a diameter of 10 μm, 15 μm and 20 μm were listed and compared with respect to computational time as shown in Table 1. The system size refers to the total number of particles, containing RBC vertices and solvent particles.

Table 1 System sizes and computational times
Full size table

3 Results and discussion

3.1 Modeling parameters and validation

Different types of DPD particles are employed to distinguish different components in the computational domain, enabling the fluid–structure interactions easier to deal with. The blood was modeled as a suspension of highly deformable RBCs. Each RBC consists of 640 particles and is 7.82 µm in diameter. It has a thickness at the thickest point of 2.5 µm and a minimum thickness in the center of 1 µm. The parameters of plasma and RBCs can refer to (Xiao et al. 2016b) and those of the RBC aggregation model are listed in Table 2. The DPD repulsion force between the membrane and fluid particles was introduced to represent the membrane impenetrability approximately. No-slip boundary condition was imposed near the wall, and a periodic boundary condition was applied along the flow. To drive the flow, a uniform body force f was applied to all particles in the flow direction, which is equivalent to the pressure gradient \(\Delta P/L = \rho f\), where \(\Delta P\) is the pressure drop over the tube length and \(\rho\) is the suspension’s mass density. Each simulation was run for sufficient time to achieve steady state, which is around 0.5 s in physical units in this study.

Table 2 Simulation parameters of RBC aggregation model
Full size table

To validate the blood flow model, blood flows in a straight microvessel with a diameter of 10, 15, 20 µm are simulated. And the simulated results are compared with the experimental ones. In the vessels larger than 200 µm, the blood can be simplified as a nearly homogenous Newtonian fluid, while in smaller vessels, such as arterioles and venules (10–25 µm in diameter), especially in capillaries (5–10 µm in diameter), the RBCs are not uniformly dispersed, so the discrete motion of RBCs is necessary to be considered. To quantitatively investigate the effect of the particulate nature of blood on the flow resistance, the relative apparent viscosity is introduced, which is defined as

$$\eta_{\text{rel}} = \frac{{\eta_{\text{app}} }}{{\eta_{\text{s}} }}$$
(5)

where \(\eta_{\text{s}}\) refers to the viscosity of the plasma and \(\eta_{\text{app}}\) represents the apparent viscosity of blood even if particulate nature of blood becomes significant in narrow tubes. The apparent viscosity is equivalent to the viscosity of a homogeneous Newtonian fluid under the same flow rate in the tube with same tube length, diameter and pressure drop as the blood flow. For a steady flow of a homogeneous Newtonian fluid through a circular cylindrical tube, the volume flow rate Q is expressed by \(Q = \pi \Delta PD^{4} /128\eta L = \pi D^{4} \bar{v}/4\), where Q is volume flow rate, L is the tube length, η is the fluid viscosity and \(\bar{v}\) is the mean blood flow velocity. Therefore, if \(\Delta P\), D, \(\bar{v}\), L are measured or known, then the apparent viscosity can be calculated

$$\eta_{\text{app}} = \frac{{\pi \Delta PD^{4} }}{128QL} = \frac{{\Delta PD^{2} }}{{32\bar{v}L}}$$
(6)

The mean blood flow velocity is defined as

$$\bar{v} = Q/A = \int_{A} {v(r){\text{d}}A_{\text{c}} /A_{\text{c}} }$$
(7)

where Ac is the area of cross section. The pseudo‐shear rate is represented by \(\overline{\gamma } = \overline{v} /D\). Most of the pseudo‐shear rates for the blood flow in straight microvessels are above or around 30 s−1, owing to the fact that the typical shear rates in in vitro and in vivo experiments are above this value.

Numerous in vitro experiments have been conducted to measure the apparent viscosity of blood in narrow glass. A decrease in the apparent blood viscosity with decreasing tube diameter was observed firstly by Fahraeus and Lindqvist in 1931. Pries et al. (1992) provided the empirical relationship between the relative apparent viscosity \(\eta_{\text{rel}}\) and tube diameter D, discharge hematocrit \(H_{\text{d}}\) based on previous literature data regarding relative blood viscosity in tube flow in vitro.

$$\eta_{\text{rel}} = 1 + (\eta_{{{\text{rel}},{\kern 1pt} {\kern 1pt} 0.45}} - 1) \cdot \frac{{(1 - H_{\text{d}} )^{c} - 1}}{{(1 - 0.45)^{c} - 1}}$$
(8)

where \(\eta_{{{\text{rel}},{\kern 1pt} {\kern 1pt} 0.45}}\) is the relative viscosity for a hematocrit of 0.45 and the parameter c is a function of diameter. They are given by empirical equations:

$$\eta_{{{\text{rel}},{\kern 1pt} {\kern 1pt} 0.45}} = 220 \cdot {\text{e}}^{ - 1.3D} + 3.2 - 2.44 \cdot {\text{e}}^{{ - 0.06D^{0.645} }}$$
(9)
$$C = (0.8 + {\text{e}}^{ - 0.075D} ) \cdot \left( { - 1 + \frac{1}{{1 + 10^{ - 11} \cdot D^{12} }}} \right) + \frac{1}{{1 + 10^{ - 11} \cdot D^{12} }}$$
(10)

The tendency of RBCs to migrate toward the center of the tube results in higher mean velocity of RBCs compared with the plasma. This leads to an increased value of discharge hematocrit, \(H_{\text{d}}\), when the cells leave the tube exit. It was firstly discovered by Fahraeus in in vitro experiments of blood flow in glass tubes. An empirical description of in vitro experimental data for \(H_{\text{d}}\) as a function of \(H_{\text{t}}\) and diameter D was presented by Pries et al. (1992), which is expressed by

$$\frac{{H_{\text{t}} }}{{H_{\text{d}} }} = H_{\text{d}} + (1 - H_{\text{d}} )(1 + 1.7{\text{e}}^{ - 0.35D} - 0.6{\text{e}}^{ - 0.01D} )$$
(11)

Figure 3a, b shows the instantaneous RBC distribution for the blood flow without considering RBC aggregation and with De= 1 μJ/m2. With the increase in the intercellular interaction strength, a distinct rouleaux structure can be observed under the relatively flow rate. Figure 3c presents the relative apparent viscosities obtained from the simulation results and compares these simulated values with the empirical fit to experiments (Pries et al. 1992). The findings showed a pronounced decrease in the relative apparent viscosity as the microvessel diameter decreases. It can be seen that the simulation results for the blood flow without considering RBC aggregation or with relatively weak RBC aggregation overpredict the relative apparent viscosity for Ht = 0.3. But, in such straight cylindrical microvessels, the apparent viscosity decreases with the increased intercellular interaction strength. That is due to the fact that RBC aggregation leads to contracted RBC core and enhanced cell-free layer near the vessel wall, which has been observed in previous studies (Bishop et al. 2001; Cokelet and Goldsmith 1991). The resulting decrease in the apparent viscosity is the combined effect of the cell-free layer with low viscosity and the RBC core with high viscosity (Baskurt and Meiselman 2007). The net result of enhanced aggregation depends on the balance between these two effects. When the intercellular interaction strength increases to 0.5 µJ/m2, the relative apparent viscosity decreases to the value nearly same as the empirical description. The relative apparent viscosity for De = 1.0 µJ/m2 is slightly lower than the corresponding empirical value. In fact, during the RBC doublet formation and disruption, the aggregating and disaggregating forces between a pair of RBCs in autologous plasma have been probed by optical tweezers (Lee et al. 2016). The RBC pair’s interaction energy density for the aggregation and disaggregation processes, which matches the intercellular interaction strength in the adopted “depletion layer” model, is about 0.4 µJ/m2 and 2–6 µJ/m2 (Lee et al. 2016) separately. It indicates that this blood flow model with considering RBC aggregation can precisely reproduce Fahraeus–Lindqvist effect.

Fig. 3
figure 3

Snapshots of instantaneous RBC distribution for De= 0 μJ/m2 (a) and De= 1 μJ/m2 (b), and comparison of relative apparent viscosity between the simulation results and empirical description in Eq. (11) (c)

Full size image

The Fahraeus–Lindqvist effect is directly attributed to the formed cell-free layer near the microvessel wall. In large blood vessels, as the thickness of CFL is much smaller compared with the tube diameter, its effect can be neglected. While for the small microvessels, the presence of the CFL significantly decreases the apparent viscosity. To determine the thickness of cell-free layer, the distance between the outer edge of the cell and the wall was measured, as illustrated in Fig. 4. Take the samples of CFL thickness every 0.5 µm along the flow direction and per 9° in a counterclockwise direction from a single snapshot, and the thickness over all segments and a period time was averaged.

Fig. 4
figure 4

Illustration of CFL measurement

Full size image

Figure 5 shows that cell-free layer thickness for different tube diameters. It is found that the thickness of cell-free layer increases with the tube diameter and increased RBC aggregation. This trend is in a good agreement with previous experimental findings (Maeda et al. 1996; Soutani et al. 1995). The strong RBC aggregability, generating strong attractive force, tends to attract the RBCs closer. The shear forces applied by the plasma cannot dissociate the aggregates, and a more concentrated RBC core with high viscosity produces. In fact, a similar discovery has been reported in in vivo experiments by Maeda et al. (1996) and in vitro experiments by Kaliviotis et al. (2017). Specifically, the flowing individual cells in the cell-rich core were visible separately at a low concentration of dextran while in a high-dextran concentration, the cell core was more compactly packed and the boundary among cells was indistinct. And the thickness of cell-free layer was found to increase with increasing dextran concentration. Reinke et al. (1987) compared the thickness of cell-free layer in saline, plasma and dextran solutions. They demonstrated a significant effect of the aggregation on the thickness of cell-free layer with the decrease in the tube diameter at shear rate of around 30 s−1 and an obvious reduction in relative apparent viscosity as a consequence of an increased tendency of the RBCs to form aggregates, which also can be found in Fig. 4. The discrepancy between simulated results and in vivo results may ascribe to several reasons such as vessel elasticity, close proximity of the site of CFL measurements to vessel bifurcations, spatial resolution of the measurements (Fedosov 2010). Also, the microvessel wall was assumed to be rigid in our simulation while the in vivo experiment had an elastic wall. Maeda et al. (1996) reported that the CFL of an elastic vessel was 0.4 μm thinner than that of the hardened vessel at high hematocrits (30% ≤ Ht≤ 45%), but thicker than the hardened vessel at low hematocrits (Ht= 8%). Furthermore, there is no significant effect of the aggregation on the cell-free layer thickness for high‐shear rates, which were estimated at \(\overline{\gamma } > 50\;{\text{s}}^{ - 1}\) (Reinke et al. 1987). Here, the blood flow over 50 s−1 is not considered in the following study. Since the simulation results are nearly in agreement with the experimental findings, the blood flow model is able to capture the blood flow properties in microvessels.

Fig. 5
figure 5

CFL thickness obtained in the simulated blood flows in microvessels with different diameters in comparison with experimental data (Soutani et al. 1995), Dc represents the concentration of Dextran T-70, which affects the velocity of the RBC rouleaux formation

Full size image

3.2 The microvascular blood flow in the presence of a stenosis

Few studies have been conducted on the local hemodynamics at the microvessel stenosis. This study aims to predict the blood flow properties in a stenosed microvessel. To mimic the stenosed microvessel, a rigid cylindrical channel with a constriction of symmetrical geometry is employed, as shown in Fig. 6. The length of stenosis counts for 30% of the whole length. When the RBCs pass through such a long stenosis, the cells have enough time to interact with the stenosis and recover their approximately parachute shape (Isfahani and Freund 2012). An area blockage, B, is introduced to define as the ratio of the blockage cross-sectional area at the throat of the constriction to the nominal cross-sectional area of the vessel far away from the constriction. Here, the diameter of the throat is denoted by Dth, so the area blockage B is

Fig. 6
figure 6

Schematic illustration of geometry of a stenosed microvessel

Full size image
$$B = 1 - \left( {\frac{{D_{\text{th}} }}{D}} \right)^{2}$$
(12)

In order to investigate the effects of the presence of stenosis on the blood flow, B = 0.36 is used first to simulate the blood flow in the microvessel with a diameter of 10 μm, 15 μm and 20 μm, respectively.

Figure 7a shows the instantaneous RBC distribution for the blood flow in a stenosed microvessel for D = 20 μm and labels different streamwise locations: far upstream (location a) and downstream (location d), and upstream and downstream close to the throat of the stenosis (location b and c). Significantly, the RBC clusters in front of the stenosis have a high concentration, as shown in Fig. 7a. The velocity profiles at these locations are normalized by the time-averaged flow velocity \(v(r)/\bar{v}\). From Fig. 7b, it can be seen that the velocity profiles are not asymmetric up- and downstream the stenosis along the flow direction though the microvessel is symmetric in geometry. At same distance from the throat, the upstream profile is flatter than the downstream profile as multiple RBCs enter simultaneously into the stenosis.

Fig. 7
figure 7

Snapshot of instantaneous RBC distribution (a) and time-averaged velocity profiles at different locations (b)

Full size image

To determine the CFL thickness, the distance between the outer edge of the cell and the wall, as shown in Fig. 8a, was measured and averaged over a period of time. Due to the dispersive effect of RBCs in the blood flow, the thickness of the cell-free layer displayed spatial and temporal fluctuations, as shown in Fig. 8a. The CFL thickness also exhibits asymmetric before and after the stenosed region, especially for the case of considering the intercellular interaction, as shown in Fig. 8b–d. The increased RBC aggregability reduces the intercellular distance and then increases the CFL thickness and further aggravates the asymmetry of CFL thickness. It can be observed that cell crowding occurs at the entrance of the stenosed region, causing a thinner CFL than that obtained in the downstream in Fig. 7a, which is similar to the experimental findings (Kang et al. 2008). An increased CFL thickness exists upstream the stenosis, which is more evident in larger microvessels, as shown in Fig. 8b–d. In larger microvessels, the CFL thickness downstream the stenosis experiences a slighter fluctuation when the RBC aggregation is not considered.

Fig. 8
figure 8

Illustration of CFL measurement for the blood flow in a stenosed microvessel (a) and time-averaged spatial variation in CFL thickness for stenosed and non-stenosed microvessels of D = 20 µm (b), D = 15 µm (c) and D = 10 µm (d)

Full size image

Moreover, to evaluate the effects of the presence of stenosis on the blood flow, the relative flow resistance R was introduced, which is defined by

$$R = \frac{{\eta_{\text{stenosis}} }}{{\eta_{\text{straight}} }}$$

where \(\eta_{\text{stenosis}}\) and \(\eta_{\text{straight}}\) represent the apparent viscosities of blood flow in the stenosed and straight microvessel, respectively. The relationship between the relative blood flow resistance and microvessel diameter is plotted in Fig. 9. It demonstrates that the presence of the stenosis leads to a pronounced increase in the flow resistance. Also, the difference in the relative flow resistance for stenosed microvessel increases with increasing diameter, which is similar to the discovery found by Vahidkhah et al. (2016). This means that an enhanced Fahraeus–Lindqvist effect arises for the blood flow in stenosed microvessels. Obviously, the apparent viscosity decreases significantly and the rate of decrease in the apparent viscosity with decreasing diameter is higher if consider the RBC aggregation.

Fig. 9
figure 9

Effect of the presence of stenosis on Fahraeus–Lindqvist effect

Full size image

The discussion of CFL thickness and velocity profiles mentioned above helps to explain the augmentation of Fahraeus–Lindqvist effect. Owing to the interaction between the RBCs and constricted geometry, in addition to deforming and delivering the RBCs, the driving force is spent on additional deformation that the cells experience as they squeeze through the stenosis, which also causes additional frictional loss and then leads to a reduction in the mean flow velocity. In contrast, the average CFL thickness decreases in the stenosed microvessels by comparing that in the non-stenosed microvessels, as shown in Fig. 8b–d. The thinner CFL with low viscosity and the RBC-rich core with high viscosity result in increasing apparent blood viscosity in the presence of stenosis. In larger microvessels, the CFL thickness downstream the stenosis experiences a slighter fluctuation when RBC aggregation is not considered, which increases the difference in the average CFL thickness compared to the non-stenosed microvessels. As a result, the flow resistance increases at a greater rate as the vessel diameter increases. In addition, the difference in the CFL thickness for the blood flow with and without considering the intercellular interaction decreases slowly as the vessel diameter decreases. It contributes to the small gap between the relative flow resistance for the blood flow with and without considering the RBC aggregation.

3.3 Effects of increased RBC aggregation combined with decreased stenosis on the blood flow

To investigate the effects of decreased stenosis coupled with increased RBC aggregation, B = 0.36, 0.64 are employed to characterize the stenoses of different levels of blockage in the microvessel of D = 20 μm. Meanwhile, De = 0, 0.02, 0.2, 0.4, 0.5 μJ/m2 are selected to qualify different intercellular interaction strengths (Lee et al. 2016; Zhang et al. 2009).

Figure 10 demonstrates the effect of varying the intercellular interaction strength on the velocity profiles upstream the throat (location b labeled in Fig. 7a) for the blood flow in the stenosed microvessels of different values of B. If B increases from 0.36 to 0.64, the flow velocity decreases by nearly 50% under no RBC aggregation while it decreases by approximately 2/3 under the strong RBC aggregation. For B = 0.36, the elevated RBC aggregation helps to increases the flow velocity and promote the RBC clusters enter into the stenosis. However, a reverse trend can be found for B = 0.64, which means that strengthening the intercellular interaction notably slows the passage of RBCs through the decreased stenosis.

Fig. 10
figure 10

Time-averaged velocity profiles at location b (see Fig. 7a) for the flow of RBCs with different intercellular interaction strengths in stenosed microvessels (B = 0.36 and B = 0.64)

Full size image

To further investigate the effect of enhanced RBC aggregation on the trajectories of the RBCs through the decreased stenosis, the displacements of two individual RBCs located in the center of vessel and nearby the vessel wall are measured. Evidently, at the same time instants, for De = 0.2 μJ/m2, the RBCs move faster, especially when they enter into the stenosis, and the concentration of the RBC core after the stenosis is higher, as shown in Fig. 11. Also, for De = 0.5 μJ/m2, the CFL becomes thinner at the throat while becomes thicker downstream the throat. The RBC core under stronger intercellular interaction strength is more compactly packed at the narrowest region of the stenosis and cannot break up into small pieces of RBC aggregates or individual cells easily, which prolongs the transit time of RBC clusters through the stenosis.

Fig. 11
figure 11

Snapshots of RBCS motion through the stenosis for De = 0.2 μJ/m2 (left column, a–d) and 0.5 μJ/m2 (right column, e–h) at t = 0 ms (a, e), 73.2 ms (b, f), 146.4 ms (c, g) and 219.6 ms (d, h), “green” and “blue” represent the RBC located near the vessel wall and in the center of the microvessel, respectively, and corresponding displacements along the flow direction of green RBC and blue RBC (i)

Full size image

Furthermore, the diameters of the RBC core for the blood flows under different intercellular interaction strengths in two different stenosed microvessels are measured, which are scaled by the diameter of the throat. From Fig. 12, it can be seen that the RBC core close to the entrance of the stenosed region reaches its peak, which means that the RBC cluster crowd upstream the stenosis generating thinner CFL. Generally speaking, a strong attractive force generated by the increasing interaction strength attracts the RBCs closer and leads to a more concentrated RBC core. It is evident that the diameter of the RBC core far away from the stenosis decreases with increasing intercellular interaction strength. For B = 0.36, the size of RBC core upstream the stenosis is smaller than and even same as that of the throat when the RBC aggregation is not considered. While for B = 0.64, the RBC core increases to 1.5 times the diameter of the throat before entering into the stenosed region. This RBC cluster has to deform largely to adapt to the decreased stenosis, and then, it prolongs its dwell time when passing through the stenosis. During this time of period, increasing the intercellular interaction strength thickens the RBC core at the throat, as shown in Fig. 12, which may cause blood occlusion as the elapse of time.

Fig. 12
figure 12

Spatial variation in the diameter of RBC core scaled by that of throat for B = 0.36 and B = 0.64

Full size image

In Fig. 13, the effect of increasing intercellular interaction strength on the relative flow resistance of blood flowing in the microvessels is investigated. For B = 0 (non-stenosed microvessel) and B = 0.36, the relative flow resistance decreases gradually with increasing intercellular interaction strength. But with the decrease in the size of stenosis, the weak RBC aggregability reduces the flow resistance to a certain degree while continuing to further increase RBC aggregability augments the flow resistance significantly. Based on the analysis of velocity profile and spatial variation in RBC core for B = 0.64, it suggests that under the weak RBC aggregation, the shear force caused by the flow velocity at the stenosis is strong enough to divide the RBC cluster into fragments of RBC aggregates or individual RBCs. So when the diameter of RBC core is larger than that of the throat, the RBC suspension under weak aggregation can flow through the stenosis smoothly, producing low flow resistance.

Fig. 13
figure 13

Effect of intercellular interaction strength on the relative flow resistance for various B

Full size image

4 Conclusions

The effects of the presence of stenosis as well as the aggregation on the blood flow in microvessels were investigated. The blood is represented by a suspension of RBCs, and the intercellular interaction is modeled by a Morse potential. The blood flow model is validated by comparing the simulation results of Fahraeus–Lindqvist effect in the straight microvessels with the empirical fit to experiments. Then, the blood flows in symmetrical stenosed microvessels were simulated and the results showed that the CFL thickness and velocity profiles exhibit asymmetry along the flow direction. The RBC clusters crowd upstream the stenosis, generating thinner CFL as well as reduced flow velocity. Consequently, the blood flow resistance increases largely and an enhanced Fahraeus–Lindqvist effect can be found in the presence of stenosis. If consider the RBC aggregation, a more concentrated RBC core forms upstream the stenosed region. If the throat of the stenosis is comparable to the formed RBC core in diameter, the blood flow resistance decreases with increasing intercellular interaction strength due to the elevated CFL thickness. But if the stenosis continually decreases by 50%, the RBC core is 1.5 times the throat of the stenosis. Under the weak RBC aggregation, the relative apparent viscosity decreases slightly, the driving force is strong enough to break the RBC clusters up into pieces when the RBCs squeezing through the stenosis. While under the strong RBC aggregation, the generated strong attractive force packs the RBC core compactly upstream the stenosis. The RBC cluster should deform as a whole to adapt to the geometry of the stenosis, which prolongs its residence time in the constricted zone and this leads to a pronounced increase in RBC concentration at the stenosis. Therefore, the CFL becomes thinner in the stenosed region and the flow resistance increases largely.