1 Introduction

Various natural phenomena and technological processes are associated with the filtration of suspensions and colloids in porous media: oil production, soil strengthening, treatment of industrial and municipal wastewater, the spread of bacteria and viruses in groundwater, biological restoration of reservoirs, and much more [1,2,3,4,5,6,7].

In the course of filtration in a porous medium, the tiny particles are transported by the carrier fluid through the pores. During deep bed filtration, particles are retained not only at the inlet, but also in the entire depth of the porous medium and form a stationary deposit [8,9,10,11,12]. Depending on the physicochemical properties of the particles and of the porous medium, the particles are blocked by electrostatic, hydrodynamic and gravitational forces [13,14,15,16]. The retained particles either clog the pore throats singly (size-exclusion), or in groups (bridging), or enter dead-end pores, or settle on the walls of wide pores (attachment) [17,18,19,20,21].

If a suspension or colloid is filled with identical particles, it is called monodisperse; polydisperse suspensions contain particles of different sizes or different properties. A bidisperse suspension or colloid contains two types of particles.

The simplest macroscopic dimensionless model of filtration of a monodisperse suspension or colloid in a porous medium with a size-exclusion retention mechanism is used when the porous medium contains pores of both small and large sizes in comparison with the particle diameter. The model includes the equation for the balance of the suspended and retained particles concentrations \(C(x,t),\,\,\,S(x,t)\) and the kinetic equation for the deposit growth [22, 23]

$$\frac{\partial C}{{\partial t}} + \frac{\partial C}{{\partial x}} + \frac{\partial S}{{\partial t}} = 0,\,\,\,\,\,\,\frac{\partial S}{{\partial t}} = \lambda \left( {1 - \frac{S}{{S_{m} }}} \right)C.$$
(1)

Here \(S_{m}\) is the maximum concentration of retained particles.

When the number of particles in the carrier fluid is small, the growth of the retained particles concentration is proportional to the first degree of the suspended particles concentration. The proportionality coefficient depends on the retained concentration and is called the filtration function. Even when the filtration function is linear as in Eq. (1), the system of equations is quasilinear and the model generates nonlinear effects. When the retained particles concentration reaches the limit value, all the pores which are small in cross section are blocked by the retained particles and the suspended particles are being freely transported through the large pores without formation of deposit.

The initial and boundary conditions for the system (1)

$$x = 0:\,\,\,C = 1,\,\,\,\,\,t = 0:\,\,\,C = 0,\,\,\,S = 0$$
(2)

correspond to the injection of a suspension or a colloid with the constant concentration 1 into a porous medium filled with a pure fluid without suspended and retained particles.

The exact solution to the system (1) with the conditions (2) has a discontinuity on the concentration front \(t = x\)

$$C(x,t) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {t < x,} \hfill \\ {\frac{{e^{{\lambda (t - x)/S_{m} }} }}{{e^{{\lambda (t - x)/S_{m} }} + e^{\lambda x} - 1}},} \hfill & {t > x;} \hfill \\ \end{array} } \right.\quad S(x,t) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {t < x,} \hfill \\ {\frac{{S_{m} (e^{{\lambda (t - x)/S_{m} }} - 1)}}{{e^{{\lambda (t - x)/S_{m} }} + e^{\lambda x} - 1}},} \hfill & {t > x.} \hfill \\ \end{array} } \right.$$

For the investigation of the filtration process, it is important to know the behavior of the retention profile, i.e. the dependence of the retained particles concentration on the x coordinate at a fixed time t. Differentiating the second solution \(S(x,t)\) with respect to the variable x, we see that \(\partial S/\partial x < 0\), so the retention profile of identical particles decreases monotonically at any time t.

Exact solutions to one‐dimensional filtration problems for monodiperse suspensions and colloids with any arbitrary filtration function are obtained in [24, 25]. However, the exact solutions were unknown for the problem of filtration of bidisperse suspensions and colloids. In a number of papers, the bidisperse filtration in a porous medium is studied experimentally and numerically [26,27,28,29,30,31,32,33,34,35]. It is shown that the total and partial retention profiles can be non-monotonic. However, there was no theoretical explanation for the profile non-monotonicity. This article provides an explanation for the non-monotonicity of the retention profiles. The exact solution of a 4 × 4 system for bidisperse suspension or colloid filtration in a porous medium is obtained, and the profiles of total and partial retained concentrations are studied. The conditions for the monotonicity/non-monotonicity of the total and partial retention profiles are obtained. Some of the results of the present paper were announced in a brief form and without proof in [36].

Section 2 presents a macroscopic deep bed filtration model for bidisperse suspensions and colloids in porous media; a solution in the form of a traveling wave is obtained. The main results are formulated in Sect. 3. Section 4 is devoted to proving the existence and uniqueness theorems for the solution. The theorems concerning the properties of retention profiles are proved in Sect. 5. Numerical calculations and profile plots are given in Sect. 6. Discussion and Conclusions in Sects. 7 and 8 end the article.

2 Mathematical model for the binary system

Let us consider deep bed filtration of a binary mixture in porous media. The particles, rock, and carrier water are incompressible. The additivity of volumes for both populations in water during retention is assumed (Amagat’s law [1]). It allows introducing volumetric concentration of retained and suspended particles. The volume of retained particles is significantly lower than the porous space, so the porosity is assumed to remain constant. For each population, the retention rate is proportional to its suspension concentration and to the vacant concentration on the rock surface (Langmuir’s blocking [4, 37]); the proportionality constants λi, i = 1, 2 are called the filtration coefficients, which are assumed to be constant. Filtration coefficient is the particle capture probability per unit length of its trajectory [38]. The term “vacant” is attributed to various particle capture mechanisms, like attachment, straining, size exclusion, and interception under electrostatic attraction [37]; to be specific, in this paper we consider particle attachment alone. We discuss the colloidal transport with a constant flow rate. This model describes suspension-colloidal-nano-transport of binary mixtures with retention and competition for free sites on the surface of a porous medium. Those assumptions are typical in the modelling of suspension-colloid-nano-transport in porous media and its numerous applications [4, 7, 12, 16, 21, 28].

In the quadrant \(\Omega = \{ x \ge 0,\,\,t \ge 0\}\) consider the system

$$\frac{{\partial c_{i} }}{\partial t} + \frac{{\partial c_{i} }}{\partial x} + \frac{{\partial s_{i} }}{\partial t} = 0,$$
(3)
$$\frac{{\partial s_{i} }}{\partial t} = (1 - b)\lambda_{i} c_{i} ,\quad b = B_{1} c_{1}^{0} s_{1} + B_{2} c_{2}^{0} s_{2} ,\quad i = 1,2,$$
(4)

where \(\lambda_{i} ,\,\,B_{i} ,\,\,c_{i}^{0}\) are positive constants and \(\lambda_{1} > \lambda_{2} ,\,\,\,\,\,\,\,c_{1}^{0} + c_{2}^{0} = 1\). Here \(c_{i} ,\,\,\,s_{i} ,\,\,\,\,\,i = 1,2\) are the suspended and retained particles concentrations, respectively, b is the concentration of occupied sites, \(B_{i}\) is the individual area that an attached particle occupies at the rock surface, and \(c_{i}^{0}\) are the particle concentrations in the injected suspension.

Consider the solution of the system (3), (4) in the form of travelling wave [39]:

$$c_{i} = c_{i} (w),\,\,\,s_{i} = s_{i} (w),\,\,\,w = x - ut,\,\,\,i = 1,2,$$
(5)

where u is the yet unknown constant velocity of the traveling wave.

The substitution of the expressions (5) into the system (3), (4) yields a system of ordinary differential equations

$$(1 - u)c^{\prime}_{i} - us^{\prime}_{i} = 0,\,\,\,\,\, - us^{\prime}_{i} = (1 - b)\lambda_{i} c_{i} ,\,\,\,\,\,\,i = 1,2.$$
(6)

For the uniqueness of the solution, the conditions are set at infinity:

$$w \to + \infty :\,\,\,c_{i} \to 0,\,\,\,s_{i} \to 0,\,\,\,i = 1,2;\,\,\,\,\,\,\,\,w \to - \infty :\,\,\,c_{i} \to c_{i}^{0} ,\,\,\,\,i = 1,2.$$
(7)

Integrate the first Eq. (6) taking into account the conditions (7) at \(w \to + \infty\)

$$(1 - u)c_{i} = us_{i} ,\,\,\,\,i = 1,2.$$
(8)

Substitute the second Eq. (6) into the first one

$$(1 - u)c^{\prime}_{i} + (1 - b)\lambda_{i} c_{i} = 0,\,\,\,\,\,\,i = 1,2.$$
(9)

and express the term \(1 - b\)

$$1 - b = - \frac{{(1 - u)c^{\prime}_{i} }}{{\lambda_{i} c_{i} }},\,\,\,\,\,\,i = 1,2.$$
(10)

Equating the right-hand parts of Eqs. (10) at \(i = 1\) and \(i = 2\) and integrating them in w with conditions (7) at \(w \to - \infty\), we obtain

$$c_{2} = c_{2}^{0} \left( {\frac{{c_{1} }}{{c_{1}^{0} }}} \right)^{{\lambda_{2} /\lambda_{1} }} .$$
(11)

Substitute the formulae (8), (11) into Eq. (9) for \(i = 1\):

$$(1 - u)c^{\prime}_{1} + \lambda_{1} c_{1} \left( {1 - \frac{1 - u}{u}B_{1} c_{1}^{0} c_{1} - \frac{1 - u}{u}B_{2} (c_{2}^{0} )^{2} \left( {\frac{{c_{1} }}{{c_{1}^{0} }}} \right)^{{\lambda_{2} /\lambda_{1} }} } \right) = 0.$$
(12)

To single out a specific solution of Eq. (12), one should specify the solution at a given point, say, at w = 0:

$$\left. {c_{1} } \right|_{w = 0} = c_{1}^{0} p,\,\,\,\,0 < p < 1.$$
(13)

The solution of Eq. (12) with the condition (13) is

$$\int\limits_{{c_{1}^{0} p}}^{{c_{1} }} {\frac{dc}{{c\left( {\frac{u}{1 - u} - B_{1} c_{1}^{0} c - B_{2} (c_{2}^{0} )^{2} \left( {\frac{c}{{c_{1}^{0} }}} \right)^{{\lambda_{2} /\lambda_{1} }} } \right)}}} = - \lambda_{1} \frac{w}{u}.$$
(14)

From the formula (14) and the condition (7) at \(w \to - \infty\), we obtain the travelling wave velocity

$$u = \frac{{B_{1} (c_{1}^{0} )^{2} + B_{2} (c_{2}^{0} )^{2} }}{{1 + B_{1} (c_{1}^{0} )^{2} + B_{2} (c_{2}^{0} )^{2} }}.$$
(15)

The solution (14) decreases monotonically from \(c_{1}^{0}\) at \(w \to - \infty\) to 0 at \(w \to + \infty\).

The formulae (8), (11) and (14) determine the solution of the system (3), (4) in the form of travelling wave.

Consider the initial-boundary conditions for the system (3), (4)

$$x = 0:\,\,\,c_{i} = c_{i}^{0} ,\,\,\,\,t = 0:\,\,\,c_{i} = 0,\,\,\,s_{i} = 0,\,\,\,\,i = 1,\,2.$$
(16)

The solutions \(c_{1} (x,t),\,\,\,c_{2} (x,t)\) have a discontinuity on the characteristic line \(t = x\), because the initial and boundary conditions do not match at the origin. The line \(t = x\) is the concentration front Γ of the suspended and retained particles which divides the interior \(\Omega^{0}\) of the quadrant Ω into two zones [40]. In the domain \(\Omega_{0} = \{ x > 0,\,\,0 < t < x\}\) the problem has a zero solution; in the domain \(\Omega_{1} = \{ x > 0,\,\,t > x\}\) the solution is positive (see Theorem 2). It is shown below that in the domain \(\Omega_{1}\) the solution is given by formulae similar to (11), (14).

Using formula (11) the system (3), (16) can be reduced to a 3 × 3 system for the overall suspended and retained particles concentrations and the concentration of occupied sites. Denote

$$s = s_{1} + s_{2} ,\,\,\,\,\,\,c = c_{1} + c_{2} ,\,\,\,\,\,\,f(c) = \lambda_{1} c_{1} + \lambda_{2} c_{2} ,\,\,\,\,\,\,d(c) = B_{1} \lambda_{1} c_{1}^{0} c_{1} + B_{2} \lambda_{2} c_{2}^{0} c_{2} ,\,\,\,\,\,\,\,w(c) = \int\limits_{c}^{1} {\frac{{{\text{d}}(y)}}{f(y)}{\text{d}}y} .$$

\(f(c)\) and \(d(c)\) are called the suspension and occupation functions.

Adding in pairs at \(i = 1\) and \(i = 2\) Eqs. (3), (4) and (4) multiplied by \(B_{1} c_{1}^{0}\) and \(B_{2} c_{2}^{0}\) yields a system of equations for three unknowns b, s, c:

$$\frac{\partial b}{{\partial t}} = (1 - b)d(c),\,\,\,\,\,\,\,\frac{\partial s}{{\partial t}} = (1 - b)f(c),\,\,\,\,\,\,\,\,\frac{\partial c}{{\partial t}} + \frac{\partial c}{{\partial x}} = - (1 - b)f(c).$$

The initial-boundary conditions for this system follow from the conditions (16):

$$x = 0:\,\,\,c = 1,\,\,\,\,\,\,t = 0:\,\,\,c = 0,\,\,\,b = 0,\,\,\,s = 0.$$

Similar to the system (3), (16), in the domain \(\Omega_{0}\) the solution to the system 3 × 3 is zero; in the domain \(\Omega_{1}\) the solution is positive. On the concentration front \(t = x\), the solution c is discontinuous, the solutions s and b are continuous, and \(s = b = 0\). In the domain \(\Omega_{1}\) the solution is given by the formulae [41, Sect. 5.2]

$$\int\limits_{{c^{ - } (x)}}^{c(x,t)} {\frac{{{\text{d}}y}}{f(y)w(y)}} = t - x,\quad b(x,t) = 1 - \frac{{w\left( {c(x,t)} \right)}}{{w\left( {c^{ - } (x)} \right)}},\quad s(x,t) = \frac{{c(x,t) - c^{ - } (x)}}{{w\left( {c^{ - } (x)} \right)}},$$

where \(c^{ - }\) is the solution on the concentration front defined implicitly by the relation \(\int\limits_{{c^{ - } (x)}}^{1} {\frac{dy}{{f(y)}}} = x.\)

3 Main results

Since the solutions are discontinuous in Ω on the line \(t = x\), consider weak solutions of the system (3) [42]. A function φ is said to be piecewise continuous in a domain Ω if it is continuous in the closures \(\overline{\Omega }_{0}\) and \(\overline{\Omega }_{1}\) of the domains \(\Omega_{0}\) and \(\Omega_{1}\) and is discontinuous on the boundary Γ of these domains. A function φ is called piecewise smooth if its partial derivatives \(\varphi^{\prime}_{t}\) and \(\varphi^{\prime}_{x}\) are piecewise continuous in Ω.

Definition 1

A weak solution to the system (3), (4) with the conditions (16) is such a set of functions \(c_{i} ,\,\,\,s_{i} ,\,\,\,i = 1,\,2\) that

  • a) the functions \(c_{1} ,\,\,\,c_{2}\) are piecewise differentiable in Ω;

  • b) the functions \(s_{1} ,\,\,\,s_{2}\) are piecewise differentiable and continuous in Ω;

  • c) Eqs. (3), (4) are satisfied in the weak sense, i.e. any function \(\varphi (x,t) \in C_{0}^{\infty } (\Omega^{0} )\) satisfies the equalities

    $$\iint\limits_{\Omega } {\left( {(c_{i} + s_{i} )\frac{\partial \varphi }{{\partial t}} + c_{i} \frac{\partial \varphi }{{\partial x}}} \right)}{\text{d}}x{\text{d}}t = 0,\quad \iint\limits_{\Omega } {\left( {s_{i} \frac{\partial \varphi }{{\partial t}} + \lambda_{i} (1 - b)c_{i} \varphi } \right)}{\text{d}}x{\text{d}}t = 0,\quad i = 1,\,2,$$

  • d) the conditions (16) are satisfied in the strong sense (pointwise).

Theorem 1

In the domain Ω there exists a weak unique solution of the system (3), (4) with the conditions (16).

Denote the distance between points \((t,x) \in \Omega_{1}\) and \((x,x) \in \Gamma\)

$$\rho = t - x.$$

Theorem 2

  • 1. The solution to the problem (3), (4), (16) is zero in the domain \(\Omega_{0}\) and positive in the domain \(\Omega_{1}\).

  • 2. In the domain \(\overline{\Omega }_{1}\), the solution is given by the formulae

    $$\begin{gathered} \int\limits_{{c_{1}^{ - } }}^{{c_{1} }} {\frac{dc}{{c\left( {B_{1} c_{1}^{0} (c_{1}^{0} - c) + B_{2} c_{2}^{0} \left( {c_{2}^{0} - c_{2}^{0} \left( {\frac{c}{{c_{1}^{0} }}} \right)^{{\lambda_{2} /\lambda_{1} }} } \right)} \right)}}} = \lambda_{1} \rho , \hfill \\ \int\limits_{{c_{2}^{ - } }}^{{c_{2} }} {\frac{dc}{{c\left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{0} \left( {\frac{c}{{c_{2}^{0} }}} \right)^{{\lambda_{1} /\lambda_{2} }} ) + B_{2} c_{2}^{0} \left( {c_{2}^{0} - c} \right)} \right)}}} = \lambda_{2} \rho , \hfill \\ \end{gathered}$$
    (17)
    $$s_{i} = \frac{{c_{i} - c_{i}^{ - } }}{{B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )}},\,\,\,\,i = 1,\,2,$$
    (18)

where

$$c_{i}^{ - } = c_{i} (x,x) = c_{i}^{0} e^{{ - \lambda_{i} x}}$$
(19)

is the solution on the concentration front Γ.

In particular, at the inlet \(x = 0\) the solution (18) takes the form

$$s_{i}^{0} (t) = \frac{{\lambda_{i} c_{i}^{0} }}{B}(1 - e^{ - Bt} ),\quad i = 1,\,2,\quad B = \lambda_{1} B_{1} (c_{1}^{0} )^{2} + \lambda_{2} B_{2} (c_{2}^{0} )^{2} .$$
(20)

Corollary 1

At \(x > 0,\,\,\,\rho \to \infty\).

$$c_{i} \to c_{i}^{0} ,\quad s_{i} \to \frac{{c_{2}^{0} - c_{i}^{ - } }}{{B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )}},\quad i = 1,\,2.$$
(21)

The following theorems are devoted to the retention profiles.

Theorem 3

In the domain \(\overline{\Omega }_{1}\) the partial and total retention profiles \(s_{1} (x,t),\,\,s_{2} (x,t),\,\,s(x,t)\) monotonously decrease

1. for a fixed \(\,t > 0\) at \(x \to t\),

2. for a fixed \(\,x \ge 0\) at \(t \to x\).

Theorem 4

Let \(\lambda_{1} > \lambda_{2}\). For a fixed \(x > 0\) at \(t \to \infty\).

1. the profile \(s_{1} (x,t)\) monotonously decreases;

2. the profile \(s_{2} (x,t)\) monotonously increases;

3. the profile \(s(x,t)\) monotonously increases if \(B_{1} c_{1}^{0} > B_{2} c_{2}^{0}\), and monotonously decreases if \(B_{1} c_{1}^{0} < B_{2} c_{2}^{0}\).

Denote

$$t_{0} = \frac{1}{B}\ln \frac{{D + \lambda_{2} B}}{{D + B^{2} - B\sqrt {B^{2} + 2D + (\lambda_{2} )^{2} } }},\,\,\,\,\,\,\,T_{0} = \frac{1}{B}\ln \frac{\lambda D + \mu B}{{\lambda (D + B^{2} ) - B\sqrt {\lambda^{2} (B^{2} + 2D) + \mu^{2} } }},$$

where

\(\lambda = \lambda_{1} c_{1}^{0} + \lambda_{2} c_{2}^{0} ,\,\,\,\,\,\,D = (\lambda_{1} )^{2} B_{1} (c_{1}^{0} )^{2} + (\lambda_{2} )^{2} B_{2} (c_{2}^{0} )^{2} ,\,\,\,\,\,\,\mu = (\lambda_{1} )^{2} c_{1}^{0} + (\lambda_{2} )^{2} c_{2}^{0}\).

Theorem 5

Let \(\lambda_{1} > \lambda_{2}\). In the domain \(\overline{\Omega }_{1}\) at \(x \to 0\).

1. The partial retention profile \(s_{1} (x,t)\) decreases monotonically for all \(t > x\);

2. The partial retention profile \(s_{2} (x,t)\) decreases monotonically for \(x < t < t_{0}\) and increases monotonically for \(t > t_{0}\) ;

3. The total retention profile \(s(x,t)\) decreases monotonically for all \(t > x\) if \(B_{1} c_{1}^{0} < B_{2} c_{2}^{0}\) ; decreases monotonically at \(x < t < T_{0}\) and increases monotonically at \(t > T_{0}\) if \(B_{1} c_{1}^{0} > B_{2} c_{2}^{0}\) .

It follows from Theorems 3–5 that any non-monotonic retention profile has a maximum point. Theorem 6describes the positions of the maximum points of the profiles at large t and x.

Theorem 6

Let \(\lambda_{1} > \lambda_{2}\). Then

1. The integral

$$I = \int\limits_{0}^{{c_{2}^{0} }} {\left( {\frac{1}{{c\left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{0} \left( {\frac{c}{{c_{2}^{0} }}} \right)^{{\lambda_{1} /\lambda_{2} }} ) + B_{2} c_{2}^{0} \left( {c_{2}^{0} - c} \right)} \right)}} - \frac{{\lambda_{2} }}{{B(c_{2}^{0} - c)}} - \frac{1}{Ac}} \right)dc}$$

converges;

2. In the domain \(\Omega_{1}\) at \(x \to \infty ,\,\,\,\rho \to \infty\) the coordinates of the maximum points \(t_{m} (x)\) and \(T_{m} (x)\) of the profiles \(s_{2} (x,t)\) and \(s(x,t)\) allow estimates

$$t_{m} (x) = \left( {\frac{{\lambda_{2} }}{B} + \frac{1}{A} + 1} \right)x + \frac{I}{{\lambda_{2} }} - \frac{1}{B}\ln \frac{{\lambda_{2} B_{1} (c_{1}^{0} )^{2} }}{B} + O(e^{{ - \lambda_{2} x}} + e^{{ - (\lambda_{1} - \lambda_{2} )x}} ),$$
(22)
$$T_{m} (x) = \left( {\frac{{\lambda_{2} }}{B} + \frac{1}{A} + 1} \right)x + \frac{I}{{\lambda_{2} }} - \frac{1}{B}\ln \frac{{(\lambda_{2} )^{2} c_{1}^{0} c_{2}^{0} (B_{1} c_{1}^{0} - B_{2} c_{2}^{0} )}}{{B(\lambda_{1} c_{1}^{0} + \lambda_{2} c_{2}^{0} )}} + O(e^{{ - \lambda_{2} x}} + e^{{ - (\lambda_{1} - \lambda_{2} )x}} ),$$
(23)

at \(t \to \infty\) the maximum values of the profiles \(s_{2} (x,t)\) and \(s(x,t)\) tend to \(c_{2}^{0} /A\) and \(1/A\), respectively. Here

$$A = B_{1} (c_{1}^{0} )^{2} + B_{2} (c_{2}^{0} )^{2} .$$

Remark 1

After neglecting the residuals in formulae (22) and (23), we obtain linear expressions in x representing the asymptotes with respect to \(t_{m}\) and \(T_{m}\).

Remark 2

At \(x \to \infty ,\,\,\,\rho \to \infty\) the limit speeds of the maximum points of the profiles \(s_{2} (x,t)\) and \(s(x,t)\) coincide and are equal to

\(v = 1/\left( {\frac{{\lambda_{2} }}{B} + \frac{1}{A} + 1} \right)\).

4 Proof of Theorems 1, 2

To prove Theorem 1, assume at first that a solution \(c_{i} ,\,\,\,s_{i} ,\,\,\,i = 1,2\) to the problem (3), (4), (16) exists and then derive the formulae of Theorem 2 for the solution. This will prove the uniqueness of the solution: if there exists a solution, then it is necessarily given by these formulae. To prove the existence of the solution, one should reverse the reasoning used to prove the uniqueness of the solution: the functions given by formulae (17)–(20) are a solution to the problem (3), (4), (16). (For brevity, these arguments are omitted.)

4.1 Proof of item 1 of Theorem 2

Substitute Eqs. (4) into (3)

$$\frac{{\partial c_{i} }}{\partial t} + \frac{{\partial c_{i} }}{\partial x} + (1 - b)\lambda_{i} c_{i} = 0,\,\,\,\,i = 1,2,$$
(24)

and then apply the standard method of characteristics [43] to Eqs. (24). The characteristic equations corresponding to the system (24) have the form

$$\dot{t} = 1,\,\,\,\dot{x} = 1,\,\,\,\,\dot{c}_{i} + (1 - b)\lambda_{i} c_{i} = 0,\,\,\,\,i = 1,\,2,$$
(25)

where the dot means the derivative by τ (the intrinsic time along the characteristics). The conditions for the system (25) in the domains \(\overline{\Omega }_{0}\) and \(\overline{\Omega }_{1}\) are determined by the initial and boundary conditions (16). In the domain \(\overline{\Omega }_{0}\)

$$\left. t \right|_{\tau = 0} = 0,\,\,\,\left. x \right|_{\tau = 0} = x_{0} ,\,\,\,\,\left. {c_{i} } \right|_{\tau = 0} = 0,\,\,\,\,i = 1,\,2;$$
(26)

in the domain \(\overline{\Omega }_{1}\)

$$\left. t \right|_{\tau = 0} = t_{0} ,\,\,\,\left. x \right|_{\tau = 0} = 0,\,\,\,\,\left. {c_{i} } \right|_{\tau = 0} = c_{i}^{o} ,\,\,\,\,i = 1,\,2.$$
(27)

The characteristics, being the solutions of the system (25) with the conditions (26) and (27), are straight lines \(x = t + x_{0} ,\,\,\,x = t - t_{0}\), everywhere densely filling the domains \(\overline{\Omega }_{0}\) and \(\overline{\Omega }_{1}\). In the domain \(\overline{\Omega }_{0}\) the solutions \(c_{i} = 0,\,\,\,\,i = 1,2\); according to the initial conditions (16), the solutions to Eqs. (4) are also zero. In the domain \(\Omega_{1}\), the solution \(c_{i} = c_{i}^{o} \exp \left( { - \lambda_{i} \int\limits_{0}^{\tau } {(1 - b)d\tau } } \right),\,\,\,\,\,\,i = 1,\,2\) to Eqs. (25) with the conditions (27) is positive.

Multiply Eqs. (4) by \(B_{i} c_{i}^{0}\) and add them together. The resulting equation has the form

$$\frac{\partial b}{{\partial t}} = (B_{1} c_{1}^{0} \lambda_{1} c_{1} + B_{2} c_{2}^{0} \lambda_{2} c_{2} )(1 - b).$$
(28)

The condition for Eq. (28) follows from the initial conditions (16):

$$t = 0:\,\,\,b = 0.$$
(29)

The solution of Eq. (28) with the condition (29) can be written in the form \(b = 1 - exp\left( { - \int\limits_{0}^{t} {(B_{1} c_{1}^{0} \lambda_{1} c_{1} + B_{2} c_{2}^{0} \lambda_{2} c_{2} ){\text{d}}t} } \right)\). Consequently, \(1 - b > 0\) and the solution \(s_{i} = \int\limits_{0}^{t} {(1 - b){\text{d}}t,} \,\,\,\,i = 1,\,2\) of Eqs. (4) with the conditions (16) is positive in \(\Omega_{1}\).

Item 1 of Theorem 2 is proved.

4.2 Proof of item 2 of Theorem 2

Let us prove the validity of the formulae (19), (20). At the inlet \(x = 0\) Eqs. (4) take the form

$$\frac{{\partial s_{i} }}{\partial t} = (1 - b)\lambda_{i} c_{i}^{0} ,\,\,\,\,i = 1,2.$$
(30)

Multiply Eqs. (30) by \(B_{i} c_{i}^{0}\) and add them together. According to the formula (4), the resulting equation has the form

$$\frac{\partial b}{{\partial t}} = (1 - b)B.$$
(31)

The solution of Eq. (31) with the initial condition (29) is

$$b(0,t) = 1 - e^{ - Bt} .$$
(32)

The substitution of (32) into Eq. (30) and the integration in t taking into account the initial conditions (16) yield the formulae (20).

Since the solutions \(s_{i} ,\,\,\,\,i = 1,\,2\) are continuous in the domain Ω, then in \(\overline{\Omega }_{1}\) on the concentration front Γ the solution b is zero and Eqs. (24) take the form

$$\frac{{\partial c_{i} }}{\partial t} + \frac{{\partial c_{i} }}{\partial x} + \lambda_{i} c_{i} = 0,\,\,\,\,i = 1,2.$$
(33)

The solution of Eqs. (33) with the boundary conditions (16) is given by the formulae (19).

Proposition 1

In the domain \(\overline{\Omega }_{1}\) the solutions \(c_{1} (x,t),\,\,\,c_{2} (x,t)\) satisfy the relations

$$c_{1} = c_{1}^{0} \left( {\frac{{c_{2} }}{{c_{2}^{0} }}} \right)^{{\lambda_{1} /\lambda_{2} }} ,\quad c_{2} = c_{2}^{0} \left( {\frac{{c_{1} }}{{c_{1}^{0} }}} \right)^{{\lambda_{2} /\lambda_{1} }} .$$
(34)

Proof

Express \((1 - b)\) from Eq. (24)

$$1 - b = - \frac{1}{{\lambda_{i} c_{i} }}\left( {\frac{{\partial c_{i} }}{\partial t} + \frac{{\partial c_{i} }}{\partial x}} \right),\,\,\,\,i = 1,2.$$
(35)

Equating the right-hand sides of Eqs. (35) at \(i = 1\) and \(i = 2\), integrating the resulting equation in x and taking into account the boundary conditions (16), we obtain

$$\frac{1}{{\lambda_{1} }}\ln \frac{{c_{1} }}{{c_{1}^{0} }} = \frac{1}{{\lambda_{2} }}\ln \frac{{c_{2} }}{{c_{2}^{0} }}.$$
(36)

The formulae (34) follow from the relation (36). Proposition 1 is proved.

To prove the formulae (17), substitute (4) into relation (34) for \(i = 1\) and express \(s_{2}\):

$$s_{2} = \frac{{1 - B_{1} c_{1}^{0} s_{1} }}{{B_{2} c_{2}^{0} }} + \frac{1}{{\lambda_{1} c_{1} B_{2} c_{2}^{0} }}\left( {\frac{{\partial c_{1} }}{\partial t} + \frac{{\partial c_{1} }}{\partial x}} \right).$$
(37)

The substitution of (35) for \(i = 1\) and of (37) into Eq. (4) for \(i = 2\) yields

$$\frac{\partial }{\partial t}\left( {\frac{{1 - B_{1} c_{1}^{0} s_{1} }}{{B_{2} c_{2}^{0} }} + \frac{1}{{\lambda_{1} c_{1} B_{2} c_{2}^{0} }}\left( {\frac{{\partial c_{1} }}{\partial t} + \frac{{\partial c_{1} }}{\partial x}} \right)} \right) = - \frac{{\lambda_{2} c_{2} }}{{\lambda_{1} c_{1} }}\left( {\frac{{\partial c_{1} }}{\partial t} + \frac{{\partial c_{1} }}{\partial x}} \right).$$
(38)

Since the function \(\ln c_{1} (x,t)\) is continuous and piecewise smooth, its derivatives in the sense of distributions coincide with the classical derivatives. This yields the chain of relations

$$\frac{\partial }{\partial t}\left( {\frac{1}{{c_{1} }}\frac{{\partial c_{1} }}{\partial x}} \right) = \frac{\partial }{\partial t}\left( {\frac{\partial }{\partial x}\ln c_{1} } \right) = \frac{\partial }{\partial x}\left( {\frac{\partial }{\partial t}\ln c_{1} } \right) = \frac{\partial }{\partial x}\left( {\frac{1}{{c_{1} }}\frac{{\partial c_{1} }}{\partial t}} \right).$$

Equation (3) at \(i = 1\) can be written in a form

$$\frac{{\partial s_{1} }}{\partial t} = - \left( {\frac{{\partial c_{1} }}{\partial t} + \frac{{\partial c_{1} }}{\partial x}} \right).$$

Using formula (34) with \(i = 2\), transform the right-hand side of Eq. (38)

$$- \frac{{\lambda_{2} c_{2} }}{{\lambda_{1} c_{1} }}\left( {\frac{{\partial c_{1} }}{\partial t} + \frac{{\partial c_{1} }}{\partial x}} \right) = - \left( {\frac{{\partial c_{2} }}{\partial t} + \frac{{\partial c_{2} }}{\partial x}} \right).$$

Now (38) becomes

$$\left( {\frac{\partial }{\partial t} + \frac{\partial }{\partial x}} \right)\left( {\frac{{B_{1} c_{1}^{0} c_{1} + \frac{{\partial c_{1} /\partial t}}{{\lambda_{1} c_{1} }}}}{{B_{2} c_{2}^{0} }} + c_{2} } \right) = 0.$$
(39)

Lower the order of Eq. (39)

$$\frac{{B_{1} c_{1}^{0} c_{1} + \frac{{\partial c_{1} /\partial t}}{{\lambda_{1} c_{1} }}}}{{B_{2} c_{2}^{0} }} + c_{2} = K(t - x).$$
(40)

The integration constant \(K(t - x)\) is determined from the boundary conditions (16):

$$K = \frac{{B_{1} \left( {c_{1}^{0} } \right)^{2} + B_{2} \left( {c_{2}^{0} } \right)^{2} }}{{B_{2} c_{2}^{0} }}.$$

Equation (40) takes the form

$$\frac{{\partial c_{1} /\partial t}}{{\lambda_{1} c_{1} }} = B_{1} c_{1}^{0} \left( {c_{1}^{0} - c_{1} } \right) + B_{2} c_{2}^{0} \left( {c_{2}^{0} - c_{2} } \right).$$
(41)

The first formula (17) is the solution of Eq. (41) with the initial condition (19) on the concentration front \(t = x\). The second formula (17) is obtained similarly.

To prove the formulae (18), differentiate equalities (17) with respect to t and x

$$\begin{gathered} \frac{1}{{c_{i} \left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1} ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2} )} \right)}}\frac{{\partial c_{i} }}{\partial t} = \lambda_{i} , \hfill \\ \frac{1}{{c_{i} \left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1} ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2} )} \right)}}\frac{{\partial c_{i} }}{\partial x} - \frac{1}{{c_{i}^{ - } \left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )} \right)}}\frac{{\partial c_{i}^{ - } }}{\partial x} = - \lambda_{i} ,\,\,i = 1,\,2. \hfill \\ \end{gathered}$$
(42)

Add Eqs. (42) together for i = 1:

$$\frac{1}{{c_{1} \left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1} ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2} )} \right)}}\left( {\frac{{\partial c_{1} }}{\partial t} + \frac{{\partial c_{1} }}{\partial x}} \right) - \frac{1}{{c_{1}^{ - } \left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )} \right)}}\frac{{\partial c_{1}^{ - } }}{\partial x} = 0$$

Transform this relation using Eqs. (3), (4) at \(i = 1\) and the formula (19):

$$\frac{{ - \lambda_{1} (1 - b)}}{{B_{1} c_{1}^{0} (c_{1}^{0} - c_{1} ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2} )}} + \frac{{\lambda_{1} }}{{B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )}} = 0$$

and then express the function b:

$$b = 1 - \frac{{B_{1} c_{1}^{0} (c_{1}^{0} - c_{1} ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2} )}}{{B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )}}.$$
(43)

The substitution of the first relation (42) and the formula (43) into Eq. (4) at \(i = 1\) gives

$$\frac{{\partial s_{1} }}{\partial t} = \frac{1}{{B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )}}\frac{{\partial c_{1} }}{\partial t}.$$
(44)

The continuity of the solution \(s_{i} (x,t),\,\,\,i = 1,2\) in Ω and item 1 of Theorem 2 imply the following condition on the concentration front:

$$t = x:\,\,\,s_{i} = 0,\,\,\,i = 1,2.$$
(45)

Integrating Eq. (44) in the variable t from x to t, we obtain the formula (18) at \(i = 1\). For \(i = 2\) the proof is similar.

Theorem 2 is proved.

From Theorem 2 it follows that the solution of the problem (3), (4), (16) must be given by formulae (17)–(20). Consequently, the problem has at most one solution. Inverting the proof of Theorem 2, we obtain the existence of a solution to the problem (3), (4), (16). Theorem 1 is proved.

5 Proof of Theorems 3–6

To calculate the derivatives of the solutions \(s_{1} (x,t),\,\,\,s_{2} (x,t)\) and of \(s = s_{1} + s_{2}\) with respect to the variable x differentiate formula (18):

$$\frac{{\partial s_{i} }}{\partial x} = \frac{{\left( {\frac{{\partial c_{i} }}{\partial x} - \frac{{\partial c_{i}^{ - } }}{\partial x}} \right)\left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )} \right) + \left( {c_{i} - c_{i}^{ - } } \right)\left( {B_{1} c_{1}^{0} \frac{{\partial c_{1}^{ - } }}{\partial x} + B_{2} c_{2}^{0} \frac{{\partial c_{2}^{ - } }}{\partial x}} \right)}}{{\left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )} \right)^{2} }},\,\,\,i = 1,\,2.$$
(46)

Express the derivatives \(\partial c_{i} /\partial x,\,\,\,\partial c_{i}^{ - } /\partial x\) using solution (19) and the second formula (42)

$$\frac{{\partial c_{i}^{ - } }}{\partial x} = - \lambda_{i} c_{i}^{ - } ,\,\,\,\,\frac{{\partial c_{i} }}{\partial x} = - \lambda_{i} c_{i} \left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1} ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2} )} \right)\left( {1 + \frac{1}{{B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } )}}} \right).$$

Formulae (46) take the form

$$\frac{{\partial s_{i} }}{\partial x} = \frac{{ - \lambda_{i} c_{i} \left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1} ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2} )} \right)\left( {1 + G(x)} \right) + \lambda_{i} c_{i}^{ - } G(x) - \left( {c_{i} - c_{i}^{ - } } \right)\left( {\lambda_{1} B_{1} c_{1}^{0} c_{1}^{ - } + \lambda_{2} B_{2} c_{2}^{0} c_{2}^{ - } } \right)}}{{G^{2} (x)}},$$
(47)

where

$$G(x) = B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{ - } ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2}^{ - } ).$$

Adding formulae (47) at \(i = 1\) and \(i = 2\) gives the derivative of \(s = s_{1} + s_{2}\):

$$\begin{aligned} \frac{\partial s}{{\partial x}} & = \frac{{ - (\lambda_{1} c_{1} + \lambda_{2} c_{2} )\left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1} ) + B_{2} c_{2}^{0} (c_{2}^{0} - c_{2} )} \right)\left( {1 + G(x)} \right)}}{{G^{2} (x)}} \\ & \quad + \frac{{(\lambda_{1} c_{1}^{ - } + \lambda_{2} c_{2}^{ - } )G(x) - \left( {c_{1} + c_{2} - c_{1}^{ - } - c_{2}^{ - } } \right)\left( {\lambda_{1} B_{1} c_{1}^{0} c_{1}^{ - } + \lambda_{2} B_{2} c_{2}^{0} c_{2}^{ - } } \right)}}{{G^{2} (x)}}. \\ \end{aligned}$$
(48)

In the domain \(\Omega_{1}\) the monotonicity of the partial and total retained concentration profiles \(s_{1} (x,t),\,\,\,s_{2} (x,t),\,\,\,s(x,t)\) for fixed \(t \ge x\) depends on the signs of derivatives (47), (48).

Proof of Theorem 3:

Both cases of Theorem 3 (\(x \to t\) and \(t \to x\)) mean that \(\rho = t - x \to 0\), so the solutions \(c_{1} \to c_{1}^{ - } ,\,\,\,c_{2} \to c_{2}^{ - }\). Application of the mean value theorem to the integrals on the left-hand side of (17) gives the representation.

$$c_{i} = c_{i}^{ - } + O(\rho ),\,\,\,\,i = 1,\,2.$$
(49)

Substitute the expansions (49) into derivatives (47), (48)

$$\frac{{\partial s_{i} }}{\partial x} = - \lambda_{i} c_{i} + O(\rho ),\,\,\,\,\,i = 1,\,2,$$
(50)
$$\frac{\partial s}{{\partial x}} = - (\lambda_{1} c_{1} + \lambda_{2} c_{2} ) + O(\rho ).$$
(51)

For small ρ the derivatives (50), (51) are negative and the partial and total retained concentration profiles are monotonously decreasing in x at \(\rho \to 0\).

Theorem 3 is proved.

Proof of Theorem 4:

The signs of derivatives (47), (48) coincide with the signs of its numerators. If \(t \to \infty\), then the solution \(c_{1} \to c_{1}^{0} ,\,\,\,c_{2} \to c_{2}^{0}\). The numerators of the derivatives (47), (48) can be expanded in a form.

$$\begin{gathered} N_{1} = B_{2} c_{2}^{0} F(\lambda_{1} ,\lambda_{2} ,x) + O\left( {(c_{2}^{0} - c_{2} ) + (c_{1}^{0} - c_{1} )} \right), \hfill \\ N_{2} = - B_{1} c_{1}^{0} F(\lambda_{1} ,\lambda_{2} ,x) + O\left( {(c_{2}^{0} - c_{2} ) + (c_{1}^{0} - c_{1} )} \right), \hfill \\ N = \left( {B_{2} c_{2}^{0} - B_{1} c_{1}^{0} } \right)F(\lambda_{1} ,\lambda_{2} ,x) + O\left( {(c_{2}^{0} - c_{2} ) + (c_{1}^{0} - c_{1} )} \right), \hfill \\ \end{gathered}$$
(52)

where

$$F(\lambda_{1} ,\lambda_{2} ,x) = \lambda_{1} c_{1}^{ - } (c_{2}^{0} - c_{2}^{ - } ) - \lambda_{2} c_{2}^{ - } (c_{1}^{0} - c_{1}^{ - } ) = c_{1}^{0} c_{2}^{0} \left( {\lambda_{1} e^{{ - \lambda_{1} x}} (1 - e^{{ - \lambda_{2} x}} ) - \lambda_{2} e^{{ - \lambda_{2} x}} (1 - e^{{ - \lambda_{1} x}} )} \right).$$
(53)

At the inlet \(x = 0\) the function (53) is zero. The sign of (53) at \(x > 0\) is determined by Proposition 2.

Proposition 2

Let \(\lambda_{1} > \lambda_{2}\). Then the function (53) is negative for all \(x > 0\).

Proof

Transform the function (53) as follows:

$$F(\lambda_{1} ,\lambda_{2} ,x) = c_{1}^{0} c_{2}^{0} \frac{{\lambda_{1} (e^{{\lambda_{2} x}} - 1) - \lambda_{2} (e^{{\lambda_{1} x}} - 1)}}{{e^{{\lambda_{1} x}} e^{{\lambda_{2} x}} }}.$$
(54)

Consider the numerator

$$F_{1} (\lambda_{1} ,\lambda_{2} ,x) = \lambda_{1} (e^{{\lambda_{2} x}} - 1) - \lambda_{2} (e^{{\lambda_{1} x}} - 1).$$

At \(x = 0\) the numerator \(F_{1} (\lambda_{1} ,\lambda_{1} ,0) = 0\). If \(x > 0\), then

$$F^{\prime}_{1} (\lambda_{1} ,\lambda_{2} ,x) = \lambda_{1} \lambda_{2} (e^{{\lambda_{2} x}} - e^{{\lambda_{1} x}} ) < 0,$$

and the function \(F_{1} (\lambda_{1} ,\lambda_{2} ,x)\) is decreasing at \(x > 0\). Therefore, the numerator \(F_{1} (\lambda_{1} ,\lambda_{2} ,x)\) is negative.

The denominator of the ratio (54) is positive, so the function \(F(\lambda_{1} ,\lambda_{2} ,x)\) is negative at \(x > 0\).

Proposition 2 is proved.

Theorem 4 follows from the formulae (52) and Proposition 2.

Proof of Theorem 5

Represent the solution of the problem (3), (4), (16) in the form of a series in the powers of x with coefficients depending on \(\rho = t - x\):

$$c_{i} = c_{i}^{0} + c_{i}^{1} (\rho )x + O(x^{2} ),\,\,\,s_{i} = s_{i}^{0} (\rho ) + s_{i}^{1} (\rho )x + O(x^{2} ),\,\,\,i = 1,\,2,$$
(55)

where the functions \(s_{i}^{0}\) are given by the formulae (20). Then the functions \(s(x,t),\,\,\,b(x,t)\) are expanded in series as follows:

$$\begin{aligned} s & = s^{0} (\rho ) + s^{1} (\rho )x + O(x^{2} ),\,\,\,\,s^{0} (\rho ) = s_{1}^{0} (\rho ) + s_{2}^{0} (\rho ),\,\,\,\,s^{1} (\rho ) = s_{1}^{1} (\rho ) + s_{2}^{1} (\rho ), \\ b & = b_{0} (\rho ) + b_{1} (\rho )x + O(x^{2} ),\,\,\,\,\,b_{0} = B_{1} c_{1}^{0} s_{1}^{0} + B_{2} c_{2}^{0} s_{2}^{0} ,\,\,\,\,\,\,b_{1} = B_{1} c_{1}^{0} s_{1}^{1} + B_{2} c_{2}^{0} s_{2}^{1} \,. \\ \end{aligned}$$

Substituting the expansions (55) into Eqs. (3), (4) and equating the coefficients at equal powers of x, we obtain:

$$c_{i}^{1} = - (1 - b_{0} )\lambda_{i} c_{i}^{0} ,\,\,\,i = 1,\,2;\,\,\,\,\left( {s_{i}^{1} } \right)^{\prime } = - b_{1} \lambda_{i} c_{i}^{0} + (1 - b_{0} )\lambda_{i} c_{i}^{1} ,\,\,\,i = 1,\,2.$$
(56)

Substitute the first Eq. (56) into the second one

$$\left( {s_{i}^{1} } \right)^{\prime } = - b_{1} \lambda_{i} c_{i}^{0} - (1 - b_{0} )^{2} (\lambda_{i} )^{2} c_{i}^{0} ,\,\,\,i = 1,\,2.$$
(57)

Multiply Eqs. (57) by \(B_{i} c_{i}^{0}\) and add them together:

$$b_{1}^{\prime } = - Bb_{1} - D(1 - b_{0} )^{2} ,$$
(58)

where

$$B = \lambda_{1} B_{1} (c_{1}^{0} )^{2} + \lambda_{2} B_{2} (c_{2}^{0} )^{2} ,\,\,\,\,\,D = (\lambda_{1} )^{2} B_{1} (c_{1}^{0} )^{2} + (\lambda_{2} )^{2} B_{2} (c_{2}^{0} )^{2}$$

The initial condition for Eq. (58) follows from the conditions (45) on the concentration front

$$\rho = 0:\,\,\,b_{1} = 0.$$
(59)

Using the formula (32), the solution to Eq. (58) with the condition (59) is obtained:

$$b_{1} = \frac{D}{B}e^{ - B\rho } (e^{ - B\rho } - 1).$$
(60)

Substitute the formulae (32), (60) in Eq. (57):

$$\left( {s_{i}^{1} } \right)^{\prime } = \lambda_{i} c_{i}^{0} \frac{D}{B}e^{ - B\rho } \left( {1 - e^{ - B\rho } } \right) - (\lambda_{i} )^{2} c_{i}^{0} e^{ - 2B\rho } ,\,\,\,i = 1,\,2.$$
(61)

The integration of Eqs. (61) with the conditions (45) gives

$$s_{i}^{1} = \frac{{\lambda_{i} c_{i}^{0} }}{{2B^{2} }}\left( {1 - e^{ - B\rho } } \right)\left( {(D - \lambda_{i} B) - (D + \lambda_{i} B)e^{ - B\rho } } \right),\,\,\,i = 1,\,2.$$
(62)

Represent the functions (20), (62) in the form

$$s_{i}^{0} (\rho ) = s_{i}^{0} (t) - \lambda_{i} c_{i}^{0} e^{ - Bt} x + O(x^{2} ),\,\,\,\,\,\,s_{i}^{1} (\rho ) = s_{i}^{1} (t) + O(x),\,\,\,\,i = 1,\,2$$
(63)

and substitute the expansions (63) into the second formula (55):

$$s_{i} (x,t) = \frac{{\lambda_{i} c_{i}^{0} }}{B}(1 - e^{ - Bt} ) + \frac{{\lambda_{i} c_{i}^{0} }}{{2B^{2} }}\left( {\left( {1 - e^{ - Bt} } \right)\left( {(D - \lambda_{i} B) - (D + \lambda_{i} B)e^{ - Bt} } \right) - 2B^{2} e^{ - Bt} } \right)x + O(x^{2} ),\,\,\,i = 1,2.$$
(64)

At small x the monotonicity of the profiles \(s_{i} (x,t)\) is determined by the sign of the coefficient at x in the expansion (64). The monotonicity of the total retention profile \(s(x,t)\) is determined by the sign of the coefficient at x in the sum of the expansions (64) at \(i = 1\) and \(i = 2\).

Denote

$$z = e^{ - Bt} ,\,\,\,0 < z \le 1,$$

and consider the coefficients at x in (64):

$$w_{i} (z) = (1 - z)\left( {(D - \lambda_{i} B) - (D + \lambda_{i} B)z} \right) - 2B^{2} z,\,\,\,i = 1,\,2.$$

Proposition 3

Let \(\lambda_{1} > \lambda_{2}\) . Then the function

1. \(w_{1} (z)\) is negative for all \(z \in [0,1][0,1]\);

2. \(w_{2} (z)\) is negative for \(z_{0} < z \le 1\) and positive for \(0 \le z < z_{0}\), where \(z_{0} = \frac{{D + B^{2} - B\sqrt {B^{2} + 2D + (\lambda_{2} )^{2} } }}{{D + \lambda_{2} B}} \in (0,\,1)\);

3. \(W(z) = w_{1} (z) + w_{2} (z)\) is negative for all \(z \in [0,1]\) if \(B_{1} c_{1}^{0} \le B_{2} c_{2}^{0}\); \(W(z)\) is negative for \(Z_{0} < z \le 1\) and positive for \(0 \le z < Z_{0}\), where \(Z_{0} = \frac{{\lambda (D + B^{2} ) - B\sqrt {\lambda^{2} (B^{2} + 2D) + \mu^{2} } }}{\lambda D + \mu B} \in (0,\,1),\,\,\,\,\lambda = \lambda_{1} c_{1}^{0} + \lambda_{2} c_{2}^{0}\), \(\mu = (\lambda_{1} )^{2} c_{1}^{0} + (\lambda_{2} )^{2} c_{2}^{0}\), if \(B_{1} c_{1}^{0} > B_{2} c_{2}^{0}\).

Proposition 3follows from the properties of the square trinomials \(w_{1} (z)\) and \(w_{2} (z)\).

Theorem 5follows from the formulae (64) and Proposition 3.

Proof of Theorem 6

1. If \(\rho \to \infty ,\,\,\,x \to \infty\), then solutions \(c_{2} \to c_{2}^{0} ,\,\,\,c_{2}^{ - } \to 0\). The denominator \(R(c) = c\left( {B_{1} c_{1}^{0} \left( {c_{1}^{0} - c_{1}^{0} (c/c_{2}^{0} )^{{\lambda_{1} /\lambda_{2} }} } \right) + B_{2} c_{2}^{0} (c_{2}^{0} - c)} \right)\) of the first term in the integral I has singularities at the points \(c = c_{2}^{0} ,\,\,\,c = 0\) and admits the following estimates in vicinities of the singular points:

$$R(c) = B(c_{2}^{0} - c)/\lambda_{2} + O(c_{2}^{0} - c)^{2} ,\,\,\,\,\,R(c) = Ac\left( {B_{1} (c_{1}^{0} )^{2} + B_{2} (c_{2}^{0} )^{2} } \right) + O(c^{2} ).$$
(65)

Consequently, the integrand of the integral I is bounded at \(c \to c_{2}^{0}\) and \(c \to 0\), and the integral I converges.

  1. 2.

    The integral on the left-hand side of the second formula (17) can be represented as

    $$\begin{aligned} & \int\limits_{{c_{2}^{ - } }}^{{c_{2} }} {\frac{dc}{{c\left( {B_{1} c_{1}^{0} (c_{1}^{0} - c_{1}^{0} \left( {\frac{c}{{c_{2}^{0} }}} \right)^{{\lambda_{1} /\lambda_{2} }} ) + B_{2} c_{2}^{0} \left( {c_{2}^{0} - c} \right)} \right)}}} = I - \int\limits_{{c_{2} }}^{{c_{2}^{0} }} {g(c)dc} - \int\limits_{0}^{{c_{2}^{ - } }} {g(c)dc + \int\limits_{{c_{2}^{ - } }}^{{c_{2} }} {\left( {\frac{{\lambda_{2} }}{{B(c_{2}^{0} - c)}} + \frac{1}{Ac}} \right)dc} } \\ & = \frac{1}{A}\ln \frac{{c_{2} }}{{c_{2}^{ - } }} - \frac{{\lambda_{2} \,}}{B}\ln \frac{{c_{2}^{0} - c_{2} }}{{c_{2}^{0} - c_{2}^{ - } }} + I + O(c_{2}^{0} - c_{2} ) + O(c_{2}^{ - } )\,. \\ \end{aligned}$$
    (66)

Here \(g(c)\) is the integrand of the integral I.

Substitute the expansion (66) into the second formula (17) and express the difference \(c_{2}^{0} - c_{2}\):

$$c_{2}^{0} - c_{2} = c_{2}^{0} e^{{ - B(t - x - x/A - I/\lambda_{2} )}} \left( {1 + O(e^{ - B(t - x - x/A)} + e^{{ - \lambda_{2} x}} )} \right).$$

The first formula in (34) implies the estimate

$$c_{1}^{0} - c_{1} = \frac{{c_{1}^{0} }}{{c_{2}^{0} }}\frac{{\lambda_{1} }}{{\lambda_{2} }}(c_{2}^{0} - c_{2} ) + O(c_{2}^{0} - c_{2} )^{2} .$$

The asymptotics of the maximum point \(t_{m} (x)\) can be determined from the equation \(\partial s_{2} /\partial x = 0\). Using the estimates of the differences \(c_{i}^{0} - c_{i}\), we represent the numerator in the formula (47) in the form

$$N_{2} (x,t) = - Bc_{2}^{0} e^{{ - B(t - x - x/A - I/\lambda_{2} )}} + (c_{1}^{0} )^{2} c_{2}^{0} B_{1} (\lambda_{2} e^{{ - \lambda_{2} x}} - \lambda_{1} e^{{ - \lambda_{1} x}} ) + O\left( {e^{ - B(t - x - x/A)} + e^{{ - \lambda_{2} x}} } \right)^{2} .$$

The formula (22) is obtained by solving the equation \(N_{2} (x,t) = 0\).

Arguing similarly to the investigation of the profile \(s_{2} (x,t)\), we represent the numerator of the derivative (48) of the total retention profile \(s(x,t)\) in the form

$$\begin{aligned} N(x,t) & = (c_{2}^{0} - c_{2} )\left( { - \lambda_{1} B_{1} (c_{1}^{0} )^{2} \frac{{c_{1}^{0} }}{{c_{2}^{0} }}\frac{{\lambda_{1} }}{{\lambda_{2} }} - \lambda_{1} B_{2} c_{2}^{0} c_{1}^{0} - \lambda_{2} B_{1} c_{1}^{0} c_{2}^{0} \frac{{c_{1}^{0} }}{{c_{2}^{0} }}\frac{{\lambda_{1} }}{{\lambda_{2} }} - \lambda_{2} B_{2} (c_{2}^{0} )^{2} } \right) - \lambda_{1} B_{1} c_{1}^{0} c_{2}^{0} c_{1}^{ - } \\ & \quad + \lambda_{1} B_{2} (c_{2}^{0} )^{2} c_{1}^{ - } + \lambda_{2} B_{1} (c_{1}^{0} )^{2} c_{2}^{ - } - \lambda_{2} B_{2} c_{2}^{0} c_{1}^{0} c_{2}^{ - } \\ & \quad + O\left( {(c_{2} - c_{2}^{0} )^{2} + (c_{2} - c_{2}^{0} )e^{{ - \lambda_{2} x}} + e^{{ - (\lambda_{1} + \lambda_{2} )x}} } \right)\,. \\ \end{aligned}$$

Solving the equation \(N(x,t) = 0\), we obtain the asymptotics (23) of the maximum point \(T_{m} (x)\) of the total retention profile \(s(x,t)\).

The limit maximum values of the profiles \(s_{2} (x,t)\) and \(s(x,t)\) follow from formulae (21).

Theorem 6 is proved.

Examples

When calculating filtration problems, explicit finite difference schemes are usually used. The ratio of steps in time and coordinate must satisfy the Courant condition to ensure the convergence of the difference solution to the exact one [44]. Since the solution is zero ahead of the concentration front, the construction of a discontinuous solution on the front can be bypassed by considering the problem only behind the front, where the solution is continuous and positive. In a triangular domain \(\{ x \ge 0,\,\,t \ge x\}\), the Goursat problem is solved with conditions at the inlet \(x = 0\) and on the front \(t = x\) [45].

The authors use a different approach based on the known exact solution of the problem. The calculation of the solution is carried out according to the formulas (17), (18). Numerical calculation of examples is given below. The Python program code for calculating integrals can be seen in the Supplement.

The examples illustrate the change in the monotonicity of the retention profiles and the movement of the maximum points. Numerical calculations were performed at \(\lambda_{1} = 24,\,\,\,\lambda_{2} = 6,\,\,\,\,c_{1}^{0} = 0.6,\,\,\,\,\,\,c_{2}^{0} = 0.4\).

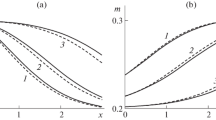
Figure 1 shows that when \(B_{1} c_{1}^{0} < B_{2} c_{2}^{0}\), the retention profiles \(s_{1} (x,t)\) and \(s(x,t)\) always decrease monotonically in x, the profile \(s_{2} (x,t)\) being not monotonic in x at \(t > 0.66\).

Fig. 1
figure 1

Total and partial retention profiles at \(B_{1} = 0.1,\,\,\,B_{2} = 0.5\). a t = 0.1, b t = 0.5, c t = 3

Full size image

When \(B_{1} c_{1}^{0} > B_{2} c_{2}^{0}\), the retention profiles \(s_{2} (x,t)\) and \(s(x,t)\) are not monotonic in x (see Fig. 2). The peak appears on the partial profile \(s_{2} (x,t)\) at \(t_{0} = 0.21\) and on the total retention profile \(s(x,t)\) at \(T_{0} = 0.73\).

Fig. 2
figure 2

Total and partial retention profiles at \(B_{1} = 0.5,\,\,\,B_{2} = 0.1\). a t = 0.1, b t = 0.5, c t = 3

Full size image

In Fig. 3, the graphs of the maximum points \(x_{\max } (t)\) of the profiles \(s_{2} (x,t)\) and \(s(x,t)\) are shown. According to Remark 1 of Theorem 6, two graphs have parallel asymptotes.

Fig. 3
figure 3

Dynamics of maximum points of retention profiles at \(B_{1} = 0.5,\,\,\,B_{2} = 0.1\)

Full size image

Since the limit speed of the maximum points of the non-monotonic retention profiles is constant and less than the speed \(v = 1\) of the concentration front Γ, it is useful to consider the profiles in the normalized coordinates \((t,\,X),\,\,\,X = x/t,\,\,\,X \in [0;1]\): \(S_{2} (X,t) = s_{2} (Xt,t)\) and \(S(X,t) = s(Xt,t)\). According to Theorem 6, the position of both peaks approaches the point \(X = 0.13\), the limit maximum values of the profiles \(S_{2} (X,t)\) and \(S(X,t)\) are 2.04 and 5.1 (see Fig. 4).

Fig. 4
figure 4

Partial and total retention profiles at \(B_{1} = 0.5,\,\,\,B_{2} = 0.1\) in coordinates \((t,\,X)\). a \(S_{2} (X,t)\) b \(S(X,t)\)

Full size image

6 Discussion

The size-exclusion retention mechanism assumes that particles freely pass through large pores and get stuck at the throats of pores that are smaller than the particles diameter. This retention mechanism occurs if the particle and pore size distributions overlap. In this case, large particles get stuck in the pores more often than small ones. According to Eqs. (4), the deposit growth rate is proportional to the coefficient \(\lambda_{i}\). Therefore, the condition \(\lambda_{1} > \lambda_{2}\) means that particles of type 1 are larger than particles of type 2. Note that such a description of the types of particles is rather arbitrary. The particles can have the same size and differ in form, density or other physicochemical properties.

The profile maximum point appears at the inlet \(x = 0\) at the moment \(t_{0} > 0\) and moves deep into the porous medium. For a porous sample of finite length l, at some instant \(t_{1} > t_{0}\), the maximum point reaches the outlet \(x = l\) and the profile \(s_{2} (x,t)\) becomes monotonically increasing in x. This means that the retained concentration of small particles is maximum at the outlet. Since the retention profile \(s_{1} (x,t)\) always decreases monotonically, the retained concentration of large particles is maximum at the porous medium inlet. Thus, the long-term deep bed filtration of a bidisperse suspension or colloid in a porous medium makes it possible to separate large and small retained particles from each other.

For a water injection problem in a well, water is pumped down a wellbore and then dispersed radially into the formation. Assuming radial symmetry, this process is actually a radial flow scheme with an explicit radius dependency. For a monodisperse suspension, we obtain a one-dimensional filtration problem with a filtration function that depends on the coordinate. It corresponds to the filtration of suspension or colloid in a porous medium with variable porosity. The problem is reduced to a single first-order equation, which in the general case does not have an analytical solution [46]. The filtration problem in polar coordinates for a bidisperse suspension requires a separate study.

If the number of particle types \(n > 2\), then the properties of the profiles of the polydisperse suspensions or colloids are not known. This problem will be considered later.

To calculate the pressure distribution in the porous medium during particle transport and retention, it is necessary to set the empirical function of permeability \(k(s_{1} ,s_{2} )\) and viscosity of the carrier water \(\mu (c_{1} ,c_{2} )\). Then pressure is determined using the Darcy’s law with varying permeability and viscosity [1].

7 Conclusions

The study of a one-dimensional deep bed filtration model of bidisperse suspensions and colloids in a porous medium leads to the following conclusions:

  • The existence and the uniqueness of the solution to the bidisperse filtration problem are proved.

  • Exact analytical formulae for the solution have been obtained.

  • Retention profiles of large particles always decrease monotonically; the profiles of small particles are non-monotonic.

  • The condition for the monotonicity/non-monotonicity of the total retention profile has been obtained.

  • Starting from a certain moment of time, each non-monotonic profile has a maximum point.