1 Introduction

Bentonite is a common material used in various civil engineering applications, such as landfill liners, cutoff walls and nuclear waste repositories, due to its low hydraulic conductivity (Kazemain and Huat 2009). Recently, El Mohtar et al. (2008, 2013), Yoon and El Mohtar (2013a), and Rugg et al. (2011) proposed the application of bentonite suspension in permeation grouting to improve the engineering performance of granular soils under static and cyclic loading conditions. In this application, bentonite suspensions are injected into loose saturated granular soil deposits at low pressures without disturbing the existing soil structures. Due to the thixotropic nature of bentonite suspension, the injected bentonite suspension forms gel-like structures inside pore spaces, increasing resistance of the treated soils to static and cyclic loading. While concentrated bentonite suspensions are required to achieve the appropriate engineering properties of the treated soils, the high concentrations limit their application in permeation grouting due to low penetrability through soils. In order to overcome the limitation, the rheological properties of the suspensions such as yield stress and viscosity should be improved to increase the penetration depth. Santagata and Santagata (2003) reported that the penetration of microfine cement grouts through sand columns significantly increased with the decrease in their viscosity. In this study, an ionic additive, sodium pyrophosphate (SPP), was utilized to control rheological properties of bentonite suspensions since SPP shows pronounced dispersing capability (Abend and Lagaly 2000; Penner and Lagaly 2001) and allows time-dependent recovery of the rheological properties by formation of 3D network structures in the suspensions (Tchillingarian 1952). The mobility of the treated bentonite suspensions is reduced with time since the mobility of bentonite suspension is controlled by the network formed in the suspension (Goh et al. 2011). The time-dependent recovery is a unique character of the SPP modified bentonite suspensions compared to bentonite suspensions treated with other ionic additives such as sodium hydroxide (Tchillingarian 1952).

The groutability of a soil with a specific grout is a measure of the ability of the grout to permeate through the soil. Although cement-based and bentonite grout are both particulate grouts, it is challenging to apply the existing groutability criteria developed for cement-based grouts to bentonite grouts due to their difference in rheological properties, particle size and shape. The existing criteria are mostly based on the groutability number (N), which only accounts for the relative grain size of the soils and cements (Bell 1993; Burwell 1958; Incecik and Ceran 1995), and do not reflect the change in chemical and rheological properties when different types of materials (with the same particle size distribution) or chemical modifications are utilized. Markou and Atmatzidis (2002) reported that the relative grain size criteria produced relatively optimistic prediction in the groutability of soils with fly ash grouts. Akbulut and Saglamer (2002) suggested an advanced criterion accounting for different parameters, of both soils and grouts, affecting groutability of granular soils such as fines content (FC), injection pressure (P), relative density (Dr), and water/cement ratios (W/C). However, this advanced criterion also did not reflect the effect of super-plasticizers, leading to the same groutability for a given soil and water/cement ratio regardless of the presence of super-plasticizers. This is a major limitation due to the fact that the super-plasticizer changes the rheological properties of the cement-based grouts affecting its permeation through soils (Santagata and Santagata 2003).

While the rheological properties of a grout govern its flow through soils when filtration is negligible (Raffle and Greenwood 1961; Jefferis 1992; Jancsecz and Steiner 1994; Gustafson and Stille 1996), the grout flow stops due to filtration, which typically occurs during injection process of particulate grouts (Gustafson and Stille 1996). The filtration affects the grout flow depending on rheological properties and grain size of a grout, and grain size of sand, resulting in the limited penetration of the grout (Herzig et al. 1970; Axelsson et al. 2009; Kim and Whittle 2009). Previous research proposed macroscopic models to simulate grout propagation based on the filtration phenomenon (Bouchelaghem and Vulliet 2001; Saada et al. 2005; Chupin et al. 2007; Kim and Whittle 2009). The models, however, do not take into account for the change in filtration due to the chemical modification of grouts to improve the depth of its penetration. Moreover, the models cannot directly predict groutability of a soil, and therefore, requiring additional experimental and theoretical studies.

This study presents a new approach to evaluate the groutability of granular soils using the SPP modified bentonite grouts based on a filtration model that incorporates the change in chemical and rheological properties of bentonite grouts due to SPP modification. The rheological tests are performed to investigate the effect of SPP on the apparent viscosity of bentonite grouts. The apparent viscosity describes the variation of the resistance to a flow at a particular shear rate, which is related to the flow rate or pressure drop in a porous medium (De Paoli et al. 1992a). Low apparent viscosity indicates high mobility of the grout. Conventional sand column tests are conducted at various experimental conditions such as effective grain size and injection pressure. A 1D filtration model is then calibrated with injected volumes of bentonite grouts, producing the lumped parameters that illuminate the filtration property of the SPP modified bentonite grout through a granular soil. A new groutability criterion for bentonite grout is proposed based on this lumped parameter.

2 Particle Transport and Deposition Model

The analysis of the suspended particles through a porous medium is represented by a macroscopic problem of solute transport through a homogeneous medium with a mass transfer. The governing equation for this type of problem is given by the advection-dispersion equation (Eq. 1). The equation is derived from mass conservation law by spatially averaging the macroscopic equation over the characteristic volume including both the solid and liquid phase (Raupach and Shaw 1982). Since the system and microscopic scale is 10–100 cm and 10\(^{-3}\)–10\(^{-2}\) cm, respectively, the size of the averaging volume ranges from 0.1 to 1 cm (Ni and Beckermann 1991). The governing equation (Kim and Whittle 2009) is expressed as:

$$\begin{aligned} \frac{\partial }{\partial t}\left( {nC} \right) +\mathbf{v}\cdot \nabla \left( C \right) +\nabla \cdot \left( {n\mathbf{D}\nabla C} \right) =-\frac{\partial \sigma }{\partial t}, \end{aligned}$$
(1)

where n is the “skeletal” porosity based on solid phase consisting of sand grains only, C is the concentration of a solute, v is the fluid velocity, D is the hydrodynamic dispersion tensor (dimension of L\(^{2}\)/T), \(\sigma \) is the specific deposit, which is defined as the mass per initial unit pore volume. Although the deposition rate changes as the deposition covers the wide area of the porous medium (Herzig et al. 1970; Tien 1989), the most commonly applied kinetics for filtration rate through clean sand is the first-order law (Iwasaki 1937):

$$\begin{aligned} \frac{\partial \sigma }{\partial t}=\lambda C, \end{aligned}$$
(2)

where \(\lambda \) is the filtration coefficient with a dimension of 1/T.

In order to implement the governing equation, the following assumptions were established: (1) the flow is 1D and steady, (2) the sedimentation of particles is neglected due to the colloidal characteristic of bentonite in aqueous medium, (3) the dilution of grout by hydrodynamic dispersion was ignored since previous research showed that the effect is small enough to ignore and the filtration is a dominant phenomenon in grout flow (Zebovitz et al. 1989; Saada et al. 2005; Kim and Whittle 2009), (4) it was assumed that particle diffusion is negligible since the average particle size of bentonite is larger than 1 \(\upmu \)m (Herzig et al. 1970), (5) since the model in this study is based on macroscopic phenomenon which does not capture the microscale variations, the detachment of deposited particles, which occurs due to the collision of the moving particles with the deposited particles by a localized pressure or flow rate variation, and the global change of the flow rate in whole bed such as reversing the flow direction, were not considered, and (6) soil matrix was regarded as rigid (Bouchelaghem and Vulliet 2001; Saada et al. 2005). Although the displacement of sand grains may occur during injection of grouts, the displacement is considered small enough to ignore. Bouchelaghem and Vulliet (2001) reported strains of the order of 10\(^{-6}\), (7) the change in porosity is insignificant (\(\partial n\)/\(\partial t \approx \) 0) (Reddi and Bonala 1997).

Based on the assumptions above and the first-order law of filtration (Eq. 2), Eq. (1) becomes

$$\begin{aligned} \frac{\partial C}{\partial t}+V\frac{\partial C}{\partial x}+\lambda C=0, \end{aligned}$$
(3)

where V is the pore velocity, \(V=v/n\) (v is the Darcian velocity, n is the porosity).

If the porous medium is sufficiently deep, the grout needs a substantial time to pass through it; accordingly, the moment when the grout reaches an element in the porous medium, the porous medium is not the same all along its depth. Thus, the elements in the porous medium should be compared at the same time scale. The retention age can be expressed as follows (Herzig et al. 1970):

$$\begin{aligned} \xi \left( {x,t} \right) =t-\frac{x}{V}. \end{aligned}$$
(4)

The term x/V is the time needed for the grout to reach a bed depth x. By adopting the concept of retention age, the partial differential equation is reduced to ordinary differential equation. Reddi and Bonala (1997) provided the solution:

$$\begin{aligned} C\left( {x,t} \right) =f_1 \left( \xi \right) \exp \left( {-\lambda \frac{x}{V}} \right) U\left( \xi \right) +f_2 \left( {-\xi V} \right) \exp \left( {-\lambda t} \right) U\left( {-\xi } \right) , \end{aligned}$$
(5)

where \(f_{1}\) is the function of boundary conditions and \(f_{2}\) is the function of initial conditions and U is the heaviside unit step function. The equation can be solved by adopting the following initial and boundary conditions

$$\begin{aligned} C(x,0)=0=f_{2}(x)=0, f_{1}(t)=c(0,t)= C_{o}. \end{aligned}$$
(6)

The concentration of grouts are obtained by

$$\begin{aligned} C\left( {x,t} \right) =C_{o} \exp \left( {-\frac{\lambda }{V}x} \right) U\left( {t-\frac{x}{V}} \right) . \end{aligned}$$
(7)

The amount of grout particles deposited in the soil matrix per initial unit pore volume is expressed by

$$\begin{aligned}&\sigma \left( {x,t} \right) =0\left( {t-\frac{x}{V}<0} \right) , \end{aligned}$$
(8)
$$\begin{aligned}&\sigma \left( {x,t} \right) =\int \limits _{x/V}^t {\lambda C_{o} } \exp \left( {-\frac{\lambda }{V}x} \right) dt\left( {t-\frac{x}{V}>0} \right) . \end{aligned}$$
(9)

By integrating Eq. (9), the amount of grout particles retained in the soil matrix per initial unit pore volume is obtained as follows:

$$\begin{aligned} \sigma \left( {x,t} \right) =\lambda C_{o} \left( {t-\frac{x}{V}} \right) \exp \left( {-\frac{\lambda }{V}x} \right) . \end{aligned}$$
(10)

In order to implement filtration modeling, the geometric properties of the soil (pore size distribution, location, orientation, and connectivity) should be investigated. It may be possible to obtain a spatial configuration of pore space by using stochastic simulation techniques from experimental data (Tsakiroglou and Pyatakes 1990) or nondestructive techniques such as X-ray or magnetic resonance microtomography (Vogel and Roth 2001). Moreover, geometric parameters, corresponding to characterize pore space, can be derived by fitting the experimentally measured pressure–saturation relations using mercury intrusion porosimetry (Tsakiroglou and Pyatakes 1990). The derivation of the deposition rate by Reddi and Bonala (1997) estimated pore sizes from the known particle size distribution, which is originally proposed by Arya and Paris (1981) and updated by Arya and Dierolf (1989) for predicting moisture characteristic curves of partially saturated soils. The particle size distribution curve is subdivided into i size ranges with average diameter, 2\(r_\mathrm{{i}}\), weight fraction, \(w_\mathrm{{i}}\). Within each size range of the pore volume is represented by a single pore of radius \(R_\mathrm{{i}}\) at the known macroscopic void ratio, e. Arya and Dierolf (1989) provided the updated model that relates pore radii (r) to particle radii (R):

$$\begin{aligned} r_{ i} =\left[ {\frac{4eR_\mathrm{{i}}^3 }{3\alpha ^{*}}} \right] ^{1/2}, \end{aligned}$$
(11)

where e is the void ratio, \(R_\mathrm{{i}}\) is the particle radius (mm), \(\alpha \)* is the parameter representing the effective pore length associated with each particle, and \(r_{ i}\) is the radius of pore (mm). Arya and Dierolf (1989) found that \(\alpha \)* varies from 3 to 15 mm for coarse sand to silts (the particle radius is from 10\(^{-3}\) to 1 mm). Moreover, the predicted pore radii showed a good agreement with the measured ones using the value of 9.11 mm. However, the particle deposition cannot be estimated directly using Eq. (10) due to the assumptions of a constant porosity (or low concentration) and particle deposition. Kim et al. (2009) reported that Eq. (10) could overestimate particle deposition, possibly due to the assumption of a constant particle deposition rate that should vary with time. In order to consider those variations, this study utilized the step-wise calculation method (Kim et al. 2009) to calculate the particle deposition. Details for the deposition coefficient with step-wise calculation are presented in Sect. 3.2.

3 Experimental Program

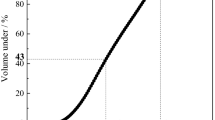
Three different sands with different effective grain size (\(D_{10})\) were used in this study. Based on a USCS classification, the sands were classified as a poorly graded sand (SP). Table 1 summarizes the index properties of the tested sands based on ASTM standards (ASTM D422, D854, D4253, and D4254). Wyoming sodium-bentonite (CP-200, CETCO) was used to prepare the grouts. The raw bentonite was screened through a No. 200 sieve to minimize the large-sized impurities such as plagioclase feldspar, orthoclase, and muscovite minerals (Abend and Lagaly 2000; Clarke 2008). This process produced approximately 95 % of particles less than 25 \(\upmu \)m and 50 % of particles less than 1 \(\upmu \)m. The specific gravity (Gs), plastic limit (PL) and liquid limit (LL) of bentonite were 2.70, 38, and 440 %, respectively. The cation exchange capacity (CEC) and specific surface area (SS) measured using methylene blue adsorption technique were 91 meq/100 g and 712 m\(^{2}\)/g. The SS area was calculated based on the method suggested by Santamarina et al. (2002). The swelling capacity of the bentonite was 8 ml/g. The grain size distribution curves for the tested sands and sieved bentonite (ASTM D422) are shown in Fig. 1.

Table 1 Index properties of the tested sands
Full size table
Fig. 1
figure 1

Grain size distribution curves for the tested sands and sieved bentonite

Full size image

The chemical analysis was performed using Philips/FEI XL30 environmental scanning electron microscope (ESEM) equipped with energy diffraction analysis of X-ray (EDX) to characterize chemical composition of the sieved bentonite powder. A gaseous secondary electron (GSE) detector was utilized with frame and spot mode of EDX. The chemical components of bentonite were oxygen (53.05 % by weight), silicone (28.77 %), aluminum (9.07 %), iron (2.31 %), sodium (2.27 %), magnesium (1.52 %), and calcium (1.2 %). the bentonite also included small amounts of other chemical components such as phosphorus, sulfur, and titanium. The molar ratio of the sieved bentonite, which is the critical parameter affecting rheological properties of bentonite suspensions (Brandenburg and Lagaly 1988), was 1.9. The pH of bentonite grouts was measured using JENCO 60 pH meter and showed a strong alkalinity with an average pH of 9.3, standard deviation and the coefficient of variation (COV) of 0.3 and 0.03, respectively.

Commercially available SPP decahydrate (Na\(_{4}\)P\(_{2}\)O\(_{7}\!\cdot \!10\)H\(_{2}\)O) was utilized in this study. Since the amount of SPP needed for each batch was very small, a 5 % SPP solution was prepared in advance and the appropriate amount of solution was added to the water and bentonite to increase the accuracy of the measurements. The average pH of the 5 % SPP solution was 9.5. De-ionized water with constant ionic concentration of 2\(\times \)10\(^{-5}\) mm was used for preparing all the bentonite grouts and SPP solution.

3.1 Apparent Viscosity Measurement

A Physica MCR 301 rheometer equipped with a vane was utilized in this study to perform the rheological tests on the bentonite grouts. The vane used is a six-bladed vane, each blade having a thickness of 1 mm and a length of 16 mm. The radius of the vane is 11 mm, resulting in a 3.46 mm of gap between the cup and the vane. Sample volume was maintained at 37 ml, which allows the vane to penetrate approximately twice its depth into the grouts. All tests were performed at a temperature of 22 \(^\circ \)C (\(\pm \)0.03 \(^\circ \)C); the temperature was controlled using the built-in Peltier temperature control system in the rheometer.

The screened bentonite powder was mixed with de-ionized water; the weight fraction of bentonite grouts was calculated as the weight ratio of bentonite to the total weight of grouts. In the calculation of bentonite fraction, the water content of the bentonite in its storing condition was accounted for by calculating the weight of the dry bentonite. The concentration of SPP was calculated as the weight ratio of dry SPP to dry bentonite. The mixing process of the bentonite grouts included three steps; each step consisted of 5 min of high shear mixing of the suspensions followed by manual scraping of the sides and base of the mixing cup to remove any attached bentonite flocs.

The stress ramp technique, a stress-controlled test, was utilized in this study. In the technique, the stress levels are increased in step-wise. At each step, a constant stress level of 3 Pa was maintained for 12 s and the torsional strain was recorded at the end of each interval. The apparent viscosity (shear stress/shear rate) was then calculated based on the shear rate and the stress applied. The samples were rested for 2 min after inserting the vane to provide a consistent initial condition. The stress ramp technique was selected since it covers a wide range of shear rates, and thus apparent viscosities. Figure 2 shows apparent viscosity of bentonite grouts with stress ramp technique. At high shear rates, it reaches a steady state (or equilibrium state), producing essentially constant apparent viscosity. Since the apparent viscosity at high shear rate is more important than that at low shear rate when analyzing the injection process (Markou and Atmatzidis 2002), it was considered appropriate to use the apparent viscosities at the equilibrium state as the model parameters. This selection of apparent viscosity at equilibrium already assumes a shear rate in the range of the expected value during injection, and therefore, eliminates the need to include the apparent viscosity as a function of shear rate; this process allows for using a single value for the apparent viscosity when comparing its effect on the permeation of the grout. Moreover, the apparent shear rates approximated using Eq. (12) suggested by Metzner and Reed (1955) produced the apparent shear rates of 250–450 1/s where the apparent viscosities of the tested grouts reached the equilibrium viscosities. In the equation, the grout flow through granular soils is idealized as a flow through a bundle of capillary tubes. In addition, the rheological behavior of the bentonite grouts is represented as a power law equation (\(\tau =\mu \cdot {\dot{\gamma }}^{n{\prime }})\) by fitting the experimental data to the model. The apparent shear rate is calculated by

$$\begin{aligned} \mathop {\gamma _\mathrm{{a}} }\limits ^\cdot =\left( {\frac{3n^{{\prime }}+1}{4n^{{\prime }}}} \right) \left( {\frac{8V_\mathrm{{c}} }{D_\mathrm{{c}}}} \right) , \end{aligned}$$
(12)

where \({\dot{\gamma }}_\mathrm{{a}}\) is the apparent shear rate, \(n'\) is the flow behavior index from power law equation, \(V_\mathrm{{c}}\) is the pore velocity, and \(D_\mathrm{{c}}\) is the diameter of a capillary tube.

Fig. 2
figure 2

Determination of equilibrium apparent viscosity

Full size image

3.2 1D Sand Column Test and Model Simulation

One-dimensional sand column tests has been a conventional technique conducted in laboratory to investigate groutability and penetrability in granular soils, even though it does not reflect multistage injection as typically performed in the field and tends to overestimate the filtration compared to 3D test (Santagata and Santagata 2003; Yoon 2011). A schematic of the injection test setup used in this study is depicted in Fig. 3. The grouting cell is transparent and has a 3.8 cm in diameter and is 21 or 45 cm in height. Clean sands were carefully air-pluviated with a funnel into the grouting cell. The free drop height was adjusted to achieve the desired relative densities (30 and 80 %). Both the loose and dense specimens were initially pluviated as a slightly loose state, and then the grouting cell was gently tapped on the sides to decrease the void ratio to the target values. The specimens were then slowly flushed with water from the bottom to the top to minimize any particle movement through the specimens. A filter material, consisting of a 12.5-mm-thick layer of coarse sand (1.2 mm \(< D_\mathrm{{f}} < 1.7\) mm) and a 12.5-mm-thick-layer of pea gravel (\(D_\mathrm{{f}}> 4.75\) mm), was placed on the top and bottom of the sand column to help produce a uniform supply of bentonite grouts throughout the cross-section of the sand column. The coarse sand layer prevented the sand grains from falling into the large voids in pea gravel layer.

Fig. 3
figure 3

Schematic of 1D sand column test setup. (The solid and dashed lines represent a flow of air-pressure and liquid, respectively)

Full size image

The air-pluviated sand columns were initially saturated with slow flushing of de-aired water (at least three pore volumes) from bottom to top, and then more pore volume of water (at least three pore volumes) was flushed at a pressure of 35 kPa to remove air bubbles in the specimen (ASTM D4320/D4320M-09). The effect of degree of saturation in penetration of grouts was not considered through this study by performing all the tests at nearly saturated condition. The hydraulic conductivity of the sand columns fell into the range of \(\pm \)25 % (ASTM D5084) from the reference hydraulic conductivity of the tested sands that were measured in the fully saturated condition, indicating a high degree of saturation.

Bentonite grouts were placed into a pressure cell within 2 min after mixing for consistency with rheological tests. The bentonite grouts were then injected into the sand columns using a pressure panel at the constant pressures of 35 and 140 kPa. A balance was placed to measure weight of effluents during testing. The volume of effluent water was considered the same as the volume of the injected grouts. The completion of permeation was determined as the moment that the weight of outflow does not vary for at least 10 min. The Reynolds numbers ranged from approximately \(10^{-4}\)–\(10^{-3}\), indicating laminar flow.

The model calculation was implemented in step-wise similar to the method proposed by Kim et al. (2009) for 3D spherical flow. A sand column was divided into infinitesimal volume blocks with the height of \(\Delta h\) (\(h_{i}\)-\(h_{i-1}\)) and the width of 38 mm (diameter of the grouting cell). Although the factors affecting the grout permeation (e.g., pore fluid velocity, porosity, and filtration coefficient) vary with time, it is considered as a constant within the descritized infinitesimal volume block. The injection time at each block is calculated by

$$\begin{aligned} \Delta t_{i,j} =\frac{\left( {\mu _\mathrm{{g}} } \right) _{i,j} n_{j,j} \Delta h}{K_{i,j} \left( {\gamma _\mathrm{{g}} } \right) _{i,j} i}, \end{aligned}$$
(13)

where the subscripts i and j are the spatial node and time step, respectively (when \(i\le j\)), \(\Delta h\) is the distance of the zone between \(h_{i-1 }\) to \(h_{i}\), \(n_{j,j}\) is the porosity in the zone between \(h_{i-1 }\) to \(h_{i}\), \(K_{i,j }\) is the intrinsic permeability in the zone between \(h_{i-1}\) to \(h_{i}\), \((\gamma _\mathrm{{g}})_{i,j}\) is the unit weight of grout in the zone between \(h_{i-1}\) to \(h_{i}\) and \((\mu _{g})_{i,j}\) is the apparent viscosity of grout in the zone between \(h_{i-1}\) to \(h_{i}\), i is the hydraulic gradient (=\(\Delta P\)/\(L\gamma _\mathrm{{w}}\)) that is assumed to be constant during the injection process. The pore fluid velocity is calculated by

$$\begin{aligned} V_{i,j} =\frac{n_{j,j} \Delta h}{\Delta t_{j} n_{i,j}}. \end{aligned}$$
(14)

The filtration rate (deposition coefficient, \(\lambda )\) is an important parameter in filtration modeling. Since the coefficient is difficult to estimate due to the dynamic nature of the filtration process, it should be obtained through back-analysis based on experimental results (Bouchelaghem and Vulliet 2001; Kim and Whittle 2009). The coefficient is also influenced by the chemical reaction and velocity of the grouts and geometrical characteristics of the porous medium. Reddi and Bonala (1997) proposed the closed form expression of the filtration rate based on particle capture probability approach. The concept is that the probability of particle capture in a pore tube is equivalent to fraction of total flow in annulus between r and \(r-\theta \cdot a\) (r is the radius of the pore tube, a is the particle radius, and \(\theta \) is the lumped parameter). They selected this approach because it determines the probability of capturing particles through a pore larger than the particle size, which is a similar condition to the particle deposition during filtration. The relation determines the fraction of flow in annulus size of \(\theta \cdot a\) under the laminar flow condition. The parameter, \(\theta \), accounts for the effect of ionic strength, pH, and fluid velocity. The higher \(\theta \) values suggest higher filtration potential. The \(\theta \) value is postulated as an exponential function:

$$\begin{aligned} \theta =\theta _\mathrm{{o}} \cdot \exp \left( {-\frac{v}{v_\mathrm{{cr}}}} \right) , \end{aligned}$$
(15)

where \(\theta _\mathrm{{o}}\) is a constant, depending on ionic conditions, v is the velocity of flow in the pore tube, and \(v_\mathrm{{cr}}\) is the critical velocity where no particle deposition is likely. For filter soils, \(v_\mathrm{{cr}}\) is close to 0.1 cm/s (Reddi et al. 2000). The \(\theta \) value becomes close to the \(\theta _\mathrm{{o}}\) when the velocity of the flow is much slower than the critical velocity, which is a normal flow condition in soil. Since the deposition coefficient depends on the velocity of the pore fluids, the deposition coefficient is expressed as:

$$\begin{aligned} \lambda _{i,j} =\frac{V_{i,j} }{\alpha ^{*}e^{2\left( {b^{2}+m} \right) }}\left[ {4 \left( {a\cdot \theta } \right) ^{2}-4 \left( {a\cdot \theta } \right) ^{3} e^{\left( {b^{2}-2m} \right) /2}+\left( {a\cdot \theta } \right) ^{4} e^{2\left( {b^{2}-m} \right) }} \right] , \end{aligned}$$
(16)

where \(V_{i,j}\) is the pore velocity in the zone between \(h_{i-1 }\) and \(h_{i}\), a is the migrating particle radius, b and m are the mean and standard deviation of natural log a, respectively, and \(\alpha \)* is the parameter representing the effective pore length associated with each particle, and \(\theta \) is the lumped parameter. With the deposition coefficient, the deposition of particles in the element can be calculated at the center of the element and the total deposition of particles is calculated as the summation of the depositions in each element:

$$\begin{aligned} \Delta \sigma _{i,j} =\lambda _{i,j} C_{i,j} \left( {\Delta t_{i,j} -\frac{h_i +\Delta h/2}{V_{i,j}}} \right) \exp \left( {-\lambda _{i,j} \frac{h_i +\Delta h/2}{V_{i,j}}} \right) . \end{aligned}$$
(17)

By using the density relationship, the change in porosity of porous medium becomes

$$\begin{aligned} n_{i,j} =n_\mathrm{{o}} -\frac{\sum \nolimits _{m=i}^j {\Delta \sigma _{i,m} } }{G_\mathrm{{s}} \gamma _\mathrm{{w}}}, \end{aligned}$$
(18)

where \(n_{i,j}\) is the changed porosity due to filtration in the zone between \(h_{i-1 }\) and \(h_{i}\), \(n_\mathrm{{o}}\) is the initial porosity of porous medium, \(\sigma _{i,j}\) is the mass of the filtered particles per unit volume of porous medium in the zone between \(h_{i-1 }\) and \(h_{i}\), \(G_\mathrm{{s}}\) is the specific gravity of solid particles, and \(\gamma _\mathrm{{w}}\) is the unit weight of water.

Based on the permeability relationships (Kozeny–Carman equation with hydraulic radius model), the variation of the intrinsic permeability is estimated by

$$\begin{aligned} \frac{K_{i,j+1} }{K_{i,j}}=\left( {\frac{n_{i,j+1} }{n_{i,j} }} \right) ^{3}\left( {\frac{1-n_{i,j} }{1-n_{i,j+1}}} \right) ^{2}. \end{aligned}$$
(19)

The concentration of the suspensions may be reduced as filtration proceeds due to the particle loss in the previous block, affecting both the unit weight and apparent viscosity. The change in the particle concentration, unit weight, and apparent viscosity was calculated by

$$\begin{aligned}&C_{i,j} =C_{i-1,j} -\Delta \sigma _{i-1,j} , \end{aligned}$$
(20)
$$\begin{aligned}&(\gamma _\mathrm{{g}})_{i,j} =1+C_{i,j} \left( {1-\frac{1}{G_\mathrm{{s}}}} \right) , \end{aligned}$$
(21)
$$\begin{aligned}&\mu _{i,j} =\mu _\mathrm{{w}} \left( {1+\left( {\frac{\mu _\mathrm{{eq}} }{\mu _\mathrm{{w}} }-1} \right) } \right) \left( {\frac{\phi _{p_{i,j} } }{\phi _{p_o } }} \right) , \end{aligned}$$
(22)

where \(\mu _\mathrm{{w}}\) and \(\mu _\mathrm{{eq}}\) are the viscosity of water and the initial equilibrium viscosity of grout, respectively, \({\phi }_\mathrm{{po}}\) is the initial particle fraction in grout, and \({\phi _\mathrm{{p}}}\) is the current particle fraction in grout. Due to the relatively short injection time, the time-dependent change in apparent viscosity is not considered in this study.

Since the grouting process occurs simultaneously, the coupling between the volume blocks should be taken into account. This effect is considered by calculating the maximum travel time at each block, which governs the whole grouting process at the time step j

$$\begin{aligned} \Delta t_j =\max \left( {\Delta t_{1,j} ,\Delta t_{2,j} ,\Delta t_{3,j} ...\Delta t_{j,j} } \right) . \end{aligned}$$
(23)

With the determined time, the amount of filtration, change of intrinsic permeability, and corresponding volume response were calculated at the middle of the elements using Eqs. (14) through (17). The numerical calculation was coded using Visual basic embedded in Microsoft Excel in accordance with the mathematical formulation and the calculation algorithm.

4 Results and Discussion

4.1 Rheological Test

Figure 4 depicts the equilibrium apparent viscosity of bentonite grouts at different SPP concentration. All the apparent viscosity values reported are the average of at least three measurements on three different samples; the different samples showed similar measured properties with a COV of 0.01–0.2. The equilibrium apparent viscosities were reduced by approximately 50 % for 7.5, 10, and 12 % grouts with 2, 3, and 4 % SPP, respectively. However, the change in the apparent viscosity from 1 to 2 % SPP at 7.5 % grout resulted in only 3 % difference. This implies that the small amount of SPP is effective to reduce the apparent viscosity of concentrated bentonite grouts, but the effect of SPP on the apparent viscosity is minimal beyond a threshold percentage of SPP. Similarly, Yoon and El Mohtar (2013b) reported that the yield stress, which is a threshold shear stress to initiate flow, becomes approximately zero with 2, 3, and 4 % SPP concentrations. Since the penetration length of the grout through soils is inversely proportional to the yield stress (Gustafson and Stille 1996), the grout mixes having zero yield stress provide theoretically infinite penetration length. Therefore, the SPP concentrations of 1, 3, and 4 % for 7.5, 10, and 12 % grouts were mainly utilized through this study as an upper bound dosage of SPP. With the SPP concentration, the bentonite grouts did not show any coagulation, indicating that the SPP concentration was still less than the critical coagulation concentration (the concentration of an ion where coagulation induces (Penner and Lagaly 2001)).

In order to incorporate the change in apparent viscosity into the filtration model, an empirical relationship was found using regression analyses based on bentonite fraction in grouts and SPP concentrations. Because the equilibrium apparent viscosity increased with bentonite fraction and decreased with SPP concentrations exponentially, the equilibrium apparent viscosity can be expressed as:

$$\begin{aligned} \mu _\mathrm{{eq}}=14.61\cdot \mathrm{{EXP}}\left( {0.278\cdot B-0.214\cdot \mathrm{{SPPC}}} \right) , \end{aligned}$$
(24)

where \(\mu _\mathrm{{eq}}\) (mPa\(\cdot \)s) is the equilibrium apparent viscosity, B (%) is the bentonite fraction in grouts (dry weight of bentonite to total weight of grout) and SPPC (%) is the SPP concentration (dry weight of SPP to dry weight of bentonite). As shown in Fig. 4, the proposed model well captured the overall variation of the equilibrium viscosity based on bentonite fraction and SPP concentration. However, it should note that the proposed viscosity model would be reasonable for the range of bentonite fraction from 5 to 12 % and SPP concentration from 0 to 4 %.

Fig. 4
figure 4

Equilibrium apparent viscosity of bentonite grouts based on SPP concentration: 7.5, 10, and 12 % grouts with 0–4 % SPP

Full size image

Figure 5 shows the injected pore volume based on equilibrium apparent viscosity for 7.5, 10, and 12 % bentonite suspensions with 0–4 % SPP. Since the sand columns were prepared based on the relative densities of 30 and 80 %, the sand columns consisting of different types of sands have different porosities at the two relative densities. In order to correct the difference in porosity, the injected volumes of the grouts were normalized by pore volume of each sand column. As can be seen, the injected pore volume consistently increased with the decrease in equilibrium apparent viscosity (\(R^{2}=0.950\)). The addition of 3 % SPP to 10 % grout increased the injected pore volume approximately 100 % compared to that in unmodified 10 % grout. This indicates that the SPP modification of bentonite grout effectively increases the amount of grout flow through the sand columns and the rheological properties of bentonite grouts significantly affect the grout flow through soils.

Fig. 5
figure 5

Injected pore volume based on equilibrium apparent viscosity of bentonite grouts: 7.5, 10, and 12 % grouts with 0–4 % SPP

Full size image

4.2 Evaluation of Lump Parameter

With the equilibrium apparent viscosities and parameters presented in Table 2, the numerical calculation was performed. The lognormal pore size distributions in three sands are shown in Fig. 6. The shape of the pore size distribution was similar in all three sands. The pore sizes of sand B were relatively well distributed compared to the others. The lumped parameters (\(\theta )\) were determined by calibrating the model to the volume intakes (\(\pm \)1.5 %) from the experimental measurements. Figure 7a and b shows the measured injected volume per unit cross-sectional area of grouts over time and the comparison of the calculated and measured volume evolution with the injection time. The injected volume of grouts rapidly increases at the beginning of the test, but the rate decreases as the injection time elapses. The model could capture the overall volumetric response well with the \(\theta \) values of 6.5–18. The wide range of \(\theta \) values is attributed to the fact that the ionic strength of bentonite grout is widely changed with SPP modification (Abend and Lagaly 2000). Rege and Fogler (1988) reported the theta values ranges from 0 to 15 for KCl modified bentonite suspensions. Moreover, Kim et al. (2009) found the values of \(\theta \) to range from 2.8 to 4.0 for microfine cement grout.

Fig. 6
figure 6

Grain and lognormal pore radius distribution of the tested sands

Full size image
Fig. 7
figure 7

a Measured injected volume per unit cross-sectional area with time, b comparison of model and measured injected volume with time

Full size image
Table 2 Parameters used in calculation
Full size table

Figure 8a–d describes the variation of the \(\theta \) value based on effective grain size of sand, equilibrium apparent viscosity, and injection pressure. Figure 8a shows the effect of the effective grain size of sand (\(D_{10})\) on \(\theta \) using 12 % bentonite suspensions with 4 % SPP. As the effective grain size of the tested sand increased, the \(\theta \) values consistently decreased. Sand C (\(D_{10 }=0.31\) mm) produced 55 % smaller \(\theta \) value compared to that of Sand A (\(D_{10 }=0.20\) mm). This indicates that less amount bentonite particles are captured in pore spaces when the grout flows through the soil having larger effective grain size. Previous studies reported that the injected volume of grout (grout intake) increased with the increase of the effective grain size of sand when chemical and cement-based grouts are utilized (Akbulut and Saglamer 2002; Santagata and Santagata 2003; Ozgurel and Vipulanandan 2005).

Fig. 8
figure 8

Effect of a effective grain size of sand, b equilibrium apparent viscosity for 10 % grouts with 0–3 % SPP, c injection pressure, d relative density on lump parameter (The lines are drawn for visual aids)

Full size image

Figure 8b depicts the effect of equilibrium apparent viscosity on the \(\theta \) value. The \(\theta \) value increased with the increase of equilibrium apparent viscosity in bentonite grout. With 3 % SPP concentration, the \(\theta \) of 10 % bentonite grout was reduced by approximately 27 % compared to that of the unmodified 10 % grout. The unmodified grout consists of aggregated particles with 3D network structures having yield stress (Yoon and El Mohtar 2012). Under flow condition, the yield stress partially contributes to the apparent viscosity. Since the addition of SPP disrupts the buildup of network structures in bentonite grout, the modified bentonite grouts include less network structures (more delaminated particles) than the unmodified ones and the contribution of yield stress to the apparent viscosity is reduced. Therefore, the apparent viscosity of SPP modified grout becomes lower than that of unmodified bentonite grouts, leading to the low chance for the particles to be captured in pore spaces, and thus low degree of filtration compared to the unmodified bentonite grouts.

Figure 8c shows the effect of injection pressures on the \(\theta \) value. As the injection pressure increased, the \(\theta \) values decreased approximately 7–25 %, depending on bentonite fraction. The decrease in the \(\theta \) values was not uniformly proportional to the increase in applied pressure and the effect was reduced as the bentonite fraction increased (12 %). Although a higher injection pressure can lower the \(\theta \) values under some of the testing conditions, and thus more injected pore volumes can be achieved, fracturing the soils structure may be induced by increasing injection pressure beyond 140 kPa (Rugg et al. 2011).

Figure 8d shows the effect of relative density on the \(\theta \) value. As the relative density of sand column increased, the \(\theta \) values decreased approximately 2–20 %, depending on bentonite fraction. The effect of relative density decreased as the bentonite fraction increases similar to the effect of injection pressure. This is possibly due to the decrease in the flow velocity of grouts, resulting in a decreased filtration in the dense specimens. The results presented in Fig. 8 imply that filtration cannot be evaluated with a single experimental parameter because the \(\theta \) value is not uniquely dependent on either of them.

4.3 New Groutability Criterion

Figure 9a shows the relationship between the injected pore volume and \(\theta \) from the filtration model. The injected pore volume decreased exponentially as the lumped parameter increased. Since the lumped parameter is correlated to the injected pore volumes (\(R^{2}=0.736\)), a quantitative evaluation of successful grouting is possible based on the injected pore volumes (i.e., at least 1 Pv). Based on this criterion, it was found that a soil is “groutable” if \(\theta \) was less than 12, and “ungroutable” if \(\theta \) is larger than 14. When the \(\theta \) lies between 12 and 14, experimental grouting tests are recommended.

Fig. 9
figure 9

a Proposed groutability criteria for bentonite grout, b groutability of Sand A using different type of bentonite

Full size image

However, the lumped parameter should be obtained by calibrating the complex model to the experimental data, losing its predictive capability. Therefore, an empirical model to predict the lump parameter was proposed based on the relationship between the lumped parameter and normalized effective grain size, equilibrium apparent viscosity, relative density, and injection pressure. The lumped parameter plotted with each parameter (effective grain size, apparent viscosity, relative density, and injection pressures), produced a function of the form of \(\theta =f(N_\mathrm{{c}})+f(\mu /P)-f(D_\mathrm{{r}})\). Based on this function, an empirical equation to estimate the lumped parameter considering how it is affected by each component was proposed as follows:

$$\begin{aligned} \theta =\phi _1 \cdot N_\mathrm{{c}} +\phi _2 \frac{\mu _r ^{\phi _3 }}{(P/1\mathrm{{atm}})^{\phi _4 }}-\left( {\frac{D_\mathrm{{r}} }{100}} \right) ^{\phi _5 }, \end{aligned}$$
(25)

where \(\theta \) is the lumped parameter (i.e., groutability of bentonite suspensions), \(\phi \) \(_{1}\),\(\phi \) \(_{2}\), \(\phi \) \(_{3}\), \(\phi \) \(_{4}\), and \(\phi \) \(_{5}\) are the empirical constants presented in Table 3, \(N_\mathrm{{c}}\) is the Burwell’s (1958) second groutability ratio (\(D_\mathrm{{10,sand}}\)(mm)/\(d_\mathrm{{95,bentonite}}\)(mm)), P is the injection pressure (kPa), \(\mu _\mathrm{{r}}\) is the relative equilibrium apparent viscosity (\(\mu _\mathrm{{grout\,at\,equilibrium}}\) (mPa\(\cdot \)s)/ \(\mu _\mathrm{{water}}\) (mPa\(\cdot \)s)), and \(D_{r}\) is the relative density of sand column.

Table 3 Empirical parameters proposed in this study
Full size table

The proposed groutability criterion was tested with the lump parameters from sand column tests performed with a different type of bentonite as shown in Fig. 9b. For these tests, the sand columns were prepared with Sand A at the relative density of 30 % and the grout was injected at the constant pressure of 35 or 140 kPa. The different type of bentonite has a similar particle size (\(d_{95}\approx 25\,\upmu \)m), but a higher Na/Ca ratio (5.1 instead of 1.9). The different Na/Ca ratio indicates that the bentonite will show different rheological properties when it is utilized as a grout. While the equilibrium apparent viscosity of the unmodified bentonite grout is reduced as the Na/Ca ratio increases due to the lack of Ca\(^{++}\) ions which exert attractive forces between bentonite particles (Brandenburg and Lagaly 1988), the SPP modified grouts displayed similar apparent viscosities to those in the unmodified grouts. For 10 % grout modified with 3 % SPP, the difference in apparent viscosity between bentonite having Na/Ca ratio of 1.9 and 5.1 was approximately less than 1 %. This is because the degree of dispersion is essentially governed by the amount of phosphate anions and shear rates. The lumped parameters produced similar results to the proposed relationship between the lumped parameter and the injected pore volume, indicating that the proposed groutability criteria is applicable for other types of bentonite grouts.

The proposed groutability criterion was evaluated by comparing it with the existing criteria. The comparison of the proposed and the existing groutability is summarized in Table 4. The initial estimation based on (1958) criterion (\(N=D_\mathrm{{15,soil}}/d_\mathrm{{85,grout}})\) produced N of 36, 46.4, and 50.9 for Sand A, B, and C, respectively, regardless of the type of the grout mix, indicating that all 18 tests are groutable (\(N>25\)). However, the injected pore volume was higher than 1 for only 6 out of these 18. The second criterion (\(N=D_\mathrm{{10,soil}}/d_\mathrm{{95,grout}})\) produced N of 8.3, 11.4, and 12.6 for Sand A, B, and C, respectively, determining only three data as groutable (\(N>11\)). All three tests reached injected pore volumes in excess of 1. On the other hand, Incecik and Ceran (1995) criterion (\(N=D_\mathrm{{10,soil}}/d_\mathrm{{90,grout}})\) estimated all of data as groutable (\(N>10\)), but approximately 67 % of data points could not be injected over 1 pore volume. Based on the comparison, it was concluded that the new proposed criteria was able to better predict the groutability of the sand.

Table 4 Comparison of groutability criteria for 18 tests
Full size table

5 Conclusions

The rheological properties of the SPP modified bentonite grouts were measured to investigate the effect of the SPP modification on groutability for granular soils. It was observed that the introduction of small amounts of SPP (1–4 % by dry weight of bentonite) could significantly reduce the equilibrium apparent viscosity of the bentonite grouts, increasing the injected pore volumes of grouts. This implies that the rheological properties of the bentonite grouts play an important role to determine the groutability of the granular soils.

The lumped parameter (\(\theta )\), which reflects the filtration property of the grout through the soil, was evaluated by calibrating a 1D filtration model to the injected volume of grouts from sand column tests. The filtration model accounts for the variation of apparent viscosity and particle deposition during the grout flow. The lumped parameter increases with the decrease in the effective grain size of the sand with the increase in the apparent viscosity of the grout. In addition, the parameter decreases with the increase in injection pressure and relative density. Based on the lumped parameter, a new groutability criterion for the SPP modified bentonite grouts is proposed. The proposed groutability accounts for a quantitative criterion (i.e., at least 1 pV) and suggests that soils are groutable when \(\theta <12\) and ungroutable when \(\theta >14\).

For the predicative application of the parameter, an empirical correlation to predict the lumped parameter is proposed based on the observed relationships between the injected pore volumes and the experimental parameters (the properties of soil and bentonite grouts, and injection pressure). The proposed criterion was tested with different type of bentonite, resulting in similar trends to what was observed in the proposed relationships. This indicates that the proposed relationship and criterion will be applicable to other types of particulate grouts as long as the rheological properties are appropriately measured.

The proposed criterion allows more accurate prediction of groutability of granular soils using the SPP modified bentonite grouts. This study showed a possible application of the SPP modified bentonite grouts in permeation grouting and the information from this work will help understand the theory behind the practical application of groutability and design grouting works.