MH-DAGMiner: maximal hierarchical sub-DAG mining in directed weighted networks

Abstract

With the easy availability of network data, there is an increasing need for extracting the compact and meaningful directed acyclic graph (DAG) patterns from network databases. There exists no specific method of sub-DAG pattern mining from the network databases with cyclic graphs. This paper presents a novel method, MH-DAGMiner, for mining maximal hierarchical sub-DAG patterns from a directed and weighted network database. To avoid the exhaustive steps of candidate generation, frequency counting and non-maximal patterns pruning, we propose a novel and effective FP-DAG structure based on edge grouping. We propose the optimum branching method to identify the vertex hierarchy within each maximal edge group generated from FP-DAG, and discover the maximal hierarchical sub-DAG patterns. The effectiveness of MH-DAGMiner is tested using several real-world network datasets and synthetic graph datasets. We analyzed the quality of MH-DAGMiner in comparison with a Naive-DAGMiner method which mines DAG patterns from a preprocessed cyclic graph (DAG) database. MH-DAGMiner is found to be more effective than Naive-DAGMiner with lower average information loss. MH-DAGMiner is also found to be more effective than the state-of-the-art benchmarking algorithms such as gSpan, FP-GraphMiner, and MFSH-TreeMiner where maximal hierarchical DAG patterns are identified with a post-processing step.

1 Introduction

Frequent pattern mining has been successfully applied to various applications presenting diverse sources of data [1, 13]. Frequent subgraph mining is popular in unstructured data domains such as bioinformatics, cheminformatics, and the web [1, 11, 13]. The majority of existing research in frequent subgraphs relates to undirected graph and ignores the edge directionality [9, 11, 18, 22]. However, an undirected graph representation loses the knowledge about the network flow and dependencies/authorities of objects. This knowledge can be vital in applications like social network hierarchy mining [7], influence maximization [15], workflow analysis [23], web navigational pattern discovery [4] and many more. There exist only a couple of frequent subgraph mining algorithms applicable to directed graphs, but they are limited to specific patterns such as rooted graph patterns [19] or abstract vertex-labeled patterns [17].

Fig. 1

A cyclic graph as shown in a can have three possible hierarchical organization of vertices as shown in b–d

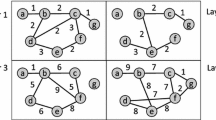
The directed acyclic graph (DAG) patterns are highly effective in applications (representing a graph data) which require the knowledge about hierarchical organization of objects. A DAG data structure presents information in a concise manner compared to sequences and trees and is not as complex as directed cyclic graphs. It is not possible to define a single hierarchy within a directed cyclic graph because cycles can lead to multiple hierarchies as shown in Fig. 1. The sequence and tree data models are found limited for representing the hierarchy, activity and information flow. A DAG, which is a compact representation of a set of sequences, can represent multiple dependencies and ancestor–descender relationships of an object without duplicating the object in representation as in the tree structure.

For the evolving networks such as social media networks, DAG pattern mining from a set of timestamped interaction networks would be able to discover valuable knowledge about the users and relationships. For example, identifying user groups who frequently share information about a particular topic and extract their hierarchical organization within the group can be useful in influential user mining [2] to benefit the applications like viral marketing and political campaigning. In the workflow data, representing a set of process sequences by compact DAG structures and then mining the frequent sub-DAG patterns can be useful for classification models in fraud detection [10]. In the web navigational pattern mining [4], the DAG patterns can be useful in identifying the hierarchical organization of web pages and developing better ranking methods.

In this paper, we propose the MH-DAGMiner method to mine DAG patterns from the network databases represented as graphs with unique vertex labels and directed weighted edges. There exist a handful of methods for DAG pattern mining from DAG databases [3, 6, 21, 25]. However, these methods cannot be applied to databases with cyclic graphs. MH-DAGMiner can be used in a network transaction setting where a database instance consists of a set of cyclic graphs, as well as, it can be applied in graph transaction setting where a database instance is a single connected cyclic graph. Figure 2 shows the difference between network and graph settings. The network setting is useful in representing social media interactions for a time period, whereas the graph setting is suitable when the dataset contains connected graphs such as activity flow graphs. To the best of our knowledge, MH-DAGMiner is the first method that can be used with both cyclic network and graph databases to mine maximal DAG patterns.

Fig. 2

a Input dataset in the graph transaction setting, b input dataset in the network transaction setting using unique vertex label representation

A common challenge with frequent subgraph mining is the sheer amount of patterns generated. Maximal pattern mining is the general approach to mine compact patterns. But it is non-trivial to use an existing maximal subgraph mining algorithm [22, 24] for DAG mining because of the complexity in modifying the processes of candidate generation and canonization in the presence of edge direction and cycles. The popular gSpan algorithm [26] can be modified to generate DAG patterns and prune the non-maximal; however (1) it compromises efficiency as canonization is designed for repeated vertex label graphs, (2) it enumerates multiple hierarchical patterns starting from each cyclic edge as shown in Fig. 1 which requires a post-processing step to select the most prominent pattern, and (3) it fails to identify multi-rooted DAG patterns.

In this paper, we show that the maximal hierarchical DAG patterns can be efficiently approximated using the vertex hierarchy derived from the optimum branching. The MH-DAGMiner method proposes a novel DAG mining framework using BitCode-based FP-DAG structure. FP-DAG, an extended version of FP-Graph [24] enables grouping of edges based on their frequency of occurrence. Each edge group is processed to identify the optimum vertex hierarchy with the optimum branching technique [5]. Finally, each vertex hierarchy is approximated to a maximal hierarchical DAG pattern with a constrain driven approach. MH-DAGMiner generates maximal hierarchical DAG patterns without an exhaustive candidate generation step since it is not necessary to enumerate all frequent patterns when the requirement is maximal pattern mining. With the use of the BitCode concept [24], the frequency of a pattern can be calculated without scanning the input database as well as the non-maximal patterns can be pruned effectively.

We empirically analyze the effectiveness of MH-DAGMiner using six real-world network datasets relating to Twitter interactions, Enron email conversations, Math Overflow interactions, Citation database, Wikipedia talk page editing and Messaging between college students. We also use a set of synthetic graph databases with different characteristics. We compare the information loss of MH-DAGMiner with a naive DAG mining approach which first removes cycles in graph database to create a DAG database and mine DAG patterns. The average information loss due to the approximation of DAG patterns from graphs is always found less than the naive method with the graph to DAG transformation. MH-DAGMiner is also found to be effective compared to the extensions of gSpan [26], FP-GraphMiner [24] and MFSH-TreeMiner [12] methods which include a post-processing step to extract maximal hierarchical DAG patterns.

The main contributions of this paper can be summarized as below;

• 1. We propose the novel MH-DAGMiner method for mining maximal hierarchical DAG patterns from a database of directed, weighted, cyclic network or graphs. It is based on the following innovative data structure/processes.

  • (a) FP-DAG structure to group edges such that all the maximal hierarchical DAG patterns are included within these groups.

  • (b) Using optimum branching-based vertex hierarchy to approximate the maximal hierarchical DAG patterns.

  • (c) Using FP-DAG structure for effective non-maximal pattern pruning.

• 2. We theoretically prove the completeness of MH-DAGMiner and analyze the computational complexity.

• 3. We empirically analyze the effectiveness of MH-DAGMiner using a set of real-world network and synthetic graph datasets.

The remainder of the paper is organized as follows. Section 2 presents the related work. Section 3 discusses the proposed method in detail with related definitions. Section 4 provides the computational complexity analysis. In Sect. 5 we analyze the experimental results and Sect. 6 concludes the paper with discussion and future work.

2 Related work

No explicit method of DAG mining from the directed cyclic network or graph databases exists with which we can compare our proposed MH-DAGMiner method. Therefore, in this section, we present the related work including maximal subgraph mining algorithms and sub-DAG mining algorithms from DAG databases.

To deal with the explosion of patterns generated in general subgraph mining algorithms, a number of closed and maximal subgraph mining algorithms including CloseGraph [27], DIGDAG [21], SPIN [9], MARGIN [22] and FP-GraphMiner [24] have been developed. Closed subgraph mining algorithms mine frequent patterns which do not have any super-graph with the same frequency in the pattern set. Maximal subgraph mining algorithms identify patterns which do not have any frequent super-graph in the pattern set. Closed or maximal subgraph mining is application dependent. If the objective is extracting compact patterns regardless of different frequency levels, maximal subgraph mining usually is found appropriate [9].

SPIN [9], the first work in maximal subgraph mining, mines all frequent tree patterns from the graph database and then reconstructs maximal subgraphs from trees. SPIN takes the advantage of less complexity inherited with tree normalization compared to graph normalization; however, it is still computationally expensive as it enumerates all frequent tree patterns and requires post-non-maximal pattern pruning. Taking a different approach, MARGIN [22] prunes the candidate patterns using the conjecture that a set of potential maximally frequent subgraphs is included in the set of frequent k subgraphs that have infrequent ($k + 1$) super-graphs. The maximal subgraphs are then identified using a post-processing step. MARGIN is claimed to be three times faster than SPIN. However, both algorithms scan the database multiple time during the mining process and designed for repeated vertex label graph representations which adversely affects the execution time when using with unique vertex label graphs. More importantly, it is non-trivial to extend these algorithms to apply in directed graph mining. A recently developed subgraph mining algorithm, FP-GraphMiner [24], has been shown to be 4 times faster than MARGIN by improving efficiency in candidate generation and frequency counting steps for unique vertex label graph databases. This algorithm scans the database once and stores the details of frequent subgraphs into a single compact undirected graph, FP-Graph, to mine frequent subgraphs with any predefined minimum support threshold $\sigma$.

The FP-Graph structure does not consider the possibility of the existence of graph patterns when there are no distinct edges corresponding to a given minimum support threshold. This issue is identified in a work related to software fault localization [12], and authors introduce the MFSH-TreeMiner based on a Tree structure. However, as we show in this paper, MFSH-TreeMiner fails to generate the complete set of patterns. We introduce the FP-DAG structure in which a depth-first search (DFS) traversal is used to mine the complete set of patterns.

A handful of work has been developed for specific types of sub-DAG mining from DAG databases. An early algorithm [3] is limited to mine pyramid patterns only, where each DAG has a single root vertex. The DIGDAG algorithm can mine closed frequent embedded sub-DAGs in unique vertex labeled DAG database [21]. It combines a closed frequent itemset mining algorithm with the item reduction technique based on ancestor–descendant edge groups to improve the efficiency of the mining process. The DAGMA algorithm mines frequent fragments in DAG databases [25] by using a new canonical form based on the topological levels of vertices. A set of rules are derived based on this topology to enumerate sub-DAG patterns efficiently. Authors in Fariha et al. [6] introduced a framework for mining frequent interaction patterns as DAGs from meeting databases.

These sub-DAG mining algorithms are designed with the assumption that the input representation does not contain cyclic relationships. For example, DAGMA [25] requires topological sorting of vertices which is infeasible in a cyclic graph. Moreover, existing DAG mining algorithms result in specific types of DAG patterns such as pyramid patterns [3], embedded patterns [21] and apply on DAG representations specific to applications like meeting interactions where the status of participants is known. It is non-trivial to extend these sub-DAG mining algorithms for cyclic network/graph input databases to mine the maximal hierarchical DAG patterns. As noted, applications like social network mining, work flow network analysis and navigational pattern mining require DAG patterns to be extracted from the graph/network databases with cyclic graphs. Graph mining algorithms such as FP-GraphMiner [24] and MFSH-TreeMiner [12] can be used for maximal subgraph mining in directed graphs, but they cannot be used for DAG mining without a post-processing step. The general-purpose gSpan [26] algorithm can be extended for maximal sub-DAG mining, but it compromises the accuracy, generates redundant patterns and unable to generate multi-rooted DAG patterns.

Based on this discussion, it can be ascertained that existing algorithms have been mainly developed for undirected graphs due to complexities involved with the edge direction in processing and the unimportance of edge direction in targeted applications and also for directed acyclic graphs focusing specific applications. However, with the recent applications such as social networks, workflow, and navigation networks, there is an increasing need to consider directed graphs for mining sub-DAG patterns that can represent hierarchy, activity and information flow. To our best knowledge, we are the first one to propose a frequent subgraph mining algorithm to generate maximal hierarchical sub-DAG patterns from the directed cyclic network/graphs.

3 The proposed method: MH-DAGMiner

3.1 Definitions

Labeled weighted graph A labeled weighted graph can be represented as $G(V,E,L_V,\varphi ,W(E))$, where V is a set of vertices, $E\subseteq (V \times V)$ is a set of edges; $L_V$ is the set of vertex labels; and $\varphi$ is a label function that defines the mapping $V \rightarrow L_V$. In this paper we assume that a label function assigns distinct labels to vertices. W(E) is the set of edge weights. G is directed if $\forall e \in E, e$ is an ordered pair of vertices. G is acyclic if it contains no cycle. If G is both directed and acyclic, it is called Directed Acyclic Graph (DAG).

Network Transaction Database A network transaction database of size n can be defined as $D=\{N_1,N_2 \ldots , N_n\}$. A network N can be represented as $N =\{G_1,\ldots G_n\}$ where $G_1,\ldots G_n$ are a set of unique vertex labeled directed weighted graphs. Graph transaction database is a special case of Network transaction database where each network N of D consists only of a single graph G.

Sub-DAG Given two unique vertex labeled DAGs $G_1(V_1,E_1)$ and $G_2(V_2,E_2)$, $G_1$ is a sub-DAG of $G_2$ if $E_1 \subseteq E_2$. In this case $G_2$ is the super-DAG of $G_1$.

DAG Isomorphism A unique vertex labeled DAG $G_1(V_1,E_1)$ is isomorphic to another DAG $G_2(V_2,E_2)$ if a bijection $f: E_1 \rightarrow E_2$ exists such that: $\forall (u,v) \in E_1, \Leftrightarrow \forall (u,v) \in E_2$. The bijection f is an isomorphism between $G_1$ and $G_2$. DAG $G_1$ is sub-DAG isomorphic to DAG G2 if there exists a sub-DAG $g \subseteq G_2$ such that $G_1$ is isomorphic to g [13].

Frequent Sub-DAG A sub-DAG g is considered to be frequent if its support is greater than the predefined minimum support threshold $\sigma$. In this paper, support of a DAG pattern is calculated using transaction-based counting as the number of network/graph transactions that g is a sub-DAG of.

Frequent Maximal Sub-DAG A DAG $G_1$ is frequent maximal if there exists no super-DAG $G_2$ of $G_1$, which is frequent.

Maximal Edge Group (MEG) A frequent edge set is defined as a maximal edge group MEG1 if there is no superset of frequent edge group MEG2 such that $MEG1 \subseteq MEG2$.

Optimum Branching A branching B of directed graph G is a subset of edges such that (1) if $(u_1,v_1), (u_2,v_2)$ are distinct edges of B with $v_1 \ne v_2$; and (2) B does not contain a cycle. There will be many such branches present in G. The optimum branching $B_o$ is the B with highest edge weight sum¹ [5]. If the branching is connected, it is called optimum arborescence.²$B_o$ is represented as a subset of edges in G.

Optimum Vertex Hierarchy The optimum vertex hierarchy of a directed graph G is defined as the hierarchical organization of vertices in the optimum branching of G.

HierarchyLevel HierarchyLevel is a discrete number between 1 and h, where h is the maximum hierarchy level.

Hierarchical DAG We define a DAG as Hierarchical DAG when it has the optimum vertex hierarchy and all the edges are directed from vertices with lower HierarchyLevel to vertices with higher HierarchyLevel.

Maximal Hierarchical DAG (MH-DAG) A DAG is defined as MH-DAG if it satisfies both frequent maximal and hierarchical DAG requirements.

Problem Definition Given a network/graph transaction database and minimum support threshold $\sigma$, the task is to extract all MH-DAG patterns with a support $\ge \sigma$.

The proposed MH-DAGMiner method achieves this by executing three main functions, (1) Frequency Table creation, (2) FP-DAG creation and (3) MH-DAG mining. The MH-DAG mining step includes sub-steps of Identifying MEGs, Optimum vertex hierarchy mining, DAG approximation and non-maximal pruning. Algorithm 1 summarizes MH-DAGMiner.

Fig. 3

a Input database (D). b Frequency table (FT)

3.2 Frequency table creation

We propose to use the edge-based representation for networks/graphs as it is known to be more efficient compared to the vertex-based adjacency matrix representation due to its reduced memory requirement [24]. With the use of unique vertex label representation, a network/graph can be presented by its edge list. For example the graph in Fig. 1a can be noted as G(AB, BC, BD, CA, CD, CE, DE). According to the Downward Closure Property (DCP) [1], a graph with $k+1$ edges cannot be frequent if it has a subgraph with k edges that is infrequent. Consequently if G is frequent, each edge in the edge set G(AB, BC, BD, CA, CD, CE, DE) needs to be frequent. This property can be used to avoid the exhaustive frequency counting step and make the mining process efficient.

Let $D=\{N_1,N_2,\ldots N_n\}$ be a network database with n networks. Each distinct edge in the network is represented as $E=\langle S,T \rangle$ where S is the source vertex and T is the target vertex.

The WeightMapwm of a distinct edge E is an array with n elements where each element represents the weight of E in the corresponding network/graph instance. The BitCodebc of E is the binary encoding of wm which can be calculated using Eq. 1. The support of E can be easily calculated by taking the sum of 1’s in the corresponding BitCode.

$$\begin{aligned} \forall i \in {0,\ldots n-1} \left( bc(i)= {\left\{ \begin{array}{ll} 1,&{} \text {if } wm(i) \ge 1 \\ 0, &{} \text {otherwise} \end{array}\right. } \right) \end{aligned}$$

(1)

The Frequency Table (FT) is defined as a collection of frequent edges in the input database in decreasing order with respect to the support of edges. Each row in the FT contains a pair $\langle \hbox {Edge,WeightMap} \rangle$. An example FT is shown in Fig. 3b, for the database illustrated in Fig. 3a.

MH-DAGMiner starts by iterating through the network instances of D to build the FT. Given the minimum support threshold $\sigma$, only the frequent edges needed to be stored in the FT. It is impossible to decide whether an edge is frequent before processing all networks and edges are added to FT as WeightMap of an edge is updated while iterating through networks. However, we can prune some of the edges, which are not going to be frequent considering $\sigma$ and the number of already processed networks. We calculate the maximum possible support value ms of an edge using Eq. 2.

$$\begin{aligned} ms = c_f(E)+ (n-n_f) \end{aligned}$$

(2)

where $c_f(E)$ is the support of edge E after processing $n_f$ number of networks from a total of n networks. When iterating though the network instances in D, from the second network we estimate ms for each distinct edge in the network, and if $ms<\sigma$, we do not add the edge into FT and remove the existing record. For example in Fig. 3a, consider the scenario where N1, N2, N3, N4 and N5 are processed in this order. Assume N1, N2 and N3 have already been processed $(n_f =3)$ and we are reading the edge $\langle F,C \rangle$ in N4. Since $\langle F,C \rangle$ does not exist in N1, N2 and N3, it is not yet included in FT $(c_f(E)=0)$. Its ms value indicates that maximum possible support value of $\langle F,C \rangle$ is 2. Given $\sigma =3$, there is no need to add $\langle F,C \rangle$ into FT as $ms <\sigma$. As shown in empirical analysis, this saves a lot of memory otherwise used for infrequent edges and improves the execution time. After processing all network instances in D, all the frequent edges are arranged in FT according to the decreasing order of edge supports.

3.3 FP-DAG creation

The next step of MH-DAGMiner is grouping the edges in FT based on BitCode and create the FP-DAG structure. We refer a group of edges as a Node. Given a set of edges $e_1,e_2, \ldots ,e_k$ with BitCodes $B_{e1}, B_{e2},\ldots , B_{ek}$, the BitCode of a Node can be derived using Eq. 3 and support of the Node can be calculated by counting 1’s in the resultant Bitcode.

$$\begin{aligned} B(\hbox {Node}) = B_{e1} \wedge B_{e2} \wedge B_{e3} \cdots \wedge B_{ek} \end{aligned}$$

(3)

Two types of Nodes namely EdgeNode and ConnectorNode are created. An EdgeNode is formed by a group of distinct edges in FT with a common BitCode. A ConnectorNode is a placeholder to represent an edge set created by combining edges of two or more EdgeNodes such that support (resultant edge set) $\ge \sigma$. The BitCodes related to the ConnectorNodes are identified by the AND operations among BitCodes of corresponding EdgeNodes. The ConnectorNodes do not include any edges but provide guidance to the DFS traversal to create a complete pattern set by connecting the EdgeNodes.

Given a Node $N_1$ with BitCode $B_1$ is a ParentNode of Node $N_2$ with BitCode $B_2$, the relationship shown in Eq. 4 should always be true. Here $N_2$ is a ChildNode of $N_1$.

$$\begin{aligned} B_1 \wedge B_2 = B_2 \end{aligned}$$

(4)

A Cluster is created by grouping the Nodes with the same support. Given t number of network instances, there can be a maximum of t Clusters. Let $C_i$, $C_j$ and $C_k$ be three successive Clusters with $support(C_i)< support(C_j) < support(C_k)$, $C_j$ and $C_k$ will be the ParentCluster and AncesstorCluster of $C_i$, respectively.

Fig. 4

a FP-DAG, b MFSH-Tree, c FP-Graph built corresponding to the example data shown in Fig. 3, d MEGs generated by FP-DAG, e edge groups generated by MFSH-Tree and f edge groups generated by FP-DAG

FP-DAG: A FP-DAG(Nodes,Edges) is a hierarchical DAG where Clusters of Nodes are arranged in the hierarchy by increasing order of support. Each Node is connected with all its ParentNodes by directed paths such that $start(path) = Node$ and $destination(path) =ParentNode$ while avoiding multiple paths between a Node and a ParentNode. Consider N1 is a ParentNode of N2 and N2 is a ParentNode of N3, there will be edges from N2 to N1 and N3 to N2 but no edge from N3 to N1 as there is a directed path from N3 to N1 via N2. The EdgeNodes are first connected with its ParentNodes in ParentCluster by directed edges. If there is no ParentNode in ParentCluster, the next AncesstorCluster in the hierarchy is considered until it is found. The EdgeNodes which generate the BitCode of a ConnectorNode is identified as the ParentNodes of that ConnectorNode and directed edges are added from ConnectorNode to the corresponding EdgeNodes.

Example 1

Suppose the input database contains five networks $N_1,N_2,N_3,N_4$ and $N_5$ as shown in Fig. 3a. With $\sigma =2$, FT (as shown in Fig. 3b) is derived where each edge is represented with a WeightMap. The WeightMap of distinct edge $\langle C,D \rangle$ [5, 6, 4, 3, 0] indicates that it appears in $N_1,N_2,N3$ and $N_4$ only. The corresponding BitCode and support can be calculated as 11110 and 4, respectively. Note that edge $\langle F,C \rangle$ of $N_4$ does not appear in the FT since it is pruned due to $support<2$.

As shown in Fig. 3b, five groups will be created based on each distinct BitCodes. Figure 4a includes these groups as EdgeNodes EN1, EN2, EN3, EN4 and EN5. EdgeNodes are grouped into four Clusters, each Cluster sharing the Nodes of same support. First each EdgeNode is connected with its ParentNodes in ParentCluster by a directed edge. For example, EN1 is a found as a ParentNode of EN2 following the ParentNode–ChildNode relationship and Eq. 4$(11111 \wedge 11110 =11110)$. Accordingly, there is a directed Edges from EN2 to EN1.

Algorithm 2 then identifies two ConnectorNodes CN6 and CN7 with supports $\ge \sigma$. CN6 will be connected with its ParentNodes EN2 and EN3 while CN7 will be connected with EN2 and EN4 as shown in Fig. 4a. The FP-Graph structure [24] only includes EdgeNodes(EN1, EN2, EN3, EN4 and EN5) and misses the ConnectorNodes(CN6, CN7) as shown in Fig. 4c. The MFSH-Tree structure [12] identifies CN6 as another EdgeNode EN6 by combining edges from EN2 and EN3, as both of these EdgeNodes belong to the same ParentCluster, however it misses CN7 where one ParentNode is in ParentCluster and another ParentNode is in an AncesstorCluster (Fig. 4b). ParentNodes of an EdgeNode can also belong to different Cluster levels. For example, EN4 and EN3 are two ParentNodes of EN5, which belong to the ParentCluster and AncesstorCluster, respectively. Both FP-Graph and MFSH-Tree structures do not identify EN3 as a ParentNode of EN5 as it does not belong to the ParentCluster of EN5 and consequently there will be no directed path from EN5 to EN3. As shown in further analyses, these processes in MH-DAGMiner ensure the generation of a complete pattern set.

Claim 1

FP-DAG contains the complete set of Nodes and Edges for generating all MH-DAG patterns.

Proof

FP-DAG is considered complete if it contains all possible Nodes with a support $\ge \sigma$, and there exist paths from each Node to all its ParentNodes. The Nodes can be either formed by an edge group where all the edges have the same BitCode value or formed by an edge group with dissimilar BitCodes, but the support of the group $\ge \sigma$. If all the edges have the same BitCode, they are available in the FT and form an EdgeNode in FP-DAG. The dissimilar BitCodes indicates a combination of two or more EdgeNodes. As detailed in Algorithm 2, the pairwise AND operation is performed for each dissimilar BitCode pair $(B_1,B_2)$ where $WT(B_1),WT(B_2) > \sigma$ and all possible BitCodes, which represent all EdgeNode combinations, are found. This ensures all possible Nodes are included in FP-DAG. Each EdgeNode is first connected with all its ParentNodes in ParentCluster. Since the ConnectorNodes result from the EdgeNode combinations, by default they become the ParentNodes. These ParentNodes are again connected with their ParentNodes and so on; thus, by considering the transitivity, we can claim that there exist paths between each Node to all its ParentNodes in ParentCluster as well as AncesstorClusters. Consequently, FP-DAG contains the complete set of Nodes and Edges in the dataset necessary for generating all MH-DAG patterns. $\square$

3.4 MH-DAG mining

3.4.1 Identifying MEGs

Depth First Search (DFS) in FP-DAG is defined as traversing FP-DAG in depth-first order starting from a given Node following the Edge direction and without visiting the same Node twice. The directed Edges in FP-DAG guarantees that only the ParentNodes are visited by DFS traversal. A Maximal Edge Group (MEG) is identified by the DFS traversal of FP-DAG starting from each LeafNode (i.e., the Nodes which does not have any incoming Edge). If the frequent mining is done in a graph transaction database, a MEG will generate a single maximal subgraph pattern. However, in a network transaction setting, a MEG can generate multiple patterns and there can be non-maximal patterns which need to be pruned.

Example 1 continues Figure 4d–f illustrates the difference between the MEGs identified by MH-DAGMiner, the maximal subgraphs identified by the FP-GraphMiner [24] and MFSH-TreeMiner [12]. Both FP-GraphMiner and MFSH-TreeMiner produce different results due to the incompleteness in FP-Graph and MFSH-Tree.

Claim 2

A DFS traversal starting from each LeafNode in FP-DAG will result in generating all MEGs existing in the dataset. The number of MEGs is equal to the number of LeafNodes.

Proof

Since FP-DAG is constructed considering minimum support threshold $\sigma$, the bottom level of FP-DAG is related to the Cluster with support $\ge \sigma$. A DFS starting from a LeafNode, LN traverses all the ParentNodes of LN and covers the largest sub-DAG DG connected to LN. Let $DG_1$ and $DG_2$ are two sub-DAGs in FP-DAG generated by LeafNodes $LN_1$ and $LN_2$, respectively. It can be inferred that $DG_1 \notin DG2$ and $DG2 \notin DG1$ due to the unique vertex label representation. Consequently edges in $DG_1$ and $DG_2$ result in two MEGs MEG1 and MEG2. BitCode of a MEG is equal to the corresponding BitCode $B_{DG}$ of DG which is calculated as follows; $B_{DG} = B_{LN} \wedge B_{PN1} \wedge B_{PN2} \cdots \wedge B_{PNn}$ where $B_{LN}$ is the BitCode of Leaf Node and $B_{PN1}, B_{PN2} \ldots B_{PNn}$ are the BitCodes of $LN's$ ParentNodes. In FP-DAG, ParentNodes are identified with the relations $B_{LN} \wedge B_{PN} = B_{LN}$ and consequently $B_{MEG}= B_{DG} = B_{LN}$. Therefore, the resultant MEGs have the BitCodes of corresponding LeafNodes and the number of MEGs is equal to the number of LeafNodes. According to the Claim 1, a complete FP-DAG ensures to have the complete set of Nodes which includes the complete set of LeafNodes. Consequently, A DFS traversal starting from each LeafNode in FP-DAG results in all MEGs existing in the dataset. $\square$

3.4.2 Optimum vertex hierarchy mining

For all MEGs identified, the maximal hierarchical DAG patterns are approximated based on the optimum vertex hierarchy. The optimum vertex hierarchy is derived using the Edmonds optimum branching algorithm³ [5]. The algorithm takes a directed weighted graph as input and returns a branching or a spanning arborescence with maximum weight, where the weight of a branching/arborescence is defined as the sum of its edge weights. The highest weighted incoming edge is chosen for each vertex. If there exists a cycle with selected edges, it removes the least weighted edge.

In MH-DAGMiner, we propose to calculate the edge weight as the sum of weights in the WeightMap relating to the BitCode of MEG. With this, edges are compared with respect to the corresponding MEG and not considering the whole input database. This guarantees to select the most prominent edges within a MEG. Edges are first prioritized based on weights, if there are multiple edges with the same weight, we apply the following heuristics for edge selection.

Heuristic 1

If there exist multiple edges with maximum weight, the edge with maximum support will get priority for the next selection.

Heuristic 2

In case of the existence of multiple edges with equal weight and support, the minimum lexicographical order of source and target vertices will be used to prioritize the selection.

Heuristic 1 considers the consistency of an edge based on its frequency in the input dataset. Heuristic 2 can be adjusted based on any feature related to the vertex. These heuristics are helpful in identifying the optimum vertex hierarchy within patterns and removing non-hierarchical edges.

Based on the optimum branching of a MEG, the optimum vertex hierarchy is identified. According to the optimum vertex hierarchy, each vertex in MEG is assigned a HierarchyLevel and stored in the HMap. HMap is a dictionary containing $\langle VertexLabel,HierarchyLevel \rangle$ pairs where VertexLabel is the key and HierarchyLevel is the value. A vertex with HierarchyLevel of 0 implies that it is not yet assigned a HierarchyLevel.

Fig. 5

a Networks generated with MEG identified in Example 1 with LeafNode CN6, b optimum branching, c HMap, d hierarchical DAG patterns

Figure 5a–c illustrates the process of identifying hierarchy levels of vertexes in the MEG identified in Ex.1 for LeafNode CN6 (Fig. 4d).

Claim 3

Optimum branching of a network N(V, E) identifies the optimum vertex hierarchy according to the edge weights and heuristics.

Proof

The Edmonds algorithm has been proved to result in the optimum branching of a graph or network [5]. This branching is constructed considering the prominent incoming edges into each vertex. The optimum branching selects the highest weighted incoming edge as the prominent edge to choose a vertex. In the case of edges with similar weight, it uses Heuristics 1 and 2 to select an edge. This process results in generating a single root vertex and at most one incoming edge for each vertex. By selecting the most prominent edge in terms of support and labels, it is able to derive a deterministic and optimum vertex hierarchy. $\square$

3.4.3 Approximating DAG patterns

The patterns generated from optimal branching are a special kind of DAG patterns called as spanning arborescence that have only one root vertex and at most one incoming edge for each vertex (as shown in Fig. 5b). This structure is not sufficient when representing multiple dependencies or authorities of objects. We extend the spanning arborescences to hierarchical DAG patterns, allowing multiple parent vertices and roots, by applying two constraints using HMap to the remaining edges in MEG (i.e., the edges do not belong to branching or the cyclic edges identified). Let S be the source vertex label and T be the target vertex label.

Constraint 1

An edge is selected if $HMap[S] = 0$ but $HMap[T] \ne 0$.

Constraint 2

An edge is selected if $HMap[S] \le HMap[T]$.

After selecting all edges with these constraints, all connected components in the selected edge set can be identified as hierarchical DAG patterns. Figure 5d shows an example of hierarchical DAG patterns.

This constraint-based hierarchical DAG approximation only loses the non-hierarchical edges that would appear in the respective cyclic graph pattern, and with the use of optimum branching we make sure that the least significant edges will be removed. It is possible for an edge to be non-hierarchical with respect to one MEG and be hierarchical within another MEG with a different set of edges. By approximating the DAG patterns with respect to a MEG, we can identify both of the patterns with and without the edge. Therefore, these heuristics do not affect the completeness of output patterns.

Claim 4

The DAG structures constructed with constraints 1 and 2 applied to MEGs will result in hierarchical DAGs.

Proof

According to constraint 1, if the source vertex of the selected edge is not assigned a hierarchy level ($HMap[S] = 0$) during the optimum vertex hierarchy mining process, it implies the following three properties. (1) The source vertex does not have any incoming edge. (2) Selected edge is not included in optimum branching because the target vertex has an incoming edge with high priority. (3) Selected edge is an isolated edge. Hence, adding this edge would not create a cycle. In this case, the value of HMap[S] will be updated to 1 and if $HMap[T] =1$, HierarchyLevel of T and its child-vertices will be increased by one. According to constraint 2, either the edges from lower HierarchyLevels to higher HierarchyLevels or edges with source and target vertices belong to the same hierarchy level ($HMap[S] == HMap[T]$) are selected. In the latter case, HMap[T] will be updated to $HMap[S]+1$ and HierarchyLevels of $T's$ child-vertices will be increased accordingly. Thus, in the output pattern there exist only the edges from lower to higher HierarchyLevels and there is no chance of creating a cycle. Consequently, these two constraints result in hierarchical DAGs. $\square$

3.4.4 Pruning non-maximal patterns

The isomorphic and non-maximal patterns have been considerably minimized by finding MEGs and then identifying DAG patterns. However, there is still the possibility of generating both isomorphic and non-maximal patterns.

Fig. 6

Examples of the cycle removal resulting in a isomorphic patterns (D1 and D2) generation, b non-maximal patterns ($D4 \subset D3$) generation

Fig. 7

Due to disconnected DAGs a isomorphic pattern (D1 and D3) generation, b non-maximal pattern ($D7 \subset D5$ and $D6 \subset D8$) generation

Cyclic edge removal Figure 6a, b shows how cyclic edge removal in two MEGs can result in the generation of isomorphic patterns (D1 and D2), or the generation of non-maximal patterns ($D4 \subset D3$).

Disconnected DAG patterns In the network transaction setting, a MEG that contains multiple graphs will result in multiple hierarchical DAGs. Figure 7a shows two MEGs MEG1 and MEG2 with isomorphic patterns D1 and D3. Similarly Fig. 7b shows two MEGs MEG1 and MEG2 can produce non-maximal patterns such as $D7 \subset D5$ and $D6 \subset D8$.

Isomorphism checking is a costly operation in frequent subgraph mining [13]. Different canonical representations have been introduced to reduce the computational cost [8, 26]. However, these canonical forms are developed for graph representations with non-unique labels. Using the same method for unique labeled graphs would add an additional overhead. A unique vertex labeled graph can simply be represented using its edge list. We propose to use an edge set-based canonical string representation. In this representation, source and target labels are separated by a comma while two edges are separated by a semi-colon. For example ‘A, C; C, D; D, E’ represents the DAG with edges AC, CD, DE. To make it unique, the edge set is sorted lexicographically(first by source label, and, in the case of same source label, by target label). Figure 8 shows a simple example of this unique encoding.

Fig. 8

Unique canonical string of two isomorphic DAG’s

PatternDictionary is a dictionary in the form of $\langle BitCode, PatternList \rangle$ where PatternList is the list of canonical strings of patterns. The BitCodes in PatternDictionary are directly related to the BitCodes of Nodes in FP-DAG.

After deriving the complete canonical string s of a pattern p, first we check whether s exists under the BitCode category of p in PatternDictionary. If so, s will not be added to PatternDictionary. If there is no similar string, we check for sub-DAG isomorphism. We use the FP-DAG structure and identify the Node related to the BitCode of the pattern and BitCodes related to all of its ParentNodes and ChildNodes. The sub-DAG isomorphism is checked within the BitCodes of Node and ChildNodes. If there exists a string related to a super-DAG of p, s will not be added to the PatternDictionary. Next, we check for patterns which can be sub-DAG of p, within the BitCode category of Node and ParentNodes. If there is a sub-DAG pattern, it will be removed from PatternDictionary. In this way, we avoid exhaustive pruning of non-maximal patterns. At the end of processing all MEGs in the input dataset, a dictionary with canonical strings of graph patterns categorized by BitCode will hold. This dictionary will also enable the user to analyze output patterns based on a support threshold and particular database instances.

Fig. 9

a DAG patterns generated from MEG for LeafNode CN7, b PatternDictionary after processing the MEG, c corresponding FP-DAG, d DAG patterns generated from MEG for LeafNode EN5, e PatternDictionary after processing MEG of EN5

Example 1 Continues Figure 9 shows an example of pruning in MH-DAGMiner with the FP-DAG (Fig. 9c). Lets consider the MEG generated from the DFS traversal starting from the LeafNode CN7. As shown in Fig. 9a, we can identify two patterns D1 with BitCode 10011 and D2 with BitCode 10010. Since the PatternDictionary is empty at this stage, both patterns are added under the respective BitCode categories (Fig. 9b). Next, lets take the patterns related to the MEG generated with LeafNode EN5. As shown in Fig. 9d, we get a single pattern D3 and BitCode 10001. There is no pattern with the same canonical string or supper-DAG pattern within the same BitCode category; hence, it will be added in the PatternDictionary. In order to check for its sub-DAG patterns, we use the FP-DAG (Fig. 9c) to identify all the ParentNodes and ChildNodes of EN5. We can identify the Nodes with BitCodes 10011, 11101, 11111 as ParentNodes and there exist no ChildNodes. Therefore, we can verify that the pattern is a maximal pattern. However, there can be sub-DAGs of this patterns within ParentNodes. By checking the patterns related to ParentNode BitCodes, we find D1 as a sub-DAG of D3 and remove D1 from the PatternDictionary as shown in Fig. 9e.

Claim 5

DAG isomorphic patterns can be pruned by searching for the exact canonical string under the pattern’s BitCode category in PatternDictionary.

Proof

Suppose, on the contrary, there exists an isomorphic pattern that has not been pruned. Regardless of the order of edges considered in deriving canonical string, the particular pattern will always have a fixed BitCode. Therefore, if there exists an isomorphic pattern, it should be stored under this BitCode category in PatternDictionary. Thus, the only possibility of creating an isomorphic pattern is considering different edge orders. Since we sort the edge set using the vertex labels, which is unique for an edge, different edge orders are not possible. Consequently, it contradicts the assumption and all isomorphic patterns will be pruned. $\square$

Claim 6

Sub-DAG isomorphism for a pattern p is needed to be checked only within the patterns under $p's$ BitCode category and BitCodes related to the ChildNodes(identified from FP-DAG) in PatternDictionary.

Proof

Lets consider all the possibilities of having a super-DAG for p. (1) Extending p using the edges of Nodes in higher Cluster levels of FP-DAG: Resulting pattern will have the BitCode of p or BitCode of a ChildNode. (2) Extending p using edges of Nodes in the same Cluster levels of FP-DAG: Resulting pattern will have the BitCode of a ChildNode. (3) Extending p using edges of Nodes in lower Cluster levels of FP-DAG: Resulting pattern will have the BitCode of a ChildNode. So in every possibility, it creates a pattern with a canonical string that is stored under either BitCode category of p or ChildNode in PatternDictionary.

$\square$

Claim 7

MH-DAGMiner generates the complete set of MH-DAG Patterns.

Proof

Given M number of distinct frequent edges, there can be a maximum of $2^M -1$ frequent DAG Patterns. The number of maximal DAGs is always $< 2^M-1$ as one maximal DAG subsumes many frequent DAGs. The EdgeNodes of FP-DAG create a frequent DAG pattern such that all the edges have the same BitCode. Since a larger maximal DAG pattern can be created by combining two or more of these DAG patterns and, it is not necessary for all edges of maximal DAG to have the same BitCode as long as the resultant DAG has a support $\ge \sigma$, MH-DAGMiner considers all possible EdgeNode combinations. For example if Node3 has two parents Node1 and Node2, by combining edges from Node1, Node2 and Node3 a MEG is created such that $(Node1 \cup Node2) \subset (Node1 \cup Node2 \cup Node3)$ and $(Node1 \cup Node3) \subset (Node1 \cup Node2 \cup Node3)$ and $(Node2 \cup Node3) \subset (Node1 \cup Node2 \cup Node3)$.

EdgeNode combinations can be taken in two ways such that (1) one EdgeNode is a ParentNode of the other and (2) EdgeNodes either have same support or different supports ($>\sigma$) but not hold a parent–child relationship. With the Claim 1 showing FP-DAG is complete, (1) each Node in FP-DAG is connected with all of its ParentNodes by Edges and (2) FP-DAG includes the ConnectorNodes as placeholders to indicate the combination of EdgeNodes which does not have a parent–child relationship. According to Claim 2, a DFS starting from a LeafNode in FP-DAG will result in the MEG related to that LeafNode. Since a complete FP-DAG and DFS guarantee to identify the complete set of LeafNodes and corresponding MEGs, respectively, we ascertain that MH-DAGMiner generates the complete set of MH-DAG Patterns. $\square$

4 Computational complexity analysis

In this section, we provide the computational complexity analysis of proposed MH-DAGMiner considering different steps in the process. Let k be the number of database instances, m be the total number of edges in the dataset, M be the total number of distinct edges in the dataset, $\sigma$ be the minimum support threshold, N be the Nodes in FP-DAG and P be the number of output patterns.

FT Creation All the distinct edges in the k graphs are scanned in FT creation with the complexity of O(m). The distinct edges in the FT are sorted by the descending order of BitCode with O(MlogM) complexity. This yields the total complexity of $O(m+MlogM)$ [24].

MEG Creation For k database instances with only frequent edges, there can be $N,(N < 2^k -1)$ nodes in FP-DAG. In order to identify the set of ConnectorNodes, the Node list is traversed and the Node pairs are processed. This operation has a time complexity of $O(N^2)$ at worst case. Let the number of LeafNode be $N_l(\left( {\begin{array}{c}n\\ k\end{array}}\right) = \frac{k!}{\sigma ! (k-\sigma )!})$, the average number of ParentNodes of a LeafNode l be V and the number of links connecting the ParentNodes of a LeafNode l be E, identifying the MEGs connected to LeafNode with DFS traversal has a time complexity of $O(N_l(V+E))$.

Optimum vertex hierarchy mining Let the average number of vertices and edges in a MEG be v and e, respectively. Edmonds algorithm has the time complexity of $O(v^2)$ for dense graphs/networks and O(elogv) for sparse graph/networks [20]. Therefore, in the worst case, this step has a time complexity of $O(N_l(v^2))$.

DAG Mining Let the number of branching edges be $b_e$, vertices be $b_v$, cyclic edges identified by the Edmond’s algorithm be $c_e$ for a MEG, the number of remaining edges will be $e_r =e-(b_e+c_e)$. On this edge set, constraints are applied and HMap is updated, this step has a complexity of $O(e_r+b_e+b_v)$. Let the total number of selected edges after applying constraints be $e_s$. Identifying connected components and canonical mapping will have the time complexity of $O(e_s log e_s)$. Overall, it has a time complexity of $O(N_l(e_r+b_e+b_v+e_s log e_s))$.

Pruning Let the number of output patterns be P. In the worst case, let’s assume all the patterns are in the same BitCode category which is really a rare case. In this case, pruning operation has a time complexity of $O(P^2)$. However, in practice, it’s way less than this bound due to the use of the FP-DAG structure for identifying BitCode categories which could include super-/sub-DAG patterns.

According to this analysis, the time complexity of MH-DAGMiner is highly depended on MEG creation and non-maximal pattern pruning steps. Overall worst-case complexity will be $O(N^2+P^2)$. Both FP-GraphMiner [24] and MFSH-TreeMiner [12] have similar theoretical complexity. However, due to the incompleteness of FP-Graph and MFSH-Tree structures, these methods either generate less number of output patterns with less execution time or generate more isomorphic patterns with greater execution time in comparison with MH-DAGMiner.

5 Empirical analysis

In this section, we present the results of experiments conducted with MH-DAG-Miner. All experiments have been conducted on a single processor of 1.2 GHz Intel(R) Xeon(R) with 264 GB main memory and running Red-Hat Linux 6.4. MH-DAGMiner and all benchmarking methods are implemented using C++ programming language and compiled using g++ and C++11 optimizations.

5.1 Datasets

We use both the real-world and synthetic datasets to analyze the performance of MH-DAGMiner. The real-world datasets collected from various networks are used to analyze the performance in network transaction setting. Synthetic data sets are used to analyze the performance in graph transaction setting. Table 1 lists the parameters used for creating datasets with different characteristics.

Table 1 Parameters for defining the characteristics of datasets

5.1.1 Real-world datasets

We use six real-world network datasets as follows: (1) Twitter interactions on the discovery of Higgs boson between 1st and 7th July 2012,⁴ (2) Interactions on the stack exchange web site Math Overflow from 2014 to 2016,⁵ (3) Email conversations among employees in Enron between 2000 and 2002,⁶ (4) Citations in the field of data mining between 1990 and 2007,⁷ (5) Interactions based on Wikipedia talk page editing between 2003 and 2007⁸ and (6) Messages sent on an online social network at the University of California, Irvine between April 2004 and October 2004.⁹ Table 2 details the characteristics of these datasets.

Table 2 Real-world network data sets

5.1.2 Synthetic datasets

The real-world network datasets consist of both small and large sized input networks. In order to evaluate the completeness of MH-DAGMiner and its performance in a larger database under different levels of correlation among the database instances and output pattern sizes, we generate a set of synthetic graph databases with properties as detailed in Table 3.

To evaluate the completeness of the proposed method we create a ground-truth pattern set (synth-data1) in a database starting from a small set of seed single rooted DAG patterns planted with 100% support, then their expanded and merged patterns (including single/multi-rooted DAGs and cyclic graphs) are planted with 80%, 60%, 40%, and 20% supports, respectively. Each pattern is represented by the edge set-based canonical string, and output patterns are verified with a simple string matching.

The rest of the synthetic datasets are created as follows. We first create a large complete graph (i.e., a reference graph) using the graph generator tool [14]. A number of graph instances are then generated by extracting subgraphs connected to randomly selected vertices with desired sizes. To generate the highly correlated graph instances (for reflecting datasets such as process logs), the reference graph is generated with the same number of vertices as expected graphs instances. To generate graph instances with less correlation (for reflecting datasets like social media interactions or navigational patterns), a reference graph is generated with at least twice the number of vertices of the expected graph. To generate a dataset with the desired output pattern size, input graphs are generated with the same number of V, E, H as the output and duplicated within the database.

Table 3 Synthetic graph data sets

5.2 Benchmarking and evaluation measures

There exists no algorithm of sub-DAG mining from graph databases that can be used for direct comparison. We propose to conduct the evaluation of MH-DAGMiner by benchmarking methods in two ways. Evaluation method 1: Preprocessing the graph data to form DAG data and find MH-DAG patterns. Evaluation method 2: Mine subgraph patterns from the graph data using the state-of-the-art maximal subgraph mining methods and apply post-processing to generate MH-DAG patterns.

Fig. 10

a Input database with four graph instances, b MH-DAG patterns identified with preprocessed database (edge DA in G1 is removed to make it DAG) and c MH-DAG patterns identified with original input database with $\sigma =3$

Evaluation method 1 The existing sub-DAG mining algorithms require a preprocessed database such that all the cyclic relationships are removed (DAG database). This type of preprocessing could lead to a high information loss. For example in Fig. 10a, G1 is a cyclic graph which can be preprocessed to make a DAG by removing edge $D \rightarrow A$ since its the least weighted edge in the cycle $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$. Figure 10b, c shows the MH-DAG patterns identified with and without this preprocessing step, respectively, with $\sigma =3$. Due to the removal of edge $D \rightarrow A$, there is only two MH-DAG patterns are identified whereas with original database three patterns are identified. Therefore, it is clear that an early preprocessing can result in an incomplete set of MH-DAG patterns and cause an information loss.

We implemented a Naive-DAGMiner method which uses the optimum branching technique to remove cycles in the input database and then mine MH-DAG patterns following the same approach as MH-DAGMiner skipping the optimum vertex hierarchy mining step. We empirically validate this scenario using real-world network datasets. We define a measure Average Removed Edge Weight Ratio (AREWR) for measuring the information loss which is being calculated using the following equation.

$$\begin{aligned} \hbox {AREWR} = \frac{1}{P}\left( \forall _{p\in P} \left( \frac{\sum _{(u,v) \in p_mg} W_{(u,v)}-\sum _{(u,v) \in p} W_{(u,v)}}{\sum _{(u,v) \in p_mg} W_{(u,v)}}\right) \right) \end{aligned}$$

(5)

where P is the total number of output patterns, p is a single pattern, and $p_mg$ is the corresponding cyclic graph pattern. If there is no corresponding cyclic graph for a pattern ($p_mg=p$), information loss gets a value of 0. AREWR calculates the average ratio of removed edge weights to total edge weights. Lower the value of AREWR, the higher the quality of DAG mining method. We use AREWR to validate the effectiveness of MH-DAGMiner over the process of preprocessing and applying existing DAG mining methods.

Evaluation method 2 The other possible way of sub-DAG Mining from cyclic graphs/networks is using existing subgraph mining algorithms with a post-processing step. The gSpan [26] algorithm is a popular general-purpose algorithm with the flexibility to extend for maximal sub-DAG mining. We use gSpan to show the ineffectiveness in (1) generating all candidate DAG patterns and pruning the non-maximal, (2) using an algorithm designed for a repeated vertex labeled representation with a unique vertex labeled database and (3) generating redundant patterns. The gSpan algorithm is modified for directed graph mining as proposed in Leung [16], and pattern growth is restricted to DAGs. FP-GraphMiner [24] and MFSH-TreeMiner [12] are the only two maximal subgraph mining algorithms that can be modified for DAG mining with an additional post-processing step.

Completeness of MH-DAGMiner is evaluated based on Precision and Recall values calculated with the ground-truth data set (synth-data1).

$$\begin{aligned} \hbox {Precision}= & {} \frac{\#\text {Relevant Output Patterns}}{\#\text {Output Patterns}} \end{aligned}$$

(6)

$$\begin{aligned} \hbox {Recall}= & {} \frac{\#\text {Relevant Output Patterns}}{\#\text {Ground truth Patterns}} \end{aligned}$$

(7)

Effectiveness of MH-DAGMiner(MHDM) is evaluated by the execution time (in seconds), memory consumption (in MB) and soundness (number of Nodes, Edges in FP-DAG and MH-DAG patterns) on real-world network datasets by comparing to the state-of-the-art gSpan (gSpan-DAGMiner/gSDM), FP-Graph-Miner (FP-DAGMiner/FPDM) and MFSH-TreeMiner (MFSH-DAG-Miner/MFSHDM). The MH-DAGMiner is also evaluated in graph databases under different characteristics of datasets such as the level of correlation and the average size of output patterns. In all experiments, execution is aborted after 7200 s.

Table 4 Evaluation method 1: AREWR ($\%$) values for real-world data sets using different Minimum support thresholds (%)

5.3 Evaluation method 1: DAG mining from graph database (MHDM) versus DAG mining from preprocessed DAG database (NDM)

Table 4 reports the AREWR (%) values for MH-DAGMiner and Naive-DAGMiner for all the real-world datasets using different minimum support values. MH-DAGMiner patterns always show an equal or lower AREWR value compared to Naive-DAGMiner patterns. In the majority of the cases, the equal AREWR values are due to the non-existence of cyclic relationships. AREWR depends on the proportion of maximal cyclic patterns generated and the edge weights which do not have a relation with the minimum supports. Therefore, we can expect a fluctuation with increasing/decreasing minimum supports. We are not comparing MH-DAGMiner with other benchmarking methods based on AREWR measure because these methods are modified for DAG mining using a similar optimum vertex hierarchy mining approach and consequently the results will be similar. Therefore, we can validate that MEG/maximal graph mining and cycles removing are more effective than removing cycles first and then mining DAG patterns.

Fig. 11

Evaluation method 2: left: precision and right: recall calculated for the output patterns of synth-data1 dataset

5.4 Evaluation method 2: DAG mining from the graph database (MHDM) versus DAG mining by post-processing graph patterns

5.4.1 Completeness of output patterns

We use precision and recall to measure the completeness of output patterns generated with the synth-data1 dataset which has a ground truth pattern set. As shown in Fig. 11, MH-DAGMiner is able to generate the complete pattern sets for all support threshold ($\sigma$) as indicated by the precision and recall values of 1. Both FP-DAGMiner and MFSH-DAGMiner show similar performance at higher threshold (e.g., $\sigma \ge$ 80 %). However, the performance degrades at lower threshold (e.g., $\sigma \le 60\%$) because of the missing ConnectorNodes to represent the EdgeNode combinations. Even though MFSH-Tree includes additional EdgeNodes to represent the EdgeNode combinations missing in FP-Graph, the Edge removal to make a tree structure affects the precision and recall to be lower than that of FP-GraphMiner. Performance of gSpan-DAGMiner is same as MH-DAGMiner when the input contains no cycles (e.g., $\sigma = 100\%$). The cyclic edges lead to the generation of multiple DAG patterns per a cyclic graph which decreases the precision. Moreover, the inability to identify multi-rooted patterns as a single pattern causes low recall values in low minimum support thresholds.

5.4.2 Soundness of output patterns

It is difficult to validate the completeness of output in real-world datasets due to absence of the output (patterns) information. Therefore, in this section, we evaluate the soundness of MH-DAGMiner and other benchmarking methods based on the number of patterns generated. Table 5 includes the number of patterns generated by each method for the datasets at different minimum support thresholds. For MH-DAGMiner, FP-DAGMiner, and MFSH-DAGMiner, we also include the number of Nodes and Edges in FP-DAG, FP-Graph, and MFSH-Tree, respectively.

Table 5 Evaluation method 2: soundness of output patterns, $\#\hbox {Patterns}$ ($\#\hbox {Nodes}$, $\#\hbox {Edges}$ in corresponding edge group structures)

As expected, the number of patterns generated by each method increases when $\sigma$ decreases. The gSpan-DAGMiner method generates equal number of patterns than other methods at higher $\sigma$; however, it generates far more patterns comparatively at lower $\sigma$ values. It generates an equal number of patterns when there is no cyclic relationship in input or when there is no multi-rooted DAG pattern in output. In other cases, it generates redundant patterns because of the cyclic relationships and the inability to process a multi-rooted pattern as a single pattern.

All the other methods generate the same number of patterns when FP-DAG, FP-Graph, and MFSH-Tree have a single Node and no Edges (when $\sigma = 100\%$) as all the maximal patterns are included within this Node. Despite the equal number of Nodes and Edges, in some cases (in Math Overflow dataset, when $\sigma = 80\%$) a different number of patterns can be generated by these methods. Through manual checking, we identified that FP-DAGMiner and MFSH-DAGMiner miss some patterns due to the use of DFS walk. It only identifies the patterns included within paths in FP-Graph and MFSH-Tree, whereas MH-DAGMiner uses DFS traversal to identify the patterns within maximal sub-DAGs of the FP-DAG. MH-DAGMiner generates more patterns than FP-DAGMiner/MFSH-DAGMiner in this case. In certain cases, it generates lesser number of patterns by subsuming two or more patterns which have been identified as maximal patterns by FP-DAGMiner/MFSH-DAGMiner. However, there can be datasets like citation network where DFS walk and DFS traversal do not make any difference given the same number of Nodes and Edges. A possible reason could be the high density of the graphs/network and the existence of only a few disconnected graphs in the network. In other datasets, MH-DAGMiner identifies more patterns with the FP-DAG structure having more Nodes or Edges than FP-Graph and MFSH-Tree. These results show the soundness of MH-DAGMiner in identifying the correct set of maximal hierarchical DAG patterns.

5.4.3 Execution time and Memory consumption

Figure 12 reports the execution time and memory consumption on real-world network datasets. MH-DAGMiner has a better execution time and less memory consumption in all datasets especially at lower $\sigma$ values. With the unique vertex labeled-based canonical representation, MH-DAGMiner performs isomorphism testing efficiently with the use of BitCode categories and FP-DAG. Consequently, it does not explode with the increase in output pattern size, whereas FP-DAGMiner and MFSH-DAGMiner consume more time and space as they produce more isomorphic patterns with DFS walk in the incomplete FP-Graph/MFSH-Tree. As they do not include isomorphic testing, these non-maximal patterns are removed as an additional post-processing step. The frequency-based edge pruning approach introduced in MH-DAGMiner FT creation significantly reduces time and memory consumption at higher $\sigma$. At lower $\sigma$, this effect is not at play.

gSpan-DAGMiner was found to be the least scalable method which was able to successfully execute only at higher $\sigma$. Even at high $\sigma$ values, the output pattern analysis reveals the existence of redundant patterns and inability to identify multi-rooted patterns. As shown in Table 5, the number of output patterns increases when $\sigma$ decreases; consequently, the pruning of non-maximal involves high computational cost. Moreover, it requires a high computational cost for canonization as the required number of comparisons becomes high to validate whether the DFS code is minimum [26].

Fig. 12

Evaluation method 2: left: execution time versus $\sigma$, right: memory consumption versus $\sigma$ for a Higgs Twitter, b Math Overflow, c Enron email, d Citation, e Wikitalk, f CollegeMsg

Since the real-world networks contain only a few database instances, we use synthetic graph databases to validate the performance of MH-DAGMiner in large-sized databases. According to the computational complexity of MH-DAGMiner, the performance highly depends on the number of Nodes in FP-DAG and on the number of output patterns. When database instances are highly correlated, there will be only a few Nodes in the FP-DAG as the edges have a similar occurrence patterns in the database; consequently, there will be only a few output patterns. In contrast, a database with less correlation will generate a higher number of Nodes and output patterns. Therefore, we first analyze the performance of MH-DAGMiner in large-sized graph databases with low and high correlation as shown in Fig. 13a, b.

Fig. 13

Evaluation method 2: left: execution time versus $\sigma$, right: memory consumption versus $\sigma$ for a synth-data2 (low correlation), b synth-data3 (high correlation)

The performance of gSpan-DAGMiner is similar on both datasets. It is aborted at $\sigma \le 80\%$ due to the complexity relating to canonization in large (in size) output patterns. For the low-correlated dataset (Fig. 13a), MH-DAGMiner consumes least execution time at high $\sigma$ values. It is interesting to see MFSH-DAGMiner executes (time) similar to MH-DAGMiner. As shown in previous experiments, MFSH-Tree is not always complete and can generate isomorphic patterns. However, in graph transaction setting, isomorphic patterns are rarely produced; therefore, the time performance of MFSH-DAGMiner comes close to MH-DAGMiner at lower $\sigma$. Due to the incompleteness in FP-Graph, FP-DAGMiner generates a higher number of patterns and it reflects in its time and memory consumption. performance than MH-DAGMiner and MFSH-DAGMiner methods and increases the computational complexity.

For the high-correlated dataset (Fig. 13b), a different performance can be seen. Due to high correlation among graph instances, only a few large (in size) sub-DAG patterns should be generated. The execution time and memory consumption of MH-DAGMiner increases rapidly with decreasing $\sigma$ and becomes more than that of FP-DAGMiner and MFSH-DAGMiner. When there is a high correlation, the FP-DAG/FP-Graph/MFSH-Tree structures include only a few Nodes and Edges. Finding missing Nodes or Edges increases the complexity of MH-DAGMiner without any significant contribution in identifying the complete pattern set.

Fig. 14

Evaluation method 2: left: execution time, right: memory consumption versus average size of output patterns O(V, E, H) on synth-data4 (5, 4, 3), synth-data5 (50, 49, 6) and synth-data6 (500, 499, 12)

Next, we compare the performance of MH-DAGMiner with different values O(V, E, H) of output patterns in order to validate the effectiveness of non-maximal pattern pruning technique used in MH-DAGMiner with compared to minimum DFS Code-based canonization in gSpan-DAGMiner and naive approach of comparing each pattern with the rest of the patterns in FP-DAGMiner and MFSH-DAGMiner. The datasets are created in a way that only five maximal patterns are generated by all methods which help to compare the performance only based on the size of output patterns.

As shown in Fig. 14, gSpan-DAGMiner is highly sensitive to the size of output patterns. As the size of patterns increases, execution time and memory consumption explode proving the inefficiency of using minimum DFS code canonization with unique vertex label graph representation. Execution time and memory consumption of MH-DAGMiner, FP-DAGMiner and MFSH-DAGMiner increase with the size of output patterns where MH-DAGMiner is the least expensive method. Considering the fact that these results are for only five patterns, we can expect a significant performance improvement in MH-DAGMiner over other methods when there are a large number of output patterns with higher values of O(V, E, H).

6 Conclusion and future work

In this paper, we present a novel algorithm (MH-DAGMiner) to mine maximal hierarchical DAG patterns from a directed weighted and cyclic network/graph database. A novel frequency-based edge grouping method using the FP-DAG structure is developed to identify MEGs in the dataset. These MEGs are approximated using the optimum branching technique to generate maximal hierarchical DAG patterns. We theoretically prove the completeness of MH-DAGMiner based on the FP-DAG Structure.

The extensive empirical analysis is conducted with several synthetic and real-world datasets exhibiting diverse characteristics. The approach of MH-DAGMiner is found to be effective compared to DAG mining from the preprocessed DAG database. MH-DAGMiner is also benchmarked with the state-of-the-art graph mining algorithms after extending them for DAG mining with a post-processing step. Results show that MH-DAGMiner is scalable for large network and graph datasets as well as efficient in terms of reduced execution cost and memory consumption. MH-DAGMiner shows better performance in network transaction setting with real-world data sets compared to graph transaction setting. In the graph transaction setting, MH-DAGMiner shows better performance with non-correlated datasets. With the unique vertex-labeled, edge-based canonical representation, MH-DAGMiner can handle large (in size) output patterns with a high number of hierarchy levels efficiently.

As expected, when the number of output patterns explodes, the performance degrades which indicates that maximal pattern mining alone is not sufficient when the requirement is identifying most significant patterns. We also found interesting insights on Twitter interactions and Enron email conversations which proves the applicability of MH-DAGMiner in applications like hierarchy mining, role mining and influence mining. In the future, we will investigate the use of MH-DAG patterns in these application areas.