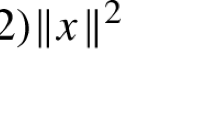Level-set methods for convex optimization

Abstract

Convex optimization problems arising in applications often have favorable objective functions and complicated constraints, thereby precluding first-order methods from being immediately applicable. We describe an approach that exchanges the roles of the objective with one of the constraint functions, and instead approximately solves a sequence of parametric level-set problems. Two Newton-like zero-finding procedures for nonsmooth convex functions, based on inexact evaluations and sensitivity information, are introduced. It is shown that they lead to efficient solution schemes for the original problem. We describe the theoretical and practical properties of this approach for a broad range of problems, including low-rank semidefinite optimization, sparse optimization, and gauge optimization.

1 Introduction

We demonstrate a method for solving constrained convex optimization problems that interchanges the objective with one of the constraint functions. This interchange defines a convex and nonsmooth univariate optimal-value function $v(\tau )$, which is parameterized by the level values of the original objective. A solution of the original problem can then be obtained by computing a root $\tau _*$ of a single nonlinear equation of the form

$$\begin{aligned} v(\tau )=\sigma , \end{aligned}$$

(1.1)

where the root corresponds to the desired optimal level value. This approach has been used to develop a variety of solution methods—some dating back to antiquity; see Sect. 1.3. Particular implementations of this idea, however, are all tied to specific choices of the algorithm used to approximate the function value $v(\tau _k)$ and the algorithm used to update the sequence of level values $\tau _k\rightarrow \tau _*$. Our proposed approach only requires a fixed relative accuracy between upper and lower bounds on $v(\tau _k)$. In doing so, we give an algorithm with an overall iteration complexity that is only a log factor of the iteration complexity needed to approximate $v(\tau _k)$. This results in a framework that decouples the method for approximating $v(\tau )$ from the method for solving (1.1) and thereby allows for the specification of a wide range of new approaches to constrained convex optimization.

The story behind our approach begins with the SPGL1 algorithm for basis pursuit [52, 53]. Although neither SPGL1 nor basis pursuit are our focus, they provide a concrete illustration of the ideas we pursue. Recall that the goal of the basis pursuit problem is to recover a sparse n-vector x that approximately satisfies the linear system $Ax=b$. This task often arises in applications such as compressed sensing and statistical model selection. Standard approaches, based on convex optimization, rely on solving one of the following formulations.

BP$_{\sigma }$	LS$_{\tau }$	QP$_{\lambda }$
$\displaystyle \min _{x} \Vert x\Vert _{1}$	$\displaystyle \min _{x} \frac{1}{2}\Vert Ax-b\Vert ^2_{2}$	$\displaystyle \min _{x} \frac{1}{2}\Vert Ax-b\Vert ^2_{2} + \lambda \Vert x\Vert _{1}$
$\text {s.t.} \frac{1}{2}\Vert Ax-b\Vert ^2_{2}\le \sigma$	$\text {s.t.} \Vert x\Vert _{1}\le \tau$

Computationally, BP$_{\sigma }$ is perceived to be the most challenging of the three formulations because of the complicated geometry of the feasible region. For example, projected- or proximal-gradient methods for LS$_{\tau }$ or QP$_{\lambda }$ require at each iteration applications of the operator A and its adjoint, and computing either a Euclidean projection onto the 1-norm ball or a proximal step, which cost $\mathcal {O}\!\left( n\log n \right)$ and $\mathcal {O}\!\left( n \right)$ operations, respectively. As a result, solvers such as FISTA [3] and SPARSA [58], target either LS$_{\tau }$ and QP$_{\lambda }$. The Homotopy algorithm [44] and alternating direction method of multipliers (ADMM) [11, 26] can be applied in various ways to solve BP$_{\sigma }$, but available implementations require solving a linear system at each iteration, which is not always practical for large problems. Inexact variants of ADMM, such as linearized Bregman [59], do not require a linear solution, but may compromise by solving an approximation of the problem [59].

This paper targets optimization problems that generalize the formulations BP$_{\sigma }$ and LS$_{\tau }$. To set the stage, consider the pair of convex problems

where $\mathcal {X}\subseteq \mathbb {R}^n$ is a closed convex set, the functions $\varphi :\mathbb {R}^n\rightarrow \overline{\mathbb {R}}:= \mathbb {R}\cup \{+\infty \}$ and $\rho :\mathbb {R}^n\rightarrow \overline{\mathbb {R}}$ are closed convex functions, and A is a linear map. Such formulations are ubiquitous in contemporary optimization and its applications, and often $\varphi$ may be regarded as a regularizer on the solution x, and $\rho$ may be regarded as a measure of misfit between a linear model Ax and observations b. Other formulations are available, of course, that may be more natural in a particular context (such as redefining $\rho$ so that A and b are not explicit). We choose this formulation because it most closely represents a large class of problems that might appear in practice.

Our working assumption is that the level-set problem $\mathcal {Q}_\tau$ is easier to solve than $\mathcal {P}_\sigma$ in the sense that there exists a specialized algorithm for its solution, but that a comparably-efficient solver does not exist for $\mathcal {Q}_\tau$. In Sect. 4, we discuss a range of optimization problems, including problems with nonsmooth regularization, and conic constraints, that have this property.

Our main contribution is to develop a practical and theoretically rigorous algorithmic framework to harness existing algorithms for $\mathcal {Q}_\tau$ to efficiently solve the $\mathcal {P}_\sigma$ formulation. As a consequence, we make explicit the fact that in typical circumstances both problems are essentially equivalent from the viewpoint of computational complexity. Hence, there is no reason not to choose any one preferred formulation based on computational considerations alone. This observation is very significant in applications since, although the formulations $\mathcal {P}_\sigma$, $\mathcal {Q}_\tau$, and their penalty-function counterparts are, in a sense, mathematically and computationally equivalent, they are far from equivalent from a modeling perspective. Practitioners should instead focus on choosing the formulation best suited to their applications. Our second contribution is to provide an algorithmic recipe for achieving the same computational complexity for a wide range of regularized data-fitting problems, listed in Sect. 1.2.

1.1 Approach

The proposed approach, which we will formalize shortly, approximately solves $\mathcal {P}_\sigma$ in the sense that it generates a point $x\in \mathcal {X}$ that is super-optimal and $\epsilon$-feasible:

$$\begin{aligned} \varphi (x)\le \text {OPT} \quad \text {and}\quad \rho (Ax-b)\le \sigma +\epsilon , \end{aligned}$$

(1.2)

where OPT is the optimal value of $\mathcal {P}_\sigma$. This optimality concept was introduced by Harchaoui et al. [28], and we adopt it here. Our proposed strategy exchanges the roles of the objective and constraint functions in $\mathcal {P}_\sigma$, and approximately solves a sequence of level-set problems $\mathcal {Q}_\tau$ for varying parameters $\tau$. There are many precursors for this level set approach, which we summarize in Sect. 1.3.

How does one use approximate solutions of $\mathcal {Q}_\tau$ to obtain a super-optimal and $\epsilon$-feasible solution of $\mathcal {P}_\sigma$, the target problem? We answer this by recasting the problem in terms of the value function for $\mathcal {Q}_\tau$:

$$\begin{aligned} v(\tau ):=\min _{x\in \mathcal {X}}\left\{ \,\rho (Ax-b)\,\left| \ \varphi (x)\le \tau \right. \right\} . \end{aligned}$$

(1.3)

This value function is nonincreasing and convex [50, Theorem 5.3]. Under the mild assumption that the constraint $\rho (Ax-b)\le \sigma$ is active at any optimal solution of $\mathcal {P}_\sigma$, it is evident that the value $\tau _*:=\text{ OPT }$ satisfies the Eq. (1.1). Conversely, it is immediate that for any $\tau \le \tau _*$ satisfying $v(\tau ) \le \sigma + \epsilon$, solutions of $\mathcal {Q}_\tau$ are super-optimal and $\epsilon$-feasible for $\mathcal {P}_\sigma$, as required. Figure 1a illustrates the set of admissible solutions.

In summary, we have translated problem $\mathcal {P}_\sigma$ to the equivalent problem of finding the minimal root of the nonlinear univariate equation (1.1). Aravkin et al. [1, Theorem 2.1] formally establish the validity of that translation. We show in Sect. 2 how approximate solutions of $\mathcal {Q}_\tau$ can serve as the basis for two Newton-like root-finding algorithms for this key equation.

Fig. 1

a The shaded area indicates the set of allowable solutions $\tau \in [\tau _{\scriptscriptstyle L},\tau _*]$ to the root-finding problem (1.1), and corresponds to the set of super-optimal solutions x that satisfy (1.2); b the root may be a minimizer of v, and then $\tau _*$ corresponds to the left-most root

In principle, any root-finding algorithm can be used. However, it must be able to obtain the left-most root, which is the only permissible solution in the case when there are multiple roots, as illustrated in Fig. 1b. Several algorithms are available for the root-finding problem (1.1), including bisection, secant, Newton, and their variants. These methods all require an initial estimate of the left-most root $\tau _*$. Bisection requires two initial estimates that bracket the root, and thus it may not always be suitable in this context because it must be initialized with an upper bound on the optimal value $\tau _*= \text{ OPT }$, which may be costly to compute. (Any feasible solution of ($\mathcal {P}_\sigma$) yields an upper bound, though obtaining it may be as costly as computing an optimal solution.) On the other hand, both secant and Newton can use initializations that underestimate the optimal value. In many important cases, this is trivial: for example, if $\phi$ is a norm, then $\tau =0$ is an obvious candidate. Secant, of course, requires a second initial point, which may not be obviously available. The root-finding algorithm should also allow for inexact evaluations of the value function, and hence allow for approximate and efficient solutions of the subproblems that define (1.3). If the algorithm used to solve the subproblems is a feasible method, efficiencies may be gained if the root-finding algorithm generates iterates that are monotonically increasing, because then solutions for one subproblem are immediately feasible for the next subproblem in the sequence.

We focus on variants of secant and Newton methods that accommodate inexact oracles for v, and which enjoy an unconditional global linear rate of convergence. The secant method requires an inexact evaluation oracle that provides upper and lower bounds on v (Definition 2.1). The Newton method additionally requires a global affine minorant (Definition 2.2). Both algorithms exhibit the desirable monotonicity property described above. Coupled with an evaluation oracle for v that has a cost that is sublinear in $\epsilon$, we obtain an algorithm with an overall cost that is also sublinear in $\epsilon$, modulo a logarithmic factor.

1.2 Roadmap

We prove in Sect. 2 complexity bounds and convergence guarantees for the level-set scheme. We note that the iteration bounds for the root-finding schemes are independent of the slope of v at the root. This implies that the proposed method is insensitive to the “width” of the feasible region in $\mathcal {P}_\sigma$. Such methods are well-suited for problems $\mathcal {P}_\sigma$ for which the Slater constraint qualification fails or is close to failing (cf. Example 4.2). In Sect. 3, we consider refinements to the overall method, focusing on linear least-squares constraints and recovering feasibility. Section 4 explores level-set methods in notable optimization domains, including semi-definite programming, gauge optimization, and regularized regression. We also describe the specific steps needed to implement the root-finding approach for some representative applications, including low-rank matrix completion [35, 47], and sensor-network localization [7,8,9].

1.3 Related work

The intuition for interchanging the role of the objective and constraint functions has a distinguished history, appearing even in antiquity. Perhaps the earliest instance is Queen Dido’s problem and the fabled origins of Carthage [22, Page 548]. In short, that problem is to find the maximum area that can be enclosed by an arc of fixed length and a given line. The converse problem is to find an arc of least length that traps a fixed area between a line and the arc. Although these two problems reverse the objective and the constraint, the solution in each case is a semi-circle. The interchange of constraint and objective is at the heart of Markowitz mean-variance portfolio theory [37], where the objective and constraint roles correspond to the rate of return and variance of a portfolio. The great variety of possible modern applications is formalized by the inverse function theorem in Aravkin et al. [1, Theorem 2.1]. More generally, trade-offs between various objectives form the foundations for multi-objective optimization [39].

The idea of rephrasing a constrained optimization problem as a root-finding problem has been used for at least half a century to the work of Morrison [40] and Marquadt [38]. The approach there is to minimize a quadratic function q(x) subject to the trust-region constraint:

$$\begin{aligned} \displaystyle \mathop {\hbox {minimize}}_{x\in \mathbb {R}^n}\,q(x) \,\mathop {\hbox {subject to}}\,\Vert x\Vert _2\le \varDelta . \end{aligned}$$

Newton’s method is used to compute a root for the equation $\Vert x(\lambda )\Vert _2^2-\varDelta =0$, where $x(\lambda )$ is the solution of a parameterized unconstrained problem. This is the basis for the family of trust-region algorithms for constrained and unconstrained optimization. Newton’s method for the trust-region subproblem motivated the SPGL1 algorithm [52, 53] for the 1-norm regularized least-squares problem and its extensions [1]. A shortcoming of the numerical theory to date is the absence of practical complexity and convergence guarantees. In this work, we take a fresh new look at this general framework and provide rigorous convergence guarantees. Several examples illustrate the vast applicability of the approach, and show how the proposed framework can be instantiated in concrete circumstances.

The root-finding approach is central to the ideas pioneered by Lemaréchal et al. [33], who propose a level bundle method for convex optimization [32, 56]. They consider the convex optimization problem

$$\begin{aligned} \displaystyle \mathop {\hbox {minimize}}_{x\in \mathcal {X}} \, f_0(x) \,\mathop {\hbox {subject to}}\, f_j(x)\le 0 \quad \text{ for } j=1,\dots ,m, \end{aligned}$$

(1.4)

where each function $f_j$ is convex and $\mathcal {X}$ is a nonempty closed convex set. The root-finding equation is based on the function

$$\begin{aligned} g(\tau ):=\min _{x\in \mathcal {X}}\ \max \ \{f_0(x)-\tau ,\, f_1(x),\dots ,\, f_m(x)\}, \end{aligned}$$

and their algorithm constructs the smallest solution $\tau _*$ to the equation $g(\tau )=0$, which corresponds to the optimal value (1.4). This method is also analyzed in depth by Nesterov [42, §3.3.4]

More recently, Harchaoui et al. [28] present an algorithm focusing on instances of $\mathcal {P}_\sigma$where the constraint function $\rho$ is smooth and $\varphi$ is a gauge function defined by the intersection of a unit ball for a norm and a closed convex cone. Their zero-finding method is coupled with the Frank–Wolfe algorithm, which generates lower bounds and affine minorants on the value function. In contrast, our root finding phase does not depend on the algorithm used to solve the subproblems, as is the case in the approaches described by Aravkin et al. [1] and van den Berg and Friedlander [52, 53]. In particular, the approach we take can use any affine minorant obtained from a dual certificate, as we describe in Sect. 2.3. Primal-dual algorithms can generate such certificates, but are not always practical for large-scale problems. On the other hand, first-order methods are often more suitable for large problems, but it not always obvious how to generate such certificates. Affine minorants can derived from the Frank–Wolfe algorithm (cf. Sect. 2.3), and from other families of first-order methods [19]. One approach that may be used in practice is to apply first-order methods in parallel to the the primal and dual problems.

1.4 Notation

The notation we use is standard, and closely follows that of Rockafellar [50]. For any function $f:\mathbb {R}^n\rightarrow \overline{\mathbb {R}}$, we use the shorthand $[f \le \alpha ] := \{x \mid f(x)\le \alpha \}$ to denote the $\alpha$-sublevel set. An affine minorant of f is any affine function g satisfying $g(x)\le f(x)$ for all x. For any set $\mathcal {C}\subseteq \mathbb {R}^n$, we define the associated indicator function $\delta _\mathcal {C}$ vanishes over $\mathcal {C}$ and is infinite elsewhere. The p-norms and corresponding closed unit balls are denoted, respectively, by $\Vert \cdot \Vert _p$ and $\mathbb {B}_{p}$. For any convex cone ${\mathcal {K}}$ defined over a Euclidean space, the dual cone is defined by ${\mathcal {K}}^*:=\left\{ y\,\left| \ {{\langle }x},{y{\rangle }} \ge 0 \text{ for } \text{ all } x\in {\mathcal {K}}\right. \right\} .$ The norm on that space is given by $\Vert x\Vert =\sqrt{{{\langle }x},{x{\rangle }}}$.

We endow the space of real $m\times n$ matrices with the trace product $\langle X,Y\rangle :=\mathrm {tr}\,(X^TY)$ and the induced Frobenius norm $\Vert X\Vert _F:=\sqrt{\langle X,X \rangle }$. The Euclidean space of real $n\times n$ symmetric matrices, written as $\mathcal {S}^n$, inherits the trace product $\langle X,Y\rangle :=\mathrm {tr}\,(XY)$ and the corresponding norm. The closed, convex cone of $n\times n$ positive semi-definite matrices is denoted by $\mathcal {S}^n_+=\{X\in \mathcal {S}^n \mid X\succeq 0\}$.

2 Root-finding with inexact oracles

Algorithms that provides approximate solutions of $\mathcal {Q}_\tau$ are central to our framework because these constitute the oracles through which we access v. In this section, we describe the complexity guarantees associated with two types of oracles: an inexact-evaluation oracle that provides upper and lower bounds on $v(\tau )$, and an affine-minorant oracle that additionally provides a global linear underestimator on v. For example, any primal-dual algorithm provides the required upper and lower bounds, and algorithms such as Frank–Wolfe [24, 29] automatically provide a global linear minorant, which gives approximate derivative information. The ability to use inexact solutions is crucial in practice, where the effort needed for each oracle call must be bounded.

As a counterpoint to the global complexity guarantees for inexact oracles that we describe later in this section, Theorem 2.1 describes the asymptotic superlinear rate of convergence for the secant and Newton methods with exact evaluations of any nonsmooth convex function. To our knowledge, the superlinear convergence of the secant method for convex root finding does not appear in the literature and so we provide the proof of this result in the appendix.

Theorem 2.1

(Superlinear convergence of secant and Newton methods) Let $f:\mathbb {R}\rightarrow \mathbb {R}$ be a decreasing, convex function on the interval [a, b]. Suppose that the point $\tau _*:=\inf \left\{ \tau \,\left| \ f(\tau )\le 0\right. \right\}$ lies in (a, b) and the non-degeneracy condition $g_*:=\inf \left\{ g\,\left| \ g\in \partial f(\tau _*)\right. \right\} <0$ holds. Fix two points $\tau _0, \tau _1\in (a,b)$ satisfying $\tau _0<\tau _1< \tau _*$ and consider the following two iterations:

and

If either sequence terminates finitely at some $\tau _k$, then it must be the case $\tau _k=\tau _*$. If the sequence $\{\tau _k\}$ does not terminate finitely, then $|\tau _*-\tau _{k+1}|\le (1-g_*/\gamma _k)|\tau _* -\tau _k|,\ k=1,2,\dots$, where $\gamma _k=g_k$ for the Newton sequence and $\gamma _k$ is any element of $\partial f(\tau _{k-1})$ for the secant sequence. In either case, $\gamma _k\uparrow g_*$ and $\tau _k\uparrow \tau _*$ globally q-superlinearly.

The algorithms presented here apply to any convex decreasing function $f:\mathbb {R}\rightarrow \mathbb {R}$ for which the equation $f(\tau )=0$ has a solution. In the following discussion, $\tau _*$ denotes a minimal root of $f(\tau )=0$. Given a tolerance $\epsilon >0$, the algorithms we discuss yield a point $\tau \le \tau _*$ satisfying $0\le f(\tau )\le \epsilon$.

2.1 Inexact secant

Our first root-finding algorithm is an inexact secant method, and is based on an oracle that provides upper and lower bounds on the value $f(\tau )$.

Definition 2.1

(Inexact evaluation oracle) For a function $f:\mathbb {R}\rightarrow \mathbb {R}$ and $\epsilon \ge 0$, an inexact evaluation oracle is a map $\mathcal {O}_{f,\epsilon }$ that assigns to each pair $(\tau ,\alpha )\in [f > 0]\times [1,\infty )$ real numbers $(\ell ,u)$ such that $\ell \le f(\tau )\le u$ and either $u\le \epsilon$, or $u > \epsilon$ and $1\le u/\ell \le \alpha$.

This oracle guarantees that either (i) we obtained an $\epsilon$-accurate solution $\tau$, or (ii) that $\ell > 0$ and $1 \le u/\ell \le \alpha$. The ratio $u/\ell$ measures the relative optimality of the point $\tau$. In contrast to the absolute gap $u-\ell$, it allows the oracle to be increasingly inexact for larger values of $f(\tau )$. The relative-accuracy condition is no less general than one based on an absolute gap. In particular, we can verify that if the absolute gap satisfies the condition $u-\ell \le (1-1/\alpha )\epsilon$, then u and $\ell$ satisfy the conditions required by the inexact evaluation oracle. Indeed, provided that $u>\epsilon$, we deduce $u/\ell \le 1+(1-1/\alpha )\epsilon /\ell \le 1+(1-1/\alpha )u/\ell$. After rearranging terms, this yields the desired inequality $1\le u/\ell \le \alpha$.

Algorithm 2.1 outlines a secant method based on the inexact evaluation oracle. Theorem 2.2 establishes the corresponding global convergence guarantees; the proof appears in Appendix A.

Theorem 2.2

(Linear convergence of the inexact secant method) The inexact secant method (Algorithm 2.1) terminates after at most

$$\begin{aligned} k\le \max \left\{ 2 + \log _{2/\alpha }\! \left( 2 C/\epsilon \right) ,\, 3 \right\} \end{aligned}$$

iterations, where $C := \max \{ |s_1|(\tau _*-\tau _1),\, \ell _1 \}$ and $s_1:=(u_{0}- \ell _1)/(\tau _{0}-\tau _1)$.

The iteration bound of the inexact secant method is indifferent to the slope of the function f at the minimal root $\tau _*$ because termination depends on function values rather than proximity to $\tau _*$. The plots in Fig. 2 illustrate this behavior: panel (a) shows the iterates for $f_1(\tau )=(\tau -1)^2-10$, which has a nonzero slope at the minimal root $\tau _*=1-\sqrt{10}\approx -2.2$ and so has a non-degenerate solution; panel (c) shows the iterates for $f_2(\tau ) = \tau ^2$, which is clearly degenerate at the solution. The algorithm behaves similarly on both problems. When applied to the value function v to find a root of (1.1), the algorithm’s indifference to degeneracy translates to an insensitivity to the width [48] of the feasible region of $\mathcal {P}_\sigma$ —a consequence of the fact that the scheme maintains infeasible iterates for $\mathcal {P}_\sigma$. Such methods are well-suited for problems $\mathcal {P}_\sigma$ for which the Slater constraint qualification is close to failing.

The iteration bound in Theorem 2.2 is infinite for $\alpha \ge 2$. This is not an artifact of the proof. As illustrated by Fig. 2b, the inexact secant method behaves poorly for $\alpha$ close to 2. Indeed, it can fail to converge linearly (or at all) to the minimal root for any $\alpha \ge 2$, as the following example shows. Consider the linear function $f(\tau )=-\tau$ with lower and upper bounds $\ell _k:=-2\tau _k/(1+\alpha )$ and $u_k:=-2\alpha \tau _k/(1+\alpha )$. A quick computation shows that the quotients $q_k:=\tau _k/\tau _{k-1}$ of the iterates satisfy the recurrence relation $q_{k+1}=(1-\alpha )/(q_k-\alpha )$. It is then immediate that for all $\alpha \ge 2$, the quotients $q_k$ tend to one, indicating that the method stalls.

Fig. 2

Inexact secant method (top row) and Newton method (bottom row) for root finding on the functions $f_1(\tau )=(\tau -1)^2-10$ (first two columns) and $f_2(\tau )=\tau ^2$ (last column). Below each panel, $\alpha$ is the oracle accuracy, and k is the number of iterations needed to converge, i.e., to reach $f_i(\tau _k)\le \epsilon$. For all problems, $\epsilon =10^{-2}$; the horizontal axis is $\tau$, and the vertical axis is $f_i(\tau )$

2.2 Inexact Newton

The secant method can be improved by using approximate derivative information (when available) to design a Newton-type method. We design an inexact Newton method around an improved oracle that provides global linear under-estimators of f. This approach has two main advantages over the secant method. First, it is guaranteed to take longer steps than the inexact secant method. Second, it locally converges quadratically whenever f is smooth, the values $f(\tau )$ are computed exactly, and the function has a nonzero (left) derivative at the minimal root. To formalize these ideas, we use the following strengthened version of an inexact evaluation oracle.

Definition 2.2

(Affine minorant oracle) For a function $f:\mathbb {R}\rightarrow \mathbb {R}$ and $\epsilon \ge 0$, an affine minorant oracle is a mapping $\mathcal {O}_{f,\epsilon }$ that assigns to each pair $(\tau , \alpha ) \in [f > 0] \times [1,\infty )$ real numbers $(\ell ,u,s)$ such that $\ell \le f(\tau )\le u$, and either $u\le \epsilon$, or $u > \epsilon$ and $1\le u/\ell \le \alpha$. The affine function ${\bar{\tau }} \mapsto \ell + s ({\bar{\tau }} - \tau )$ globally minorizes f.

Algorithm 2.2 gives a Newton method based on the affine minorant oracle. The inexact Newton method has global convergence guarantees analogous to those of the inexact secant method, as described in Theorem 2.3. A proof is given in Appendix A.

Theorem 2.3

(Linear convergence of the inexact Newton method) The inexact Newton method (Algorithm  2.2) terminates after at most

$$\begin{aligned} k\le \max \left\{ 1 + \log _{2/\alpha }\! \left( 2 C /\epsilon \right) ,\, 2 \right\} \end{aligned}$$

iterations, where $C := \max \{ |s_0|(\tau _*-\tau _0),\, \ell _0 \}$.

When we compare the two algorithms, it is easy to see that the Newton steps are never shorter than the secant steps. Indeed, let $(\ell _{k-1},u_{k-1},s_{k-1})=\mathcal {O}_f(\tau _{k-1},\alpha )$ and $(\ell _{k},u_{k},s_{k})=\mathcal {O}_f(\tau _{k},\alpha )$ be the triples returned by an affine minorant oracle at $\tau _{k-1}$ and $\tau _{k}$, respectively. Then

$$\begin{aligned} u_{k-1}\ge f(\tau _{k-1})\ge \ell _k + s_k (\tau _{k-1} - \tau _k), \end{aligned}$$

which implies

$$\begin{aligned} s^{\hbox {secant}}_k := (u_{k-1}-\ell _k)/(\tau _{k-1}-\tau _k)\le s_k =: s^{\hbox {newton}}_k. \end{aligned}$$

Therefore, the Newton step length $-\ell _k/s^{\hbox {newton}}_k$ is at least as large as the secant step length $-\ell _k/s^{\hbox {secant}}_k$.

The Newton method often outperforms the secant method in practice. The bottom row of panels in Fig. 2 shows the progress of the Newton method on the same test problems specfied earlier. The Newton method performs relatively well even when $\alpha$ is near its upper limit of 2; compare panels (b) and (e) in the figure. In this set of experiments, we chose an oracle that has the same quality lower and upper bounds as the experiments with secant, but has the least favorable (i.e., steepest) slope that still results in a global minorant.

2.3 Lower minorants via duality

When are affine minorant oracles of the value function v readily available? Suppose we can express the value function in dual form,

$$\begin{aligned} v(\tau )=\max _{y\in \mathbb {R}^m}\ \varPhi (y,\tau ), \end{aligned}$$

where $\varPhi$ is concave in y and convex in $\tau$. For example, appealing to Fenchel duality, we may write

$$\begin{aligned} \begin{aligned} v(\tau )&= \min _{x\in \mathcal {X}}\ \left\{ \rho (Ax-b)\,\left| \ \varphi (x)\le \tau \right. \right\} \\&= \min _{x\in \mathbb {R}^n}\ \rho (Ax-b) + \delta _{\mathcal {X}\cap \,[\varphi \le \tau ]}(x) \\&= \max _{y\in \mathbb {R}^m}\ {{\langle }y},{b{\rangle }} - \rho ^{\star }(-y) - \delta ^{\star }_{\mathcal {X}\cap \,[\varphi \le \tau ]}(A^* y), \end{aligned} \end{aligned}$$

where the last equality holds provided that either the primal or the dual problem has a strictly feasible point [10, Theorem 3.3.5]. Hence, the Fenchel dual objective

$$\begin{aligned} \varPhi (y,\tau ):={{\langle }b},{y{\rangle }} -\rho ^{\star }(-y) -\delta ^{\star }_{\mathcal {X}\cap [\varphi \le \tau ]}(A^* y) \end{aligned}$$

(2.1)

yields an explicit representation for $\varPhi$, which is concave in $\tau$, as shown by Lemma A.1.

Many standard first-order methods that might be used as an oracle for evaluating $v({\bar{\tau }})-\sigma$, and generate both a lower bound ${\bar{\ell }}$ and a dual certificate $\bar{y}$ that satisfy the equation ${\bar{\ell }}=\varPhi (\bar{y},\bar{\tau })-\sigma$. Examples include saddle-prox [41], Frank–Wolfe [24, 29], some projected subgradient methods [2], and accelerated versions [43, 51]. Whenever such a dual certificate $\bar{y}$ is available, we have

$$\begin{aligned} \begin{aligned} v(\tau )-\sigma \ge \varPhi (\bar{y},\tau )-\sigma&= \big (\varPhi (\bar{y},\bar{\tau })-\sigma \big ) + \big (\varPhi (\bar{y},\tau )-\varPhi (\bar{y},\bar{\tau })\big ) \\&\ge \bar{\ell }+\bar{s}(\tau -\bar{\tau }), \end{aligned} \end{aligned}$$

(2.2)

where $\bar{s}\in \partial _{\tau }\delta ^{\star }_{\mathcal {X}\cap \, [\varphi \le \tau ]}(A^* y)$. Hence, any dual certificate $\bar{y}$ is valid if it generates an affine minorant oracle where ${\bar{\ell }}$ satisfies the accuracy condition required by Definition 2.2. In summary, if $y_k$ is a valid dual certificate, we may take

$$\begin{aligned} \ell _k := \varPhi (y_k,\tau _k) -\sigma \quad \text{ and } \text{ any }\quad s_k \in \partial _{\tau }\delta ^{\star }_{\mathcal {X}\cap \, [\varphi \le \tau _k]}(A^* y_k). \end{aligned}$$

We derive in Sect. 4 subdifferential formulas for a large class of contemporary problems, including conic and gauge optimization (cf. Tables 1 and 2). More general rules for computing subdifferential formulas are outlined by Aravkin et al. [1, Equations 5.1(d,e), 6.13, 6.26].

2.4 Lower minorants via Frank–Wolfe

In some instances, lower-bounds on the optimal value of $\mathcal {Q}_\tau$ that is provided by an algorithm are seemingly not related to a dual solution. A notable example of such a scheme is the Frank–Wolfe algorithm, which has recently received much attention. Suppose that the function $\rho$ is smooth. The Frank–Wolfe method applied to the problem $\mathcal {Q}_\tau$ is based on the following two-step iteration:

$$\begin{aligned} \begin{aligned} z_{k}&= \mathop {\mathrm {argmin}}\ \left\{ {{\langle }A^*\nabla \rho (Ax_k-b)},{z{\rangle }} \mid z\in \mathcal {X}\cap [\varphi \le \tau ] \right\} \\x_{k+1}&= x_k+t_k(z_k-x_k) \end{aligned} \end{aligned}$$

for an appropriately chosen sequence of step-sizes $t_k$ (e.g., $t_k=\frac{2}{k+2}$). As the method progresses, it generates the upper bounds $u_k=\min _{i=1,\ldots ,k} \rho (Ax_i-b)$ on the optimal value of $\mathcal {Q}_\tau$. Moreover, it is easy to deduce from convexity that the following are valid lower bounds:

$$\begin{aligned} \ell _k=\max _{i=1,\ldots ,k} \left\{ \rho (Ax_i-b)+ \langle A^* \nabla \rho (Ax_i-b) , z_i-x_i\rangle \right\} . \end{aligned}$$

Jaggi [29] provides an extensive discussion. If the step sizes $t_k$ are chosen appropriately, the gap satisfies $u_k-\ell _k\le \mathcal {O}(D^2L/k)$, where the diameter D of the feasible region and the Lipschitz constant L of the gradient of the objective function of $\mathcal {Q}_\tau$ are measured in an arbitrary norm. Harchaoui et al. [28] observe how to deduce from such lower bounds $\ell _k$ an affine minorant of the value function v.

On the other hand, one can also show that the lower bounds $\ell _k$ are indeed generated by an explicit candidate dual solution, and hence the Frank–Wolfe algorithm (and its variants) fit perfectly in the above framework based on dual certificates. To see this, consider the Fenchel dual

$$\begin{aligned} \displaystyle \mathop {\hbox {maximize}}_{y\in \mathbb {R}^m}\quad \varPhi (y,\tau )={{\langle }y},{b{\rangle }} - \rho ^{\star }(-y) - \delta ^{\star }_{\mathcal {X}\cap [\varphi \le \tau ]}(A^* y) \end{aligned}$$

of $\mathcal {Q}_\tau$. Then for the candidate dual solutions $y_i:=-\nabla \rho (Ax_i-b)$, we deduce

$$\begin{aligned} \varPhi (y_i,\tau )&=\langle y_i,b\rangle -\rho ^{\star }(-y_i)-\langle A^* y_i,z_i\rangle \\&=\langle y_i,b\rangle +\Big (\rho (Ax_i-b)+\langle y_i, Ax_i-b\rangle \Big ) -\langle A^* y_i,z_i\rangle \\&=\rho (Ax_i-b)+\langle A^T\nabla \rho (Ax_i-b),z_i-x_i\rangle . \end{aligned}$$

Thus, the lower bounds $\ell _k$ are simply equal to $\ell _k=\max _{i=1,\ldots ,k} \varPhi (y_i,\tau )$, and affine minorants on the value function v are readily computed from the dual iterates $y_k$ and the derivatives $\partial _{\tau }\delta ^{\star }_{\mathcal {X}\cap \, [\varphi \le \tau ]}(A^* y_k)$.

3 Special cases

This section can be considered as an aside in our main exposition. We address in this section two questions that arise in the application of our root-finding approach: how best to apply the algorithm to problems with linear least-squares constraints, and how to recover a feasible point.

3.1 Least-squares misfit and degeneracy

Particularly important instances of problem $\mathcal {P}_\sigma$ arise when the misfit between Ax and b is measured by the 2-norm, i.e., $\rho =\Vert \cdot \Vert _2$. In this case, the objective of the level-set problem $\mathcal {Q}_\tau$ is $\Vert Ax-b\Vert _2$, which is not differentiable whenever $Ax=b$. Rather than applying a nonsmooth optimization scheme, an apparently easy fix is to replace the constraint in $\mathcal {P}_\sigma$ with its equivalent formulation $\tfrac{1}{2}\Vert Ax-b \Vert _2^2\le \tfrac{1}{2}\sigma ^2$, leading to the pair of problems

However, this reformulation presents some numerical difficulties. Below we describe the potential pitfalls and a simple alternative.

For this section only, define

$$\begin{aligned} f_1(\tau ) := v(\tau )-\sigma \qquad \text{ and }\qquad f_2(\tau ):=\tfrac{1}{2}v^2(\tau )-\tfrac{1}{2}\sigma ^2, \end{aligned}$$

where v is the value function corresponding to the original (unsquared) level-set problem $\mathcal {Q}_\tau$. Throughout this section, the problems $\mathcal {P}_\sigma$ and $\mathcal {Q}_\tau$ continue to define the original formulations without the squares.

A direct application of the root-finding procedure for $\mathcal {P}_\sigma ^2$ would be applied to the function $f_2$, which is degenerate at each of its roots. As a result, the secant and Newton root-finding methods would not converge locally superlinearly—even if the values $v(\tau )$ are evaluated exactly; see Theorem 2.1. Moreover, we have observed empirically that this issue can in some cases cause numerical schemes to stagnate.

A simple alternative avoids this pitfall: apply the root-finding procedure to the function $f_1$, but approximately solve $\mathcal {Q}_\tau ^2$ to obtain bounds on v. The oracle definitions required for the secant (Algorithm 2.1) and Newton (Algorithm 2.2) methods require suitable modification. For secant, the modifications are straightforward, but for Newton, care is needed in order to obtain the correct affine minorants of $f_1$. The required modifications for secant and Newton are described below.

Secant For the secant method applied to the function $f_1$, we derive an inexact evaluation oracle from an inexact evaluation oracle for $f_2$ as follows. Suppose that we have approximately solved $\mathcal {Q}_\tau ^2$ by an inexact-evaluation oracle

$$\begin{aligned} \mathcal {O}_{f_2, \epsilon }\big (\tau , \alpha ^2\big ) = \left( \tfrac{1}{2}\ell ^2-\tfrac{1}{2}\sigma ^2,\ \tfrac{1}{2}u^2-\tfrac{1}{2}\sigma ^2\right) , \end{aligned}$$

(3.1)

where we have specified the relative accuracy between the lower and upper bounds to be $\alpha ^2$. Assume, without loss of generality, that $u,\ell \ge 0$. Then clearly u and $\ell$ are upper and lower bounds on $v(\tau )$, respectively. It is now straightforward to deduce

$$\begin{aligned} 0\le \ell -\sigma \le f_1(\tau ) \le u-\sigma \qquad \hbox {and}\qquad \frac{ u-\sigma }{\ell -\sigma } \le \sqrt{\frac{ u^2-\sigma ^2}{ \ell ^2-\sigma ^2}}\le \alpha . \end{aligned}$$

(3.2)

Hence an inexact function evaluation oracle for $f_2$ yields an inexact evaluation oracle for $f_1$.

Newton Newton’s method in this setting is slightly more intricate because of the formulas required for obtaining a valid affine minorant of $f_1$. We use the respective objectives of the dual problems corresponding to $\mathcal {Q}_\tau$ and $\mathcal {Q}_\tau ^2$, given by

$$\begin{aligned} \varPhi _1(y,\tau )&:= {{\langle }b},{y{\rangle }} - \delta ^{\star }_{\mathcal {X}\cap [\varphi \le \tau ]}(A^* y) - \delta _{\mathbb {B}_2}(y), \\ \varPhi _2(y,\tau )&:= {{\langle }b},{y{\rangle }} -\delta ^{\star }_{\mathcal {X}\cap [\varphi \le \tau ]}(A^* y) -\tfrac{1}{2}\Vert y\Vert ^2_2. \end{aligned}$$

As described by (3.1), an inexact solution of $\mathcal {Q}_\tau ^2$ delivers values $\ell$ and u that satisfy (3.2). Let y be the valid dual certificate that generated the lower bound $\ell$, so that $\varPhi _2(y,\tau )=\tfrac{1}{2}\ell ^2$. (See the discussion in Sect. 2.3 regarding valid dual certificates.) Let $s\in \partial _{\tau } \varPhi _2(y,\tau )$ be any subgradient. The following result establishes that $(\hat{\ell },\, u,\, s/\Vert y\Vert _2)$, with $\hat{\ell }:=\varPhi _1\left( y/\Vert y\Vert _2,\,\tau \right) ,$ defines a valid affine minorant for $f_1$.

Proposition 3.1

The inequalities

$$\begin{aligned} 0\le \hat{\ell }-\sigma \le f_1(\tau ) \le u-\sigma \qquad \hbox {and}\qquad (u-\sigma )/(\hat{\ell }-\sigma ) \le \alpha \end{aligned}$$

hold, and the linear functional $\tau ' \mapsto (\hat{\ell }-\sigma )-(s/\Vert y\Vert _2)(\tau '-\tau )$ minorizes $f_1$.

The proof is given in Appendix A. In summary, if we wish to obtain a super-optimal and $\epsilon$-feasible solution to $\mathcal {P}_\sigma$, in each iteration of the Newton method we must evaluate $f_2(\tau )$ up to an absolute error of at most $\frac{1}{2}(1-1/\alpha )^2\epsilon ^2$. Indeed, suppose that in the process of evaluation, the oracle $\mathcal {O}_{f_2}\big (\tau , \alpha ^2\big )$ achieves u and l satisfying $\tfrac{1}{2}u^2-\tfrac{1}{2}\ell ^2\le \tfrac{1}{2}(1-1/\alpha )^2\epsilon ^2.$ Then we obtain the inequality

$$\begin{aligned} u-\ell = \sqrt{(u-\ell )^2} \le \sqrt{u^2-\ell ^{2}} \le (1-1/\alpha )\epsilon . \end{aligned}$$

Thus, by the discussion following Definition 2.1, either the whole Newton scheme can now terminate with $f_1(\tau )\le \epsilon$ or we have achieved the relative accuracy $(u-\sigma )/(\ell -\sigma )\le \alpha$ for the oracle.

4 Some problem classes

A wide variety of problems can be treated by the root-finding approach, including sparse optimization, with applications in compressed sensing and sparse recovery, and conic optimization, including semidefinite programming (SDP). The following sections give recipes for applying the root-finding approach in different contexts.

4.1 Conic optimization

The general conic problem (CP) has the form

where ${\mathcal {A}}: E_1 \rightarrow E_2$ is a linear map between Euclidean spaces, and ${\mathcal {K}}\subset E_1$ is a proper, closed, convex cone. The familiar forms of this problem include linear programming (LP), second-order cone programming (SOCP), and semidefinite programming (SDP). Ben-Tal and Nemirovski [5] survey an enormous number of applications and formulations captured by conic programming.

There are at least two possible approaches for applying the level-set framework to this problem. The first approach exchanges the roles of the original objective ${{\langle }c},{x{\rangle }}$ with the linear constraint $Ax=b$, and brings a least-squares term into the objective. The second approach moves the cone constraint $x\in {\mathcal {K}}$ into the objective with the aid of a suitable distance function. This yields two distinct algorithms for the conic problem. The two approaches are summarized in Table 1. Note that it is possible to consider conic problems with the more general constraint $\rho (Ax-b)\le \sigma$, but here we restrict our attention to the simpler affine constraint, which conforms to the standard form of conic optimization.

4.1.1 First approach: least-squares level set

In this section we describe an application of the level-set approach to (CP) that exchanges the roles of the linear functions, and derive the overall complexity guarantees. This approach relies on a simple transformation that guarantees a lower bound on the objective value. To this end, we make the blanket assumption that there is available a strictly feasible vector ${\widehat{y}}$ the dual of (CP)

$$\begin{aligned} \displaystyle \mathop {\hbox {maximize}}_{y} \quad {{\langle }b},{y{\rangle }} \quad \mathop {\hbox {subject to}}\quad c-\mathcal {A}^*y\in {\mathcal {K}}^*. \end{aligned}$$

Thus ${\widehat{y}}$ satisfies ${\widehat{c}}:=c - {\mathcal {A}}^* {\widehat{y}}\in {{\mathrm{int}}}\mathcal {K}^*$. A simple calculation shows that minimizing the new objective ${{\langle }{\widehat{c}}},{x{\rangle }}$ only changes the objective of CP by a constant: for all x feasible for CP, we now have

$$\begin{aligned} {{\langle }{\widehat{c}}},{x{\rangle }}={{\langle }c},{x{\rangle }}-{{\langle }{\mathcal {A}}x},{{\widehat{y}}{\rangle }}={{\langle }c},{x{\rangle }}-{{\langle }b},{{\widehat{y}}{\rangle }}. \end{aligned}$$

In particular, we may assume $b \ne 0$, since otherwise, the origin is the trivial solution for the shifted problem. Note that in the important case $c\in {{\mathrm{int}}}\mathcal {K}$, we can simply set ${\widehat{y}}=0$, which yields the equality $c={\widehat{c}}$.

We now illustrate the computational complexity of applying the root-finding approach to solve (CP) using the level-set problem

$$\begin{aligned} \displaystyle \mathop {\hbox {minimize}}_{x} \quad \Vert {\mathcal {A}}x - b\Vert _2 \quad \mathop {\hbox {subject to}}\quad {{\langle }{\widehat{c}}},{x{\rangle }} \le \tau ,\ x\in {\mathcal {K}}. \end{aligned}$$

(4.1)

Our aim is then to find a root of (1.1), where v is the value function of (4.1). The top row of Table 1, gives the corresponding dual

$$\begin{aligned} \displaystyle \mathop {\hbox {maximize}}_{y,~\,\mu \ge 0} \quad {{\langle }b},{y{\rangle }} - \mu \tau \quad \mathop {\hbox {subject to}}\quad \Vert y\Vert _2\le 1,\ \mu c - {\mathcal {A}}^* y \in \mathcal {K}^* \end{aligned}$$

of the level-set problem. We use $\tau _0=0$ as the initial root-finding iterate. Because of the inclusion ${\widehat{c}}\,\in {{\mathrm{int}}}\mathcal {K}^*$, we deduce that $x=0$ is the only feasible solution to (4.1), which yields $v(0) = \Vert b\Vert _2$ and the exact lower bound $\ell _0=\Vert b\Vert _2$. The corresponding dual certificate is $(\bar{y},\bar{\mu }) = (b/\Vert b\Vert _2, \bar{\mu })$, where

$$\begin{aligned} \bar{\mu }:=\min _\mu \left\{ \mu {\widehat{c}}-(\mathcal {A}^*b)/\Vert b\Vert _2\in {\mathcal {K}}^*\right\} . \end{aligned}$$

(4.2)

Note the inequality $\bar{\mu }>0$, because otherwise we would deduce $\mathcal {A}^*b\in -\mathcal {K}^*$, implying the inequality $\Vert b\Vert ^2_2=\langle b,\mathcal {A}x\rangle =\langle \mathcal {A}^*b, x\rangle \le 0$ for any feasible x. This contradicts our assumption that b is nonzero. In the case where ${\mathcal {K}}$ is the nonnegative orthant and ${\widehat{c}}=e$, the number $\bar{\mu }$ is simply the maximal coordinate of $\mathcal {A}^*b/\Vert b\Vert _2$; if ${\mathcal {K}}$ is the semidefinite cone and ${\widehat{c}}=I$, the number $\bar{\mu }$ is the maximal eigenvalue of $\mathcal {A}^*b/\Vert b\Vert _2$.

Table 1 Least-squares and conic level-set problems for conic optimization

Let OPT denote the optimal value of CP. Theorem 2.3 asserts that within $\mathcal {O}\big (\log _{2/\alpha } 2C/\epsilon \big )$ inexact Newton iterations, where $\alpha$ is the accuracy of each subproblem solve and

$$\begin{aligned} C = \max \left\{ \bar{\mu } \cdot (\text {OPT} - {{\langle }b},{{\widehat{y}}{\rangle }} ),\ \Vert b\Vert _2 \right\} , \end{aligned}$$

the point $x\in \mathcal {K}$ that yields the final upper bound in (4.1) is a super-optimal and $\epsilon$-feasible solution of the shifted CP. Thus, x satisfies

$$\begin{aligned} {{\langle }{\widehat{c}}},{x{\rangle }} \le \hbox {OPT}-{{\langle }{\widehat{y}}},{b{\rangle }} \quad \text{ and }\quad \Vert \mathcal {A}x-b\Vert _2\le \epsilon . \end{aligned}$$

To see how good the obtained point x is for the original CP (without the shift), note that

$$\begin{aligned} {{\langle }{\widehat{c}}},{x{\rangle }} ={{\langle }c},{x{\rangle }} - {{\langle }\mathcal {A}^*{\widehat{y}}},{x{\rangle }}= & {} {{\langle }c},{x{\rangle }} -{{\langle }{\widehat{y}}},{\mathcal {A}x-b{\rangle }} -{{\langle }{\widehat{y}}},{b{\rangle }}\\\ge & {} {{\langle }c},{x{\rangle }}-{{\langle }{\widehat{y}}},{b{\rangle }}-\epsilon \Vert {\widehat{y}}\Vert _2, \end{aligned}$$

and hence $\langle c,x\rangle \le \hbox {OPT}+\epsilon \Vert {\widehat{y}}\Vert _2$. In the important case where $c\in {{\mathrm{int}}}{\mathcal {K}}^*$, we deduce super-optimality $\langle c,x\rangle \le \hbox {OPT}$ for the target problem CP.

Each Newton root-finding iteration requires an approximate solution of (4.1). As described in Sect. 3.1, we obtain this approximation by instead solving its smooth formulation with the squared objective $(1/2)\Vert {\mathcal {A}}x-b\Vert _2^2$. Let $L:=\Vert {\mathcal {A}}\Vert ^2_2$, where $\Vert {\mathcal {A}}\Vert _2$ is the operator norm induced by the Euclidean norms on the spaces $E_1$ and $E_2$, be the Lipschitz constant for the gradient ${\mathcal {A}}^*({\mathcal {A}}\cdot -b)$. Also, let D be the diameter of the region $\{x\mid {{\langle }{\widehat{c}}},{x{\rangle }} = 1,\ x\in {\mathcal {K}}\}$, which is finite by the inclusion ${\widehat{c}}\in {{\mathrm{int}}}{\mathcal {K}}^*$. Thus, in order to evaluate v to an accuracy $\epsilon$, we may apply an accelerated projected-gradient method on the squared version of the problem to an additive error of $\frac{1}{2}(1-1/\alpha )^2\epsilon ^2$ (see end of Sect. 3.1), which terminates in at most

$$\begin{aligned} \mathcal {O}\left( \frac{\sqrt{L} \cdot \tau D}{\epsilon (1-1/\alpha )} \right) = \mathcal {O}\left( \frac{\Vert {\mathcal {A}}\Vert _2\cdot D\cdot \left( \hbox {OPT}-{{\langle }b},{{\widehat{y}}{\rangle }}\right) }{\epsilon (1-1/\alpha )} \right) \end{aligned}$$

iterations [6, §6.2]. Here, we have used the monotonicity of the root finding scheme to conclude $\tau \le \hbox {OPT}-\langle b,{\widehat{y}}\rangle$. When $\mathcal {K}$ is the non-negative orthant, each projection can be accomplished with $\mathcal {O}(n)$ floating point operations [12], while for the semidefinite cone each projection requires an eigenvalue decomposition. More generally, such projections can be quickly found as long as projections onto the cone $\mathcal {K}$ are available; see Remark A.1. An improved complexity bound can be obtained for the oracles in the LP and SDP cases by replacing the Euclidean projection step with a Bregman projection derived from the entropy function; see e.g., Beck and Teboulle [4] or Tseng [51, §3.1]. We leave the details to the reader.

In summary, we can obtain a point $x\in \mathcal {K}$ that satisfies $\langle c,x\rangle \le \hbox {OPT}+\epsilon \Vert {\widehat{y}}\Vert _2$ and $\Vert {\mathcal {A}}x-b\Vert _2\le \epsilon$ in at most

$$\begin{aligned} \mathcal {O}\left( \frac{\Vert A\Vert _2\cdot D\cdot \left( \hbox {OPT}-\langle b,{\widehat{y}}\rangle \right) }{\epsilon (1-1/\alpha )} \right) \cdot \mathcal {O}\left( \log _{2/\alpha } \frac{\max \left\{ \bar{\mu }\cdot \left( \text {OPT}- \langle b,{\widehat{y}}\rangle \right) ,\Vert b\Vert _2 \right\} }{\epsilon } \right) \end{aligned}$$

iterations of an accelerated projected-gradient method, where $\bar{\mu }$ is defined in (4.2).

Fig. 3

Progress of the least-squares level-set method for a linear program (cf. Sect. 4.1.1). The panels on the left depict the graph of $v(\tau )$ (solid line), and the squares and circles, respectively, show the upper and lower bounds computed using an optimal projected-gradient method. The horizontal log scale results in a value function that appears nonconvex. The panels on the right show the number of projected-gradient iterations for each Newton step. Top panels: $\alpha =1.8$. Bottom panels: $\alpha =1.01$

Figure 3 shows the convergence behaviour of this approach applied to a randomly-generated linear program with 256 constraints and 1024 variables.

4.1.2 Second approach: conic level set

Renegar’s recent work [49] on conic optimization inspires a possible second level-set approach based on interchanging the roles of the affine objective and the conic constraint in (CP). A key step is to define a convex function $\kappa$ that is nonnegative on the cone ${\mathcal {K}}$, and positive elsewhere, so that it acts as a surrogate for the conic constraint, i.e.,

$$\begin{aligned} \kappa (x)\le 0 \quad \text{ if } \text{ and } \text{ only } \text{ if }\quad x\in {\mathcal {K}}. \end{aligned}$$

(4.3)

The conic optimization problem can be expressed in entirely functional form as

$$\begin{aligned} \displaystyle \mathop {\hbox {minimize}}_{x} \quad {{\langle }c},{x{\rangle }} \quad \mathop {\hbox {subject to}}\quad {\mathcal {A}}x=b,\ \kappa (x)\le 0, \end{aligned}$$

which allows us to define the level-set function

$$\begin{aligned} v(\tau ) = \inf _x \left\{ \kappa (x) \mid {\mathcal {A}}x=b,\ {{\langle }c},{x{\rangle }} \le \tau \right\} . \end{aligned}$$

(4.4)

Renegar gives a procedure for constructing a suitable surrogate function $\kappa$ under the assumption that ${\mathcal {K}}$ has a nonempty interior: choose a point $e\in {{\mathrm{int}}}{\mathcal {K}}$ and define $\kappa (x)=-\lambda _{\min }(x)$, where

$$\begin{aligned} \lambda _{\min }(x) := \inf \, \{ \lambda \mid x - \lambda e \not \in {\mathcal {K}}\}. \end{aligned}$$

In the case of the PSD cone, we may take $e = I$, and then $\lambda _{\min }$ yields the minimum eigenvalue function. As is shown in [49, Prop. 2.1], the function $\lambda _{\min }$ is Lipschitz continuous (with modulus one) and concave, as would be necessary to apply a subgradient method for minimizing $\kappa$. The dual of the resulting level-set problem, needed to apply the lower affine-minorant root-finding method, is shown in the second row of Table 1, and can be derived using the conjugate of $\lambda _{\min }$; see Lemma A.2.

Renegar derives a novel algorithm along with complexity bounds for CP using the $\lambda _{\min }$ function. A rigorous methodology for applying the level-set scheme, as described in the current paper, requires further research. It is an intriguing research agenda to unify Renegar’s explicit complexity bounds with the proposed level-set approach. It is not clear, however, that this approach holds any practical advantage over the least-squares approach described in Sect. 4.1.1.

The function $\lambda _{\min }$ is only one example of a surrogate function that satisfies (4.3). Other choices are available for $\kappa$ that yield suitable value functions (4.4). The best choice ultimately depends on the algorithms that are available for the inexact solution of the corresponding subproblems. For example, we might choose to define the differentiable surrogate function

$$\begin{aligned} \kappa = \tfrac{1}{2}\hbox {dist}_{\mathcal {K}}^2, \quad \text {where}\ \ \hbox {dist}_{\mathcal {K}}(x):=\inf _{z\in {\mathcal {K}}}\ \Vert x-z \Vert \end{aligned}$$

measures the distance to the cone ${\mathcal {K}}$.

Note the significant differences between the least-squares and conic level-set problems (4.1) and (4.4). For the sake of discussion, suppose that ${\mathcal {K}}$ is the positive semidefinite cone. The least-squares level-set problem has a smooth objective whose gradient can be easily computed by applying the operator ${\mathcal {A}}$ and its adjoint, but the constraint set still contains the explicit cone. Projected-gradient methods, for example, require a full eigenvalue decomposition of the steepest-descent step, while the Frank–Wolfe method requires only a single rightmost eigenpair computation. The latter level-set problem, however, can require a potentially more complex procedure to compute a gradient or subgradient, but has an entirely linear constraint set. In this case, projected (sub)gradient methods require a least-squares solve for the projection step.

Table 2 Nonsmooth regularized data-fitting

4.2 Gauge optimization

We now apply the level-set approach to regularized data-fitting problems, restricting the convex functions $\varphi$ and $\rho$ to be gauges—i.e., functions that are additionally nonnegative, positively homogeneous, and vanish at the origin. We assume that the side constraint $x\in \mathcal {X}$ is absent from the formulation $\mathcal {P}_\sigma$. Problems of this type occur in sparsity optimization; basis pursuit (and its “denoising” variant BP$_\sigma$) [18] was our very first example in Sect. 1. The first two columns of Table 2 describe various formulations of current interest, including basis pursuit denoising (BPDN), low-rank matrix recovery [14, 23], a sharp version of the elastic-net problem [62], and gauge optimization [25] in its standard form. The third column shows the level-set problem $\mathcal {Q}_\tau$ needed to evaluate the value function $v(\tau )$, while the fourth column shows the slopes needed to implement the Newton scheme; cf. 2.3.

The dual representation (2.1) can be specialized for this family, and requires some basic facts regarding a gauge function f and its polar

$$\begin{aligned} f^\circ (y):=\inf \left\{ \mu >0\,\left| \ {{\langle }x},{y{\rangle }} \le \mu f(x) \text{ for } \text{ all } x\right. \right\} . \end{aligned}$$

When f is a norm, the polar $f^\circ$ is simply the familiar dual norm. There is a close relationship between gauges, their polars, and the support functions of their sublevel sets, as described by the identities [25, Prop. 2.1(iv)]

$$\begin{aligned} f^{\circ } = \delta ^{\star }_{[f\le 1]} \quad \hbox {and}\quad f^{\star }=\delta _{[f^{\circ }\le 1]}. \end{aligned}$$

We apply these identities to the quantities involving $\rho$ and $\varphi$ in the expression for the dual representation $\varPhi$ in (2.1), and deduce

$$\begin{aligned} \delta ^{\star }_{[\varphi \le \tau ]} = \tau \delta ^{\star }_{[\varphi \le 1]} = \tau \varphi ^\circ \quad \hbox {and}\quad \rho ^{\star } = \delta _{[\rho ^\circ \le 1]}. \end{aligned}$$

Substitute these into $\varPhi$ to obtain the equivalent expression

$$\begin{aligned} \varPhi (y,\tau ) = {{\langle }b},{y{\rangle }} - \delta _{[\rho ^\circ \le 1]}(-y) - \tau \varphi ^\circ (A^* y). \end{aligned}$$

We can now write an explicit dual for the level-set problem $\mathcal {Q}_\tau$:

$$\begin{aligned} \displaystyle \mathop {\hbox {maximize}}_{y}\quad {{\langle }b},{y{\rangle }}-\tau \varphi ^{\circ }(A^* y) \quad \mathop {\hbox {subject to}}\quad \rho ^{\circ }(-y)\le 1. \end{aligned}$$

In the last three rows of the table, we set $\rho =\Vert \cdot \Vert _2$, which is self polar. For BPDN, $\varphi =\Vert \cdot \Vert _1$, whose polar is the dual norm $\varphi ^\circ =\Vert \cdot \Vert _\infty$. For matrix completion, $\varphi =\Vert \cdot \Vert _*:=\sum _{i=1}^{\min \{m,n\}}\sigma _i(\cdot )$ is the nuclear norm of a n-by-m matrix, which is polar to the spectral norm $\varphi ^\circ = \sigma _1(\cdot )$.

4.3 Low-rank matrix completion

A range of useful applications that involve missing data can be modeled as matrix completion problems. This modeling approach extends to robust principal-component analysis (RPCA), where we decompose a signal into low-rank and sparse components, and its variants, including its stable version, which allows for noisy measurements. Important examples include applications in recommender systems and system identification [47], alignment of occluded images [45], scene triangulation [60], model selection [17], face recognition, and document indexing [13].

These problems can be formulated generally as

$$\begin{aligned} \displaystyle \mathop {\hbox {minimize}}_{X\in \mathbb {R}^{m\times n}}\quad \varphi (X) \quad \mathop {\hbox {subject to}}\quad \rho ({\mathcal {A}}X- b)\le \sigma , \end{aligned}$$

(4.5)

where b is a vector of observations, the linear operator ${\mathcal {A}}$ encodes information about the measurement process, the objective $\varphi$ encourages the low-rank and possibly other structure in the solution, and the constraint $\rho$ measures the misfit between ${\mathcal {A}}X$ and b. If we wish to require ${\mathcal {A}}X=b$, we can simply set $\sigma =0$ and choose any nonnegative convex function $\rho$ that vanishes only at the origin, e.g., the 2-norm.

We categorize the family of low-rank problems into symmetric and asymmetric classes. For each case, we describe a basic formulation and how the level-set approach leads to implementable algorithms with computational kernels that scale well with problem size.

4.3.1 Symmetric problems

The symmetric class of problems aims to recover a low-rank PSD matrix, with a linear operator ${\mathcal {A}}$ that maps between the space of symmetric $n\times n$ matrices and m-vectors. We define the objective of (4.5) by

$$\begin{aligned} \varphi _1(X) = \mathrm {tr}\,(X) + \delta _{\mathcal {S}^n_+}(X). \end{aligned}$$

(4.6)

Problem (4.5) then reduces to finding a PSD matrix with minimum trace that satisfies the constraints $\rho ({\mathcal {A}}X-b)\le \sigma$. It is straightforward to extend this formulation to optimization over Hermitian matrices, so that it includes important applications such as phase retrieval, which aims to recover phase information about a signal (e.g., and image) from a series of magnitute-only measurements [16, 36, 54]. For simplicity, we focus here only on real-valued matrices.

4.3.2 Asymmetric problems

The asymmetric class of matrix-recovery problems does not require definiteness of X. In this case, the linear operator ${\mathcal {A}}$ on $\mathbb {R}^{m\times n}$ is not restricted to symmetric matrices. We define the objective of (4.5) by

$$\begin{aligned} \varphi _2(X) = \left| \left| X \right| \right| _* \end{aligned}$$

(4.7)

This formulation captures matrix completion [46], bi-convex compressed sensing [35], and robust PCA [15, 61].

Example 4.1

(Robust PCA) We give an example of how to a problem that is not in the form of (4.5) can be recast to fit into the required formulation. The stable version of the RPCA problem [57] aims to decompose an m-by-n matrix B as a sum of a low-rank matrix and a sparse matrix via the problem

$$\begin{aligned} \displaystyle \mathop {\hbox {minimize}}_{L,S}\quad \lambda _{\scriptscriptstyle L}\Vert L\Vert _* + \lambda _{\scriptscriptstyle S}\Vert S\Vert _1 + \tfrac{1}{2}\Vert \mathcal {A}[L-B]-S\Vert _F^2. \end{aligned}$$

(4.8)

Here the operator $\mathcal {A}$ is often a mask for the known elements of B. The goal is to obtain a low-rank approximation to Y where the deviation from the known elements of B are sparse. The positive parameters $\lambda _{\scriptscriptstyle L}$ and $\lambda _{\scriptscriptstyle S}$ balance the rank of L against the sparsity of the residual S, and the least-squared misfit.

We show how this model might be recast within the formulation (4.5). The first step is based on the observation that, as a function of S, the objective is the Moreau envelope of the 1-norm evaluated at ${\mathcal {A}}(L-B)$, or equivalently, the Huber function on ${\mathcal {A}}(L-B)$. In particular,

$$\begin{aligned} \inf _S \left\{ \lambda _{\scriptscriptstyle S}\Vert S\Vert _1 + \tfrac{1}{2}\Vert {\mathcal {A}}[L-B]-S\Vert _F^2\right\} = \rho _{\lambda _{\scriptscriptstyle S}} ({\mathcal {A}}[L-B]), \end{aligned}$$

where

$$\begin{aligned} \rho _\alpha (R) = \sum _{i,j} {\left\{ \begin{array}{ll} \tfrac{1}{2}r_{ij}^2 &{} \hbox {if }|r_{ij}|\le \alpha , \\ \alpha (|r_{ij}|-\tfrac{1}{2}\alpha ) &{} \hbox {otherwise,} \end{array}\right. } \end{aligned}$$

is the Huber function. For some nonnegative parameter $\sigma$, we can then reinterpret (4.8) as the problem of finding the lowest-rank approximation to B subject to a bound on a robust measure of misfit. This yields the related problem

$$\begin{aligned} \displaystyle \mathop {\hbox {minimize}}_{L}\quad \left| \left| L \right| \right| _* \quad \mathop {\hbox {subject to}}\quad \rho _{\lambda _{\scriptscriptstyle L}}(\mathcal {A}[L-B]) \le \sigma . \end{aligned}$$

In some contexts, this formulation may be preferable to (4.8) if there is a target level of misfit as measured by the constraint.

4.3.3 Level-set approach and the Frank–Wolfe oracle

We apply the level-set approach to (4.5) and exchange the roles of the regularizing function $\varphi$ and the misfit $\rho ({\mathcal {A}}X-b)$. The objective function $\varphi _1$ for the symmetric case vanishes at the origin, and is convex and positively homogeneous; it is thus a gauge. The second objective function $\varphi _2$ is simply a norm. For both cases, we can use the first row of Table 2 to determine the corresponding level-set subproblem and affine minorants based on dual certificates. The corresponding level-set subproblem $\mathcal {Q}_\tau$, which defines the value function, is

$$\begin{aligned} v(\tau ) := \min _{X}\, \left\{ \rho ({\mathcal {A}}X-b)\,\left| \ \varphi (X) \le \tau \right. \right\} . \end{aligned}$$

We use the polar calculus described by Friedlander et al. [25, §7.2.1] and the definition of the dual norm to obtain the required polar functions

$$\begin{aligned} \varphi _1^\circ (Y) = \max \{0,\ \lambda _1(Y) \} \qquad \text {and}\qquad \varphi _2^\circ (Y) = \sigma _1(Y) \end{aligned}$$

for the symmetric (4.6) and asymmetric (4.7) cases, respectively.

The evaluation of the affine minorant oracle requires an approximate solution of the optimization problem that defines the value function v, and computation of either an extreme eigenvalue or singular value to determine an affine minorant. The Frank–Wolfe algorithm [24, 29] is well suited for evaluating the required quantities, Each iteration of Frank–Wolfe updates the solution estimate via $X^+\leftarrow X + \alpha (\widehat{X}-X)$, where $\alpha$ is a step length, $\widehat{X}$ is a solution of the linearized subproblem

$$\begin{aligned} \displaystyle \mathop {\hbox {maximize}}_{\widehat{X}} \, {{\langle }G},{\widehat{X}{\rangle }} \,\mathop {\hbox {subject to}}\, \varphi (\widehat{X})\le \tau , \end{aligned}$$

(4.9)

and $G:={\mathcal {A}}^*\nabla \rho ({\mathcal {A}}X-b)$ is the gradient of the constraint function evaluated at the current primal iterate X. Note that the steplength in this case is easily obtained as the minimizer of the quadratic objective along the intersection of $[\varphi \le \tau ]$ and the ray $X+\mathbb {R}_+(\widehat{X}-X)$.

Solutions of the subproblem (4.9) depend on the extreme eigenvalues or singular values of G [29, §4.2]. For the symmetric case (4.6), the constraint

$$\begin{aligned} \varphi _1(\widehat{X})=\mathrm {tr}\,(\widehat{X}) + \delta _{\mathcal {S}^n_+}(\widehat{X})\le \tau \quad \hbox {is equivalent to}\quad \mathrm {tr}\,(\widehat{X})\le \tau ,\ \widehat{X}\succeq 0. \end{aligned}$$

For the asymmetric case, the constraint $\varphi _2(\widehat{X})\le \tau$ is simply $\Vert \widehat{X}\Vert _*\le \tau$. The solutions $\widehat{X}_1$ and $\widehat{X}_2$, respectively, of the subproblems (4.9) corresponding to the symmetric and asymmetric cases, have the form

$$\begin{aligned} \begin{aligned} \widehat{X}_1&= U \text{ Diag }\,(\xi _i) U^T, \\ \widehat{X}_2&= U \text{ Diag }\,(\xi _i) V^T, \end{aligned} \qquad \hbox {with}\qquad \sum _{i=1}^{k}\xi _i=\tau ,\ \xi _i\ge 0. \end{aligned}$$

For the symmetric case, the orthonormal n-by-k matrix U collects the k eigenvectors of G corresponding to $\lambda _1(G)$. For the asymmetric case, the m-by-k matrix U and n-by-k matrix V, respectively, collect the k left- and right-singular vectors of G corresponding to the leading singular value $\sigma _1(G)$. In both cases, Krylov-based eigensolvers, such as ARPACK [31] can be used for the required eigenvalue and singular-value computation. If matrix-vector products with the matrix $\mathcal {A}^*y$ and its adjoint are computationally inexpensive, the computation of a few rightmost eigenvalue/eigenvector pairs (resp., maximum singular value/vector pairs) is much cheaper than the computation of the entire spectrum, as required by a method based on projections onto the feasible region. Such circumstances are common, for example when the operator $\mathcal {A}$ is sparse or it is accessible through a fast Fourier transform.

The next example illustrates an application where the operator $\mathcal {A}$ is accessibly only via its action on a matrix. It also gives us an opportunity to describe how the level-set method can be easily adapted to to solve a maximization problem, which requires computing the right-most root to the corresponding value function.

Example 4.2

(Euclidean distance completion) A common problem in distance geometry is the inverse problem: given only local pairwise Euclidean distance measurements among a set of points, recover their location in space. Formally, given a weighted undirected graph $G=(V,E,\omega )$ with a vertex set $V=\{1,\ldots ,n\}$, and a target dimension r, the Euclidean distance completion problem asks to determine a collection of points $p_1,\ldots , p_n$ in $\mathbb {R}^r$ approximately satisfying

$$\begin{aligned} \Vert p_i-p_j\Vert ^2=\omega _{ij} \quad \text {for all edges}\quad ij\in E. \end{aligned}$$

This problem is also often called $\ell _2$ graph embedding and appears in wireless networks, statistics, robotics, protein reconstruction, and manifold learning [34].

A popular convex relaxation for this problem was introduced by Weinberger et al. [55] and extensively studied by a number of authors [8, 21, 27]:

$$\begin{aligned} \displaystyle \mathop {\hbox {maximize}}_{X} \, \mathrm {tr}\,(X) \quad \text{ subject } \text{ to }\quad \begin{aligned} \Vert \mathcal {P}_E\circ \mathcal {K}(X)-\omega \Vert&\le \sigma , \\ Xe=0,\ X&\succeq 0, \end{aligned} \end{aligned}$$

(4.10)

where $\mathcal {K}:\mathcal {S}^n\rightarrow \mathcal {S}^n$ is the mapping $[\mathcal {K}(X)]_{ij}=X_{ii}+X_{jj}-2X_{ij}$ and $\mathcal {P}_E(\cdot )$ is the canonical projection of a matrix onto entries indexed by the edge set E. Indeed, if X is a rank r feasible matrix, we may factor it into $X=PP^T$, where P is an $n\times r$ matrix; the rows of P are the points $p_1,\ldots ,p_n\in \mathbb {R}^r$ we seek. The constraint $Xe=0$ ensures that the points $p_i$ are centered around the origin. Note that this formulation maximizes the trace $\mathrm {tr}\,(X)= \frac{1}{2n}\sum ^n_{i,j=1} \Vert p_i-p_j\Vert ^2$, which helps to “flatten” the realization of the graph.

It is well-known that for $\sigma =0$, the constraints of problem (4.10) do not admit a strictly feasible solution [20, 21, 30]. In particular, for small positive $\sigma$, the feasible region is very thin and the solution to the problem is unstable. As a result, algorithms maintaining feasibility are likely to have difficulties. In contrast, the level-set approach is an infeasible method, and hence the poor conditioning of the underlying problem does not play a major role.

The least-squares level-set problem that corresponds to the minimization formulation of (4.10) is

$$\begin{aligned} \begin{aligned}{}\begin{array}[t]{l@{\quad }l} \mathop {\hbox {minimize}}&{} \Vert \mathcal {P}_E\circ \mathcal {K}(X)-\omega \Vert \\ \mathop {\hbox {subject to}}&{} \mathrm {tr}\,(X)\ge \tau ,\ Xe=0,\ X\succeq 0. \end{array} \end{aligned} \end{aligned}$$

(4.11)

The inequality $\mathrm {tr}\,(X)\ge \tau$ takes into account that the original formulation (4.10) is a maximization problem. As a result, the root-finding method on the value function corresponding to (4.11) approaches the optimal value $\tau _*=\hbox {OPT}$ from the right. To initialize the approximate Newton scheme, we need an upper bound $\tau _0$ on the objective function, which is easily available from the diameter of the graph.

Fig. 4

A plot of the value function $v(\tau )$ of (4.11). Newton’s method converges to either the min- or max-trace solution, depending on initialization. To solve (4.10), we need the maximal root. Here, $\sigma =0.25$, indicated by the solid horizontal line

The gradient of the objective function is as sparse as the edge set E, and the linear subproblem over the feasible region requires computing only a maximal eigenvalue on a sparse matrix [21]. This makes the problem (4.11) ideally suited for the Frank–Wolfe algorithm. The dual problem of (4.11) takes the form

$$\begin{aligned} \displaystyle \mathop {\hbox {maximize}}_{y\in \mathbb {R}^{E},\ \Vert y\Vert _2\le 1} \quad \varPhi (y,\tau ):={{\langle }y},{\omega {\rangle }}-2\tau \lambda ^{e^{\perp }}_1(\text{ Diag }\,(Ye)-Y), \end{aligned}$$

where $\lambda ^{e^{\perp }}_1(A)$ is the maximal eigenvalue of the restriction of the matrix A to the space orthogonal to e, and $Y=\mathcal {P}^*_E(y)$ is diagonal matrix formed from the vector y padded with zeros. The expression of the dual objective follows from the fact that ${\mathcal {K}}^*\mathcal {P}^*_E(y)=2(\text{ Diag }\,(Ye)-Y)$. As described in Sect. 2.4, we use the sequence $\{y_i\}$ of dual certificates generated by the Frank–Wolfe algorithm to establish at iteration k an affine minorant at defined by

$$\begin{aligned} \ell _k = \min _{i=1,\ldots ,k}\varPhi (y_i,\tau ) \quad \text{ and }\quad s_k = 2\lambda _1^{e^\perp }(\text{ Diag }\,(Y_ke)-Y_k) \end{aligned}$$

where $Y_k=\mathcal {P}^*_E(y_k)$. A full derivation and extensive numerical results are given [21]. Figure 4 shows the iterations of Newton’s method applied to this problem.

A Proofs

Proof

(Proof of Theorem 2.1) Since f is convex, the subdifferential $\partial f(\tau )$ is nonempty for all $\tau \in (a,b)$. The claim concerning finite termination is easy to deduce from convexity; we leave the details to the reader. Suppose neither sequence terminates finitely at $\tau _*$. Let us first consider the Newton iteration. Convexity of f immediately implies that the sequence $\tau _i$ is well-defined and satisfies $\tau _0<\tau _1<\tau _2<\dots < \tau _*$. Monotonicity of the subdifferential then implies $g_0\le g_1\le g_2\le \dots \le g_*<0$. Due to the inequalities $f(\tau _*)+\bar{g}(\tau _k-\tau _*)\le f(\tau _k)$ and $g_k<0$, we have

$$\begin{aligned} \frac{f(\tau _k)-f(\tau _*)}{g_k}\le -\frac{g_*}{g_k}(\tau _*-\tau _k), \end{aligned}$$

and so

$$\begin{aligned} 0<\tau _*-\tau _{k+1}= \tau _*-\tau _k+\frac{f(\tau _k)-f(\tau _*)}{g_k} \le \left( 1-\frac{g_*}{g_k}\right) (\tau _*-\tau _k). \end{aligned}$$

Upper semi-continuity of $\partial f$ on its domain implies $g_k\uparrow g_*$. Hence $\tau _k$ converge q-superlinearly to $\tau _*$.

Now consider the secant iteration. As in the Newton iteration, it is immediate from convexity that the sequence $\tau _i$ is well-defined and satisfies $\tau _0<\tau _1<\tau _2<\dots <\tau _*$. Monotonicity of the subdifferential then implies $g_0\le g_1\le g_2\le \dots \le g_*<0$. We have

$$\begin{aligned}0< g_*(\tau _k- \tau _*)\le f(\tau _k)-f(\tau _*),\end{aligned}$$

and $f(\tau _{k-1})+g_{k-1}(\tau _k-\tau _{k-1})\le f(\tau _k)$, and hence

$$\begin{aligned} \frac{\tau _k-\tau _{k-1}}{f(\tau _k)-f(\tau _{k-1})}(f(\tau _k)-f(\tau _*)) \le \frac{f(\tau _k)-f(\tau _*)}{g_{k-1}}<0. \end{aligned}$$

Combining the two inequalities yields

$$\begin{aligned} \frac{f(\tau _k)-f(\tau _*)}{f(\tau _k)-f(\tau _{k-1})}(\tau _k-\tau _{k-1}) \le \frac{f(\tau _k)-f(\tau _*)}{g_{k-1}}\le \frac{g_*}{g_{k-1}}(\tau _k-\tau _*)<0. \end{aligned}$$

Consequently, we deduce

$$\begin{aligned} 0<\tau _* -\tau _{k+1}=\tau _*-\tau _k+ \frac{f(\tau _k)-f(\tau _*)}{f(\tau _k)-f(\tau _{k-1})}(\tau _k-\tau _{k-1}) \le \left( 1-\frac{g_*}{g_{k-1}}\right) (\tau _*-\tau _k). \end{aligned}$$

The result follows. $\square$

Proof

(Proof of Theorem 2.2) It is easy to see by convexity that the iterates $\tau _k$ are strictly increasing and satisfy $f(\tau _k) >0$. For each index $j \ge 2$ for which the algorithm has not terminated, define the following quantities:

$$\begin{aligned} h_{j}:=\tau _j-\tau _{j-1},\quad \quad \theta _j:=\frac{s_{j}}{s_{j-1}},\quad \text { and } \quad \gamma _j:=\frac{\ell _j}{\ell _{j-1}}. \end{aligned}$$

Note that using the equation $\tau _{j-1}-\tau _j = \frac{\ell _{j-1}}{s_{j-1}}$, we can write $\theta _j=\frac{u_{j-1} - \ell _j}{\ell _{j-1}}$. Clearly then the bound, $0\le \theta _j\le \alpha -\gamma _j$, is valid. Define now constants $\beta _j\in [0,1]$ by the equation $\gamma _j = \beta _j \alpha$. Suppose $k \ge 2$ is an index at which the algorithm has not terminated, i.e., $u_k > \epsilon$. Taking into account the inequality $\ell _k \ge \frac{u_k}{\alpha }> \frac{\epsilon }{\alpha }$, we deduce

$$\begin{aligned} \frac{\epsilon }{\alpha } \le \ell _k = \ell _1 \prod _{j=2}^k \gamma _j \le C \alpha ^{k-1} \prod _{j=2}^k \beta _j .\ \end{aligned}$$

(A.1)

The defining equation for $\tau _{k+1}$ and the definition of $\theta _j$ yield the equality

$$\begin{aligned} h_{k+1} = \frac{\ell _k}{|s_k|} = \frac{\ell _k}{|s_1|} \cdot \prod _{j=2}^k \theta _j^{-1}. \end{aligned}$$

The bounds $\tau _* - \tau _1 \ge h_{k+1}$, $\ell _k \ge \frac{\epsilon }{\alpha }$, and $\theta _j \le \alpha - \gamma _j$ imply

$$\begin{aligned} \tau _*-\tau _1 \ge \frac{\ell _k}{|s_1|} \cdot \prod _{j=2}^k \theta _j^{-1} \ge \frac{\epsilon }{\alpha |s_1|} (\alpha ^{-1})^{k-1} \prod _{j=2}^k (1-\beta _j)^{-1}, \end{aligned}$$

and rearranging gives

$$\begin{aligned} \epsilon \le (\tau _*-\tau _1) | s_1 | \alpha ^k \prod _{j=2}^k (1 - \beta _j) \le C \alpha ^k \prod _{j=2}^k (1 - \beta _j). \end{aligned}$$

(A.2)

Combining (A.1) and (A.2), we get

$$\begin{aligned} \epsilon \le C \alpha ^k \min \left\{ \prod _{j=2}^k \beta _j, \ \prod _{j=2}^k (1 - \beta _j) \right\} . \end{aligned}$$

(A.3)

One the other hand, observe

$$\begin{aligned} \left( \prod _{j=2}^k \beta _j\right) \left( \prod _{j=2}^k ( 1- \beta _j)\right) = \prod _{j=2}^k \beta _j( 1- \beta _j) \le 0.5^{2(k-1)}, \end{aligned}$$

and hence

$$\begin{aligned} \min \left\{ \prod _{j=2}^k \beta _j, \ \prod _{j=2}^k (1 - \beta _j) \right\} \le 0.5^{k-1}. \end{aligned}$$

(A.4)

Combining Eqs. (A.4) and (A.3), the claimed estimate $k-1 \le \log _{2/\alpha } \left( \frac{ \alpha C }{ \epsilon } \right)$ follows.

Proof

(Proof of Theorem 2.3) The proof is identical to the proof of Theorem 2.2, except for some minor modifications. The only nontrivial change is how we arrive at the bound $\theta _j \le \alpha - \gamma _j$. For this, observe $\tau _{j-1} - \tau _j = \ell _{j-1}/s_{j-1}$, and because the function $\tau \mapsto \ell _j + s_j ( \tau - \tau _j)$ minorizes f, we see

$$\begin{aligned} u_{j-1}&\ge \ell _j + s_j( \tau _{j-1} - \tau _j ) = \ell _j + s_j \left( \frac{\ell _{j-1}}{s_{j-1}} \right) = \ell _j + \theta _j \ell _{j-1}. \end{aligned}$$

After rearranging, we get the desired upper bound on $\theta _j$:

$$\begin{aligned} \theta _j&\le \frac{u_{j-1} - \ell _j}{\ell _{j-1}} \le \alpha - \gamma _j. \end{aligned}$$

Finally, we remark that with the approximate Newton method, we can start indexing at $j = 0$ instead of $j = 1$. This explains the different constants in the convergence result.

Lemma A.1

(Concavity of the parametric support function) For any convex function $f:\mathbb {R}^n\rightarrow \overline{\mathbb {R}}$ and vector $z\in \mathbb {R}^n$, the univariate function $t\mapsto \delta ^*_{[f\le t]}(z)$ is concave.

Proof

It follows from convexity of f that

$$\begin{aligned} \lambda \cdot [f\le a]+(1-\lambda ) \cdot [f\le b]\subseteq [f\le \lambda a+(1-\lambda ) b] \qquad \forall a,b\in \mathbb {R}\text { and } \lambda \in [0,1], \end{aligned}$$

where $[f\le \alpha ]$ defines the $\alpha$-level set of f, and the summation of the level sets indicates their Minkowski (i.e., direct) sum. Moreover, for any convex sets $\mathcal C$ and $\mathcal D$ such that $\mathcal C\subseteq \mathcal D$, $\delta ^*_{\mathcal C}\le \delta ^*_{\mathcal D}$. Thus,

$$\begin{aligned} \lambda \cdot \delta ^*_{[f\le a]}(z)+(1-\lambda ) \cdot \delta ^*_{[f\le b]}(z)=\delta ^*_{\lambda \cdot [f\le a]+(1-\lambda ) \cdot [f\le b]}(z)\le \delta ^*_{[f\le \lambda a+(1-\lambda ) b]}(z), \end{aligned}$$

which implies concavity of the function at hand..

Proof

(Proof of Proposition 3.1) For this proof only, let $\Vert \cdot \Vert$ denote the 2-norm. Note the inclusion $s/\Vert y\Vert \in \partial _{\tau }\varPhi _1\left( y/\Vert y\Vert ,\,\tau \right)$. Use the same computation from (2.2) to deduce that the affine function

$$\begin{aligned} \tau '\mapsto (\hat{\ell }-\sigma )-\frac{s}{\Vert y\Vert }(\tau '-\tau ) \end{aligned}$$

minorizes $f_1$.

From the definition of $\hat{\ell }$, $\varPhi _1$, and $\varPhi _2$, it follows that

$$\begin{aligned} \begin{aligned} \frac{u-\sigma }{\hat{\ell }-\sigma } = \frac{(u-\sigma )\Vert y\Vert }{\varPhi _2(y,\tau ) + \frac{1}{2}\Vert y\Vert ^2 - \sigma \Vert y\Vert } = \frac{2(u-\sigma )\Vert y\Vert }{\ell ^2 + \Vert y\Vert ^2 - 2\sigma \Vert y\Vert }. \end{aligned} \end{aligned}$$

(A.5)

Taking into account the equivalence

$$\begin{aligned} \frac{u-\sigma }{\ell -\sigma } \le \alpha \quad \iff \quad \frac{u + (\alpha -1)\sigma }{\alpha } \le \ell , \end{aligned}$$

we deduce

$$\begin{aligned} \ell ^2+\Vert y\Vert ^2-2\sigma \Vert y\Vert\ge & {} \alpha ^{-2} \Big ( (u+(\alpha -1)\sigma )^2+\Vert \alpha y\Vert ^2-2\sigma \alpha \Vert \alpha y\Vert \Big )\\\ge & {} 2\alpha ^{-1}(u-\sigma )\Vert y\Vert , \end{aligned}$$

where the rightmost inequality follows from the computation

$$\begin{aligned} \begin{aligned} (u + [\alpha - 1]\sigma )^2&+ \Vert \alpha y\Vert ^2 - 2\alpha \sigma \Vert \alpha y\Vert - 2(u-\sigma )\Vert \alpha y\Vert \\ {}&= \left( u + [\alpha -1]\sigma \right) ^2 + \Vert \alpha y\Vert ^2 - 2\Vert \alpha y\Vert (u + [\alpha -1]\sigma ) \\ {}&= \left( u + [\alpha -1]\sigma - \Vert \alpha y\Vert \right) ^2 \ge 0. \end{aligned} \end{aligned}$$

Because the right-hand side of (A.5) is non-negative, we can deduce that $\hat{\ell }\ge \sigma$. Finally, the required inequality $(u-\sigma )/(\hat{\ell }-\sigma )\le \alpha$ also follows from (A.5).

Lemma A.2

$(-\lambda _{\min })^{\star }(y) = \delta _\mathcal {S}(-y)$, where $\mathcal {S}= {\mathcal {K}}^{*} \cap \left\{ x \mid {{\langle }e},{x{\rangle }} = 1 \right\}$.

Proof

The following formula is established in [49]:

$$\begin{aligned} \partial (-\lambda _{\min }) ( x ) = \left\{ -y \mid {{\langle }y},{e{\rangle }} = 1, \ {{\langle } y},{ z - (x - \lambda _{\min }(x) e ) {\rangle }} \ge 0 \text { for all } z \in \mathcal {K} \right\} \end{aligned}$$

or equivalently

$$\begin{aligned} \partial (-\lambda _{\min }) ( x )&= \left\{ -y \,\left| \ {{\langle }y},{e{\rangle }} = 1, -y\in N_{\mathcal {K}}\left( x - \lambda _{\min }(x) e\right) \right. \right\} \\&= \left\{ -y\,\left| \ {{\langle }y},{e{\rangle }} = 1, \ y \in \mathcal {K}^*, \ 0 = \lambda _{\min }(x) - {{\langle }y},{x{\rangle }} \right. \right\} . \end{aligned}$$

Here the symbol $N_{\mathcal {K}}$ denotes the normal cone to $\mathcal {K}$. Now for any $y\in \partial (-\lambda _{\min }) ( x )$, we have $\langle x,y\rangle =-\lambda _{\min }(x)$. Observe $\mathrm {range}\,\partial (-\lambda _{\min })=-\mathcal {S}$. Hence by the equality in the Fenchel-Young inequality, for any $y\in -\mathcal {S}$, we have $(-\lambda _{\min })^{\star }(y)=0$. On the other hand, for any y with $\langle y,e\rangle \ne -1$, we have $(-\lambda _{\min })^{\star }(y)\ge \langle te,y\rangle -(-\lambda _{\min })(te)=t(\langle y,e\rangle +1)$ for any $t \ge 0$. Letting $t\rightarrow \infty$, we deduce $(-\lambda _{\min })^{\star }(y)=+\infty$. Similarly, consider $y\notin -\mathcal {K}^*$. Then we may find some $x\in \mathcal {K}$ satisfying $\langle x,y\rangle >0$. We deduce $(-\lambda _{\min })^{\star }(y)\ge \langle tx,y\rangle -(-\lambda _{\min })(tx)=t(\langle y,x\rangle -(-\lambda _{\min })(x))$ for any $t \ge 0$. Letting $t\rightarrow \infty$, we deduce $(-\lambda _{\min })^{\star }(y)=+\infty$. We deduce that $(-\lambda _{\min })^{\star }$ is the indicator function of $-\mathcal {S}$, as claimed. $\square$

Remark A.1

(Projection onto a conic slice sets) This remark is standard. Fix a proper convex cone ${\mathcal {K}}$ and consider the projection problem

$$\begin{aligned} \min _{x}\ \left\{ \tfrac{1}{2}\Vert x-z\Vert ^2\,\left| \ \langle c,x\rangle =1,\, x\in \mathcal {K}\right. \right\} . \end{aligned}$$

Equivalently, we can consider the univariate concave maximization problem

$$\begin{aligned} \max _{\beta }\min _{x\in {\mathcal {K}}}\, L(x,\beta )&= \max _{\beta }\min _{x\in {\mathcal {K}}}\, \tfrac{1}{2}\Vert x-z\Vert ^2+\beta (\langle c,x\rangle -1)\\&=\max _{\beta }\min _{x\in {\mathcal {K}}}\, \tfrac{1}{2}\Vert x-(z-\beta c)\Vert ^2+\beta (\langle c,z\rangle -1)-\tfrac{1}{2}\beta ^2\Vert c\Vert ^2\\&=\max _{\beta }~ \tfrac{1}{2}\hbox {dist}^2_{\mathcal {K}}(z-\beta c)+\beta (\langle c,z\rangle -1)-\tfrac{1}{2}\beta ^2\Vert c\Vert ^2. \end{aligned}$$

We can solve this problem for example by bisection, provided projections onto ${\mathcal {K}}$ are available.