1 Introduction

Let \({\mathcal {S}}^n\) denote the vector space of real symmetric \(n\times n\) matrices. The standard inner product on \({\mathcal {S}}^n\) is

$$\begin{aligned} A\bullet B=\mathrm{tr}(AB) =\sum _{i,j}A_{ij}B_{ij} \quad \mathrm{and} \quad \mathrm{tr}(\cdot )=\mathrm{trace}(\cdot ). \end{aligned}$$

By \(X\succeq 0\)\((X \succ 0)\), where \(X \in {\mathcal {S}}^n\), we mean that X is positive semidefinite (positive definite). Consider the following convex semidefinite programming (SDP) problem

$$\begin{aligned} \begin{array}{rcl} \min \limits _{X\in {\mathcal {S}}^n} &{} &{} f(X) \\ \mathrm{s.t.\ } &{} &{}A_k\bullet X= b_k, \ k=1,\dots ,m,\\ &{} &{} X\succeq 0, \end{array} \end{aligned}$$
(P)

where \(f : {\mathcal {S}}^n \rightarrow R\) is convex and continuously differentiable, \(b\in R^m\), and \(A_k\in {\mathcal {S}}^n\), \(k=1,\dots ,m\). As a blanket assumption, we assume that the optimal value for problem (P) is finite and attainable, therefore, we use \(\min \) rather than \(\inf \) in problem (P).

The following notations will be used in our subsequent discussions

$$\begin{aligned}&{R^n_+}=\{x \in R^n| x\ge 0\}, \quad {R^n_{++}}=\{x \in R^n| x > 0 \},\\&{{\mathcal {S}}^n_+}=\{X \in {\mathcal {S}}^n| X\succeq 0\}, \quad {{\mathcal {S}}^n_{++}}=\{X \in {\mathcal {S}}^n| X \succ 0 \},\\&\mathcal{P^+}=\{X \in {\mathcal {S}}^n|A_k\bullet X= b_k, \ k=1,\dots ,m,\ X\succeq 0\},\\&\mathcal{P^{++}}=\{X \in {\mathcal {S}}^n|A_k\bullet X= b_k, \ k=1,\dots ,m, \ X \succ 0 \}. \end{aligned}$$

A comprehensive study of SDP with linear objective function can be found in [35].

There are many interior point algorithms for solving problem (P), for example, [1, 16, 17, 19, 25, 28, 38] for f(X) being linear, [12, 21, 30, 31] for f(X) being convex quadratic, and [36, 37] for general nonlinear semidefinite programming. Some related continuous trajectories were studied for semidefinite programming, for instance, [8, 10, 11, 13, 15]. Most of interior point algorithms are primal–dual path-following algorithms that are extensions of primal–dual path-following algorithm for linear programming (LP). The affine scaling algorithm for LP was originally proposed by Dikin [5], and further discussed by Barnes [2], and Vanderbei et al. [33]. For more details on the development of the affine scaling algorithm, see [7, 20], and the references therein. Unfortunately, the affine scaling algorithm for linear SDP with either the short or the long step version may fail [20], even though the affine scaling continuous trajectory, which is contained in Cauchy trajectories, converges to the optimal solution set of problem (P) [13].

In [20], Muramatsu gave an example of linear SDP such that the affine scaling algorithm converges to a non-optimal point. In that example, for both the short and the long step version of the affine scaling algorithm, there exists a region of starting points such that the generated sequence converges to a non-optimal point. In the concluding remarks of [20], Muramatsu pointed that it may still be possible to prove the global convergence from well-chosen starting points, or by allowing variable step sizes. In this paper, we focus on the second strategy—allowing variable step sizes, and propose a new step size rule which is similar to the Armijo-type rule [3]. Under this new rule of step size, we can prove that starting from any interior feasible point, every accumulation point of the affine scaling algorithm is an optimal solution of problem (P). It should be noted that Renegar and Sondjaja studied a polynomial-time affine scaling method for linear semidefinite and hyperbolic programming in [22], where the method is actually a variant of Dikin’s affine scaling method. The algorithm in [22] shares the similar spirit as Dikin’s method in that at each iteration, the cone in the original optimization problem is replaced by an ellipsoidal cone centered at the current iterate, rather than an ellipsoid as in Dikin’s method. The algorithm differs from Dikin’s method in that at each iteration, the ellipsoidal cone is chosen to contain the original cone rather than to be contained by it.

In Sect. 5, we will consider a special case where X and \(A_i\) (\(i = 1,\ldots ,m\)) are all diagonal in (P) and with a slightly different but less restrictive step size rule. In this special case, problem (P) becomes linearly constrained convex programming which has been studied in [7] in the context of affine scaling algorithms and in [32] through a first-order interior point method, which includes the affine scaling algorithm as a special case. However, to ensure optimality, they both require nondegeneracy assumptions, and the strong convergence of the (first-order) affine scaling algorithm is still open. The line search procedure in [7] is quite general, in order to guarantee optimality, the step size in [32] needs to be bounded. The second-order affine scaling algorithm for linearly constrained convex programming has been studied in [18, 27]. In [27], Sun proved the global convergence at a local linear rate under a Hessian similarity condition of the objective function, and an \(\epsilon \)-optimal solution can be obtained if the step size is in the order of \(O(\epsilon )\) without nondegeneracy assumptions. In [18], Monteiro and Wang studied a version of the second-order affine scaling algorithm in which a fraction of the ellipsoid used at each iteration is selected according to a trust region strategy for linearly constrained convex and concave programs. In the convex case of [18], optimality is obtained under the primal nondegeneracy assumption, and it was shown that the sequences of iterates and objective function values generated by the algorithm converge R-linearly and Q-linearly, respectively, under certain invariance condition on the Hessian of the objective function.

For simplicity, in what follows, we use \(\Vert \cdot \Vert \) to denote either the 2-norm of vector or the spectral norm of matrix, and use \(\Vert \cdot \Vert _F\) to denote the Frobenius norm of matrix. \(x_i\) denotes the ith component of a vector x, and I stands for the identity matrix whose dimension will be clear from the context. \(\mathrm{diag}(x)\) for the vector x denotes the diagonal matrix whose diagonal entries are that of x. For any \(Q\in {{\mathcal {S}}^n}\), \(\lambda _{\min }(Q)\) denotes the smallest eigenvalue of Q.

The definition of the affine scaling direction in linear semidefinite programming can be found in [6] or [20]. In the convex case, the affine scaling direction can be defined similarly. Similar to [20], the affine scaling direction for problem (P) can be obtained by first defining the associated dual estimate. For a point \(X \in \mathcal{P^{++}}\), we define the dual estimate \((u(X), S(X)) \in R^m \times {\mathcal {S}}^n\) as the unique solution of the following optimization problem

$$\begin{aligned} \begin{array}{rcl} \min \limits _{S\in {\mathcal {S}}^n, u\in R^m} &{} &{} \Vert X^{\frac{1}{2}}SX^{\frac{1}{2}}\Vert _F^2 \\ \mathrm{s.t. \ }&{} &{} S + \sum \limits _{i=1}^m u_iA_i = \frac{\partial f}{\partial X}, \end{array} \end{aligned}$$
(1)

where \(X^\frac{1}{2} \in {{\mathcal {S}}^n_{++}}\) is the unique square root matrix of X. Using the KKT condition of problem (1), (u(X), S(X)) can be solved as (see (4) in [20])

$$\begin{aligned} u(X) = G(X)^{-1}p(X), \ \ \ S(X) = \frac{\partial f}{\partial X} - \sum \limits _{i=1}^m u_i(X)A_i, \end{aligned}$$
(2)

where \(G(X) \in {\mathcal {S}}^m\) and \(p(X) \in R^m\) are such that \(G_{ij}(X) = \mathrm{tr}(A_iXA_jX)\) and \(p_j(X) = \mathrm{tr}(A_jX\frac{\partial f}{\partial X}X)\) for \(i, j = 1, 2,\ldots , m\), respectively. Assumption 2 below guarantees that G(X) is invertible (see Proposition 1 in [20]).

Then the affine scaling direction D(X) for problem (P) can be defined as

$$\begin{aligned} D(X) = -\, XS(X)X = -\,X \left( \frac{\partial f}{\partial X} - \sum \limits _{i=1}^m u_i(X)A_i \right) X. \end{aligned}$$
(3)

The rest of this paper is organized as follows. In Sect. 2, we study some properties of the affine scaling direction. In Sect. 3, we propose an affine scaling algorithm with a new step size rule, which is similar to the Armijo-type rule. In Sect. 4, we prove that any accumulation point of the affine scaling algorithm with the new step size rule is an optimal solution of problem (P) for any starting interior feasible point without nondegeneracy assumptions. In Sect. 5, we consider a special case of problem (P) where X and \(A_i\)’s are diagonal. A slightly different step size rule, which is less restrictive, is proposed for the affine scaling algorithm. For any accumulation point of the resulting algorithm, optimality is obtained as well. In Sect. 6, the convergence of our affine scaling algorithm on the counter example in [20] and on some randomly generated linear SDP problems are illustrated. Finally, some concluding remarks are drawn in Sect. 7.

2 Properties of the affine scaling direction

The following assumptions are made throughout this paper.

Assumption 1

\(\mathcal{P^{++}}\) is nonempty.

Assumption 2

The matrix \(\mathcal {A}\) has full row rank m.

Assumption 3

The optimal solution set of problem (P) is nonempty and bounded.

Now we introduce another form of the affine scaling direction D(X) in (3). Firstly we need the following notations.

  • We define the map \(\mathrm{svec}:\ {{\mathcal {S}}^n} \rightarrow R^{n(n+1)/2}\) as

    $$\begin{aligned} \mathrm{svec}(U) := (u_{11}, \sqrt{2}u_{21}, \dots , \sqrt{2}u_{n1}, u_{22}, \sqrt{2}u_{32}, \dots , \sqrt{2}u_{n2}, \dots , u_{nn})^T, \end{aligned}$$

    where \(U \in {\mathcal {S}}^n\) and “T” is the transpose.

  • The symmetrized Kronecker product \(\circledast \) is defined as

    $$\begin{aligned} (G\circledast K)\mathrm{svec}(H)=\frac{1}{2}\mathrm{svec}(KHG^T+GHK^T), \end{aligned}$$

    where \(G, K \in R^{n\times n}\) and \(H\in {\mathcal {S}}^n\). The properties of operator \(\circledast \) can be found in the Appendix of [1, 24].

  • Let matrix \(\mathcal {A}\) be defined as follows

    $$\begin{aligned} \mathcal{A}=\begin{pmatrix} \mathrm{svec}(A_1)^T \\ \vdots \\ \mathrm{svec}(A_m)^T \end{pmatrix} \in R^{m\times {n(n+1)/2}}. \end{aligned}$$

From (2), we can rewrite \(G_{ij}(X)\) and \(p_j(X)\) as \(\mathrm{svec}(A_i)(X\circledast X)\mathrm{svec}(A_j)\) and \(\mathrm{svec}(A_j)(X\circledast X)\mathrm{svec}\left( \frac{\partial f}{\partial X}\right) \), respectively. Therefore, G(X) and p(X) can be denoted as \(\mathcal{{A}}(X\circledast X)\mathcal{{A}}^T\) and \(\mathcal{{A}}(X\circledast X)\mathrm{svec}\left( \frac{\partial f}{\partial X}\right) \), respectively, consequently

$$\begin{aligned} u(X) = (\mathcal{{A}}(X\circledast X)\mathcal{{A}}^T)^{-1}\mathcal{{A}}(X\circledast X)\mathrm{svec}\left( \frac{\partial f}{\partial X}\right) , \end{aligned}$$
(4)

and

$$\begin{aligned} \mathrm{svec}(S(X)) = ( I-P_{\mathcal{{A}}X}(X\circledast X))\mathrm{svec}\left( \frac{\partial f}{\partial X} \right) , \end{aligned}$$
(5)

where we denote \(P_{\mathcal{{A}}X}=\mathcal{{A}}^T(\mathcal{{A}}(X\circledast X)\mathcal{{A}}^T)^{-1}\mathcal{{A}}\) for simplicity. Now we can present another form of the affine scaling direction D(X) as

$$\begin{aligned} \mathrm{svec}(D(X))= -\,\left( I-(X\circledast X)P_{\mathcal{{A}}X}\right) (X\circledast X)\mathrm{svec}\left( \frac{\partial f}{\partial X} \right) . \end{aligned}$$
(6)

Using the above notations, the affine scaling direction in (3) can be also derived from the following optimization problem

$$\begin{aligned} \begin{array}{rcl} \min \limits _{D\in R^{n\times n}} &{} &{} \frac{\partial f}{\partial X}\bullet D \\ \mathrm{s.t.\ } &{} &{}A_k\bullet D= 0, \ k=1,\dots ,m,\\ &{} &{} \Vert X^{-\frac{1}{2}}DX^{-\frac{1}{2}} \Vert _F^2 \le {{\tilde{\beta }}}^2 <1, \end{array} \end{aligned}$$
(7)

where \(X^{-\frac{1}{2}}\) is the inverse of \(X^{\frac{1}{2}}\). In fact, if the current point \(X \in \mathcal{P^{++}}\) is not an optimal solution of problem (P), then by the KKT condition of problem (7), it is not difficult to obtain the solution of problem (7) as

$$\begin{aligned} \mathrm{svec}(D) = -\,\frac{{{\tilde{\beta }}}\left( I-(X\circledast X)P_{\mathcal{{A}}X}\right) (X\circledast X)\mathrm{svec}\left( \frac{\partial f}{\partial X} \right) }{\left\| \left( I-\left( X^{\frac{1}{2}}\circledast X^{\frac{1}{2}}\right) P_{\mathcal{{A}}X}\left( X^{\frac{1}{2}}\circledast X^{\frac{1}{2}}\right) \right) \left( X^{\frac{1}{2}}\circledast X^{\frac{1}{2}}\right) \mathrm{svec}\left( \frac{\partial f}{\partial X} \right) \right\| }, \end{aligned}$$

or equivalently

$$\begin{aligned} D = -\,\frac{{{\tilde{\beta }}}XS(X)X}{\Vert X^{\frac{1}{2}}S(X)X^{\frac{1}{2}} \Vert _F}. \end{aligned}$$

We can see this D and the D(X) in (3) represent the same direction.

For linear SDP, the properties of the affine scaling direction have been discussed in [20]. For convex SDP, these properties can be obtained similarly. The proof of Theorem 1 below can be obtained identically from the proof of Proposition 2 in [20] except replacing matrix C with \(\frac{\partial f}{\partial X}\), hence the proof is omitted.

Theorem 1

We have

$$\begin{aligned} A_i\bullet D(X) = 0, \end{aligned}$$
(8)

for all \(i=1,\ldots ,m\), and

$$\begin{aligned} \frac{\partial f}{\partial X}\bullet D(X) = -\,\Vert X^{\frac{1}{2}}S(X)X^{\frac{1}{2}}\Vert _F^2. \end{aligned}$$
(9)

3 A new step size rule

It has been shown in [20] that the affine scaling algorithm for linear SDP can fail no matter it uses a long step strategy or a short step strategy. Hence here we design a new step size strategy which is similar to the Armijo-type rule [3]. For any initial point \(X_0 \in \mathcal{P^{++}}\), the iterations in the affine scaling algorithm have the form

$$\begin{aligned} X_{k+1} = X_{k} + \alpha ^kD(X_k),\ k=0,1,\ldots , \end{aligned}$$
(10)

where \(\alpha ^k > 0\) is the step size and D(X) is given in (3). In order to state our step size strategy, we first introduce some notations. Let

$$\begin{aligned} \rho (X) = \sup \{ \rho >0 | X + \rho D(X) \succ 0 \}, \end{aligned}$$

for any \(X \in {{\mathcal {S}}^n_{++}}\) and select a positive sequence \(\{ a_i\}_{i=0}^{+\infty }\) such that \(\lim \nolimits _{i\rightarrow +\infty } a_i= 0\) and \(\lim \nolimits _{s\rightarrow +\infty } \sum \nolimits _{i=0}^sa_i = +\,\infty \). For instance, the sequence can be \(\{ \frac{1}{(i+1)^\alpha }\}_{i=0}^{+\infty }\) with \(0<\alpha \le 1\) or \(\{ \frac{1}{\ln (i+2)}\}_{i=0}^{+\infty }\). Then \(\alpha ^k\) in (10) can be defined from the following two steps:

  • Step 1:

    $$\begin{aligned} \alpha _0^k = \min \left\{ \frac{a_k}{\Vert S_kX_k\Vert c(\Vert S_k\Vert )}, \tau \rho (X_k) \right\} >0 , \end{aligned}$$
    (11)

    where \(S_k = S(X_k)\), \(0< \tau < 1 \) is a constant, and c(x) is a scalar function which satisfies \(c_1x \le c(x) \le \max (c_2x, c_3)\), where \(0<c_1 \le c_2\), \(c_3>0\) are constants.

  • Step 2:\(\alpha ^k\) is the largest \(\alpha \in \{ \alpha _0^k \beta ^l \}_{l=0,1,\ldots }\) satisfying

    $$\begin{aligned} f(X_k + \alpha D(X_k)) \le f(X_k) + \sigma \alpha G_k\bullet D(X_k), \end{aligned}$$
    (12)

    where \(G_k = \frac{\partial f}{\partial X}|_{X=X_k}\), \(0< \beta , \ \sigma <1\) are constants.

It should be noticed that in (11) \(S_k\) should be a nonzero matrix. In fact, if \(S_k = 0\), then it is easy to verify that \(X_k\) is actually an optimal solution from the KKT condition, and the iteration should stop, hence we will not consider this trivial case for brevity.

4 Optimality of the affine scaling algorithm

In this section, we will show that the affine scaling algorithm with our step size strategy (12) will succeed without nondegeneracy assumptions. We begin our discussions with the following lemmas.

Lemma 1

(Section 3.1.3, [4]) Suppose f is differentiable (i.e., its gradient \(\nabla f\) exists at each point in domf). Then f is convex if and only if domf is convex and

$$\begin{aligned} f(y) \ge f(x)+\nabla f(x)^T(y-x) \end{aligned}$$
(13)

holds for all x, \(y\in dom f\).

According to [9], a vector \(\beta \) is said to majorize a vector \(\alpha \) if

$$\begin{aligned} \min \left\{ \sum _{j=1}^k \beta _{i_j}: 1\le i_1<\cdots<i_k\le n \right\} \ge \min \left\{ \sum _{j=1}^k \alpha _{i_j}: 1\le i_1<\cdots <i_k\le n \right\} , \end{aligned}$$

for any \(k=1,2,\dots ,n\) with equality for \(k=n\).

Lemma 2

(Theorem 4.3.26, [9]) Let A be Hermitian. Then the vector composed of the diagonal entries of A majorizes the vector composed of the eigenvalues of A.

Lemma 3

The level set \(\mathcal{{F}} = \{ X\in \mathcal{P^+} | f(X) \le f(X_0) \}\) is bounded.

Proof

Let \(\delta _{\mathcal{P^+}}(X)\) be the indicator function of \(\mathcal{P^+}\) which is defined by

$$\begin{aligned} \delta _\mathcal{P^+}(X) = {\left\{ \begin{array}{ll} 0 &{}\quad \text{ if } X\in \mathcal{P^+},\\ +\,\infty &{}\quad \text{ Otherwise }. \end{array}\right. } \end{aligned}$$

Then \(f(X) + \delta _{\mathcal{P^+}}(X)\) is a closed proper convex function, and the optimal solution set of problem (P) can be expressed as

$$\begin{aligned} \{ X\in {\mathcal {S}}^n | f(X) + \delta _{\mathcal{P^+}}(X) \le f^* \}, \end{aligned}$$

where \(f^*\) is the optimal objective value for problem (P). According to Assumption 3, the optimal solution set of problem (P) is nonempty and bounded, hence Corollary 8.7.1 in [23] implies that

$$\begin{aligned} \{ X\in {\mathcal {S}}^n | f(X) + \delta _{\mathcal{P^+}}(X) \le f(X_0) \} = \mathcal{{F}} = \{ X\in \mathcal{P^+} | f(X) \le f(X_0) \} \end{aligned}$$
(14)

is also bounded. \(\square \)

Theorem 2

Let \(\{ X_k \}\) be generated by the affine scaling algorithm (10) with the step size \(\{ \alpha ^k \}\) chosen by (12). Then

  1. (i)

    \(X_k \in \mathcal{P^{++}}\), \(\{ f(X_k) \}\) is nonincreasing, \(\{X_k \}\) and \(\{D(X_k) \}\) are bounded;

  2. (ii)

    every accumulation point of \(\{X_k \}\) is an optimal solution for problem (P).

Proof

Proof of (i). Since \(X_0 \in \mathcal{P^{++}}\) and \(\alpha ^k \le \tau \rho (X_k)\) at each step, by using an induction argument on k, we have that \(X_k \in {{\mathcal {S}}^n_{++}}\) for all k. Moreover, from (8) in Theorem 1 and \(X_0 \in \mathcal{P^{++}}\), we have \(X_k \in \mathcal{P^{++}}\) for all k. Also, since f(X) is continuously differentiable and \(\alpha ^k_0 > 0\), \(0<\sigma <1\) in (12), we know \(\alpha ^k>0\) for all k.

Combining (9) and (12), we have for all k

$$\begin{aligned} f(X_{k+1}) - f(X_k)\le \sigma \alpha ^k G_k\bullet D(X_k) = -\, \sigma \alpha ^k \left\| X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\right\| _F^2 \le 0, \end{aligned}$$
(15)

thus \(\{ f(X_k) \}\) is nonincreasing. Then \(X_k \in \mathcal{{F}}\) for all k. Since the level set \(\mathcal{{F}}\) in (14) is bounded from Lemma 3, we know \(\{X_k \}\) is bounded as well. For \(D(X_k)\), since

$$\begin{aligned} \mathrm{svec}(D(X_k)) = \left( X_k^{\frac{1}{2}}\circledast X_k^{\frac{1}{2}}\right) \mathcal{{P}}_k\left( X_k^{\frac{1}{2}}\circledast X_k^{\frac{1}{2}}\right) G_k, \end{aligned}$$

where \(\mathcal{{P}}_k = I - (X_k^{\frac{1}{2}}\circledast X_k^{\frac{1}{2}})P_{\mathcal{{A}}X_k}(X_k^{\frac{1}{2}}\circledast X_k^{\frac{1}{2}})\) is an idempotent matrix which implies \(\Vert \mathcal{{P}}_k\Vert \le 1\) for all k. Then along with the facts that \(\{X_k \}\) is bounded and f(X) is continuously differentiable, we have \(\{D(X_k) \}\) is also bounded.

Proof of (ii). From (i), we have \(\{X_k \}\) is bounded, hence \(\{X_k \}\) must have at least one accumulation point. Let \({\bar{X}}\) be any accumulation point of \(\{X_k \}\), we will show it is actually an optimal solution for problem (P) by contradiction.

Assume \({\bar{X}}\) is not an optimal solution of problem (P). First, since \(X_k \in \mathcal{P^{++}}\), we have \({\bar{X}} \in \mathcal{P^{+}}\). From Assumption 3, we can choose a point \(X^* \in \mathcal{P^{+}}\) such that \(X^*\) is an optimal solution for problem (P). According to the hypothesis and the fact that \(\{ f(X_k) \}\) is nonincreasing from (i), we have

$$\begin{aligned} f(X_0) \ge f({\bar{X}}) = \lim \limits _{k\rightarrow +\infty } f(X_k) > f(X^*). \end{aligned}$$

Let us define

$$\begin{aligned} {\bar{Y}}=\frac{f({\bar{X}})-f(X^*)}{2(f(X_0)-f(X^*))}X_0+ \left[ 1-\frac{f({\bar{X}})-f(X^*)}{2(f(X_0)-f(X^*))}\right] X^*, \end{aligned}$$

then \({\bar{Y}} \in \mathcal{P^{++}}\). Since f(X) is convex, we have

$$\begin{aligned} f({\bar{Y}})\le & {} \frac{f({\bar{X}})-f(X^*)}{2(f(X_0)-f(X^*))}f(X_0) + \left[ 1-\frac{f({\bar{X}})-f(X^*)}{2(f(X_0)-f(X^*))}\right] f(X^*)\\= & {} \frac{f({\bar{X}})+f(X^*)}{2}. \end{aligned}$$

Let us define

$$\begin{aligned} V(X) = \ln \det X + \mathrm{tr}(X^{-1}{\bar{Y}}), \end{aligned}$$

where \(X \in {{\mathcal {S}}^n_{++}}\). (Remark: The definition of V(x) is inspired by the potential function in Losert and Akin [14].) Then at \(X_k\), we can define a scalar function \(V_k(\alpha )\) as

$$\begin{aligned} V_k(\alpha ) = V(X_k+\alpha D(X_k)), \end{aligned}$$

where \(0\le \alpha \le \alpha ^k_0\). Obviously, \(V_k(0) = V(X_k)\) and \(V_k(\alpha ^k) = V(X_{k+1})\). Moreover,

$$\begin{aligned} \frac{dV_k(\alpha )}{d\alpha }= & {} \mathrm{tr}(X(\alpha )^{-1}D(X_k)) - \mathrm{tr}(X(\alpha )^{-1}{{\bar{Y}}}X(\alpha )^{-1}D(X_k))\\= & {} \mathrm{tr}\left[ (X(\alpha )-{\bar{Y}})X(\alpha )^{-1}D(X_k)X(\alpha )^{-1}\right] \\= & {} \mathrm{tr}\left[ ({\bar{Y}}-X(\alpha ))X(\alpha )^{-1}X_kS_kX_kX(\alpha )^{-1}\right] , \end{aligned}$$

where \(X(\alpha ) = X_k + \alpha D(X_k) = X_k - \alpha X_kS_kX_k\). Notice \(X_k^{-1}X(\alpha ) = I - \alpha S_kX_k\), which implies

$$\begin{aligned} X(\alpha )^{-1}X_k = I + \alpha S_kX_k(I-\alpha S_kX_k)^{-1}, \end{aligned}$$
(16)

hence

$$\begin{aligned} \frac{dV_k(\alpha )}{d\alpha }= & {} \mathrm{tr}\left[ ({\bar{Y}}-X(\alpha ))X(\alpha )^{-1}X_kS_kX_kX(\alpha )^{-1}\right] \\= & {} \mathrm{tr}\left\{ ({\bar{Y}}-X(\alpha ))\left[ I + \alpha S_kX_kW \right] S_k\left[ I + \alpha W^TX_kS_k \right] \right\} \\= & {} \mathrm{tr}\left\{ ({\bar{Y}}-X(\alpha ))\left[ S_k + \alpha S_kX_kWS_k \right] \right\} \\&+\,\mathrm{tr}\left\{ ({\bar{Y}}-X(\alpha ))\left[ \alpha S_kW^TX_kS_k + {\alpha }^2S_kX_kWS_kW^T X_kS_k\right] \right\} , \end{aligned}$$

where \(W = X(\alpha )^{-1}X_k = (I-\alpha S_kX_k)^{-1}\). Next we show that when \(0\le \alpha \le \alpha ^k\), \(\frac{dV_k(\alpha )}{d\alpha }\) is always negative if k is large enough. Since the level set \(\mathcal{{F}}\) in (14) is bounded and f(X) is continuously differentiable, there exist \(M_1, \ M_2 > 0\) such that \(\Vert X\Vert \le M_1\), \(\Vert \frac{\partial f}{\partial X}\Vert \le M_2\) if \(X \in \mathcal{{F}}\). From Theorem 1 and Lemma 1, we have

$$\begin{aligned} \mathrm{tr}(({\bar{Y}} - X_k)S_k)= & {} \mathrm{tr}(({\bar{Y}} - X_k)G_k) \le f({\bar{Y}}) - f(X_k)\\\le & {} f({\bar{Y}}) - f({\bar{X}}) \le \frac{f(X^*)-f({\bar{X}})}{2} < 0, \end{aligned}$$

which implies

$$\begin{aligned} \frac{f({\bar{X}})-f(X^*)}{2} \le \mathrm{tr}((X_k -{\bar{Y}})S_k) \le \Vert X_k -{\bar{Y}}\Vert \cdot \Vert S_k\Vert \le 2M_1\Vert S_k\Vert , \end{aligned}$$

thus

$$\begin{aligned} \Vert S_k\Vert \ge \frac{f({\bar{X}})-f(X^*)}{4M_1}, \end{aligned}$$
(17)

for all k. Then when \(0\le \alpha \le \alpha ^k\) we have

$$\begin{aligned} \mathrm{tr}(({\bar{Y}} - X(\alpha ))S_k)= & {} \mathrm{tr}\left[ ({\bar{Y}} - X_k + \alpha X_kS_kX_k)G_k\right] \\\le & {} \frac{f(X^*)-f({\bar{X}})}{2} + \alpha M_1M_2\Vert S_kX_k\Vert \\\le & {} \frac{f(X^*)-f({\bar{X}})}{2} + M_1M_2\frac{a_k}{c_1\Vert S_k\Vert } \\\le & {} \frac{f(X^*)-f({\bar{X}})}{2} + \frac{4M_1^2M_2a_k}{c_1(f({\bar{X}})-f(X^*))}. \end{aligned}$$

From (16), if \(0< a_k < \frac{c_1(f({\bar{X}})-f(X^*))}{4M_1}\) and \(0\le \alpha \le \alpha ^k\), we have

$$\begin{aligned} \Vert W\Vert \le 1 + \alpha \Vert S_kX_k\Vert \cdot \Vert W\Vert \le 1 + \frac{4M_1a_k}{c_1(f({\bar{X}})-f(X^*))}\Vert W\Vert , \end{aligned}$$

which indicates that

$$\begin{aligned} \Vert W^T\Vert = \Vert W\Vert \le \frac{1}{1-\frac{4M_1a_k}{c_1(f({\bar{X}})-f(X^*))}}. \end{aligned}$$
(18)

Therefore if \(0< a_k < \frac{c_1(f({\bar{X}})-f(X^*))}{4M_1}\) and \(0\le \alpha \le \alpha ^k\), we have

$$\begin{aligned} \frac{dV_k(\alpha )}{d\alpha }\le & {} \frac{f(X^*)-f({\bar{X}})}{2} + \frac{4M_1^2M_2a_k}{c_1(f({\bar{X}})-f(X^*))} + 4\alpha M_1\Vert S_kX_k\Vert \cdot \Vert W\Vert \cdot \Vert S_k\Vert \\&+\, 2\alpha ^2M_1\Vert S_kX_k\Vert ^2\cdot \Vert W\Vert ^2\cdot \Vert S_k\Vert \\\le & {} \frac{f(X^*)-f({\bar{X}})}{2} + \frac{4M_1^2M_2a_k}{c_1(f({\bar{X}})-f(X^*))} + \frac{4M_1a_k\Vert W\Vert }{c_1} + \frac{2M_1a_k^2\Vert W\Vert ^2}{c_1^2\Vert S_k\Vert }, \end{aligned}$$

then from (17), (18), and the fact that \(\lim \nolimits _{k\rightarrow +\infty } a_k= 0\), we know there exists a \(K > 0\) such that for all \(k\ge K\), if \(0\le \alpha \le \alpha ^k\), then \(\frac{dV_k(\alpha )}{d\alpha } < 0\). Especially, we have

$$\begin{aligned} V(X_{k+1}) = V_k(\alpha ^k) < V_k(0) = V(X_k), \end{aligned}$$

for all \(k\ge K\). Hence there exists an \(M_3 \in R\) such that \(V(X_k) \le M_3\) for all k. When \(X \in {{\mathcal {S}}^n_{++}}\), let \(X=Q\Lambda Q^T\) be an eigenvalue decomposition of X, and \(\{\lambda _i\}_{i=1}^n\) be the eigenvalues of X. Then

$$\begin{aligned} V(X) = \ln \det X + \mathrm{tr}\big ( Q{\Lambda }^{-1}Q^T{{\bar{Y}}}\big ) = \sum _{i=1}^n \ln \lambda _i + \mathrm{tr}\big ( {\Lambda }^{-1}Q^T{{\bar{Y}}}Q \big ), \end{aligned}$$

since \({{\bar{Y}}}\in \mathcal{P}^{++}\), we have

$$\begin{aligned} \lambda _{\min }(Q^T{{\bar{Y}}}Q) = \lambda _{\min }({\bar{Y}}) > 0. \end{aligned}$$

Therefore from Lemma 2, we have

$$\begin{aligned} V(X)= & {} \sum _{i=1}^n \ln \lambda _i + \mathrm{tr}({\Lambda }^{-1}Q^T{{\bar{Y}}}Q)\\\ge & {} \sum _{i=1}^n \ln \lambda _i + \sum _{i=1}^n {\lambda _i}^{-1}\lambda _{\min }({\bar{Y}})\\= & {} \sum _{i=1}^n (\ln \lambda _i + {\lambda _i}^{-1}\lambda _{\min }({\bar{Y}}) ). \end{aligned}$$

For each i, \(\ln \lambda _i + {\lambda _i}^{-1}\lambda _{\min }({\bar{Y}}) \ge \ln \lambda _{\min }({\bar{Y}}) + 1\) and \(\lim \nolimits _{\lambda _i \rightarrow 0}[\ln \lambda _i + {\lambda _i}^{-1}\lambda _{\min }({\bar{Y}})] = +\infty \). Thus, by \(V(X_k) \le M_3\) for all k, we know there exists an \(M_4>0\) such that for all k, we have

$$\begin{aligned} \lambda _{\min }(X_k) \ge M_4 > 0. \end{aligned}$$

Let us define

$$\begin{aligned} \mathcal{H} = \{ X\in {{\mathcal {S}}^n_{++}} | \ \lambda _{\min }(X)\ge M_4 \}. \end{aligned}$$

Then for all k, \(X_k \in \mathcal{H} \cap \mathcal{{F}}\) which implies \(\Vert X_k^{-\frac{1}{2}}\Vert \le \frac{1}{\sqrt{M_4}}\). Along with (17), we get for all k,

$$\begin{aligned} \left\| X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\right\| _F \ge \left\| X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\right\| \ge \frac{\Vert S_k\Vert }{\Vert X_k^{-\frac{1}{2}}\Vert ^2} \ge \frac{M_4(f({\bar{X}})-f(X^*))}{4M_1} > 0. \end{aligned}$$
(19)

From (15), (19), and \(\lim \nolimits _{k \rightarrow +\infty } f(X_{k+1})-f(X_k) = 0\), we know \(\lim \nolimits _{k\rightarrow +\infty } \alpha ^k = 0\). Next we show that the index set

$$\begin{aligned} \mathcal{I} = \{ \ k \ | \ \alpha ^k = \alpha _0^k \beta ^l ,\ l\ge 1 \ \text{ in } \ (12) \} \end{aligned}$$

is finite. If not, then we can choose a subsequence \(\{X_k\}_{k\in \mathcal{K}}\) (\(\mathcal{K} \subseteq \{ 0, 1, \ldots \}\)) such that \(\mathcal{K} \subseteq \mathcal{I}\) and \(\lim \nolimits _{k\in \mathcal{K}, \ k\rightarrow +\infty } X_k = {\tilde{X}} \in \mathcal{H} \cap \mathcal{{F}}\). Then for \(k\in \mathcal{K}\), the condition (12) is violated by \(\alpha = \alpha ^k/\beta \), i.e.,

$$\begin{aligned} \frac{f\left( X_k + \frac{\alpha ^k}{\beta }D(X_k)\right) - f(X_k)}{\frac{\alpha ^k}{\beta }} > \sigma G_k \bullet D(X_k). \end{aligned}$$
(20)

Since \(\lim \nolimits _{k\rightarrow +\infty } \alpha ^k = 0\) and f(X) is continuously differentiable, from (20) we have \({\tilde{G}} \bullet D({{\tilde{X}}}) \ge \sigma {\tilde{G}} \bullet D({\tilde{X}})\) where \({\tilde{G}} = \frac{\partial f}{\partial X}|_{X={\tilde{X}}}\), which implies

$$\begin{aligned} -\,\left\| {{\tilde{X}}}^{\frac{1}{2}}S({\tilde{X}}){{\tilde{X}}}^{\frac{1}{2}}\right\| ^2_F = {\tilde{G}} \bullet D({\tilde{X}}) \ge 0, \end{aligned}$$

but this contradicts with (19). Thus the index set \(\mathcal{I}\) is finite and there must exist an \(N_1 > 0\) such that for all \(k\ge N_1\), \(\alpha ^k = \alpha ^k_0\) in (12). From (4), we know \(\Vert u(X)\Vert \) is a continuous function on \(\mathcal{H} \cap \mathcal{{F}}\) which is closed and bounded, thus \(\Vert u(X)\Vert \) will be bounded on \(\mathcal{H} \cap \mathcal{{F}}\). Along with (2) and (17), there exists an \(M_5>0\) such that for all k, \(\Vert S_k\Vert \le M_5\) and

$$\begin{aligned} \frac{c_1(f({\bar{X}})-f(X^*))}{4M_1} \le c(\Vert S_k\Vert ) \le M_5. \end{aligned}$$
(21)

Since \(\lim \nolimits _{k \rightarrow +\infty } a_k = 0\), there exists an \(N_2>0\) such that for all \(k \ge N_2\), we have \(a_k < \frac{\tau c_1 (f({\bar{X}})-f(X^*))}{4M_1}\). Then for \(k\ge N_2\), by using Theorem 1.3.20 in [9] and (21), for \(\alpha = \frac{a_k}{\tau \Vert S_kX_k\Vert c(\Vert S_k\Vert )}\), we have

$$\begin{aligned} \left\| \alpha X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\right\|= & {} \alpha r\left( X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\right) = \alpha r(S_kX_k)\\\le & {} \alpha \Vert S_kX_k\Vert = \frac{a_k}{\tau c(\Vert S_k\Vert )} \le \frac{4M_1a_k}{\tau c_1 (f({\bar{X}})-f(X^*))} < 1, \end{aligned}$$

where r(A) denotes the spectral radius of matrix A, this implies

$$\begin{aligned} X_k + \alpha D(X_k) = X_k^{\frac{1}{2}}\left( I - \alpha X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\right) X_k^{\frac{1}{2}} \in {{\mathcal {S}}^n_{++}}, \end{aligned}$$

therefore \(\alpha \le \rho (X_k)\) and then \(\frac{a_k}{\Vert S_kX_k\Vert c(\Vert S_k\Vert )} \le \tau \rho (X_k)\). Thus for all \(k\ge N_2\), by (21) we have

$$\begin{aligned} \alpha ^k_0 = \frac{a_k}{\Vert S_kX_k\Vert c(\Vert S_k\Vert )} \ge \frac{a_k}{\Vert S_k\Vert \cdot \Vert X_k\Vert c(\Vert S_k\Vert )} \ge \frac{a_k}{M_1M_5^2}. \end{aligned}$$
(22)

Combining (15), (19), and (22), we know for all \(k\ge N_3 = \max (N_1, N_2)\),

$$\begin{aligned} f(X_{k+1}) - f(X_k) \le -\,\sigma \alpha ^k_0 \frac{M_4^2(f({\bar{X}})-f(X^*))^2}{16M_1^2} \le -\,\frac{\sigma M_4^2(f({\bar{X}})-f(X^*))^2}{16M_1^3M_5^2}a_k, \end{aligned}$$

this implies

$$\begin{aligned} f({\bar{X}}) - f(X_{N_3}) \le -\,\frac{\sigma M_4^2(f({\bar{X}})-f(X^*))^2}{16M_1^3M_5^2}\sum \limits _{k\ge N_3}^{+\infty } a_k = -\,\infty , \end{aligned}$$

which is a contradiction. Therefore any accumulation point of \(\{X_k \}\) is an optimal solution for problem (P). \(\square \)

5 A special case of problem (P)

In this section, we consider a special case of problem (P) where X and \(A_i\) (\(i = 1,\ldots ,m\)) are all diagonal. The results of this section are therefore applicable to the linearly constrained convex programming. We will show that in this special case, the step size can be larger in (12) in the sense that the positive sequence \(\{ a_i\}_{i=0}^{+\infty }\) is not required. If \(X = \mathrm{diag}(x)\), where \(x \in R^n_{++}\), then S(X), D(X), and \(\frac{\partial f}{\partial X}\) are all diagonal matrices. Let \(A \in R^{m\times n}\) such that \(A_{ij} = (A_i)_{jj}\) and \(\nabla f \in R^n\) such that \((\nabla f)_i = (\frac{\partial f}{\partial X})_{ii}\). Then from (4), u(X) can be denoted as

$$\begin{aligned} u(X) = (AX^2A^T)^{-1}AX^2\nabla f. \end{aligned}$$
(23)

In this special case, the step size \(\alpha ^k\) is also chosen by (12) but \(\alpha ^k_0\) is defined as

$$\begin{aligned} 0 < \alpha _0^k = \min \left\{ \frac{c_5}{\Vert S_kX_k\Vert ^{c_4}}, \tau \rho (X_k) \right\} , \end{aligned}$$
(24)

where \(0\le c_4<1\), \(c_5>0\) are constants.

Theorem 3

Let \(\{ X_k \}\) be generated by the affine scaling algorithm (10) with the step size \(\{ \alpha ^k \}\) chosen by (12) and (24). Then

  1. (i)

    \(X_k \in \mathcal{P^{++}}\), \(\{ f(X_k) \}\) is nonincreasing, \(\{X_k \}\) and \(\{D(X_k) \}\) are bounded;

  2. (ii)

    \(\lim \nolimits _{k \rightarrow +\infty } \Vert X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\Vert _F = 0\);

  3. (iii)

    every accumulation point of \(\{X_k \}\) is an optimal solution for problem (P).

Proof

Proof of (i). Similar to the proof of (i) in Theorem 2.

Proof of (ii). We prove this by contradiction. Assume \(\lim \nolimits _{k \rightarrow +\infty } \Vert X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\Vert _F = 0\) is not true, then since \(\{X_k \}\), \(\{D(X_k) \}\) are both bounded, there must exist a subsequence \(\{X_k\}_{k\in \mathcal{K}}\) (\(\mathcal{K} \subseteq \{ 0, 1, \ldots \}\)) and an \({{\bar{M}}}_1 > 0\) such that \(\lim \nolimits _{k\in \mathcal{K},\ k \rightarrow +\infty } \Vert X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\Vert _F = {{\bar{M}}}_1\), \(\lim \nolimits _{k\in \mathcal{K},\ k \rightarrow +\infty } X_k = {\hat{X}}\), and \(\lim \nolimits _{k\in \mathcal{K},\ k \rightarrow +\infty } D(X_k) = {\hat{D}}\).

Then from (15) and \(\lim \nolimits _{k\rightarrow +\infty } f(X_{k+1})-f(X_k) = 0\), we know

$$\begin{aligned} \lim \limits _{k\in \mathcal{K},\ k \rightarrow +\infty } \alpha ^k = 0. \end{aligned}$$
(25)

From Lemma 3 and the Remark in Sun [26], we know that if \(x>0\), then every entry of \((AX^{2}A^T)^{-1}AX^{2}\) is bounded, and the bound depends only on A and n. Thus from (23), we know that \(u(X_k)\) is bounded which implies that \(S(X_k)\) is also bounded. Hence there exists an \({{\bar{M}}}_2 > 0\) such that \(\Vert S_kX_k\Vert \le {{\bar{M}}}_2\) for all k. If \(\alpha = \frac{1}{2{{\bar{M}}}_2}\), then

$$\begin{aligned} \left\| \alpha X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\right\| = \alpha \Vert S_kX_k\Vert < 1, \end{aligned}$$

which implies

$$\begin{aligned} X_k + \alpha D(X_k) = X_k^{\frac{1}{2}}\left( I - \alpha X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\right) X_k^{\frac{1}{2}} \in {{\mathcal {S}}^n_{++}}, \end{aligned}$$

therefore \(\rho (X_k) \ge \frac{1}{2{{\bar{M}}}_2}\) for all k. Let \({{\bar{M}}}_3 = \min (\frac{c_5}{{{{\bar{M}}}_2}^{c_4}}, \tau \frac{1}{2{{\bar{M}}}_2})\). Then from (24), we have \(\alpha ^k_0 \ge {{\bar{M}}}_3 > 0\). Hence from (25), we know for all \(k \in \mathcal{K}\) sufficiently large, \(\alpha ^k < \alpha ^k_0\), which implies that condition (12) is violated by \(\alpha = \alpha ^k/\beta \), i.e.,

$$\begin{aligned} \frac{f\left( X_k + \frac{\alpha ^k}{\beta }D(X_k)\right) - f(X_k)}{\frac{\alpha ^k}{\beta }} > \sigma G_k \bullet D(X_k). \end{aligned}$$
(26)

Since \(\lim \nolimits _{k \in \mathcal{K},\ k\rightarrow +\infty } \alpha ^k = 0\) and f(X) is continuously differentiable, from (26) we have \({\hat{G}} \bullet {\hat{D}} \ge \sigma {\hat{G}} \bullet {\hat{D}}\) where \({\hat{G}} = \frac{\partial f}{\partial X}|_{X={\hat{X}}}\), which implies

$$\begin{aligned} {\hat{G}} \bullet {\hat{D}} = 0, \end{aligned}$$

but this contradicts with \(\lim \nolimits _{k\in \mathcal{K},\ k \rightarrow +\infty } \Vert X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\Vert _F = {{\bar{M}}}_1 > 0\). Hence the hypothesis is not true, and \(\lim \nolimits _{k \rightarrow +\infty } \Vert X_k^{\frac{1}{2}}S_kX_k^{\frac{1}{2}}\Vert _F = 0\).

Proof of (iii). Similar to Theorem 2, we also prove this by contradiction. From (ii), we have

$$\begin{aligned} 0\le \lim \inf \limits _{k\rightarrow +\infty } \alpha ^k \Vert S_kX_k\Vert\le & {} \lim \sup \limits _{k\rightarrow +\infty } \alpha ^k \Vert S_kX_k\Vert \\\le & {} \lim \sup \limits _{k\rightarrow +\infty } \alpha ^k_0 \Vert S_kX_k\Vert \le \lim \sup \limits _{k\rightarrow +\infty } c_5 \Vert S_kX_k\Vert ^{1-c_4} =0, \end{aligned}$$

which implies \(\lim \nolimits _{k\rightarrow +\infty }\alpha ^k\Vert S_kX_k\Vert = 0\). Moreover, \(\Vert S_k\Vert \) is also bounded, hence similar to the proof of Theorem 2, we can also get (19) (\(M_1, M_4>0\) may be different), but this contradicts with (ii). Hence every accumulation point of \(\{X_k \}\) is an optimal solution for problem (P). Thus the proof is complete. \(\square \)

6 Numerical experiments

In this section, we provide computational results of our affine scaling algorithm on the counter example in [20] and on some randomly generated linear SDP problems. The algorithm is implemented in Matlab (version 2017a) on a PC, and it should be mentioned that the main goal of this paper is on the theoretical aspect, hence the program is coded only for the demonstration purpose. In our algorithm, for linear SDP, \(\alpha ^k = \alpha _0^k\), and for simplicity, we set \(c_1=c_2=c_3=1\) and \(c(\Vert S_k\Vert ) = \Vert S_k\Vert \) in the following numerical experiments.

The example in [20] is the following SDP problem:

$$\begin{aligned} \min \limits _{X\in {\mathcal {S}}^n} \begin{pmatrix}1 &{} 0\\ 0 &{} 1\end{pmatrix} \bullet X \ \ \mathrm{s.t.\ } \begin{pmatrix}0 &{} 1 \\ 1 &{} 0\end{pmatrix} \bullet X= 2, \ X\succeq 0. \end{aligned}$$
(27)

The equality constraint in problem (27) implies that \(X = \begin{pmatrix} x &{} 1\\ 1 &{} y\end{pmatrix}\) for \(x, y\in R\). In fact, problem (27) has the following equivalent form (see (18) in [20]):

$$\begin{aligned} \min \limits _{x, y\in R} x+y \ \ \mathrm{s.t.\ } x\ge 0, \ \ y\ge 0, \ \ xy\ge 1. \end{aligned}$$
(28)

More details related to problem (27) can be found in Sect. 3 in [20]. From (24)-(26) in [20], we have

$$\begin{aligned} u(X) = \frac{x+y}{xy+1}, \ \ \ S(X) = \begin{pmatrix} 1 &{} -\,u(X) \\ -\,u(X) &{} 1 \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} D(X) = -\,\frac{xy-1}{xy+1}\begin{pmatrix} x^2-1 &{} 0 \\ 0 &{} y^2-1 \end{pmatrix}. \end{aligned}$$

The initial point \((x^0, y^0)\) in [20] is chosen from the set

$$\begin{aligned} \mathcal{{L}} = \{ (x, y) | xy>1, \ x<1, \ y>1 \}, \end{aligned}$$

and in this situation, from Proposition 3 and (32) in [20], we can obtain

$$\begin{aligned} \rho (X) = \frac{xy+1}{xy-1}\cdot \frac{-\,(x+y)+\sqrt{(x+y)^2+4R(x,y)}}{2R(x,y)}, \end{aligned}$$

where \(R(x,y) = \frac{(1-x^2)(y^2-1)}{xy-1}\). In the numerical tests, we also choose the initial point \((x^0, y^0)\) from \(\mathcal{{L}}\). In particular, we choose an \(x^0\) in (0, 1) and set \(\epsilon (x^0) = \frac{1-x^0}{2}\). Finally, we choose a \(y^0>1\) such that

$$\begin{aligned} \sqrt{x^0y^0-1} < \frac{\tau ^2\epsilon (x^0)(1-\epsilon (x^0)-x^0)}{2}. \end{aligned}$$

From Theorem 7 in [20], the limit point of the iterations \(\{(x^k, y^k) \}\) will be contained in the closure of \(\mathcal{{L}}_{\epsilon (x^0)} = \{ (x, y)\in \mathcal{{L}} | x<1-\epsilon (x^0) \}\) if \(\alpha ^k = \tau \rho (X_k)\) at each iteration. In the numerical tests, we set \(a_k = \frac{1}{\sqrt{x^0y^0-1}\cdot \ln (2+k)}\) to make \(a_0\) and \(\rho (X_0)\) have the same magnitude.

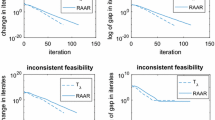
The following two tables list the numerical results of our algorithm for problem (27) with different \(\tau \) values and initial points. The unique solution of problem (28) is (1, 1), and the stopping criterion of the program is \(|x+y-2|<10^{-6}\). \(Iter_{es}\) denotes the iteration number when \((x^k, y^k)\) escaped from \(\mathcal{{L}}_{\epsilon (x^0)}\) the first time, and Iter denotes the total iteration number when the algorithm stopped. We also report the behaviors of the long step affine scaling algorithm in [20]. We set \(\alpha ^k = \tau \rho (X_k)\) at each iteration and use \(x_f\) to denote the value of x after \(10^7\) iterations.

Table 1 Numerical results for problem (27) with \(\tau =0.5\)
Full size table
Table 2 Numerical results for problem (27) with \(\tau =0.9\)
Full size table

From Tables 1 and 2, we can see for the long step affine scaling algorithm where \(\alpha ^k = \tau \rho (X_k)\) at each iteration, the numerical results confirm the findings of Theorem 7 in [20], and even after \(1.0\times 10^7\) iterations, \((x^k, y^k)\) is still contained in \(\mathcal{{L}}_{\epsilon (x^0)}\). However, by adopting our new step size rule, we can obtain the optimal solution within \(10^{-6}\) accuracy successfully in all cases.

Next we report the numerical results of our affine scaling algorithm on some randomly generated linear SDP problems. Let \(C\bullet X\) be the objective function of randomly generated linear SDP. Then each element of C and \(A_i \ (i = 2,\ldots ,m)\) is chosen randomly and uniformly in \([-\,1, 1]\), while \(A_1\) is set at the identity matrix I. Finally, we set \(b_i = A_i\bullet I \ (i=1, \ldots , m)\). In this way, I will be an interior feasible point for problem (P), and we use I as the initial point in our numerical experiments. These randomly generated SDP problems are actually the same as the ones in Section 4.1 of [34].

In our tests, after a linear SDP problem is generated, we firstly use SDPT3 [29] to obtain the optimal objective function value \(f^*\) with the default accuracy tolerance of \(10^{-8}\). Then we run our program from the initial point \(X_0 = I\), and the stopping criterion is set as \(\frac{|f(X_k) - f^*|}{|f^*|+1} < 10^{-6}\). For each (m, n) pair, we run the program for 20 times, and each number reported in Table 3 is the average of 20 runs. In all of our tests, we set \(a_k = \frac{mn}{\ln (k+2)}\) and \(\tau = 0.5\).

Table 3 Numerical results for randomly generated linear SDPs
Full size table

7 Concluding remarks

In this paper, an affine scaling algorithm with a new step size rule for linearly constrained convex semidefinite programming is proposed. It is proven that, starting from any feasible interior point, the accumulation points of the sequence generated by this algorithm are optimal solutions if the optimal solution set is nonempty and bounded. This global convergence does not depend on nondegeneracy assumptions. This confirms our conjecture that by just selecting a suitable step size at each iteration, the affine scaling algorithm can be made convergent even if it is applied to semidefinite programming, which includes linearly constrained convex programming as a special case.

A possible future topic of research is the convergence of the generated sequence, which we call strong convergence. Even in the special case where X is diagonal, as far as we know, the strong convergence of the affine scaling algorithm for convex programming has not been resolved. Tseng et al. [32] showed that for some first-order interior point method, the strong convergence can be obtained for the quadratic case, but not for the affine scaling algorithm. It would be of theoretical interest to know if this is true if we allow more flexibility in selecting the step size or initial points.