On the pervasiveness of difference-convexity in optimization and statistics

Abstract

With the increasing interest in applying the methodology of difference-of-convex (dc) optimization to diverse problems in engineering and statistics, this paper establishes the dc property of many functions in various areas of applications not previously known to be of this class. Motivated by a quadratic programming based recourse function in two-stage stochastic programming, we show that the (optimal) value function of a copositive (thus not necessarily convex) quadratic program is dc on the domain of finiteness of the program when the matrix in the objective function’s quadratic term and the constraint matrix are fixed. The proof of this result is based on a dc decomposition of a piecewise $\hbox {LC}^1$ function (i.e., functions with Lipschitz gradients). Armed with these new results and known properties of dc functions existed in the literature, we show that many composite statistical functions in risk analysis, including the value-at-risk (VaR), conditional value-at-risk (CVaR), optimized certainty equivalent, and the expectation-based, VaR-based, and CVaR-based random deviation functionals are all dc. Adding the known class of dc surrogate sparsity functions that are employed as approximations of the $\ell _0$ function in statistical learning, our work significantly expands the classes of dc functions and positions them for fruitful applications.

1 Introduction

Long before their entry into the field of optimization in the early 1980’s [19, 20, 36, 54], difference-of-convex (dc) functions have been studied extensively in the mathematics literature; the 1959 paper [18] cited a 1950 paper [2] where dc functions were considered. The paper [18] contains a wealth of fundamental results on dc functions that lay the foundation for this class of non-convex functions. While focused on the more general class of “delta-convex functions” in abstract spaces, the thesis [55] contains the very important mixing property of dc functions that in today’s language is directly relevant to the dc property of piecewise functions. The most recent paper [4] adds to this literature of the mathematics of dc functions with a summary of many existing properties of dc functions. As noted in the last paper, the mapping that Nash employed to show the existence of a mixed equilibrium strategy in his celebrated 1951 paper [30] turns out to be defined by dc functions. This provides another evidence of the relevance of dc functions more than half a century ago. In the optimization literature, applications of the dc methodology to nonconvex optimization problems are well documented in the survey papers [23, 24] and in scattered papers by the pair of authors of the latter papers and their collaborators; adding to these surveys, the paper [22] discusses an application of dc programming to the class of linear programs with complementarity constraints; the most recent paper [25] documents many contemporary applied problems in diverse engineering and other disciplines.

Our own interest in dc functions stemmed from the optimization of some physical layer problems in signal processing and communication [1, 3, 34]. Most worthy of note in these references are the following. In [34], a novel class of dc functions was identified and an iterative algorithm was described to compute a directional stationary point of a convex constrained dc program; extensions of the algorithm to dc constraints were also presented. In [1], a unified dc representation was given for a host of surrogate sparsity functions that were employed as approximations of the $\ell _0$ function in statistical learning; such a representation further confirms the fundamental importance of dc functions in the latter subject that is central to today’s field of big-data science and engineering. The paper [33] investigates decomposition methods solving a class of multi-block optimization problems with coupled constraints and partial dc-structure.

The present paper was initially motivated by the desire to understand the dc property of composite risk/deviation functions arising from financial engineering [44,45,46]; see Sect. 2 for a formal definition of these functions. Roughly speaking, these are functions defined as the compositions of some well-known statistical quantities, such as variance, standard deviation, and quantiles, with some random functionals such as the uncertain return of an investment portfolio [42, 43, 47] or the second-stage recourse function [35] in stochastic programming [8, 51]. Initially, we were intrigued by the question of whether the value-at-risk (VaR) functional of a random portfolio return was a dc function of the asset holdings. It turns out that this question already has an affirmative answer given in the paper [57] where a formula linking the VaR and CVaR is obtained. In our work, we provide an alternative expression connecting these two risk quantities that is based on linear programming duality. We also extend our formula to the more general context of the optimized certainty equivalent introduced by Ben-Tal and Teboulle [5, 6] that predates the work of Rockafellar and Uryasev [42, 43]. Our next investigation pertains to a composite risk function involving a recourse function defined by a random quadratic program parameterized by the first-stage decision variable. Our analysis pertains to the general problem where the latter quadratic recourse program is nonconvex. A second contribution of our work is a detailed proof showing that the (optimal) value function of a quadratic program (QP) is dc on the domain of finiteness of the program when the matrix in the objective function’s quadratic term and the constraint matrix are fixed, under the assumption that the former matrix is copositive on the recession cone of the constraint region. Such a copositive assumption is essential because without it the quadratic program is unbounded below on any non-empty feasible set. In turn, the proof of the said dc property of the QP value function is based on an explicit dc decomposition of a piecewise function with Lipschitz gradients that is new by itself. In addition to these specialized results pertaining to statistical optimization and two-stage stochastic programming, we obtain a few general dc results that supplement various known facts in the literature; e.g., the decompositions in part (c) of Lemma 3 and Propositions 5 and 6.

1.1 Significance of the dc property

Besides the mathematical interest, the dc property of a function can be used profitably for the design of convex program based optimization algorithms. Indeed, the backbone of the classical dc algorithm [23, 24, 36] and its recent enhancements [33, 34] is a given dc decomposition of the functions involved in the optimization problem. Such a decomposition provides a convenient convex majorization of the functions that can be used as their surrogates to be optimized [38, 39]. In a nutshell, the benefit of a dc-based iterative algorithm is that it provides a descent algorithm without either a line search or a trust region step; as a result, parallel and/or distributed implementations of such an algorithm can be easily designed without centralized coordination [37, 40, 41, 49, 50] when the given problem has certain partitioned structure. More interestingly, a certain class of dc programs is the only class of nonconvex, nondifferentiable programs for which a directional derivative based stationary point can be computed [34]; such a stationarity concept is the sharpest one among all “first-order” stationarity concepts. In particular, directional stationarity is significantly sharper than the convex-analysis based concept of a critical point of a dc program [23, 24, 36], which is a relaxation of a Clarke stationary point [10] under the dc property. Here sharpness refers to the property that under various first-order stationarity definitions, the corresponding sets of stationary points contain the set of directional stationary points. The papers [1, 9] examine how directional stationarity is instrumental in the characterization of local minimizers of nonconvex and nondifferentiable optimization problems under piecewise linearity and/or second-order conditions.

The dc algorithm and its variants have been employed in many applied contexts; see the recent survey [25]. For many existing applications, the resulting convex programs can be solved very easily; see e.g. [16, 26] in the area of sparse optimization that has attracted much interest in recent years. In general, deciding whether a given nonconvex function is dc is not necessarily an easy task. In situations where a function can be shown to be dc, a dc decomposition offers the first step to design an efficient algorithm by readily providing a convex majorant of the function to be minimized and enabling the investigation and computation of sharp stationary solutions. A novel case in point is the family of nonconvex, nondifferentiable composite programs arising from piecewise affine statistical regression and multi-layer neural networks with piecewise affine activation functions. For these applied problems, the convex subprograms are not straightforward to be solved; nevertheless, they are amenable to efficient solution by a semi-smooth Newton method [13, Section 7.5]. Details of this dc approach to the numerical solution of these advanced statistical learning problems can be found in the most recent Ref. [11].

In summary, a dc decomposition offers both a computational venue and a theoretical framework for the understanding and numerical solution of nonconvex nondifferentiable optimization problems. In this paper we collect in one place many nonconvex functions that are not previously known to be of the dc kind and establish their dc property. These function arise from 3 different areas: (a) composite risk functionals, (b) statistical estimation and learning, and (c) quadratic recourse in stochastic programming. Further study of how the dc property of these functions can benefit algorithmic design for solving the optimization problems involving these functions is beyond the scope of this paper. As word of caution: the obtained dc decompositions for the functions studied in this paper may not be the most conducive for numerical use; nevertheless, they offer a formal demonstration of the dc property of the functions that are not previously known to have this property.

1.2 Organization of the paper

In the next section, we introduce several classes of composite risk and statistical functions to be studied subsequently. These include the renowned Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR) [42, 43], their extensions to a utility based Optimized Certainty Equivalent (OCE) [5,6,7], and maximum likelihood functions (Sect. 2.2) derived from one-parameter exponential densities composite with a statistical estimation model. In Sect. 3, we give proofs of the difference-convexity of the composite risk and statistical functions, providing in particular an alternative expression connecting the VaR with the CVaR in Sect. 3.1 that is extended to the OCE in Sect. 3.2. Section 3.3 deals with the composite statistical functions such as the variance, standard deviations and certain composite density functions. Section 4 shows that the optimal objective value of a copositive quadratic program for a fixed constraint matrix is a dc function of the linear term of the objective and the right-hand side of the constraints; such a value function arises as the recourse of a two-stage stochastic program with the copositivity assumption generalizing the positive semi-definiteness of the quadratic form and making the objective function nonconvex in general. Specialized to a linear program, this dc property is a new result in the vast literature of linear programming theory and provides a first step in expanding the two-stage stochastic programming domain beyond the much focused paradigm of linear recourse. Lastly in Sect. 5 we give a necessary and sufficient condition for a univariate folded concave function to be dc. Such a function provides a unification of all the surrogate sparsity functions that have a fundamental role to play in nonconvex sparsity optimization.

2 Composite risk and statistical functions

For a given scalar $\lambda > 0$ and decision variable $x \in \mathbb {R}^n$, consider the function

$$\begin{aligned} {\mathcal {R}}_{\lambda }(x) \, \triangleq \, \mathbb {E}{\mathcal {Z}}(x;\widetilde{\omega }) + \lambda \, {\mathcal {D}}\left[ {\mathcal {Z}}(x;\widetilde{\omega }) \right] \end{aligned}$$

where $\mathbb {E}$ is the expectation operator with respect to the random variable $\widetilde{\omega }$ defined on the probability space $(\Omega ,{\mathcal {F}}, \mathbb {P})$, with $\Omega$ being the sample space, ${\mathcal {F}}$ being the $\sigma$-algebra generated by subsets of $\Omega$, and $\mathbb {P}$ being a probability measure defined on ${\mathcal {F}}$; $\lambda > 0$ is a given parameter that balances the expectation (for risk neutrality) and the deviation measure ${\mathcal {D}}$ (representing risk aversion); for a random variable ${\mathcal {Z}}$, ${\mathcal {D}}( {\mathcal {Z}} )$ is a expectation-based, CVaR-based, or VaR-based deviation measure:

	Expectation based	(C)VaR based
$\bullet$ Variance:	$\sigma ^2({\mathcal {Z}}) \triangleq \mathbb {E}\left[ \, {\mathcal {Z}} - \mathbb {E}{\mathcal {Z}} \, \right] ^2$	$\mathbb {E}\left[ \, {\mathcal {Z}} - \text{(C)VaR }({\mathcal {Z}}) \, \right] ^2$
$\bullet$ Standard deviation:	$\sigma ({\mathcal {Z}}) \triangleq \sqrt{\sigma ^2({\mathcal {Z}})}$	$\sqrt{\mathbb {E}\left[ \, {\mathcal {Z}} - \text{(C)VaR }({\mathcal {Z}}) \, \right] ^2}$
$\bullet$ Absolute semi-deviation (ASD):	$\text{ ASD }({\mathcal {Z}}) \triangleq \mathbb {E}\left[ {\mathcal {Z}} - \mathbb {E}{\mathcal {Z}} \right] _+$	$\mathbb {E}\left[ {\mathcal {Z}} - \text{(C)VaR }({\mathcal {Z}}) \right] _+$
$\bullet$ Absolute deviation (AD):	$\text{ AD }({\mathcal {Z}}) \triangleq \mathbb {E}\left| \, {\mathcal {Z}} - \mathbb {E}{\mathcal {Z}} \, \right|$	$\mathbb {E}\left| \, {\mathcal {Z}} - \text{(C)VaR }({\mathcal {Z}}) \, \right|$

where $[ \bullet ]_+ \triangleq \max ( 0, \bullet )$, and the expressions of $\text{ CVaR }_{\alpha }(\bullet )$ and $\text{ VaR }_{\alpha }(\bullet )$ are as follows:

$$\begin{aligned} \begin{array}{lll} \text{ CVaR }_{\alpha }({\mathcal {Z}}) &{} = &{} \displaystyle { \mathop {\text{ minimum }}\limits _{t \in \mathbb {R}} } \, \left[ \, t + \displaystyle { \frac{1}{1 - \alpha } } \, \mathbb {E}\left[ \, {\mathcal {Z}} - t \, \right] _+ \, \right] \\ \text{ VaR }_{\alpha }({\mathcal {Z}}) &{} = &{} \text{ minimum }\left\{ \, t^{\, \prime } \, \mid \, t^{\, \prime } \, \in \displaystyle { \mathop {\text{ argmin }}\limits _{t \in \mathbb {R}} } \, \left[ \, t + \displaystyle { \frac{1}{1 - \alpha } } \, \mathbb {E}\left[ \, {\mathcal {Z}} - t \, \right] _+ \, \right] \, \right\} . \end{array} \end{aligned}$$

The case where ${\mathcal {D}}({\mathcal {Z}})$ is itself $\text{ CVaR }_{\alpha }({\mathcal {Z}})$ or $\text{ VaR }_{\alpha }({\mathcal {Z}})$ is also covered by our analysis. Unlike the equality $\text{ AD }({\mathcal {Z}}) = 2\text{ ASD }({\mathcal {Z}})$, it is in general not true that $\mathbb {E}\left| {\mathcal {Z}} - \text{ CVaR }_{\alpha }({\mathcal {Z}}) \right| = 2 \mathbb {E}\left[ {\mathcal {Z}} - \text{ CVaR }_{\alpha }({\mathcal {Z}}) \right] _+$. For a recent survey on the connection between risk functions and deviation measures and their applications in risk management and statistical estimation, see [44].

Admittedly, the (C)Var-based deviation measure is a non-traditional quantity that is not commonly employed in risk analysis. Nevertheless, as a quantile of a random variable that includes for instance the median as a special case, we feel that it is important to consider the deviation from such a fundamental statistical quantity and understand its generalized convexity properties (if applicable) when its optimization is called for. The resulting deviations are the analogs of the classical variance family of deviations that are based on the mean of the random variable.

Extending the (C)VaR, the Optimized Certainty Equivalent (OCE) of a random variable is defined by a proper, concave, non-decreasing, lower semi-continuous utility function $u : \mathbb {R} \rightarrow [ \, -\infty , \, \infty \, )$ with a non-empty effective domain $\text{ dom }(u) \triangleq \left\{ \, t \in \mathbb {R} \mid u(t) > -\infty \, \right\}$ such that $u(0) = 0$ and $1 \in \partial u(0)$, where $\partial u$ denotes the subdifferential map of u. Thus in particular,

$$\begin{aligned} \begin{array}{ll} u(t) \ge 0, &{}\quad \forall \, t \ge 0, \quad \text{ and } \\ u(t) \le t, &{}\quad \forall \, t \in \mathbb {R}. \end{array} \end{aligned}$$

Let ${\mathcal {U}}$ be the family of these univariate utility functions. For an essentially bounded random variable ${\mathcal {Z}}$ satisfying $\sup _{\omega \in \Omega } \, | \, {\mathcal {Z}}(\omega ) \, | \, < \, \infty$, the optimized certainty equivalent (OCE) of ${\mathcal {Z}}$ with respect to a utility function $u \in {\mathcal {U}}$ is defined as

$$\begin{aligned} {\mathcal {O}}_u({\mathcal {Z}}) \, \triangleq \, \displaystyle { \sup _{\eta \in \mathbb {R}} } \, \left[ \, \eta + \mathbb {E}u( {\mathcal {Z}} - \eta ) \, \right] . \end{aligned}$$

The choice of $u(t) \triangleq \frac{1}{1 - \alpha } \, \min (0,t)$ yields ${\mathcal {O}}_u({\mathcal {Z}}) = -\text{ CVaR }_{\alpha }(-{\mathcal {Z}})$. Proposition 2.1 in [7] shows that for a random variable ${\mathcal {Z}}$ whose support is a compact interval, then the supremum in ${\mathcal {O}}_u({\mathcal {Z}})$ is attained; in this case, we may consider the largest such maximizer,

$$\begin{aligned} m_u({\mathcal {Z}}) \, \triangleq \, \max \left\{ \, \eta ^{\, \prime } \, \mid \, \eta ^{\, \prime } \, \in \displaystyle { \mathop {\text{ argmax }}\limits _{\eta \in \mathbb {R}} } \, \left[ \, \eta + \mathbb {E}u( {\mathcal {Z}} - \eta ) \, \right] \, \right\} , \end{aligned}$$

which is the utility-based extension of VaR that pertains to a given choice of u. As explained in [7], the deterministic quantity $m_u({\mathcal {Z}})$ can be interpreted as the largest optimal allocation between present and future consumption if ${\mathcal {Z}}$ represents an uncertain income of ${\mathcal {Z}}$ dollars, largest as a way to break ties among multiple optimal allocations if such allocation is not unique.

2.1 Quadratic recourse function

Besides the bilinear ${\mathcal {Z}}(x;\omega ) = x^T\omega$ that is quite common in portfolio management with $\omega$ representing the uncertain asset returns and x the holdings of the assets, we shall treat carefully a quadratic recourse function given by

$$\begin{aligned} \begin{array}{llll} \psi (x;\omega ) &{} \triangleq &{} \displaystyle { \mathop {\text{ minimum }}\limits _{z}} &{} \left[ \, f(\omega ) + G(\omega )x \, \right] ^Tz + {\textstyle {\frac{1}{2}}}\, z^TQz\\ &{} &{} \text{ subject } \text{ to } &{} C(\omega )x + Dz \, \ge \, \xi (\omega ), \end{array} \end{aligned}$$

(1)

where $Q \in \mathbb {R}^{m \times m}$ is a symmetric, albeit not necessarily positive or negative semi-definite, matrix; D is a $k \times m$ matrix, $f : \Omega \rightarrow \mathbb {R}^m$ and $\xi : \Omega \rightarrow \mathbb {R}^k$ are vector-valued random functions, and $G : \Omega \rightarrow \mathbb {R}^{m \times n}$ and $C : \Omega \rightarrow \mathbb {R}^{k \times n}$ are matrix-valued random functions. Besides the main dc result of the composite function ${\mathcal {R}}_{\lambda }(x)$, the proof that the value function $\psi (\bullet ;\omega )$ is dc on its domain of finiteness is a major contribution of this work that is of independent interest. This result will be discussed in detail in Sect. 4. There are several noteworthy points of our analysis: (a) the matrix Q is not required to be positive semi-definite; thus we allow our recourse function to be derived from an indefinite quadratic program; (b) the first-stage variable x appears in both the objective function and the constraint; this is distinguished from much of the stochastic (linear) programming literature where x appears only in the constraint; and (c) it follows from our result that the value function of a linear program:

$$\begin{aligned} \begin{array}{cccl} \varphi (b,c) &{} \triangleq &{} \displaystyle { \mathop {\text{ minimum }}\limits _{z} } &{} c^Tz \\ &{} &{} \text{ subject } \text{ to } &{} Az \, = \, b \quad \text{ and } \quad z \ge 0, \end{array} \end{aligned}$$

is a dc function on its domain of finiteness. This is a new result by itself because existing results in parametric linear programming deal only with the concavity/convexity of $\varphi (b,c)$ when b (c respectively) is fixed; there does not exist a (non-)convexity analysis of the optimal objective value as a function jointly of b and c.

Like the deviations from the (C)VaR, recourse-function based deviations are not common in the stochastic programming literature. Part of the reason for this lack of attention might be due to the computational challenge of dealing with the recourse function itself, which is further complicated when coupled with the statistical functions, such as variances, standard deviations, or semi-deviations. Hopefully, understanding the structural properties of the composite recourse-based deviations could open a path for solving the advanced stochastic programs for risk-averse players who might be interested in reducing their risk exposure of deviation from the second-stage decisions. In such a situation, the composite deviations would provided a reasonable measure of the risk to be reduced.

In the analysis of the value function $\psi (\bullet ;\omega )$, we are led to a detailed study of the dc property of piecewise functions. Specifically, a continuous function $\theta$ defined on an open set ${\mathcal {O}} \subseteq \mathbb {R}^n$ is piecewise C$^k$ [13, Definition 4.5.1] for an integer $k \ge 0$ if there exist finitely many C$^k$ functions $\{ \theta _i\}_{i=1}^I$ for some integer $I > 0$, all defined on ${\mathcal {O}}$, such that $\theta (x) \in \{ \theta _i(x) \}_{i=1}^I$ for all $x \in {\mathcal {O}}$. A major focus of our work is the case of a piecewise quadratic (PQ) $\theta$, which has each $\theta _i$ being a (possibly nonconvex) quadratic function. It is a well-known fact that a general quadratic function must be dc; subsequently, we extend this fact to a piecewise quadratic function with an explicit dc representation in terms of the pieces. While our analysis relies on several basic results of dc functions that can be found in [4, 18] (see also [53, Chapter 4]), we also discover a number of new results concerning PQ functions that are of independent interest. Summarized below, these results are the pre-requisites to establish the dc property of the composite-risk functions with quadratic recourse.

• The optimal objective value of the quadratic program (QP):

  $$\begin{aligned} \begin{array}{lll} \text{ qp }_{\mathrm{opt}}(q,b) \, \triangleq &{} \quad \displaystyle { \mathop {\text{ minimum }}\limits _{z} } &{} \zeta (z) \, \triangleq \, q^Tz + {\textstyle {\frac{1}{2}}}\, z^TQz\\ &{}\quad \text{ subject } \text{ to } &{} z \, \in \, {\mathcal {P}}_D(b) \, \triangleq \, \left\{ \, z \, \in \, \mathbb {R}^m \, \mid \, Dz \, \ge \, b \, \right\} , \end{array} \end{aligned}$$

  (2)

  is a dc function of (q, b) on the domain $\text{ dom }(Q,D) \triangleq \left\{ ( q,b ) \in \mathbb {R}^{m+k} \mid -\infty<\right. \left. \text{ qp }_{\mathrm{opt}}(q,b) < \infty \right\}$ of finiteness of the problem, for a fixed pair (Q, D) with Q being a symmetric matrix that is copositive on the recession cone of the feasible region ${\mathcal {P}}_D(b)$; i.e., provided that $v^TQv \ge 0$ for all $v \in D_{\infty } \triangleq \left\{ v \in \mathbb {R}^m \mid Dv \ge 0 \right\}$. We let $\text{ qp }_{\mathrm{sol}}(q,b)$ denote the optimal solution set of (2), which is empty for $(q,b) \not \in \text{ dom }(Q,D)$. It turns out that the analysis of (2) in such a copositive case is not straightforward and uses significant background about the problem and polyhedral theory.

• Motivated by the value function $\text{ qp }_{\mathrm{opt}}(q,b)$, we obtain an explicit min–max (dc) representation of a general (not necessarily convex) piecewise quadratic function with given pieces, extending the work [52] that studies the special case when such a function is convex and also the max–min representation of a piecewise linear function [32, 48], as well as the so-called mixing property of dc functions [55, Lemma 4.8] on open convex sets extended to the family of PQ functions whose domains are closed sets.

2.2 One-parameter exponential densities

A random variable Y belongs to a one-parameter exponential family if its density (or mass) function can be written in the form

$$\begin{aligned} g(y;\theta ) \, = \, a(y) \exp \left\{ \, y \theta - b(\theta ) \, \right\} , \end{aligned}$$

where $\theta$ is the canonical parameter, and a and b are given functions with b being convex and increasing. In the presence of covariates X, we model the conditional distribution of $Y|X = x$ as a one-parameter exponential family member with parameter $\theta = m(x;\Theta )$ that depends on the realization x of Y|X and where $m(\bullet ;\Theta )$ is a parametric statistical (e.g. linear) model with the parameter $\Theta \in \mathbb {R}^n$ in the latter model being computed by maximzing the expected log-likelihood function $\mathbb {E}_{Y|X}\left[ \, \log g(y;m(x;\Theta )) \, \right]$. When discretized with respect to the given data $\{ (y_s;x^s) \}_{s=1}^N$, the latter optimization problem is equivalent to

$$\begin{aligned} \displaystyle { \mathop {\text{ maximize }}\limits _{\Theta } } \, \displaystyle { \frac{1}{N} } \displaystyle { \sum _{s=1}^N } \, \left[ \ y_s \, m(x^s;\Theta ) - b \circ m(x^s;\Theta ) \, \right] . \end{aligned}$$

In the recent paper [17], a piecewise affine statistical estimation model was proposed with $m(\bullet ;\Theta )$ being a piecewise affine function. Per the representation results of [48, 52], every such function can be expressed as the difference of two convex piecewise affine functions, and is thus dc. This motivates us to ask the question of whether the composite function $b \circ m(\bullet ;\Theta )$ is dc, and more generally, if $\mathbb {E}\log f(\Theta ;\widetilde{\omega })$ is dc if $f(\bullet ;\omega )$ is dc for each $\omega \in \Omega$.

3 Proof of difference-convexity

We show that if the random function ${\mathcal {Z}}(x;\omega ) = p(x,\omega ) - q(x,\omega )$ where $p(\bullet ,\omega )$ and $q(\bullet ,\omega )$ are both convex functions on a domain ${\mathcal {D}}$ for every fixed $\omega \in \Omega$, then all the expectation based and (C)VaR based risk measures ${\mathcal {R}}_{\lambda }(x)$ are dc on ${\mathcal {D}}$, so are the OCE extensions ${\mathcal {O}}_u({\mathcal {Z}}(x;\widetilde{\omega }))$ and $m_u({\mathcal {Z}}(x;\widetilde{\omega }))$ with a piecewise linear utility function u. In turn, it suffices to show that the following functions are dc with ${\mathcal {Z}} = {\mathcal {Z}}(x;\widetilde{\omega })$:

• $\text{ CVaR }_{\alpha }({\mathcal {Z}})$ and $\text{ VaR }_{\alpha }({\mathcal {Z}})$;

• the OCE extensions ${\mathcal {O}}_u({\mathcal {Z}})$ and $m_u({\mathcal {Z}})$ with a piecewise linear utility function u;

• $\sigma ^2({\mathcal {Z}})$ and $\sigma ({\mathcal {Z}})$.

Once these are shown, using known properties of dc functions (such as the nonnegative part of a dc function is dc), we can readily establish the dc-property of the following functions and also yield their dc decompositions:

• $\text{ ASD }({\mathcal {Z}}) = {\textstyle {\frac{1}{2}}}\text{ AD }({\mathcal {Z}})$;

• $\mathbb {E}\left[ {\mathcal {Z}} - \text{(C)VaR }_{\alpha }({\mathcal {Z}}) \right] ^2$ and $\sqrt{\mathbb {E}\left[ {\mathcal {Z}} - \text{(C)VaR }_{\alpha }({\mathcal {Z}}) \right] ^2}$; and

• $\mathbb {E}\left[ {\mathcal {Z}} - \text{(C)VaR }_{\alpha }({\mathcal {Z}}) \right] _+$ and $\mathbb {E}\left| {\mathcal {Z}} - \text{(C)VaR }_{\alpha }({\mathcal {Z}}) \right|$.

Among the former three families of composite functions, the proof of $\text{ VaR }_{\alpha }({\mathcal {Z}}(x;\widetilde{\omega }))$, $m_u({\mathcal {Z}}(x;\widetilde{\omega }))$, $\sigma ({\mathcal {Z}}(x;\widetilde{\omega }))$ requires the random variable $\widetilde{\omega }$ to be discretely distributed.

3.1 CVaR and VaR

The following result shows that $\text{ CVaR }_{\alpha }(f(x,\widetilde{\omega }))$ is a dc function if $f(\cdot ,\omega )$ is dc for fixed realization $\omega$.

Proposition 1

For every $\omega \in \Omega$, let $f(x,\widetilde{\omega }) = p(x,\widetilde{\omega }) - q(x,\widetilde{\omega })$ be the dc decomposition of $f(\bullet ,\omega )$ on a convex set ${\mathcal {D}} \subseteq \mathbb {R}^n$. Then for every $\alpha \in ( 0,1 )$,

$$\begin{aligned} \text{ CVaR }_{\alpha }(f(x,\widetilde{\omega }))= & {} \underbrace{\min _{t \in \mathbb {R}}\, \left\{ \, t + \displaystyle { \frac{1}{1 - \alpha } } \, \mathbb {E}\max \left( \, p(x,\widetilde{\omega }) - t, q(x,\widetilde{\omega }) \, \right) \, \right\} }_{\text{ cvx } \text{ in } x}\\&- \underbrace{\displaystyle { \frac{1}{1 - \alpha } } \, \mathbb {E}q(x,\widetilde{\omega })}_{\text{ cvx } \text{ in } x}. \end{aligned}$$

Proof

The equality is fairly straightforward. The convexity of the minimum is due to the joint convexity of the function $(x,t) \mapsto t + \frac{1}{1 - \alpha } \, \mathbb {E}\max \left( \, p(x,\widetilde{\omega }) - t, q(x,\widetilde{\omega }) \, \right)$. $\square$

A formula that connects $\text{ VaR }_{\alpha }({\mathcal {Z}})$ to $\text{ CVaR }_{\alpha }({\mathcal {Z}})$ for a discretely distributed random variable ${\mathcal {Z}}$ was obtained in [57]; this formula can be used to establish the dc property of $\text{ VaR }_{\alpha }(f(x,\widetilde{\omega }))$ when $f(\bullet ,\widetilde{\omega })$ is dc. In what follows, we derive an alternative expression connecting $\text{ VaR }({\mathcal {Z}})$ and $\text{ CVaR }({\mathcal {Z}})$ using simple linear programming duality when the sample space $\Omega = \left\{ \omega ^1, \ldots , \omega ^S \right\}$ for some integer $S > 0$. Let $\left\{ p_1, \ldots , p_S \right\}$ be the associated family of probabilities of the discrete realizations of the random variable $\widetilde{\omega }$. Writing $z_s \triangleq f(x,\omega ^s)$, we then have

where the last equality follows by the substitution: $v_0=\sum _{s=1}^S \, v_s - 1$ and by noticing that the nonnegativity of $v_0$ can be dropped, provided that $\{ v_s \}_{s=1}^S$ belongs to the fixed set:

$$\begin{aligned} {\mathcal {W}} \, \triangleq \, \left\{ \, v \, \in \, \mathbf {R}^S_+ \, \mid \, \underbrace{\frac{-p_s}{1 - \alpha } \, \left[ \, \sum _{s^{\, \prime } = 1}^S \, v_{s^{\, \prime }} - 1 \, \right] + v_s \, \le \, 0, \quad s \, = \, 1, \ldots , S}_{\text{ can } \text{ be } \text{ written } \text{ as } \left[ \, \mathbb {I}_S - \frac{1}{1 - \alpha } \, p \mathbf {1}_S^T \, \right] v + \frac{p}{1 - \alpha } \, \le \, 0} \right\} , \end{aligned}$$

where $\mathbb {I}_S$ is the identity matrix of order S, p is the S-vector of probabilities $\{ p_s \}_{s=1}^S$, and $\mathbf {1}_S$ is the S-vector of ones. Let $\left\{ v^j \triangleq ( v^j_s )_{s=1}^S \right\} _{j=1}^J$ be the finite family of extreme points of ${\mathcal {W}}$ for some integer $J > 0$. We then obtain the expression:

$$\begin{aligned} \text{ VaR }_{\alpha }( f(x,\widetilde{\omega }) )= & {} \text{ CVaR }_{\alpha }( f(x,\widetilde{\omega }) )\nonumber \\&+\,\displaystyle { \mathop {\text{ maximum }}\limits _{1 \le j \le J} } \ \displaystyle { \sum _{s=1}^S } \, \left[ \, f(x,\omega ^s) - \text{ CVaR }_{\alpha }( f(x,\widetilde{\omega }) ) \, \right] \, v_s^j, \end{aligned}$$

(3)

which shows that $\text{ VaR }_{\alpha }( f(x,\widetilde{\omega }) )$ is the pointwise maximum of a finite family of dc functions. As such it is itself a dc function of x, by known properties of difference-convexity. The above expression is different from the one in [57, page 866] that has the following form for the case $f(x,\widetilde{\omega }) = x^T \widetilde{\omega }$:

$$\begin{aligned} \text{ VaR }_{\alpha }( x^T\widetilde{\omega } ) \, = \, \displaystyle { \frac{\alpha }{\gamma } } \, \text{ CVaR }_{\alpha }( x^T\widetilde{\omega } ) + \left( \, 1 - \displaystyle { \frac{\alpha }{\gamma } } \, \right) \, \text{ CVaR }_{\alpha - \gamma }( x^T\widetilde{\omega } ) \end{aligned}$$

(4)

where $\gamma \in ( 0,\alpha )$ is a constant that is independent of x. [The bilinearity of the portfolio return $x^T\widetilde{\omega }$ is not essential.] When the scenarios have equal probabilities, the constant $\gamma$ can easily be determined. In the general case of un-equal scenario probabilities, the constant $\gamma$ can still be obtained by solving a bin packing problem. In the considered examples in the cited reference, it was observed that a small $\gamma$ relative to the scenario probabilities was sufficient to validate the formula. In contrast, our dc decomposition of $\text{ VaR }_{\alpha }( f(x,\widetilde{\omega }) )$ replaces the bin-packing step by the enumeration of the extreme points of the special polyhedron ${\mathcal {W}}$. Detailed investigation of the connection of these two formulae of VaR in terms of CVaR and how the alternative expression (3) can be used for algorithmic design are beyond the scope of this paper. In the next subsection, we extend the above derivation to a piecewise linear utility based OCE.

The family $\left\{ v^j \triangleq ( v^j_s )_{s=1}^S \right\} _{j=1}^J$ of extreme points of the special set ${\mathcal {W}}$ depends only on the probabilities $\{ p_s \}_{s=1}^S$ and not on the realizations $\{ \omega ^s \}_{s=1}^S$. Properties of these extreme points are not known at the present time; understanding the polytope ${\mathcal {W}}$ and its extreme points could benefit the design of efficient descent algorithms for optimizing $\text{ VaR }_{\alpha }( f(x,\widetilde{\omega }) )$. This is a worthwhile investigation that is left for future research. In the special case where the scenario probabilities $\{ p_s \}_{s=1}^S$ are all equal, we expect that the formula (3) can be significantly simplified.

3.2 Extension to an OCE with piecewise linear utility

Consider the function $m_u( f(x,\widetilde{\omega }) )$ with a concave piecewise linear utility function $u(t) \triangleq \min _{1 \le i \le I} \, a_i t + \alpha _i$ for some positive integer I and scalars $\{ a_i,\alpha _i \}_{i=1}^I$ with each $a_i \ge 0$. Omitting the derivation which is similar to the above for the VaR, we can show that

$$\begin{aligned} m_u( f(x,\widetilde{\omega }) )= & {} {\mathcal {O}}_u( f(x,\widetilde{\omega }) )\\&+\,\displaystyle { \mathop {\text{ minimum }}\limits _{1 \le j \le J} } \, \displaystyle { \sum _{i=1}^I } \, \displaystyle { \sum _{s=1}^S } \, \left\{ \, a_i \, \left[ \, f(x,\omega ^s) - {\mathcal {O}}_u( f(x,\widetilde{\omega })) \, \right] + \alpha _i \, \right\} \, \varphi _{is}^j \end{aligned}$$

where each $\varphi ^j = \left( \varphi ^j_{is} \right) _{(i,s) = 1}^{(I,S)}$ is an extreme point of a corresponding set

$$\begin{aligned} \Phi \, \triangleq \, \left\{ \, \varphi \, \in \mathbb {R}_+^{IS} \, \mid \, \displaystyle { \sum _{i=1}^I } \, \displaystyle { \sum _{s^{\prime }=1}^S } \, \left( \, p_s \, a_i - \delta _{s^{\prime } s} \, \right) \, \varphi _{is^{\prime }} \, = \, p_s, \ \forall \, s \, = \, 1, \ldots , S \, \right\} , \end{aligned}$$

where $\delta _{s^{\prime } s} \triangleq \left\{ \begin{array}{ll} 1 &{}\quad \text{ if }\quad s^{\prime } = s \\ 0 &{}\quad \text{ if }\quad s^{\prime } \ne s \end{array} \right.$. Similar to Proposition 1, the following result shows that ${\mathcal {O}}_u( f(x,\widetilde{\omega }))$ is a dc function of x provided that $f(\bullet ,\omega )$ is. Thus so is $m_u( f(\bullet ,\widetilde{\omega }) )$.

Proposition 2

For every $\omega \in \Omega$, let $f(x,\omega ) = p(x,\omega ) - q(x,\omega )$ be the dc decomposition of $f(\bullet ,\omega )$ on a convex set ${\mathcal {D}} \subseteq \mathbb {R}^n$. For a concave piecewise linear utility function $u(t) \triangleq \min _{1 \le i \le I} \, a_i t + \alpha _i$ for some positive integer I and scalars $\{ a_i,\alpha _i \}_{i=1}^I$ with each $a_i \ge 0$, it holds that

$$\begin{aligned}&{\mathcal {O}}_u(f(x,\widetilde{\omega })) \, = \, \underbrace{\left( \, \displaystyle { \sum _{i=1}^I } \, a_i \, \right) \, \mathbb {E}p(x,\widetilde{\omega })}_{\text{ cvx } \text{ in } x} \\&\quad + \underbrace{\displaystyle { \max _{\eta \in \mathbb {R}} } \, \left[ \, \eta - \mathbb {E}\displaystyle { \max _{1 \le i \le I} } \, \left\{ \, \left( \, \displaystyle { \sum _{i^{\, \prime } \ne i} } \, a_{i^{\, \prime }} \, \right) p(x,\widetilde{\omega }) + a_i \left( \, q(x,\widetilde{\omega }) + \eta \, \right) - \alpha _i \, \right\} \, \right] }_{\text{ cve } \text{ in } x}. \end{aligned}$$

Proof

We have, for each $\omega \in \Omega$,

$$\begin{aligned} \begin{array}{lll} u( f(x,\omega ) - \eta ) &{} = &{} \displaystyle {\min _{1 \le i \le I}} \, \left\{ \, a_i \, \left[ \, p(x,\omega ) - q(x,\omega ) - \eta \, \right] + \alpha _i \, \right\} \\ &{} = &{} \left( \, \displaystyle { \sum _{i=1}^I } \, a_i \, \right) \, p(x,\omega ) \\ &{}&{}- \underbrace{\displaystyle { \max _{1 \le i \le I} } \, \left\{ \, \left( \, \displaystyle { \sum _{i^{\, \prime } \ne i} } \, a_{i^{\, \prime }} \, \right) \, p(x,\omega ) + a_i \, \left( \, q(x,\omega ) + \eta \, \right) - \alpha _i \, \right\} }_{\text{ jointly } \text{ cvx } \text{ in } (x,\eta )}. \end{array} \end{aligned}$$

Thus the desired expression of ${\mathcal {O}}_u(f(x,\widetilde{\omega }))$ follows readily. $\square$

3.3 Variance, standard deviation, and exponential densities

We next show that the composite variance and standard deviations of dc functionals are dc, and so are the composite logarithmic and exponential functions. The proof of the former functions is based on several elementary facts of dc functions, which we summarize in Lemma 3 below. While these facts all pertain to composite functions and are generally known in the dc literature (see e.g. [18, Theorem II, page 708] and [4, 56]), we give their proofs in order to highlight the respective dc decompositions of the functions in question. Such explicit decompositions are expected to be useful in applications.

Lemma 3

Let ${\mathcal {D}}$ be a convex subset in $\mathbb {R}^n$. The following statements are valid:

• (a) The square of a dc function on ${\mathcal {D}}$ is dc on ${\mathcal {D}}$.

• (b) The product of two dc functions on ${\mathcal {D}}$ is dc on ${\mathcal {D}}$.

• (c) Let $f_i(x) = g_i(x) - h_i(x)$ be a dc decomposition of $f_i$ on ${\mathcal {D}}$, for $i = 1, \ldots , I$. Then $\Vert F(x) \Vert _2$ is a dc function on ${\mathcal {D}}$, where $F(x) \triangleq \left( f_i(x) \right) _{i=1}^I$.

Proof

• (a) Let $f = g - h$ be a dc decomposition of f with g and h being both nonnegative convex functions. We have

  $$\begin{aligned} f^2 \, = \, 2 \, ( \, g^2 + h^2 \, ) - ( \, g + h \, )^2. \end{aligned}$$

  (5)

  This gives a dc representation of $f^2$ because the square of a nonnegative convex function is convex.

• (b) Let $\widehat{f}$ and $\widetilde{f}$ be any two dc functions on ${\mathcal {D}}$, we can write

  $$\begin{aligned} \widehat{f}(x) \, \widetilde{f}(x) \, = \, {\textstyle {\frac{1}{2}}}\, \left[ ( \, \widehat{f}(x) + \widetilde{f}(x) \, )^2 - \widehat{f}(x)^2 - \widetilde{f}(x)^2 \, \right] , \end{aligned}$$

  which shows that the product $\widehat{f} \widetilde{f}$ is dc.

• (c) Using the fact that $\Vert v \Vert _2 = \max _{u: \Vert u \Vert _2 = 1} \, u^Tv$, we can express

  $$\begin{aligned} \Vert \, F(x) \, \Vert _2= & {} \displaystyle { \max _{u:\Vert u \Vert _2 = 1} } \, \displaystyle { \sum _{i=1}^I } \, u_i \, (g_i(x) - h_i(x)) \\= & {} \displaystyle { \sum _{i=1}^I } \, \left[ \underbrace{-g_i(x) - h_i(x)}_{\text{ cve } \text{ function }} \, \right] \\&+\displaystyle { \max _{u:\Vert u \Vert _2 = 1} } \, \displaystyle { \sum _{i=1}^I } \, \left[ \, \underbrace{(u_i + 1 ) \, g_i(x) + (1 - u_i) \, h_i(x)}_{{\triangleq \varphi _i(x,u_i)}} \, \right] . \end{aligned}$$

Since each $\varphi _i(\bullet ,u_i)$ is a convex function and the pointwise maximum of a family of convex functions is convex, the above identity readily gives a dc decomposition of $\Vert F(x) \Vert _2$. $\square$

Remark

It follows from the above proof in part (c) that the function $\Vert F(x) \Vert _2 + \sum _{i=1}^I \, \left( g_i(x) + h_i(x) \right)$ is convex. This interesting side-result is based on a pointwise maximum representation of the convex Euclidean norm function; the result can be extended to the composition of a convex with a dc function by using the conjugacy theory of convex functions; see Proposition 6 for an illustrative result of this kind. $\square$

Utilizing the expression (5), we give a dc decomposition of $\sigma ^2(f(x,\widetilde{\omega }))$.

Proposition 4

For every $\omega \in \Omega$, let $f(x,\omega ) = p(x,\omega ) - q(x,\omega )$ be a dc decomposition of $f(\bullet ,\omega )$ on ${\mathcal {D}} \subseteq \mathbb {R}^n$ with $p(\bullet ,\omega )$ and $q(\bullet ,\omega )$ both nonnegative and convex. Then

$$\begin{aligned} \sigma ^2(f(x,\widetilde{\omega })) \, = \, 2 \, \underbrace{\mathbb {E}\left[ \, p(x,\widetilde{\omega })^2 + q(x,\widetilde{\omega })^2 \, \right] + \left\{ \, \mathbb {E}p(x,\widetilde{\omega }) + \mathbb {E}q(x,\widetilde{\omega }) \, \right\} ^2}_{\text{ cvx } \text{ in } x} \nonumber \\ \quad - \left\{ \, \underbrace{\mathbb {E}\left[ \, p(x,\widetilde{\omega }) + q(x,\widetilde{\omega }) \, \right] ^2 + 2 \left[ \, \left( \, \mathbb {E}p(x,\widetilde{\omega }) \, \right) ^2 + \left( \, \mathbb {E}q(x,\widetilde{\omega }) \, \right) ^2 \, \right] }_{\text{ cvx } \text{ in } x} \, \right\} . \end{aligned}$$

(6)

Proof

We have

$$\begin{aligned} \sigma ^2(f(x,\widetilde{\omega }))= & {} \mathbb {E}f(x,\widetilde{\omega })^2 - \left( \, \mathbb {E}f(x,\widetilde{\omega }) \, \right) ^2 \\= & {} \mathbb {E}\left[ 2 \left\{ \, p(x,\widetilde{\omega })^2 + q(x,\widetilde{\omega })^2 \, \right\} - \left\{ \, p(x,\widetilde{\omega }) + q(x,\widetilde{\omega }) \, \right\} ^2 \, \right] \\&-\,\left[ \, 2 \left\{ \, \left( \, \mathbb {E}p(x,\widetilde{\omega }) \, \right) ^2 + \left( \, \mathbb {E}q(x,\widetilde{\omega }) \, \right) ^2 \, \right\} - \left\{ \, \mathbb {E}p(x,\widetilde{\omega }) + \mathbb {E}q(x,\widetilde{\omega }) \, \right\} ^2 \right] , \end{aligned}$$

from which (6) follows readily. $\square$

The proof that $\sigma (f(x,\widetilde{\omega }))$ is dc requires $\widetilde{\omega }$ to be discretely distributed and is based on the expression:

$$\begin{aligned} \sigma (f(x,\widetilde{\omega })) \, = \, \sqrt{ \displaystyle { \sum _{s=1}^S } \, p_s \, \left[ \, \underbrace{f(x,\omega ^s) - \sum _{s^{\, \prime }=1}^S \, p_{s^{\, \prime }} \, f(x,\omega ^{s^{\, \prime }})}_{\text{ dc } \text{ in } x} \, \right] ^2}; \end{aligned}$$

thus, $\sigma (f(x,\widetilde{\omega }))$ is the 2-norm of the vector dc function $x \mapsto \left( \sqrt{p_s} \left[ f(x,\omega ^s) -\right. \right. \left. \left. \sum _{s^{\, \prime }=1}^S \, p_{s^{\, \prime }} \, f(x,\omega ^{s^{\, \prime }}) \right] \right) _{s=1}^S$ (i.e., all its components are dc functions). As such, the dc-property of $\text{ std }(f(\bullet ,\widetilde{\omega }))$ follows from part (c) of Lemma 3.

We end this section by addressing two key functions in the one-parameter exponential density estimation discussed in Sect. 2.2. In generic notation, the first function is the composite $b \circ m(x)$ for x in a convex set ${\mathcal {D}} \subseteq \mathbb {R}^n$. The univariate function m is convex and non-decreasing, and admits a special dc decomposition $m(x) = p(x) - \max _{1 \le i \le I} \, \left[ \, ( a^i )^Tx + \alpha _i \, \right]$, where p is a convex function on ${\mathcal {D}}$ and each pair $( a^i,\alpha _i ) \in \mathbb {R}^{n+1}$; such a function m includes as a special case a piecewise affine function where p is also the pointwise maximum of finitely many affine functions. The second function is $\log f(x)$, where f is a dc function bounded away from zero. Extensions of these deterministic functions to the expected-value function $\mathbb {E}\left[ \log (f(x,\widetilde{\omega })) \right]$ is straightforward when the random variable is discretely distributed so that

$$\begin{aligned} \mathbb {E}\left[ \log (f(x,\widetilde{\omega })) \right] \, = \, \displaystyle { \sum _{s=1}^S } \, p_s \, \log ( f(x,\omega ^s) ). \end{aligned}$$

Proposition 5

Let $b : \mathbb {R} \rightarrow \mathbb {R}$ be a convex non-decreasing function and $m(x) = p(x) - \max _{1 \le i \le I} \, \left[ \, ( a^i )^Tx + \alpha _i \, \right]$ with p being a convex function on the convex set ${\mathcal {D}} \subseteq \mathbb {R}^n$. It holds that the composite function $b \circ m$ is dc on ${\mathcal {D}}$.

Proof

By the non-decreasing property of b, we can write

$$\begin{aligned} b \circ m(x) \, = \, \displaystyle { \min _{1 \le i \le I} } \, b\left( \, p(x) - ( a^i )^Tx - b_i \, \right) , \end{aligned}$$

with each function $x \mapsto b\left( \, p(x) - ( a^i )^Tx - b_i \, \right)$ being convex. The above expression shows that the composite $b \circ m(x)$ is the pointwise minimum of finitely many convex functions; hence $b \circ m$ is dc. $\square$

Remark

While it is known that the composition of two dc functions is dc if their respective domains have some openness/closedness properties; see e.g. [18, Theorem II]. The dc decomposition of the composite function is rather complex and not as simple as the one in the special case of Proposition 5. Whether the latter decomposition can be extended to the general case where the pointwise (finite) maximum term in the function m(x) is replaced by an arbitrary convex function is not known at the present time. $\square$

Proposition 6

Let $\theta (x) = -\log ( f(x) )$ where $f(x) = p(x) - q(x)$ is a dc function on a convex set ${\mathcal {D}} \subseteq \mathbb {R}^n$ where $\inf _{x \in {\mathcal {D}}} \, f(x) > 0$. Then there exists a scalar $M > 0$ such that the function $\theta (x) + M \, p(x)$ is convex on ${\mathcal {D}}$; thus $\theta$ has the dc decomposition $\theta (x) \, = \, \left[ \, \theta (x) + M \, p(x) \, \right] - M \, p(x)$ on ${\mathcal {D}}$.

Proof

Let $1/M \triangleq \inf _{x \in {\mathcal {D}}} \, f(x)$. Consider the conjugate function of the univariate convex function $\zeta (t) \triangleq -\log (t)$ for $t > 0$. We have

$$\begin{aligned} \zeta ^*(v) \, \triangleq \displaystyle { \sup _{t > 0} } \, \left\{ \, v \, t + \log (t) \, \right\} \, = \, -1 - \log (-v), \quad \text{ for }\quad v <0. \end{aligned}$$

Hence, by double conjugacy,

$$\begin{aligned} -\log (t) \, = \, \displaystyle { \sup _{v < 0} } \, \left\{ \, v \, t + 1 + \log (-v) \, \right\} , \quad \text{ for }\quad t \, > \, 0, \end{aligned}$$

where the sup is attained at $v = -1/t$. Since $p(x) - q(x) \ge 1/M$ on ${\mathcal {D}}$, it follows that

$$\begin{aligned} -\log \left( p(x) - q(x) \right)= & {} \displaystyle { \sup _{v< 0} } \, \left\{ \, v \, ( \, p(x) - q(x) \, ) + 1 + \log (-v) \, \right\} \\= & {} \displaystyle { \sup _{-M \le v< 0} } \, \left\{ \, v \, ( \, p(x) - q(x) \, ) + 1 + \log (-v) \, \right\} \\= & {} \displaystyle { \sup _{-M \le v < 0} } \, \left\{ \, \underbrace{( \, v + M \, ) \, p(x) + ( \, -v \, ) \, q(x) + 1 + \log (-v)}_{\text{ cvx } \text{ in } x} \, \right\} \\&-\,M \, p(x). \end{aligned}$$

This shows that $\theta (x) + M \, p(x)$ is equal to the pointwise maximum of a family of convex functions, hence is convex. $\square$

4 A study of the value function $\text{ qp }_\mathrm{opt}(q,b)$

Properties of the QP-value function are clearly important for the understanding of the quadratic recourse function $\psi (x,\omega )$, which is equal to $\text{ qp }_\mathrm{opt}(q(x,\omega ),b(x,\omega ))$ where $q(x,\omega ) \triangleq f(\omega ) + G(\omega )x$ and $b(x,\omega ) \triangleq \xi (\omega ) - C(\omega )x$. In the analysis of the general QP (2), we do not make a semi-definiteness assumption on Q. Instead the copositivity of Q on $D_{\infty }$ is essential because if there exists a recession vector v in this cone such that $v^TQv < 0$, then for all b for which ${\mathcal {P}}_D(b) \ne \emptyset$, we have $\text{ qp }_\mathrm{opt}(q,b) = -\infty$ for all $q \in \mathbb {R}^n$.

We divide the derivation of the dc property (and an associated dc representation) of $\text{ qp }_\mathrm{opt}(q,b)$ into two cases: (a) when Q is positive definite, and (b) when Q is copositive on $D_{\infty }$. In the former case, the dc decomposition is easy to derive and much simpler, whereas the latter case is much more involved. Indeed, when Q is positive definite, we have

(7)

The lemma below shows that the minimum of the second summand in the above expression is a convex function of the right-hand vector $b^{\, \prime }$. This yields a rather simple dc decomposition of $\text{ qp }_\mathrm{opt}(q,b)$. The proof of the lemma is easy and omitted.

Lemma 7

Let $f : \mathbb {R}^m \rightarrow \mathbb {R}$ be a strongly convex function and let $D \in \mathbb {R}^{k \times m}$. The value function:

$$\begin{aligned} \begin{array}{lll} \varphi (b) \, \triangleq &{} \displaystyle { \mathop {\mathrm{minimum}}\limits _y } &{} f(y) \\ &{} \mathrm{subject\,to} &{} Dy \, \ge \, b \end{array} \end{aligned}$$

is a convex function on the domain $\text{ Range }(D) - \mathbb {R}^k_+$ which consists of all vectors b for which there exists $y \in \mathbb {R}^m$ satisfying $Dy \ge b$. $\square$

It is worthwhile to point out that while it is fairly easy to derive the above “explicit” dc decomposition of $\text{ qp }_\mathrm{opt}(q,b)$ when Q is positive definite, the same cannot be said when Q is positive semidefinite. Before proceeding further, we refer the reader to the monograph [27] for an extensive study of indefinite quadratic programs. Yet results therein do not provide clear descriptions of the structure of (a) the optimal solution set of the QP (2) for fixed (q, b) and (b) the domain $\text{ dom }(Q,D)$ of finiteness, and (c) the optimal value function $\text{ qp }_\mathrm{opt}(q,b)$, all when Q is an indefinite matrix. Instead we rely on an early result [15] and the recent study [21] to formally state and prove these desired properties of the QP (2) when Q is copositive on the recession cone of the feasible region. This is the main content of Proposition 9 below. The key to this proposition is the following consequence of a well-known property of a quadratic program which was originally due to Frank–Wolfe and subsequently refined by Eaves [12]; see [27, Theorem 2.2]. In the lemma below and also subsequently, the $\perp$ notation denotes perpendicularity, which expresses the complementarity condition between two nonnegative vectors.

Lemma 8

Suppose that Q is copositive on $D_{\infty }$. A pair $(q,b) \in \text{ dom }(Q,D)$ if and only if ${\mathcal {P}}_D(b) \ne \emptyset$ and

$$\begin{aligned} \left. \begin{array}{r} Qv - D^{\, T}\eta \, = \, 0 \\ 0 \, \le \, \eta \, \perp \, Dv \, \ge \, 0 \\ Dz \, \ge \, b \end{array} \right\} \ \Rightarrow \ ( \, q + Qz \, )^Tv \, \ge \, 0. \end{aligned}$$

(8)

Proof

By [27, Theorem 2.2], $(q,b) \in \text{ dom }(Q,D)$ if and only if ${\mathcal {P}}_D(b) \ne \emptyset$ and

$$\begin{aligned} \left. \begin{array}{r} v^TQv \, = \, 0, \quad Dv \, \ge \, 0 \\ Dz \, \ge \, b \end{array} \right\} \ \Rightarrow \ ( \, q + Qz \, )^Tv \, \ge \, 0. \end{aligned}$$

(9)

By the copositivity of Q on $D_{\infty }$, we have

$$\begin{aligned} \begin{array}{lll} \left[ \, v^TQv \, = \, 0, \quad Dv \, \ge \, 0 \, \right] &{} \Leftrightarrow &{} v \text{ is } \text{ a } \text{ minimizer } \text{ of } {\textstyle {\frac{1}{2}}}\, u^TQu \text{ for } u \, \in \, D_{\infty } \\ &{} \Leftrightarrow &{} \exists \, \eta \text{ such } \text{ that } \left\{ \begin{array}{l} Qv - D^{\, T}\eta \, = \, 0 \\ 0 \, \le \, \eta \, \perp \, Dv \, \ge \, 0. \end{array} \right. \end{array} \end{aligned}$$

Thus (9) and (8) are equivalent. $\square$

Interestingly, while the result below is well known in the case of a positive semidefinite Q, its extension to a copositive Q turns out to be not straightforward, especially under no boundedness assumption whatsoever. There is an informal assertion, without proof or citation, of the result below (in particular, part (c)) for a general qp without the copositive assumption [29, page 88]. This is a careless oversight on the authors’ part as the proof below is actually quite involved.

Proposition 9

Suppose that Q is copositive on $D_{\infty }$. The following statements hold:

• (a) $\text{ qp }_\mathrm{opt}(q,b)$ is continuous on $\text{ dom }(Q,D)$;

• (b) $\text{ dom }(Q,D)$ is the union of finitely many polyhedra (thus is a closed set);

• (c) There exists a finite family ${\mathcal {F}} \triangleq \{ S_F \}$ of polyehdra in $\mathbb {R}^{m+k}$ on each of which $\text{ qp }_\mathrm{opt}(q,b)$ is a (finite-valued) quadratic function; hence $\text{ qp }_\mathrm{opt}(q,b)$ is a piecewise quadratic function on $\text{ dom }(Q,D)$;

• (d) For each pair $(q,b) \in \text{ dom }(Q,D)$, the optimal solution set of the QP (2) is the union of finitely many polyhedra.

Proof

(a) Let $\{ (q^{\nu },b^{\nu }) \} \subseteq \text{ dom }(Q,D)$ be a sequence of vectors converging to the pair $( q^{\infty },b^{\infty })$. For each $\nu$, let $z^{\nu } \in \text{ qp }_\mathrm{sol}(q^{\nu },b^{\nu })$. Note that this sequence $\{ z^{\nu } \}$ need not be bounded. Nevertheless, by the renowned Hoffman error bound for linear inequalities [13, Lemma 3.2.3], it follows that the following two properties hold: (a) ${\mathcal {P}}_D(b^{\infty }) \ne \emptyset$ and there exists a sequence $\{ \bar{z}^{\, \nu } \} \subseteq {\mathcal {P}}_D(b^{\infty })$ such that $\{ \bar{z}^{\nu } - z^{\nu } \} \rightarrow 0$; and (b) for every $z \in {\mathcal {P}}_D(b^{\infty })$, there exists, for every $\nu$ sufficiently large, a vector $y^{\nu } \in {\mathcal {P}}_D(b^{\nu })$ such that the sequence $\{ y^{\nu } \}$ converges to z. Hence, for every $( \eta ,v )$ satisfying the left-hand conditions in (8), we have

$$\begin{aligned} ( \, q^{\infty } + Qz \, )^Tv \, = \, \displaystyle { \lim _{\nu \rightarrow \infty } } \, ( \, q^{\nu } + Qy^{\nu } \, )^Tv \, \ge \, 0. \end{aligned}$$

Hence $\text{ qp }_\mathrm{sol}(q^{\infty },b^{\infty }) \ne \emptyset$; thus $( q^{\infty },b^{\infty } ) \in \text{ dom }(Q,D)$. Moreover, by taking the vector $z \in \text{ qp }_\mathrm{sol}(q^{\infty },b^{\infty })$, we have

$$\begin{aligned} \text{ qp }_\mathrm{opt}(q^{\infty },b^{\infty }) \,= & {} \, \zeta (z) \, = \, \displaystyle { \lim _{\nu \rightarrow \infty } } \, \zeta (y^{\nu }) \, \ge \, \displaystyle { \limsup _{\nu \rightarrow \infty } } \, \zeta (z^{\nu }) \, = \, \displaystyle { \limsup _{\nu \rightarrow \infty } } \, \zeta ( \bar{z}^{\nu }) \,\\\ge & {} \, \displaystyle { \liminf _{\nu \rightarrow \infty } } \, \zeta ( \bar{z}^{\nu }) \, \ge \, \text{ qp }_\mathrm{opt}(q^{\infty },b^{\infty }) \end{aligned}$$

from which it follows that $\lim _{\nu \rightarrow \infty } \, \text{ qp }_\mathrm{opt}(q^{\nu },b^{\nu }) = \lim _{\nu \rightarrow \infty } \, \zeta (z^{\nu })$ exists and equals to $\text{ qp }_\mathrm{opt}(q^{\infty },b^{\infty })$. Thus (a) holds.

To prove (b), we use an early result of quadratic programming [15] stating that for a pair (q, b) in $\text{ dom }(Q,D)$, the value $\text{ qp }_\mathrm{opt}(q,b)$ is equal to the minimum of the quadratic objective function $\zeta (z)$ on the set of stationary solutions of the problem, and also use the fact [28] that the set of values of $\zeta$ on the set of stationary solutions is finite. More explicitly, the stationarity conditions of (2), or Karush–Kuhn–Tucker (KKT) conditions, are given by the following mixed complementarity conditions:

$$\begin{aligned}&q + Qz - D^{\, T}\eta \, = \, 0 \nonumber \\&0 \, \le \, \eta \, \perp \, Dz - b \, \ge \, 0. \end{aligned}$$

(10)

In turn the above conditions can be decomposed into a finite, but exponential, number of linear inequality systems by considering the index subsets ${\mathcal {I}} \subseteq \{ 1, \ldots , k \}$ each with complement ${\mathcal {J}}$ such that

$$\begin{aligned} \begin{array}{lll} q + Qz - ( D_{{\mathcal {I}} \bullet } )^T \eta _{\mathcal {I}} &{} = &{} 0, \\ D_{{\mathcal {I}} \bullet }z - b_{\mathcal {I}} \, = \, 0 &{} \le &{} \eta _{\mathcal {I}} \\ D_{{\mathcal {J}} \bullet }z - b_{\mathcal {J}} \, \ge \, 0 &{} = &{} \eta _{\mathcal {J}}. \end{array} \end{aligned}$$

(11)

The above linear inequality system defines a polyhedral set in $\mathbb {R}^{m+k}$, which we denote $\text{ KKT }({\mathcal {I}})$. Alternatively, a tuple (q, b) satisfies (11) if and only if

$$\begin{aligned} \left( \begin{array}{l} q \\ b_{\mathcal {I}} \\ b_{\mathcal {J}} \end{array} \right) \, \in \, \left[ \begin{array}{ccc} -Q &{} ( D_{{\mathcal {I}} \bullet } )^T &{} 0\\ D_{{\mathcal {I}} \bullet } &{} 0 &{} 0 \\ D_{{\mathcal {J}} \bullet } &{} 0 &{} -\mathbb {I}_{| {\mathcal {J}} |} \end{array} \right] \left( \begin{array}{c} \mathbb {R}^m \\ \mathbb {R}_+^{| {\mathcal {I}} |} \\ \mathbb {R}_+^{| {\mathcal {J}} |} \end{array} \right) \, \triangleq \, \underbrace{\text{ QD }({\mathcal {I}})}_{\text{ a } \text{ polyhedral } \text{ cone }}. \end{aligned}$$

The recession cone of $\text{ KKT }({\mathcal {I}})$, denoted $\text{ KKT }({\mathcal {I}})_{\infty }$, is a polyhedral cone defined by the following homogeneous system in the variables $( v,\xi )$:

$$\begin{aligned} \begin{array}{lll} Qv - ( D_{{\mathcal {I}} \bullet } )^T \xi _{\mathcal {I}} &{} = &{} 0, \\ D_{{\mathcal {I}} \bullet }v \, = \, 0 &{} \le &{} \xi _{\mathcal {I}} \\ D_{{\mathcal {J}} \bullet }v \, \ge \, 0 &{} = &{} \xi _{\mathcal {J}}. \end{array} \end{aligned}$$

This cone is the conical hull of a finite number of generators, which we denote $\left\{ \left( v^{{\mathcal {I}},\ell },\xi ^{{\mathcal {I}},\ell } \right) \right\} _{\ell =1}^{L_{\mathcal {I}}}$ for some integer $L_{\mathcal {I}} > 0$. Notice that these generators depend only on the pair (Q, D). In terms of them, the implication (8) is equivalent to

$$\begin{aligned} Dz \, \ge \, b \ \Rightarrow \ ( \, q + Qz \, )^Tv^{{\mathcal {I}},\ell } \, \ge \, 0, \quad \forall \, \ell \, = \, 1, \ldots , L_{\mathcal {I}} \text { and all subsets } {\mathcal {I}} of \{ 1, \ldots , k \}. \end{aligned}$$

In turn, for a fixed pair $( {\mathcal {I}},\ell )$, the latter implication holds if and only if

$$\begin{aligned} \begin{array}{llllll} 0 &{} \le &{} q^Tv^{{\mathcal {I}},\ell } + &{} \displaystyle { \mathop {\text{ minimum }}\limits _{Dz \, \ge \, b} } &{} \left( \, Qv^{{\mathcal {I}},\ell } \, \right) ^Tz \\ [0.1in] &{} = &{} q^Tv^{{\mathcal {I}},\ell } + &{} \displaystyle { \mathop {\text{ maximize }}\limits _{\mu \ge 0} } &{} b^{\, T}\mu \qquad \qquad \text{ by } \text{ linear } \text{ programming } \text{ duality } \\ &{} &{} &{} \text{ subject } \text{ to } &{} D^T\mu \, = \, Qv^{{\mathcal {I}},\ell }. \end{array} \end{aligned}$$

Let ${\mathcal {E}}({\mathcal {I}},\ell ) \triangleq \{ \mu ^{{\mathcal {I}},\ell ,\kappa } \}_{\kappa =1}^{E({\mathcal {I}},\ell )}$ be the finite set of extreme points of the polyhedron $\left\{ \mu \in \mathbb {R}^k_+ \mid D^T\mu \, = \, Qv^{{\mathcal {I}},\ell } \right\}$ for some positive integer $E({\mathcal {I}},\ell )$. Again these extreme points depend on the pair (Q, D) only. It then follows that (8) holds if and only if for every pair $( {\mathcal {I}},\ell )$ with ${\mathcal {I}}$ being a subset of $\{ 1, \ldots , k \}$ and $\ell = 1, \ldots , L_{\mathcal {I}}$, there exists $\mu ^{{\mathcal {I}},\ell ,\kappa } \in {\mathcal {E}}({\mathcal {I}},\ell )$ such that $0 \le q^Tv^{{\mathcal {I}},\ell } + b^{\, T} \mu ^{{\mathcal {I}},\ell ,\kappa }$. Together with the feasibility condition $b \in \text{ range }(D) - \mathbb {R}^k_+$, each of the latter inequalities in (q, b) defines a polyhedron that defines a piece of $\text{ dom }(Q,D)$. Specifically let ${\mathcal {V}} \triangleq \prod _{( {\mathcal {I}},\ell )} \, {\mathcal {E}}({\mathcal {I}},\ell )$ where the Cartesian product ranges over all pairs $( {\mathcal {I}},\ell )$ with ${\mathcal {I}}$ being a subset of $\{ 1, \ldots , k \}$ and $\ell = 1, \ldots , L_{\mathcal {I}}$. An element $\varvec{\mu } \in {\mathcal {V}}$ is a tuple of extreme points $\mu ^{{\mathcal {I}},\ell ,\kappa }$ over all pairs $( {\mathcal {I}},\ell )$ as specified with $\kappa$ being one element in $\{ 1, \ldots , E({\mathcal {I}},\ell ) \}$ corresponding to the given $\varvec{\mu }$; every such element $\varvec{\mu }$ defines a system of $\sum _{{\mathcal {I}} \subseteq \{ 1, \ldots , k \}} \, | \, L_{\mathcal {I}} \, |$ linear inequalities each of the form:

$$\begin{aligned} q^Tv^{{\mathcal {I}},\ell } + b^{\, T} \mu ^{{\mathcal {I}},\ell ,\kappa } \, \ge \, 0, \end{aligned}$$

Consequently, it follows that

$$\begin{aligned}&\text{ dom }(Q,D) \, \\&\quad = \, \displaystyle { \bigcup _{\varvec{\mu } \in {\mathcal {V}}} } \, \left\{ \, ( \, q,b \, ) \, \in \, \mathbb {R}^m \, \times \, \left[ \, D\mathbb {R}^m - \mathbb {R}^k_+ \, \right] \, \mid \, \underbrace{q^Tv^{{\mathcal {I}},\ell } + b^{\, T} \mu ^{{\mathcal {I}},\ell ,\kappa } \, \ge \, 0}_{\text{ there } \text{ are } \displaystyle { \sum _{{\mathcal {I}} \subseteq \{ 1, \ldots , k \}} } \, | \, L_{\mathcal {I}} \, | \text {of these}} \, \right\} , \end{aligned}$$

proving that $\text{ dom }(Q,D)$ is a union of finitely (albeit potentially exponentially) many polyhedra, each denoted by $\text{ dom }^{\varvec{\mu }}(Q,D)$ for $\varvec{\mu } \in {\mathcal {V}}$.

To prove (c), let ${\mathcal {F}}$ be the family of polyhedra

$$\begin{aligned} \left\{ \, \text{ dom }^{\varvec{\mu }}(Q,D) \, \cap \, \text{ QD }({\mathcal {I}}^{\, \prime }) \, \mid \, \varvec{\mu } \, \in \, {\mathcal {V}} \text{ and } {\mathcal {I}}^{\, \prime } \, \subseteq \, \{ 1, \ldots , k \} \, \right\} . \end{aligned}$$

For each polyhedron in this family, the system KKT$({\mathcal {I}}^{\, \prime })$ has a solution $( z,\eta _{{\mathcal {I}}^{\, \prime }} )$ satisfying:

$$\begin{aligned} \begin{array}{lll} q + Qz - ( D_{{\mathcal {I}}^{\, \prime } \bullet } )^T \eta _{{\mathcal {I}}^{\, \prime }} &{} = &{} 0, \\ D_{{{\mathcal {I}}^{\, \prime }} \bullet }z - b_{{\mathcal {I}}^{\, \prime }} \, = \, 0 &{} \le &{} \eta _{{\mathcal {I}}^{\, \prime }} \\ D_{{{\mathcal {J}}^{\, \prime }} \bullet }z - b_{{\mathcal {J}}^{\, \prime }} \, \ge \, 0, \end{array} \end{aligned}$$

(12)

where ${\mathcal {J}}^{\, \prime }$ is the complement of ${\mathcal {I}}^{\, \prime }$ in $\{ 1, \ldots , k \}$. The system (12) can be written as:

$$\begin{aligned} \left[ \begin{array}{ccc} -Q &{} ( D_{{\mathcal {I}}^{\, \prime } \bullet } )^T &{} 0 \\ D_{{{\mathcal {I}}^{\, \prime }} \bullet } &{} 0 &{} 0 \\ D_{{{\mathcal {J}}^{\, \prime }} \bullet } &{} 0 &{} -\mathbb {I}_{| {\mathcal {J}}^{\, \prime } | } \end{array} \right] \left( \begin{array}{c} z \\ \eta _{{\mathcal {I}}^{\, \prime }} \\ s_{{\mathcal {J}}^{\, \prime }} \end{array} \right) \, = \, \left( \begin{array}{c} q \\ b_{{\mathcal {I}}^{\, \prime }} \\ b_{{\mathcal {J}}^{\, \prime }} \end{array} \right) , \quad ( \, \eta _{{\mathcal {I}}^{\, \prime }}, s_{{\mathcal {J}}^{\, \prime }} \, ) \, \ge \, 0. \end{aligned}$$

By elementary linear-algebraic operations similar to the procedure of obtaining a basic feasible solution from an arbitrary feasible solution to a system of linear inequalities in linear programming, it follows that there exists a matrix $M({\mathcal {I}}^{\, \prime })$, dependent on the pair (Q, D) only, such that (12) has a solution with $z = M({\mathcal {I}}^{\, \prime })\left( \begin{array}{c} q \\ b \end{array} \right)$; i.e., (12) has a solution that is linearly dependent on the pair (q, b). It is not difficult to show that the objective function $\zeta (z)$ is a constant on the set of solutions of (12) [in fact, this constancy property is the source of the finite number of values attained by the quadratic function $\zeta$ on the set of stationary solutions of the QP (2)], it follows that this constant must be a quadratic function of the pair (q, b). Since for a fixed pair $(q,b) \in \text{ dom }(Q,D)$, $\text{ qp }_\mathrm{opt}(q,b)$ is the minimum of these constants over all polyhedra in the family ${\mathcal {F}}$ that contains the pair (q, b), part (c) follows.

Lastly, to prove (d), it suffices to note that for a given pair $(q,b) \in \text{ dom }(Q,D)$, the solution set of the QP (2) is equal to set of vectors z for which there exists $\eta$ such that the pair $(z,\eta )$ satisfies the linear equality system $\text{ KKT }({\mathcal {I}})$ and ${\textstyle {\frac{1}{2}}}\, ( q^Tz + b^T \eta ) = \text{ qp }_\mathrm{opt}(q,b)$ for some index subset ${\mathcal {I}}$ of $\{ 1, \ldots , k \}$. $\square$

4.1 Proof the dc property

Based on Proposition 9 and known properties of piecewise dc functions in general, the following partial dc property of the value function $\text{ qp }_\mathrm{opt}(q,b)$ can be proved.

Corollary 10

Suppose that Q is copositive on $D_{\infty }$. The value function $\text{ qp }_\mathrm{opt}(q,b)$ is dc on any open convex set contained in $\text{ dom }(Q,D)$.

Proof

This follows from the mixing property of piecewise dc functions; see [4, Proposition 2.1] which has its source from [55, Lemma 4.8]. $\square$

Since $\text{ dom }(Q,D)$ is a closed set, the above corollary does not yield the difference-convexity of $\text{ qp }_\mathrm{opt}(q,b)$ on its full domain. We give a formal statement of this property in Theorem 12 under the assumption that $\text{ dom }(Q,D)$ is convex. The proof of this desired dc property is based on a more general Proposition 11 pertaining to piecewise $\hbox {LC}^{\, 1}$ functions that does not require the pieces to be quadratic functions nor the polyehdrality of the sub-domains.

Recall that a function $\theta$ is LC$^1$ (for Lipschitz continuous gradient) on an open set ${\mathcal {O}}$ in $\mathbb {R}^n$ if $\theta$ is differentiable and its gradient is a Lipschitz continuous function on ${\mathcal {O}}$. It is known that a LC$^1$ function is dc with the decomposition $\theta (x) = \left( \theta (x) + \frac{M}{2} \, x^Tx \right) - \frac{M}{2} \, x^Tx$, where M is a positive scalar larger than the Lipschitz modulus of the gradient function $\nabla \theta$. Another useful fact [31, 3.2.12] about LC$^{\, 1}$ functions is the inequality (13) that is a consequence of a mean-value function theorem of multivariate functions: namely, if $\theta$ is LC$^{\, 1}$ with $L > 0$ being a Lipschitz modulus of $\nabla \theta$ on an open convex convex set ${\mathcal {O}}$, then for any two vectors x and y in ${\mathcal {O}}$,

$$\begin{aligned} \theta (x) - \theta (y) \, \le \, \nabla \theta (y)^T(x - y) + \displaystyle { \frac{L}{2} } \, \Vert \, x - y \, \Vert _2^2. \end{aligned}$$

(13)

Proposition 11

Let $\theta (x)$ be a continuous function on a convex set ${\mathcal {S}} \triangleq \bigcup _{i=1}^I \, S^{\, i}$ where each $S^{\, i}$ is a closed convex set in $\mathbb {R}^N$. Suppose there exist LC$^1$ functions $\{ \theta _i(x) \}_{i=1}^I$ defined on an open set ${\mathcal {O}}$ containing ${\mathcal {S}}$ such that $\theta (x) = \theta _i(x)$ for all $x \in S^{\, i}$ and that each difference function $\theta _{ji}(x) \triangleq \theta _j(x) - \theta _i(x)$ has dc gradients on ${\mathcal {S}}$. It holds that $\theta$ is dc on ${\mathcal {S}}$.

Proof

Let $L_{ji}$ be the Lipschitz modulus of $\nabla \theta _{ji}$ on ${\mathcal {O}}$ and let $L_i \triangleq \max _{1 \le j \le I} \, L_{ji}$. Let $\text{ dist }(x;S^{\, i}) \triangleq \min _{z \in S^{\, i}} \, \Vert \, x - z \, \Vert _2 = \Vert \, x - \Pi _{S^{\, i}}(x) \, \Vert _2$ be the distance function to the set $S^{\, i}$ with $\Pi _{S^{\, i}}(x)$ being the Euclidean projection (i.e., closest point) of the vector x onto $S^{\, i}$. We note that both $\text{ dist }(\bullet ;S^{\, i})$ and $\left[ \, \text{ dist }(\bullet ;S^{\, i}) \, \right] ^2$ are convex functions. Define

$$\begin{aligned} \phi _i(x) \, \triangleq \, \underbrace{\text{ dist }(x;S^{\, i})}_{\text{ cvx } \text{ in } x} \, \underbrace{\max _{1 \le j \le I} \, \Vert \nabla \theta _{ji}(x) \Vert _2}_{\text{ dc } \text{ in } x} + \frac{3 \, L_i}{2} \, \left[ \, \text{ dist }(x;S^{\, i}) \, \right] ^2, \quad x \, \in \, \mathbb {R}^N \end{aligned}$$

and let $\psi _i(x) \triangleq \, \theta _i(x) + \phi _i(x)$. The first summand, $\text{ dist }(x;S^{\, i}) \, \max _{1 \le j \le I} \, \Vert \nabla \theta _{ji}(x) \Vert _2$, being the product of two dc functions is dc, by Lemma 3. Hence each function $\psi _i$ is dc. We claim that

$$\begin{aligned} \theta (x) \, = \, \displaystyle { \min _{1 \le i \le I} } \, \psi _i(x), \quad \forall \, x \, \in \, {\mathcal {S}}. \end{aligned}$$

(14)

Since the pointwise minimum of finitely many dc functions is dc [53, Proposition 4.1], the expression (14) is enough to show that $\theta$ is dc on ${\mathcal {S}}$. In turn since $\psi _i(x) = \theta _i(x)$ for all $x \in S^{\, i}$, to show (14), it suffices to show that $\psi _i(x) \ge \theta (x)$ for all $x \in {\mathcal {S}} {\setminus } S^{\, i}$. For such an x, let $\bar{x}^i \triangleq \Pi _{S^{\, i}}(x)$. Since ${\mathcal {S}}$ is convex, the line segment joining x and $\bar{x}^i$ is contained in ${\mathcal {S}}$. Hence, there exists a finite partition of the interval [0, 1]:

$$\begin{aligned} 0 \, = \, \tau _0 \,< \, \tau _1< \cdots< \tau _T \, < \, \tau _{T+1} \, = \, 1 \end{aligned}$$

and corresponding indices $i_t \in \{ 1, \ldots , I \}$ for $t = 1, \ldots , T+1$ so that $\theta (x) = \theta _{i_t}(x)$ for all x in the (closed) sub-segment joining $x^{t-1} \triangleq x + \tau _{t-1} ( \bar{x}^i - x )$ to $x^t \triangleq x + \tau _t ( \bar{x}^i - x )$. We have

$$\begin{aligned}&\theta (x) - \theta _i(x) \, = \, \theta (x) - \theta (\bar{x}^i) + \theta _i(\bar{x}^i) - \theta _i(x) \quad \text{ because } \theta (\bar{x}^i) = \theta _i(\bar{x}^i) \\&\quad = \, \displaystyle { \sum _{t=1}^{T+1} } \, \left[ \, \theta _{i_t}(x^{t-1}) - \theta _{i_t}(x^t) \, \right] - \displaystyle { \sum _{t=1}^{T+1} } \, \left[ \, \theta _i(x^{t-1}) - \theta _i(x^t) \, \right] \\&\qquad \qquad \text{ because } \theta (x^{t-1}) = \theta _{i_t}(x^{t-1})\text { and }\theta (x^t) = \theta _{i_t}(x^t) \\&\quad = \, \displaystyle { \sum _{t=1}^{T+1} } \, \left[ \, \theta _{i_t}(x^{t-1}) - \theta _i(x^{t-1}) \, \right] - \displaystyle { \sum _{t=1}^{T+1} } \, \left[ \, \theta _{i_t}(x^t) - \theta _i(x^t) \, \right] \\&\quad = \, \displaystyle { \sum _{t=1}^{T+1} } \, \left[ \, \theta _{i_t i}(x^{t-1}) - \theta _{i_t i}(x^t) \, \right] \\&\quad \le \, \displaystyle { \sum _{t=1}^{T+1} } \, \left[ \, \nabla \theta _{i_t i}(x^t)^T( \, x^{t-1} - x^t \, ) + \displaystyle { \frac{L_{i_t i}}{2} } \, \Vert \, x^{t-1} - x^t \, \Vert _2^2 \, \right] \quad \text{(by } (13))\\&\quad \le \, \displaystyle { \sum _{t=1}^{T+1} } \, \left\{ \, \nabla \theta _{i_ti}(x)^T( \, x^{t-1} - x^t \, ) + \left[ \, \nabla \theta _{i_t i}(x^t) - \nabla \theta _{i_t i}(x) \right] ^T ( \, x^{t-1} - x^t \, ) \, \right\} \\&\qquad + \displaystyle { \frac{\displaystyle { \max _{1 \le j \le I} } \, L_{ji}}{2} } \, \displaystyle { \sum _{t=1}^{T+1} } \, \Vert \, x^{t-1} - x^t \, \Vert _2^2 \\&\quad \le \, \displaystyle { \max _{1 \le j \le I} } \, \Vert \, \nabla \theta _{ji}(x) \, \Vert _2 \, \displaystyle { \sum _{t=1}^{T+1} } \, \Vert \, x^{t-1} - x^t \, \Vert _2 \\&\qquad + \displaystyle { \max _{1 \le j \le I} } \, L_{ji} \, \Vert \, x - \bar{x}^i \, \Vert _2 \, \displaystyle { \sum _{t=1}^{T+1} } \, \Vert \, x^{t-1} - x^t \, \Vert _2 \\&\qquad + \displaystyle { \frac{L_i}{2} } \, \Vert \, x - \bar{x}^i \, \Vert _2^2 \\&\quad = \, \displaystyle { \max _{1 \le j \le I} } \, \Vert \, \nabla \theta _{ji}(x) \, \Vert _2 \, \Vert \, x - \bar{x}^i \, \Vert _2 + \displaystyle { \frac{3 \, L_i}{2} } \, \Vert \, x - \bar{x}^i \, \Vert _2^2 \, = \, \phi _i(x) \quad \\&\qquad \qquad \text{ because } \Vert \, x - \bar{x}^i \, \Vert _2 = \text{ dist }(x;S^{\, i}), \end{aligned}$$

where the last inequality holds by the Cauchy–Schwartz inequality, the Lipschitz property of $\nabla \theta _{i_t i}$, and the identity $\sum _{t=1}^{T+1} \, \Vert x^{t-1} - x^t \Vert _2 = \Vert x - \bar{x}^i \Vert$. Thus $\psi _i(x) \ge \theta (x)$ for all $x \in \mathcal{{S}} {\setminus } S^{\, i}$ as claimed, and (14) follows readily. $\square$

We are now ready to formally state and prove the following main result of this section.

Theorem 12

Suppose that Q is copositive on $D_{\infty }$ and that $\text{ dom }(Q,D)$ is convex. Then the value function $\text{ qp }_\mathrm{opt}(q,b)$ is dc on $\text{ dom }(Q,D)$.

Proof

This follows readily from Proposition 11 by letting each pair $(S_i,\theta _i)$ be the quadratic piece identified in part (c) of Proposition 9. $\square$

Several remarks about the above results are in order. First, when each $\theta _i(x) = x^Ta^i + \alpha _i$ is an affine function for some N-vector $a^i$ and scalar $\alpha _i$, the representation (14) of the function $\theta$ becomes

$$\begin{aligned} \theta (x) \, = \, \displaystyle { \min _{1 \le i \le I} } \, \left[ \, \theta _i(x) + \text{ dist }(x;S^{\, i}) \, \displaystyle { \max _{1 \le j \le I} } \, \Vert \, a^j - a^i \, \Vert _2 \, \right] , \end{aligned}$$

which provides an alternative min–max representation of the piecewise affine function $\theta$ with affine pieces $\theta _i$; this is distinct from the max–min representation of such a piecewise function in [32, 48]. Second, when Q is positive semi-definite, $\text{ dom }(Q,D)$ is known to be convex; in fact, it is equal to the polyhedron $\left[ \begin{array}{cc} Q &{} -D^{\, T} \\ D &{} 0 \end{array} \right] \left( \mathbb {R}^m \times \mathbb {R}^k_+ \right) - \left( \{ 0 \} \times \mathbb {R}^k_+ \right)$, which is the set of pairs (q, b) for which the linear constraints (without the complementarity condition) of the KKT system (10) are feasible. Third, there are copositive, nonconvex QPs for which $\text{ dom }(Q,D)$ is convex. For instance, for a symmetric, (entry-wise) positive matrix Q and an identity matrix D, $\text{ dom }(Q,D)$ is equal to the entire space $\mathbb {R}^{m+k}$. More generally, if $D_{\infty } = \{ 0 \}$, then for any symmetric matrix Q, $\text{ dom }(Q,D) = \mathbb {R}^m \times \left[ \, D\mathbb {R}^m - \mathbb {R}^k_+ \, \right]$ is a convex polyhedron. Fourth, the convexity of ${\mathcal {S}}$ in Proposition 11 is a reasonable assumption because convex, and thus dc, functions are defined only on convex sets. Hence, the convexity requirement of $\text{ dom }(Q,D)$ in Theorem 12 is needed for one to speak about the dc property of $\text{ qp }_\mathrm{opt}(q,b)$. Admittedly, the dc representation in Theorem 12 is fairly complex, due to the possibly exponentially many quadratic pieces of the value function (cf. the proof of Proposition 9). This begs the question of whether a much simpler representation exists when the matrix Q is positive semi-definite (cf. the rather straightforward representation (7) in the positive definite case). There is presently no resolution to this question.

5 Univariate folded concave functions

The family of univariate folded concave functions was introduced [14] in the literature of sparsity representation as approximations of the univariate non-zero count function $\ell _0(t) \triangleq \left\{ \begin{array}{ll} 1 &{}\quad \text{ if }\quad t \ne 0 \\ 0 &{}\quad \text{ otherwise. } \end{array} \right.$ Formally, such a function is given by $\theta (t) \triangleq f( | t |)$, where f is a continuous, univariate concave function defined on $\mathbb {R}_+$. Since we take the domain of f to be the closed interval $[ 0, \infty )$, the composition property of dc functions [18, Theorem II, page 708] is not applicable to directly deduce that $\theta$ is dc. We formally state and prove the following result that is a unification of all the special cases discussed in [1]. Proposition 6 in [26] gives a different dc decomposition of such a folded concave function $\theta (t)$.

Proposition 13

Let f be a (continuous) univariate concave function defined on $\mathbb {R}_+$. The composite function $\theta (t) \triangleq f( | t |)$ is dc on $\mathbb {R}$ if and only if $f^{\, \prime }(0;+)$ exists and is finite, where

$$\begin{aligned} f^{\, \prime }(0;+) \, \triangleq \, \displaystyle { \lim _{\tau \downarrow 0} } \, \displaystyle { \frac{f(\tau ) - f(0)}{\tau } } \, = \, -\displaystyle { \lim _{\tau \uparrow 0} } \, \displaystyle { \frac{f(-\tau ) - f(0)}{\tau }}. \end{aligned}$$

(15)

Proof

Since a dc function must be directionally differentiable, a property inherited from a convex function, it suffices to prove the sufficiency claim of the result. Since f is concave on $\mathbb {R}_+$, it follows that

$$\begin{aligned} f(t) \, \le \, f(0) + f^{\, \prime }(0;+) \, t, \quad \forall \, t \, \ge \, 0. \end{aligned}$$

(16)

Fig. 1

$g(t)= \max \left( f_1(t),f_2(t) \right)$. Case (a): $f(|t|)=-|t|^2-1$; case (b)1: $f(|t|)=- 2(|t|-1)^2+3$; case (b)2: $f(|t|)=\sqrt{(|t|+1)}$

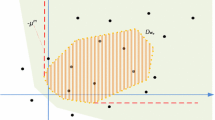
The proof is divided into 2 cases: (a) $f^{\, \prime }(0;+) \le 0$, or (b) $f^{\, \prime }(0;+) > 0$. (See Figure 1 for illustration.) In case (a), it follows that $t = 0$ is a maximum of the function $\theta$ on the interval $( -\infty ,\infty )$ by (16). Further, we claim that the function $\theta$ is concave on the real line in this case. To prove the claim, it suffices to show that if $t_1> 0 > t_2$, then the secant, denoted S, joining the two points $( t_1, \theta (t_1) )$ and $( t_2, \theta (t_2) )$, where $\theta (t_1) = f(t_1)$ and $\theta (t_2) = f(-t_2)$, on the curve of $\theta (t)$ is below the curve $\theta (t)$ itself for t in the interval $( t_2, t_1 )$. This can be argued as follows. The secant S can be divided into two sub-secants, one, denoted $S_1$, starting at the end point $( t_1, \theta (t_1) )$, and ending at $\left( 0, \theta (t_2) - \frac{\theta (t_1) - \theta (t_2)}{t_1 - t_2} \, t_2 \right)$; and the other, denoted $S_2$, starting at the latter end point and ending at $( t_2, \theta (t_2) )$. It is not difficult to see that the sub-secant $S_1$ lies below the line segment joining $( t_1, \theta (t_1) )$ and $(0,\theta (0))$, which in turn lies below the curve of $\theta (t)$ for $t \in ( t_1, 0)$ by concavity of f; furthermore, for the same token, the sub-secant $S_2$ lies below the line segment joining $(0,\theta (0))$ to $( t_2, \theta (t_2) )$, which in turn lies below the curve of $\theta (t)$ for $t \in ( 0, t_2 )$. This establishes the concavity of $\theta$ in case (a).

Consider case (b); i.e., suppose $f^{\, \prime }(0;+) > 0$. Consider the half-line $t \mapsto f(0) + f^{\, \prime }(0;+) t$ emanating from the point (0, f(0)) for $t < 0$. Let $t_-^* < 0$ be the right-most $t < 0$ such that this line meets the curve $\theta (t) = f(-t)$ to the left of the origin. If this does not happen, we let $t_-^* = -\infty$. Define the function:

$$\begin{aligned} \begin{array}{ll} f_1(t) \, \triangleq \, \left\{ \begin{array}{ll} f(t) &{}\quad \text{ if }\quad t \, \ge \, 0 \\ f(0) + f^{\, \prime }(0;+) t &{}\quad \text{ if }\quad t \, \in \, [ \, t_-^*,0 \, ] \\ f(-t) &{}\quad \text{ if }\quad t \, < \, t_-^*, \end{array} \right\} &{}\quad \text{ if }\quad t_-^* > -\infty \\ f_1(t) \, \triangleq \, \left\{ \begin{array}{ll} f(t) &{}\quad \text{ if }\quad t \, \ge \, 0 \\ f(0) + f^{\, \prime }(0;+) t &{}\quad \text{ if }\quad t \, \in \, ( \, -\infty , 0 \, ] \end{array} \right\}&\quad \text{ if }\quad t_-^* = -\infty \end{array} \end{aligned}$$

We claim that this function is concave on $\mathbb {R}$ and $f_1(t) \le f(-t)$ for $t \in ( \, t_-^*,0 \, ]$. Indeed, since $f^{\, \prime }(0;+) > 0$, it follows that $f(-t) > f(0) + f^{\, \prime }(0;+) \, t$ for all $t \in ( t_-^*,0 )$ by the definition of $t_-^*$. The concavity of $f_1(t)$ can be proved in a way similar to the above proof of case (a), by considering sub-segments. Details are omitted. Similarly, define $t_+^* > 0$ as the left-most $t > 0$ such that half-line $t \mapsto f(0) - f^{\, \prime }(0;+) \, t$ meets the curve $\theta (t) = f(t)$ to the right of the origin and let $t_+^* = \infty$ if this does not happen. Define the function:

$$\begin{aligned} \begin{array}{ll} f_2(t) \, \triangleq \, \left\{ \begin{array}{ll} f(-t) &{}\quad \text{ if }\quad t \, \le \, 0 \\ f(0) - f^{\, \prime }(0;+) t &{}\quad \text{ if }\quad t \, \in \, [ \, 0, t_+^* \, ] \\ f(t) &{}\quad \text{ if }\quad t \, > \, t_+^*, \end{array} \right\} &{}\quad \text{ if }\quad t_+^* < \infty \\ f_2(t) \, \triangleq \, \left\{ \begin{array}{ll} f(-t) &{}\quad \text{ if }\quad t \, \le \, 0 \\ f(0) - f^{\, \prime }(0;+) t &{}\quad \text{ if }\quad t \, \in \, [ \, 0, \infty \, ) \end{array} \right\}&\quad \text{ if }\quad t_+^* = \infty \end{array} \end{aligned}$$

We can similarly show that $f_2(t)$ is concave on $\mathbb {R}$ and $f_2(t) \le f(t)$ for $t \in [ \, 0, t_+^* \, )$. Now define $g(t) \triangleq \max \left( f_1(t),f_2(t) \right)$ for all $t \in \mathbb {R}$. As the pointwise maximum of two concave functions, g is dc. It remains to show that $g(t) = \theta (t)$ for all $t \in \mathbb {R}$. This can be divided into 2 cases: $t \ge 0$ and $t \le 0$. In each case, the above established properties of the two functions $f_1$ and $f_2$ can be applied to complete the proof. $\square$

Remarks

Being not dc, the univariate function $\theta (t) \triangleq \sqrt{| \, t \, |}$ provides a counter-example to illustrate the important role of the existence of the limit (15). Another relevant remark is that the following fact is known [18, page 707]: “if ${\mathcal {D}}$ is a (bounded or unbounded) interval, then the univariate function f is dc on ${\mathcal {D}}$ if and only if f has left and right derivatives (where these are meaningful) and these derivatives are of bounded variation on every closed bounded interval interior to ${\mathcal {D}}$”. We have not applied this fact to prove Proposition 13 because our proof provides a simple construction of the dc representation of the function $\theta$ in terms of the function f. $\square$