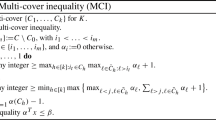1 Introduction

For \(n>0\), define the vector \(\lambda =\{\lambda _i,i=1,\ldots ,n\}\) where \(\lambda _i=i/n\). The vector \(\lambda \) is referred to as the lineality of n. A master knapsack problem of order n is defined to be

$$\begin{aligned} \max&vt, \end{aligned}$$
(1)
$$\begin{aligned} st&\sum _{i=1}^{n}\lambda _it_i = 1, \end{aligned}$$
(2)
$$\begin{aligned}&t \ge 0, \end{aligned}$$
(3)
$$\begin{aligned}&t_i\hbox { are integers}, \end{aligned}$$
(4)

where \(v\ge 0\). The constraints (2), (3) and (4) define the master knapsack problem K(n). The convex hull of the solutions to K(n) is denoted by P(K(n)) and referred to as the master knapsack polytope. The dimension of P(K(n)) is \(n-1\) and the non-negativity constraints (3) are facet defining for \(i\ge 2\): \(t_1\ge 0\) is not facet defining. (See Shim [14] and Shim and Johnson [15].) We call the facet-defining non-negativity constraints as trivial facets. The other facets are called knapsack facets. Since P(K(n)) is not full dimensional, each knapsack facet has infinitely many representations.

In Fulkerson’s blocking framework of the cyclic group and the knapsack problems, Gomory [8] and Aráoz [1] preferred subadditive relations of \(\pi \)-variables for characterizing the facets; in particular, knapsack facets are represented by \(\pi t\ge \pi _n\) for P(K(n)), where \(\pi \) is the length n row vector of coefficients. In this paper, we use an alternative characterization \(\xi =-\pi \) of knapsack facets \(\xi t\le 1\) using superadditive relations between components of the vector \(\xi \) once we fix \(\xi _1=0\) and \(\xi _n=1\). This characterization is inspired by the characterization of packing knapsack facets in Hunsaker [13]. The superadditive characterization of knapsack facets allows us to identify some classes of strong facets for which Chopra et al. [4] develop efficient separation algorithm. This would not be possible with the subadditive representation. Given our representation, we define a coefficient vector \(\xi \) to be a 1 / k -facet if k is the smallest integer such that

$$\begin{aligned} \left. \begin{array}{ll} {\xi }_i\in \left\{ {0}/{k},{1}/{k},{2}/{k},\ldots ,{k}/{k}\right\} &{}\hbox { for all }i\hbox { for { k} even},\\ {\xi }_i\in \left\{ {0}/{k},{1}/{k},{2}/{k},\ldots ,{k}/{k}\right\} \cup \left\{ {1}/{2}\right\} &{}\hbox { for all }i\hbox { for { k} odd}. \end{array} \right\} \end{aligned}$$
(5)

1 / k-facets build on 1-facets (\(k=1\)) first defined by Aráoz et al. [2]. In Sect. 2, we introduce the knapsack facets dealt with in this paper.

The ultimate value of studying the master knapsack polytope comes from our ability to use this information to solve the general integer knapsack problem where some of the variables \(t_i\) are missing (or set to 0). We believe that 1 / k-facets for small values of k can play an important role in this regard. This paper shows that 1 / k-facets for small values of k are “strong” for the master knapsack polytope. Our work in Chopra et al. [4] shows that 1 / k-facets can be separated effectively for small k. As a result 1 / k-facets for small k can be used effectively when solving the general knapsack problem.

There have been a variety of approaches used to define the strength of a facet defining inequality. Gomory introduced the shooting experiment as a way to measure the size of a facet (see Gomory et al. [12].) The shooting experiment shoots arrows in random directions from the origin and counts the number of shots that hit each facet. The size of each facet is proportional to the number of shots absorbed by it. Goemans [7] provides an alternative approach to understand the strength of a class of facet defining inequalities for the traveling salesman problem (TSP). In his approach, if P and Q are polyhedra in \({\mathbb R}^n\) where P is a relaxation of Q obtained by dropping some inequalities from Q, then the strength of the dropped inequalities from Q can be measured by the ratio

$$\begin{aligned} t(P,Q)=\sup _{c\in {\mathbb R}^n_+}\frac{\min \{ cx:x\in Q\}}{\min \{ cx:x\in P\}}. \end{aligned}$$

Given that our goal is to identify strong knapsack facets, we use a similar approach to identify the strength of 1 / k-facets. For any knapsack facet \(\xi t\le 1\) define \(P(K(n)-\xi )\) to be the polytope obtained by eliminating the inequality \(\xi t\le 1\) from a minimal complete inequality description of P(K(n)). Using Goemans’ terminology, \(P(K(n)-\xi )\) is a relaxation of P(K(n)). Let \(z^{LP(\xi )}(v)=\max \{ vt: t\in P(K(n)-\xi )\}\) and \(z^{IP}(v)=\max \{ vt:t\in P(K(n))\}\). We thus measure the strength of the knapsack facet \(\xi t\le 1\) through its \(\xi \)-relaxation gap given by the ratio

$$\begin{aligned} \max _{v\in {\mathbb R}^n_+}\frac{z^{LP(\xi )}(v)}{z^{IP}(v)}. \end{aligned}$$

Observe that the \(\xi \)-relaxation gap for an inequality \(\xi t\le 1\) is obtained when \(v=\xi \). If \(\xi t\le 1\) is a facet defining inequality, \(z^{IP}(\xi )=1\). We thus obtain

$$\begin{aligned} \max _{v\in {\mathbb R}^n_+}\frac{z^{LP(\xi )}(v)}{z^{IP}(v)}=\frac{z^{LP(\xi )}(\xi )}{z^{IP}(\xi )}=z^{LP(\xi )}(\xi ). \end{aligned}$$
(6)

The larger the \(\xi \)-relaxation gap, the stronger the corresponding inequality is because its removal from a complete inequality description increases the worst case objective function value by a large amount. In this paper, we use the \(\xi \)-relaxation gap to characterize the strength of 1 / k-facets.

We initiated our research by explicitly evaluating the \(\xi \)-relaxation gap for all knapsack facets of the master knapsack polytopes P(K(n)) for \(n\le 26\). Our computational analysis for \(n\le 26\) showed the following patterns:

  1. 1.

    The \(\xi \)-relaxation gaps of all the knapsack facets are \(\le 1+{1}/{2}\).

  2. 2.

    The 1-facets have \(\xi \)-relaxation gaps of \(1+1/2\), \(1+1/3\) or \(1+1/4\).

  3. 3.

    The 1-facets are strongest (i.e. have the largest \(\xi \)-relaxation gap) and all other knapsack facets have \(\xi \)-relaxation gaps \(<1+1/4\).

  4. 4.

    The next strongest knapsack facets are 1 / 3-facets and 1 / 4-facets with \(\xi \)-relaxation gap of \(1+1/6\).

In Sects. 4 and 5, we prove the \(\xi \)-relaxation gaps of the 1-facets to be \(1+1/2\), \(1+1/3\) or \(1+1/4\) for all n as suggested in Observation 2. In Sect. 6, we prove that \(\xi \)-relaxation gap of 1 / 3-facets is at most 1+1/6 as mentioned in Observation 4. In Sect. 7, we prove the \(\xi \)-relaxation gap of 1 / 4-facets is strictly less than 1+1/4. In Sect. 8, we show that the \(\xi \)-relaxation gaps of the knapsack facets except the 1-facets are strictly less than \(1+1/2\). That is, the upper bound \(1+1/2\) is achieved only among the 1-facets, which verifies Observation 1 and provides some support for Observation 3.

For large values of n it is very time consuming to evaluate the \(\xi \)-relaxation gap. Thus, we used the shooting experiment to estimate the size of 1 / k-facets for large values of n (see Chopra et al. [4]). The shooting experiment results further validated Observations 1–4 and provided the following further observations:

  1. 5.

    The size of 1 / k-facets decreases as k grows.

  2. 6.

    The size of 1 / k-facets is smaller for k odd and larger for k even.

  3. 7.

    There are spikes of the size of 1 / k-facets at k where \(k+1\) divides \(n+1\).

While Observation 7 is previously known from Gomory et al. [12], all other Observations 1-6 are new. In Sect. 9, we perform the worst case analysis for a subset of 1 / k-facets defined in closed form by Aráoz et al. [2]. Consistent with Observation 5, we identify upper bounds of these 1 / k-facets to be \(1+1/k\) which decreases as k grows. We identify tighter upper bounds \(1+1/2k\) for k odd, providing support for Observation 6.

Following Gomory, several authors have studied polyhedra corresponding to binary and cyclic groups. For example, Gomory and Johnson [9, 10] defined two-slope facets for master cyclic group polyhedra, and Cornuejols and Molinaro [6] and Basu et al. [3] have defined other families of facets for such polyhedra, including three-slope and \((k + 1)\)-slope facets. Shu et al. [16] gave a new class of 1/3- and 1/4-facets with no 0-valued coefficient for master binary group polyhedra. Araoz et al. [2] studied the relation between cyclic group and knapsack facets, and defined strong families of knapsack facets that mainly came from 2-slope facets in the subadditive representation.

2 Characterization of 1 / k-facets

The work of Gomory [8] and Araoz [1] allows us to obtain all knapsack facets \(\xi t \le 1\) as the extreme points of a polytope described by polynomially many relations:

Theorem 2.1

The coefficient vectors \(\xi \) of the knapsack facets \(\xi t\le 1\) of P(K(n)) with \(\xi _1=0\) and \(\xi _n=1\) are the extreme points of the system of linear constraints

$$\begin{aligned} \xi _i+\xi _j\le & {} \xi _{i+j} \quad \hbox { whenever }i+j<n, \end{aligned}$$
(7)
$$\begin{aligned} \xi _i+\xi _{n-i}= & {} 1 \qquad \; \hbox { for }1\le i\le n/2, \end{aligned}$$
(8)
$$\begin{aligned} \xi _1= & {} 0, \end{aligned}$$
(9)
$$\begin{aligned} \xi _n= & {} 1. \end{aligned}$$
(10)

All feasible solutions to the system give valid inequalities \(\xi t\le 1\) for P(K(n)).

Fixing \(\xi _1=0\) is inspired by the characterization of the packing knapsack facets in Hunsaker [13]. The knapsack facets become perpendicular to the first non-negativity constraint \(t_1\ge 0\) by fixing \(\xi _1=0\).

The relations (7) and (8) are referred to as superadditivities and complementarities respectively. Due to superadditivities (7) and the fact that \(\xi _1=0\), the coefficients of every knapsack facet \(\xi \) must be a non-decreasing sequence, i.e.,

$$\begin{aligned} \xi _i=\xi _1+\xi _i\le \xi _{i+1}\hbox { for all }i=1,\ldots ,n-1. \end{aligned}$$
(11)

If \(\xi \) is a 1 / k-facet, due to the complementarities (8), \(\xi \) is symmetric in that if \(\xi _i=m/k\) then \(\xi _{n-i}=(k-m)/k\). Let \(\xi \) be a symmetric non-decreasing vector as defined in (5). Then, \(\xi \) is uniquely determined by a non-decreasing sequence of indices \((a_m=\min \{i:\xi _i\ge m/k\})\) (or \((a^k_m)\) if we need distinguish k from others) where \(a_m\) represents the first index i such that \(\xi _i\ge m/k\). Such a vector \(\xi \) will be denoted by \(\xi ^{k - (a_m)}\). In this paper, a 1 / k-facet \(\xi t\le 1\) will sometimes be denoted by \(\xi ^{k - (a_m)}\) and at other times in terms of its individual components \(\xi _i\) or \(\xi (i)\).

Observe that k / 2 is not an integer for k odd but is required to obtain the coefficient 1 / 2. Also, because of symmetry, the number of \(\xi _i\)’s of value m / k must equal the number of those of value \((k-m)/k\). Thus, \(a_m\) for \(m=1,\ldots ,k/2\) are enough to define \(\xi ^{k - (a_m)}\) where \(a_{k/2}\) corresponds to the first index i such that \(\xi _i=1/2\). For any knapsack facet \(\xi ^{k - (a_m)}\), the interval \(a_{k/2}\) to \(n - a_{k/2}\) with all coefficients having value 1 / 2 is referred to as the half landing. We can easily see that \(a_{k/2} > n/3\) (this implies that \(n - a_{k/2} < 2n/3\)). A 1 / k-facet is a special case for a 1 / k-inequality defined in Chopra et al. [4]. In the rest of this section we introduce a variety of 1 / k-facets that will be studied in the paper. Each special case introduced by us can be described in closed form.

2.1 The 1-facets

The 1-facets are the 1 / k-facets with \(k = 1\). A 1-facet \(\xi ^{1 - (a_{1/2},a_1)}\) is thus defined by the indices \(\{ a_{1/2}, a_1\}\) where \(a_{1/2}\) is the first index with coefficient at least 1 / 2 and \(a_1\) is the first index with coefficient 1. If \(a_{1/2} = a_1\), there is no half landing. If \(a_{1/2} < a_1\), the half-landing of the 1-facet is from \(a_{1/2}\) to \(n-a_{1/2}=a_1 - 1\). One of \(a_{1/2}\) and \(a_1\) is enough to decide the other and therefore define the 1-facet. Shim and Johnson [15] defined the rank r of a 1-facet as

$$\begin{aligned} r=\left\lceil \frac{n}{2}\right\rceil -a_{1/2}. \end{aligned}$$

The largest possible rank of a 1-facet is denoted by R(n) which is the largest integer satisfying

$$\begin{aligned} R(n)<\left\lceil \frac{n}{2}\right\rceil -\frac{n}{3}. \end{aligned}$$

Figure 1 illustrates the coefficients of the 1-facet of rank 2 for P(K(16)). Observe that \(\xi _i=0\) for \(0\le i\le 5\), \(\xi _i=1/2\) for \(6\le i\le 10\), and \(\xi _i=1\) for \(11\le i\le 16\).

2.2 The 1 / 3-facets and the 1 / 4-facets

The 1 / 3- and 1 / 4-facets are the 1 / k-facets with \(k=3\) and \(k=4\) respectively. Figure 2 illustrates a 1 / 3-facet of P(K(19)). A 1 / 3-facet \(\xi ^{3 - (a_m)}\) is determined by the first index \(i=a_1\) of \(\xi _i=1/3\) and the first index \(i=a_{3/2}\) of \(\xi _i\ge 1/2\). We see that \(a_2=n-a_{3/2}+1\) and \(a_3=n-a_1+1\) and simply denote \(\xi ^{3 - (a_1,a_{3/2},a_2,a_3)}\) by \(\xi ^{3 - (a_1,a_{3/2})}\). Chopra et al. [5] have given the following characterization of the 1 / 3-facets by restrictions to and relations between \(a_1\) and \(a_{3/2}\).

Fig. 1
figure 1

The graph \(\left( i,\xi ^{1 - (6,11)}_i\right) \) of a 1-facet of P(K(16))

Full size image

Theorem 2.2

(Chopra et al. [5]) Let \(\xi ^{3 - (a^3_1,a^3_{3/2})}\) be a symmetric non-decreasing vector given by \(a^3_1<a^3_{3/2}\le (n+1)/2\). It is a knapsack facet, if and only if

$$\begin{aligned} 2a^3_1+a^3_{3/2}\ge & {} n+1,\hbox { and} \end{aligned}$$
(12)
$$\begin{aligned} 3a^3_1\le & {} n. \end{aligned}$$
(13)
Fig. 2
figure 2

Knapsack facet \({\xi }^{3 - (5,10)}\) of P(K(19))

Full size image

Likewise, a 1 / 4-facet \(\xi ^{4 - (a_1,a_2)}\) is determined by \(a_1\) and \(a_{2}=a_{4/2}\). The 1 / 4-facets can be characterized as follows:

Theorem 2.3

(Chopra et al. [5]) The vector \(\xi ^{4 - (a_1,a_2)}\) is a knapsack facet, if and only if

$$\begin{aligned} a_2\ge & {} \frac{n-a_1+1}{2}, \end{aligned}$$
(14)
$$\begin{aligned} a_2\le & {} 2a_1,\hbox { and } \end{aligned}$$
(15)
$$\begin{aligned} a_2\le & {} n-2a_1. \end{aligned}$$
(16)
Fig. 3
figure 3

The coefficients of the regular 1 / 6-facet of rank 1 for P(K(18))

Full size image

2.3 The regular 1 / k-facets

Aráoz et al. [2] defined regular 1 / k-facets as follows. Let \(n=kd\) with divisors \(k\ge 3\) and \(d\ge 3\). The regular 1 / k-facet \(\xi ^{k - (a_m)}\) of rank r is the 1 / k-facet given by

$$\begin{aligned} a_m= & {} md\hbox { for }m<\frac{k}{2}\hbox { and } \end{aligned}$$
(17)
$$\begin{aligned} \frac{n-d+1}{2}\le a_{k/2}= & {} \left\lceil \frac{n}{2}\right\rceil -r\le \frac{n+1}{2}. \end{aligned}$$
(18)

The largest rank is denoted by \(R^k(n)\). Observe that regular 1 / k-facets are a subset of all 1 / k-facets where each coefficient m / k for \(1\le m< k/2\) (for \(k/2<m\le n\)) begins (ends) at regular intervals at the index md where \(n=kd\). For general 1 / k-facets the starting index \(a_m\) for each coefficient m / k need not be regularly distributed.

Figure 3 illustrates the coefficients of the regular 1 / 6-facet of rank \(r=1\) for P(K(18)). Observe that the coefficients of the facet coincide with the coefficients of the lineality \(\lambda =(1/n,2/n,\ldots ,n/n)\) for every index \(i=md\) for \(m\in \{ 0,1,..,k\}\). Also observe that the coefficients to the left of the half landing are less than or equal to the corresponding coefficients in the lineality \(\lambda \). The coefficients to the right of the half landing are greater than or equal to the corresponding coefficients in the lineality \(\lambda \). As k grows, the regular 1 / k-facet of rank 0 converges to the lineality \(\lambda \).

3 A general approach to finding the \(\xi \)-relaxation gap

In this section we describe the general approach used in the rest of the paper to find the \(\xi \)-relaxation gap and also give some preliminary results that are used later in the proofs. Assume that we know the complete inequality description of the polytope P(K(n)). For any objective \(v\ge 0\), the primal linear program over P(K(n)) can be written as

$$\begin{aligned} \max \left\{ vt:\ \lambda t=1,\ t\ge 0\hbox { and }\xi ^lt\le 1\hbox { for }l=1,\ldots ,K\right\} , \end{aligned}$$
(19)

where \(\lambda =(1/n,2/n,\ldots ,n/n)\) and \(\xi ^l, l=1,\ldots ,K,\) are all the knapsack facets. The dual problem can be written as

$$\begin{aligned} \min&x_0+x_1+\cdots +x_K, \end{aligned}$$
(20)
$$\begin{aligned} st&x_0 \lambda + x_1\xi ^1+\cdots +x_K\xi ^K\ge v, \end{aligned}$$
(21)
$$\begin{aligned}&x_i\ge 0\hbox { for }i=1,\ldots ,K. \end{aligned}$$
(22)

Given any knapsack facet \(\xi ^l t\le 1\) from the complete inequality description, define \(P(K(n)-\xi ^l)\) to be the polytope obtained by deleting the inequality \(\xi ^l t\le 1\) from P(K(n)), where we keep all \(t_i\ge 0\) including \(t_1\ge 0\) though it is not facet-defining for P(K(n)). To obtain the \(\xi \)-relaxation gap \(z^{LP(\xi ^l)}(\xi ^l)\) we proceed as follows. The first step is to obtain a primal feasible solution \(\hat{t}\) (referred to as the primal certificate) to

$$\begin{aligned} \max \{ \xi ^l t : t\in P(K(n)-\xi ^l) \}. \end{aligned}$$

The next step is to obtain a dual feasible solution x satisfying (21) and (22) with \(x_l=0\) (referred to as the dual certificate) such that the primal and dual objectives have the same value. We then obtain

$$\begin{aligned} z^{LP(\xi ^l)}(\xi ^l)=\xi ^l \hat{t}. \end{aligned}$$

3.1 Some useful results

In this section, we prove some lemmas that are used for proving theorems throughout this paper. Our first result gives a minimal representation of the system (7)–(10):

Lemma 3.1

(Shim [14]) A minimal representation of the system (7)–(10) is given by replacing the inequalities (7) with

$$\begin{aligned}&\xi _i+\xi _j\le \xi _{i+j}\hbox { for }i\le j<i+j<n/2, \end{aligned}$$
(23)
$$\begin{aligned}&\xi _i+\xi _j+\xi _{n-i-j}\le 1\hbox { for }i\le j\le n-i-j<n/2, \end{aligned}$$
(24)
$$\begin{aligned}&\hbox { and }2\xi \left( \frac{n}{4}\right) \le \xi \left( \frac{n}{2}\right) =\frac{1}{2} \hbox { if }n\equiv 0\mod 4. \end{aligned}$$
(25)

The next lemmas give a sufficient condition for an inequality \(\xi ^{k - (a_m)}\) to be a knapsack facet. Chopra et al. [4] discover that the super-additivity relations of \(\xi _i\) are equivalent to the subadditivity relations of \(a_m\). The main idea is that \((m_1 + m_2)/k = \xi (a_{m_1}) + \xi (a_{m_2}) \le \xi (a_{m_1} + a_{m_2})\) implies \(a_{m_1+m_2} \le a_{m_1} + a_{m_2}\) by the definition of \(a_{m_1+m_2}\). The next lemma is a special case for strict (including all multiples of 1 / k) 1 / k-inequalities \(\xi \).

Lemma 3.2

Let \(\xi ^{k -(a_m)}\) have all the multiples of 1 / k except 1/2; i.e.,

$$\begin{aligned} \xi ^{k -(a_m)} (a_m) = \frac{m}{k}\hbox { for all }m\ne \frac{k}{2}. \end{aligned}$$
(26)

It satisfies (7) if and only if

$$\begin{aligned} a_{m_1}+a_{m_2}\ge a_{\lceil m_1+m_2\rceil }\hbox { for all }m_1\le m_2\hbox { with }\lceil m_1+m_2\rceil \le k. \end{aligned}$$
(27)

Lemma 3.3

Let \(\xi ^{k - (a_m)}\) satisfy (26) and (27). The inequality \(\xi ^{k - (a_m)}\) is a knapsack facet if

  1. (a)

    \(\xi ^{k - (a_m)}(a_1)+\xi ^{k - (a_m)}(a_{m-1})=\xi ^{k - (a_m)}(a_1+a_{m-1})\) for \(1<m<k/2\), and

  2. (b)

    \(\xi ^{k - (a_m)}(a_{m_1})+\xi ^{k - (a_m)}(a_{m_2})=\xi ^{k - (a_m)}(a_{m_1}+a_{m_2})\) for some \(m_1\le m_2<k/2\) with \(k/2\le m_1+m_2< k\).

Proof

Let \(\xi \) satisfy all binding constraints of \(\xi ^{k - (a_m)}\) among (7)–(10) as equalities. We show that \(\xi \) is uniquely determined to be \(\xi =\xi ^{k - (a_m)}\), which will complete the proof of the lemma.

We easily see that \(\xi _1+\xi _{i-1}=\xi _{i-1}=\xi _i\) for \(i\ne a_m\) imply

$$\begin{aligned} \begin{array}{ll} \xi _i=\xi (a_m)&{}\hbox { for }a_m\le i<a_{m+1}\hbox { for } k ~\hbox {even}\\ \xi _i=\xi (a_m)&{}\hbox { for }\left\{ \begin{array}{l} a_m\le i<a_{m+1},m+1\le \lfloor \frac{k}{2}\rfloor ,\hbox { for } k ~\hbox {odd}\\ a_m\le i<a_{k/2},m=\lfloor \frac{k}{2}\rfloor ,\hbox { for } k ~\hbox {odd}. \end{array} \right. \end{array} \end{aligned}$$
(28)

Now, we only need to show that \(\xi (a_m) = m\xi (a_1) = m/k\) for \(m\ne k/2\), and \(\xi (a_{k/2})=1/2\) if \(a_{k/2}<a_{\lfloor k/2+1\rfloor }\).

From (28) and complementarities (8), we see

$$\begin{aligned} \xi (a_m) = 1-\xi (a_{k-m}) \hbox { (in particular, } \xi (a_{k/2})=1-\xi (a_{k/2})=1/2) \end{aligned}$$
(29)

unless \(m=k/2\) and \(a_{k/2}=a_{\lfloor k/2+1\rfloor }\). From (28), (a) implies that

$$\begin{aligned} \xi (a_1)+\xi (a_{m-1})=\xi (a_1+a_{m-1})=\xi (a_m)\hbox { for }1<m<k/2 \end{aligned}$$

and therefore

$$\begin{aligned} \xi (a_m) = m\xi (a_1)\hbox { for }1<m<k/2. \end{aligned}$$
(30)

From (28), (b) is followed by

$$\begin{aligned} \xi (a_{m_1}+a_{m_2})=\xi (a_{m_1+m_2}). \end{aligned}$$
(31)

From (30), (31) and (29), (b) implies

$$\begin{aligned} (m_1+m_2)\xi (a_1)= & {} \xi (a_{m_1})+\xi (a_{m_2})=\xi (a_{m_1}+a_{m_2})\\= & {} \xi (a_{m_1+m_2})=1-\xi (a_{k-m_1-m_2})\\= & {} 1-(k-m_1-m_2)\xi (a_1). \end{aligned}$$

Thus, we have \(\xi (a_1)=1/k\) and so \(\xi (a_m) = m/k=\xi ^{k - (a_m)}(a_m)\), completing the proof of the lemma. \(\square \)

The next lemma shows that the 1-facets have the smallest support.

Lemma 3.4

Let \(a_{1/2}(R(n))\) be the first index of the half landing of the 1-facet of the largest rank R(n). If a knapsack facet \(\xi \) with \(\xi _1=0\) and \(\xi _n=1\) has \(\xi _{a_{1/2}(R(n))-1}=0\), then \(\xi \) is a 1-facet.

Proof

Let \(\xi ^{1 - (a_{1/2})}\) be the 1-facet with \(a_{1/2}\) equal to the index of the first non-zero component (which must be 1/2 or 1) of \(\xi \). That is, \(\xi _{a_{1/2}}> 0\) and \(\xi _i=0\) for all \(i<a_{1/2}\). The knapsack facet \(\xi \) satisfies n linearly independent equality constraints including the equalities in (8)–(10) and binding constraints from (23) and (24). Note that \(\xi \) does not satisfy (25) as equality because \(\xi \left( \frac{n}{4}\right) =0\) when \(n\equiv 0\mod 4\).

We show that all the binding constraints from (23) and (24) are satisfied as equalities by \(\xi ^{1 - (a_{1/2})}\). Since \(i\le j<i+j<n/2\) implies \(i<n/4<a_{1/2}(R(n))\) and therefore \(\xi _i=0\), every binding constraint from (23) is written as

$$\begin{aligned} \xi _i+\xi _j=0+\xi _j=\xi _{i+j}. \end{aligned}$$

Given that it is satisfied as equality by \(\xi ^{1 - (a_{1/2})}\), we have

$$\begin{aligned} \xi ^{1 - (a_{1/2})}_i+\xi ^{1 - (a_{1/2})}_j=0+\xi ^{1 - (a_{1/2})}_j=\xi ^{1 - (a_{1/2})}_{i+j}=0\hbox { or }\frac{1}{2}. \end{aligned}$$

Since \(i\le j\le n-i-j<n/2\) implies \(i\le n/3<a_{1/2}(R(n))\) and therefore \(\xi _i=0\), every binding constraint from (24) is of the form

$$\begin{aligned} \xi _i+\xi _j+\xi _{n-i-j}=0+\xi _j+\xi _{n-i-j}=1. \end{aligned}$$

From \(\xi _j\le 1/2\) and \(\xi _{n-i-j}\le 1/2\), we have

$$\begin{aligned} \xi _j=\xi _{n-i-j}=\xi ^{1 - (a_{1/2})}_j=\xi ^{1 - (a_{1/2})}_{n-i-j}=\frac{1}{2}. \end{aligned}$$

The binding constraint is satisfied as equality by \(\xi ^{1 - (a_{1/2})}\). Thus, the n constraints uniquely determine \(\xi =\xi ^{1 - (a_{1/2})}\) completing the proof. \(\square \)

4 The 1-facet of rank 0

In this section, we show that the \(\xi \)-relaxation gap for any 1-facet \(\xi t\le 1\) of rank 0 is 1+1/2 for \(n\not \equiv 0\mod 4\) and 1+1/3 for \(n=0\mod 4\) as mentioned in Observation 2. Given a 1-facet \(\xi ^{1 - (a_{1/2})}\) of rank 0, let \(a_1\) be the index of the first coefficient equal to 1. We observe that \(a_1\) is the smallest integer that is larger than n / 2.

To prove the worst case bound, we provide a primal certificate \(\hat{t}\in P( K(n)-\xi ^{1 - (a_{1/2})})\) with objective function value 3/2 if \(n\not \equiv 0\mod 4\) and 4/3 if \(n\equiv 0\mod 4\). We then provide a dual certificate with only one non-zero component which is shown to be 3 / 2 if \(n\not \equiv 0\mod 4\) and 4/3 if \(n\equiv 0\mod 4\). Thus, the primal objective value is the same as the dual objective value, proving the \(\xi \)-relaxation gap of the 1-facet of rank 0 by strong duality. We first prove the result for \(n\not \equiv 0\mod 4\).

Lemma 4.1

Let \(n\not \equiv 0\mod 4\) and let \(a_1\) denote the index of the first coefficient equal to 1 of the 1-facet of rank 0. If a knapsack facet \(\xi \) satisfies

$$\begin{aligned} \xi _{a_1}>2/3, \end{aligned}$$
(32)

then it must be the 1-facet of rank 0.

Proof

We show that if (32) holds or equivalently if it holds that

$$\begin{aligned} \xi _{n-a_1}=1-\xi _{a_1}<1-\frac{2}{3}=\frac{1}{3}, \end{aligned}$$
(33)

then \(\xi \) is the 1-facet of rank 0. For the knapsack facet \(\xi \), consider the binding constraints from (8)–(10) and (23)–(24). (Since \(n\not \equiv 0\mod 4\), we don’t have to consider (25).) We show that none of the binding constraints comes from (24) and therefore the 1-facet of rank 0 is uniquely determined to be \(\xi \) by the binding constraints.

By complementarities (8), (24) is equivalent to

$$\begin{aligned} \xi _i+\xi _j\le 1-\xi _{n-i-j}=\xi _{i+j}, \end{aligned}$$

where \(i\le j<n/2<i+j\) implies

$$\begin{aligned} \xi _i+\xi _j \le \xi _{n-a_1}+\xi _{n-a_1}< \frac{1}{3} + \frac{1}{3} = \frac{2}{3}<\xi _{a_1}\le \xi _{i+j}. \end{aligned}$$
(34)

Therefore, \(\xi \) does not satisfy any constraint in (24) as equality, and the 1-facet of rank 0 satisfies all binding constraints of \(\xi \), completing the proof of \(\xi \) being the 1-facet of rank 0. \(\square \)

In the next result, we obtain our primal certificate.

Lemma 4.2

Let \(n\not \equiv 0\mod 4\) and let \(a_1\) denote the index of the first coefficient equal to 1 of the 1-facet \(\xi ^{1 - (a_{1/2})}\) of rank 0. Then, \(\hat{t}\) given by

$$\begin{aligned} \hat{t}_i =\left\{ \begin{array}{ll} n-{3a_1}/{2}&{}\hbox { for }i=1,\\ 3/2&{}\hbox { for }i=a_1,\\ 0&{}\hbox { for }i\ne 1\hbox { or }a_1 \end{array} \right. \end{aligned}$$
(35)

is a feasible solution to the LP problem maximizing \(\xi ^{1 - (a_{1/2})} t\) over \(P\left( K(n)-\xi ^{1 - (a_{1/2})}\right) \).

Proof

Considering

$$\begin{aligned} \xi \cdot \hat{t}=\xi _{a_1}\cdot \hat{t}_{a_1}=\xi _{a_1}\cdot \frac{3}{2}, \end{aligned}$$

\(\hat{t}\) is feasible for \(P\left( K(n)-\xi ^{1 - (a_{1/2})}\right) \) by Lemma 4.1. \(\square \)

We now identify the inequalities over which our dual certificate will have a non-zero component.

Lemma 4.3

For \(n\not \equiv 0\mod 4\),

$$\begin{aligned} \hat{\xi }^1= & {} \xi ^{3 - (q+1,2q+1)}\hbox { for }n=4q+1, \end{aligned}$$
(36)
$$\begin{aligned} \hat{\xi }^2= & {} \xi ^{6 - (q,q+1,2q+1)}\hbox { for }n=4q+2, \end{aligned}$$
(37)
$$\begin{aligned} \hat{\xi }^3= & {} \xi ^{3 - (q+1,2q+2)}\hbox { for }n=4q+3, \end{aligned}$$
(38)

are knapsack facets.

Proof

By Theorem 2.2, \(\hat{\xi }^1\) and \(\hat{\xi }^3\) are knapsack facets. By Lemmas 3.2 and 3.3, \(\hat{\xi }^2\) is a knapsack facet, where (b) of Lemma 3.3 may be satisfied by \(m_1=m_2=2\).

We now show that 3 / 2 is the non-zero component in the dual certificate.

Lemma 4.4

For \(n=4q+i,\ i=1,2,3\), \(\hat{\xi }=\hat{\xi }^i\) in (36)–(38) satisfies

$$\begin{aligned} \xi ^{1 - (a_{1/2})}\le & {} \frac{3}{2}\hat{\xi }. \end{aligned}$$

Proof

Note that \(\hat{\xi }_{a_1}=2/3\), where \(a_1\) is the first index larger than n / 2.

We now prove that the \(\xi \)-relaxation gap is \(1+1/2\).

Theorem 4.5

For \(n\not \equiv 0\mod 4\), the \(\xi \)-relaxation gap of the 1-facet \(\xi ^{1 - (a_{1/2})}\) of rank 0 is \(1+1/2\).

Proof

Lemma 4.2 gives a feasible solution \(\hat{t}\) with value 3 / 2 to the primal LP problem of maximizing \(\xi ^{1 - (a_{1/2})} t\) over \(P\left( K(n)-\xi ^{1 - (a_{1/2})}\right) \). Lemma 4.3 gives knapsack facets \(\hat{\xi }\) such that

$$\begin{aligned} \hat{\xi }_{a_1}= & {} 2/3\hbox { if }n\not \equiv 0\mod 4. \end{aligned}$$

Lemma 4.4 gives a dual feasible solution with only one nonzero component equal to 3 / 2 at the dual variable corresponding to \(\hat{\xi }\). The dual objective value is 3 / 2 (equal to the primal objective value) completing the proof of the theorem. \(\square \)

The next set of results show the \(\xi \)-relaxation gap to be 4 / 3 if \(n\equiv 0\mod 4\). The proofs of Lemmas 4.6–4.8 are similar to those of Lemmas 4.1–4.3 (except that we use Theorem 2.3 in the proof of Lemma 4.8) and are thus included in the “Appendix”.

Lemma 4.6

Let n be a multiple of 4 and let \(a_1\) denote the index of the first coefficient equal to 1 of the 1-facet of rank 0. If a knapsack facet \(\xi \) satisfies

$$\begin{aligned} \xi _{a_1}>3/4, \end{aligned}$$
(39)

then it must be the 1-facet of rank 0.

The next result provides the primal certificate with objective function value 4/3 if \(n\equiv 0\mod 4\).

Lemma 4.7

Let \(n\equiv 0\mod 4\) and let \(a_1\) denote the index of the first coefficient equal to 1 of the 1-facet of rank 0. Let \(\xi t \le 1\) be a knapsack facet of K(n) with \(\xi _1=0\) and \(\xi _n=1\). Then, \(\hat{t}\) given by

$$\begin{aligned} \hat{t}_i =\left\{ \begin{array}{ll} n-4a_1/3&{}\hbox { for }i=1,\\ 4/3&{}\hbox { for }i=a_1,\\ 0&{}\hbox { for }i\ne 1\hbox { or }a_1 \end{array} \right. \end{aligned}$$
(40)

is a feasible solution to the LP problem maximizing \(\xi ^{1 - (a_{1/2})} t\) over \(P\left( K(n)-\xi ^{1 - (a_{1/2})}\right) \).

Lemma 4.8

For \(n=4q\), \(\hat{\xi }=\xi ^{4 - (q,2q)}\) is a knapsack facet.

The next result provides the dual certificate with 4 / 3 as the only non-zero component and thus an objective function value of 4/3.

Lemma 4.9

For \(n=4q\), \(\hat{\xi }=\xi ^{4 - (q,2q)}\) satisfies

$$\begin{aligned} \xi ^{1 - (a_{1/2})}\le & {} \frac{4}{3}\hat{\xi }. \end{aligned}$$

As in the proof of Theorem 4.5, we can show that the \(\xi \)-relaxation gap is 1+1/3 if \(n\equiv 0\mod 4\) by showing the equality of the primal and dual objective function values.

Theorem 4.10

For \(n\equiv 0\mod 4\), the \(\xi \)-relaxation gap of the 1-facet of rank 0 is \(1+1/3\).

5 The 1-facets of positive rank

In this section, we show primal certificates (41) and dual certificates (53)–(54) which prove the following theorem:

Theorem 5.1

The \(\xi \)-relaxation gap for any 1-facet \(\xi \) of rank \(r>0\) is \(1+{1}/{4}\).

5.1 A primal certificate

Given a 1-facet \(\xi ^{1 - (a_{1/2}(r))}\) of rank r where \(0<r\le R(n)\), our first step is to obtain a primal feasible solution for \(P\left( K(n)-\xi ^{1 - (a_{1/2}(r))}\right) \). In Lemma 5.2 we define a primal feasible solution \(\hat{t}\) with objective function value \(\xi ^{1 - (a_{1/2}(r))}\hat{t}=1+1/4\), which leads to

$$\begin{aligned} {z^{LP(\xi )}(\xi )}\ge \xi ^{1 - (a_{1/2}(r))}\hat{t}=1+\frac{1}{4}. \end{aligned}$$
(41)

Lemma 5.2

Let \(0<r\le R(n)\) and let \(a_{1/2}(r)\) denote the first index of the half landing of the 1-facet of rank r. A fractional solution

$$\begin{aligned} \hat{t} =&\left( t_1=\frac{a_{1/2}(r)}{2}-1;\ t_{a_{1/2}(r)}=\frac{1}{2};\ t_{n-a_{1/2}(r)+1}=1;\ t_i=0\hbox { otherwise}\right) ,\nonumber \\ \end{aligned}$$
(42)

is feasible for \(P(K(n)-\xi ^{1 - (a_{1/2}(r))})\).

Proof

We assume \(\xi t\le 1\) is a knapsack facet that is violated by \(\hat{t}\), and only need to show that \(\xi =\xi ^{1 - (a_{1/2}(r))}.\) This would prove that \(\hat{t}\) is feasible for \(P\left( K(n)-\xi ^{1 - (a_{1/2}(r))}\right) \). Our assumption that \(\xi t\le 1\) is violated by \(\hat{t}\) can be written as

$$\begin{aligned} \frac{1}{2}\xi _{a_{1/2}(r)}+\xi _{n-a_{1/2}(r)+1}>1. \end{aligned}$$

By substituting complementarity \(\xi _{a_{1/2}(r)-1}+\xi _{n-a_{1/2}(r)+1}=1\), it is equivalent to

$$\begin{aligned} 2\xi _{a_{1/2}(r)-1}<\xi _{a_{1/2}(r)}. \end{aligned}$$
(43)

There are n linearly independent binding constraints including the equalities in (8)–(10). We may assume that the other binding constraints are from (23)–(25). We show that (43) allows only three cases (44), (46) and (51) of the binding constraints, and we see that they are all satisfied by \(\xi ^{1 - (a_{1/2}(r))}\) as equalities.

For the indices in (23), there are four possible cases

$$\begin{aligned}&i\le j<i+j<a_{1/2}(r)<n/2 \end{aligned}$$
(44)
$$\begin{aligned}&i\le j<a_{1/2}(r)\le i+j<n/2 \end{aligned}$$
(45)
$$\begin{aligned}&i< a_{1/2}(r)\le j< i+j < n/2 \end{aligned}$$
(46)
$$\begin{aligned}&a_{1/2}(r)\le i\le j< i+j < n/2. \end{aligned}$$
(47)

Case (47) provides a contradiction because

$$\begin{aligned} \frac{n}{3}<a_{1/2}(r)\le i\le j< i+j < n/2. \end{aligned}$$

From (43), case (45) is also forbidden, because it would be followed by

$$\begin{aligned} \xi _i+\xi _j\le 2\xi _{a_{1/2}(r)-1}<\xi _{a_{1/2}(r)}\le \xi _{i+j}. \end{aligned}$$
(48)

Since \(i=j=\frac{n}{4}\le a_{1/2}(r)-1\) and \(a_{1/2}(r)<\frac{n}{2}\) in (48), inequality (25) is forbidden when \(n\equiv 0\mod 4\). Therefore, only two cases (44) and (46) are possible for the indices in (23).

For the indices in (24), there are four possible cases

$$\begin{aligned}&i\le j\le n-i-j< a_{1/2}(r)<n/2 \end{aligned}$$
(49)
$$\begin{aligned}&i\le j< a_{1/2}(r)\le n-i-j<n/2 \end{aligned}$$
(50)
$$\begin{aligned}&i< a_{1/2}(r)\le j\le n-i-j<n/2 \end{aligned}$$
(51)
$$\begin{aligned}&a_{1/2}(r)\le i\le j\le n-i-j<n/2. \end{aligned}$$
(52)

From (43), cases (49) and (50) are forbidden by

$$\begin{aligned} \xi _i+\xi _j+\xi _{n-i-j}\le 2\xi _{a_{1/2}(r)-1}+\frac{1}{2}<\xi _{a_{1/2}(r)}+\frac{1}{2}\le \frac{1}{2}+\frac{1}{2}=1. \end{aligned}$$

Case (52) provides a contradiction

$$\begin{aligned} \frac{n}{3}<a_{1/2}(r)\le i\le j\le n-i-j<n-\frac{n}{3}-\frac{n}{3}=\frac{n}{3}. \end{aligned}$$

Therefore, (51) is only possible case for the indices in (24).

Since inequalities (23) in cases (44) and (46) and inequalities (24) in case (51) are satisfied by \(\xi ^{1 - (a_{1/2}(r))}\) as equalities, the n binding constraints uniquely determine \(\xi ^{1 - (a_{1/2}(r))}\) completing the proof of the lemma. \(\square \)

5.2 Dual certificates

Our next step is to identify dual feasible solutions with a weight of 0 on the deleted 1-facet \(\xi ^{1 - (a_{1/2}(r))}\) and an objective value 5/4. For \(\xi =\xi ^{1 - (a_{1/2}(r))}\) with \(r>0\), we show that if \(n=2\mod 3\hbox { and }r=R(n)\),

$$\begin{aligned} \xi ^{1 - (a_{1/2}(r))}\le \frac{5}{4}\cdot \hat{\xi }\hbox { for a knapsack facet }\hat{\xi }. \end{aligned}$$
(53)

Thus a dual solution with weight 5/4 on \(\hat{\xi }\) and 0 elsewhere is feasible and has objective value 5/4. For all other cases we show that

$$\begin{aligned} \xi ^{1 - (a_{1/2}(r))}\le 1\cdot \hat{\xi }+\frac{1}{4}\cdot {\xi }^{1 - (a_{1/2}(0))}\hbox { for a knapsack facet }\hat{\xi }. \end{aligned}$$
(54)

Thus a dual solution with weight 1 on \(\hat{\xi }\), 1/4 on \(\xi ^{1 - (a_{1/2}(0))}\) and 0 elsewhere is feasible and has objective value 5/4. They certify that the \(\xi \)-relaxation gap of \(\xi ^{1 - (a_{1/2}(r))}\) with \(r>0\) is less than or equal to \(1+1/4\). We first consider the case when \(n\equiv 2\mod 3\).

5.2.1 The 1-facet of the largest rank R(n) in case \(n=2~\mathrm{mod}~3\)

If \(n\equiv 2\mod 3\), then either \(n\equiv 2\mod 6\) or \(n\equiv 5\mod 6\). We show that (53) holds in either case.

Lemma 5.3

Let \(n\equiv 2\mod 6\) and let \(R(n)\ge 2\) be the largest rank of a 1-facet for P(K(n)). Then, \(n=6R(n)+2\) and the 1 / 5-facet \(\hat{\xi }=\xi ^{5 - (a^5_1,a^5_2,a^5_{5/2})}\) given by \(a^5_1=R(n)+1\), \(a^5_2=2R(n)+1\) and \(a^5_{5/2}=3R(n)+1\) satisfies

$$\begin{aligned} \xi ^{1 - (a_{1/2}(R(n)))}\le \frac{5}{4}\cdot \hat{\xi }. \end{aligned}$$

Lemma 5.4

Let \(n=5\mod 6\) and let \(R(n)\ge 2\) be the largest rank of a 1-facet for P(K(n)). Then, \(n=6R(n)-1\) and the 1 / 5-facet \(\hat{\xi }=\xi ^{5 - (a^5_1,a^5_2,a^5_{5/2})}\) given by \(a^5_1=R(n)\), \(a^5_2=2R(n)\) and \(a^5_{5/2}=3R(n)\) satisfies (53), i.e.

$$\begin{aligned} \xi ^{1 - (a_{1/2}(R(n)))}\le \frac{5}{4}\cdot \hat{\xi }. \end{aligned}$$

5.2.2 All the other 1-facets of rank \(r>0\)

We now show that (54) holds in all other cases. Unless \(n=2\mod 3\) and \(r=R(n)\), each rank r satisfies

$$\begin{aligned} r<\frac{n+1}{6}&\hbox { whenever }n\hbox { is odd}\\ r<\frac{n-2}{6}&\hbox { whenever }n\hbox { is even}, \end{aligned}$$

which imply \(n+1-2a_{1/2}(r)<a_{1/2}(r)\). We use this observation to define \(\hat{\xi }\) in the following lemma.

Lemma 5.5

Assume that \(n\ne 2\mod 3\) or \(r\ne R(n)\). Let \(a_{1/2}(r)\) be the first index of the half landing of the 1-facet of rank r and let

$$\begin{aligned} m=\max \left\{ \left\lceil \frac{a_{1/2}(r)}{2}\right\rceil ,n+1-2a_{1/2}(r)\right\} . \end{aligned}$$

Then, \(m<a_{1/2}(r)\) and therefore \(\hat{\xi }={\xi }^{4 - (m,a_{1/2}(r))}\) is well-defined. It is a knapsack facet satisfying (54), i.e.,

$$\begin{aligned} \xi ^{1 - (a_{1/2}(r))}\le 1\cdot \hat{\xi }+\frac{1}{4}\cdot \xi ^{1 - (a_{1/2}(0))}. \end{aligned}$$

The results in Sects. 5.1 and 5.2 together prove Theorem 5.1.

6 The \(\frac{1}{3}\)-facets

In this section, consistent with Observation 4 we first show that the gap of a 1 / 3-facet is less than or equal to \(1+1/6\). Then, we identify a strong 1 / 3-facet with gap \(1+1/6\) for every \(n\equiv 3\mod 4\). It shows that 1+1/6 is the best achievable gap for 1 / 3-facets.

6.1 The bound of the gap of the 1 / 3-facets

Theorem 6.1

The \(\xi \)-relaxation gap of a \(\frac{1}{3}\)-facet \(\xi ^{3 - ({a_1},a_{3/2})}\) is less than or equal to \(1+1/6\).

Proof

To prove the result we need to find dual feasible solutions with a value of \(1+1/6\) and a weight of 0 on the selected 1 / 3-facet. The case when \(a_1 = n/3\) is included in the more general result in Theorem 9.2. We thus assume that \({a_1}<n/3\). From (12) in Theorem 2.2 we need to consider two cases, \(2{a_1}+a_{3/2}-1>n\) and \(2{a_1}+a_{3/2}-1=n\).

Firstly, let \(2{a_1}+a_{3/2}-1>n\). Then, \(\xi ^{3 - ({a_1},a_{3/2}-1)}\) is a knapsack facet, and

$$\begin{aligned} \xi ^{3 - ({a_1},a_{3/2})}\le \xi ^{3 - ({a_1},a_{3/2}-1)}+\frac{1}{6}\xi ^{1 - (a_{1/2}(0))} \end{aligned}$$

follows from

$$\begin{aligned}&\xi ^{3 - ({a_1},a_{3/2})}-\xi ^{3 - ({a_1},a_{3/2}-1)}\\&\quad =0\le \frac{1}{6}\xi ^{1 - (a_{1/2}(0))}_i\hbox { for }i\ne \{1,\ldots ,n\}\setminus \{a_{3/2}-1,n-a_{3/2}+1\},\\&\quad =\frac{1}{3}-\frac{1}{2}=-\frac{1}{6}\le 0=\frac{1}{6}\xi ^{1 - (a_{1/2}(0))}_i\hbox { for }i= a_{3/2}-1,\\&\quad =\frac{2}{3}-\frac{1}{2}=\frac{1}{6}=\frac{1}{6}\cdot 1=\frac{1}{6} \xi ^{1 - (a_{1/2}(0))}_i\hbox { for }i= n-a_{3/2}+1. \end{aligned}$$

The dual feasible solution thus assigns weight 1 to \(\xi ^{3 - ({a_1},a_{3/2}-1)}\) and weight 1/6 to \(\xi ^{1 - (a_{1/2}(0))}\). Thus, the theorem is true when \(2{a_1}+a_{3/2}-1>n\).

Secondly, let \(2{a_1}+a_{3/2}-1=n\). Given \(a_1\), the half landing is then largest possible and, therefore, \(\xi ^{3 - ({a_1},a_{3/2}-1)}\) is not a knapsack facet. Theorem 6.4 will show the \(\xi \)-relaxation gap equals \(1+1/6\) if \(2{a_1}+a_{3/2}-1=n\) and \(n\equiv 3\mod 4\). We thus assume here that \(n\not \equiv 3\mod 4\). Instead of \(\xi ^{3 - ({a_1},a_{3/2}-1)}\), we consider \({\xi }^{6 - (a^6_m)}\) given by \(a^6_1=a_1-1\), \(a^6_2=a_1\) and \(a^6_3=a_{3/2}\). This inequality is a knapsack facet by Lemmas 3.2 and 3.3 with \(m_1=m_2=2\) in (b) of Lemma 3.3. We then obtain

$$\begin{aligned} \xi ^{3 - ({a_1},a_{3/2})}\le {\xi }^{6 - (a^6_m)}+\frac{1}{6}\xi ^{1 - (a_{1/2}(0))}. \end{aligned}$$

In this case, the dual feasible solution assigns weight 1 to \(\xi ^{6 - (a^6_m)}\) and 1/6 to \(\xi ^{1 - (a_{1/2}(0))}\) and 0 elsewhere. This completes the proof of the theorem. \(\square \)

6.2 Strong 1 / 3-facets with \(\xi \)-relaxation gap \(1+1/6\)

Now we identify a set of 1 / 3-facets that achieve the upper bound gap of \(1+1/6\) showing that a gap of \(1+1/6\) is the best achievable for 1 / 3-facets. We show that the 1 / 3-facet \(\xi ^{3 - (q+1,2q+2)}\) for \(n=4q+3\) achieves the \(\xi \)-relaxation gap of \(1+1/6\), the largest achievable for 1 / 3-facets. We do so by defining suitable primal and dual certificates.

The first step is to obtain a primal certificate \(\hat{t}\) with objective function value \(\xi ^{3 - (q+1,2q+2)}\hat{t}=7/6\).

Lemma 6.2

Let \(n=4q+3\). Then,

$$\begin{aligned} \hat{t}= & {} \left( \hat{t}_1= n-\frac{7}{2}(q+1);\ \hat{t}_{q+1}=\frac{7}{2};\ \hat{t}_{i}=0\hbox { for } i \ne 1\hbox { or }q+1\right) \end{aligned}$$
(55)

is feasible for \(P(K(n)-\xi ^{3 - (q+1,2q+2)})\).

Proof

See the online appendix. \(\square \)

The next step is to obtain a dual feasible solution with value 7 / 6 and weight 0 on the inequality \(\xi ^{3 - (q+1,2q+2)}\).

Lemma 6.3

Let \(n=4q+3\). A 1 / 7-facet \(\hat{\xi }={\xi }^{7 - (a^7_m)}\) given by \(a^7_1=q\), \(a^7_2=q+1\), \(a^7_3=2q+1\) and \(a^7_{7/2}=2q+2\) satisfy

$$\begin{aligned} \xi ^{3 - (q+1,2q+2)}\le \frac{7}{6}\cdot \hat{\xi }. \end{aligned}$$
(56)

Proof

Inequality \({\xi }^{7 - (a^7_m)}\) is a knapsack facet by Lemmas 3.2 and 3.3 with \(m_1=m_2=2\) in (b) of Lemma 3.3. Then, \(a^7_2=q+1\) and \(a^7_{7/2}=2q+2\) imply (56).

Theorem 6.4

Let \(n=4q+3\). The \(\xi \)-relaxation gap of 1 / 3-facet \(\xi ^{3 - (q+1,2q+2)}\) is \(1+1/6\).

Proof

Lemma 6.2 gives a feasible solution \(\hat{t}\) with value 7 / 6 to the primal LP problem of maximizing \(\xi ^{3 - (q+1,2q+2)} t\) over \(P\left( K(n)-\xi ^{3 - (q+1,2q+2)}\right) \). Lemma 6.3 gives a dual feasible solution with only one nonzero component equal to 7 / 6 at the dual variable corresponding to \(\hat{\xi }\). The dual objective value is 7 / 6 completing the proof of the theorem.

7 The \(\frac{1}{4}\)-facets

In this section, we show that the gap for a 1 / 4-facet is strictly less than \(1+1/4\). Then, we identify a 1 / 4-facet with gap \(1+1/6\) for every \(n\equiv 4\mod 6\). This still leaves some room between \(1+1/6\) and \(1+1/4\) in terms of the best achievable gap for 1 / 4-facets. In our computational experiment we did not find any 1 / 4-facets with gap larger than \(1+1/6\).

7.1 A strict bound of the gap for 1 / 4-facets

Theorem 7.1

The \(\xi \)-relaxation gap for a 1 / 4-facet \(\xi ^{4 - (a_1,a_2)}\) is strictly less than \(1+1/4\).

Proof

To prove the result we identify a dual feasible solution with objective value strictly less than \(1+1/4\). Given 1 / 4-facet \(\xi ^{4 - (a_1,a_2)}\), there exists a 1-facet \(\xi ^{1 - (a_{1/2}(r))}\) with \(a_2\) as the first index of the half landing; i.e.,

$$\begin{aligned} a_{1/2}(r)=a_2, \end{aligned}$$
(57)

because Theorem 2.3 implies \(\frac{n}{5}<a_1<\frac{n}{3}\) and (14) implies

$$\begin{aligned} a_2\ge \frac{n-a_1+1}{2}=\frac{n+1}{2}-a_1\cdot \frac{1}{2}>\frac{n+1}{2}-\frac{n}{3}\cdot \frac{1}{2}=\frac{n}{3}+\frac{1}{2}>\frac{n}{3}. \end{aligned}$$

Let \(\xi ^{1 - (a_{1/2}(r))}\) satisfy (57). Given lineality \(\lambda \), in order to prove the theorem, we only need to show

$$\begin{aligned} \frac{n}{4a_1}\cdot \lambda +\left( \frac{5}{4}-\frac{n}{4a_1}-\varepsilon \right) \cdot \xi ^{1 - (a_{1/2}(r))}\ge \xi ^{4 - (a_1,a_2)} \hbox { for a small }\varepsilon >0. \end{aligned}$$
(58)

If we can prove (58) we obtain the appropriate dual feasible solution by assigning weight \(\frac{n}{4a_1}\) to the lineality \(\lambda \), \(\left( \frac{5}{4}-\frac{n}{4a_1}-\varepsilon \right) \) to \(\xi ^{1 - (a_{1/2}(r))}\) and 0 to all other inequalities. We prove (58) by showing

$$\begin{aligned} \frac{n}{4a_1}\cdot \frac{i}{n}+\left( \frac{5}{4}-\frac{n}{4a_1}-\varepsilon \right) \cdot 0\ge \frac{1}{4}&\hbox { for }i\ge a_1 \end{aligned}$$
(59)
$$\begin{aligned} \ \frac{n}{4a_1}\cdot \frac{i}{n}+\left( \frac{5}{4}-\frac{n}{4a_1}-\varepsilon \right) \cdot \frac{1}{2}\ge \frac{1}{2}&\hbox { for }i\ge a_2 \end{aligned}$$
(60)
$$\begin{aligned} \frac{n}{4a_1}\cdot \frac{i}{n}+\left( \frac{5}{4}-\frac{n}{4a_1}-\varepsilon \right) \cdot 1\ge \frac{3}{4}&\hbox { for }i\ge n-a_2+1 \end{aligned}$$
(61)
$$\begin{aligned} \frac{n}{4a_1}\cdot \frac{i}{n}+\left( \frac{5}{4}-\frac{n}{4a_1}-\varepsilon \right) \cdot 1\ge 1&\hbox { for }i>n-a_1. \end{aligned}$$
(62)

We can immediately see that (59) holds, because \(\frac{i}{4a_1}\ge \frac{1}{4}\) is equivalent to \(i\ge a_1\).

We show (60) by (14) in Theorem 2.3 which implies

$$\begin{aligned} i\ge a_2\ge \frac{n-a_1+1}{2}=\frac{n-a_1}{2}+\frac{1}{2}>\frac{n-a_1}{2}. \end{aligned}$$

The strict inequality \(i>\frac{n-a_1}{2}\) is equivalent to

$$\begin{aligned} \frac{i}{4a_1}+\frac{1}{8}>\frac{n}{8a_1}. \end{aligned}$$

It implies that

$$\begin{aligned} \frac{n}{4a_1}\cdot \frac{i}{n}+\left( \frac{5}{4}-\frac{n}{4a_1} \right) \cdot \frac{1}{2}=\frac{i}{4a_1}+\frac{1}{8}+\frac{1}{2}-\frac{n}{8a_1}>\frac{1}{2}, \end{aligned}$$

completing the proof of (60).

We show (61) by (15) in Theorem 2.3 which implies \(a_2\le 2a_1\) and therefore \(i\ge n-a_2+1>n-2a_1\). The strict inequality \(i>n-2a_1\) is equivalent to

$$\begin{aligned} \frac{i}{4a_1}+\frac{1}{2}>\frac{n}{4a_1}. \end{aligned}$$

It implies that

$$\begin{aligned} \frac{n}{4a_1}\cdot \frac{i}{n}+\left( \frac{5}{4}-\frac{n}{4a_1} \right) \cdot 1=\frac{i}{4a_1}+\frac{1}{2}+\frac{3}{4}-\frac{n}{4a_1} > \frac{3}{4}, \end{aligned}$$

completing the proof of (61).

We now show (62). The assumption \(i>n-a_1\) is equivalent to

$$\begin{aligned} \frac{i}{4a_1}+\frac{1}{4}>\frac{n}{4a_1}. \end{aligned}$$

It implies that

$$\begin{aligned} \frac{n}{4a_1}\cdot \frac{i}{n}+\left( \frac{5}{4}-\frac{n}{4a_1} \right) \cdot 1=\frac{i}{4a_1}+\frac{1}{4}+1-\frac{n}{4a_1}>1, \end{aligned}$$

completing the proof of (62). Thus, (58) holds completing the proof of the theorem. \(\square \)

7.2 Strong 1 / 4-facets with gap \(1+1/6\)

We now define a set of 1 / 4-facets with a provable \(\xi \)-relaxation gap of \(1+1/6\). We show that the \(\xi \)-relaxation gap for \(\xi ^{4 - (2q+1,2q+2)}\) for \(n=6q+4\) is \(1+1/6\) by defining suitable primal and dual certificates.

To prove the primal certificate, we restrict some components of the knapsack facet.

Lemma 7.2

Let \(n=6q+4\) and let a knapsack facet \(\xi \) with \(\xi _1=0\) and \(\xi _n=1\) satisfy

$$\begin{aligned} \frac{2}{3}\xi _{2q+1}+2\xi _{2q+2}>1. \end{aligned}$$
(63)

Then, it holds that

$$\begin{aligned}&\xi _{2q}< \frac{2}{10}, \end{aligned}$$
(64)
$$\begin{aligned}&\xi _{2q+1}\le \frac{3}{10}, \end{aligned}$$
(65)
$$\begin{aligned}&\hbox {and }\xi _{2q+2}> \frac{4}{10}. \end{aligned}$$
(66)

Proof

Since (63) and (65) imply (66) and (64) by

$$\begin{aligned}&\xi _{2q+2}>\frac{1}{2}\times \left( 1-\frac{2}{3}\xi _{2q+1}\right) \ge \frac{1}{2}\times \left( 1-\frac{2}{3}\times \frac{3}{10}\right) =\frac{4}{10}\hbox { and }\\&\xi _{2q}=1-\xi _{4q+4}\le 1-\left( \xi _{2q+2}+\xi _{2q+2}\right) <1-2\times \frac{4}{10}=\frac{2}{10}, \end{aligned}$$

we only need to show (65). Since \(3\times ({2q+1})\le 6q+4=n\) implies \(3\xi _{2q+1}\le 1\), we have

$$\begin{aligned} \xi _{2q+1}\le \frac{1}{3}. \end{aligned}$$
(67)

We denote the initial upper bound in (67) by \(U_{2q+1}^0=1/3\) and show a decreasing sequence \(\left( U_{2q+1}^{k}\right) _{k=1}^{\infty }\) with \(\xi _{2q+1}<U_{2q+1}^{k}\) converging to 3 / 10.

From (63) and (67), we have that

$$\begin{aligned} \xi _{2q+2}>\frac{1}{2}\times \left( 1-\frac{2}{3}\xi _{2q+1}\right) \ge \frac{1}{2}\times \left( 1-\frac{2}{3}U_{2q+1}^0\right) =\frac{1}{2}-\frac{1}{3}U_{2q+1}^0. \end{aligned}$$
(68)

Complementarity (8) and (68) imply

$$\begin{aligned} \xi _{4q+2}=1-\xi _{2q+2}<1-\left( \frac{1}{2}-\frac{1}{3}U_{2q+1}^0\right) =\frac{1}{2}+\frac{1}{3}U_{2q+1}^0. \end{aligned}$$
(69)

As a result we have

$$\begin{aligned} \xi _{2q+1}=\frac{1}{2}\left( \xi _{2q+1}+\xi _{2q+1}\right) \le \frac{1}{2}\xi _{4q+2}<\frac{1}{2}\left( \frac{1}{2}+\frac{1}{3}U_{2q+1}^0\right) =\frac{1}{4}+\frac{1}{6}U_{2q+1}^0. \end{aligned}$$

We now define new strict upper bound \(U_{2q+1}^{1}\) given by

$$\begin{aligned} \xi _{2q+1}<U_{2q+1}^1=\frac{1}{4}+\frac{1}{6}U_{2q+1}^0. \end{aligned}$$
(70)

We repeat the process above to recursively define an infinite sequence \(\left( U_{2q+1}^k\right) _{k=1}^{\infty }\) of strict upper bounds of \(\xi _{2q+1}\) by

$$\begin{aligned} U_{2q+1}^k=\frac{1}{4}+\frac{1}{6}U_{2q+1}^{k-1} =\frac{5}{6}\times \frac{3}{10}+\frac{1}{6}U_{2q+1}^{k-1}\hbox { for }k=1,2,\ldots \end{aligned}$$
(71)

Since \(U_{2q+1}^k\) is a convex combination of 3 / 10 and \(U_{2q+1}^{k-1}\) in (71), we have

$$\begin{aligned} U_{2q+1}^0=\frac{1}{3}>U_{2q+1}^{1}>U_{2q+1}^2>\cdots >\frac{3}{10}. \end{aligned}$$

For \(k=0,1,2,\ldots \), we can write \(U_{2q+1}^k\) explicitly as

$$\begin{aligned} U_{2q+1}^k= & {} \frac{3}{10}+\left( U_{2q+1}^0-\frac{3}{10}\right) \times \left( \frac{1}{6}\right) ^{k} =\frac{3}{10}+\left( \frac{1}{3}-\frac{3}{10}\right) \times \left( \frac{1}{6}\right) ^{k}\\= & {} \frac{3}{10}+\frac{1}{30}\times \left( \frac{1}{6}\right) ^{k}. \end{aligned}$$

Since \(\left( U_{2q+1}^k\right) _{k=1}^{\infty }\) is a decreasing sequence converging to 3 / 10 such that \(\xi _{2q+1}<U_{2q+1}^k,\) it holds that

$$\begin{aligned} \xi _{2q+1}\le \frac{3}{10}, \end{aligned}$$

completing the proof of the lemma. \(\square \)

We now define our primal certificate \(\hat{t}\):

Lemma 7.3

Let \(n=6q+4\), \(q\ge 1\). Then,

$$\begin{aligned} \hat{t}= & {} \bigg (\hat{t}_1{=} n-\frac{16}{3}q-\frac{14}{3};\ \hat{t}_{2q+1}{=}\frac{2}{3};\ \hat{t}_{2q+2}=2;\ \hat{t}_{i}=0\hbox { for } i\ne 1, 2q+1 or 2q+2\bigg )\nonumber \\ \end{aligned}$$
(72)

is feasible for \(P\left( K(n)-\xi ^{4 - (2q+1,2q+2)}\right) \).

Proof

In order to show that \(\hat{t}\) in (72) is feasible for \(P\left( K(n)-\xi ^{4 - (2q+1,2q+2)}\right) \), we only need to show that all knapsack facets \(\xi \) except \({\xi }^{4 - (2q+1,2q+1)}\) satisfy

$$\begin{aligned} \xi \hat{t}=\frac{2}{3}\xi _{2q+1}+2\xi _{2q+2}\le 1. \end{aligned}$$
(73)

Equivalently, we show that, if a knapsack facet \(\xi \) satisfies (63), then \(\xi ={\xi }^{4 - (2q+1,2q+2)}\). Let \(\xi \) be a knapsack facet satisfying (63). Then, there are n linearly independent relations binding at \(\xi \) which include the equalities in (8)–(10) and relations from (23)–(25). By Lemma 7.2, they are all shown to be equalities at \(\xi ={\xi }^{4 - (2q+1,2q+2)}\), which will complete the proof of the lemma. (See the online appendix for more details.) \(\square \)

We now define the appropriate dual certificate.

Lemma 7.4

Let \(n=6q+4\), \(q\ge 1\). Then, \(\hat{\xi }=\xi ^{10 - (a^{10}_m)}\) defined by \(a^{10}_1=q\), \(a^{10}_2=q+1\), \(a^{10}_3=2q+1\), \(a^{10}_4=2q+2\) and \(a^{10}_5=3q+2\) is a knapsack facet and satisfies

$$\begin{aligned} {\xi }^{4 - (2q+1,2q+2)}\le \frac{5}{6}\hat{\xi }+\frac{1}{3}\xi ^{1 - (a_{1/2}(R(n)))}. \end{aligned}$$
(74)

Proof

We prove this lemma in a similar way to the proof of Lemma 6.3. \(\square \)

Theorem 7.5

Let \(n=6q+4\), \(q\ge 1\). The \(\xi \)-relaxation gap of 1 / 4-facet \(\xi ^{4 - (2q+1,2q+2)}\) is \(1+1/6.\)

Proof

Lemma 7.3 gives a feasible solution \(\hat{t}\) with value 7 / 6 for the primal LP problem of maximizing \(\xi ^{4 - (2q+1,2q+2)} t\) over \(P\left( K(n)-\xi ^{4 - (2q+1,2q+2)}\right) \). Lemma 7.4 gives a dual feasible solution with two nonzero components, 5 / 6 and 1 / 3, as the dual variables corresponding to the knapsack facet \(\hat{\xi }\) (defined in Lemma 7.4) and the 1-facet \(\xi ^{1 - (a_{1/2}(R(n)))}\) of the largest rank. The dual objective value is \(7/6=5/6+1/3\) completing the proof of the theorem. \(\square \)

8 A global upper bound for the \(\xi \)-relaxation gap

Consistent with Observations 1 and 2, we show that \(1+1/2\) is an upper bound over all the knapsack facets and can be achieved only among the 1-facets.

Proposition 8.1

Let \(\xi \) be a knapsack facet with \(\xi _1=0\) and \(\xi _n=1\), and let \(m\ge 2\). Then,

$$\begin{aligned} \xi _i\le \frac{\xi _{i_0}}{m}\hbox { whenever }i\le \frac{i_0}{m}. \end{aligned}$$

Proof

By super-additivities (7),

$$\begin{aligned} m\xi _i\le (m-2)\xi _i+\xi _{2i}\le (m-3)\xi _i+\xi _{3i}\le \cdots \le \xi _i+\xi _{(m-1)i}\le \xi _{mi}\le \xi _{i_0}. \end{aligned}$$

\(\square \)

Theorem 8.2

Let \(\xi \) be a knapsack facet with \(\xi _1=0\) and \(\xi _n=1\). If \(\xi \) is not a 1-facet,

$$\begin{aligned} {z^{LP(\xi )}(\xi )}<1+\frac{1}{2}. \end{aligned}$$
(75)

Proof

Recall that \(\lambda \) is the lineality of n. We first show that for \(i\not \in \left( \frac{n}{2},\frac{2n}{3}\right) ,\)

$$\begin{aligned} \xi _i<\left( 1+\frac{1}{2}\right) \cdot \frac{i}{n}=\left( 1+\frac{1}{2}\right) \cdot \lambda _i. \end{aligned}$$
(76)

For \(\frac{n}{m+1}<i\le \frac{n}{m}\) where \(m\ge 2\), substituting \(i_0=n\) for Proposition 8.1 gives

$$\begin{aligned} \xi _i\le \frac{1}{m}. \end{aligned}$$

Since \(m\ge 2\) and \(i>\frac{n}{m+1}\), we obtain

$$\begin{aligned} \xi _i\le \frac{1}{m}\le \frac{3}{2(m+1)}<\frac{3}{2}\cdot i\cdot \frac{1}{n}. \end{aligned}$$

Therefore, (76) holds for all \(i\le n/2\). For \(i> \frac{2n}{3}\),

$$\begin{aligned} \xi _i\le 1=\frac{3}{2}\cdot \frac{2n}{3}\cdot \frac{1}{n}<\frac{3}{2}\cdot i\cdot \frac{1}{n}=\frac{3}{2}\cdot \lambda _i. \end{aligned}$$

Since \(\xi \) is not a 1-facet, Lemma 3.4 implies

$$\begin{aligned} \xi _i< 1 = \frac{3}{2}\cdot \frac{i}{n}=\frac{3}{2}\cdot \lambda _i \end{aligned}$$

for \(i=\frac{2n}{3}\) when n is a multiple of 3. Thus, for every \(i\le \frac{n}{2}\) and for every \(i\ge \frac{2n}{3}\), (76) holds. If \(\xi \) satisfies (76) for \(\frac{n}{2}<i<\frac{2n}{3}\), it satisfies (75).

Now, we assume that \(\xi \) does not satisfy (76) for some \(\frac{n}{2}<i<\frac{2n}{3}\); i.e.,

$$\begin{aligned} \xi _i\ge \frac{3}{2}\cdot \frac{i}{n}. \end{aligned}$$
(77)

Let \(\bar{i}_1\) be the first index satisfying (77), and let \(i_1=n-\bar{i}_1\). Then, \(i_1\) is the last index in \(\frac{n}{3}<i_1<\frac{n}{2}\) which satisfies

$$\begin{aligned} \xi _{i_1}\le \frac{3}{2}\cdot \frac{i_1}{n}-\frac{1}{2}. \end{aligned}$$
(78)

Let \(\hat{i}\) be the first index satisfying

$$\begin{aligned} \xi _{\hat{i}}\ge \frac{\hat{i}}{n}=\lambda _{\hat{i}}. \end{aligned}$$

Then, for all \(i<\hat{i}\),

$$\begin{aligned} \xi _i<\frac{i}{n}=\lambda _i. \end{aligned}$$
(79)

We show that \(i_1<\hat{i}\), and that for all i,

$$\begin{aligned} \xi _i<\lambda _i+\frac{1}{2}\xi ^{1 - (a_{1/2}(r))}_i, \end{aligned}$$
(80)

where the rank r of \(\xi ^{1 - (a_{1/2}(r))}\) is set up for \(\hat{i}\) to be the first index of the half-landing of \(\xi ^{1 - (a_{1/2}(r))}\) (\(r=0\) if \(\hat{i}\ge \frac{n}{2}\)).

Firstly, we show that \(i_1<\hat{i}\). For \(i\le \frac{i_1}{2}\), (78) and Proposition 8.1 imply that for \(\frac{i_1}{3}<i\le \frac{i_1}{2}\) with \(m=2\),

$$\begin{aligned} \xi _i\le & {} \frac{1}{2}\xi _{i_1} \le \frac{1}{2}\cdot \left( \frac{3}{2}\cdot \frac{i_1}{n}-\frac{1}{2}\right) =\frac{1}{2}\cdot \frac{i_1}{n}+\frac{1}{4}\cdot \frac{i_1}{n}-\frac{1}{4}\\<&\frac{1}{2}\cdot \frac{1}{2}+\frac{i_1}{3}\cdot \frac{1}{n}-\frac{1}{4} <\frac{1}{4}+i\cdot \frac{1}{n}-\frac{1}{4}=\frac{i}{n}, \end{aligned}$$

and that for \(\frac{i_1}{m+1}<i\le \frac{i_1}{m}\) with \(m\ge 3\),

$$\begin{aligned} \xi _i\le & {} \frac{1}{m}\xi _{i_1} \le \frac{1}{m}\cdot \left( \frac{3}{2}\cdot \frac{i_1}{n}-\frac{1}{2}\right) =\frac{3i_1-n}{2nm}\\<&\frac{3(m+1)i-n}{2nm} =\frac{2mi+mi+3i-n}{2nm} =\frac{i}{n}+\frac{(m+3)i-n}{2nm}\\\le & {} \frac{i}{n}+\frac{2mi-n}{2nm} \le \frac{i}{n}+\frac{2i_1-n}{2nm} <\frac{i}{n}+\frac{0}{2nm}=\frac{i}{n}. \end{aligned}$$

For \(\frac{i_1}{2}<i\le i_1\),

$$\begin{aligned} \xi _i\le & {} \xi _{i_1}\le \frac{3}{2}\cdot \frac{i_1}{n}-\frac{1}{2} =\frac{1}{2}\cdot \frac{i_1}{n}+\frac{i_1}{n}-\frac{1}{2}\\<&\frac{1}{2}\cdot \frac{i_1}{n}+\frac{1}{2}-\frac{1}{2} =\frac{i_1}{2}\cdot \frac{1}{n}<\frac{i}{n}. \end{aligned}$$

Thus, (79) holds for all \(i\le i_1\), and therefore by the definition of \(\hat{i}\)

$$\begin{aligned} \frac{n}{3}<i_1<\hat{i}. \end{aligned}$$
(81)

It implies that \(\xi ^{1 - (a_{1/2}(r))}\) with \(\hat{i}\) as the first index of its half-landing (\(r=0\) if \(\hat{i}\ge \frac{n}{2}\)) is well-defined and (80) holds for all \(i<\hat{i}\). Thus,

$$\begin{aligned} \xi _i<\lambda _i=\lambda _i+\frac{1}{2}\cdot 0<\lambda _i+\frac{1}{2}\xi ^{1 - (a_{1/2}(r))}_i. \end{aligned}$$

Secondly, we show that (80) holds for all \(i\ge \hat{i}\). If \(\hat{i}\ge \frac{n}{2}\), (80) is trivial for all \(i\ge \hat{i}\). We assume that \(\hat{i}<\frac{n}{2}\). For \(\hat{i}\le i\le \frac{n}{2}\), (81) implies that

$$\begin{aligned} \xi _i\le & {} \frac{1}{2}=\frac{1}{3}+\frac{1}{6}<\frac{i}{n}+\frac{1}{3}\cdot \frac{1}{2}= \frac{i}{n}+\frac{1}{3}\xi ^{1 - (a_{1/2}(r))}_i\\< & {} \frac{i}{n}+\frac{1}{2}\xi ^{1 - (a_{1/2}(r))}_i =\lambda _i+\frac{1}{2}\xi ^{1 - (a_{1/2}(r))}_i. \end{aligned}$$

For \(\frac{n}{2}<i\le n-\hat{i}\), (81) implies that

$$\begin{aligned} \xi _i\le & {} \xi _{n-\hat{i}}=1-\xi _{\hat{i}}<1-\frac{1}{3}=\frac{1}{2}+\frac{1}{6}<\frac{i}{n}+\frac{1}{3}\cdot \frac{1}{2} =\frac{i}{n}+\frac{1}{3}\cdot \xi ^{1 - (a_{1/2}(r))}_i\\< & {} \frac{i}{n}+\frac{1}{2}\cdot \xi ^{1 - (a_{1/2}(r))}_i =\lambda _i+\frac{1}{2}\cdot \xi ^{1 - (a_{1/2}(r))}_i. \end{aligned}$$

For \(i>n-\hat{i}>\frac{n}{2}\),

$$\begin{aligned} \xi _i\le & {} 1=\frac{1}{2}+\frac{1}{2}\\< & {} \frac{i}{n}+\frac{1}{2}\cdot 1 =\frac{i}{n}+\frac{1}{2}\cdot \xi ^{1 - (a_{1/2}(r))}_i =\lambda _i+\frac{1}{2}\cdot \xi ^{1 - (a_{1/2}(r))}_i, \end{aligned}$$

completing the proof of the theorem. \(\square \)

9 A decreasing and oscillating bound for the \(\xi \)-relaxation gap

In this section, we prove two results. Consistent with Observation 5, we provide a bound for the \(\xi \)-relaxation gap of regular 1 / k-facets that decreases as k grows. Consistent with Observation 6 we show that the bound for the \(\xi \)-relaxation gap for regular 1 / k-facets is smaller for k odd compared to k even.

Theorem 9.1

Let \(k\ge 3\). The \(\xi \)-relaxation gap of the regular 1 / k-facets \(\xi ^{k - (a_m)}\) is strictly less than \(1+1/k.\)

Proof

Let \(a_{k/2}\) denote the first index of the half landing of \(\xi ^{k - (a_m)}\). For \(i<a_{k/2}\) and \(\varepsilon >0\),

$$\begin{aligned} \xi ^{k - (a_m)}_i-\lambda _i= & {} \frac{1}{k}\cdot \left\lfloor \frac{i}{d}\right\rfloor -\frac{i}{kd} =\frac{1}{k}\cdot \left( \left\lfloor \frac{i}{d}\right\rfloor -\frac{i}{d}\right) \nonumber \\ \le \frac{1}{k}\cdot 0= & {} 0 =\left( \frac{1}{k}-\varepsilon \right) \cdot 0=\left( \frac{1}{k}-\varepsilon \right) \xi ^{1 - (a_{1/2}(r))}_i. \end{aligned}$$
(82)

Let the 1-facet \(\xi ^{1 - (a_{1/2}(r))}\) of rank r have the same half landing as that of \(\xi ^{k - (a_m)}\); i.e.,

$$\begin{aligned} a_{1}(r)=a_{k/2}. \end{aligned}$$

For \(a_{k/2}\le i\le n-a_{k/2}\), the lower bound in (18) implies

$$\begin{aligned}&\xi ^{k - (a_m)}_i-\lambda _i = \frac{1}{2}-\frac{i}{n}\le \frac{1}{2}-\frac{a_{k/2}}{n}\nonumber \\&\quad <\frac{1}{2}-\frac{1}{2}\cdot \left( 1-\frac{1}{k}\right) =\frac{1}{k}\cdot \frac{1}{2} =\frac{1}{k}\xi ^{1 - (a_{1/2}(r))}_i. \end{aligned}$$
(83)

For \(i>n-a_{k/2}\),

$$\begin{aligned} \xi ^{k - (a_m)}_i-\lambda _i= & {} 1-\frac{1}{k}\cdot \left\lfloor \frac{n-i}{d}\right\rfloor -\frac{i}{n}\nonumber \\= & {} \left( 1-\frac{i}{n}\right) -\frac{1}{k}\cdot \left\lfloor \frac{n-i}{d}\right\rfloor =\frac{n-i}{n}-\frac{1}{k}\cdot \left\lfloor \frac{n-i}{d}\right\rfloor \nonumber \\= & {} \frac{n-i}{kd}-\frac{1}{k}\cdot \left\lfloor \frac{n-i}{d}\right\rfloor =\frac{1}{k}\cdot \left( \frac{n-i}{d}-\left\lfloor \frac{n-i}{d}\right\rfloor \right) \nonumber \\< & {} \frac{1}{k}\cdot 1=\frac{1}{k}\xi ^{1 - (a_{1/2}(r))}_i. \end{aligned}$$
(84)

From (82), (83) and (84), we have

$$\begin{aligned} \xi ^{k - (a_m)}-\lambda \le \left( \frac{1}{k}-\varepsilon \right) \xi ^{1 - (a_{1/2}(r))} \end{aligned}$$

for a small \(\varepsilon >0\), completing the proof of the theorem. \(\square \)

Theorem 9.1 shows that as k gets larger, the \(\xi \)-relaxation gap approaches 1. In other words a regular 1 / k-facet for small k is much stronger than a 1 / k-facet with large k.

Theorem 9.2

If \(k\ge 3\) is odd, the \(\xi \)-relaxation gap of the regular 1 / k-facets \(\xi ^{k - (a^k_m(r))}\) of any rank r are less than or equal to \(1+1/(2k)\).

Proof

If \(r<R^k(n)\), we easily see that

$$\begin{aligned} \xi ^{k - (a^k_m(r))}\le \xi ^{k - (a^k_m(r+1))}+\frac{1}{2k}\xi ^{1 - (a_{1/2}(0))}. \end{aligned}$$

We assume \(r=R^k(n)\). Then, \(\xi ^{2k - (a^{2k}_m)}\) given by \(a^{2k}_{k}=a^{k}_{k/2}\) and

$$\begin{aligned} a^{2k}_{2m}=a^{k}_{m}=md \hbox { and } a^{2k}_{2m-1}=a^{k}_{m}-1=md-1\hbox { for }1\le m<\frac{k}{2}, \end{aligned}$$

is a knapsack facet by Lemmas 3.2 and 3.3. This facet satisfies

$$\begin{aligned} \xi ^{k - (a^k_m(R^k(n)))}\le \xi ^{2k - (a^{2k}_m)}+\frac{1}{2k}\xi ^{1 - (a_{1/2}(0))}, \end{aligned}$$

completing the proof of the theorem. \(\square \)

Comparing Theorems 9.1 and 9.2 we see that the bound for the \(\xi \)-relaxation gap for regular 1 / k-facets with k odd is less than that for k even. This provides support for Observation 6 from our computational experiments that 1 / k-facets for k even are “stronger” than 1 / k-facets for k odd.