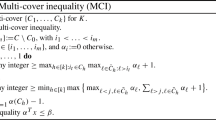Multi-cover Inequalities for Totally-Ordered Multiple Knapsack Sets

Abstract

We propose a method to generate cutting-planes from multiple covers of knapsack constraints. The covers may come from different knapsack inequalities if the weights in the inequalities form a totally-ordered set. Thus, we introduce and study the structure of a totally-ordered multiple knapsack set. The valid multi-cover inequalities we derive for its convex hull have a number of interesting properties. First, they generalize the well-known (1, k)-configuration inequalities. Second, they are not aggregation cuts. Third, they cannot be generated as a rank-1 Chvátal-Gomory cut from the inequality system consisting of the knapsack constraints and all their minimal covers. Finally, we provide conditions under which the inequalities are facet-defining for the convex hull of the totally-ordered knapsack set.

1 Introduction

We study cutting-planes related to covers of 0–1 knapsack sets. For a 0–1 knapsack set

$$\begin{aligned} K_{{\textsc {knap}}}:= \{x \in \{0,1\}^n \mid a^T x \le b\}, \end{aligned}$$

with $(a, b) \in \mathbb {Z}^{n+1}_+$, a cover is any subset of elements $C \subseteq [n]$ such that $\sum _{j \in C} a_j > b$. The cover inequality (CI)

$$ \sum _{j \in C} x_j \le |C| - 1 $$

is a valid inequality for the knapsack polytope ${\text {conv}}(K_{{\textsc {knap}}})$ that separates the invalid characteristic vector of C. There is a long and rich literature on (lifted) cover inequalities for the knapsack polytope [1, 7, 8, 10, 15], and the readers are directed to the recent survey of [9] for a more complete background.

For the binary-valued set

$$\begin{aligned} X = \{x \in \{0,1\}^n \mid Ax \le b\}, \end{aligned}$$

where $[A, b] \in \mathbb {Z}^{m \times (n+1)}_+$, a standard and computationally-useful way for generating valid inequalities to improve the linear programming relaxation of X is to generate lifted cover inequalities for the knapsack sets defined by the individual constraints of X [4]. In this way, the extensive literature regarding valid inequalities for ${\text {conv}}(K_{{\textsc {knap}}})$ can be leveraged to solve integer programs whose feasible region is X. In contrast to $K_{{\textsc {knap}}}$, very little is known about polyhedra that arise as the convex hull of the intersection of multiple knapsack sets. In this paper, we introduce a family of cutting-planes, called (antichain) multi-cover inequalities ((A)MCIs), that are derived by simultaneously considering multiple covers which satisfy some particular condition. The covers may come from any inequality in the formulation, so long as the weights appearing in the knapsack inequalities are totally-ordered.

More formally, we give a new approach to generate valid inequalities for a special multiple knapsack set, called the totally-ordered multiple knapsack set (TOMKS). Given a constraint matrix $A \in \mathbb {Z}^{m \times n}_+$ whose columns $\{A_1, A_2, \ldots , A_n\}$ form a chain ordered by component-wise order, i.e., $A_1 \ge A_2 \ldots \ge A_n,$ and a right-hand-side vector $b \in \mathbb {Z}_+^m$, the TOMKS is the set

$$\begin{aligned} K = \{x \in \{0,1\}^n \mid Ax \le b\}. \end{aligned}$$

(1)

TOMKS can arise in the context of chance-constrained programming. Specifically, consider a knapsack constraint where the weights of the items (a) depend on a random variable $(\xi$), and we wish to satisfy the chance constraint

$$\begin{aligned} \mathbb {P} \{ a(\xi )^T x \le \beta \} \ge 1-\epsilon , \end{aligned}$$

(2)

selecting a subset of items ($x \in \{0,1\}^n$) so that the likelihood that these items fit into the knapsack is sufficiently high. In the scenario approximation approach proposed in [3, 12], an independent Monte Carlo sample of N realizations of the weights $(a(\xi ^1), \ldots a(\xi ^N))$ is drawn and the deterministic constraints

$$\begin{aligned} a(\xi ^i)^T x \le \beta \quad \forall i=1\ldots ,N \end{aligned}$$

(3)

are enforced. In [11] it is shown that if the sample size N is sufficiently large:

$$\begin{aligned} N \ge \frac{1}{2 \epsilon ^2} \left( \log \left( \frac{1}{\delta } \right) + n \log (2) \right) , \end{aligned}$$

then any feasible solution to (3) satisfies the constraint (2) with probability at least $1-\delta$. If the random weights of the items $a_1(\xi ), a_2(\xi ), \ldots a_n(\xi )$ are independently distributed with means $\mu _1 \ge \mu _2 \ldots \ge \mu _n$, then the feasible region in (3) may either be a TOMKS, or the constraints can be (slightly) relaxed to obey the ordering property.

But the TOMKS may arise in more general situations as well. For a general binary set X, if two knapsack inequalities $a_1^T x \le b_1$ and $a_2^T x \le b_2$ have non-zero coefficients in very few of the same variables, their intersection may be totally-ordered, and the (A)MCI would be applicable in this case. In the special case where the multiple covers come from the same knapsack set, the (A)MCI can also produce interesting inequalities. For example, the well-known (1, k)-configuration inequalities for ${\text {conv}}(K_{{\textsc {knap}}})$ [13] are a special case of (A)MCI where all covers come from the same inequality (see Proposition 4). We also give an example where a facet of ${\text {conv}}(K_{{\textsc {knap}}})$ found by a new lifting procedure described in [10] is a MCI.

A MCI is generated by a simple algorithm (given in Algorithm 1) that takes as input a special family of covers $\mathscr {C}= \{C_1, C_2, \ldots C_k\}$ that obeys a certain maximality criterion (defined in Definition 3). For many types of cover families $\mathscr {C}$, the MCI may be given in closed-form. In the case that the family of covers $\mathscr {C}$ is an antichain in a certain partial order, the resulting MCI has the interesting property that it simultaneously cuts off at least two of the characteristic vectors of the covers in $\mathscr {C}$. We also give conditions under which the MCI yields a facet for ${\text {conv}}(K)$ in Sect. 5.

The MCI may be generated by simultaneously considering multiple knapsack inequalities defining K. Another mechanism to generate inequalities taking into account information from multiple constraints of the formulation is to aggregate inequalities together, forming the set

$$\begin{aligned} \mathcal {A}(A,b) := \bigcap _{\lambda \in \mathbb {R}^m_+} {\text {conv}}(\{x \in \{0,1\}^n \ \mid \lambda ^T A x \le \lambda ^T b \}). \end{aligned}$$

Inequalities valid for $\mathcal {A}(A,b)$ are known as aggregation cuts, and have been shown to be quite powerful from both an empirical [6] and theoretical [2] viewpoint. The well-known Chvátal-Gomory (CG) cuts, lifted knapsack cover inequalities, and weight inequalities [14] are all aggregation cuts. In Example 3, we show that MCI are not aggregation cuts. Further, in Example 4, we show that MCI cannot be obtained as a (rank-1) Chvátal-Gomory cut from the linear system consisting of all minimal cover inequalities from K.

The paper is structured as follows: In Sect. 2, we define a certain type of dominance relationship between covers that is necessary for MCI. The MCI is defined in Sect. 3, where we also give many examples to demonstrate that MCIs are not dominated by other well-known families of cutting-planes. In Sect. 4, we propose a strengthening of MCI in the case that the cover-family forms an antichain in a certain partially ordered set. Section 5 provides sufficient condition for the MCI to be a facet-defining inequality for ${\text {conv}}(K)$.

Notation. For a positive integer n, we denote by $[n] := \{1,\dots ,n\}$. For $x \in \mathbb {R}^n$, ${\text {supp}}(x): = \{i \in [n] \mid x_i \ne 0\}$ denotes the support of x. The characteristic vector of a set $S \subseteq [n]$ is denoted by $\chi ^S$. Therefore, given a TOMKS K, we say that a set $S \subseteq [n]$ is a cover for K if $\chi ^S \notin K$. For a vector $x \in \mathbb {R}^n$ and a set $S \subseteq [n]$, we define $x(S) := \sum _{i \in S} x_i$. This in particular means $x(\emptyset ) = 0.$ We denote the power set of a set S by $2^S$, which is the set of all subsets of S.

2 A Dominance Relation

In this section we define and provide some properties of a type of dominance relationship between covers.

Definition 1

(Domination). For $S_1, S_2 \subseteq [n]$, we say that $S_1$ dominates $S_2$ and write $S_1 \triangleright S_2$, if there exists an injective function $f: S_2 \rightarrow S_1$ with $f(i) \le i \ \forall i \in S_2$.

The dominance relation in Definition 1 is reflexive, antisymmetric, and transitive, so $(2^{[n]}, \triangleright )$ forms a partially ordered set (poset). For two sets $S_1, S_2 \subseteq [n]$, we say $S_1$ and $S_2$ are comparable if $S_1 \triangleright S_2$ or $S_2 \triangleright S_1$.

The dominance relation has a natural use in the context of covers. In fact, if $C_2$ is a cover for a TOMKS K and $C_1$ dominates $C_2$, then $C_1$ is also a cover for K. Next, we present two technical lemmas. The proofs are technical and can be found in the full version of the paper [5].

Lemma 1

Let $S_1, S_2 \subseteq [n]$ with $S_1 \ne S_2$. Then for any $S' \subseteq S_1 \cap S_2$, $S_1 \triangleright S_2$ if and only if $S_1 \setminus S' \triangleright S_2 \setminus S'$.

Lemma 2

Let $S \subseteq [n]$ and let $S_1 ,S_2 \subseteq S$. Then, $S_1\triangleright S_2$ if and only if $S \setminus S_2 \triangleright S \setminus S_1$.

3 Multi-cover Inequalities

Throughout this section, we consider a TOMKS $K : = \{x \in \{0,1\}^n \mid Ax \le b\}$, and we introduce the multi-cover inequalities (MCIs), which form a novel family of valid inequalities for K. Each MCI can be obtained from a special family of covers $\{C_1, \ldots , C_k\}$ for K that we call a multi-cover. In order to define a multi-cover, we first introduce the discrepancy family.

Definition 2

(Discrepancy family). For a family of sets $\mathscr {C}= \{C_1, \ldots , C_k\}$, we say that $\{C_1 \setminus \cap _{h=1}^k C_h, \ldots , C_k \setminus \cap _{h=1}^k C_h\}$ is the discrepancy family of $\mathscr {C}$, and we denote it by $\mathcal D(\mathscr {C})$.

Now we can define the concept of a multi-cover.

Definition 3

(Multi-cover). Let $\mathscr {C}$ be a family of covers for K. We then say that $\mathscr {C}$ is a multi-cover for K if for any set $T \subseteq \cup _{D \in \mathcal D(\mathscr {C})} D$ with $T \notin \mathcal {D}(\mathscr {C})$, there exists some $D' \in \mathcal {D}(\mathscr {C})$ such that T is comparable with $D'$.

For a given family of covers $\{C_1, \ldots , C_k\}$ for K, throughout this paper, for ease of notation we define $C_0 := \cap _{h=1}^k C_h$, $C := \cup _{h=1}^k C_h$, $\bar{C}_h: = C \setminus C_h$ for $h \in [k]$, and similarly $\bar{T} := C \setminus T$ for any $T \subseteq C$.

We are now ready to introduce our multi-cover inequalities for K. These inequalities are defined by the following algorithm.

We remark that in Algorithm 1, in the case where we take the minimum or maximum over an empty set (see Step 4 and 6), the corresponding minimum or maximum is defaulted to take the value zero.

For the above algorithm, we have the following easy observations.

Observation 1

Given a multi-cover $\{C_h\}_{h=1}^k$, Algorithm 1 performs a number of operations that is polynomial in |C| and k. Furthermore, ${\text {supp}}(\alpha ) = C$.

The main result of this section is that, given a multi-cover for K, the corresponding MCI is valid for ${\text {conv}}(K)$. Before presenting the theorem, we will need the following auxiliary result.

Proposition 1

Let $\{C_h\}_{h=1}^k$ be a multi-cover and let $\alpha ^T x \le \beta$ be the associated MCI. If there exists $T \subseteq C \setminus C_0, T \notin \{\bar{C}_h\}_{h=1}^k,$ with $T \triangleright \bar{C}_{h'}$ for some $h' \in [k]$, then $\alpha (T) > \alpha (\bar{C}_{h'})$.

Proof

Let T and $\bar{C}_{h'}$ be the sets as assumed in the statement of this proposition, with $T \triangleright \bar{C}_{h'}$. Denote $T_0: = T \cap \bar{C}_{h'}, T_1: = T \setminus T_0,$ and $T_2: = \bar{C}_{h'} \setminus T_0$. Then $T = T_0 \cup T_1, \bar{C}_{h'} = T_0 \cup T_2$. Since $T \ne \bar{C}_{h'}$ and $T \triangleright \bar{C}_{h'}$, then we know $T_1 \ne \emptyset$. By Lemma 1, we know that $T_1 \triangleright T_2$. If $T_2 = \emptyset$, then $\alpha (T) = \alpha (T_0) + \alpha (T_1) > \alpha (T_0) = \alpha (\bar{C}_{h'})$. Hence we assume $T_2 \ne \emptyset$. Denote $T_2: = \{j_1, \ldots , j_t\}$. Since $T_1 \triangleright T_2$ and $T_1 \cap T_2 = \emptyset$, we know there exists $\{k_1, \ldots , k_t\} \subseteq T_1$ such that $k_1< j_1, \ldots , k_t < j_t$.

W.l.o.g., consider $k_1$ and $j_1$. By definition, there is $k_1 < j_1, k_1 \notin \bar{C}_{h'}, j_1 \in \bar{C}_{h'}$, which is just saying: $k_1 < j_1, k_1 \in C_{h'}, j_1 \in \bar{C}_{h'}$. Therefore, $j_1 \in \{\ell \mid \ell > k_1, \ell \in \bar{C}_{h'}, k_1 \in C_{h'}\}$. By Step 4 of Algorithm 1, we know that $\alpha _{k_1} > \alpha _{j_1}$. For the remaining $j_2$ and $j_2, \ldots , k_t$ and $j_t$ we can do the exact same argument and obtain $\alpha _{k_2}> \alpha _{j_2}, \ldots , \alpha _{k_t} > \alpha _{j_t}$.

Therefore, $\alpha (T) = \alpha (T_1) + \alpha (T_0) \ge \alpha _{k_1} + \ldots + \alpha _{k_t} + \alpha (T_0) > \alpha _{j_1} + \ldots + \alpha _{j_t} + \alpha (T_0) = \alpha (\bar{C}_{h'})$, which concludes the proof.    $\square$

Now we are ready to present the first main result of this paper.

Theorem 1

Given a multi-cover $\{C_h\}_{h=1}^k$ for a TOMKS K, the MCI produced by Algorithm 1 is valid for ${\text {conv}}(K)$.

Proof

Since ${\text {supp}}(\alpha ) = C$, in order to show that $\alpha ^T x \le \beta$ is valid to ${\text {conv}}(K)$, it suffices to show that, for any $T \subseteq C$ with $\alpha (T) \ge \beta + 1$, T must be a cover to K. Note that from Step 7 there is $\beta + 1= \max _{h=1}^k \alpha (C_h)$, and for any $T_1, T_2 \subseteq C$, $\alpha (T_1) \ge \alpha (T_2)$ is equivalent to $\alpha (\bar{T}_1) \le \alpha (\bar{T}_2)$, furthermore from Lemma 2, therefore it suffices for us to show that: for any $T \subseteq C$ with $\alpha (\bar{T}) \le \min _{h=1}^k\alpha (\bar{C}_h)$, there must exist some $h^* \in [k]$ such that $\bar{C}_{h^*} \triangleright \bar{T}$. We will assume that $T \notin \{C_h\}_{h=1}^k$ since otherwise $\bar{C}_{h^*} \triangleright \bar{T}$ trivially holds. In the following, the proof is subdivided into two cases, depending on whether $\bar{T} \cap C_0 = \emptyset$ or not.

First, we consider the case $\bar{T} \cap C_0 = \emptyset$. In this case, there is $C_0 \subseteq T$. by Definition 3 of multi-cover, we know there must exist $h^* \in [k]$ such that either $C_{h^*} \setminus C_0 \triangleright T \setminus C_0$, or $T \setminus C_0 \triangleright C_{h^*} \setminus C_0$. By the above assumption $C_0 \subseteq T$ and Lemma 1, we know that either $C_{h^*} \triangleright T$ or $T \triangleright C_{h^*}$. If $T \triangleright C_{h^*}$, then Lemma 2 implies $\bar{C}_{h^*} \triangleright \bar{T}$, which completes the proof. So we assume $C_{h^*} \triangleright T$, or equivalently, $\bar{T} \triangleright \bar{C}_{h^*}$. Since $\bar{T} \subseteq C \setminus C_0$ and $\bar{T} \notin \{\bar{C}_h\}_{h=1}^k$, By Proposition 1 we obtain that $\alpha (\bar{T}) > \alpha (\bar{C}_{h^*})$, and this contradicts to the assumption of $\alpha (\bar{T}) \le \min _{h=1}^k\alpha (\bar{C}_h)$.

Next, we consider the case $\bar{T} \cap C_0 \ne \emptyset$. In this case, we want to construct a $\bar{D} \subseteq C$ with $\bar{D} \cap C_0 = \emptyset , \alpha (\bar{D}) \le \alpha (\bar{T})$, and $\bar{D} \triangleright \bar{T}$. Then since $\alpha (\bar{T}) \le \min _{h=1}^k\alpha (\bar{C}_h)$, we have $\alpha (\bar{D}) \le \min _{h=1}^k\alpha (\bar{C}_h)$ where $\bar{D} \cap C_0 = \emptyset$. According to our discussion in the previous case, we know there exists some $h^* \in [k]$ such that $\bar{C}_{h^*} \triangleright \bar{D}$, which implies $\bar{C}_{h^*} \triangleright \bar{T}$ since $\triangleright$ forms a partial order, and the proof is completed.

Arbitrarily pick $t^* \in \bar{T} \cap C_0$. Then by Step 6, we know there exists $h^* \in [k]$ such that $\alpha _{t^*} = \max \big \{ \min _{\ell <t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell , \sum _{t>t^*, t \in \bar{C}_{h^*}} \alpha _t + 1 \big \}$. If $\{\ell \in \bar{C}_{h^*} \mid \ell < t^*\} \subseteq \bar{T}$, then we have $\alpha (\bar{T}) \ge \sum _{\ell < t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell + \alpha _{t^*}$, which is at least $\sum _{\ell < t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell + \sum _{t>t^*, t \in \bar{C}_{h^*}} \alpha _t + 1$. Since $t^* \notin \bar{C}_{h^*}$, we know that $\sum _{\ell < t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell + \sum _{t>t^*, t \in \bar{C}_{h^*}} \alpha _t + 1 = \alpha (\bar{C}_{h^*}) + 1$. Hence $\alpha (\bar{T}) > \alpha (\bar{C}_{h^*})$, and this contradicts to the initial assumption of $\alpha (\bar{T}) \le \min _{h=1}^k\alpha (\bar{C}_h)$. Therefore we can find some $\ell ^* \in \bar{C}_{h^*}, \ell ^* < t^*$ such that $\ell ^* \notin \bar{T}$. Now define $\bar{D}: = \bar{T} \cup \{\ell ^*\} \setminus \{t^*\}$. Since $\ell ^* < t^*$, clearly $\bar{D} \triangleright \bar{T}$. Also $\alpha (\bar{T}) - \alpha (\bar{D}) = \alpha _{t^*} - \alpha _{\ell ^*}$, since $\alpha _{t^*} \ge \max _{\ell <t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell$, we know that $\alpha (\bar{T}) - \alpha (\bar{D}) \ge 0$. If $\bar{D} \cap C_0 = \emptyset$, then we are done. Otherwise, we can replace $\bar{T}$ by $\bar{D}$, consider any index in $\bar{D} \cap C_0$ and do the above discussion one more time. Every time we are able to obtain a set $\bar{D}$ with $|\bar{D} \cap C_0|$ decreasing by 1. In the end we will obtain a set $\bar{D}$ with the desired property: $\bar{D} \cap C_0 = \emptyset , \alpha (\bar{D}) \le \alpha (\bar{T})$, and $\bar{D} \triangleright \bar{T}$. This completes the proof for the case $\bar{T} \cap C_0 \ne \emptyset$.

Therefore, from the discussion for the above two cases, we have concluded the proof of MCI $\alpha ^T x \le \beta$ being a valid inequality for ${\text {conv}}(K)$.    $\square$

For some multi-covers with a special discrepancy family, we are able to write the associated MCI in closed form. We provide two examples.

Example 1

Consider $\{C_1, C_2\}$ with discrepancy family $\{\{i_1, i_{t+1}\}, \{i_2, \ldots , i_t\}\}$ for some $t \ge 3$, with $i_1< \ldots < i_{t+1}$. Easy to verify that such $\{C_1, C_2\}$ is a multi-cover, and the obtained MCI is:

$$\begin{aligned} \begin{aligned}&\sum _{i<i_1, i \in C} (2t - 1) x_i + \sum _{i_1 \le i< i_2, i \in C} (2t - 3) x_i + \sum _{\ell =3}^{t} \sum _{i_{\ell -1}< i< i_\ell , i \in C} (2t-2\ell +3) x_i \\&+ \sum _{\ell =2}^t 2 x_{i_\ell } + \sum _{i_t< i< i_{t+1}, i \in C} 2 x_i + x_{i_{t+1}} + \sum _{i > i_{t+1}, i \in C} 2x_i \le \alpha (C_1) - 1, \end{aligned} \end{aligned}$$

(4)

where $\alpha$ is the vector associated with the left-hand-side term.    $\diamond$

Example 2

Consider $\{C_1, C_2, C_3\}$ with discrepancy family $\{\{i_1, i_3\},\{i_1, i_4, i_5\},$ $\{i_2, i_3, i_5\}\}$, with $i_1< \ldots < i_{5}$. Here the family of covers $\{C_1, C_2, C_3\}$ is a multi-cover, and the obtained MCI is:

$$\begin{aligned} \begin{aligned}&\sum _{i< i_1, i \in C} 5x_i + \sum _{i_1 \le i< i_2, i \in C} 3x_i + 2 x_{i_2} + \sum _{i_2< i< i_3, i \in C} 3x_i + 2x_{i_3}\\&+ \sum _{i_3< i< i_4, i \in C} 2x_i + x_{i_4} + \sum _{i_4< i < i_5, i \in C} 2x_i + x_{i_5} + \sum _{i > i_5, i \in C} 2x_i \le \alpha (C_1) - 1, \end{aligned} \end{aligned}$$

(5)

where $\alpha$ is the vector associated with the left-hand-side term.    $\diamond$

Next, we present some illustrative examples to showcase the novelty of MCIs. The first example shows that, unlike lifted cover inequalities or CG cuts, MCIs are not aggregation cuts of the original linear system.

Example 3

Consider the TOMKS:

$$\begin{aligned}&K: = \{x \in \{0,1\}^5 \mid 19 x_1 + 11x_2 + 5x_3 + 4x_4 + 2x_5 \le 31, \\&\qquad \qquad \qquad \qquad \,\,\, 16 x_1 + 10 x_2 + 7 x_3 + 5 x_4 + 3 x_5 \le 30\}. \end{aligned}$$

Then $\{C_1, C_2\} := \{\{1,2,5\},\{1,3,4,5\}\}$ is a multi-cover for K, point $\chi ^{C_1}$ only violates the first knapsack constraint, and point $\chi ^{C_2}$ only violates the second knapsack constraint. The associated MCI is

$$\begin{aligned} 3 x_ 1 + 2 x_2 + x_3 + x_4 + x_5 \le 5, \end{aligned}$$

(6)

and (6) is violated by both $\chi ^{C_1}$ and $\chi ^{C_2}$.

Now consider an aggregation of the knapsack inequalities of K given by $\lambda _1 (19,11,5,4,2)^T x + \lambda _2 (16,10,7,5,3)^T x \le 31\lambda _1 + 30 \lambda _2$, where $\lambda _1, \lambda _2 \ge 0$. For any choice of $\lambda _1 \ge 0, \lambda _2 \ge 0$, it can be verified that $C_1$ and $C_2$ cannot both be covers to the knapsack set given by this single inequality, so any aggregation cut for K can cut off at most one of $\chi ^{C_1}$ and $\chi ^{C_2}$. Therefore, the inequality (6) is not an aggregation cut. In some cases, it may be possible to obtain an MCI as a CG cut of the original linear system augmented with its minimal cover inequalities. In this example, consider the set

$$\begin{aligned} K_{CI} : = \{x \in \{0,1\}^5 \mid&\ 19 x_1 + 11x_2 + 5x_3 + 4x_4 + 2x_5 \le 31, \\&16 x_1 + 10 x_2 + 7 x_3 + 5 x_4 + 3 x_5 \le 30,\\&x_1 + x_2 + x_3 \le 2, x_1 + x_2 + x_4 \le 2,\\&x_1 + x_2 + x_5 \le 2, x_1 + x_3 + x_4 + x_5 \le 3 \}. \end{aligned}$$

The inequality (6) is indeed a CG cut with respect to $K_{CI}$, as shown by multipliers $\frac{1}{12} \cdot (19, 11, 5,4,2) + \frac{1}{4} \cdot (1,1,1,0,0) + \frac{1}{3} \cdot (1,1,0,1,0) + \frac{1}{2} \cdot (1,1,0,0,1) + \frac{1}{3} \cdot (1,0,1,1,1) = (3,2,1,1,1), \frac{1}{12} \cdot 31 + \frac{1}{4} \cdot 2 + \frac{1}{3} \cdot 2 + \frac{1}{2} \cdot 2 + \frac{1}{3} \cdot 3 = 5.75.$ Hence $(3,2,1,1,1)^T x \le \lfloor 5.75 \rfloor = 5$ is a CG cut for $K_{CI}$.    $\diamond$

Example 3 demonstrates that MCI can be obtained from multiple knapsack sets simultaneously. Specifically, the inequality (6) is facet-defining for ${\text {conv}}(K)$, but it is neither valid for $\{x \in \{0,1\}^5 \mid 19 x_1 + 11x_2 + 5x_3 + 4x_4 + 2x_5 \le 31 \}$ nor $\{x \in \{0,1\}^5 \mid 16 x_1 + 10 x_2 + 7 x_3 + 5 x_4 + 3 x_5 \le 30\}$. Example 3 also shows that an MCI can be a CG cut for the linear system given by the original knapsack constraints along with all their minimal cover inequalities. In the next example, we will see that this is not always the case.

Example 4

Consider the following TOMKS:

$$\begin{aligned}&K: = \{x \in \{0,1\}^8 \mid \ 28 x_1 + 24x_2+20x_3+19x_4+15x_5+10x_6+7x_7+6x_8 \le 96, \\&\qquad \qquad \qquad \qquad \,\,\,\,\, 27x_1+24x_2+21x_3+19x_4+13x_5+12x_6+7x_7+4x_8 \le 96\}. \end{aligned}$$

Consider the family of covers $C_1 = \{2,3,4,5,6,7,8\}$, $C_2 = \{1,3,4,5,6,8\},$ $C_3 = \{1,2,3,5,6\}$, $C_4 = \{1,2,3,5,7,8\}$. We have $C = [8]$, $C_0 = \{3,5\}$, and the discrepancy family is $\mathcal {D}(\mathscr {C}) = \{\{2,4,6,7,8\}, \{1,4,6,8\}, \{1,2,6\}, \{1,2,7,8\}\} =: \{D_1, D_2, D_3, D_4\}$.

First, we verify that $\mathscr {C}$ is a multi-cover. For any set $S \subseteq C \setminus C_0$ and $S \notin \mathcal {D}(\mathscr {C})$, if $1 \in S, |S| = 2$, then it is clearly dominated by either $D_2, D_3$ or $D_4$. If $1 \in S, |S| = 3$, then either $S \triangleright D_3$ or $D_3 \triangleright S$. If $1 \in S, |S| = 4$, then S must be comparable with $D_2$ or $D_3$. If $1 \in S, |S| = 5$, then $S \triangleright D_1$. If $1 \notin S,$ then clearly $D_1 \triangleright S$ since $S \subseteq D_1$. Hence for any $S \subseteq C \setminus C_0$ and $S \notin \mathcal {D}(\mathscr {C})$, S must be comparable with some set in $\mathcal {D}(\mathscr {C})$. Therefore, $\mathscr {C}$ is a multi-cover.

When Algorithm 1 is applied to $\mathscr {C}$, we obtain the inequality

$$\begin{aligned} \alpha ^T x \le \beta := 4x_1+3x_2+3x_3+2x_4+3x_5+2x_6+x_7+x_8 \le 14, \end{aligned}$$

(7)

and it can be shown that (7) is a facet-defining inequality for ${\text {conv}}(K)$.

Consider the linear system given by all the minimal cover inequalities for K, as well as the original two linear constraints. We refer to this linear system as $K_{CI}$, which consists of 30 inequalities. Solving $\max \{\alpha ^T x \mid x \in K_{CI}\}$ gives optimal value 15.307, so any corresponding CG cut with respect to $K_{CI}$ is $\alpha ^T x \le 15$, and it is weaker than inequality (7).    $\diamond$

Even when the cover-family consists of covers all coming from the same knapsack inequality, the MCI can produce interesting inequalities. In the next example, we show a MCI that cannot be obtained as a standard lifted cover inequality, regardless of the lifting order.

Example 5

(Example 3 in [10]). Let $K := \{x \in \{0,1\}^5 \mid 10 x_1 + 7 x_2 + 7 x_3 + 4 x_4 + 4 x_5 \le 16\}$, and consider the multi-cover $\mathscr {C}: = \{ \{1, 3\}, \{1, 4, 5\}, \{2, 3, 5\}\}$. From inequality (5) of Example 2, we know that the corresponding MCI is

$$\begin{aligned} 3x_1 + 2x_2 + 2x_3 + x_4 + x_5 \le 4. \end{aligned}$$

(8)

The inequality (8) is the same inequality produced by the new lifting procedure described in [10], and the authors of [10] state that (8) is both a facet of ${\text {conv}}(K)$ and cannot be obtained from any cover inequality by standard sequential lifting methods, regardless of the lifting order. $\diamond$

4 Antichain Multi-cover Inequalities

In this section we propose a way to strengthen MCI when the associated multi-cover forms an antichain in a certain poset. Recall that in order theory, an antichain is a subset of a poset such that any two distinct elements in the subset are incomparable, and a maximal antichain is an antichain that is not a proper subset of any other antichain.

Definition 4

(Antichain multi-cover). Let $\mathscr {C}$ be a family of covers for K. Then we say $\mathscr {C}$ is an antichain multi-cover for K, if $\mathcal D(\mathscr {C})$ is a maximal antichain of the poset $(2^{\cup _{D \in \mathcal D(\mathscr {C})} D}, \triangleright )$.

We are now ready to define our antichain multi-cover inequalities (AMCIs) by Algorithm 2. AMCIs have the interesting property (proved in Theorem 3) that they cut off at least two characteristic vectors of covers in the antichain multi-cover $\mathscr {C}$.

Note that an AMCI is not necessarily different from its corresponding MCI, it depends on if condition 2 is satisfied or not.

First, we show that Algorithm 2 can perform all required steps. The only nontrivial step is Step 3. Thus, we only need to prove the following proposition.

Proposition 2

In Step 3, for any $h \in [k]$, there exists an index $i_{t^*}$ in $\{i_1, \ldots , i_{m}\}$ such that $|C_{h} \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| = 1.$

Proof

First, we claim that there exists $t^\circ \in [m]$, such that

$$\begin{aligned} |C_{h} \cap \{i_1, \ldots , i_{t^\circ }\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^\circ }\}| \ge 1. \end{aligned}$$

(9)

We prove this claim by contradiction. Thus we assume that for every $t \in [m]$ we have $|C_h \cap \{i_1, \ldots , i_t\}| - |C_{h^*} \cap \{i_1, \ldots , i_t\}| \le 0$. Let $C_h \setminus C_0 = \{j_1, \ldots , j_{\ell }\} \subseteq \{i_1, \ldots , i_m\}$ with $j_1< \cdots < j_{\ell }$. To prove our claim it suffices to construct an injective function $f : C_h \setminus C_0 \rightarrow C_{h^*} \setminus C_0$ such that $f(j_1) \le j_1, \dots , f(j_\ell ) \le j_\ell$. In fact, Definition 1 then implies $C_{h^*} \setminus C_0 \triangleright C_h \setminus C_0$, which gives us a contradiction since by Definition 4 of antichain multi-cover, the discrepancy family $\{C_h \setminus C_0\}_{h \in [k]}$ forms an antichain. Let $s_1 \in [m]$ be an index such that $i_{s_1} = j_1$. From our assumption, we know that $|C_{h^*} \cap \{i_1, \ldots , i_{s_1}\}| \ge |C_h \cap \{i_1, \ldots , i_{s_1}\}| = 1$. So we can find $i_{r_1} \in C_{h^*}$ with $i_{r_1} \le i_{s_1} = j_1$, and let $f(j_1): = i_{r_1}$. Now let $s_2$ such that $i_{s_2} = j_2$. From our assumption, we know that $|C_{h^*} \cap \{i_1, \ldots , i_{s_2}\}| \ge |C_h \cap \{i_1, \ldots , i_{s_2}\}| = 2$, thus $|(C_{h^*} \setminus \{i_{r_1}\}) \cap \{i_1, \ldots , i_{s_2}\}| \ge 1$. So we can find $i_{r_2} \in C_{h^*}$ with $i_{r_2} \ne i_{r_1}$ and $i_{r_2} \le i_{s_2} = j_2$. We then set $f(j_2): = i_{r_2}$. Recursively, we can then construct an injective function $f : C_h \setminus C_0 \rightarrow C_{h^*} \setminus C_0$ such that $f(j_1) \le j_1, \dots , f(j_\ell ) \le j_\ell$. This concludes the proof of (9).

For every $t \in [m-1]$, we clearly have $0 \le |C_{h} \cap \{i_1, \ldots , i_{t+1}\}| - |C_{h} \cap \{i_1, \ldots , i_t\}| \le 1$, and the same observation holds if we replace h with $h^*$. Thus

$$\begin{aligned} -1 \le \qquad&(|C_{h} \cap \{i_1, \ldots , i_{t+1}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t+1}\}|) \\&- (|C_{h} \cap \{i_1, \ldots , i_t\}| - |C_{h^*} \cap \{i_1, \ldots , i_t\}|) \qquad \le 1. \end{aligned}$$

From $|C_{h} \cap \{i_1\}| - |C_{h^*} \cap \{i_1\}| \le 1$ and (9), we then obtain that there must exist some $t^* \in [t^\circ ]$, such that $|C_{h} \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| = 1$.    $\square$

Next, we show that AMCIs are valid for K. The validity proof is analogous to that of Theorem 1, which also requires the following auxiliary result.

Proposition 3

Let $\{C_h\}_{h=1}^k$ be an antichain multi-cover and let $\alpha ^T x \le \beta$ be the associated AMCI. If there exists $T \subseteq C \setminus C_0, T \notin \{\bar{C}_h\}_{h=1}^k,$ with $T \triangleright \bar{C}_{h'}$ for some $h' \in [k]$, then $\alpha (T) > \alpha (\bar{C}_{h'})$.

Proof

We will assume that the condition at Step 2 in Algorithm 2 is satisfied, since if not, then the AMCI coincides with its MCI, and the statement of this proposition coincides with Proposition 1. Let T and $\bar{C}_{h'}$ be the sets as assumed in the statement of this proposition, with $T \triangleright \bar{C}_{h'}$. Denote $T_0: = T \cap \bar{C}_{h'}, T_1: = T \setminus T_0,$ and $T_2: = \bar{C}_{h'} \setminus T_0$. Then $T = T_0 \cup T_1, \bar{C}_{h'} = T_0 \cup T_2$. Since $T \ne \bar{C}_{h'}$ and $T \triangleright \bar{C}_{h'}$, then we know $T_1 \ne \emptyset$. By Lemma 1, we know that $T_1 \triangleright T_2$. If $T_2 = \emptyset$, then $\alpha (T) = \alpha (T_0) + \alpha (T_1) > \alpha (T_0) = \alpha (\bar{C}_{h'})$. Hence we assume $T_2 \ne \emptyset$. Denote $T_2: = \{j_1, \ldots , j_t\}$. Since $T_1 \triangleright T_2$ and $T_1 \cap T_2 = \emptyset$, we know there exists $\{k_1, \ldots , k_t\} \subseteq T_1$ such that $k_1< j_1, \ldots , k_t < j_t$.

Let $\gamma ^T x \le \theta$ be the MCI of antichain multi-cover $\{C_h\}_{h=1}^k$. From the proof of Proposition 1, we know that $\gamma _{k_1}> \gamma _{j_1}, \ldots , \gamma _{k_t} > \gamma _{j_t}$. By Step 5 and 6, we know for any $i \in C \setminus C_0, \alpha _i = \gamma _i + \delta \cdot \mathbbm {1}\{i \le i_{t^*}\}$. Since $k_1< j_1, \ldots , k_t < j_t$, therefore we have $\mathbbm {1}\{k_1 \le i_{t^*}\} \ge \mathbbm {1}\{j_1 \le i_{t^*}\}, \ldots , \mathbbm {1}\{k_t \le i_{t^*}\} \ge \mathbbm {1}\{j_t \le i_{t^*}\}$. Hence $\alpha _{k_1} = \gamma _{k_1} + \delta \cdot \mathbbm {1}\{k_1 \le i_{t^*}\} > \gamma _{j_1} + \delta \cdot \mathbbm {1}\{j_1 \le i_{t^*}\} = \alpha _{j_1}$, and similarly there is also $\alpha _{k_2}> \alpha _{j_2}, \ldots , \alpha _{k_t} > \alpha _{j_t}$.

Therefore, $\alpha (T) = \alpha (T_1) + \alpha (T_0) \ge \alpha _{k_1} + \ldots + \alpha _{k_t} + \alpha (T_0) > \alpha _{j_1} + \ldots + \alpha _{j_t} + \alpha (T_0) = \alpha (T_2) + \alpha (T_0) = \alpha (\bar{C}_{h'})$.    $\square$

Given the above proposition, the proof of the following theorem is exactly the same as that of Theorem 1. For the completeness of this paper, we present its proof in the following.

Theorem 2

Given an antichain multi-cover $\mathscr {C}$ for a TOMKS K, the AMCI produced by Algorithm 2 is valid for ${\text {conv}}(K)$.

Proof

Since ${\text {supp}}(\alpha ) = C$, in order to show that AMCI $\alpha ^T x \le \beta$ is valid to ${\text {conv}}(K)$, it suffices to show that, for any $T \subseteq C$ with $\alpha (T) \ge \beta + 1$, T must be a cover to K. Note that from Step 7 there is $\beta + 1= \max _{h=1}^k \alpha (C_h)$, and for any $T_1, T_2 \subseteq C$, $\alpha (T_1) \ge \alpha (T_2)$ is equivalent to $\alpha (\bar{T}_1) \le \alpha (\bar{T}_2)$, furthermore from Lemma 2, therefore it suffices for us to show that: for any $T \subseteq C$ with $\alpha (\bar{T}) \le \min _{h=1}^k\alpha (\bar{C}_h)$, there must exist some $h^* \in [k]$ such that $\bar{C}_{h^*} \triangleright \bar{T}$. We will assume that $T \notin \{C_h\}_{h=1}^k$ since otherwise $\bar{C}_{h^*} \triangleright \bar{T}$ trivially holds. In the following, the proof is subdivided into two cases, depending on whether $\bar{T} \cap C_0 = \emptyset$ or not.

First, we consider the case $\bar{T} \cap C_0 = \emptyset$. In this case, there is $C_0 \subseteq T$. by Definition 3 of multi-cover, we know there must exist $h^* \in [k]$ such that either $C_{h^*} \setminus C_0 \triangleright T \setminus C_0$, or $T \setminus C_0 \triangleright C_{h^*} \setminus C_0$. By the above assumption $C_0 \subseteq T$ and Lemma 1, we know that either $C_{h^*} \triangleright T$ or $T \triangleright C_{h^*}$. If $T \triangleright C_{h^*}$, then Lemma 2 implies $\bar{C}_{h^*} \triangleright \bar{T}$, which completes the proof. So we assume $C_{h^*} \triangleright T$, or equivalently, $\bar{T} \triangleright \bar{C}_{h^*}$. Since $\bar{T} \subseteq C \setminus C_0$ and $\bar{T} \notin \{\bar{C}_h\}_{h=1}^k$, By Proposition 3 we obtain that $\alpha (\bar{T}) > \alpha (\bar{C}_{h^*})$, and this contradicts to the assumption of $\alpha (\bar{T}) \le \min _{h=1}^k\alpha (\bar{C}_h)$.

Next, we consider the case $\bar{T} \cap C_0 \ne \emptyset$. In this case, we want to construct a $\bar{D} \subseteq C$ with $\bar{D} \cap C_0 = \emptyset , \alpha (\bar{D}) \le \alpha (\bar{T})$, and $\bar{D} \triangleright \bar{T}$. Then since $\alpha (\bar{T}) \le \min _{h=1}^k\alpha (\bar{C}_h)$, we have $\alpha (\bar{D}) \le \min _{h=1}^k\alpha (\bar{C}_h)$ where $\bar{D} \cap C_0 = \emptyset$. According to our discussion in the previous case, we know there exists some $h^* \in [k]$ such that $\bar{C}_{h^*} \triangleright \bar{D}$, which implies $\bar{C}_{h^*} \triangleright \bar{T}$ since $\triangleright$ forms a partial order, and the proof is completed.

Arbitrarily pick $t^* \in \bar{T} \cap C_0$. Then by Step 6, we know there exists $h^* \in [k]$ such that $\alpha _{t^*} = \max \big \{ \min _{\ell <t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell , \sum _{t>t^*, t \in \bar{C}_{h^*}} \alpha _t + 1 \big \}$. If $\{\ell \in \bar{C}_{h^*} \mid \ell < t^*\} \subseteq \bar{T}$, then we have $\alpha (\bar{T}) \ge \sum _{\ell < t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell + \alpha _{t^*}$, which is at least $\sum _{\ell < t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell + \sum _{t>t^*, t \in \bar{C}_{h^*}} \alpha _t + 1$. Since $t^* \notin \bar{C}_{h^*}$, we know that $\sum _{\ell < t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell + \sum _{t>t^*, t \in \bar{C}_{h^*}} \alpha _t + 1 = \alpha (\bar{C}_{h^*}) + 1$. Hence $\alpha (\bar{T}) > \alpha (\bar{C}_{h^*})$, and this contradicts to the initial assumption of $\alpha (\bar{T}) \le \min _{h=1}^k\alpha (\bar{C}_h)$. Therefore we can find some $\ell ^* \in \bar{C}_{h^*}, \ell ^* < t^*$ such that $\ell ^* \notin \bar{T}$. Now define $\bar{D}: = \bar{T} \cup \{\ell ^*\} \setminus \{t^*\}$. Since $\ell ^* < t^*$, clearly $\bar{D} \triangleright \bar{T}$. Also $\alpha (\bar{T}) - \alpha (\bar{D}) = \alpha _{t^*} - \alpha _{\ell ^*}$, since $\alpha _{t^*} \ge \max _{\ell <t^*, \ell \in \bar{C}_{h^*}} \alpha _\ell$, we know that $\alpha (\bar{T}) - \alpha (\bar{D}) \ge 0$. If $\bar{D} \cap C_0 = \emptyset$, then we are done. Otherwise, we can replace $\bar{T}$ by $\bar{D}$, consider any index in $\bar{D} \cap C_0$ and do the above discussion one more time. Every time we are able to obtain a set $\bar{D}$ with $|\bar{D} \cap C_0|$ decreasing by 1. In the end we will obtain a set $\bar{D}$ with the desired property: $\bar{D} \cap C_0 = \emptyset , \alpha (\bar{D}) \le \alpha (\bar{T})$, and $\bar{D} \triangleright \bar{T}$. This completes the proof of the case $\bar{T} \cap C_0 \ne \emptyset$.    $\square$

The next theorem shows that each AMCI cuts off at least two characteristic vectors of covers from the associated antichain multi-cover.

Theorem 3

Given an antichain multi-cover $\mathscr {C}$, the AMCI produced by Algorithm 2 is violated by at least two characteristic vectors of covers in $\mathscr {C}$.

Proof

Let $\mathscr {C}: = \{C_h\}_{h \in [k]}$. When the “if” condition 2 does not hold, meaning there already exist at least two covers $C_{h_1}$ and $C_{h_2}$ from $\mathscr {C}$, such that $\alpha (C_{h_1}) = \alpha (C_{h_2}) = \max _{h=1}^k \alpha (C_h)$. Then according to Step 9, we know that $\alpha ^T x \le \beta$ cuts off $\chi ^{C_{h_1}}$ and $\chi ^{C_{h_2}}$.

Now assuming the condition 2 is satisfied. For any $i \in C \setminus C_0$, denote the intermediate coefficient of $\alpha _i$ at Step 2 before the updating operation 5 and 6 to be $\gamma _i$. Then according to the algorithm, there is $\gamma (C_{h^*}) = \max _{h=1}^k \gamma (C_h), \delta = \min \{\gamma (C_{h^*}) - \gamma (C_h) : |C_h \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| = 1\}$ where $i_{t^*}$ is defined by Step 3, and $\alpha _i = \gamma _i + \delta$ for any $i = i_1, \ldots , i_{t^*}$. Let $C_{h^{**}}$ be the cover which satisfies $|C_{h^{**}} \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| = 1$ and $\gamma (C_{h^*}) - \gamma (C_{h^{**}}) = \delta$. Next we are going to show that: $\alpha (C_{h^*}) = \alpha (C_{h^{**}}) = \max _{h=1}^k \alpha (C_h)$. Since $\alpha (C_{h^*}) - \alpha (C_{h^{**}}) = \gamma (C_{h^*}) - \gamma (C_{h^{**}}) + \delta \cdot |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| - \delta \cdot |C_{h^{**}} \cap \{i_1, \ldots , i_{t^*}\}|$, then we obtain that $\alpha (C_{h^*}) = \alpha (C_{h^{**}})$.

Claim

$\alpha (C_{h^*}) = \max _{h=1}^k \alpha (C_h)$.

Proof of claim

Arbitrarily pick $h \in [k], h \ne h^*, h \ne h^{**}$, we want to show that $\alpha (C_{h^*}) \ge \alpha (C_h)$.

If $|C_h \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| = 1$, then by definition of $\delta$, we have $\gamma (C_{h^*}) - \gamma (C_h) \ge \delta$. Therefore $\alpha (C_{h^*}) - \alpha (C_h) = \gamma (C_{h^*}) + \delta \cdot |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| - (\gamma (C_h) + \delta \cdot |C_h \cap \{i_1, \ldots , i_{t^*}\}|) = \gamma (C_{h^*}) - \gamma (C_h) - \delta \cdot (|C_h \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}|) = \gamma (C_{h^*}) - \gamma (C_h) - \delta \ge 0$.

If $|C_h \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| \le 0$, then $\alpha (C_{h^*}) - \alpha (C_h) = \gamma (C_{h^*}) - \gamma (C_h) - \delta \cdot (|C_h \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}|) \ge 0$. Here the last inequality is because $\gamma (C_{h^*}) = \max _{h=1}^k \gamma (C_h)$.

If $|C_h \cap \{i_1, \ldots , i_{t^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t^*}\}| > 1$, then because $|C_h \cap \{i_1\}| - |C_{h^*} \cap \{i_1\}| \le 1$ and $(|C_h \cap \{i_1, \ldots , i_{t + 1}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t+1}\}|) - (|C_h \cap \{i_1, \ldots , i_{t}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{t}\}|) \le 1$, we know there must exist some $i_{\ell ^*} < i_{t^*}$, such that $|C_h \cap \{i_1, \ldots , i_{\ell ^*}\}| - |C_{h^*} \cap \{i_1, \ldots , i_{\ell ^*}\}| = 1$, which contradicts to the minimum choice of $i_{t^*}$ at Step 3.    $\diamond$

Hence we have shown that $\alpha (C_{h^*}) = \alpha (C_{h^{**}}) = \max _{h=1}^k \alpha (C_h)$. According to the definition of $\beta$ at Step 9, we know that $\alpha ^T x \le \beta$ cuts off $\chi ^{C_{h^*}}$ and $\chi ^{C_{h^{**}}}$.    $\square$

Note that the multi-covers in Example 1 and Example 2 are both antichain multi-covers, and the corresponding MCIs are violated by the characteristic vectors of all covers. Therefore the AMCIs of those examples coincide with their MCIs. Next, we give an example where an AMCI is different from the corresponding MCI.

Example 6

Consider $\{C_1, C_2\}$ with discrepancy family $\{\{i_1\}, \{i_2, \ldots , i_t\}\}$ for some $t \ge 3$, with $i_1< \ldots < i_{t}$. $\{C_1, C_2\}$ is obviously an antichain multi-cover, and the obtained MCI is:

$$\begin{aligned} \begin{aligned} \gamma ^T x&:= \sum _{i<i_1, i \in C} 3 x_i + \sum _{i_1 \le i< i_2, i \in C} 2 x_i + \sum _{\ell =3}^{t} \sum _{i_{\ell -1}< i < i_\ell , i \in C} 2 x_i\\&\quad \;+ \sum _{\ell =2}^t x_{i_\ell } + \sum _{i>i_t, i \in C} x_i \le \gamma (C_2) - 1. \end{aligned} \end{aligned}$$

(10)

This MCI is different from the corresponding AMCI obtained by Algorithm 2:

$$\begin{aligned} \begin{aligned} \alpha ^T x&:= \sum _{i<i_1, i \in C} t x_i + \sum _{i_1 \le i< i_2, i \in C} (t-1) x_i + \sum _{\ell =3}^{t} \sum _{i_{\ell -1}< i < i_\ell , i \in C} (t-\ell +2) x_i\\&\quad \;+ \sum _{\ell =2}^t x_{i_\ell } + \sum _{i>i_t, i \in C} x_i \le \alpha (C_1) - 1. \end{aligned} \end{aligned}$$

(11)

   $\diamond$

The next result states that the well-known (1, k)-configuration inequality can be obtained from the AMCI (11) in Example 6.

Proposition 4

Consider a knapsack set $K = \{x \in \{0,1\}^n \mid a^T x \le b\}$, a nonempty subset $N \subseteq [n]$, and $t \in [n] \setminus N$. Assume that $\sum _{i \in N}a_i \le b$ and that $H \cup \{t\}$ is a minimal cover for all $H \subset N$ with $|H| = k$. Then for any $T(r) \subseteq N$ with $|T(r)| = r$, $k \le r \le |N|$, the (1, k)-configuration inequality $(r-k+1) x_t + \sum _{j \in T(r)}x_j \le r$ can be obtained from an AMCI (11) associated with an antichain multi-cover of a knapsack set.

Proof

When $r = k$, then the above inequality reduces to a cover inequality. Hence we assume $r > k$. W.l.o.g. assuming $a_1 \ge \ldots \ge a_n$. Consider a new knapsack set $K': = \{x \in \{0,1\}^{n+1} \mid a^{\prime T} x \le b\}$, with $a'_i = a_i \ \forall i \le t, a'_{t+1} = a_t, a'_j = a_{j-1} \ \forall j > t+1.$ Then clearly there is also $a'_1 \ge \ldots \ge a'_{n+1}$.

Since for any $H \subset N$ with $|H| = k$, $H \cup \{t\}$ is a cover to K, we know for any $j \in N, N \cup \{t\} \setminus \{j\}$ is also a cover to K, which means $\sum _{i \in N} a_i - a_j + a_t > b$. From the assumption that $\sum _{i \in N}a_i \le b$, we have $a_t > a_j$, or equivalently, $t < j$ for any $j \in N$. Now for any $T(r) \subseteq N$ with $|T(r)| = r$, $k \le r \le |N|$, denote $T(r): = \{j_1, \ldots , j_r\}$ with $j_1< \ldots < j_r$, so we have $t < j_1$ from above. Then consider $C_1: = \{t\} \cup \{j_{r-k+1}, \ldots , j_r\},C'_1: = \{t\} \cup \{j_{r-k+1} + 1, \ldots , j_r + 1\}, C'_2 : = \{t+1\} \cup \{j_{1} + 1, \ldots , j_r + 1\}$. Since $\{j_{r-k+1}, \ldots , j_r\} \subset N$ with $|\{j_{r-k+1}, \ldots , j_r\}| = k$, we know that $C_1$ is a cover to K, so $C'_1$ is a cover to $K'$ from the construction of $K'$. Furthermore it is obvious that $C'_2$ is also a cover to $K'$ since $a'_{t+1} = a'_t$. Note that the discrepancy family of $\{C'_1, C'_2\}$ is $\{\{t\}, \{t+1, j_1 + 1, \ldots , j_{r-k} + 1\}\}$, then from the AMCI (11) of Example 6, we obtain the AMCI associated with $\{C'_1, C'_2\}$ for $K'$:

$$ (r-k+1) x_t + x_{t+1} + \sum _{\ell =1}^r x_{j_\ell + 1} \le r. $$

Since K can be obtained by simply projecting out of the $x_{t+1}$ variable of $K'$, therefore we obtain that the following inequality is valid for K:

$$ (r-k+1) x_t + \sum _{\ell =1}^r x_{j_\ell } = (r-k+1) x_t + \sum _{j \in T(r)}x_j \le r. $$

   $\square$

5 Facet-Inducing MCI

In this section we provide a sufficient condition for the the MCI to define a facet of ${\text {conv}}(K)$. The proof can be found in the full version of the paper [5].

Given a multi-cover $\{C_1,\dots ,C_k\}$ with its corresponding MCI $\alpha ^T x \le \beta$, we denote by $\{i_{t,1}, \ldots , i_{t, n_t}\}: = \{i \in C \setminus C_0 \mid \alpha _i = t\}$, with $i_{t, 1}< \ldots < i_{t, n_t}$.

Theorem 4

Let $\{C_1,\dots ,C_k\}$ be a multi-cover for a TOMKS K, and let $\alpha ^T x \le \beta$ be the associated MCI. Assume that the following conditions hold:

• 1. $C_0 = \emptyset$;

• 2. For each $h \in [k]$, cover $C_h$ is a minimal cover;

• 3. For any $t = 2, \ldots , \max _{i=1}^n \alpha _i$, there exist some $i_{t-1, \ell _t} \notin C_{h_t} \in \{C_h\}_{h=1}^k$ with $i_{t,1} \in C_{h_t}$ and $i_{1,n_1} \in C_{h_t}$, such that $C_{h_t} \cup \{i_{t-1, \ell _t}\} \setminus \{i_{t, n_t}\}$ is not a cover;

• 4. There exists some $C_{h_1} \in \{C_h\}_{h=1}^k$, such that $i_{1, 1} \in C_{h_1}$ and for any $i' \notin C$, $C_{h_1} \cup \{i'\} \setminus \{i_{1, 1}\}$ is not a cover.

• 5. For any $t = 1, \ldots , \max _{i=1}^n \alpha _i$, $\alpha (C_{h_t}) = \beta + 1$.

Then $\alpha ^T x \le \beta$ is a facet-defining inequality for ${\text {conv}}(K)$.

Example 7

Consider the TOMKS and the multi-cover in Example 5. We have $C_1 = \{1, 3\}$, $C_2 = \{1, 4, 5\}$, $C_3 = \{2, 3, 5\}$, and the associated MCI $\alpha ^T x \le \beta$ is $3x_1 + 2x_2 + 2x_3 + x_4 + x_5 \le 4$, here $i_{1,1} = 4, i_{1,2} = 5, i_{2,1} = 2, i_{2,2} = 3, i_{3,1} = 1$.

Clearly condition 1 in Theorem 4 holds. Since $\alpha (C_1) - \alpha _3 = 10 \le 16$, $\alpha (C_2) - \alpha _5 = 14 \le 16$, $\alpha (C_3) - \alpha _5 = 14 \le 16$, condition 2 holds as well. For $t = 2,$ let $C_{h_2} = C_3$, then $i_{1,1} \notin C_{h_2}, i_{1,2} \in C_{h_2}, i_{2,1} \in C_{h_2}$, and $C_{h_2} \cup \{i_{1,1}\} \setminus \{i_{2,2}\} = \{2, 4, 5\}$ is not a cover. For $t = 3$, let $C_{h_3} = C_2$, then $i_{2,1} \notin C_{h_3}, i_{1,2} \in C_{h_3}, i_{3,1} \in C_{h_3}$, and $C_{h_3} \cup \{i_{2,1}\} \setminus \{i_{3,1}\} = \{2,4,5\}$ is not a cover. Therefore condition 3 holds. Let $C_{h_1} = C_2$, then $i_{1,1} \in C_{h_1}$, since here $C = [5]$, condition 4 holds. Lastly, $\alpha (C_{h_1}) = \alpha (C_{h_2}) = \alpha (C_{h_3}) = 5$, so condition 5 also holds. Hence Theorem 4 yields that this MCI is a facet-defining inequality for ${\text {conv}}(K)$.

6 Conclusion

In this work, we give a new family of valid inequalities for the intersection of knapsack sets and demonstrate several ways in which the inequalities are not implied by other known cutting-plane methods. We are aware of very little work that explicitly studies the polyhedral structure of the intersection of multiple knapsack sets, and we hope the ideas presented here will give rise to new methods for generating strong valid inequalities for complex binary sets that arise in practical settings.