Tractable approximations of sets defined with quantifiers

Abstract

Given a compact basic semi-algebraic set $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m$, a simple set $\mathbf {B}$ (box or ellipsoid), and some semi-algebraic function $f$, we consider sets defined with quantifiers, of the form

$$\begin{aligned} \mathbf {R}_f:=\{\mathbf {x}\in \mathbf {B}&: f(\mathbf {x},\mathbf {y})\le 0 \,\, \text{ for } \text{ all } \,\, \mathbf {y}\,\, \text{ such } \text{ that }\quad (\mathbf {x},\mathbf {y})\in \mathbf {K}\}\\ \mathbf {D}_f:=\{\mathbf {x}\in \mathbf {B}&: f(\mathbf {x},\mathbf {y})\ge 0 \,\, \text{ for } \text{ some } \,\, \mathbf {y}\quad \text{ such } \text{ that }\quad (\mathbf {x},\mathbf {y})\in \mathbf {K}\}. \end{aligned}$$

The former set $\mathbf {R}_f$ is particularly useful to qualify “robust” decisions $\mathbf {x}$ versus noise parameter $\mathbf {y}$ (e.g. in robust optimization on some set $\varvec{\Omega }\subset \mathbf {B}$) whereas the latter set $\mathbf {D}_f$ is useful (e.g. in optimization) when one does not want to work with its lifted representation $\{(\mathbf {x},\mathbf {y})\in \mathbf {K}: f(\mathbf {x},\mathbf {y})\ge 0\}$. Assuming that $\mathbf {K}_\mathbf {x}:=\{\mathbf {y}:(\mathbf {x},\mathbf {y})\in \mathbf {K}\}\ne \emptyset$ for every $\mathbf {x}\in \mathbf {B}$, we provide a systematic procedure to obtain a sequence of explicit inner (resp. outer) approximations that converge to $\mathbf {R}_f$ (resp. $\mathbf {D}_f$) in a strong sense. Another (and remarkable) feature is that each approximation is the sublevel set of a single polynomial whose vector of coefficients is an optimal solution of a semidefinite program. Several extensions are also proposed, and in particular, approximations for sets of the form

$$\begin{aligned} \mathbf {R}_F:=\{\mathbf {x}\in \mathbf {B}\,:\, (\mathbf {x},\mathbf {y})\in F \,\, \text{ for } \text{ all }\,\, \mathbf {y}\,\, \text{ such } \text{ that }\,\, (\mathbf {x},\mathbf {y})\in \mathbf {K}\} \end{aligned}$$

where $F$ is some other basic-semi algebraic set, and also sets defined with two quantifiers.

1 Introduction

Consider two sets of variables $\mathbf {x}\in \mathbb {R}^n$ and $\mathbf {y}\in \mathbb {R}^m$ coupled with a constraint $(\mathbf {x},\mathbf {y})\in \mathbf {K}$, where $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m$ is some compact basic semi-algebraic set¹ defined by:

$$\begin{aligned} \mathbf {K}\,:=\,\{(\mathbf {x},\mathbf {y})\in \mathbb {R}^n\times \mathbb {R}^m\,:\,\mathbf {x}\in \mathbf {B};\,\, g_j(\mathbf {x},\mathbf {y})\,\ge \,0,\,j=1,\ldots ,s\} \end{aligned}$$

(1)

for some polynomials $g_j$, $j=1,\ldots ,s$, and let $\mathbf {B}\subset \mathbb {R}^n$ be a simple set (e.g. some box or ellipsoid).

With $f:\mathbf {K}\rightarrow \mathbb {R}$ a given semi-algebraic function on $\mathbf {K}$ (that is, a function whose graph $\varPsi _f:=\{(\mathbf {x},f(\mathbf {x})):\mathbf {x}\in \mathbf {K}\}$ is a semi-algebraic set), and

$$\begin{aligned} \mathbf {K}_\mathbf {x}\,:=\,\{\mathbf {y}\,\in \,\mathbb {R}^m\,:\,(\mathbf {x},\mathbf {y})\,\in \,\mathbf {K}\,\},\quad \forall \mathbf {x}\in \mathbf {B}, \end{aligned}$$

(2)

consider the two sets:

$$\begin{aligned} \mathbf {R}_f\,:=\,\{\,\mathbf {x}\in \mathbf {B}\,:\,f(\mathbf {x},\mathbf {y})\le 0\,\, \text{ for } \text{ all }\quad \mathbf {y}\in \mathbf {K}_\mathbf {x}\,\}, \end{aligned}$$

(3)

and

$$\begin{aligned} \mathbf {D}_f\,:=\,\{\,\mathbf {x}\in \mathbf {B}\,:\,f(\mathbf {x},\mathbf {y})\ge 0 \,\, \text{ for } \text{ some }\quad \mathbf {y}\in \mathbf {K}_\mathbf {x}\,\}. \end{aligned}$$

(4)

Both sets $\mathbf {R}_f$ and $\mathbf {D}_f$ which include a quantifier in their definition, are semi-algebraic and are interpreted as robust sets of variables $\mathbf {x}$ with respect to the other set of variables $\mathbf {y}$, and to some performance criterion $f$.

Indeed in the first case (3) one may think of “$\mathbf {x}$” as decision variables which should be robust with respect to some noise (or perturbation) $\mathbf {y}$ in the sense that no matter what the admissible level of noise $\mathbf {y}\in \mathbf {K}_\mathbf {x}$ is, the constraint $f(\mathbf {x},\mathbf {y})\le 0$ is satisfied whenever $\mathbf {x}\in \mathbf {R}_f$. For instance, such sets $\mathbf {R}_f$ are fundamental in robust control and robust optimization on a set $\varvec{\Omega }\subset \mathbf {B}$ (in which case one is interested in $\mathbf {R}_f\cap \varvec{\Omega }$). Instead of considering $\varvec{\Omega }$ directly in the definition (3) of $\mathbf {R}_f$ one introduces the simple set $\mathbf {B}\supset \varvec{\Omega }$ because moments of the Lebesgue measure on $\mathbf {B}$ (which are needed later) are easy to compute (in contrast to moments of the Lebesgue measure on $\varvec{\Omega }$). For a nice treatment of robust optimization the interested reader is referred to Ben-Tal et al. [2] where a particular emphasis is put on how to model the uncertainty so as to obtain tractable formulations for robust counterparts of some (convex) conic optimization problems. We are here interested in (converging) approximations of sets $\mathbf {R}_f$ in the general framework of polynomials.

On the other hand, in the second case (4) the vector $\mathbf {x}$ should be interpreted as design variables (or parameters) and the set $\mathbf {K}_\mathbf {x}$ defines a set of admissible decisions $\mathbf {y}\in \mathbf {K}_\mathbf {x}$ within the framework of design $\mathbf {x}$. And so $\mathbf {D}_f$ is the set of robust design parameters $\mathbf {x}$, in the sense that for every value of the design parameter $\mathbf {x}\in \mathbf {D}_f$, there is at least one admissible decision $\mathbf {y}\in \mathbf {K}_\mathbf {x}$ with performance level $f(\mathbf {x},\mathbf {y})\ge 0$. Notice that $\mathbf {D}_{f}\supseteq \overline{\mathbf {B}{\setminus }\mathbf {R}_f}$, and in a sense robust optimization on $\mathbf {R}_f$ is dual to optimization on $\mathbf {D}_f$.

The semi-algebraic function $f$ as well as the set $\mathbf {K}$ can be fairly complicated and therefore in general both sets $\mathbf {R}_f$ and $\mathbf {D}_f$ are non convex so that their exact description can be fairly complicated as well! Needless to say that robust optimization problems with constraints of the form $\mathbf {x}\in \mathbf {R}_f$, are very difficult to solve. In principle when $\mathbf {K}$ is a basic semi-algebraic set, quantifier elimination is possible via algebraic techniques; see e.g. Bochnak et al. [4]. However, in practice (exact) quantifier elimination is very costly and limited to problems of very modest size.

On the other hand, optimization problems with a constraint of the form $\mathbf {x}\in \mathbf {D}_f$ (or $\mathbf {x}\in \mathbf {D}_f\cap \varvec{\Omega }$ for some $\varvec{\Omega }$) can be formulated directly in the lifted space of variables $(\mathbf {x},\mathbf {y})\in \mathbb {R}^n\times \mathbb {R}^m$ (i.e. by adding the constraints $f(\mathbf {x},\mathbf {y})\ge 0;\,(\mathbf {x},\mathbf {y})\in \mathbf {K}$) and so with no approximation. But sometimes one may be interested in getting a description of the set $\mathbf {D}_f$ itself in $\mathbb {R}^n$ because its “shape” is hidden in the lifted $(\mathbf {x},\mathbf {y})$-description, or because optimizing over $\mathbf {K}\cap \{(\mathbf {x},\mathbf {y}):f(\mathbf {x},\mathbf {y})\ge 0\}$ may not be practical. However, if the projection of a basic semi-algebraic set (like e.g. $\mathbf {D}_f$) is semi-algebraic, it is not necessarily basic semi-algebraic and could be a complicated union of several basic semi-algebraic sets (hence not very useful in practice).

So a less ambitious but more practical goal is to obtain tractable approximations of such sets $\mathbf {R}_f$ (or $\mathbf {D}_f$). Then such approximations can be used for various purposes, optimization being only one among many potential applications.

Contribution In this paper we provide a hierarchy $(\mathbf {R}^k_f)$ (resp. $(\mathbf {D}_f^k)$), $k\in \mathbb {N}$, of inner approximations for $\mathbf {R}_f$ (resp. outer approximations for $\mathbf {D}_f$). These two hierarchies have three essential characteristic features:

• (a) Each set $\mathbf {R}_f^k\subset \mathbb {R}^n$ (resp. $\mathbf {D}_f^k$), $k\in \mathbb {N}$, has a very simple description in terms of the sublevel set $\{\mathbf {x}\in \mathbf {B}: p_k(\mathbf {x})\le 0\}$ (resp. $\{\mathbf {x}\in \mathbf {B}: p_k(\mathbf {x})\ge 0\}$) associated with a single polynomial $p_k$.

• (b) Both hierarchies $(\mathbf {R}_f^k)$ and $(\mathbf {D}_f^k)$, $k\in \mathbb {N}$, converge in a strong sense since we prove that (under some conditions) $\mathrm{vol}\,(\mathbf {R}_f{\setminus } \mathbf {R}^k_f)\rightarrow 0$ (resp. $\mathrm{vol}\,(\mathbf {D}_f^k{\setminus } \mathbf {D}_f)\rightarrow 0$) as $k\rightarrow \infty$ (and where “$\mathrm{vol}(\cdot )$” denotes the Lebesgue volume). In other words, for $k$ sufficiently large the inner approximations $\mathbf {R}_f^k$ (resp. outer approximations $\mathbf {D}_f^k$) coincide with $\mathbf {R}_f$ (resp. $\mathbf {D}_f$) up to a set of very small Lebesgue volume.

• (c) Computing the vector of coefficients of the above polynomial $p_k$ reduces to solving a semidefinite program whose size is parametrized by $k$.

As one potential application, the constraint $p_k(\mathbf {x})\le 0$ (resp. $p_k(\mathbf {x})\ge 0$) can be used in any robust (resp. design) optimization problem on $\varvec{\Omega }\,\subseteq \mathbf {B}$ as a substitute for $\mathbf {x}\in \mathbf {R}_f\cap \,\varvec{\Omega }$ (resp. $\mathbf {x}\in \mathbf {D}_f\cap \,\varvec{\Omega }$), thereby eliminating the variables $\mathbf {y}$. One then obtains a standard polynomial minimization problem $\mathbf {P}$ for which one may apply the hierarchy of semidefinite relaxations defined in [11] to obtain a sequence of lower bounds on the optimal value (and sometimes an optimal solution if the size of the resulting is moderate or if some sparsity pattern can be used for larger size problems). For more details, the interested reader is referred to [11] (and Waki et al. [16] for semidefinite relaxations that use a sparsity pattern). This approach was proposed in [12] for robust optimization (and in [9] with some convergence guarantee). But the sets $\mathbf {R}_f^k$ can also be used in other applications to provide a certificate for robustness as membership in $\mathbf {R}_f^k$ is easy to check and the approximation is from inside.

We first obtain inner (resp. outer) approximations of $\mathbf {R}_f$ (resp. $\mathbf {D}_f$) when $f$ is a polynomial. To do so we extensively use a previous result of the author [10] which allows to approximate in a strong sense the optimal value function of a parametric optimization problem. We then describe how the methodology can be extended to the case where $f$ is a semi-algebraic function on $\mathbf {K}$, whose graph $\varPsi _f$ is explicitly described by a basic semi-algebraic set.² This methodology had been already used in Henrion and Lasserre [5] to provide (convergent) inner approximations for the particular case of a set defined by matrix polynomial inequalities. The present contribution can be viewed as an extension of [5] to the more general framework (3)–(4) and with $f$ semi-algebraic.

Finally, we also provide several extensions, and in particular, we consider:

• The case where one also enforces the computed inner or outer approximations to be a convex set. This can be interesting for optimization purposes but of course, in this case convergence as in (b) is lost.

• The case where $f(\mathbf {x},\mathbf {y})\le 0$ is now replaced with a polynomial matrix inequality $\mathbf {F}(\mathbf {x},\mathbf {y})\preceq 0$, i.e., $\mathbf {F}(\cdot ,\cdot )$ is a real symmetric $m\times m$ matrix such that $\mathbf {F}_{ij}\in \mathbb {R}[\mathbf {x},\mathbf {y}]$ for each entry $(i,j)$. One then retrieves the methodology already used in Henrion and Lasserre [5] to provide (convergent) inner approximations of the set $\{\mathbf {x}\in \mathbf {B}: \mathbf {F}(\mathbf {x})\succeq 0\}$ for some polynomial matrix inequality.

• The case where $\mathbf {R}_f$ is now replaced with the set $\mathbf {R}_F$ defined by:

  $$\begin{aligned} \mathbf {R}_F\,=\,\{\mathbf {x}\in \mathbf {B}\,:\, (\mathbf {x},\mathbf {y})\in F\,\, \text{ for } \text{ all }\,\, \mathbf {y}\,\, \text{ such } \text{ that }\,\, (\mathbf {x},\mathbf {y})\in \mathbf {K}\}, \end{aligned}$$

  where $F$ is some basic-semi-algebraic set.

• The case where we now how have two quantifiers, like for instance,

  $$\begin{aligned} \mathbf {R}_f\,=\,\{\mathbf {x}\in \mathbf {B}_\mathbf {x}\,:\,\exists \,\mathbf {y}\in \mathbf {B}_\mathbf {y} \text{ s.t. } f(\mathbf {x},\mathbf {y},\mathbf {u})\le 0,\,\forall \mathbf {u}:\,(\mathbf {x},\mathbf {y},\mathbf {u})\in \mathbf {K}\}, \end{aligned}$$

  for some boxes $\mathbf {B}_\mathbf {x}\subset \mathbb {R}^n$, $\mathbf {B}_\mathbf {y}\subset \mathbb {R}^m$, and some compact set $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m\times \mathbb {R}^s$.

• The case where $\mathbf {K}$ is a semi-algebraic (but not basic semi-algebraic) set.

2 Notation and definitions

In this paper we use some material which is now more or less standard in what is called Polynomial Optimization. The reader not totally familiar with such notions and concepts, will find suitable additional material and details in the sources [3, 11] and [14].

Let $\mathbb {R}[\mathbf {x}]$ denote the ring or real polynomials in the variables $\mathbf {x}=(x_1,\ldots ,x_n)$, and let $\mathbb {R}[\mathbf {x}]_d$ be the vector space of real polynomials of degree at most $d$. Similarly, let $\Sigma [\mathbf {x}]\subset \mathbb {R}[\mathbf {x}]$ denote the convex cone of real polynomials that are sums of squares (SOS) of polynomials, and $\Sigma [\mathbf {x}]_d\subset \Sigma [\mathbf {x}]$ its subcone of SOS polynomials of degree at most $2d$. Denote by $\mathcal {S}^m$ the space of $m\times m$ real symmetric matrices. For a given matrix $\mathbf {A}\in \mathcal {S}^m$, the notation $\mathbf {A}\succeq 0$ (resp. $\mathbf {A}\succ 0$) means that $\mathbf {A}$ is positive semidefinite (resp. positive definite), i.e., all its eigenvalues are real and nonnegative (resp. positive). For a Borel set $B\subset \mathbb {R}^n$ let $\mathrm{vol}(B)$ denote its Lebesgue volume.

Moment matrix With $\mathbf {z}=(z_\alpha )$ being a sequence indexed in the canonical basis $(\mathbf {x}^\alpha )$ of $\mathbb {R}[\mathbf {x}]$, let $L_\mathbf {z}:\mathbb {R}[\mathbf {x}]\rightarrow \mathbb {R}$ be the so-called Riesz functional defined by:

$$\begin{aligned} f\quad \left( =\sum _{\alpha }f_{\alpha }\,\mathbf {x}^\alpha \right) \quad \mapsto \quad L_\mathbf {z}(f)\,=\,\sum _{\alpha }f_{\alpha }\,z_{\alpha }, \end{aligned}$$

and let $\mathbf {M}_d(\mathbf {z})$ be the symmetric matrix with rows and columns indexed in the canonical basis $(\mathbf {x}^\alpha )$, and defined by:

$$\begin{aligned} \mathbf {M}_d(\mathbf {z})(\alpha ,\beta )\,:=\,L_\mathbf {z}(\mathbf {x}^{\alpha +\beta })\,=\,z_{\alpha +\beta },\quad \alpha ,\beta \in \mathbb {N}^n_d \end{aligned}$$

(5)

with $\mathbb {N}^n_d:=\{\alpha \in \mathbb {N}^n\,:\,\vert \alpha \vert \,(=\sum _i\alpha _i)\le d\}$.

If $\mathbf {z}$ has a representing measure $\mu$, i.e., if $z_\alpha =\int \mathbf {x}^\alpha d\mu$ for every $\alpha \in \mathbb {N}^n$, then

$$\begin{aligned} \langle \mathbf {f},\mathbf {M}_d(\mathbf {z})\mathbf {f}\rangle \,=\,\int f(\mathbf {x})^2\,d\mu (\mathbf {x})\,\ge \,0,\qquad \forall \,f\in \mathbb {R}[\mathbf {x}]_d, \end{aligned}$$

and so $\mathbf {M}_d(\mathbf {z})\succeq 0$. In particular, if $\mu$ has a density $h$ with respect to the Lebesgue measure, positive on some open set $B$, then $\mathbf {M}_d(\mathbf {z})\succ 0$ because

$$\begin{aligned} 0\,=\,\langle \mathbf {f},\mathbf {M}_d(\mathbf {z})\mathbf {f}\rangle \,\ge \,\int _B f(\mathbf {x})^2\,h(\mathbf {x})d\mathbf {x}\quad \Rightarrow \quad f=0. \end{aligned}$$

Localizing matrix Similarly, with $\mathbf {z}=(z_{\alpha })$ and $g\in \mathbb {R}[\mathbf {x}]$ written

$$\begin{aligned} \mathbf {x}\mapsto g(\mathbf {x})\,=\,\sum _{\gamma \in \mathbb {N}^n}g_{\gamma }\,\mathbf {x}^\gamma , \end{aligned}$$

let $\mathbf {M}_d(g\,\mathbf {y})$ be the symmetric matrix with rows and columns indexed in the canonical basis $(\mathbf {x}^\alpha )$, and defined by:

$$\begin{aligned} \mathbf {M}_d(g\,\mathbf {z})(\alpha ,\beta )\,:=\,L_\mathbf {z}\left( g(\mathbf {x})\,\mathbf {x}^{\alpha +\beta }\right) \,=\,\sum _{\gamma }g_{\gamma }\, z_{\alpha +\beta +\gamma },\qquad \forall \, \alpha ,\beta \in \mathbb {N}^n_d. \end{aligned}$$

(6)

If $\mathbf {z}$ has a representing measure $\mu$, then $\langle \mathbf {f},\mathbf {M}_d(g\,\mathbf {z})\mathbf {f}\rangle =\int f^2gd\mu$, and so if $\mu$ is supported on the set $\{\mathbf {x}\,:\,g(\mathbf {x})\ge 0\}$, then $\mathbf {M}_d(g\,\mathbf {z})\succeq 0$ for all $d=0,1,\ldots$ because

$$\begin{aligned} \langle \mathbf {f},\mathbf {M}_d(g\,\mathbf {z})\mathbf {f}\rangle \,=\,\int f(\mathbf {x})^2g(\mathbf {x})\,d\mu (\mathbf {x})\,\ge \,0,\qquad \forall \,f\in \mathbb {R}[\mathbf {x}]_d. \end{aligned}$$

(7)

In particular, if $\mu$ is the Lebesgue measure and $g$ is positive on some open set $B$, then $\mathbf {M}_d(g\,\mathbf {z})\succ 0$ because

$$\begin{aligned} 0\,=\,\langle \mathbf {f},\mathbf {M}_d(g\,\mathbf {z})\mathbf {f}\rangle \,\ge \,\int _B f(\mathbf {x})^2\,g(\mathbf {x})d\mathbf {x}\quad \Rightarrow \quad f=0. \end{aligned}$$

3 Main result

Let $\mathbf {K}$ be the basic semi-algebraic set defined in (1) for some polynomials $g_j\subset \mathbb {R}[\mathbf {x},\mathbf {y}]$, $j=1,\ldots ,s$, and with simple set (box or ellipsoid) $\mathbf {B}\subset \mathbb {R}^n$.

Denote by $L_1(\mathbf {B})$ the Lebesgue space of measurable functions $h:\mathbf {B}\rightarrow \mathbb {R}$ that are integrable with respect to the Lebesgue measure on $\mathbf {B}$, i.e., such that $\int _\mathbf {B}\vert h\vert d\mathbf {x}<\infty$.

Given $f\in \mathbb {R}[\mathbf {x},\mathbf {y}]$, consider the mapping $\overline{J_f}:\mathbf {B}\rightarrow \mathbb {R}\cup \{-\infty \}$ defined by:

$$\begin{aligned} \mathbf {x}\mapsto \overline{J_f}(\mathbf {x})\,:=\,\displaystyle \max _{\mathbf {y}}\,\{f(\mathbf {x},\mathbf {y}):\mathbf {y}\in \,\mathbf {K}_\mathbf {x}\},\qquad \mathbf {x}\,\in \,\mathbf {B}. \end{aligned}$$

(8)

Therefore the set $\mathbf {R}_f$ in (3) reads $\{\mathbf {x}\in \mathbf {B}: \overline{J_f}(\mathbf {x})\le 0\}$ whereas $\mathbf {D}_f$ in (4) reads $\{\mathbf {x}\in \mathbf {B}: \overline{J_f}(\mathbf {x})\ge 0\}$.

Lemma 1

The function $\overline{J_f}$ is upper semi-continuous.

Proof

With $\mathbf {x}\in \mathbf {B}$ let $(\mathbf {x}_n)\subset \mathbf {B}$, $n\in \mathbb {N}$, be a sequence such that $\mathbf {x}_n\rightarrow \mathbf {x}$ and $\limsup _{\mathbf {z}\rightarrow \mathbf {x}}\overline{J_f}(\mathbf {z})=\lim _{n\rightarrow \infty }\overline{J_f}(\mathbf {x}_n)$. As $\mathbf {K}$ is compact, for every $n\in \mathbb {N}$, $\overline{J_f}(\mathbf {x}_n)=f(\mathbf {x}_n,\mathbf {y}_n)$ for some $\mathbf {y}_n\in \mathbf {K}_{\mathbf {x}_n}$. Therefore there is some subsequence $(n_k)$, $k\in \mathbb {N}$, and some $\mathbf {y}$ with $(\mathbf {x},\mathbf {y})\in \mathbf {K}$, such that$(\mathbf {x}_{n_k},\mathbf {y}_{n_k})\rightarrow (\mathbf {x},\mathbf {y})\in \mathbf {K}$ as $k\rightarrow \infty$. Hence

$$\begin{aligned} \limsup _{\mathbf {z}\rightarrow \mathbf {x}}\overline{J_f}(\mathbf {z})&= \lim _{k\rightarrow \infty }\overline{J_f}(\mathbf {x}_{n_k})\,=\,\lim _{k\rightarrow \infty }f(\mathbf {x}_{n_k},\mathbf {y}_{n_k})\\&= f(\mathbf {x},\mathbf {y})\le \max _\mathbf {z}\,\{\,f(\mathbf {x},\mathbf {z}):\mathbf {z}\in \mathbf {K}_\mathbf {x}\,\}\,=\,\overline{J_f}(\mathbf {x}), \end{aligned}$$

i.e., $\limsup _{\mathbf {z}\rightarrow \mathbf {x}}\overline{J_f}(\mathbf {z})\le \overline{J_j}(\mathbf {x})$, the desired result. $\square$

We will need also the following intermediate result.

Theorem 1

Let $\mathbf {B}\subset \mathbb {R}^n$ be a compact set and $\overline{J_f}:\mathbf {B}\rightarrow \mathbb {R}$ be a bounded and upper semi-continuous function. Then there exists a sequence of polynomials $\{p_k:k\in \mathbb {N}\}\subset \mathbb {R}[\mathbf {x}]$ such that $p_k(\mathbf {x})\ge \overline{J_f}(\mathbf {x})$ for all $\mathbf {x}\in \mathbf {B}$ and

$$\begin{aligned} \lim _{k\rightarrow \infty }\,\int _\mathbf {B}\vert \,p_k(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}\,=\,0\quad \mathrm{[}{Convergence\,in}\,\, L_1(\mathbf {B})\mathrm{]}. \end{aligned}$$

(9)

Proof

To prove (9) observe that $\overline{J_f}$ being bounded and upper semi-continuous on $\mathbf {B}$, there exists a nonincreasing sequence $(f_k)$, $k\in \mathbb {N}$, of bounded continuous functions $f_k:\mathbf {B}\rightarrow \mathbb {R}$ such that $f_k(\mathbf {x})\downarrow \overline{J_f}(\mathbf {x})$ for all $\mathbf {x}\in \mathbf {B}$, as $k\rightarrow \infty$; see e.g. Ash [1, Theorem A6.6, p. 390]. Moreover, by the Monotone Convergence Theorem:

$$\begin{aligned} \int _{\mathbf {B}} f_k(\mathbf {x})\,d\mathbf {x}\,\rightarrow \,\int _{\mathbf {B}} \overline{J_f}(\mathbf {x})\,d\mathbf {x}\qquad \text{ as }\,\, k\rightarrow \infty , \end{aligned}$$

and so

$$\begin{aligned} \int _{\mathbf {B}} \vert f_k(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}\,=\, \int _{\mathbf {B}} (f_k(\mathbf {x})-\overline{J_f}(\mathbf {x}))\,d\mathbf {x}\,\rightarrow \,0\qquad \text{ as }\,\, k\rightarrow \infty , \end{aligned}$$

that is, $f_k\rightarrow \overline{J_f}$ for the $L_1(\mathbf {B})$-norm. Next, by the Stone-Weierstrass theorem, for every $k\in \mathbb {N}$, there exists $p^{\prime }_k\in \mathbb {R}[\mathbf {x}]$ such that $\sup _{\mathbf {x}\in \mathbf {B}}\vert p^{\prime }_k-f_k\vert <(2k)^{-1}$ and so $p_k:=p^{\prime }_k+(2k)^{-1}\ge f_k\ge \overline{J_f}$ on $\mathbf {B}$. In addition,

$$\begin{aligned} \lim _{k\rightarrow \infty }\int _{\mathbf {B}}\vert p_k(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}&= \lim _{k\rightarrow \infty }\int _{\mathbf {B}}\underbrace{\vert p_k(\mathbf {x})-f_k(\mathbf {x})\vert }_{\le k^{-1}}+\vert f_k(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}\\&\le \lim _{k\rightarrow \infty }\left( k^{-1}\mathrm{vol}(\mathbf {B})+\int _\mathbf {B}\vert f_k(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}\right) \\&\le \lim _{k\rightarrow \infty }\int _\mathbf {B}\vert f_k(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}\,=\,0.\qquad \end{aligned}$$

The following result is an immediate consequence of Theorem 1.

Corollary 2

Let $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m$ be compact and let $\overline{J_f}$ be as in (8). If $\mathbf {K}_\mathbf {x}\ne \emptyset$ for every $\mathbf {x}\in \mathbf {B}$, there exists a sequence of polynomials $\{p_k:k\in \mathbb {N}\}\subset \mathbb {R}[\mathbf {x}]$, such that $p_k(\mathbf {x})\ge f(\mathbf {x},\mathbf {y})$ for all $\mathbf {y}\in \mathbf {K}_\mathbf {x}$, $\mathbf {x}\in \mathbf {B}$, and

$$\begin{aligned} \lim _{k\rightarrow \infty }\,\int _\mathbf {B}\vert \,p_k(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}\,=\,0\quad \mathrm{[}{Convergence\, in}\,\, L_1(\mathbf {B})\mathrm{]}. \end{aligned}$$

(10)

3.1 Inner approximations of $\mathbf {R}_f$

Let $\mathbf {K}$ be as in (1) with $\mathbf {K}_\mathbf {x}$ as in (2) and assume that $\mathbf {B}$ and $\mathbf {R}_f$ in (3) have nonempty interior.

Theorem 3

Let $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m$ in (1) be compact and $\mathbf {K}_\mathbf {x}\ne \emptyset$ for every $\mathbf {x}\in \mathbf {B}$. Assume that $\{\mathbf {x}\in \mathbf {B}: \overline{J_f}(\mathbf {x})\,=\,0\}$ has Lebesgue measure zero, and for every $k\in \mathbb {N}$, let $\mathbf {R}_f^k:=\{\mathbf {x}\in \mathbf {B}:p_k(\mathbf {x})\le 0\}$, where $p_k\in \mathbb {R}[\mathbf {x}]$ is as in Corollary 2. Then $\mathbf {R}_f^k\subset \mathbf {R}_f$ for every $k$, and

$$\begin{aligned} \mathrm{vol}\left( \mathbf {R}_f{\setminus } \mathbf {R}_f^k\right) \,\rightarrow \,0\quad \text{ as } k\rightarrow \infty . \end{aligned}$$

(11)

Proof

By Corollary 2, $p_k\rightarrow \overline{J_f}$ in $L_1(\mathbf {B})$ as $k\rightarrow \infty$. Therefore by [1, Theorem 2.5.1], $p_k$ converges to $\overline{J_f}$ in measure, that is, for every $\epsilon >0$,

$$\begin{aligned} \lim _{k\rightarrow \infty }\,\mathrm{vol}\left( \{\,\mathbf {x}\,:\,\vert p_k(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,\ge \,\epsilon \}\right) \,=\,0. \end{aligned}$$

(12)

Next, as $\overline{J_f}$ is upper semi-continuous on $\mathbf {B}$, the set $\{\mathbf {x}: \overline{J_f}(\mathbf {x})<0\}$ is open and as the set $\{\mathbf {x}\in \mathbf {B}:\overline{J_f}(\mathbf {x})=0\}$ has Lebesgue measure zero,

$$\begin{aligned} \mathrm{vol}(\mathbf {R}_f)&= \mathrm{vol}\left( \{\mathbf {x}\in \mathbf {B}: \overline{J_f}(\mathbf {x})<0\}\right) \nonumber \\&= \mathrm{vol}\left( \bigcup _{\ell =1}^\infty \{\mathbf {x}\in \mathbf {B}: \overline{J_f}(\mathbf {x})\le -1/\ell \}\right) \nonumber \\&= \lim _{\ell \rightarrow \infty }\mathrm{vol}\left( \{\mathbf {x}\in \mathbf {B}: \overline{J_f}(\mathbf {x})\le -1/\ell \}\right) \nonumber \\&= \lim _{\ell \rightarrow \infty }\mathrm{vol}\left( \mathbf {R}_f(\ell )\right) , \end{aligned}$$

(13)

where $\mathbf {R}_f(\ell ):=\{\mathbf {x}\in \mathbf {B}:\overline{J_f}(\mathbf {x})\le -1/\ell \}$. Next, $\mathbf {R}_f(\ell )\subseteq \mathbf {R}_f$ for every $\ell \ge 1$, and

$$\begin{aligned} \mathrm{vol}\,(\mathbf {R}_f(\ell ))\,=\,\mathrm{vol}\left( \mathbf {R}_f(\ell )\cap \{\mathbf {x}: p_k(\mathbf {x})>0\}\right) +\mathrm{vol}\left( \mathbf {R}_f(\ell )\cap \{\mathbf {x}: p_k(\mathbf {x})\le 0\}\right) . \end{aligned}$$

Observe that by (12), $\mathrm{vol}\left( \mathbf {R}_f(\ell )\cap \{\mathbf {x}: p_k(\mathbf {x})>0\}\right) \rightarrow 0$ as $k\rightarrow \infty$. Therefore,

$$\begin{aligned} \mathrm{vol}(\mathbf {R}_f(\ell ))&= \lim _{k\rightarrow \infty } \mathrm{vol}\left( \mathbf {R}_f(\ell )\right. \cap \underbrace{\left. \{\mathbf {x}: p_k(\mathbf {x})\le 0\}\right) }_{=\mathbf {R}_f^k}\nonumber \\&\le \lim _{k\rightarrow \infty }\mathrm{vol}\,(\mathbf {R}_f^k)\,\le \,\mathrm{vol}\,(\mathbf {R}_f). \end{aligned}$$

(14)

As $\mathbf {R}_f^k\subset \mathbf {R}_f$ for all $k$, letting $\ell \,\rightarrow \infty$ and using (13) yields the desired result. $\square$

Theorem 3 states that the (potentially complicated) set $\mathbf {R}_f$ can be approximated arbitrary well from inside by sublevel sets of polynomials. In particular, for application in robust optimization problems where one wishes to optimize a function over some set $\varvec{\Omega }\,\cap \mathbf {R}_f$ for some $\varvec{\Omega }\subset \mathbf {B}$, one may reinforce the complicated (and intractable) constraint $\mathbf {x}\in \mathbf {R}_f\cap \,\varvec{\Omega }$ by instead considering the inner approximation $\{\mathbf {x}\in \varvec{\Omega }:p_k(\mathbf {x})\le 0\}$ obtained with the two much simpler constraints $\mathbf {x}\in \varvec{\Omega }$ and $p_k(\mathbf {x})\le 0$. The resulting conservatism becomes negligible as $k$ increases.

3.2 Outer approximations of $\mathbf {D}_f$

Let $\mathbf {B}$ and $\mathbf {D}_f$ in (4) have nonempty interior.

Corollary 4

Let $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m$ in (1) be compact and $\mathbf {K}_\mathbf {x}\ne \emptyset$ for every $\mathbf {x}\in \mathbf {B}$. Assume that $\{\mathbf {x}\in \mathbf {B}:\overline{J_f}(\mathbf {x})\,=\,0\}$ has Lebesgue measure zero, and for every $k\in \mathbb {N}$, let $\mathbf {D}_f^k:=\{\mathbf {x}\in \mathbf {B}:p_k(\mathbf {x})\ge 0\}$, where $p_k\in \mathbb {R}[\mathbf {x}]$ is as in Corollary 2. Then $\mathbf {D}_f^k\supset \mathbf {D}_f$ for every $k$, and

$$\begin{aligned} \mathrm{vol}(\mathbf {D}_f{\setminus } \mathbf {D}_f^k)\,\rightarrow \,0\quad \text{ as } k\rightarrow \infty . \end{aligned}$$

(15)

Proof

The proof uses same arguments as in the proof of Theorem 3. Indeed, $\mathbf {D}_f=\mathbf {B}{\setminus }\varDelta _f$ with

$$\begin{aligned} \varDelta _f&:= \{\mathbf {x}\in \mathbf {B}\,:\, f(\mathbf {x},\mathbf {y})\,<\,0 \text{ for } \text{ all }\,\, \mathbf {y}\in \mathbf {K}_\mathbf {x}\}\\&= \{\mathbf {x}\in \mathbf {B}\,:\, \sup _\mathbf {y}\{\,f(\mathbf {x},\mathbf {y})\,:\,\mathbf {y}\in \mathbf {K}_\mathbf {x}\}\,<\,0\}\\&= \{\mathbf {x}\in \mathbf {B}\,:\, \overline{J_{f}}(\mathbf {x})\,<\,0\}, \end{aligned}$$

and since $\{\mathbf {x}\in \mathbf {B}\,:\, \overline{J_f}(\mathbf {x})\,=\,0\}$ has Lebesgue measure zero,

$$\begin{aligned} \mathrm{vol}(\varDelta _f)=\mathrm{vol}\left( \{\mathbf {x}\in \mathbf {B}\,:\, \overline{J_{f}}(\mathbf {x})\,\le \,0\}\right) . \end{aligned}$$

Hence by Theorem 3,

$$\begin{aligned} \lim _{k\rightarrow \infty }\mathrm{vol}\left( \{\mathbf {x}\in \mathbf {B}\,:\,p_k(\mathbf {x})\le 0\}\right) \,=\,\mathrm{vol}\left( \varDelta _f\right) , \end{aligned}$$

which in turn implies the desired result

$$\begin{aligned} \lim _{k\rightarrow \infty }\mathrm{vol}\left( \{\mathbf {x}\in \mathbf {B}\,:\,p_k(\mathbf {x})\ge 0\}\right)&= \lim _{k\rightarrow \infty }\mathrm{vol}\left( \{\mathbf {x}\in \mathbf {B}\,:\,p_k(\mathbf {x})>0\}\right) \\&= \mathrm{vol}\left( \mathbf {B}{\setminus }\varDelta _f\right) \,=\,\mathrm{vol}\left( \mathbf {D}_f\right) , \end{aligned}$$

because $\mathrm{vol}\left( \{\mathbf {x}\in \mathbf {B}:p_k(\mathbf {x})=0\}\right) =0$ for every $k$. $\square$

Corollary 4 states that the set $\mathbf {D}_f$ can be approximated arbitrary well from outside by sublevel sets of polynomials. In particular, if $\varvec{\Omega }\subset \mathbf {B}$ and one wishes to work with $\mathbf {D}_f\cap \,\varvec{\Omega }$ and not its lifted representation $\{f(\mathbf {x},\mathbf {y})\ge 0;,\mathbf {x}\in \varvec{\Omega };\,(\mathbf {x},\mathbf {y})\in \mathbf {K}\}$, one may instead use the outer approximation $\{\mathbf {x}\in \varvec{\Omega }:p_k(\mathbf {x})\ge 0\}$. The resulting laxism becomes negligible as $k$ increases.

3.3 Practical computation

In this section we follow [10] and show how to compute a sequence of polynomials $(p_k)\subset \mathbb {R}[\mathbf {x}]$, $k\in \mathbb {N}$, as defined in Theorem 3. With $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m$ as in (1) and compact, we assume that we know some $M>0$ such that $M-\Vert \mathbf {y}\Vert ^2\ge 0$ whenever $(\mathbf {x},\mathbf {y})\in \mathbf {K}$. Next, and possibly after a re-scaling of the $g_j$’s, we may and will set $M=1$, $\mathbf {B}=[-1,1]^n$. Next, let

$$\begin{aligned} \gamma _\alpha \,:=\,&= \frac{1}{\lambda (\mathbf {B})}\int _\mathbf {B}\mathbf {x}^\alpha \,d\lambda (\mathbf {x}),\qquad \alpha \in \mathbb {N}^n\\&= \left\{ \begin{array}{l}0 \quad \text{ if }\,\, \alpha _i \,\, \text{ is } \text{ odd } \text{ for } \text{ some }\,\, i\\ \displaystyle \prod \nolimits _{i=1}^n (\alpha _i+1)^{-1}\quad \text{ otherwise }\end{array}\right. ; \end{aligned}$$

be the moments of the (scaled) Lebesgue measure $\lambda$ on $\mathbf {B}$. In fact, as already mentioned, one may consider any set $\mathbf {B}$ for which all moments of the Lebesgue measure (or any Borel measure with support exactly equal to $\mathbf {B}$) are easy to compute (for instance an ellipsoid).

Moreover, letting $g_{s+1}(\mathbf {y}):=1-\Vert \mathbf {y}\Vert ^2$, and $x_i\mapsto \theta _i(\mathbf {x}):=1-x_i^2$, $i=1,\ldots ,n$, for convenience we redefine $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m$ to be the basic semi-algebraic set

$$\begin{aligned} \mathbf {K}\,=\,\{(\mathbf {x},\mathbf {y})\,:\,g_j(\mathbf {x},\mathbf {y})\,\ge \,0,\quad j=1,\ldots ,s+1;\,\theta _i(\mathbf {x})\ge 0,\,i=1,\ldots ,n\},\quad \end{aligned}$$

(16)

and let $g_0\in \mathbb {R}[\mathbf {x},\mathbf {y}]$ be the constant polynomial equal to $1$. With $v_j:=\lceil \mathrm{deg}(g_j)/2\rceil$, $j=0,\ldots ,m$, and for fixed $k\ge \max _{j}[v_j]$, consider the following optimization problem:

$$\begin{aligned} \begin{array}{rl} \rho _k=\displaystyle \min _{p,\sigma _j,\psi _i}&{}\displaystyle \int _{\mathbf {B}} p(\mathbf {x})\,d\lambda (\mathbf {x})\\ \text{ s.t. }&{}p(\mathbf {x})-f(\mathbf {x},\mathbf {y})=\displaystyle \sum _{j=0}^{s+1}\sigma _j(\mathbf {x},\mathbf {y})\,g_j(\mathbf {x},\mathbf {y})+\sum _{i=1}^n \psi _i(\mathbf {x},\mathbf {y})\,\theta _i(\mathbf {x})\\ &{}p\in \mathbb {R}[\mathbf {x}]_{2k};\,\sigma _j\in \Sigma _{k-v_j}[\mathbf {x},\mathbf {y}],\,j=0,\ldots ,s+1\\ &{}\psi _i\in \Sigma _{k-1}[\mathbf {x},\mathbf {y}],\,i=1,\ldots ,n. \end{array} \end{aligned}$$

(17)

For a feasible solution $p\in \mathbb {R}[\mathbf {x}]_{2k}$ of (17) the constraint certifies that $p(\mathbf {x})-f(\mathbf {x},\mathbf {y})\ge 0$ for all $(\mathbf {x},\mathbf {y})\in \mathbf {K}$, and therefore, $p(\mathbf {x})\ge \overline{J_f}(\mathbf {x})$ for all $\mathbf {x}\in \mathbf {B}$. As minimizing $\int _\mathbf {B}p(\mathbf {x})d\lambda (\mathbf {x})$ is the same as minimizing $\int _\mathbf {B}(p(\mathbf {x})-\overline{J_j}(\mathbf {x}))d\lambda (\mathbf {x})$, by solving (17) one tries to obtain a polynomial of degree at most $2k$ which dominates $\overline{J_f}$ on $\mathbf {B}$ and minimizes the $L_1$-norm $\int _\mathbf {B}(\vert p-\overline{J_j}\vert d\lambda$. In other words, an optimal solution of (17) is the best $L_1$-norm approximation in $\mathbb {R}[\mathbf {x}]_{2k}$ of $\overline{J_f}$ on $\mathbf {B}$ (from above).

It turns out that problem (17) is a semidefinite program. Indeed :

• The criterion $\int _\mathbf {B}p(\mathbf {x})\,d\lambda (\mathbf {x})$ is linear in the coefficients $\mathbf {p}=(p_\alpha )$, $\alpha \in \mathbb {N}^n_{2k}$, of the unknown polynomial $p\in \mathbb {R}[\mathbf {x}]_k$. In fact,

  $$\begin{aligned} \int _\mathbf {B}p(\mathbf {x})\,d\lambda (\mathbf {x})\,=\,\sum _{\alpha \in \mathbb {N}^n_{2k}}p_\alpha \,\underbrace{\int _\mathbf {B}\mathbf {x}^\alpha \,d\lambda (\mathbf {x})}_{\gamma _\alpha }\,=\,\sum _{\alpha \in \mathbb {N}^n_{2k}}p_\alpha \,\gamma _\alpha . \end{aligned}$$

• The constraint

  $$\begin{aligned} p(\mathbf {x})-f(\mathbf {x},\mathbf {y})=\displaystyle \sum _{j=0}^{s+1}\sigma _j(\mathbf {x},\mathbf {y})\,g_j(\mathbf {x},\mathbf {y})+\sum _{i=1}^n \psi _i(\mathbf {x},\mathbf {y})\,\theta _i(\mathbf {x}), \end{aligned}$$

  with $p\in \mathbb {R}[\mathbf {x}]_{2k};\,\sigma _j\in \Sigma _{k-v_j}[\mathbf {x},\mathbf {y}],\,j=0,\ldots ,s$, and $\psi _i\in \Sigma _{k-1}[\mathbf {x},\mathbf {y}],\,k=1,\ldots ,n$, reduces to

  • linear equality constraints between the coefficients of the polynomials $p,\sigma _j$ and $\psi _i$, to satisfy the identity, and

  • Linear Matrix Inequality (LMI) constraints to ensure that $\sigma _j$ and $\psi _i$ are all SOS polynomials of degree bounded by $2(k-v_j)$ and $2(k-1)$ respectively.

The dual of the semidefinite program (17) reads:

$$\begin{aligned} \begin{array}{rl} \rho _k^*=\displaystyle \min _{\mathbf {z}}&{}L_\mathbf {z}(f)\\ \text{ s.t. }&{}\mathbf {M}_{k-v_j}(g_j\,\mathbf {z})\,\succeq \,0,\quad j=0,\ldots ,s+1\\ &{}\mathbf {M}_{k-1}(\theta _i\,\mathbf {z})\,\succeq \,0,\quad i=1,\ldots ,n\\ &{}L_\mathbf {z}(\mathbf {x}^\alpha )\,=\,\gamma _\alpha ,\quad \alpha \in \mathbb {N}^n_{2k}, \end{array} \end{aligned}$$

(18)

where $\mathbf {z}=(z_{\alpha \beta })$, $(\alpha ,\beta )\in \mathbb {N}^{n+m}_{2k}$, and $L_\mathbf {z}:\mathbb {R}[\mathbf {x},\mathbf {y}]\rightarrow \mathbb {R}$ is the Riesz functional introduced in §2. Similarly, $\mathbf {M}_k(g_j\,\mathbf {z})$ (resp. $\mathbf {M}_k(\theta _i\,\mathbf {z})$) is the localizing matrix associated with the sequence $\mathbf {z}$ and the polynomial $g_j$ (resp. $\theta _i$), also introduced in Sect. 2 (but now with $(\mathbf {x},\mathbf {y})$ instead of $\mathbf {x}$).

Next we extend [10, Theorem3.5] and prove that both (17) and its dual (18) have an optimal solution whenever $\mathbf {K}$ has nonempty interior.

Theorem 5

Let $\mathbf {K}$ be as in (16) with nonempty interior, and assume that $\mathbf {K}_\mathbf {x}\ne \emptyset$ for every $\mathbf {x}\in \mathbf {B}$. Then:

There is no duality gap between the semidefinite program (17) and its dual (18). Moreover (17) (resp. (18)) has an optimal solution $p_k^*\in \mathbb {R}[\mathbf {x}]_{2k}$ (resp. $\mathbf {z}^*=(z^*_{\alpha \beta })$, $(\alpha ,\beta )\in \mathbb {N}^{n+m}_{2k}$), and

$$\begin{aligned} \lim _{k\rightarrow \infty }\,\int _\mathbf {B}\vert p^*_{k}(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}\,=\,0\quad \mathrm{[}{Convergence\, in}\,\, L_1(\mathbf {B})\mathrm{]}. \end{aligned}$$

(19)

Proof

As $\mathbf {K}$ has a nonempty interior it contains an open set $O\subset \mathbb {R}^n\times \mathbb {R}^m$. Let $O_\mathbf {x}\subset \mathbf {B}$ be the projection of $O$ onto $\mathbf {B}$, so that its ($\mathbb {R}^n$) Lebesgue volume is positive. Let $\mu$ be the finite Borel measure on $\mathbf {K}$ defined by

$$\begin{aligned} \mu (A\times B)\,:=\,\int _{A}\phi (B\,\vert \,\mathbf {x})\,d\lambda (\mathbf {x}),\qquad A\in \mathcal {B}(\mathbb {R}^n),\,B\in \mathcal {B}(\mathbb {R}^m), \end{aligned}$$

where for every $\mathbf {x}\in O_\mathbf {x}$, $\phi (d\mathbf {y}\,\vert \,\mathbf {x})$ is the probability measure on $\mathbb {R}^m$, supported on $\mathbf {K}_\mathbf {x}$, and defined by:

$$\begin{aligned} \phi (B\,\vert \,\mathbf {x})=\mathrm{vol}\,\,(\mathbf {K}_\mathbf {x}\cap B)/\mathrm{vol}(\mathbf {K}_\mathbf {x}),\qquad \forall B\in \mathcal {B}(\mathbb {R}^m). \end{aligned}$$

On $\mathbf {B}{\setminus } O_\mathbf {x}$ the probability $\phi (d\mathbf {y}\,\vert \,\mathbf {x})$ is an arbitrary probability measure on $\mathbf {K}_\mathbf {x}$.

Let $\mathbf {z}=(z_{\alpha \beta })$, $(\alpha ,\beta )\in \mathbb {N}^{n+m}_{2k}$, be the moments of $\mu$. As $\mathbf {K}\supset O$, $\mathbf {M}_{k-v_j}(g_j\,\mathbf {z})\succ 0$ (resp. $\mathbf {M}_{k-1}(\theta _i\,\mathbf {z})\succ 0$) for $j=0,\ldots ,s+1$ (resp. for $i=1,\ldots ,n$). Indeed for all non zero vectors $\mathbf {u}$ (indexed by the canonical basis $(\mathbf {x}^\alpha \mathbf {y}^\beta )$),

$$\begin{aligned} \langle \mathbf {u},\mathbf {M}_{d-v_j}(g_j\,\mathbf {z})\mathbf {u}\rangle&= \int _\mathbf {K}u(\mathbf {x},\mathbf {y})^2g_j(\mathbf {x},\mathbf {y})\,d\mu (\mathbf {x},\mathbf {y})\\&> \int _O u(\mathbf {x},\mathbf {y})^2g_j(\mathbf {x},\mathbf {y})\,d\mu (\mathbf {x},\mathbf {y})\,>\,0 \end{aligned}$$

(as $\mathbf {u}$ is supposed to be non trivial). Moreover, by construction of $\mu$, its marginal on $\mathbf {B}$ is the (scaled) Lebesgue measure $\lambda$ on $\mathbf {B}$ and so

$$\begin{aligned} L_\mathbf {z}(\mathbf {x}^\alpha )\,=\,\int _\mathbf {B}\mathbf {x}^\alpha \,d\lambda (\mathbf {x})\,=\,\gamma _\alpha ,\qquad \alpha \in \mathbb {N}^n_{2k}. \end{aligned}$$

In other words, $\mathbf {z}$ is a strictly feasible solution of (18), i.e., Slater’s condition holds for the semidefinite program (18). By a now standard result in convex optimization, this implies that $\rho _k=\rho ^*_k$, and (17) has an optimal solution if $\rho _k$ is finite. So it remains to show that indeed $\rho _k$ is finite and (18) is solvable.

Observe that from the definition of the scaled Lebesgue measure $\lambda$ on $\mathbf {B}$, $L_\mathbf {z}(1)=\gamma _0=1$. In addition, from the constraint $\mathbf {M}_{k-1}(g_{s+1}\,\mathbf {z})\succeq 0$, and $\mathbf {M}_{k-1}(\theta _i\,\mathbf {z})\succeq 0$, $i=1,\ldots ,n$, we deduce that any feasible solution $\mathbf {z}$ of (18) satisfies:

$$\begin{aligned} L_\mathbf {z}(y_\ell ^{2k})\,\le \,1,\quad \forall \ell =1,\ldots ,m;\qquad L_\mathbf {z}(x_i^{2k})\,\le \,1,\quad \forall i=1,\ldots ,n. \end{aligned}$$

Hence by [11, Proposition3.6] this implies $\vert z_{\alpha \beta }\vert \le \max [\gamma _0,1]=1$ for all $(\alpha ,\beta )\in \mathbb {N}^{n+m}_{2k}$. Therefore, the feasible set is compact as closed and bounded, which in turn implies that (18) has an optimal solution $\mathbf {z}^*$. And as Slater’s condition holds for (18) the dual (17) also has an optimal solution. Finally (19) follows from [10, Theorem3.5]. $\square$

Remark 6

In fact, in Theorem 3 one may impose the sequence $(p_k)\subset \mathbb {R}[\mathbf {x}]$, $k\in \mathbb {N}$, to be monotone, i.e., such that $\overline{J_f}\le p_k\le \overline{p_{k-1}}$ on $\mathbf {B}$, for all $k\ge 2$. And similarly for Corollary 4. For the practical computation of such a monotone sequence, in the semidefinite program (17) it suffices to include the additional constraint (or positivity certificate)

$$\begin{aligned} p^*_{k-1}(\mathbf {x})-p(\mathbf {x})\,=\,\sum _{i=0}^n\phi _i(\mathbf {x})\,\theta _i(\mathbf {x}),\quad \phi _0\in \Sigma [\mathbf {x}]_k,\,\phi _i\in \Sigma [\mathbf {x}]_{k-1},\,i\ge 1, \end{aligned}$$

where $\theta _0=1$ and $p^*_{k-1}\in \mathbb {R}[\mathbf {x}]_{k-1}$ is the optimal solution computed at the previous step $k-1$. In this case the inner approximations $(\mathbf {R}_f^k)$, $k\in \mathbb {N}$, form a nested sequence since $\mathbf {R}_f^{k}\subseteq \mathbf {R}_f^{k+1}$ for all $k$. Similarly the outer approximations $(\mathbf {D}_f^k)$, $k\in \mathbb {N}$, also form a nested sequence since $\mathbf {D}_f^{k+1}\subseteq \mathbf {D}_f^{k}$ for all $k$.

4 Extensions

4.1 Semi-algebraic functions

Suppose for instance that given $q_1,q_2\in \mathbb {R}[\mathbf {x},\mathbf {y}]$, one wants to characterize the set

$$\begin{aligned} \{\mathbf {x}\in \mathbf {B}: \, \min \,[q_1(\mathbf {x},\mathbf {y}),q_2(\mathbf {x},\mathbf {y})]\,\le \,0\,\,\text{ for } \text{ all }\,\, \mathbf {y}\in \mathbf {K}_\mathbf {x}\}, \end{aligned}$$

where $\mathbf {K}_\mathbf {x}$ has been defined in (2), i.e., the set $\mathbf {R}_f$ associated with the semi-algebraic function $(\mathbf {x},\mathbf {y})\mapsto f(\mathbf {x},\mathbf {y})=\min [q_1(\mathbf {x},\mathbf {y}),q_2(\mathbf {x},\mathbf {y})]$. If $f$ would be the semi-algebraic function $\max [q_1(\mathbf {x},\mathbf {y}),q_2(\mathbf {x},\mathbf {y})]$, characterizing $\mathbf {R}_f$ would reduce to the polynomial case (with some easy adjustments) as $\mathbf {R}_f=\mathbf {R}_{q_1}\cap \mathbf {R}_{q_2}$. But for $f=\min [q_1,q_2]$ this characterization is not so easy, and in fact is significantly more complicated. However, even though $f$ is not a polynomial any more, we shall next see that the above methodology also works for semi-algebraic functions, a much larger class than the class of polynomials. Of course there is no free lunch and the resulting computational burden increases because one needs additional lifting variables to represent the semi-algebraic function.

With $\mathbf {S}\subset \mathbb {R}^n$ being semi-algebraic, recall that a continuous function $f:\mathbf {S}\rightarrow \mathbb {R}$ is a semi-algebraic function if its graph $\{(\mathbf {x},f(\mathbf {x})):\mathbf {x}\in \mathbf {S}\}$ is a semi-algebraic set. And in fact, the graph of every semi-algebraic function is the projection of some basic semi-algebraic set in a lifted space. For more details the interested reader is referred to e.g. Lasserre and Putinar [13, p. 418].

So with $\mathbf {K}\subset \mathbb {R}^n\times \mathbb {R}^m$ as in (1), let $f:\mathbf {K}\rightarrow \mathbb {R}$ be a semi-algebraic function whose graph $\varPsi _f=\{\,(\mathbf {x},\mathbf {y},f(\mathbf {x},\mathbf {y})):\,(\mathbf {x},\mathbf {y})\in \mathbf {K}\,\}$ is the projection $\{(\mathbf {x},\mathbf {y},v)\in \mathbb {R}^n\times \mathbb {R}^m\times \mathbb {R}\}$ of a basic semi-algebraic set $\widehat{\mathbf {K}}\subset \mathbb {R}^n\times \mathbb {R}^m\times \mathbb {R}^r$, i.e.:

$$\begin{aligned} v\,=\,f(\mathbf {x},\mathbf {y}) \text{ and } (\mathbf {x},\mathbf {y})\,\in \,\mathbf {K}\,\Longleftrightarrow \,\exists \,\mathbf {w} \text{ s.t. } (\mathbf {x},\mathbf {y},v,\mathbf {w})\,\in \,\widehat{\mathbf {K}}. \end{aligned}$$

Letting $\widehat{f}:\widehat{\mathbf {K}}\rightarrow \mathbb {R}$ be such that $\widehat{f}(\mathbf {x},\mathbf {y},v,\mathbf {w}):=v$, we have

$$\begin{aligned} \mathbf {R}_f\,&= \,\{\,\mathbf {x}\in \mathbf {B}\,:\,f(\mathbf {x},\mathbf {y})\,\le \,0 \text{ for } \text{ all }\,\, \mathbf {y}\,\,\text{ such } \text{ that }\,\, (\mathbf {x},\mathbf {y})\in \mathbf {K}\,\}\\&= \{\,\mathbf {x}\in \mathbf {B}\,:\,\widehat{f}(\mathbf {x},\mathbf {y},v,\mathbf {w}))\,\le \,0 \text{ for } \text{ all }\,\, (\mathbf {y},v,\mathbf {w})\,\, \text{ such } \text{ that }\,\, (\mathbf {x},\mathbf {y},v,\mathbf {w}))\in \widehat{\mathbf {K}}\,\}. \end{aligned}$$

Hence this is just a special case of has been considered in Sect. 3 and therefore converging inner approximations of $\mathbf {R}_f$ can be obtained as in Theorems 3 and 5.

Example 1

For instance suppose that $f:\mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}$ is the semi-algebraic function $(\mathbf {x},\mathbf {y})\mapsto f(\mathbf {x},\mathbf {y}):=\min [q_1(\mathbf {x},\mathbf {y}),q_2(\mathbf {x},\mathbf {y})]$. Then using $a\wedge b=\frac{1}{2}(a+b-\vert a-b\vert )$ and $\vert a-b\vert =\theta \ge 0$ with $\theta ^2=(a-b)^2$,

$$\begin{aligned} \widehat{\mathbf {K}}&= \left\{ (\mathbf {x},\mathbf {y},v,w)\right. : (\mathbf {x},\mathbf {y})\in \mathbf {K};\,w^2=(q_1(\mathbf {x},\mathbf {y})-q_2(\mathbf {x},\mathbf {y}))^2; \quad w\ge 0;\\&\left. 2v=q_1(\mathbf {x},\mathbf {y})+q_2(\mathbf {x},\mathbf {y})-w\right\} , \end{aligned}$$

and

$$\begin{aligned} \varPsi _f\,=\,\{\,(\mathbf {x},\mathbf {y},f(\mathbf {x},\mathbf {y})):(\mathbf {x},\mathbf {y})\in \mathbf {K}\,\}\,=\,\{(\mathbf {x},\mathbf {y},v):\,(\mathbf {x},\mathbf {y},v,w)\,\in \,\widehat{\mathbf {K}}\}. \end{aligned}$$

4.2 Convex inner approximations

It is worth mentioning that enforcing convexity of inner approximations of $\mathbf {R}_f$ is easy. But of course there is some additional computational cost and the convergence in Theorem 3 is lost in general.

To enforce convexity of the level set $\{\mathbf {x}\in \mathbf {B}: p^*_k(\mathbf {x})\le 0\}$ it suffices to require that $p^*_k$ is convex on $\mathbf {B}$, i.e., adding the constraint

$$\begin{aligned} \langle \mathbf {u},\nabla ^2 p^*_k(\mathbf {x})\,\mathbf {u}\rangle \,\ge \,0,\qquad \forall (\mathbf {x},\mathbf {u})\in \mathbf {B}\times \mathbf {U}, \end{aligned}$$

where $\mathbf {U}:=\{\mathbf {u}\in \mathbb {R}^n:\Vert \mathbf {u}\Vert ^2\le 1\}$. The latter constraint can in turn be enforced by the Putinar positivity certificate

$$\begin{aligned} \langle \mathbf {u},\nabla ^2 p^*_k(\mathbf {x})\,\mathbf {u}\rangle \,=\,\sum _{i=0}^{n}\omega _i(\mathbf {x},\mathbf {u})\,\theta _i(\mathbf {x}) +\omega _{n+1}(\mathbf {x},\mathbf {u})\,\theta _{n+1}(\mathbf {x},\mathbf {u}), \end{aligned}$$

(20)

for some SOS polynomials $(\omega _i)\subset \Sigma [\mathbf {x},\mathbf {u}]$ (and where $\theta _{n+1}(\mathbf {x},\mathbf {u})=1-\Vert \mathbf {u}\Vert ^2$).

Then (20) can be included in the semidefinite program (17) with $\omega _0\in \Sigma [\mathbf {x},\mathbf {u}]_{k}$, and $\omega _i\in \Sigma [\mathbf {x},\mathbf {u}]_{k-1}$, $i=1,\ldots \,n+1$. However, now $\mathbf {z}=(z_{\alpha ,\gamma ,\beta })$, $(\alpha ,\beta ,\gamma )\in \mathbb {N}^{2n+m}$, and so solving the resulting semidefinite program is more demanding.

4.3 Polynomial matrix inequalities

Let $\mathbf {A}_\alpha \in \mathcal {S}_m$, $\alpha \in \mathbb {N}^n_d$, be real symmetric matrices and let $\mathbf {B}\subset \mathbb {R}^n$ be a given box. We first consider the set

$$\begin{aligned} \mathbf {S}:=\{\mathbf {x}\in \mathbf {B}:\,\mathbf {A}(\mathbf {x})\succeq 0\}, \end{aligned}$$

(21)

where $\mathbf {A}\in \mathbb {R}[\mathbf {x}]^{m\times m}$ is the matrix polynomial

$$\begin{aligned} \mathbf {x}\mapsto \,\mathbf {A}(\mathbf {x})\,:=\,\sum _{\alpha \in \mathbb {N}^n_d}\mathbf {x}^\alpha \,\mathbf {A}_\alpha . \end{aligned}$$

If $\mathbf {A}(\mathbf {x})$ is linear in $\mathbf {x}$ then $\mathbf {S}$ is convex and (21) is an LMI description of $\mathbf {S}$ which is very nice as it can be used efficiently in semidefinite programming.

In the general case the description (21) of $\mathbf {S}$ is called a Polynomial Matrix Inequality (PMI) and cannot be used as efficiently as in the convex case. Indeed $\mathbf {S}$ is a basic semi-algebraic set with an alternative description in terms of the box constraint $\mathbf {x}\in \mathbf {B}$ and $m$ additional polynomial inequality constraints (including the constraint $\mathrm{det}(\mathbf {A}(\mathbf {x}))\ge 0$). However, this latter description may not be very appropriate either because the degree of polynomials involved in that description is potentially as large as $d^m$ which precludes its use for practical computation (e.g., for optimization purposes).

On the other hand, for polynomial optimization problems with a PMI constraint $\mathbf {A}(\mathbf {x})\succeq 0$, one may still define an appropriate and ad hoc hierarchy of semidefinite relaxations, as described in Hol and Scherer [7, 8], and Henrion and Lasserre [6]. But even if more economical than the hierarchy using the former description of $\mathbf {S}$ with $m$ (high degree) polynomials, this latter approach may not still be ideal. In particular it is not clear how to detect (and then take benefit of) some possible structured sparsity to reduce the computational cost.

So in the general case and when $d^m$ is not small, one may be interested in a description of $\mathbf {S}$ simpler than the PMI (21) so that it can used more efficiently.

Let $\mathbf {Y}:=\{\,\mathbf {y}\in \mathbb {R}^m: \Vert \mathbf {y}\Vert ^2=1\,\}$ denote the unit sphere of $\mathbb {R}^m$. Then with $(\mathbf {x},\mathbf {y})\mapsto f(\mathbf {x},\mathbf {y}):=-\langle \mathbf {y},\mathbf {A}(\mathbf {x})\mathbf {y}\rangle$, the set $\mathbf {S}$ has the alternative and equivalent description

$$\begin{aligned} \mathbf {S}\,=\,\{\mathbf {x}\in \mathbf {B}:\,f(\mathbf {x},\mathbf {y})\,\le \,0,\,\forall \mathbf {y}\in \mathbf {Y}\}\,=:\,\mathbf {R}_f, \end{aligned}$$

(22)

which involves the quantifier “$\forall$”. Therefore the machinery developed in Sect. 3 can be applied to define the hierarchy of inner approximations $\mathbf {R}_f^k\subset \mathbf {S}$ in Theorem 3, where for each $k$, $\mathbf {R}^k_f=\{\mathbf {x}\in \mathbf {B}: p_k(\mathbf {x})\le 0\}$ for some polynomial $p_k$ of degree $k$. Theorem 5 is still valid even though $\mathbf {K}$ has now empty interior. Observe that if $\mathbf {x}\mapsto \mathbf {A}(\mathbf {x})$ is not a constant matrix, then with

$$\begin{aligned} \mathbf {x}\mapsto \overline{J_f}(\mathbf {x})\,:=\,\sup _\mathbf {y}\,\{f(\mathbf {x},\mathbf {y}):\,\mathbf {y}\in \mathbf {Y}\},\qquad \mathbf {x}\in \mathbf {B}, \end{aligned}$$

the set $\{\mathbf {x}:\overline{J_f}(\mathbf {x})=0\}$ has Lebesgue measure zero because $\overline{J_f}(\mathbf {x})$ is the largest eigenvalue of $-\mathbf {A}(\mathbf {x})$. Hence by Theorem 3

$$\begin{aligned} \mathrm{vol}\left( \mathbf {R}_f^k\right) \,\rightarrow \,\mathrm{vol}(\mathbf {S}),\qquad \text{ as }\,\, k\rightarrow \infty . \end{aligned}$$

Notice that computing $p_k$ has required to introduce the $m$ additional variables $\mathbf {y}$ but the degree of $f$ is not larger than $d+2$ if $d$ is the maximum degree of the entries.

Importantly for computational purposes, structure sparsity can be exploited to reduce the computational burden. Write the polynomial

$$\begin{aligned} (\mathbf {x},\mathbf {y})\mapsto f(\mathbf {x},\mathbf {y})\,=\,-\langle \mathbf {y},\mathbf {A}(\mathbf {x})\,\mathbf {y}\rangle \,=\,\sum _{\alpha \in \mathbb {N}^n}h_\alpha (\mathbf {y})\,\mathbf {x}^\alpha ,\quad (\mathbf {x},\mathbf {y})\in \mathbb {R}^n\times \mathbb {R}^m, \end{aligned}$$

for finitely many quadratic polynomials $\{h_\alpha \in \mathbb {R}[\mathbf {y}]_2:\alpha \in \mathbb {N}^m\}$. Suppose that the polynomial

$$\begin{aligned} \mathbf {x}\mapsto \theta (\mathbf {x})\,:=\,\sum _{\alpha \in \mathbb {N}^n}h_\alpha (\mathbf {y})\,\mathbf {x}^\alpha ,\qquad \mathbf {x}\in \mathbb {R}^n, \end{aligned}$$

has some structured sparsity. That is, $\{1,\ldots ,n\}=\cup _{\ell =1}^s I_\ell$ (with possible overlaps) and $\theta (\mathbf {x})=\sum _{\ell =1}^s\theta _\ell (\mathbf {x}_\ell )$ where $\mathbf {x}_\ell =\{x_i: i\in I_\ell \}$. Then $(\mathbf {x},\mathbf {y})\mapsto f(\mathbf {x},\mathbf {y})$ inherits the same structured sparsity (but with now $\cup _{\ell =1}^sI'_\ell$ where $I'_\ell =\{x_i,y_1,\ldots y_m:i\in I_\ell \}$). And so in particular, for computing $p_k$ one may use the sparse version of the hierarchy of semidefinite relaxations introduced in Waki et al. [16] which permits to handle problems with a significantly large number of variables.

Example 2

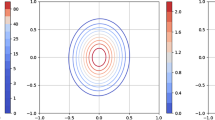
The following illustrative example is taken from Henrion and Lasserre [5]. With $n=2$, let $\mathbf {B}\subset \mathbb {R}^2$ be the unit disk $\{\mathbf {x}\,:\,\Vert \mathbf {x}\Vert ^2\le 1\}$, and let

$$\begin{aligned} \mathbf {A}(\mathbf {x})\,:=\,\left[ \begin{array}{c@{\quad }c} 1-16x_1x_2 &{} x_1 \\ x_1 &{} 1-x_1^2-x_2^2 \end{array}\right] ;\quad \mathbf {S}:=\{\mathbf {x}\in \mathbf {B}\,:\,\mathbf {A}(\mathbf {x})\,\succeq \,0\}. \end{aligned}$$

In Fig. 1 is displayed $\mathbf {S}$ and the degree two $\mathbf {R}_f^1$ and four $\mathbf {R}_f^2$ inner approximations of $\mathbf {S}$, whereas in Fig. 2 are displayed the $\mathbf {R}_f^3$ and $\mathbf {R}_f^4$ inner approximations of $\mathbf {S}$. One may see that with $k=4$, $\mathbf {R}_f^4$ is already a quite good approximation of $\mathbf {S}$.

Fig. 1

Example 2: $\mathbf {R}_f^1$ (left) and $\mathbf {R}_f^2$ (right) inner approximations (light gray) of $\mathbf {S}$ (dark gray) embedded in unit disk $\mathbf {B}$ (dashed)

Fig. 2

Example 2: $\mathbf {R}_f^3$ (left) and $\mathbf {R}_f^4$ (right) inner approximations (light gray) of $\mathbf {S}$ (dark gray) embedded in unit disk $\mathbf {B}$ (dashed).

Next, with $\mathbf {K}$ as in (1) consider now sets of the form

$$\begin{aligned} \mathbf {R}_f:=\{\mathbf {x}\in \mathbf {B}: \mathbf {F}(\mathbf {x},\mathbf {y})\preceq 0\quad \text{ for } \text{ all }\,\, \mathbf {y}\,\,\text{ in }\,\, \mathbf {K}_\mathbf {x}\}, \end{aligned}$$

where $\mathbf {F}\in \mathbb {R}[\mathbf {x},\mathbf {y}]^{m\times m}$ is a polynomial matrix in the $\mathbf {x}$ and $\mathbf {y}$ variables. Then letting $\mathbf {Z}:=\{\mathbf {z}\in \mathbb {R}^m:\Vert \mathbf {z}\Vert =1\}$, $\widehat{\mathbf {K}}:=\mathbf {K}\times \mathbf {Z}$, and $f:\widehat{\mathbf {K}}\rightarrow \mathbb {R}$, defined by:

$$\begin{aligned} (\mathbf {x},\mathbf {y},\mathbf {z})\mapsto f(\mathbf {x},\mathbf {y},\mathbf {z})\,:=\,\langle \mathbf {z},\mathbf {F}(\mathbf {x},\mathbf {y})\,\mathbf {z}\rangle ,\qquad (\mathbf {x},\mathbf {y},\mathbf {z})\in \widehat{\mathbf {K}}, \end{aligned}$$

the set $\mathbf {R}_f$ has the equivalent description:

$$\begin{aligned} \mathbf {R}_f:=\{\mathbf {x}\in \mathbf {B}: f(\mathbf {x},\mathbf {y},\mathbf {z})\le 0\quad \text{ for } \text{ all }\,\, (\mathbf {y},\mathbf {z})\,\, \text{ in }\,\, \widehat{\mathbf {K}}_\mathbf {x}\}, \end{aligned}$$

and the methodology of Sect. 3 again applies even though $\widehat{\mathbf {K}}$ has now empty interior.

4.4 Several functions $f$

We next consider sets of the form

$$\begin{aligned} \mathbf {R}_F:=\{\mathbf {x}\in \mathbf {B}:\, (\mathbf {x},\mathbf {y})\in \mathbf {F}\,\, \text{ for } \text{ all }\,\, \mathbf {y}\,\, \text{ such } \text{ that } \, (\mathbf {x},\mathbf {y})\in \mathbf {K}\} \end{aligned}$$

where $\mathbf {F}\subset \mathbb {R}^n\times \mathbb {R}^m$ is a basic-semi algebraic set defined by

$$\begin{aligned} \mathbf {F}\,:=\,\{(\mathbf {x},\mathbf {y})\in \mathbb {R}^n\times \mathbb {R}^m:\,f_\ell (\mathbf {x},\mathbf {y})\,\le \,0,\quad \forall \ell =1,\ldots ,q\}, \end{aligned}$$

for some polynomials $(f_\ell )\subset \mathbb {R}[\mathbf {x},\mathbf {y}]$, $\ell =1,\ldots ,q$. In other words,

$$\begin{aligned} \mathbf {R}_f\,=\,\{\mathbf {x}\in \mathbf {B}:\, \mathbf {K}_\mathbf {x}\,\subset \,\mathbf {F}_\mathbf {x}\}, \end{aligned}$$

where $\mathbf {F}_\mathbf {x}:=\{\,\mathbf {y}:\,(\mathbf {x},\mathbf {y})\,\in \,\mathbf {F}\}$.

Of course it is a particular case of the previous section with the semi-algebraic function $f=\max [f_1,\ldots ,f_q]$, but in this case a simpler approach is possible. Let $p_{k\ell }\in \mathbb {R}[\mathbf {x}]$ be an optimal solution of (17) associated with $f_\ell$, $\ell =1,\ldots ,q$, and let the set $\mathbf {R}_F^k$ be defined by

$$\begin{aligned} \mathbf {R}_F^k\,:=\,\{\mathbf {x}\in \mathbb {R}^n:p_{k\ell }(\mathbf {x})\,\le \,0,\,\, \ell =1,\ldots ,q\}\,=\,\bigcap _{\ell =1}^q\,\mathbf {R}^k_{f_\ell }, \end{aligned}$$

where for each $\ell =1,\ldots ,q$, the set $\mathbf {R}_{f_\ell }^k$ is defined in the obvious manner.

The sets $(\mathbf {R}_F^k)\subset \mathbf {R}_F$, $k\in \mathbb {N}$, provide a sequence of inner approximations of $\mathbf {R}_F$ with the nice property that

$$\begin{aligned} \lim _{k\rightarrow \infty }\,\mathrm{vol}\left( \mathbf {R}_F^k\right) \,=\,\mathrm{vol}\left( \mathbf {R}_F\right) , \end{aligned}$$

whenever the set $\{\,\mathbf {x}\in \mathbf {B}:\max _{\ell }\overline{J_{f_\ell }}(\mathbf {x})\,=0\,\}$ has Lebesgue measure zero.

4.5 Sets defined with two quantifiers

Consider three types of variables $(\mathbf {x},\mathbf {y},\mathbf {u})\in \mathbb {R}^n\times \mathbb {R}^m\times \mathbb {R}^s$, a box $\mathbf {B}_\mathbf {x}\subset \mathbb {R}^n$, a box $\mathbf {B}_\mathbf {y}\subset \mathbb {R}^m$, and a compact basic semi-algebraic set $\mathbf {K}\subset \mathbf {B}_\mathbf {x}\times \mathbf {B}_\mathbf {y}\times \mathbf {U}$. It is assumed that for each $(\mathbf {x},\mathbf {y})\in \mathbf {B}_{\mathbf {x}\mathbf {y}}\,(=\mathbf {B}_\mathbf {x}\times \mathbf {B}_\mathbf {y})$,

$$\begin{aligned} \mathbf {K}_{\mathbf {x}\mathbf {y}}\,:=\,\{\mathbf {u}\in \mathbf {U}\,:\,(\mathbf {x},\mathbf {y},\mathbf {u})\,\in \,\mathbf {K}\}\,\ne \,\emptyset . \end{aligned}$$

Sets with $\mathbf {\exists }$, $\mathbf {\forall }$. Consider a set $\mathbf {D}_f'$ of the form

$$\begin{aligned} \mathbf {D}_f'\,:=\,\{\mathbf {x}\in \mathbf {B}_\mathbf {x}\,:\, \exists \,\mathbf {y}\in \mathbf {B}_\mathbf {y}\,\, \text{ such } \text{ that }\,\, f(\mathbf {x},\mathbf {y},\mathbf {u})\le 0\,\, \text{ for } \text{ all }\,\, \mathbf {u}\in \mathbf {K}_{\mathbf {x}\mathbf {y}}\}. \end{aligned}$$

(23)

Such a set is not easy to handle, in particular for optimizing over it. So it is highly desirable to approximate as closely as possible the set $\mathbf {D}'_f$ with a set having a much simpler description, and in particular a description with no quantifier. We propose to use the methodology of Sect. 3 to provide such approximations. Consider the lift of $\mathbf {D}'_f$ given by:

$$\begin{aligned} \mathbf {H}_f&:= \{(\mathbf {x},\mathbf {y})\in \mathbf {B}_{\mathbf {x}\mathbf {y}}:f(\mathbf {x},\mathbf {y},\mathbf {u})\,\le \,0\,\, \text{ for } \text{ all }\,\, \mathbf {u}\in \mathbf {K}_{\mathbf {x}\mathbf {y}}\}\\&= \{(\mathbf {x},\mathbf {y})\in \mathbf {B}_{\mathbf {x}\mathbf {y}}:\overline{J_f}(\mathbf {x},\mathbf {y})\le 0\}, \end{aligned}$$

where $\overline{J_f}(\mathbf {x},\mathbf {y}):=\max _\mathbf {u}\,\{\,f(\mathbf {x},\mathbf {y},\mathbf {u}):(\mathbf {x},\mathbf {y},\mathbf {u})\in \mathbf {K}\,\}$. Using results of Sect. 3 we can find inner approximations $(\mathbf {H}^k_f)$ of the form:

$$\begin{aligned} \mathbf {H}^k_f\,:=\,\{(\mathbf {x},\mathbf {y})\in \mathbf {B}_{\mathbf {x}\mathbf {y}}:p_k(\mathbf {x},\mathbf {y})\le 0\}\,\subset \,\mathbf {H}_f,\quad k\in \mathbb {N}, \end{aligned}$$

for some polynomials $(p_k)\subset \mathbb {R}[\mathbf {x},\mathbf {y}]$. This then gives inner approximations $(\mathbf {D}^k_f)$ of $\mathbf {D}'_f$ of the form:

$$\begin{aligned} \mathbf {D}^k_f\,=\,\{\mathbf {x}\in \mathbf {B}_{\mathbf {x}}:p_k(\mathbf {x},\mathbf {y})\,\le \,0\quad \text{ for } \text{ some }\,\, \mathbf {y}\in \mathbf {B}_\mathbf {y}\}\,\subset \,\mathbf {D}'_f,\quad k\in \mathbb {N}. \end{aligned}$$

Considering again results of Sect. 3 we can find outer approximations of these inner approximations, of the form:

$$\begin{aligned} \mathbf {D}^{k\ell }_f\,=\,\{\mathbf {x}\in \mathbf {B}_{\mathbf {x}}:p_{k\ell }(\mathbf {x})\,\le \,0\}\,\supset \,\mathbf {D}^{k}_f,\quad k,\ell \in \mathbb {N}, \end{aligned}$$

for some polynomials $(p_{k\ell })\subset \mathbb {R}[\mathbf {x}]$. Unfortunately obtaining (some type of) convergence $\mathbf {D}_f^{k\ell }\rightarrow \mathbf {D}'_f$ is much more difficult and requires additional hypotheses.

Sets with $\forall$, $\exists$. Consider now a set $\mathbf {R}'_f$ of the form

$$\begin{aligned} \mathbf {R}'_f\,:=\,\{\mathbf {x}\in \mathbf {B}_\mathbf {x}\,:\, \forall \,\mathbf {y}\in \mathbf {B}_\mathbf {y},\,\exists \,\mathbf {u}\in \mathbf {K}_{\mathbf {x}\mathbf {y}} \,\, \text{ such } \text{ that }\,\, f(\mathbf {x},\mathbf {y},\mathbf {u})\ge 0\}. \end{aligned}$$

(24)

As for $\mathbf {D}'_f$, such a set is not easy to handle, in particular for optimizing over it. So again it is highly desirable to approximate as closely as possible the set $\mathbf {R}'_f$ with a set having a much simpler description, and in particular a description with no quantifier. So proceeding in a similar fashion as before,

$$\begin{aligned} \mathbf {R}'_f=\{\mathbf {x}\in \mathbf {B}_\mathbf {x}: \, \overline{J_f}(\mathbf {x},\mathbf {y})\ge 0 \quad \text{ for } \text{ all }\,\, \mathbf {y}\in \mathbf {B}_\mathbf {y}\}, \end{aligned}$$

and from Sect. 3 we can provide outer approximations $(\mathbf {R}^k_f)$ of $\mathbf {R}'_f$ of the form:

$$\begin{aligned} \mathbf {R}'_f\subset \mathbf {R}_f^k\,=\{\mathbf {x}\in \mathbf {B}_\mathbf {x}: p_k(\mathbf {x},\mathbf {y})\ge 0\quad \text{ for } \text{ all }\,\, \mathbf {y}\in \mathbf {B}_\mathbf {y}\},\quad k\in \mathbb {N}, \end{aligned}$$

for some polynomials $(p_k)\subset \mathbb {R}[\mathbf {x},\mathbf {y}]$. Considering again results of Sect. 3 we can find inner approximations of these outer approximations, of the form:

$$\begin{aligned} \mathbf {R}^{k\ell }_f\,=\,\{\mathbf {x}\in \mathbf {B}_{\mathbf {x}}:p_{k\ell }(\mathbf {x})\,\ge \,0\}\,\subset \,\mathbf {R}^k_f,\quad k,\ell \in \mathbb {N}, \end{aligned}$$

for some polynomials $(p_{k\ell })\subset \mathbb {R}[\mathbf {x}]$. Unfortunately, as for approximating $\mathbf {D}'_f$, obtaining (some type of) convergence $\mathbf {R}^{k\ell }_f\rightarrow \mathbf {R}'_f$ is also much more difficult and requires additional hypotheses.

4.6 General semi-algebraic set

We finally briefly discuss the case where the set $\mathbf {K}\subset \mathbb {R}^{n+m}$ in (1) is semi-algebraic but not basic semi-algebraic. Of course $\mathbf {K}$ can be always represented as the projection of some basic semi-algebraic set $\widehat{\mathbf {K}}$ defined in a higher dimensional space $\mathbb {R}^{n+m+t}$ for some $t\in \mathbb {N}$. That is

$$\begin{aligned} \mathbf {K}\,=\,\{(\mathbf {x},\mathbf {y}):\,\exists \,\mathbf {z} \text{ such } \text{ that } (\mathbf {x},\mathbf {y},\mathbf {z})\in \widehat{\mathbf {K}}\,\}. \end{aligned}$$

If $\widehat{\mathbf {K}}$ is known (i.e. $\mathbf {K}$ is known implicitly from $\widehat{\mathbf {K}}$) then sets of the form $\mathbf {D}_f$ in (4) can be approximated as we have done in Sect. 3. Indeed,

$$\begin{aligned} \mathbf {D}_f&= \{\,\mathbf {x}\in \mathbf {B}\,:\,f(\mathbf {x},\mathbf {y})\ge 0\,\, \text{ for } \text{ some }\,\, \mathbf {y}\in \mathbf {K}_\mathbf {x}\,\}\\&= \{\,\mathbf {x}\in \mathbf {B}\,:\,f(\mathbf {x},\mathbf {y})\ge \,\, 0 \text{ for } \text{ some }\,\, (\mathbf {y},\mathbf {z})\in \widehat{\mathbf {K}}_\mathbf {x}\,\}, \end{aligned}$$

where for every $\mathbf {x}\in \mathbf {B}$, $\widehat{\mathbf {K}}_\mathbf {x}:=\{\,(\mathbf {y},\mathbf {z}):(\mathbf {x},\mathbf {y},\mathbf {z})\in \widehat{\mathbf {K}}\,\}$. (Sets $\widehat{\mathbf {K}}$ with empty interior may be tolerated.) Similarly, sets of the form $\mathbf {R}_f$ in (3) can be also approximated as we have done in Sect. 3 because

$$\begin{aligned} \mathbf {R}_f&= \{\,\mathbf {x}\in \mathbf {B}\,:\,f(\mathbf {x},\mathbf {y})\le 0\,\, \text{ for } \text{ all } \,\,\mathbf {y}\in \mathbf {K}_\mathbf {x}\,\}\\&= \{\,\mathbf {x}\in \mathbf {B}\,:\,f(\mathbf {x},\mathbf {y})\le 0\,\, \text{ for } \text{ all } \,\,(\mathbf {y},\mathbf {z})\in \widehat{\mathbf {K}}_\mathbf {x}\,\}. \end{aligned}$$

Finite union of basic semi-algebraic sets. Alternatively, a general semi-algebraic set $\mathbf {K}$ is often described as the finite union $\cup _t\mathbf {K}_t$ (with possible overlaps) of basic compact semi-algebraic sets $\mathbf {K}_t$, $t\in T$, defined by:

$$\begin{aligned} \mathbf {K}_t\,=\,\{\,(\mathbf {x},\mathbf {y})\in \mathbb {R}^{n+m}:\,g_{tj}(\mathbf {x},\mathbf {y})\,\ge \,0,\,\, j=1,\ldots ,s_t\,\},\quad t\in T, \end{aligned}$$

for some polynomials $(g_{tj})\subset \mathbb {R}[\mathbf {x},\mathbf {y}]$, $j=1,\ldots ,s_t$, $t\in T$.

Again the function

$$\begin{aligned} \mathbf {x}\mapsto \overline{J_f}(\mathbf {x})\,:=\,\max _\mathbf {y}\,\{\,f(\mathbf {x},\mathbf {y}):(\mathbf {x},\mathbf {y})\,\in \,\mathbf {K}\,\},\quad \mathbf {x}\in \mathbf {B}, \end{aligned}$$

is upper semicontinuous on $\mathbf {B}$ and so Corollary 2 applies.

Therefore we can apply again the methodology of Sect. 3 with ad hoc adjustments.

In particular, for practical computation of a sequence of polynomials $(p_k)\subset \mathbb {R}[\mathbf {x}]$ of increasing degree and with $p_k\ge \overline{J_f}$ for all $k$, and $\int _\mathbf {B}\vert p_k-\overline{J_f}\vert \,d\lambda \rightarrow 0$ as $k\rightarrow \infty$, the analogue of the semidefinite program (17) reads:

$$\begin{aligned} \begin{array}{rl} \rho _k=\displaystyle \min _{p,\sigma _{tj},\psi _{ti}}&{}\displaystyle \int _{\mathbf {B}} p(\mathbf {x})\,d\lambda (\mathbf {x})\\ \text{ s.t. }&{}p-f=\displaystyle \sum _{j=0}^{s_t+1}\sigma _{tj}\,g_{tj}+\sum _{i=1}^n \psi _{ti}\,\theta _i,\quad t\in T\\ &{}p\in \mathbb {R}[\mathbf {x}]_{2k};\,\sigma _{tj}\in \Sigma _{k-v_j}[\mathbf {x},\mathbf {y}],\,j=0,\ldots ,s_t+1;\,t\in T\\ &{}\psi _{ti}\in \Sigma _{k-1}[\mathbf {x},\mathbf {y}],\,i=1,\ldots ,n;\,t\in T. \end{array} \end{aligned}$$

(25)

If $\mathrm{int}\,(\mathbf {K}_t)\ne \emptyset$ for every $t\in T$ and $\mathbf {K}_\mathbf {x}:=\{\mathbf {y}:(\mathbf {x},\mathbf {y})\in \mathbf {K}\,\}\ne \emptyset$ for every $\mathbf {x}\in \mathbf {B}$, then the analogue of Theorem 5 is valid (in fact, sets $\mathbf {K}_{t}$ with empty interior may also be tolerated).

Namely, the semidefinite program (25) has an optimal solution $p^*_k\in \mathbb {R}[\mathbf {x}]_{2k}$ with the desired convergence property:

$$\begin{aligned} \lim _{k\rightarrow \infty }\,\int _\mathbf {B}\vert p^*_{k}(\mathbf {x})-\overline{J_f}(\mathbf {x})\vert \,d\mathbf {x}\,=\,0\quad \mathrm{[}{Convergence\, in}\,\, L_1(\mathbf {B})\mathrm{]}. \end{aligned}$$

5 Conclusion

We have seen how to approximate some semi-algebraic sets defined with quantifiers by a monotone sequence of sublevel sets associated with appropriate polynomials of increasing degree. Each polynomial of the sequence is computed by solving a semidefinite program whose size increases with the degree of the polynomial and convergence of the approximations takes place in a strong sense. Several extensions have also been provided. Of course, solving the resulting hierarchy of semidefinite programs is computationally expensive and so far, in its present form the methodology is limited to problems of modest size only. Fortunately, larger size problems with some structured sparsity pattern can be attacked by applying techniques already used in [16]. However, evaluating (and improving) the efficiency of this methodology on a sample of problems of significant size is a topic of further investigation.