1 Introduction

Production very often leads to wear and tear of resources such as tools or machine components that need to be replaced routinely in order to maintain the operational capability of the production system. It is quite common within time-based maintenance approaches to schedule these maintenance activities periodically and in advance at an aggregate time scale and to schedule setup and production operations for the remaining time in between the maintenance activities. Many practitioners and academics have for a long time claimed that a use-based or condition-based approach to maintenance could be more efficient if maintenance itself is expensive and/or time-consuming. In order to avoid unplanned disruptions of the production process, wear and tear models are required to predict when preventive maintenance activities will be necessary.

In this paper we study the special case that some of these maintenance activities have to be performed quite frequently due to wear and tear of what we call a “critical resource” that is used for production. In order to maintain this critical resource, the production process has to be stopped until it has been restored. Such a situation could on the one hand be due to resources such as tools that wear down quickly. However, the critical resource could on the other hand also be a material held in a limited and closed material storage like, e.g., a tank that needs discrete re-filling operations in order to resume production. Both possible cases call for a tight coupling of the production process, the wear and tear process, and the maintenance process in order to model short-term production and maintenance planning and scheduling. To this end we use a relatively simple model of a wear and tear function that can also naturally model the dynamic depletion of a material storage. This model serves as link between short-term lot-sizing and scheduling on the one hand and predictive and use-based maintenance on the other hand.

As we aim at a generic model, we consider different forms of maintenance as well as different forms of interaction between maintenance and setup operations. The lot-sizing part of our generic model can be interpreted as a hybrid between a General Lotsizing and Scheduling Problem as proposed by Fleischmann and Meyr (1997) and the Proportional Lotsizing and Scheduling Problem developed by Drexl and Haase (1995). Based on this very detailed lotsizing modeling approach we can represent and anticipate the state of the critical resource at the required level of detail and accuracy.

The resulting mixed-integer linear program, however, can only be solved for very small problem instances using standard solvers like CPLEX. For this reason, we develop a heuristic decomposition approach based on the Fix-and-Optimize heuristic presented in Helber and Sahling (2010), also known as the “Exchange” approach proposed by Pochet and Wolsey (2006). In order to evaluate the performance of this heuristic, we further present the results of an extensive numerical study. In addition, we use our model to analyze the impact of simultaneous as opposed to sequential planning of production and maintenance operations.

The remainder of the paper is structured as follows: In Sect. 2 we discuss different forms of maintenance and maintenance planning. In addition, we present different approaches to deal with the interdependencies between production and maintenance planning that have been proposed in the literature. In Sect. 3 we first introduce the assumptions and notation and then develop the generic lot-sizing and maintenance scheduling model including the formal wear and tear function. Section 4 is devoted to the description of the Fix-and-Optimize algorithm and Sect. 5 to the numerical experiments. Conclusions and directions for future research are presented in Sect. 6.

2 Production and maintenance planning in an intensive wear and tear situation

2.1 Forms and interactions of production and maintenance operations

In our short-term perspective, we assume that production of a set of different products facing a dynamic demand takes place on a single capacity-constrained resource, e.g., a machine. In order to be able to produce a specific type of product, the machine needs to be set up which takes a setup time and may result in a setup cost. Production of a single unit of any product type requires a type-specific processing time. We assume that as a result of these production operations, the stock of wear-out of a critical resource required in the process like, e.g., a tool or a material in a limited material storage decreases over time as in Fig. 1 for the case of the continuous production of a single product type, see (Jacobs et al. 2009, p. 1267).

Fig. 1
figure 1

Depletion of a critical and renewable resource

Full size image

The state of this critical resource is always between a maximum and minimum level. It can be increased through maintenance activities. The linear function depicted in Fig.  1 is only an approximation if wear and tear also depend on factors other than production time, for example production intensities or environmental conditions.

In order to lay both the conceptional and notational foundation for a generic model, we now introduce a notation of the form \((\alpha , \beta , \gamma )\) with \(\alpha , \beta , \gamma \in \{0, 1\}\) to describe different forms of maintenance and their interaction with setup operations.

If the minimum state of the critical resource has been reached, production has to stop until maintenance has been performed. This stop of production can interact with the setup state of the resource: During the maintenance activity, the setup state can be either be preserved \((\alpha = 1)\) or lost \((\alpha = 0)\).

The maintenance activity itself can be partial \((\beta = 1)\) so that after the maintenance activity the new level of the critical resource can still be below the maximum state or it can be complete \((\beta = 0)\) in the sense that the maintenance activity always leads to the maximum state of the critical resource.

Finally, setup and maintenance operations may have to be performed serially \((\gamma = 1)\), or it may be possible to perform these two types of operation simultaneously, i.e., in parallel, \((\gamma = 0)\). These three problem dimensions lead to eight different combinations of problem features as depicted in Fig. 2.

Fig. 2
figure 2

Possible combinations of problem aspects

Full size image

In the generic model presented in Sect. 3, we use these binary incidence parameters \(\alpha , \beta \), and \(\gamma \) to activate those elements of the model that are required in the respective case and to de-activate the others.

As we are dealing with intensive and short-term wear and tear, we have to model the state of the critical resource at a detailed level so that we eventually have to decide about both lot sizes and sequences on the one hand and to schedule the maintenance activities on the other hand.

2.2 Review of the literature

The problem studied in this paper addresses both lot-sizing and scheduling and maintenance planning and scheduling. A rich body of literature addresses these two fields, but usually in isolation from each other.

Several authors reviewed the lot-sizing literature, typically from a specific perspective, in particular with respect to heuristic solution approaches. Such reviews were given by Bahl et al. (1987), Brahimi et al. (2006), Drexl and Kimms (1997), Jans and Degraeve (2007), Karimi et al. (2003), Kuik et al. (1994), Maes and Wassenhove (1988), Salomon et al. (1991), Staggemeier and Clark (2001), Wolsey (1995) and recently Buschkuehl et al. (2010). Dynamic lot-sizing models are often classified as either of the “big bucket” or the “small bucket” type. “Big” time bucket models are based on longer time periods like weeks so that to each week several production lots are assigned, giving rise to a further sequencing decision for the lots assigned to each of those periods. In the “small” time bucket models, however, the length of a period is shorter (hours or a few days) and only one or at most two different product types are assigned to a small time bucket. This modeling approach simultaneously addresses the lot sizing and the lot scheduling problem in a short-term perspective. It is therefore a natural starting point for our model development which requires a detailed representation of the consumption of the critical resource over time. One of the two most relevant models in our context is the Proportional Lotsizing and Scheduling Problem (PLSP), see Drexl and Haase (1995). It is based on the assumption that in each small time period, at most one setup can occur so that at most two different product types can be produced during such a short period, one before and one after the setup. The total length of each of the short periods, however, is exogenously given. By contrast, the so-called General Lotsizing and Scheduling Problem by Fleischmann and Meyr (1997) combines an exogenous and fixed time grid of “big” time buckets, to which dynamic demands are assigned, with a second flexible time grid of “small” time periods. Only one product type can be assigned to each of these small periods. The characteristic feature of this model is that the size of the respective lots endogenously determines the length of the small time periods. We combine elements from both models in Sect. 3 as we integrate lot-sizing and maintenance scheduling.

With respect to the maintenance of production systems that face an uncertain wear and tear, many authors derive production policies, often using dynamic stochastic programming and often considering constant demand rates in continuous time. They determine when and how much to maintain, setup, produce etc. as the state of the system evolves over time. In these models, the working life of the critical resource is often modeled as a random variable. Examples of this type of work are found in Boukas and Haurie (1990), Chelbi and Ait-Kadi (2004), Iravani and Duenyas (2002), Kenné and Nkeungoue (2008), Liberopoulos and Caramanis (1994) and Yao et al. (2005), Suliman and Jawad (2012), Zhang et al. (2014), Liu et al. (2015) to name but a few. Other authors tackle the problem to incorporate cyclic maintenance operations in discrete time models, e. g., Yalaoui et al. (2014).

Several other authors tackle deterministic sequencing and scheduling problems for deterministic production systems, very often focussing on a single or at most two successive production stages. Common approaches to deal with maintenance are to assume that either machines are temporarily unavailable due to time-based maintenance or that maintenance activities have to be scheduled together with the production activities. The length of the production jobs (reflecting in our context the lot size), however, is often assumed to be exogenously given. Examples of this type of work are found in Allaoui et al. (2008), Chen (2006), Gharbi et al. (2007), Kubzin and Strusevich (2006), Qi et al. (1999) and Yuan et al. (2008).

Another branch of the literature addresses sequencing and scheduling problems for machines that are subject to random failures. Cassady and Kutanoglu (2005), e.g., assume on the one hand that the sequence of the jobs processed by a single machine has to be determined. On the other hand, immediately prior to each of these jobs, preventive maintenance (PM) can be performed. This PM reduces the probability that a random machine failure during the processing time of this job requires a repair or corrective maintenance. As these failures are random events, the job completion times are random as well. A possible objective is to minimize the expected total completion time or tardiness. Other papers in this field are Cassady and Kutanoglu (2003), Guo et al. (2007), Lee and Lin (2001), and Sortrakul et al. (2005). As in the previously mentioned deterministic models, lot-sizing problems do not occur.

Several works consider the coordination of production and maintenance activities for the special case of process industries in which liquids or other continuous goods like dry chemicals are treated, see, e.g., Ashayeri et al. (1996), Dedopoulos and Shah (1995), Goel et al. (2003), Pistikopoulos et al. (2001), Sanmarti et al. (1997), Suryadi and Papageorgiou (2004) and Vassiliadis et al. (2000). Often “state-task-networks” are used to represent production processes within discrete-time mixed-integer linear programming models.

One of the papers that are most closely related to the problem treated in this paper has been presented by Aghezzaf et al. (2007) who study different versions of dynamic lot-sizing models in which the objective function is augmented by a term dealing with the cost of preventive and corrective maintenance based on a probabilistic failure rate function for the case of cyclic preventive maintenance activities. The other closely related paper was presented by Jacobs et al. (2009). They develop an integrated model dealing with multiple machines, products and periods and determine both production quantities and maintenance activities via a deterministic wear and tear function that is conceptionally similar to the one used in this paper. They minimize the total cost of production and maintenance using a mixed-integer linear model. However, like many other authors, they do not consider setup costs or times and hence any lot-sizing problem.

Lu et al. (2013) consider a big-bucket capacitated lot sizing problem (CLSP) with maintenance operations, but without setup times, so that the interaction of the times required for setups and maintenance cannot be modeled. In Ramezanian et al. (2013), a discrete time lot sizing and maintenance scheduling model is presented which assumes that maintenance tasks are explicitly given, i. e., a wear and tear function like the one presented in Fig. 1 is not considered. Fitouhi and Nourelfath (2012) propose a lot sizing model and present a solution method for a case with non-cyclical maintenance operations in which the expected cost and capacity reduction due to random repairs is considered.

Based on the discussion of the literature we are not aware of any paper dealing with a generic and integrated lot-sizing and maintenance scheduling model using a wear and tear function. We hence present such a model in the next section.

3 Model formulation

3.1 Assumptions and notation

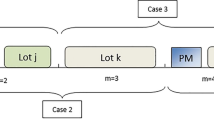
In our generic model, both setup and production operations with specific production quantities (lot sizes) as well as various kinds of maintenance activities are considered over multiple products and periods. In order to integrate maintenance planning, it is necessary to track the state of the critical resource on a lot-for-lot basis which requires the knowledge of the production sequences. For this reason, it appears to be natural to work with a fine and flexible time grid to integrate lot-sizing and scheduling. To further integrate maintenance, a combination of the proportional lotsizing and scheduling problem (PLSP) by Drexl and Haase (1995) and the general lotsizing and scheduling oroblem (GLSP) by Fleischmann and Meyr (1997) is used, combining exogenous macroperiods with given length and demand with endogenous microperiods with flexible length. In a PLSP, the production quantity of product k in a microperiod t is given either by the decision variable \(Q^1_{kt}\) if it uses a setup state carried over from a previous period \(t-1\) or by the decision variable \(Q^2_{kt}\) if it follows a setup operation in this microperiod, see Fig. 3. In a GLSP, the length of the microperiod is endogenous.

Fig. 3
figure 3

First production operation, setup operation and second production operation within a single microperiod

Full size image

The following general set of assumptions holds for all variants of the generic model:

  • Different product types \(k=1, \ldots ,K\) are produced.

  • The planning horizon is divided into macroperiods \(\tau = 1,\ldots ,P\). Each macroperiod \(\tau \) consists of K consecutive microperiods. Hence, there are \(t=1,\ldots ,T=P\cdot K\) microperiods. Denote with \(\fancyscript{T}\fancyscript{M}=\{K, 2K,\ldots ,P\cdot K\}\) the set of the last microperiods assigned to the macroperiods and with \(TP_\tau \) the set of microperiods within macroperiod \(\tau \).

  • The demand \(d_{kt}\) which has to be satisfied is given for each product k and each last microperiod \(t \in \fancyscript{T}\fancyscript{M}\) of the macroperiods.

  • The production of the K products takes place on a machine with limited exogenous capacity \(c_\tau \) per macroperiod \(\tau \). The capacity \(C_t\) in each microperiod and hence the length of the microperiod t is determined endogenously.

  • The unit processing time of product k is \(tp_k\).

  • Setting up the machine for product k causes a setup cost \(cs_k\) per setup and takes a setup time \(ts_k\).

  • At most one setup is allowed in each microperiod. The setup state can be carried over into the next microperiod. Hence, at most two different products can be produced in each microperiod.

  • The inventory of product k at the end of microperiod t is given by \(I_{kt}\).

Note our assumption that setup times are not sequence-dependent. It is a technical assumption to avoid an extremely large number of binary setup variables leading to an extremely challenging lot sizing problem, even without considering maintenance. With respect to wear and tear as well as maintenance of the critical resource, several modeling assumptions hold for every possible maintenance case from Sect. 2.1:

  • The state of the critical resource is at any moment in time between the minimum state \(s^{\min }\) and the maximum state \(s^{\max }\).

  • It is reduced by \(a_k\) units for each produced unit of product k.

  • Maintenance activities can be performed to increase the state of the resource again if it is below the maximum state \(s^{\max }\).

  • If the state of the resource reaches the minimum state \(s^{\min }\), production stops until a maintenance activity increased the state again.

In order to track the state of the critical resource over time, four different variables are used and related to different moments in time within in a microperiod t. The variable \(S^1_t\) gives the state of the critical resource immediately before the start of the production of quantity \(Q^1_{kt}\) while variable \(S^2_t\) gives the state after the end of the production of quantity \(Q^1_{kt}\). Likewise, the variable \(S^3_t\) gives the state immediately before the production of quantity \(Q^2_{kt}\) and \(S^4_t\) the state at the end of microperiod t. The example in Fig. 4 shows the use of these variables for the special case of setup state preservation (\(\alpha =1\)), complete maintenance (\(\beta =0\)), and serial maintenance and setup operations (\(\gamma =1\)).

Fig. 4
figure 4

State variables for case \(\alpha =1, \beta =0, \gamma =1\)

Full size image
Table 1 General notation
Full size table

The first and general part of the notation used in the generic model is presented in Table 1. We now further present the specific assumptions and notational elements (see Table 2) that apply to the specific cases maintenance depicted in Fig. 2.

Table 2 Maintenance-specific notation
Full size table

If a maintenance activity preserves the setup state of the machine (\(\alpha =1\)), at most two maintenance activities are possible in each microperiod t, one at the beginning of the microperiod and one before the setup in the microperiod, as shown in Fig. 4. However, if the setup state is lost during maintenance (\(\alpha =0\)), at most one maintenance operation is possible in each microperiod t, right before the setup in this microperiod, which implies \(S^4_{t-1}=S^1_t\) in this case, see Fig. 5 as opposed to Fig. 4.

For the case of partial maintenance (\(\beta =1\)), the following assumptions hold:

  • The state of the critical resource is lifted by integer multiples of the state increase pm for a single discrete unit of maintenance to a state below or up to \(s^{\max }\). The unit state increase pm is assumed to be large enough to avoid too short maintenance operations.

  • The integer variables \(U^{1}_t\) and \(U^{2}_t\) give the scheduled number of partial maintenance units pm prior to the production of the first and second quantities \(Q^1_{kt}\) and \(Q^2_{kt}\) in this period, respectively.

  • Each unit of partial maintenance requires tm time units of the machine capacity and causes a partial maintenance unit costs cm.

Figure 6 shows the time structure of a microperiod in the case of partial maintenance.

Fig. 5
figure 5

State variables for case \(\alpha =0, \beta =0, \gamma =1\)

Full size image
Fig. 6
figure 6

State variables for case \(\alpha =1, \beta =1, \gamma =1\)

Full size image

For the case of complete maintenance (\(\beta =0\)), the following assumptions apply:

  • A complete maintenance activity always results in the maximal state \(s^{\max }\) of the resource.

  • One complete maintenance activity causes costs cv and requires time tv time units, independent of the state prior to the maintenance operation.

  • Binary variables \(\mu ^{1}_t\) and \(\mu ^{2}_t\) indicate whether a complete maintenance operation is scheduled prior to the production of the first and second production quantities \(Q^1_{kt}\) and \(Q^2_{kt}\) in this period, respectively.

  • The variables \(SI^{1}_t\) and \(SI^{2}_t\) give the required state increase of the critical resource to reach the maximal state \(s^{\max }\) for the first and second maintenance operation in the period, respectively.

If maintenance and setup operations can be performed in parallel (\(\gamma =0\)), the continuous variable \(CB_t\) gives the capacity bonus due to performing setup and maintenance operations in parallel, which is zero if maintenance and setup have to be performed serially (\(\gamma =1\)).

Note that both a complete and a partial maintenance can only be scheduled as a first operation preceding \(Q^1_{kt}\) in microperiod t if the setup state is preserved during maintenance, i.e., case \(\alpha =1\). In Fig. 4, the time structure of a microperiod in the case of serial and complete maintenance is shown. Figure 7 shows the time structure of a microperiod in the case of parallel and complete maintenance.

Fig. 7
figure 7

State variables for case \(\alpha =1, \beta =0, \gamma =0\)

Full size image

3.2 Description of the model

With the above mentioned notation, the General Lotsizing and Maintenance Scheduling Problem (GLMSP) is defined. It is a generic model as specific parts are only (de-)activated for specific values of the incidence parameters \(\alpha \), \(\beta \) and \(\gamma \).

The objective function (1) minimizes the total costs:

$$\begin{aligned} \min z= & {} \sum _{ k\in \fancyscript{K}}\sum _{ t\in \fancyscript{T}\fancyscript{M}} ci_k \cdot I_{kt}+\sum _{ k\in \fancyscript{K}}\sum _{ t\in \fancyscript{T}} \big (cs_k \cdot \delta _{kt} + ce_k \cdot X_{kt} \big )\nonumber \\&+ \sum _{ t\in \fancyscript{T}} \Big (\beta \cdot cm \cdot (\alpha \cdot U^{1}_t + U^{2}_t) + (1-\beta ) \cdot cv \cdot (\alpha \cdot \mu ^{1}_t + \mu ^{2}_t ) \Big ) \end{aligned}$$
(1)

The total costs consist of the inventory costs at the end of each macroperiod, the setup costs and the (penalty) cost of planned external supply \(X_{kt}\). We finally add the respective costs of partial or complete maintenance.

Equation (2) are the inventory balance constraints. Restrictions (3) and (4) are the production and rough capacity constraints per microperiod. Restrictions (5) are the setup constraints and restrictions (6) are the setup carry-over constraints.

$$\begin{aligned}&I_{k,t-1} + Q^1_{kt} + Q^2_{kt} - I_{kt} + X_{kt}= d_{kt} \cdot \mathbb {1}_{\{\forall t\in \fancyscript{T}\fancyscript{M} \}}&\qquad \quad \forall k\in \fancyscript{K},\forall t\in \fancyscript{T} \end{aligned}$$
(2)
$$\begin{aligned}&Q^1_{kt} \le \frac{c_{\tau }}{tp_{k}} \cdot \omega _{k,t-1}&\qquad \quad \forall k\in \fancyscript{K},\forall \tau \in \fancyscript{P},\forall t\in \fancyscript{T}\fancyscript{P}_{\tau } \end{aligned}$$
(3)
$$\begin{aligned}&Q^2_{kt} \le \frac{c_{\tau }}{tp_{k}} \cdot \omega _{kt}&\qquad \quad \forall k\in \fancyscript{K},\forall \tau \in \fancyscript{P},\forall t\in \fancyscript{T}\fancyscript{P}_{\tau } \end{aligned}$$
(4)
$$\begin{aligned}&\sum _{ k\in \fancyscript{K}} \omega _{kt} \le 1&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(5)
$$\begin{aligned}&\delta _{kt} \ge \omega _{kt}-\omega _{k,t-1}&\qquad \quad \forall k\in \fancyscript{K},\forall t\in \fancyscript{T} \end{aligned}$$
(6)

The indicator function \(\mathbb {1}_{\{\forall t\in \fancyscript{T}\fancyscript{M} \}}\) in the inventory balance Eq. (2) is used as demand is only assigned to the last microperiod within each macroperiod. In each of the microperiods, we permit an external supply \(X_{kt}\), so that formally any problem instance is capacity-feasible. We use prohibitively high (penalty) cost parameters \(ce_k\) on external supply to eventually price out any external supply if possible in the implementation of our decomposition algorithm. Inequalities (3) and (4) ensure the resource is set up for product k in order to produce product k. Restrictions (5) state that the resource can be set up for at most one product at the end of microperiod t. Restrictions (6) model the carry-over of the setup state into the next microperiod. The following restrictions (7) and (8) are the capacity constraints with variables \(C_t\) and parameters \(c_\tau \) expressed in time units.

$$\begin{aligned}&\sum _{ k\in \fancyscript{K}} (tp_{k} \cdot (Q^1_{kt} + Q^2_{kt}) + ts_k \cdot \delta _{kt}) + \beta \cdot tm \cdot (\alpha \cdot U^{1}_t + U^{2}_t) \nonumber \\&\quad + (1-\beta ) \cdot tv \cdot ( \alpha \cdot \mu ^{1}_t + \mu ^{2}_t) = C_t + (1-\gamma ) \cdot CB_t&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(7)
$$\begin{aligned}&\sum _{ t\in \fancyscript{T}\fancyscript{P}_{\tau }} C_t \le c_{\tau }&\qquad \quad \forall \tau \in \fancyscript{P} \end{aligned}$$
(8)

The constraints (7) determine the required capacity \(C_t\) in each microperiod t and hence implicitly its length. The capacity constraints (8) make sure that the time needed for production, setup and maintenance in a microperiod t belonging to a macroperiod \(\tau \) does not exceed the available capacity \(c_\tau \) of that macroperiod \(\tau \). The capacity consumption due to partial \((\beta =1)\) or complete maintenance \((\beta =0)\), a potential loss of the setup state (\(\alpha =0\)) and a capacity bonus \(CB_t\) in case of parallel setup and maintenance operations (\(\gamma =0\)) are reflected in constraints (7).

The next restrictions (9)–(14) track the state of the critical resource.

$$\begin{aligned}&S^4_{t-1} + \alpha \cdot ( \beta \cdot pm \cdot U^{1}_t + (1-\beta ) \cdot SI^{1}_t) = S^1_t&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(9)
$$\begin{aligned}&S^1_t - \sum _{ k\in \fancyscript{K}} a_k \cdot Q^1_{kt} = S^2_t&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(10)
$$\begin{aligned}&S^2_t + \beta \cdot pm \cdot U^{2}_t + (1-\beta ) \cdot SI^2_t = S^3_t&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(11)
$$\begin{aligned}&S^3_t - \sum _{ k\in \fancyscript{K}} a_k \cdot Q^2_{kt} = S^4_t&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(12)
$$\begin{aligned}&S^1_t, S^2_t, S^3_t, S^4_t \le s^{\max }&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(13)
$$\begin{aligned}&s^{\min } \le S^1_t, S^2_t, S^3_t, S^4_t&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(14)

Restrictions (9) to (12) connect the state variables \(S^1_t\) to \(S^4_t\) and account for both wear and maintenance. In restrictions (9), the state increase due to maintenance operations at the beginning of microperiods is considered. The state decrease prior to a setup operation in a microperiod is accounted for in restrictions (10). In a similar way restrictions (11) and (12) model the state increase or decrease due to maintenance or production adjacent to the setup process of microperiod t.

Restrictions (13) and (14) make sure that the state of the critical resource is always in the interval \([s^{\min }, s^{\max }]\).

The following restrictions (15)–(18) are only activated in the case of complete maintenance (\(\beta =0\)).

$$\begin{aligned}&S^1_t \ge s^{\max } \cdot \mu ^{1}_t&\qquad \quad \forall t\in \fancyscript{T}, \alpha =1, \beta =0 \end{aligned}$$
(15)
$$\begin{aligned}&SI^{1}_t \le s^{\max } \cdot \mu ^{1}_t&\qquad \quad \forall t\in \fancyscript{T}, \alpha =1, \beta =0 \end{aligned}$$
(16)
$$\begin{aligned}&S^3_t \ge s^{\max } \cdot \mu ^{2}_t&\qquad \quad \forall t\in \fancyscript{T}, \beta =0 \end{aligned}$$
(17)
$$\begin{aligned}&SI^{2}_t \le s^{\max } \cdot \mu ^{2}_t&\qquad \quad \forall t\in \fancyscript{T}, \beta =0 \end{aligned}$$
(18)

Restrictions (15) and (16) make sure that the state of the resource is equal to \(s^{\max }\) after a maintenance activity at the beginning of microperiod t. Likewise, restrictions (17) and (18) guarantee that the state of the resource equals \(s^{\max }\) after the maintenance activity before or parallel to the setup operation. A further set of restrictions (19)–(20) is used to determine the capacity bonus \(CB_t\) for the case of parallel maintenance (\(\gamma =0\)) to determine the overlap of maintenance and setup operations, see restriction (7).

$$\begin{aligned}&CB_t \le \sum _{k\in \fancyscript{K}} ts_k \cdot \delta _{kt}&\qquad \quad \forall t\in \fancyscript{T},\gamma =0 \end{aligned}$$
(19)
$$\begin{aligned}&CB_t \le \beta \cdot tm \cdot U^2_t + (1-\beta ) \cdot tv \cdot \mu ^{2}_t&\qquad \quad \forall t\in \fancyscript{T},\gamma =0 \end{aligned}$$
(20)

In the capacity constraint (7), the capacity consumption for setup as well as maintenance operations is considered. If these operations can be performed in parallel, the capacity bonus \(CB_t\) cannot exceed the minimum of the time required for these two operations, see (19) and (20). Note that a possible maintenance operation prior to a setup operation during that microperiod cannot result in a capacity bonus as there cannot be a parallel setup process.

Restrictions (21) are only required if a maintenance operation leads to a loss of the setup state (\(\alpha =0\)) and ensure that a new setup has to be carried out in order to continue production.

$$\begin{aligned} \sum _{ k\in \fancyscript{K}} \delta _{kt} + 1 \ge \beta \cdot \frac{pm \cdot U^{2}_t}{s^{\max }} + (1-\beta ) \cdot \mu ^{2}_t + \sum _{ k\in \fancyscript{K}} \omega _{kt}&\forall t\in \fancyscript{T}, \alpha =0 \end{aligned}$$
(21)

Note that it is not possible to have a a maintenance operation prior to a setup operation during that microperiod if the setup state is lost (\(\alpha =0\)) during maintenance.

Constraints (22)–(27) give the starting values for the state of the resource, the inventory and the setup state of the resource and define the domains of the different variables.

$$\begin{aligned}&s_0 = s^{\max }&\qquad \quad \end{aligned}$$
(22)
$$\begin{aligned}&I_{k0}=0&\qquad \quad \forall k\in \fancyscript{K} \end{aligned}$$
(23)
$$\begin{aligned}&\omega _{k0}=0&\qquad \quad \forall k\in \fancyscript{K} \end{aligned}$$
(24)
$$\begin{aligned}&C_t, CB_t, I_{kt}, Q^1_{kt}, Q^2_{kt}, S^1_t, S^2_t, S^3_t, S^4_t, SI^{1}_t, SI^{2}_t, X_{kt} \ge 0&\qquad \quad \forall k\in \fancyscript{K},\forall t\in \fancyscript{T} \end{aligned}$$
(25)
$$\begin{aligned}&U^{1}_t, U^{2}_t \in \mathbb {N}_0&\qquad \quad \forall t\in \fancyscript{T} \end{aligned}$$
(26)
$$\begin{aligned}&\delta _{kt}, \omega _{kt}, \mu ^{1}_t, \mu ^{2}_t \in \{0,1\}&\qquad \quad \forall k\in \fancyscript{K},\forall t\in \fancyscript{T} \end{aligned}$$
(27)

Equation (22) initialize the state of the resource at the beginning of the first period to \(s^{\max }\). Equation (23) set the inventory level at the beginning of the planning horizon to zero. Eq. (24) prohibit an initial setup state. Restrictions (25)–(27) are the nonnegativity, integer and binary constraints of the model.

It should be noted that a more compact and mathematically equivalent formulation of this model is possible. We chose the presented version to serve the ease of presentation.

4 Adapted fix-and-optimize heuristic

Standard solvers for mixed-integer programs (MIPs) like CPLEX can only solve very small instances of the problem presented in the previous section due to its combinatorial structure. To solve large problem instances, we developed a decomposition heuristic of the Fix-and-Optimize type as proposed by Helber and Sahling (2010). In this approach, the original problem is decomposed into interrelated subproblems that are solved iteratively. In each such subproblem, all real-valued decision variables, but only a (usually small) subset of the binary decision variables of the original problem are endogenously optimized while the other binary variables of the original problem are assigned a fixed value and hence treated as an exogenous parameter within the subproblem. As this fixation results in a limited number of the binary variables, it is often possible to solve each subproblem to (sub)optimality in moderate time using any standard solver for MIPs. Most of the original binary variables that are optimized in one subproblem are fixed in the following subproblem. For this reason, the decomposition algorithm sequentially explores different areas of the solution space.

For the Fix-and-Optimize decomposition algorithm, a set \(\fancyscript{K}\fancyscript{T}\) of product-period combinations is firstly defined, i.e., \(\fancyscript{K}\fancyscript{T} = \{1,\ldots ,K\} \times \{1,\ldots ,T\}\). To identify those setup operation and setup state variables \(\delta _{kt}\) and \(\omega _{kt}\) of the original problem, that are either fixed or optimized in the current subproblem, the following disjunctive subsets \(\fancyscript{K}\fancyscript{T}_{\delta }^{fix} \subseteq \fancyscript{K}\fancyscript{T}\), \(\fancyscript{K}\fancyscript{T}_{\delta }^{opt} \subseteq \fancyscript{K}\fancyscript{T}\), \(\fancyscript{K}\fancyscript{T}_{\omega }^{fix} \subseteq \fancyscript{K}\fancyscript{T}\) and \(\fancyscript{K}\fancyscript{T}_{\omega }^{opt} \subseteq \fancyscript{K}\fancyscript{T}\) are defined.

Table 3 Additional notation for each subproblem GPLSM-Sub
Full size table

As explained in Sect. 3, see also Table 1, the binary variables \(\mu ^{1}_t\) and \(\mu ^{2}_t\) are only required in the case of complete maintenance to define the precise timing of maintenance operations within each period. For this reason, we also introduce disjunctive subsets \(\fancyscript{T}_{\mu }^{fix} \subseteq \fancyscript{T}\) and \(\fancyscript{T}_{\mu }^{opt} \subseteq \fancyscript{T}\) to determine which of these variables are fixed or optimized within each subproblem. Using the additional notation in Table 3, we can state the subproblem GLMSP-Sub as (1)–(27) extended by the following additional constraints:

$$\begin{aligned}&\delta _{kt} = \overline{\delta }_{kt}&\qquad \quad \forall (k,t) \in \fancyscript{K}\fancyscript{T}_{\delta }^{fix} \end{aligned}$$
(28)
$$\begin{aligned}&\omega _{kt} = \overline{\omega }_{kt}&\qquad \quad \forall (k,t) \in \fancyscript{K}\fancyscript{T}_{\omega }^{fix} \end{aligned}$$
(29)
$$\begin{aligned}&\mu ^{1}_t = \overline{\mu }^{1}_t&\qquad \quad \forall t \in \fancyscript{T}_{\mu }^{fix},\alpha =1, \beta =0 \end{aligned}$$
(30)
$$\begin{aligned}&\mu ^{2}_t = \overline{\mu }^{2}_t&\qquad \quad \forall t \in \fancyscript{T}_{\mu }^{fix}, \beta =0 \end{aligned}$$
(31)

The additional constraints (28)–(31) limit the optimization of the binary setup variables \(\delta _{kt}\) to the subset \(\fancyscript{K}\fancyscript{T}_{\delta }^{opt} = \fancyscript{K}\fancyscript{T} \backslash \fancyscript{K}\fancyscript{T}_{\delta }^{fix}\), of the binary setup state variables \(\omega _{kt}\) to the subset \(\fancyscript{K}\fancyscript{T}_{\omega }^{opt} = \fancyscript{K}\fancyscript{T} \backslash \fancyscript{K}\fancyscript{T}_{\omega }^{fix}\), and of the binary complete maintenance variables to the subset \(\fancyscript{T}_{\mu }^{opt} = \fancyscript{T} \backslash \fancyscript{T}_{\mu }^{fix}\).

We start our iterative decomposition algorithm with a trivial solution. As the number of microperiods per macroperiod equals the number of products, we initially schedule a setup operation for product 1 in microperiod 1 (\(\delta _{1,1}=1\)), for product 2 in microperiod 2 (\(\delta _{2,2}=1\)) etc. In the first microperiod of the second macroperiod, we again schedule a setup operation for product 1 and so on. This way the setup operation and setup state variables are assigned initial variables. In the case of complete maintenance (\(\beta =0\)), we furthermore need initial values of the binary variables \(\mu ^{1}_t\) for the maintenance activities at the beginning of each microperiod t as well as the binary variables \(\mu ^{2}_t\) for the maintenance activities before and during setup, respectively. If the entire setup pattern is assigned the initial values just mentioned, we can initially solve the augmented problem GLMSP-Sub (1)–(31) by fixing all setup variables, i.e., setting \(\fancyscript{K}\fancyscript{T}_{\delta }^{fix} = \fancyscript{K}\fancyscript{T}_{\omega }^{fix} =\fancyscript{K}\fancyscript{T}\) and optimizing over all real-valued as well as all binary maintenance variables, i.e., setting \(\fancyscript{T}_{\mu }^{opt} = \fancyscript{T}\). For a given setup pattern, the latter optimization can be performed quickly.

In the Fix-and-Optimize algorithm, we solve a sequence of subproblems (1)–(31) which only differ with respect to the set of currently fixed binary variables of the original problem. Those variables are set to the values that were either determined or optimized in the previous subproblem or already fixed in the last subproblem which led to an improvement of the solution. For a detailed description of the Fix-and-Optimize heuristic and its decomposition strategies see Sahling (2010) as well as Helber and Sahling (2010).

In our implementation, we start with a single round of a period-oriented decomposition which is followed by a single round or a product-oriented decomposition. In the period-oriented decomposition all binary setup operation, setup state and maintenance variables \(\delta _{kt}\), \(\omega _{kt}\), \(\mu ^1_t\) and \(\mu ^2_t\) optimized within a time-window of \(\kappa \) consecutive microperiods. The remaining binary variables outside this time-window are fixed to the values of the last subproblem that improved the incumbent solution. Beginning in the first microperiod, this time-window is shifted by \(\lambda \) microperiods into the future to create the next subproblem until the end of the planning horizon is reached. We then perform a product-oriented decomposition where pairs of two products are treated within a subproblem. The binary setup operation variables \(\delta _{kt}\), setup state variables \(\omega _{kt}\) and maintenance variables \(\mu ^{1}_t\) and \(\mu ^{2}_t\) are optimized over all microperiods \(\forall t\in \fancyscript{T}\) for those two products of the current subproblem. The binary variables of all other products are fixed to the values of the incumbent solution. Beginning with the pair of products 1 and 2 and continuing with the pair of products 1 and 3 etc., the pair of products is switched successively until every possible combination of two products was tried once. Whenever a subproblem leads to a solution with lower cost than the current incumbent solution, it becomes the new incumbent solution. Extensive numerical pre-tests showed that this simple algorithmic design combines a good relationship between solution quality and computer runtime.

5 Numerical experiments

5.1 Purpose and outline of the numerical experiments

In our numerical experiments, we want to address two different questions. The first question is related to the numerical tractability of the model developed in Sect. 3. We ask for the computational effort as well as the solution quality if either a standard branch&bound algorithm for mixed-integer linear programs like CPLEX or the specialized Fix-and-optimize heuristic from Sect. 4 is used to solve the model. The second question is more management-related and asks for the impact of simultaneously vs. sequentially scheduling setup, production, and maintenance operations. The aim is to identify those conditions which call for a simultaneous approach or suggest a possibly less sophisticated sequential approach.

5.2 Test instances, computational environment, and solution metrics

For the numerical investigation we define two problem classes A and B differing in the number K of products and T of periods. Generally speaking, the instances of problem class A are small while those of B are substantially larger, see Table 4. For each of the eight possible combinations of the maintenance cases \((\alpha / \beta / \gamma )\) from Fig. 2 and each of the two problem classes numerous (artificial) test instances (TI) are defined by systematically varying different parameters of the model. Table 5 gives a selection of the different parameter values used the two problem classes. A document with the complete description the data set leading to a total of 1152 test instances can be found at http://www.prod.uni-hannover.de/GLMSP-testinstances.

Table 4 Problem classes
Full size table
Table 5 Selection of parameters for the test instances
Full size table

The model formulation presented in Sect. 3 and the Fix-and-optimize heuristic in Sect. 4 were implemented in GAMS 23.7.3. We used CPLEX 12.3 to solve the models and to determine reference values. All computations were performed at the parallel cluster system of Leibniz Universität Hannover’s IT Services. This is a highly powerful and flexible scientific computing system which allows the user to specify the number of processor cores or threads as well as the RAM used to solve a MIP instance, see http://www.rrzn.uni-hannover.de/scientific_computing_doku.html?&L=1 for details. Due to the high number of processors operating in parallel, we were able to perform an extremely time-consuming analysis of our large test bed, both for applying the Fix-and-Optimize heuristic and for computing CPLEX reference values directly. For the Fix-and-optimize heuristic we used two parallel threads with 2.93 GHz, 4 GB of RAM and a time limit of 15 s per subproblem. For each problem instance, this led to a solution with an objective function value denoted as \( Z^{F \& O}\).

To compute a reference value, we furthermore solved for each of the 1152 test instances the model in Sect. 3 directly. As this turned out to be extremely time-consuming, we provided to CPLEX the solution from the Fix-and-optimize heuristic as a starting solution to speed up the branch and bound process. CPLEX was then given 1 h of CPU time for each of the test instances of Class A and 10 h for each of the test instances of Class B. Here we used four parallel threads with 2.93 GHz and 32 GB of RAM in an attempt to find reference solutions that are better than those found by the Fix-and-optimize heuristic. The objective function values of these reference values were denoted as \(Z^{\textit{CPLEX}}\). Note that \( Z^{F \& O} \ge Z^{\textit{CPLEX}}\) holds and that both \( Z^{F \& O}\) and \(Z^{\textit{CPLEX}}\) are upper bounds on the optimal objective function value. When CPLEX terminated its attempt to determine reference values, it also reported the final lower bound on the objective function value, denoted here as \(Z^{\textit{LB}}\). Note that when for a problem instance \(Z^{\textit{CPLEX}}=Z^{\textit{LB}}\) holds, then CPLEX was able to solve the problem instance to proven optimality. This was possible for 43.92 % of the instances of problem class A, but none of problem class B.

As an upper bound on the relative deviation from the optimal objective function value we determined the following gaps:

$$ \begin{aligned} \textit{GAP}^{F \& O}&= \displaystyle \frac{Z^{F \& O} - Z^{\textit{LB}} }{ Z^{\textit{LB}} } \end{aligned}$$
(32)
$$\begin{aligned} \textit{GAP}^{\textit{CPLEX}}&= \displaystyle \frac{Z^{\textit{CPLEX}} - Z^{\textit{LB}} }{ Z^{\textit{LB}} } \end{aligned}$$
(33)

We furthermore asked to which extent the initial solution from the Fix-and-optimize heuristic could actually be improved in the attempt to compute a reference value. To this end, the relative deviation of the objective function value of the heuristic from the objective function value of CPLEX is determined as follows:

$$ \begin{aligned} DevCpx = \displaystyle \frac{ Z^{F \& O} - Z^{\textit{CPLEX}} }{ Z^{\textit{CPLEX}} } \end{aligned}$$
(34)

In both approaches explained so far, setup, production, and maintenance operations were treated simultaneously. In order to analyze the benefits of such a simultaneous approach, we compared it to two different (non-simultaneous) approaches which reflect to some extent the usual industrial practice to separate production and maintenance planning. The common feature of both non-simultaneous approaches is that in a first step decisions about production operations are made under the (preliminary) assumption that wear and tear does not occur (i.e., by setting \(a_k=0, \forall k\)). In this setting, maintenance operations are not necessary and hence not included in the schedule. We use the Fix-and-optimize heuristic in this first step to solve the model. This leads to a setup pattern and time-phased production and inventory quantities. In the second step, we eliminate this preliminary assumption \((a_k=0, \forall k)\) again and determine a schedule for the maintenance activities that is compatible with those decisions that are adopted from the first step. For this second step, we used CPLEX right away for the remaining problem. CPLEX was given 1 h for each instance of problem class A and 10 h for each instance of class B for this second step.

In the first alternative approach (denoted as the “sequential approach”), we adopt in the second step only the setup pattern from the first step, i.e., the values of the binary variables \(\delta _{kt}\) and \(\omega _{kt}\). Given this setup pattern, we then determine simultaneously values for all the maintenance-related variables as well as (new and compatible) values for the production, inventory and external supply quantities. This approach can still be interpreted as a partial coordination of production and maintenance decisions.

For the second alternative approach (denoted as the “independent approach”), we adopt in the second step both the setup pattern and the inventory quantities \(I_{kt}\) from the first step. We furthermore try to retain the production quantities from the first step to the extent that this is possible, while at the same time including in the schedule compatible maintenance operations to the extent that this is necessary. However, due to the capacity restrictions, maintenance operations cannot simply be “added” for the given production quantities \(Q^1_{kt}\) and \(Q^2_{kt}\) from step 1 unless there is substantial slack capacity. For this reason, we compute from the results of the first step a parameter \(Q^{fix,S1}_{kt}\) as follows:

$$\begin{aligned} Q^{fix,S1}_{kt}:=Q^1_{kt}+Q^2_{kt} + X_{kt}&\qquad \quad \forall k\in \fancyscript{K}, \forall t\in \fancyscript{T} \end{aligned}$$
(35)

In the second step a new restriction is added to the model, which allows to re-compute \(Q^1_{kt}\) and \(Q^2_{kt}\) and substitute production quantities with (additional) external supply \(X_{kt}\):

$$\begin{aligned} Q^{fix}_{kt}=Q^1_{kt}+Q^2_{kt}+X_{kt}&\qquad \quad \forall k\in \fancyscript{K}, \forall t\in \fancyscript{T} \end{aligned}$$
(36)

This way we can ensure that the end-of-period inventory levels are not changed in the solution related to the second step. In the solution to the second step, the re-computed production quantities \(Q^1_{kt}\) and \(Q^2_{kt}\) are again compatible with the maintenance decisions.

Both the sequential approach (SA) and the independent approach (IA) tend to lead to an increase of the external supply. As it is punished in the objective function, the objective function values of the corresponding schedules tend to increase. We denote with \(Z^{\textit{SA}}\) and \(Z^{\textit{IA}}\) the respective objective function values. The relative deviation from the best available solution to a problem instance is computed as follows:

$$\begin{aligned} DevCpx^{\textit{SA}}&= \displaystyle \frac{ Z^{\textit{SA}} - Z^{\textit{CPLEX}}}{ Z^{\textit{CPLEX}} } \end{aligned}$$
(37)
$$\begin{aligned} DevCpx^{\textit{IA}}&= \displaystyle \frac{ Z^{\textit{IA}} - Z^{\textit{CPLEX}}}{ Z^{\textit{CPLEX}} } \end{aligned}$$
(38)

It shows to which extent costs increase do to the increased external supply which becomes necessary if setup, production, and maintenance operations are not coordinated simultaneously.

5.3 Numerical results

First we compare the solutions found by the heuristic with the solutions found by CPLEX. In Table 6 the numerical results are presented for Class A and in Table 7 for Class B. The averages of the gaps for the Fix-and-optimize heuristic (32) and CPLEX (33) are reported in the columns “AvgGAP”, together with the average computation times. The average of the improvement (34) by CPLEX over the Fix-and-optimize solution is reported in column “AvgDevCpx”. In a similar manner we report for the sequential and the independent approach the average of the relative cost increase (37) and (38) as well as the average fraction of the demand that has to be supplied externally.

Table 6 Numerical results for problem Class A
Full size table
Table 7 Numerical results for problem Class B
Full size table

The results indicate that the specialized Fix-and-optimize heuristic can solve both problem classes, irrespective of the problem aspects from Table 5. Even if CPLEX is given a good initial solution and a lot of additional computation time, it cannot improve the Fix-and-optimize solution substantially. For problem class A, the solutions are close to optimal and found quickly. For problem class B, the averages of the upper bounds on the relative deviation from the optimal solutions are relatively large. This might be due to the weak lower bounds from the LP-relaxation used in the branch and bound process. Note that the many fractional values of the originally binary or integer variables created in the LP-relaxation of the branch and bound process lead to many nodes in the branch and bound tree that are not integer feasible such that finding feasible solutions by applying CPLEX to the monolithic model can be extremely time-consuming. Again, the specialized heuristic outperforms the standard solver and we conclude that it can solve medium-sized problems.

On average, the solutions from the sequential approach (SA) as well as those from the independent approach (IA) are much more costly than those from the simultaneous approach, even if only a small fraction of the demand is supplied externally. This is due to the high penalty costs \(ce_k\) for the external supply, see Table 5 and indicates that it can be economically important to solve the problem simultaneously. It should be noted that this cost increase is much higher for problem class A than for problem class B. The reason is that in problem class B the number of both the products and the periods is substantially larger, which apparently leads to a larger and better structured solution space and more options to include maintenance operations in a partially determined production schedule.

A comparison of the average values of the best solutions (column “AvgBestSol”) shows the expected behavior, for example that average total costs decrease as the time between maintenance operations (TBM) increases from 0.5 to 2 macroperiods or that they increase as the relative maintenance cost \(cm^{rel}\) increase from 0.5 to 2.

6 Conclusion and future research

In this paper we have presented a new and generic lot sizing and maintenance scheduling model including a formal wear and tear function. This way we established a simultaneous planning approach that can be more cost-efficient than a traditional sequential planning approach. The solution of the model results in an integrated production and maintenance schedule for the case of intensive and predictable wear and tear. The model is generic in the sense that a total of eight different problem constellations can be treated. A specialized Fix-and-optimize heuristic has been developed and shown to be powerful in a extensive numerical study.

Future research could address the case of nonlinear wear and tear functions as well as the case of different components that are subject to wear and tear. In addition, one could treat the case of multiple machines that compete for a limited maintenance crew. In such a setting, production and maintenance schedules have to be coordinated over several machines.