A two-stage coupled algorithm for an integrated maintenance planning and flowshop scheduling problem with deteriorating machines

Abstract

We address a novel integrated maintenance and production scheduling problem in a multi-machine and multi-period production system, considering maintenance as a long-term decision. Deterioration of machines over time decreases production capacity. Since maintenance activities not only improve machine conditions, increasing production capacity, but also take time that cannot be used for production, the challenge is to assign maintenance to periods and to schedule maintenance and production activities within each period to minimize the combined cost of maintenance and lost production over the planning horizon. Motivated by logic-based Benders decomposition, we design an integrated two-stage algorithm to solve the problem. The first stage assigns maintenance to machines and time periods, abstracting the scheduling problem, while the second stage creates a schedule for the current time period. The first stage is then re-solved using feedback from the schedule. This iteration between maintenance planning and scheduling continues until the solution costs in two stages converge. The integrated approach models the interdependencies between maintenance and scheduling decisions in highly coupled processes such as wafer fabrication in the semiconductor manufacturing. Our results demonstrate that the benefit of integrated decision making increases when maintenance is less expensive relative to lost production cost and that a longer horizon for maintenance planning is beneficial when maintenance cost increases.

1 Introduction

Production scheduling addresses the problem of allocating the available production capacity to competing customer orders to optimize the performance of the system. In many manufacturing systems, the production capacity decreases over time as machines deteriorate. For example, a dull drill bit, a contaminated cooling system, or a worn-out crankshaft sensor in manufacturing slow the operations, increasing the number of orders that cannot be delivered by their due dates. However, maintenance improves machine conditions, restoring the production capacity, while using potential production time that could be otherwise allocated to processing the customer orders. Therefore, scheduling maintenance to minimize the disruption of the production process is a challenging problem. In this paper, we explore how information about machine conditions and operational information including workloads and due dates can be integrated to simultaneously schedule maintenance and production activities, increasing the number of orders satisfied by their due dates.

Maintenance planning and production scheduling are often viewed as separate and sequential decisions in contexts such as wafer fabrication in the semiconductor manufacturing (Yao et al. 2004). In this process, wafer lots (production jobs) flow through the system, requiring several operations to be performed by various cluster tools (machines) (Kumar and Kumar 2001). The flow of the wafers in a fab forms a reentrant line, a manufacturing configuration between classical flowshop and jobshop (Uzsoy et al. 1992; Kumar and Kumar 2001; Mönch et al. 2011). In the fabrication process, on the higher level, the preventive maintenance frequency is first planned mainly based on the state of tools, such as their age (Yao et al. 2004) and provided as inputs to the scheduling system. Knowing the information about which tools are under preventive maintenance and the maintenance duration, scheduling decisions then find the optimal allocation of the available tools to competing wafer lots over time. The goal is to increase the capability of meeting due dates for optimal customer satisfaction, one of the most important objectives in the semiconductor market (Mönch et al. 2011). However, this division ignores the dependency between maintenance planning and scheduling (Yao et al. 2004): it may be globally optimal to schedule maintenance earlier or later. As an example, if the fab process is heavily loaded, there is an opportunity for significant financial gains by delaying maintenance (Yao et al. 2004). Therefore, incorporating the operational state of the process such as workloads and due dates into maintenance decisions leads to a better allocation of resources to maintenance and wafer lots.

There are two areas in the scheduling literature that study the dependency between maintenance planning and production scheduling. The first addresses the limited availabilities of machines due to maintenance requirements (Ma et al. 2010), and the second area models the effect of maintenance on processing times by considering maintenance as a rate-modifying activity (Lee and Leon 2001). However, there is no decision regarding planning maintenance since the time windows for maintenance are typically given [e.g., Kuo and Yang (2008), Mosheiov and Sidney (2010), Kellerer et al. (2013)]. To address the interdependency between maintenance and scheduling decisions in highly coupled processes such as wafer fabrication (Yao et al. 2004), in this paper, we consider a flowshop system with multiple machines over multiple time periods where maintenance concepts are modeled as defined in the maintenance research literature (McCall 1965; Cho and Parlar 1991; Dekker et al. 1997; Wang 2002; Nicolai and Dekker 2008). We explicitly model the effect of machine conditions on processing times and consider maintenance as a long-term decision.

Motivated by logic-based Benders decomposition approach (Hooker 2005, 2007), we design an integrated two-stage algorithm where the maintenance and scheduling decisions are tackled in different, coupled stages. The first stage finds the optimal maintenance plan, abstracting the production scheduling problem. It has a long-term view over the time periods where information about the customer orders is available and seeks to minimize the sum of maintenance and a lower bound on the lost production costs. The maintenance plan determines the assignment of maintenance activities to machines and time periods. The second stage has a short-term view over the current period, finding the optimal schedule of maintenance and production activities given the specified maintenance plan. The real lost production cost is then communicated via a constraint to the first stage so that the maintenance plan can be revised if it is no longer optimal. The decision stages iterate until the optimal solution is found, i.e., the relaxation of lost production cost in the first stage solution is equal to the actual lost production cost.

We experimentally compare the performance of this integrated algorithm with three other approaches: hierarchical decision making where there is no feedback between decision stages, a short-term model where maintenance planning and scheduling are done together for each period, and a heuristic model. Our empirical results demonstrate that the integrated and long-term decision making results in higher solution quality. It is further shown that the benefit of integrated decision making increases as the ratio of maintenance cost to lost production cost decreases while planning maintenance for multiple periods is beneficial when the ratio increases.

The following section provides an overview of the relevant literature. We then formally define our problem, describe the proposed solution approaches, present our experiments and discuss the results. Finally, we end with conclusion and directions for future work.

2 Literature review

In this section, we review the literature on integrating maintenance and production scheduling problems and provide necessary background on logic-based Benders decomposition, an inspiration for our integrated approach.

2.1 Integrated maintenance planning and production scheduling

The problem of maintenance planning and production scheduling has been studied in the scheduling literature from two perspectives. The first deals only with the fact that a machine undergoing maintenance is unavailable for production jobs (Schmidt 2000; Lee 2004; Ma et al. 2010; Hadidi et al. 2012a). The second perspective models different processing times for a production job depending on whether it is scheduled before or after maintenance (Lee and Leon 2001). Both perspectives typically consider single-machine problems and focus on analyzing the computational complexity of the problems and/or deriving the properties of the optimal schedules. The derived properties are used to develop polynomial-time approximation algorithms or efficient heuristics, or are modeled as extra constraints to reduce the computational effort.

A problem of the first category can be defined as follows. A set of jobs $\mathcal {J}=\{J_i|i=1,\ldots ,n\}$ and a set of machines $\mathcal {M}=\{M_j|j=1,\ldots ,m\}$ are given. Machine $M_j$ is not available for processing the jobs within $S_j$ time intervals $[B^s_j,F^s_j],~s=1,\ldots ,S_j$ where $B^s_j$ and $F^s_j$ denote the start time and the finish time of the $s$-th unavailability interval (Ma et al. 2010). The goal of the problem is to pack the jobs into the gaps created between unavailability intervals, optimizing an operational performance measure such as finishing all the jobs as soon as possible. In different problem variations, jobs may be resumable (i.e., the job continues its processing after the unavailability period) (Lee 1996), non-resumable (i.e., it is re-started if interrupted by the unavailability period) (Lee 1996), or semi-resumable (i.e., the disrupted job has to re-do part of its processing when the machine becomes available again) (Lee 1999). One or several unavailability intervals (maintenance periods) might be considered where their start and end times are either known or decision variables. A number of different combinations of the unavailability intervals and job characteristics have been studied (Lee 1996; Liao and Chen 2003; Akturk et al. 2004; Chen 2006; Ji et al. 2007; Kovacs and Beck 2007; Xu et al. 2010; Yu et al. 2014). While the majority of this literature deals with deterministic problems where limited availabilities of machines only result from planned maintenance, a number of authors have studied a single- machine scheduling problem assuming that the machine is not continuously available due to both planned maintenance and random machine breakdowns (Cassady and Kutanoglu 2003, 2005; Kuo and Chang 2007; Hadidi et al. 2011, 2012b).

The problem of integrated maintenance planning and production scheduling of the first category has also been extended to flowshop setting that is similar to the manufacturing configuration of the fabrication process in the semiconductor industry (Allaoui and Artiba 2004). Different computationally efficient solution approaches are developed to find a good schedule. Some examples of the solution approaches are meta-heuristic algorithms including genetic algorithm, tabu search (Aggoune 2004; Ruiz et al. 2007), and variable neighborhood search (Naderi et al. 2009); a heuristic algorithm combining dispatching rules, simulated annealing, and simulation (Allaoui and Artiba 2004); and a branch-and-bound algorithm (Allaoui and Artiba 2006). A detailed review of this literature can be found in Naderi et al. (2009).

The above scheduling problems do not model any correlation between machine conditions and processing times, ignoring the effect of maintenance on machine deterioration and restoration processes (Rustogi and Strusevich 2012; Kellerer et al. 2013). Lee and Leon (2001) were the first to introduce such maintenance considerations into the scheduling literature, initiating the study of the second category of problems. More specifically, the authors defined maintenance as a rate-modifying activity that changes the processing times of production jobs scheduled after maintenance to $\lambda _j p_j$ where $0<\lambda _j<1$ and $p_j$ represents the processing time of job $j$ before maintenance. In the work of Lee and Leon and many subsequent models [e.g., Mosheiov and Sarig (2009), Mosheiov and Sidney (2010)], only a single rate-modifying activity is considered and the processing time of a job does not depend on its position in the schedule or its start time, only whether it comes before or after maintenance. However, recent work has studied the problem of dividing the jobs into groups where the number of groups indicates the number of maintenance activities and the processing time of each job depends both on its assigned group and its position within the group (Kuo and Yang 2008; Yang and Yang 2010; Lodree and Geiger 2010; Rustogi and Strusevich 2012; Kellerer et al. 2013; Kim and Ozturkoglu 2013). The focus of such work is the development of polynomial-time algorithms for single-machine problems.

In the scheduling literature, unlike the broader maintenance literature (Dekker et al. 1996; Wang 2002; Nicolai and Dekker 2008; Pintelon and Parodi-Herz 2008), maintenance is considered as a short-term decision when reasoning about it in combination with production scheduling. That is, the problem is defined over a fixed horizon where maintenance and machine deterioration act on the same time-scale as the production jobs. In practice, a machine does not deteriorate as fast as the production jobs are processed and so maintenance decisions are naturally made over longer time horizons than detailed scheduling decisions (Cassady and Kutanoglu 2005; Budai et al. 2006; Grigoriev et al. 2006; Aghezzaf and Najid 2008).

In this paper, we study a scheduling problem where maintenance is considered as a long-term decision and where there is an explicit model representing the deterioration processes of machines and their effects on the processing times. This perspective on the problem takes into account common conceptualizations of maintenance as they appear in the maintenance literature (McCall 1965; Dekker et al. 1997; Wang 2002; Pintelon and Parodi-Herz 2008) and introduce them to the scheduling literature. Furthermore, we study the problem in a multi-machine flowshop environment rather than a single-machine problem.

2.2 Logic-based Benders decomposition

Our integrated two-stage approach is motivated by logic-based Benders decomposition. The classical Benders decomposition (Benders 1962; Geoffrion and Graves 1974) is a mathematical programming approach for solving large-scale mixed integer programming models. It partitions the problem into a mixed integer master problem (MP), which is a relaxation of the global model, and a set of linear sub-problems (SPs). Solving a problem by classical Benders involves iteratively solving the MP to optimality and using the solution to generate the sub-problems. The linear programming dual of the SPs is then solved to derive the tightest bound on the global cost function. If this bound is less than or equal to the current MP solution (assuming a minimization problem), the MP solution and the SP solutions constitute a globally optimal solution. Otherwise, a constraint, a Benders cut, is added to the MP to express the violated bound and another iteration is performed.

Logic-based Benders decomposition (Hooker and Yan 1995; Hooker and Ottosson 2003) was developed excluding the necessity that the MP must be a mixed integer model and the SPs linear. Therefore, the inference duals (Hooker 2005) of the SPs are solved rather than the linear duals to find the tightest bound on the global cost function from the original constraints and the current MP solution. Although logic-based Benders decomposition has more flexibility in modeling the problems, there is no standard procedure to derive the Benders cuts, it is problem-specific and requires creative effort. Nonetheless it has been successfully applied to a number of combinatorial optimization problems, often reporting computational results that are several orders of magnitude better than the previous state-of-the-art (Hooker 2005, 2007; Beck 2010; Fazel-Zarandi and Beck 2011; Aramon Bajestani and Beck 2013).

The formal representation of logic-based Benders decomposition can be found in Hooker (2007).

3 Problem definition

We consider a multi-machine flowshop production environment, producing multiple products over a finite planning horizon. There are $K$ discrete time periods, each $T$ time units long. Machines deteriorate as they are used for production. To model each machine deterioration process, we assume that the speed of a machine decreases as the number of time periods since preventive maintenance increases. A machine, $m \in \{1,2,\ldots ,M\}$, is in state $s_m \in \{0,1, \ldots , \mathcal {S}_m\}$, if its most recent preventive maintenance was $s_m$ time periods ago. In state $s_m$, machine $m$ operates at speed $\nu ^m_{s_m}$. Without loss of generality, it is assumed that the speed of machine $m$ in state $s_m=0$ is $\nu ^m_0=1$ and $\nu ^m_0 > \nu ^m_1 > \cdots > \nu ^m_{\mathcal {S}_m}=0$. In the semiconductor manufacturing, one of the commonly used tool parameters is the throughput rate, i.e., the number of wafers produced per time unit by each tool (Ramíez-Hernández and Fernández-Gaucherand 2003), that can be seen as equivalent to the speed used here. Performing a preventive maintenance job, $p$, at any point on machine $m$ takes $t^m_p$ units of time, costs $\tau ^m_p$, and changes the machine’s speed to $\nu ^m_0$. In other words, preventive maintenance makes the machine as good as new such that it operates at the highest speed. Since the complex machines such as cluster tools in the semiconductor manufacturing require highly skilled technicians for maintenance (Yao et al. 2004), we assume that the number of machines that can be maintained in each period is limited to $\mathcal {C}$. The initial state of machine $m$ at the beginning of the planning horizon is known and denoted as $\alpha _m$.

At the beginning of each time period, the set of production jobs is known for the next $L$ periods where $L<K$. The set of production jobs at time period $k \in \{1,2,\ldots ,K\}$ is denoted as $\mathcal {J}_k$. The production jobs are not carried over time periods: job $j$ in time period $k$, $j \in \mathcal {J}_k$, can only be processed during time period $k$. Furthermore, job $j$ has to be processed on all machines in sequence, requires processing time $p_{jm}$ on machine $m$, and has the due date $d_j$. The processing time of job $j$ on machine $m$ is $\frac{n_{jm}}{\nu ^m_{s_m}}$ where $n_{jm}$ is the processing time of job $j$ at $s_m = 0$, the best state of the machine. The due date $d_j$ corresponds to the latest possible completion time of job $j$ and is a time point within the $k$-th period. If a job is not finished by its due date, it is lost at cost $h_k$.

The goal of the problem is to allocate preventive maintenance to machines and time periods over the planning horizon and to assign start times to both production jobs and preventive maintenance activities, if any, within each time period such that the total cost of lost jobs and performing maintenance is minimized.

4 Problem formulation

We use the following decision variables to formulate the problem.

$y_{mk}$ :

$y_{mk}=1$ if machine $m$ at time period $k$ is maintained, and $y_{mk}=0$, otherwise.

$u_j$ :

$u_j=1$ if job $j$ is lost and $u_j=0$, otherwise.

$N_m(k)$ :

The state of machine $m$ in period $k$ before performing maintenance.

$st_{jm}$ :

The start time of job $j$ on machine $m$.

$p_{jm}$ :

The processing time of job $j$ on machine $m$.

$st_{pm}$ :

The start time of preventive maintenance job $p$ on machine $m$.

$x_{jim}$ :

$x_{jim} = 1$ if job $j$ is processed before job $i$ on machine $m$.

$b_{jm}$ :

$b_{jm}=1$ if job $j$ is processed before preventive maintenance on machine $m$.

The objective function (1) minimizes the sum of lost production and maintenance cost over the planning horizon.

$$\begin{aligned} \text{ min }&\sum _{k=1}^{K}\sum _{j \in {\mathcal {J}}_k} h_ku_j +\sum _{k=1}^{K} \sum _{m=1}^{M} \tau ^m_p y_{mk}&\end{aligned}$$

(1)

The problem is subject to maintenance planning and maintenance/production scheduling constraints which are defined below.

Maintenance planning constraints Since in any time period, there is a limit on the number of machines that can be maintained denoted as $\mathcal {C}$, Constraints (2) enforce the maintenance capacity limit in each time period.

$$\begin{aligned}&\sum _{m=1}^{M} y_{mk} \le \mathcal {C},&\qquad \qquad \quad \forall k \end{aligned}$$

(2)

Maintenance/production scheduling constraints The detailed descriptions of the maintenance/production scheduling constraints in period $k$ are provided below:

• In Constraints (3), $N_m(k)$ defines the state of machine $m$ at time period $k$ before performing maintenance. Defining the dummy variable $y_{m0}=1$ and the indicator function $I(x)$ being equal to 1 if $x$ is true and to 0 otherwise, we have (i) if machine $m$ is not maintained in any of the previous periods, $I(\max \{l|y_{ml}=1, 0 \le l < k\}=0)$ equals 1 and machine $m$’s state is $k-1+\alpha _m$, or (ii) if the most recent maintenance on machine $m$ is in period $l >0$, $I(\max \{l|y_{ml}=1, 0 \le l < k\}>0)$ is equal to 1 and machine $m$ is in state $k-l$.

  $$\begin{aligned} N_m(k)&=(k-1+\alpha _m)&\nonumber \\&\quad \times I(\max \{l|y_{ml}=1, 0 \le l < k\}=0)&\nonumber \\&\quad + (k-\max \{l|y_{ml}=1, 0 \le l < k\})&\nonumber \\&\quad \times I(\max \{l|y_{ml}=1, 0 \le l < k\}>0), \forall m&\end{aligned}$$

  (3)

• Constraints (4) denote the processing times of jobs in time period $k$. If job $j$ is scheduled before maintenance on machine $m$ ($b_{jm}=1$), the state of the machine is $N_m(k)$ and if scheduled after maintenance, the machine is in state 0.

  $$\begin{aligned}&p_{jm}= \frac{n_{jm}}{\nu ^m_{N_m(k)}}b_{jm}+\frac{n_{jm}}{\nu ^m_0}(1-b_{jm}) ,\forall j \in \mathcal {J}_k,\forall m&\end{aligned}$$

  (4)

• Constraints (5) enforce the precedence constraints: the job should be finished on an upstream machine before its processing starts on downstream machines.

  $$\begin{aligned}&st_{jm} + p_{jm} \le st_{j(m+1)}, \forall j \in \mathcal {J}_k, ~\forall m~(m \ne M)&\end{aligned}$$

  (5)

• Constraints (6) ensure that maintenance activities on machines requiring maintenance at time period $k$ ($y_{mk}=1$) are scheduled within the length of the time period where $\mathcal {B}$ is a big value.

  $$\begin{aligned}&st_{pm} + t^m_p + \mathcal {B}(y_{mk}-1) \le T, ~\forall m&\end{aligned}$$

  (6)

• Constraints (7), (8), and (9) define the relationships between the binary decision variables $b_{jm}$ and the maintenance decisions. Respectively, the constraints guarantee that if a job is processed before maintenance ($b_{jm}=1$), then its processing is finished before maintenance is started; if a job is processed after maintenance ($b_{jm}=0$), then maintenance is performed before processing the job is started; if a machine does not require maintenance ($y_{mk}=0$), all jobs are processed before maintenance ($b_{jm}=1$).

  $$\begin{aligned}&st_{jm} + p_{jm} \le st_{pm} + \mathcal {B}(1-b_{jm}), \forall j \in \mathcal {J}_k, ~\forall m&\end{aligned}$$

  (7)
  $$\begin{aligned}&st_{pm} + t^m_p \le st_{jm} + \mathcal {B} b_{jm}, ~\forall j \in \mathcal {J}_k, ~\forall m&\end{aligned}$$

  (8)
  $$\begin{aligned}&1-b_{jm} \le y_{mk}, ~\forall j \in \mathcal {J}_k, ~\forall m&\end{aligned}$$

  (9)

• Since $M$ is the last machine, Constraints (10) define whether job $j$ in time period $k$ is lost or not. If a job is not finished before or at its due date, it is then lost.

  $$\begin{aligned}&st_{jM}+p_{jM} \le d_j + \mathcal {B}u_j, ~ \forall j \in \mathcal {J}_k&\end{aligned}$$

  (10)

• Constraints (11) and (12) are disjunctive constraints ensuring that all jobs on a machine form a total ordering, meaning that no two jobs execute at the same time.

  $$\begin{aligned} st_{jm} + p_{jm}&\le st_{im} + \mathcal {B}(1-x_{jim}), \forall j,i \in \mathcal {J}_k~ (j>i), \nonumber \\&\qquad \qquad \qquad \qquad \forall m \end{aligned}$$

  (11)
  $$\begin{aligned} st_{im} + p_{im}&\le st_{jm} + \mathcal {B}x_{jim}, \forall j,i \in \mathcal {J}_k ~ (j>i), \nonumber \\&\qquad \qquad \qquad \qquad \forall m \end{aligned}$$

  (12)

Since the number of production jobs is only known for the next $L$ periods, we use a rolling horizon approach to make the decisions at the beginning of each period. Without loss of generality, the current period is considered as the first period and the future periods where the number of production jobs is known are numbered from 2 to $L$. Defining maintenance assignment decisions as $Y=\{y_{mk}|\forall m, ~ \forall k\}$ and the scheduling decisions as $S=\{st_{jm}|j \in \mathcal {J}_k,~\forall m,~\forall k\}$, the optimization problem for making the current time period decisions is shown in Model 1. The schedule is executed for the current time period; the decision horizon is then extended, and the same procedure repeats until the end of the planning horizon.

The optimization problem in Model 1 is a non-linear mixed integer programming model since Constraints (3), defining the state of machines at each period, and Constraints (4), denoting the processing times of the jobs, are non-linear.

Fig. 1

The schematic representation of the logic-based Benders decomposition approach

5 Solution approaches

To solve the optimization problem (Model 1) at the beginning of each period, we design a two-stage decomposed but coupled approach, Integrated, where each stage is modeled as a mixed integer linear program (MILP).

In this section, the Integrated approach and three alternative approaches, Non-integrated, Short-term, and Heuristic are presented.

5.1 The Integrated approach

There are two different decisions in the problem: (i) assigning maintenance to machines and time periods and (ii) scheduling the production jobs and maintenance activities, if any, in each period. Therefore, similar to a logic-based Benders decomposition (LBBD), the global problem (Model 1) can be decomposed into a maintenance planning problem (MPP) and $L$ production scheduling problems (PSP). The MPP is the master problem assigning maintenance to machines and time periods and each PSP defines one sub-problem, finding the schedule of a period. However, solving the problem using the logic-based Benders decomposition framework is computationally expensive, though both MPP and PSPs are mixed integer linear models (see Sect. 7.1). Therefore, as illustrated in Figs. 1 and 2, we adjust the LBBD such that only one PSP problem is solved at each iteration.

Fig. 2

The schematic representation of the Integrated approach

In the Integrated algorithm, the MPP is solved in the first stage to determine the assignment of maintenance to machines and time periods, minimizing the sum of maintenance and lost production costs over the $L$ time periods where the production jobs are known. In the MPP, the PSPs and the production capacity are relaxed, discarding the scheduling combinatorics. Therefore, the lost production cost in the first stage is a lower bound on the actual lost production cost.

The PSP in the second stage creates a production and maintenance schedule for the first period, minimizing the actual lost production cost of the first period given the maintenance plan specified by the MPP. If the achieved lost production cost is equal to the lower bound computed on the lost cost of the first period in the MPP, the computed schedule is executed. Otherwise, a constraint expressing a new bound on the lost production cost of the first period, called a cut, is added to the MPP and the MPP is re-solved. The iteration between MPP and PSP continues until the lower bound on the lost production cost of the first period in the MPP is equal to the cost calculated in the PSP. The finite convergence of the Integrated approach is demonstrated below in Sect. 5.1.3.

The decision horizon then rolls over one time period, the initial state of each machine ($\alpha _m$) is updated, the customer orders become known for time period $L+1$, and the solution procedure repeats.

In the balance of this section, we present our optimization models for both MPP and PSP, the cut, and the relaxation of the PSPs in the MPP. We have proved a number of structural properties about the PSP but our early experimentation showed that none of them had significant impact on the performance of the solver (Aramon Bajestani and Beck 2012).

5.1.1 The maintenance planning problem (MPP)

To model the MPP as a MILP, we change the maintenance binary decision variable from $y_{mk}$ to $y^m_{lk}$ that equals 1 if machine $m$ at time period $k$ is most recently maintained in time period $l$ where $l \le k$. We further define the new variable $\varLambda _k$ as the lost cost decision variable of time period $k$. To abstract production scheduling problems in the MPP and to find a lower bound on the lost cost decision variables, we assume that maintenance is performed at the beginning of the period with negligible time and define the following notation where 0 is a dummy period. Let $N^m_{lk}$ denote the state of machine $m$ in period $k$ after performing the most recent maintenance in period $l$.

$$\begin{aligned} N^m_{lk}= \left\{ \begin{array}{llll} 0 &{}\quad k=l\\ k-1+\alpha _m &{}\quad k>l,~l=0 \\ k-l &{}\quad k>l,~l>0 \end{array} \right. \end{aligned}$$

To explain the notation defined above, we distinguish three cases:

• 1. $k=l$: Machine $m$ is maintained at period $k$, i.e., $y^m_{kk}=1$. Maintenance makes machine $m$ as good as new, setting its state to the best value, $0$.

• 2. $k>l,~l=0$: Machine $m$ at time period $k$ has not been maintained in any of the previous periods, i.e., $y^m_{0k}=1$. Machine $m$’s state is equal to $k-1+\alpha _m$.

• 3. $k>l,~l>0$: Machine $m$ at time period $k$ is previously maintained at time period $l,~l>0$, i.e., $y^m_{lk}=1$. Machine $m$ is then at state $k-l$.

The MILP model for MPP in the first time period is shown in Model 2.

The MPP objective function (13) minimizes the total cost composed of the lower bound on the lost cost of $L$ periods and maintenance cost. Constraints (14) and (15) ensure the feasibility of the maintenance plan where the former defines the previous maintenance period on machine $m$ at time period $k$ and the latter guarantees that if time period $l,~l<k$, is the previous maintenance period on machine $m$ before the $k$-th period, then $l$ is also the previous maintenance period before period $k-1$. Constraints (16) enforce the maintenance capacity limit in each time period. Constraints (17) are the relaxations of PSPs, calculating the lower bound on the lost cost at period $k$ where $|\mathcal {J}_k|$ is the number of production jobs at time period $k$. In a flowshop system, the upper bound on total number of products produced is equal to the minimum number of products produced over all machines. The upper bound on the number of finished jobs on machine $m$ given that it was last maintained in period $l$, i.e., $y^m_{lk}=1$, equals $\frac{\nu ^m_{N^m_{lk}} \times T}{\underset{j \in \mathcal {J}_k}{\min }(n_{jm})}$ where the numerator is the upper bound on the total available processing time and the denominator is the minimum processing time required by a job on machine $m$ in period $k$. The cuts are explained in Sect. 5.1.3.

The non-linear Constraints (17) are replaced by the following two constraints where $\delta _k$ is a dummy decision variable.

$$\begin{aligned}&\varLambda _k \ge h_k (|\mathcal {J}_k| - \delta _k),&\forall k \in \{1,\ldots ,L\} \\&\delta _k \le \sum _{l=0}^k \frac{\nu ^m_{N^m_{lk}} \times T}{\underset{j \in \mathcal {J}_{k}}{\min }(n_{jm})} y^m_{lk},&\forall m, ~\forall k \in \{1,\ldots ,L\} \end{aligned}$$

5.1.2 The production scheduling problem (PSP)

After the maintenance assignment decisions denoted as $y^{mh}_{lk}$ are found by the MPP in iteration $h$, the states of machines are known. The PSP model for finding the optimal maintenance and production schedule in the first time period for a given maintenance plan by the MPP is shown in Model 3 where in Constraints (4) to (12): (i) $k$ equals 1; (ii) $y_{m1}$ changes to $y^{mh}_{11}$; and (iii) $N_m(1)$ equals $\alpha _m$ denoting the state of machine $m$ before performing maintenance at the first period.

If we relax the PSP by assuming there is no deterioration and that $|M| = 2$, then the PSP problem corresponds to a two-machine flowshop with the objective of minimizing the number of tardy jobs, an NP-complete problem (Lenstra et al. 1977).

Fig. 3

The optimal schedules

5.1.3 The MPP cuts

As noted above, the MPP and PSP are iteratively solved with each optimal MPP solution defining a PSP and each PSP returning cuts if the lost production cost of the first period from the MPP cannot be achieved. Assume that in iteration $h$, the first period lost production cost in the MPP is less than the optimal lost production cost in the PSP, represented as $\varLambda _1^h$. The cut after iteration $h$ is

$$\begin{aligned}&\varLambda _1 \ge \varLambda _1^h \left( 1 - \sum _{m \in Q^h} (1-y^m_{11}) - \sum _{m \notin Q^h} y^m_{11}\right) \end{aligned}$$

(18)

where $Q^h=\{m| y^{mh}_{11}=1\}$ denotes the set of machines requiring maintenance in iteration $h$ found in the MPP.

The cut is a no-good cut guaranteeing that if the same set of machines are maintained ($m \in Q^h$) and the same set of machines are not maintained ($m \notin Q^h$) in the current first period, the lost production cost of the first period in the MPP ($\varLambda _1$) should be greater than or equal to $\varLambda _1^h$. As the MPP and the PSP find, respectively, a lower bound and an upper bound on the lost production cost of the first period in each iteration, iterating between stages terminates when the bounds are equal. Furthermore, the finite number of possible maintenance plans guarantees the finite convergence of the Integrated approach.

Changing the cut to $\varLambda _1 \ge \varLambda _1^h (1 - \sum _{m \notin Q^h} y^m_{11})$ would make it stronger, but is unsound due to the non-monotonic behavior of $Q^h$: depending on the problem, maintaining a subset of $Q^h$ can decrease or increase the lost production cost making the stronger cut invalid (see Example 1 below). The stronger cut is not valid unless we make further assumptions. For example, if we assume that the maintenance duration of all machines is less than the increase in the processing times of all jobs, then maintaining fewer machines never decreases the lost production cost, making the stronger cut valid. However, we do not make such an assumption here.

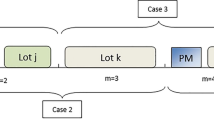
Example 1

A facility with 3 machines (M1, M2, M3) and 2 production jobs (J1, J2) is considered where the length of the time period is 40, the due dates of production jobs are 24 and 35, the processing time of each production job on each of three machines is 10 and decreases to 5 if scheduled after maintenance. The durations of maintenance activities on machines (P1, P2, P3) are 30, 5, and 15, respectively.

Assuming that the MPP at iteration $h$ decides to maintain machines 1, 2, and 3 ($Q^h=\{1,2,3\}$), the optimal schedule is shown in Fig. 3 where the number of on-time jobs is one. If the subset $\{1,2\}$ is maintained in the next iteration, none of the jobs is then on-time, increasing the lost production cost. However, maintaining the subset $\{2,3\}$ makes both jobs on-time decreasing the lost production cost.

5.1.4 Relaxation of the PSP in the MPP

As noted, Constraints are the relaxation of the PSPs in the MPP, expressing a lower bound on the lost production cost. We tighten the lower bound for the first time period by applying Moore’s algorithm on the last machine. Moore’s algorithm finds the optimal number of tardy jobs in a single-machine problem when all jobs are ready at time 0 with the computational complexity of $O(n\log n)$ (Pinedo 2002).

The last machine is considered as a single-machine where the due dates of the production jobs are changed to $d^{\prime }_j=d_j-\varDelta$ since all are not available at time 0. $\varDelta$ corresponds to the sum of the minimum processing times of the jobs on the upstream machines denoted as $\sum _{m=1}^{M-1} \underset{j \in \mathcal {J}_1}{\min } (n_{jm})$. Since $\varDelta$ is calculated assuming that all previous machines are processing at their best states and that there is no precedence constraint, then the following constraint, added to the MPP, is a lower bound on the lost production cost of the first time period.

$$\begin{aligned}&\varLambda _1 \ge h_1U^1y^M_{11} + h_1U^0y^M_{01}&\end{aligned}$$

(19)

$U^1$ and $U^0$ represent the value of Moore’s algorithm when the last machine is maintained and is not, respectively. Similarly, the processing times of the jobs on the last machine are $n_{jM}$ or $\frac{n_{jM}}{\nu ^M_{\alpha _M}}$ in Moore’s algorithm. Note that, Moore’s algorithm to find $U^1$ and $U^0$ is just applied before starting to iterate. We use both relaxations, i.e., Constraints and (19), in our model.

5.2 The Non-integrated approach

The Non-integrated approach (Fig. 4) is the standard hierarchical decision-making procedure where there is no iteration between the MPP and PSP. The MPP (Model 2) solves the maintenance planning problem over $L$ periods minimizing the sum of maintenance and a lower bound on the lost production costs. The PSP (Model 3) then finds the optimal lost production cost for the current time period given the maintenance activities specified by the MPP. The schedule is executed, the decision horizon then rolls over one time period updating the machine states ($\alpha _m$), and the same procedure repeats.

Fig. 4

The schematic representation of the Non-integrated approach

Fig. 5

The schematic representation of the Short-term approach

5.3 The Short-term approach

The Short-term approach has a reasoning horizon of one time period (Fig. 5) considering maintenance as a short-term decision. The maintenance and production scheduling problem (MPSP) determines machines for maintenance and finds the optimal schedule, minimizing the sum of maintenance and lost production costs simultaneously. The computed schedule is then executed, the machine states ($\alpha _m)$ are updated, and the same procedure repeats for the next time period.

The MPSP model for the first period is shown in Model 4, where $k=1$ and $N_m(1)=\alpha _m$ in Constraints (2) and Constraints (4) to (12).

5.4 Heuristic approaches

We investigate two heuristic approaches for the PSP and the MPSP models inspired by Moore’s algorithm.

5.4.1 A heuristic for the PSP

In the heuristic algorithm, the maintenance activities are performed first on machines that have to be maintained, i.e., $\forall m \in Q^1$. $Q^1$ is the set of machines determined for maintenance in the first iteration of the MPP. Moore’s algorithm is then applied on the last machine, $M$, as explained in Sect. 5.1.4 where

$$\begin{aligned}&\varDelta = \sum _{\begin{array}{c} m \in Q^1 \\ m \ne M \end{array}} \left( t^m_p+\underset{j \in \mathcal {J}_1}{\min } (n_{jm})\right) + \sum _{\begin{array}{c} m \notin Q^1 \\ m \ne M \end{array}} \underset{j \in \mathcal {J}_1}{\min }\left( \frac{n_{jm}}{\nu ^m_{\alpha _m}}\right)&\\&d^{\prime }_j= \left\{ \begin{array}{llll} d_j - (\varDelta +t^M_p) &{}\quad \text{ if } M \in Q^1 \\ d_j -\varDelta &{}\quad \text{ if } M \notin Q^1 \end{array} \right. \end{aligned}$$

The sequence found by Moore’s algorithm is used to schedule the jobs on all machines.

5.4.2 A heuristic for the MPSP

The heuristic is the same as one for the PSP with the only difference that the decision on which machines require maintenance is also incorporated. Machines are ordered in increasing order of their indices and the first $\mathcal {C}$ machines in an initial state greater than or equal to $\frac{\mathcal {S}_m}{2}$ are maintained. Recall that $\mathcal {S}_m$ is the worst state of machine $m$. The maintained machines then form set $Q^1$ and the Heuristic for the PSP is applied to find a feasible schedule.

6 Computational study

The next sub-section describes the problem instances and the experimental details. We then compare the performance of the solution approaches experimentally and present insights into each algorithm’s performance through a deeper analysis of the results.

6.1 Experimental setup

The problem instances have $M \in \{3, 4, 5, 6\}$ machines and $|\mathcal {J}| \in \{5, 10, 15\}$ jobs in each time period. Note that in our experimental study, the number of jobs at each time period is equal, i.e., $|\mathcal {J}_k|=|\mathcal {J}|$ in a given instance. Twenty instances for each combination of parameters are generated, resulting in 240 instances.

Machines Each machine has five states and is randomly assigned to one of the deterioration processes shown in Table 1. The deterioration process is classified into three categories of slow, medium, or fast, defining the speed of the machine in different states. The initial state of each machine, $\alpha _m$, is drawn from the discrete uniform distribution $[0,3]$ assuming that no machine is in the worst state at the beginning of the planning horizon. The maintenance cost for each machine, $\tau _p^m$, is generated from the discrete uniform distribution $[50, 100]$.

Table 1 The speed of a machine at each state in different deterioration processes

Time periods The length of time period, $T$, is set at 79, 152, and 224 in instances with 5, 10, and 15 jobs, respectively. As with the maintenance cost, the lost production cost per each job at time period $k$, $h_k$, is generated from the discrete uniform distribution $[50, 100]$. The maintenance capacity at each time period, $\mathcal {C}$, is equal to $\lfloor \frac{M}{2}\rfloor$.

Production jobs To generate the processing times of the jobs at the best state of machines, i.e., $n_{jm}$, we assume that they are uniformly distributed with mean $\mu$ and variance $\sigma ^2$. Further we assume that $\nu _a$ denotes the average speed of a machine. The average processing time of a job on a machine regardless of its state is then uniformly distributed with mean $\frac{\mu }{\nu _a}$ and variance $\frac{\sigma ^2}{\nu _a^2}$. The sum of the average processing times of all jobs has an approximately normal distribution with mean $|J| \times \frac{\mu }{\nu _a}$ and variance $|J| \times \frac{\sigma ^2}{\nu _a^2}$. Setting $\nu _a=0.5$, $\mu$ and $\sigma ^2$ are found such that the probability that the sum of the average processing times of all jobs is less than eighty percent of the length of the time period equals 0.75. In our experiment, $\mu$ and $\sigma ^2$ equal 5.5 and 6.75 in all instances and the length of the time periods are set based on the number of jobs, as described above. $n_{jm}$ is then drawn from the discrete uniform distribution $[1, 10]$. The due date of job $j$ is generated from the discrete uniform distribution $[f^d \times \sum _{m=1}^M n_{jm}, \max (T,f^d \times \sum _{m=1}^M n_{jm})]$, where $f^d = 1.5$ and $T$ is the length of each time period.

Maintenance Activities The maintenance duration on machine $m$, $t_p^m$, is drawn from the discrete uniform distribution $[0.05 \times T, 0.15 \times T]$.

There are $K=24$ time periods in the planning horizon where the number of production jobs are always known for the next $L=4$ periods. The CPU time limit to find the maintenance and production schedule at each time period is 900 s. As noted above, the length of the time periods varies between 79, 152, and 224 time units. Since it is not uncommon in practice to have one time unit correspond to 10 or 15 minutes, the CPU time limit being less than 2 % of the length of the time period is compatible with the on-line execution requirement. We execute the best feasible maintenance and production schedule found by the time-limit if an algorithm times out. In the case that no feasible solution is found before the time limit, the schedule found by a heuristic is executed: Heuristic for the PSP is executed when the PSP times out and Heuristic for the MPSP is executed when the MPSP times out.

All experiments were run on an AMD 270 CPU with 1 MB cache per core, 4 GB of main memory, running Red Hat Enterprise Linux 4. The MILP solver is CPLEX 12.3.

6.2 Computational results

In this section, we discuss our results to compare the performance of different algorithms on the total cost of maintenance and lost production. The total cost is calculated over the first 21 time periods to reduce end-of-horizon effects. The algorithms are Integrated, Non-integrated, Short-term, and Heuristic. The Heuristic algorithm refers to the Heuristic for the MPSP defined in Sect. 5.4.2.

Figure 6 shows the mean and the standard error of the normalized total cost for different algorithms and different number of jobs. The number of jobs is 5, 10, and 15, each representing a different problem set with 80 instances. The total cost of each instance for each algorithm is normalized by dividing to the total cost achieved using the Heuristic algorithm. The graph shows a lower mean and standard error for the Integrated approach for all problem sets, indicating its superiority over the other three approaches. Table 2 presents further data for each algorithm and each problem set: the mean and the standard error of the normalized total cost, the number of instances for which the best known solution is found, and the number of timed-out instances. An instance is counted as a timed-out if it reaches the time limit without finding the optimal solution in at least one time period.

Fig. 6

The mean and the standard error of the normalized total cost for different algorithms and different number of jobs

Table 2 The mean and the standard error (se) of the normalized total cost, the number of instances for which the best known solution is found (best), and the number of timed-out instances for different algorithms

Integrated vs. Non-integrated The Integrated approach outperforms the Non-integrated, achieving a lower normalized total cost and finding the best known solutions on 99 % of the instances.

Integrated vs. Short-term The Integrated algorithm results in a lower normalized total cost on 73 % of the problem instances and a higher value on 27 %. A closer look to the results shows that for 89 % of the instances where Short-term outperforms Integrated, both algorithms time out. If the Integrated approach times out, it executes the best feasible schedule found for that time period. Therefore, the comparison between the performance of the algorithms reduces to comparison between different heuristics.

Integrated vs. Heuristic Although the Heuristic approach is fast, the Integrated algorithm has a significant superiority over it, decreasing the mean normalized cost by 42 % and resulting in a lower normalized total cost for all problem instances.

7 Discussion

The results in Table 2 provide evidence that solving the production scheduling problem (PSP) of each period to optimality can improve the performance of the Integrated approach. As shown in Table 2, the PSP in the Integrated approach times out at least in one time period in all instances having 15 jobs and in instances with 10 jobs and 6 machines. The existing literature on the flowshop scheduling problem with the objective of minimizing the number of tardy jobs (Gupta and Stafford 2006; Shabtay 2012) can be investigated in the future to tighten the relaxation of the PSP in the maintenance planning problem, to design a stronger cut, and to develop more efficient dominance properties in order to decrease the run-time of the PSP.

Furthermore, the results in Table 2 show that the Integrated, the Non-integrated, and the Short-term approaches outperform the Heuristic approach though they are computationally more expensive and their implementation requires investment in data analysis and software development. However, since the maintenance cost of the cluster tools in the semiconductor manufacturing has the largest share in the total cost, i.e., 80 % of $2.5 billion (Ramíez-Hernández and Fernández-Gaucherand 2003; Blau 2003), the capital cost in software development will trade off with savings that will be achieved by considering the process interdependencies in planning and scheduling maintenance operations.

A more detailed analysis of our experimental results suggest that the superiority of the Integrated over the Non-integrated and the Short-term decreases as the maintenance becomes more expensive and more inexpensive, respectively.

In both Integrated and Non-integrated algorithms, the maintenance decision is made primarily based on long-term reasoning and both decide to do the same amount of maintenance over the MPP horizon. However, having the same number of maintenance jobs does not mean that the two approaches find the same schedule. In particular, recall that the iterations of the Integrated approach result in the total lost production cost over the MPP horizon being composed of the actual lost production cost in the first period plus a lower bound from the later periods. This asymmetry results in the Integrated approach preferring to schedule its maintenance in the first period because that leads to reduced lost production cost. The outcome therefore is that Integrated adopts a schedule which is less expensive than Non-integrated but which tends to schedule its maintenance in the first period. When maintenance cost is high, the bias to perform maintenance earlier in each MPP horizon tends to result in more frequent maintenance over the planning horizon. Therefore, a higher maintenance cost over the 21 time periods results in a higher total cost since the savings on the lost production costs is insignificant compared to the maintenance cost. Adjusting the Integrated approach to have a symmetric view over all periods such that the total lost production cost consists of the actual lost costs of all periods in the MPP horizon is likely to remove the bias of the Integrated approach (see Sect. 7.1).

Turning to the comparison of Integrated and Short-term, the primary difference is the long-term maintenance reasoning done by the former. A limitation of the Integrated compared to the Short-term is likely to arise when maintenance is inexpensive. If maintenance costs less than failing to satisfy a customer order, then it is almost always best to do more maintenance. Furthermore, the Short-term approach will be able to find such solutions because maximizing maintenance is worthwhile both in the long and short runs.

To verify our interpretations, we define $\rho =\frac{\tau ^m_p}{h_k}$ as the ratio of maintenance cost to lost production cost and use the 240 problem instances as defined in Sect. 6.1 running two other experiments with the modification that the maintenance cost of each machine is multiplied by 0.5 and 1.5, respectively: $0.5 \le \rho \le 2$ in the first experiment is changed to $0.25 \le \rho \le 1$ and $0.75 \le \rho \le 3$. Figure 7 illustrates the mean and the standard error of normalized total cost for different algorithms and different $\rho$ values over all 240 problem instances.

Fig. 7

The mean and the standard error of the normalized total cost for different algorithms and different $\rho$ values

Table 3 shows the difference between the means of normalized total costs for different algorithms. As the $\rho$ values increase, i.e., performing maintenance becomes more expensive, the difference between the Non-integrated and the Integrated approaches decreases while the difference between the Short-term and the Integrated increases, supporting our interpretations.

Table 3 The difference between the means of normalized total costs for different algorithms and different $\rho$ values

7.1 The Extended Integrated approach

As already discussed, the Integrated approach has an asymmetric view over the PSPs in the MPP horizon: because the MPP lost cost value in the current period converges to the actual lost cost but the same value is represented only by a lower bound in later periods, the Integrated approach has a bias to perform immediate maintenance. The lost cost is essentially more expensive in the current period than in subsequent periods. Adjusting the Integrated approach to represent the actual lost production cost from all periods will remove this bias while also allowing the MPP to reason with more accurate lost cost information.

We can therefore use the logic-based Benders decomposition representation of the problem shown in Fig. 1, called the Extended Integrated approach. The extension is that for each MPP solution, a PSP for each period within the known horizon is solved to find the actual lost costs for each of the $L$ time periods. While this increases the number of PSPs, given a maintenance plan, each PSP is independent and they can be solved in parallel with multiple processors.

While the Extended Integrated approach is actually a standard logic-based Benders decomposition, the approach has two critical weaknesses in our context.

• 1. Observe that the lost production cost of time period $k$ is dependent on both the set of maintained machines in period $k$ and the machine speeds, and therefore the machine conditions, at the beginning of the period. While the $L$ PSPs can be solved independently, a cut for a time period $k, ~k > 1$, cannot simply refer to the maintenance decisions in period $k$. In a subsequent iteration, a change in maintenance decisions in an earlier period would change the machine conditions at the beginning of period $k$ and, therefore, would change the lost cost impact of the maintenance decisions in period $k$. A cut that only includes the maintenance decisions for time period $k$ is therefore invalid. In fact, a valid cut for period $k$ in the Extended Integrated approach must refer to the maintenance decisions for the first $k$ periods and provide a bound on the sum of the lost costs over the first $k$ periods. Formally, the cuts after iteration $h$ are:

  $$\begin{aligned} \sum _{i=1}^{k} \varLambda _i \ge&\left( \sum _{i=1}^{k}\varLambda _i^h\right) \left( 1- \sum _{i=1}^{k}\sum _{m \in Q^h_i} (1-y^m_{ii})\right. \nonumber \\&\left. - \sum _{i=1}^{k}\sum _{m \notin Q^h_i} y^m_{ii}\right) , \forall k \in \{1,\ldots ,L\} \end{aligned}$$

  (20)

  $Q^h_k$ indicates the set of machines maintained in period $k$ in iteration $h$. The iterations between the MPP and the PSPs continue until the total lost cost over $L$ time periods is equal to the one computed in the MPP.

• 2. At each iteration of the MPP, the PSPs return cuts until the convergence criterion is achieved. The maximum number of iterations therefore equals the maximum number of times that the PSPs might return cuts to the MPP. Since the cuts in the Integrated approach (Eq. 18) involve only the lost production cost variable for the first period, the maximum number of iterations is $\sum _{i=0}^{\mathcal {C}} \left( {\begin{array}{c}M\\ i\end{array}}\right)$, enumerating all possible ways of assigning maintenance to $i$ machines and the first period considering the maintenance capacity limit of $C$. However, the cuts in the Extended Integrated approach (Eq. 20) involve the lost production cost variables for all $L$ periods. The maximum number of iterations consequently increases to $(\sum _{i=0}^{\mathcal {C}} \left( {\begin{array}{c}M\\ i\end{array}}\right) )^L$. The Extended Integrated approach will then be expected to have an extremely high computational expense not because of the linear increase in the number of PSPs in each MPP iteration (i.e., solving $L-1$ more PSPs), but because of the exponential increase in the number of iterations.

These weaknesses make the Extended Integrated model unlikely to be successful. To confirm this analysis, we ran it on the 240 problem instances of Sect. 6.1 where $0.5 \le \rho \le 2$ and where the CPU time limit is 900 s for each period. As expected, it times out on 198 problem instances and the mean of the normalized total cost over all instances marginally increases to 0.59 compared to 0.58 for the Integrated approach in Table 2.

7.2 Job-dependent lost production cost

Although in the Integrated approach we assume that the lost production cost, $h_k$, is only dependent on the time period, our solution approach can be adapted for a problem where the lost production cost is dependent on both the time period and the job, i.e., $h_{kj}$. To calculate a lower bound on the lost cost of all periods, we replace $h_k$ in Eq. with $\min _{j \in \mathcal {J}_k}(h_{kj})$. Similar to Sect. 5.1.4, to tighten the lower bound on the first period, we consider the last machine as a single-machine where the due dates of jobs are changed to $d^{\prime }_j=d_j-\varDelta$, but we use a dynamic programming to minimize the weighted number of tardy jobs on the last machine (Pinedo 2002; Cai and Vairaktarakis 2012). Constraint (19) is therefore replaced with

$$\begin{aligned}&\varLambda _1 \ge \bar{U}^1y^M_{11} + \bar{U}^0y^M_{01},&\end{aligned}$$

(21)

where $\bar{U}^1$ and $\bar{U}^0$ are the optimal values of dynamic programming when the last machine is maintained and is not, respectively. Similarly, the processing times of the jobs on the last machine are $p_{jM}=n_{jM}$ or $p_{jM}=\frac{n_{jM}}{\nu ^M_{\alpha _M}}$ in dynamic programming. To calculate $\bar{U}^1$ or $\bar{U}^0$, we first assume the jobs are indexed in Earliest Due Date (EDD) order and let $F_j(t)$ be the minimum weighted number of tardy jobs for the first $j$ jobs such that the processing time of the on-time jobs is at most $t$. Defining the initial conditions as:

$$\begin{aligned} F_j(t)= \left\{ \begin{array}{llll} \infty &{}\quad \text{ for } t<0, ~ j=1, 2, \ldots , |\mathcal {J}_1| \\ 0 &{}\quad \text{ for } t \ge 0, ~ j=0 \end{array} \right. , \end{aligned}$$

we use the following recursive equations for $j=1, \ldots , |\mathcal {J}_1|$ and $T=\sum _{j=1}^{|\mathcal {J}_1|} p_{jM}$.

$$\begin{aligned}&F_j(t)\\&\quad = \left\{ \begin{array}{llll} \min \{F_{j-1}(t-p_{jM}), F_{j-1}(t)+h_{j1}\} &{}\quad 0 \le t \le d_j &{}\\ F_j(d_j) &{}\quad d_j < t \le T \end{array} \right. . \end{aligned}$$

The optimal weighted number of tardy jobs is then $F_{|\mathcal {J}_1|}(d_{|\mathcal {J}_1|})$. The dynamic programming algorithm is pseudopolynomial with the computational complexity of $O(|\mathcal {J}_1|T)$ (Pinedo 2002).

To investigate the performance of the algorithms with job-dependent lost production cost, we consider the 80 problem instance of Sect. 6.1 with $|\mathcal {J}| = 5$ jobs and generate the lost production cost of each job at each time period, $h_{jk}$, from the discrete uniform distribution $[50, 100]$. Our results on the 80 problem instances show that the Integrated approach decreases the total cost on average by 31 and 29 % compared with the Non-integrated when the lost costs are job-dependent and job-independent, respectively.¹ Therefore, the superiority of the Integrated approach is preserved with different lost production cost per job. However, when the lost production cost is job-dependent, we expect the lower bounds on the lost costs of the future periods are weaker than the lower bounds with job-independent lost cost. As a result, the tendency of the Integrated approach to perform more frequent maintenance is likely to increases due to the asymmetrical representation of the lost costs of the PSPs in the MPP horizon and the superiority of the Integrated over the Non-integrated decreases more as the maintenance cost becomes more expensive.

8 Conclusion and future work

In this paper, we address an integrated maintenance planning and production scheduling problem that arises in highly coupled processes such as wafer fab in the semiconductor manufacturing: a multi-machine production system where production capacity decreases as machines deteriorate and where each customer order has specific processing requirements and due date. At the beginning of each time period, two decisions are made: which machines are to be maintained, if any, and when each production and each maintenance activity should be executed in order to minimize the total maintenance and lost production costs over the planning horizon.

Our problem has two novel features: (i) a multi-machine scheduling problem is studied and (ii) maintenance concepts are modeled as they appear in the maintenance research literature: maintenance is considered as a long-term decision and there is an explicit model representing the effect of machine deterioration and restoration processes on processing times.

To precisely model the production capacity as a function of both machine states and scheduling combinatorics including due dates and workloads, we propose an integrated two-stage algorithm. In the first stage of the algorithm, maintenance planning is done over time periods where the customer orders are known. The production scheduling problem and production capacity are abstracted in the first stage and the objective is to find a maintenance plan for each machine, minimizing the sum of maintenance cost and a lower bound on lost production cost. The second stage then schedules maintenance and production activities in the current period, minimizing the actual lost production cost assuming the given maintenance plan. The iteration between two stages continues, with feedback, until the lower bound and the actual lost production cost of the current period converge.

The computational results demonstrate that the Integrated approach yields lower total cost than three other approaches tested: a Non-integrated approach, a Short-term, integrated approach, and a Heuristic approach. The benefit for Integrated decision making over Non-integrated, furthermore, increases for lower maintenance cost relative to lost production cost. Finally, the benefit of long-term decision making in the Integrated approach over a myopic, Short-term approach increases with higher relative maintenance cost. These observations suggest that at extreme low or high relative maintenance cost, Short-term and Non-Integrated approaches should be adopted. However, for a broad range of intermediate relative costs, Integrated provides superior quality solutions.

Our investigation of the integrated maintenance planning and scheduling for long horizon and multi-machine problems opens substantial scope for future work. In particular, the investigation of real world maintenance planning and scheduling problems is likely to inspire a variety of problem definitions, formulations, and solution approaches that may be complementary to and improve upon the work presented here. The most interesting extension is to model problem characteristics such as customer orders, machine state, and the effect of maintenance on machine state as stochastic variables, requiring a combination of tools from stochastic maintenance planning (Sloan 2004, 2008; Nicolai and Dekker 2008) and stochastic scheduling (Cai et al. 2003, 2004; Beck and Wilson 2007). For work in this direction, see Aramon Bajestani et al. (Aramon Bajestani et al. 2014).