1 Introduction

Polar forms are one of the most powerful methods for developing the theory of Bézier and B-spline curves and surfaces not only in polynomial and piecewise polynomial spaces [24] but also in non polynomial and non piecewise polynomial spaces such as Q-splines [14], exponential splines [12], hyperbolic splines [15], trigonometric splines [16] and Chebyshev splines [23].

Classical polar forms satisfy three axioms; symmetry, multi-affinity, and a simple diagonal property. Replacing the standard multi-affine property of polar forms by the trigonometric multi-barycentric property defines polar forms for trigonometric polynomials [11]. This trigonometric multi-barycentric property can be used to develop circular analogues of Bernstein Bézier polynomials [2] and trigonometric B-splines [16]. The geometric properties of trigonometric splines can be investigated by introducing control curves [13]. The same class of trigonometric spaces can also be investigated by means of control polygons instead of control curves [18]. Using this approach it can be shown that this class of trigonometric spaces has optimal shape preserving properties [18].

Chebyshev B-splines are investigated extensively in the literature [4, 19, 21–23]. Barry [4] uses an extension of the de Boor-Fix dual functionals to construct generalizations of algorithms for piecewise polynomial B-spline curves to Chebyshev B-spline curves. Algorithms for and shape preserving properties of the polynomial Bernstein–Bézier and B-spline bases can also be generalized to Chebyshev spaces by using the notion of polar forms; see, for example [19, 21–23] and references therein. The existence of polar forms guarantees the existence of Bernstein–Bézier and B-spline bases in Chebyshev spaces. For example, in [22], the existence of B-spline bases in 4-dimensional extended Chebyshev spaces is derived from the existence of polar forms constructed by intersecting appropriate osculating flats.

Conditions for the existence of B-splines for piecewise exponential spline spaces are given in [17] by studying null spaces of linear differential operators with constant coefficients and no complex roots. Since hyperbolic spaces are special cases of piecewise exponential spaces and exponential spaces are extended Chebyshev spaces (see [17]), polar forms for Chebyshev spaces can also be applied to exponential B-splines and hyperbolic B-splines. Polar forms for Q-splines and the corresponding non-affine subdivision algorithm are derived in [14] using pseudo Bézier points. For more information about these generalizations see [12, 14–16, 20, 21, 23] and references therein.

Polar forms for Chebyshev spaces have been constructed by replacing the multi-affine property by a pseudo-affine property (see [1, 20, 23]). These polar forms can be used to construct Bernstein Bézier bases for Chebyshev spaces and B-spline bases for Chebyshev splines. In contrast, in [8], we construct polar forms for non-polynomial Bernstein Bézier curves by keeping the multi-linear property and changing instead the diagonal property. The advantage of our approach is that the computations and proofs are still simple, since we retain the simple multi-linear property. By altering the diagonal property of the polar form for homogeneous polynomials, we developed a unified theory of Bézier curves for infinitely many diverse type of spaces, including trigonometric polynomials, hyperbolic polynomials and special Müntz spaces. In this paper, as a sequel to [8], we develop a unified theory of B-splines for the corresponding spline spaces.

This paper is organized in the following fashion. In Sect. 2, we review a variant of the homogeneous polar form where we alter the diagonal property. This variant will play a central role in our construction and analysis of spline spaces and B-spline basis functions. A variant of the local de Boor algorithm is presented in Sect. 3 and a global de Boor type algorithm is derived in Sect. 4 where we prove that B-splines of degree n with no multiple knots are \( C^{n-1} \) continuous. In Sect. 5 we show that every spline curve is a B-spline curve and we also analyse the effect of multiple knots on smoothness. Section 6 deals with knot insertion algorithms and a proof of the variation diminishing property. Finally in Sect. 7 we construct B-spline basis functions and study properties and identities for these basis functions such as the dual functional property, Marsden’s identity, partition of unity, curvilinear precision, interpolation, and differentiation.

2 Functional polar forms

We begin by reviewing the notion of homogeneous polar forms, which play a central role in our construction and analysis of B-splines.

Let \(\gamma _{1}\) and \(\gamma _{2}\) be two differentiable, locally linearly independent functions. By locally linearly independent we mean that there is an open interval \(I\subseteq supp(\gamma _{1})\cap supp(\gamma _{2})\) such that \(\gamma _{1}\) and \(\gamma _{2}\) are linearly independent on I. Set

$$\begin{aligned} \pi _{n}(\gamma _{1},\gamma _{2})=\text {span}\left\{ \gamma _{1}^{n-k}\gamma _{2}^{k}\right\} _{k=0}^{n}. \end{aligned}$$
(1)

Thus \(\pi _{n}(\gamma _{1},\gamma _{2})\) is the space of homogeneous polynomials of degree n in the functions \(\gamma _{1},\gamma _{2}.\)

Dişibüyük and Goldman [8] introduce the notion of a polar form for functions \(G \in \pi _{n}(\gamma _{1},\gamma _{2}).\) The homogeneous polar form or homogeneous blossom of G(x) is the unique symmetric, multi-linear function \(g((u_{1},w_{1}),\ldots , (u_{n},w_{n}))\) that reduces to G(x) along the \((\gamma _{1},\gamma _{2})\) diagonal. That is, \(g((u_{1},w_{1}),\ldots , (u_{n},w_{n}))\) is the unique function that satisfies the following three axioms:

  1. (a)

    Symmetry property: for every permutation \([\sigma _{1},\ldots ,\sigma _{n}]\) of \([1,\ldots ,n]\)

    $$\begin{aligned} g((u_{\sigma _{1}},w_{\sigma _{1}}),\ldots , (u_{\sigma _{n}},w_{\sigma _{n}}))=g((u_{1},w_{1}),\ldots , (u_{n},w_{n})) \end{aligned}$$
  2. (b)

    Multi-linear property: for \(i=1,\ldots ,n,\)

    $$\begin{aligned} g((u_{1}&,w_{1}), \ldots , a(u_{i},w_{i})+b(v_{i},y_{i}) ,\ldots , (u_{n},w_{n}))\\&=a g((u_{1},w_{1}),\ldots , (u_{i},w_{i}) ,\ldots , (u_{n},w_{n}))\\&\quad \,+b g((u_{1},w_{1}),\ldots , (v_{i},y_{i}) ,\ldots , (u_{n},w_{n})) \end{aligned}$$
  3. (c)

    Diagonal Property: g is equal to G on the \((\gamma _{1},\gamma _{2})\) diagonal i.e.

    $$\begin{aligned} g((\gamma _{1}(x),\gamma _{2}(x)),\ldots ,(\gamma _{1}(x),\gamma _{2}(x)))=G(x). \end{aligned}$$

The existence and uniqueness of this polar form are established in [8].

Consider the planar parametric curve \(\Gamma (t)=(\gamma _{1}(t),\gamma _{2}(t)), a\leqslant t\leqslant b.\) The barycentric coordinates of a point \(\Gamma (x)=(\gamma _{1}(x),\gamma _{2}(x)), a\leqslant x\leqslant b,\) on this curve relative to the end points of the arc of \(\Gamma (t)\) from \(\Gamma (a)=(\gamma _{1}(a),\gamma _{2}(a))\) to \(\Gamma (b)=(\gamma _{1}(b),\gamma _{2}(b))\) are the solutions \(\alpha (x,a,b),\,\beta (x,a,b)\) of the linear system

$$\begin{aligned} \alpha \gamma _{1}(a) + \beta \gamma _{1}(b)&= \gamma _{1}(x)\nonumber \\ \alpha \gamma _{2}(a) + \beta \gamma _{2}(b)&= \gamma _{2}(x). \end{aligned}$$
(2)

Solving these equations gives \(\alpha (x,a,b)=\frac{d(x,b)}{d(a,b)}\) and \(\beta (x,a,b)=\frac{d(a,x)}{d(a,b)},\) where \(d(u,v)=\gamma _{1}(u)\gamma _{2}(v)-\gamma _{2}(u)\gamma _{1}(v).\) Now the following multi-barycentric property is an immediate consequence of (2) and the multi-linear property of the polar form.

Multi-barycentric property:

Let g be the polar form of \(G\in \pi _{n}(\gamma _{1},\gamma _{2}).\) Then

$$\begin{aligned} g(\ldots ,(\gamma _{1}(x),\gamma _{2}(x)),\ldots )&=\frac{d(x,b)}{d(a,b)} g(\ldots ,(\gamma _{1}(a),\gamma _{2}(a)),\ldots )\nonumber \\&\quad +\frac{d(a,x)}{d(a,b)}g(\ldots ,(\gamma _{1}(b),\gamma _{2}(b)),\ldots ) \end{aligned}$$
(3)

Just like the homogeneous polar form for homogeneous polynomials in two variables, this homogeneous polar form can be used to compute the derivatives of functions \(G\in \pi _{n}(\gamma _{1},\gamma _{2}).\) Let g be the polar form of G. Then by the chain rule and the symmetry of the polar form, the first derivative of G(x) is given by [8]

$$\begin{aligned} G'(x)=ng((\gamma '_{1}(x),\gamma '_{2}(x)),(\gamma _{1}(x),\gamma _{2}(x)), \ldots , (\gamma _{1}(x),\gamma _{2}(x))) \end{aligned}$$
(4)

In order to compute the kth derivative of G(x) in terms of the polar form, we need to invoke the notion of integer partitions.

An integer partition of a positive integer k is a set of positive integers \(l=\{ l_{1},l_{2},\ldots ,l_{r} \}\) such that \(\sum _{i=1}^{r}l_{i}=k.\) For example, all the integer partitions of 4 are \(\{4\},\) \(\{3,1\},\) \(\{2,2\},\) \(\{2,1,1\}\) and \(\{1,1,1,1\}.\) For detailed information about integer partitions, see [3]. We denote the set of all the integer partitions of k by \(\lambda (k)\) and we denote the set of the integer partitions that have at most n elements by \(\lambda _{n}(k).\) For example,

$$\begin{aligned} \lambda (4)&= \{ \{4\}, \{3,1\}, \{2,2\}, \{2,1,1\}, \{1,1,1,1\} \}\\ \lambda _{2}(4)&= \{ \{4\}, \{3,1\}, \{2,2\} \},\\ \lambda _{3}(4)&= \{ \{4\}, \{3,1\}, \{2,2\}, \{2,1,1\} \}. \end{aligned}$$

Finally, let \(\delta (l)\) be the set of all permutations of the elements of l. Denote the number of elements of \(\delta (l)\) by \(|\delta (l)|\) and the number of elements of l by |l|. For example, for \(l=\{2,1,1\}\in \lambda (4),\) the set of permutations is \(\delta (\{2,1,1\})=\{\{2,1,1\}, \{1,2,1\} \{1,1,2\}\}.\) Hence we have \( |\delta (\{2,1,1\})|=3=|l|.\)

Let g be the polar form of \(G\in \pi _{n}(\gamma _{1},\gamma _{2}).\) To simplify our notation, we define

$$\begin{aligned} g^{(a)}=g\left( \left( \frac{d ^{a_{1}}\gamma _{1}}{dx^{a_{1}}},\frac{d ^{a_{1}}\gamma _{2}}{dx^{a_{1}}}\right) ,\ldots , \left( \frac{d ^{a_{n}}\gamma _{1}}{dx^{a_{n}}},\frac{d ^{a_{n}}\gamma _{2}}{dx^{a_{n}}}\right) \right) , \end{aligned}$$

where \(a = (a_{1},a_{2}, \ldots ,a_{n})\) is a multi-index. We also define \(a + b =(a_{1} + b_{1},\ldots ,a_{n} + b_{n})\) and the elementary unit multi-index \(e_{j}\) by

$$\begin{aligned} e_{j}=\left( 0,\ldots ,0,\underbrace{1}_{jth\ term},0,\ldots ,0\right) . \end{aligned}$$

For example, we write

$$\begin{aligned} g^{(e_{k})}=g\left( (\gamma _{1}(x),\gamma _{2}(x)),\ldots ,\underbrace{ \left( \frac{d \gamma _{1}}{dx},\frac{d \gamma _{2}}{dx}\right) }_ {kth\ term}, \ldots , (\gamma _{1}(x),\gamma _{2}(x))\right) . \end{aligned}$$

Since the polar form g is multi-linear, it follows by the chain rule that

$$\begin{aligned} \frac{dg}{dx}=\sum _{k=1}^{n}g^{(e_{k})}. \end{aligned}$$

Theorem 1

kth derivative of G : Let g be the polar form of \(G\in \pi _{n}(\gamma _{1},\gamma _{2})\). Then

$$\begin{aligned} G^{(k)}(x)=\sum _{l\in \lambda _{n}(k)}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|g^{\left( \tilde{l}\right) }, \end{aligned}$$
(5)

where \(l_{i},i=1\ldots |l|\) are the elements of l and \(\tilde{l}=(l_{1},\ldots l_{|l|},\underbrace{0,\ldots ,0}_{n-|l|\ terms}).\)

Proof

By the diagonal property of the polar form

$$\begin{aligned} G(x)=g(\gamma _{1}(x),\gamma _{2}(x),\ldots ,(\gamma _{1}(x),\gamma _{2}(x))). \end{aligned}$$

Now differentiating both sides k times with respect to x and using the chain and product rules, we have

$$\begin{aligned} G^{(k)}(x)=\sum _{j_{1}=1}^{n}\cdots \sum _{j_{k}=1}^{n}g^{(e_{j_{1}}+\cdots +e_{j_{k}})}. \end{aligned}$$

Since \(j_{i},\ i=1,\ldots ,k\) may be repeated, there exist \(l\in \lambda _{n}(k)\) such that \((e_{j_{1}}+\cdots + e_{j_{k}})\) can be generated by changing exactly |l| zeros of \((\underbrace{0,\ldots ,0}_{n\, \mathrm{zeroes}})\) to \(l_{i},\ i=1\ldots |l|.\) The number of ways of choosing |l| zeros from n zeros is \(\displaystyle \left( {\begin{array}{c}n\\ |l|\end{array}}\right) ,\) and for \(l=\{l_{1},\ldots ,l_{|l|}\}\) there are \(\displaystyle \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) \) ways of distributing k elements into the |l| distinct positions such that each position \(i=1\ldots , |l|\) includes exactly \(l_{i}\) elements. Finally, since the number of permutations of l is \(|\delta (l)|,\) by the symmetry property both of the polar form and of the multinomial coefficients we obtain

$$\begin{aligned} G^{(k)}(x)=\sum _{l\in \lambda _{n}(k)}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|g^{\left( \tilde{l}\right) }, \end{aligned}$$

where \(\tilde{l}=\{l_{1},\ldots ,l_{|l|},\underbrace{0,\ldots ,0}_{n-|l|\, \mathrm{zeroes}}\}.\) \(\square \)

Remark 1

For classical homogeneous polynomials \( \gamma _{1}=t \) and \( \gamma _{2}=w. \) Therefore for classical polynomials the only partition \(l\in \lambda _{n}(k)\) for which \( g^{(l)}\ne 0 \) is \( l=(\underbrace{1,\ldots ,1}_{k\, \mathrm{times}}). \) Thus for classical polynomials after dehomogenization the summation on the right-hand side of Eq. (5) reduces to the single term:

$$\begin{aligned} \frac{n!}{(n-k)!}g\left( \underbrace{(1,0),\ldots ,(1,0)}_{k\, \mathrm{terms}},\underbrace{(t,1),\ldots ,(t,1)}_{n-k\, \mathrm{terms}}\right) . \end{aligned}$$

The many terms on the right-hand side of Eq. (5) are what distinguishes polynomials in \( (\gamma _{1},\gamma _{2}) \) from classical polynomials and makes the proofs of differentiability much harder for spline functions with segments in \( \pi _{n}(\gamma _{1},\gamma _{2}). \) See, for example, the proofs presented below of Theorem 2 and Lemma 1.

Remark 2

If \(\gamma _{1}\) and \(\gamma _{2}\) are continuous and non-negative functions on an interval I such that \(\frac{\gamma _{2}}{\gamma _{1}}\) is increasing on I and satisfies

$$\begin{aligned} \inf _{x\in I}\left\{ \frac{\gamma _{2}}{\gamma _{1}}\right\} =0, \quad \sup _{x\in I}\left\{ \frac{\gamma _{2}}{\gamma _{1}}\right\} =+\infty , \end{aligned}$$

then the basis in (1) is a B-basis and has optimal shape preserving properties [18].

Note that if \(\gamma _{1}\) and \(\gamma _{2}\) are non-negative functions and \(\frac{\gamma _{2}}{\gamma _{1}}\) is an increasing function then \(d(u,v)>0\) for all \( u<v \). Thus for any \(x_{0}<\cdots < x_{n},\) the determinant of the collocation matrix [7] is

$$\begin{aligned} \det \left( \left( \gamma _{1}^{n-i}(x_{j})\gamma _{2}^{i}(x_{j})\right) _{i,j=0}^{n}\right) =\prod _{j<i}^{n}d(x_{j},x_{i})>0. \end{aligned}$$

Using the positivity of \(\gamma _{1}\) and \(\gamma _{2},\) it can be shown that every submatrix of this collocation matrix has a positive determinant, which is the requirement for totally positivity of the basis in (1).

3 The local de Boor algorithm

We will now construct B-spline curves by introducing a variant of the de Boor algorithm. We will begin with a local version of this de Boor algorithm specifically adapted to \(\pi _{n}(\gamma _{1},\gamma _{2}).\) But before we can construct this local de Boor algorithm, we first need the notion of a progressive sequence.

Definition 1

Let \( \gamma _{1}\) and \( \gamma _{2} \) be two locally linearly independent functions and let \(d(a,b)=\gamma _{1}(a)\gamma _{2}(b)-\gamma _{1}(b)\gamma _{2}(a).\) A sequence \( \{x_{i}\}_{i=1}^{2n} \) of 2n real numbers satisfying the constraints \( d(x_{j},x_{i+n})\ne 0 \) for all \(i\leqslant j\leqslant n\) is called a d-progressive sequence or more simply just a progressive sequence.

The local de Boor algorithm evaluates recursively a function \(G\in \pi _{n}(\gamma _{1},\gamma _{2})\) starting from \(n+1\) values of the polar form of G evaluated at a progressive sequence. To generate the local de Boor algorithm, we first construct a recursive evaluation algorithm for the polar form of G.

Recursive evaluation algorithm for polar forms:

Let \( \{x_{i}\}_{i=1}^{2n} \) be a progressive sequence and let \(G\in \pi _{n}(\gamma _{1},\gamma _{2}).\) Set

$$\begin{aligned} b^{0}_{k}=g((\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),\ldots , (\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n}))),\quad k=0,1,\ldots ,n \end{aligned}$$

and

$$\begin{aligned} b^{r}_{k}=\frac{d(u_{r},x_{k+n+1})}{d(x_{k+r},x_{k+n+1})}b^{r-1}_{k} + \frac{d(x_{k+r},u_{r})}{d(x_{k+r},x_{k+n+1})}b^{r-1}_{k+1},\quad k=0,1,\ldots ,n-r \end{aligned}$$
(6)

and \(r=1,\ldots ,n.\) Then it follows easily by induction on r and the symmetry and multi-barycentric properties of the polar form that

$$\begin{aligned} b^{r}_{k}= & {} g((\gamma _{1}(x_{k+r+1}),\gamma _{2}(x_{k+r+1})),\ldots , (\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n})),\\&(\gamma _{1}(u_{1}),\gamma _{2}(u_{1})),\ldots , (\gamma _{1}(u_{r}),\gamma _{2}(u_{r}))) \end{aligned}$$

for \(k=0,1,\ldots ,n-r,\) and \(r=0,1,\ldots ,n.\) In particular

$$\begin{aligned} b^{n}_{0}&= g((\gamma _{1}(u_{1}),\gamma _{2}(u_{1})),\ldots , (\gamma _{1}(u_{n}),\gamma _{2}(u_{n}))). \end{aligned}$$

Note that this evaluation algorithm is well defined since the denominators in (6) never vanish because \( \{x_{i}\}_{i=1}^{2n} \) is a progressive sequence. This algorithm is illustrated for the case \(n=3\) in Fig. 1.

Fig. 1
figure 1

The recursive evaluation algorithm (6) for polar forms. Here \(x_{i},\ i=1,\ldots 6\) is a progressive sequence and uvw denotes \(g((\gamma _{1}(u),\gamma _{2}(u)),(\gamma _{1}(v),\gamma _{2}(v)),(\gamma _{1}(w),\gamma _{2}(w))) \)

Full size image

Since g reduces to G on the \((\gamma _{1},\gamma _{2})\) diagonal, setting \(u_{i}=x\) provides a recursive evaluation algorithm for a curve \(G\in \pi _{n}(\gamma _{1},\gamma _{2}).\) In analogy with classical B-splines, we call this recursive evaluation algorithm the local de Boor algorithm.

The local de Boor algorithm:

Let \( \{x_{i}\}_{i=1}^{2n} \) be a progressive sequence and let \(G\in \pi _{n}(\gamma _{1},\gamma _{2}).\) Set

$$\begin{aligned} P^{0}_{k}=g(\gamma _{1}(x_{k+1}), \gamma _{2}(x_{k+1})),\ldots , (\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n})),\quad k=0,\ldots ,n, \end{aligned}$$

and define \(P^{r}_{k}\) recursively by

$$\begin{aligned} P^{r}_{k}=\frac{d(x,x_{k+n+1})}{d(x_{k+r},x_{k+n+1})}P^{r-1}_{k} + \frac{d(x_{k+r},x)}{d(x_{k+r},x_{k+n+1})}P^{r-1}_{k+1} \end{aligned}$$
(7)

for \( k=1,\ldots ,n-r \) and \(r=1,\ldots ,n.\) In this case

$$\begin{aligned} P^{r}_{k}=&g((\gamma _{1}(x_{k+r+1}), \gamma _{2}(x_{k+r+1})),\ldots , (\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n})),\\&\quad (\gamma _{1}(x),\gamma _{2}(x)),\ldots , (\gamma _{1}(x),\gamma _{2}(x))) \end{aligned}$$

for \(k=0,1,\ldots ,n-r,\) and \(r=0,1,\ldots ,n.\) In particular,

$$\begin{aligned} P^{n}_{0}=g((\gamma _{1}(x),\gamma _{2}(x)),\ldots , (\gamma _{1}(x),\gamma _{2}(x)))=G(x). \end{aligned}$$

In Fig. 2 the local de Boor algorithm is illustrated for the case \(n=3.\)

Fig. 2
figure 2

The local de Boor evaluation algorithm (7). Here \(x_{i},\ i=1,\ldots 6\) is a progressive sequence and uvw denotes \(g((\gamma _{1}(u),\gamma _{2}(u)),(\gamma _{1}(v),\gamma _{2}(v)),(\gamma _{1}(w),\gamma _{2}(w)))\)

Full size image

Let \( B_{j,n} \) be the function generated by the local de Boor algorithm for a fixed progressive sequence \( \{x_{i}\}_{i=1}^{2n} \) with the initial values \( b^{0}_{k}=\delta _{jk}. \) That is, \( B_{j,n}(x) \) is the sum of the products along all paths from the jth position at the base to the apex of the local de Boor algorithm. Then since every function \(G\in \pi _{n}(\gamma _{1},\gamma _{2})\) has a polar form, it follows by linearity that

$$\begin{aligned} G(x)=\sum \limits _{k=0}^{n}B_{k,n}(x)g((\gamma _{1}(x_{k+1}), \gamma _{2}(x_{k+1})),\ldots , (\gamma _{1}(x_{k+n}),{\gamma _{2}(x_{k+n})))}. \end{aligned}$$
(8)

Thus the functions \( B_{0,n},\ldots B_{n,n} \) span the space \(\pi _{n}(\gamma _{1},\gamma _{2}).\) Since \(\dim \pi _{n}(\gamma _{1},\gamma _{2}) =n+1\) (see [8]), we conclude that the functions \( B_{0,n},\ldots B_{n,n} \) form a basis for the space \( \pi _{n}(\gamma _{1},\gamma _{2}). \) Therefore the coefficients of G relative to the basis \( B_{0,n},\ldots B_{n,n} \) are unique. Hence from (8), we have the following dual functional property.

Dual functional property:

Let \(G(x)=\sum _{k=0}^{n}P_{k}B_{k,n}(x)\) and let g be the polar form of G. Then

$$\begin{aligned} P_{k}=g((\gamma _{1}(x_{k+1}), \gamma _{2}(x_{k+1})),\ldots , (\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n}))). \end{aligned}$$

The special progressive sequence \( x_{i}=a,\ i=1,2,\ldots n \) and \( x_{s}=b,\ s=n+1,n+2,\ldots ,2n \) with the control points \(P_{k}=\delta _{jk}\) generates the Bernstein-Bézier basis functions

$$\begin{aligned} B_{k,n}(x)=\left( {\begin{array}{c}n\\ k\end{array}}\right) \left( \frac{d(a,x)}{d(a,b)}\right) ^{k}\left( \frac{d(x,b)}{d(a,b)}\right) ^{n-k}, \quad k=0,1,\ldots ,n \end{aligned}$$
(9)

defined on the interval [a, b] (see [8]). In this case the local de Boor algorithm reduces to the de Casteljau evaluation algorithm for Bernstein–Bézier curves in \(\pi _{n}(\gamma _{1},\gamma _{2})\). For the special properties of these Bernstein–Bézier curves, see [8].

4 The global de Boor algorithm

The local de Boor evaluation algorithm computes points along a single segment in \( \pi _{n}(\gamma _{1},\gamma _{2}) \). As in the case of classical B-splines, for a given set of control points \(\{P_{j}\}\) and an increasing knot sequence \(\{x_{i}\},\) where each consecutive set of 2n knots form a progressive sequence, the global de Boor algorithm produces smooth piecewise curves, where each segment lies in \( \pi _{n}(\gamma _{1},\gamma _{2}). \) In analogy with the classical piecewise polynomial theory we call these curves B-spline curves (In this section we are restricting to the case of simple knots; multiple knots will be discussed in Sect. 5). A B-spline segment of degree n is defined by 2n progressive knots \( \{x_{i}\}_{i=1}^{2n} \) and \(n+1\) arbitrary control points \(\{P_{j}\}_{j=0}^{n}\) by placing the control points at the base of the local de Boor algorithm and the knots as parameters in the function d along the edges (Fig. 2). If we are given one additional knot \(x_{2n+1}\) and one additional control point \(P_{n+1},\) then we can evaluate a new segment by shifting all the indices in the local de Boor algorithm by 1 . The case where \( n=3 \) is illustrated in Fig. 3.

Fig. 3
figure 3

Evaluating a new segment by shifting all the indices in the local de Boor algorithm by 1

Full size image

Since these two segments share common control points, as well as nodes and edges with common labels, we may overlap the diagrams in Figs. 2 and 3. We illustrate this overlap in Fig. 4.

Fig. 4
figure 4

The global de Boor algorithm for two segments of a cubic B-spline curve

Full size image

Notice that the symbols xxx at the apexes represent the values of distinct curves in \( \pi _{n}(\gamma _{1},\gamma _{2}) \) over distinct parameter intervals with distinct knot sequences,

$$\begin{aligned} G_{1}(x)=g_{1}((\gamma _{1}(x),\gamma _{2}(x)),(\gamma _{1}(x),\gamma _{2}(x)),(\gamma _{1}(x),\gamma _{2}(x))) \end{aligned}$$

and

$$\begin{aligned} G_{2}(x)=g_{2}((\gamma _{1}(x),\gamma _{2}(x)),(\gamma _{1}(x),\gamma _{2}(x)),(\gamma _{1}(x),\gamma _{2}(x))). \end{aligned}$$

In order to investigate the continuity of two adjacent segments, we will start with the case \( n=3\) as an illustration before we launch into a formal proof of the general case. Note that the diagrams also overlap in the general case.

As in the case of classical B-splines (see [10]), the first apex in Fig. 4 represents the curve segment for \(x_{3}\leqslant x \leqslant x_{4}\) and the second apex represents the curve segment for \(x_{4}\leqslant x \leqslant x_{5}.\) Since \(d(x,x)=0,\) if we evaluate \(G_{1}\) and \(G_{2}\) at \(x=x_{4},\) then the left arrow of the top level of the first segment and the right arrow of the top level of the second segment both evaluate to zero and their adjacent arrows evaluate to one. Hence evaluating both segments at \(x=x_{4}\) gives the same result denoted in Fig. 4 by \(x_{4}xx\). Therefore these two curve segments meet continuously at \(x=x_{4}.\)

To show that \(G_{1}\) and \(G_{2}\) meet with \(C^{1}\)-continuity at \(x=x_{4},\) we will use the formula for the derivative in terms of the polar form. By (4)

$$\begin{aligned} G'_{1}(x)= 3 g_{1}((\gamma '_{1}(x),\gamma '_{2}(x)),(\gamma _{1}(x),\gamma _{2}(x)),(\gamma _{1}(x),\gamma _{2}(x))). \end{aligned}$$

Similarly,

$$\begin{aligned} G'_{2}(x) = 3 g_{2}((\gamma '_{1}(x),\gamma '_{2}(x)),(\gamma _{1}(x),\gamma _{2}(x)),(\gamma _{1}(x),\gamma _{2}(x))). \end{aligned}$$

Differentiating (2) with \(a=x_{k}\) and \(b=x_{j}\) yields

$$\begin{aligned} \alpha ' (\gamma _{1}(x_{k}),\gamma _{2}(x_{k})) + \beta ' (\gamma _{1}(x_{j}),\gamma _{2}(x_{j}))=(\gamma '_{1}(x),\gamma '_{2}(x)). \end{aligned}$$

Solving this equation gives

$$\begin{aligned} \alpha ' = \frac{\gamma '_{1}(x)\gamma _{2}(x_{j})-\gamma _{1}(x_{j})\gamma '_{2}(x)}{\gamma _{1}(x_{k})\gamma _{2}(x_{j})-\gamma _{1}(x_{j})\gamma _{2}(x_{k})} = \frac{d}{dx} \left( \frac{d(x,x_{j})}{d(x_{k},x_{j})}\right) \end{aligned}$$

and

$$\begin{aligned} \beta ' = \frac{\gamma _{1}(x_{k})\gamma '_{2}(x)-\gamma '_{1}(x)\gamma _{2}(x_{k})}{\gamma _{1}(x_{k})\gamma _{2}(x_{j})-\gamma _{1}(x_{j})\gamma _{2}(x_{k})} = \frac{d}{dx} \left( \frac{d(x_{k},x)}{d(x_{k},x_{j})}\right) \end{aligned}$$

which are the barycentric coordinates of \((\gamma '_{1}(x),\gamma '_{2}(x))\) with respect to the points \((\gamma _{1}(x_{k}),\gamma _{2}(x_{k}))\) and \((\gamma _{1}(x_{j}),\gamma _{2}(x_{j})).\)

Therefore by (4) to compute \(G'_{1}(x)\) and \(G'_{2}(x)\) using polar forms, we may differentiate the first level of the algorithm and multiply the result by 3. (see Fig. 5). Thus to compute \(G'_{1}\) and \(G'_{2}\) from the diagram, we need to replace the labels along the arrows of the first level

Fig. 5
figure 5

Derivative of two adjacent segments of a cubic B-spline curve. Here \(x '\) denotes the homogeneous polar form evaluated at \((\gamma '_{1}(x),\gamma '_{2}(x))\)

Full size image
figure a

by

figure b

Since the labels along the arrows entering the two apexes in the Fig. 4 do not change, we see that \(G_{1}\) and \(G_{2}\) meet with \(C^{1}\)-continuity because once again when \(x=x_{4}\) the left arrow entering the first apex and the right arrow entering the second apex are zero and their adjacent arrows evaluate to 1.

Thus we can see from the diagram that \(C^{k}\)-continuity holds as long as the top level in the diagram does not change. From Theorem 1, since \(\lambda _{3}(2)=\left\{ \{2\},\{1,1\}\right\} ,\) the second derivative of \(G_{1}\) and \(G_{2}\) can be evaluated from the diagram by differentiating the first level twice (corresponding to \(l=\{2\}\)) and by differentiating the first two levels once (corresponding to \(l=\{1,1\}\)). These derivatives do not affect the top level of the algorithm; hence by the same reasoning as for \(C^{1}\)-continuity, \(G_{1}\) and \(G_{2}\) meet with \(C^{2}\)-continuity. But for the third derivative we have \(\lambda _{3}(3)=\left\{ \{3\},\{2,1\},\{1,1,1\}\right\} \) and all three levels of the diagram corresponding to \(l=\{1,1,1\}\) are differentiated. In this case we do not have \(C^{3}\)-continuity, since the expressions on the left arrow entering the first apex and the right arrow entering the second apex are no longer zero.

In general, a similar argument shows that two B-spline curve segments of degree n joined at \(x=x_{j}\) meet with \(C^{s}\)-continuity as long as the sth derivative of the two adjacent segments does not change the top level of the algorithm. Since our diagrams are just graphical realizations of the algorithm, in the following discussion we shall speak of the diagram and the algorithm interchangeably; levels in the diagram correspond to levels in the algorithm, and labels along the edges of the diagram correspond to coefficients in the algorithm. The diagrams, however, are easier to visualize and therefore help to simplify our understanding and analysis of the algorithm.

Consider the de Boor evaluation algorithm for a degree n B-spline curve, where the nodes are represented by values of the polar form. To replace the ith component \((\gamma _{1}(x),\gamma _{2}(x))\) of the polar form by \((\gamma ^{(r)}_{1}(x),\gamma ^{(r)}_{2}(x))\) in the diagram, we can differentiate the functions along the edges at the ith level of the diagram r times, since by differentiating r times we solve the equation

$$\begin{aligned} \alpha ^{(r)} (\gamma _{1}(x_{k}),\gamma _{2}(x_{k})) + \beta ^{(r)} (\gamma _{1}(x_{j}),\gamma _{2}(x_{j})) = (\gamma ^{(r)}_{1}(x),\gamma ^{(r)}_{2}(x)). \end{aligned}$$

Thus there is a recursive algorithm for each term in the derivative formula (5). A term \(g^{\left( \tilde{l}\right) }\) has a recursive evaluation algorithm with the functions \(\displaystyle \frac{d^{l_{j}}}{dx^{l_{j}}} \left( \frac{d(x,x_{k+n+1})}{d(x_{k+j},x_{k+n+1})}\right) \) and \(\displaystyle \frac{d^{l_{j}}}{dx^{l_{j}}}\left( \frac{d(x_{k+j},x)}{d(x_{k+j},x_{k+n+1})}\right) \) on level \(j,j{\,=\,}1,\ldots ,|l|,\) and the functions \(\displaystyle \frac{d(x,x_{k+n+1})}{d(x_{k+r},x_{k+n+1})}\) and \(\displaystyle \frac{d(x_{k+r},x)}{d(x_{k+r},x_{k+n+1})}\) on the remaining \(n-|l|\) levels from \(r=|l|+1\) to \(r=n.\) Since the functions \(\displaystyle \frac{d(x,x_{k+n+1})}{d(x_{k+n},x_{k+n+1})}\) and \(\displaystyle \frac{d(x_{k+n},x)}{d(x_{k+n},x_{k+n+1})}\) appear on level n,  when evaluated at the join \(x=x_{k+n+1},\) the segments agree for this term and this agreement holds for every term. This agreement holds until \(|l|=n\) or equivalently until the partition \(\{1,\ldots ,1\},\) when the last level must be differentiated.

The main point here is that, for the sth derivative of B-spline curve, if \(s \geqslant n,\) then there will be a term in the formula for the derivative where every element inside the polar form is differentiated. In this case the coefficients on all the levels including the top level are differentiated and the argument for continuity breaks down. But if \(s < n,\) then we never need to differentiate the top level of the diagram; all the derivatives can be distributed to lower levels of the algorithm.

Note that the ith level of the diagram is associated with the ith component of the polar form. Therefore by Theorem 1 two adjacent segments of a degree n B-spline curve meet with \(C^{s}\)-continuity as long as every element l of \(\lambda _{n}(s)\) satisfies \(|l|<n.\) Since |l| cannot exceed s,  \(C^{s}\)-continuity holds for every \(s<n;\) that is, two adjacent segments of a degree n B-spline curve meet with \(C^{n-1}\)-continuity. Hence we have proved the following theorem:

Theorem 2

B-spline curves of degree n with no multiple knots are \(C^{n-1}\)-continuous at the knots.

5 All splines are B-splines

A spline is a piecewise function whose segments \(G_{k}\in \pi _{n} (\gamma _{1},\gamma _{2})\) meet smoothly up to some order at the joins. A B-spline curve is a spline generated by the de Boor algorithm. For a fixed progressive knot sequence, let \(\sigma _{n} (\gamma _{1},\gamma _{2})\) denotes the spaces of splines whose segments lie in \(\pi _{n}(\gamma _{1},\gamma _{2})\) where \( \gamma _{1},\gamma _{2} \) are two differentiable, locally linearly independent functions. The goal of this section is to prove that all splines from the space \(\sigma _{n} (\gamma _{1},\gamma _{2})\) can be generated by the de Boor algorithm. To begin, we need to prove the following analogue of [10, pp. 364, Lemma 7.2].

Lemma 1

Let F and G be two functions in \(\pi _{n}(\gamma _{1},\gamma _{2})\) and let f and g be the polar forms of F and G . If \(\gamma _{1}(\xi )\gamma '_{2}(\xi )-\gamma '_{1}(\xi )\gamma _{2}(\xi )\ne 0,\) then the following statements are equivalent.

  1. 1.
    $$\begin{aligned} F^{(j)}(\xi )=G^{(j)}(\xi ),\quad 0\leqslant j \leqslant k \leqslant n. \end{aligned}$$
  2. 2.
    $$\begin{aligned}&f((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j})\\&\quad =g((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j}) \end{aligned}$$

    for any parameters \(u_{1},\ldots ,u_{j},w_{1},\ldots ,w_{j},0\leqslant j \leqslant k \leqslant n,\) where

    $$\begin{aligned} (\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j}=\underbrace{(\gamma _{1}(\xi ),\gamma _{2}(\xi )),\ldots ,(\gamma _{1}(\xi ),\gamma _{2}(\xi ))}_{n-j\text { times}} \end{aligned}$$

Proof

\(1\Rightarrow 2.\) Suppose that \(F^{(j)}(\xi )=G^{(j)}(\xi ),\ 0\leqslant j \leqslant k \leqslant n.\) By Theorem 1

$$\begin{aligned} F^{(j)}(\xi )=\sum _{l\in \lambda _{n}(j)}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}j\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|f^{\left( \tilde{l}\right) }(\xi ) \end{aligned}$$

and

$$\begin{aligned} G^{(j)}(\xi )=\sum _{l\in \lambda _{n}(j)}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}j\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|g^{\left( \tilde{l}\right) }(\xi ). \end{aligned}$$

Now we will use strong induction on k. Clearly, if \(F(\xi )=G(\xi ),\) then by the diagonal property

$$\begin{aligned} f((\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n})=g((\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n}). \end{aligned}$$
(10)

Hence, statement 2 is true for \(k=0.\) For \(k=1\) by (4), \(F'(\xi )=G'(\xi )\) implies

$$\begin{aligned} n\,f((\gamma '_{1}(\xi ),\gamma '_{2}(\xi )),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-1}) =n\,g((\gamma '_{1}(\xi ),\gamma '_{2}(\xi )),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-1}).\nonumber \\ \end{aligned}$$
(11)

Now for the solutions \(\displaystyle \alpha (u_{1},w_{1},\xi )=\frac{u_{1}\gamma _{2}'(\xi )-\gamma _{1}'(\xi )u_{2}}{\gamma _{1}(\xi )\gamma '_{2}(\xi )-\gamma '_{1}(\xi )\gamma _{2}(\xi )}\) and \(\displaystyle \beta (u_{1},w_{1},\xi )=\frac{\gamma _{1}(\xi )u_{2}-u_{1}\gamma _{2}(\xi )}{\gamma _{1}(\xi )\gamma '_{2}(\xi )-\gamma '_{1}(\xi )\gamma _{2}(\xi )}\) of the system

$$\begin{aligned} \alpha (u_{1},w_{1},\xi )(\gamma _{1}(\xi ),\gamma _{2}(\xi ))+\beta (u_{1},w_{1},\xi )(\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))=(u_{1},w_{1}), \end{aligned}$$

the multilinear property of polar forms implies

$$\begin{aligned}&\alpha (u_{1},w_{1},\xi )f((\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n})+\beta (u_{1},w_{1},\xi )f((\gamma '_{1}(\xi ),\gamma '_{2}(\xi )),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-1})\\&\quad =f((u_{1},w_{1}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-1}). \end{aligned}$$

Similarly,

$$\begin{aligned}&\alpha (u_{1},w_{1},\xi )g((\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n})+\beta (u_{1},w_{1},\xi )g((\gamma '_{1}(\xi ),\gamma '_{2}(\xi )),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-1})\\&\quad =g((u_{1},w_{1}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-1}). \end{aligned}$$

Hence for \(k=0,1,\) statement 2 is true by (10) and (11). Now assume that statement 2 is true for \(0\leqslant j \leqslant k-1 < n\). We need to show that if \(F^{(j)}(\xi )=G^{(j)}(\xi ), 0\leqslant j \leqslant k \leqslant n,\) then

$$\begin{aligned}&f((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j})\nonumber \\&\quad =g((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j}) \end{aligned}$$
(12)

for \(0\leqslant j \leqslant k \leqslant n.\) But certainly if \(F^{(j)}(\xi )=G^{(j)}(\xi ),\text { for } 0\leqslant j \leqslant k \leqslant n,\) then \(F^{(j)}(\xi )=G^{(j)}(\xi ),\text { for } 0\leqslant j \leqslant k-1<n.\) Therefore by the inductive hypothesis

$$\begin{aligned}&f((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j})\nonumber \\&\quad =g((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j}),\ 0\leqslant j\leqslant k-1<n. \end{aligned}$$
(13)

On the other hand since \(F^{(k)}(\xi )=G^{(k)}(\xi ),\) by Theorem 1 we have

$$\begin{aligned} \sum _{l\in \lambda _{n}(k)}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|f^{\left( \tilde{l}\right) }(\xi )=\sum _{l\in \lambda _{n}(k)}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|g^{\left( \tilde{l}\right) }(\xi ). \end{aligned}$$
(14)

The left hand side of (14) can be written as

$$\begin{aligned}&\sum _{\begin{array}{c} l\in \lambda _{n}(k) \\ |l|<k \end{array}}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|f^{\left( \tilde{l}\right) }(\xi )\nonumber \\&\quad +\left( {\begin{array}{c}n\\ k\end{array}}\right) \left( {\begin{array}{c}k\\ 1\ \cdots \ 1\end{array}}\right) |\delta (\{1,\ldots ,1\})|f((\gamma '_{1}(\xi ) ,\gamma '_{2}(\xi ))^{k}, (\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-k}). \end{aligned}$$
(15)

Similarly the right hand side of (14) is

$$\begin{aligned}&\sum _{\begin{array}{c} l\in \lambda _{n}(k) \\ |l|<k \end{array}}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|g^{\left( \tilde{l}\right) }(\xi ) \nonumber \\&\quad +\left( {\begin{array}{c}n\\ k\end{array}}\right) \left( {\begin{array}{c}k\\ 1\ \cdots \ 1\end{array}}\right) |\delta (\{1,\ldots ,1\})|g((\gamma '_{1}(\xi ) ,\gamma '_{2}(\xi ))^{k}, (\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-k}). \end{aligned}$$
(16)

The terms with \(|l|<k\) in the summations of the Eqs. (15) and (16) are identical by Eq. (13). That is

$$\begin{aligned} \sum _{\begin{array}{c} l\in \lambda _{n}(k) \\ |l|<k \end{array}}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|f^{\left( \tilde{l}\right) }(\xi )=\sum _{\begin{array}{c} l\in \lambda _{n}(k) \\ |l|<k \end{array}}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}k\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) \delta (l)|g^{\left( \tilde{l}\right) }(\xi ). \end{aligned}$$
(17)

Thus from (14) and (17), we conclude that

$$\begin{aligned} \left( {\begin{array}{c}n\\ k\end{array}}\right)&k!f((\gamma '_{1}(\xi ) ,\gamma '_{2}(\xi ))^{k},(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-k})\\&=\left( {\begin{array}{c}n\\ k\end{array}}\right) k!g((\gamma '_{1}(\xi ) ,\gamma '_{2}(\xi ))^{k},(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-k}). \end{aligned}$$

Therefore we have

$$\begin{aligned}&f((\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))^{j},(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j})\\&\quad =g((\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))^{j},(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j}),\quad j=0,\ldots ,k, \end{aligned}$$

where \((\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))^{j}=\underbrace{(\gamma '_{1}(\xi ),\gamma '_{2}(\xi )),\ldots ,(\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))}_{j\text { times}}.\) Now starting with \(k+1\) polar form values

$$\begin{aligned} f_{j}^{0}=f((\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))^{j},(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j}),\quad j=0,\ldots ,k, \end{aligned}$$

define

$$\begin{aligned} f^{r}_{j}=\alpha (u_{r},w_{r},\xi )f^{r-1}_{j}+\beta (u_{r},w_{r},\xi )f^{r-1}_{j+1} \end{aligned}$$

for \(r=1,\ldots ,k\) and \(j=0,\ldots ,n-r,\) where \(\alpha (u_{r},w_{r},\xi )\) and \(\beta (u_{r},w_{r},\xi )\) are the solutions of the system

$$\begin{aligned} \alpha (u_{r},w_{r},\xi )(\gamma _{1}(\xi ),\gamma _{2}(\xi ))+\beta (u_{r},w_{r},\xi )(\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))=(u_{r},w_{r}). \end{aligned}$$

As a consequence of the multilinear property of the polar form, it follows by induction on r that

$$\begin{aligned} f^{r}_{j}=f((u_{1},w_{1}),\ldots ,(u_{r},w_{r}),(\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))^{j},(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-r-j}) \end{aligned}$$

for \(r=1,\ldots ,k,\) and \(j=0,\ldots ,k-r.\) Similarly, the same algorithm, starting with the \(k+1\) values of the polar form

$$\begin{aligned} g_{j}^{0}=g((\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))^{j},(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j}),\quad j=0,\ldots ,k, \end{aligned}$$

generates the values of the polar form

$$\begin{aligned} g_{j}^{r}=g((u_{1},w_{1}),\ldots ,(u_{r},w_{r}),(\gamma '_{1}(\xi ),\gamma '_{2}(\xi ))^{j},(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-r-j}) \end{aligned}$$

for \(r=1,\ldots ,k,\) and \(j=0,\ldots ,k-r.\) Since the input to these two algorithms is the same, the output must also be the same. Therefore

$$\begin{aligned} f^{j}_{0}&=f((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j})\\&=g((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j})=g^{j}_{0} \end{aligned}$$

for any parameters \(u_{1},\ldots ,u_{j},w_{1},\ldots ,w_{j},\ 0\leqslant j \leqslant k \leqslant n.\)

\(2\Rightarrow 1.\) For any parameters \(u_{1},\ldots ,u_{j},w_{1},\ldots ,w_{j},\ 0\leqslant j \leqslant k \leqslant n\) suppose that

$$\begin{aligned}&f((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j})\\&\quad =g((u_{1},w_{1}),\ldots ,(u_{j},w_{j}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-j}). \end{aligned}$$

Then for any \(0\leqslant j \leqslant k \leqslant n\) one may write

$$\begin{aligned}&\sum _{l\in \lambda _{n}(j)}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}j\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|f((u_{l_{1}} ,w_{l_{1}}),\ldots (u_{l_{|l|}}, w_{l_{|l|}}),(\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-|l|})\\&\quad =\sum _{l\in \lambda _{n}(j)}^{}\left( {\begin{array}{c}n\\ |l|\end{array}}\right) \left( {\begin{array}{c}j\\ l_{1}\ \cdots \ l_{|l|}\end{array}}\right) |\delta (l)|g((u_{l_{1}} ,w_{l_{1}}),\ldots (u_{l_{|l|}}, w_{l_{|l|}}),\\&\quad \qquad (\gamma _{1}(\xi ),\gamma _{2}(\xi ))^{n-|l|}) \end{aligned}$$

Setting \((u_{l_{i}},w_{l_{i}})=(\gamma ^{(l_{i})}_{1}(\xi ),\gamma ^{(l_{i})}_{2}(\xi ))\) and applying Theorem 1 gives \(F^{(j)}(\xi )=G^{(j)}(\xi ),\ 0\leqslant j \leqslant k \leqslant n.\) \(\square \)

Theorem 3

Every spline curve is a B-spline curve.

Proof

Let \(S\in \sigma _{n}(\gamma _{1},\gamma _{2})\) be a spline curve defined over the knot intervals \([x_{k},x_{k+1}]\) by functions \(S_{k}\in \pi _{n}(\gamma _{1},\gamma _{2}),\) with polar forms \(s_{k},k=n,n+1,\ldots ,m.\) Suppose further that for each k, 

$$\begin{aligned} S_{k}^{(j)}(x_{k+1})=S_{k+1}^{(j)}(x_{k+1}),\quad j=0,1,\ldots ,n-1. \end{aligned}$$

We need to find a collection of points \(\{P_{k}\}\) such that the B-spline curve in \(\sigma _{n}(\gamma _{1},\gamma _{2})\) generated by the knot sequence \(\{x_{k}\}\) and by the control points \(\{P_{k}\}\) is S. Consider the first segment \(S_{n}\) over the interval \([x_{n},x_{n+1}].\) Let

$$\begin{aligned} P_{j}=s_{n}((\gamma _{1}(x_{j+1}),\gamma _{2}(x_{j+1})),\ldots (\gamma _{1}(x_{j+n}),\gamma _{2}(x_{j+n}))),\quad j=0,1\ldots ,n. \end{aligned}$$

Then by (8), the local de Boor algorithm for the knots \(x_{1},x_{2},\ldots ,x_{2n}\) and the control points \(P_{0},P_{1},\ldots , P_{n}\) generates the function \(S_{n}(x).\) Similarly, if we set

$$\begin{aligned} Q_{j}=s_{n+1}((\gamma _{1}(x_{j+2}),\gamma _{2}(x_{j+2})),\ldots (\gamma _{1}(x_{j+n+1}),\gamma _{2}(x_{j+n+1}))),\quad j=0,1\ldots ,n, \end{aligned}$$

then the local de Boor algorithm for the knots \(x_{2},x_{3},\ldots , x_{2n+1}\) and the control points \(Q_{0},Q_{1},\ldots ,Q_{n}\) generates the function \(S_{n+1}(x).\) It remains to show that \(P_{j}=Q_{j-1}\) or equivalently,

$$\begin{aligned}&s_{n}((\gamma _{1}(x_{j+1}),\gamma _{2}(x_{j+1})),\ldots (\gamma _{1}(x_{j+n}),\gamma _{2}(x_{j+n})))\\&\quad =s_{n+1}((\gamma _{1}(x_{j+1}),\gamma _{2}(x_{j+1})),\ldots (\gamma _{1}(x_{j+n}),\gamma _{2}(x_{j+n}))) \end{aligned}$$

for \(j=1,2,\ldots ,n.\) But by assumption

$$\begin{aligned} S_{n}^{(j)}(x_{n+1})=S_{n+1}^{(j)}(x_{n+1}),\quad j=0,1,\ldots ,n-1. \end{aligned}$$

Therefore by Lemma 1

$$\begin{aligned}&s_{n}((u_{1}w_{1}),\ldots ,(u_{n-1},w_{n-1}),(\gamma _{1}(x_{n+1}),\gamma _{2}(x_{n+1})))\\&\quad =s_{n+1}((u_{1},w_{1}),\ldots ,(u_{n-1},w_{n-1}),(\gamma _{1}(x_{n+1}),\gamma _{2}(x_{n+1}))). \end{aligned}$$

But notice that

$$\begin{aligned} (\gamma _{1}(x_{n+1}),\gamma _{2}(x_{n+1}))\in \{(\gamma _{1}(x_{j+1}),\gamma _{2}(x_{j+1})),\ldots , (\gamma _{1}(x_{j+n}),\gamma _{2}(x_{j+n}))\} \end{aligned}$$

for all \(j=1,2,\ldots ,n.\) Hence for a fixed j and \(i=1,2,\ldots ,n-1,\) setting

$$\begin{aligned} (u_{i},w_{i})=\left\{ \begin{array}{ll} (\gamma _{1}(x_{i+j}),\gamma _{2}(x_{i+j})),&{}\quad \text {if }i+j<n+1\\ &{} \\ (\gamma _{1}(x_{i+j+1}),\gamma _{2}(x_{i+j+1})),&{}\quad \text {if }i+j\geqslant n+1 \end{array}\right. \end{aligned}$$

gives

$$\begin{aligned} s_{n}&((\gamma _{1}(x_{j+1}),\gamma _{2}(x_{j+1})),\ldots , (\gamma _{1}(x_{j+n}),\gamma _{2}(x_{j+n})))\\&=s_{n+1}((\gamma _{1}(x_{j+1}),\gamma _{2}(x_{j+1})),\ldots , (\gamma _{1}(x_{j+n}),\gamma _{2}(x_{j+n}))) \end{aligned}$$

for \(j=1,2,\ldots ,n.\) Thus these two segments form a B-spline curve. In the same manner using the local de Boor algorithm, we can generate more segments that match the segments of the given spline S. By the same argument, these new segments share common control points; therefore, they form a B-spline curve. Since the entire curve is generated by the global de Boor algorithm, it follows that every spline curve is a B-spline curve. \(\square \)

5.1 Multiple Knots

Consider a B-spline curve of degree n for an increasing sequence of knots, \(x_{1}<x_{2}<x_{3}<\cdots .\) The first segment on the interval \([x_{n},x_{n+1}]\) is generated from the knots \(\{x_{i}\}_{i=1}^{2n}.\) Similarly the second segment over the interval \([x_{n+1},x_{n+2}]\) is generated from the knots \(\{x_{i}\}_{i=2}^{2n+1}.\) In Sect. 4 we showed that these two curve segments meet with order \(n-1\) continuity at \(x=x_{n+1}.\) What happens if \(x_{n+1}=x_{n+2}?\) In this case, the knot interval \([x_{n+1},x_{n+2}]\) collapses to a single point. Hence to investigate continuity, we must examine the first and third segments. The third curve segment is generated from the knots \(\{x_{i}\}_{i=3}^{2n+2}.\) Consider the diagram generated by the global de Boor algorithm that corresponds to the intervals \([x_{n},x_{n+1}]\) and \([x_{n+2},x_{n+3}]\) (see Fig. 6).

Fig. 6
figure 6

Two apexes corresponding to the intervals \([x_{n},x_{n+1}]\) and \([x_{n+2},x_{n+3}]\)

Full size image

In Fig. 6 we illustrate the final two levels of these algorithms. When \(x=x_{n+1}\) and \(x_{n+1}=x_{n+2},\) then since all the functions along the leftmost arrows in the left triangle and all the functions along the rightmost arrows in the right triangle evaluate to zero, the only nonzero paths from the base to the apexes are through the right edge of the first apex and the left edge of the second apex. Moreover the values of the functions along these nonzero arrows are 1. Therefore both segments meet continuously at \(x=x_{n+1}.\) Using the same arguments as in Sect. 4, we conclude that if \(x_{n+1}=x_{n+2},\) then by Theorem 1 the two adjacent segments that meet at \(x=x_{n+1}\) meet with \(C^{n-2}\)-continuity. We can generalize this result as follows:

Theorem 4

At a knot of multiplicity \(\mu ,\) a B-spline curve from the space \(\sigma _{n}(\gamma _{1},\gamma _{2})\) has \(n-\mu \) continuous derivatives.

Proof

This proof is modelled on the proof of [25, Theorem 6.2]. Let \(\{x_{i}\}\) be a nondecreasing knot sequence where each consecutive set of 2n knots form a progressive sequence and let S be a spline defined by the de Boor algorithm over the intervals \([x_{i},x_{i+1}]\) by functions \(S_{i}\in \pi _{n}(\gamma _{1},\gamma _{2}),\ i=n,n+1,\ldots \) with the control points \(P_{i-n},\ldots ,P_{i}.\) Suppose that \(x_{k+1}=x_{k+2}=\cdots =x_{k+\mu }\) and \(x_{k+\mu +1}\ne x_{k+\mu }\) for some \(\mu \leqslant n.\) We need to show that for every \(m=0,\ldots ,n-\mu ,\)

$$\begin{aligned} S^{(m)}_{k}(x_{k+1})=S^{(m)}_{k+\mu }(x_{k+1}). \end{aligned}$$
(18)

The curves \(S_{k}\) and \(S_{k+\mu }\) have \(n+1-\mu \) common control points \(P_{k-n+\mu },\ldots ,P_{k}\) and \(2n-\mu \) common knots \(x_{k-n+\mu +1},\ldots x_{k+n}.\) Now let \(s_{j}\) denote the polar form of \(S_{j},j=n,n+1,\ldots .\) Then by the dual functional property

$$\begin{aligned} P_{i}&=s_{k}\left( (\gamma _{1}(x_{i+1}),\gamma _{2}(x_{i+1})),\ldots ,(\gamma _{1}(x_{i+n}),\gamma _{2}(x_{i+n}))\right) \nonumber \\&=s_{k+\mu }\left( (\gamma _{1}(x_{i+1}),\gamma _{2}(x_{i+1})),\ldots ,(\gamma _{1}(x_{i+n}),\gamma _{2}(x_{i+n}))\right) \end{aligned}$$
(19)

for \(i=k-n+\mu ,\ldots ,k.\) The common knots that appear as common parameters in the polar forms of these common control points are \(\{x_{k+1},\ldots ,x_{k+\mu }\}.\) Now consider the symmetric, multilinear functions

$$\begin{aligned}&\tilde{s}_{k}((u_{1},w_{1}),\ldots ,(u_{n-\mu },w_{n-\mu }))\\&\quad =s_{k}((\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),\ldots ,(\gamma _{1}(x_{k+\mu }),\gamma _{2}(x_{k+\mu })),(u_{1},w_{1}),\ldots ,(u_{n-\mu },w_{n-\mu })) \end{aligned}$$

and

$$\begin{aligned}&\tilde{s}_{k+\mu }((u_{1},w_{1}), \ldots ,(u_{n-\mu },w_{n-\mu }))\\&\quad =s_{k+\mu }\!((\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),\ldots ,(\gamma _{1}(x_{k+\mu }),\gamma _{2}(x_{k+\mu })),(u_{1},w_{1}),\ldots ,(u_{n-\mu },w_{n-\mu }))\!. \end{aligned}$$

From (19) it follows that

$$\begin{aligned} \tilde{s}_{k}&((\gamma _{1}(x_{k-n+\mu +1}),\gamma _{2}(x_{k-n+\mu +1})),\ldots ,(\gamma _{1}(x_{k}),\gamma _{2}(x_{k})))\\&=\tilde{s}_{k+\mu }((\gamma _{1}(x_{k-n+\mu +1}),\gamma _{2}(x_{k-n+\mu +1})),\ldots ,(\gamma _{1}(x_{k}),\gamma _{2}(x_{k}))),\\ \tilde{s}_{k}&((\gamma _{1}(x_{k-n+\mu +2}),\gamma _{2}(x_{k-n+\mu +2})),\ldots ,(\gamma _{1}(x_{k}),\gamma _{2}(x_{k})),(\gamma _{1}(x_{k+\mu +1}),\gamma _{2}(x_{k+\mu +1})))\\&=\tilde{s}_{k+\mu }((\gamma _{1}(x_{k-n+\mu +2}),\gamma _{2}(x_{k-n+\mu +2})),\ldots ,(\gamma _{1}(x_{k}),\gamma _{2}(x_{k})),(\gamma _{1}(x_{k+\mu +1}),\\&\qquad \gamma _{2}(x_{k+\mu +1}))),\\&\qquad \vdots \\ \tilde{s}_{k}&((\gamma _{1}(x_{k+\mu +1}),\gamma _{2}(x_{k+\mu +1})),\ldots ,(\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n})))\\&=\tilde{s}_{k+\mu }((\gamma _{1}(x_{k+\mu +1}),\gamma _{2}(x_{k+\mu +1})),\ldots ,(\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n}))). \end{aligned}$$

That is, for the knot vector \((x_{k-n+\mu +1},\ldots ,x_{k},x_{k+\mu +1},\ldots ,x_{k+n})\) of size \(2(n-\mu ),\) the functions \(\tilde{s}_{k}\) and \(\tilde{s}_{k+\mu }\) agree at each sequence of \(n-\mu \) consecutive knots. Therefore by the recursive evaluation algorithm for symmetric multilinear functions, it follows that

$$\begin{aligned} \tilde{s}_{k}((u_{1},w_{1}),\ldots ,(u_{n-\mu },w_{n-\mu }))=\tilde{s}_{k+\mu }((u_{1},w_{1}),\ldots ,(u_{n-\mu },w_{n-\mu })) \end{aligned}$$

or equivalently

$$\begin{aligned} s_{k}&((\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),\ldots ,(\gamma _{1}(x_{k+\mu }),\gamma _{2}(x_{k+\mu })),(u_{1},w_{1}),\ldots ,(u_{n-\mu },w_{n-\mu }))\\&=s_{k+\mu }((\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),\ldots ,(\gamma _{1}(x_{k+\mu }),\gamma _{2}(x_{k+\mu })),(u_{1},w_{1}),\ldots ,(u_{n-\mu },w_{n-\mu })). \end{aligned}$$

But by assumption \(x_{i}=x_{k+1},\ i=k+1,\ldots ,k+\mu .\) Therefore for any \(0\leqslant m\leqslant n-\mu ,\) and any \(l\in \lambda _{n}(m),\) setting

$$\begin{aligned} (u_{r},w_{r})=\left\{ \begin{array}{ll} (\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),&{}\quad r> |l|\\ \left( \gamma _{1}^{(l_{r})}(x_{k+1}),\gamma ^{(l_{r})}_{2}(x_{k+1})\right) ,&{}\quad r\leqslant |l| \end{array} \right. \end{aligned}$$

we conclude that

$$\begin{aligned}&s_{k}\left( \left( \gamma _{1}^{(l_{1})}\right. \right. (x_{k+1})\left. \left. ,\gamma ^{(l_{1})}_{2}(x_{k+1})\right) ,\ldots \left( \gamma _{1}^{(l_{|l|})}(x_{k+1}),\gamma ^{(l_{|l|})}_{2}(x_{k+1})\right) ,\left( \gamma _{1}(x_{k+1}),\right. \right. \nonumber \\&\quad \quad \left. \left. \gamma _{2}(x_{k+1})\right) ^{n-|l|}\right) \nonumber \\&\quad =s_{k+\mu }\left( \left( \gamma _{1}^{(l_{1})}(x_{k+1}),\gamma ^{(l_{1})}_{2}(x_{k+1})\right) ,\ldots \left( \gamma _{1}^{(l_{|l|})}(x_{k+1}),\gamma ^{(l_{|l|})}_{2}(x_{k+1})\right) ,\left( \gamma _{1}(x_{k+1}),\right. \right. \nonumber \\&\quad \quad \left. \left. \gamma _{2}(x_{k+1})\right) ^{n-|l|}\right) , \end{aligned}$$
(20)

for all \(l\in \lambda _{n}(m).\) Thus (18) follows from Theorem 1 and (20). \(\square \)

Theorem 5

Let \(S\in \sigma _{n}(\gamma _{1},\gamma _{2})\) be defined over the knot sequence \(\{\xi _{i}\}_{i=1}^{l}\) with \(C^{n-\mu _{i}}\) continuity at the knot \(\xi _{i},\ i=2,\ldots ,l-1.\) Then S is a B-spline curve.

Proof

Let \(S_{i}\) denotes the curve segment of S over the interval \([\xi _{i},\xi _{i+1}]\) and let \(s_{i}\) be the polar form of \(S_{i}.\) By assumption

$$\begin{aligned} S^{(m)}_{i-1}(\xi _{i})=S^{(m)}_{i}(\xi _{i}), \end{aligned}$$
(21)

\(m=0,\ldots ,n-\mu _{i},\ i=2,\ldots ,l-1.\) Set \(k_{1}=n,\ k_{2}=n+1\) and define recursively

$$\begin{aligned} k_{i+1}=k_{i}+\mu _{i},\quad i=2,\ldots ,l-1. \end{aligned}$$

Now set \(x_{k_{i}}=\xi _{i},\ i=1,\ldots ,l\) and \(x_{k}=x_{k_{i}},\) \(k=k_{i}+1,\ldots ,k_{i+1}-1,\) \(i=2,\ldots ,l-1.\) Then the rest of the proof is similar to the proof of [25, Theorem 6.3] and follows from (21) and Theorem 1. \(\square \)

6 Knot insertion

For classical splines, knot insertion is a powerful method for analyzing B-spline curves. There are two standard knot insertion algorithms: Boehm’s knot insertion algorithm and the Oslo algorithm. Boehm’s knot insertion algorithm inserts one new knot at a time [5]; in contrast, the Oslo algorithm inserts many distinct knots simultaneously [6].

In Boehm’s knot insertion algorithm if we wish to insert a knot t into the interval \([x_{i},x_{i+1}],\) then the new knot splits the original polynomial that corresponds to the interval \([x_{i},x_{i+1}]\) into two new polynomial segments. Using the polar form of the control points for the two new segments, Goldman [9] shows that Boehm’s knot insertion algorithm is a subset of the de Boor algorithm. That is, the new control points of the new segments are exactly the values computed in the first level of the polar form algorithm for the original B-spline curve.

Using the same point of view, Goldman [9] also shows that the values of the polar form for each new control point generated from the Oslo algorithm can be evaluated by the recursive evaluation algorithm for the polar form of the original B-spline curve. That is, the Oslo algorithm is the polar form evaluation algorithm. An improved version of the Oslo algorithm is also given in [9].

Since we define the de Boor evaluation algorithm using the recursive evaluation algorithm for homogeneous polar forms, we also have analogous knot insertion algorithms for non polynomial B-spline curves. Similar to classical B-splines to find new control points using Boehm’s knot insertion algorithm, we run the de Boor evaluation algorithm one level and read the new control points from the polar forms on the first level of the algorithm. For Goldman’s improved Oslo algorithm the new control points can be computed by running the polar form evaluation algorithm twice and reading the new control points off the left and right lateral edges of the algorithm. For details see [9].

Naturally, one may ask under what conditions the control polygons generated by knot insertion for splines in \(\sigma _{n}(\gamma _{1},\gamma _{2})\) converge to the original spline curve? For two differentiable, locally linearly independent functions \( \gamma _{1} \) and \( \gamma _{2} \) the control polygons generated by knot insertion algorithms converge to the original B-spline curve if the function \(d(a,b)=\gamma _{1}(a)\gamma _{2}(b)-\gamma _{1}(b)\gamma _{2}(a)\) never vanishes for arbitrary values of \(a\text { and }b.\) Convergence is guaranteed by the diagonal property; that is, the control polygons generated by knot insertion converge to the B-spline curve for the original control polygon as the knot spacing approaches zero. The proof is identical to the proof for classical B-splines [10]; simply replace the classical polar form by the homogeneous polar form.

6.1 Conversion to piecewise Bernstein Bézier form

By applying knot insertion algorithms to a B-spline curve, we can express the same B-spline curve with respect to another knot sequence. We can also apply knot insertion algorithms to convert from B-spline to piecewise Bernstein-Bézier form. This approach allows us to analyse B-spline curves, simply by analysing the corresponding Bernstein Bézier curve segments.

Consider a B-spline curve segment \(G_{j}\) of degree n defined over a knot sequence \(x_{j+1},x_{j+2},\ldots ,x_{j+2n}\) and let \(g_{j}\) bt the polar form of \(G_{j}.\) Here, we are interested only in the interval \([x_{j+n},x_{j+n+1}].\) By the dual functional property, the B-spline control points of \(G_{j}\) are

$$\begin{aligned} g_{j}((\gamma _{1}(x_{j+1+k}),\gamma _{2}(x_{j+1+k})),\ldots ,(\gamma _{1}(x_{j+n+k}),\gamma _{2}(x_{j+n+k}))), \quad k=0,1,\ldots ,n. \end{aligned}$$

It is shown in [8] that the Bernstein Bézier control points of \(G_{j}\) are

$$\begin{aligned} g_{j}\left( (\gamma _{1}(x_{j+n}),\gamma _{2}(x_{j+n}))^{n-k},(\gamma _{1}(x_{j+n+1}),\gamma _{2}(x_{j+n+1}))^{k}\right) ,\quad k=0,1,\ldots ,n. \end{aligned}$$

Thus, we can get the Bernstein Bézier control points from the B-spline control points by inserting the knots \( \underbrace{x_{j+n},\ldots ,x_{j+n}}_{n-1\text { times}},\underbrace{x_{j+n+1},\ldots ,x_{j+n+1}}_{n-1\text { times}} \) between the knots \(x_{j+n}\) and \(x_{j+n+1}.\)

Next, we are going to use the Bernstein Bézier representation of B-spline curves to establish necessary conditions for the variation diminishing property to hold for B-spline curves. A curve S(x) with control points \(\{P _0,P _1,\ldots , P _m\}\) is said to be variation diminishing if for any hyper-plane h the number of intersections of h and S(x) is bounded by the number of intersections of h with the control polygon generated by the control points \(\{P _0,P _1,\ldots , P _m\}.\) The following result on the variation diminishing property for Bernstein Bézier curves is proved in [8].

Proposition 1

If \(\frac{d}{dx}\left( \frac{d(a,x)}{d(a,b)}\right) >0,\) and \(\frac{d}{dx}\left( \frac{d(x,b)}{d(a,b)}\right) <0\) on [a, b],  and the Bernstein basis functions on [a, b] form a partition of unity, then the corresponding Bernstein Bézier curves are variation diminishing.

Theorem 6

If \(1\in {\text {span}}\{\gamma _{1},\gamma _{2}\},\) \(\displaystyle \frac{d(x,x_{k+n+1})}{d(x_{k+r},x_{k+n+1})}\) and \(\displaystyle \frac{d(x_{k+r},x)}{d(x_{k+r},x_{k+n+1})},\) \(k=1,\ldots , n-r,\) \(r=1,\ldots ,n\) are positive and \(\displaystyle \frac{d}{dx}\left( \frac{d(x_{i},x)}{d(x_{i},x_{i+1})}\right) >0,\) \(\displaystyle \frac{d}{dx}\!\left( \frac{d(x,x_{i+1})}{d(x_{i},x_{i+1})}\right) <0,\) for all i,  then the corresponding B-spline curves are variation diminishing.

Proof

If \(1\in {\text {span}}\{\gamma _{1},\gamma _{2}\},\) then for any a, b with \(d(a,b)\ne 0,\) \(\displaystyle \frac{d(x,b)}{d(a,b)}\) and \(\displaystyle \frac{d(a,x)}{d(a,b)}\) sum to one (see [8]). Hence the Bernstein basis functions \( B^{n}_{k}(x) \) on [a, b] form a partition of unity since by [8]

$$\begin{aligned} \sum _{k=0}^{n}B^{n}_{k}(x)=\left( \frac{d(x,b)}{d(a,b)} + \frac{d(a,x)}{d(a,b)}\right) ^{n}=1. \end{aligned}$$

On the other hand, since \(\displaystyle \frac{d(x,x_{k+n+1})}{d(x_{k+r},x_{k+n+1})}\) and \(\displaystyle \frac{d(x_{k+r},x)}{d(x_{k+r},x_{k+n+1})}\) are positive and sum to one, the de Boor algorithm is a corner-cutting procedure. Since knot insertion is the polar form interpretation of the de Boor algorithm, knot insertion is also a corner-cutting procedure. Therefore, the control polygon for the piecewise Bernstein Bézier representation of the original B-spline curve is variation diminishing with respect to the original B-spline control polygon. But by Proposition 1 each Bernstein Bézier segment is variation diminishing with respect to its Bernstein Bézier control polygon whenever \(\displaystyle \frac{d}{dx}\left( \frac{d(x_{i},x)}{d(x_{i},x_{i+1})}\right) >0,\) \(\displaystyle \frac{d}{dx}\left( \frac{d(x,x_{i+1})}{d(x_{i},x_{i+1})}\right) <0,\) for all i. Hence the entire curve must be variation diminishing with respect to the original B-spline control polygon. \(\square \)

For example if \( \gamma _{1}(x)=\sinh ^{2}(x) \) and \( \gamma _{2}(x)=\cosh ^{2}(x), \) then by Theorem 6 the B-spline curve of degree n with an increasing knot sequence \(x_{1}<x_{2}<\cdots < x_{2n}<\cdots \) is variation diminishing whenever \(x_{i}>0\) for all i or \(x_{i}<0\) for all i.

7 B-spline basis functions

Just like classical B-spline curves, B-spline curves in \(\sigma _{n}(\gamma _{1},\gamma _{2})\) can be represented in terms of compactly supported basis functions. For any B-spline curve \(S\in \sigma _{n}(\gamma _{1},\gamma _{2})\) with control points \(P_{k}\) and knot sequence \(\{x_{k}\},\) we seek functions \(\{N_{k,n}\in \sigma _{n}(\gamma _{1},\gamma _{2})\}\) such that

$$\begin{aligned} S(x)=\sum \limits _{k}^{}N_{k,n}(x)P_{k}. \end{aligned}$$
(22)

The basis functions \(N_{k,n}\) can be computed from the global de Boor algorithm by setting

$$\begin{aligned} P_{j}=\left\{ \begin{array}{ll} 0,&{}\quad j\ne k\\ 1,&{}\quad j=k. \end{array} \right. \end{aligned}$$

Now (22) follows by linearity.

As in the classical case the functions \(\{N_{k,n}\}\) are called the B-spline basis functions. Also as in the classical case (see [10]), the B-spline basis functions can be computed by placing 1 at each apex and reversing all the arrows in the global de Boor algorithm. In this case, the B-spline basis functions emerge at the base of the diagram. It follows that the B-spline basis functions satisfy the following recurrence.

$$\begin{aligned} N_{k,0}(x)=\left\{ \begin{array}{ll} 1,&{}\quad \text {if } x_{k}\leqslant x< x_{k+1}\\ 0,&{}\quad \text {otherwise.} \end{array} \right. \end{aligned}$$
$$\begin{aligned} N_{k,n}(x)=\frac{d(x_{k},x)}{d(x_{k},x_{k+n})}N_{k,n-1}(x)+ \frac{d(x,x_{k+n+1})}{d(x_{k+1},x_{k+n+1})}N_{k+1,n-1}(x). \end{aligned}$$
(23)

Thus it follows easily by induction on n that \(supp\{N_{k,n}\}=[x_{k},x_{k+n+1}].\)

Example 1

If \(\gamma _{1}(x)=1,\,\gamma _{2}(x)=x,\) then \(\pi _{n}(\gamma _{1},\gamma _{2})\) is the space of polynomials of degree n and \(d(a,b)=b-a.\) Thus

$$\begin{aligned} N_{k,n}(x)=\frac{x-x_{k}}{x_{k+n}-x_{k}}N_{k,n-1}(x)+ \frac{x_{k+n+1}-x}{x_{k+n+1}-x_{k+1}}N_{k+1,n-1}(x) \end{aligned}$$

are the classical B-spline basis functions.

Example 2

If \(\gamma _{1}(x)=\sin (x),\gamma _{2}(x)=\cos (x),\) then \(\pi _{n}(\gamma _{1},\gamma _{2})\) is the space of trigonometric polynomials of degree n (see [11]). In this case \(d(a,b)=\sin (a-b)\) and

$$\begin{aligned} N_{k,n}(x)=\frac{\sin (x_{k}-x)}{\sin (x_{k}-x_{k+n})}N_{k,n-1}(x)+ \frac{\sin (x-x_{k+n+1})}{\sin (x_{k+1}-x_{k+n+1})}N_{k+1,n-1}(x) \end{aligned}$$

are the trigonometric B-spline basis functions (see [16]).

Example 3

If \(\gamma _{1}(x)=\sin ^{2}(x),\gamma _{2}(x)=\cos ^{2}(x),\) then \( d(a,b)=\frac{1}{2}\big (\cos (2b) - \cos (2a)\big ). \) Thus,

$$\begin{aligned} N_{k,n}(x)=\frac{\cos (2x) - \cos (2x_{k})}{\cos (2x_{k+n}) - \cos (2x_{k})}N_{k,n-1}(x)+ \frac{\cos (2x_{k+n+1}) - \cos (2x)}{\cos (2x_{k+n+1}) - \cos (2x_{k+1})}N_{k+1,n-1}(x). \end{aligned}$$

Example 4

If \(\gamma _{1}(x)=\sinh (x),\gamma _{2}(x)=\cosh (x),\) then \(d(a,b)=\sinh (a-b)\) and

$$\begin{aligned} N_{k,n}(x)=\frac{\sinh (x_{k}-x)}{\sinh (x_{k}-x_{k+n})}N_{k,n-1}(x)+ \frac{\sinh (x-x_{k+n+1})}{\sinh (x_{k+1}-x_{k+n+1})}N_{k+1,n-1}(x) \end{aligned}$$

are the hyperbolic B-spline basis functions.

Example 5

If \(\gamma _{1}(x)=\sinh ^{2}(x),\gamma _{2}(x)=\cosh ^{2}(x),\) then \( d(a,b)=\frac{1}{2}\big (\cosh (2a) - \cosh (2b)\big ). \) Thus,

$$\begin{aligned} N_{k,n}(x)= & {} \frac{\cosh (2x) - \cosh (2x_{k})}{\cosh (2x_{k+n}) - \cosh (2x_{k})}N_{k,n-1}(x)\\&+ \frac{\cosh (2x_{k+n+1}) - \cosh (2x)}{\cos (2x_{k+n+1}) - \cos (2x_{k+1})}N_{k+1,n-1}(x). \end{aligned}$$

Example 6

If \(\gamma _{1}(x)=x^{i}\) and \(\gamma _{2}(x)=x^{j},\) then \(\pi _{n}(\gamma _{1},\gamma _{2})\) is a Müntz space generated by \(\{x^{(n-k)i+kj}\}_{k=0}^{n}.\) In this case \(d(a,b)=a^{i}b^{j}-a^{j}b^{i}\) and

$$\begin{aligned} N_{k,n}(x)= & {} \frac{(x_{k})^{i}x^{j}-(x_{k})^{j}x^{i}}{(x_{k})^{i}(x_{k+n})^{j}-(x_{k})^{j}(x_{k+n})^{i}}N_{k,n-1}(x)\\&+\frac{x^{i}(x_{k+n+1})^{j}-x^{j}(x_{k+n+1})^{i}}{(x_{k+1})^{i}(x_{k+n+1})^{j}-(x_{k+1})^{j}(x_{k+n+1})^{i}}N_{k+1,n-1}(x). \end{aligned}$$

Notice here that i and j may be either positive or negative numbers.

Example 7

If \(\gamma _{1}(x)=\left\{ \begin{array}{ll} -x^{4},&{}\quad x<\frac{3}{2},\\ x-\frac{105}{16},&{}\quad x\geqslant \frac{3}{2} \end{array}\right. \) and \(\gamma _{2}(x)=x,\) then for any \(u<v\) we have

$$\begin{aligned} d(u,v)=\left\{ \begin{array}{ll} -u^{4}v+v^{4}u,&{}\quad v<\frac{3}{2},\\ -u^{4}v-\left( v-\frac{105}{16}\right) u,&{}\quad u<\frac{3}{2}\leqslant v,\\ \left( u-\frac{105}{16}\right) v-\left( v-\frac{105}{16}\right) u,&{}\quad \frac{3}{2}\leqslant u. \end{array}\right. \end{aligned}$$

In this case; if the support of the B-spline basis functions contains the value \(\frac{3}{2},\) then the B-splines are not differentiable at that point.

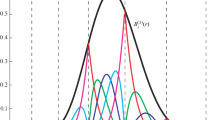
By changing the functions \(\gamma _{1}(x)\) and \(\gamma _{2}(x)\) it is possible to generate infinitely many distinct B-spline bases. Some illustrations of B-splines are given in Figs. 7, 8, 9, 10. In each case the knot sequence is \(\{1.2,1.3,\ldots ,1.8\}.\)

Fig. 7
figure 7

B-splines in \(\sigma _{3}(\gamma _{1},\gamma _{2})\) for \(\gamma _{1}(x)=\cos ^{2}(x)\) and \(\gamma _{2}(x)=\sin ^{2}(x)\)

Full size image
Fig. 8
figure 8

B-splines in \(\sigma _{3}(\gamma _{1},\gamma _{2})\) for \(\gamma _{1}(x)=x^{-0.5}\) and \(\gamma _{2}(x)=x^{2}\)

Full size image
Fig. 9
figure 9

B-splines in \(\sigma _{3}(\gamma _{1},\gamma _{2})\) for \(\gamma _{1}(x)=\cosh ^{2}x\) and \(\gamma _{2}(x)=\sinh ^{2}x\)

Full size image
Fig. 10
figure 10

B-splines in \(\sigma _{3}(\gamma _{1},\gamma _{2})\) for \(\gamma _{1}(x)=(-x^{4},x<3/2,x-105/16,x\geqslant 3/2)\) and \(\gamma _{2}(x)=x\)

Full size image

7.1 Properties and identities for B-spline basis functions

In this section we study properties and identities for the B-spline basis functions, including the dual functional property, Marsden’s identity, partition of unity, curvilinear precision, interpolation and differentiation.

Proposition 2

(Dual functional property) Let \(G(x)=\sum _{k}^{}P_{k}N_{k,n}(x)\) be a B-spline curve with knots \(\{x_{i}\}.\) Then

$$\begin{aligned} P_{k}=g((\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),\ldots ,(\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n}))). \end{aligned}$$
(24)

Proof

This result follows easily from (8). \(\square \)

Theorem 7

(Marsden Identity)

$$\begin{aligned} \left( d(x,t)\right) ^{n}=\sum _{k}^{}\left[ \prod _{i=1}^{n}d(x_{k+i},t)\right] N_{k,n}(x). \end{aligned}$$
(25)

Proof

Since \(d(x,t)=\gamma _{1}(x)\gamma _{2}(t)-\gamma _{1}(t)\gamma _{2}(x)\) is a linear combination of \(\gamma _{1}(x)\) and \(\gamma _{2}(x),\) \(\left( d(x,t)\right) ^{n}\in \pi _{n}(\gamma _{1},\gamma _{2}).\) The polar form of \(G(x)=\left( d(x,t)\right) ^{n}\) is

$$\begin{aligned} g((u_{1},w_{1}),\ldots ,(u_{n},w_{n}))=\prod _{i=1}^{n}\left( u_{i}\gamma _{2}(t)-\gamma _{1}(t)w_{i}\right) \end{aligned}$$

since the right-hand side is symmetric, multi-linear, and reduces G(x) along the \((\gamma _{1},\gamma _{2})\) diagonal. Thus by the dual functional property (24)

$$\begin{aligned} \left( d(x,t)\right) ^{n}=&\sum _{k}^{}g((\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),\ldots ,(\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n})))N_{k,n}(x)\\ =&\sum _{k}^{}\left[ \prod _{i=1}^{n}d(x_{k+i},t)\right] N_{k,n}(x). \end{aligned}$$

\(\square \)

Theorem 8

(Partition of unity) If \(1\in \pi _{n}(\gamma _{1},\gamma _{2}),\) then \(\sum _{k}^{}N_{k,n}(x)=1.\)

Proof

The polar form of the function \(G(x)=1\) is \(g((u_{1},w_{1}),\ldots ,(u_{n},w_{n}))=1.\) Therefore this result follows immediately from the dual functional property. \(\square \)

For curves the variation diminishing property (Theorem 6) is important for design. Another essential property for curves, weaker than the variation diminishing property, is the convex hull property. The following theorem presents a convex hull property for B-spline curves.

Theorem 9

If \(1\in \pi _{n}(\gamma _{1},\gamma _{2})\) and the functions \( \frac{d(x_{k},x)}{d(x_{k},x_{k+n})},\ \frac{d(x,x_{k+n+1})}{d(x_{k+1},x_{k+n+1})} \) in (23) are positive then the basis functions form a convex partition of unity. Therefore in this case the corresponding B-spline curves lie in the convex hull of their control points.

Proof

Clearly since the coefficients in (23) are positive, the basis functions are positive. Thus this result follows form Theorem 8. \(\square \)

For example if \(\frac{\gamma _{2}}{\gamma _{1}}\) is an increasing function, then since \(d(u,v)>0\) for all \(u<v,\) the functions \( \frac{d(x_{k},x)}{d(x_{k},x_{k+n})}, \) and \( \frac{d(x,x_{k+n+1})}{d(x_{k+1},x_{k+n+1})} \) are positive in the support of \(N_{k,n}.\) Hence any B-spline curve of the form \(\sum _{k}P_{k}N_{k,n}\) lies in the convex hull of the control points \(\{P_{k}\}.\)

Theorem 10

(Curvilinear precision) If \(1\in \text {span}\{\gamma _{1},\gamma _{2}\},\) then for any \(c_{1},c_{2}\in \mathbb {R}\)

$$\begin{aligned} c_{1}\gamma _{1}(x)+c_{2}\gamma _{2}(x)=\sum _{k}^{}\left[ \sum _{i=1}^{n}\frac{c_{1}\gamma _{1}(x_{k+i})+c_{2}\gamma _{2}(x_{k+i})}{n}\right] N_{k,n}(x). \end{aligned}$$
(26)

Proof

If \(1\in \text {span}\{\gamma _{1},\gamma _{2}\},\) then \(1\in \pi _{n-1}(\gamma _{1},\gamma _{2})\) so \(\gamma _{1},\gamma _{2}\in \pi _{n}(\gamma _{1},\gamma _{2}).\) Moreover the polar forms of the functions \(\gamma _{1}(x)\) and \(\gamma _{2}(x)\) are \(\displaystyle \frac{u_{1}+\cdots +u_{n}}{n}\) and \(\displaystyle \frac{w_{1}+\cdots +w_{n}}{n}.\) Hence this result follows from the dual functional property of B-spline curves and the linearity of the polar forms. \(\square \)

Theorem 11

Let \(x_{k+1}=x_{k+2}=\cdots =x_{k+n}.\) Then the B-spline curve interpolates the control point \(P_{k}.\)

Proof

Suppose that \(x_{k+1}=x_{k+2}=\cdots =x_{k+n}\) and consider the B-spline segment \(S_{k+n}\) over the knot interval \([x_{k+n},x_{k+n+1}].\) Then by dual functional property the initial control point of this segment is

$$\begin{aligned} P_{k}&=s_{k+n}((\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1})),\ldots ,(\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n})))\\&=s_{k+n}((\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n})),\ldots ,(\gamma _{1}(x_{k+n}),\gamma _{2}(x_{k+n})))\\&=S_{k+n}(x_{k+n}). \end{aligned}$$

\(\square \)

We close with a recurrence for the derivatives of the B-spline basis functions. But first we need some preliminary results.

Theorem 12

(Recurrence for the polar form of the B-spline basis functions) Let \(\tilde{n}_{k,n}\) denote the polar form of the B-spline basis function \(N_{k,n}.\) Then

$$\begin{aligned}&\tilde{n}_{k,n}((\gamma _{1}(u_{1}),\gamma _{2}(u_{1})),\ldots ,(\gamma _{1}(u_{n}),\gamma _{2}(u_{n})))\nonumber \\&\quad =\frac{d(x_{k},u_{1})}{d(x_{k},x_{k+n})}\tilde{n}_{k,n-1}((\gamma _{1}(u_{2}),\gamma _{2}(u_{2})),\ldots ,(\gamma _{1}(u_{n}),\gamma _{2}(u_{n}))) \nonumber \\&\qquad +\frac{d(u_{1},x_{k+n+1})}{d(x_{k+1},x_{k+n+1})}\tilde{n}_{k+1,n-1}((\gamma _{1}(u_{2}),\gamma _{2}(u_{2})),\ldots ,(\gamma _{1}(u_{n}),\gamma _{2}(u_{n}))) \end{aligned}$$
(27)

Proof

By the recursive evaluation algorithm for polar forms (6), the polar form of a B-spline curve \(G\in \sigma _{n}(\gamma _{1},\gamma _{2})\) with control points \(\{P^{0}_{j}\}\) satisfies

$$\begin{aligned}&g((\gamma _{1}(u_{1}),\gamma _{2}(u_{1})),\ldots ,(\gamma _{1}(u_{n}),\gamma _{2}(u_{n})))\nonumber \\&\quad =\sum _{i}^{}P^{0}_{i}\, \tilde{n}_{i,n}((\gamma _{1}(u_{1}),\gamma _{2}(u_{1})),\ldots ,(\gamma _{1}(u_{n}),\gamma _{2}(u_{n})))\nonumber \\&\quad =\sum _{i}^{}P^{1}_{i}\, \tilde{n}_{i+1,n-1}((\gamma _{1}(u_{2}),\gamma _{2}(u_{2})),\ldots ,(\gamma _{1}(u_{n}),\gamma _{2}(u_{n}))), \end{aligned}$$
(28)

where

$$\begin{aligned} P^{1}_{i}=\frac{d(u_{1},x_{i+n+1})}{d(x_{i+1},x_{i+n+1})}P^{0}_{i}+\frac{d(x_{i+1},u_{1})}{d(x_{i+1},x_{i+n+1})}P^{0}_{i+1}. \end{aligned}$$

Now setting \(P^{0}_{i}=\delta _{i,k}\) gives (27). \(\square \)

Consider the recursive evaluation algorithm (6) for the polar form of a function \(G\in \pi _{n}(\gamma _{1},\gamma _{2}).\) What happens if we modify the recurrence by differentiating the recurrence at level \(r=1\) with respect to \(u_{1}\) and do not change the recurrence for the subsequent levels \(r\geqslant 2?\) In this case the coefficients in the first level of the algorithm turn into the solutions of the system

$$\begin{aligned} a(\gamma _{1}(x_{k+1}),\gamma _{2}(x_{k+1}))+b(\gamma _{1}(x_{k+n+1}),\gamma _{2}(x_{k+n+1}))=\!\left( \frac{\partial }{\partial u_{1}}\gamma _{1}(u_{1}),\frac{\partial }{\partial u_{1}}\gamma _{2}(u_{1})\!\right) .\nonumber \\ \end{aligned}$$
(29)

Hence the function \(\tilde{b}^{n}_{0}\) that emerges at the apex of the modified algorithm is

$$\begin{aligned} \tilde{b}^{n}_{0}(u_{1},\ldots ,u_{n})= & {} g\left( \left( \frac{\partial }{\partial u_{1}}\gamma _{1}(u_{1}),\frac{\partial }{\partial u_{1}}\gamma _{2}(u_{1})\right) ,(\gamma _{1}(u_{2}),\gamma _{2}(u_{2})),\ldots ,\right. \nonumber \\&\left. (\gamma _{1}(u_{n}),\gamma _{2}(u_{n}))\right) . \end{aligned}$$
(30)

Setting \(u_{i}=x,\) for \(i=1,\ldots ,n\) in (30) gives

$$\begin{aligned} \tilde{b}^{n}_{0}(x,\ldots ,x)=g((\gamma '_{1}(x),\gamma '_{2}(x)),(\gamma _{1}(x),\gamma _{2}(x))^{n-1}). \end{aligned}$$
(31)

Theorem 13

$$\begin{aligned} \frac{d}{dx}N_{k,n}(x)= & {} n\left[ \left( \frac{d}{dx}\frac{d(x_{k},x)}{d(x_{k},x_{k+n})}\right) N_{k,n-1}(x)\right. \nonumber \\&+\left. \left( \frac{d}{dx}\frac{d(x,x_{k+n+1})}{d(x_{k+1},x_{k+n+1})}\right) N_{k+1,n-1}(x) \right] \end{aligned}$$
(32)

Proof

This result follows immediately from (27), (31) and (4). \(\square \)