Introduction

The artificial ground freezing (AGF) method is a special reinforcement technology widely used in soft soil areas or water-rich strata that has the characteristics of strong adaptability and non-pollution (Kang et al. 2016). The AGF method has been widely applied in the construction of coal mine shafts (Vitel et al. 2016), subway shafts (Kim et al. 2012; Yang et al. 2017), subway tunnels (Pimentel et al. 2012; Vitel et al. 2015), and subway cross passages (Fan and Yang 2019; Wu et al. 2021; Yan et al. 2017). The basic principle of the AGF method, mainly composed of the water, brine, and refrigeration circulation systems, is illustrated in Fig. 1 (Yan et al. 2019). The frozen curtain formed by the AGF method is a high strength and impermeable temporary support structure, while the safety of engineering construction could be reliably ensured.

Fig. 1
figure 1

A typical AGF system

Full size image

So far, AGF has attracted extensive attention from researchers all over the world. Scholars have conducted a great deal of research focusing on the expansion characteristics of the temperature field (Alzoubi et al. 2018; Anagnostou et al. 2012; Kim et al. 2012; Lackner et al. 2005; Pimentel et al. 2012; Zueter et al. 2021), the mechanical properties of frozen soil (Lackner et al. 2008; Ou et al. 2009), the thermo-hydro-mechanical coupling (Casini et al. 2016; Marwan et al. 2016; Tounsi et al. 2019), and the frost heave and thaw displacement (Zhou and Tang 2015, 2018). However, by comparison, very limited research has been performed on the damage of artificial frozen soil in AGF. The damage to artificial frozen soil will cause strength deterioration and a reduction in the bearing capacity of the frozen curtain, which will threaten the safety of the AGF project.

As X-ray computed tomography (CT) scanning can realize non-destructive testing and observe the internal structure of the specimen that cannot be observed by the naked eye (Torrance et al. 2008), it has been applied to the research of frozen soil by a large number of scholars in recent years (Starkloff et al. 2017; Zhao et al. 2022). Wu et al. (Wu et al. 1996) monitored and analyzed the structure change in frozen soil through CT scanning. Liu et al. (Liu et al. 2002) conducted the relationship between density and CT number of frozen soil based on an additional damage concept. Tang et al. (Tang et al. 2018) proposed a multi-scale method to investigate the microstructural and mechanical changes of expansive soils exposed to freeze-thaw cycles. Ala et al. (Ala et al. 2017) presented the soil structure of fine-grained soil with the CT scanning method. Zhang et al. (Zhang et al. 2019) conducted a series of triaxial compression tests to investigate the micromechanical analysis of the frozen silty clay-sand mixtures with real-time CT scanning. From the aforementioned literature review, it is found that the CT scanning test has been playing an irreplaceable role in the field of geotechnical engineering worldwide.

In the above-mentioned research, scholars primarily focused on the fine-grained soil, which is quite different from the sandy gravel that belongs to the coarse-grained soil with large porosity and high moisture content. Due to the randomness and inhomogeneity of gravel distribution, the mechanical properties of sandy gravel are significantly different from those of fine-grained soil. However, little research has been conducted on coarse-grained soil via CT scanning. Takano et al. (Takano et al. 2015) studied the characteristics of internal strain in wide-grained sand using triaxial compression and CT scanning tests. Li et al. (Li et al. 2021) conducted several triaxial compression and CT scanning tests to explore the dynamic characteristics and microstructural changes of sandy gravel in a frozen region. Zhang et al. (Zhang et al. 2021) used CT scanning tests to study the inner structural characteristics of a clay-gravel composite. The damage law of frozen soil was examined using microscopic techniques in the aforementioned researches. Besides, in terms of macroscopic damage, Lemaitre et al. (Lemaitre and Chaboche 1994) introduced the method of calculating damage at the plastic hardening stage of the stress-strain curve. Liu et al. (Liu et al. 2005) calculated the plastic damage of Lanzhou loess through uniaxial compression tests according to continuous damage mechanics theory. To the best knowledge of the authors, no one has combined macroscopic damage and microscopic damage to study the damage evolution law of frozen sandy gravel.

In this paper, a thorough investigation has been performed to study the damage evolution characteristics of artificial frozen sandy gravel by triaxial compression and CT scanning tests. Combining the experiment results, macro-plastic damage calculation theory, and micro-crack damage calculation theory, the concept of cross-scale modified damage is proposed, which is beneficial to reveal the damage evolution of frozen sandy gravel at both macroscopic and microscopic scales. More importantly, this study will directly provide valuable references to the constitutive model of the artificial frozen sandy gravel and pave the way for the design and numerical simulation of similar AGF projects.

Materials and methods

Experimental sandy gravel

The experimental sandy gravel soil is taken from the strata in the No.1 cross passage of Chengdu Metro Line 10. The test sieves of 10 mm, 5 mm, 2 mm, 1 mm, 0.5 mm, 0.25 mm, and 0.075 mm are used to analyze the particle-size grading of the sandy gravel, as shown in Fig. 2. According to the actual engineering situation, the cross passage is below the groundwater level, and the soil is regarded as saturated. Therefore, the saturated soil is selected in this paper. The sandy gravel is dried and has a saturated moisture content of 19.9%. The saturated sandy gravel is reconstructed according to the dry density of 1.73 g/cm3. The saturated sandy gravel is packed in a sealed container and left for 24 hours. After the moisture is uniform, the specimens are prepared using a standard prototype that consists of the main engine, control box, soil sample box, unloading box, and drainage system. The specimens are standard cylindrical samples with a diameter of 61.8 mm and a height of 125.0 mm. Five layers are tamped and compacted during mold loading. The prepared specimens are first put into cold storage at an ambient temperature of −30 °C for rapid freezing for more than 48 hours. Then the specimens are unmolded and placed in a thermostatic box, where the freezing temperature is set according to the test requirements. After being placed in the thermostatic box for 48 hours, the low-temperature triaxial tests are conducted.

Fig. 2
figure 2

Particle-size grading of experimental sandy gravel

Full size image

Triaxial compression test

The triaxial compression tests of saturated frozen sandy gravel were carried out in the State Key Laboratory of Frozen Soil Engineering, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences. The test instrument is the MTS-810 low-temperature triaxial material test machine, as presented in Fig. 3. The range of the MTS-810 temperature control system is +30 °C to −30.0 °C, with an accuracy of ±0.1 °C. Moreover, the maximum axial loading displacement of the MTS-810 is 50 mm, the maximum axial load is 50 kN, and the maximum confining pressure is 12.0 MPa. The instrument has stress, strain, and multi-channel control modes. In this paper, the control mode of the frozen sandy gravel triaxial compression test is the axial strain control mode, and the loading rate is 1.25 mm/min. Additionally, confining pressure and axial pressure could be controlled synchronously. The triaxial compression test is automatically controlled by the computer, and the data such as time, load, and axial displacement are collected automatically in real time until the end of the test.

Fig. 3
figure 3

MTS-810 low-temperature triaxial material test machine

Full size image

The triaxial tests were conducted in accordance with the national standard of the People’s Republic of China “Standard for Geotechnical Test Methods” GB/T50123–2019(Ministry of Water Resources 2019). On the basis of the design scheme of the actual cross passage AGF project, the design average temperature of the frozen curtain is −10 °C, while the brine temperature is about −25 °C to −30 °C during the active freezing period. Therefore, five negative temperature triaxial compression tests, which are set at −1 °C (determined based on the freezing temperature test results), −5 °C, −10 °C, −15 °C, and − 20 °C, are carried out. Furthermore, the confining pressure of the triaxial compression test should also be consistent with the corresponding stratum pressure where the cross passage is located. When the buried depth is 18–32 m, the stratum pressure is calculated as 0.36–0.64 MPa. Therefore, four confining pressures are designed for each temperature in this triaxial test: 0 kPa, 300 kPa, 600 kPa, and 900 kPa. Under each temperature and confining pressure condition, a sandy gravel specimen is loaded. Firstly, the specimens are put into a cold storage room with an ambient temperature of −30 °C for rapid freezing that lasts more than 48 hours. Secondly, put the specimens into the thermostatic box for more than 24 hours while the freezing temperature is set according to the test requirements. Thirdly, the specimens are put into the pressure chamber and kept at the design experimental temperature for 3–4 hours. Afterwards, the axial pressure and confining pressure are simultaneously applied to the design value and maintained for 2 hours before the triaxial compression test under constant confining pressure. The test is terminated when the specimen develops a 20% strain.

CT scanning test

The CT scanner is a PHILIPS Brilliance16 spiral multi-energy CT scanner, as presented in Fig. 4 (Chen et al. 2017). The CT scanner features 0.208 mm of spatial resolution, 0.3% of density resolution, 90–140 kV of scanning tube voltage, and 30–500 mA of scanning tube current. It has a workstation for processing CT images.

Fig. 4
figure 4

PHILIPS Brilliance16 Spiral X-ray CT scanner

Full size image

As the design average temperature of the frozen curtain is −10 °C, and the average formation pressure calculated according to the burial depth of the cross passage is 600 kPa. The saturated frozen sandy gravel specimens adopted for CT scanning tests are subjected to a temperature of −10 °C and a confining pressure of 600 kPa. The CT scanning test protocol is shown in Fig. 5(a), and it is scanned once when the strain is 0%, 35%, 70%, 100%, and 130% of the failure strain, respectively. Through the triaxial compression tests, the failure strain of the specimen is about 8% when the temperature is −10 °C and the confining pressure is 600 kPa. Therefore, it is set to scan once when the strain is 0, 2.8%, 5.6%, 8%, and 10.4%, respectively. The scanning layers of each specimen are about 40 layers at an interval of 3 mm, as illustrated in Fig. 5(b).

Fig. 5
figure 5

CT scanning test protocol

Full size image

It is not possible to scan while loading because of the constraints placed on the CT scanner. For the CT scanning tests, five specimens that matched the scanning strain were employed, as indicated in Fig. 6. The test is designed to reduce variations brought on by human factors. The five specimens used in this CT scanning test were created from the same batch of soil, and the specimen preparation procedure followed the same national standard.

Fig. 6
figure 6

Specimens after CT scanning test

Full size image

Result analysis

Macro-plastic damage

Deviatoric stress-strain curve

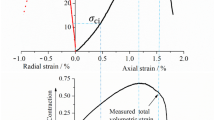
The deviatoric stress-strain curve of the frozen sandy gravel is obtained in Fig. 7. Figure 7 illustrates how, at constant temperature, the deviatoric stress-strain curves of various confining pressures follow the same pattern. However, as confining pressure increases, the bonding force between soil particles and gravels likewise does so, increasing both the peak stress and the accompanying strain. For instance, the peak stress is 4.4 MPa and the corresponding strain is 7% when the temperature is −5 °C and the confining pressure is 0 kPa. While the peak stress is 4.9 MPa and the corresponding strain is 10% when the confining pressure rises to 900 kPa. Moreover, temperature will affect the unfrozen water content in the frozen soil, which in turn affects the bonding strength between soil particles and gravels. The bonding strength between the soil particles and gravels and the deformation ability are stronger at lower temperatures because there is less unfrozen water and more ice. As a result, temperature has a big impact on the peak strength and mechanical characteristics of frozen sandy gravel. Additionally, the peak stress increases with decreasing temperature under the same confining pressure. For instance, with a confining pressure of 300 kPa, the peak stress is around 2.5 MPa at a temperature of −1 °C and 7.8 MPa at −15 °C.

Fig. 7
figure 7

Deviatoric stress-strain curve of frozen sandy gravel

Full size image

The deviatoric stress-strain curve of frozen sandy gravel roughly consists of the following three stages. (1) Initial linear elastic stage. The deviatoric stress grows quickly and approximately in a straight line when the axial strain is less than 1%, demonstrating an elastic feature. The curve has properties of linear elastic because the initial frozen sandy gravel is quite compact and there is little internal damage to the specimen. Additionally, the yield stress in the linear elastic stage considerably rises with lower temperatures. The cause is because the low temperature causes the ice-water phase change in the sandy gravel, which improves the connection between the soil particles, gravel, and ice. (2) Pre-peak plastic stage. The curve gradually shifts from linear to nonlinear as the strain increases. Additionally, the slope of the curve is always greater than 0 prior to the stress peak and steadily lowers with increasing strain. At this stage, irreversible plastic deformation and internal damage have been caused in the frozen specimens, and the anti-deformation ability has been diminished. Additionally, the pre-peak plastic stage lasts longer at higher temperatures. (3) Post-peak stage. The slope of the curve turns negative when the stress peaks, and the stress gradually declines until the specimen collapses. Various confining pressures have different properties in terms of the curve’s form. When the confining pressure is low, the curve exhibits weak post-peak strain softening features, indicating that there is a clear stress peak in this situation. Additionally, the curve displays ideal elastic-plastic properties when the confining pressure is high. The ideal elastic-plastic properties also become more apparent as the temperature drops.

Macro-plastic damage calculation theory

According to the literature (Lemaitre and Chaboche 1994), both thermodynamic and phenomenological experiments in solid physics have confirmed that there is no coupling effect between the elasticity and plasticity of solid materials. In other words, the material deformation can be divided into reversible elastic deformation εe and irreversible inelastic deformation εp. Moreover, εp can be subdivided into hysteretic elastic deformation, plastic deformation, and viscoplastic deformation. Therefore, in the elastic-plastic range, there are:

$${\varepsilon}_p=\varepsilon -{\varepsilon}_e$$
(1)

Each point on the monotonic hardening curve can be regarded as a point representing the plasticity threshold, so the hardening characteristic equation can be written as follows:

$${\sigma}_s={g}^{-1}\left({\varepsilon}_p\right)$$
(2)

When σ = σs, there is plastic flow:

$$\left\{\begin{array}{l}\sigma <{\sigma}_s\to {\dot{\varepsilon}}_p=0\\ {}\sigma ={\sigma}_s\to {\dot{\varepsilon}}_p\ne 0\end{array}\right.$$
(3)

In order to simulate the hardening function, many analytical expressions have been proposed. The expression based on dislocation theory is used in this paper, and the following formula shows that the stress threshold is proportional to the square root of the dislocation density ρd (Lemaitre and Chaboche 1994):

$${\sigma}_s=\kappa b{\rho}_d^{1/2}$$
(4)

In fact, even in the initial state, the dislocation density is never equal to zero. Let ρd0 be the dislocation density corresponding to the elastic limit σy, then:

$${\sigma}_s={\sigma}_y+\kappa b{\left({\rho}_d-{\rho}_{d0}\right)}^{1/2}$$
(5)

The above formula can be expressed by the macroscopic strain as:

$${\sigma}_s={\sigma}_y+{K}_y{\varepsilon_p}^{1/{M}_y}$$
(6)

This equation is known as the Ramberg-Osgood equation, which can be converted into:

$${\varepsilon}_p=g\left({\sigma}_s\right)={\left\langle \frac{\sigma_s-{\sigma}_y}{K_y}\right\rangle}^{M_y}$$
(7)

where σy represents the elastic yield strength of the stress-strain curve; Ky denotes the plastic resistance coefficient; My is the hardening parameter.

After getting σy from the stress-strain curve, Ky and My can be obtained from the double logarithmic curve of ln(σs − σy) and ln(εp) by fitting the following equation:

$$\ln \left({\sigma}_s-{\sigma}_y\right)=\ln {K}_y+\frac{1}{M_y}\ln {\varepsilon}_p$$
(8)

In the monotonic hardening process, once the damage becomes noticeable, that is, ε > εv, where εv is the strain corresponding to the peak stress strength. Based on the principle of strain equivalence related to the concept of effective stress, the above equation can be written as:

$${\varepsilon}_p=\frac{1}{K_y^{M_y}}{\left\langle \frac{\sigma_s}{1-D}-{\sigma}_y\right\rangle}^{M_y}$$
(9)

When Ky and My are known, for the case of ε < εv, the damage Dp in the monotonic plastic hardening stage can be obtained from the stress-strain curve by the following formula:

$${D}_p=1-\frac{\sigma_s}{K_y{\varepsilon_p}^{\frac{1}{M_y}}+{\sigma}_y}$$
(10)

where Dp is the plastic damage at a certain point in the monotonic plastic hardening stage; σs represents the stress at this point; εp denotes the plastic strain at this point.

Macro-plastic damage calculation results

Given that the design average temperature of the frozen curtain is −10 °C, and the average formation pressure calculated according to the buried depth of the cross passage is about 600 kPa. Therefore, the triaxial test result with a temperature of −10 °C and a confining pressure of 600 kPa is selected to calculate the macro-plastic damage. In this paper, the tangent modulus determination method is used, in which the slope of two points on the front straight section of the stress-strain curve is selected to calculate the deformation modulus. According to Fig. 7(c), the linear elastic stage can be determined to be ε = 0%–0.47% depending on the variation of the deformation modulus. As a result, the yield strain at the elastic stage is 0.47%, and the corresponding yield stress is 2.72 MPa. The relationship curve between σ − σy and εp is illustrated in Fig. 8.

Fig. 8
figure 8

Relationship between σ − σy and εp

Full size image

On the basis of the macro-plastic damage calculation theory, the relationship between ln(σ − σy) and ln(εp) is drawn as Fig. 9. Additionally, Eq. 8 is fitted, and the fitting results are also shown in Fig. 9. It can be obtained that ln(Ky) = 0.71366 and 1/My = 0.54326, i.e., Ky = 2.0414 and My = 1.8407.

Fig. 9
figure 9

Fitting results of plastic damage parameters Ky and My

Full size image

In addition, after Ky and My are obtained, the macro-plastic damage Dp is calculated according to Eq. 10, and the results are presented in Table 1.

Table 1 Calculation results of macro-plastic damage Dp
Full size table

Micro-crack damage

Binarized CT image

In the analysis of the CT images of the specimens, factors such as size effect, visual error, and boundary effect, will cause the difference of the damage evolution law. It is difficult to obtain the changes of the damaged structure with the naked eye only from conventional CT images. Therefore, the authors adopt a qualitative analysis method, in which converts the CT images obtained in the CT scanning test into binarized CT images through MATLAB. Compared with CT images, binarized CT images can display the damaged area more intuitively. The scanning layers at the specimen’s two ends are removed, and the specimen’s central 90-mm area is chosen in order to lessen the impact of the end effect. Seven scanning layers spaced 15 mm apart of each specimen are studied, as presented in Fig. 10.

Fig. 10
figure 10

Scanning layers of binarized CT image analysis

Full size image

The binarized CT images of each scanning strain of the frozen sandy gravel specimens during the triaxial compression tests are shown in Figs. 11, 12, 13, 14, and 15. Control the appropriate threshold to separate low-density area where may exist cracks and voids from gravels and high-density soil area. Comparing to the white color, the black color means that the CT number and material density of this part is low.

Fig. 11
figure 11

CT binarization image when ε1 = 0%

Full size image
Fig. 12
figure 12

CT binarization image when ε1 = 2.8%

Full size image
Fig. 13
figure 13

CT binarization image when ε1 = 5.6%

Full size image
Fig. 14
figure 14

CT binarization image when ε1 = 8.0%

Full size image
Fig. 15
figure 15

CT binarization image when ε1 = 10.4%

Full size image

It can be observed from Fig. 11 that when the strain is 0%, which is the initial state, there are some low-density areas inside the specimen. In layers D3, D4, and D6, there are some sporadic initial damages that cannot be noticed by naked eyes. In addition, when the strain is 2.8%, the D1 and D2 layers are relatively intact, and the low-density areas in the D3, D4, and D7 layers develop. Moreover, when the strain is loaded to 5.6%, a large number of low-density areas occur in D5 and D6, and there are large gravels in the middle of these two layers. Additionally, when the strain increases to 8%, the separation of the gravels from the soil particles can be clearly noticed in D1, D2, and D3, and obvious low-density areas appear around the gravels. After the strain reaches the post-peak stage, which is 10.4%, gravels and soil particles are completely separated from each other in the middle area of layers D4, D6, and D7. The size of each gravel can be clearly seen, and the specimen is almost completely destroyed. The boundaries of gravel are very clear, and damage exists in almost every scanning layer at this time. Therefore, it can be inferred that the contact surface between the gravel and the soil particles is fragile, and the low-density area often starts from these contact surfaces. This phenomenon is obviously distinct from the failure state of fine-grained soil, while the crack generation of fine-grained soil is often accompanied by randomness and suddenness. It’s worth mentioning that the internal low-density areas are difficult to detect by the naked eye but can be easily noticed by a CT scanner, which reflects the value of the CT scanning test.

Micro-crack damage calculation theory

At present, in classical damage mechanics, the density change is often adopted to define the damage (Zheng et al. 2011),namely:

$$D=1-\frac{\rho_j}{\rho_0}=1-\frac{m_j{v}_0}{m_0{v}_j}$$
(11)

where D represents the damage; ρ0, m0, and v0 denotes the initial state density, mass and volume of the soil, respectively; ρj, mj, and vj is the density, mass, and volume of the soil when it is loaded to time j, respectively.

For rock or non-frozen soil, it can be assumed that the mass of each component is constant and incompressible, that is, the true density is constant. Thus, there are:

$$D=1-\frac{\rho_j}{\rho_0}=1-\frac{v_0}{v_j}$$
(12)

When the damage is expressed by density change, it can only reflect the overall volume change of the specimen, which includes the generation and expansion of voids and micro-cracks. Additionally, it can be expected that for frozen soil, during loading, the specimen’s overall mass will not change. However, since compression melting and recrystallization of ice may take place when the specimen is loaded, it cannot be believed that the mass of each component stays the same. The damage represented by density change cannot reflect the real alteration in the specimen’s interior structure.

The CT principle states that a material’s CT number is inversely correlated with its X-ray absorption coefficient, and various material components have varying X-ray absorption coefficients. Additionally, the interior structure of the specimen will vary during the mechanical test, and this will influence each component’s X-ray absorptivity. Therefore, when the damage is represented by the change in CT number, the change in X-ray absorption coefficient of each component can reflect internal structural changes like local ice compression melting and recrystallization, the phase change between ice and water, and the directional arrangement and refinement of soil particles. As a result, the micro-crack damage factor Dc is defined using the change in CT number in this paper.

When a specific spatial resolution is met, the image CT number is defined by the convolution technique (Chen et al. 2017):

$$H=1000\frac{\left({\mu}_{rm}-{\mu}_w\right)}{\mu_w}$$
(13)

where, H represents the CT number of a pixel point; μrm is the X-ray absorption or attenuation coefficient of a substance; μw denotes the X-ray absorption or attenuation coefficient of water.

The density of the material being viewed is proportional to the CT number, and the larger the CT number, the denser the material is. The CT number of water is 0 when measured in HU, while the CT number of air is −1000 HU. The absorption coefficient μrm of the detected substance to X-ray can be expressed as:

$${\mu}_{rm}={\mu}_m\rho$$
(14)

where, ρ is the density of a substance; μm represents the mass absorption coefficient of a substance.

Substituting Eq. 14 into Eq. 13, and obtain:

$$\rho =\frac{\mu_w\left(1+\frac{H}{1000}\right)}{\mu_m}$$
(15)

When Eq. 15 is substituted into Eq. 11, there is:

$$D=\frac{\frac{\mu_w\left(1+\frac{H_i}{1000}\right)}{\mu_{mi}}-\frac{\mu_w\left(1+\frac{H_0}{1000}\right)}{\mu_{m0}}}{\frac{\mu_w\left(1+\frac{H_0}{1000}\right)}{\mu_{m0}}}$$
(16)

The components inside the specimen will not change during the mechanical test, so there is μm0 = μmi, and then:

$$D=\frac{H_i-{H}_0}{1000+{H}_0}$$
(17)

Considering that different CT scanners have varied resolutions, the micro-crack damage Dc defined by the CT number is expressed as:

$${D}_c=\frac{1}{{n_0}^2}\left(\frac{H_i-{H}_0}{1000+{H}_0}\right)$$
(18)

where, n0 denotes the spatial resolution of a CT scanner, which is 0.416 in this experiment. H0 represents the mean CT number of the frozen soil specimen in the initial state. Hi is the mean CT number of the frozen soil specimen at time i.

Micro-crack damage calculation results

Figure 16 presents the three-dimensional CT images of the frozen sandy gravel specimens at ε = 5.6%. White patches in the illustration show a high absorption coefficient at this place, which reflects a high CT value and high density at this place. The dark color of the CT image means low CT value and density, as well as the possibility of cracks or voids. Therefore, the change in the internal meso-structure and the emergence of cracks in the frozen sandy gravel specimens may be intuitively recognized through the brightness difference at various points of the CT image. The 3D CT image also makes it easy to see the gravel’s size, shape, and location. The meso-structures of the sandy gravel specimens differ significantly between the layers as a result of the gravel’s erratic distribution. The gravel and soil particles are dispersed alternately and erratically across the interior of the same layer, which is likewise not uniform.

Fig. 16
figure 16

CT image of frozen sandy gravel at ε = 5.6%

Full size image

In addition, the mean value (Hmean) of the CT number of the scanning layers D1–D7 as shown in Fig. 10 in various strain stages is also obtained using the DICOM Viewer. Table 2 presents the statistical outcomes.

Table 2 Statistical results of Hmean of CT numbers (HU)
Full size table

Table 2 shows that the Hmean of different sections of the same specimen is different, indicating that each section’s density varies and the specimen’s starting state is not uniform. Hmean progressively declines as strain increases. When ε = 0% develops to ε = 2.8%, Hmean falls from 1579 to 1566, and the decline ratio is 0.82%. The phenomena of growth and expansion occur in the microcracks. The micro-crack damage now starts to evolve. Additionally, Hmean decreases from 1566 to 1521 with a drop rate of 2.87% when ε changes from 2.8% to 5.6%. The growth of cracks worsens the specimen’s damage as the old micro-cracks and voids rapidly expand while new micro-cracks and voids are also produced. Additionally, when ε varies from 5.6% to 8%, Hmean falls from 1521 to 1512, falling by 0.59%. In addition, Hmean dramatically declines from 1512 to 1419 in the stage of 8%–10.4%. At this point, the Hmean of each layer rapidly decreases as micro-crack damage rapidly develops following the stress peak. The specimen fails as a result of the macro-cracks that are produced when the micro-cracks and voids meet horizontally and longitudinally. Combined with Table 2 and the micro-crack damage calculation theory defined by CT number, the micro-crack damage Dc is calculated as Table 3.

Table 3 Calculation results of micro-crack damage Dc
Full size table

Discussion

On the basis of continuum mechanics and solid material mechanics, the macro-plastic damage calculation theory has been developed. It is a set of presumptions-based macroscopic damage calculation theories. The micro-crack damage calculation theory, on the other hand, is microscopic damage and is based on classical damage mechanics. Despite having the same stress-strain curve as their common foundation, the two damage calculation models use very different theoretical approaches. They are distinct from one another and connected. Additionally, only the plastic stage can be used for the production of the Dp. Dc claims that there is also damage to the elastic stage, though. Dc is 0.0119 when the elastic stage’s final strain is 0.47%. Moreover, the Dp is significantly bigger than the Dc in the plastic stage. As a result, the author suggests modifying the Dp using the discovered Dc in order to more precisely characterize how damage develops during both the elastic and plastic stages. The cross-scale modified damage Dm is defined by adding and averaging the Dp and Dc calculations above. Table 4 lists the findings of Dm’s calculation.

Table 4 Calculation results of cross-scale modified damage Dm
Full size table

The stress-strain curve, macro-plastic damage Dp, micro-crack damage Dc, and cross-scale modified damage Dm are all plotted in Fig. 17. The Dp is only produced when the elastic stage concludes and moves into the plastic stage (0.47%). However, the Dc exists no matter if it is in the elastic or plastic stage. When 2.8% < ε < 10.4%, Dp increases faster and is significantly greater than Dc. The values of Dp and Dc are practically comparable at 10.4% axial strain. Additionally, the growth rate of Dp between 8% and 10.4% is similar to that between 5.6% and 8%. For Dc, however, there is a noticeable rise as the strain goes from 8% to 10.4%, and the specimen is seriously harmed. To investigate the reason, Dp is calculated by idealized mathematical formulas based on a series of assumptions. It is not taken into account how the change in microstructure during the loading process affects macroscopic mechanical properties. The author thinks that damage happens in both the elastic and plastic stages, in accordance with the outcomes of the actual microscopic testing. The elastic stage is frequently ignored by the classical damage hypothesis, which frequently solely focuses on the plastic stage. Therefore, it is of positive significance to modify the macroscopic plastic damage Dp with the microscopic crack damage Dc.

Fig. 17
figure 17

Damage evolution of frozen sandy gravel

Full size image
$${D}_m={\textrm{e}}^{\hbox{-} 4.55437+0.54055\varepsilon -0.0197{\varepsilon}^2}0\le \varepsilon \le 10.4\%$$
(19)

The modified results show that the Dm maintains an upward trend with the strain. When ε ≤ 2.8%, Dm growth is quite gentle. The specimen exhibits strong compressive resistance at the early loading stage. At this time, the strain is small, the coordination deformation ability of the ice-water-soil-gravel four-phase medium is strong, and the damage increases less. When the strain increases from 2.8% to 5.6%, there is a significant increase in Dm. The author believes that there is an ice compress melting phenomenon at the contact point of gravels with increasing strain, which reduces the ice content of the specimen, weakens the ice bonding, and increases the damage. In the pre-peak plastic stage, when the strain is 5.6% to 8%, the Dm increases less than in the previous stage. When the strain is over 8% during the post-peak stage, Dm grows more quickly. At this time, the microcracks and micropores in the specimen have rapidly developed into macroscopic cracks. The discordant deformation of the ice-water-soil-gravel four-phase medium occurs, and the Dm reaches 0.35. The relationship between Dm and ε is fitted by several relation points in the form of an exponential function, as illustrated in Eq. 19, and the fitting correlation coefficient R2 is 0.96593.

Conclusion and future works

This paper proposes a novel idea to study the macroscopic and microscopic damage of artificial frozen sandy gravel through triaxial compression and X-ray CT scanning tests. The microscopic damage is calculated based on macro-plastic damage calculation theories and triaxial compression test results when the temperature is −10 °C and the confining pressure is 0.6 MPa. Moreover, the microscopic damage is obtained by micro-crack calculation theories and CT scanning test results at the same temperature and confining pressure. The evolution laws of the two damages are similar as they have the same stress-strain curve as their common foundation. However, the values of the two damage calculation models are different as they use very different theoretical approaches. On the whole, the value of macro-plastic damage is larger than that of micro-crack damage and cannot reflect the damage of the elastic stage. Therefore, this paper proposes to use micro-crack damage to modify macro-plastic damage to obtain cross-scale modified damage to more precisely characterize how damage develops during both the elastic and plastic stages. Furthermore, the relationship between the cross-scale modified damage and the strain is fitted by an exponential function. The fitting function will provide essential references and guidance for the numerical modeling of AGF in similar engineering projects. Future work can be conducted focusing on the secondary development of the frozen sandy gravel damage constitutive model in the finite element model.