Introduction

In recent years, the artificial ground freezing (AGF) technique has been widely used in many geotechnical engineering projects, such as shafts, tunnels, subways, deep foundations, and ground source heat pumps (Wagner 2013; Russo et al. 2015), because it is a highly adaptable and economical method for dealing with weak and low-strength strata (Jones and Brown 1979; Russo et al. 2015). With the further development of the underground space and coal mining, the AGF technique will play a crucial role in these projects (Yang et al. 2014). In addition, with the application of the “one belt and one way” strategy, many infrastructures will be constructed in cold regions (Ma et al. 2017), and these projects will certainly involve frozen rocks. As noted by Duca et al. (2015), the study of the mechanical properties of frozen rock (soil) has an important theoretical value and a practical significance for geotechnical engineering and disaster prevention. Therefore, it is necessary for people to better grasp the strength characteristics of frozen rock for good design and construction in frozen soil engineering.

As the main load bearing elements of the AGF method, the strength of frozen walls is expected to play a crucial role in engineering stability. After the soft rock in the freezing circle is excavated, the frozen wall will bear the external load. It is known that during the loading process the cracks in the rock will propagate or close and finally destroy the stability of the structures (Xue et al. 2014). From the viewpoint of damage mechanics, the failure process of rock is a process of continuous crack evolution and expansion under external load (Lemaitre 1985; Cerfontaine et al. 2017). To accurately assess the damage degree of the rock, the key point is to determine the crack evolution rule. Generally, cracks are randomly distributed in the rock, where the number and size of the cracks follow definite statistical distributions (Dougill et al. 1976; Li et al. 2012). Therefore, the mesoscopic method and statistical principles were suggested to describe the crack evolution in rock under the loading function (Krajcinovic and Silva 1982).

Many studies have focused on the statistical damage constitutive model of rock (Lemaitre 1985; Wang et al. 2007; Li et al. 2012; Xu et al. 2018; Huang et al. 2018). These models have two key points in common: (1) application of the strain equivalent hypothesis and (2) the microunit strength subject to some types of random distribution, such as Weibull distribution, normal distribution, Harris function distribution, and power function distribution. In addition, these models also have diversity: (1) The damage variables are different, including the axial strain, tensile strain, and elastic modulus (Li et al. 2012; Xu et al. 2018; Huang et al. 2018), and (2) the failure criterion is different, involving the Drucker-Prager (D-P) criterion and the Mohr–Coulomb (M-C) criterion (Deng and Gu 2011; Zhou et al. 2017; Xie et al. 2020). As mentioned above, the microunit strength and its probability density distribution are the two key factors for determining the crack evolution rule and estimating the degree of damage. Moreover, these studies mainly focus on the damage characteristics of rock at room and high temperatures.

Compared to room and high temperatures, negative temperatures can enhance the strength of rock (Yamabe and Neaupanek 2001; Bayram 2012; Gautam et al. 2016; Qu et al. 2018). In artificial ground freezing method, the strength of the frozen wall is of great significance for the structural design and risk control (Jiang et al. 2012). In the design and calculation of artificial ground freezing, to accurately describe the mechanical behavior of frozen rocks, it is necessary to adopt the damage constitutive model while considering negative temperatures. To accomplish this goal, the strength characteristics of frozen sandstone were analyzed based on the results of triaxial tests. After that, a statistical damage constitutive model of frozen sandstone was presented and verified using the experimental data. Then the key parameters influencing the damage process of frozen sandstone were discussed. Finally, the effect of temperature on the strength of frozen sandstone was analyzed.

Characteristics of rock deformation and the failure process

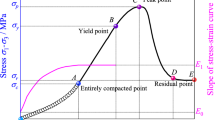
The typical stress–strain curve of rock is shown in Fig. 1. This curve can generally be divided into five stages: the compaction stage, elastic stage, steady crack development stage, non-steady crack development stage, and post-peak stage (Martin and Chandler 1994; Cai et al. 2004; Xue et al. 2014; Li et al. 2020). However, the compaction stage is not intrinsic for the rock. For some intact rocks with few initial cracks, this stage may not be observed. As the stress level gradually increases, the crack volumetric strain decreases gradually, and the deformation enters the elastic stage (Cai et al. 2004; Xue et al. 2014; Li et al. 2020). A new crack then forms with a further increase in the axial stress, which indicates the beginning of the steady crack development stage. The axial stress at this point is the crack initiation stress \(\left({\sigma }_{ci}\right)\). At this stage, both the total volumetric strain and the crack volumetric strain increase gradually. As the axial stress increases, many cracks will form and coalesce, with the total volumetric strain reaching its peak value. The axial stress at this moment is the crack dilation stress \(\left({\sigma }_{cd}\right)\). When the sample cannot support an increase in the axial stress, rupture will eventually occur. The largest axial stress is the peak stress \(\left({\sigma }_{f}\right)\).

Fig. 1
figure 1

Triaxial stress–strain curves of the frozen rock sample (\({\sigma }_{ci}\) is crack initiation stress; \({\sigma }_{cd}\) is crack dilation stress; \({\sigma }_{f}\) is peak stress)

Full size image

The development of cracks is determined by three characteristic stresses: crack initiation stress, crack dilatation stress, and peak stress (Cai et al. 2004; Li et al. 2020). As seen in Fig. 1, the crack volumetric strain changes continuously during the loading process due to the closure and generation of cracks. Compared with crack closure, crack generation is highly detrimental for engineering structures. Therefore, this paper focuses on the mechanism of crack generation in frozen rock.

To obtain the crack initiation stress and the crack dilation stress, the first step is to determine the crack volumetric strain. In general, the crack volumetric strain can be calculated using the following steps.

The total volumetric strain \(\left({\varepsilon }_{v}\right)\) can be calculated by the axial strain \(\left({\varepsilon }_{1}\right)\) and radial strain \(\left({\varepsilon }_{3}\right)\),

$${\varepsilon }_{v}={\varepsilon }_{1}+{2\varepsilon }_{3}$$
(1)

The total volumetric strain \({\varepsilon }_{v}\) can also be divided into elastic volumetric strain \({\varepsilon }_{ve}\) and inelastic volumetric strain \({\varepsilon }_{vie}\). Martin and Chandler (1994) defined the inelastic volumetric strain \({\varepsilon }_{vie}\) as the crack volumetric strain \({\varepsilon }_{vc}\), which is attributed to axial cracking. Therefore, the total volumetric strain \({\varepsilon }_{v}\) can be divided into the elastic volumetric strain \({\varepsilon }_{ve}\) and the crack volumetric strain \({\varepsilon }_{vc}\) (Xue et al. 2014; Liu et al. 2019)

$${\varepsilon }_{v}={\varepsilon }_{ve}+{\varepsilon }_{vc}$$
(2)

According to Hook’s law, the elastic volumetric strain \({\varepsilon }_{ve}\) can be expressed as

$${\varepsilon }_{ve}={\varepsilon }_{1e}+{\varepsilon }_{2e}+{\varepsilon }_{3e}=\frac{1-2v}{E}\left({\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}\right)$$
(3)

where \({\sigma }_{1}\), \({\sigma }_{2}\), and \({\sigma }_{3}\) are the principal stresses and \({\varepsilon }_{1e}\), \({\varepsilon }_{2e}\), and \({\varepsilon }_{3e}\) are the corresponding principal strains.

Substituting Eqs. (1) and (3) into Eq. (2), the crack volumetric strain \({\varepsilon }_{vc}\) can be expressed as

$${\varepsilon }_{vc}={\varepsilon }_{1}+{2\varepsilon }_{3}-\frac{1-2v}{E}\left({\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}\right)$$
(4)

where \(v\) is the Poisson ratio and \(E\) is the elastic modulus.

Once the crack volumetric strain is calculated using Eq. (4), the crack initiation stress and the crack dilation stress can be obtained through the stress–strain curve, as shown in Fig. 1.

Laboratory test

Sample preparation

Red sandstone taken from a frozen shaft in a coal mine was used as the testing sample. According to the standard testing method of the International Society for Rock Mechanics (ISRM), the samples were made into columns with a diameter of 50 mm and a height of 100 mm and wrapped with cling film to avoid moisture loss.

In western China, Cretaceous sandstone is a kind of non-continuous, nonlinear, and anisotropic material (Yang et al. 2019). Figure 2 presents an SEM photograph of the red sandstone. As seen in Fig. 2, some clay minerals exist in the sample. In general, the size of the sandstone particle is distributed in the range of 0.25–0.50 mm. This means that the testing sample is medium sandstone. Because the strata are located in water-rich areas, the rock sample can be treated as saturated sandstone.

Fig. 2
figure 2

Photograph of the scanning electron microscope (SEM)

Full size image

After the cylinder samples were prepared, the ultrasonic method was used to select the samples with a good integrity (acoustic velocity in the range of 2046 ± 150 m/s) for conducting follow-on tests. From the selected samples, three specimens were handpicked in order to measure the basic physical parameters. The measuring process was as follows:

  1. (1)

    The specimens were placed in an oven at 105 °C

  2. (2)

    Twenty-four hours later, the specimens were removed, and their size and weight were measured.

  3. (3)

    The dry specimens were placed in a vacuum saturator for 12 h and then weighed. The size variation can be ignored during the saturation processes.

The average value of the three specimens was used to determine the basic physical parameters of the red sandstone. The tested results are listed in Table 1.

Table 1 Basic physical parameters of red sandstone
Full size table

Test condition

In freezing shaft sinking engineering, the average temperature of the freezing wall decreases with an increasing burial depth. To reflect this characteristic, the test temperatures were determined to be−5 °C,−10 °C,−15 °C,−20 °C,−25 °C, and−30 °C. According to the industry standard (artificial frozen soil physics mechanics performance test Part 5: artificial frozen soil triaxial shear test method (No. MT/T593.1–2011)), the confining pressure in the triaxial test can be calculated by

$${P}_{0}=0.013H$$
(5)

where \({P}_{0}\) is the horizontal ground pressure, in megapascals; \(H\) is the buried depth, in meters.

Substituting the buried depth of 300–350 m into Eq. (5), a horizontal ground pressure of 3.90 ~ 4.55 MPa can be obtained. Therefore, the confining pressures in the test were set to 2 MPa, 4 MPa and 6 MPa.

Test apparatus

The triaxial compression tests were performed in the laboratory by using a low-temperature triaxial testing system (Fig. 3). The low-temperature triaxial testing system consists of four components: a loading system, a temperature control system, a data collection system, and a data processing system (Fig. 3a). The temperature range of the temperature control system is−40 ~ 90 °C, with an accuracy of ± 0.1 °C. By using an external temperature sensor, the sample temperature can be dynamically controlled via the proportion-integral-derivative (PID) controller. The maximum axial force and confining pressure are 1000 kN and 140 MPa, respectively.

Fig. 3
figure 3

Low-temperature triaxial testing system (LVDT stands for linear variable differential transducer, which is used to measure the deformation of frozen rock in this system). (a) Key components of the low-temperature triaxial testing system. (b) Detail of deformation measurer. (c) Temperature controlling

Full size image

Test procedure

The steps of the triaxial compression test were as follows:

  1. (1)

    The rock sample was covered with a rubber film; the axial and radial strain sensors were installed in the middle of the sample (Fig. 3b). After the sample was put into the pressure chamber, the pressure chamber cover was put down, and silicon oil was fed into the pressure chamber (Fig. 3a).

  2. (2)

    The temperature of the cooling system was set to the required temperature. When activating the cooling system, refrigeration circulation was performed. With the coolant inflow and outflow of the pressure chamber cover (Fig. 3c), the temperature of the silicon oil and specimens gradually decreased to the required temperature by heat conduction.

  3. (3)

    After 12 h, when the temperature of the silicon oil dropped to the required temperature, the confining pressure was applied at a rate of 0.05 MPa/s.

  4. (4)

    Two hours later, deviatoric stress was applied at a rate of 0.5 MPa/s. When the loss value of the peak deviatoric stress reached 30%, the test was stopped.

Experimental results

Triaxial compression test

Figure 4 shows the macroscopic failure modes of the rock sample at different temperatures. There is a shear crack on each sample, and the shear cracks are similar at different temperatures. The relationships between the deviatoric stress \(\left({\sigma }_{1}-{\sigma }_{3}\right)\), the axial strain \(\left({\varepsilon }_{1}\right)\), and the radial strain \(\left({\varepsilon }_{3}\right)\) under different test conditions are shown in Fig. 5. According to the triaxial data, the peak deviatoric stresses of the frozen red sandstone are obtained, as presented in Table 2.

Fig. 4
figure 4

Failure morphology of sandstone at different temperatures (the confining pressure is 6 MPa)

Full size image
Fig. 5
figure 5

Stress–strain curves of frozen red sandstone at different temperatures. (a)−5 °C (b)−10 °C (c)−15 °C (d)−20 °C. (e)−25 °C. (f)−30 °C

Full size image
Table 2 Triaxial compression strength of sandstone at different temperatures (unit: MPa)
Full size table

As seen in Fig. 5, the stress–strain curve of the red sandstone samples is a concave function rather than a linear function. This indicates that the elastic modulus increases at the compaction stage. In general, this stage is a compaction stage because the crack volumetric strain gradually decreases (Xue et al. 2014; Qu et al. 2018). As shown in Fig. 5, the compaction stage gradually becomes inconspicuous with decreasing temperature. This can be explained that when the temperature is lower than the freezing point, the pores are filled with ice due to the phase change. The connection between the rock particles has been strengthened by ice, and the voids in frozen sandstone are relatively hard to compress. Therefore, the compaction stage becomes less unapparent. Moreover, compared with the rock particles, ice has a strong plastic property. With more ice formed in the rock sample, the plastic characteristics of the sample become obvious. As seen in Fig. 5, the failure strain increases with decreasing temperature, which means that the plastic property has been strengthened.

At a given confining pressure, the peak strength of red sandstone increases with a decreasing temperature (Table 2). For instance, with a confining pressure of 6 MPa, the peak strengths at−5 °C,−10 °C,−15 °C,−20 °C,−25 °C, and−30 °C are 32.25 MPa, 47.60 MPa, 54.29 MPa, 55.35 MPa, 57.02 MPa, and 59.89 MPa, respectively, which are 1.00, 1.47, 1.68, 1.71, 1.77, and 1.86 times the peak strength at−5 °C, respectively. This indicates that frozen rock exhibits obvious temperature-dependent behaviors. This can be explained by the fact that at a negative temperature (below the freezing point), ice is formed in water-filled pores and the pore ice enhances the cementation between the rock particles. It shows a better strengthening effect when the artificial freezing method is applied in water-rich soft rock strata (Yang et al. 2014). The results confirmed that the stress–strain of sandstones showed different performances at different temperatures, which demonstrated that the sandstone constitutive models have an inseparable relation to the temperature.

Characteristic stresses

At different deformation stages, the characteristic stresses of rock materials are different (Cai et al. 2004). For engineering design and practice, it is necessary to know the characteristic stresses associated with these deformation stages. Therefore, the influence of temperature on the characteristic stresses is analyzed in this section. Based on the calculated method mentioned in “Characteristics of rock deformation and the failure process,” the characteristic stresses of frozen sandstone at different temperatures can be obtained, as shown in Table 3.

Table 3 Crack initiation and dilatation stresses at different temperatures
Full size table

Under the same confining pressure, both the crack initiation stress and the crack damage stress increase with a decreasing temperature (Table 3). At−10 °C, the crack level \(\left({\sigma }_{ci}/{\sigma }_{f}\right)\) is 0.20 ~ 0.24 with an average value of 0.22, and the dilation level \(\left({\sigma }_{cd}/{\sigma }_{f}\right)\) is 0.91 ~ 0.94 with an average value of 0.93. At−20 °C, the crack level \({\sigma }_{ci}/{\sigma }_{f}\) is 0.22 ~ 0.28 with an average value of 0.26, and the dilation level \(\left({\sigma }_{cd}/{\sigma }_{f}\right)\) is 0.93 ~ 0.97 with an average value of 0.95. At−30 °C, the crack level \(\left({\sigma }_{ci}/{\sigma }_{f}\right)\) is 0.33 ~ 0.49 with an average value of 0.41, and the dilation level \(\left({\sigma }_{cd}/{\sigma }_{f}\right)\) is 0.84 ~ 0.97 with an average value of 0.91. The results indicate that a negative temperature can improve the crack initiation stress and the crack dilation stress. Moreover, the crack initiation stress slightly increases with increasing confining pressure. This means that the initiation of new cracks is slightly inhibited by the confining stress.

As shown in Table 3, there is no distinct rule for the crack initiation strain and crack dilation strain, but the failure strain increases with a decreasing temperature. The results show that the freezing action can result in an increase in the plastic deformation stage and a decrease in the brittleness due to the water ice phase change (Liu et al. 2019). As a result, the reserve capacity for plastic deformation is inadequate, which means that the rock will be damaged quickly once the frozen sandstone enters the plastic state. Therefore, both the strength and deformation characteristics should be considered in the design of frozen walls.

Damage constitutive model

The characteristic stresses cannot reflect the entire failure process of frozen rocks. To describe the failure process of frozen rocks, it is necessary to adopt the damage constitutive model while considering negative temperatures.

Model building

Assuming that the micro unit strength of rock \(\left(F\right)\) meets the Weibull distribution, the probability density function of the micro unit strength can be expressed as (Weibull 1951),

$$p\left(F\right)=\frac{m}{{F}_{0}}{\left(\frac{F}{{F}_{0}}\right)}^{m-1}\mathrm{exp}\left[-{\left(\frac{F}{{F}_{0}}\right)}^{m}\right]$$
(6)

where \(p\left(F\right)\) is the probability density function of stress; \(m\) and \({F}_{0}\) are the distribution parameters.

When the stress level reaches the microelement strength variable, the microelement will be damaged. Assuming that \(F\) obeys some kinds of the probability distribution, \(d{N}_{d}\) in any stress level \(\left[F,F+dF\right]\) can be described as

$$d{N}_{d}=Np\left(F\right)dF$$
(7)

When the stress increases from 0 to \(F\), \({N}_{d}\) can be calculated as

$${N}_{d}={\int }_{0}^{F}Np\left(F\right)dF$$
(8)

The damage variable \(\left(D\right)\) is defined as the ratio of the number of failed microscopic elements \(\left({N}_{d}\right)\) to the total number of microscopic elements \(\left(N\right)\),

$$D=\frac{{N}_{d}}{N}$$
(9)

Substituting Eqs. (6) and (8) into Eq. (9), \(D\) can be expressed as

$$D=\left\{\begin{array}{l}1-\mathrm{exp}\left[{-\left(\frac{F}{{F}_{0}}\right)}^{m}\right]\\ 0\end{array}\begin{array}{c}F\ge 0\\ F<0\end{array}\right.$$
(10)

According to the hypothesis of strain equivalence (Lemaitre, 1985),

$$\left[\varepsilon \right]=\frac{\left[\sigma \right]}{\left[E\right]}=\frac{\left[\sigma \right]}{\left[E\right]}=\frac{\left[\sigma \right]}{\left(1-D\right)\left[E\right]}$$
(11)

where \(\left[E\right]\) is the elastic matrix of the damaged material and \(\left[E\right]\) is the elastic matrix of the nondestructive material.

Most elastic–plastic constitutive models currently only consider the linear phase and the yield stage and ignore the initial compaction stage. For rock with a larger porosity, the initial compaction process is obvious, so the variation in porosity needs to be considered in the constitutive model,

$$\left[\varepsilon \right]=\frac{\left[\sigma \right]}{\left(1-n\right)\left(1-D\right)\left[E\right]}$$
(12)

Based on Eq. (12), the following formula can be obtained,

$${\sigma }_{1}=E{\varepsilon }_{1}\left(1-D\right)\left(1-n\right)+2\nu {\sigma }_{3}$$
(13)

The porosity \(\left(n\right)\) can be calculated by the volumetric strain \(\left({\varepsilon }_{\nu }\right)\) and the initial porosity \(\left({n}_{0}\right)\),

$$n=\frac{{n}_{0}-{\varepsilon }_{\nu }}{1-{\varepsilon }_{\nu }}$$
(14)

For the triaxial compression test, the confining pressure is first applied followed by the deviatoric stress. However, the initial strain \(\left({\varepsilon }_{10}\right)\) caused by the confining pressure was not included in the deviatoric stress–strain curve data. To truly reflect the stress–strain relationship, the initial strain \(\left({\varepsilon }_{10}\right)\) should be considered. According to the generalized Hooke's law, \(\left({\varepsilon }_{10}\right)\) can be calculated,

$${\varepsilon }_{10}=\frac{{\sigma }_{3}}{E}\left(1-2\nu \right)$$
(15)

Therefore, the actual axial strain is

$${\varepsilon }_{1}={\varepsilon }_{1b}+{\varepsilon }_{10}$$
(16)

where \({\varepsilon }_{1b}\) is the measured axial strain in the deviatoric stress–strain curve data.

Substituting Eq. (16) into Eq. (13),

$${\sigma }_{1}=E\left({\varepsilon }_{1b}+{\varepsilon }_{10}\right)\left(1-D\right)\left(1-n\right)+{2\nu \sigma }_{3}$$
(17)

Substituting Eqs. (10) and (13) into Eq. (17), the damage constitutive model can be described as

$${\sigma }_{1}=\left\{\begin{array}{l}E\left({\varepsilon }_{1b}+{\varepsilon }_{10}\right)\left(\frac{1-{n}_{0}}{1-{\varepsilon }_{\nu }}\right)\mathrm{exp}\left[{-\left(\frac{F}{{F}_{0}}\right)}^{m}\right]+{2\nu \sigma }_{3}\\ E\left({\varepsilon }_{1b}+{\varepsilon }_{10}\right)\left(\frac{1-{n}_{0}}{1-{\varepsilon }_{\nu }}\right)+{2\nu \sigma }_{3}\end{array}\begin{array}{l}F\ge 0\\ F<0\end{array}\right.$$
(18)

Determination of parameters \(m\) and \({F}_{0}\)

From Eq. (18), it can be seen that a key issue is how to determine \({F}_{0}\) in a logical form. Considering the mechanical response commonly related to the various stress states of rocks, it can be determined that the Drucker-Prager criterion can reasonably reflect the cohesive force and the friction effect of geotechnical materials (Deng and Gu 2011; Xu et al. 2018; Lin et al. 2019). The Drucker-Prager criterion is adopted to determine the parameter \(F\), which can be described as

$$F={\sigma }_{1}\left(1+\frac{\sqrt{3}\mathrm{sin}\phi }{3\sqrt{3+{\mathrm{sin}}^{2}\phi }}\right)-{\sigma }_{3}\left(1-\frac{2\mathrm{sin}\phi }{3\sqrt{3+{\mathrm{sin}}^{2}\phi }}\right)=\frac{3c\mathrm{cos}\phi }{\sqrt{3+{\mathrm{sin}}^{2}\phi }}$$
(19)

where \(c\) is the cohesion and \(\phi\) is the internal friction angle.

Based on the relationship between the equivalent stress \(\left[\sigma \right]\) and the stress \(\left[\sigma \right]\), Eq. (19) can be rewritten as

$$F=\frac{{\sigma }_{1}}{\left(1-D\right)}\left(1+\frac{\sqrt{3}\mathrm{sin}\phi }{3\sqrt{3+{\mathrm{sin}}^{2}\phi }}\right)-\frac{{\sigma }_{3}}{\left(1-D\right)}\left(1-\frac{2\mathrm{sin}\phi }{3\sqrt{3+{\mathrm{sin}}^{2}\phi }}\right)$$
(20)

In this paper, the stress \(\left({\sigma }_{1p}\right)\) and strain \(\left({\varepsilon }_{1p}\right)\) at the peak of the stress–strain curve are used as specific macroscopic parameters to determine the model parameters. In the stress–strain curve, \({\sigma }_{1p}\) and \({\varepsilon }_{1p}\) satisfy the following conditions:

$${\sigma }_{1b}={\sigma }_{1p}$$
(21)
$${\varepsilon }_{1b}={\varepsilon }_{1p}$$
(22)

The derivative of stress with respect to the axial strain is zero at the peak point,

$${\left.\frac{d\sigma }{d{\varepsilon }_{1}}\right|}_{\begin{array}{c}\sigma ={\sigma }_{1p}\\ \varepsilon ={\varepsilon }_{1p}\\ F={F}_{1p}\end{array}}=0$$
(23)

Substituting Eq. (18) into Eq. (23),

$$\begin{aligned}\frac{d{\sigma }_{1}}{d{\varepsilon }_{1}}=&E\left(\frac{1-{n}_{0}}{1-{\varepsilon }_{\nu }}\right)\mathrm{exp}\left[{-\left(\frac{F}{{F}_{0}}\right)}^{m}\right]+E{\varepsilon }_{1}\left(\frac{1-{n}_{0}}{1-{\varepsilon }_{\nu }}\right)\\ &\mathrm{exp}\left[{-\left(\frac{F}{{F}_{0}}\right)}^{m}\right]\left({-m\left(\frac{F}{{F}_{0}}\right)}^{m-1}\frac{1}{{F}_{0}}\right)\\&\frac{dF}{d{\varepsilon }_{1}}=E\left(\frac{1-{n}_{0}}{1-{\varepsilon }_{\nu }}\right)\mathrm{exp}\left[{-\left(\frac{F}{{F}_{0}}\right)}^{m}\right]\\ &\left({1-{\varepsilon }_{1}m\left(\frac{F}{{F}_{0}}\right)}^{m-1}\frac{1}{{F}_{0}}\frac{dF}{d{\varepsilon }_{1}}\right)=0\end{aligned}$$
(24)

Rearranging Eq. (24) gives

$$1-{\varepsilon }_{1}m{\left(\frac{F}{{F}_{0}}\right)}^{m-1}\frac{1}{{F}_{0}}\frac{dF}{d{\varepsilon }_{1}}=0$$
(25)

Specifically, the distributed variable F is given as Eq. (26) following the D-P criterion (Liu and Dai 2018),

$$F=\left(\alpha {I}_{1}+\sqrt{{J}_{2}}\right)\frac{E{\varepsilon }_{1}}{{\sigma }_{1}}$$
(26)

The following equation can be easily achieved using Eq. (26):

$${\varepsilon }_{1}\frac{dF}{d{\varepsilon }_{1}}=F$$
(27)

Substituting Eq. (27) into Eq. (25),

$${F}_{0}={F}_{p}{\left(m\right)}^{1/m}$$
(28)

At the point of peak stress, the following equation can be easily obtained by Eq. (18):

$${\sigma }_{1p}=E\left({\varepsilon }_{1p}+{\varepsilon }_{10}\right)\left(\frac{1-{n}_{0}}{1-{\varepsilon }_{\nu }}\right)\mathrm{exp}\left[{-\left(\frac{{F}_{p}}{{F}_{0}}\right)}^{m}\right]+{2\nu \sigma }_{3}$$
(29)

Substituting Eq. (28) into Eq. (29), the following formula can be obtained:

$$m=\frac{-1}{\mathrm{ln}\frac{{\sigma }_{1p}-{2\nu \sigma }_{3}}{E\left({\varepsilon }_{1p}+{\varepsilon }_{10}\right)\left(\frac{1-{n}_{0}}{1-{\varepsilon }_{\nu }}\right)}}$$
(30)

Model validation

Based on the measured stress–strain curves, the model parameters \(m\) and \({F}_{0}\) can be calculated by Eqs. (28) and (30). According to the state reference < Standard for test methods of engineering rock mass > (GB/T 50,226–2013), the elastic modulus \(E\) and Poisson ratio \(\nu\) can be obtained from the experimental results, as presented in Table 4.

Table 4 Model parameters used in the model
Full size table

Substituting these parameters into Eq. (18), the predicted stress–strain curves of frozen rock can be obtained. Figure 6 shows the comparison between the measured and predicted results. The predicted results have a changing trend that is similar to the experimental results. This indicates that, to some degree, the presented constitutive model can predict the stress–strain characteristics of frozen sandstone during the loading process. However, the presented model is hard to describe the variation of the stress–strain in the post-peak phase.

Fig. 6
figure 6

Comparison between the measured and predicted results. (a) −5°C (b) −10°C (c) −15°C (d) −20°C (e) −25°C (f) −30°C

Full size image

Discussion

Relationship between the porosity and axial strain

The variation in porosity is influenced by the tested temperatures during the loading process. Based on the experimental results, the relationship between the axial strain and porosity can be calculated using Eq. (14), as shown in Fig. 7. The development of porosity can be divided into three stages: the decreasing stage, the gradual increasing stage, and the sharp increasing stage. According to the stress–strain curves, when the stress level is low than crack initiation stress, the sandstone sample is at the compaction stage and the porosity decreases with increasing deviatoric stress. As the deviatoric stress reaches the crack initiation stress, the cracks will be extended. As a result, the porosity has a slight increase. When the deviatoric stress reaches the crack damage stress, the propagation of cracks is intensified, and the final porosity is greater than the initial porosity. In addition, it is shown in Fig. 8 that at the same confining pressure, the lower the temperature is, the larger the porosity change is. This can be explained by the fact that the strength of sandstone increases with a decreasing temperature, which means that the rock can bear a larger loading and deformation. Therefore, the sample at a lower temperature has a densification state and a smaller porosity during the loading process.

Fig. 7
figure 7

Variation in the porosity with axial strain under different temperatures

Full size image
Fig. 8
figure 8

Damage evolution under different temperatures

Full size image

Relationship between the damage variable and deviatoric stress

The relationship between the damage degree and the deviatoric stress can be obtained by Eq. (17). As shown in Fig. 8, the damage degree curves have a similar change rule at different temperature conditions: the degree of damage is zero when the stress is at a lower level; when the stress reaches a certain stress level (e.g., crack dilation stress), the degree of damage begins to increase with the increase in the deviatoric stress. When the deviatoric stress approaches the peak stress, the damage degree increases dramatically. Taking the results of−10 °C as an example, when the deviatoric stress is less than 47.26 MPa, the degree of damage is zero; when the deviatoric stress is greater than 47.26 MPa, the degree of damage begins to increase, while the deviatoric stress approaches 50.93 MPa, the damage degree increases rapidly. The main reason for these results is that with an increase in the deviatoric stress, the cracks have gone through different developmental stages (Cai et al. 2004; Xue et al. 2014). Before the deviatoric stress increases to the crack initiation stress, the microcracks will be extended or closed, and the pore volume strain has little change. As the deviatoric stress increases to the crack initiation stress, few new cracks form, and the damage degree slightly increases. After the deviatoric stress reaches the crack dilation stress, many new cracks are generated, and the damage degree increases quickly. It can also be seen from Fig. 8 that the starting stresses of the increase in the damage variable are discrepant at different temperatures. For example, at−20 °C it is 47.26 MPa, and at−30 °C it is 62.21 MPa. This can be explained by the fact that, according to the Drucker-Prager criterion, an increase in the rock strength results in an increase in the yield stress. Therefore, as the peak strength increases with a decreasing temperature, the yield stress gradually increases. In other words, a lower temperature will enhance the ability to resist damage.

From the abovementioned, it can be concluded that when the deviatoric stress exceeds the crack initiation stress, the crack volumetric strain increases gradually. In some degree, the crack initiation stress can be used to determine the lower limit of the long-term strength (Diederichs et al. 2004). When the deviatoric stress exceeds the crack dilatation stress, the crack volumetric strain increases dramatically, and the degree of damage begins to increase. As the crack dilatation stress marks the yielding strength of frozen rock, the crack dilatation stress can be used to estimate the upper limit of the long-term strength for rock (Martin and Chandler 1994; Diederichs 2003). In conclusion, these two stresses can be treated as a warning indicator for frozen rock rupture, to some degree.

Variation in parameters \(m\) and \({F}_{0}\) at different temperatures

Previous studies have indicated that the parameters \(m\) and \({F}_{0}\) can describe the features of micro internal defects of rock (Xu and Wei 2002; Li et al. 2012). At negative temperatures, the water–ice phase change results in a change in the internal micro-defects and leads to changes in \({F}_{0}\) and \({F}_{0}\). Based on the experimental results, the parameters \(m\) and \({F}_{0}\) can be easily obtained by using Eqs. (28) and (30). The variations in \(m\) and \({F}_{0}\) are shown in Figs. 9 and 10. The results show that the dropping temperature results in a decrease in \(m\) and an increase in \({F}_{0}\). For the rock material, the sample with a larger \(m\) has an obvious brittleness (Xu and Wei 2002). Figure 9 indicates that the negative temperature weakens the brittleness of rock, and that the most direct manifestation is an increase in the failure strain. Figures 5 and 10 show that both decreasing the temperature and increasing the confining pressure cause an increase in the strength and parameter \({F}_{0}\). Therefore, to a certain extent \({F}_{0}\) can be considered as a parameter that describes the rock strength. In conclusion, \(m\) can represent the brittleness and strength of rock, \({F}_{0}\) can represent the strength of the rock, and the two parameters depend on one another.

Fig. 9
figure 9

Relationship between \(m\) and temperature

Full size image
Fig. 10
figure 10

Relationship between \({F}_{0}\) and temperature

Full size image

As shown in Figs. 9 and 10, the parameters \(m\) and \({F}_{0}\) are influenced by the confining pressure and temperature. By means of the regression analysis method of mathematical logic, the following formulas can be obtained:

$$m=20.537+0.491T-1.218{\sigma }_{3}-0.029T{\sigma }_{3}$$
(31)
$${F}_{0}=26.985-1.045T+0.302{\sigma }_{3}-0.307T{\sigma }_{3}$$
(32)

where \(T\) is the negative temperature, in degree Celsius, and \({\sigma }_{3}\) is the confining pressure, in megapascals.

Effect of a negative temperature on the strength of frozen sandstone

The shear strength of rock reflects its ability to resist damage, and it contains two indicators: the cohesion force and the internal friction angle. In general, the cohesion force mainly reflects the cementation between the rock particles, and the internal friction angle reflects the friction properties of the rock particles (Xi and Xu 2016). Based on the triaxial test results, the cohesion force and internal friction angle are determined by Mohr’s circle graphic method. As listed in Table 5, both the cohesion force and internal friction angle increase with a decreasing temperature. Compared with the results at−5 °C, the cohesion force and internal friction angle at−30 °C increase by 47.37% and 15.38%, respectively, which indicates that the cohesion force is more sensitive to temperature.

Table 5 Variation of shear strength indicators
Full size table

According to Fig. 2, a sketch of the mesostructures of frozen red sandstone is redrawn and shown in Fig. 11. Generally, the saturated frozen rock is composed of clay minerals, ice, water, and rock particles. The influence of the temperature on the cohesive force and internal friction angle can be explained as follows: (1) Pore ice enhances the cementation performance between the rock particles and improves the cohesion force of rock. (2) The friction effect between rock particles and ice particles is more evident than that between the rock particles and water. Therefore, the internal friction angle of sandstone is enhanced. As a result, the cohesive force and the friction angle both increase with a decreasing temperature. For further decreases in temperature, the increment of ice crystals becomes small. Consequently, the contribution of ice crystals to cementation and friction becomes small (Yamabe and Neaupanek 2001). Therefore, the increasing ratio of cohesive force and internal friction angle gradually slows.

Fig. 11
figure 11

Sketch of the mesostructures of the frozen red sandstone

Full size image

Moreover, during the loading process the rock particles undergo three processes: elastic deformation, particle sliding, and pore closure (Liu et al. 2019). The changes in the temperature and confining pressure enhance the friction effect between rock particles and ice particles. Increasing the confining pressure decreases the porosity, and the friction effect between particles becomes more apparent, so the relative slip between particles has been hindered (Kodama et al. 2013). With increasing confining pressure the pores are squeezed, and the deformation of the sample is reduced. In conclusion, the shear strength indexes of frozen rock are enhanced by negative temperatures.

According to Eq. (19), the Drucker-Prager criterion can be written as

$$F=k=\alpha {I}_{1}+\sqrt{{J}_{2}}=\frac{3c\mathrm{cos}\phi }{\sqrt{3+{\mathrm{sin}}^{2}\phi }}$$
(33)

where \({I}_{1}\) is the first invariant of the stress tensor; \({J}_{2}\) is the second invariant of the deviatoric stress tensor; and \(\alpha\) and \(k\) are the parameters determined by the cohesion force and internal friction angle.

Substituting the cohesion force and the internal friction angle (in Table 5) into Eq. (33), the variation in the rock microelement strength \(k\) with temperature can be obtained, as shown in Fig. 12. The rock microelement strength increases with decreasing temperature. This means that the negative temperature gives the rock samples a better ability to resist damage. In other words, the rock will be damaged at a higher stress level. Therefore, the starting stress of the increase in the damage variable is postponed by the decreasing temperatures, as shown in Fig. 8.

Fig. 12
figure 12

Relationship between the rock microelement strength \(k\) and the temperature

Full size image

Conclusions

This study aimed to provide more realistic essential parameters of frozen rock in artificial ground freezing. By conducting a series of experiments on sandstone at negative temperatures, the mechanical properties of frozen sandstone were analyzed, and a damage constitutive model was established. Based on the results, the following conclusions can be drawn:

  1. (1)

    Both the cohesion force and the internal friction angle increase significantly with a decreasing temperature, and the cohesion force is more sensitive to the negative temperature. The crack initiation stress, peak stress, and failure strain of the frozen sandstone increase with decreasing temperature. The crack damage threshold increases as the frozen sandstone strength increases. The negative temperature enhances the strength of the rock microelement and inhibits the damage evolution.

  2. (2)

    When the deviator stress reaches the crack initiation stress, damage begins to occur. When the deviator stress reaches the crack damage stress, the propagation of cracks is intensified. The damage variable increases rapidly when the deviator stress approaches the peak strength. The evolvement of the porosity experiences different phases: the decreasing stage, the gradual increasing stage, and the sharp increasing stage. The crack damage threshold can be treated as a reliable indicator for predicting the damage and failure of the frozen sandstone.

  3. (3)

    The presented model considers the impact of the threshold on rock damage. To reflect the damage evolution process, a statistical damage model was proposed to describe the failure process of frozen sandstone. The verified results indicate the feasibility and capability of the proposed model. The parameters in the model have a good relationship with the temperature and confining pressure. \({F}_{0}\) reflects the strength of rock, and \(m\) reflects both the strength and the brittleness of rock.