Introduction 

High-energy massive rockburst disasters are very likely to occur in the rock surrounding tunnels constructed in an environment under high stress, high temperature, high karst water pressure, and mining disturbance (Zhang et al. 2018; Oge and Cirak 2019; Li et al. 2019; Jendryś et al. 2021). When a rockburst occurs, damage phenomena including burst, loosening, and ejection occur in the surrounding rock, which occur sudden, posing a hazard. How to predict and avoid rockburst disasters has become one of the key challenges that limit development of deep underground spaces (Chen et al. 2017; Hradecký and Pánek 2008; Afraei et al. 2018; Feng et al. 2019; Roohollah and Abbas 2019; Zubíček et al. 2020).

The properties of the rock determine whether a rockburst occurs during the construction of a deep underground space or not, so their mechanical behaviors are critical for exploring the evolution mechanism and prediction and early warning of rockbursts. When a rockburst occurs, the stress on surrounding rocks has reached the ultimate strength of rocks, making this a problem of rock failure; however, it is difficult to study the failure behaviors of rockburst-prone surrounding rocks under full-scale excavation due to the complex field geological conditions. At present, commonly used research methods mainly include laboratory uniaxial tests (Gu et al. 2014), biaxial tests (Yun et al. 2010), and true triaxial tests (Su et al. 2017; Akdag et al. 2018; Si et al. 2020; Si et al. 2021). Uniaxial tests are mainly applicable to rockbursts of rock pillars; triaxial tests can be used to study rockbursts during unloading and stress concentration of surrounding rocks. However, most of these methods ignore any influences of different tangential stress gradients of surrounding rocks in the stress field on the disaster-causing mechanism of rockbursts. After rocks are excavated, a large tangential stress of surrounding rocks is observed on tunnel walls, which decreases to the interior of the surrounding rock at a certain rate (Liu et al. 2019); therefore, Xia et al. (2014) investigated the fractal features of the debris mass and shape of models during rockbursts under different loading and unloading paths. They also established the relationship between the rockburst intensity of the model and fractal dimension of debris under different loading and unloading paths. They found the fractal dimension of debris of the model during rockbursts in the unloading process of low confining pressure is larger than that during unloading of high confining pressure. By conducting true triaxial tests, Liu et al. (2021) studied the damage phenomena of the model during rockbursts under different stress gradients by conducting true triaxial tests. They found that as the stress gradient increases, the rockbursts become more intense and the failure load decreases. By conducting gradient tests, Huo et al. (2020) explored the infrared features of unloading on certain faces under different gradient loads. Test results are of important significance for studying rockbursts. However, the rockburst mechanism under gradient stresses of surrounding rocks was not revealed based on test results and the significant difference in failure modes of surrounding rocks under loading conditions with different stress gradients was not explained. Therefore, developing a mesoscopic mechanical model for surrounding rocks under gradient stresses is conducive to explaining various mechanical behaviors of rockburst-prone surrounding rocks from the perspective of the failure mechanism.

A mesoscopic simulation model of rockbursts under gradient stresses was established using a discrete element method based on the particle flow code (PFC). The model was used to simulate features of acoustic emission (AE) events, including the spatio-temporal distribution, and fracture strength during rockbursts under loading conditions with different stress gradients. Moreover, the induction mechanism of rockbursts under gradient stresses was revealed from perspectives of the rockburst intensity and failure modes. The research provides a basis for understanding the failure mechanism of rockbursts under gradient stresses and scientifically evaluating the stability of engineering operations at depth in rock.

Simulation and verification of rockbursts during loading of gradient stresses

Rockburst model during loading of gradient stresses

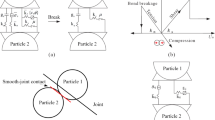
The collection, machining, and loading of large natural rock samples are limited by many aspects including actual conditions and requirements for experimental equipment. Additionally, defects such as joints and fractures in large natural rock samples; the heterogeneity of rock samples also affect the test results. Therefore, natural rock samples in the tests are generally replaced with and simulated by high-strength gypsum (Li et al. 2014; Amad et al. 2020; Zhao et al. 2021). Relevant physico-mechanical parameters are shown in Table 1 and the dimensions of the rockburst model and the process of application of gradient stresses are illustrated in Fig. 1. The impact energy index KE (Ghasemi et al. 2020) is the ratio of the deformation energy accumulated before the peak and the deformation energy consumed after the peak in the stress–strain curve under uniaxial loading. It is generally believed that the larger the KE, the higher the elastic energy release rate during rockburst failure, and the more favorable to the occurrence of strong rockburst.

Table 1 Material parameters of the model and indices of rockburst proneness  
Full size table
Fig. 1
figure 1

Dimensions of the model and the loading process of gradient stresses 

Full size image

As shown in Fig. 1a, before excavation, the rock is under three principal stresses such that σ1 ≥ σ2 ≥ σ3; after excavation unloading, the radial stresses on the unloading face are σr = σ3 = 0, providing a free face for failure of surrounding rocks under stress. The tangential stress σθ is concentrated on the unloading face and changes from uniform distribution σθ = σ1 before excavation along the gradient distribution. That is, the tangential gradient stress is large on tunnel walls, and decreases to the interior of the surrounding rock (gradient 1 = σ1-1 > gradient 2 = σ1-2 > gradient 3 = σ1-3 > gradient 4 = σ1-4), as shown in Fig. 1b. The axial stress remains unchanged before and after excavation (σr = σ2), and failure of surrounding rocks is related to the minimum and maximum principal stresses (Taromi et al. 2017; Li et al. 2017). The rockburst occurs in the loading process with concentration of tangential stress after unloading excavation of the tunnel.

Inversion of mesoscopic parameters and model verification

The linear parallel bond contact model was adopted. It can resist tension, shearing, and the rotation of particles with many previous numerical studies (Potyondy and Cundall 2004; Potyondy 2012; Cao et al. 2018; Duan et al. 2021) demonstrating that the PBM can be used to simulate the mechanical behavior of rock. As shown in Fig. 2, a full-system model of rockburst under gradient loading was established based on the mesoscopic discrete element code PFC2D to reveal the rockburst and fracture mechanism of the model under different stress gradients from the mesoscopic perspective. The test simulation system included a model sample under stress and a stress loading system in the test process. To apply load in the test, the servo-motor-controlled loading boundary was adopted as the loading boundary of rockbursts in the PFC model, and the dimensions of specimens were identical to those used in the test.

Fig. 2
figure 2

Simulation of stress states before and after tunnel excavation

Full size image

According to the correspondence between mesoscopic parameters of particle elements and macroscopic physical and mechanical properties of materials in previous research (Su et al. 2019; Lu et al. 2021; Song et al. 2022), the steps for determining the mesoscopic parameters are described as follows:

  1. (1)

    According to the size of samples, the radius of particle elements that constitute the model is set to 1.2 to 1.8 mm and meets the Gaussian random distribution. The particle density is calculated based on the density of concrete and the porosity of the model. The coefficient of friction between particles is set to 0.5;

  2. (2)

    The normal contact stiffness \({k}_{n}\) and bonding stiffness \({\overline{k} }_{n}\) of particles can be converted into the elastic modulus En = kn/2t and \({\overline{E} }_{n}={\overline{k} }_{n}\)/(RA + RB). It is supposed that \({E}_{n}\)/\({\overline{E} }_{n}\) = 1; t is the model thickness (generally set to 1); RA and RB are the radii of particles in mutual contact;

  3. (3)

    Each component \({k}_{n}\)/\({k}_{s}\) is inverted according to the relationship between \({k}_{n}\)/\({k}_{s}\) and the Poisson’s ratio, where \({k}_{\mathrm{s}}\) represents the tangential stiffness;

  4. (4)

    The stiffness \({k}_{n}, { k}_{s}, {\overline{k} }_{n}, \mathrm{and} {\overline{k} }_{s}\) of each component is inverted based on the elastic modulus E of the test material, in which \({\overline{k} }_{s}\) denotes the tangential bonding stiffness; and

  5. (5)

    According to the Brazilian splitting tests and triaxial tests, the bonding strength \({\tilde{\sigma }}_{c} \mathrm{and} {\overline{\tau }}_{c}\) of each component can be inverted, which is a major step of the mesoscopic parameter calibration. According to the comparison of mechanical parameters between the laboratory test of gypsum samples and the PFC simulation results (Fig. 3 and Fig 4), the error between the peak strength of the stress–strain curve is small. In addition, the failure modes of the samples are basically consistent.

Fig. 3
figure 3

Comparison diagram of Brazilian splitting tests

Full size image
Fig. 4
figure 4

Comparison diagram of triaxial compression test

Full size image

In the test process, the initial confining pressure (σ1 = 2 MPa, σ3 = 1 MPa) was applied to each face of the model using multi-stage loading. The horizontal confining pressure on a face was unloaded after loading to the initial confining pressure state of the model. According to Fig. 1, the vertical load was applied at multiple levels after excavation unloading in the simulation. The stress was increased by 0.5 MPa at gradient 1; while the stress was simplified as follows at other gradients:

$$y=an{\overline{e} }^{mx}+c$$
(1)

where y represents the tangential stress on a point in surrounding rocks of an underground tunnel (MPa); x is the radial distance from a point in the model to the unloading face (m); n denotes the loading steps related to time in the tunnel-excavation process; a represents the loading step sizes in the vertical stress concentration process on the unloading face of the model after excavation in the simulation (MPa); c is the initial top compressive stress of the model (MPa); m denotes the coefficient of stress gradients (m ≥ 0). Therein, different coefficients m of stress gradients can reflect the distributions of different vertical stress gradients in the model. The larger the value of m, the greater the vertical stress gradient, which corresponds to a greater tangential stress gradient of surrounding rocks. In the present research, gradient loading tests with m set to 0, 2, 4, and 6 were selected for inversion (Liu et al. 2021). The mesoscopic parameters attained through inversion are listed in Table 2.

Table 2 Mesoscopic parameters of the model
Full size table

Damage phenomena attained through inversion and the result comparison are shown in Figs. 5, 6, 7, and 8, wherein the blue color represents the model while particle clusters in other colors denote debris. The red and black cracks are shear and tensile cracks, respectively. The failure stresses of rockbursts acquired in the tests and simulation are listed in Table 3.

Fig. 5
figure 5

Crack propagation results of the model with m = 0

Full size image
Fig. 6
figure 6

Crack propagation results of the model with m = 2

Full size image
Fig. 7
figure 7

Crack propagation results of the model with m = 4

Full size image
Fig. 8
figure 8

Crack propagation results of the model with m = 6

Full size image
Table 3 Comparison of failure stresses of rockbursts: physical tests and numerical simulation
Full size table

As shown in Figs. 5, 6, 7, and 8 and Table 3, the macroscopic and microscopic failure phenomena in model tests of rockbursts are relatively consistent with the results of numerical simulation. Due to influences of side resistance in these tests, the failure load in the tests is higher than that in the numerical simulation (in general). In Fig. 5, when the coefficient of applied stress gradients m is 0, the cracks in the simulation correspond to those in the laboratory test results and cracks mainly propagate along the unloading excavation face of the model. Wedge-shaped failure occurs to the top of samples in both the model test and simulation results, and the failure structures at the bottom are also consistent. It can be seen from Fig. 6 that the failure mode in the numerical model is almost consistent with that in the laboratory test when the coefficient of applied stress gradients m is 2. Tabular debris falls from the upper part of the unloading face of the model and in the interior of the model, vertical cracks run through the model. As the applied stress gradient increases (m = 4, Fig. 7), the samples all show step-like crack propagation faces, the cracks propagate to the center of the model, and the severity of the damage increases, with subsequent debris ejection. Figure 8 indicates that during numerical simulation, a tilted triangular failure zone appears in the top of the unloading face, cracks on side faces of the model propagate to form a concave cavity, and a partial nucleation zone appears in the model when the coefficient of applied stress gradients m is 6. Meanwhile, many particles and small blocky debris are ejected from the unloading face at rockburst failure, indicative of high rockburst intensity, which also agrees with the fracture mode and rockburst intensity of the model in the laboratory tests.

Comparison of the aforementioned test results and simulation results in crack propagation implies that mesoscopic PFC simulation of rockburst tests of physical models under loading conditions of different stress gradients is consistent with test results, from failure phenomena to mechanical properties, thereby verifying the numerical model.

Crack propagation and energy evolution process

Crack propagation and fracture modes

Microstructures are constantly deteriorated during the loading of the model. As the load increases, new micro-cracks maintain their stable growth. Figure 9 simulates changes in the total number of cracks as well the numbers of tensile cracks and shear cracks in the model in loading environments with different stress gradients.

Fig. 9
figure 9

Crack propagation process in the numerical model under different stress gradients

Full size image

From the time of crack propagation in Fig. 9, the model enters the stable crack propagation stage after unloading. The cracks increase rapidly in the model during loading at stress gradients with m = 0 and m = 2; when the coefficient of stress gradient is m = 4 and m = 6, cracks propagate slowly and tensile cracks predominate. When loading to the critical value, crack propagation begins to accelerate, and the model enters the failure and crack-coalescence stage. When the coefficient of stress gradient m = 0 and m = 2, cracks increase albeit slightly; at m = 4 and m = 6, cracks inducing failure of the model increase in both number and length and do so rapidly. As the coefficient increases from m = 0 to m = 6, the numbers of cracks at rockburst failure of the model are 3.25 × 103, 2.7 3 × 103, 2.38 × 103, and 2.12 × 103, respectively. Under any stress gradient, tensile cracks account for a larger proportion in the whole failure process of the model before rockbursts. However, as the coefficient of applied stress gradients rises, the proportion of shear cracks gradually enlarges, separately to 26.2%, 37.5%, 46.8%, and 64.3%, namely, the tensile shear failure ratio is 2.81, 1.66, 1.14, and 0.56 respectively. This indicates that rockburst failure of the model is dominated by tensile failure under a small applied stress gradient; while with the increase in the applied stress gradient, the contribution of shear failure to the overall failure increases.

According to the spatial locations of crack propagation in the model (Fig. 9), cracks in the model show a similar spatial propagation process during rockbursts under different stress gradients applied. In the stable crack propagation stage, many cracks are initiated and gather in the upper part of the model; these are mainly tensile cracks, accompanied by a small number of shear cracks. Then, a small number of tensile-shear cracks develop in the lower part of the model. When loading to the failure and crack coalescence stage, cracks on the unloading face of the model propagate simultaneously from the upper and lower parts and coalesce at the center of the model, with a greater extent of crack propagation evident in the upper part than in the lower part. When the coefficient of stress gradient is m = 0 and m = 2, the through-going cracks mainly are tensile cracks. When m = 4, tensile-shear cracks overlap and run through the model. When the coefficient is m = 6, the through-going cracks mainly are shear cracks.

Energy evolution process

In laboratory tests, the energy evolution in the model during rockbursts under loading conditions of different stress gradients was generally characterized by AE data. To reproduce the real-time evolution process of each physical energy in the rockburst process of the model, the FISH language was adopted to embed each energy-releasing event in the rockburst process to the PFC.

Here, it is supposed that the whole rockburst test system is a closed system without any energy exchange with the outside. If the total energy input generated by the work done by external forces (work done by the load platens on the top of the model) is U, then the following is obtained according to the first law of thermodynamics (Meng et al. 2020):

$$U={U}_{d}+{U}_{e}$$
(2)

where Ud represents the dissipated energy of particles in the loading process of the model; Ue denotes the releasable elastic strain energy stored in the rockburst model.

In the rockburst simulation test based on PFC, the total external energy input U of the model can be acquired using the following equation:

$$U={U}_{pre}+\left({F}_{1}{\Delta D}_{1}+{F}_{2}{\Delta D}_{2}+{F}_{3}3+{F}_{4}{\Delta D}_{4}\right)$$
(3)

where Upre denotes the total energy input when loading to a certain time step; F1, F2, F3, and F4 separately represent the forces applied by four gradient loading platens at the beginning of the next time step; ΔD1, ΔD2, ΔD3, and ΔD4 separately refer to the displacements of corresponding loading platens.

The elastic strain energy Ue of the aggregate of particles in the PFC parallel bonding model consists of two parts: strain energy of particles Uc and strain energy under parallel bonding Upb, which are separately expressed as follows (Luo et al. 2020):

$${U}_{e}={U}_{c}+{U}_{pb}$$
(4)
$${U}_{c}=\frac{1}{2}\sum_{{N}_{c}}\left({\left|{\overline{F} }_{i}^{n}\right|}^{2}/{k}^{n}+{\left|{F}_{i}^{s}\right|}^{2}/{k}^{s}\right)$$
(5)
$${U}_{pb}=\frac{1}{2}\sum_{{N}_{pb}}\left[{\left|{\overline{F} }_{i}^{n}\right|}^{2}/\left(A {\overline{k} }^{n}\right)+{\left|{\overline{F} }_{i}^{s}\right|}^{2}/\left(A {\overline{k} }^{s}\right)+{\left|\overline{M }\right|}^{2}/\left(I{ \overline{k} }_{n}\right)\right]$$
(6)

The dissipated energy Ud is attained by substituting Eqs. (3) to (6) into Eq. (2).

Damage evolution in the model under loads is mainly driven by the dissipated energy (Zhang et al. 2017), while rockbursts are mainly triggered by the release of elastic strain energy. Therefore, Eqs. (2) to (6) are written in PFC using FISH, which enables discussion of the evolution of dissipated energy and elastic strain energy in the rockburst-development process of the model. Figure 10 shows the energy evolution process of the model during rockbursts under loading attained through numerical simulation. Therein, the post-peak stage of elastic strain energy is regarded as one of rapid energy release, during which the change rate is measured in terms of the quantity v/10–6 aJ·Pa−1.

Fig. 10
figure 10

The energy evolution process in the PFC2D model during rockbursts

Full size image

As illustrated in Fig. 10, the PFC model exhibits similar energy evolution during rockbursts in the loading environment with different stress gradients. The overall energy evolution in the rockburst process can be divided into the elastic stage, dissipation stage, and accelerated release stage. In the initial stress loading process (gradient 1 < 2 MPa), the model is in the elastic stage. In the deformation of the model under stress, the work done by each gradient loading platen is stored in the model as elastic strain energy, as evinced by the overlapping of the input energy curve and the strain energy curve. As the gradient stress applied to the model increases, micro-cracks begin to be initiated in the model, which marks the beginning of the energy dissipation stage; because the generation and propagation of micro-cracks entail dissipation of energy, the energy absorbed by the model is not completely transformed into elastic strain energy. The dissipated energy corresponding to damage to the model gradually increases, and the rate of growth of releasable stored elastic energy decreases, as evinced by the phenomenon that the input energy curve and the strain energy curve begin to deviate from each other. If the applied stress reaches that for a rockburst, the releasable elastic strain energy stored in the model is released rapidly, as evinced by the substantial decrease in the accumulation of elastic strain energy.

Each stage in the energy evolution in the model is similar during rockbursts under different applied stress gradients, whereas as the applied stress gradient increases, the magnitude of each energy changes to different extents. Table 4 lists changes in each component of the energy stored in the model under different applied stress gradients; Fig. 11 illustrates the relationship between the stress gradient and the energy.

Table 4 Statistics pertaining to energy in the model during a rockburst failure
Full size table
Fig. 11
figure 11

Relationship between applied stress gradients and energy in rockburst tests

Full size image

As shown in Table 4 and Fig. 11, the total energy input by each loading platen decreases from 1.13 kN·m to 0.69 kN·m with increasing applied stress gradient. The peak elastic energy storage varies slightly while the proportion of elastic strain energy (peak elastic strain energy/total energy input) increases from 0.29 to 0.49, suggesting that the proportion of elastic strain energy increases before a rockburst occurs. Moreover, the rate at which elastic energy is released increases from 0.23 to 0.55, suggesting that the rate of energy release in the model increases with increasing m. The rapidly released energy imposes greater impact damage, and the energy needed for dynamic cracking is much lower than that needed for steady crack propagation (Wu et al. 2015a). Therefore, more energy is transformed into kinetic energy for ejection of debris, and the ejection becomes more intense in the rockburst process.

These results imply that the development and occurrence of rockbursts are related to the growth and decline of each component of stored energy in the model. The rockburst failure of the model is shown as a process going from local damage (energy dissipation) to overall failure (energy release). As the applied stress gradient in increased, the proportion of elastic energy storage increases before a rockburst and the rate of release of energy increases thereafter.

AE during rockbursts in the model

AE simulation based on PFC

To study features of rockburst events of the model, including the spatio-temporal distribution and fracture strength, the AE process was simulated using PFC. In the discrete element method of particle simulation, it is easy to calculate the moment tensor according to changes in the contact force of surrounding particles at bond failure because stress and motion of particles can be directly acquired in the model. The moment tensor component was obtained via summation operation after multiplying variations of all contact forces on source particles with the corresponding arm of force (distance from the contact point to the center of the micro-cracks), as expressed below (Zhao et al. 2021):

$${\sum }_{s}\left(\Delta {F}_{i}{R}_{j}\right)$$
(7)

where △Fi is the ith component of the variation of the contact force; Rj represents the jth component of the distance from the contact point to the center of the micro-cracks. If an AE event only involves a micro-crack, then the spatial location of the AE event is the center of the micro-crack; if an AE event is induced by multiple micro-cracks, the geometrical center of all micro-cracks is the spatial location of the AE event.

Figure 12 illustrates the AE event caused by a tensile micro-crack. In Fig. 12a, the velocity vector of particles after formation of the micro-crack indicates that source particles move rapidly to both sides along the direction normal to the micro-crack. In Fig. 12b, the lengths and directions of the two arrows are calculated and represented by eigenvalues of the moment tensor matrix.

Fig. 12
figure 12

An AE event caused by a tensile micro-crack (Zhao et al. 2021)

Full size image

Multiple AE test results indicate that energy released by AE events constantly evolves over time. Therefore, the moment tensor can be represented as a function of time. In PFC, to improve the efficiency of calculation, the moment tensor with the maximum scalar torque is adopted as the moment tensor of each AE event and saved. According to the moment tensor matrix, the scalar torque is expressed as follows:

$${M}_{0}={\left(\frac{{\sum }_{j=i}^{3}{M}_{j}^{2}}{2}\right)}^{1/2}$$
(8)

where mj denotes the jth eigenvalue of the moment tensor matrix. Based on the peak scalar torque of moment tensors of AE events, the fracture strength M of AE events can be calculated using the following equation (Barton and Shen 2018):

$$M=\frac{2}{3}log{M}_{0}-6$$
(9)

Spatio-temporal-strength characteristics of rockbursts in the model

The spatial distribution of AE intensity of the model during rockbursts under different applied stress gradients as obtained in PFC simulation is shown in Fig. 13. In the figure, the red represents the high intensity AE event, and the AE event intensity gradually decreases as the color tends toward blue.

Fig. 13
figure 13

Spatial distribution of AE count and intensity during rockbursts of the model under loading conditions of different stress gradients

Full size image

It can be seen from Fig. 13 that the AE count is normally distributed with changes in the strength M. In addition, high-intensity AE events increase in number and samples are severely damaged. As the applied stress gradient is increased, the maximum AE count arises when M is between 2 × 10–4 and 3 × 10–4, 3 × 10–4 and 4 × 10–4, 5 × 10–4 and 6 × 10–4, and 7 × 10–4 and 8 × 10–4. The result suggests the increase in the overall AE intensity at fracture points on the unloading face of the model. Points with large AE intensity generally correspond to shear fracture points. This is mainly because the burst and loosening of surrounding rocks dominated by tensile failure belong to brittle failure of surrounding rocks under a low stress; compression and shear-dominated failure involves extremely intense failure of rocks under a high stress, and the energy release during shear failure is greater than that during tensile failure (Zhang et al. 2018).

The temporal distribution of the AE intensity of the model during rockbursts under different stress gradients applied obtained through PFC simulation is shown in Fig. 14.

Fig. 14
figure 14

Temporal distribution of the AE count and intensity during rockbursts of the model under loading conditions of different stress gradients

Full size image

According to temporal distribution of the AE count and intensity in the rockburst process in the model subject to different stress gradients (Fig. 14), the AE intensity characteristics differ significantly; when loaded to the critical value, the model shows accelerated energy release once failure begins. The accumulation of AE energy is rapid, indicative of high critical sensitivity and temporal heterogeneity. As the coefficient m relating to the applied stress gradient is increased, this phenomenon becomes increasingly prominent, suggesting that the rate of release of energy increases in the model failure process. The energy needed for dynamic cracking is much lower than that needed for steady crack propagation (Wu et al. 2015b), so there is more energy transformed into kinetic energy driving the ejection of debris; therefore, the magnitude of m affects the temporal distribution in the energy release process during rockbursts. The larger m is, the more concentrated the energy release immediately before a rockburst.

Conclusions

Based on the numerical software PFC2D, the research simulated the whole rockburst process of the model from the mesoscopic perspective. Combined with rockburst tests on a macroscopic model under gradient loading, the initiation, propagation, and coalescence of micro-cracks during rockburst events, along with the energy transformation of the system, were studied. The main conclusions are as follows:

  1. (1)

    Comparison of the PFC2D numerical simulation with laboratory test results of the rockburst model reveals that the simulated results are consistent with the laboratory rockburst test results, verifying the effectiveness of the numerical model.

  2. (2)

    The increase of the applied stress gradient accelerates the deterioration of materials during rockbursts and promotes rapid propagation of the dominant main crack. In addition, the number of secondary cracks and the total number of cracks are significantly reduced. As the applied stress gradient is increased from m = 0 to m = 6, the numbers of cracks at rockburst failure of the model are 3.25 × 103, 2.73 × 103, 2.37 × 103, and 2.12 × 103, respectively. Under any gradient stress, tensile cracks predominate in the early stage of loading. At rockburst failure, the proportion of shear cracks gradually increases to 26.2%, 37.5%, 46.8%, and 54.3% as the applied stress gradient is increased.

  3. (3)

    The energy evolution in the rockburst process is divided into an elastic stage, energy-dissipation stage, and energy-release stage; the energy evolution process is closely related to the applied stress gradient. With increasing applied stress gradient, the proportion of elastic energy storage at rockbursts increases from 0.29 to 0.49 and the rate at which energy is released increases from 0.25 to 0.53, indicating more severe damage.

  4. (4)

    The AE count shows a normal distribution with changes in the strength M. As the applied stress gradient is increased, the number of high-intensity AE events increases and damage to the samples tends to be more severe. The magnitude of the stress gradient affects the temporal distribution of the AE intensity during rockbursts. The greater the applied stress gradient, the more concentrated the high-intensity AE points at the critical point of the rockburst.