Introduction

Owing to the complex formation conditions and long-term geological tectonics, rocks often contain various types of microscopic cracks, which directly affect their mechanical properties (Perie and Monteiro 1991; Liu et al. 1998). In rock mechanics, the specimen size is a negligible factor which may influence micro-defects and the corresponding mechanical properties. Meanwhile, rock deformation and failure are state instability phenomenon driven by energy, whose essential characteristic is energy transformation (Xie et al. 2005; Li and Cai 2021; Su et al. 2021). Thus, it is significant to investigate the size effect of rocks from an energy point of view.

Many experimental studies and numerical simulations have been carried out to investigate the size effect on mechanical properties. The peak compressive strength decreases with L/D regardless of material types (John 1972; Hawkins 1998; You and Zou 2000; Lei et al. 2019), loading rates (Liang et al. 2013; Meng et al. 2016), and temperature (Su et al. 2015). Meanwhile, several models which reflect relationship between the peak strength and diameters were proposed, such as an exponential function suggested by Liu et al. (1998), the H-B model (Hoek and Brown 1980), and MFSL model (Carpinteri et al. 1995). Many experimental data were used for validating and modifying these models by later researchers (Hawkins 1998; Pells 2004; Darlington et al. 2011; Masoumi et al. 2016; Darbor et al. 2019; Rong et al. 2018). When the length-to-diameter ratio (L/D) varies from 1 to 3, Thuro et al. (2001) pointed out that the size effect on rock damage and elastic modulus is quite remarkable. Under uniaxial compression (UC) and uniaxial cyclical compression tests, Guo et al. (2017) noted that AE counts and AE energy decrease with an increase in the L/D ratio. Walton (2018) pointed out that crack initiation and damage stresses are not related to specimen sizes. Wu et al. (2021) conducted UC tests on specimens with a small size (D = 20~50 mm) and analyzed the reason for size effects through CT scanner and 3D profilometer. Li et al. (2021) modified the universal equation derived from Song et al. (2018) to describe the relationship among the peak strength, specimen size, and loading direction. Kasyap and Senetakis (2022) observed small-scale size effects through various parameters (displacements at peak stress, tangential stiffness, and shear band formations) from shearing tests.

In addition to mechanical properties of rocks, energy is also an important topic on which researchers focus. Gong et al. (2018, 2019) found that the elastic strain energy (ESE) and dissipation strain energy (DSE) linearly increase with the input strain energy (ISE), which are named linear energy storage (LES) law and linear energy dissipation (LED) law, respectively. Khoramishad et al. (2014) studied size effects on the fracture energy of rocks and modified Bazant’s (1984) size effect law based on the fracture process zone. Meng et al. (2016) and Liang et al. (2016) pointed out that strain energy parameters (ISE, ESE, and DSE) decrease with L/D regardless of strain rates and described relationships between strain energy parameters and L/D with a power function (Meng et al. 2016) and a logarithmic regression function (Liang et al. 2016). In unloading rockburst tests, Zhao and He (2017) pointed out that fragment kinetic energy is not sensitive to sample size when the height-to-thickness ratio is less than 3. Zhao et al. (2022) discussed the energy storage limit and failure mode of sandstone under different L/D. Kasyap et al. (2022) analyzed relationships between the energy loss and fracture width and studied the total kinetic energy under different fracture distances.

Most investigations concentrated on the size effect from the aspect of mechanical properties, but the size effect on rock energy characteristics has less well been investigated. Furthermore, present research mostly focused on the relationship between strain energy parameters and L/D, but rarely investigated the internal relationships among strain energy parameters under different specimen sizes. In addition, it is generally known that energy storage and dissipation are inevitable in the process of rock damage and failure. Gong et al. (2018) defined the energy storage coefficient (ESC) and energy dissipation coefficient (EDC), among them, ESC can reflect the storage capacity of ESE during loading. The ESE at the peak strength can be accurately obtained through ESC, thus improving a series of rockburst proneness criteria (Gong et al. 2020, 2021a, 2022). EDC can be widely used in proposing a new damage variable and establishing a damage constitutive model based on energy dissipation (Gong et al. 2021b). Therefore, investigating internal relationships among strain energy parameters under different specimen sizes and studying the size effect on ESC and EDC is of great significance.

In this study, five groups of single-cycle loading–unloading uniaxial compression (SCLUC) tests were performed on red sandstone using an INSTRON 1346 testing system. The rock specimens had the constant L/D = 2/1 and five contrasting diameters: 25, 37, 50, 75, and 100 mm. Based on test results, relationships among ISE, ESE, and DSE under different specimen sizes were clearly presented, and size effects on ESC and EDC were analyzed. This study would extend the applicable scope of LES and LED laws and enrich energy-based research on rock materials.

Experimental methodology

Specimen preparation

Rock specimens used in this study was red sandstone collected from Wuding County, Yunnan Province, China. The rock cores were first sampled from the same intact rock block, which had a uniform texture. Then, these cores were processed into cylindrical specimens. The L/D of the prepared specimens was 2, and the specimen diameters were 25, 37, 50, 75, and 100 mm, respectively (see Fig. 1). The prepared specimens had integrated and compact textures, and there were no visible cracks on their surfaces. The average density and P-wave velocity of the rock specimens were 2450 kg/m3 and 3411 m/s, respectively. Specific data are presented in Table 1. The specimen identification (ID) was organized in the form of “C-D-b,” wherein “C” means the compression test, “a” means the specimen diameter (mm), and “b” denotes the serial number of specimens in the “D” diameter group. Noteworthy, “b = 0” represents that the specimens are used to perform UC tests while “b = 1~6” on behalf of SCLUC tests with various unloading stress levels.

Fig. 1
figure 1

Photograph of the typical prepared specimens of different sizes

Full size image
Table 1 Basic parameters of specimens
Full size table

Test equipment

An electro-hydraulic servo-controlled testing system (INSTRON 1346) shown in Fig. 2 was used for the experiment. This test system comprises a control and data collection system, a loading system, a hydraulic transmission system, and a 2.5-mm-displacement extensometer. During the compression tests, the maximum axial loading force is 2000 kN. The strain and stress were obtained through a displacement extensometer and a hydraulic transmission system. An extensometer was used to measure the axial deformation of specimens. It was noted that two rigid blocks were placed between the specimen and equipment indenters to reduce the end friction effect. For the purpose of obtaining actual axial deformations of specimens, the axial deformation of these two rigid blocks was deducted.

Fig. 2
figure 2

INSTRON 1346 test system

Full size image

Test process

A monotonic UC test and five to six SCLUC tests were performed on specimens of each size group to investigate the size effect of red sandstone. For the monotonic UC test, one to three rock specimens were tested with a monotonically increasing loading until failure to obtain the (average) peak strength σc. For SCLUC tests, according to the obtained σc, five unloading stresses were preset as kσc (where the preset unloading stress level k = 0.1, 0.3, 0.5, 0.7, and 0.9). In SCLUC tests, the specimen was first loaded, then unloaded once it reached the preset unloading stress, and a second loading was applied until it failed. The loading path of the SCLUC test is shown in Fig. 3.

Fig. 3
figure 3

Load path of the SCLUC test: a stress–time diagram, and b stress–strain diagram

Full size image

The monotonic UC test and SCLUC tests were performed for specimens in each size group. Notably, the actual unloading stress level i is the ratio of the unloading stress to the actual peak strength under SCLUC tests (\(i = k\sigma_{{\mathrm{c}}} /\sigma_{\mathrm{c}}^{k}\)). The loading rate of the monotonic UC test was 1 MPa/s; for SCLUC tests, in order to prevent specimens from sudden failure near the peak point, a force-controlled and then displacement-controlled loading mode was used. In specific, the loading rate of the initial loading and unloading processes was 1 MPa/s, and the loading rate of the second loading process was 1 MPa/s before 0.8σc, then 0.001 mm/s until failure.

Energy calculation method

According to the thermodynamics law, the relationship between ISE, ESE, and DSE is as follows (Kidybinski 1981):

$$E_{{\mathrm{i}}}^{i} = E_{{\mathrm{e}}}^{i} + E_{{\mathrm{d}}}^{i}$$
(1)

where i is the actual unloading stress level (\({0} \le i \le 1\)), \(E_{{\mathrm{i}}}^{i} , \ E_{\mathrm{e}}^{i}\ ,{\mathrm{and}}\ E_{{\mathrm{d}}}^{i}\) are the ISE, ESE, and DSE at the actual unloading stress level i, respectively.

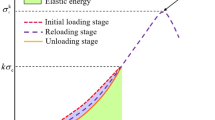
According to the schematic diagram shown in Fig. 4, strain energy parameters at the unloading point could be determined. ISE is the total input strain energy resulting from the work done by external forces and ISE is equal to the area between the initial loading curve and the horizontal axis (Eq. (2)). ESE could be determined as the area between the unloading curve and the horizontal axis (Eq. (3)). DSE equals ISE minus ESE (Eq. (4)). The specific equations are shown as follows:

$$E_{{\mathrm{i}}}^{i} = \int_{0}^{{\varepsilon_{{\mathrm{u}}} }} {f(\varepsilon )} \, d\varepsilon$$
(2)
$$E_{{\mathrm{e}}}^{i} = \int_{{\varepsilon_{0} }}^{{\varepsilon_{{\mathrm{u}}} }} {f_{{\mathrm{u}}} (\varepsilon )} \, d\varepsilon$$
(3)
$$E_{{\mathrm{d}}}^{i} = E_{{\mathrm{i}}}^{i} - E_{{\mathrm{e}}}^{i} = \int_{0}^{{\varepsilon_{{\mathrm{u}}} }} {f(\varepsilon )} \, d\varepsilon - \int_{{\varepsilon_{0} }}^{{\varepsilon_{{\mathrm{u}}} }} {f_{{\mathrm{u}}} (\varepsilon )} \, d\varepsilon$$
(4)

where \(f(\varepsilon )\) and \(f_{{\mathrm{u}}} (\varepsilon )\) are the curvilinear functions of initial loading process and the unloading process, respectively. \(\varepsilon_{{0}}\) is the permanent strain after unloading, and \(\varepsilon_{{\mathrm{u}}}\) is the strain at the unloading point.

Fig. 4
figure 4

Schematic of the energy calculation method at the actual unloading stress level

Full size image

Results

Mechanical properties of red sandstone with different sizes

Stress–strain curves of red sandstone specimens of different sizes are shown in Fig. 5. The concavity of stress–strain curves slightly decreased with the specimen size; thus, the elastic modulus increased. Stress–strain curves dropped steeply when reaching the peak point regardless of specimen sizes, exhibiting brittle failure characteristic. Specimens of D = 25 mm showed the largest peak strain, and the peak strain varied slightly for specimens from D = 37 to D = 100 mm. When the diameter of specimens changed from 37 to 100 mm, the peak compression strength increased slightly. For specimens with a diameter of 25 mm, the peak compression strength was at a medium level.

Fig. 5
figure 5

Stress–strain curves of specimens of different sizes under different unloading stress level: a k = 0, b k = 0.1, c k = 0.3, d k = 0.5, e k = 0.7, and f k = 0.9

Full size image

From stress–strain curves of SCLUC tests shown in Fig. 5b~f, it was observed that the secondary loading curve passed the unloading point. This finding confirms that the single-cycle loading and unloading processes have no effect on its full UC process. In addition, the unloading curves no longer returned to the coordinate origin (0,0), indicating that there was a permanent plastic strain after unloading and energy dissipation existed during the loading and unloading process.

Failure characteristics of red sandstone with different sizes

Figure 6 shows pictures of specimens after failure. The failure mode of red sandstone was axial splitting failure regardless of specimen sizes. In Fig. 6a and c, there was one main crack approximately along the loading direction and several small cracks appeared near the main crack. In Fig. 6b, numerous axial cracks along the loading direction appeared in the outer surface of the rock specimen, exhibiting obvious splitting failure characteristics. Figure 6d and e exhibited multiple failure surfaces and rock fragments were mostly in block and flake forms. As specimen sizes increased, the number of rock fragments increased. For specimens of small diameters in Fig. 6a~c, only a small number of rock fragments fell inside the equipment pressure head. While for specimens of larger diameters in Fig. 6d and e, lots of fragments dropped from the rock parent body and fell outside the equipment indenter. The remaining rock specimen body after failure were in the form of two cones. Conical failure shown in Fig. 6d and e was caused by the “end friction effect” that the friction between specimen ends and loading plates limited the radial deformation at both specimen ends (Wu 2021).

Fig. 6
figure 6

Failure characteristics of specimens with different sizes: a C-25–4, b C-37–1, c C-50–5, d C-75–2, and e C-100–2

Full size image

Gong et al. (2018) defined the far-filed ejection mass ratio as a semi-quantitative indicator to evaluate rockburst proneness. However, the far-field and near-field were defined according to standard specimens (D × L = 50 mm × 100 mm). Whether this indicator could be used for non-standard specimens needed further research, because the range of near-field would increase with the specimen diameter. Herein, based on the experimental data and failure characteristics of standard specimens, red sandstone had a far-field ejection mass ratio of 0.13 that a small number of blocks were ejected and mostly fell within the equipment indenter. Additionally, through applying rockburst proneness criteria suggested in Gong et al. (2018) for quantitative analysis, the residual elastic energy was 97.4 kJ/m3. These results indicates that red sandstone had a low rockburst proneness.

Energy evolution characteristics of red sandstone with different sizes

Invoking the energy calculation method in the “Energy calculation method” section, the ISE, ESE, and DSE at different i were achieved. When analyzing the energy evolution characteristics of red sandstone with i, a coordinate origin (0,0) was added to represent the initial state where all strain energy parameters could be zero. The ISE, ESE, and DSE of specimens with different sizes under different unloading stress levels were shown in Fig. 7. The ISE, ESE, and DSE all nonlinearly increased with the i regardless of specimen sizes. Relationships between \(E_{{\mathrm{i}}}^{i} , \, E_{{\mathrm{e}}}^{i} {, }E_{{\mathrm{d}}}^{i}\) and i were fitted with quadratic functions. Specific fitting equations and their coefficients of determination (R2) were also expressed in Fig. 7. It was found that there were uniform nonlinear relationships between \(E_{{\mathrm{i}}}^{i} , \, E_{{\mathrm{e}}}^{i} {, }E_{{\mathrm{d}}}^{i}\) and i in the range of D = 25 ~ 100 mm with the R2 of 0.9674, 0.9657, and 0.9620, respectively. These high R2 values showed that specimen size did not have significant impacts on the variation rate of strain energy parameters with i. During the deformation and failure process of rock, the ISE converted into the ESE and DSE. Additionally, the ISE has the fastest increasing rate while DSE has the slowest one with i. The specimen size would not change this energy conversion mechanism that ESE was always larger than DSE, indicating that most of the ISE was stored as the ESE and a limited portion was dissipated. Through these relationships, strain energy parameters at any unloading stress levels with any specimen sizes could be obtained.

Fig. 7
figure 7

Relationships between the actual unloading stress level i and a ISE, b ESE, and c DSE

Full size image

Linear energy storage and dissipation laws of red sandstone with different sizes

For specimens with five different diameters, relationships between the ISE and ESE, DSE were shown in Fig. 8. During data fitting, the point (0, 0) was artificially added for the correction deviation; this coordinate origin corresponds to the ideal situation in which both the ESE and DSE are 0 when the ISE is 0. Figure 8 shows that ISE has good linear correlations with both ESE and DSE regardless of specimen sizes, which could be described as the LES law and LED law, respectively. The LES and LED laws under different specimen sizes could be expressed as followed:

$$E_{{\mathrm{e}}}^{D} = aE_{{\mathrm{i}}}^{D} + b$$
(5)
$$E_{{\mathrm{d}}}^{D} = (1 - a)E_{{\mathrm{i}}}^{D} - b = cE_{{\mathrm{i}}}^{D} - b$$
(6)

where \(E_{{\mathrm{i}}}^{D}\), \(E_{{\mathrm{e}}}^{D}\), and \(E_{{\mathrm{d}}}^{D}\) are ISE, ESE, and DSE of specimens of diameter D (mm), respectively, and a and b are fitting parameters. “a” and “c” can be defined as compression energy storage coefficient (ESC) and compression energy dissipation coefficient (EDC), respectively.

Fig. 8
figure 8

LES law and LED law of red sandstone with different sizes

Full size image

For specimens with D = 25, 37, 50, 75, and 100 mm, R2 of linear fitting functions between the ISE and ESE were 0.9998, 0.9991, 0.9979, 0.9985, and 0.9998, respectively, whereas R2 of the fitting functions between the ISE and DSE were 0.9993, 0.9967, 0.9934, 0.9957, and 0.9998, respectively. High fitting levels demonstrate that the LES and LED laws exist for specimens of any size, further extending the application scope of linear laws.

Through comparing a, b, and c, it was observed that b was much smaller than a and c. Therefore, when discussing size effect on linear energy storage and dissipation laws, the intercept b could be ignored. Thus, the size effect on the LES and LED laws could be evaluated through researching the ESC and EDC of specimens of different sizes. For specimens of five various diameters, values of ESC were 0.6688, 0.6487, 0.6439, 0.6306, and 0.6505, respectively, whereas values of EDC were 0.3312, 0.3513, 0.3561, 0.3694, and 0.3494, respectively (see Fig. 9). The difference between the maximum ESC (or EDC) and minimum ESC (or EDC) was only 0.0382, indicating that ESC and EDC changed slightly with the variation of specimen diameters. Consequently, unified LES and LED laws can be proposed for specimens of D = 25~100 mm (Fig. 10) whose R2 are 0.9981 and 0.9936, respectively. ESC and EDC of unified linear laws were 0.6488 and 0.3512, respectively. Based on the unified LES and LED laws, as long as the ISE was calculated through integration, accurate ESE and DSE of specimens of any diameters could be obtained.

Fig. 9
figure 9

The ESC and EDC of different specimen sizes

Full size image
Fig. 10
figure 10

Unified LES law and unified LED law of specimens with different sizes

Full size image

Discussion

Size effect on peak strength of specimens with L/D of 2

To investigate the size effect on the peak strength for specimens whose L/D is 2, results in this study and previous research were analyzed. Table 2 summarized conclusions about the size effect on the uniaxial compressive strength in reported literature. Conclusions resulted from different literature were different. From the point of view of statistical distribution, rock specimens contained micro-defects of different scales, and rock specimens with larger size were possible to contain more micro-defect, thus leading to lower strength (Çelik 2017). In addition, friction force existed between the rigid block and end faces more or less, resulting in a lateral binding force near the end face. Therefore, the peak compressive strength of rocks was negatively correlated with length and positively correlated with diameter. The size effect of rock materials on the peak strength was caused by a combination of several factors (Yang et al. 2005), and thus conclusions obtained from different studies might vary.

Table 2 Summary of the size effect on the peak strength
Full size table

To obtain a general law which describes a relationship between the peak strength and diameter, Fig. 11a shows the peak strength in this study and previous research (i.e., this work and previous studies by Nishimatsu et al. 1969, Hoskins and Horino 1969, Hawkins 1998, Thuro et al. 2001, Pells 2004, Darlington et al. 2011, Masoumi et al. 2016, Komurlu 2018, Walton 2018, Faramarzi and Rezaee 2018, Rong et al. 2018, and Darbor et al. 2019). Due to the reason that the peak strength of various rock types was distinctly different, data were scattered and accurate law was hardly to be observed. Therefore, the peak strength was normalized according to the approach proposed by Hoek and Brown (1980). In Fig. 11b, normalized strength equaled peak strength value divided by the peak strength of 50-mm diameter specimen. The formula can be shown as follows:

$$\sigma_{{{\mathrm{cn}}}} = \frac{{\sigma_{{\mathrm{c}}}^{D} }}{{\sigma_{{\mathrm{c}}}^{50} }}$$
(7)

where \(\sigma_{{{\mathrm{cn}}}}\) is normalized peak strength of specimens and \(\sigma_{{\mathrm{c}}}^{D}\) is the peak strength of “D” diameter specimens.

Fig. 11
figure 11

Relationships between specimen diameter and: a peak strength and b normalized strength (data from this study and Nishimatsu et al. 1969, Hoskins and Horino 1969, Hawkins 1998, Thuro et al. 2001, Pells 2004, Darlington et al. 2011, Masoumi et al. 2016, Komurlu 2018, Walton 2018, Faramarzi and Rezaee 2018, and Rong et al. 2018, Darbor et al. 2019)

Full size image

Notably, some studies did not include results of D = 50-mm specimens and \(\sigma_{{\mathrm{c}}}^{50}\) would be replaced by the peak strength of specimens whose diameter was close to 50 mm. Figure 11b reveals that the peak strength increases at first and then decreases slightly with specimen diameters. Specimens whose diameter was ranged from 40 to 60 mm usually had the largest peak strength. Because of the dispersion among peak strength of rock samples, the result in this study was not fully consistent to this general law. Therefore, this conclusion just reflects the general law for the size effect on peak strength, and additional analysis is also needed for specific types of rock.

Size-independent effect on ESC

In the “Linear energy storage and dissipation laws of red sandstone with different sizes” section, it was found that ESC and EDC were not sensitive to specimen sizes by comparing ESC and EDC of specimens of different diameters. However, whether ESC could be considered as an essential property measuring the energy storage capacity of rocks, the variation degree of each parameter under different sizes needed to be compared. As we all known, the P-wave velocity and density were inherent properties whose values were only relevant to rock types, internal components, and structure. On the contrary, mechanical properties such as the peak strength, peak strain, and elastic modulus varied with external loading conditions (e.g., loading rates). In this paper, the coefficient of variation (CoV) was used to evaluate the variation degree of each parameter at different size. The CoV can be defined as follows:

$${\mathrm{CoV}} = \frac{\beta }{\mu } \times 100\%$$
(8)

where β represents the standard deviation and \(\mu\) denotes the average value.

CoV values of ESC and other five common parameters were shown in Fig. 12. CoV values of density, ESC, P-wave velocity, peak strain, elastic modulus, and peak strength were 1.30%, 1.89%, 2.37%, 7.7%, 11.33%, and 12.21%, respectively. CoV of the ESC was smaller than that of mechanical properties (peak strain, elastic modulus, and peak strength). Meanwhile, CoV of the ESC was among the range of CoV values of inherent properties (density and P-wave velocity). Hence, ESC reflecting the energy storage capacity of rocks could be considered as an essential property, which did not vary with external loading conditions.

Fig. 12
figure 12

Coefficients of variation of the ESC and other common parameters

Full size image

Conclusions

In this study, several groups of UC and SCLUC tests were performed on red sandstone specimens of constant L/D and five different diameters using INSTRON 1346 test system. According to experimental results, effects of specimen size on mechanical properties and failure modes were analyzed. Furthermore, size effects on energy distribution and evolution laws of red sandstone were investigated. The relevant conclusions are as follows:

  1. 1.

    When specimen diameters increased, the concavity of stress–strain curves slightly decreased and the elastic modulus increased. Peak strength increased when D increased from 37 to 100 mm. Peak strain of specimens of D = 25 mm was obviously larger than that of other diameters.

  2. 2.

    The failure mode of red sandstone specimens of various diameters was axial splitting failure. The rock failure degree and amounts of rock fragments increased with specimen size. According to analytical results of standard specimens (D × L = 50 mm × 100 mm), red sandstone had a low rockburst proneness.

  3. 3.

    The input strain energy (ISE), elastic strain energy (ESE), and dissipation strain energy (DSE) nonlinearly increased with the actual unloading stress level. Unified nonlinear relationships were obtained for specimens whose diameter was from 25 to 100 mm. When the actual unloading stress level increased, ISE had the largest growth rate and DSE had the smallest one.

  4. 4.

    The ESE and DSE linearly increased with the ISE regardless of specimen sizes, i.e., the linear energy storage and dissipation laws also existed for specimens with non-standard sizes. The energy storage coefficient and energy dissipation coefficient were not dependent on specimen sizes. Furthermore, the energy storage coefficient was an essential property of rock materials which reflected the energy storage capacity of rock materials.