Investigation on the Linear Energy Storage and Dissipation Laws of Rock Materials Under Uniaxial Compression

Abstract

To investigate the energy evolution characteristics of rock materials under uniaxial compression, the single-cyclic loading–unloading uniaxial compression tests of four rock materials (Qingshan granite, Yellow sandstone, Longdong limestone and Black sandstone) were conducted under five unloading stress levels. The stress–strain curves and failure characteristics of rock specimens under the single-cyclic loading–unloading uniaxial compression tests basically corresponded with those of under uniaxial compression, which indicates that single-cyclic loading–unloading has minimal effects on the variations in the loading–deformation response of rocks. The input energy density, elastic energy density and dissipated energy density of four rocks under five unloading stress levels were calculated using the graphical integration method, and variation characteristics of those three energy density parameters with different unloading stress levels were explored. The results show that all three energy density parameters above increased nonlinearly with increasing unloading stress level as quadratic polynomial functions. Meanwhile, both the elastic and dissipated energy density increased linearly when the input energy density increased, and the linear energy storage and dissipation laws for rock materials were observed. Furthermore, a linear relationship between the dissipated and elastic energy density was also proposed. Using the linear energy storage or dissipation law, the elastic and dissipated energy density at any stress levels can be calculated, and the internal elastic (or dissipated) energy density at peak compressive strength (the peak elastic and dissipated energy density for short) can be obtained. The ratio of the elastic energy density to dissipated energy density with increasing input energy density was investigated using a new method, and the results show that this ratio tends to be constant at the peak compressive strength of rock specimens.

1 Introduction

The process of rock fracture and failure is essentially an energy transfer and exchange event, and the energy-related characteristics are important and effective in describing the mechanical properties of rock materials. The rock deformation and failure process is intrinsically driven by energy evolution activities that include energy input, storage, dissipation and release (Brady and Brown 2006; Xie et al. 2005; Mcsaveney and Davies 2009; Wasantha et al. 2014; Park et al. 2014; Wang et al. 2017; Gong et al. 2018a). Many researchers have conducted experimental studies from different aspects to investigate the energy evolution characteristics of rock materials. Based on uniaxial compression (UC) tests, Tsoutrelies and Exadaktylos (1993) studied the effects of rock discontinuities on the ratio of surface energy to the volume elastic strain energy. Hua and You (2001) concluded that the strain energy is stored in rocks during the loading stage, and the energy will be released when it is sufficiently large, causing rock failure. Huang and Li (2014) investigated the characteristics of strain energy accumulation, dissipation and release in three stages, including elastic compression, pre-peak unloading and post-peak fracturing. Li et al. (2014) analyzed the strain rate dependency of rock strain energy and observed that the pre-peak absorbs strain energy, while damage strain energy and elastic strain energy increase with the strain rate. Meng et al. (2016, 2018) revealed the acoustic emission characteristics of rocks and identified the relationships between the elastic energy, dissipated energy and axial loading stress of rock specimens. Xu and Cai (2018) investigated the influence of the strain energy released from a UC test machine on the rock failure process. Gong et al. (2018b, c) studied the energy storage and dissipation evolution process and characteristics of red sandstone and marble in three tension-type failure tests (including Brazilian test, point load test and semi-circular bending test), and found that there are linear relationships between the internal elastic and dissipated and external input energy. On the other hand, triaxial compression tests have also been performed to investigate energy transformation during deformation and failure process of rock. Peng et al. (2015) obtained the relationship between energy transformation and coal failure with conventional triaxial compression tests under five different confining pressures. Yang et al. (2016) proposed energy dissipation and energy release rules to characterize crack growth under different triaxial stress and explained the relationships between the releasable elastic strain energy, the dissipated energy density and the confining pressure. Zhang et al. (2017) explored the influence of confining pressure on the energy evolution characteristics and distribution relationships through triaxial cyclic loading–unloading compression tests. Torabi and Zarifi (2014) investigated the energy propagation in rock cataclastic bands. Castanon-Jano et al. (2017) designed energy dissipating devices from the perspective of energy conversion. Li et al. (2019) studied the energy attenuation characteristics of rock masses with different joint roughness using the modified SHPB device. Furthermore, certain rockburst proneness indexes were also proposed based on energy analysis (Kidybinski 1981; Singh 1988; Wang and Park 2001). Jiang et al. (2010) and Li et al. (2012) used a new energy index LERR (local energy release rate) to simulate and analyze the conditions causing rockburst in the deeply buried tunnels of Jinping II hydropower station. Cai (2016) and Miao et al. (2016) analyzed rockburst disasters in rock engineering from the prospect of energy accumulation theory. Gong et al. (2019) proposed a peak strength strain energy storage index to estimate and classify the rockburst proneness of nine rock materials.

According to the existing literature studies, most of the relevant research studies focus on the relationships between the elastic energy (or dissipated energy) and the stress or strain of rock specimen during the loading process. Few studies have emphasized the relationships between the input energy density (IED), elastic energy density (EED) and dissipated energy density (DED). In the present study, four rock materials (Qingshan granite, Yellow sandstone, Longdong limestone and Black sandstone) were investigated by single-cyclic loading–unloading uniaxial compression (SCLUC) tests under five unloading stress levels. The conversion characteristics of three energy density parameters (IED, EED and DED) with unloading stress levels were studied. Additionally, the relationships among the EED, DED and IED were analyzed in detail. The results show that there are strong linear relationships between the EED, DED and IED for every rock type tested. Based on the linear energy storage law, the EED or DED can be calculated at any stress levels. The proportional relationships between the EED and DED with increasing IED were also discussed.

2 Experimental Study

2.1 Rock Specimens and Preparation

A series of tests were carried out on four rock materials taken from different quarry in China; Qingshan granite and Longdong limestone materials were obtained from the city of Changsha in the Hunan Province, and Yellow sandstone and Black sandstone were taken from the city of Zigong in the Sichuan province. All the rock materials had favorable integrities and compactness without surface cracks. Cylindrical specimens were obtained by drilling core. The diameter ($D$) of the rock specimens was 50 mm, and the height ($H$) was 100 mm. The sides and end faces of the rock specimens were smoothed before testing. The nonparallel end faces and axial deviation were in the allowable ranges according to the standards of the International Society for Rock Mechanics (ISRM) standard (Fairhurst and Hudson 1999). Six specimens of each rock material with good homogeneity were selected for testing, and photographs of these specimens are shown in Fig. 1. The basic parameters of each rock specimen were determined, and the results are presented in Table 1. The density ($\rho$) of the Qingshan granite, Yellow sandstone, Longdong limestone and Black sandstone varied from 2.63 to 2.66 g/cm³, 2.57 to 2.58 g/cm³, 2.68 to 2.70 g/cm³ and 2.58 to 2.60 g/cm³, respectively. The longitudinal wave velocities ($v$) ranges were 3937.60–4248.83 m/s, 3872.17–4036.47 m/s, 6096.66–6193.23 m/s and 3645.34–3792.08 m/s, respectively.

Fig. 1

Photographs of rock specimens (left to right): Qingshan granite, Yellow sandstone, Longdong limestone, Black sandstone (color figure online)

Table 1 Basic parameter of rock specimens

2.2 Test Instrument and Test Schemes

The tests on the four rocks were all carried out with INSTRON 1346 testing system (Fig. 2). The testing system includes a control computer, loading system, pressure chambers, hydraulic transmission system and data acquisition system. During the tests, the axial forces of the rock specimens were obtained through the pressure sensor of the testing machine. The axial displacement of rock specimens was measured by linear variable differential transformers (LVDTs). First, the uniaxial compressive strength ($\sigma_{{\rm c}}^{{\rm e}}$) of a rock specimen was obtained by UC test and was taken as the initial estimated peak compressive strength. Second, the setting unloading stress level (k  = 0.1, 0.3, 0.5, 0.7, 0.9) of unloading point was determined in accordance with the $\sigma_{{\rm c}}^{{\rm e}}$ of rocks, and thus, the unloading stress $k\sigma_{{\rm c}}^{{\rm e}}$ was obtained. Then, SCLUC tests under different setting unloading stress levels were performed, and the peak compressive strength $\sigma_{\text{c}}^{k}$ of every specimen was obtained. After obtaining the $\sigma_{{\rm c}}^{k}$, the actual unloading stress level i of every specimen was calculated as follows:

Fig. 2

INSTRON 1346 testing machine

$$ i = {{k\sigma_{\text{c}}^{\text{e}} } \mathord{\left/ {\vphantom {{k\sigma_{{\text{c}}}^{{\rm e}} } {\sigma_{{\text{c}}}^{k} }}} \right. \kern-0pt} {\sigma_{\text{c}}^{k} }}. $$

(1)

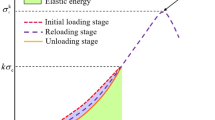
The stress–strain curves of the rock specimens under SCLUC paths are shown in Fig. 3. The entire loading process was divided into three stages, namely initial loading stage, unloading stage and secondary loading stage.

Fig. 3

Stress–strain curve of rock specimen under SCLUC path

3 Stress–Strain Curves and Failure Characteristics of Rock Specimens

The stress–strain curves of four rock materials under the UC and SCLUC tests are presented in Figs. 4 and 5. The specific parameters of each rock specimen are shown in Table 2. It can be observed that the peak compressive strength of different specimens for each rock material is very similar. The secondary loading curves will intersect the unloading curve at a stress slightly smaller than $k\sigma_{{\rm c}}^{{\rm e}}$ and continue to develop along the development trend of the initial loading line, which demonstrates that rock material possesses a memory function and the SCLUC process has little effect on the variation trend of stress–strain curves. Figure 5 also shows that the strain of the unloading curve will not reach zero point when the unloading stress is zero. There is an obvious area between the initial loading curve and unloading curve, which represents energy that was dissipated (Jaeger et al.; 2007).

Fig. 4

Stress–strain curves of rock specimens in the UC test

Fig. 5

Stress–strain curves of rock specimens in SCLUC test under different unloading stress level k

Table 2 Parameters of rock specimens at different unloading points

The failure characteristics of the rock specimens under UC are shown in Fig. 6. Figure 6a, b, d shows that failure modes of Qingshan granite, Yellow sandstone and Black sandstone specimens are all shear failure. In Fig. 6c, the Longdong limestone specimens mainly fail by splitting. All the failures occurred instantaneously, while the crack initiation and propagation in the failure process were unapparent. Regardless of whether the specimens were under UC or SCLUC, the failure modes of specimens for each rock material were the same, which indicates that the SCLUC has no effect on the failure characteristics.

Fig. 6

Failure models of four rocks after UC and SCLUC tests

4 Energy Conversion Characteristics During Loading Process

4.1 Energy Calculation Method of Three Energy Parameters

Based on the energy equation of rocks during loading process proposed by Xie et al. (2009), the equivalent relationship among three energy parameters of rock specimens under the actual unloading stress level i can be expressed as

$$ u_{i}^{{\rm o}} = u_{i}^{{\rm e}} + u_{i}^{{\rm d}} , $$

(2)

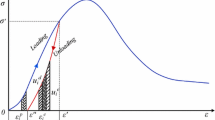
where $u_{i}^{{\rm o}}$ is the IED at the actual unloading stress level i, $u_{i}^{{\rm e}}$ is the EED at the actual unloading stress level i, and $u_{i}^{{\rm d}}$ is the DED at the actual unloading stress level i. Furthermore, the relationship among the peak IED ($u^{\text{o}}$), peak EED ($u^{{\rm e}}$) and peak DED ($u^{{\rm d}}$) can also be expressed as

$$ u_{{}}^{{\rm o}} = u_{{}}^{{\rm e}} + u_{{}}^{{\rm d}} . $$

(3)

The product of the IED and the volume of a rock specimen is equivalent to the total work performed by the testing machine on the specimen. The product of the EED and volume of a rock specimen is the elastic energy stored in rock, which can be regenerated during the unloading process. The dissipated energy is equivalent to the product of the DED and volume of rock specimen, which is used for crack propagation, rock plastic deformation, thermal energy, acoustic emission energy and so on (Song et al. 2012; Ai et al. 2016).

The IED, EED and DED can be obtained by integrating the enclosed area. The integration area of different energy density parameters is shown in Fig. 7. Under different unloading stress levels, the IED of a rock specimen is estimated as the area enclosed by the initial loading stress–strain curve and the abscissa axis. The EED is calculated by the area under the unloading stress–strain curve and the abscissa axis, and the enclosed area of the initial loading and unloading curve is DED (Kidybiński 1981; Zhang and Gao 2015).

Fig. 7

Integration area of different energy density parameters

4.2 Energy Evolution of Rock Specimens Under Different Actual Unloading Stress Levels

Using the calculation method mentioned in Sect. 4.1, the IED, EED and DED of rock specimens under different actual unloading stress levels were obtained (see Table 3).

Table 3 Values of IED, EED and DED under the different actual unloading stress levels

Figure 8 shows the change rule of IED, EED and DED with the actual unloading stress level. To improve the fitting accuracy, an extra (0, 0) point was added in each figure. As given by Fig. 8, the IED, EED and DED of the four rock materials all present nonlinear growth with increasing unloading stress level. The IED grows the most rapidly of the three energy densities, followed by the EED and then DED. The curve of the EED is closer to the IED, which indicates that a larger amount of the external input energy is transformed into the elastic energy, and the dissipated energy only occupies a small part of the input energy. In addition, it can be seen from Fig. 8 that the higher the compressive strength of the rock (the average compressive strengths of Qingshan granite, Yellow sandstone, Longdong limestone and Black sandstone are 156.64, 117.62, 161.53 and 87.16 MPa, respectively), the closer the EED is to the IED. This result indicates that a higher compressive strength usually represents a stronger energy storage capacity and more obvious elastic brittleness in rock, which corresponds the general understanding of the energy storage characteristics of rock materials. These characteristics are also confirmed in Figs. 4 and 5. The post-peak curves of Longdong limestone are relatively short, while those of Yellow sandstone and Black sandstone are relatively long.

Fig. 8

The change laws of three energy density parameters with the actual stress level i

To further assess the relationships between the IED, EED and DED and the actual unloading stress level, a quadratic polynomial function was used to fit the variation laws. The nonlinear relationships between $u_{i}^{\text{o}}$, $u_{i}^{\text{e}}$, $u_{i}^{\text{d}}$ and i of Qingshan granite, Yellow sandstone, Longdong limestone and Black sandstone are shown in Table 4. It can be seen from Table 4 that the coefficient correlation R² of the fitting functions is all greater than 0.98. A quadratic polynomial function can describe the relationship between the three energy density parameters and actual unloading stress level well. Figure 9 shows the variation of the ratios $u_{i}^{{\rm e}}$ / $u_{i}^{\text{o}}$ and $u_{i}^{{\rm d}}$ / $u_{i}^{\text{o}}$ under different actual unloading stress levels. In Fig. 9a, c, the values of ${{u_{i}^{{\text e}} } \mathord{\left/ {\vphantom {{u_{i}^{{\text e}} } {u_{i}^{{\text o}} }}} \right. \kern-0pt} {u_{i}^{\text o} }}$ are obviously higher than those of ${{u_{i}^{{\text d}} } \mathord{\left/ {\vphantom {{u_{i}^{{\text d}} } {u_{i}^{{\text o}} }}} \right. \kern-0pt} {u_{i}^{\text o} }}$, fluctuating around a constant value. These results also indicate that the input energy of Qingshan granite and Longdong limestone is mainly transformed into elastic energy. In Fig. 9b, d, when the unloading stress level is relatively low (less than 0.1–0.2), values of ${{u_{i}^{{\rm d}} } \mathord{\left/ {\vphantom {{u_{i}^{d} } {u_{i}^{{\rm o}} }}} \right. \kern-0pt} {u_{i}^{{\rm o}} }}$ are higher than those of ${{u_{i}^{{\rm e}} } \mathord{\left/ {\vphantom {{u_{i}^{{\rm e}} } {u_{i}^{{\rm o}} }}} \right. \kern-0pt} {u_{i}^{{\rm o}} }}$, indicating that energy consumption is the main factor. When the unloading stress level increases, the values of ${{u_{i}^{{\rm e}} } \mathord{\left/ {\vphantom {{u_{i}^{e} } {u_{i}^{o} }}} \right. \kern-0pt} {u_{i}^{{\rm o}} }}$ become greater than those of ${{u_{i}^{{\rm d}} } \mathord{\left/ {\vphantom {{u_{i}^{{\rm d}} } {u_{i}^{{\rm o}} }}} \right. \kern-0pt} {u_{i}^{{\rm o}} }}$, and ${{u_{i}^{{\rm e}} } \mathord{\left/ {\vphantom {{u_{i}^{{\rm e}} } {u_{i}^{{\rm o}} }}} \right. \kern-0pt} {u_{i}^{{\rm o}} }}$ first increases and then decreases. Furthermore, Fig. 9 also shows that when the unloading stress level increases (more than 0.2), the higher the compressive strength of rock, the larger the mean value of the gap between ${{u_{i}^{{\rm e}} } \mathord{\left/ {\vphantom {{u_{i}^{{\rm e}} } {u_{i}^{{\rm o}} }}} \right. \kern-0pt} {u_{i}^{{\rm o}} }}$ and ${{u_{i}^{{\rm d}} } \mathord{\left/ {\vphantom {{u_{i}^{{\rm d}} } {u_{i}^{{\rm o}} }}} \right. \kern-0pt} {u_{i}^{{\rm o}} }}$, which indicates that the compressive strength of rock is positively correlated with its elastic energy storage capacity.

Table 4 Fitting functions and R² between $u_{i}^{{\rm o}}$, $u_{i}^{{\rm e}}$, $u_{i}^{{\rm d} }$ and i

Fig. 9

Variation of the energy ratios of rock specimens with the actual stress level i

4.3 Relationships Among the IED, EED and DED

The relationships between the EED, DED and IED under different unloading stress levels were further investigated. Based on the data in Table 3, relationship curves are obtained in which the abscissa represents the IED, and the ordinate represents the EED and DED, respectively (shown in Fig. 10). Figure 10 shows that both $u_{i}^{{\rm e}}$ and $u_{i}^{{\rm d}}$ gradually increase with the increase of $u_{i}^{{\rm o}}$, and there is an obvious linear correlation between $u_{i}^{{\rm e}}$ and $u_{i}^{\text d}$ and $u_{i}^{{\rm o}}$. The fitting functions can be expressed as follows:

Fig. 10

Relationships between the EED and DED and IED

$$ u_{i}^{{\rm e}} = au_{i}^{{\rm o}} + b, $$

(4)

$$ u_{i}^{{\rm d}} = (1 - a)u_{i}^{{\rm o}} - b, $$

(5)

where a and b are the fitting parameters obtained from experimental data. The fitting functions between $u_{i}^{{\rm e}}$ and $u_{i}^{{\rm d}}$ and $u_{i}^{{\rm o}}$ of the four rocks are presented in Table 5. The coefficients correlation R² of all the fitting functions range from 0.9377 to 0.9998, showing that there are strong linear relationships between them.

Table 5 Fitting functions and R² among $u_{i}^{{\rm o}}$, $u_{i}^{{\rm e}}$ and $u_{i}^{{\rm d}}$

Taking Qingshan granite as an example, in Eq. (4), the slope a and intercept b are equal to 0.8010 and 0.0010, respectively. The coefficient b is very small compared with a, being only 0.12% of a. When the $u_{i}^{{\rm o}}$ increases, the effect of b on the function relation can gradually be ignored, and the fitting function simplifies to the form of $u_{i}^{{\rm e}} = au_{i}^{{\rm o}}$ ($u_{i}^{{\rm e}} = 0.8010u_{i}^{{\rm o}}$). The coefficient a reflects the ability to convert the input energy into elastic energy. Furthermore, the relationship between $u_{i}^{{\rm d}}$ and $u_{i}^{{\rm o}}$ can be similarly described. The fitting function between $u_{i}^{{\rm d}}$ and $u_{i}^{{\rm o}}$ can be approximated to $u_{i}^{\text{d}} = (1 - a)u_{i}^{\text{o}}$ ($u_{i}^{{\rm d}} = 0.1990u_{i}^{{\rm o}}$). The coefficient (1−a) reflects the proportion of dissipated energy in the input energy. The above analysis is also applicable to Yellow sandstone, Longdong limestone and Black sandstone. The two constants a and (1−a) can be regarded as the compression energy storage coefficient and the compression energy dissipation coefficient of rock materials separately.

Figure 11 shows the relationships between $u_{i}^{{\rm e}}$ and $u_{i}^{{\rm d}}$, and the relationship is also a linear functional correlation as follows:

Fig. 11

Relationships between the dissipated and elastic energy density

$$ u_{i}^{{\rm d}} = cu_{i}^{{\rm e}} + d, $$

(6)

where c and d are fitting parameters obtained from experimental data. The R² of the linear function is all greater than 0.91 (shown in Table 5), showing that there is also a strong linear relationship between them. This function reflects the proportional relationship between the elastic energy and dissipated energy of rock specimen during loading process. In the case of achieving the EED, the DED can be obtained.

4.4 Application of the Linear Energy Storage or Dissipation Law

Using the obtained linear energy storage law, the EED or DED at any stress levels can be calculated for a rock material, especially at the peak strength of rock specimen. According to Eqs. (3)–(5) and $u_{{}}^{{\rm o}}$ obtained from the stress–strain curve, $u_{{}}^{{\rm e}}$ and $u_{{}}^{{\rm d}}$ can be given as

$$ u^{{\rm e}} = au^{{\rm o}} + b, $$

(7)

$$ u^{{\rm d}} = (1 - a)u^{\text{o}} - b, $$

(8)

Table 6 presents the $u_{{}}^{{\rm o}}$, $u_{{}}^{{\rm e}}$ and $u_{{}}^{{\rm d}}$ of the specimen in the UC and SCLUC tests. All the $u_{{}}^{{\rm o}}$ s of the four rocks are compared in Fig. 12. The results show that all the $u_{{}}^{{\rm o}}$ are random and that SCLUC operation produces a negligible effect compared with UC.

Table 6 The $u_{{}}^{{\rm o}}$, $u_{{}}^{{\rm e}}$, $u_{{}}^{{\rm d}}$ and $W_{{\rm et}}^{{\rm p}}$ of rock specimens using the new method

Fig. 12

The $u_{{}}^{{\rm o}}$ of rock specimens in UC and SCLUC tests

5 Discussion

The peak EED ($u^{{\rm e}}$) plays an important role in investigating the mechanical characteristics of rocks. This term has attracted the attention of many researchers and has been used widely in many rock mechanic problems. Wang and Park (2001) reported that Kwasniewski et al. scaled the occurrence of shock and rockburst with $u^{{\rm e}}$ in their Scientific Report from 1994, and a criterion of elastic strain energy was presented to predict rockburst in Kwasniewski’s private communication in 2000. Wang and Park (2001) applied this rockburst criterion to evaluate the rockburst proneness of rock in Linglong gold mine. Zhu et al. (2002) presented a new index of rockburst proneness using $u^{{\rm e}}$. Xie et al. (2009) given the expression of $u^{{\rm e}}$ under the UC tests in establishing the overall failure criterion of the rock. Tarasov and Randolph (2011), Tarasov and Potvin (2013) discussed the superbrittleness of rocks and universal criteria for rock brittleness considering $u^{{\rm e}}$. Li et al. (2014) investigated the strain rate dependency of $u^{{\rm e}}$ under UC tests on coarse crystal marble. Huang and Li (2014) studied the conversion of $u^{{\rm e}}$ of marble in triaxial unloading tests. Munoz et al. (2016) proposed an energy-based brittleness index with $u^{{\rm e}}$. Ai et al. (2016) gave two new brittleness indices including $u^{{\rm e}}$. Cai (2016) and Miao et al. (2016) used $u^{{\rm e}}$ to estimate the rockburst proneness of six rocks in Sanshandao Gold Mine. Liu et al. (2017) introduced the peak elastic energy release rate using $u^{{\rm e}}$.

The above research studies show that the accurate acquisition of $u^{{\rm e}}$ is very important and will directly affect the reliability and accuracy of analysis results. However, in actual UC tests, due to the discreteness and uncertainty of peak strength of rock specimens, it is impossible to unload in time enough at the peak strength of the specimen, and $u^{{\rm e}}$ cannot be obtained by calculating the area under the unloading curve. In most cases, the approximate expression of $u^{{\rm e}}$ is as follows (shown in Fig. 13):

Fig. 13

Schematic drawing of traditional calculation of $u^{{\rm e}}$

$$ u^{{\rm e}} = {{\sigma_{{\rm c}}^{2} } \mathord{\left/ {\vphantom {{\sigma_{{\rm c}}^{2} } {2E}}} \right. \kern-0pt} {2E}}_{{\rm u}} , $$

(9)

where $\sigma_{{\rm c}}$ is the peak strength of rock specimen in a UC test; E_u is regarded as the linear modulus of an ideal unloading curve at the peak strength point, and has different names in different literatures. When Eq. (9) was used to calculate the value of $u^{{\rm e}}$, two methods were often used to obtain E_u: (i) E_u is equal to the unloading tangential modulus E_s (Wang and Park, 2001, shown in Fig. 14a) (ii) E_u is equal to the Young’s modulus of the loading curve E_l (Zhu et al. 2002 and Munoz et al. 2016, shown in Fig. 14b).

Fig. 14

Schematic drawing of calculation of E_u

Two basic assumptions of Eq. (9) are: (i) the elastic modulus E_u is constant, that is, the unloading curve is a straight line; (ii) the unloading modulus E_u at the peak strength is equal to the unloading modulus E_s at a certain point before the peak strength. The aforementioned two basic assumptions are valid only for ideal linear elastic materials (shown in Fig. 15a). For natural rock materials, the unloading curve is not usually a straight line (shown in Fig. 15b). Since the unloading curve is not a straight line, E_u and E_s are not constants, and further E_u cannot be equal to E_s.

Fig. 15

Unloading curves of ideal linear elastic material and natural rock material

However, in our research in Sect. 4.4, there is a linear law between the EED, DED and IED. The $u_{{}}^{{\rm o}}$ can be calculated using the graphical integration method in the stress–strain curve, and then $u_{{}}^{{\rm e}}$ and $u_{{}}^{{\rm d}}$ can be calculated easily using Eqs. (7) and (8). The presented method solves the problem that E_u cannot be obtained scientifically and accurately.

After obtaining $u_{i}^{{\rm e}}$ and $u_{i}^{{\rm d}}$, the variation of the ratio $u_{i}^{{\rm e}}$ / $u_{i}^{{\rm d}}$ ($W_{\text{et}}^{i}$) was also investigated. Equation (10) presents the formula of the traditional definition of $W_{\text{et}}^{i}$ and the results of $W_{\text{et}}^{i}$ are listed in Table 3.

$$ W_{\text{et}}^{i} = \frac{{u_{i}^{{\rm e}} }}{{u_{i}^{{\rm d}} }}. $$

(10)

According to Eqs. (4) and (5), we give a new method for calculating dynamic $W_{\text{et}}^{{\rm d}}$ as follows:

$$ W_{\text{et}}^{{\rm d}} = \frac{{au_{{\rm d}}^{{\rm o}} + b}}{{(1 - a)u_{{\rm d}}^{{\rm o}} - b}}, $$

(11)

where $u_{{\rm d}}^{{\rm o}}$ is the IED at any loading time before the peak compressive strength and $W_{\text{et}}^{{\rm d}}$ is the dynamic ratio of the EED to DED. The peak $W_{\text{et}}^{{\rm d}}$ is marked as $W_{\text{et}}^{{\rm p}}$ and can be expressed as follows:

$$ W_{\text{et}}^{{\rm p}} = \frac{{au^{{\rm o}} + b}}{{(1 - a)u^{{\rm o}} - b}} = \frac{{u^{{\rm e}} }}{{u^{{\rm d}} }}. $$

(12)

Figure 16 shows the variation trend of the ratio EED/DED from the traditional method and new method. With increasing IED, the volatility of $W_{\text{et}}^{i}$ obtained by the traditional method is high, and $W_{\text{et}}^{i}$ finally seems to converge, which might require more experimental data for verification. However, the change curve of $W_{\text{et}}^{{\rm d}}$ tends to gradually converge with increasing IED increases. The values of $W_{\text{et}}^{{\rm p}}$ for the four rocks are given in Table 6. For comparison, the calculating results of ${{u_{{}}^{{\rm e}} } \mathord{\left/ {\vphantom {{u_{{}}^{{\rm e}} } {u_{{}}^{{\rm d}} }}} \right. \kern-0pt} {u_{{}}^{{\rm d}} }}$ using two traditional methods are also shown in Tables 7 and 8. The results of the three methods are compared as shown in Fig. 17. It can be seen that most of the u^e/u^ds using Method 1 are large than $W_{\text{et}}^{{\rm p}}$ s, while the u^e/u^d s using Method 2 are smaller than $W_{\text{et}}^{{\rm p}}$ s. The reason for this characteristic is attributed to the hypothesis of two traditional methods. In addition, the randomness and dispersion of u^e/u^d s using two traditional methods are obvious. However, the values of $W_{\text{et}}^{{\rm p}}$ for every rock are very close to each other. The results indicate that $W_{\text{et}}^{{\rm p}}$ may be regarded as a constant that reflects the proportional of the elastic energy to the dissipation energy of rock material.

Fig. 16

Relationships between $W_{\text{et}}^{i}$ and $W_{\text{et}}^{d}$ and IED

Table 7 The peak EED of rock specimens [the method of Zhu et al. (2002) and Munoz et al. (2016)]

Table 8 The peak EED of rock specimens [the method of Wang and Park (2001)]

Fig. 17

The peak EED of rock specimens using three methods [Method 1: Zhu et al. (2002) and Munoz et al. (2016); Method 2: Wang and Park (2001)]

6 Conclusions

This paper investigated the energy evolution characteristics of four rock materials (Qingshan granite, Yellow sandstone, Longdong limestone and Black sandstone) under uniaxial compression using a series of SCLUC tests. Based on the test results, the following conclusions can be drawn:

• (1) In SCLUC tests, the secondary loading curves of rocks intersected the unloading curve at a stress slightly smaller than unloading stress and continued to develop according to the development trend of the initial loading curve. The four rock materials possess memory, and the SCLUC process has minimal effect on the variation of the stress–strain curves. In addition, the failure modes of SCLUC are the same as those of UC.

• (2) The nonlinear characteristics of the energy evolution for four rock materials under different unloading stress levels were determined. Based on the analysis of the energy density parameters under different unloading stress levels, the IED, EED and DED all increase with increasing stress as quadratic polynomial functions. The IED has the most rapid growth, following the EED, and finally the DED.

• (3) The linear relationships between EED and DED, and IED were obtained. The test results indicate that the EED and DED all increase linearly with increasing IED, and the linear energy storage or dissipation laws of rock materials were observed and confirmed. The EED and DED at any stress levels (including the peak compressive strength level) can be obtained using the linear energy storage or dissipation law above.

• (4) The ratio EED/DED with the increase of IED was investigated. Due to the heterogeneity of natural rock materials, when the ratios EED/DED are directly calculated at different unloading stress levels using the experimental data, the ratio greatly fluctuates. In this research, we develop a new method to calculate the ratio EED/DED. The results show that the change curve of the ratio tends to gradually converge as the IED increases. The ratio obtained at the peak compressive strength tends to be constant, which shows that there is a stable ratio EED/DED under UC of rock materials.