Introduction

Soils in engineering geology are defined by their grain size distribution (GSD) and their classification (e.g., ASTM D2487 2017). A companion paper (Chapuis 2021a) has listed many applications and use of the GSD in different research domains. The GSD is used to predict physical properties of soils such as (a) their saturated and unsaturated hydraulic conductivities (Chapuis 2012a, 2016); (b) their specific surface area, (c) their total porosity, (d) their effective porosity for tracer tests (Chapuis 2019a, (e) their pore size distribution, and (f) their water retention curve. The GSD is also used in erosion studies, in designing filters and in preventing internal erosion problems. The GSD is used to study the history of sediments. Combined with the porosity, n, or the void ratio, e, the GSD is used to predict mechanical properties of soils, landslides, and settlements. The GSD of air-borne particles is used in air and environmental studies, in correlation with health issues. The GSD of powders is used in powder technology and pharmaceutical manufacturing.

Different techniques give a GSD, such as sieving, sedimentation, elutriation, analysis of photographs, and laser diffraction. These methods make different assumptions and thus, may yield different GSD data for the same specimen.

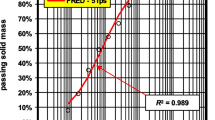
A companion paper (Chapuis 2021a) has reviewed the different methods that were proposed to fit a GSD: usually, their coefficient of determination, R2, is in the 0.5–0.9 range (Buchan et al. 1993; Hwang et al. 2002; Bah et al. 2009; Weipeng et al. 2015; Esmaeelnejad et al. 2016). A modal decomposition method, MDM, was developed (Chapuis 2010; Chapuis et al. 2014) to extract from a GSD its sub-populations or modes, proportions, and specific surface area. This new MDM is easy to use in a spreadsheet and yields a R2 value typically over 0.999. As a result, the GSD is described mathematically, which improves the quality of studies (Chapuis 1995). For example, when soil samples are taken in boreholes with a split-spoon, information on stratification is lost, but the MDM was shown to recover information. The MDM improves the prediction of field permeability in stratified soils, which is critical for groundwater and pollution studies (Chapuis 2010; Chapuis et al. 2014, 2021b), For example, the large-scale K value, as derived from pumping tests, was found to be correctly predicted by the composed small-scale K values of the stratified aquifer, as quantified with the MDM (Chapuis 2013; Chapuis et al. 2005), which eliminates the need for a so-called scale-effect (Chapuis 2019b, 2021b). Single layers in stratified soils are unimodal, with a single population of grains. Multimodal soils are either homogeneous (till, crushed stone) or stratified (sandy aquifers). Borehole samples may have up to four modes in their GSDs. This is why a four-mode MDM spreadsheet and instructions are made freely available to readers in the web site of Scholar Portal Database (Chapuis 2020).

A companion article (Chapuis 2021a) has quantified continuity between different types of sand. It has found, with several examples, that if the sand coefficient of uniformity, CU, is higher than 3, the sand is stratified.

The objective of this article is to show diverse possibilities offered by the MDM of a GSD, for studies and researches in engineering geology. Examples are provided for investigating problems such as improving the quantitative description of a GSD, improving the current filter criteria that are used for drainage and filtering projects, including those of earth dams, and improving the design rules to avoid the risk of internal erosion in earth dams, and in structural layers of streets and highways.

Background

The GSD is plotted as the percentage p of solid mass smaller than size d (mm) against log (d / 1 mm) = log (D), which yields a curve p(D). The GSD is a cumulative distribution function, defined as the integral of the probability density mass distribution of grain sizes (PDDGS). A grain size dx is defined as the size such as x % of the solid mass is smaller than dx.

Many soil GSDs are poly-disperse collections of particles. The soil in this article has a geotechnical definition, not an agricultural definition. For example, soil samples taken in boreholes may be mixtures of thin layers. Each of them results from several factors including different origins, means of transport, erosion, and deposition. Identifying the different sources, and their respective inputs, is important for correctly assessing natural and anthropogenic impacts upon environmental and health issues.

Chapuis et al. (2014) proposed a modal decomposition method, MDM, to describe mathematically the mixture and its specific surface, including the percentage and own GSD of each layer or sub-population, or mode. Each mode was assumed to be defined by a lognormal distribution, which may cover a wide range of grain sizes. A unimodal GSD results from a single series of processes. Individually sampled layers in a stratified aquifer, and most natural clays, were shown to be unimodal (Chapuis et al. 2014). A multimodal GSD results from several series of processes. Split-spoon samples in stratified sand yield a multimodal GSD. The MDM provides a closed-form equation for the specific surface, SS, whose values were verified against those given by the previous method of Chapuis and Légaré (1992), which uses Riemann sums.

To analyze GSDs series for a geological unit, one must follow a single standard for sieving and sedimentation, respects the needed minimum solid mass, and does not mix GSDs obtained by different methods (e.g., sieving and laser). The MDM can accurately decompose man-made soil mixtures and thus, retrieve information, but may be inaccurate for a mode fraction below 2% (Chapuis et al. 2014).

The MDM key equations are summarized hereafter as Eqs. 1–4. The GSD is described by a function F:

$$F\left(D\right)=p\left[\ln D\right]=\sum_{j=1}^Nm_jp_j\left[\ln D\right]$$
(1)

where D = d (mm)/ 1 mm. The mode j (index j from 1 to N) contributes for mj (%) to the solid mass:

$$\sum_{j=1}^N{}m_j=1\;or\;100\%$$
(2)

The GSD of each mode j is described by pj[ln D], or pj(x) where x = ln D, which is a lognormal distribution with a mean μj and a standard deviation σj (or a variance σj2). Its derivative is

$$\frac{d{p}_{j}}{dx}\left(x;{\mu }_{j},{\sigma }_{j}\right)=\frac{1}{{\sigma }_{j}\sqrt{2\pi }}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{{\left(x-{\mu }_{j}\right)}^{2}}{2{\sigma }_{{}^{j}}^{2}}\right]$$
(3)

The probability density distribution of the grain size, PDDGS, is therefore obtained by summation of the (dpj/dx) functions. The function F(D) is then defined by the summation of integrals, yielding

$$F=p\left[\mathrm{l}\mathrm{n}(\frac{dmm}{1mm})\right]=p\left[\mathrm{l}\mathrm{n}(D)\right]=\sum _{j=1}^{N}{m}_{j}\left(\frac{1}{2}+\frac{1}{2} \text{erf}\left[\frac{\left(\mathrm{l}\mathrm{n}D-{\mu }_{j}\right)}{{\sigma }_{j}\sqrt{2}}\right]\right)$$
(4)

where erf is the error function.

After having reminded basic information on the MDM (see Chapuis 2021a for more equations), this article provides interesting potential applications of the MDM for engineering geology. Three applications are examined, those linked to (1) an accurate quantification of the GSD, (2) filter criteria for materials undergoing seepage forces, and (3) internal erosion issues, which are critical for earth dams and structural layers of highways and streets.

Possible tools for research with the GSD

By providing an accurate GSD description, the MDM has an attractive potential for innovative research. Usually, geological engineers and specialists in geotechnique describe a soil with its GSD, its coefficients of uniformity, CU, and curvature CC. The CU value reflects the steepness of the GSD in its central part, whereas the CC value, below or above unity, reflects how the real GSD deviates from a normal distribution. These are defined as \(C_U=d_{60}/d_{10}\) and \(C_C=d_{30}^2/(d_{60}d_{10})\) .

Many soils (geotechnical definition) are found to be unimodal by their MDM: their CU and CC values depend upon the μ and σ values. Any size dx of a unimodal soil is also related to μ and σ. Its value can be extracted using the function erfc−1 that can be found in textbooks and is available in most mathematical codes. A few equations are given hereafter to link the usual geotechnical parameters of the GSD and the new parameters of μ and σ for a unimodal soil: these relationships of Eqs. 5–12 are shown in Figs. 1 and 2.

$$d_{50} = \exp (\mu ),$$
(5)
$$\sigma=\ln\left[d_{84.1}/d_{50}\right]=\ln\left[d_{50}/d_{15.9}\right]=\frac12\ln\left[d_{84.1}/d_{15.9}\right],$$
(6)
$${d_5}/{d_{50}} = \exp ( - 1.6449\,\sigma )\;or\;{d_5} = \exp (\mu - 1.6449\sigma ),$$
(7)
$${d_{10}}/{d_{50}} = \exp ( - 1.2816\,\sigma ),$$
(8)
$${d_{30}}/{d_{50}} = \exp ( - 0.4959\,\sigma ),$$
(9)
$${d_{60}}/{d_{50}} = \exp (0.2533\,\sigma ),$$
(10)
Fig. 1
figure 1

Relationships between dx/d50 and σ for unimodal GSDs

Full size image
Fig. 2
figure 2

Relationships between CU, CC, and σ for unimodal GSDs

Full size image
$$C_U=\exp\left(1.5349\;\sigma\right),\;\mathrm{and}\;C_C=\exp(0.0365\;\sigma)$$
(11)
$$S_S(m^2/kg)=\frac6{\rho_s}\sum_{j=1}^Nm_j\frac{\mathrm e\mathrm x\mathrm p\;(\sigma_j^2)}{0.001\;\mathrm e\mathrm x\mathrm p\;(\mu_j)}=\frac6{\rho_s}\sum_{j=1}^Nm_j\frac{\mathrm e\mathrm x\mathrm p\;(\sigma_j^2)}{0.001\;d_{50}(in\;mm)}$$
(12)

It is worth noting that in practice, the σ value of a unimodal soil rarely exceeds 3. A high σ value is found for clay, whereas a low σ value is found for an individual sand layer. For a soil that has a multimodal GSD, it is mathematically impossible to derive similar simple expressions for the sizes dx and the coefficients CU and CC. These sizes depend upon the total set of mj, μj, and σj values. However, the mathematical code used for the MDM can easily find all the numerical values of the dx, as target values and then, those of CU and CC for any multimodal soil.

The usual filter criteria

Filter criteria are important in geotechnical design. They were derived initially from laboratory tests with uniform base soil (the finer soil, the one to be protected) and protective (coarse) soil filter (Terzaghi 1939; Bertram 1940; USACE 1953; USBR 1974; Sherard et al. 1984; Kenney et al. 1985; NRCS 1994). The common and old criteria involve specific particle sizes, d15, d50, and d85 with an extra index B or F for the base and filter, respectively. For example, the common criteria for cohesionless uniform base and filter are (USBR 1974):

$$4d_{15B}\leq d_{15F}\leq4d_{85B}.$$
(13)

These were obtained for uniform (probably unimodal) GSDs, but cannot be simply applied to soils having irregular or multimodal GSDs (Honjo and Veneziano 1989; Foster and Fell 2001). To avoid this difficulty and derive better criteria, several researchers proposed to study not the relationship between the two GSDs but the relationship between the base GSD and the filter constriction size distribution or CSD (Kenney et al. 1985; Indraratna et al. 2007; Raut and Indraratna 2008; Reboul et al. 2010).

In this article, because the mathematical treatment for multimodal GSDs is fairly complex and will take more research time, only the simple case of well-graded or unimodal bases and filters is examined. In this simple case, the d15 and d85 sizes are given by simple relationships (Fig. 3):

$${d_{15}}/{d_{50}} = \exp ( - 1.0364\,\sigma )\;or\;{d_{15}} = \exp (\mu - 1.0364\,\sigma ),$$
(14)
$${d_{85}}/{d_{50}} = \exp (1.0364\,\sigma )\;or\;{d_{85}} = \exp (\mu + 1.0364\sigma ).$$
(15)
Fig. 3
figure 3

Relating the ratios d15/d50 and d85/d50 to σ for unimodal GSDs (Eqs. (14)–(15) and afterwards verification of filter criteria

Full size image

As a result, the criteria of Eq. (13) become.

$${d}_{15F}=\mathrm{e}\mathrm{x}\mathrm{p}\left({\mu }_{F}-1.0364{\sigma }_{F}\right)\ge 4{d}_{15B}=4\mathrm{e}\mathrm{x}\mathrm{p}\left({\mu }_{B}-1.0364{\sigma }_{B}\right), \mathrm{a}\mathrm{n}\mathrm{d}$$
(16)
$${d_{15F}} = \exp ({\mu _F} - 1.0364\,{\sigma _F}) \leqslant 4\,{d_{85B}} = 4\exp ({\mu _B} + 1.0364\,{\sigma _B}).$$
(17)

Taking the natural logarithms of both sides in Eqs. (16)–(17), it comes:

$$({\mu }_{F}-1.0364{\sigma }_{F})\ge \mathrm{l}\mathrm{n}(4)+\left({\mu }_{B}-1.0364{\sigma }_{B}\right)\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}$$
(18)
$$(\mu_F-1.0364\,\sigma_F)\leq\ln(4)+(\mu_B+1.0364\,\sigma_B).$$
(19)

Equations (18)–(19) are rearranged to give:

$$\left({\mu }_{F}-{\mu }_{B}\right)\ge 1.3863+1.0364\left({\sigma }_{F}-{\sigma }_{B}\right),\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}$$
(20)
$$(\mu_F-\mu_B)\leq1.3863+1.0364\,\left(\sigma_B+\,\sigma_F\right).$$
(21)

Thus, for well-graded or unimodal bases and filters, the filter criteria of Eq. (13) become the inequalities of Eqs. (20)–(21). These involve the difference of the two means (μF − μB), the sum and the difference of the two standard deviations (σF + σB) and (σF − σB).

The simplest filter case is that of two materials made of equal spheres, of size dB for the base and dF for the filter, for which σF = σB = 0. Equation (17) predicts that the filtration will work if μF − μB)<1.386 which means also dF/dB < 4. The large sphere diameter cannot exceed 4 times the small sphere diameter to be able to stop the movement of small spheres: this rule is safe for filtration according to physical tests of Ghidaglia et al. (1996) and numerical simulations of randomly loosely packed equal spheres (Roozbahani et al. 2014). The latter have shown that all small spheres up to 0.15 times the large sphere size pass through the loose pack, whereas small spheres of diameter 0.25 times are stopped, which corresponds to dF/dB < 4.

In field conditions, when an aquifer is stratified, its adjacent sub-layers must have respected some natural filter criteria. The MDM provides the μ and σ values of the sub-layers. The collected data for seven stratified aquifers are used here to assess the terms on each side of inequalities in Eqs. (20)–(21), for the M1 and M2 modes, and then for the M2 and M3 modes, when all GSDs are decomposed with a 3-mode MDM. The data for Eq. (20) are plotted in Fig. 4, whereas those for Eq. (21) are plotted in Fig. 5.

Fig. 4
figure 4

Verifying Eq. (20), equivalent to the Eq. (13) left side for the usual filter criterion relating the d15 values for adjacent lognormal modes

Full size image
Fig. 5
figure 5

Verifying Eq. (21) (equivalent to Eq. (13) right side) for the usual filter criterion relating the d15F and the d85B for adjacent lognormal modes

Full size image

Most data in Fig. 4 respect the left side of Eq. (13), or Eq. (20), for the usual filter criterion involving the two d15 values. There are, however, six outlier points in Fig. 4. A few outliers may be expected for at least two reasons: first, the MDM is an inverse method, which means it may have several solutions, and second, the MDM was done initially with only three possible modes. The GSDs for the outlier points in Fig. 4 were reanalyzed with a MDM allowing four possible modes. The arrows in Fig. 4 indicate the displacements that occur when allowing 4 instead of 3 modes. All data now fall on or above the line, thus verify the left side of Eq. (13) for loose uniform soils.

According to Fig. 4, stratified sand GSDs must not be fitted with three modes because the assumed three modes may not respect the filter criteria. This is a new finding. When a 3-mode MDM is used, and there are two asymmetrical peaks in the PDDGS, the 3-mode MDM fits one peak with one mode and the other peak with the two other modes. This type of fit (even with a R2 of 0.999) was inadequate as shown in Fig. 4 for six specimens, which needed a four-mode MDM.

It must be noted that Fig. 4 was plotted by assuming that the modes follow the order M1-M2-M3 or M1-M2-M3-M4 in field conditions, following the order of means μ1 to μ4. This may be incorrect when M1 and M2 are close (or M3 and M4 are close). Then, in the field, the order may be M1-M3-M2-M4 or M1-M4-M2-M3 instead of M1-M2-M3-M4, because M1 and M2 were created by the same physical phenomena with variations in parameter intensities. If the order M1-M3-M2-M4 is taken to plot the 4 M data in Fig. 4, then the points move upward (this is not shown in Fig. 4) and thus better respect the left side of Eq. (13) or the Eq. (21), for the filter criterion involving the two d15 values.

All data in Fig. 5 respect the right side of Eq. (13) or Eq. (21) for the criterion with the d15F and d85B values. The points close to the equality line are for those specimens giving outliers in Fig. 4, and thus. they were reanalyzed with a 4-mode MDM. A few displacements that result with 4 instead of 3 modes are shown by arrows in Fig. 5. All data now fall above the line, thus verify the right side of Eq. (13) for uniform soils.

It seems that the criterion could be moved up by at least 0.25 in Fig. 5. The constant 1.3863 in Eqs. (20)–(21) would become 1.6363, which is the natural logarithm of 5.14. More simply stated, from Figs. 4 and 5, it appears that the cohesionless uniform sand sub-layers in natural conditions and usually loose field compactness verify

$$\left(d_{15F}/d_{15B}\right)\geq4\;and\;\left(d_{15F}/d_{85B}\right)\leq5.$$
(22)

As stated before, this verification for field conditions is valid only with well-graded or unimodal bases and filters for which the filter criteria of Eq. (13) become the inequalities of Eqs. (20)–(21). Figure 6 illustrates the physical meaning of these filter equations that use the difference of means (μF − μB), the sum, and the difference of standard deviations (σF + σB) and (σF − σB). It is worth noticing, and this is another new finding to be added to those from Figs. 4 and 5, that it is certainly not a coincidence if the experimental data of earlier researchers pointed out the key role of d15 and d85 for filter criteria, because d15 and d85 are close to (μ + σ) and (μ − σ), respectively, as stated by Eqs. (14)–(15).

Fig. 6
figure 6

Illustration of filter criteria for a unimodal base and a unimodal filter. Note that d50 = μ and d15 ≈ μ – σ, and d85 ≈ μ + σ—see Eqs. (6), (14), and (15)

Full size image

As indicated previously, the filter criteria currently used in civil engineering have evolved to take different forms, depending upon the CU and CC values, the convex or concave shape of the GSD, and the density index. The latter depends upon the maximum and minimum values of porosity, which depend upon the particle shape (Youd 1973; Chapuis 2012b; Chang et al. 2018), and influence also the pore detailed geometry, which should be viewed as a key factor for filtration. Because soil filtering is complex, its translation into new criteria relating individual modes of the filter and base will need long and detailed investigations. This is why the article has not presented other cases than the simple one described. It proves the need for a 4-mode MDM, which is interesting because it allows us to better quantify and understand all the processes involved in filtration.

The usual criteria for internal erosion

The example 5 in Chapuis (2021a) was for a 0–20-mm crushed stone that is prone to internal erosion according to usual criteria and as confirmed by laboratory tests (Chapuis et al. 1996; Chapuis and Saucier 2020). These usual criteria for internal erosion involve GSD parameters, but not the soil porosity n or void ratio e, which should be taken into account in improved criteria (Chapuis 1992).

The “usual” criteria of Kezdi (1969), Sherard (1979), and Kenney and Lau (1985, 1986) first split a GSD into a fine (index f) and a coarse portion (index c). Then, they apply filter criteria to the two portions to verify whether the solids of the fine portion can move in the pores of the coarse portion. More recent geometric criteria were proposed for well-graded and gap-graded GSDs (Perzlmaier et al. 2007; Wan and Fell 2008; Li and Fannin 2008, 2012; Chang and Zhang 2013a, b; Ahlinhan and Adjovi 2019).

The usual internal erosion criteria can be expressed as similar equations and geometric rules (Chapuis 1992; Chapuis and Tournier 2006). The criterion of Kezdi (1969) uses Eq. (13), and it became the following: if the GSD slope is flatter than 24.9% per log cycle at a size dx, the soil voids cannot retain particles finer than dx (Chapuis 1992). The criterion of Sherard (1979) uses Eq. (22) and became as follows: if the GSD slope is flatter than 21.5% per log cycle at a size dx, the soil voids cannot retain particles finer than dx (Chapuis 1992). The criterion of Kenney and Lau (1985, 1986) was built upon the theory of Lubochkov (1965, 1969). It became as follows: the particles finer than d0 at a point of ordinate p0 will move in the pore space if the GSD slope falls below the slope of curve of Eq. (23) (Chapuis and Tournier 2006) at this pivot point (d0, p0):

$$\frac{p}{{{p_0}}} = {\left( {\frac{d}{{{d_0}}}} \right)^{0.7213}}$$
(23)

Equation (23) is easily plotted over the GSD plot in a spreadsheet. The usual predictive methods (the two slope criteria plus Eq. (23) agree that the solid grains smaller than d0 ≈ 2.5 mm will move in the pores of the coarse grains of the soil having the GSD of Fig. 7.

Fig. 7
figure 7

The GSD of a crushed stone and the usual predictive methods for internal erosion (Kezdi 1969; Sherard 1979; Kenney and Lau 1985, 1986), written as equations (Chapuis 1992; Chapuis and Tournier 2006)

Full size image

Predicting internal erosion is simplified when using the PDDGS, which plots the GSD slope. The criteria of Kezdi (1969) and Sherard (1979) become horizontal lines; that of Kenney and Lau (1985, 1986) is the derivative of Eq. (23). All criteria agree that particles smaller than d0 ≈ 4 mm will move in the pores of the coarse particles of the soil having the PDDGS of Fig. 8. There is a small difference (2.5 or 4 mm) between the GSD (integral) and the PDDGS (derivative).

Fig. 8
figure 8

Using the PDDGS of the crushed stone to express geometrically the internal filter criteria using the equations of Chapuis (1992) and Chapuis and Tournier (2006)

Full size image

The criteria are easily verified in Fig. 7 for 0–20-mm crushed stone, which had internal erosion in laboratory tests. However, if example 1 in Chapuis (2021a, its Fig. 1a) for uniform sand is examined, its slope becomes lower than 21.5% per log cycle at a size dx ≈ 0.33 mm but everyone experienced with filters will sustain that this sand is not prone to internal erosion.

This example 1 in Chapuis (2021a) is thus indicating that current slope criteria are insufficient and other criteria should be added. In the PDDGS, a first visible difference is the d-length over which the slope criterion is not respected. A second difference is the position of this d-length that may be at the end of the GSD or in its middle. This d-length exceeds one log cycle in Fig. 7, but it is quite short (about 0.2 log cycle) in the Fig. 1b of Chapuis (2021a). This d-length and its position should be taken into account to better predict whether or not a gap-graded GSD is prone to internal erosion. Therefore, the MDM makes it clear that new criteria are needed to help future research on internal erosion, which is another new result, derived from the use of the MDM. In parallel, new techniques are needed to better quantify the internal erosion process, such as tracer tests (Molina-Gomez and Chapuis 2021).

As a result, the MDM with its best fits for the GSD and PDDGS appears as a promising tool. Because internal erosion is complex to quantify, it will need long and detailed investigations to develop new criteria involving the soil own modes or sub-populations of particles. This is why this article has not analyzed other cases than simple unimodal ones. By better quantifying the GSD modes, the MDM should help to develop better criteria for internal erosion and filtration.

Discussion

The modal decomposition method, MDM, was proposed and developed for two reasons. First, a soil mixture and a stratified soil have different small- and large-scale K values. Second, sampling a stratified aquifer with a split-spoon yields class-4 samples, which are remolded. Therefore, information on the detailed stratigraphy may be lost and each GSD may be questioned. A major issue is this loss of information about stratification, which is important for geomechanical and hydraulic properties. Initially, the purpose of the MDM (Chapuis 2010; Chapuis et al. 2014) was to better evaluate local- and large-scale K values (pumping tests), and also the effective porosity and longitudinal dispersivity for the migration of tracers or dissolved contaminants (Chapuis 2019a). Thus, initially, the MDM was essential to quantify stratification and better understand the geological processes that have created a soil layer and its resulting characteristics.

The capacities of the MDM were shown in Chapuis et al. (2014) and Chapuis (2021a). This article has examined different possibilities offered by the MDM for future research in engineering geology. First, in order to have a reliable GSD, the analyzed solid mass must exceed the minimum value of standards (e.g., ASTM C136/C136M 2014). In addition, for sieving gravel and sand, it would be wise to add a few in-between sieves to those that are used habitually. The usual sieves may be not enough to describe correctly a multi-modal GSD. A good practice would be to insert an intermediate-size sieve between each sieve that is overloaded and the regular sieve just above that overloaded sieve. The laser diffraction method may be a good complement to sieving for sand and silt. In this case, it would be wise to perform firstly a sieve analysis with a solid mass respecting the standard minimum requirement, and afterward select a fraction smaller than 0.63 or 0.315 mm to perform laser GSDs with a-few-grams specimens. This will allow the MDM to better quantify the different sub-populations that may exist in stratified sands.

Afterward, the MDM gives accurate mathematical equations for the GSD and its derivative, PDDGS, which closely fit the experimental data. This means that the MDM has the capacity to organize in a single equation all information previously obtained with the use of d5, d10, d15, d30, d60, d85, CU, and CC, plus qualitative words. This capacity should prove useful for future research about correlations between the GSD, plus other parameters, and the mechanical and hydraulic properties of the tested soil.

A preliminary study of field conditions, with a 4-mode MDM, has reached new findings about filter criteria. It has shown that stratified sand aquifers verify the usual criteria between the sand individual layers, which were already known to be unimodal. It has also clarified the physical meaning of usual filter criteria, through the closed link between d15, d50, d85, and the mean, μ, and standard deviation, σ, of a 1-mode GSD. More research is needed for filter criteria with man-made polymodal mixtures, and gap-graded GSDs.

A preliminary study of internal erosion criteria has also reached new findings. Recently, Chapuis and Saucier (2020) found that a material undergoing internal erosion is more complex than the association of a coarse solid skeleton and a sub-population of mobile solids. They have found that the soil may have 3 modes: the mode 1 being that of mobile fine solids and the modes 2 and 3 forming altogether a solid skeleton supporting effective stresses. During an internal erosion test, modes 2 and 3 stay immobile, whereas only the solids of mode 1 migrate through the pores of the solid skeleton formed by modes 2 and 3. In this article, the use of the MDM has shown that current slope criteria are necessary but not sufficient, and probably two other criteria should be added. An improved understanding will require long and detailed investigations to develop new criteria involving the soil own modes or sub-populations of particles.

Conclusions

Many studies need the GSD of solid particles. Most specimens are poly-disperse populations of grains of different sizes, reflecting a variety of origins, transport, and alteration processes. The MDM of a GSD gives its lognormal components, their own GSDs, and their proportions in the specimen.

The MDM gives an equation with 1- to 4-modes, and 2, 5, 8, or 11 parameters (1 to 4 means, 1 to 4 standard deviations, and 1 or 2 or 3 percentages). Note that more than four modes may be used. The MDM advantage over previous methods is that it fits the GSD by an accurate equation with an R2 value usually over 0.999. In stratified aquifers, the MDM was shown to help in better predicting the small- and large-scale values of hydraulic conductivity and also its anisotropy, which are key parameters for the design of dewatering or remediation facilities, and for assessing the groundwater velocities and fate of dissolved contaminants.

This article has examined a few possibilities for future research. First, it gives new equations to link the GSD usual geotechnical parameters (CU, CC, d10, d15 …) and the new parameters μ and σ for a unimodal soil. The usual geotechnical parameters are used in relationships with extreme values of porosity, packing condition, permeability, elastic modulus, shear strength, etc. More research will be needed to develop similar relationships with the new parameters.

Second, for stratified formations, new original results were obtained: the sub-populations or modes of grains in the field were shown to respect usual filter criteria for the case of well-graded or unimodal bases and filters. Homogeneous formations (e.g., tills) and man-made (reworked by excavating, mixing, and transporting) materials are more complex and will need more research.

Third, the MDM has opened a new window that should help to better define the conditions for internal erosion. Using the MDM made it clear that the usual criteria are not enough and two criteria seem to be needed, about the d-length over which the GSD slope criterion is not respected and its position: this is another new result that should interest many researchers.

In short, the MDM appears as a promising and useful tool for future research in engineering geology because it gives close-to-perfect fits for the GSD. By better quantifying the GSDs, the MDM should help to unify several concepts while helping researchers to develop better predictions, and better define both filter conditions and internal erosion conditions.