Introduction

The slope stability analysis has always been a classical issue in the geotechnical engineering field (Sloan 2013). In general, the slope stability analysis consists of two components: calculating the safety factor and searching for the critical sliding surface (Kim and Lee 1997; Zheng et al. 2009). Many different analysis methods can be classified into two types: (1) a series of potential critical sliding surfaces are pre-assumed; then, the safety factors for each surface are calculated; finally, the minimum safety factor and corresponding slip surface are determined; and (2) the safety factor of slope is first acquired; then, its corresponding critical sliding surface is determined according to the stress, strain or displacement distributions of the slope at the critical state (Zheng et al. 2005; Cheng et al. 2007; Lin et al. 2009, 2019; Zheng et al. 2009; Wang et al. 2016; Tu et al. 2016; Sun et al. 2016, 2020). The limit equilibrium method (LEM) undoubtedly belongs to the first type, whilst the strength reduction method (SRM) is classified as the second type. The dominant methods in the slope stability analysis have always been the traditional limit equilibrium methods in the previous decades and will remain unchanged for some time to come. However, by comparing the LEM with the SRM, Duncan (1996) and Krahn (2007) coincidentally thought that the LEM has its essential shortcomings, and the LEM does not satisfy the deformation compatibility. The SRM has many particular advantages over the LEM in many aspects, so it has received increasing attention and broad acceptance from many researchers in slope stability analysis (Zheng et al. 2005; Xu et al. 2009).

In the traditional SRM, the cohesion (c) and friction coefficient (tanϕ) are reduced by the same reduction parameter (i.e., the equivalent proportional reduction method), and the reduction parameter that leads the slope to the critical state is considered the safety factor of this slope. However, many researchers have introduced different viewpoints about this reduction method and thought that there might be a more appropriate approach to reduce the shear strength parameters. The first typical perspective is that the reduction approach should represent the weakening rate of c and tanϕ during the process of slope progressive failure and reflect different contributions of c and tanϕ in maintaining the slope stability. The reduction of the shear strength parameters based on a single reduction coefficient implies that c and tanϕ have identical safety reservations, and their weakening degree are treated as identical, which obviously conflicts with the actual process of slope progressive failure. Thus, a selection of two appropriate reduction-parameters for c and tanϕ can compensate for the drawbacks of the equivalent proportional reduction method (Suo 2010; Pantelidis and Griffiths 2012; Yuan et al. 2013; Jiang et al. 2013; Bai et al. 2014; Deng et al. 2017; Chen and Lin 2018). Another perspective is that the process of strength reduction is similar to the strain-softening behaviour of geotechnical materials; the reduction of c and tanϕ should be along their softening pathway. By introducing this correlation into the SRM, the non-proportional correlative reduction method is proposed (Conte et al. 2010; Xue et al. 2016). The third perspective is that there are infinitely many combinations of (tanϕ, c) that lead the slope to its critical state, and the curve composed of these combinations is defined as the critical state curve. The shortest pathway from the initial friction coefficient and cohesion to the critical state curve is considered the most appropriate reduction approach (Isakov and Moryachkov 2014; Yuan et al. 2016; Tang et al. 2017). Regardless of how the reduction approach is selected, the core goal is that the slope can reach a critical state much closer to reality using the strength reduction method. However, there is no obvious consensus on this issue.

Compared with the traditional SRM, a key issue for SRM based on two reduction parameters is how to define a global safety factor to estimate the slope stability. In general, the global factor of safety (Fgcf) is the function of Fsc and Fsf, where Fsc and Fsf are the reduction parameters of the cohesion and friction coefficient that lead the slope to the critical state, respectively. At present, there are several typical definitions as follows (Jiang et al. 2013):

$$ {F}_{gcf}=\frac{F_{sc}+{F}_{sf}}{2}. $$
(1)
$$ {F}_{gcf}=\frac{\sqrt{2}{F}_{sc}\cdotp {F}_{sf}}{\sqrt{F_{sc}^2+{F}_{sf}^2}}\ \left(\mathrm{Yuan}\ \mathrm{et}\ \mathrm{al}.\kern0.5em 2013\right). $$
(2)
$$ {F}_{gcf}=\frac{1}{1-\frac{L}{\sqrt{2}}},\kern0.5em L=\sqrt{{\left(1-\frac{1}{F_{sc}}\right)}^2+{\left(1-\frac{1}{F_{sf}}\right)}^2}\ \left(\mathrm{Isakov}\ \mathrm{and}\ \mathrm{Moryachkov}\ 2014\right). $$
(3)
$$ {F}_{gcf}=\sqrt{F_{sc}\cdotp {F}_{sf}}\left(\mathrm{Yuan}\ \mathrm{et}\ \mathrm{al}.\kern0.5em 2016\right). $$
(4)

Except for the above definitions, Bai et al. (2015) thought that it was not necessary to define the global safety factor by establishing a pure mathematical relationship among Fgcf, Fsc and Fsf. The global safety factor can be defined as:

$$ {F}_{gcf}=\frac{\varPsi_{ini}}{\varPsi_{cri}} $$
(5)

where Ψ is a physical index that represents the overall situation of the slope, and subscripts ini and cri denote the initial state and critical state of the slope, respectively. However, the suitable physical index to define the global safety factor has not been noted in this cited reference.

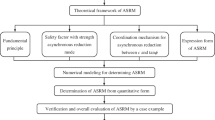
In summary, the essential questions for the SRM based on two reduction parameters are the selection of the appropriate reduction pathway of c and tanϕ and the definition of the global safety factor. In this paper, the authors propose a new SRM that simultaneously satisfies the upper and lower limit theorems and provide a new definition of the global safety factor. To verify the feasibility of the proposed method, five simple slope examples are used as research objects to find the differences between the traditional SRM and the proposed method.

“\( \tan \phi -\frac{c}{\gamma H} \)” critical state curve

Upper bound limit analysis

The upper bound limit analysis method, which is known as the energy analysis method, is established on the virtual work principle. This method assumes that slope failure would occur if the external work rate from soil gravity (Wext) exceeds the internal energy dissipation rate (Wint). When Wext tends to be equal to Wint, the slope will reach the critical state. Obviously, the complex stress-strain analysis can be avoided in this method (Chen and Liu 1990; Tang et al. 2017).

Figure 1 shows a rotational failure mechanism of a simple homogeneous slope used to build the work-energy balance equation. According to the work-energy balance equation Wert = Wint, the critical height of the slope is:

$$ H=\frac{c}{\gamma}\cdotp f\left({\theta}_h,{\theta}_0,{\beta}^{\prime}\right)\ \left(\mathrm{Chen}\ \mathrm{and}\ \mathrm{Liu}\ 1990\right) $$
(6)
Fig. 1
figure 1

Rotational failure mechanism of a simple homogeneous slope (Chen and Liu 1990)

Full size image

where f(θh, θ0, β′) is expressed as:

$$ f\left({\theta}_h,{\theta}_0,{\beta}^{\prime}\right)=\frac{\left[{e}^{2\left({\theta}_h-{\theta}_0\right)\tan \phi }-1\right]\cdotp \left[\sin {\theta}_h\cdot {e}^{\left({\theta}_h-{\theta}_0\right)\tan \phi }-\sin {\theta}_0\right]}{2\tan \phi \cdotp \left({f}_1-{f}_2-{f}_3-{f}_4\right)}\ \left(\mathrm{Chen}\ \mathrm{and}\ \mathrm{Liu}\ 1990\right). $$
(7)

f1~f4 are given as:

$$ \left\{\begin{array}{c}{f}_1=\frac{1}{3\left(1+9{\tan}^2\varphi \right)}\left[\left(3\tan \varphi \cdotp \cos {\theta}_h+\sin {\theta}_h\right)\cdotp {e}^{3\left({\theta}_h-{\theta}_0\right)\tan \varphi }-\left(3\tan \varphi \cdotp \cos {\theta}_0+\sin {\theta}_0\right)\right]\\ {}{f}_2=\frac{1}{6}\frac{L}{r_0}\left(2\cos {\theta}_0-\frac{L}{r_0}\right)\sin {\theta}_0\\ {}{f}_3=\frac{1}{6}{e}^{\left({\theta}_h-{\theta}_0\right)\tan \varphi}\cdotp \left[\sin \left({\theta}_h-{\theta}_0\right)-\frac{L}{r_0}\sin {\theta}_h\right]\cdotp \left[\cos {\theta}_0-\frac{L}{r_0}+\cos {\theta}_h\cdotp {e}^{\left({\theta}_h-{\theta}_0\right)\tan \varphi}\right]\\ {}{f}_4={\left(\frac{H}{r_0}\right)}^2\frac{\sin \left(\beta -{\beta}^{\prime}\right)}{2\sin \beta \cdotp \sin {\beta}^{\prime }}\left[\cos {\theta}_0-\frac{L}{r_0}-\frac{1}{3}\frac{H}{r_0}\left(\cot \beta +\cot {\beta}^{\prime}\right)\right]\end{array}\right.\ \left(\mathrm{Chen}\ \mathrm{and}\ \mathrm{Liu}\ 1990\right) $$
(8)

r0 and θ0 are the initial polar radius and polar angle of log spiral, respectively; ϕ and γ are the internal friction angle and unit weight of soil, respectively; β is the slope angle. The meanings of the other parameters are shown in Fig. 1.

Next, we study the relationship among the geometrical and mechanical parameters of the slope when it reaches the critical failure state according to Eq. 6. If we take the partial derivative of Eq. 7 with respect to θh, θ0 and β′, when ∂f/∂θh = 0, ∂f/∂θ0 = 0 and ∂f/∂β′ = 0 make sense, the minimum of f(θh, θ0, β′) is acquired and marked as minf. Its corresponding minimum upper limit of the slope height is expressed as Hcu. Thus, the critical state of the slope that satisfies the upper limit theorem is:

$$ \frac{c}{\gamma {H}_{cu}}=\frac{1}{\min f} $$
(9)

where minf is an implicit function of the internal friction angle of soil and slope angle. Once the slope angle has been determined, there are multiple combinations of (tanϕ, c/γHcu) that make Eq. (9) true. The curve that consists of these (tanϕ, c/γHcu) combinations is named the critical state curve (CSC). The key issue to establish the CSC is searching for the minimum value of f(θh, θ0, β′) under the limiting conditions (Eq. (10)). Considering the mathematical optimization method, the CSCs that satisfy the upper limit theorem for different slope angles are shown in Fig. 2.

$$ \left\{\begin{array}{c}{\theta}_0<{\theta}_h<\pi \\ {}0<{\theta}_0<\pi /2\\ {}0<{\beta}^{\prime }<\beta \\ {}\phi \le \beta \end{array}\right. $$
(10)
Fig. 2
figure 2

Critical state curves that satisfy the upper limit theorem for different slope angles

Full size image

As shown in Fig. 2, all critical state curves for different slope angles have identical characteristics: c/γHcu first sharply drops and subsequently slowly decreases with the increase in tanϕ, which performs as a hyperbolic function. Thus, the relationship between c/γHcu and tanϕ can be fitted by the following expression:

$$ \frac{c}{\gamma {H}_{cu}}=\frac{m_u}{\tan \phi +{n}_u}-{h}_u $$
(11)

where mu, nu and hu are the undetermined coefficients that vary with the change in slope angle. The fitting results of Eq. (11) for different slope angles are shown in Table 1. All relevant coefficients are greater than 0.99 and very close to 1.0. Thus, the hyperbolic function can perfectly represent the relationship between c/γHcu and tanϕ.

Table 1 Coefficients of the critical state curves based on the upper bound theorem
Full size table

Lower bound limit analysis

Eq. (6) shows the upper bound of the slope height at the ultimate state according to the upper bound limit analysis. Obviously, there must be a lower bound for the slope height, and the lower bound limit analysis method can provide a solution approach for this issue. The basic description of the lower bound theorem is as follows: all possible external loads that satisfy the statically admissible stress field are less than the real ultimate load (Chen and Liu 1990). The mathematical expressions for the statically admissible stress filed are:

$$ Staticequilibriumcondition:\kern0.5em {\sigma}_{ij,j}+{F}_i=0\ \left(\mathrm{Chen}\ \mathrm{and}\ \mathrm{Liu}\ 1990\right) $$
(12)
$$ Yieldcriterion:\kern0.5em f\left({\sigma}_{ij}\right)\le 0\ \left(\mathrm{Chen}\ \mathrm{and}\ \mathrm{Liu}\ 1990\right) $$
(13)
$$ Boundarycondition:\kern0.5em {\sigma}_{ij}{n}_j={T}_i\ \left(\mathrm{Chen}\ \mathrm{and}\ \mathrm{Liu}\ 1990\right) $$
(14)

where Fi is the body force vector; f is the yield function; nj is the normal vector of the stress boundary; σij is the stress tensor; Ti is the surface force vector applied on the stress boundary. For a slope without external loads (i.e., Ti = 0), if the function of Fi is assigned, the goal of the lower bound theorem is to search for a slope with the maximal geometric size that makes Eqs. (12) and (13) true. Thus, the lower bound theorem can be expressed in another manner: the maximum possible slope height that satisfies the statically admissible stress filed is a lower bound of the slope height at the real ultimate state.

It is challenging to destruct a statically admissible stress field of the entire slope in the actual engineering. However, Chen and Morgenstern (1983) have proposed a vertical slice method that strictly satisfies the lower bound theorem to analyse the slope stability. In this method, a mass of probable slide surfaces is first presumed to cover the entire slope; then, the force and moment balance equations of each slice embraced by a presumed slide surface are simultaneously established. Obviously, this process is equivalent to the destruction of the statically admissible stress field.

In this paper, this method is used to establish the relationship between the slope height and other influence factors associated with the slope at the critical state. The procedure is as follows:

  1. (1)

    Many slope models with different heights, slope angles and soil weights are established.

  2. (2)

    For each slope model, more than 5000 presumed possible slide surfaces are assigned to cover the entire slope profile. The safety factors associated with each potential sliding surface are calculated based on Chen and Morgenstern’s vertical slide method.

  3. (3)

    The minimum safety factor is selected and made to be 1.0 by adjusting c and tanϕ of the soil. Obviously, there are many combinations of (c, tan ϕ) that make the minimum safety factor equal to 1.0.

  4. (4)

    According to all combinations of (c, tan ϕ) for each slope model, the relationships between the slope height and c, tanϕ and γ for different slope angles are established through the multiple nonlinear fitting method.

The orthogonal experimental design method is used to design various slope models. Thus, the slope height, slope angle and soil weight are considered the impact factors, and each impact factor has been specified with five values: the slope height is equal to 20 m, 50 m, 80 m, 110 m or 140 m; the slope angle is equal to 15°, 30°, 45°, 60°or 75°; and the soil weight is equal to 10 kN/m3, 15 kN/m3, 20 kN/m3, 25 kN/m3 or 30 kN/m3. According to the orthogonal array L25(35), the final designing scheme for slope models is shown in Table 2.

Table 2 Designing scheme for the slope models
Full size table

Based on the above calculation procedure, the combinations of (c, tan ϕ) for each slope model in Table 2 at the critical state are obtained. Similarly, let us suppose that the abscissa denotes the friction coefficient (tanϕ) and the ordinate denotes non-dimensional number (c/γH). The combinations of (tanϕ, c/γH) for the slope with different slope angles can form a curve, which is named the critical state curve (CSC) and satisfies the lower bound theorem. Figure 3 shows the CSC for different slope angles. As observed in Fig. 3, their morphological characteristics are very close to the CSC that satisfies the upper bound theorem in Fig. 2. Thus, the relationship between tanϕ and c/γH can also be established by the multiple nonlinear fitting method in the basis of the hyperbolic function:

$$ \frac{c}{\gamma {H}_{cL}}=\frac{m_L}{\tan \phi +{n}_L}-{h}_L $$
(15)

where HcL is the critical slope height resulting from the lower bound analysis method; mL, nL and hL are undetermined coefficients that vary with the change in slope angle. Fortunately, all relevant coefficients of the fitting functions for different slope angles in Table 2 are greater than 0.99 and very close to 1.0. Thus, the CSC that satisfies the lower bound theorem can also be accurately represented by the hyperbolic curve. In view of this conclusion, the CSC for the other slope angles except those in Table 2 can be obtained by identical procedures, and their undetermined coefficients (mL, nL, hL) are shown in Table 3.

Fig. 3
figure 3

Critical state curves that satisfy the lower limit theorem for different slope angles

Full size image
Table 3 Coefficients of the critical state curves based on the lower bound theorem
Full size table

Relationship between two types of critical state curves

Undoubtedly, these two types of critical state curves are very close to each other instead of actually coinciding with each other in the same “tanϕ − c/γH” coordinate system. For example, for slope angle = 20,40,60 and 80°, their two types of CSCs are shown in Fig. 4. All CSCs that satisfy the upper bound theorem are first above and subsequently below the CSCs satisfying lower bound theorem along with the increasing of tanϕ. Each group of CSC has an intersection point, and it is indicated that this point simultaneously satisfies Eqs. (11) and (15). In other words, once a slope angle is determined, the c, γ,H and tanϕ attached to this intersection point can bring this slope to the ultimate state, which simultaneously satisfies the upper and lower bounds. Obviously, this ultimate state of slope can be considered its realistic critical state, and this intersection point can be named the optimal critical point (OCP). The coordinates of the OCP for different slope angles can be acquired by solving Eqs. (11) and (15), as shown in Table 4.

Fig. 4
figure 4

Two types of critical state curves in the same coordinate system for the slope angle of 20°, 40°, 60°and 80°

Full size image
Table 4 Coordinates of the optimal critical point for different slope angles
Full size table

Strength reduction method using two reduction parameters

Reduction path for c and tan ϕ

The essence of SRM is to make the slope as close to the realistic ultimate state as possible. In this section, we propose a new SRM using two reduction parameters based on CSC.

As shown in Fig. 5, two solid lines represent two types of CSC for an arbitrary slope. Pi denotes the initial state of this slope with the initial coordinates of \( \left(\tan {\phi}_i,\frac{c_i}{\gamma H}\right) \), and OCP is the optimal critical point with the coordinates of (XOCP, YOCP). Obviously, there are many paths for Pi to reach the red or blue solid lines, such as L1, L2, L3, L4 and L5. Each path means a different reduction method for ci and tanϕi. For example, with L2, P1 and P2 are the intersection points of L2 with the red solid line and blue solid line, respectively, and their coordinates should be \( \left(\mathit{\tan}{\phi}_1,\frac{c_1}{\gamma H}\right) \) and \( \left(\tan {\phi}_2,\frac{c_2}{\gamma H}\right) \). In view of P1, P2, Pi and O on the same straight line, the following equation holds:

$$ \frac{\raisebox{1ex}{${c}_i$}\!\left/ \!\raisebox{-1ex}{$\gamma H$}\right.}{\tan {\phi}_i}=\frac{\raisebox{1ex}{${c}_1$}\!\left/ \!\raisebox{-1ex}{$\gamma H$}\right.}{\tan {\phi}_1}=\frac{\raisebox{1ex}{${c}_2$}\!\left/ \!\raisebox{-1ex}{$\gamma H$}\right.}{\tan {\phi}_2}\Rightarrow \frac{c_i}{c_1}=\frac{\tan {\phi}_i}{\tan {\phi}_1}=\frac{c_i}{c_2}=\frac{\tan {\phi}_i}{\tan {\phi}_2}=K $$
(16)

where K is the equivalent proportional reduction parameter. Thus, path L2 based on the traditional SRM is only one of many possible paths that lead the slope to the critical state. In particular, it is difficult to make the slope close to the realistic ultimate state along path L2 because the upper and lower bound theorems only provide a range of realistic ultimate states that follow this path. In other words, the realistic critical point of path L2 lies between P1 and P2. Similarly, other paths such as L1, L4 and L5 cannot accurately lead the slope to the realistic ultimate state.

Fig. 5
figure 5

Discussion on the reduction path of the strength reduction method

Full size image

Because OCP is a critical point that simultaneously satisfies the upper and lower bound theorems, the reduction path from the initial point Pi towards OCP is a feasible path to search for the realistic ultimate state of the slope, which is named the optimal reduction path. Thus, the final realistic reduction parameters for ci and tanϕi can be depicted as:

$$ {K}_{\phi }=\frac{\tan {\phi}_i}{X_{OCP}}\kern0.5em {K}_c=\frac{1}{\gamma H}\cdotp \frac{c_i}{Y_{OCP}} $$
(17)

The ratio of Kc to Kϕ is defined as the mating coefficient Φ:

$$ \varPhi =\frac{K_c}{K_{\phi }}=\frac{1}{\gamma H}\frac{c_i}{\tan {\phi}_i}\frac{X_{OCP}}{Y_{OCP}} $$
(18)

Obviously, Φ is not a constant and varies with the slope angle, initial state, soil weight and slope height. The core of the slope stability analysis based on the double reduction parameters is first to calculate the mating coefficient. To ensure that the reduction of ci and tanϕi are exactly consistent with the optimal reduction path, the ratio of Fsc to Fsf at each reduction step should be assigned to be equal to Φ. During the entire reduction process, we should continue adjusting Fsc and Fsf to acquire new ci and tanϕi; then, the elasto-plastic calculation for the slope is executed by importing these new shear strength parameters. Once the slope reaches the critical state, the reduction process should be terminated, and its corresponding Fsc and Fsf are considered the final reduction parameters. Thus, the procedures of SRM using two reduction parameters are shown in Fig. 6.

Fig. 6
figure 6

Procedures of the strength reduction method using two reduction parameters

Full size image

Definition of the global safety factor of the slope

In essence, the global safety factor of the slope should reflect the secure situation of the slope at the initial state using its critical state as a reference. The definition of the global safety factor based on pure mathematical relations (as shown in Eqs. (1)~(4)) may lack a certain mechanical significance. Thus, this paper attempts to provide a definition of the global safety factor based on Eq. (5). Specifically, the global sliding resistance force on the critical sliding surface is selected as a physical index to represent the overall situation of the slope.

As shown in Fig. 7, the right slope at the critical state is considered the reference, and the left slope is the objective slope at the initial state. When the slope has developed from the initial state to the critical state by SRM, the stress field and critical sliding surface at the critical state can be determined. The global sliding resistance force at the critical state can be acquired by integrating the shear strength of each point along the critical surface. Simultaneously, the location of the critical sliding surface is transplanted into the left slope, and the global sliding resistance force at the initial state can be similarly obtained. The ratio of these two sliding resistance forces is considered the global safety factor of slope:

$$ {F}_{gsf}=\frac{\underset{l}{\int}\left({\sigma}_i\tan {\phi}_i+{c}_i\right) dl}{\underset{l}{\int}\left({\sigma}_c\tan {\phi}_c+{c}_c\right) dl} $$
(19)

where σi and σc denote the normal stress of each point on the critical sliding surface for the initial state and critical state, respectively; tanϕi and ci are the friction coefficient and cohesion of the slope at the initial state; tanϕc and cc are the friction coefficient and cohesion of the slope at the critical state.

Fig. 7
figure 7

Definition of the global safety factor based on the relationship of the global sliding resistance force between the initial state and the critical state of slope

Full size image

Examples

Five slopes with different slope angles are used to demonstrate the slope stability analysis based on SRM using two reduction parameters. The geometrical and mechanical parameters of the five examples are shown in Table 5.

Table 5 Geometrical and mechanical parameters for the slope stability analysis
Full size table

The slope with slope angle = 75°is taken as an example to illustrate the searching procedures of its critical state and the calculation of its global safety factor in detail. According to the geometrical and mechanical parameters of this slope, the coordinates of its initial state point in the “tanϕ − c/γH” coordinate system are Pi(0.7813, 0.0500), and the coordinates of the optimal critical point are OCP(0.4684, 0.1132). According to Eq. (18), the mating coefficient Φ is equal to 0.2648. Thus, during the process of adjusting the reduction parameters of ci and tanϕi in each reduction step, the ratio of Fsc to Fsf is identically equal to 0.2684. When Fsc = 0.5 and Fsf = 1.89, this slope reaches the ultimate state. According to the displacement field of the critical state of the slope, the critical sliding surface is acquired (its displacement nephogram and corresponding critical sliding surface are shown in Fig. 8). Note that the searching processes for the critical sliding surface refer to the approach proposed by Wang et al. (2016). Next, the normal stress of each point on the critical sliding surface associated with initial stress field and critical stress field are obtained. In addition, the shear strength parameters for the initial state and critical state are determined: ci = 50KPa, tanϕi = 0.7813, cc = 100KPa and tanϕc = 0.4138. According to the normal stress, the shear strength of each point on the same critical sliding surface for the initial state and critical state can be obtained, as shown in Fig. 9. Finally, based on the data in Fig. 9, the global safety factor is calculated to be 0.9853 according to Eq. 19.

Fig. 8
figure 8

Displacement nephogram and the corresponding critical sliding surface (slope angle = 75 °)

Full size image
Fig. 9
figure 9

Shear strength of each point on the same critical sliding surface for the initial state and critical state (slope angle = 75 °)

Full size image

Table 6 shows the global safety factors of five slope examples resulted from the traditional SRM and the proposed method in this paper. The curves of all safety factors vary with the increase in slope angle as shown in Fig. 10. The definition approach of the global safety factors based on two reduction parameters can significantly affect their results. The final global safety factors resulted from Eq. (1) ~Eq. (4) and Eq. (19) are notably different. Undoubtedly, when the slope height, mechanical parameters and other influence factors are identical, the stability of the slope decreases with the increase in slope angle, and the global safety factor should reflect this basic rule. However, the global safety factors acquired from Eq. (1), Eq. (2) and Eq. (3) do not monotonically decrease with the increase in slope angle. Thus, these three definitions have drawbacks. A comparison of the proposed method to the traditional SRM shows that the evolution laws of the global safety factors resulted from these two methods coincide with each other. In addition, for each slope angle, all global safety factors resulted from the proposed method are greater than that resulted from the traditional SRM. Thus, the traditional SRM based on the lower bound theorem may underrate the slope stability.

Table 6 Global safety factors for five slope examples based on different SRMs
Full size table
Fig. 10
figure 10

Variation of all safety factors with increasing slope angles

Full size image

Figure 11 shows the critical sliding surfaces of five slopes resulted from the traditional SRM and the proposed method in this study. For each slope, the sliding area resulted from the traditional SRM is less than that from the proposed method. The reason is that the critical state induced by the traditional SRM generally satisfies the upper bound theorem, which may underestimate the weakening degree of the shear strength parameters of soil, i.e., the cohesion and friction coefficient. Thus, its corresponding sliding area may be less than that resulted from the proposed method, which can lead the slope into the critical state that simultaneously satisfies the upper and lower bound theorems. In addition, for the slope with a small slope angle, i.e., β = 15°and β = 30°in this study, the sliding surfaces acquired by the proposed method contain a straight line at their back edge, which indicates that the tensile failure induces a drawing open surface at the back edge of the sliding surface. However, the entire sliding surface for each slope with a small slope angle acquired by the traditional SRM performs as a gradually varied curve without any straight segment, which implies that the entire sliding body only exhibits shear failure without tensile failure. In fact, when the slope is led to the critical state in real engineering, a series of approximately upright tensile cracks may appear at the back edge of the sliding body. Thus, compared with the traditional SRM, the proposed method in this paper can obtain a much more reasonably realistic sliding surface.

Fig. 11
figure 11

Critical sliding surfaces of five slopes resulted from the traditional SRM and the proposed method in this paper (The green and red solid lines represent the critical sliding surfaces resulted from the proposed method and traditional SRM, respectively)

Full size image

Conclusions

This paper has proposed a new strength reduction method using two reduction parameters to search for the critical state of slope. The slope critical state obtained by the proposed method in this paper simultaneously satisfies the upper and lower bound theorem, which is considered the realistic ultimate state. In addition, this paper has proposed a definition approach for the global safety factor, which is not built on the pure mathematical function of two reduction parameters but established on the relationship of the sliding resistance force between the initial state and the critical state of a slope. The definition of the global safety factor in this paper has definite physical and mechanical meanings. The results of the stability analysis for five slope examples show that the global safety factor acquired by the proposed method is greater than that obtained through the traditional SRM for all situations. The critical sliding surface obtained from the proposed method is also much more reasonable than that from the traditional SRM.